Space-Charge Driven Second Harmonic Generation in Nanometric Conductors

1. Introduction

Second harmonic generation (SHG) at frequency $2\omega$ has been initially investigated in case of an electromagnetic wave of frequency $\omega$ interacting with molecular dipoles, lacking inversion symmetry, but such that the energy difference between the electronic ground- and excited states, making up each dipole, is close to $2\hslash \omega$[1]. Therefore subsequent observation of SHG, over a broad frequency range, in bulk materials displaying conversely inversion symmetry[2,3] or at their surface [4,5], for which the incident light was coupled with valence and conduction electrons rather than molecules, was bound to require new interpretations. The corresponding hydrodynamic and quantum arguments were further extended to account tentatively for SHG data, measured in metallic samples [6,7,8] of nanometric ($\approx 10$ nm) dimension. Remarkably those various explanations shared a common feature, since all of them dealt with conduction electrons coupled with an electromagnetic field [2,3,4,9,10,11], obeying Maxwell’s equations [12] and thence not allowing for 3-dimensional space-charge for some reason to be developed in the conclusion. Therefore this work is aimed at devising the first theory of space-charge waves in conducting materials. Its potential will then be illustrated by investigating SHG induced in samples of nanometric length. As a matter of fact SHG will turn out to stem from the quadratic term, showing up in the expressions of the drift current and the polarisation of conduction electrons. Actually space-charge solitons have already been invoked to account for the Gunn effect [13] and acousto-electric instabilities observed in piezoelectric semi-conductors [14,15], but the corresponding theoretical treatments were empirical, which prevented any conclusive statement regarding their validity. By contrast, the self-consistent analysis, laid out below, yields the explicit dependence of the SHG signal on the sample length, electron concentration and frequency $\omega$ for the sake of comparison with measurements.

The outline is as follows : the dispersion curve of space-charge waves will be worked out in section 1 with help of Newton and Gauss’ equations and the charge conservation law, whereas section 2 will deal with the procedure permitting to match together an electromagnetic wave with a space-charge one of same frequency; SHG will be analysed in section 3, while the main results will be summarised in the conclusion.

2. 1-Dispersion Curve

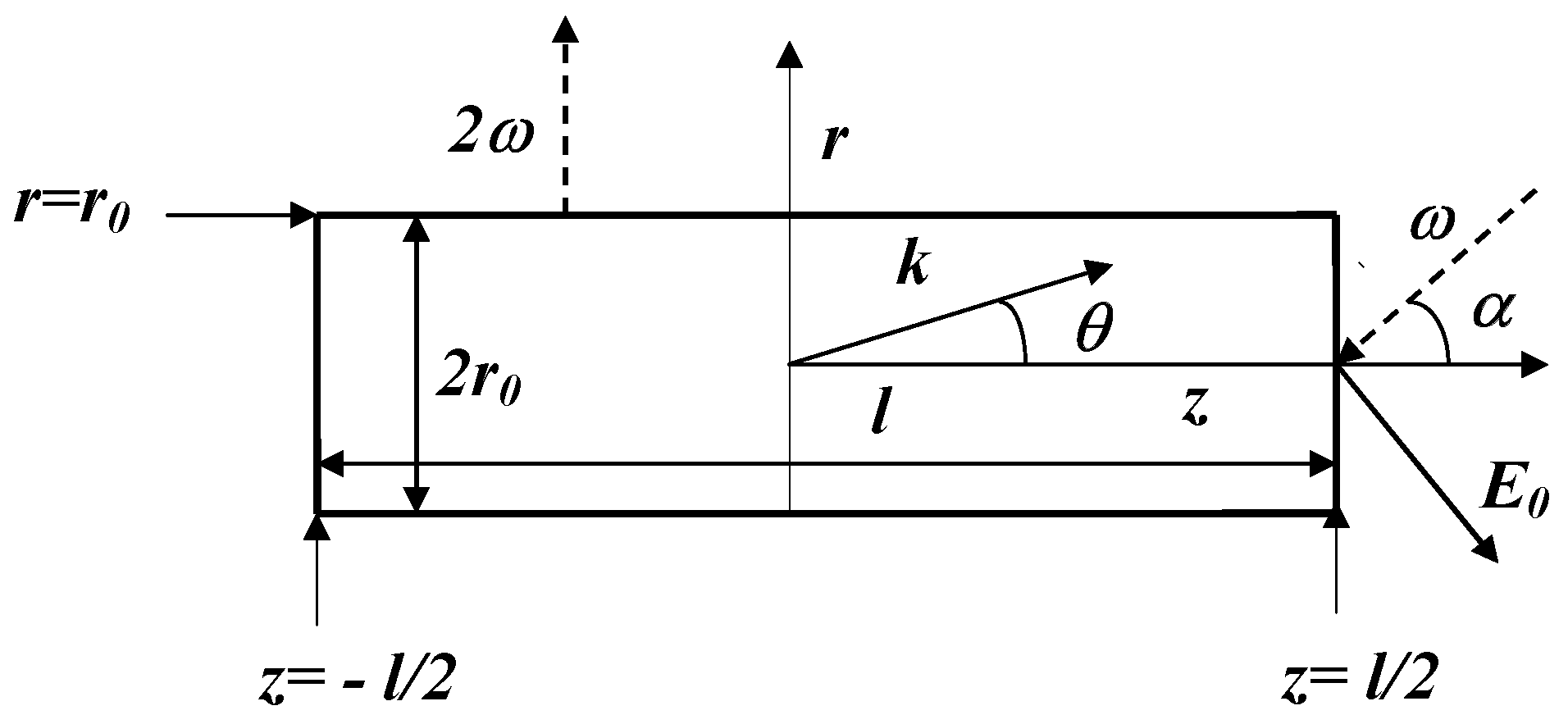
Though various geometrical shapes, such as silver-coated nanocones and bowtie antennas [6], gold nanospheres [7] and V-groove nanoparticle [8], have been discussed by other authors, we shall focus for simplicity upon the wire, sketched in Figure 1, containing conduction electrons of charge e, effective mass m and concentration $c_0$ and located in a cylindrical frame $r,\varphi ,z$. It is assumed to sustain a wave, travelling along the z axis and conveying an electric field E, parallel to the z direction and taken to read

Figure 1. Cross section of a cylindrical wire of length l and radius $r_0$ in the $\varphi =0,z$ plane; the dashed lines labelled $\omega ,2\omega$ designate respectively the incoming electromagnetic wave of frequency $\omega$, making an angle $\alpha$ with the z direction, and the outgoing one of frequency $2\omega$, parallel to the radial axis; the solid lines labelled k, $E_0$ refer, respectively, to a one-electron wave-vector, making an angle $\theta$ with the z direction and the electric field carried along by the incoming wave.

Figure 1. Cross section of a cylindrical wire of length l and radius $r_0$ in the $\varphi =0,z$ plane; the dashed lines labelled $\omega ,2\omega$ designate respectively the incoming electromagnetic wave of frequency $\omega$, making an angle $\alpha$ with the z direction, and the outgoing one of frequency $2\omega$, parallel to the radial axis; the solid lines labelled k, $E_0$ refer, respectively, to a one-electron wave-vector, making an angle $\theta$ with the z direction and the electric field carried along by the incoming wave.

$$E(t,z,x)=E_z\left(\omega \right)g\left(x\right)e^{K\left(\omega \right)z+i\omega t},$$

with t standing for time, x being the coordinate along the $\varphi =0$ radial axis and the complex unknowns $E_z\left(\omega \right),g\left(x\right),K\left(\omega \right)$ to be assigned below. The field E sets the electrons in motion in compliance with Newton’s law as

$$m{\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}=eE-{\displaystyle \frac{m}{\tau }}{\displaystyle \frac{\partial u}{\partial t}}-{\displaystyle \frac{\partial p}{c_e\partial z}},$$

(1)

with $u=u_z\left(\omega \right)g\left(x\right)e^{Kz+i\omega t},\tau ,p\left(z\right),c_e\left(z\right)$ designating the displacement coordinate of the electron mass center, parallel to the z axis, Drude’s collision time [12,16], the z-dependent pressure and electron concentration, respectively. In addition to the usual inertial $\left(\propto {\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}\right)$, electrostatic $\left(\propto E\right)$ and friction $\left(\propto {\displaystyle \frac{\partial u}{\partial t}}\right)$ terms [12,16], Equation (1) is seen to display a pressure induced force $\left(\propto {\displaystyle \frac{\partial p}{\partial z}}\right)$ to be derived now.

To that end, let us begin with writing the expression of the force $d{f}_p$ exerted by p upon a cylinder of axis z, length $dz<<l$, section $S=\pi r_0^2$, containing thence $d{n}_e=Sdz{c}_e\left(z\right)$ of electrons

$$d{f}_p=S\left(p\left(z\right)-p(z+dz)\right).$$

Then

$${\displaystyle \frac{d{f}_p}{d{n}_e}}(dz\to 0)=-{\displaystyle \frac{\partial p}{c_e\partial z}},$$

showing up in the right-hand side of Equation (1), is identified as the force exerted on a single electron. The expression of ${\displaystyle \frac{\partial p}{\partial z}}$ will be worked out now by resorting to usual thermodynamical definitions [16,17], while assuming a unique temperature T all over the wire

$$\left.\begin{array}{c}p=-{\displaystyle \frac{\partial \left(V{F}_H\right)}{\partial V}}\hfill \\ E_F={\displaystyle \frac{\partial F_H}{\partial c_e}}\hfill \end{array}\right\}\Rightarrow p=c_e{E}_F-F_H\Rightarrow {\displaystyle \frac{\partial p}{c_e\partial z}}={\displaystyle \frac{\partial E_F}{\partial c_e}}{\displaystyle \frac{\partial \rho }{e\partial z}},$$

with $V,F_H\left(z\right),E_F\left(z\right),\rho$ referring to a small volume, containing $n_e$ of electrons $(\Rightarrow c_e={\displaystyle \frac{n_e}{V}})$, local Helmholz free energy per unit-volume, Fermi energy, known as the chemical potential of independent electrons and space-charge density $(\Rightarrow c_e\left(z\right)=c_0+{\displaystyle \frac{\rho \left(z\right)}{e}})$, respectively. Thus the pressure gradient ${\displaystyle \frac{\partial p}{\partial z}}\ne 0$ is realized to ensue from the finite space-charge density ${\displaystyle \frac{\partial \rho }{\partial z}}\ne 0$. Note also that the macroscopic pressure p is unrelated to the so called quantum pressure, considered by other authors [4,9,10].

Besides, the field E induces [12,16,18] a dielectric displacement D, parallel to the z direction

$$D={ϵ}_{0}E+\left(c_{0}e+\rho \right)u,$$

(2)

with ${ϵ}_0$ referring to the vacuum permittivity. Noteworthy is that the polarisation term ${ϵ}_0(n^2-1)E$ (n stands for the refractive index), originating from the filled bands and contributing to ${\displaystyle \frac{\partial D}{\partial t}}$ in the Ampère-Maxwell equation, is lacking in Equation (2), because the corresponding electrons contribute nothing to $\rho$. Linearising further D by dropping $\rho u$ in Equation (2) $\left(\Rightarrow D={ϵ}_{0}E+c_{0}eu\right)$ and Fourier transforming it with respect to t yields

$$\begin{array}{c}D(t,z,x)=D_z\left(\omega \right)g\left(x\right)e^{Kz+i\omega t}\hfill \\ c_{0}e{u}_z\left(\omega \right)-D_z\left(\omega \right)=-{ϵ}_0{E}_z\left(\omega \right)\hfill \end{array}.$$

(3)

The space-charge density $\rho (t,z,x)\propto e^{K\left(\omega \right)z+i\omega t}$ is given by Gauss’ equation [18], reading in this unidimensional analysis as

$$\rho =\nabla .D={\displaystyle \frac{\partial D}{\partial z}}.$$

(4)

At last substituting ${\displaystyle \frac{\partial E_F}{\partial c_e}}{\displaystyle \frac{\partial \rho }{e\partial z}}$ to ${\displaystyle \frac{\partial p}{c_e\partial z}}$ in Equation (1) and Fourier transforming the resulting expression with respect to $t,z$, while taking advantage of Equation (4), gives

$$m\omega \left(\omega -{\displaystyle \frac{i}{\tau }}\right)u_z\left(\omega \right)-{\displaystyle \frac{\partial E_F}{\partial c_e}}{\displaystyle \frac{K^2}{e}}{D}_z\left(\omega \right)=-e{E}_z\left(\omega \right).$$

(5)

Thus combining Equations (3,5) together is seen to make up a $2\times 2$ Cramer system in terms of the unknowns $u_z\left(\omega \right),D_z\left(\omega \right)$, to be solved as

$$\begin{array}{c}{u}_z\left(\omega \right)=\chi \left(\omega \right)E_z\left(\omega \right),D_z\left(\omega \right)={ϵ}_0ϵ\left(\omega \right)E_z\left(\omega \right)\\ \chi \left(\omega \right)={\displaystyle \frac{ie\tau }{m\omega }}{\displaystyle \frac{\frac{\partial E_F}{\partial c_e}\frac{{ϵ}_0{K}^2}{e^2}-1}{B}},ϵ\left(\omega \right)={\displaystyle \frac{1+i\omega \tau \left(1-\frac{{\omega }_p^2}{{\omega }^2}\right)}{B}}\\ B=1+i\omega \tau \left(1-{\displaystyle \frac{\partial E_F}{\partial c_e}}{\displaystyle \frac{c_0{K}^2}{m{\omega }^2}}\right)\end{array},$$

(6)

with ${\omega }_p=\sqrt{{\displaystyle \frac{c_0{e}^2}{{ϵ}_{0}m}}}$ being the plasma frequency [12]. Those expressions of $\chi ,ϵ$ are seen to be quite different from the corresponding formulae, valid for an electromagnetic wave [12] which can be deduced from Equation (1), after deleting ${\displaystyle \frac{\partial p}{c_e\partial z}}$, as

$$\chi \left(\omega \right)=-{\displaystyle \frac{ie\tau }{m\omega \left(1+i\omega \tau \right)}},ϵ\left(\omega \right)=1-{\displaystyle \frac{i{\omega }_p^2\tau }{\omega \left(1+i\omega \tau \right)}}.$$

(7)

The charge conservation law [18] can be recast, by taking advantage of Equation (4) while assuming $K\ne 0$, as

$$\begin{array}{c}\nabla .j+{\displaystyle \frac{\partial \rho }{\partial t}}={\displaystyle \frac{\partial }{\partial z}}\left(j+{\displaystyle \frac{\partial D}{\partial t}}\right)=K\left(j+{\displaystyle \frac{\partial D}{\partial t}}\right)=0\Rightarrow \\ j+{\displaystyle \frac{\partial D}{\partial t}}=0\end{array}.$$

(8)

Comparing Equation (8) with the Ampère-Maxwell equation [12] enables one to realise that the space-charge wave conveys no magnetic field, unlike electromagnetic waves.

The current density in Equation (8) is defined as $j=j_1+j_2$ with $j_1,j_2$ referring to the drift[12,16] and diffusion[13,14,15] components, respectively, both flowing along the z axis. They read [13,14,15,16]

$$j_1=\left(c_{0}e+\rho \right){\displaystyle \frac{\partial u}{\partial t}},j_2=-D_n{\displaystyle \frac{\partial \rho }{\partial z}},$$

(9)

with $D_n$ being a diffusion coefficient [13,14,15]. Linearising $j_1$ by dropping $\rho {\displaystyle \frac{\partial u}{\partial t}}$ in Equation (9) and Fourier transforming the resulting expression of $j_1=c_{0}e{\displaystyle \frac{\partial u}{\partial t}}$ with respect to t and that of $j_2$ with respect to z lead to

$$\begin{array}{c}{j}_{i=1,2}(t,z,x)=j_{i=1,2}\left(\omega \right)g\left(x\right)e^{Kz+i\omega t}\\ j_1\left(\omega \right)={\sigma }^{*}{E}_z\left(\omega \right),{\sigma }^{*}=\sigma {\displaystyle \frac{1-\frac{\partial E_F}{\partial c_e}\frac{{ϵ}_0{K}^2}{e^2}}{B}}\\ j_2\left(\omega \right)=-D_n{K}^2{D}_z\left(\omega \right)\end{array},$$

(10)

with $\sigma ={\displaystyle \frac{c_0{e}^2\tau }{m}}$ standing for Drude’s conductivity [12,16] and B given by Equation (6). The expression of $j_1\left(\omega \right)$ in Equation (10) is to be compared with that of a current $j\left(\omega \right)$, aroused by an electromagnetic wave and obeying thence Ohm’s law [12,16]

$$j\left(\omega \right)={\displaystyle \frac{\sigma }{1+i\omega \tau }}{E}_z\left(\omega \right).$$

(11)

At last, Fourier transforming the charge conservation law in Equation (8) with respect to $t,z$, while taking advantage of Equations (6,10), yields eventually the dispersion relation $K\left(\omega \right)=K_R\left(\omega \right)+i{K}_I\left(\omega \right)$ as

$$\begin{array}{c}{\sigma }^{*}{E}_z\left(\omega \right)+\left(i\omega -D_n{K}^2\right)D_z\left(\omega \right)=0\Rightarrow \hfill \\ {\sigma }^{*}+{ϵ}_0ϵ\left(\omega \right)\left(i\omega -D_n{K}^2\right)=0\Rightarrow \hfill \\ K^2\left(\omega \right)={\displaystyle \frac{i\omega \left(1-2\frac{{\omega }_p^2}{{\omega }^2}-\frac{i}{\omega \tau }\right)}{D_n\left(1-\frac{{\omega }_p^2}{{\omega }^2}-\frac{i}{\omega \tau }\right)-\frac{\partial E_F}{\partial c_e}\frac{i{ϵ}_0{\omega }_p^2}{e^2\omega }}}\hfill \end{array}.$$

(12)

Explicit expressions are needed now for $D_n,{\displaystyle \frac{\partial E_F}{\partial c_e}}$. To that end, the set of conduction electrons is assumed to make up an isotropic, 3-dimensional Fermi gas, either degenerate (metal) or not (semi-conductor). The one-electron energy $\epsilon$ and the corresponding density of states ${\rho }_d$ read in both cases

$$\epsilon \left(\mathbf{k}\right)={\displaystyle \frac{{\hslash }^2{k}^2}{2m}},{\rho }_d\left(\mathbf{k}\right)={\displaystyle \frac{sin\theta k^2}{4{\pi }^3}},$$

wherein $k=\left|\mathbf{k}\right|$ and $\mathbf{k},\theta$ are defined in the caption of Figure 1. Moreover the origin of energy $\epsilon (\mathbf{k}=0)=0$ is taken at the bottom of the conduction band. Due to the electron velocity being equal to ${\displaystyle \frac{\hslash \mathbf{k}}{m}}$, each electron contributes $j_2\left(\mathbf{k}\right)$ to $j_2$

$$\begin{array}{c}{j}_2\left(\mathbf{k}\right)=e{\displaystyle \frac{\hslash k}{m}}cos\theta F\left(\mathbf{k}\right)\hfill \\ F\left(\mathbf{k}\right)=f(\mathbf{k},E_F(z-{\displaystyle \frac{l_a}{2}}))-f(\mathbf{k},E_F(z+{\displaystyle \frac{l_a}{2}}))\hfill \end{array},$$

(13)

with

$$f(\mathbf{k},E_F)={\left(1+e^{{\displaystyle \frac{\epsilon \left(\mathbf{k}\right)-E_F}{k_{B}T}}}\right)}^{-1}$$

being the Fermi-Dirac distribution [16], whereas $k_B,l_a\left(\mathbf{k}\right)={\displaystyle \frac{\hslash k}{m}}cos\theta \tau$ refer, respectively, to Boltzmann’s constant and the mean free path, projected onto the z axis. Remarkably the conduction electrons are to be described below as a Fermi gas at local thermal equilibrium, characterised by a uniqueT, yet zdependent$E_F$. The diffusion current density $j_2$ is then obtained by integrating $j_2\left(\mathbf{k}\right)$ over $\mathbf{k}$ in reciprocal space

$$j_2=2\pi {\int }_{\theta =0}^{{\displaystyle \frac{\pi }{2}}}{\int }_{k=0}^{k_M}{j}_2\left(\mathbf{k}\right){\rho }_d(k,\theta )d\theta dk,$$

(14)

with $k_M={\displaystyle \frac{\sqrt[3]{6{\pi }^2}}{a}}$ being the radius of the spherical Brillouin zone and $a^3$ standing for the volume of the unit-cell, accommodating at most 2 electrons. Hence $\epsilon \left({\mathbf{k}}_M\right)$ is inferred to be the upper bound of the conduction band. After integration with respect to $\theta$, Equation (14) is recast into

$$\begin{array}{c}{j}_2={\displaystyle \frac{e\tau }{6}}{\left({\displaystyle \frac{\hslash }{\pi m}}\right)}^2{\displaystyle \frac{\partial E_F}{\partial c_e}}{\displaystyle \frac{\partial c_e}{\partial z}}{\int }_{k=0}^{k_M}{\displaystyle \frac{\partial f}{\partial \epsilon }}{k}^{4}dk\Rightarrow \hfill \\ D_n=-{\displaystyle \frac{\tau \sqrt{2m}}{3{\pi }^2{\hslash }^3}}{\displaystyle \frac{\partial E_F}{\partial c_e}}{\int }_0^{\epsilon \left({\mathit{k}}_M\right)}{\displaystyle \frac{\partial f}{\partial \epsilon }}\sqrt{{\epsilon }^3}d\epsilon \hfill \end{array}.$$

(15)

Note that $\left|{\displaystyle \frac{\rho \left(z\right)}{e}}\right|<<c_0$ entails $c_e\left(z\right)\approx c_0,\forall z$. The calculation of $j_2$ proceeds differently for a metal or a semi-conductor.

Since the T dependence of $E_F$ is negligible [16] in a metal up to room temperature, the calculation of ${\displaystyle \frac{\partial E_F}{\partial c_e}}$ will be made at $T=0$, which yields

$${\displaystyle \frac{\partial E_F}{\partial c_e}}={\displaystyle \frac{{\hslash }^2{\left(3{\pi }^2\right)}^{\frac{2}{3}}}{3m\sqrt[3]{c_e}}}={\displaystyle \frac{{\hslash }^2{\left(3{\pi }^2\right)}^{\frac{2}{3}}a}{3m}},$$

by assuming a half-filled band $\left(\Rightarrow c_e\approx c_0=a^{-3}\right)$. Performing further the integration in Equation (15) owing to Sommerfeld’s expansion [16] gives eventually

$$D_n={\left(3{\pi }^2\right)}^{{\displaystyle \frac{2}{3}}}{\displaystyle \frac{\tau }{6}}{\left({\displaystyle \frac{\hslash }{ma}}\right)}^2.$$

By contrast, the conduction electron properties prove strongly T-dependent in semi-conductors [16], which implies near room temperature

$${\displaystyle \frac{\partial E_F}{\partial c_e}}=e^{-{\displaystyle \frac{E_F}{k_{B}T}}}{\displaystyle \frac{{\pi }^2{\hslash }^3}{\sqrt{2m^3{k}_{B}T}{\int }_0^{\infty }{e}^{-v}\sqrt{v}dv}}={\displaystyle \frac{k_{B}T}{c_D}},$$

for which $c_D$ designates the donor concentration. At last $D_n$ is inferred to read

$$D_n={\displaystyle \frac{\tau k_{B}T}{3m}}{\displaystyle \frac{{\int }_0^{\infty }{e}^{-v}\sqrt{v^3}dv}{{\int }_0^{\infty }{e}^{-v}\sqrt{v}dv}}.$$

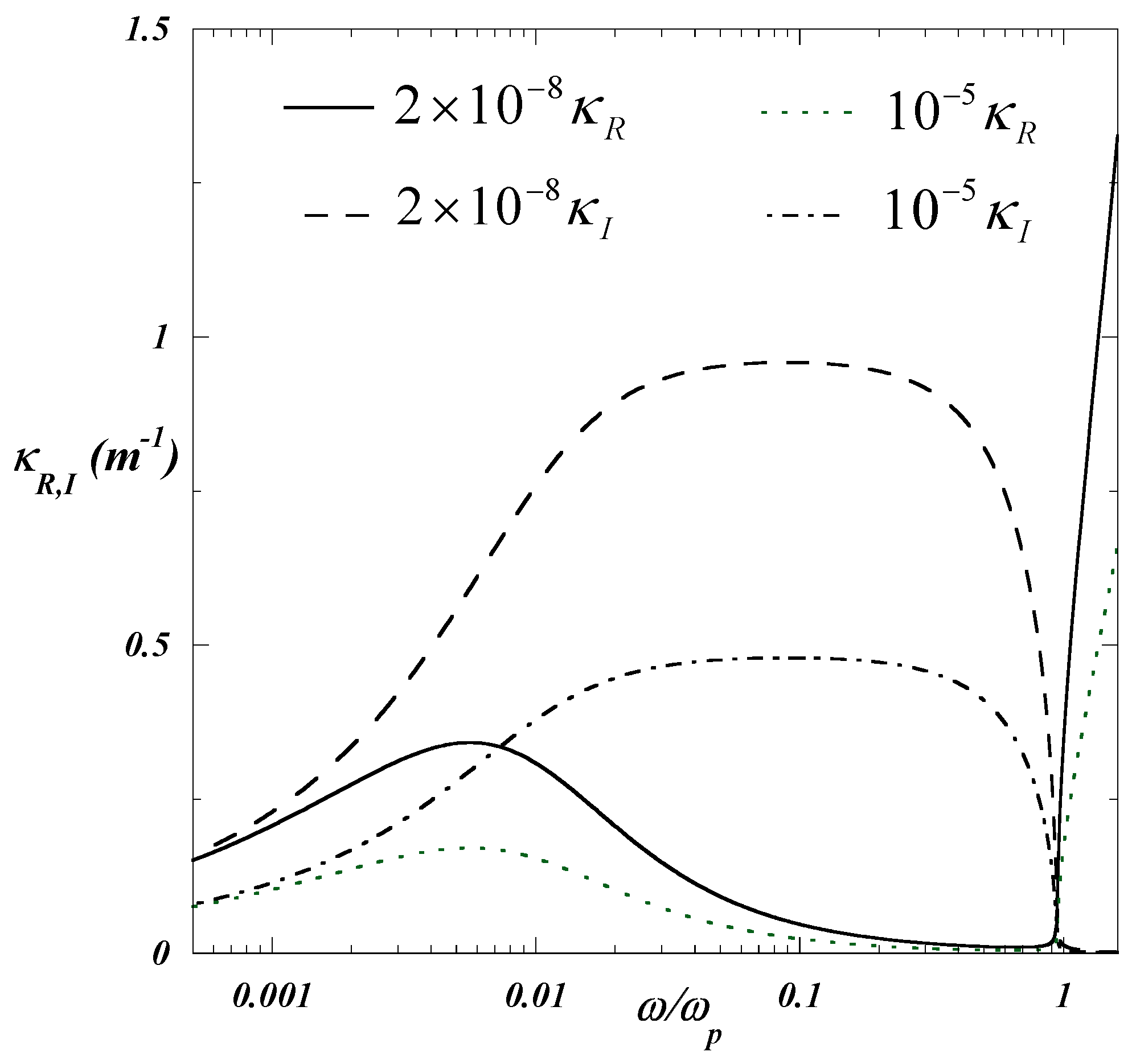
The dispersion curve $K\left(\omega \right)$, ensuing from Equation (12), has been plotted in Figure 2. For $\omega <.8{\omega }_p$ there is $K_R\left(\omega \right)\approx K_I\left(\omega \right)\approx \sqrt{{\displaystyle \frac{\omega }{D_n}}}$, whereas there is $K_R\left(\omega \right)\approx K_I\left(\omega \right)\approx \sqrt{{\displaystyle \frac{\omega }{2D_n}}}$ for $\omega >\sqrt{2}{\omega }_p$.

3. 2-Matching Procedure

The electric field E can be now expressed as

$$E=E_{\omega }\left(z\right)g\left(x\right)e^{i\omega t},E_{\omega }\left(z\right)=E_1{e}^{Kz}+E_2{e}^{-Kz},$$

(16)

with the unknowns $E_{i=1,2}\left(\omega \right)$ to be assigned below. To that end, it ought to be noted that, since the longitudinal space-charge wave is to be aroused by an external transverse electromagnetic wave, the only practical way to couple both waves together consists of having the electromagnetic wave impinging upon the edge of the wire, as pictured in Figure 1. Thus requiring the projection of the dielectric displacement D onto the z axis to be continuous at $z=\pm l/2$ implies

$$\begin{array}{c}{E}_{\omega }\left({\displaystyle \frac{l}{2}}\right)={\displaystyle \frac{E_{+}}{ϵ\left(\omega \right)}},E_{\omega }\left(-{\displaystyle \frac{l}{2}}\right)=0\hfill \\ E_{+}=E_{0}sin\alpha ,g\left(x\right)=e^{{\displaystyle \frac{i\omega sin\alpha }{c}}x}\hfill \end{array}.$$

(17)

$ϵ\left(\omega \right)$ is given by Equation (6) and $c,E_0,E_{+}$ are respectively the light velocity, the amplitude of the electric component of the incoming wave, making an angle ${\displaystyle \frac{\pi }{2}}-\alpha$ with the z axis (see Figure 1) and its projection onto the z axis, whereas $g\left(x\right)$ is identified as the phase-shift of the incoming beam along the $\varphi =0$ radial axis.

Actually allowing for $E_{\omega }\left({\displaystyle \frac{l}{2}}\right)\ne {\displaystyle \frac{E_{+}}{ϵ\left(\omega \right)}}$ would give rise to a superficial charge density $q_{+}$

$$q_{+}={ϵ}_0\left(E_{+}-ϵ\left(\omega \right)E_{\omega }\left({\displaystyle \frac{l}{2}}\right)\right),$$

(18)

in accordance [18] with Equation (4). However, let us prove by contradiction that it cannot be so. Accordingly taking advantage [18] of ${\displaystyle \frac{d{q}_{+}}{dt}}=j\left({\displaystyle \frac{l}{2}}\right)$ and Equation (8) implies

$$i\omega q_{+}=j\left({\displaystyle \frac{l}{2}}\right)=-i\omega D\left({\displaystyle \frac{l}{2}}\right)=-i\omega {ϵ}_0ϵ\left(\omega \right)E_{\omega }\left({\displaystyle \frac{l}{2}}\right).$$

Thence inserting the latter expression of $q_{+}$ into Equation (18) enables us to deduce $E_{+}=0\Rightarrow E_0=0$, contradicting thereby our assumption $E_0\ne 0$. At last, by substituting the expressions of $E_{\omega }\left(\pm {\displaystyle \frac{l}{2}}\right)$, as given in Equation (16), to $E_{\omega }\left(\pm {\displaystyle \frac{l}{2}}\right)$ in Equation (17), Equation (17) is turned into a $2\times 2$ Cramer system, the unknowns $E_{i=1,2}\left(\omega \right)$ of which are found to read

$$\begin{array}{c}{E}_1={\displaystyle \frac{E_{+}}{ϵ\left(\omega \right)\left(e^{\frac{Kl}{2}}-e^{-\frac{3Kl}{2}}\right)}},E_2={\displaystyle \frac{E_{+}}{ϵ\left(\omega \right)\left(e^{-\frac{Kl}{2}}-e^{\frac{3Kl}{2}}\right)}}\hfill \end{array}.$$

(19)

4. 3-SHG

The polarisation $P_{2\omega }(t,z,x)=\rho u$ and current density $j_{2\omega }(t,z,x)=\rho {\displaystyle \frac{\partial u}{\partial t}}$ which have been discarded while linearising $D,j_1$ in Equations (2,9), are both realised to oscillate like $e^{2\left(K\left(\omega \right)z+i\omega t\right)}$ and are thence recognised as the only source of SHG in this work. They read

$$\begin{array}{c}{P}_{2\omega }(t,z,x)=P_{2\omega }\left(z\right)g^2\left(x\right)e^{2\left(K\left(\omega \right)z+i\omega t\right)}\hfill \\ j_{2\omega }(t,z,x)=j_{2\omega }\left(z\right)g^2\left(x\right)e^{2\left(K\left(\omega \right)z+i\omega t\right)}\hfill \end{array},$$

which entails for their time-Fourier transforms $P_{2\omega }\left(z\right),j_{2\omega }\left(z\right)$ owing to Equations (4,6)

$$\begin{array}{c}{P}_{2\omega }\left(z\right)={ϵ}_0ϵ\left(\omega \right){\displaystyle \frac{\partial E_{\omega }}{\partial z}}\chi \left(\omega \right)E_{\omega }\left(z\right)={ϵ}_0ϵ\left(\omega \right)\chi \left(\omega \right){\displaystyle \frac{\partial E_{\omega }^2}{2\partial z}}\hfill \\ j_{2\omega }\left(z\right)=i\omega P_{2\omega }\left(z\right)\hfill \end{array}.$$

The average values of $P_{2\omega }\left(z\right),j_{2\omega }\left(z\right)$ over $z\in \left[-{\displaystyle \frac{l}{2}},{\displaystyle \frac{l}{2}}\right]$ are needed to proceed further. They are inferred to read, thanks to Equations (16,19)

$$\begin{array}{c}{P}_{2\omega }={\int }_{-{\displaystyle \frac{l}{2}}}^{{\displaystyle \frac{l}{2}}}{P}_{2\omega }\left(z\right){\displaystyle \frac{dz}{l}}\hfill \\ ={\displaystyle \frac{{ϵ}_0ϵ\left(\omega \right)\chi \left(\omega \right)sinh\left(K\left(\omega \right)l\right)\left(E_1^2\left(\omega \right)-E_2^2\left(\omega \right)\right)}{l}}\hfill \\ j_{2\omega }={\int }_{-{\displaystyle \frac{l}{2}}}^{{\displaystyle \frac{l}{2}}}{j}_{2\omega }\left(z\right){\displaystyle \frac{dz}{l}}=i\omega P_{2\omega }\hfill \end{array}.$$

(20)

The SHG signal to be addressed now consists for $r>r_0$ in an electromagnetic wave of frequency $2\omega$ propagating outward along the radial direction (see Figure 1) and carrying an electric component, parallel to the z axis

$$E(t,r)=E_z\left(2\omega \right)e^{i\left(2\omega t-\kappa \left(2\omega \right)r\right)},$$

with the wave number $\kappa ={\displaystyle \frac{2\omega }{c}}$. However for $r\in \left[0,r_0\right]$, $E(t,r)$ induces in addition a drift current density $j(t,r)$, obeying Ohm’s law (see Equation (11)) and a dielectric displacement $D(t,r)$, both aligned with the z axis and reading [12]

$$\begin{array}{c}j(t,r)={\displaystyle \frac{\sigma }{1+2i\omega \tau }}E(t,r)\hfill \\ D(t,r)={ϵ}_0\left(n^2-1+ϵ\left(2\omega \right)\right)E(t,r)\hfill \end{array},$$

with $ϵ\left(2\omega \right)$ given by Equation (7). The complex number $\kappa (r\le r_0)$ will be calculated now with help of the wave-equation [12]

$$\begin{array}{c}{ϵ}_0{c}^2\nabla \times \nabla \times E+{\displaystyle \frac{\partial j}{\partial t}}+{\displaystyle \frac{{\partial }^{2}D}{\partial t^2}}=0\Rightarrow \hfill \\ {\kappa }^2\left(2\omega \right)={\left({\displaystyle \frac{2n\omega }{c}}\right)}^2-{\left({\displaystyle \frac{2{\omega }_p}{c}}\right)}^2{\displaystyle \frac{i\omega \tau }{1+2i\omega \tau }}\hfill \end{array}.$$

(21)

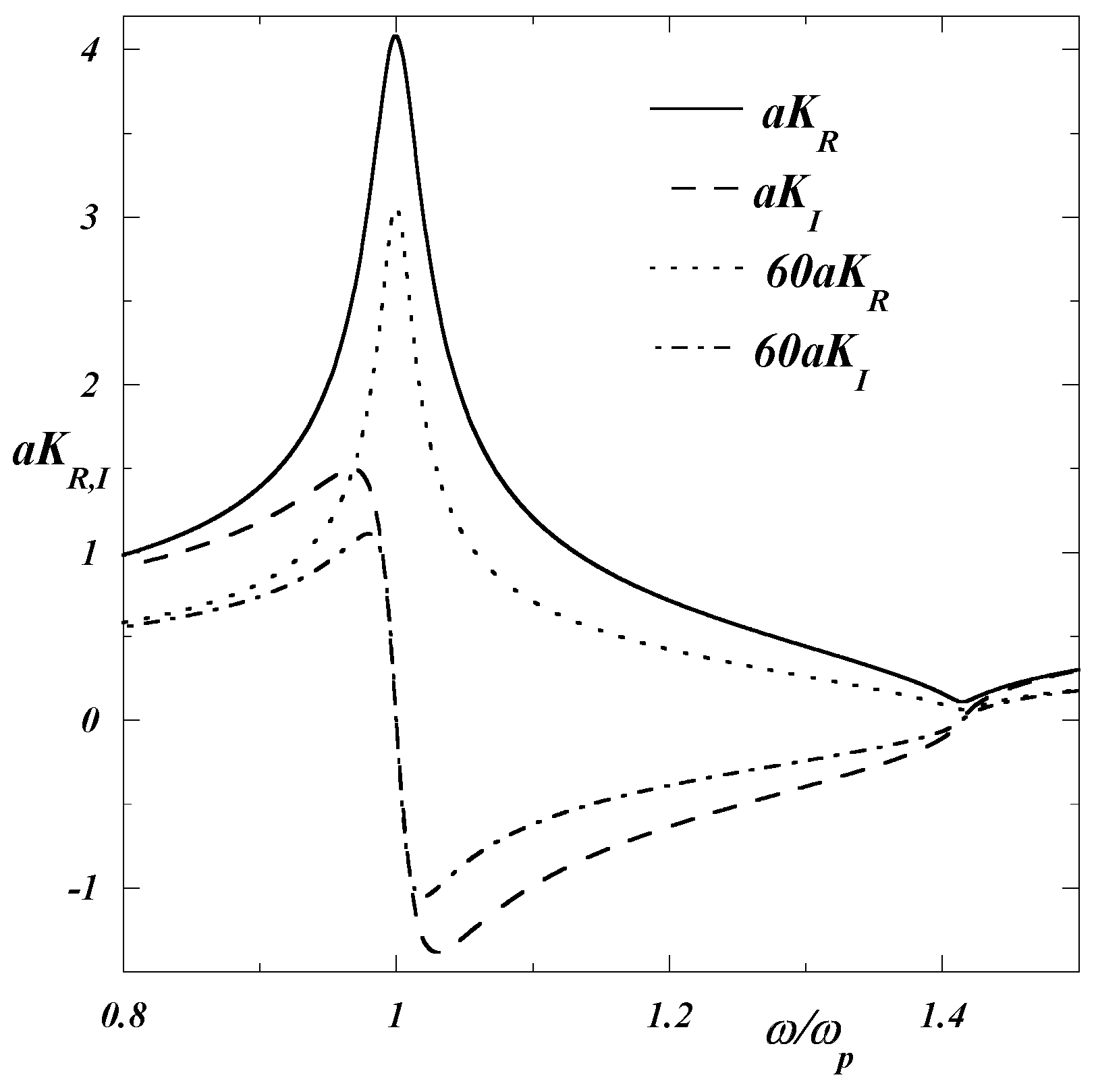
The dispersion curve of electromagnetic waves

$$\kappa \left(\omega \right)={\kappa }_R\left(\omega \right)+i{\kappa }_I\left(\omega \right),$$

plotted in Figure 3, turns out to differ markedly from that of space-charge waves $K\left(\omega \right)$, pictured in Figure 2. Likewise, there is

$${\kappa }_R\left(\omega \right)\approx {\kappa }_I\left(\omega \right)\approx {\displaystyle \frac{{\omega }_p}{c}}\sqrt{\omega \tau },$$

for $\omega \tau <<1\Rightarrow \omega <<{\omega }_p$, whereas there is

$${\kappa }_R\left(\omega \right)\approx {\displaystyle \frac{\sqrt{{\left(n\omega \right)}^2-2{\omega }_p^2}}{c}},{\kappa }_I\left(\omega \right)\approx 0,$$

for $\omega >{\omega }_2={\omega }_p{\displaystyle \frac{\sqrt{2}}{n}}$. Actually, the conditions $\omega <{\omega }_2$ and $\omega >{\omega }_2$ characterise, respectively, the surface plasmon-polaritons [11,12], for which the electromagnetic field is confined inside a narrow range $r\in \left[r_0-{\displaystyle \frac{1}{\left|{\kappa }_I\left(\omega \right)\right|}},r_0\right]$ in accordance with the skin effect [19], and three-dimensional plasmons, penetrating deeply into bulk matter due to ${\kappa }_I\left(\omega \right)\approx 0$. At last, it is worth noting that there is $K\left({\omega }_1={\omega }_p\sqrt{2}\right)=\kappa \left({\omega }_2\right)=0$, as inferred from Equations (12,21) for $\tau \to \infty$, which entails that the associated space-charge and electromagnetic waves are identical in this particular case, since both are characterised by

$$u_z\left({\omega }_{i=1,2}\right)\ne 0,E_z\left({\omega }_{i=1,2}\right)\ne 0,$$

but vanishing space-charge density and magnetic field. Besides, the plasma oscillation ought to take place at ${\omega }_2$ rather than ${\omega }_p$, as arbitrarily purported in textbooks [12,16,20] to ensue from $ϵ\left({\omega }_p\right)=0$ with $ϵ\left(\omega \right)$ defined in Equation (7).

The unknown $E_z\left(2\omega \right)$ will be assigned thanks to Equations (11,20), by substituting $j_{2\omega }{e}^{i\left(2\omega t-\kappa \left(2\omega \right)r_0\right)},\left({ϵ}_0{n}^2{E}_z\left(2\omega \right)+P_{2\omega }\right)e^{i\left(2\omega t-\kappa \left(2\omega \right)r_0\right)}$ to $j(t,r_0),D(t,r_0)$, respectively, in the wave-equation (21), which yields finally

$$\begin{array}{c}\left({\displaystyle \frac{\sigma }{1+2i\omega \tau }}+2i\omega {ϵ}_0\left(n^2-1+ϵ\left(2\omega \right)\right)\right)E_z\left(2\omega \right)=\hfill \\ j_{2\omega }+2i\omega \left({ϵ}_0{n}^2{E}_z\left(2\omega \right)+P_{2\omega }\right)\Rightarrow \hfill \\ \left({\displaystyle \frac{\sigma }{1+2i\omega \tau }}+2i\omega {ϵ}_0\left(ϵ\left(2\omega \right)-1\right)\right)E_z\left(2\omega \right)=\hfill \\ j_{2\omega }+2i\omega P_{2\omega }=3i\omega P_{2\omega }=3j_{2\omega }\Rightarrow \hfill \\ E_z\left(2\omega \right)={\displaystyle \frac{3\left(1+2i\omega \tau \right)}{2\sigma }}{j}_{2\omega }\hfill \end{array}.$$

(22)

with $ϵ\left(2\omega \right)$ given by Equation (7).

The incoming electromagnetic power $W_{\omega }$ and the outgoing one $W_{2\omega }$ can thence be inferred to read

$$\begin{array}{c}{W}_{\omega }=\pi r_0^2{ϵ}_{0}ccos\alpha {\left|E_{+}\right|}^2=\pi r_0^2{ϵ}_{0}ccos\alpha {sin}^2\alpha E_0^2\hfill \\ W_{2\omega }=2\pi r_{0}l{ϵ}_{0}c{\left|E_z\left(2\omega \right)\right|}^2\hfill \end{array}.$$

The property

$$W_{2\omega }\propto E_{+}^4\Rightarrow W_{2\omega }\propto W_{\omega }^2$$

is a signature of the non-linear character of SHG [1]. Moreover $W_{\omega }$ reaches its upper bound for $\alpha =54.7$deg.

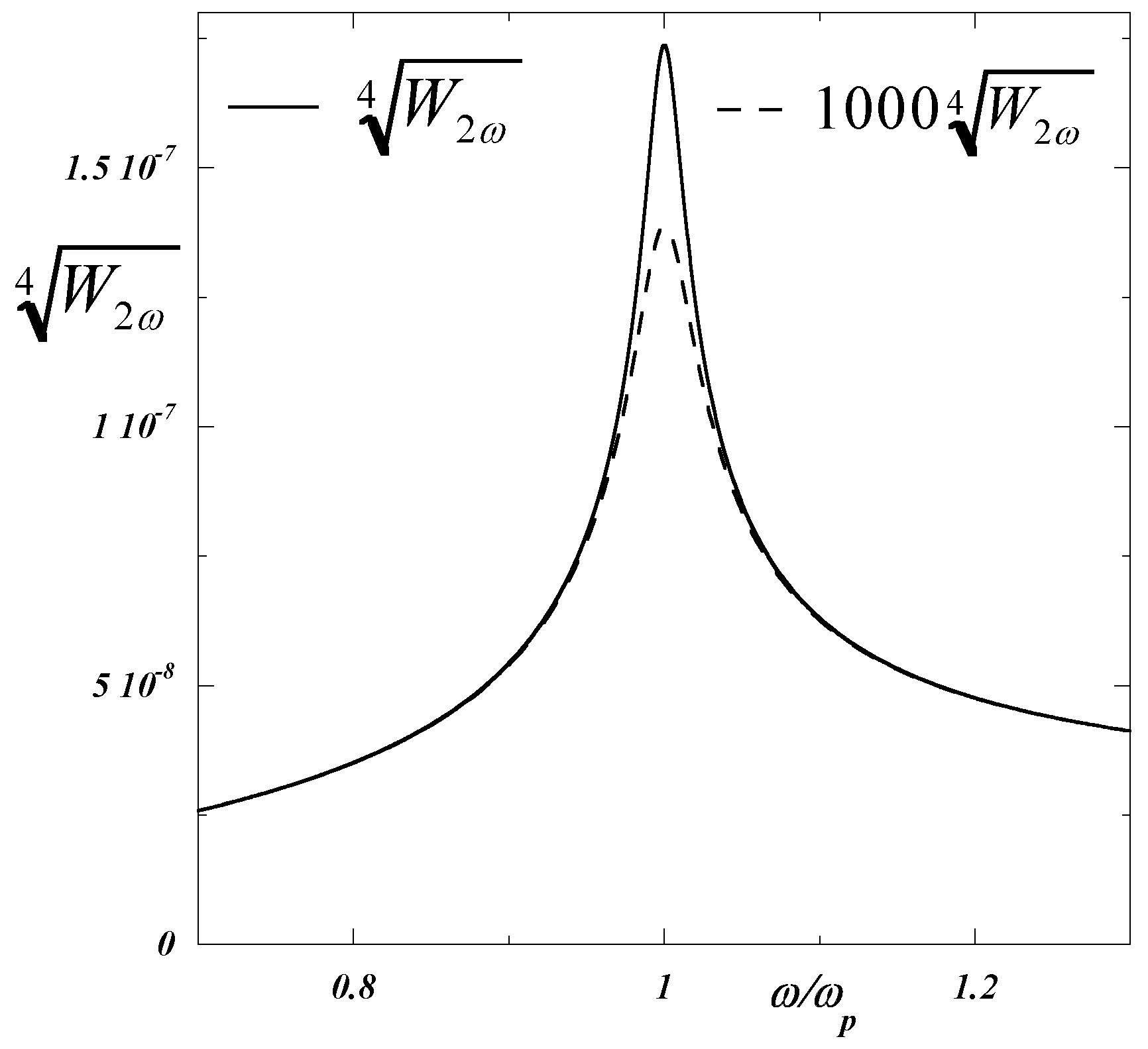
The outgoing power $W_{2\omega }\left(\omega \right)$ has been plotted in Figure 4 for a metal and a semi-conductor. Both plots exhibit a sharp maximum at $\omega ={\omega }_p$, ensuing from $W_{2\omega }\left(\omega \right)\propto {ϵ}^{-4}\left(\omega \right)$ with $ϵ\left({\omega }_p\right)\approx 0$, as inferred from Equation (6) for ${\omega }_p\tau =100>>1$. $W_{2\omega }$ decreases to 0 with $\omega \to 0$, whereas it reaches a plateau $\approx .003W_{2\omega }\left({\omega }_p\right)$ for $\omega \to \infty$. The huge ratio $W_{2\omega }$(semi-conductor)$/W_{2\omega }$(metal)$\approx {10}^{12}$, conspicuous in Figure 4, stems from

$$W_{2\omega }(\omega \ge {\omega }_p)\propto {\displaystyle \frac{1}{c_0^{2}l}}.$$

Such a behaviour, ensuing from

$$j_{2\omega }\propto 1/l,E_z\left(2\omega \right)\propto 1/\sigma \Rightarrow E_z\left(2\omega \right)\propto 1/c_0,$$

in Equations (20,22), respectively, is thence realised to concur with the ratio of $c_0$-values, assumed in Figs.2,4. Therefore choosing a semi-conducting sample of short length l is likely to greatly enhance the SHG efficiency. Besides, semi-conductors exhibit two additional merits :

• semi-conductors, unlike metals of fixed $c_0$, enable one to tune ${\omega }_p$ to the searched frequency, either by controlling the doping rate $c_D$ or monitoring the temperature;
• the relatively low value of ${\omega }_p\approx {10}^{13}$rad/s, typical of donor-like semi-conductors permits to benefit from a broader frequency range above ${10}^{13}$rad/s than in metals and acceptor-like semi-conductors, for which this threshold is pushed up above ${10}^{16}$rad/s. Moreover this analysis breaks down in the microscopic limit for $K\left(\omega \right)a>1$, which, in view of Equation (12), sets upper limits $\omega <{10}^{16}$rad/s and $\omega <{10}^{17}$rad/s for metals and semi-conductors, respectively.

Figure 4. Plot of the SHG power $\sqrt[4]{W_{2\omega }\left(\omega \right)}$ at frequency $2\omega$, expressed in $\sqrt[4]{W}$ with $E_{+}=1$V/m, $l=10$nm, $r_0=100$nm; the solid and dashed lines depict the data reckoned for a semi-conductor and a metal, respectively; the various parameters, used for the calculations, have been assigned to the same values, as already taken for Figure 2.

Figure 4. Plot of the SHG power $\sqrt[4]{W_{2\omega }\left(\omega \right)}$ at frequency $2\omega$, expressed in $\sqrt[4]{W}$ with $E_{+}=1$V/m, $l=10$nm, $r_0=100$nm; the solid and dashed lines depict the data reckoned for a semi-conductor and a metal, respectively; the various parameters, used for the calculations, have been assigned to the same values, as already taken for Figure 2.

5. Conclusions

The properties of longitudinal space-charge waves have been worked out with help of Equations (1,4,8) and strong emphasis has been put on their being quite different from transverse electromagnetic waves which are rather solutions of Maxwell’s equations [12,18]. Accordingly, a space-charge wave carries no magnetic field, whereas an electromagnetic wave carries no three-dimensional space-charge, even though the electromagnetic field may be strongly spatially inhomogeneous [9,10,11]. However most of textbooks [12,20] purport wrongly that the same dielectric displacement D comes up, on the one hand, in the Ampère-Maxwell equation and on the other hand, in Gauss’ equation (see Equation (4)) and the charge conservation law (see Equation (8)). Unfortunately such a claim is inconsistent in two respects :

• as already recalled above, D contains only the polarisation, stemming from the conduction electrons in Gauss’ equation and the charge conservation law, whereas D includes in addition that of filled bands in the Ampère-Maxwell equation;
• there is $\nabla .D\ne 0$ for Gauss’ equation and the charge conservation law versus $\nabla .D=0$ for the Ampère-Maxwell equation.

Hopefully this work will help dispel this ubiquitous and harmful confusion.

Figure 1 illustrates how matching both waves together might provide with a novel mechanism of SHG, instrumental over a wide frequency range in semi-conductors. Light has been shed on the advantage offered by nanometric samples. The concentration dependence of $W_{2\omega }\propto 1/c_0^2$ turns out to be redolent of a similar behaviour of the Hall voltage, varying [21] like $1/c_0$. Note also that the $\mathit{3}$-dimensional space charge discussed here, is quite different from the $\mathit{2}$-dimensional superficial charge density, conveyed by a surface plasmon polariton [11,12]. Last but not least, the $l,c_0,\omega$ dependences of $W_{2\omega }$, unveiled here, lend themselves to an experimental check.