Submitted:
25 February 2025
Posted:
27 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Material System
2.2. Single-tow Tension Tests
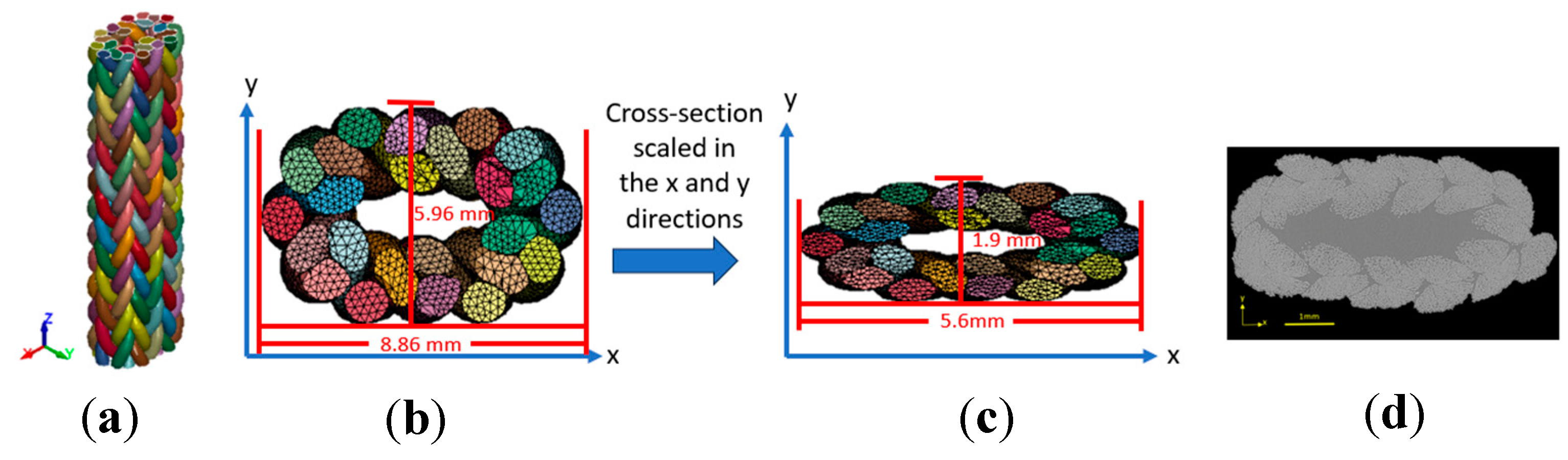
2.3. Braid Geometry: Dimensions and Features
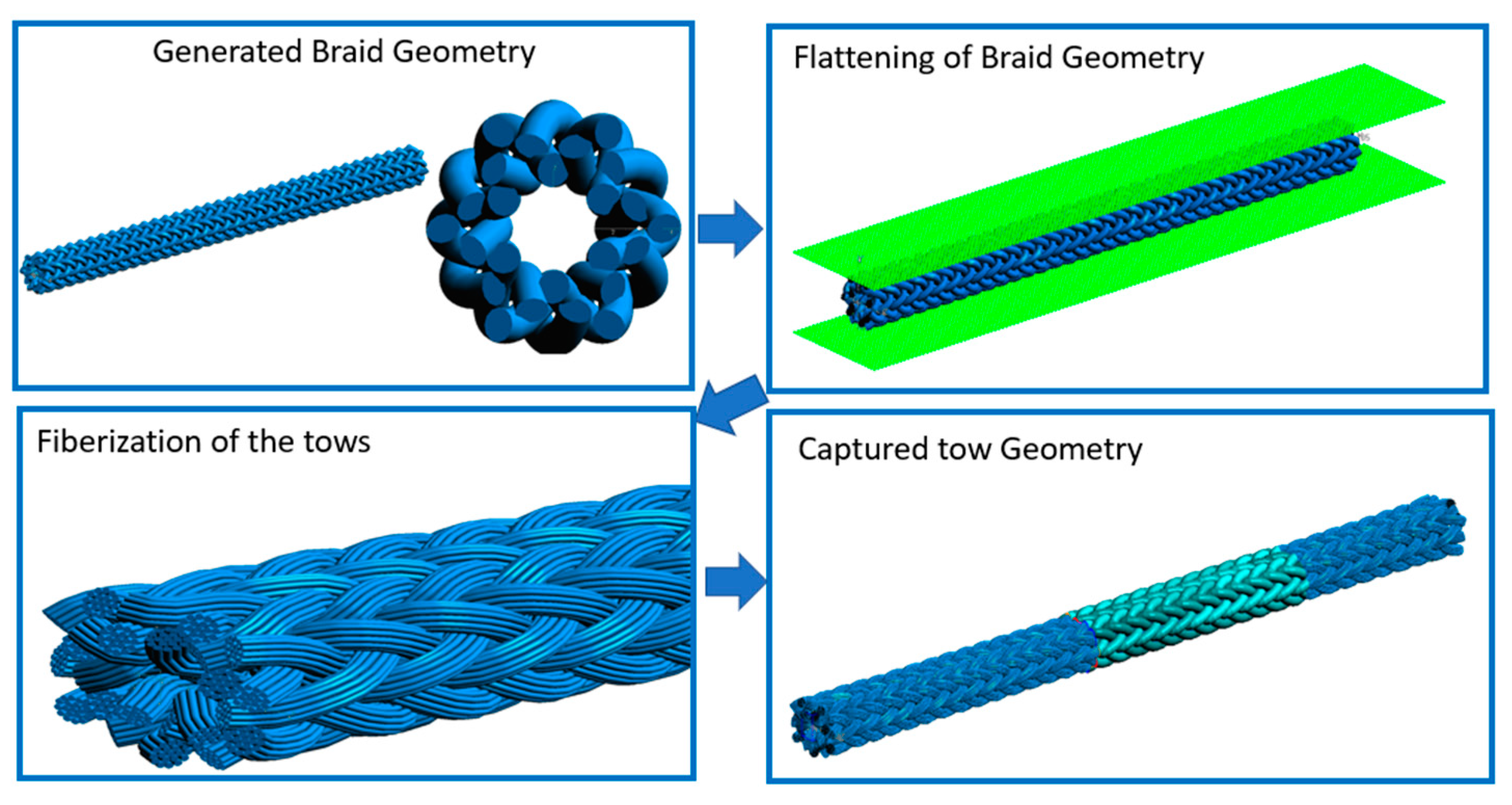
2.4. Braid Geometry: Modeling
2.5. Material Model
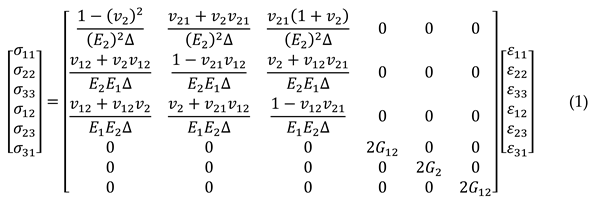
2.6. Single-Tow Model
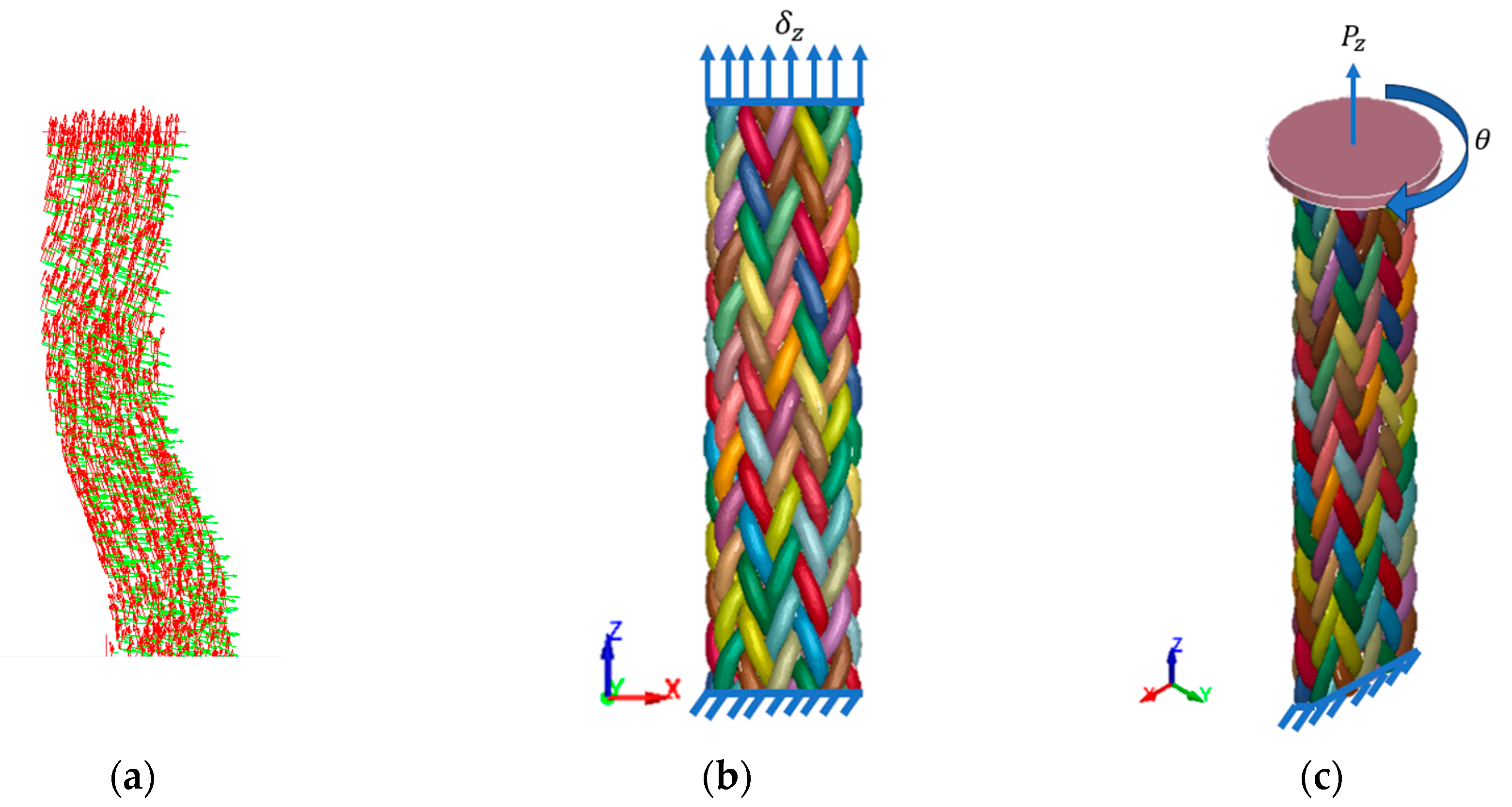
2.7. Model of the Tensile Test of the Full Braid
2.8. Modeling of the Torsion Test of the Full Braid
3. Results and Discussion
3.1. Braid Geometry: Dimensions and Features
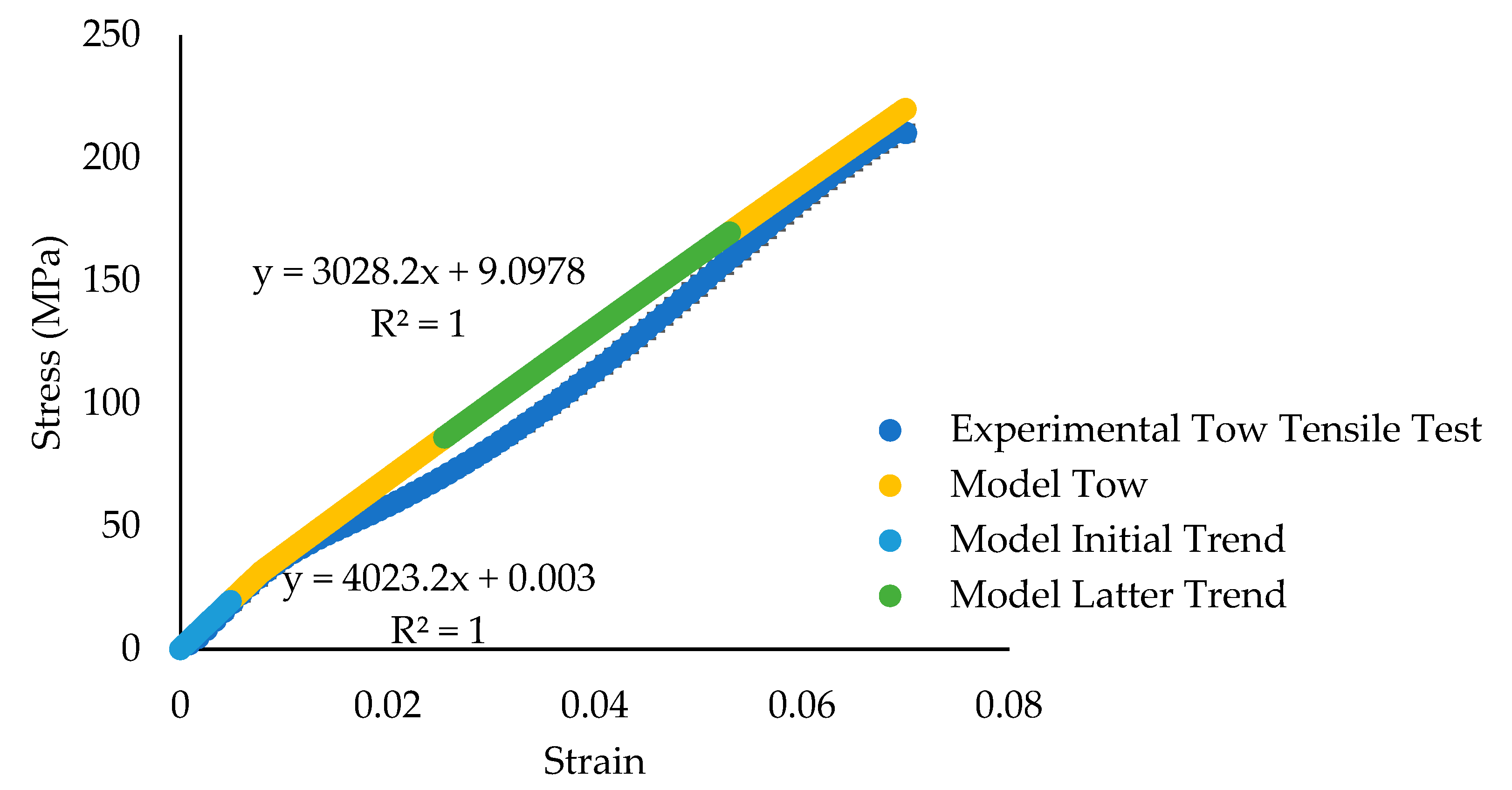
3.2. Single-Tow Tension Tests
3.3. Single-Tow Finite Element Model
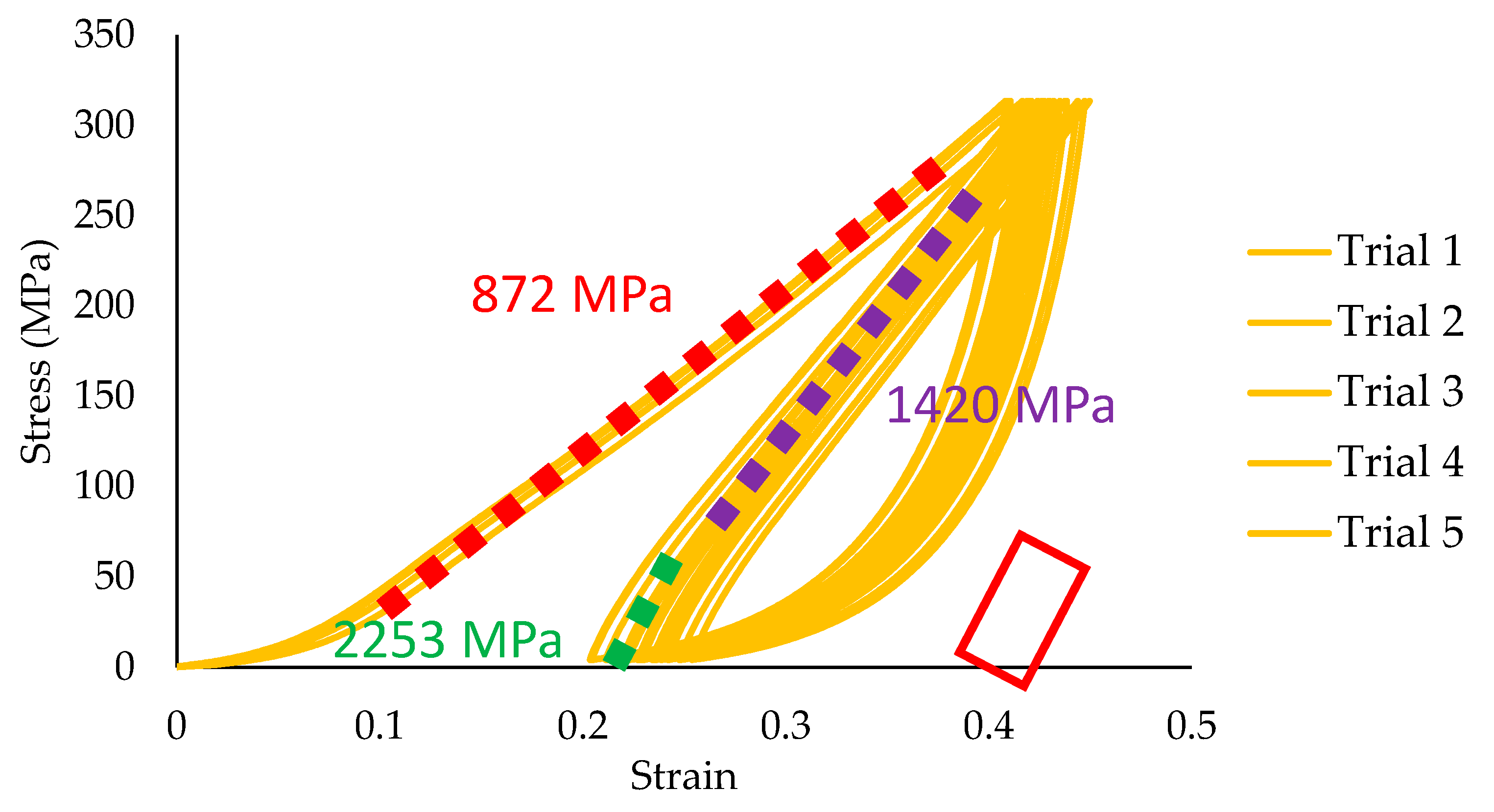
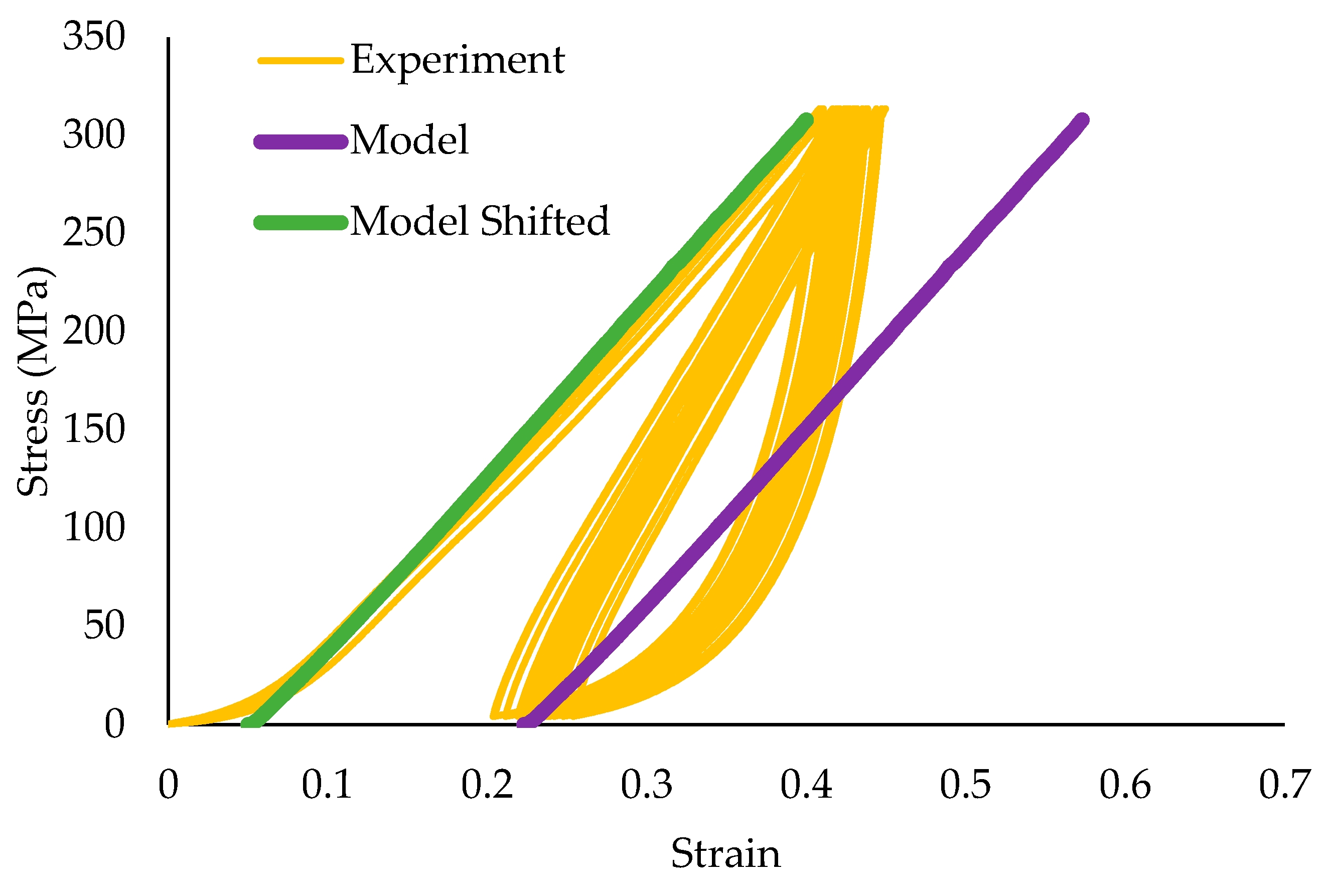
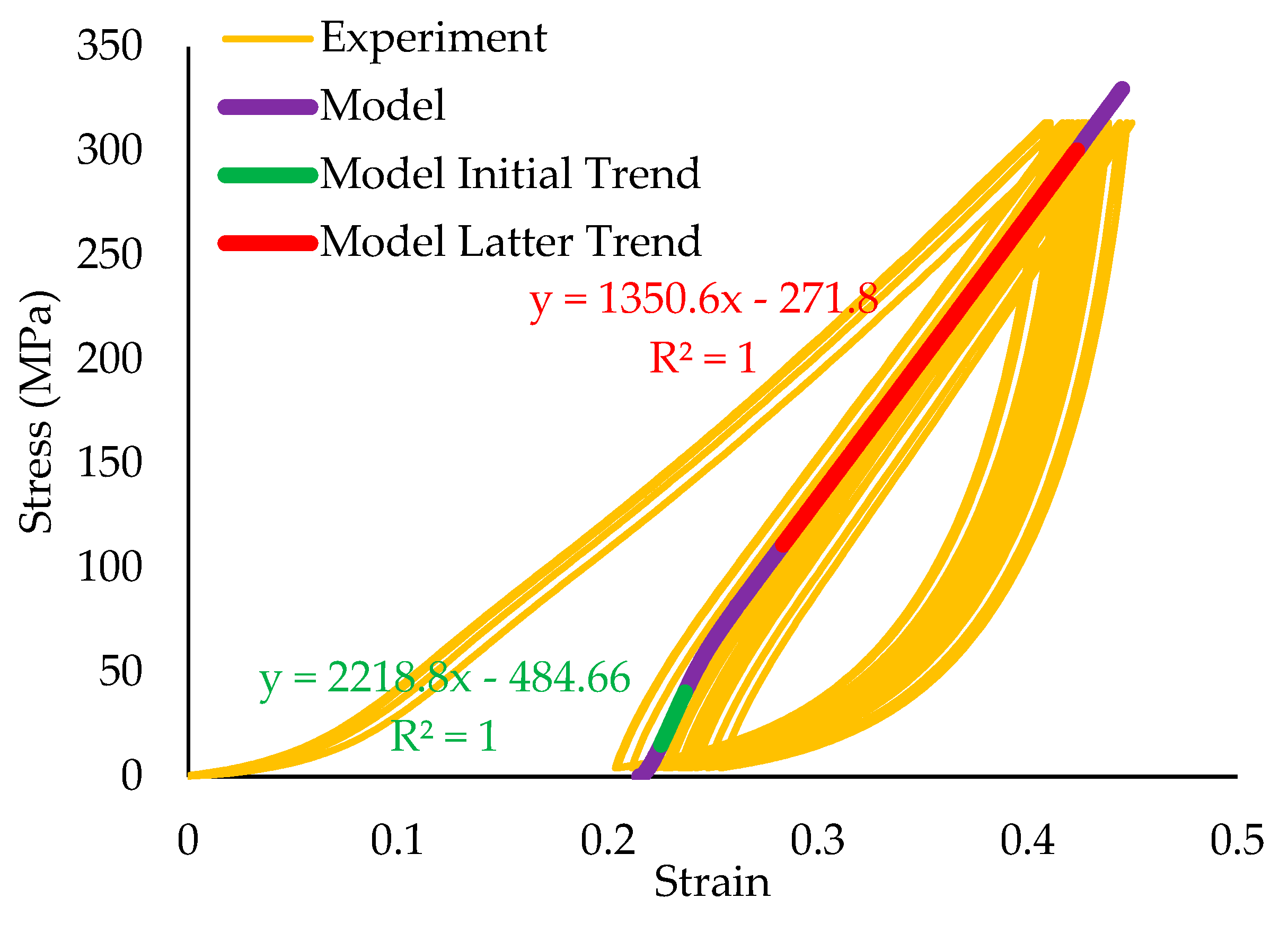
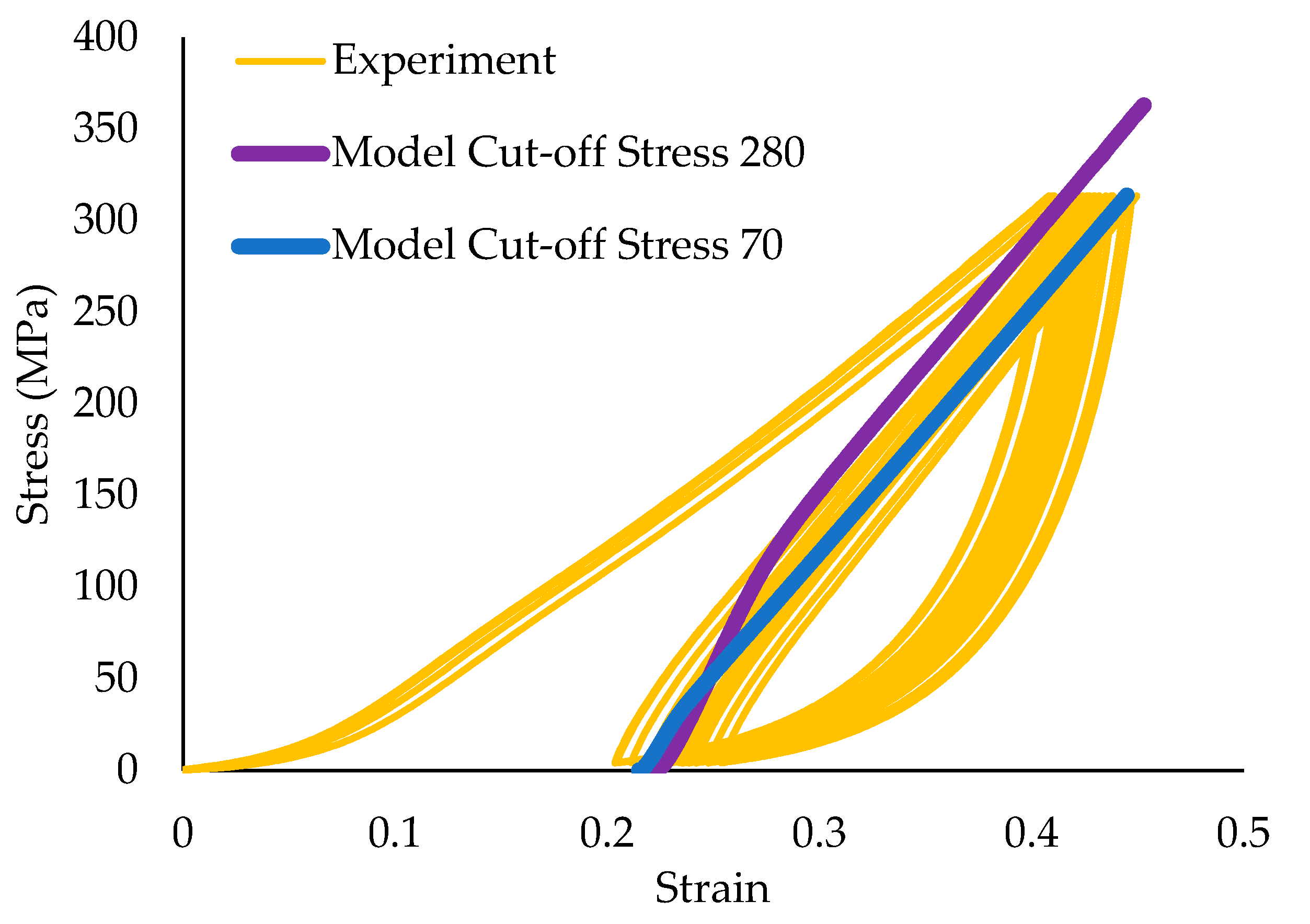
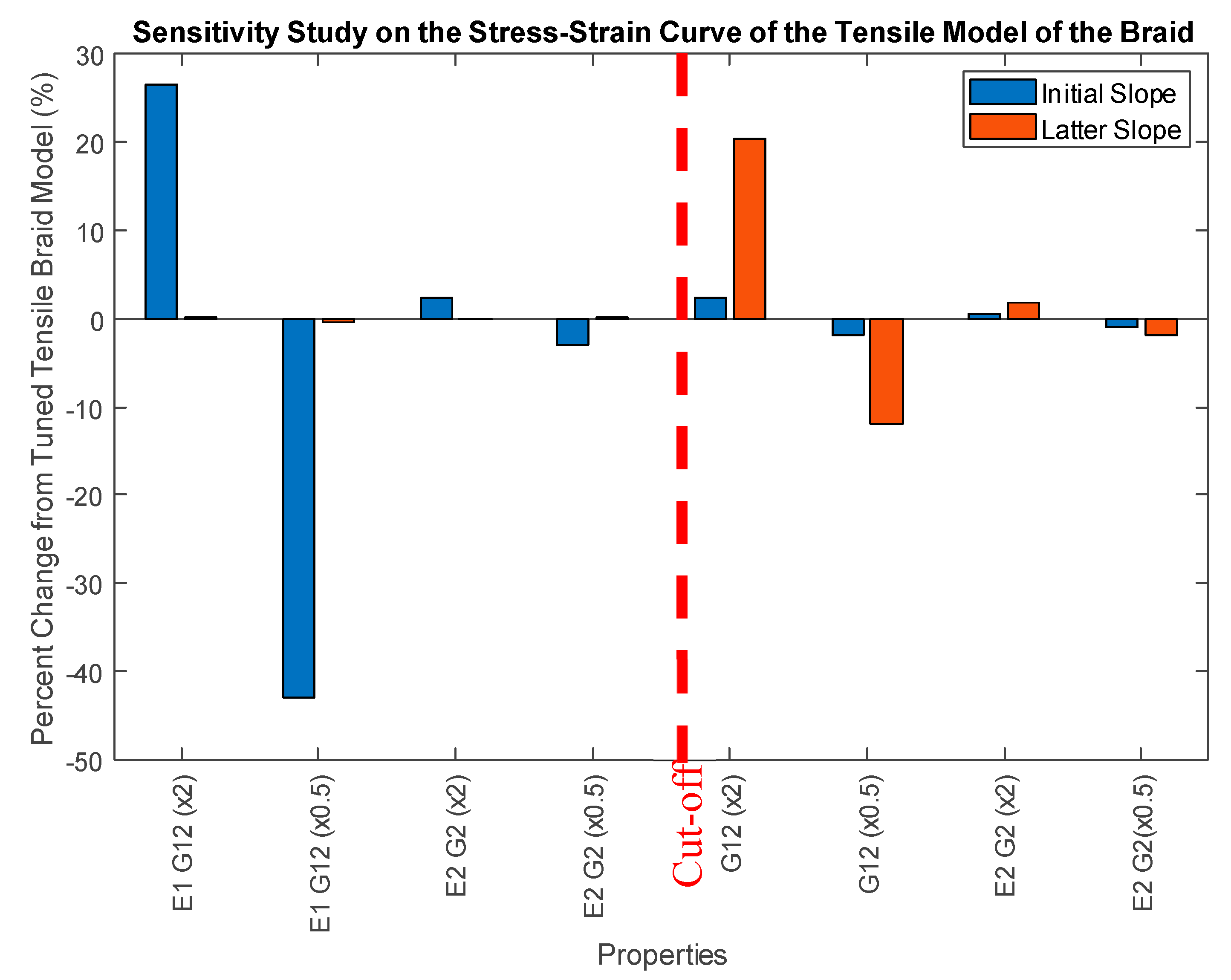
3.4. Modeling of the Tensile Test of the Braided Cord
3.5. Modeling if the Torsion Test
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lingard, S., “Basic Analysis of Ram-Air Parachute,” in Precision Aerial Delivery Systems: Modeling, Dynamics, and Control, (Progress in Astronautics and Aeronautics: American Institute of Aeronautics and Astronautics, Inc., 2015, pp. 73-125.
- Omeroglu, S., “The effect of braiding parameters on the mechanical properties of braided ropes,” Fibres and Textiles in Eastern Europe, vol. 14, pp. 53-57, 01/01 2006.
- Raoof, M.; Davies, T., “Determination of the bending stiffness for a spiral strand,” The Journal of Strain Analysis for Engineering Design, vol. 39, no. 1, pp. 1-13, 2004.
- Chiang, Y.J., “Characterizing simple-stranded wire cables under axial loading,” Finite Elements in Analysis and Design, vol. 24, no. 2, pp. 49-66, 1996/12/16/ 1996. [CrossRef]
- Hussain, N.; Baharom, M.B., “Analysis of optimum wire rope configuration for equal unidirectional torsional stiffness for flexible steering shaft,” in MATEC Web of Conferences, 2016, vol. 74: EDP Sciences, p. 00017.
- Goldberg, R.K.; Blinzler, B.J.; Binienda, W.K., “Modification of a Macromechanical Finite Element–Based Model for Impact Analysis of Triaxially Braided Composites,” Journal of Aerospace Engineering, vol. 25, no. 3, pp. 383-394, 2011.
- King, M.J.; Jearanaisilawong, P.; Socrate, S., “A continuum constitutive model for the mechanical behavior of woven fabrics,” International Journal of Solids and Structures, vol. 42, no. 13, pp. 3867-3896, 2005/06/01/ 2005. [CrossRef]
- Peng, X.; Cao, J., “A continuum mechanics-based non-orthogonal constitutive model for woven composite fabrics,” Composites part A: Applied Science and manufacturing, vol. 36, no. 6, pp. 859-874, 2005.
- Shahkarami, A.; Vaziri, R., “A continuum shell finite element model for impact simulation of woven fabrics,” International Journal of Impact Engineering, vol. 34, no. 1, pp. 104-119, 2007/01/01/ 2007. [CrossRef]
- Xue, P.; Peng, X.; Cao, J., “A non-orthogonal constitutive model for characterizing woven composites,” Composites part A: Applied Science and manufacturing, vol. 34, no. 2, pp. 183-193, 2003.
- Yu, W.R.; Pourboghrat, F.; Chung, K.; Zampaloni, M.; Kang, T.J., “Non-orthogonal constitutive equation for woven fabric reinforced thermoplastic composites,” Composites Part A: Applied Science and Manufacturing, vol. 33, no. 8, pp. 1095-1105, 2002/08/01/ 2002. [CrossRef]
- Zhang, C.; Curiel-Sosa, J.L.; Bui, T.Q., “Meso-scale progressive damage modeling and life prediction of 3D braided composites under fatigue tension loading,” Composite Structures, vol. 201, pp. 62-71, 2018/10/01/ 2018. [CrossRef]
- Zhang, C.; Binienda, W.K.; Goldberg, R.K.; Kohlman, L.W., “Meso-scale failure modeling of single layer triaxial braided composite using finite element method,” Composites Part A: Applied Science and Manufacturing, vol. 58, pp. 36-46, 2014/03/01/ 2014. [CrossRef]
- Wu, L.; Gu, B., “Fatigue behaviors of four-step three-dimensional braided composite material: a meso-scale approach computation,” Textile Research Journal, vol. 84, no. 18, pp. 1915-1930, 2014/11/01 2014. [CrossRef]
- Tabatabaei, S.A.; Lomov, S.V., “Eliminating the volume redundancy of embedded elements and yarn interpenetrations in meso-finite element modelling of textile composites,” Computers & Structures, vol. 152, pp. 142-154, 2015/05/01/ 2015. [CrossRef]
- Nguyen, Q.T.; Vidal-Sallé, E.; Boisse, P.; Park, C.H.; Saouab, A.; Bréard, J.; Hivet, G., “Mesoscopic scale analyses of textile composite reinforcement compaction,” Composites Part B: Engineering, vol. 44, no. 1, pp. 231-241, 2013/01/01/ 2013. [CrossRef]
- Lomov, S.V.; Ivanov, D.S.; Verpoest, I.; Zako, M.; Kurashiki, T.; Nakai, H.; Hirosawa, S., “Meso-FE modelling of textile composites: Road map, data flow and algorithms,” Composites Science and Technology, vol. 67, no. 9, pp. 1870-1891, 2007/07/01/ 2007. [CrossRef]
- Lomov, S.V.; Gusakov, A.V.; Huysmans, G.; Prodromou, A.; Verpoest, I., “Textile geometry preprocessor for meso-mechanical models of woven composites,” Composites Science and Technology, vol. 60, no. 11, pp. 2083-2095, 2000/08/01/ 2000. [CrossRef]
- Li, D.-S.; Fang, D.-N.; Jiang, N.; Xuefeng, Y., “Finite element modeling of mechanical properties of 3D five-directional rectangular braided composites,” Composites Part B: Engineering, vol. 42, no. 6, pp. 1373-1385, 2011/09/01/ 2011. [CrossRef]
- Grail, G.; Hirsekorn, M.; Wendling, A.; Hivet, G.; Hambli, R., “Consistent Finite Element mesh generation for meso-scale modeling of textile composites with preformed and compacted reinforcements,” Composites Part A: Applied Science and Manufacturing, vol. 55, pp. 143-151, 2013/12/01/ 2013. [CrossRef]
- Doitrand, A.; Fagiano, C.; Irisarri, F.X.; Hirsekorn, M., “Comparison between voxel and consistent meso-scale models of woven composites,” Composites Part A: Applied Science and Manufacturing, vol. 73, pp. 143-154, 2015/06/01/ 2015. [CrossRef]
- Badel, P.; Vidal-Sallé, E.; Maire, E.; Boisse, P., “Simulation and tomography analysis of textile composite reinforcement deformation at the mesoscopic scale,” Composites Science and Technology, vol. 68, no. 12, pp. 2433-2440, 2008/09/01/ 2008. [CrossRef]
- Durville, D., “Simulation of the mechanical behaviour of woven fabrics at the scale of fibers,” International Journal of Material Forming, vol. 3, no. 2, pp. 1241-1251, 2010/09/01 2010. [CrossRef]
- Grujicic, M.; Hariharan, A.; Pandurangan, B.; Yen, C.F.; Cheeseman, B.A.; Wang, Y.; Miao, Y.; Zheng, J.Q., “Fiber-Level Modeling of Dynamic Strength of Kevlar® KM2 Ballistic Fabric,” Journal of Materials Engineering and Performance, vol. 21, no. 7, pp. 1107-1119, 2012/07/01 2012. [CrossRef]
- Huang, L.; Wang, Y.; Miao, Y.; Swenson, D.; Ma, Y.; Yen, C.-F., “Dynamic relaxation approach with periodic boundary conditions in determining the 3-D woven textile micro-geometry,” Composite Structures, vol. 106, pp. 417-425, 2013/12/01/ 2013. [CrossRef]
- Zhou, G.; Sun, X.; Wang, Y., “Multi-chain digital element analysis in textile mechanics,” Composites Science and Technology, vol. 64, no. 2, pp. 239-244, 2004/02/01/ 2004. [CrossRef]
- Xiang, L.; Wang, H.Y.; Chen, Y.; Guan, Y.J.; Wang, Y.L.; Dai, L.H., “Modeling of multi-strand wire ropes subjected to axial tension and torsion loads,” International Journal of Solids and Structures, vol. 58, pp. 233-246, 2015/04/01/ 2015. [CrossRef]
- Zhang, D.; Ostoja-Starzewski, M., “Finite Element Solutions to the Bending Stiffness of a Single-Layered Helically Wound Cable With Internal Friction,” Journal of Applied Mechanics, vol. 83, no. 3, pp. 031003-031003-8, 2015. [CrossRef]
- Ghoreishi, S.R.; Cartraud, P.; Davies, P.; Messager, T., “Analytical modeling of synthetic fiber ropes subjected to axial loads. Part I: A new continuum model for multilayered fibrous structures,” International Journal of Solids and Structures, vol. 44, no. 9, pp. 2924-2942, 2007/05/01/ 2007. [CrossRef]
- Vu, T.D.; Durville, D.; Davies, P., “Finite element simulation of the mechanical behavior of synthetic braided ropes and validation on a tensile test,” International Journal of Solids and Structures, vol. 58, pp. 106-116, 2015/04/01/ 2015. [CrossRef]
- Stanova, E.; Fedorko, G.; Fabian, M.; Kmet, S., “Computer modelling of wire strands and ropes part II: Finite element-based applications,” Advances in Engineering Software, vol. 42, no. 6, pp. 322-331, 2011/06/01/ 2011. [CrossRef]
- Nawrocki, A.; Labrosse, M., “A finite element model for simple straight wire rope strands,” Computers & Structures, vol. 77, no. 4, pp. 345-359, 2000/07/07/ 2000. [CrossRef]
- PIA-C-2754C, ParachuteIndustryAssociation, 2011.
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W., “NIH Image to ImageJ: 25 years of image analysis,” Nature methods, vol. 9, no. 7, pp. 671-675, 2012.
- Barry, C.P.; Olson, B.G.; Willis, D.J.; Bergeron, K.; Charrette, C.; Noetscher, G.M.; Amirkhizi, A.; Sherwood, J.A., “The experimental characterization of the torsional and transverse stiffnesses of a braided parachute suspension line,” Journal of Engineered Fibers and Fabrics, vol. 19, p. 15589250241291167, 2024.
- Aktaş, B.; Narang, Y.S.; Vasios, N.; Bertoldi, K.; Howe, R.D., “A modeling framework for jamming structures,” Advanced Functional Materials, vol. 31, no. 16, p. 2007554, 2021.





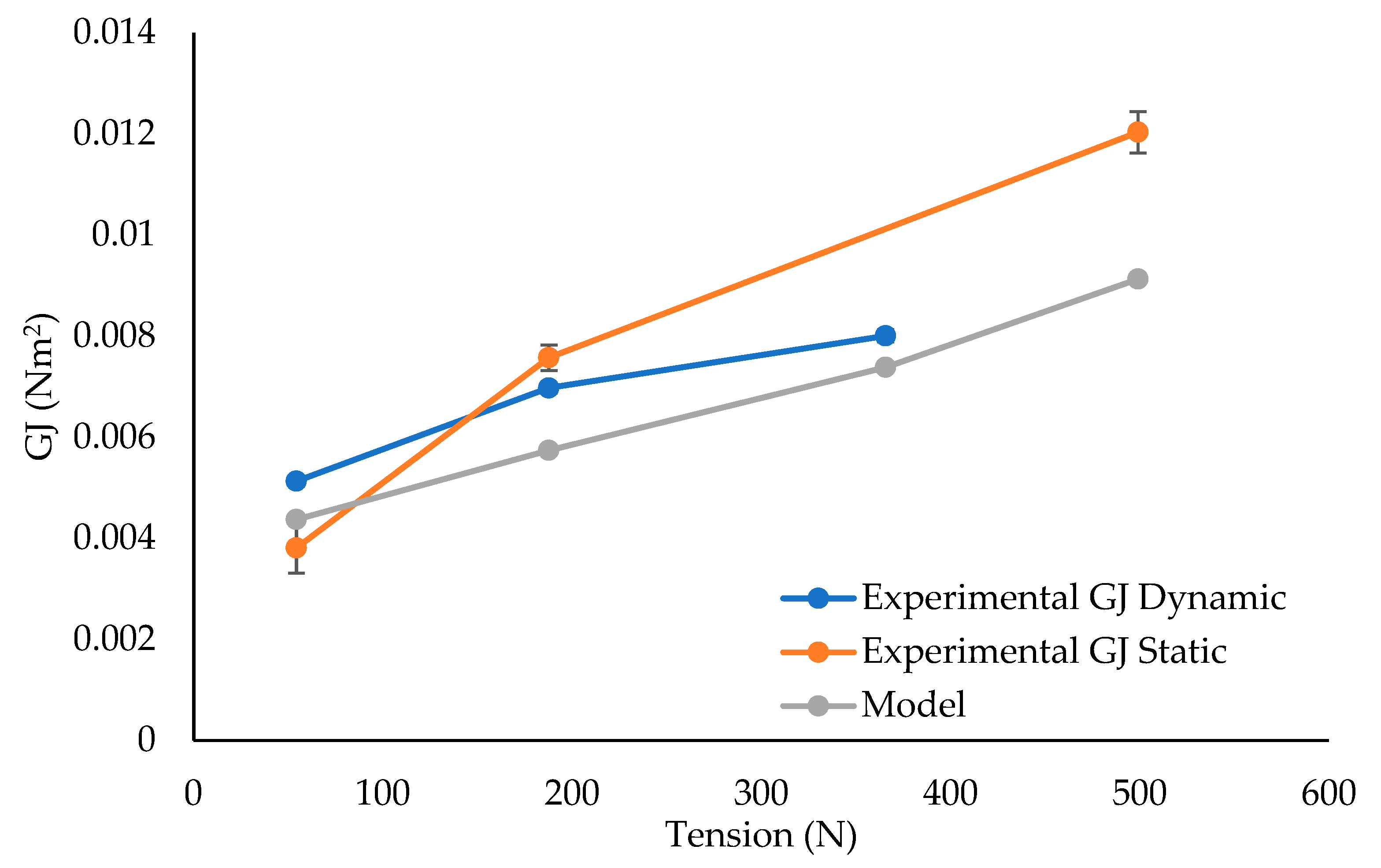
| Characteristic | PIA C 2754 Type II | |
|---|---|---|
| Number of carriers | 24 | |
| Ends per carrier | 3 | |
| Total ends | 72 | |
| Basic yarn denier | 1100 | |
| Yarn ply | Single | |
| Picks per inch | 10-12 | |
| Length per pound, feet (minimum) | 120 | |
| Breaking strength, pounds (minimum) | 1000 | |
| Elongation percent (at 75% of the specified breaking strength) | Minimum | 7 |
| Maximum | 11 | |
| Braid Parameter | Value |
|---|---|
| Tow Diameter | 1.57±0.12 mm |
| Braid Angle | 56.14±5.48o |
| Braid Diameter | 5.58 mm |
| σ < 30 MPa | σ > 30 MPa | All σ | ||||
|---|---|---|---|---|---|---|
| E1 (MPa) | 4,100 | E1 (MPa) | 3,200 | ν2 | 0.49 | |
| G12 (MPa) | 2,050 | G12 (MPa) | 1,600 | ν21 | 0 | |
| E2 (MPa) | 5,000 | E2 (MPa) | 5,000 | ν12 | 0 | |
| G2 (MPa) | 1,678 | G2 (MPa) | 1,678 | |||
| σ < 140 MPa | σ > 140 MPa | All σ | |||
|---|---|---|---|---|---|
| E1 (MPa) | 12,000 | E1 (MPa) | 3,200 | ν2 | 0.49 |
| G12 (MPa) | 6,000 | G12 (MPa) | 42,000 | ν21 | 0 |
| E2 (MPa) | 5,000 | E2 (MPa) | 100,000 | ν12 | 0 |
| G2 (MPa) | 1,678 | G2 (MPa) | 33,557 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





