Parallel Machine Scheduling Problem with Machine Rental Cost and Shared Service Cost

1. Introduction

Shared manufacturing, relying on new infrastructures such as 5G, artificial intelligence, the industrial Internet, and the Internet of Things, has quietly emerged and shown a booming development [1,2]. Shared manufacturing is the reuse of idle production capacity, which can optimize resource allocation, break information asymmetry, reduce manufacturing costs, expand effective supply, and enhance manufacturing service capabilities and levels [3]. As a result, shared manufacturing has become one of the key themes driving the high-quality and sustainable development of the manufacturing industry, aligning with the trend towards intelligent, efficient, and service-oriented economic development.

Under the impetus of development demands and policy support, many Chinese enterprises have achieved fruitful practices in implementing sharing systems. For example, the "Oscar COSMOPlat" has connected 900,000 enterprises, the INDICS platform has integrated over 1.7 million pieces of industrial equipment, and Tao Factory has enabled online collaboration for millions of factories and traders. In addition, there are also Mould Lao crowd creative space, Shugen Internet, China Aerospace Cloud Platform, Haichuanghui, and the Shenyang Machine Tool Sharing Platform, among others. However, the supply and demand configuration of enterprise resources under shared manufacturing still faces many new challenges. These are primarily reflected in the lack of effective guidance for enterprises in sharing both internal and external manufacturing resources. Additionally, there are ongoing issues with the full utilization of resources and the optimization of manufacturing costs [1]. China’s small and medium-sized manufacturing enterprises are characterized by their relatively small scale and limited investment. They are often at a disadvantage in terms of human and material resources. However, these enterprises are numerous and densely distributed. If external shared resources can be reasonably scheduled, it will effectively compensate for the shortage of manufacturing resources, thereby improving production efficiency, profitability, and customer satisfaction.

Production scheduling, as a crucial component of real-world production management, significantly impacts the production efficiency, cost, and competitiveness of enterprises [4,5]. However, most existing research on production scheduling focuses solely on the scheduling of enterprises’ own machines. In the context of shared manufacturing, optimizing the rental costs of shared machines while enhancing the production efficiency of small and medium-sized manufacturing enterprises with limited production capacity is essential. Formulating a rational and efficient machine renting and scheduling scheme is thus an urgent problem to be addressed. This paper investigates the offline scheduling problem of identical parallel machines, considering fixed rental costs, unit variable rental costs, and shared service costs. The objective is to minimize the sum of the maximum completion time (makespan) and the total shared costs. The study aims to provide a scientific basis for schedulers to make informed decisions regarding resource sharing and scheduling schemes. By doing so, it helps enterprises reduce sharing costs while improving production efficiency and customer satisfaction, ultimately promoting accurate and efficient matching of the supply and demand of manufacturing resources.

The main contributions of this work are as follows:

(1)

In the context of shared manufacturing, we incorporate shared machines with rental costs and shared service costs into the classic parallel machine scheduling problem. We investigate how machine sharing influences the production scheduling decisions of enterprises.

(2)

We establish an integer programming model, analyze the properties of the problem, and provide the optimal scheduling case without renting machines, the range of the number of machine rentals, and the upper bound of the problem.

(3)

We propose a heuristic algorithm based on the number of shared machine rentals to address large-scale instances of the considered problem.

The rest of this paper is organized as follows. Section 2 reviews the relevant papers in the literature. Section 3 describes the considered problem and constructs an integer programming model. Section 4 analyzes the properties of the problem. Section 5 proposes a heuristic algorithm. In Section 6, the experimental results, together with the sensitivity analysis, are presented. Finally, Section 7 concludes this work and suggests future research directions.

2. Literature Review

Manufacturing resource sharing offers new insights for optimizing resource allocation in the scheduling domain. Efficient resource utilization is closely tied to the rational design of sharing strategies and scheduling optimization. Existing related studies have analyzed the sharing strategies for various manufacturing resources, including processing capacity [6], multi-skilled human resources [7], orders [8], and information [9]. Since this paper primarily investigates the sharing and scheduling scheme of machine resources, this section focuses on reviewing studies related to the scheduling optimization of shared machine resources in detail. Additionally, this section also reviews the scheduling optimization research on the use costs of identical parallel machines, which is closely related to this paper.

2.1. Shared Machine Resource Scheduling Problem

Dereniowski and Kubiak [10,11] considered the preemptive job situation, assuming that each job could be executed on its private processor and simultaneously on possibly many processors shared. Their goal was to maximize the total weighted overlap of all jobs. Ji et al. [12] proposed a shared parallel machine scheduling model with machine processing set restrictions, aiming at minimizing the sum of makespan and total shared service cost. They proved that this problem is NP-hard and designed a fully polynomial-time approximation scheme. Wei and Wu [13] studied two two-machine hybrid flow-shop problems with fixed processing sequences in the context of shared manufacturing. Xu et al. [14] assumed that when a manufacturer with a certain number of parallel machines uses shared machines, it will obtain a certain proportion of shared benefits. They considered the time value of money and the due date-to-deadline window, with the objective of maximizing the total future value of profits. They designed a genetic algorithm and a heuristic algorithm. Zheng et al. [15] described a sharing platform as one parallel machine scheduling problem with machine-order type matching and order splitting. Their objective was to minimize the sum of the total processing cost of machines used and the total completion time of orders. They designed a Capability-Based Greedy heuristic and an improved Genetic Algorithm. Fu et al. [16] proposed a stochastic bi-objective two-stage open shop scheduling problem for shared professional equipment, aiming to minimize total tardiness and processing costs subject to various resource constraints. They designed a hybrid multiobjective migrating bird optimization combined with a genetic operation and a discrete event system. Xu et al. [17,18] studied the online scheduling optimization problem of shared parallel machines, considering the shared machine rental costs and discounts. They designed a competitive strategy.

2.2. Scheduling Problem with the Use Cost of Identical Parallel Machines

Ruiz-Torres et al. [19] assumed that machine costs consist of a fixed cost and a variable cost. For machine costs with concave functions, they derived general characteristics of optimal solutions regarding decisions on the number of machines to use and the way to load machines. Rustogi and Strusevich [20] assumed that the machine cost is a linear function of the number of machines used. They examined the impact of increasing the number of machines on both makespan and total flow time. Lee et al. [21] assumed that each job-machine combination may have a different cost. They studied two bi-criteria scheduling problems, proposed fast heuristics, and established the corresponding worst-case performance bounds. Li Kai et al. believed that each machine has a cost per unit of time that differs from machine to machine. They considered the problem of minimizing the makespan or the total completion time [22] and the problem of minimizing the maximum lateness [23]. Jiang et al. [24] assumed that each machine has a different constant processing cost per unit of time and designed corresponding approximation algorithms for two different production objectives. Anghinolfi et al. [25] considered the energy consumption rate and the time-of-use electricity prices of different machines. They designed an ad-hoc heuristic method to minimize both the makespan and the total energy consumption. Jarboui et al. [26] assumed that each machine has a fixed energy consumption rate and a positive energy price in each period. They explored the multiobjective problem of minimizing both the makespan and the total energy cost simultaneously and proposed an Epsilon Oscillation Algorithm. Wu et al. [27] considered the fixed usage cost of each machine. $\epsilon$-LO-MILP, $\epsilon$-LBBD, and NSGA-II are presented to solve the bi-objective scheduling problem of minimizing the maximum completion time and the total cost including machine usage cost and resource consumption cost.

Existing scheduling literature considering machine costs assumes that the machines have the same cost components and that the scheduling scope is limited to self-owned machines. However, there are only a few studies on shared machine resource scheduling that consider both own machines’ scheduling schemes and shared machines’ renting and scheduling schemes. The differences from this paper mainly include the cost components, optimization objectives, problem characteristics, and optimization methods. This paper focuses on the fixed rental cost, unit variable rental cost, and shared service cost associated with shared machines. The goal is to provide a scientific basis for the formulation of resource-sharing and optimized scheduling schemes for small and medium-sized manufacturing enterprises with insufficient production capacity, thereby promoting the sustainable development of manufacturing enterprises.

3. Problem Description

Consider a machine set $\mathcal{M}=\left\{Mi\right|i=1,2,\dots ,m+k\}$ consisting of $m+k$ parallel machines with the same processing speed. Here, $m\ge 2$ represents the number of machines owned by the manufacturer, and $k\ge 1$ denotes the number of shared machines that can be rented on the sharing platform. Let h be the number of shared machines actually rented. Given a set of jobs $\mathcal{J}=\left\{J_j\right|j=1,2,\dots ,n\}$, $p_j$ ($p_j>0$) denotes the processing time of job $J_j$. It is assumed that any job $J_j$ can be processed either on the manufacturer’s own machines or on a rented external machine. The manufacturer must pay a fixed rental cost a (e.g., preparation and cleaning costs of the shared machine) and a unit variable rental cost b for renting a shared machine $M_i$ ($m+1\le i\le m+k$). Specifically, the rental cost of the machine is $a+b{C}_i$, where $C_i$ represents the completion time of machine $M_i$. In addition, we consider the shared service cost $c_{ij}$ (e.g., transportation cost for raw materials or finished products, processing preparation cost, service cost, etc., collectively referred to as shared service cost) incurred when renting machine $M_i$ ($m+1\le i\le m+k$) to process job $J_j$. Here it is assumed that all shared parallel machines have the same fixed rental cost and unit variable rental cost. That is, for $\forall i\in [m+1,m+k]$, $a_i=a$, $b_i=b$. Meanwhile, we do not consider the existing sunk cost associated with the manufacturer’s own machines. Therefore, for $\forall i\in [1,m]$, $a_i=b_i=c_{ij}=0$.

Without loss of generality, some basic assumptions are made [25]: (1) Each job is assigned to only one selected machine for processing; (2) Each machine only processes one job at a time; (3) Preemption is not allowed.

Let $\sigma$ denote a feasible scheduling scheme. The problem is to find the optimal scheduling scheme ${\sigma }^{*}$ that minimizes the sum of the makespan and the total shared cost. The three-parameter representation of the problem can be expressed as $P_{m+k}\parallel C_{max}+\sum S_i$, where $P_{m+k}$, $C_{max}$, and $\sum S_i$ denote the identical parallel machine, the maximum completion time and the total shared cost (the sum of the total machine rental cost and the total shared service cost), respectively. If job $J_j$ is scheduled to be processed on machine $M_i$, let $x_{ij}=1$, otherwise, $x_{ij}=0$. If machine $M_i$ is used, let ${\alpha }_i=1$, otherwise, ${\alpha }_i=0$. Therefore, the shared cost of machine $M_i$ is $S_i=a_i{\alpha }_i+b_i{\sum }_{j=1}^n{p}_j{x}_{ij}+{\sum }_{j=1}^n{c}_{ij}{x}_{ij}$. When $\forall b_i=0$, the problem reduces to a scheduling problem considering only the fixed rental cost and the shared service cost of shared machines. When $\forall c_{ij}=0$, the problem reduces to a scheduling problem considering the fixed rental cost and the unit variable cost of shared machines. It can be seen that this problem is more general.

4. Model Formulation

In this section, we introduce the notations, formulate the mathematical model based on the fixed rental cost, unit variable rental cost, and shared service cost associated with the shared machines, and provide detailed explanations of the constraints.

4.1. Notations

The indices, parameters, and decision variables used in the model are defined as follows:

Indices:

i: the index of machines, $i=1,2,\dots ,m+k$;

j: the index of jobs, $j=1,2,\dots ,n$.

Parameters:

m: the number of own machines;

k: the number of shared machines;

n: the number of jobs;

$a_i$: the fixed rental cost, $a_i=a$ if machine $M_i$ ($i=m+1,m+2,\dots ,m+k$) is a shared machine, and $a_i=0$, otherwise;

$b_i$: the unit variable rental cost, $b_i=b$ if machine $M_i$ ($i=m+1,m+2,\dots ,m+k$) is a shared machine, and $b_i=0$, otherwise;

$p_j$: the processing time of job $J_j$, $j=1,2,\dots ,n$;

$c_{ij}$: the shared service cost, $c_{ij}>0$ if job $J_j$ is processed on shared machine $M_i$ ($i=m+1,m+2,\dots ,m+k$), and $c_i=0$, otherwise;

Decision variables

$C_{max}$: the makespan;

$S_i$: the shared cost of machine $M_i$;

${\alpha }_i$: binary variable, ${\alpha }_i=1$ when machine $M_i$ is used;

$x_{ij}$: binary variable, $x_{ij}=1$ when job $J_j$ is processed on machine $M_i$.

4.2. Mathematical Model

Based on the settings of the above parameters and variables, the established integer programming model is as follows:

$$minZ=C_{max}+\sum _{i=1}^{m+k}{S}_i$$

(1)

Subject to:

$$S_i=a_i{\alpha }_i+b_i\sum _{j=1}^n{p}_j{x}_{ij}+\sum _{j=1}^n{c}_{ij}{x}_{ij},i=1,\dots ,m+k$$

(2)

$$\sum _{i=1}^{m+k}{x}_{ij}=1,j=1,\dots ,n$$

(3)

$$\sum _{j=1}^n{p}_j{x}_{ij}\le C_{max},i=1,\dots ,m+k$$

(4)

$$x_{ij}\le {\alpha }_i,i=1,\dots ,m+k;j=1,\dots ,n$$

(5)

$$x_{ij}\in \{0,1\},{\alpha }_i\in \{0,1\},i=1,\dots ,m+k;j=1,\dots ,n$$

(6)

The objective function in Equation (1) aims to minimize the sum of the maximum completion time and the total shared cost over the planning time period. Constraint (2) indicates the shared cost of machine $M_i$. Constraint (3) ensures that each job must be scheduled on a certain machine. Constraint (4) indicates that the completion time of machine $M_i$ is not greater than the maximum completion time $C_{max}$. Constraint (5) establishes the relationship between variables ${\alpha }_i$ and $x_{ij}$, indicating that only the machines that are used will be assigned jobs. Constraint (6) specifies the value ranges of the decision variables.

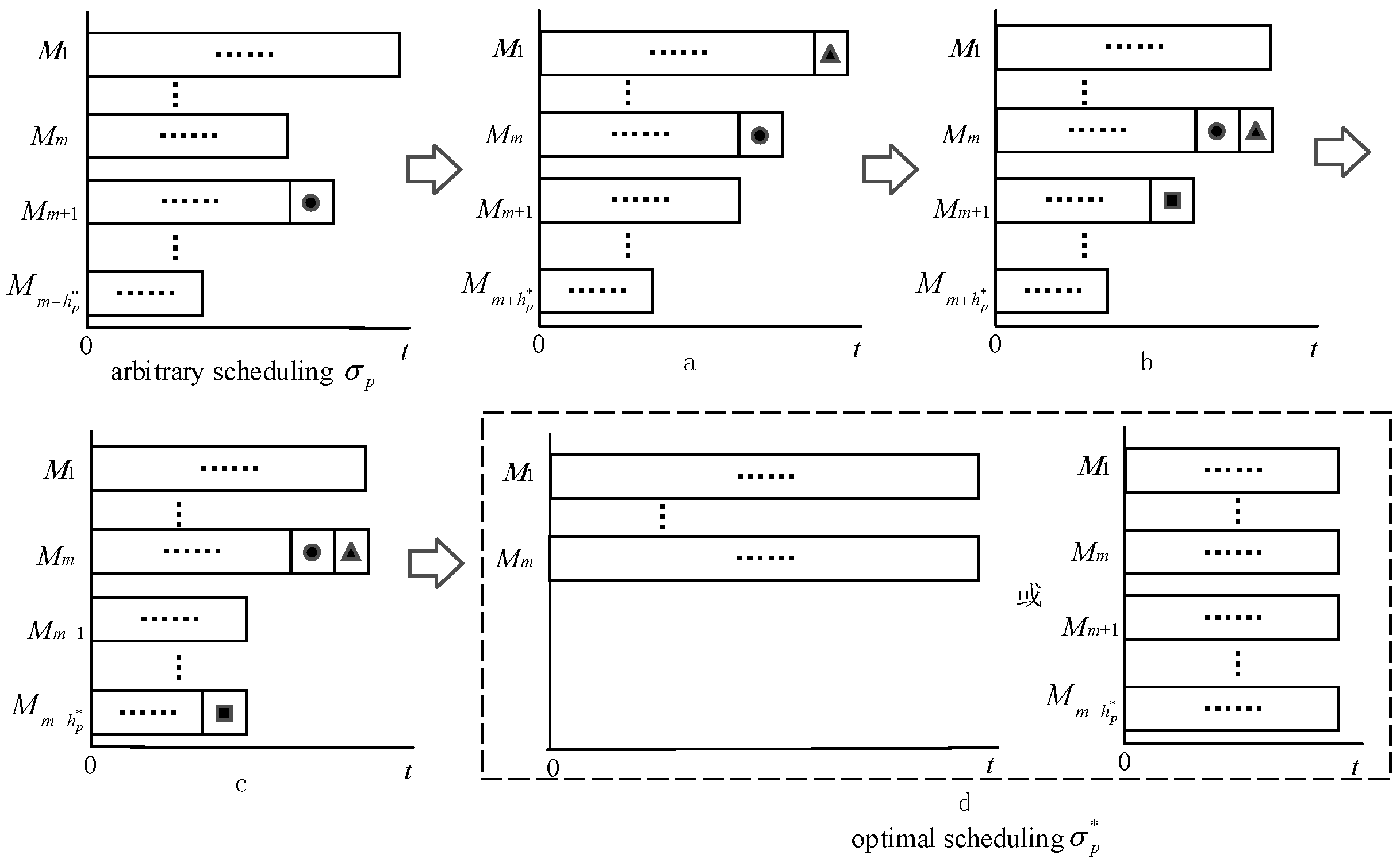
5. Problem property

In this section, some problem-specific properties are derived for in-depth understanding and solving the problem $P_{m+k}\parallel C_{max}+\sum S_i$.

When $a\to \infty$ or $a=0$, $b=0$, $\forall c_{ij}=0$, the problem simplifies to $P\parallel C_{max}$, which is known to be strong NP-hard [28]. Consequently, the problem $P_{m+k}\parallel C_{max}+\sum S_i$ is also a strong NP-hard problem. When $a=0$, the problem can be regarded as a special case of the problem discussed in the literature [12]. Therefore, we will focus on the case where $a>b\ge 0$ in the following discussion. When job $J_j$ is assigned to a shared machine $M_i$ ($m+1\le i\le m+k$) for processing, $C_{max}$ can decrease by at most $p_j$, while the rental cost will increase by at least $b{p}_j+c_{ij}$. If $b\ge 1$, the optimal scheduling would not involve renting the shared machine $M_i$. Hence, we will restrict our discussion to the case where $0\le b<1$.

Let $p_{max}={max}_{j=1}^n\left\{p_j\right\}$, $P={\sum }_{j=1}^n{p}_j$. For the problem $P\left|pmtn\right|C_{max}$, where $pmtn$ indicates that jobs are interruptible, McNaughton’s wrap-around rule [29] provides the optimal solution $C_{max}^{*}=max\{p_{max},P/m\}$. When jobs are non-interruptible, the optimal maximal completion time satisfies $C_{max}^{*}\ge p_{max}$ and $C_{max}^{*}\ge P/m$. Therefore, properties 1 and 2 can be readily derived. In Property 1, $\lceil P/p_{max}\rceil$ denotes the minimum number of machines required such that the maximum processing time of all jobs is greater than or equal to the average completion time of the machines. Consequently, when the number of owned machines is greater than or equal to this value, the optimal scheduling does not involve renting shared machines. When the fixed rental cost a of the shared machine is sufficiently large, the optimal scheduling also avoids renting machines. Property 2 specifies the value range of a in this scenario.

Property 1. 

For problem $P_{m+k}\parallel C_{max}+\sum S_i$, if $m\ge \lceil P/p_{max}\rceil$, then the optimal scheduling does not rent shared machines, and the optimal objective value is $p_{max}$.

Property 2. 

For problem $P_{m+k}\parallel C_{max}+\sum S_i$, if $a\ge \lfloor P/(m+1)\rfloor$, then the optimal scheduling does not rent shared machines.

As mentioned above, if job $J_j$ is assigned to the shared machine $M_i$ ($m+1\le i\le m+k$), $C_{max}$ will decrease by at most $p_j$, and the rental cost will increase by at least $b{p}_j+c_{ij}$. If $c_{ij}\ge (1-b)p_j$, then $b{p}_j+c_{ij}\ge p_j$, and the optimal scheduling will not rent the shared machine $M_i$ to process job $J_j$. Therefore, Property 3 can be obtained.

Property 3. 

For problem $P_{m+k}\parallel C_{max}+\sum S_i$, if $c_{ij}\ge (1-b)p_j$, the optimal scheduling will not assign job $J_j$ to the shared machine $M_i$ for processing.

Before arranging the processing sequence of jobs, it is necessary to first determine the number of rented machines. Property 4 provides a range of the possible number of machines to be rented for optimal scheduling.

Property 4. 

Let the optimal scheduling ${\sigma }^{*}$ rent $h^{*}$ machines, then $h^{*}$ satisfies:

(1) When $1-bm>0$, if $\sqrt{P(1-bm)/a}-m\le 0$, $h^{*}=0$, if $0<\sqrt{P(1-bm)/a}-m<k$, $h^{*}\le \lceil \sqrt{P(1-bm)/a}\rceil -m$, and if $\sqrt{P(1-bm)/a}-m\ge k$, $h^{*}\le k$.

(2) When $1-bm\le 0$, $h^{*}=0$.

In the research problem, the manufacturer decides whether to rent a machine based on actual conditions in order to reduce the maximum completion time of the jobs. Therefore, when renting a shared machine is not considered, the maximum completion time $C^{LPT}$ obtained by scheduling all jobs on the manufacturer’s own machines using the LPT rule is an upper bound of the problem, i.e. Property 5.

Property 5. 

For problem $P_{m+k}\parallel C_{max}+\sum S_i$, $Z^{*}\le C^{LPT}$, where $C^{LPT}$ is the maximum completion time obtained using the LPT rule on own machines.

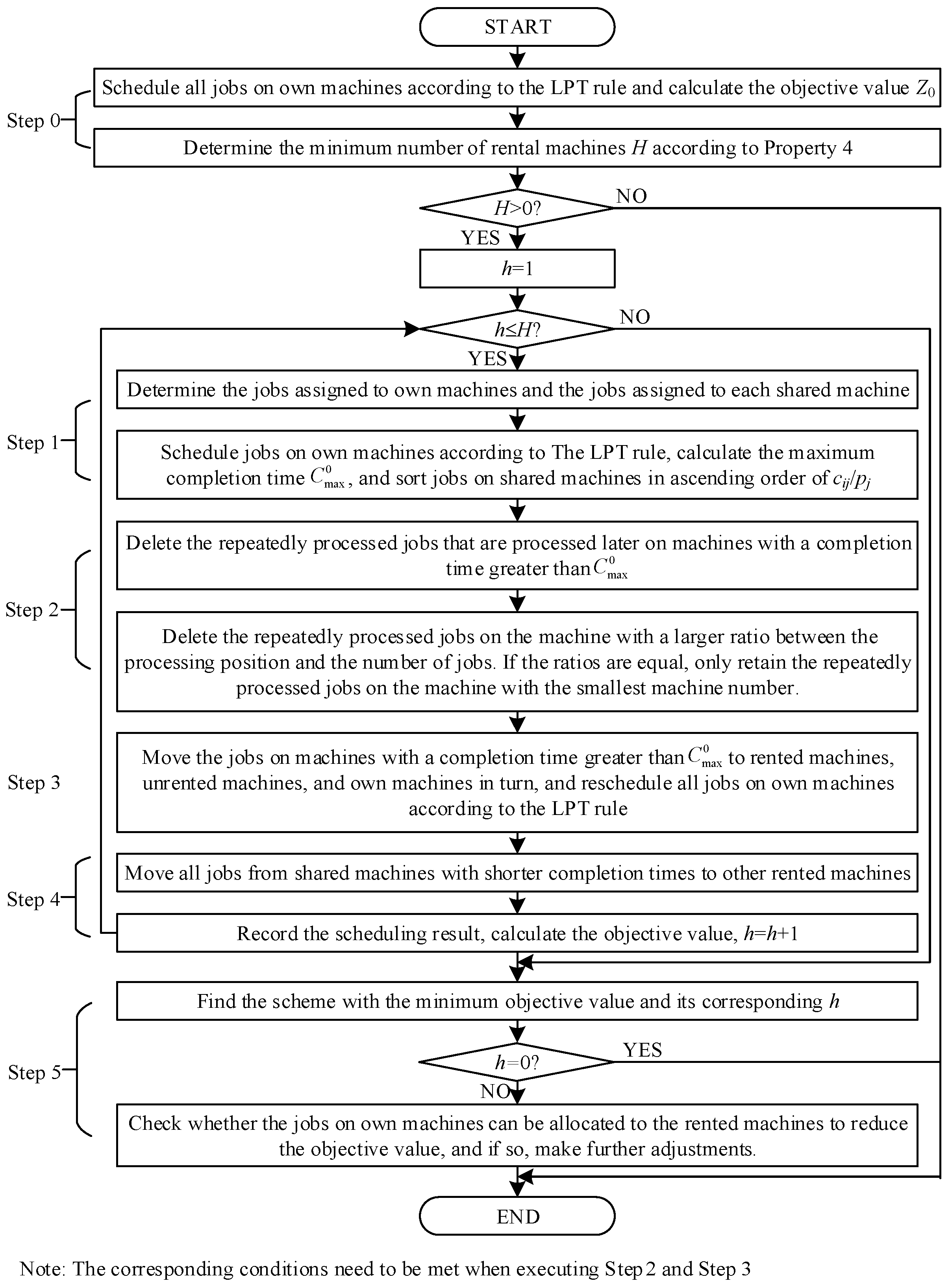
6. Solution Approach

Although the optimal solution can be obtained using mathematical programming models, the computation time may be excessively long, particularly for large-scale problems. To provide decision-makers with an efficient scheduling solution in a timely manner, this section designs a heuristic algorithm based on the number of shared machine rentals (Number of shared machine-dependent heuristic, NSMD-H). This algorithm builds upon the results of the problem property analysis. According to the properties discussed in Section 5, when $m\ge \lceil P/p_{max}\rceil$ or $a\ge \lfloor P/(m+1)\rfloor$ or $1-bm\le 0$ or $1-bm>0$ and $\sqrt{P(1-bm)/a}-m\le 0$, the optimal scheduling does not involve renting shared machines. At this time, the LPT rule is applied to schedule jobs on the manufacturer’s own machines, ensuring that $C^{LPT}\le ({\displaystyle \frac{4}{3}}-{\displaystyle \frac{1}{3m}})C_{max}^{*}$[30]. When none of the above four conditions hold, the heuristic algorithm NSMD-H is employed to solve the problem. If the LPT rule is still used to schedule jobs on the own machines, then the performance ratio is $Z\left(LPT\right)/Z^{*}=O(k/m)$. For example, consider a scenario with $n\to \infty$ jobs, each with a processing time of p, which can be processed on m own machines and k shared machines, where n is a multiple of m and $m+k$. Let $a\to 0$, $b=0$, and $\forall c_{ij}=0$. In this case, the performance ratio is given by: $Z\left(LPT\right)/Z^{*}=(np/m)/[(np/(m+k)+ak]=1+k/m$.

The main idea of the heuristic algorithm NSMD-H is to first determine the number of rented machines and then obtain the minimum value of the maximum completion time for the own machines. Based on this value and the ratio of service cost to job processing length, the algorithm determines which jobs should be assigned to the own machines and which to the shared machines. It then schedules and adjusts the jobs accordingly. Specifically, the algorithm proceeds as follows:

(1) Initial Scheduling: Schedule all jobs on the own machines using the LPT rule.

(2) Determine Number of Rented Machines: According to Property 4, determine the minimum number of rented machines H. If $H>0$, iterate over the number of rented machines h from 1 to H and perform the following steps for each h:

(i) Job Assignment: Determine the jobs assigned to the own machines and each shared machine. Schedule jobs on the own machines using the LPT rule, and sort jobs on the shared machines in non-decreasing order based on the ratio of service cost to job processing time.

(ii) Remove Duplicates: Eliminate any jobs that are scheduled multiple times on the shared machines to ensure each job is processed only once.

(iii) Adjust Shared Machine Jobs: For shared machines with completion times exceeding those of the own machines, adjust the job assignments to balance the load.

(iv) Optimize Machine Utilization: Adjust jobs on shared machines with lower completion times to minimize the number of rented machines and reduce the overall objective value.

(v) Reassignment Check: Evaluate whether jobs initially assigned to the own machines can be reassigned to rented shared machines to further reduce the objective value.

(vi) Output Results: Record the scheduling result and the corresponding objective value for each h.

(3) Select Optimal Solution: After completing the above steps for all possible values of h, select the scheduling scheme with the smallest objective value as the final result of the algorithm.

The execution flow of NSMD-H is illustrated in Figure 1. The specific algorithm is described as follows:

Step 0 Assign all jobs to own machines according to the LPT rule to obtain the initial schedule ${\sigma }_0$ and the target value $Z_0$. According to Property 4, if $\sqrt{P(1-bm)/a}-m\le 0$, then let $H=0$. If $0<\sqrt{P(1-bm)/a}-m<k$, then set $H=\lceil \sqrt{P(1-bm)/a}-m\rceil$. If $\sqrt{P(1-bm)/a}-m\ge k$, then set $H=k$. If $H>0$, then for each h from 1 to H, execute Steps 1 to 4 in sequence. Otherwise, proceed to Step 5.

Step 1 Sort the jobs in non-increasing order based on $\underset{i\in \{m+1,\dots ,m+k\}}{\min }{c}_{ij}/p_j$. Select the jobs sequentially until the sum of the processing times of the selected jobs exceeds $Pm/(m+h)$, and assign these selected jobs to own machines. Then, assign the jobs that satisfy $\underset{i\in \{m+1,\dots ,m+k\}}{\min }{c}_{ij}\ge (1-b)p_j$ to own machines according to Property 3. The jobs of own machines are scheduled according to the LPT rule, and the maximum completion time $C_{max}^0$ is calculated. The jobs on shared machines are sorted in non-decreasing order according to $c_{ij}/p_j$, and the completion times of these machines are calculated. Let the set of completion times for the shared machines be $\mathcal{CI}=\{C_{m+1},\dots ,C_{m+k}\}$. If there are jobs that are processed repeatedly on the shared machines, run Step 2. Otherwise, obtain the feasible schedule ${\sigma }_h$ and determine whether there is a value greater than $C_{max}^0$ in $\mathcal{CI}$, if so, run Step 3, otherwise, run Step 4.

Step 2 Delete the repeatedly processed jobs, which mainly involves the following two steps:

Step 2.1 Let the set of repeatedly processed jobs on the shared machines be denoted by ${\mathcal{J}}_r$, and let $\mathcal{CI}’=\mathcal{CI}$. If $max\{\mathcal{CI}’\}>C_{max}^0$, determine whether there are any repeatedly processed jobs on the machine with a completion time equal to $max\{\mathcal{CI}’\}$. If so, delete the job with the largest processing position among the repeatedly processed jobs, update $\mathcal{CI}$, $\mathcal{CI}’$, and ${\mathcal{J}}_r$. If not, set the completion time of the corresponding machine in $\mathcal{CI}’$ equal to 0, and repeat this step until $max\{\mathcal{CI}’\}\le C_{max}^0$.

Step 2.2 If ${\mathcal{J}}_r\ne \varnothing$, for each repeatedly processed job, retain only the instance on the machine with the smallest ratio of the job processing position to the number of jobs. If multiple machines have equal ratios, retain the job on the machine with the smallest machine number and delete the repeatedly processed jobs on the remaining machines. Sort the jobs on the shared machines by $c_{ij}/p_j$ in a non-decreasing order, update $\mathcal{CI}$, and obtain the schedule ${\sigma }_h$. If $max\left\{\mathcal{CI}\right\}>C_{max}^0$, run Step 3, otherwise, run Step 4.

Step 3 Let $M_I$ be the shared machine with a completion time equal to $max\left\{\mathcal{CI}\right\}$. If there are already rented machines with completion times less than $C_{max}^0$ (denoted by the set $\overline{\mathcal{M}}$ ), proceed to Step 3.1. Then, if $C_I>C_{max}^0$, and there are unrented machines (denoted by the set ${\mathcal{M}}_0$), and $k-|{\mathcal{M}}_0|<h$, let the number of machines that need to be rented be $h_0=min\{\lceil (C_I-C_{max}^0)/C_{max}^0\rceil ,h-(k-|{\mathcal{M}}_0\left|\right)\}$, and run Step 3.2. Then, if $C_I>C_{max}^0$, proceed to Step 3.3. Repeat this step until $max\left\{\mathcal{CI}\right\}\le C_{max}^0$.

Step 3.1 Adjust the jobs on $M_I$ in sequence. For example, consider the job $J_g$ on $M_I$. Sort the machines in $\overline{\mathcal{M}}$ according to $c_{ig}$ (where $i\in \overline{\mathcal{M}}$) in non-decreasing order, and determine whether $J_g$ can be moved to each machine for processing in sequence. For instance, consider $M_l$ in $\overline{\mathcal{M}}$. If $J_g$ is moved to $M_l$, the following conditions must be satisfied: (1) $c_{lg}-c_{Ig}\le z$ (where $z=p_g$ if $max\left\{\mathcal{CI}\right\}-C_{max}^0\ge p_g$, and $z=max\left\{\mathcal{CI}\right\}-C_{max}^0$ otherwise); (2) $C_l\le C_{max}^0$; (3) $c_{lg}<(1-b)p_g$. If all these conditions are met, move $J_g$ to $M_l$, update $\mathcal{CI}$ and ${\sigma }_h$, and do not consider other adjustable machines after $M_l$. If $C_I\le C_{max}^0$, there is no need to adjust any other jobs on $M_I$ after $J_g$.

Step 3.2 If $(C_I-C_{max}^0)/C_{max}^0\ge 1$, set $D=C_{max}^0$, otherwise, set $D=C_I-C_{max}^0$. Each machine in ${\mathcal{M}}_0$ performs the following operations in sequence. For example, consider machine $M_q$ in ${\mathcal{M}}_0$: The jobs on $M_I$ are sorted by $c_{qj}/p_j$ in non-decreasing order, and the processing times of the jobs that satisfy $c_{qj}<(1-b)p_j$ are added in sequence. When the cumulative sum of the jobs’ processing times $SP$ is greater than D, stop the summation. Let ${\mathcal{J}}_q$ be the set of jobs whose processing times are summed. If $C_I-SP\ge C_{max}^0$, set $W_q=SP-(a+\Delta c)$, otherwise, set $W_q=(C_I-SP)-(a+\Delta c)$, where $\Delta c$ represents the increase in service cost after adjusting the job. After all machines in ${\mathcal{M}}_0$ complete these operations, obtain the sets $\mathcal{W}$ and $\mathcal{J}$. If $max\left\{\mathcal{W}\right\}\ge 0$, identify the machine $M_u$ corresponding to $max\left\{\mathcal{W}\right\}$. Move the jobs in ${\mathcal{J}}_u$ from $M_I$ to $M_u$, update $\mathcal{CI}$, ${\mathcal{M}}_0$, and ${\sigma }_h$. Perform the above operation $h_0$ times.

Step 3.3 The jobs on $M_I$ are sorted in non-increasing order based on $c_{Ij}/p_j$ and are assigned sequentially to own machines. When the sum of the processing times of the assigned jobs exceeds $m(C_I-C_{max}^0)/(m+1)$, no further jobs from $M_I$ are assigned to own machines. Update $\mathcal{CI}$, schedule the jobs on own machines according to the LPT rule, and update $C_{max}^0$ and ${\sigma }_h$.

Step 4 Let the set of rented machines be ${\mathcal{M}}_1$, and initialize $\sigma {’}_h={\sigma }_h$ and $\mathcal{CI}’=\mathcal{CI}$. If ${\mathcal{M}}_1\ne ⌀$, identify the machine with the smallest completion time in ${\mathcal{M}}_1$ as $M_s$, with completion time $C_s$. If $C_s>\left(\right|{\mathcal{M}}_1|-1)C_{max}^0-(\sum _{i\in {\mathcal{M}}_1}{C}_i-C_s)$, run Step 5. Otherwise, adjust the jobs on $M_s$ in $\sigma {’}_h$ as follows. For example, consider a job $J_G$ on $M_s$. Sort the machines in ${\mathcal{M}}_1\setminus \left\{M_s\right\}$ according to $c_{iG}$ in non-decreasing order. Initialize $loop=0$. Determine if $J_G$ can be moved to them for processing in sequence. Take the machine $M_L$ in ${\mathcal{M}}_1\setminus \left\{M_s\right\}$ as an example. If moving $J_G$ to $M_L$ satisfies both $C_L+p_G\le C_{max}^0$ and $c_{LG}<(1-b)p_G$, then move $J_G$ to $M_L$. Calculate the increase in service cost $\Delta c$. Set $loop=1$, update $\mathcal{CI}’$ and $\sigma {’}_h$. No further machines need to be considered after $M_L$. If $loop=0$, set $\sigma {’}_h={\sigma }_h$, $\mathcal{CI}’=\mathcal{CI}$. No further jobs need to be judged after $J_G$. If $a-\sum \Delta c>0$, set ${\sigma }_h=\sigma {’}_h$, $\mathcal{CI}=\mathcal{CI}’$, otherwise, set $\sigma {’}_h={\sigma }_h$, $\mathcal{CI}’=\mathcal{CI}$. Remove $M_s$ from ${\mathcal{M}}_1$${\mathcal{M}}_1={\mathcal{M}}_1\setminus \left\{M_s\right\}$, repeat the above operations until ${\mathcal{M}}_1=⌀$. Finally, calculate the target value $Z_h$ for ${\sigma }_h$.

Step 5 Select the scheduling scheme with the minimum objective value and perform local adjustments to further optimize it.

Step 5.1 Select the scheduling $\sigma$ and h corresponding to the minimum objective value from $Z_0$ and $Z=\{Z_1,Z_2,\dots ,Z_H\}$. If $h=0$, then $\sigma ={\sigma }_0$ is the scheduling result of the algorithm, with the objective value being $Z_0$. Otherwise, let the completion time of all machines be $\mathcal{C}=\{C_1,\dots ,C_{m+k}\}$, set $c_{ij}^{\prime }=c_{ij}$, let ${\mathcal{M}}_1$ be the set of rented machines, and let ${\mathcal{J}}_0$ be the set of jobs on own machines.

Step 5.2 Find the machine $M_{i^{\prime }}$ and the job $J_{j^{\prime }}$ that correspond to $\underset{i\in {\mathcal{M}}_1,j\in {\mathcal{J}}_0}{min}{c}_{ij}^{\prime }$. If assigning job $J_{j^{\prime }}$ to the machine $M_{i^{\prime }}$ and sorting the jobs on own machines according to the LPT rule results in a decrease in the objective value, then perform this operation and update $\mathcal{C}$ and ${\mathcal{J}}_0$. Otherwise, set $c_{i^{\prime }{j}^{\prime }}^{\prime }=\sum p_j$. Repeat Step 5.2 until $\forall c_{i^{\prime }{j}^{\prime }}^{\prime }=\sum p_j$, $i^{\prime }\in {\mathcal{M}}_1$, $j^{\prime }\in {\mathcal{J}}_0$ or the maximum completion time of the shared machines is greater than or equal to the maximum completion time of the own machines.

In this heuristic algorithm, the computation times of Step 0 and Step 1 are $O(nlogn)$. The computation time of Step 2 is $O\left(nk\right)$. The computation times of Step 3.1, Step 3.2, and Step 3.3 are $O\left(nk\right)$, $O\left(n{k}^2\right)$, and $O(nlogn)$, respectively. Since Step 3.1 to Step 3.3 are executed at most k times, the computation time of Step 3 is $max\{O\left(n{k}^3\right),O(knlogn)\}$. The computation times of Step 4 and Step 5 are $O\left(n{k}^2\right)$ and $O\left(nk\right)$, respectively. Since Step 1 to Step 4 are executed at most k times, the computation time complexity of NSMD-H is $max\{O\left(n{k}^4\right),O(k^{2}nlogn)\}$.

7. Computation Experiments

This section analyzes the performance of the proposed NSMD-H algorithm through numerical experiments. The mathematical programming model and the algorithm are coded on Matlab R2014a and executed on a personal computer (Intel Core i7-8550U, 8GB memory, Windows 10 64 bit). CPLEX12.5 is employed to solve the integer programming model accurately. The calculation time limit of CPLEX is set to 7200 seconds (s). The following will introduce data generation, experimental results, and analysis in sequence.

The test cases are randomly generated, and the case scale is shown in Table 1.

For the above cases, CPLEX, NSMD-H, and a Genetic Algorithm (GA) are used to solve the problem, and the LPT rule is used to schedule jobs on own machines. The results obtained from these methods are compared and analyzed. The GA algorithm in this section is based on the work in [14], which shares similarities with this paper by considering jobs on both own and external machines. The GA algorithm from [14] is known for its high computational accuracy. Therefore, the GA algorithm in this section adopts the same individual gene coding representation, mutation operator, and selection operator as in [14]. However, extensive experiments have shown that the single-point crossover operator used in [14] is not well-suited for this problem. Consequently, the GA algorithm in this section employs a two-point crossover operator, specifically for the second half of the parent chromosome. Additionally, the scheduling result obtained from the NSMD-H algorithm is transformed into a chromosome to form part of the initial population for the GA algorithm. An elite retention strategy is also implemented to preserve the individual with the highest fitness after each iteration.

A total of 51 sets of experiments are conducted, varying the number of machines, job sizes, and the values of the fixed rental cost a and the unit variable cost b of shared machines. The specific results for small-scale and large-scale cases are presented in Table 2 and Table 3 respectively. Sensitivity analysis is performed on a and b to assess their impact on the experimental results. This analysis examines how changes in a and b (while keeping other parameters constant) affected the outcomes, using the control variable method. The experimental results are shown in Table 4. The columns Z, $CPU$, and h record the objective value, calculation time (in seconds), and the number of rented machines of each method, respectively. For the GA, the results shown are the average values obtained from five runs. The relative error gap between the algorithm’s objective value and the optimal value is calculated as $gap=(Z-Z^{*})/Z^{*}\times 100\%$. Since the calculation time for scheduling jobs on own machines using the LPT rule was consistently less than 0.01 seconds across all cases, the calculation time for LPT is not listed in the tables.

Analyzing Table 2 and Table 3 the following conclusions can be drawn:

(1)

When the number of jobs and machines is small, CPLEX can accurately solve the problem. However, as the scale of the problem increases, its computation time tends to rise significantly, ranging from 0.65s to 7200s. When the number of jobs and machines is large, CPLEX becomes unstable in terms of computational efficiency. In some cases, CPLEX is unable to provide an accurate solution and corresponding scheduling scheme within two hours. For example, this occurs when there are 200 jobs, 6 own machines, 10 shared machines, and 800 jobs in total.

(2)

The NSMD-H algorithm demonstrates a short computation time, even for large-scale cases with 800 jobs, 10 own machines, and 10 shared machines, with a running time of only 2.02 seconds. In terms of computational accuracy, the NSMD-H algorithm performs well. The gap between the objective value obtained by the NSMD-H algorithm and the optimal value obtained by CPLEX ranges from 0.04% to 7.5%. The average gap values for small-scale and large-scale cases are 2.76% and 1.53%, respectively. The difference between the number of rented machines of the NSMD-H algorithm and the number of rented machines of optimal scheduling is not significant. The maximum difference observed is 2 machines. This indicates that the objective value is influenced not only by the number of rented machines but also by the scheduling arrangement of jobs.

(3)

The computation time of the GA algorithm gradually increases from 6.43s to 25.15s, indicating relatively high running efficiency. However, compared to the NSMD-H algorithm, the GA algorithm does not significantly improve solution quality. The average gap values of small-scale and large-scale cases are 1.88% and 1.50%, respectively. Additionally, the number of shared machines rented by the GA algorithm is consistent with that of the NSMD-H algorithm. The primary reason for this is that the quality of solutions generated by the GA algorithm through random chromosome initialization differs significantly from that of the NSMD-H algorithm. Consequently, the better solutions obtained during GA iterations are mostly local adjustments to the solutions initially obtained by the NSMD-H algorithm. This results in minimal changes to the objective value. Therefore, the GA algorithm, while increasing computation time, does not significantly enhance the quality of solutions obtained by the NSMD-H algorithm.

(4)

The LPT rule, which schedules jobs only on own machines without considering rented machines, has a very low computation time (no more than 0.01 seconds). However, it deviates significantly from optimal scheduling. In some cases, the maximum deviation reaches 95.25%.

The following conclusions can be drawn from analyzing Table 4:

(1)

When other parameters remain unchanged, an increase in the fixed rental cost a leads to a higher objective value and a gradual decrease in the number of shared machines rented. The same trend is observed for the unit variable rental cost b.

(2)

The conclusions drawn from analyzing Tables 2 and 3 are consistent. CPLEX exhibits significant variability in computational efficiency, with computation times ranging from 1.75 seconds to 7200 seconds. The values of parameters a and b have a substantial impact on CPLEX’s computational time, with no discernible pattern.

(3)

The NSMD-H and GA algorithms demonstrate high computational efficiency, unaffected by the values of a and b. The average computational times are 0.27 seconds and 10.22 seconds, respectively. Both algorithms achieve higher computational accuracy, with average deviations of 2.84% and 2.12%, respectively.

(4)

All jobs are scheduled on own machines using the LPT rule. The objective value is independent of the values of a and b. However, the deviation from the optimal value is significant, particularly in cases where the shared machine rental cost is low and the optimal number of rented machines is high(e.g., the 1st and 10th cases in the table). As previously noted, when parameters n, a, b, and $c_{ij}$ take extreme values, the deviation becomes unbounded.

In summary, the NSMD-H and GA algorithms are effective in solving the problem, maintaining high computational accuracy and solution efficiency even as the problem size increases. While both algorithms achieve similar levels of computational accuracy, the NSMD-H algorithm demonstrates superior computational efficiency, meeting the dual requirements of solution quality and computational speed necessary for practical production environments.

The primary motivation for studying this machine-sharing scheduling problem is to provide a theoretical foundation for enterprise managers to make informed decisions regarding the rental of shared machines and the arrangement of job production schedules. Through mathematical modeling, property analysis, algorithm design, and problem-solving, the following management insights are offered to assist enterprise decision-makers:

(1)

The rental and scheduling results of machines are influenced by multiple factors. Enterprises should comprehensively consider their own production conditions (such as the number of own machines), the characteristics of jobs to be processed (including the number of jobs and their processing times), the production goals of the enterprise, and the costs associated with shared machines (fixed rental costs, unit variable costs, shared service costs).

(2)

Enterprises can utilize the proposed model and algorithm to determine the number of shared machines to be rented and to arrange the order of jobs on their own machines and shared machines. This approach helps reduce the maximum completion time of jobs (i.e., customer waiting time) while optimizing the enterprise’s shared costs. For small-scale problems, the model can be used to obtain exact solutions. For large-scale problems, the proposed algorithm can efficiently generate near-optimal solutions to support decision-making.

8. Conclusions

This paper examines an offline scheduling problem for identical parallel machines, incorporating the practical scenario of renting shared machines in manufacturing enterprises. Manufacturers with a certain number of machines can rent additional shared machines to process jobs. However, they must incur fixed rental costs, unit variable rental costs, and shared service costs associated with both jobs and machines. The optimization objective is to minimize the sum of the makespan and the total shared cost. To address this problem, an integer programming model is first developed. Subsequently, the optimal scheduling without renting machines and the range of optimal rental quantities when renting machines are analyzed. Based on the problem’s properties, the NSMD-H algorithm is proposed. Data experiments confirm that the proposed model can accurately solve small-scale cases, while the NSMD-H algorithm can quickly obtain near-optimal solutions for both small-scale and large-scale cases.

Future research directions may include (i) designing heuristics that can solve the problem more efficiently; (ii) considering more practical conditions, such as various rental discounts and multi-resource sharing; (iii) investigating scheduling problems where jobs are processed on shared machines of different machine types (e.g., uniform parallel machines, unrelated parallel machines, etc.); and (iv) studying the problem with other objective functions, such as scheduling problems with durations (maximum delay time, delay time, number of late jobs, etc.), or multi-objective functions.