Submitted:
17 February 2025
Posted:
18 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Design and Simulation
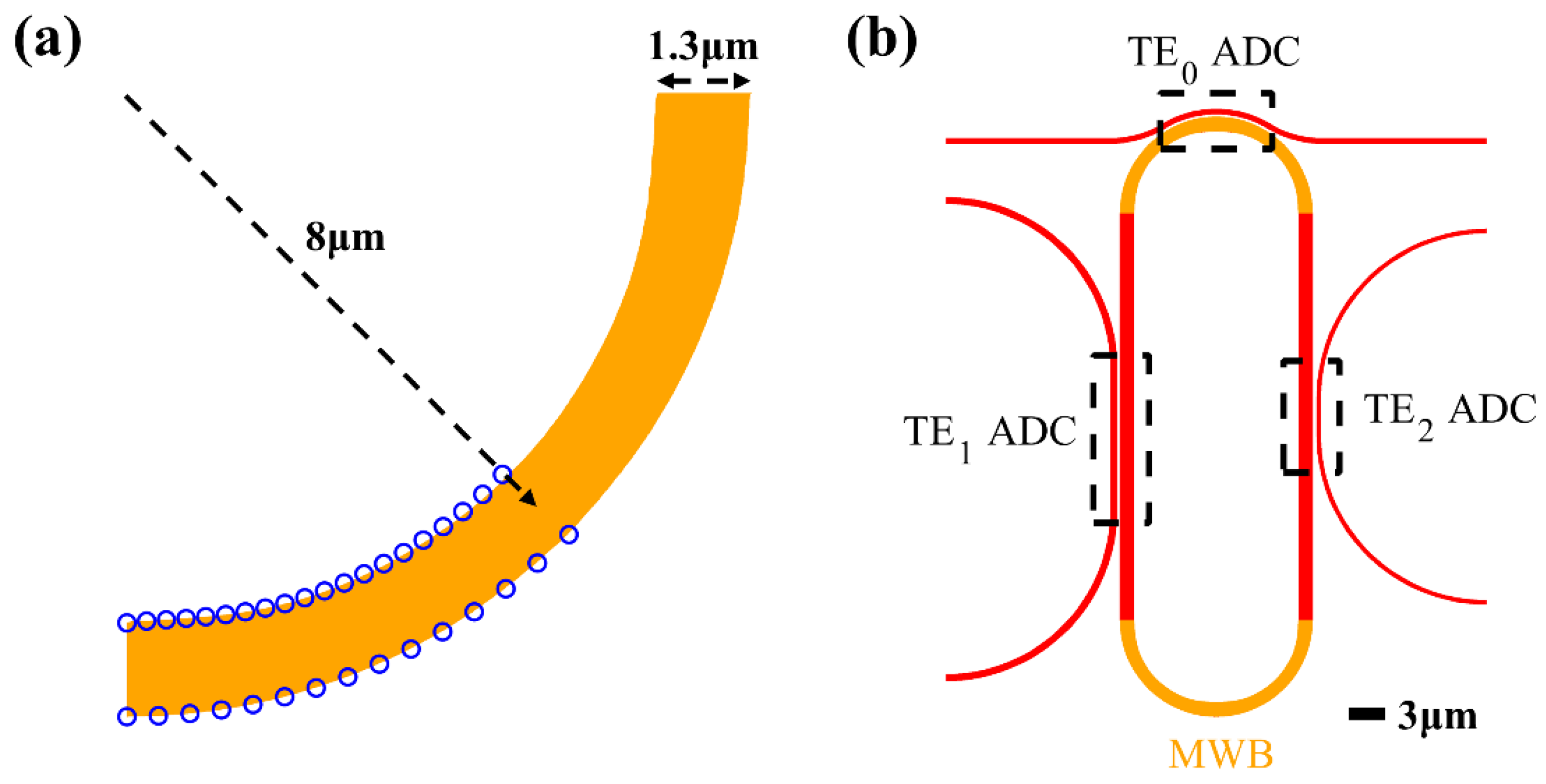
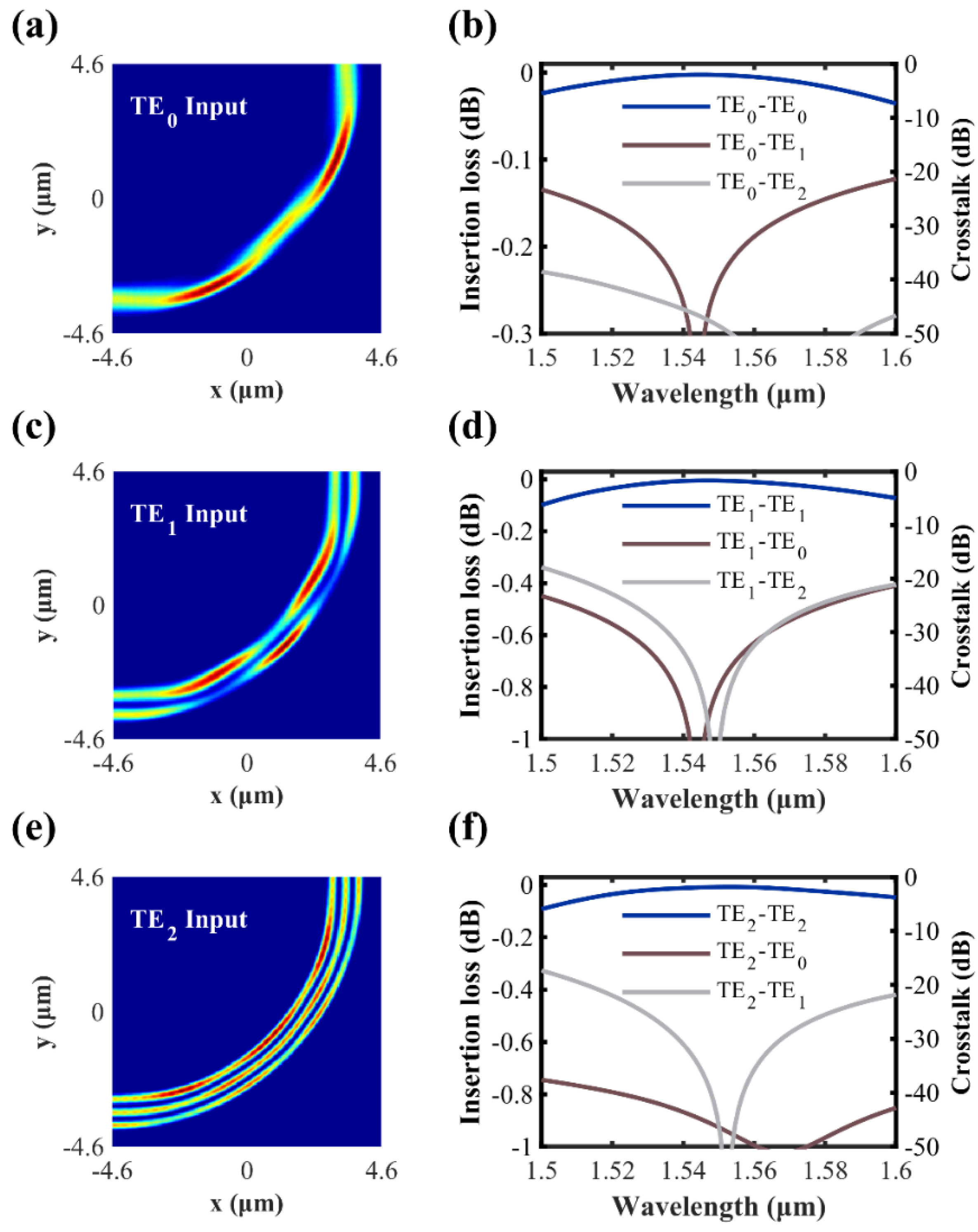
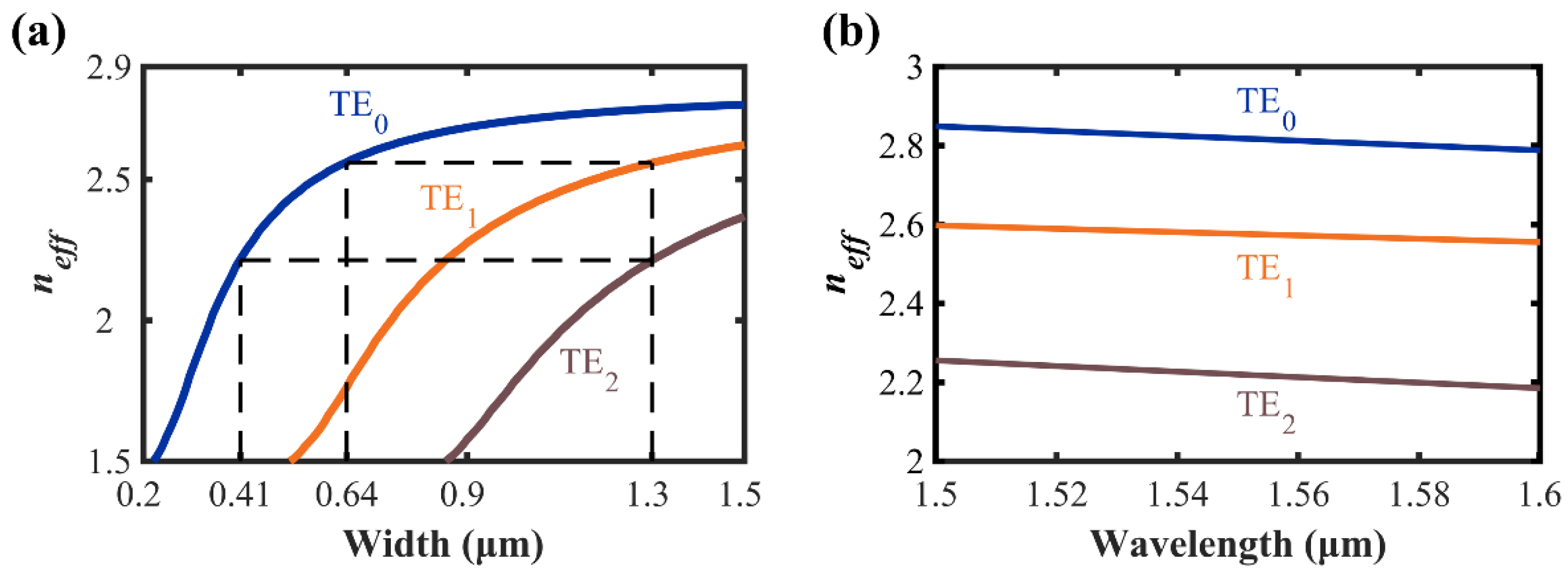
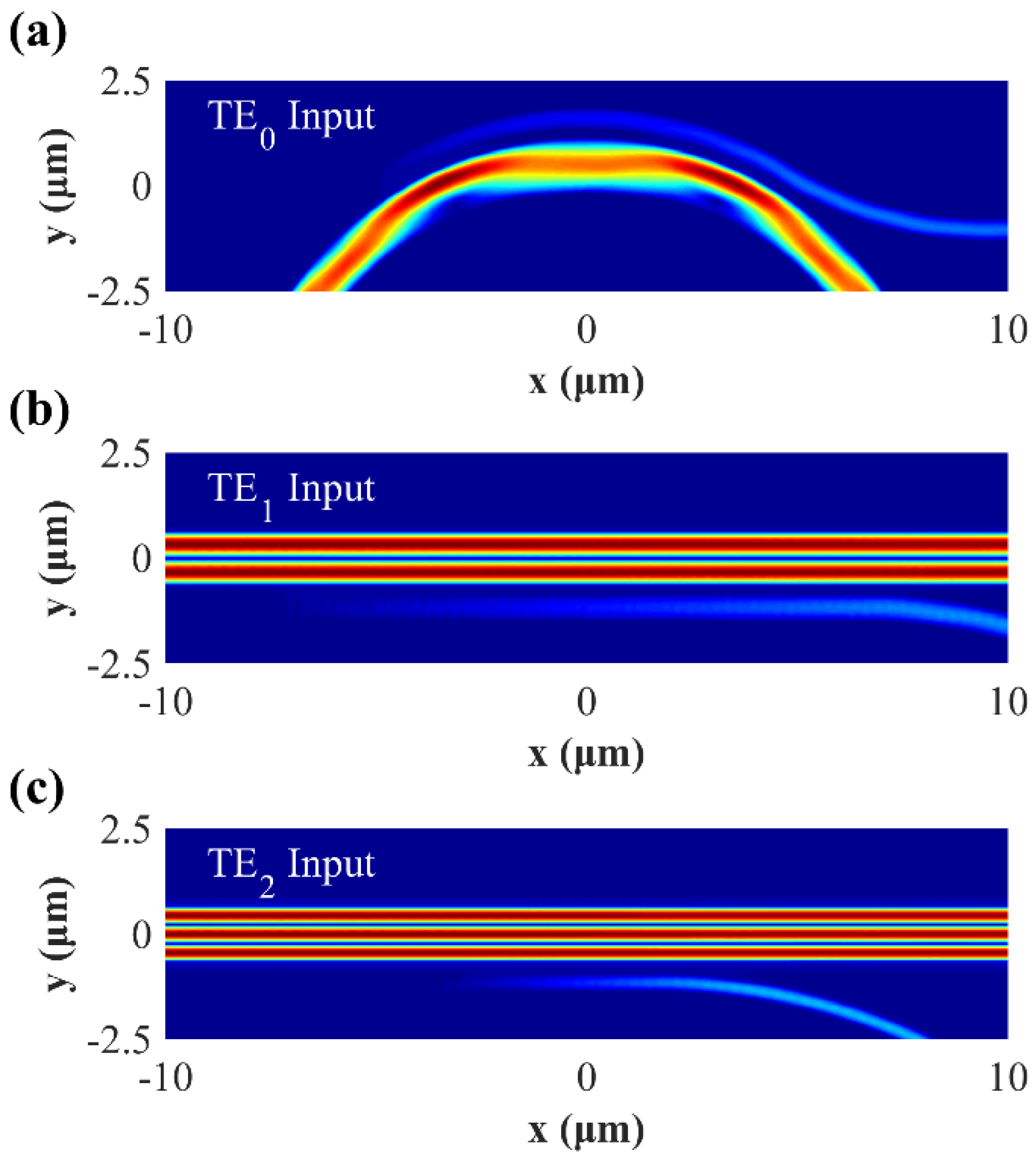
2.1. The Design of Multimode Waveguide Bend (MWB)
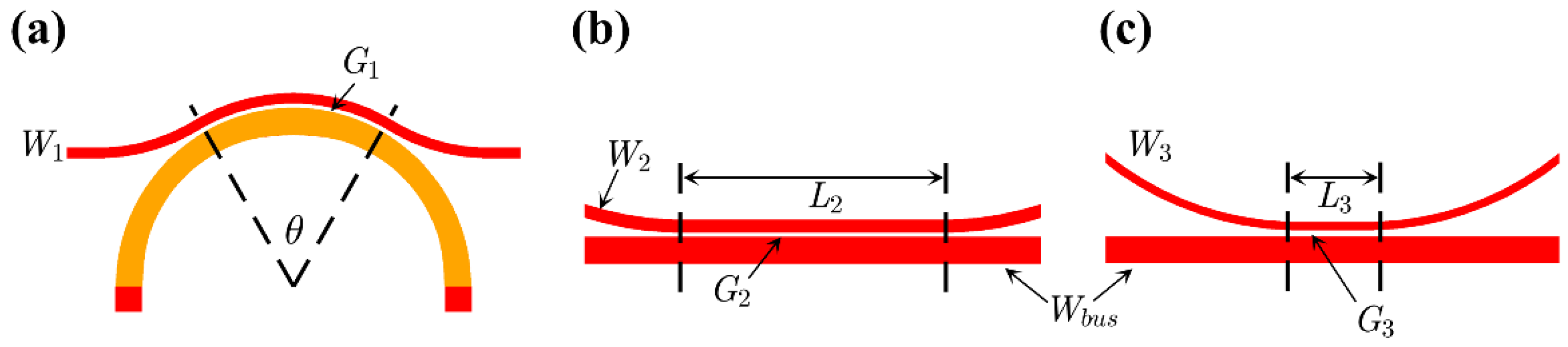
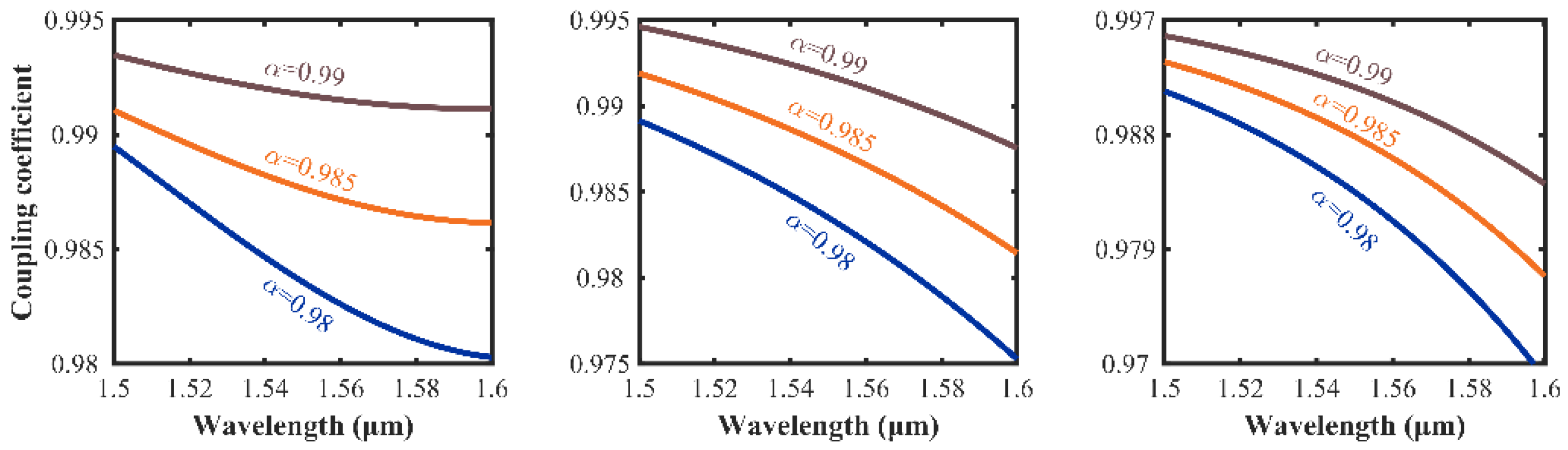
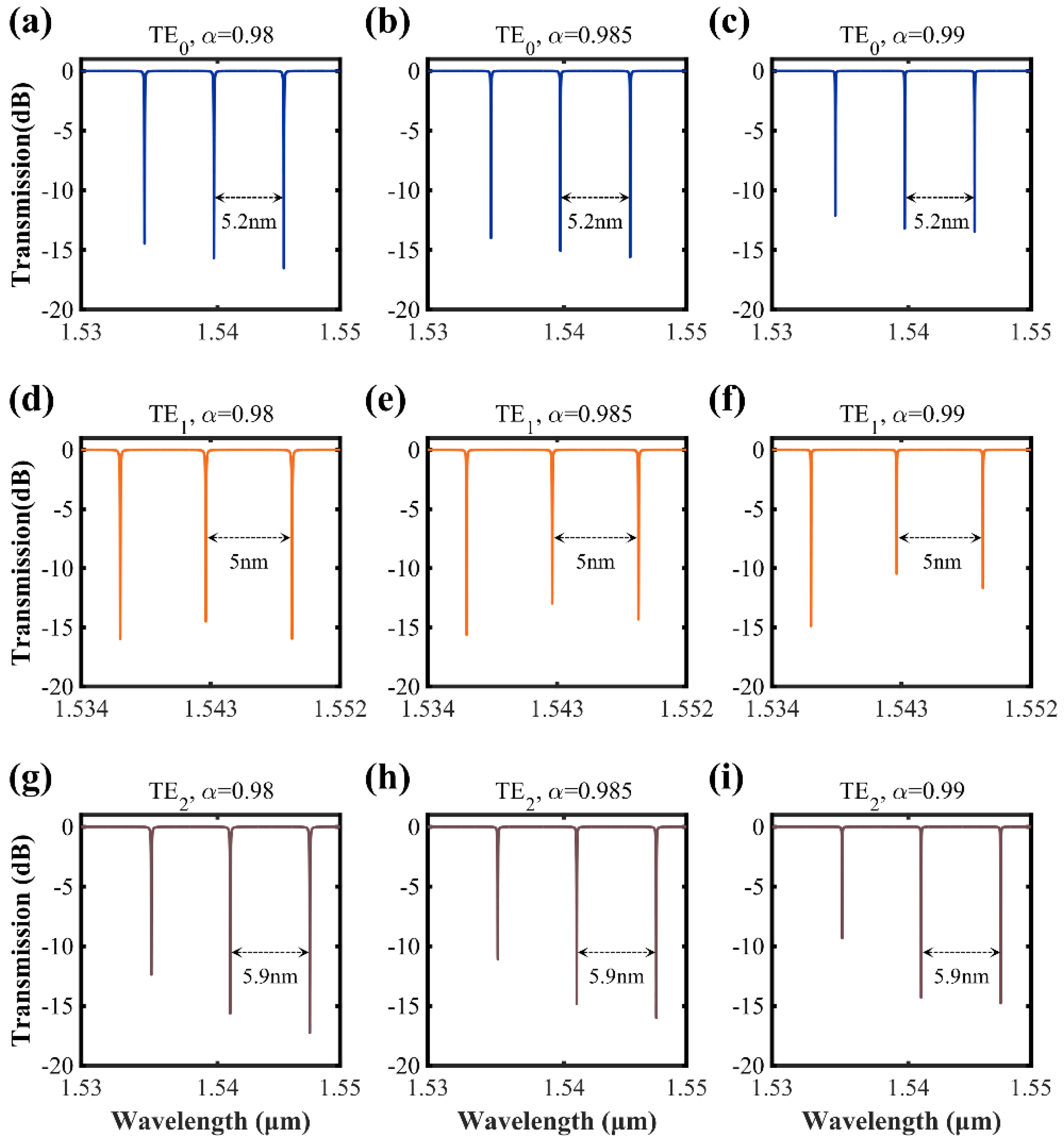
2.1. The Design of Multimode Microring Resonator (MMRR)
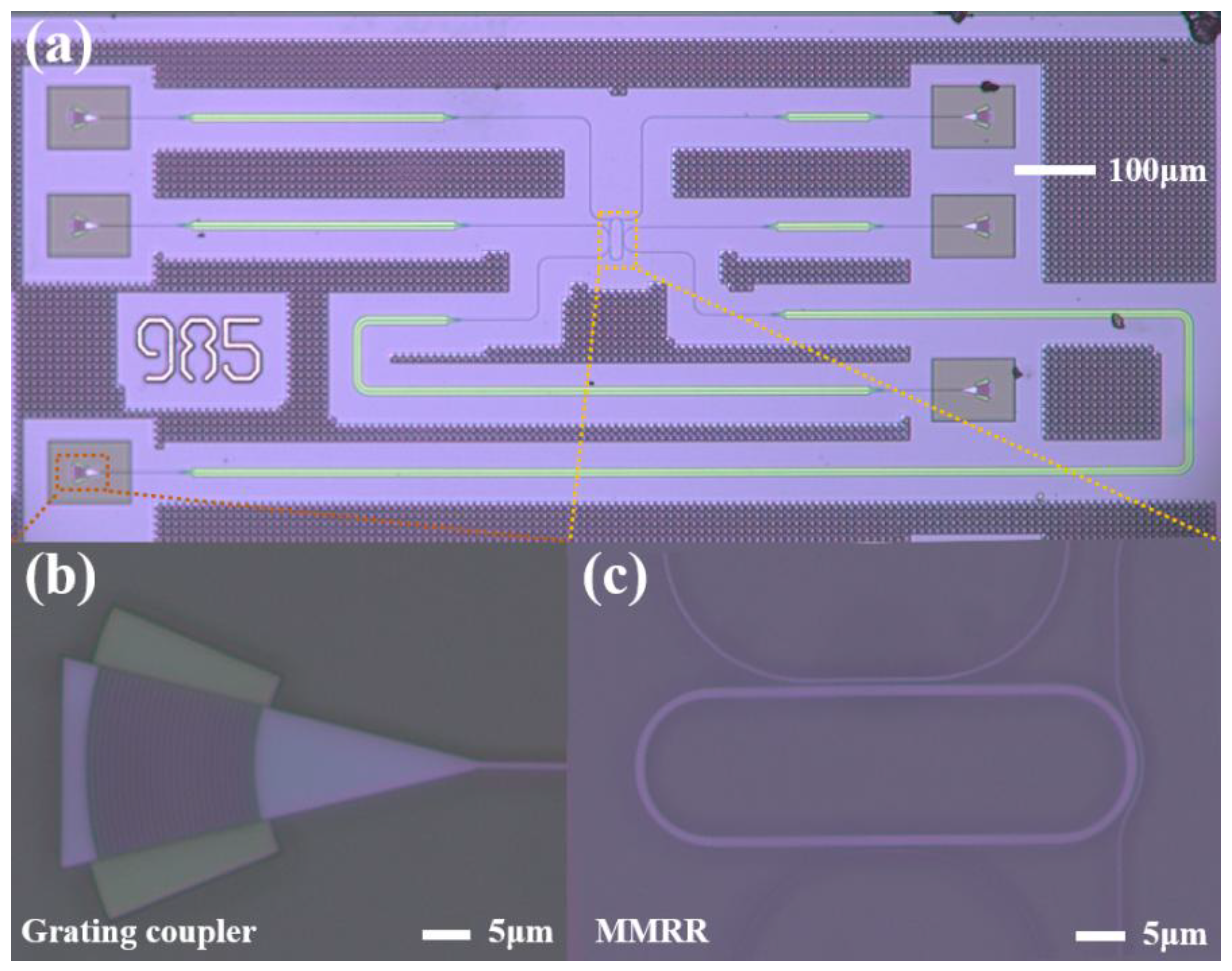
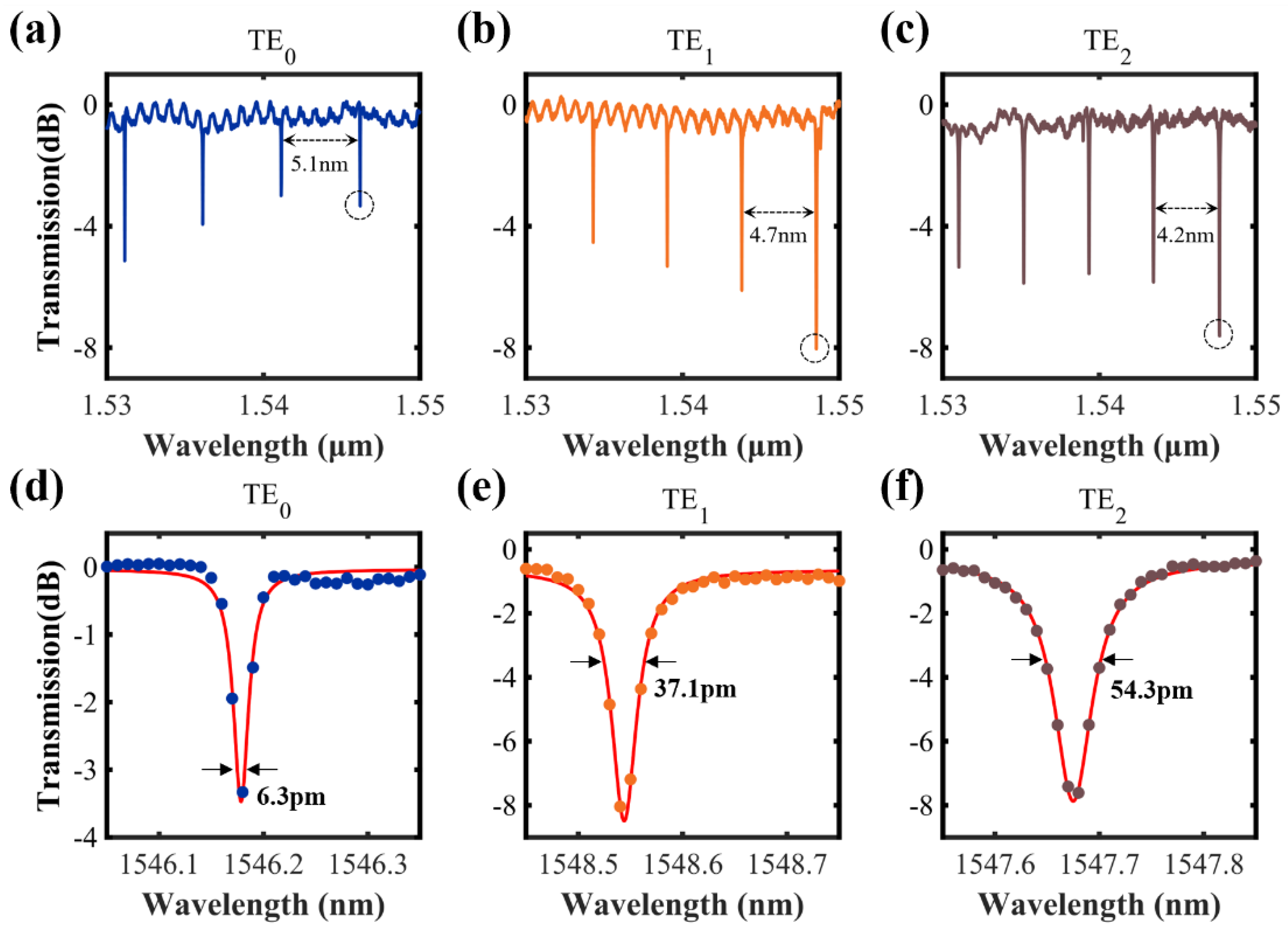
3. Fabrication and Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMRR | multimode microring resonator |
| MWB | multimode waveguide bend |
| ADC | asymmetric directional coupler |
| FSR | free spectral range |
| MDM | mode division multiplexing |
| SWG | subwavelength grating |
| IL | insertion loss |
| TIR | total internal reflection |
| SOI | silicon-on-insulator |
| FOM | figure-of-merit |
| FDTD | finite-difference time-domain |
| ER | extinction ratio |
References
- Yao, J.; Capmany, J. Microwave Photonics. Sci. China Inf. Sci. 2022, 65, 221401. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated Microwave Photonics. Nature Photon 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Zhang, J.; Liu, J.; Wang, L.; Chen, D.; Chi, N.; Xiao, X.; Yu, S. 240 Gb/s Optical Transmission Based on an Ultrafast Silicon Microring Modulator. Photon. Res. 2022, 10, 1127. [Google Scholar] [CrossRef]
- Yuan, Y.; Peng, Y.; Sorin, W.V.; Cheung, S.; Huang, Z.; Liang, D.; Fiorentino, M.; Beausoleil, R.G. A 5 × 200 Gbps Microring Modulator Silicon Chip Empowered by Two-Segment Z-Shape Junctions. Nat Commun 2024, 15, 918. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Zhao, Y.; Zhang, L.; Chen, Q.; Ding, J.; Fu, X.; Yang, L. 5-Port Optical Router Based on Si Microring Optical Switches for Photonic Networks-on-Chip. IEEE Photon. Technol. Lett. 2016, 1–1. [Google Scholar] [CrossRef]
- Liu, S.; Huo, Y.; Cheng, C.; Niu, J.; Fu, X.; Yang, L. Ultra-Compact On-Chip Silicon Photonic Polarization- and Wavelength-Selective Switch. Journal of Lightwave Technology 2024, 42, 8793–8801. [Google Scholar] [CrossRef]
- Tao, Z.; Tao, Y.; Jin, M.; Qin, J.; Chen, R.; Shen, B.; Wu, Y.; Shu, H.; Yu, S.; Wang, X. Highly Reconfigurable Silicon Integrated Microwave Photonic Filter towards Next-Generation Wireless Communication. Photon. Res. 2023, 11, 682. [Google Scholar] [CrossRef]
- Yan, H.; Xie, Y.; Zhang, L.; Dai, D. Wideband-Tunable on-Chip Microwave Photonic Filter with Ultrahigh- Q U-Bend-Mach–Zehnder-Interferometer-Coupled Microring Resonators. Laser & Photonics Reviews 2023, 2300347. [Google Scholar] [CrossRef]
- Zhao, W.; Peng, Y.; Cao, X.; Zhao, S.; Liu, R.; Wei, Y.; Liu, D.; Yi, X.; Han, S.; Wan, Y.; et al. 96-Channel on-Chip Reconfigurable Optical Add-Drop Multiplexer for Multidimensional Multiplexing Systems. Nanophotonics 2022, 11, 4299–4313. [Google Scholar] [CrossRef]
- James, A.; Novick, A.; Rizzo, A.; Parsons, R.; Jang, K.; Hattink, M.; Bergman, K. Scaling Comb-Driven Resonator-Based DWDM Silicon Photonic Links to Multi-Tb/s in the Multi-FSR Regime. Optica 2023, 10, 832. [Google Scholar] [CrossRef]
- Yi, X.; Zhao, W.; Li, C.; Zhang, L.; Xiang, Y.; Liu, C.; Shi, Y.; Liu, L.; Dai, D. Reconfigurable Optical Add-Drop Multiplexers for Hybrid Mode-/Wavelength-Division-Multiplexing Systems. Adv. Photon. Nexus 2023, 2. [Google Scholar] [CrossRef]
- Mojaver, K.R.; Safaee, S.M.R.; Morrison, S.S.; Liboiron-Ladouceur, O. Recent Advancements in Mode Division Multiplexing for Communication and Computation in Silicon Photonics. Journal of Lightwave Technology 2024, 42, 7860–7870. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode Silicon Photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Wu, X.; Huang, C.; Xu, K.; Shu, C.; Tsang, H.K. Mode-Division Multiplexing for Silicon Photonic Network-on-Chip. J. Lightwave Technol. 2017, 35, 3223–3228. [Google Scholar] [CrossRef]
- Dai, D.; Li, C.; Wang, S.; Wu, H.; Shi, Y.; Wu, Z.; Gao, S.; Dai, T.; Yu, H.; Tsang, H. 10-Channel Mode (de)Multiplexer with Dual Polarizations. Laser & Photonics Reviews 2018, 12, 1700109. [Google Scholar] [CrossRef]
- Zhao, W.; Yi, X.; Peng, Y.; Zhang, L.; Chen, H.; Dai, D. Silicon Multimode Waveguide Crossing Based on Anisotropic Subwavelength Gratings. Laser & Photonics Reviews 2022, 16, 2100623. [Google Scholar] [CrossRef]
- Chang, W.; Zhang, M. Silicon-Based Multimode Waveguide Crossings. J. Phys. Photonics 2020, 2, 022002. [Google Scholar] [CrossRef]
- Liu, R.; Lu, L.; Zhang, P.; Chang, W.; Liu, D.; Zhang, M. Integrated Dual-Mode 3-dB Power Splitter Based on Multimode Interference Coupler. IEEE Photon. Technol. Lett. 2020, 32, 883–886. [Google Scholar] [CrossRef]
- Fu, X.; Yang, S.; Niu, J.; Zhang, G.; Jia, H.; Yang, L. Carrier Depletion High-Speed Tunable Dual-Mode Converter for Mode-Division Multiplexing Networks. IEEE Photon. Technol. Lett. 2022, 34, 1242–1245. [Google Scholar] [CrossRef]
- Sun, S.; Fu, Y.; Li, S.; Ning, X.; Zhou, Z.; Zhang, D.; Wang, X. Ultra-Broadband Multimode Fiber-to-Chip Edge Coupler Based on Periodically Segmented Waveguides. Opt. Lett. 2024, 49, 6061. [Google Scholar] [CrossRef]
- Zhang, R.; Li, X.; He, Y.; Chen, G.; Xiong, L.; Chen, H.; Fontaine, N.K.; Zhang, Y.; Xie, W.; Su, Y. Ultra-High Bandwidth Density and Power Efficiency Chip-To-Chip Multimode Transmission through a Rectangular Core Few-Mode Fiber. Laser & Photonics Reviews 2023, 2200750. [Google Scholar] [CrossRef]
- Tan, J.; Xiao, H.; Ma, M.; Zhou, X.; Yuan, M.; Dubey, A.; Boes, A.; Nguyen, T.G.; Ren, G.; Su, Y.; et al. Arbitrary Access to Optical Carriers in Silicon Photonic Mode/Wavelength Hybrid Division Multiplexing Circuits. Opt. Lett. 2022, 47, 3531. [Google Scholar] [CrossRef]
- Jia, H.; Fu, X.; Zhou, T.; Zhang, L.; Yang, S.; Yang, L. Mode-Selective Modulation by Silicon Microring Resonators and Mode Multiplexers for on-Chip Optical Interconnect. Opt. Express 2019, 27, 2915. [Google Scholar] [CrossRef]
- Cai, L.; Gao, D.; Dong, J.; Hou, J.; Yang, C.; Chen, S.; Zhang, X. Compact and High Q-Factor Multimode Racetrack Ring Resonator Based on Transformation Optics. Opt. Express 2022, 30, 15766. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, M.; Zhang, L.; Zhang, Q. Compact Mode-Insensitive Ring Resonator Based on SWG Coupler and Euler Bends. In Proceedings of the AOPC 2021: Micro-optics and MOEMS; SPIE, November 24 2021; Vol. 12066; pp. 144–149. [Google Scholar]
- Ye, M.; Sun, C.; Yu, Y.; Ding, Y.; Zhang, X. Silicon Integrated Multi-Mode Ring Resonator. Nanophotonics 2021, 10, 1265–1272. [Google Scholar] [CrossRef]
- Yang, S.; Jia, H.; Niu, J.; Fu, X.; Yang, L. CMOS-Compatible Ultra-Compact Silicon Multimode Waveguide Bend Based on Inverse Design Method. Optics Communications 2022, 523, 128733. [Google Scholar] [CrossRef]
- Dou, T.; Yue, S.; Hou, Y.; Wang, R.; Shi, H.; Li, Y.; Feng, Y.; Zhang, Z. Ultra-Sharp Multimode Waveguide Bends Based on Superellipse Curves and Shallowly Etched Nanoslots Designed by an Intelligent Algorithm. J. Light. Technol. 2024, 42, 5249–5261. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Zhu, M.; Dai, D.; Shi, Y. Ultra-Compact Multimode Waveguide Bend With Optimized Dual Bezier Contours. IEEE Photon. Technol. Lett. 2023, 35, 1131–1134. [Google Scholar] [CrossRef]
- Liao, J.; Tian, Y.; Yang, Z.; Xu, H.; Dai, T.; Zhang, X.; Kang, Z. Broadband and Compact Silicon Multimode Waveguide Bends Based on Hybrid Shape Optimization. Journal of Lightwave Technology 2024, 42, 4882–4891. [Google Scholar] [CrossRef]
- Zhang, E.; Yang, S.; Zhang, L. General Waveguide Bend Design Based on Cubic Spline Interpolation and Inverse Design. J. Light. Technol. 2024, 42, 4614–4625. [Google Scholar] [CrossRef]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint Shape Optimization Applied to Electromagnetic Design. Opt. Express 2013, 21, 21693. [Google Scholar] [CrossRef]
- Georgieva, N.K.; Glavic, S.; Bakr, M.H.; Bandler, J.W. Feasible Adjoint Sensitivity Technique for EM Design Optimization. IEEE Transactions on Microwave Theory and Techniques 2002, 50, 2751–2758. [Google Scholar] [CrossRef]
- Cheng, C.; Yang, S.; Liu, W.; Liu, S.; Huo, Y.; Fu, X.; Yang, L. Ultra-Compact Inverse Designed Multimode Waveguide Bend Based on Levelset Method. IEEE Photonics Technology Letters 2024, 36, 571–574. [Google Scholar] [CrossRef]
- Discrete Global Optimization Algorithms for the Inverse Design of Silicon Photonics Devices. Photonics and Nanostructures - Fundamentals and Applications 2022, 52, 101072. [CrossRef]
- Chen, H.; Su, G.; Fu, X.; Yang, L. Ultra-Broadband and Compact 2 × 2 3-dB Silicon Adiabatic Coupler Based on Supermode-Injected Adjoint Shape Optimization. Photonics 2023, 10, 1311. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-Mode Theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Novel Ultra-Short and Ultra-Broadband Polarization Beam Splitter Based on a Bent Directional Coupler. Opt. Express, OE 2011, 19, 18614–18620. [Google Scholar] [CrossRef]
- McKinnon, W.R.; Xu, D.X.; Storey, C.; Post, E.; Densmore, A.; Delâge, A.; Waldron, P.; Schmid, J.H.; Janz, S. Extracting Coupling and Loss Coefficients from a Ring Resonator. Opt. Express 2009, 17, 18971. [Google Scholar] [CrossRef]
| α | θ (degree) | (μm) | (μm) |
|---|---|---|---|
| 0.98 | 62.57 | 12.74 | 3.27 |
| 0.985 | 51.4 | 10.57 | 2.3 |
| 0.99 | 42.86 | 8.03 | 1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




