Submitted:
11 February 2025
Posted:
13 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
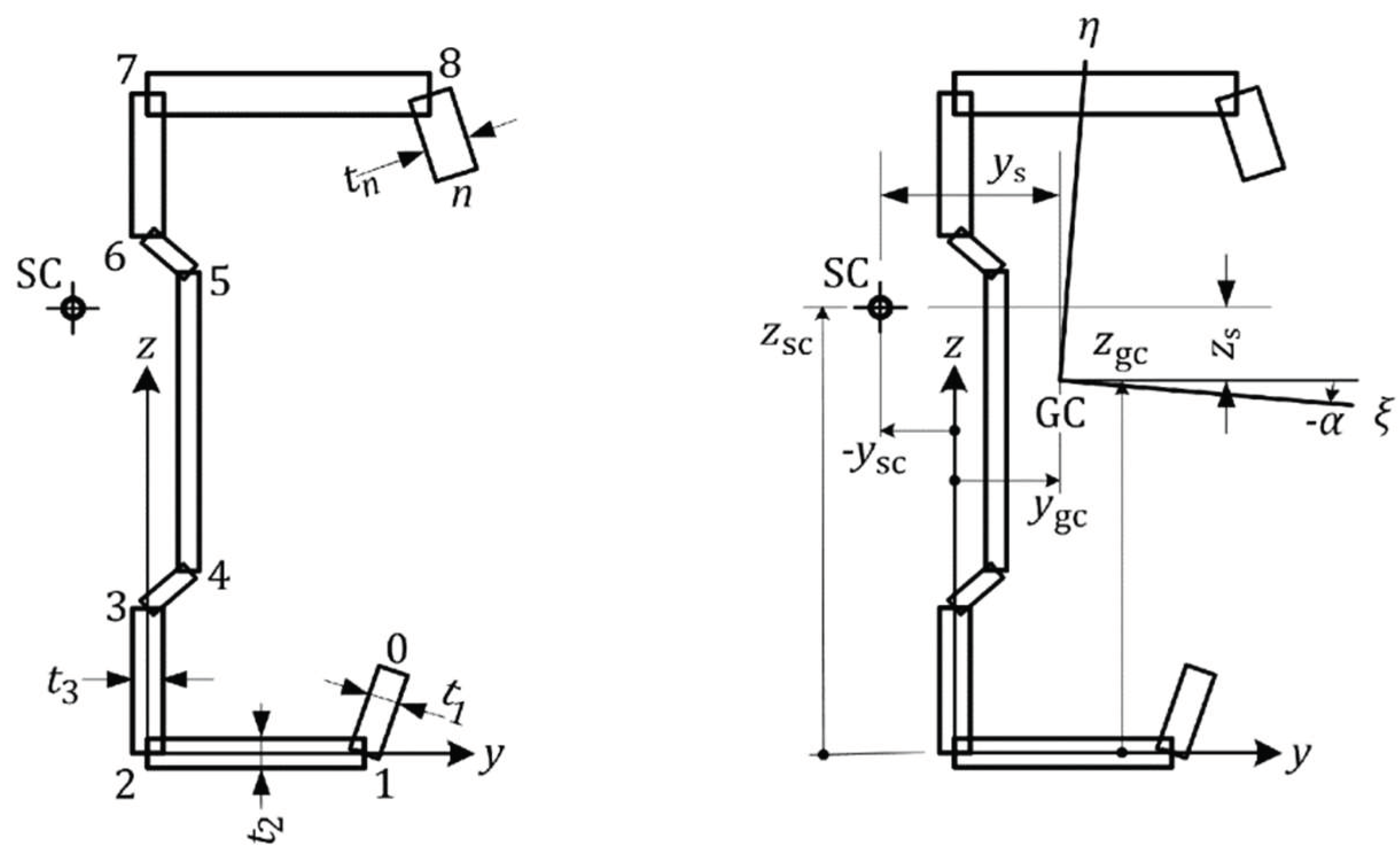
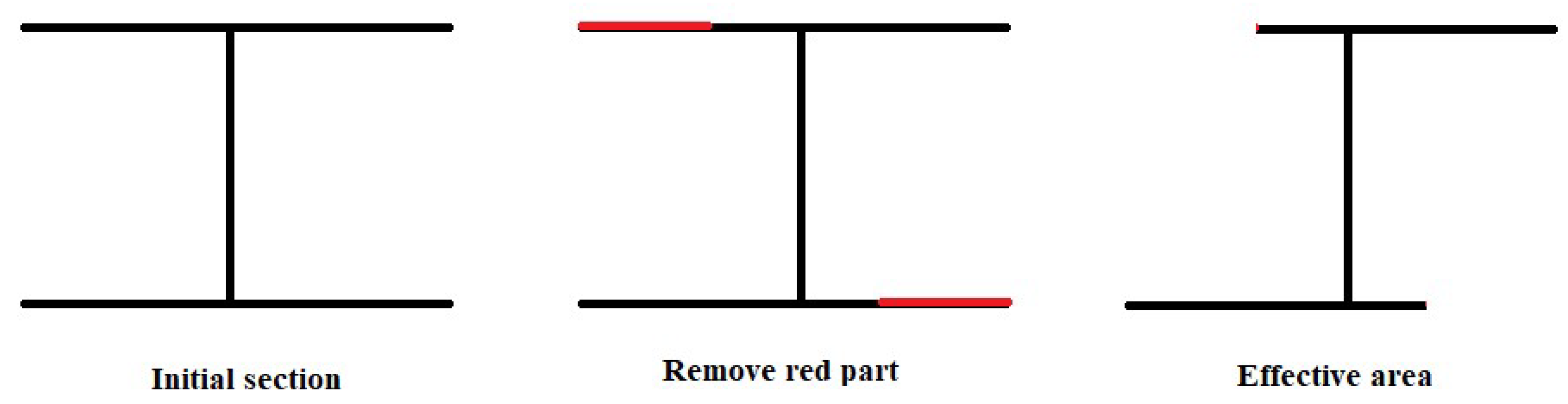
Elastic Theory
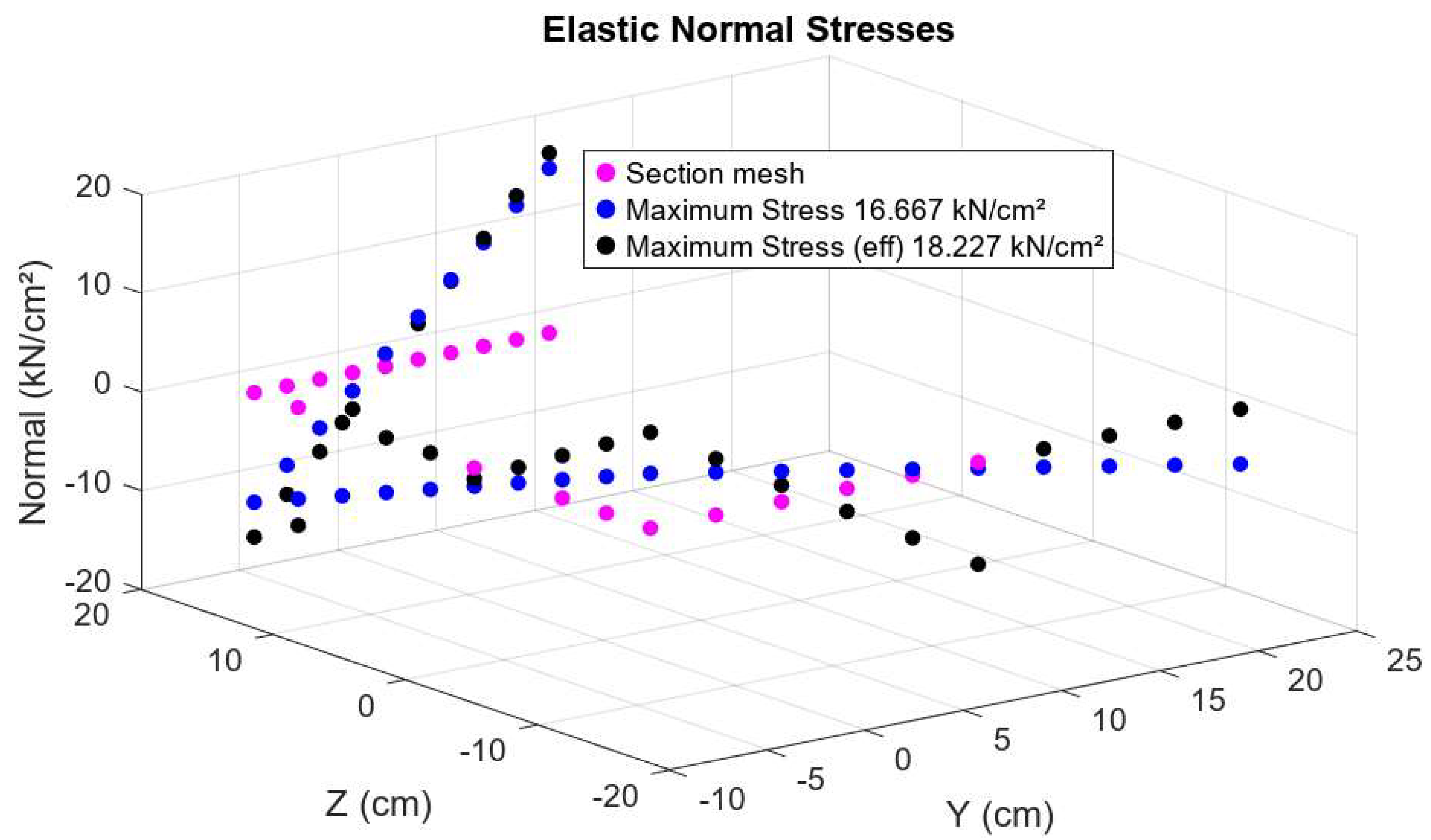
2. Numerical Examples
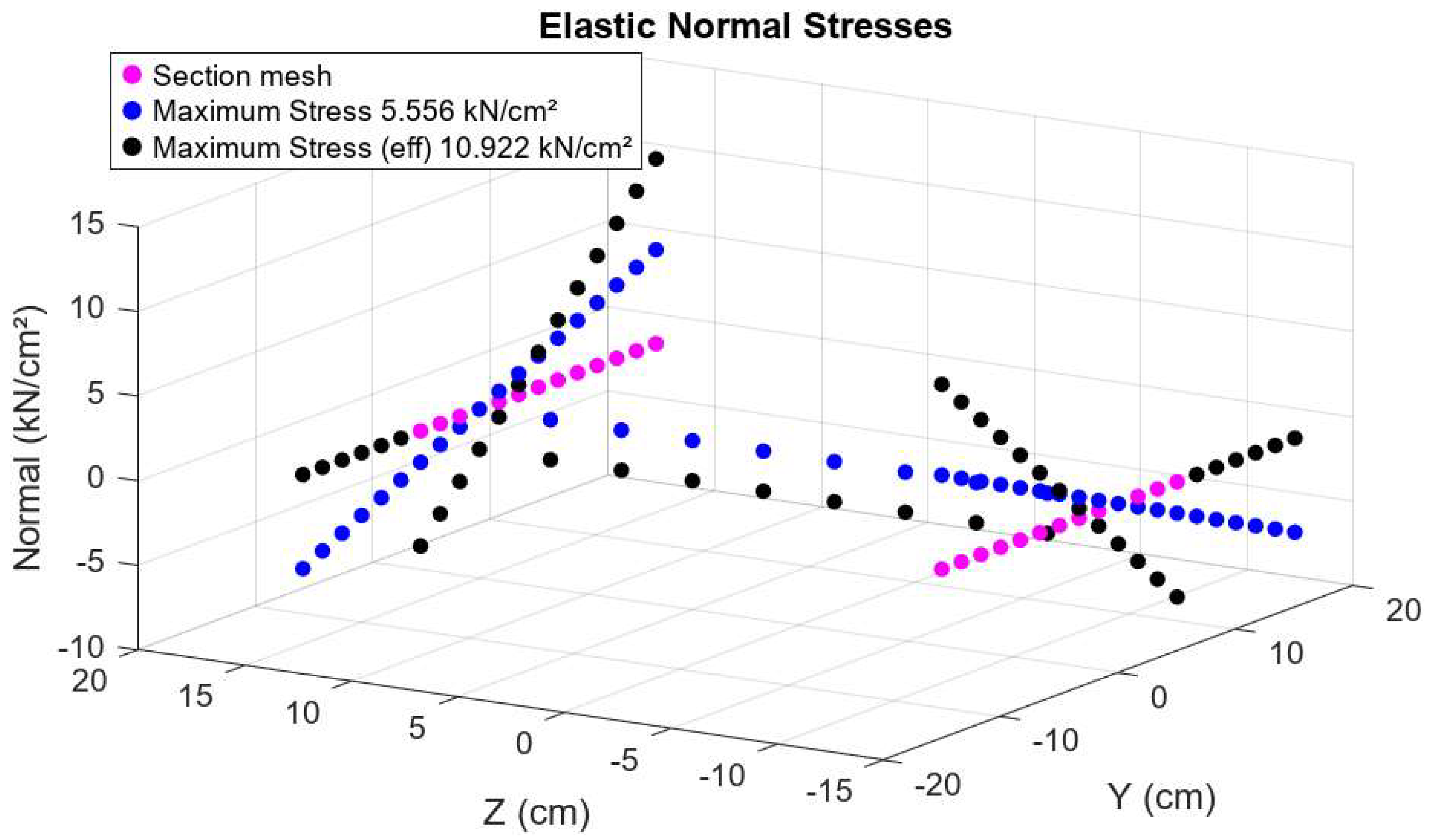
2.1. I Shape Section 2 Axes of Symmetry
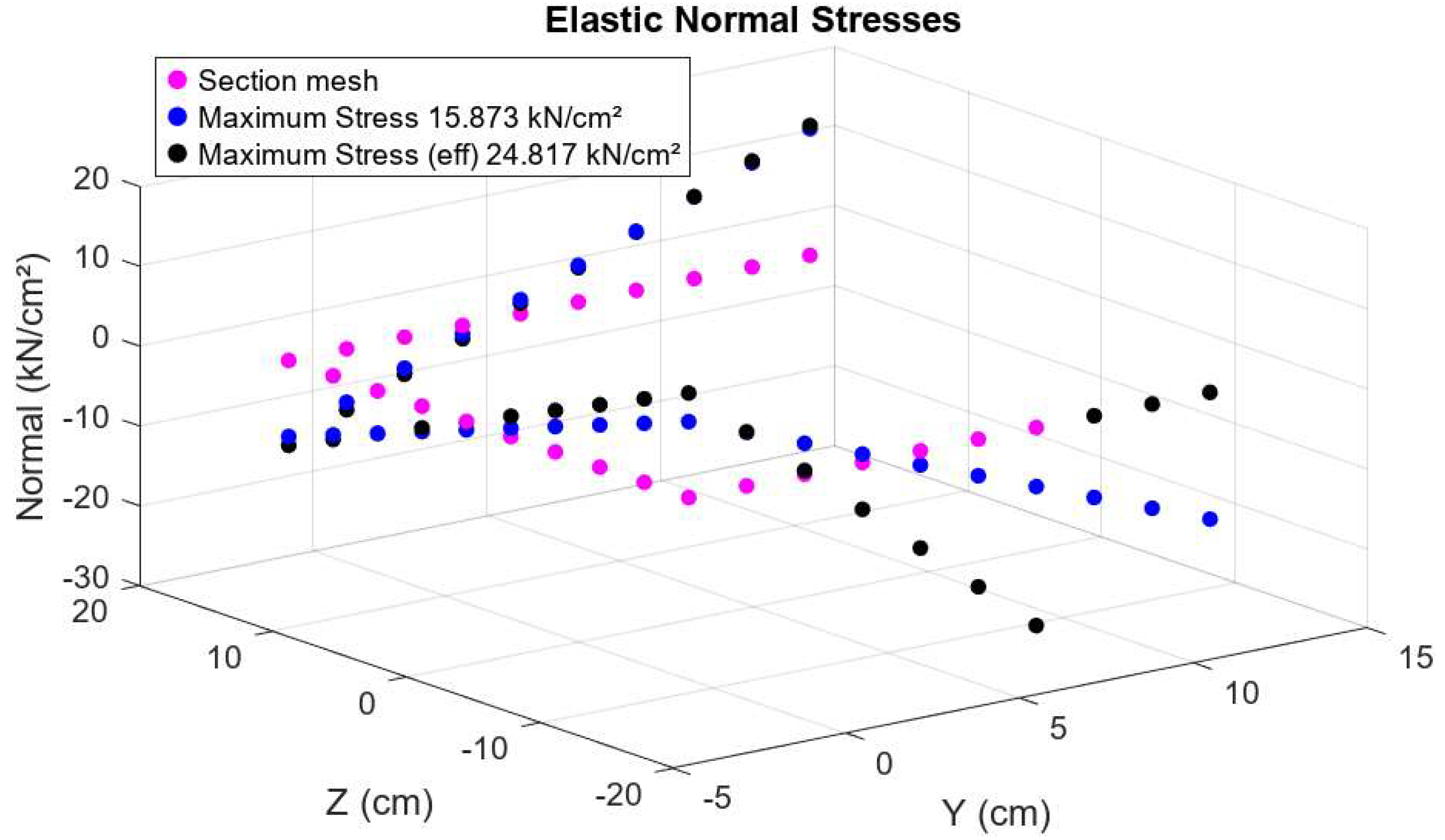
2.2. Monosymmetric Section
2.3. Non Symmetric Section
3. Conclusions
Funding
Nomenclature
References
- EN 1993-1-1:2022; Eurocode 3: Design of Steel Structures. Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2022.
- EN 1993-1-5:2006; Eurocode 3: Design of steel structures - Part 1-5: General rules - Plated structural Elements.
- Lee, C.K.; Chiew, S.P. A review of class 4 slender section properties calculation for thin-walled steel sections according to EC3. Advanced Steel Construction 2019, 15, 259–266. [Google Scholar]
- Agüero, A. , “Thin wall section Class 1,2,3 & 4” Software, Online available from https://labmatlab-was.upv.es/webapps/home/thinwallsectionmaterials_class4.html, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




