A Generalized Geometric Theoretical Framework of Centroid Discriminant Analysis for Linear Classification of Multi-dimensional Data

1. Introduction

Linear classifiers are often favored over nonlinear models, such as neural networks, for certain tasks due to their comparable performance in high-dimensional data spaces, faster training speeds, reduced tendency to overfit, and greater interpretability in decision-making ([1,2]). Notably, linear classifiers have demonstrated performance on par with convolutional neural networks (CNNs) in medical classification tasks, such as predicting Alzheimer’s disease from structural or functional brain MRI images ([3,4]).

These linear classifiers can be categorized into several types based on the principles they use to define the decision boundary or classification discriminant, as described below, where N is the number of samples, M is the number of features and k denotes an iteration term:

• The minimum distance classifier (MDC) ([5]) which is a prototype-based classifier that assigns points according to the perpendicular bisector boundary between the centroids of two groups. This classifier has $O\left(NM\right)$ training time complexity.
• Fisher’s linear discriminant analysis (LDA, specifically refer to Fisher’s LDA in this study) is a variance-based classifier which can be trained in cubic time complexity $O(N{M}^2+M^3)$. While faster implementations like spectral regression discriminant analysis (SRDA) ([6]) claim lower training time complexity, their efficiency depends on specific conditions, such as a sufficiently small iterative term and sparsity in the data. These constraints limit SRDA’s applicability in real-world classification tasks.
• Support vector machine (SVM) ([7]) with a linear kernel is a maximum-margin classifier, which has a training time complexity of $O\left(N^3\right)$. Fast implementations include Liblinear (referred to as fast SVM) and SVM-SGD, which use coordinate descent and stochastic gradients respectively, achieving quasi-quadratic time complexity $O\left(kNM\right)$.
• Perceptron ([8]) is a misclassification-triggered ruled-based classifier. Its training time complexity is $O\left(kNM\right)$.
• Logistic regression (LR) ([9]) is a statistics-based classifier. It can be trained using either maximum likelihood estimation (MLE) or iteratively reweighted least squares, with time complexity of $O(N{M}^2+M^3)$ and $O\left(N{M}^2\right)$ respectively, and with $O\left(kNM\right)$ using the same coordinate descent technique in Liblinear.

• Among linear classifiers, MDC offers the lowest training time complexity but suffers from limited performance due to its overly simplified decision boundary. Widely used methods such as LDA and SVM are often favored for their strong predictive capabilities. However, these methods can be computationally expensive, particularly for large-scale datasets. Hence, achieving both high scalability and strong predictive performance remains a challenging tradeoff, highlighting the need for new approaches that balance these competing demands.

To address this challenge, this paper makes the following 3 key contributions:

• A geometric theoretical framework for classifiers: (See Appendix A.1 for explanation of the term theoretical framework.) This study introduces a geometric framework, geometric discriminant analysis (GDA), to unify certain linear classifiers under a common theoretical model. GDA leverages a special type of centroid discriminant basis (CDB0), a vector connecting the centroids of two classes, which serves as the foundation for constructing classifier decision boundaries. The GDA framework adjusts the CDB0 through geometric corrections under various constraints, enabling the derivation of classifiers with desirable properties. Notably, we show that: MDC is a special case of GDA, where geometric corrections are not applied to CDB0; linear discriminant analysis (LDA) is a special case of GDA, where the CDB0 is corrected by maximizing the projection variance ratio.
• A high-performance and scalable linear geometric classifier: Building upon the GDA framework, we propose centroid discriminant analysis (CDA), a novel geometric classifier that iteratively adjusts the CDB through performance-dependent rotations on 2D planes. These rotations are optimized via Bayesian optimization, enhancing the decision boundary’s adaptability efficiently. CDA achieves lower training time complexity (quadratic) and is more efficient than LDA and SVM. Experimental evaluations on 27 real-world datasets of standard images, medical images and chemical property data, reveal that CDA consistently outperforms LDA, SVM and and LR in predictive performance, scalability, and stability.
• Nonlinear geometric classification via kernel method: For complex data where linear models are not enough, CDA supports nonlinear classification via kernel method. We demonstrated with challenging image and chemical datasets that kernel CDA improved over linear CDA and outperformed kernel SVM. Nonetheless, while kernel CDA offers greater expressiveness and improved capability, linear CDA remains highly valuable for real-world tasks due to its superior training efficiency, interpretability, and reduced risk of overfitting.

More importantly, we emphasize that CDA not only achieves robust predictive performance but also offers superior computational efficiency. Unlike traditional methods such as LDA and SVM, which typically exhibit cubic time complexity, CDA operates with quadratic complexity, resulting in significantly faster runtimes in practice. These advantages make CDA particularly attractive for real-world applications, where scalability, interpretability, and efficiency are essential. As linear classifiers remain widely used across scientific domains for their transparency and speed, CDA represents a valuable advancement for practitioners seeking reliable and computationally lightweight solutions. Lastly, the GDA theoretical framework, from which CDA is derived, may inspire new classifiers under the definition of different geometric constraints.

2. Geometric Discriminant Analysis (GDA)

In this study, we propose a generalized geometric theoretical framework for centroid-based linear classifiers. In geometry, the generalized definition of centroid is the weighted average of points. For binary classification problem, training a linear classifier involves finding a discriminant (perpendicular to the decision boundary) and a bias. In GDA, we focus on the centroid discriminant basis (CDB) which is defined as the unit vector from the centroid of negative class to positive class. Specifically, we focus on a particular discriminant termed as CDB0, which is constructed from centroids with uniform sample weights. GDA theoretical framework incorporates all the classifiers whose classification discriminant is CDB0 adjusted by geometric corrections on CDB0, which is described in details in the following using an instance with LDA. Moreover, in the GDA theoretical framework, the classifier discriminants are scaling-invariant, which is explained in Appendix A.2. Thus, throughout, $\gamma \ne 0$ denotes a generic constant independent of the variable of interest.

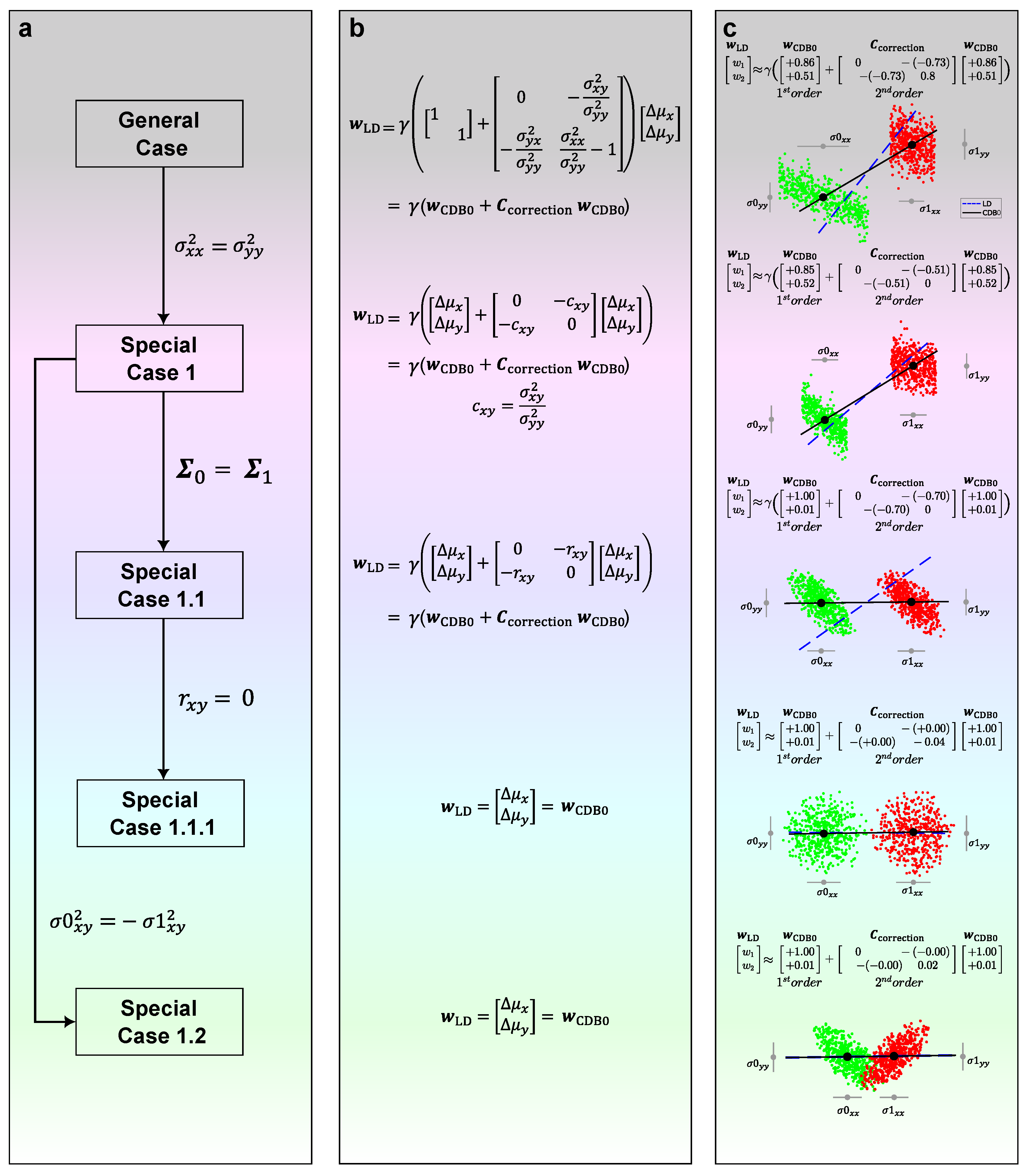
Without loss of generality, assume a two-dimensional space (see Appendix D for any-dimensional proofs). We derive the GDA theoretical framework as a generalization of Fisher’s LDA (hereafter referred to simply as LDA) and includes it under a certain geometric constraint. In LDA, the linear discriminant (LD) is derived as the maximization of between-class variance to within-class variance:

$$S={\displaystyle \frac{{\sigma }_{\mathrm{b}}^2}{{\sigma }_{\mathrm{w}}^2}}={\displaystyle \frac{{({\mathit{w}}^{\mathrm{T}}{\mathit{\nu }}_1-{\mathit{w}}^{\mathrm{T}}{\mathit{\nu }}_0)}^2}{{\mathit{w}}^{\mathrm{T}}{\mathsf{\Sigma }}_0\mathit{w}+{\mathit{w}}^{\mathrm{T}}{\mathsf{\Sigma }}_1\mathit{w}}}={\displaystyle \frac{{({\mathit{w}}^{\mathrm{T}}{\mathit{\nu }}_1-{\mathit{w}}^{\mathrm{T}}{\mathit{\nu }}_0)}^2}{{\mathit{w}}^{\mathrm{T}}({\mathsf{\Sigma }}_0+{\mathsf{\Sigma }}_1)\mathit{w}}}$$

(1)

where ${\mathit{\nu }}_0$ and ${\mathit{\nu }}_1$ are the means of negative and positive class, ${\mathsf{\Sigma }}_0$ and ${\mathsf{\Sigma }}_1$ are their covariance matrices, $\mathit{w}$ is the projection coefficient. The maximum is obtained when $N\mathsf{\Sigma }\mathit{w}={\mathit{\nu }}_1-{\mathit{\nu }}_0$ ([10]), or $N\mathsf{\Sigma }\gamma {\mathit{w}}_{\mathrm{LD}}={\mathit{\nu }}_1-{\mathit{\nu }}_0$, where ${\mathit{w}}_{\mathrm{LD}}$ is the normalized LDA discriminant in the GDA theoretical framework with a normalizing constant $\gamma$, N is the total number of samples. $\mathsf{\Sigma }$ is the sum of within-class covariance matrices of each class ${\mathsf{\Sigma }}_0+{\mathsf{\Sigma }}_1$:

$$\mathsf{\Sigma }=\left[\begin{array}{cc}\sigma 0_{xx}^2& \sigma 0_{xy}^2\\ \sigma 0_{yx}^2& \sigma 0_{yy}^2\end{array}\right]+\left[\begin{array}{cc}\sigma 1_{xx}^2& \sigma 1_{xy}^2\\ \sigma 1_{yx}^2& \sigma 1_{yy}^2\end{array}\right]=\left[\begin{array}{cc}{\sigma }_{xx}^2& {\sigma }_{xy}^2\\ {\sigma }_{yx}^2& {\sigma }_{yy}^2\end{array}\right]$$

(2)

And the inverse of the covariance matrix $\mathsf{\Sigma }$ is:

$${\mathsf{\Sigma }}^{-1}={\displaystyle \frac{adj\left(\mathsf{\Sigma }\right)}{\left|\mathsf{\Sigma }\right|}}={\displaystyle \frac{1}{{\sigma }_{xx}^2{\sigma }_{yy}^2-{\sigma }_{xy}^2{\sigma }_{yx}^2}}\left[\begin{array}{cc}{\sigma }_{yy}^2& -{\sigma }_{xy}^2\\ -{\sigma }_{yx}^2& {\sigma }_{xx}^2\end{array}\right]={\displaystyle \frac{{\sigma }_{yy}^2}{{\sigma }_{xx}^2{\sigma }_{yy}^2-{\sigma }_{xy}^2{\sigma }_{yx}^2}}\left[\begin{array}{cc}1& -{\displaystyle \frac{{\sigma }_{xy}^2}{{\sigma }_{yy}^2}}\\ -{\displaystyle \frac{{\sigma }_{yx}^2}{{\sigma }_{yy}^2}}& {\displaystyle \frac{{\sigma }_{xx}^2}{{\sigma }_{yy}^2}}\end{array}\right]$$

(3)

Where $adj\left(\mathsf{\Sigma }\right)$ is the adjugate of $\mathsf{\Sigma }$. Let $\Delta \mu$ denote the unit vector of $\Delta \mathit{\nu }$, then ${\mathit{\nu }}_1-{\mathit{\nu }}_0=\gamma ({\mu }_1-{\mu }_0)=\gamma \Delta \mu =\gamma {[\Delta {\mu }_x,\Delta {\mu }_y]}^{\mathrm{T}}$, and ${\mathit{w}}_{\mathrm{LD}}=\gamma {\mathsf{\Sigma }}^{-1}({\mathit{\nu }}_1-{\mathit{\nu }}_0)=\gamma {\mathsf{\Sigma }}^{-1}({\mu }_1-{\mu }_0)$. Further,

$${\mathit{w}}_{\mathrm{LD}}={\displaystyle \frac{\gamma {\sigma }_{yy}^2}{{\sigma }_{xx}^2{\sigma }_{yy}^2-{\sigma }_{xy}^2{\sigma }_{yx}^2}}\left[\begin{array}{cc}1& -{\displaystyle \frac{{\sigma }_{xy}^2}{{\sigma }_{yy}^2}}\\ -{\displaystyle \frac{{\sigma }_{yx}^2}{{\sigma }_{yy}^2}}& {\displaystyle \frac{{\sigma }_{xx}^2}{{\sigma }_{yy}^2}}\end{array}\right]\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right]=\gamma \left(\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]+\left[\begin{array}{cc}0& -{\displaystyle \frac{{\sigma }_{xy}^2}{{\sigma }_{yy}^2}}\\ -{\displaystyle \frac{{\sigma }_{yx}^2}{{\sigma }_{yy}^2}}& {\displaystyle \frac{{\sigma }_{xx}^2}{{\sigma }_{yy}^2}}-1\end{array}\right]\right)\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right]$$

$$=\gamma ({[\Delta {\mu }_x,\Delta {\mu }_y]}^{\mathrm{T}}+{\mathit{C}}_{\mathrm{correction}}{[\Delta {\mu }_x,\Delta {\mu }_y]}^{\mathrm{T}})$$

(4)

where ${\mathit{C}}_{\mathrm{correction}}$ is a correction matrix that acts as the second-order term associated with the sum of covariance matrices. Since ${\mathit{w}}_{\mathrm{CDB}0}$ is the unit vector constructed from centroids with uniform sample weights (i.e., arithmetic means), it can be written as ${\mathit{w}}_{\mathrm{CDB}0}={[\Delta {\mu }_x,\Delta {\mu }_y]}^{\mathrm{T}}.$ As in the covariance matrix, ${\sigma }_{xy}^2={\sigma }_{yx}^2$, and let $c_{xy}={\sigma }_{xy}^2/{\sigma }_{yy}^2$, $c_{xx/yy}={\sigma }_{xx}^2/{\sigma }_{yy}^2-1$, the linear discriminant in Eq. 4 can be compressed into the following general form (Figure A1a-c, general case):

$${\mathit{w}}_{\mathrm{GD}}={\mathit{w}}_{\mathrm{LD}}=\gamma (\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right]+\left[\begin{array}{cc}0& -c_{xy}\\ -c_{xy}& c_{xx/yy}\end{array}\right]\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right])=\gamma ({\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_{\mathrm{correction}}{\mathit{w}}_{\mathrm{CDB}0}).$$

(5)

Since from Equation (5), ${\mathit{w}}_{\mathrm{LD}}$ can be decomposed into the basis ${\mathit{w}}_{\mathrm{CDB}0}$ and a correction on the basis, we write out ${\mathit{w}}_{\mathrm{GD}}$ to indicate that ${\mathit{w}}_{\mathrm{LD}}$ is a geometrical discriminant (GD), a discriminant geometrically modified from ${\mathit{w}}_{\mathrm{CDB}0}$. This geometrical modification can be intuitively interpreted as performing rotations on ${\mathit{w}}_{\mathrm{CDB}0}$.

Starting from Equation (5), we have the following special cases to consider, which represent different forms of geometrical modification applied to ${\mathit{w}}_{\mathrm{CDB}0}$:

Special case 1. If we assume two variables have the same variance (${\sigma }_{xx}^2={\sigma }_{yy}^2$), then $c_{xx/yy}=0$. Equation (5) becomes (Figure A1, special case 1):

$${\mathit{w}}_{\mathrm{LD}}=\gamma (\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right]+\left[\begin{array}{cc}0& -c_{xy}\\ -c_{xy}& 0\end{array}\right]\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right])=\gamma ({\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_{\mathrm{correction}}{\mathit{w}}_{\mathrm{CDB}0})$$

(6)

From Equation (6), there are two special cases:

Special case 1.1. If two covariance matrices are same (${\mathsf{\Sigma }}_0={\mathsf{\Sigma }}_1$), then the following also holds: $c_{xy}={\displaystyle \frac{{\sigma }_{xy}^2}{{\sigma }_{yy}^2}}={\displaystyle \frac{\mathbb{E}\left[(x-{\mu }_x)(y-{\mu }_y)\right]}{{\sigma }_x{\sigma }_y}}=r_{xy}$ where $r_{xy}$ is the Pearson correlation coefficient (PCC) between x and y of the samples in each class. Equation (6) becomes (Figure A1, special case 1.1):

$${\mathit{w}}_{\mathrm{LD}}=\gamma (\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right]+\left[\begin{array}{cc}0& -r_{xy}\\ -r_{xy}& 0\end{array}\right]\left[\begin{array}{c}\Delta {\mu }_x\\ \Delta {\mu }_y\end{array}\right])=\gamma ({\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_{\mathrm{correction}}{\mathit{w}}_{\mathrm{CDB}0})$$

(7)

Special case 1.1.1. From Equation (7), if there is no correlation between x and y variables (e.g., $r_{xy}=0$), then the equation becomes (Figure A1, special case 1.1.1):

$${\mathit{w}}_{\mathrm{LD}}=\gamma \left({[\Delta {\mu }_x, \Delta {\mu }_y]}^{\mathrm{T}}\right)={[\Delta {\mu }_x, \Delta {\mu }_y]}^{\mathrm{T}}={\mathit{w}}_{\mathrm{CDB}0}$$

(8)

which is equivalent to MDC method except for the bias. The second equal mark is from the fact that ${[\Delta {\mu }_x, \Delta {\mu }_y]}^{\mathrm{T}}$ is already a unit vector, thus $\gamma =1$.

Special case 1.2. From Equation (6), if two classes are symmetric about one variable, i.e., $\sigma 0_{xy}^2=-\sigma 1_{xy}^2\ne 0$, then $c_{xy}={\displaystyle \frac{{\sigma }_{xy}^2}{{\sigma }_{yy}^2}}=0$. In this case, the obtained discriminant is the same as in Special case 1.1.1 (Figure A1, special case 1.2):

$${\mathit{w}}_{\mathrm{LD}}=\gamma {[\Delta {\mu }_x, \Delta {\mu }_y]}^{\mathrm{T}}={[\Delta {\mu }_x, \Delta {\mu }_y]}^{\mathrm{T}}={\mathit{w}}_{\mathrm{CDB}0}$$

(9)

Figure A1c shows how LDA applies geometric modifications to ${\mathit{w}}_{\mathrm{CDB}0}$ as a shape adjustment for different shapes of data. When two covariance matrices are similar (Special case 1.1), the correction term acts only when the variables x and y have a certain extent of correlation and increases with this correlation (Figure A1, the third row). Interestingly, when further assumptions are made that two variables have no correlation (Special case 1.1.1), or when two classes are symmetric about one variable (Special case 1.2), we can see from Equations (8)-(equation 9) that ${\mathit{w}}_{\mathrm{LD}}$ will approach ${\mathit{w}}_{\mathrm{CDB}0}$, which is indeed what we observe in the last two rows of Figure A1. Videos showing these special cases using 2D simulated data can be found from this link1.

The demonstrations of all these cases for higher-dimensional space are in the Appendix D.

From the above derivation, Equation (5)-(equation 9) show that the solution of LDA can be represented by ${\mathit{w}}_{\mathrm{CDB}0}$ superimposed with a geometric correction on ${\mathit{w}}_{\mathrm{CDB}0}$, and the geometric correction term is obtained under the constraint of Equation (1), which solves the maximization of the projection variance ratio. Without loss of generality, the conclusion can be extended to other linear classifiers with different constraints imposed on the geometric correction term, for instance MDC, where the correction terms are all zero.

Here, we propose the generalized GDA theoretical framework in which not only the geometric correction term can impose any constraint based on different principles, but also any number of correction terms can act together on ${\mathit{w}}_{\mathrm{CDB}0}$ to create the classification discriminant, given by:

$${\mathit{w}}_{\mathrm{GD}}=\gamma ({\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_1{\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_2{\mathit{w}}_{\mathrm{CDB}0}+\dots +{\mathit{C}}_n{\mathit{w}}_{\mathrm{CDB}0})$$

(10)

Figure 1 shows that LDA is derived by the general GD equation imposing one variance-based geometric correction in Figure 1b, shown in Figure 1a using an instance of 2d artificial data with specific covariance.

3. Centroid Discriminant Analysis (CDA)

Based on the GDA theoretical framework, in this study we propose an efficient geometric centroid-based linear classifier named centroid discriminant analysis (CDA), then introduce the extension to nonlinear classification via kernel method in Section 5. As described by Eq. 10 in the GDA thoery, the model of a geometric classifier can be expressed by the basis CDB0 imposed by geometric corrections on this basis. We first give the conclusion that the final discriminant of CDA after n rotations is in the form ${\mathit{w}}_{\mathrm{CDA}}^{\left(n\right)}=\gamma ({\mathit{w}}_{\mathrm{CDB}0}+{\mathit{C}}_1{\mathit{w}}_{\mathrm{CDB}0})={\mathit{w}}_{\mathrm{GD}}$, where ${\mathit{C}}_1=\mathit{I}-{\prod }^n{\mathit{A}}_{\mathrm{cda}}$ is the geometric correction operator term, $\mathit{I}$ is the identity operator, and ${\mathit{A}}_{\mathrm{cda}}$ is the operator of a single CDA rotation). The complete derivation of CDA in GDA theoretical framework can be found in Appendix E.

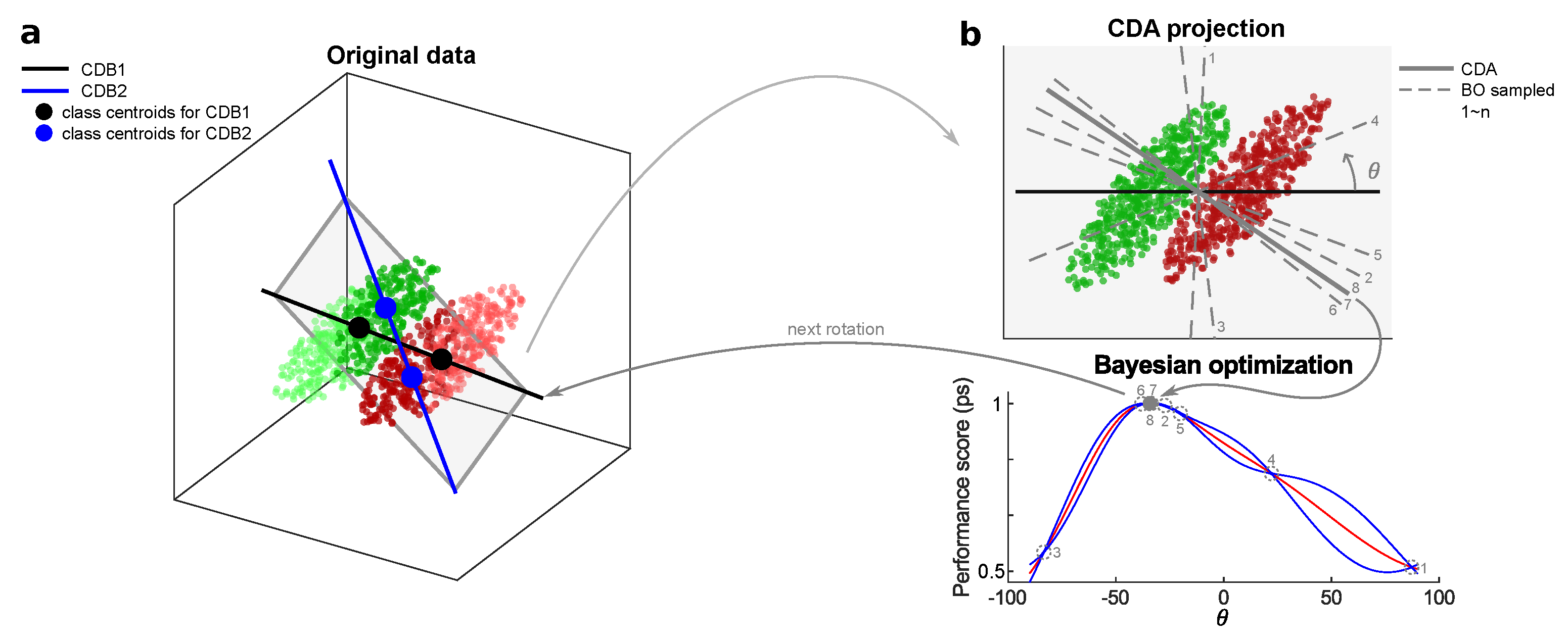
From the geometric point of view, CDA is built on the basis CDB0 in the GDA theoretical framework, then subjected to a series of geometric constraints guiding the rotations of the discriminant CDB in high-dimensional spaces. CDA follows a performance-dependent training that starting from CDB0 involves the iterative calculation of new adjusted centroid discriminant lines whose optimal rotations on the associated 2D planes are searched via Bayesian optimization. The following parts together with Figure A2 describe the CDA workflow, mechanisms and principles in detail.

Performance-associated CDB Classifier: In GDA theoretical framework, CDB is defined as the unit vector pointing from the geometric centroid of the negative class to positive class. The geometric centroid is defined in a general sense which considers the weights of the data. The space of CDB consists of unit vectors obtained with all possible weights.

Apart from the discriminant line, a bias is further required to realize classification by offering a decision boundary for data projected onto the discriminant. We perform a search for this bias by checking the middle points of every two consecutive sorted projections. Thus, given N samples, there are $N-1$ candidates. We name the best candidate as optimal operating point (OOP) and select OOP according to a performance-score, defined as $(Fscor{e}^{\mathrm{pos}}+Fscor{e}^{\mathrm{neg}}+ACscore)/3$ (see Appendix F for definitions), where pos and neg means evaluating the metric for each class. The performance score is a comprehensive metric that simultaneously considers sensitivity, recall, and specificity, providing a fair evaluation that accounts for biased models trained on imbalanced data, owing to the more conservative AC-score metric ([11]). With this OOP search strategy, any vector in the space of CDB is associated with a performance-score. The OOP search can be performed efficiently in $O\left(N\log N\right)$ time (see Algorithm A3 for pseudocode). Importantly, during each rotation within the 2D plane, CDA explicitly selects the direction that maximizes the performance score, and progressively refines this choice through continuous rotations. Because the optimization target is transparent at every step, CDA offers an inherently explainable learning process.

CDA as Consecutive Geometric Rotations of CDB in 2D planes: Our idea is to start the optimization path from CDB0, continuously rotate the classification discriminant on 2D planes on which there is a high probability of having a classification discriminant with better performance. To construct such a 2D plane with another vector, a key observation is that the samples, whose projections onto CDB are close to the decision boundary (i.e. OOP), should have more weights, because these samples are prone to overlapping with samples from the other class, causing misclassification. Thus, we compute another CDB using centroids with shifted sample weights toward OOP (see next part). On the plane formed by these two CDBs, the best rotation is found by Bayesian optimization. For clarity, we have the following definition: the first vector in each rotation is termed as CDB1, the second vector in each rotation is termed as CDB2, the CDB searched with the best performance is termed as CDA, and at the end of each rotation CDA becomes CDB1 for the next rotation. CDA rotation is used to refer to this rotation process. Figure A2a shows the diagram for the first CDA rotation, where CDB1 equals to CDB0 calculated using uniform sample weights. The CDA training stops when meeting any of the two criteria: (1) Reach the maximum 50 iterations. (2) the coefficient of variation (CV) of the last 10 performance-score is less than a threshold, indicating that the training has converged (see Algorithms A1, A2 and A4 for pseudocode).

Sample Weights Update Strategy: Given CDB1 and the associated OOP in each CDA rotation, the distance of all projections to OOP can be obtained by $d_i=|q_i-oop|,\forall i\in \{1,2,\dots ,N\}$, which is then reversed by ${\mathit{d}}_{\mathrm{r}}=|\mathit{d}-min\left(\mathit{d}\right)-max\left(\mathit{d}\right)|$, in align with the purpose that points close to decision boundary should have larger weights. Since only the relative information of sample weights is important, they are L2-normalized and decay smoothly from previous sample weights by $\mathit{\alpha }=\mathit{\alpha }\odot {\mathit{d}}_{\mathrm{r}}/{\parallel \mathit{\alpha }\odot {\mathit{d}}_{\mathrm{r}}\parallel }_2$, where ⊙ indicates the Hadamard (element-wise) product. Specifically, in the first CDA rotation, the CDB1 is obtained with uniform sample weights, which corresponds to CDB0 in the GDA theoretical framework.

Bayesian Optimization (BO): The CDA rotation aims to search for a unit vector CDB with the best performance-score, which can be efficiently realized by BO ([12]). BO is a statistical-based technique to estimate the global minimum of a function with as fewer evaluations as possible. CDA leverages this high-efficiency characteristic of BO to achieve fast training. BO has $O\left(Z^3\right)$ time complexity when it searches a single parameter, where Z is the number of sampling-and-evaluations. CDA employs a strategy that grows BO sampling times from 4 to the maximum 10 with CDA iterations (see Appendix C.1). Figure A2b shows an instance of BO working process. Algorithm A5 shows the pseudocode for the CDA rotation as the black box function to optimize by BO.

Finalization: As a finalization step, on the best plane CDA refines the discriminant with a null-model statistical test using 100 random CDB lines drawn from the plane (see Appendix C.2 and Algorithm A6).

Multiclass Prediction: Error-correcting output codes (ECOC) ([13]) is a vote/penalization-based method to make multiclass predictions from trained binary classifiers. To predict the class of a new sample, multiple scores can be obtained from the set of trained binary classifiers. These scores are interpreted as they either vote for or are against a particular class. Depending on the coding matrix and the loss function chosen, ECOC takes the class with the highest overall reward or lowest overall penalty as the predicted class. In this study, the coding matrix for one-versus-one training scheme is selected, as it creates more linear separability ([14,15]). For the type of loss function, hinge-loss is chosen, as our internal tests suggested that this loss leads to the best classification performance for all tested linear classifiers.

4. Experimental Evidences on Linear Classification of Real Data

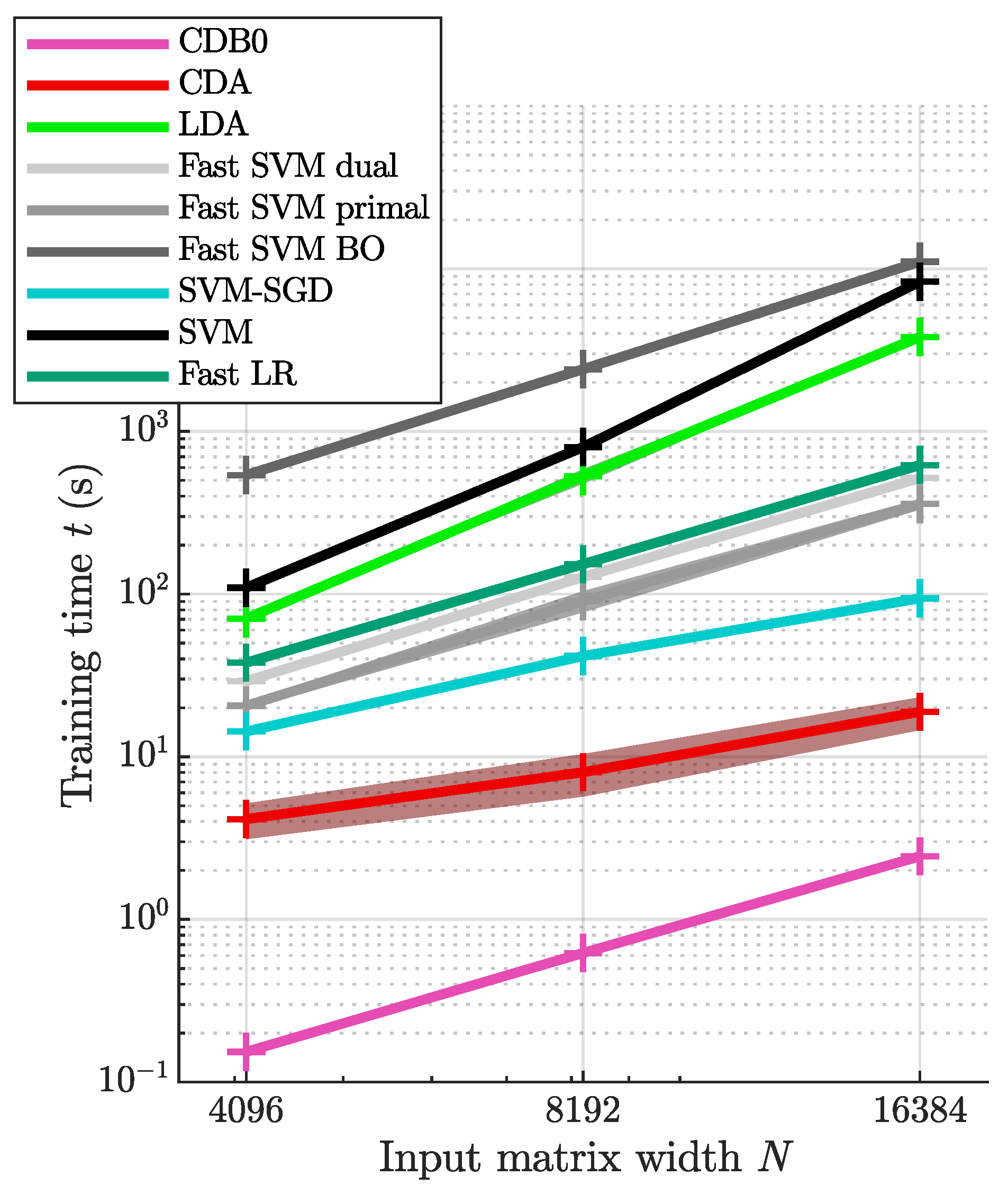
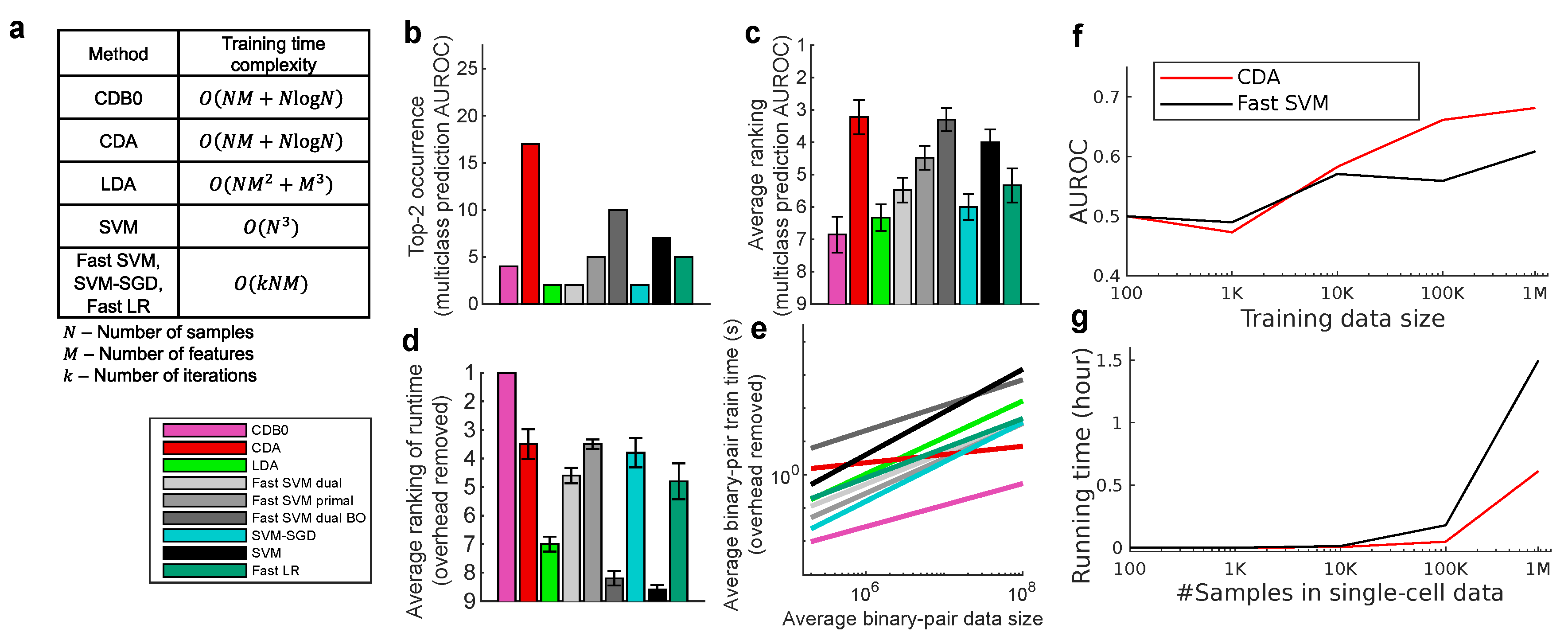
In this section, we compared the proposed CDA with other linear classifiers including LDA, SVM and LR. The 5 tested SVM variants includes the original SVM, dual and primal fast SVM implemented by Liblinear, SVM-SGD, and one fast SVM with BO hyperparameter search. LR uses fast implementation by Liblinear (fast SVM and fast LR refers to the dual version unless otherwise specified). Additionally, we include the baseline method, CDB0 (equivalent to MDC equipped with OOP bias), to quantify the improvements made by CDA over a simplistic centroid-based classification approach. Their theoretical time complexity is shown in Figure 2a. Experiment details are in Appendix I.

Classification Performance on Real Data: We assessed linear classification performance across 27 datasets, including standard image classification ([16,17,18,19,20,21,22,23,24]), medical image classification ([25]), and chemical property prediction tasks ([26]). These datasets represent a broad range of real-world applications and varying data sizes, enabling evaluations for both training speed and predictive performance. Image data were used in their original value flattened to 1d vectors; chemical formula were processed by simplified molecular input line entry system (SMILES) tokenized encoding (see Appendix J). Each dataset was split into a 4:1 ratio for training and test sets. The final model for each method was an unweighted ensemble of the five cross-validated models on the training set.

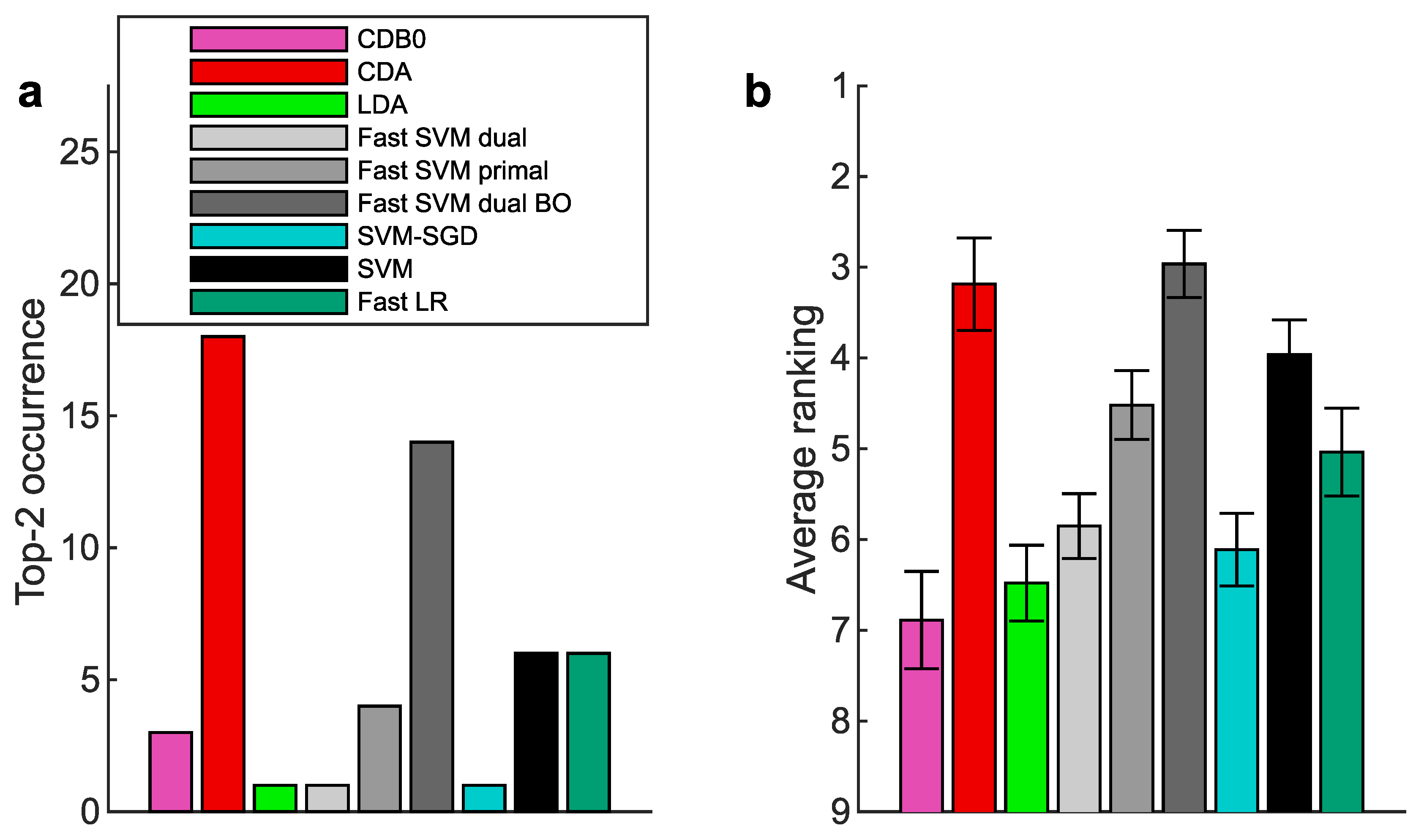
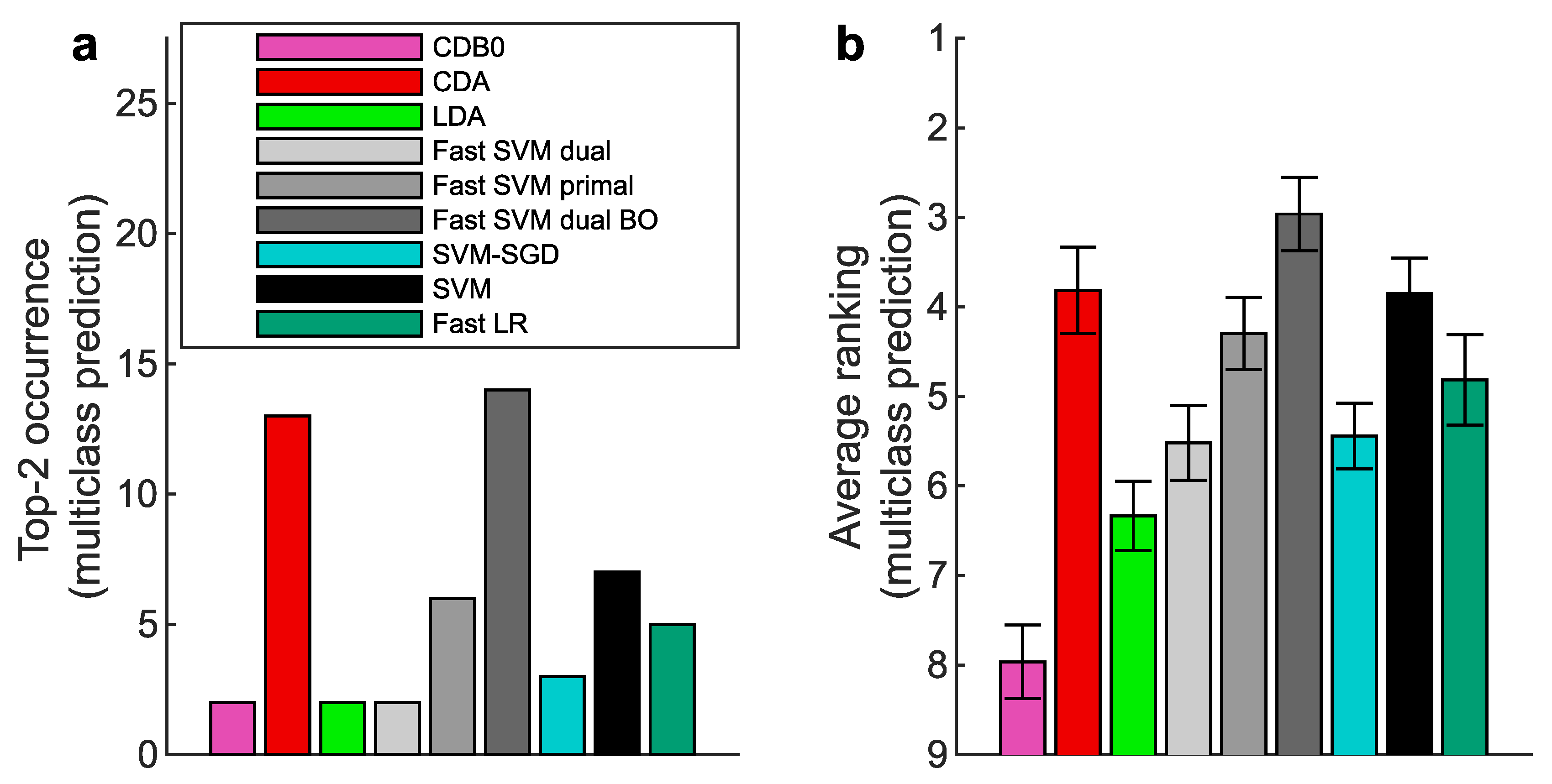
Figure 2b-e show the test set multiclass prediction performance. In Figure 2b, CDA achieved a top-2 occurrence of AUROC on 17 out of 27 datasets, outperforming all the other linear classifiers, indicating its stability and competitiveness. Figure 2c shows that CDA achieved the highest average ranking around 3.3, followed by fast SVM BO and SVM, however, their extremely low average ranking of training speed in Figure 2d indicates the impracticality for large-scale datasets (Panel (d) shows results on large datasets with average class-pair data size $N\times M>{10}^7$, because in practice we care more about the time consumption on large datasets rather than small ones). See Appendix K-Appendix L for binary classification results, ranking on other metrics, and complete performance tables.

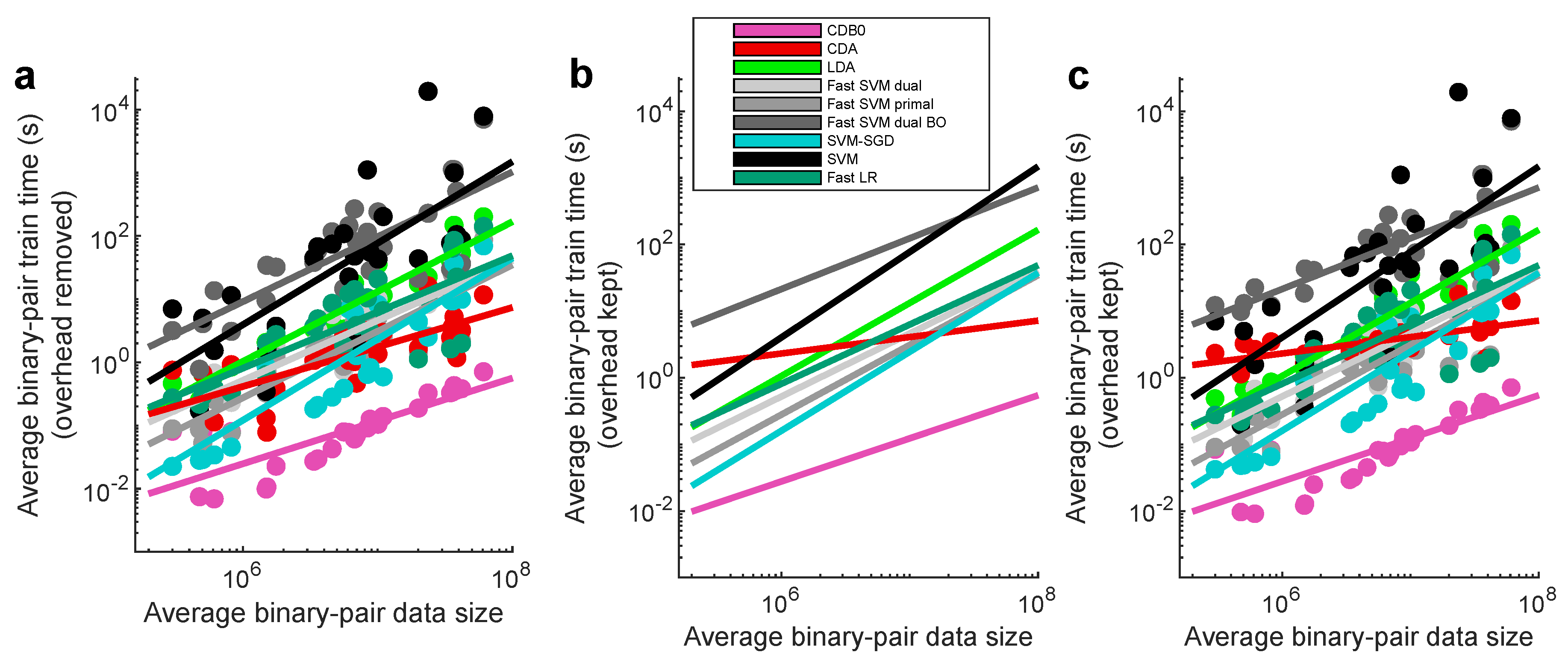
In Figure 2e we performed linear regressions between training times and data sizes averaged across binary pairs within each dataset with overhead deducted (See Figure A5a for original data points, and Figure A5b-c for results with overhead kept). The regression results show that CDB0 exhibits the best scalability due to its simplicity. SVM primal and SVM-SGD are fast for small data size, however, CDA outperforms them when data size gets large. CDA not only improves significantly over CDB0 in performance but also retains similar scalability. This improvement is driven by three key components: generalized centroids with non-uniform weights, sample weight shift strategy, and rotations by Bayesian optimization. The weighted average number of iterations required by CDA per dataset was 29.33 - a small constant that does not contribute to time complexity. In contrast, the iterations required by SVM variants increase significantly with more challenging datasets to achieve a reasonable classification performance. Considering the diversity of tested datasets, CDA demonstrates itself as a generic classifier with strong performance and scalability, making it applicable to large-scale classification tasks across various domains.

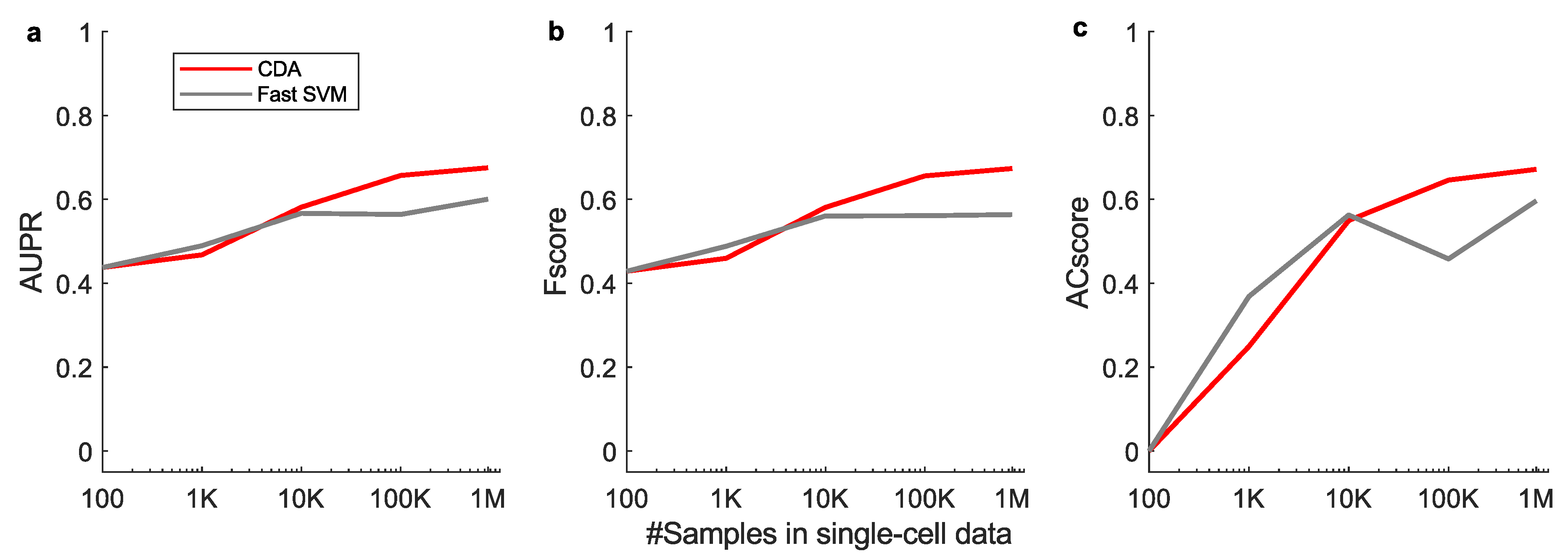
We further test CDA on a large-scale dataset, the 1.3-million-cell mouse brain dataset ([27]), with the largest two classes (See Section. Appendix G for details). The results show that with growing sample sizes, CDA outperforms fast SVM on both classification AUROC (Figure 2f and Appendix Figure A3), and training speed (Figure 2g). These results indicate that linear CDA is even more efficient and scalable than the flagship SVM method in efficiency. Hence, CDA as a fast approach has the potential to drive large-scale real-world applications in fields such as biomedicine and autonomous driving.

In addition, we made a comparison between CDA with two prevalent neural network architectures - MLP and ResNet. See Appendix M.1 for this comparison. In addition, we found that it is feasible to incorporate neural networks in CDA, using their extracted features to train CDA, which improves significantly over directly training on the original data if the data is complex. This combined approach and the associated experiment is discussed in Appendix M.2.

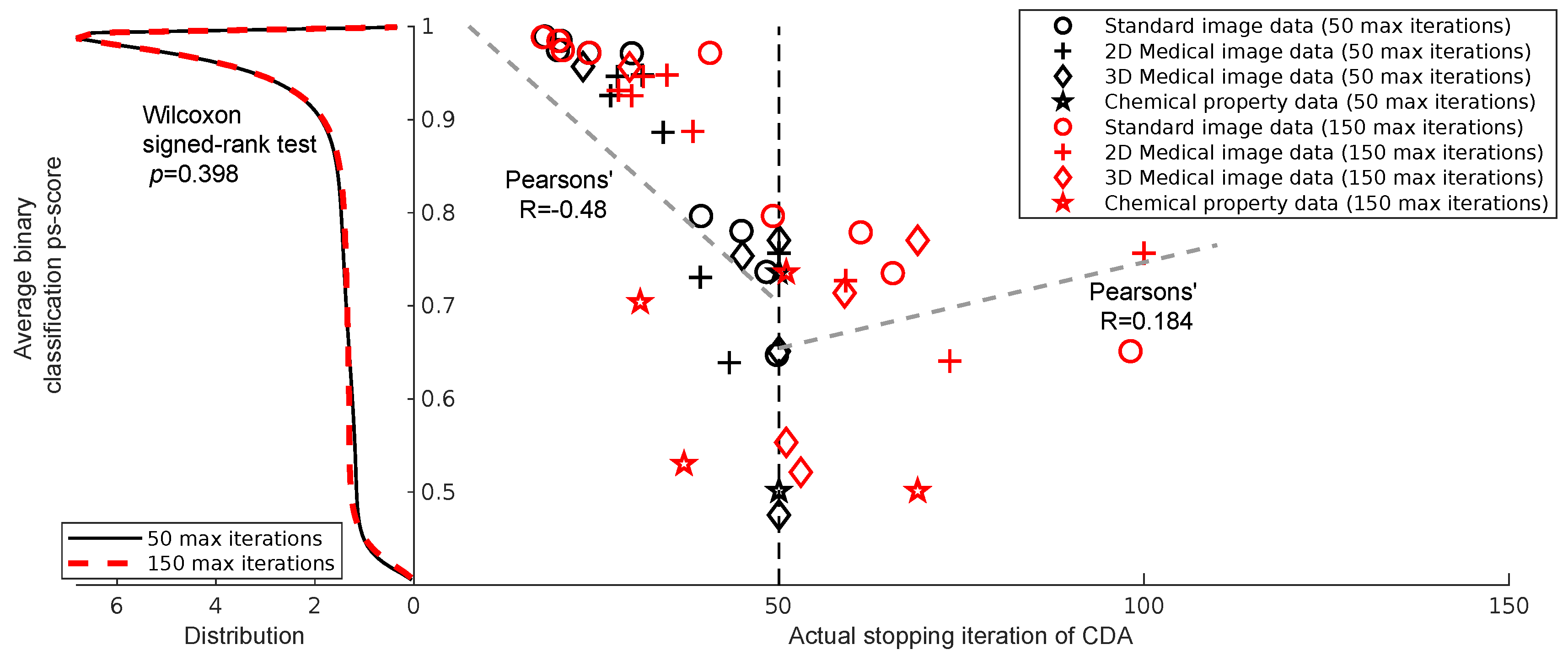
CDA’s Convergence Property: We analyzed the relationship between the actual stopping iteration of CDA and the average binary classification performance (ps-score) across different datasets and iteration limits. The results revealed two distinct regimes. In the right half of Figure 3, for tasks converging before 50 iterations, we observed a significant negative correlation (Pearson’s R = –0.48), indicating that datasets with lower performance required more iterations to converge. This highlights the importance of allowing at least 50 iterations, as early stopping before this point may prevent convergence for more challenging tasks. In contrast, for tasks exceeding 50 iterations, the correlation was weak and positive (Pearson’s R = 0.184), suggesting that beyond this threshold, the number of iterations no longer plays a significant role in ensuring convergence. This indicates that once 50 iterations are reached, CDA can stabilize regardless of the underlying task performance.

To further validate this observation, in the left half of Figure 3, we compared the distributions of ps-scores obtained under maximum iteration limits of 50 and 150. The estimated probability densities were nearly identical, and the Wilcoxon signed-rank test confirmed no significant difference between the two conditions (p=0.398). This result supports the conclusion that extending the maximum number of iterations beyond 50 does not provide systematic benefits in terms of classification performance.

5. Preliminary Test on Nonlinear Kernel CDA

When data exhibit strong nonlinearity, linear classifiers often underperform. To address this problem, models must exploit these nonlinear patterns to enhance expressiveness and improve classification performance. In fact, linear CDA can be naturally extended to a nonlinear variant using kernel method while retaining efficiency (see Appendix C.4). The main computational bottleneck lies in the kernel matrix computation, which is a common cost shared by all kernel-based classifiers.

To compare the performance of nonlinear CDA and other nonlinear classifiers, we performed tests on two challenging datasets, image dataset SVHN and chemical property dataset ClinTox (see Appendix J for data processing). We choose these datasets because they are difficult to classify with linear classifiers, and we are interested in to what extent can nonlinear classifiers improve over linear ones. We used a subset of SVHN samples (24,000) due to the time limitation to test with kernel method. We compared linear CDA, nonlinear gaussian CDA (nCDA), linear SVM, nonlinear gaussian SVM (nSVM). For kernel methods, we performed hyperparameter search for the gaussian parameter $\sigma$. The data were divided into train, validation and test set, where on the validation set the hyperparameter was tuned. The training specifics can be found in Appendix I.2. The multiclass test set results (on ClinTox binary results since it is a binary task) in Table 1 show that nonlinear kernel CDA outperforms gaussian SVM and linear methods on both the SVHN subset and ClinTox on all classification metrics. Despite the fact that gaussian CDA improves substantially over linear CDA in tasks such as the SVHN image classification, we emphasize that linear CDA is still very useful and important, with high efficiency and low resource requirement in computation, among other merits.

6. Conclusions and Discussions

Linear classifiers, while inherently simpler, are favored in certain contexts due to their reduced tendency to overfit and their interpretability in decision-making. However, achieving both high scalability and robust predictive performance simultaneously remains a significant challenge.

In this study, the introduction of the Geometric Discriminant Analysis (GDA) framework marks a notable step forward in addressing this challenge. By leveraging the geometric properties of centroids – a fundamental concept in multiple disciplines – GDA provides a unifying framework for certain linear classifiers. The core innovation lies in a special type of Centroid Discriminant Basis (CDB0), which serves as the foundation for deriving discriminants. These discriminants, when augmented with geometric corrections under varying constraints, extend the theoretical flexibility of GDA. Notably, Minimum Distance Classifier (MDC) and Linear Discriminant Analysis (LDA) are shown to be a subset of this broader framework, demonstrating how they converge to CDB0 under specific conditions. This theoretical generalization not only validates the GDA framework but also sets the stage for novel classifier designs.

A key practical contribution of this work is the Centroid Discriminant Analysis (CDA), a specialized implementation of GDA. CDA employs geometric rotations of the CDB within planes defined by centroid-vectors with shifted sample weights. These rotations, combined with Bayesian optimization techniques, enhance the method’s scalability, achieving quadratic time complexity $O(NM+N\log N)$. Across diverse datasets—including standard images, medical images, and chemical property classifications—CDA demonstrated superior performance in scalability, predictive performance, and stability. We emphasize that CDA not merely robustly outperforms most of existing linear classification methods, but crucially, it achieves this with superior computational efficiency. Specifically, CDA exhibits a quadratic time complexity in the worst-case scenario, compared to the cubic complexity typical of established methods such as LDA and SVM, with significantly shorter runtimes that highlight its practical advantage in real-world applications. These findings hold particular relevance for the broader machine learning community, as linear classifiers remain widely used across numerous scientific domains where interpretability, scalability, and computational efficiency are critical. In such contexts, practitioners often prefer models that are not only robust and fast but also transparent and easy to deploy in real-world decision-making scenarios.

In cases where the data exhibit complex nonlinear structures that linear classifiers cannot adequately capture, linear CDA can be extended to a nonlinear form via kernel methods. This generalization significantly broadens the applicability of CDA by enabling it to handle nonlinear patterns in the data. Together, linear and kernel-based CDA form a complementary toolkit for classification tasks. A practical strategy is to begin with linear CDA to see whether the predictions are satisfying, which offers fast and interpretable results. Our preliminary results also suggest that extending CDA with nonlinear kernels is a promising direction for future research, since the variety of available kernels broadens the opportunity to tailor the mapping of original data onto higher-dimensional spaces according to the specific structure of the data - where it may become more easily separable.

In conclusion, the GDA framework and its CDA implementation represent a paradigm shift in classifier design, combining the interpretability of geometric principles with state-of-the-art computational efficiency. This work not only advances the field of classification but also lays groundwork for innovative approaches to supervised learning.

Appendix A.1. Difference Between Theory and Theoretical Framework

We emphasize that GDA does not constitute a new theory, but rather a theoretical framework. A theory in data science and machine learning provides a foundational explanation often accompanied by rigorous mathematical derivations, such as performance bounds or convergence guarantees. In contrast, a theoretical framework offers a structured set of concepts and assumptions, typically formalized through equations, that guide the design of methods and the interpretation of results - without necessarily proving theoretical performance guarantees. Within this clarified scope, GDA serves as the framework under which we define and motivate an efficient geometric, centroid-based linear classification method: Centroid Discriminant Analysis (CDA), which is discussed in Section 3.

Appendix A.2. Scaling Invariance of the Discriminants in the GDA Framework

GDA is a geometrical projection-based theoretical framework. In this framework, the discriminant (the high-dimensional vector orthogonal to the classification boundary) of the involved classifiers (including CDA), is normalized to a unit vector before projecting data. The final classification depends solely on these projections; scaling the discriminant length by any factor (including terms like ${\sigma }_{yy}^2/\left|\mathsf{\Sigma }\right|$ in the derivation of GDA by LDA) uniformly scales all projections without changing their relative positions. Consequently, the optimal threshold (which can be found by search) and classification results remain unchanged. This normalization is explicitly implemented in CDA (see, for example, Appendix C.3, Algorithm 1, line 4: “Normalize ${\mathit{w}}_{\mathrm{CDB}1}$ …”), ensuring that only the direction is refined during iterations.

This property distinguishes GDA and CDA from approaches like SVM, where the magnitude of the discriminant vector is tied to the margin width during training. However, even for SVM, once the model is trained, scaling $\mathit{w}$ and b together leaves predictions unchanged because the decision function $y=H({\mathit{w}}^{\mathrm{T}}\mathit{x}+b)$ is homogeneous in $\mathit{w}$ and b. (y: predicted class; $H(·)$: Heaviside function; $\mathit{x}$: sample; b: bias). In CDA training, magnitude carries no interpretive meaning - only direction matters. These also reflect that GDA reinterprets certain existing classifiers from the geometric projection perspective, which is an innovation that inherently differs from their own interpretations.

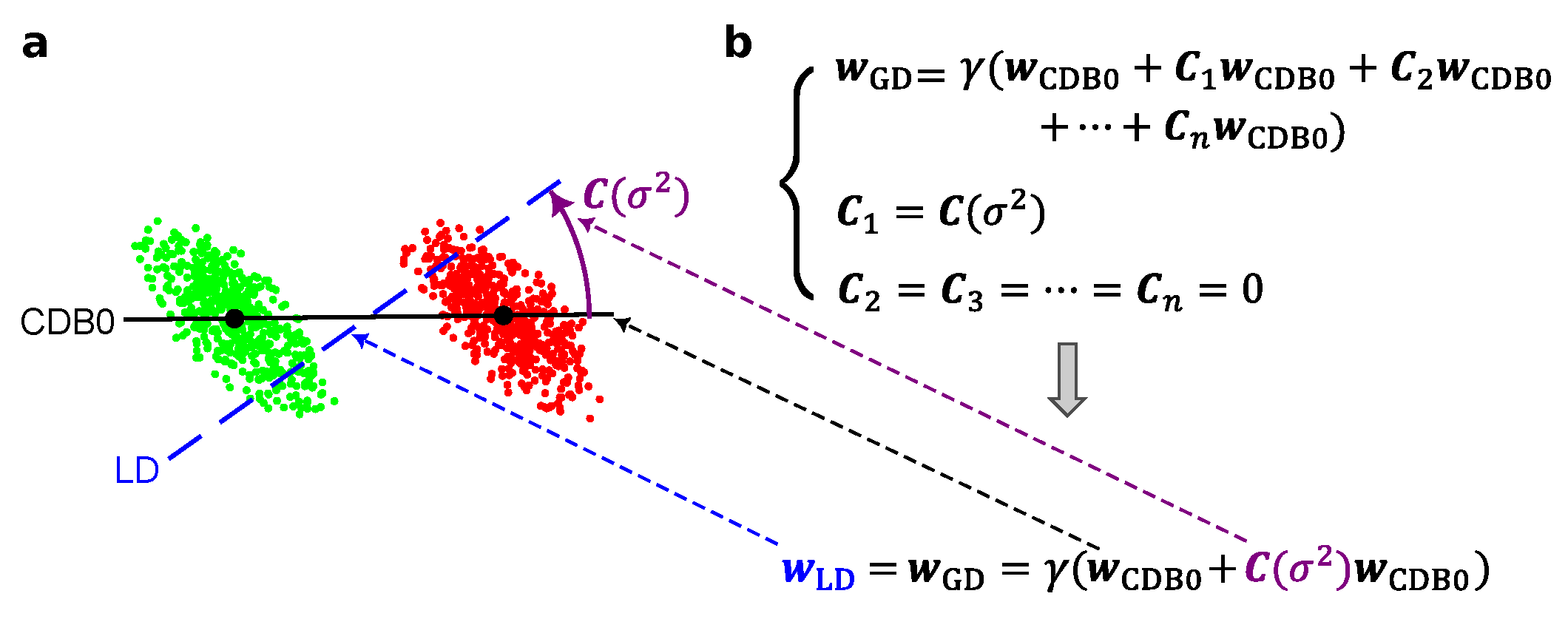
Figure A1. The GDA theoretical framework in 2 dimensions showing how the relation between LD and CDB0 evolves under specific conditions. (a) The relations between LD and CDB0 proceeding from the general case to different special cases under the conditions shown along each arrow. (b) The specific expressions of LD in terms of CDB0 and corrections corresponding to each case in column (a). (c) Binary classifications models of LD (blue dashed) and CDB0 (black solid) on different 2D data corresponding to each case in column (a). The lines show the direction instead of the unit vector of the discriminants. LD: Linear Discriminant; CDB0: Centroid Discriminant Basis 0. $\gamma$ denotes a generic normalizing factor.

Figure A1. The GDA theoretical framework in 2 dimensions showing how the relation between LD and CDB0 evolves under specific conditions. (a) The relations between LD and CDB0 proceeding from the general case to different special cases under the conditions shown along each arrow. (b) The specific expressions of LD in terms of CDB0 and corrections corresponding to each case in column (a). (c) Binary classifications models of LD (blue dashed) and CDB0 (black solid) on different 2D data corresponding to each case in column (a). The lines show the direction instead of the unit vector of the discriminants. LD: Linear Discriminant; CDB0: Centroid Discriminant Basis 0. $\gamma$ denotes a generic normalizing factor.

Appendix A.3. GDA Demonstration with 2D Artificial Data

Appendix C.1. Bayesian Optimization

One factor related to the effectiveness of CDA is the estimation with varying precision in BO. We set the number of BO sampling times to $min(3+rot, 10)$ as default parameter during the CDA rotation, where $rot$ is the $rot$-th rotation. During the first few CDA rotations, the BO estimation has relatively less precision. This gives CDA enough randomness to first enter a large region in which there are more discriminants with high performance, under the hypothesis that regions close to global optimum or suboptimum have more high-performance solutions that are more likely to be randomly selected. Starting from this large region, BO precision is gradually enhanced to refine the search in or close to this region in terms of Euclidean distance, and force CDA to converge. The upper limit of 10 CDA rotations still creates a small level of imprecision, in order to make CDA escape from small-size local minimum, to acquire higher performance, and improve training efficiency.

Appendix C.2. Refining CDA with statistical examination on 2D plane

In CDA, the plane associated with the best performance is selected, but it is uncertain whether there are higher-performance discriminants on this plane, since the precision might not be high enough with 10 BO samplings and even lower for less samplings. To determine whether the BO is precise enough, a statistical examination using p-value with respect to null-model is performed. On this best plane, we generate 100 random CDBs, run BO in turn for 10, 20 and to the maximum 30 BO samplings, until the p-value of training performance-score of the BO-estimated CDB with regard to the null model is 0, otherwise using the best random CDB. In this way, we are able to give a confidence level of the BO estimated discriminant in the best CDA rotation plane. Algorithm A6 shows the pseudocode for the refining finalization step.

Appendix C.3. Linear CDA Pseudocode

This study deals with a supervised binary classification problem on labeled data $\{\mathit{X},\mathit{y}\}={\{{\mathit{x}}_i,y_i\}}_{i=1}^N$ with N samples and M features. The samples consist of positive and negative class data ${\chi }_1$ and ${\chi }_2$ with sizes $N_1$ and $N_2$, respectively, and the corresponding labels are tokenized as 1 and 0, respectively. The sample features are flattened to 1D if they have higher dimensions, such as image data. The following section introduces CDA in pseudo-code. CDA rotations, BO sampling and p-value computing involve constant numbers, thus, they do not contribute to the time complexity.

Algorithm A1 CDA Main Algorithm (CDA)       $O(NM+N\log N)$

Input: $N\times M$ data matrix $\mathit{X}$, $N\times 1$ labels $\mathit{y}$ Initialize $\alpha ={[1;1;\dots ;1]}^{N\times 1}/\sqrt{N}$         $\left\{O\right(N\left)\right\}$ Compute ${\mathit{w}}_{\mathrm{CDB}1}={\displaystyle \sum _{c=1}^2}{(-1)}^{c+1}{\displaystyle \frac{1}{N_c}}{\displaystyle \sum _{{\mathit{x}}_i\in {\chi }_c}}{\alpha }_i{\mathit{x}}_i$       $\left\{O\right(NM\left)\right\}$ Normalize ${\mathit{w}}_{\mathrm{CDB}1}={\mathit{w}}_{\mathrm{CDB}1}/{\parallel {\mathit{w}}_{\mathrm{CDB}1}\parallel }_2$       $\left\{O\right(M\left)\right\}$ Initialize $p{s}^{\ast }=0$        $\left\{O\right(1\left)\right\}$ for $i=1$ to 50 do    $\alpha =\mathrm{updateSampleWeights}(\mathit{X}, \mathit{y}, \alpha , {\mathit{w}}_{\mathrm{CDB}1})$       $\left\{O\right(NM+N\log N\left)\right\}$    Compute ${\mathit{w}}_{\mathrm{CDB}2}={\displaystyle \sum _{c=1}^2}{(-1)}^{c+1}{\displaystyle \frac{1}{N_c}}{\displaystyle \sum _{{\mathit{x}}_i\in {\chi }_c}}{\alpha }_i{\mathit{x}}_i$       $\left\{O\right(NM\left)\right\}$    Normalize ${\mathit{w}}_{\mathrm{CDB}2}={\mathit{w}}_{\mathrm{CDB}2}/{\parallel {\mathit{w}}_{\mathrm{CDB}2}\parallel }_2$         $\left\{O\right(M\left)\right\}$    Set $N_{\mathrm{BO}}=min(i+3, 10)$       $\left\{O\right(1\left)\right\}$ Number of BO sampling    $({\mathit{w}}_{\mathrm{CDA}}, ps)=\mathrm{CdaRotation}({\mathit{w}}_{\mathrm{CDB}1}, {\mathit{w}}_{\mathrm{CDB}2}, \mathit{X}, \mathit{y}, N_{\mathrm{BO}})$       $\left\{O\right(NM+N\log N\left)\right\}$    if $ps>p{s}^{\ast }$ then      $({\mathit{w}}_{\mathrm{CDB}1}^{\ast }, {\mathit{w}}_{\mathrm{CDB}2}^{\ast }, p{s}^{\ast })=({\mathit{w}}_{\mathrm{CDB}1}, {\mathit{w}}_{\mathrm{CDB}2}, ps)$       $\left\{O\right(M\left)\right\}$    end if    if coefficient of variation of the last 10 $ps$ $<0.001$ then      break           {Early stop convergence}    end if    Update ${\mathit{w}}_{\mathrm{CDB}1}={\mathit{w}}_{\mathrm{CDA}}$         $\left\{O\right(M\left)\right\}$ end for Compute $({\mathit{w}}_{\mathrm{CDA}}, oop)=\mathrm{refineOnBestPlane}({\mathit{w}}_{\mathrm{CDB}1}^{\ast }, {\mathit{w}}_{\mathrm{CDB}2}^{\ast },\mathit{X}, \mathit{y})$       $\left\{O\right(NM+N\log N\left)\right\}$ Output: ${\mathit{w}}_{\mathrm{CDA}}, oop$

Algorithm A2 Update Sample Weights (updateSampleWeights)       $O(NM+N\log N)$

Input: $N\times M$ data matrix $\mathit{X}$, $N\times 1$ labels $\mathit{y}$, $N\times 1$ sample weights $\alpha$, $1\times M$ vector ${\mathit{w}}_{\mathrm{CDB}1}$ Initialize $oop=\mathrm{searchOOP}(\mathit{X},\mathit{w})$          $\left\{O\right(N\log N\}$ Compute $\mathit{q}=\mathit{X}{\mathit{w}}_{\mathrm{CDB}1}^{\mathrm{T}}$       $\left\{O\right(NM\left)\right\}$ Compute $d_i=|q_i-oop|,\forall i\in \{1,2,\dots ,N\}$             $\left\{O\right(N\left)\right\}$ Compute ${\mathit{d}}_r=|\mathit{d}-min\left(\mathit{d}\right)-max\left(\mathit{d}\right)|$          $\left\{O\right(N\left)\right\}$ Update $\alpha =\alpha \odot {\mathit{d}}_r/{\parallel \alpha \odot {\mathit{d}}_r\parallel }_2$                $\left\{O\right(N),\odot$ is Hadamard product} Output: $\alpha$

Algorithm A3 Search Optimal Operating Point (searchOOP)       $O\left(N\log N\right)$

Input: $N\times 1$ projected points $\mathit{q}$, $N\times 1$ labels $\mathit{y}$ Sort $(\mathit{q}, \mathit{y})$        $\{O\left(N\log N\right),$ sort according to $\mathit{q}$} Initialize $\mathit{cm}=\mathrm{evaluateMetrics}(\mathit{y}, {\left[\begin{array}{c}0;0;\dots ;0\end{array}\right]}^{N\times 1})$             $\left\{O\right(N\left)\right\}$ initial confusion matrix for $i=1$ to $N-1$ do    Update $\mathit{cm}=\mathrm{updateCM}(y_i, \mathit{cm})$        $\left\{O\right(1\left)\right\}$ scan each label and adjust cm    Compute $p{s}_i=\mathrm{evaluateMetrics}\left(\mathit{cm}\right)$          $\left\{O\right(1\left)\right\}$ end for Compute $idx=arg{max}_{i}p{s}_i$       $\left\{O\right(N\left)\right\}$ Compute $ps=max\left(\mathit{ps}\right)$       $\left\{O\right(N\left)\right\}$ Compute $oop={\displaystyle \frac{q_{idx}+q_{(idx+1)}}{2}}$        $\left\{O\right(1\left)\right\}$ Output: $oop,ps$

Algorithm A4 Approximate Optimal Line by BO (CdaRotation)       $O(NM+N\log N)$

Input: $1\times M$ lines ${\mathit{w}}_{\mathrm{CDB}1}, {\mathit{w}}_{\mathrm{CDB}2}$, $N\times M$ data matrix $\mathit{X}$, $N\times 1$ labels $\mathit{y}$, total BO iteration $N_{\mathrm{BO}}$ Compute ${\mathit{w}}_{\mathrm{orth}}={\mathit{w}}_{\mathrm{CDB}2}-{\mathit{w}}_{\mathrm{CDB}1}^{\mathrm{T}}{\mathit{w}}_{\mathrm{CDB}2}{\mathit{w}}_{\mathrm{CDB}1}$          $\left\{O\right(M\left)\right\}$ Normalize ${\mathit{w}}_{\mathrm{orth}}={\mathit{w}}_{\mathrm{orth}}/{\parallel {\mathit{w}}_{\mathrm{orth}}\parallel }_2$          $\left\{O\right(M\left)\right\}$ Estimate $\widehat{\theta }=\mathrm{BayesianOptimization}(\mathrm{evaluateRotation}(\theta ,{\mathit{w}}_{\mathrm{CDB}1},{\mathit{w}}_{\mathrm{orth}}, \mathit{X}, \mathit{y}), N_{\mathrm{BO}})$, $\theta \in [-{\displaystyle \frac{\pi }{2}}, {\displaystyle \frac{\pi }{2}}]$$\left\{O\right(NM+N\log N\left)\right\}$ Compute ${\mathit{w}}_{\mathrm{CDA}}={\mathit{w}}_{\mathrm{CDB}1}cos\widehat{\theta }+{\mathit{w}}_{\mathrm{orth}}sin\widehat{\theta }$     $\left\{O\right(M\left)\right\}$ Compute $\mathit{q}=\mathit{X}{\mathit{w}}_{\mathrm{CDA}}^T$       $\left\{O\right(NM\left)\right\}$ Get the mean of $(oop, ps)=\mathrm{searchOOP}(\mathit{q}, \mathit{y})$ with 5-fold cross-validation       $\left\{O\right(N\log N\left)\right\}$ Output: ${\mathit{w}}_{\mathrm{CDA}}, oop, ps$

Algorithm A5 Evaluate the Line with Rotation Angle (evaluateRotation)       $O(NM+N\log N)$

Input: Rotation angle $\theta$, $1\times M$ lines ${\mathit{w}}_{\mathrm{CDB}1}, {\mathit{w}}_{\mathrm{orth}}$, $N\times M$ data matrix $\mathit{X}$, $N\times 1$ labels $\mathit{y}$ Compute ${\mathit{w}}_{\mathrm{CDA}}={\mathit{w}}_{\mathrm{CDB}1}cos\theta +{\mathit{w}}_{\mathrm{orth}}sin\theta$         $\left\{O\right(M\left)\right\}$ Compute $\mathit{q}=\mathit{X}{\mathit{w}}_{\mathrm{CDA}}^T$       $\left\{O\right(NM\left)\right\}$ Get mean $ps=\mathrm{searchOOP}(\mathit{q}, \mathit{y})$ with 5-fold cross-validation scheme       $\left\{O\right(N\log N\left)\right\}$ Output: $ps$

Algorithm A6 Refine on the Best Model (refineOnBestPlane)       $O(NM+N\log N)$

Input: $1\times M$${\mathit{w}}_{\mathrm{CDB}1}$ and its orthogonal vector ${\mathit{w}}_{\mathrm{orth}}$, $N\times M$ data matrix $\mathit{X}$, $N\times 1$ labels $\mathit{y}$ for $i=1$ to 100 do    Randomly choose $\theta \in \left[-{\displaystyle \frac{\pi }{2}}, {\displaystyle \frac{\pi }{2}}\right]$       $\left\{O\right(1\left)\right\}$    Compute ${\mathit{w}}_{\mathrm{r}}={\mathit{w}}_{\mathrm{CDB}1}cos\theta +{\mathit{w}}_{\mathrm{orth}}sin\theta$       $\left\{O\right(M\left)\right\}$    Compute $\mathit{q}=\mathit{X}{\mathit{w}}_{\mathrm{r}}^{\mathrm{T}}$       $\left\{O\right(NM\left)\right\}$    Get mean ${(oo{p}_{\mathrm{r}}, p{s}_{\mathrm{r}})}_i=\mathrm{searchOOP}(\mathit{q}, \mathit{y})$ with 5-fold cross-validation       $\left\{O\right(N\log N\left)\right\}$ end for Sort $idx=\mathrm{sortIdx}\left([ps, p{s}_{\mathrm{r}}]\right)$         $\left\{O\right(1\left)\right\}$ sort returning position indices Compute $p=1-{\displaystyle \frac{\left(idx\right(1)-1)}{N_r}}$       $\left\{O\right(1\left)\right\}$ Initialize $N_{\mathrm{BO}}=0$ while $p\ne 0$ and $N_{\mathrm{BO}}<30$ do    Increment $N_{\mathrm{BO}}=N_{\mathrm{BO}}+10$    Compute $({\mathit{w}}_{\mathrm{CDA}}, oop, ps)=\mathrm{CdaRotation}({\mathit{w}}_{\mathrm{CDB}1},{\mathit{w}}_{\mathrm{CDB}2}, \mathit{X}, \mathit{y}, N_{\mathrm{BO}})$       $\left\{O\right(NM+N\log N\left)\right\}$    Sort $idx=\mathrm{sortIdx}\left([ps, {\mathrm{ps}}_r]\right)$         $\left\{O\right(1\left)\right\}$ sort returning position indices    Compute $p=1-{\displaystyle \frac{\left(idx\right(1)-1)}{N_r}}$      $\left\{O\right(1\left)\right\}$ end while if $p\ne 0$ then    Compute $i=arg{min}_{i}p{s}_{\mathrm{r}, i}$       $\left\{O\right(1\left)\right\}$    Set $({\mathit{w}}_{\mathrm{CDA}}, oop, ps)={({\mathit{w}}_r, oo{p}_{\mathrm{r}}, p{s}_{\mathrm{r}})}_i$       $\left\{O\right(1\left)\right\}$ end if Output: ${\mathit{w}}_{\mathrm{CDA}}, oop, ps$

Appendix C.4. Nonlinear kernel CDA

The CDA algorithm involves computing the CDBs using the equation provided in Appendix C.3, Algorithm 1:

$${\mathit{w}}_{\mathrm{CDB}}=\sum _{c=1}^2{(-1)}^{c+1}·{\displaystyle \frac{1}{N_c}}\sum _{{\mathit{x}}_i\in {\chi }_c}{\alpha }_i{\mathit{x}}_i$$

(A1)

Combining this with the normalization step for each CDB ${\mathit{w}}_{\mathrm{CDB}}\leftarrow {\mathit{w}}_{\mathrm{CDB}}/{\parallel {\mathit{w}}_{\mathrm{CDB}}\parallel }_2$, the equation can be rewritten as:

$${\mathit{w}}_{\mathrm{CDB}}={(\alpha \odot \mathit{n}\odot {\mathit{y}}_t·k)}^{\top }\mathit{X}={\beta }^{\top }\mathit{X},$$

(A2)

where $\alpha$ is the vector of sample weights; $\mathit{n}=[1/N_{\mathrm{map}\left(i\right)}]$ for all $i\in \{1,2,\dots ,N\}$ is the weight sum division for each class, and $\mathrm{map}\left(i\right)$ maps sample index i to class index c; ${\mathit{y}}_t={(-1)}^{c+1}$ are the tokenized labels ($+1$ or $-1$); k is the factor to normalize each CDB as a unit vector.

For the rotated CDBs used in Bayesian optimization (Appendix B, Algorithms 4–5), they can be expressed as linear combinations of CDB1 and orthogonalized CDB2, mixing their corresponding $\mathit{\beta }$ vectors. Thus, the sample coefficient $\mathit{\beta }$ is tracked throughout the training process for each CDB.

The data projection can be expressed as:

$$\mathit{q}=\mathit{X}{\mathit{w}}_{\mathrm{CDB}}^{\top }=\mathit{X}{\left({\mathit{\beta }}^{\top }\mathit{X}\right)}^{\top }=\mathit{X}{\mathit{X}}^{\top }\mathit{\beta }$$

(A3)

With this expression, the data projection can incorporate kernel methods to realize nonlinear classification, shown by the following equation.

$$\mathit{q}=Ker(\mathit{X},{\mathit{X}}^{\top })\mathit{\beta }$$

(A4)

In fact, kernel methods implicitly projects data into a high-dimensional space, then applying linear classifiers in the transformed feature space.

Appendix I.1. Linear Classifiers

Linear classifiers compared in this study include LDA, SVM, and fast SVM. Data were input to classifiers in their original values without standardization.

For CDA, the threshold for the coefficient of variation (CV) of performance-score was set to 0.001. 5-fold cross-validation is applied on the OOP search.

For LDA, the MATLAB toolbox function fitcdiscr was applied, with pseudolinear as the discriminant type, which solves the pseudo-inverse with SVD to adapt to poorly conditioned covariance matrices.

For SVM, the MATLAB toolbox function fitcsvm was applied, with sequential minimal optimization (SMO) as the optimizer. The cost function used the L2-regularized (margin) L1-loss (misclassification) form. The misclassification cost coefficient was set to $C=1$ by default. The maximum number of iterations was linked to the number of training samples in the binary pair as $100\times N_{\mathrm{train}}$. The convergence criteria were set to the default values.

For fast SVM, the LIBLINEAR MATLAB mex function was applied. For the dual form SVM using dual coordinate descent (DCD), the cost function used the L2-regularized (margin) L1-loss (misclassification) form; For the primal form SVM, both regularization and loss are in L2 form. The misclassification cost coefficient was set to $C=1$ by default. A bias term was added, and correspondingly, the data had an additional dimension with a value of 1. The convergence criteria were set to the default values. Training epochs were set to 300 in general tasks and 100 in large-scale single-cell test.

For SVM-SGD, the passes of all training data are 10; batchsize is 10; learning rate is $1/\sqrt{1+{max}_i\parallel {\mathit{x}}_i{\parallel }_2}$.

Hyperparameter tuning was performed for fast SVM to achieve the its best performance. CDA, as well as CDB0, do not require parameter tuning.

Speed tests and performance test were from different computational conditions. To obtain classification performance in a reasonable time span, GPU was enabled for SVM, and multicore was enabled for CDA and LDA. To compare speed fairly, all linear classifiers used single-core computing mode.

Appendix I.2. Nonlinear Classifiers

For the experiments on the nonlinear kernel-based approaches, on SVHN subset and chemical Clintox, the data were first divided into train+validation and test set with 5:1 and 4:1 ratio respectively, then the train+validation set was further divided into train set and validation set with a 4:1 ratio.

The gaussian kernel parameter sigma was tuned on the validation set by Bayesian optimization with 30 sampling. For the tuned gaussian parameter, on SVHN subset gaussian CDA has $coeff=0.2$ and gaussian SVM has $coeff=0.134$; on ClinTox gaussian CDA has $coeff=1.34$ and gaussian SVM has $coeff=68.9$, where in gaussian kernel ${\sigma }^2=coeff\ast \mathrm{median}(\mathrm{pairwiseSquareEuclideanDistance}\left(X_{\mathrm{train}}\right))$.

For CDA, the threshold for the coefficient of variation (CV) of performance-score was set to 0.001. For SVM, libSVM was implemented with L2-regularized (margin) L1-loss (misclassification) cost function and with default misclassification cost coefficient $C=1$.

Appendix K.1. Binary classification

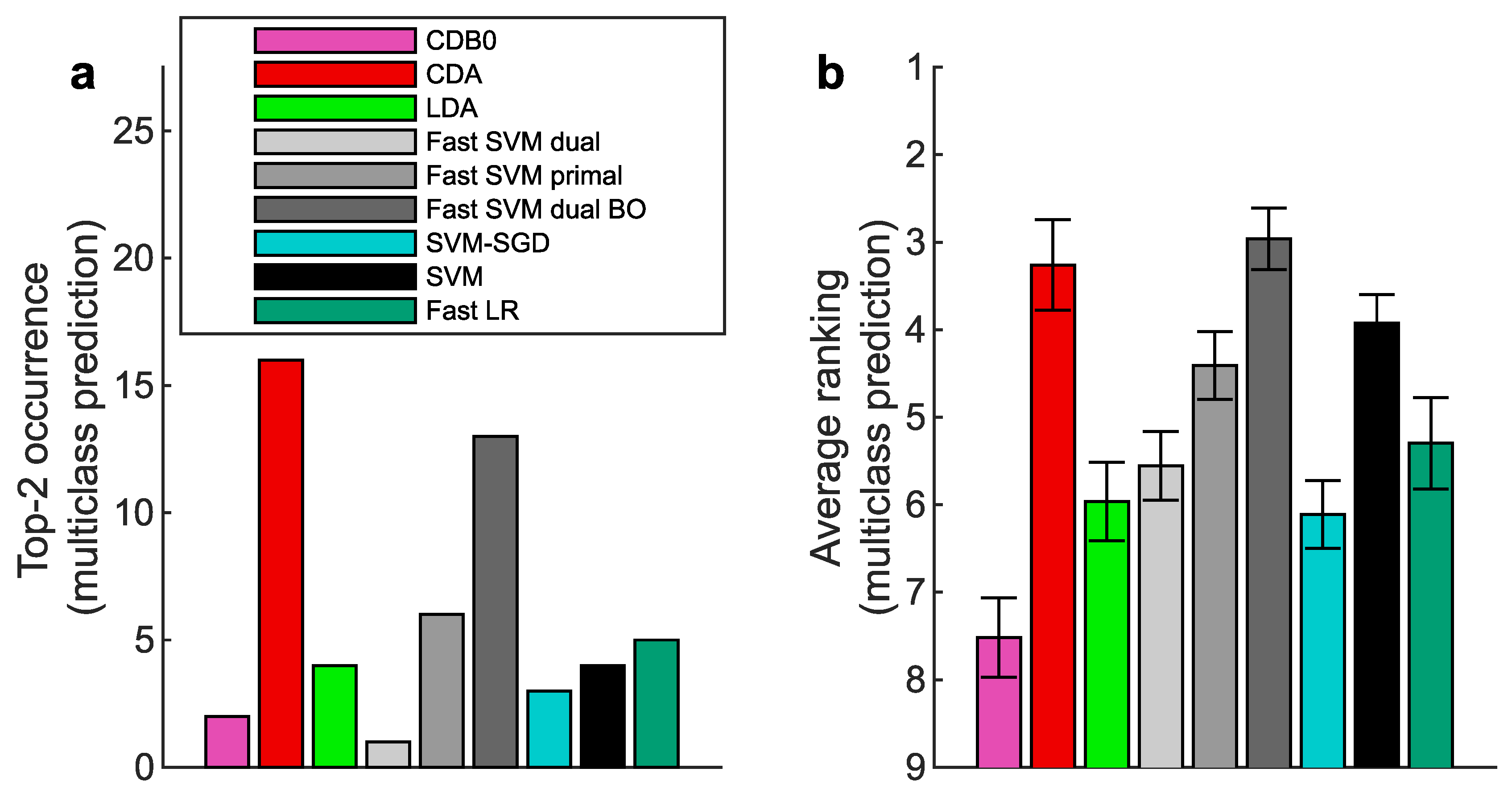
Figure A6. Binary classification performance on 27 real datasets according to AUROC. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A6. Binary classification performance on 27 real datasets according to AUROC. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A7. Binary classification performance on 27 real datasets according to AUPR. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A7. Binary classification performance on 27 real datasets according to AUPR. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A8. Binary classification performance on 27 real datasets according to F-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A8. Binary classification performance on 27 real datasets according to F-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A9. Binary classification performance on 27 real datasets according to AC-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A9. Binary classification performance on 27 real datasets according to AC-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Appendix K.2. Multiclass prediction

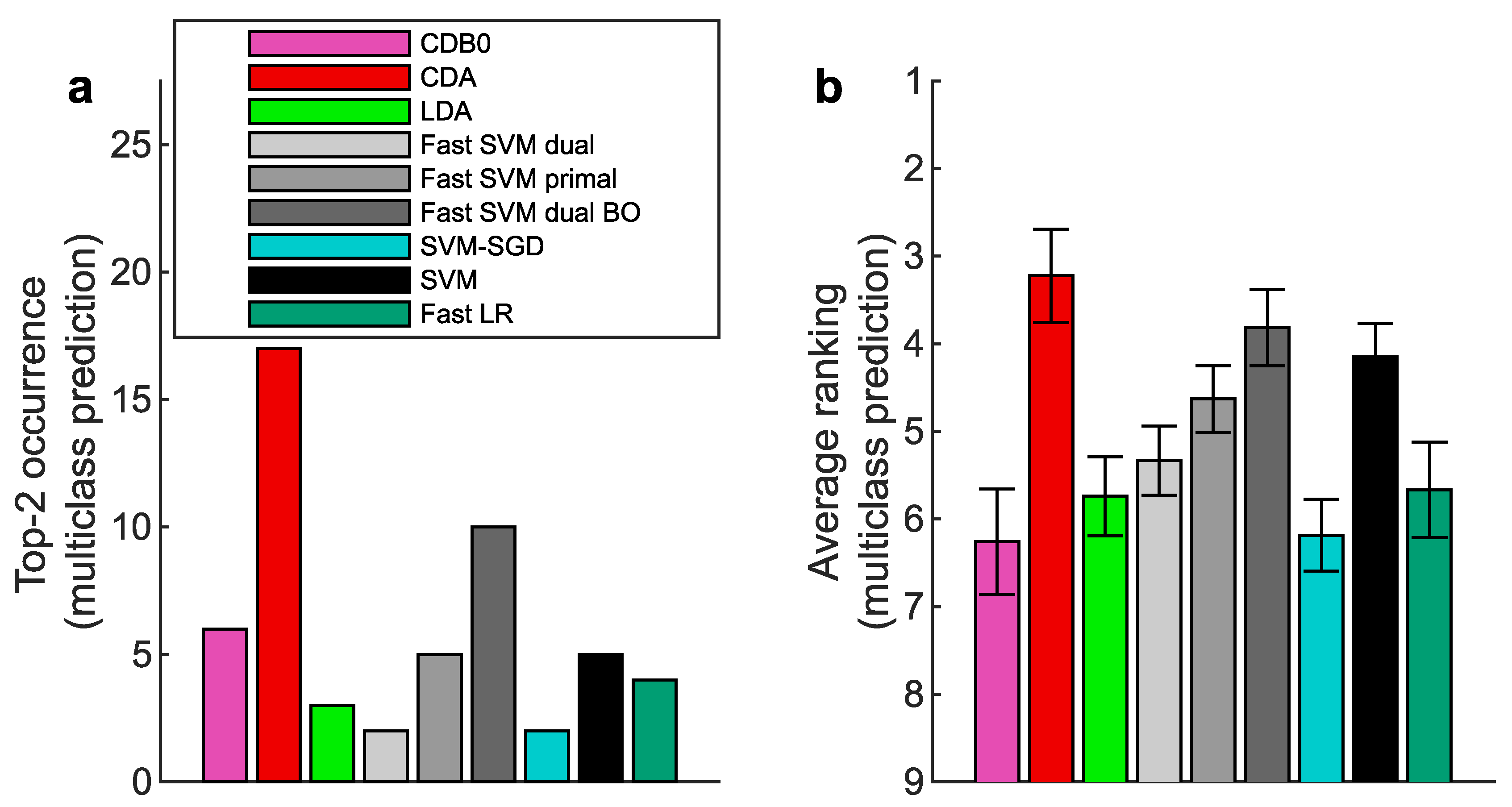
Figure A10. Multiclass prediction performance on 27 real datasets according to AUPR. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A10. Multiclass prediction performance on 27 real datasets according to AUPR. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A11. Multiclass prediction performance on 27 real datasets according to F-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A11. Multiclass prediction performance on 27 real datasets according to F-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A12. Multiclass prediction performance on 27 real datasets according to AC-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Figure A12. Multiclass prediction performance on 27 real datasets according to AC-score. (a) Top-2 occurrences of algorithms. (b) Average ranking of algorithms. Error bars represent standard errors. CDB0: Centroid Discriminant Basis 0; CDA: Centroid Discriminant Analysis; LDA: Linear Discriminant Analysis; SVM: Support Vector Machine; LR: Logistic Regression; BO: Bayesian Optimization

Appendix L.1. Binary classification

Table A2. AUROC (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.982±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.696±0.01	0.797±0.01	0.741±0.01	0.754±0.01	0.784±0.01	0.807±0.01	0.762±0.01	0.787±0.01	0.757±0.02
SVHN	0.528±0.003	0.667±0.005	0.555±0.003	0.55±0.004	0.578±0.004	0.592±0.005	0.537±0.003	0.591±0.004	0.57±0.008
flower	0.703±0.02	0.739±0.02	0.571±0.01	0.71±0.03	0.705±0.03	0.754±0.03	0.722±0.03	0.71±0.03	0.734±0.02
GTSRB	0.767±0.003	0.972±0.001	0.942±0.002	0.995±0.0004	0.995±0.0003	0.995±0.0004	0.99±0.0006	0.995±0.0004	0.994±0.0004
STL10	0.723±0.02	0.781±0.02	0.667±0.01	0.758±0.02	0.757±0.02	0.791±0.02	0.766±0.02	0.761±0.02	0.712±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
ermamnist	0.682±0.01	0.753±0.02	0.684±0.02	0.676±0.02	0.708±0.02	0.698±0.02	0.608±0.02	0.712±0.02	0.663±0.03
pneumoniamnist	0.837±0	0.933±0	0.912±0	0.941±0	0.943±0	0.941±0	0.942±0	0.941±0	0.944±0
retinamnist	0.63±0.03	0.662±0.04	0.616±0.02	0.631±0.03	0.626±0.02	0.632±0.03	0.615±0.03	0.622±0.03	0.619±0.03
breastmnist	0.66±0	0.763±0	0.703±0	0.726±0	0.757±0	0.705±0	0.734±0	0.709±0	0.688±0
bloodmnist	0.89±0.02	0.947±0.01	0.898±0.02	0.951±0.01	0.955±0.01	0.955±0.01	0.946±0.01	0.957±0.01	0.955±0.01
organamnist	0.897±0.009	0.948±0.008	0.95±0.008	0.928±0.01	0.953±0.008	0.958±0.008	0.939±0.01	0.957±0.008	0.954±0.008
organcmnist	0.89±0.01	0.925±0.01	0.908±0.01	0.895±0.01	0.913±0.01	0.928±0.01	0.911±0.01	0.919±0.01	0.902±0.02
organsmnist	0.831±0.01	0.886±0.01	0.866±0.01	0.842±0.02	0.871±0.01	0.888±0.01	0.853±0.02	0.88±0.01	0.844±0.03
organmnist3d	0.924±0.01	0.957±0.008	0.953±0.008	0.965±0.007	0.966±0.007	0.966±0.007	0.962±0.007	0.966±0.007	0.937±0.02
nodulemnist3d	0.715±0	0.781±0	0.732±0	0.687±0	0.702±0	0.735±0	0.691±0	0.724±0	0.743±0
fracturemnist3d	0.671±0.06	0.556±0.03	0.525±0.04	0.576±0.007	0.578±0.008	0.6±0.004	0.592±0.004	0.612±0.007	0.592±0.01
adrenalmnist3d	0.653±0	0.756±0	0.692±0	0.697±0	0.619±0	0.647±0	0.637±0	0.665±0	0.641±0
vesselmnist3d	0.605±0	0.685±0	0.681±0	0.61±0	0.648±0	0.628±0	0.604±0	0.6±0	0.584±0
synapsemnist3d	0.539±0	0.544±0	0.508±0	0.518±0	0.527±0	0.518±0	0.525±0	0.539±0	0.517±0
Chemical formula
bace	0.621±0	0.705±0	0.684±0	0.618±0	0.677±0	0.697±0	0.639±0	0.637±0	0.693±0
BBBP	0.711±0	0.743±0	0.693±0	0.667±0	0.707±0	0.71±0	0.646±0	0.697±0	0.712±0
clintox	0.65±0	0.575±0	0.543±0	0.517±0	0.515±0	0.519±0	0.508±0	0.514±0	0.515±0
HIV	0.6±0	0.616±0	0.537±0	0.51±0	0.506±0	0.51±0	0.505±0	0.506±0	0.51±0

Table A2. AUROC (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.982±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.696±0.01	0.797±0.01	0.741±0.01	0.754±0.01	0.784±0.01	0.807±0.01	0.762±0.01	0.787±0.01	0.757±0.02
SVHN	0.528±0.003	0.667±0.005	0.555±0.003	0.55±0.004	0.578±0.004	0.592±0.005	0.537±0.003	0.591±0.004	0.57±0.008
flower	0.703±0.02	0.739±0.02	0.571±0.01	0.71±0.03	0.705±0.03	0.754±0.03	0.722±0.03	0.71±0.03	0.734±0.02
GTSRB	0.767±0.003	0.972±0.001	0.942±0.002	0.995±0.0004	0.995±0.0003	0.995±0.0004	0.99±0.0006	0.995±0.0004	0.994±0.0004
STL10	0.723±0.02	0.781±0.02	0.667±0.01	0.758±0.02	0.757±0.02	0.791±0.02	0.766±0.02	0.761±0.02	0.712±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
ermamnist	0.682±0.01	0.753±0.02	0.684±0.02	0.676±0.02	0.708±0.02	0.698±0.02	0.608±0.02	0.712±0.02	0.663±0.03
pneumoniamnist	0.837±0	0.933±0	0.912±0	0.941±0	0.943±0	0.941±0	0.942±0	0.941±0	0.944±0
retinamnist	0.63±0.03	0.662±0.04	0.616±0.02	0.631±0.03	0.626±0.02	0.632±0.03	0.615±0.03	0.622±0.03	0.619±0.03
breastmnist	0.66±0	0.763±0	0.703±0	0.726±0	0.757±0	0.705±0	0.734±0	0.709±0	0.688±0
bloodmnist	0.89±0.02	0.947±0.01	0.898±0.02	0.951±0.01	0.955±0.01	0.955±0.01	0.946±0.01	0.957±0.01	0.955±0.01
organamnist	0.897±0.009	0.948±0.008	0.95±0.008	0.928±0.01	0.953±0.008	0.958±0.008	0.939±0.01	0.957±0.008	0.954±0.008
organcmnist	0.89±0.01	0.925±0.01	0.908±0.01	0.895±0.01	0.913±0.01	0.928±0.01	0.911±0.01	0.919±0.01	0.902±0.02
organsmnist	0.831±0.01	0.886±0.01	0.866±0.01	0.842±0.02	0.871±0.01	0.888±0.01	0.853±0.02	0.88±0.01	0.844±0.03
organmnist3d	0.924±0.01	0.957±0.008	0.953±0.008	0.965±0.007	0.966±0.007	0.966±0.007	0.962±0.007	0.966±0.007	0.937±0.02
nodulemnist3d	0.715±0	0.781±0	0.732±0	0.687±0	0.702±0	0.735±0	0.691±0	0.724±0	0.743±0
fracturemnist3d	0.671±0.06	0.556±0.03	0.525±0.04	0.576±0.007	0.578±0.008	0.6±0.004	0.592±0.004	0.612±0.007	0.592±0.01
adrenalmnist3d	0.653±0	0.756±0	0.692±0	0.697±0	0.619±0	0.647±0	0.637±0	0.665±0	0.641±0
vesselmnist3d	0.605±0	0.685±0	0.681±0	0.61±0	0.648±0	0.628±0	0.604±0	0.6±0	0.584±0
synapsemnist3d	0.539±0	0.544±0	0.508±0	0.518±0	0.527±0	0.518±0	0.525±0	0.539±0	0.517±0
Chemical formula
bace	0.621±0	0.705±0	0.684±0	0.618±0	0.677±0	0.697±0	0.639±0	0.637±0	0.693±0
BBBP	0.711±0	0.743±0	0.693±0	0.667±0	0.707±0	0.71±0	0.646±0	0.697±0	0.712±0
clintox	0.65±0	0.575±0	0.543±0	0.517±0	0.515±0	0.519±0	0.508±0	0.514±0	0.515±0
HIV	0.6±0	0.616±0	0.537±0	0.51±0	0.506±0	0.51±0	0.505±0	0.506±0	0.51±0

Table A3. AUPR (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.983±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.697±0.01	0.797±0.01	0.741±0.01	0.762±0.01	0.784±0.01	0.807±0.01	0.774±0.01	0.787±0.01	0.757±0.02
SVHN	0.528±0.003	0.682±0.006	0.559±0.003	0.577±0.005	0.604±0.004	0.638±0.006	0.566±0.005	0.634±0.006	0.587±0.009
flower	0.704±0.02	0.741±0.02	0.571±0.01	0.712±0.03	0.707±0.03	0.759±0.03	0.73±0.03	0.712±0.03	0.736±0.02
GTSRB	0.757±0.003	0.973±0.001	0.934±0.002	0.995±0.0003	0.996±0.0003	0.996±0.0003	0.991±0.0005	0.995±0.0003	0.995±0.0003
STL10	0.724±0.02	0.782±0.02	0.667±0.01	0.759±0.02	0.757±0.02	0.791±0.02	0.772±0.02	0.762±0.02	0.713±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.977±0.006
Medical images
dermamnist	0.653±0.01	0.743±0.02	0.681±0.02	0.729±0.02	0.746±0.02	0.744±0.02	0.646±0.03	0.752±0.02	0.717±0.03
pneumoniamnist	0.817±0	0.931±0	0.922±0	0.937±0	0.944±0	0.946±0	0.927±0	0.945±0	0.946±0
retinamnist	0.614±0.03	0.649±0.03	0.612±0.02	0.641±0.02	0.634±0.02	0.637±0.03	0.622±0.03	0.632±0.03	0.631±0.03
breastmnist	0.653±0	0.759±0	0.69±0	0.743±0	0.766±0	0.718±0	0.726±0	0.725±0	0.736±0
bloodmnist	0.889±0.02	0.947±0.01	0.895±0.02	0.953±0.01	0.955±0.01	0.957±0.01	0.945±0.01	0.957±0.01	0.956±0.01
organamnist	0.902±0.009	0.95±0.007	0.951±0.008	0.929±0.01	0.953±0.008	0.959±0.008	0.941±0.01	0.957±0.008	0.955±0.008
organcmnist	0.901±0.009	0.931±0.009	0.908±0.01	0.893±0.01	0.911±0.01	0.932±0.009	0.913±0.01	0.918±0.01	0.902±0.02
organsmnist	0.839±0.01	0.892±0.01	0.867±0.01	0.84±0.02	0.87±0.01	0.894±0.01	0.86±0.02	0.88±0.01	0.845±0.03
organmnist3d	0.924±0.009	0.958±0.008	0.954±0.008	0.965±0.007	0.966±0.007	0.967±0.007	0.963±0.007	0.967±0.007	0.937±0.02
nodulemnist3d	0.7±0	0.771±0	0.745±0	0.695±0	0.709±0	0.749±0	0.711±0	0.732±0	0.752±0
fracturemnist3d	0.663±0.05	0.566±0.02	0.531±0.05	0.583±0.003	0.586±0.008	0.606±0.004	0.6±0.006	0.618±0.01	0.608±0.01
adrenalmnist3d	0.65±0	0.774±0	0.705±0	0.708±0	0.627±0	0.663±0	0.657±0	0.689±0	0.665±0
vesselmnist3d	0.582±0	0.671±0	0.694±0	0.627±0	0.7±0	0.692±0	0.668±0	0.646±0	0.661±0
synapsemnist3d	0.537±0	0.542±0	0.544±0	0.533±0	0.558±0	0.533±0	0.538±0	0.572±0	0.546±0
Chemical formula
bace	0.62±0	0.704±0	0.685±0	0.643±0	0.679±0	0.699±0	0.652±0	0.64±0	0.695±0
BBBP	0.701±0	0.747±0	0.734±0	0.712±0	0.743±0	0.751±0	0.701±0	0.723±0	0.742±0
clintox	0.602±0	0.57±0	0.548±0	0.553±0	0.54±0	0.575±0	0.514±0	0.53±0	0.54±0
HIV	0.565±0	0.583±0	0.558±0	0.612±0	0.578±0	0.584±0	0.601±0	0.585±0	0.596±0

Table A3. AUPR (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.983±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.697±0.01	0.797±0.01	0.741±0.01	0.762±0.01	0.784±0.01	0.807±0.01	0.774±0.01	0.787±0.01	0.757±0.02
SVHN	0.528±0.003	0.682±0.006	0.559±0.003	0.577±0.005	0.604±0.004	0.638±0.006	0.566±0.005	0.634±0.006	0.587±0.009
flower	0.704±0.02	0.741±0.02	0.571±0.01	0.712±0.03	0.707±0.03	0.759±0.03	0.73±0.03	0.712±0.03	0.736±0.02
GTSRB	0.757±0.003	0.973±0.001	0.934±0.002	0.995±0.0003	0.996±0.0003	0.996±0.0003	0.991±0.0005	0.995±0.0003	0.995±0.0003
STL10	0.724±0.02	0.782±0.02	0.667±0.01	0.759±0.02	0.757±0.02	0.791±0.02	0.772±0.02	0.762±0.02	0.713±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.977±0.006
Medical images
dermamnist	0.653±0.01	0.743±0.02	0.681±0.02	0.729±0.02	0.746±0.02	0.744±0.02	0.646±0.03	0.752±0.02	0.717±0.03
pneumoniamnist	0.817±0	0.931±0	0.922±0	0.937±0	0.944±0	0.946±0	0.927±0	0.945±0	0.946±0
retinamnist	0.614±0.03	0.649±0.03	0.612±0.02	0.641±0.02	0.634±0.02	0.637±0.03	0.622±0.03	0.632±0.03	0.631±0.03
breastmnist	0.653±0	0.759±0	0.69±0	0.743±0	0.766±0	0.718±0	0.726±0	0.725±0	0.736±0
bloodmnist	0.889±0.02	0.947±0.01	0.895±0.02	0.953±0.01	0.955±0.01	0.957±0.01	0.945±0.01	0.957±0.01	0.956±0.01
organamnist	0.902±0.009	0.95±0.007	0.951±0.008	0.929±0.01	0.953±0.008	0.959±0.008	0.941±0.01	0.957±0.008	0.955±0.008
organcmnist	0.901±0.009	0.931±0.009	0.908±0.01	0.893±0.01	0.911±0.01	0.932±0.009	0.913±0.01	0.918±0.01	0.902±0.02
organsmnist	0.839±0.01	0.892±0.01	0.867±0.01	0.84±0.02	0.87±0.01	0.894±0.01	0.86±0.02	0.88±0.01	0.845±0.03
organmnist3d	0.924±0.009	0.958±0.008	0.954±0.008	0.965±0.007	0.966±0.007	0.967±0.007	0.963±0.007	0.967±0.007	0.937±0.02
nodulemnist3d	0.7±0	0.771±0	0.745±0	0.695±0	0.709±0	0.749±0	0.711±0	0.732±0	0.752±0
fracturemnist3d	0.663±0.05	0.566±0.02	0.531±0.05	0.583±0.003	0.586±0.008	0.606±0.004	0.6±0.006	0.618±0.01	0.608±0.01
adrenalmnist3d	0.65±0	0.774±0	0.705±0	0.708±0	0.627±0	0.663±0	0.657±0	0.689±0	0.665±0
vesselmnist3d	0.582±0	0.671±0	0.694±0	0.627±0	0.7±0	0.692±0	0.668±0	0.646±0	0.661±0
synapsemnist3d	0.537±0	0.542±0	0.544±0	0.533±0	0.558±0	0.533±0	0.538±0	0.572±0	0.546±0
Chemical formula
bace	0.62±0	0.704±0	0.685±0	0.643±0	0.679±0	0.699±0	0.652±0	0.64±0	0.695±0
BBBP	0.701±0	0.747±0	0.734±0	0.712±0	0.743±0	0.751±0	0.701±0	0.723±0	0.742±0
clintox	0.602±0	0.57±0	0.548±0	0.553±0	0.54±0	0.575±0	0.514±0	0.53±0	0.54±0
HIV	0.565±0	0.583±0	0.558±0	0.612±0	0.578±0	0.584±0	0.601±0	0.585±0	0.596±0

Table A4. F-score (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.983±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.696±0.01	0.797±0.01	0.741±0.01	0.747±0.01	0.784±0.01	0.807±0.01	0.751±0.02	0.787±0.01	0.757±0.02
SVHN	0.523±0.003	0.664±0.005	0.555±0.003	0.51±0.01	0.568±0.005	0.574±0.007	0.471±0.01	0.577±0.006	0.563±0.009
flower	0.701±0.02	0.738±0.02	0.57±0.01	0.709±0.03	0.705±0.03	0.754±0.03	0.715±0.03	0.709±0.03	0.734±0.03
GTSRB	0.743±0.003	0.972±0.001	0.931±0.002	0.995±0.0003	0.996±0.0003	0.996±0.0003	0.99±0.0005	0.995±0.0003	0.995±0.0003
STL10	0.722±0.02	0.781±0.02	0.666±0.01	0.756±0.02	0.756±0.02	0.791±0.02	0.76±0.02	0.761±0.02	0.712±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
dermamnist	0.621±0.02	0.736±0.02	0.677±0.02	0.682±0.03	0.726±0.02	0.722±0.02	0.595±0.03	0.731±0.02	0.68±0.04
pneumoniamnist	0.812±0	0.931±0	0.921±0	0.937±0	0.944±0	0.945±0	0.925±0	0.944±0	0.946±0
retinamnist	0.594±0.02	0.639±0.03	0.61±0.02	0.611±0.04	0.611±0.04	0.631±0.03	0.586±0.04	0.623±0.03	0.619±0.03
breastmnist	0.651±0	0.759±0	0.684±0	0.739±0	0.765±0	0.716±0	0.725±0	0.722±0	0.712±0
bloodmnist	0.888±0.02	0.947±0.01	0.894±0.02	0.952±0.01	0.955±0.01	0.957±0.01	0.943±0.01	0.957±0.01	0.955±0.01
organamnist	0.899±0.01	0.949±0.008	0.951±0.008	0.923±0.02	0.953±0.008	0.959±0.008	0.939±0.01	0.957±0.008	0.955±0.008
organcmnist	0.896±0.01	0.929±0.009	0.908±0.01	0.892±0.02	0.911±0.01	0.932±0.009	0.911±0.01	0.918±0.01	0.901±0.02
organsmnist	0.834±0.01	0.89±0.01	0.866±0.01	0.834±0.02	0.869±0.01	0.893±0.01	0.85±0.02	0.88±0.01	0.844±0.03
organmnist3d	0.92±0.01	0.957±0.008	0.953±0.008	0.964±0.007	0.966±0.007	0.966±0.007	0.962±0.007	0.966±0.007	0.937±0.02
nodulemnist3d	0.695±0	0.769±0	0.743±0	0.694±0	0.708±0	0.747±0	0.706±0	0.731±0	0.751±0
fracturemnist3d	0.651±0.05	0.523±0.03	0.514±0.05	0.577±0.007	0.579±0.007	0.602±0.003	0.594±0.004	0.615±0.009	0.593±0.01
adrenalmnist3d	0.65±0	0.771±0	0.703±0	0.707±0	0.625±0	0.659±0	0.651±0	0.681±0	0.656±0
vesselmnist3d	0.56±0	0.669±0	0.693±0	0.623±0	0.681±0	0.663±0	0.635±0	0.625±0	0.611±0
synapsemnist3d	0.534±0	0.539±0	0.45±0	0.493±0	0.501±0	0.493±0	0.511±0	0.522±0	0.48±0
Chemical formula
bace	0.619±0	0.704±0	0.684±0	0.569±0	0.678±0	0.698±0	0.634±0	0.637±0	0.694±0
BBBP	0.699±0	0.747±0	0.718±0	0.691±0	0.731±0	0.736±0	0.669±0	0.716±0	0.733±0
clintox	0.54±0	0.569±0	0.547±0	0.517±0	0.515±0	0.52±0	0.506±0	0.513±0	0.515±0
HIV	0.531±0	0.562±0	0.548±0	0.511±0	0.504±0	0.511±0	0.501±0	0.504±0	0.511±0

Table A4. F-score (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.983±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.928±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.97±0.001	0.973±0.001	0.97±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.696±0.01	0.797±0.01	0.741±0.01	0.747±0.01	0.784±0.01	0.807±0.01	0.751±0.02	0.787±0.01	0.757±0.02
SVHN	0.523±0.003	0.664±0.005	0.555±0.003	0.51±0.01	0.568±0.005	0.574±0.007	0.471±0.01	0.577±0.006	0.563±0.009
flower	0.701±0.02	0.738±0.02	0.57±0.01	0.709±0.03	0.705±0.03	0.754±0.03	0.715±0.03	0.709±0.03	0.734±0.03
GTSRB	0.743±0.003	0.972±0.001	0.931±0.002	0.995±0.0003	0.996±0.0003	0.996±0.0003	0.99±0.0005	0.995±0.0003	0.995±0.0003
STL10	0.722±0.02	0.781±0.02	0.666±0.01	0.756±0.02	0.756±0.02	0.791±0.02	0.76±0.02	0.761±0.02	0.712±0.03
FMNIST	0.937±0.01	0.975±0.006	0.973±0.006	0.976±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
dermamnist	0.621±0.02	0.736±0.02	0.677±0.02	0.682±0.03	0.726±0.02	0.722±0.02	0.595±0.03	0.731±0.02	0.68±0.04
pneumoniamnist	0.812±0	0.931±0	0.921±0	0.937±0	0.944±0	0.945±0	0.925±0	0.944±0	0.946±0
retinamnist	0.594±0.02	0.639±0.03	0.61±0.02	0.611±0.04	0.611±0.04	0.631±0.03	0.586±0.04	0.623±0.03	0.619±0.03
breastmnist	0.651±0	0.759±0	0.684±0	0.739±0	0.765±0	0.716±0	0.725±0	0.722±0	0.712±0
bloodmnist	0.888±0.02	0.947±0.01	0.894±0.02	0.952±0.01	0.955±0.01	0.957±0.01	0.943±0.01	0.957±0.01	0.955±0.01
organamnist	0.899±0.01	0.949±0.008	0.951±0.008	0.923±0.02	0.953±0.008	0.959±0.008	0.939±0.01	0.957±0.008	0.955±0.008
organcmnist	0.896±0.01	0.929±0.009	0.908±0.01	0.892±0.02	0.911±0.01	0.932±0.009	0.911±0.01	0.918±0.01	0.901±0.02
organsmnist	0.834±0.01	0.89±0.01	0.866±0.01	0.834±0.02	0.869±0.01	0.893±0.01	0.85±0.02	0.88±0.01	0.844±0.03
organmnist3d	0.92±0.01	0.957±0.008	0.953±0.008	0.964±0.007	0.966±0.007	0.966±0.007	0.962±0.007	0.966±0.007	0.937±0.02
nodulemnist3d	0.695±0	0.769±0	0.743±0	0.694±0	0.708±0	0.747±0	0.706±0	0.731±0	0.751±0
fracturemnist3d	0.651±0.05	0.523±0.03	0.514±0.05	0.577±0.007	0.579±0.007	0.602±0.003	0.594±0.004	0.615±0.009	0.593±0.01
adrenalmnist3d	0.65±0	0.771±0	0.703±0	0.707±0	0.625±0	0.659±0	0.651±0	0.681±0	0.656±0
vesselmnist3d	0.56±0	0.669±0	0.693±0	0.623±0	0.681±0	0.663±0	0.635±0	0.625±0	0.611±0
synapsemnist3d	0.534±0	0.539±0	0.45±0	0.493±0	0.501±0	0.493±0	0.511±0	0.522±0	0.48±0
Chemical formula
bace	0.619±0	0.704±0	0.684±0	0.569±0	0.678±0	0.698±0	0.634±0	0.637±0	0.694±0
BBBP	0.699±0	0.747±0	0.718±0	0.691±0	0.731±0	0.736±0	0.669±0	0.716±0	0.733±0
clintox	0.54±0	0.569±0	0.547±0	0.517±0	0.515±0	0.52±0	0.506±0	0.513±0	0.515±0
HIV	0.531±0	0.562±0	0.548±0	0.511±0	0.504±0	0.511±0	0.501±0	0.504±0	0.511±0

Table A5. AC-score (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.982±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.927±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.969±0.001	0.973±0.001	0.969±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.694±0.01	0.796±0.01	0.74±0.01	0.725±0.02	0.784±0.01	0.807±0.01	0.72±0.02	0.787±0.01	0.756±0.02
SVHN	0.524±0.002	0.614±0.004	0.499±0.008	0.352±0.03	0.444±0.02	0.419±0.02	0.302±0.03	0.438±0.02	0.461±0.02
flower	0.698±0.02	0.733±0.02	0.567±0.01	0.701±0.03	0.696±0.03	0.74±0.03	0.678±0.05	0.7±0.03	0.725±0.03
GTSRB	0.753±0.003	0.97±0.002	0.941±0.002	0.995±0.0004	0.995±0.0003	0.995±0.0004	0.99±0.0006	0.995±0.0004	0.994±0.0004
STL10	0.72±0.01	0.779±0.02	0.664±0.01	0.75±0.02	0.755±0.02	0.79±0.02	0.743±0.02	0.76±0.02	0.711±0.03
FMNIST	0.936±0.01	0.975±0.006	0.973±0.006	0.975±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
dermamnist	0.658±0.02	0.72±0.02	0.608±0.04	0.535±0.05	0.602±0.05	0.62±0.05	0.323±0.07	0.606±0.05	0.518±0.05
pneumoniamnist	0.837±0	0.932±0	0.908±0	0.94±0	0.942±0	0.94±0	0.942±0	0.94±0	0.943±0
retinamnist	0.62±0.03	0.639±0.05	0.567±0.03	0.513±0.07	0.543±0.04	0.544±0.05	0.448±0.08	0.518±0.06	0.501±0.06
breastmnist	0.641±0	0.751±0	0.698±0	0.682±0	0.732±0	0.658±0	0.722±0	0.661±0	0.59±0
bloodmnist	0.889±0.02	0.946±0.01	0.897±0.02	0.949±0.01	0.954±0.01	0.954±0.01	0.944±0.01	0.956±0.01	0.953±0.01
organamnist	0.892±0.01	0.946±0.008	0.949±0.008	0.919±0.02	0.952±0.009	0.958±0.008	0.935±0.01	0.956±0.008	0.954±0.008
organcmnist	0.881±0.01	0.92±0.01	0.907±0.01	0.893±0.02	0.913±0.01	0.927±0.01	0.905±0.01	0.919±0.01	0.9±0.02
organsmnist	0.822±0.01	0.88±0.01	0.862±0.01	0.833±0.02	0.868±0.01	0.884±0.01	0.828±0.02	0.877±0.01	0.839±0.03
organmnist3d	0.918±0.01	0.956±0.008	0.952±0.008	0.964±0.007	0.965±0.007	0.965±0.007	0.962±0.007	0.965±0.007	0.937±0.02
nodulemnist3d	0.707±0	0.773±0	0.693±0	0.636±0	0.657±0	0.694±0	0.623±0	0.688±0	0.71±0
fracturemnist3d	0.668±0.06	0.38±0.1	0.351±0.1	0.491±0.06	0.491±0.04	0.535±0.03	0.514±0.03	0.562±0.01	0.485±0.05
adrenalmnist3d	0.602±0	0.718±0	0.631±0	0.642±0	0.52±0	0.553±0	0.526±0	0.57±0	0.528±0
vesselmnist3d	0.547±0	0.615±0	0.58±0	0.43±0	0.488±0	0.434±0	0.376±0	0.375±0	0.313±0
synapsemnist3d	0.498±0	0.506±0	0.0612±0	0.189±0	0.19±0	0.189±0	0.253±0	0.239±0	0.137±0
Chemical formula
bace	0.62±0	0.704±0	0.678±0	0.483±0	0.673±0	0.694±0	0.583±0	0.621±0	0.688±0
BBBP	0.693±0	0.715±0	0.603±0	0.553±0	0.63±0	0.632±0	0.501±0	0.626±0	0.646±0
clintox	0.634±0	0.365±0	0.238±0	0.0869±0	0.0869±0	0.0869±0	0.0868±0	0.0869±0	0.0869±0
HIV	0.471±0	0.465±0	0.159±0	0.0407±0	0.0273±0	0.0407±0	0.0205±0	0.0273±0	0.0407±0

Table A5. AC-score (Binary Classification Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.957±0.004	0.985±0.002	0.981±0.002	0.985±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002	0.986±0.002
USPS	0.966±0.005	0.989±0.001	0.982±0.002	0.99±0.002	0.99±0.002	0.99±0.001	0.991±0.001	0.99±0.002	0.991±0.001
EMNIST	0.927±0.003	0.972±0.001	0.964±0.001	0.97±0.001	0.969±0.001	0.973±0.001	0.969±0.002	0.97±0.001	0.97±0.002
CIFAR10	0.694±0.01	0.796±0.01	0.74±0.01	0.725±0.02	0.784±0.01	0.807±0.01	0.72±0.02	0.787±0.01	0.756±0.02
SVHN	0.524±0.002	0.614±0.004	0.499±0.008	0.352±0.03	0.444±0.02	0.419±0.02	0.302±0.03	0.438±0.02	0.461±0.02
flower	0.698±0.02	0.733±0.02	0.567±0.01	0.701±0.03	0.696±0.03	0.74±0.03	0.678±0.05	0.7±0.03	0.725±0.03
GTSRB	0.753±0.003	0.97±0.002	0.941±0.002	0.995±0.0004	0.995±0.0003	0.995±0.0004	0.99±0.0006	0.995±0.0004	0.994±0.0004
STL10	0.72±0.01	0.779±0.02	0.664±0.01	0.75±0.02	0.755±0.02	0.79±0.02	0.743±0.02	0.76±0.02	0.711±0.03
FMNIST	0.936±0.01	0.975±0.006	0.973±0.006	0.975±0.006	0.976±0.006	0.978±0.005	0.975±0.006	0.976±0.006	0.976±0.006
Medical images
dermamnist	0.658±0.02	0.72±0.02	0.608±0.04	0.535±0.05	0.602±0.05	0.62±0.05	0.323±0.07	0.606±0.05	0.518±0.05
pneumoniamnist	0.837±0	0.932±0	0.908±0	0.94±0	0.942±0	0.94±0	0.942±0	0.94±0	0.943±0
retinamnist	0.62±0.03	0.639±0.05	0.567±0.03	0.513±0.07	0.543±0.04	0.544±0.05	0.448±0.08	0.518±0.06	0.501±0.06
breastmnist	0.641±0	0.751±0	0.698±0	0.682±0	0.732±0	0.658±0	0.722±0	0.661±0	0.59±0
bloodmnist	0.889±0.02	0.946±0.01	0.897±0.02	0.949±0.01	0.954±0.01	0.954±0.01	0.944±0.01	0.956±0.01	0.953±0.01
organamnist	0.892±0.01	0.946±0.008	0.949±0.008	0.919±0.02	0.952±0.009	0.958±0.008	0.935±0.01	0.956±0.008	0.954±0.008
organcmnist	0.881±0.01	0.92±0.01	0.907±0.01	0.893±0.02	0.913±0.01	0.927±0.01	0.905±0.01	0.919±0.01	0.9±0.02
organsmnist	0.822±0.01	0.88±0.01	0.862±0.01	0.833±0.02	0.868±0.01	0.884±0.01	0.828±0.02	0.877±0.01	0.839±0.03
organmnist3d	0.918±0.01	0.956±0.008	0.952±0.008	0.964±0.007	0.965±0.007	0.965±0.007	0.962±0.007	0.965±0.007	0.937±0.02
nodulemnist3d	0.707±0	0.773±0	0.693±0	0.636±0	0.657±0	0.694±0	0.623±0	0.688±0	0.71±0
fracturemnist3d	0.668±0.06	0.38±0.1	0.351±0.1	0.491±0.06	0.491±0.04	0.535±0.03	0.514±0.03	0.562±0.01	0.485±0.05
adrenalmnist3d	0.602±0	0.718±0	0.631±0	0.642±0	0.52±0	0.553±0	0.526±0	0.57±0	0.528±0
vesselmnist3d	0.547±0	0.615±0	0.58±0	0.43±0	0.488±0	0.434±0	0.376±0	0.375±0	0.313±0
synapsemnist3d	0.498±0	0.506±0	0.0612±0	0.189±0	0.19±0	0.189±0	0.253±0	0.239±0	0.137±0
Chemical formula
bace	0.62±0	0.704±0	0.678±0	0.483±0	0.673±0	0.694±0	0.583±0	0.621±0	0.688±0
BBBP	0.693±0	0.715±0	0.603±0	0.553±0	0.63±0	0.632±0	0.501±0	0.626±0	0.646±0
clintox	0.634±0	0.365±0	0.238±0	0.0869±0	0.0869±0	0.0869±0	0.0868±0	0.0869±0	0.0869±0
HIV	0.471±0	0.465±0	0.159±0	0.0407±0	0.0273±0	0.0407±0	0.0205±0	0.0273±0	0.0407±0

Appendix L.2. Multiclass prediction

Table A6. AUROC (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.897±0.01	0.963±0.005	0.958±0.006	0.965±0.005	0.965±0.005	0.967±0.004	0.965±0.005	0.966±0.005	0.967±0.004
USPS	0.914±0.01	0.971±0.004	0.969±0.006	0.974±0.005	0.974±0.005	0.973±0.004	0.974±0.004	0.973±0.005	0.976±0.004
EMNIST	0.773±0.01	0.896±0.008	0.879±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.883±0.01	0.892±0.008	0.878±0.01
CIFAR10	0.599±0.02	0.671±0.02	0.627±0.01	0.641±0.02	0.661±0.02	0.681±0.01	0.645±0.02	0.663±0.02	0.627±0.03
SVHN	0.522±0.006	0.638±0.01	0.531±0.007	0.536±0.01	0.55±0.01	0.551±0.01	0.534±0.008	0.558±0.01	0.543±0.01
flower	0.61±0.03	0.666±0.03	0.554±0.02	0.632±0.03	0.629±0.02	0.669±0.03	0.634±0.03	0.632±0.03	0.652±0.03
GTSRB	0.589±0.01	0.878±0.01	0.821±0.02	0.982±0.003	0.982±0.003	0.982±0.003	0.959±0.005	0.983±0.003	0.972±0.004
STL10	0.607±0.02	0.655±0.02	0.596±0.02	0.648±0.02	0.648±0.02	0.663±0.02	0.648±0.03	0.653±0.02	0.584±0.02
FMNIST	0.836±0.03	0.917±0.02	0.92±0.02	0.924±0.02	0.923±0.02	0.927±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.614±0.03	0.658±0.03	0.588±0.02	0.595±0.03	0.596±0.02	0.601±0.03	0.531±0.01	0.606±0.03	0.563±0.02
pneumoniamnist	0.837±0	0.933±0	0.912±8e-17	0.941±0	0.943±6e-17	0.941±0	0.942±6e-17	0.941±0	0.944±0
retinamnist	0.575±0.04	0.622±0.04	0.592±0.03	0.596±0.04	0.596±0.04	0.608±0.04	0.61±0.04	0.603±0.04	0.596±0.04
breastmnist	0.66±0	0.763±8e-17	0.703±0	0.726±0	0.757±0	0.705±0	0.734±0	0.709±0	0.688±0
bloodmnist	0.789±0.04	0.88±0.03	0.817±0.03	0.882±0.03	0.893±0.03	0.891±0.03	0.877±0.03	0.895±0.03	0.891±0.03
organamnist	0.815±0.03	0.888±0.02	0.885±0.03	0.85±0.04	0.891±0.03	0.9±0.02	0.866±0.03	0.897±0.02	0.893±0.03
organcmnist	0.809±0.03	0.869±0.03	0.833±0.03	0.811±0.04	0.839±0.03	0.862±0.03	0.833±0.03	0.847±0.03	0.798±0.05
organsmnist	0.694±0.03	0.761±0.03	0.735±0.03	0.7±0.03	0.733±0.03	0.754±0.03	0.732±0.04	0.746±0.03	0.705±0.05
organmnist3d	0.867±0.03	0.913±0.02	0.903±0.03	0.924±0.02	0.93±0.02	0.925±0.02	0.925±0.02	0.925±0.02	0.834±0.06
nodulemnist3d	0.715±0	0.781±0	0.732±8e-17	0.687±0	0.702±6e-17	0.735±6e-17	0.691±6e-17	0.724±0	0.743±0
fracturemnist3d	0.622±0.04	0.518±0.01	0.554±0.04	0.574±0.004	0.579±0.005	0.578±0.01	0.575±0.009	0.576±0.009	0.578±0.01
adrenalmnist3d	0.653±8e-17	0.756±8e-17	0.692±0	0.697±0	0.619±0	0.647±6e-17	0.637±0	0.665±6e-17	0.641±0
vesselmnist3d	0.605±8e-17	0.685±0	0.681±8e-17	0.61±0	0.648±6e-17	0.628±6e-17	0.604±0	0.6±0	0.584±0
synapsemnist3d	0.539±8e-17	0.544±8e-17	0.508±0	0.518±8e-17	0.527±6e-17	0.518±6e-17	0.525±0	0.539±0	0.517±0
Chemical formula
bace	0.621±8e-17	0.705±0	0.684±8e-17	0.618±8e-17	0.677±6e-17	0.697±0	0.639±6e-17	0.637±6e-17	0.693±6e-17
BBBP	0.711±8e-17	0.743±0	0.693±0	0.667±0	0.707±0	0.71±0	0.646±6e-17	0.697±0	0.712±0
clintox	0.65±0	0.575±0	0.543±0	0.517±0	0.515±0	0.519±6e-17	0.508±0	0.514±6e-17	0.515±0
HIV	0.6±0	0.616±8e-17	0.537±0	0.51±0	0.506±6e-17	0.51±0	0.505±6e-17	0.506±0	0.51±0

Table A6. AUROC (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.897±0.01	0.963±0.005	0.958±0.006	0.965±0.005	0.965±0.005	0.967±0.004	0.965±0.005	0.966±0.005	0.967±0.004
USPS	0.914±0.01	0.971±0.004	0.969±0.006	0.974±0.005	0.974±0.005	0.973±0.004	0.974±0.004	0.973±0.005	0.976±0.004
EMNIST	0.773±0.01	0.896±0.008	0.879±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.883±0.01	0.892±0.008	0.878±0.01
CIFAR10	0.599±0.02	0.671±0.02	0.627±0.01	0.641±0.02	0.661±0.02	0.681±0.01	0.645±0.02	0.663±0.02	0.627±0.03
SVHN	0.522±0.006	0.638±0.01	0.531±0.007	0.536±0.01	0.55±0.01	0.551±0.01	0.534±0.008	0.558±0.01	0.543±0.01
flower	0.61±0.03	0.666±0.03	0.554±0.02	0.632±0.03	0.629±0.02	0.669±0.03	0.634±0.03	0.632±0.03	0.652±0.03
GTSRB	0.589±0.01	0.878±0.01	0.821±0.02	0.982±0.003	0.982±0.003	0.982±0.003	0.959±0.005	0.983±0.003	0.972±0.004
STL10	0.607±0.02	0.655±0.02	0.596±0.02	0.648±0.02	0.648±0.02	0.663±0.02	0.648±0.03	0.653±0.02	0.584±0.02
FMNIST	0.836±0.03	0.917±0.02	0.92±0.02	0.924±0.02	0.923±0.02	0.927±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.614±0.03	0.658±0.03	0.588±0.02	0.595±0.03	0.596±0.02	0.601±0.03	0.531±0.01	0.606±0.03	0.563±0.02
pneumoniamnist	0.837±0	0.933±0	0.912±8e-17	0.941±0	0.943±6e-17	0.941±0	0.942±6e-17	0.941±0	0.944±0
retinamnist	0.575±0.04	0.622±0.04	0.592±0.03	0.596±0.04	0.596±0.04	0.608±0.04	0.61±0.04	0.603±0.04	0.596±0.04
breastmnist	0.66±0	0.763±8e-17	0.703±0	0.726±0	0.757±0	0.705±0	0.734±0	0.709±0	0.688±0
bloodmnist	0.789±0.04	0.88±0.03	0.817±0.03	0.882±0.03	0.893±0.03	0.891±0.03	0.877±0.03	0.895±0.03	0.891±0.03
organamnist	0.815±0.03	0.888±0.02	0.885±0.03	0.85±0.04	0.891±0.03	0.9±0.02	0.866±0.03	0.897±0.02	0.893±0.03
organcmnist	0.809±0.03	0.869±0.03	0.833±0.03	0.811±0.04	0.839±0.03	0.862±0.03	0.833±0.03	0.847±0.03	0.798±0.05
organsmnist	0.694±0.03	0.761±0.03	0.735±0.03	0.7±0.03	0.733±0.03	0.754±0.03	0.732±0.04	0.746±0.03	0.705±0.05
organmnist3d	0.867±0.03	0.913±0.02	0.903±0.03	0.924±0.02	0.93±0.02	0.925±0.02	0.925±0.02	0.925±0.02	0.834±0.06
nodulemnist3d	0.715±0	0.781±0	0.732±8e-17	0.687±0	0.702±6e-17	0.735±6e-17	0.691±6e-17	0.724±0	0.743±0
fracturemnist3d	0.622±0.04	0.518±0.01	0.554±0.04	0.574±0.004	0.579±0.005	0.578±0.01	0.575±0.009	0.576±0.009	0.578±0.01
adrenalmnist3d	0.653±8e-17	0.756±8e-17	0.692±0	0.697±0	0.619±0	0.647±6e-17	0.637±0	0.665±6e-17	0.641±0
vesselmnist3d	0.605±8e-17	0.685±0	0.681±8e-17	0.61±0	0.648±6e-17	0.628±6e-17	0.604±0	0.6±0	0.584±0
synapsemnist3d	0.539±8e-17	0.544±8e-17	0.508±0	0.518±8e-17	0.527±6e-17	0.518±6e-17	0.525±0	0.539±0	0.517±0
Chemical formula
bace	0.621±8e-17	0.705±0	0.684±8e-17	0.618±8e-17	0.677±6e-17	0.697±0	0.639±6e-17	0.637±6e-17	0.693±6e-17
BBBP	0.711±8e-17	0.743±0	0.693±0	0.667±0	0.707±0	0.71±0	0.646±6e-17	0.697±0	0.712±0
clintox	0.65±0	0.575±0	0.543±0	0.517±0	0.515±0	0.519±6e-17	0.508±0	0.514±6e-17	0.515±0
HIV	0.6±0	0.616±8e-17	0.537±0	0.51±0	0.506±6e-17	0.51±0	0.505±6e-17	0.506±0	0.51±0

Table A7. AUPR (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.897±0.01	0.963±0.004	0.958±0.005	0.965±0.004	0.965±0.004	0.967±0.004	0.965±0.004	0.966±0.004	0.967±0.004
USPS	0.918±0.01	0.971±0.005	0.969±0.005	0.974±0.004	0.974±0.005	0.974±0.004	0.974±0.004	0.973±0.005	0.976±0.003
EMNIST	0.774±0.01	0.896±0.008	0.88±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.884±0.009	0.892±0.008	0.878±0.01
CIFAR10	0.6±0.01	0.67±0.01	0.627±0.01	0.64±0.02	0.66±0.01	0.68±0.01	0.651±0.02	0.663±0.02	0.615±0.02
SVHN	0.528±0.009	0.666±0.01	0.533±0.006	0.546±0.005	0.572±0.006	0.589±0.007	0.565±0.01	0.597±0.005	0.552±0.01
flower	0.611±0.02	0.665±0.02	0.554±0.02	0.631±0.02	0.628±0.02	0.671±0.02	0.641±0.03	0.632±0.02	0.652±0.02
GTSRB	0.619±0.01	0.891±0.01	0.805±0.01	0.981±0.003	0.981±0.003	0.982±0.002	0.959±0.005	0.981±0.003	0.975±0.003
STL10	0.604±0.02	0.653±0.02	0.598±0.02	0.648±0.02	0.647±0.02	0.663±0.02	0.65±0.02	0.651±0.02	0.585±0.01
FMNIST	0.836±0.03	0.916±0.02	0.92±0.02	0.923±0.02	0.923±0.02	0.926±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.592±0.02	0.645±0.02	0.603±0.02	0.608±0.03	0.633±0.03	0.629±0.03	0.615±0.03	0.649±0.03	0.596±0.02
pneumoniamnist	0.817±0	0.931±0	0.922±0	0.937±0	0.944±0	0.946±0	0.927±0	0.945±0	0.946±0
retinamnist	0.568±0.03	0.621±0.04	0.594±0.03	0.589±0.04	0.593±0.04	0.608±0.04	0.632±0.03	0.608±0.04	0.598±0.04
breastmnist	0.653±0	0.759±0	0.69±0	0.743±0	0.766±0	0.718±0	0.726±0	0.725±0	0.736±0
bloodmnist	0.785±0.04	0.878±0.03	0.818±0.03	0.89±0.03	0.895±0.03	0.894±0.03	0.872±0.03	0.897±0.02	0.895±0.03
organamnist	0.82±0.03	0.892±0.02	0.889±0.02	0.851±0.03	0.892±0.02	0.903±0.02	0.871±0.03	0.898±0.02	0.895±0.02
organcmnist	0.818±0.03	0.877±0.02	0.838±0.03	0.811±0.04	0.839±0.03	0.87±0.02	0.836±0.03	0.847±0.03	0.793±0.05
organsmnist	0.697±0.02	0.764±0.03	0.741±0.03	0.703±0.03	0.736±0.03	0.763±0.03	0.734±0.03	0.748±0.03	0.698±0.04
organmnist3d	0.867±0.02	0.913±0.02	0.904±0.03	0.924±0.02	0.93±0.02	0.926±0.02	0.925±0.02	0.926±0.02	0.82±0.05
nodulemnist3d	0.7±0	0.771±0	0.745±0	0.695±0	0.709±0	0.749±0	0.711±0	0.732±0	0.752±0
fracturemnist3d	0.617±0.04	0.526±0.02	0.553±0.04	0.578±0.004	0.583±0.003	0.582±0.008	0.579±0.007	0.579±0.008	0.585±0.009
adrenalmnist3d	0.65±0	0.774±0	0.705±0	0.708±0	0.627±0	0.663±0	0.657±0	0.689±0	0.665±0
vesselmnist3d	0.582±0	0.671±0	0.694±0	0.627±0	0.7±0	0.692±0	0.668±0	0.646±0	0.661±0
synapsemnist3d	0.537±0	0.542±0	0.544±0	0.533±0	0.558±0	0.533±0	0.538±0	0.572±0	0.546±0
Chemical formula
bace	0.62±0	0.704±0	0.685±0	0.643±0	0.679±0	0.699±0	0.652±0	0.64±0	0.695±0
BBBP	0.701±0	0.747±0	0.734±0	0.712±0	0.743±0	0.751±0	0.701±0	0.723±0	0.742±0
clintox	0.602±0	0.57±0	0.548±0	0.553±0	0.54±0	0.575±0	0.514±0	0.53±0	0.54±0
HIV	0.565±0	0.583±0	0.558±0	0.612±0	0.578±0	0.584±0	0.601±0	0.585±0	0.596±0

Table A7. AUPR (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.897±0.01	0.963±0.004	0.958±0.005	0.965±0.004	0.965±0.004	0.967±0.004	0.965±0.004	0.966±0.004	0.967±0.004
USPS	0.918±0.01	0.971±0.005	0.969±0.005	0.974±0.004	0.974±0.005	0.974±0.004	0.974±0.004	0.973±0.005	0.976±0.003
EMNIST	0.774±0.01	0.896±0.008	0.88±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.884±0.009	0.892±0.008	0.878±0.01
CIFAR10	0.6±0.01	0.67±0.01	0.627±0.01	0.64±0.02	0.66±0.01	0.68±0.01	0.651±0.02	0.663±0.02	0.615±0.02
SVHN	0.528±0.009	0.666±0.01	0.533±0.006	0.546±0.005	0.572±0.006	0.589±0.007	0.565±0.01	0.597±0.005	0.552±0.01
flower	0.611±0.02	0.665±0.02	0.554±0.02	0.631±0.02	0.628±0.02	0.671±0.02	0.641±0.03	0.632±0.02	0.652±0.02
GTSRB	0.619±0.01	0.891±0.01	0.805±0.01	0.981±0.003	0.981±0.003	0.982±0.002	0.959±0.005	0.981±0.003	0.975±0.003
STL10	0.604±0.02	0.653±0.02	0.598±0.02	0.648±0.02	0.647±0.02	0.663±0.02	0.65±0.02	0.651±0.02	0.585±0.01
FMNIST	0.836±0.03	0.916±0.02	0.92±0.02	0.923±0.02	0.923±0.02	0.926±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.592±0.02	0.645±0.02	0.603±0.02	0.608±0.03	0.633±0.03	0.629±0.03	0.615±0.03	0.649±0.03	0.596±0.02
pneumoniamnist	0.817±0	0.931±0	0.922±0	0.937±0	0.944±0	0.946±0	0.927±0	0.945±0	0.946±0
retinamnist	0.568±0.03	0.621±0.04	0.594±0.03	0.589±0.04	0.593±0.04	0.608±0.04	0.632±0.03	0.608±0.04	0.598±0.04
breastmnist	0.653±0	0.759±0	0.69±0	0.743±0	0.766±0	0.718±0	0.726±0	0.725±0	0.736±0
bloodmnist	0.785±0.04	0.878±0.03	0.818±0.03	0.89±0.03	0.895±0.03	0.894±0.03	0.872±0.03	0.897±0.02	0.895±0.03
organamnist	0.82±0.03	0.892±0.02	0.889±0.02	0.851±0.03	0.892±0.02	0.903±0.02	0.871±0.03	0.898±0.02	0.895±0.02
organcmnist	0.818±0.03	0.877±0.02	0.838±0.03	0.811±0.04	0.839±0.03	0.87±0.02	0.836±0.03	0.847±0.03	0.793±0.05
organsmnist	0.697±0.02	0.764±0.03	0.741±0.03	0.703±0.03	0.736±0.03	0.763±0.03	0.734±0.03	0.748±0.03	0.698±0.04
organmnist3d	0.867±0.02	0.913±0.02	0.904±0.03	0.924±0.02	0.93±0.02	0.926±0.02	0.925±0.02	0.926±0.02	0.82±0.05
nodulemnist3d	0.7±0	0.771±0	0.745±0	0.695±0	0.709±0	0.749±0	0.711±0	0.732±0	0.752±0
fracturemnist3d	0.617±0.04	0.526±0.02	0.553±0.04	0.578±0.004	0.583±0.003	0.582±0.008	0.579±0.007	0.579±0.008	0.585±0.009
adrenalmnist3d	0.65±0	0.774±0	0.705±0	0.708±0	0.627±0	0.663±0	0.657±0	0.689±0	0.665±0
vesselmnist3d	0.582±0	0.671±0	0.694±0	0.627±0	0.7±0	0.692±0	0.668±0	0.646±0	0.661±0
synapsemnist3d	0.537±0	0.542±0	0.544±0	0.533±0	0.558±0	0.533±0	0.538±0	0.572±0	0.546±0
Chemical formula
bace	0.62±0	0.704±0	0.685±0	0.643±0	0.679±0	0.699±0	0.652±0	0.64±0	0.695±0
BBBP	0.701±0	0.747±0	0.734±0	0.712±0	0.743±0	0.751±0	0.701±0	0.723±0	0.742±0
clintox	0.602±0	0.57±0	0.548±0	0.553±0	0.54±0	0.575±0	0.514±0	0.53±0	0.54±0
HIV	0.565±0	0.583±0	0.558±0	0.612±0	0.578±0	0.584±0	0.601±0	0.585±0	0.596±0

Table A8. F-score (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.896±0.01	0.963±0.004	0.958±0.005	0.965±0.004	0.965±0.004	0.967±0.004	0.965±0.004	0.966±0.004	0.967±0.004
USPS	0.917±0.01	0.971±0.005	0.969±0.005	0.974±0.004	0.973±0.005	0.973±0.004	0.974±0.004	0.973±0.005	0.976±0.003
EMNIST	0.773±0.01	0.896±0.008	0.879±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.883±0.009	0.892±0.008	0.878±0.01
CIFAR10	0.59±0.01	0.67±0.01	0.627±0.01	0.634±0.02	0.66±0.01	0.679±0.01	0.634±0.02	0.663±0.02	0.603±0.02
SVHN	0.509±0.006	0.649±0.01	0.529±0.005	0.526±0.006	0.542±0.007	0.54±0.01	0.521±0.008	0.55±0.01	0.53±0.009
flower	0.599±0.02	0.662±0.02	0.553±0.02	0.629±0.02	0.626±0.02	0.665±0.02	0.628±0.03	0.63±0.02	0.65±0.02
GTSRB	0.586±0.01	0.886±0.01	0.782±0.01	0.98±0.003	0.981±0.003	0.982±0.003	0.957±0.005	0.98±0.003	0.974±0.003
STL10	0.601±0.02	0.653±0.02	0.597±0.02	0.646±0.02	0.646±0.02	0.662±0.02	0.641±0.02	0.651±0.02	0.57±0.02
FMNIST	0.835±0.03	0.916±0.02	0.919±0.02	0.923±0.02	0.923±0.02	0.926±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.571±0.02	0.639±0.02	0.599±0.02	0.602±0.03	0.611±0.03	0.615±0.03	0.533±0.01	0.624±0.03	0.572±0.02
pneumoniamnist	0.812±0	0.931±0	0.921±0	0.937±0	0.944±0	0.945±0	0.925±0	0.944±0	0.946±0
retinamnist	0.547±0.04	0.615±0.04	0.592±0.03	0.579±0.04	0.584±0.04	0.604±0.04	0.605±0.03	0.6±0.04	0.591±0.04
breastmnist	0.651±0	0.759±0	0.684±0	0.739±0	0.765±0	0.716±0	0.725±0	0.722±0	0.712±0
bloodmnist	0.779±0.04	0.877±0.03	0.817±0.03	0.887±0.03	0.894±0.03	0.894±0.03	0.869±0.03	0.897±0.02	0.894±0.03
organamnist	0.812±0.03	0.889±0.02	0.889±0.02	0.847±0.04	0.892±0.02	0.903±0.02	0.869±0.03	0.898±0.02	0.894±0.02
organcmnist	0.811±0.03	0.874±0.02	0.837±0.03	0.809±0.04	0.839±0.03	0.867±0.02	0.834±0.03	0.847±0.03	0.789±0.05
organsmnist	0.685±0.02	0.76±0.03	0.74±0.03	0.698±0.03	0.736±0.03	0.76±0.03	0.729±0.04	0.748±0.03	0.684±0.04
organmnist3d	0.862±0.02	0.913±0.02	0.903±0.03	0.922±0.02	0.929±0.02	0.923±0.02	0.924±0.02	0.923±0.02	0.809±0.06
nodulemnist3d	0.695±0	0.769±0	0.743±0	0.694±0	0.708±0	0.747±0	0.706±0	0.731±0	0.751±0
fracturemnist3d	0.601±0.04	0.486±0.02	0.547±0.04	0.575±0.002	0.581±0.003	0.579±0.008	0.575±0.006	0.577±0.008	0.577±0.01
adrenalmnist3d	0.65±0	0.771±0	0.703±0	0.707±0	0.625±0	0.659±0	0.651±0	0.681±0	0.656±0
vesselmnist3d	0.56±0	0.669±0	0.693±0	0.623±0	0.681±0	0.663±0	0.635±0	0.625±0	0.611±0
synapsemnist3d	0.534±0	0.539±0	0.45±0	0.493±0	0.501±0	0.493±0	0.511±0	0.522±0	0.48±0
Chemical formula
bace	0.619±0	0.704±0	0.684±0	0.569±0	0.678±0	0.698±0	0.634±0	0.637±0	0.694±0
BBBP	0.699±0	0.747±0	0.718±0	0.691±0	0.731±0	0.736±0	0.669±0	0.716±0	0.733±0
clintox	0.54±0	0.569±0	0.547±0	0.517±0	0.515±0	0.52±0	0.506±0	0.513±0	0.515±0
HIV	0.531±0	0.562±0	0.548±0	0.511±0	0.504±0	0.511±0	0.501±0	0.504±0	0.511±0

Table A8. F-score (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.896±0.01	0.963±0.004	0.958±0.005	0.965±0.004	0.965±0.004	0.967±0.004	0.965±0.004	0.966±0.004	0.967±0.004
USPS	0.917±0.01	0.971±0.005	0.969±0.005	0.974±0.004	0.973±0.005	0.973±0.004	0.974±0.004	0.973±0.005	0.976±0.003
EMNIST	0.773±0.01	0.896±0.008	0.879±0.009	0.891±0.008	0.888±0.008	0.898±0.008	0.883±0.009	0.892±0.008	0.878±0.01
CIFAR10	0.59±0.01	0.67±0.01	0.627±0.01	0.634±0.02	0.66±0.01	0.679±0.01	0.634±0.02	0.663±0.02	0.603±0.02
SVHN	0.509±0.006	0.649±0.01	0.529±0.005	0.526±0.006	0.542±0.007	0.54±0.01	0.521±0.008	0.55±0.01	0.53±0.009
flower	0.599±0.02	0.662±0.02	0.553±0.02	0.629±0.02	0.626±0.02	0.665±0.02	0.628±0.03	0.63±0.02	0.65±0.02
GTSRB	0.586±0.01	0.886±0.01	0.782±0.01	0.98±0.003	0.981±0.003	0.982±0.003	0.957±0.005	0.98±0.003	0.974±0.003
STL10	0.601±0.02	0.653±0.02	0.597±0.02	0.646±0.02	0.646±0.02	0.662±0.02	0.641±0.02	0.651±0.02	0.57±0.02
FMNIST	0.835±0.03	0.916±0.02	0.919±0.02	0.923±0.02	0.923±0.02	0.926±0.02	0.918±0.02	0.924±0.02	0.924±0.02
Medical images
dermamnist	0.571±0.02	0.639±0.02	0.599±0.02	0.602±0.03	0.611±0.03	0.615±0.03	0.533±0.01	0.624±0.03	0.572±0.02
pneumoniamnist	0.812±0	0.931±0	0.921±0	0.937±0	0.944±0	0.945±0	0.925±0	0.944±0	0.946±0
retinamnist	0.547±0.04	0.615±0.04	0.592±0.03	0.579±0.04	0.584±0.04	0.604±0.04	0.605±0.03	0.6±0.04	0.591±0.04
breastmnist	0.651±0	0.759±0	0.684±0	0.739±0	0.765±0	0.716±0	0.725±0	0.722±0	0.712±0
bloodmnist	0.779±0.04	0.877±0.03	0.817±0.03	0.887±0.03	0.894±0.03	0.894±0.03	0.869±0.03	0.897±0.02	0.894±0.03
organamnist	0.812±0.03	0.889±0.02	0.889±0.02	0.847±0.04	0.892±0.02	0.903±0.02	0.869±0.03	0.898±0.02	0.894±0.02
organcmnist	0.811±0.03	0.874±0.02	0.837±0.03	0.809±0.04	0.839±0.03	0.867±0.02	0.834±0.03	0.847±0.03	0.789±0.05
organsmnist	0.685±0.02	0.76±0.03	0.74±0.03	0.698±0.03	0.736±0.03	0.76±0.03	0.729±0.04	0.748±0.03	0.684±0.04
organmnist3d	0.862±0.02	0.913±0.02	0.903±0.03	0.922±0.02	0.929±0.02	0.923±0.02	0.924±0.02	0.923±0.02	0.809±0.06
nodulemnist3d	0.695±0	0.769±0	0.743±0	0.694±0	0.708±0	0.747±0	0.706±0	0.731±0	0.751±0
fracturemnist3d	0.601±0.04	0.486±0.02	0.547±0.04	0.575±0.002	0.581±0.003	0.579±0.008	0.575±0.006	0.577±0.008	0.577±0.01
adrenalmnist3d	0.65±0	0.771±0	0.703±0	0.707±0	0.625±0	0.659±0	0.651±0	0.681±0	0.656±0
vesselmnist3d	0.56±0	0.669±0	0.693±0	0.623±0	0.681±0	0.663±0	0.635±0	0.625±0	0.611±0
synapsemnist3d	0.534±0	0.539±0	0.45±0	0.493±0	0.501±0	0.493±0	0.511±0	0.522±0	0.48±0
Chemical formula
bace	0.619±0	0.704±0	0.684±0	0.569±0	0.678±0	0.698±0	0.634±0	0.637±0	0.694±0
BBBP	0.699±0	0.747±0	0.718±0	0.691±0	0.731±0	0.736±0	0.669±0	0.716±0	0.733±0
clintox	0.54±0	0.569±0	0.547±0	0.517±0	0.515±0	0.52±0	0.506±0	0.513±0	0.515±0
HIV	0.531±0	0.562±0	0.548±0	0.511±0	0.504±0	0.511±0	0.501±0	0.504±0	0.511±0

Table A9. AC-score (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.888±0.01	0.962±0.005	0.956±0.006	0.964±0.005	0.964±0.005	0.966±0.005	0.964±0.005	0.965±0.005	0.966±0.005
USPS	0.907±0.01	0.97±0.005	0.968±0.007	0.974±0.005	0.973±0.005	0.973±0.005	0.974±0.004	0.973±0.005	0.975±0.004
EMNIST	0.708±0.02	0.884±0.01	0.863±0.01	0.878±0.01	0.874±0.01	0.886±0.01	0.867±0.01	0.879±0.01	0.855±0.02
CIFAR10	0.404±0.05	0.562±0.03	0.48±0.03	0.491±0.05	0.542±0.03	0.579±0.03	0.487±0.06	0.548±0.03	0.431±0.08
SVHN	0.223±0.05	0.478±0.03	0.241±0.04	0.223±0.06	0.242±0.05	0.216±0.04	0.234±0.06	0.247±0.05	0.224±0.06
flower	0.492±0.07	0.597±0.05	0.417±0.05	0.545±0.05	0.542±0.04	0.591±0.05	0.518±0.08	0.546±0.05	0.576±0.04
GTSRB	0.296±0.03	0.853±0.02	0.762±0.03	0.981±0.004	0.981±0.004	0.981±0.004	0.956±0.006	0.982±0.004	0.97±0.004
STL10	0.425±0.05	0.523±0.05	0.413±0.04	0.512±0.05	0.51±0.05	0.541±0.04	0.501±0.05	0.521±0.05	0.364±0.06
FMNIST	0.801±0.05	0.909±0.02	0.912±0.02	0.916±0.02	0.915±0.02	0.92±0.02	0.91±0.02	0.917±0.02	0.917±0.02
Medical images
dermamnist	0.439±0.09	0.527±0.07	0.352±0.07	0.348±0.1	0.324±0.07	0.337±0.09	0.131±0.04	0.346±0.08	0.239±0.07
pneumoniamnist	0.837±0	0.932±0	0.908±0	0.94±0	0.942±0	0.94±0	0.942±0	0.94±0	0.943±0
retinamnist	0.377±0.1	0.506±0.07	0.444±0.08	0.401±0.1	0.404±0.1	0.433±0.1	0.422±0.1	0.426±0.1	0.405±0.1
breastmnist	0.641±0	0.751±0	0.698±0	0.682±0	0.732±0	0.658±0	0.722±0	0.661±0	0.59±0
bloodmnist	0.742±0.05	0.864±0.04	0.784±0.04	0.865±0.03	0.88±0.03	0.878±0.03	0.86±0.04	0.883±0.03	0.878±0.03
organamnist	0.771±0.05	0.872±0.03	0.868±0.03	0.814±0.05	0.874±0.03	0.887±0.03	0.84±0.04	0.883±0.03	0.877±0.03
organcmnist	0.766±0.04	0.848±0.03	0.797±0.04	0.76±0.05	0.804±0.04	0.836±0.03	0.788±0.05	0.816±0.04	0.705±0.09
organsmnist	0.58±0.06	0.69±0.05	0.653±0.04	0.589±0.06	0.649±0.05	0.677±0.05	0.624±0.07	0.669±0.05	0.54±0.1
organmnist3d	0.845±0.04	0.902±0.03	0.89±0.03	0.914±0.03	0.923±0.02	0.916±0.02	0.917±0.02	0.916±0.02	0.736±0.1
nodulemnist3d	0.707±0	0.773±0	0.693±0	0.636±0	0.657±0	0.694±0	0.623±0	0.688±0	0.71±0
fracturemnist3d	0.569±0.09	0.279±0.05	0.425±0.2	0.5±0.07	0.508±0.06	0.503±0.06	0.495±0.06	0.505±0.05	0.482±0.08
adrenalmnist3d	0.602±0	0.718±0	0.631±0	0.642±0	0.52±0	0.553±0	0.526±0	0.57±0	0.528±0
vesselmnist3d	0.547±0	0.615±0	0.58±0	0.43±0	0.488±0	0.434±0	0.376±0	0.375±0	0.313±0
synapsemnist3d	0.498±0	0.506±0	0.0612±0	0.189±0	0.19±0	0.189±0	0.253±0	0.239±0	0.137±0
Chemical formula
bace	0.62±0	0.704±0	0.678±0	0.483±0	0.673±0	0.694±0	0.583±0	0.621±0	0.688±0
BBBP	0.693±0	0.715±0	0.603±0	0.553±0	0.63±0	0.632±0	0.501±0	0.626±0	0.646±0
clintox	0.634±0	0.365±0	0.238±0	0.0869±0	0.0869±0	0.0869±0	0.0868±0	0.0869±0	0.0869±0
HIV	0.471±0	0.465±0	0.159±0	0.0407±0	0.0273±0	0.0407±0	0.0205±0	0.0273±0	0.0407±0

Table A9. AC-score (Multiclass Prediction Performance)

Dataset	CDB0	CDA	LDA	Fast SVM dual	Fast SVM primal	Fast SVM BO	SVM SGD	SVM	Fast LR
Standard images
MNIST	0.888±0.01	0.962±0.005	0.956±0.006	0.964±0.005	0.964±0.005	0.966±0.005	0.964±0.005	0.965±0.005	0.966±0.005
USPS	0.907±0.01	0.97±0.005	0.968±0.007	0.974±0.005	0.973±0.005	0.973±0.005	0.974±0.004	0.973±0.005	0.975±0.004
EMNIST	0.708±0.02	0.884±0.01	0.863±0.01	0.878±0.01	0.874±0.01	0.886±0.01	0.867±0.01	0.879±0.01	0.855±0.02
CIFAR10	0.404±0.05	0.562±0.03	0.48±0.03	0.491±0.05	0.542±0.03	0.579±0.03	0.487±0.06	0.548±0.03	0.431±0.08
SVHN	0.223±0.05	0.478±0.03	0.241±0.04	0.223±0.06	0.242±0.05	0.216±0.04	0.234±0.06	0.247±0.05	0.224±0.06
flower	0.492±0.07	0.597±0.05	0.417±0.05	0.545±0.05	0.542±0.04	0.591±0.05	0.518±0.08	0.546±0.05	0.576±0.04
GTSRB	0.296±0.03	0.853±0.02	0.762±0.03	0.981±0.004	0.981±0.004	0.981±0.004	0.956±0.006	0.982±0.004	0.97±0.004
STL10	0.425±0.05	0.523±0.05	0.413±0.04	0.512±0.05	0.51±0.05	0.541±0.04	0.501±0.05	0.521±0.05	0.364±0.06
FMNIST	0.801±0.05	0.909±0.02	0.912±0.02	0.916±0.02	0.915±0.02	0.92±0.02	0.91±0.02	0.917±0.02	0.917±0.02
Medical images
dermamnist	0.439±0.09	0.527±0.07	0.352±0.07	0.348±0.1	0.324±0.07	0.337±0.09	0.131±0.04	0.346±0.08	0.239±0.07
pneumoniamnist	0.837±0	0.932±0	0.908±0	0.94±0	0.942±0	0.94±0	0.942±0	0.94±0	0.943±0
retinamnist	0.377±0.1	0.506±0.07	0.444±0.08	0.401±0.1	0.404±0.1	0.433±0.1	0.422±0.1	0.426±0.1	0.405±0.1
breastmnist	0.641±0	0.751±0	0.698±0	0.682±0	0.732±0	0.658±0	0.722±0	0.661±0	0.59±0
bloodmnist	0.742±0.05	0.864±0.04	0.784±0.04	0.865±0.03	0.88±0.03	0.878±0.03	0.86±0.04	0.883±0.03	0.878±0.03
organamnist	0.771±0.05	0.872±0.03	0.868±0.03	0.814±0.05	0.874±0.03	0.887±0.03	0.84±0.04	0.883±0.03	0.877±0.03
organcmnist	0.766±0.04	0.848±0.03	0.797±0.04	0.76±0.05	0.804±0.04	0.836±0.03	0.788±0.05	0.816±0.04	0.705±0.09
organsmnist	0.58±0.06	0.69±0.05	0.653±0.04	0.589±0.06	0.649±0.05	0.677±0.05	0.624±0.07	0.669±0.05	0.54±0.1
organmnist3d	0.845±0.04	0.902±0.03	0.89±0.03	0.914±0.03	0.923±0.02	0.916±0.02	0.917±0.02	0.916±0.02	0.736±0.1
nodulemnist3d	0.707±0	0.773±0	0.693±0	0.636±0	0.657±0	0.694±0	0.623±0	0.688±0	0.71±0
fracturemnist3d	0.569±0.09	0.279±0.05	0.425±0.2	0.5±0.07	0.508±0.06	0.503±0.06	0.495±0.06	0.505±0.05	0.482±0.08
adrenalmnist3d	0.602±0	0.718±0	0.631±0	0.642±0	0.52±0	0.553±0	0.526±0	0.57±0	0.528±0
vesselmnist3d	0.547±0	0.615±0	0.58±0	0.43±0	0.488±0	0.434±0	0.376±0	0.375±0	0.313±0
synapsemnist3d	0.498±0	0.506±0	0.0612±0	0.189±0	0.19±0	0.189±0	0.253±0	0.239±0	0.137±0
Chemical formula
bace	0.62±0	0.704±0	0.678±0	0.483±0	0.673±0	0.694±0	0.583±0	0.621±0	0.688±0
BBBP	0.693±0	0.715±0	0.603±0	0.553±0	0.63±0	0.632±0	0.501±0	0.626±0	0.646±0
clintox	0.634±0	0.365±0	0.238±0	0.0869±0	0.0869±0	0.0869±0	0.0868±0	0.0869±0	0.0869±0
HIV	0.471±0	0.465±0	0.159±0	0.0407±0	0.0273±0	0.0407±0	0.0205±0	0.0273±0	0.0407±0

Appendix M.1. Comparison between CDA with Neural Network

Given that neural networks are prevalent, especially deep learning architectures such as ResNet, we made a comparison between linear CDA and them. Specifically, we compared CDA with ResNet-18, and included a single-hidden-layer MLP as the baseline for the simplest neural network. We tested on 6 3D medical image datasets of MedMNIST. The results are shown in Appendix Table. Table A10. The parameters of MLP and ResNet-18 are: 100 training epochs; SGDM optimizer; initial learning rate 0.01 with decay of 50% every 30 epochs. For MLP, we used ReLU activation function; the number of hidden-layer neurons was set to approximately $\sqrt{\#\mathrm{samples}\times \#\mathrm{features}}$. We can see that even compared with the more complex architecture ResNet, CDA still outperforms on the adrenalmnist3d dataset. In addition, CDA demonstrates a better performance than MLP, outperforming on 4 out of 6 datasets.

Table A10. Test set multiclass AUROC on MedMNIST3D datasets.

Method	CDA	MLP	ResNet-18
organmnist3d	0.913	0.936	0.977
nodulemnist3d	0.781	0.766	0.850
fracturemnist3d	0.518	0.564	0.611
adrenalmnist3d	0.756	0.635	0.737
vesselmnist3d	0.685	0.674	0.769
synapsemnist3d	0.544	0.507	0.656

Table A10. Test set multiclass AUROC on MedMNIST3D datasets.

Method	CDA	MLP	ResNet-18
organmnist3d	0.913	0.936	0.977
nodulemnist3d	0.781	0.766	0.850
fracturemnist3d	0.518	0.564	0.611
adrenalmnist3d	0.756	0.635	0.737
vesselmnist3d	0.685	0.674	0.769
synapsemnist3d	0.544	0.507	0.656

Appendix M.2. Combining CDA with Neural Network

Under the circumstance that the data is complex and has strong nonlinear relations, it is feasible to combine linear CDA with current prevalent deep learning architectures, leveraging their extracted features to train linear CDA for better performance. We validated this combined approach on the SVHN dataset. We took the ResNet-18 pre-trained on ImageNet, and extracted the features from the layer right before the last fully-connected layer with SVHN data as input. Then we used these extracted features to train linear CDA. For prediction on test data, we used the pretrained ResNet weights and the trained CDA weights. As shown in Appendix Table. Table A11, this combination method improves significantly over directly training linear CDA on the original data, offering a great potential for addressing complex data with strong nonlinear relations in real-world applications.

Table A11. Test set multiclass prediction performance on SVHN dataset.

Dataset	Method	AUROC	AUPR	Fscore	ACscore
SVHN	CDA	0.638±0.01	0.666±0.01	0.649±0.01	0.478±0.03
	ResNet+CDA	0.741±0.02	0.740±0.01	0.739±0.01	0.677±0.03

Table A11. Test set multiclass prediction performance on SVHN dataset.

Dataset	Method	AUROC	AUPR	Fscore	ACscore
SVHN	CDA	0.638±0.01	0.666±0.01	0.649±0.01	0.478±0.03
	ResNet+CDA	0.741±0.02	0.740±0.01	0.739±0.01	0.677±0.03