Integrated Model Selection and Scalability in Functional Data Analysis through Bayesian Learning

1. Introduction

The emergence of big data across diverse fields, such as biomedicine, finance, and physical modeling, has catalyzed the need for advanced analytical methodologies capable of handling complex, high-dimensional datasets that conventional discrete-data analysis approaches cannot always process effectively. Such datasets often require analysis that captures and interprets their continuous and potentially high-dimensional complexities–a central promise of functional data analysis (FDA) [1,2]. Foundational work established FDA’s capacity to treat each observation as an entire function [3], be it a curve, surface, or higher-dimensional structure, thereby extracting richer insights than conventional discrete-point analyses. Over the past decade, FDA’s scope has widened significantly to accommodate high-dimensional and multivariate applications with theoretical and computational advances emerging across various contexts [4,5,6].

A pivotal technique within FDA is functional principal component analysis (fPCA), which serves as a dimension-reduction tool similar to classical PCA and factor analysis. Unlike classical PCA, however, fPCA operates in principle in an infinite-dimensional function space to capture dominant modes of variation and reduce complexity [7]. Despite its conceptual elegance, existing fPCA and similar FDA models often assume that data is observed on a shared, finite grid, often relying on heuristic imputation or posterior estimation to handle any missing entries [8,9,10,11,12,13,14,15,16,17,18]. This assumption conveniently facilitates the adoption of established linear algebraic methods, but compromises the integrity of FDA by introducing significant information loss and high computational demands in high-dimensional applications.

Ideally, each function would be represented according to its naturally sampled measurement points rather than forcing all observations onto a shared grid, thus preserving crucial information and avoiding the need for heuristic resampling. This point is critical when considering that, given only a finite number of data points, infinitely many functions can interpolate these points, each reflecting different inductive biases about smoothness or shape [19]. Conventional smoothing or regridding methods (e.g., polynomial interpolation) introduce biases that may distort the underlying function’s actual behavior. In contrast, we will achieve more accurate and unbiased predictions by concurrently updating the function estimation and the population-level statistics governing the estimation, such as those encoded in the covariance operator. Such an approach requires directly modeling the function from its original measurement points rather than imposing artificial grids.

To mitigate these limitations, several studies have proposed alternative strategies. For instance, [3] developed a nonparametric technique for estimating mean and covariance for functional data under smoothness assumptions while also discussing a continuous formulation and the necessary discretization in practical applications. In [20,21], they extended fPCA to sparse and irregular longitudinal designs by smoothing the covariance estimate and then discretizing. Nonetheless, classical discretization steps often result in significant information loss and computational burdens.

As functional data size and complexity grew, researchers turned to flexible basis expansions, including sinusoids (Fourier), wavelets, polynomials, and B-splines, for a finite-dimensional representation of functional data that is convenient and accurate in computation, avoiding the drawbacks of explicit approximation and resampling [2,22,23,24,25,26]. For example, [27] utilized basis function approximations to manage irregular grids. However, a core challenge remains in selecting a suitable model. For instance, researchers must choose the number and form (e.g., smoothness), along with the dimensionality of the representational subspace. In approximation, the placement of basis functions is also essential. Evenly spaced nodes remain popular for their simplicity but may be suboptimal. Alternative node allocations may be better, like Chebyshev nodes for superior accuracy [28], or sparse grids to reduce combinatorial growth of computational complexities [29].

Existing studies tend to rely on choosing the hyperparameters manually [7,10,11,30], or cross-validation [3,25,31,32], which are known to be computationally prohibitive. Others employ approximated cross-validation [22,24] or marginal likelihood [14] but still require exhaustive testing of all candidate models. Methods with sparse Bayesian priors [8,33,34] for model selection allow model selection with a single optimization. In [35,36], they use shrinkage or sparse priors for data-adaptive basis selection to ensure minimal but effective sets of basis functions. Notably, [37] proposed Bayesian and Akaike information criterion demonstrating state-of-the-art performance in simulation studies for sparse and dense functional data.

In addition, probabilistic FDA emerges as a sophisticated adaptation of probabilistic methods tailored to incorporate the flexibility of latent variable models to manage functional data. A Bayesian latent factor regression model (LFRM) [34], for example, extends conventional regression to accommodate complex structures and dependencies in functional data, providing a robust framework to handle the complexities inherent in functional data. However, these Bayesian approaches are often limited with the computational demands of Monte Carlo methods in high dimensions [14]. To address increasingly high-dimensional FDA problems, recent efforts have emphasized scalability. For instance, [7,30,38,39] introduced FDA for 2D and 3D images with a fixed basis or grid. In [32], they further reduced complexity in 2D fPCA via tensor product B-splines. And [40] applied a Bayesian framework with basis expansion, adaptive regularization, and Gibbs sampling to 2D functional data in the form of EEG studies on children with autism. Further, [41] leverages a parsimonious basis representation and variational Bayes to achieve computational efficiency, making it suitable for 3-D brain imaging data.

In parallel, the broader field of principal component analysis (PCA) remains a fundamental and effective tool. Classical PCA, rooted in eigen-decomposition [42], effectively extracts dominant modes of variation in many settings but does not inherently accommodate the probabilistic nature of real-world data and its inherent uncertainties. Thus, [43] introduced probabilistic PCA (PPCA), which incorporates a probability distribution to manage these uncertainties more effectively. PCA has since evolved to address missing data, model selection, and complex data types [44,45,46,47]. In the context of functional data, these concepts motivate new approaches that unify probabilistic methodologies, latent factor models, and kernel expansions for continuous domains [1].

Within Bayesian machine learning, various priors have been proposed for sparse or robust formulations of PCA [48,49,50,51]. Specifically, sparse Bayesian learning (SBL) [52,53,54] with its mechanism automatic relevance determination (ARD) [55,56] has proven adept at promoting parsimonious solutions [57,58,59,60,61]. SBL has emerged in Bayesian PCA [45,62,63], applying an iterative method to evaluate the relevance of each component and select the internal dimensionality by disregarding the redundant ones. [64] applied SBL to optimize the combination of base kernels to enhance model performance. These methods often exploit variational techniques or accelerated optimization [17,64,65,66,67,68,69,70], thereby balancing model complexity with computational tractability. In functional data contexts, where representations are infinite-dimensional, SBL offers a compelling framework for advanced FDA methods by efficiently handling sparse expansions and adaptively adjusting model complexity.

In summary, despite these efforts to advance functional data analysis, several challenges persist. Existing methods often exhibit limitations in accuracy and efficiency when sampling is sparse, automatic model selection is essential, and dimensionality is high [41]. Concurrently, probabilistic PCA and SBL frameworks illustrate powerful strategies to incorporate versatility and adaptivity for such data complexities while their adaptation to FDA is still evolving. These gaps underscore a need for a robust, flexible, and computationally feasible approach, unifying ideas from FDA, PPCA, and SBL, that manages the continuous and high-dimensional intricacy of modern datasets.

1.1. Contriubutions

This manuscript proposes a novel Bayesian framework for functional principal component analysis that leverages nonparametric kernel expansions, sparse Bayesian learning for model selection, and efficient variational inference (VI). We abbreviate the proposed method as BSFDA (Bayesian Scalable Functional Data Analysis). BSFDA addresses critical gaps in existing FDA techniques with irregular sampling, high-dimensional scalability, and selection of both basis functions and principal components. Specifically, our approach offers:

• Joint selection of optimum latent factors and sparse basis functions: This eliminates constraints on parametric representation dimensionality, avoids information loss from discretization, and extends naturally to higher dimensions or non-Euclidean spaces through nonparametric kernel expansion. It further enhances interpretability by adaptively choosing model complexity without testing multiple models separately. We achieve these improvements using a Bayesian paradigm that provides robust and accurate posterior estimates while supporting uncertainty quantification [1].
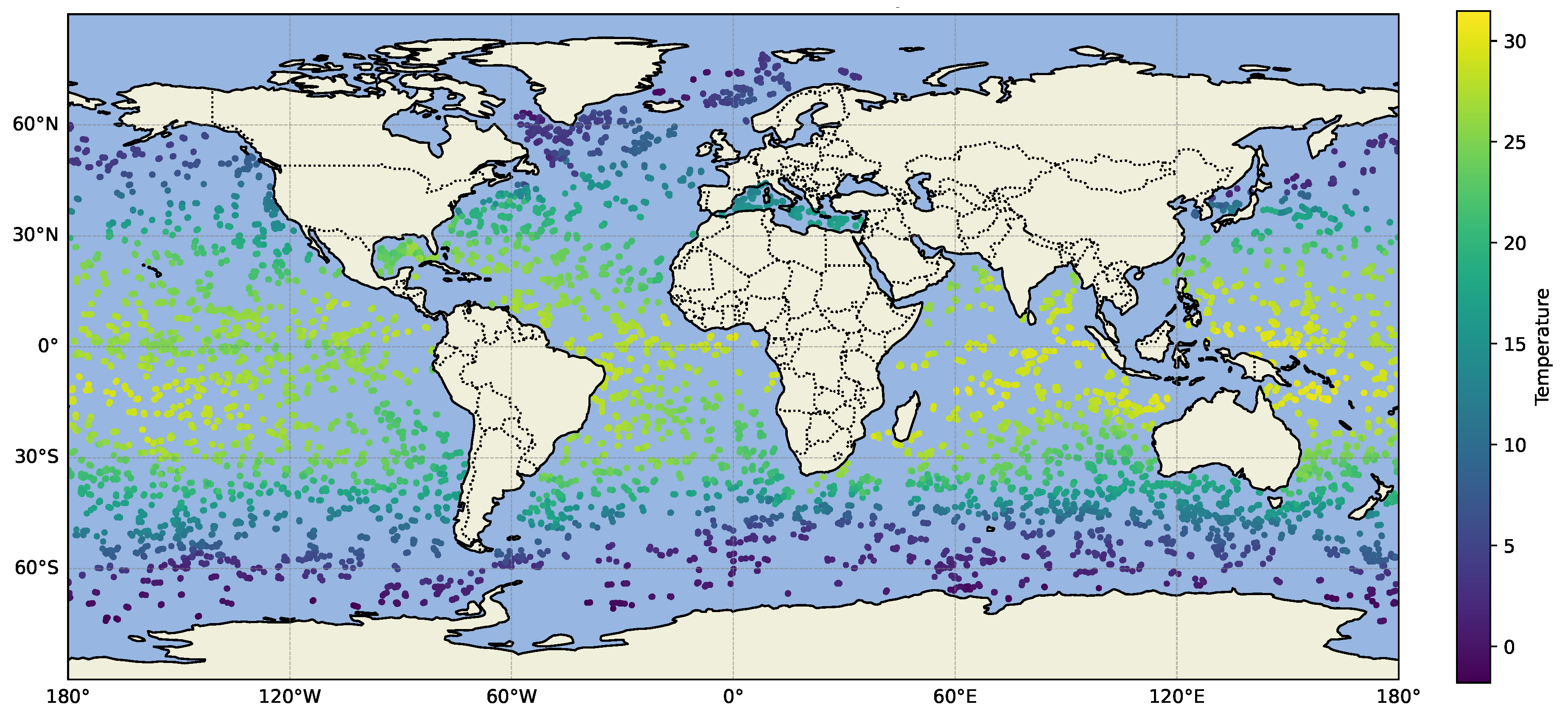
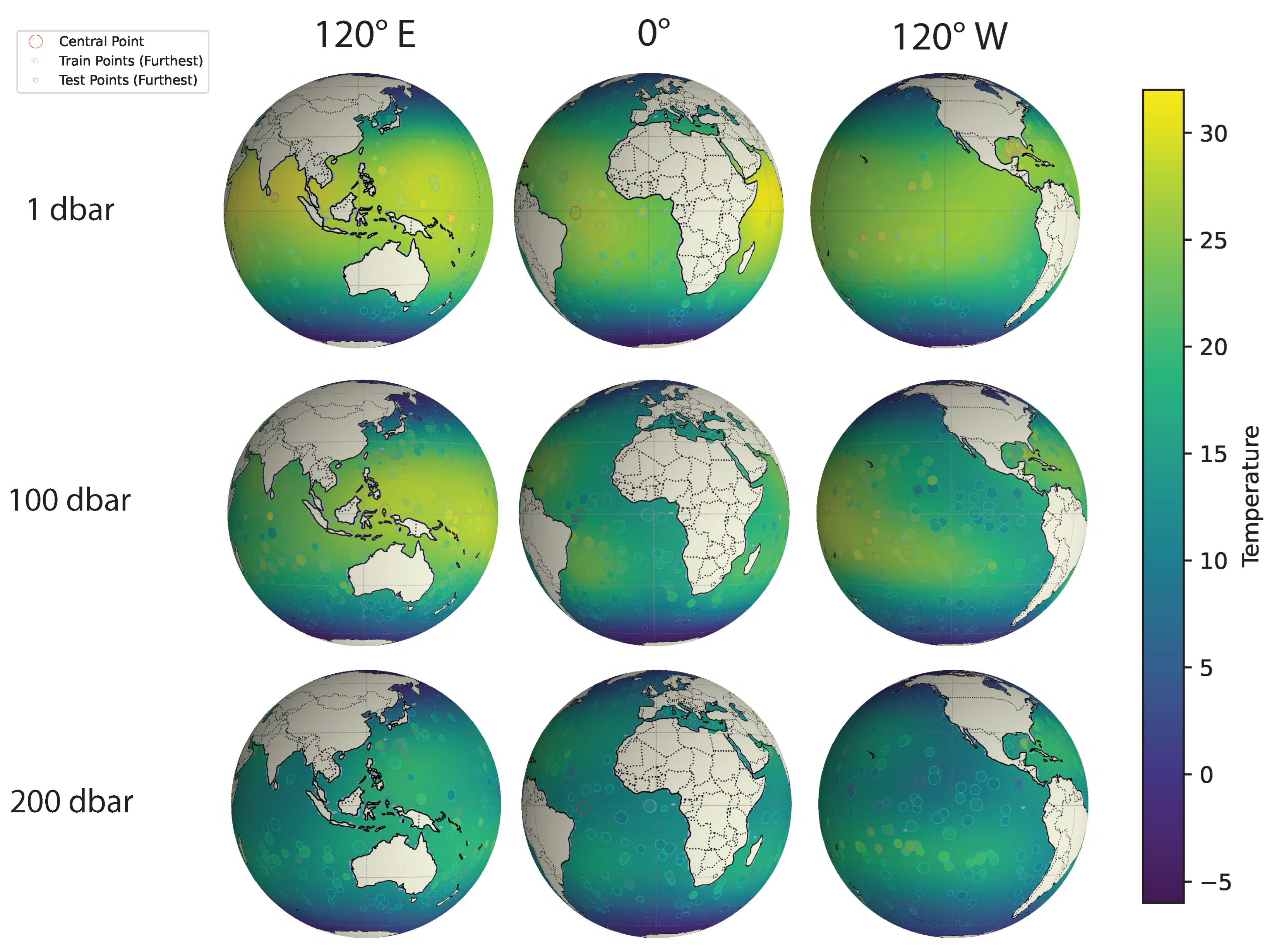
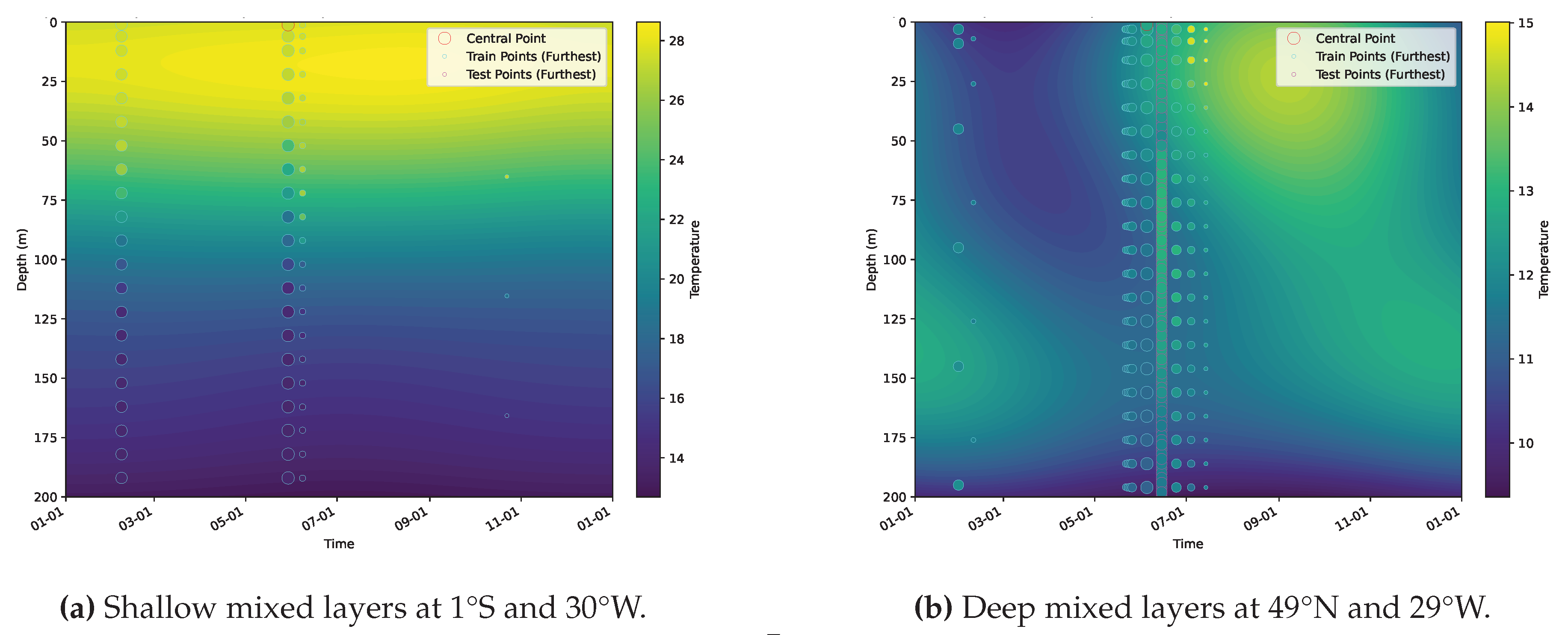
• Scalability across domain dimensionality and data size: The proposed method uses VI for faster computation compared to Markov chain Monte Carlo (MCMC) methods, while still being accurate. BSFDA reduces overall computation by partitioning the parameters into smaller update groups, and introducing a slack variable to further subdivide the weighting matrix (which is part of the kernel structure) into even smaller parts [34], updating fewer blocks at a time and considering all model options. Introducing a slack variable makes the optimization process more efficient by separating different variable groups. This approach scales well with data size and works efficiently even with large, complex datasets. We demonstrate this on the 4D global oceanic temperature data set (ARGO), which consists of 127 million data points spanning across the globe for 27 years with depths up to 200 meters [71].

1.2. Outline

Together, these contributions position our work at the intersection of functional principal component analysis [25] and sparse Bayesian learning [52], enabling robust, flexible, and computationally feasible analysis of high-dimensional functional data. The remainder of this paper is organized as follows. We first describe the proposed Bayesian functional PCA framework in detail, highlighting the nonparametric kernel expansions and sparse Bayesian priors. Next, we discuss the variational inference procedure and the reduced active block updating step, illustrating how these techniques jointly provide scalability and accuracy. We then present extensive empirical studies demonstrating factor selection accuracy, covariance operator estimation, and performance in large-scale 4D applications. Finally, we conclude with a discussion of potential extensions and open directions, emphasizing the broader implications of our work for large-scale, high-dimensional functional data analysis.

2. Formulation

The aim of the proposed method is the estimation of functions $y_i:R^M\mapsto R$ that are outcomes of an M-dimensional stochastic process. The observed data are P independent, noisy samples of the functions ${\left\{y_i\right\}}_{i=1}^P$ at index ${\{X_i\in R^{N_i\times M}\}}_{i=1}^P$ where $N_i$ is the number of measured samples for the $i^{th}$ function $y_i$ and $X_{in}\in R^M$ is the location of the $n^{th}$ measurement in the domain of the sample. The observations are ${\left\{Y_i\right\}}_{i=1}^P$, where $Y_{in}=y_i\left(X_{in}\right)+E_{in}$, where $E_{in}$ is white Gaussian noise of variance ${\sigma }^2$.

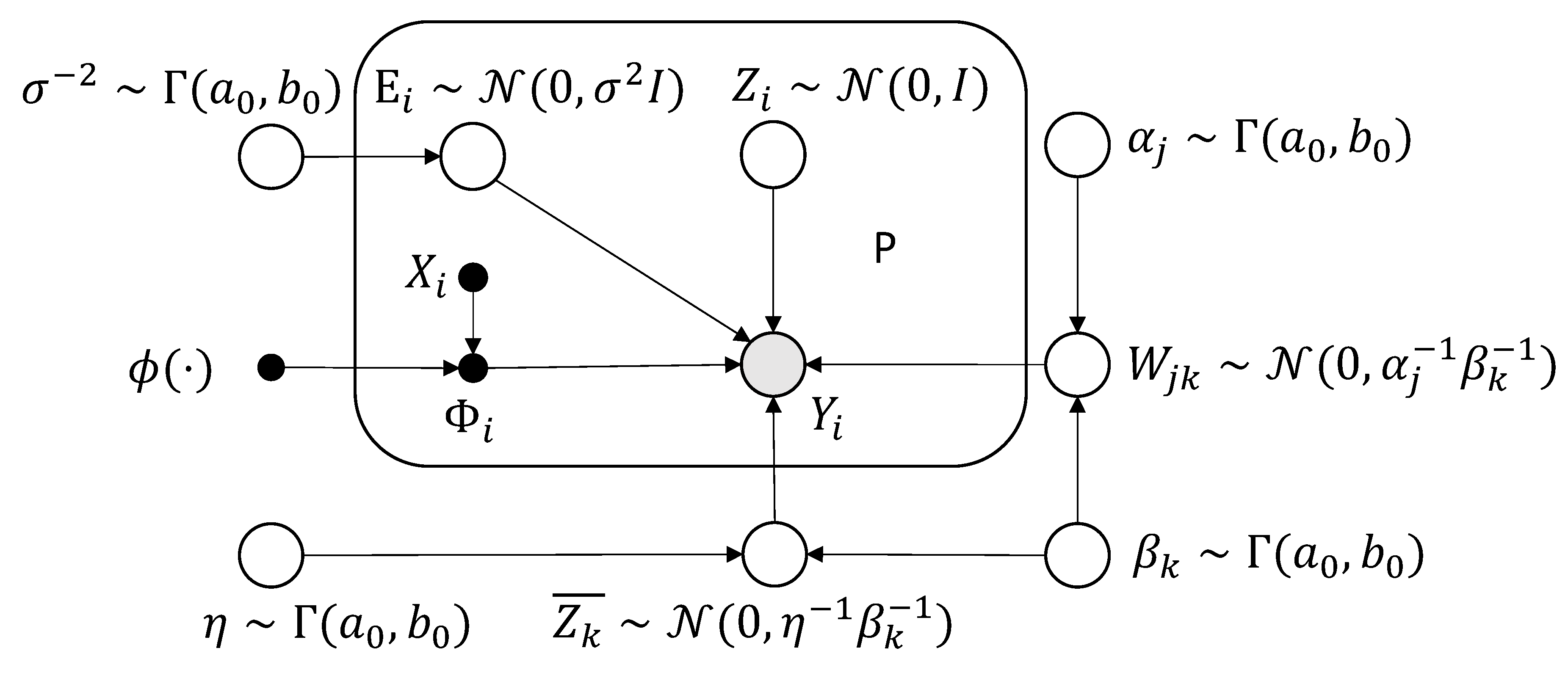
2.1. Generative model

We assume that $y_i$ is in a class of functions that can be approximated as a weighted summation of K kernel functions ${\left\{{\varphi }_k\right\}}_{k=1}^K$:

$$\begin{array}{c}\hfill y_i\left(x\right)=\sum _{k=1}^K{w}_{ik}{\varphi }_k\left(x\right),\end{array}$$

(1)

where ${\varphi }_k\left(x\right)=\mathcal{K}(x,X_{in})$, $\mathcal{K}$ is the kernel function, $X_{in}$ is the k-th location, ${\left\{w_{ik}\right\}}_{k=1}^K$ are the K coefficients of $y_i$. We also assume that the functions span a low dimensional subspace of dimension $J<<K$. We model this stochastically by assuming that the weights, $w_i\in R^K$, are given by $w_{ik}={\sum }_{j=1}^J{Z}_{ij}{W}_{jk}+{\overline{Z}}_k,$ where $W\in R^{J\times K}$ are the principal component loadings and $Z_i\in R^J$ are standard normal variables. This model is therefore:

$$\begin{array}{cc}\hfill Y_{in}& =\sum _{k=1}^K\left(\left(\sum _{j=1}^J\left(Z_{ij}{W}_{jk}\right)+{\overline{Z}}_k\right){\varphi }_k\left(X_{in}\right)\right)+E_{in}=(Z_{i}W+\overline{Z}){\Phi }_{i·n}+E_{in},\hfill \end{array}$$

(2)

where ${\Phi }_{i·n}={[{\varphi }_1\left(X_{in}\right),\dots ,{\varphi }_K\left(X_{in}\right)]}^T$ are the evaluations of the basis functions at the n-th index of the i-th sample function.

2.2. Sparse Prior

For effective model selection, we introduce a sparse prior over the coefficients of the basis functions. The sparse prior in the proposed model is based on automatic relevance detection (ARD) [62]. ARD evaluates the importance of a feature with a precision parameter estimated from the data. The model uses ${\left\{{\alpha }_j\right\}}_{j=1}^J$ and ${\left\{{\beta }_k\right\}}_{k=1}^K$ for the numbers of components and basis functions, respectively, while $\eta$ signifies the overall magnitude of the mean coefficients:

$$\begin{array}{cc}\hfill {\overline{Z}}_k& \sim \mathcal{N}(0,{\eta }^{-1}{\beta }_k^{-1}),\forall k=1:K\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill W_{jk}& \sim \mathcal{N}(0,{\alpha }_j^{-1}{\beta }_k^{-1}),\forall j=1:J,k=1:K\hfill \end{array}$$

(4)

In the model, ${\alpha }_j,{\beta }_k,\eta ,{\sigma }^{-2}$ are all variables of precision parameters, coming naturally with a conjugate prior of Gamma distribution. The probabilistic graphical model is depicted in Figure 1. Setting $a_0,b_0$ to a small value yields a vague Gamma prior that approximates a noninformative (Jeffreys-type) prior.

3. Methods

Based on the proposed formulation in Section 1.2, we estimate $Pr[\Theta |X,Y,a_0,b_0]$, the posterior of the unobserved values $\Theta =\{Z,W,\overline{Z},\sigma ,\alpha ,\beta ,\eta \}$. This inference gives the point estimates of $\Theta$ and the posterior predictive distribution of new data. For notational convenience, $X,a_0,b_0$ are omitted.

Using Bayes’ theorem, $Pr[\Theta |Y]={\displaystyle \frac{Pr\left[Y\right|\Theta ]Pr[\Theta ]}{Pr\left[Y\right]}}$, but the exact posterior distribution is intractable because the evidence $Pr\left[Y\right]=\int Pr[\Theta ,Y]d\Theta$ is intractable. Therefore, an approximate inference strategy is proposed. To facilitate this, we utilize variational inference (VI) [72], choosing a surrogate density from a parameterized family, denoted as $\mathcal{Q}$, to approximate the posterior. Compared with classical methods like Markov chain Monte Carlo (MCMC) sampling, VI is typically faster per [72]. In our experiments, VI is about 85 times faster for the original Bayesian PCA formulation [45] as shown in Section 12.2 in the supplements.

3.1. Variational Bayesian Inference

Variational inference optimizes $\mathcal{Q}$ by maximizing the lower bound $\mathcal{L}$ (minimizing the KL divergence between actual and surrogate distributions):

$$\begin{array}{c}\hfill {\mathbb{E}}_{\mathcal{Q}}\left[ln{\displaystyle \frac{Pr[\Theta ,Y]}{\mathcal{Q}(\Theta )}}\right]=-\mathrm{KL}\left(\mathcal{Q}(\Theta )\right||Pr[\Theta |Y])+lnPr\left[Y\right]\propto -\mathrm{KL}\left(\mathcal{Q}(\Theta )\right||Pr[\Theta |Y]).\end{array}$$

(5)

The mean-field variational family is used for $\mathcal{Q}$. It simplifies the optimization by assuming the surrogate posterior distributions are independent, allowing each variable in the posterior to be optimized independently: ${\mathcal{Q}}_{\Theta }={\prod }_i{\mathcal{Q}}_{{\Theta }_i}$. The posterior for each variable is chosen conjugate, further simplifying the optimization. Thus, the posteriors of the component scores Z, the weighting matrix W, and the mean weights $\overline{Z}$ are normal distributions. Here W is vectorized via $vec\left(W\right)$ without altering its normality assumption. Meanwhile, the posteriors of the precision variables of noise ${\sigma }^{-2}$, components $\alpha$, basis functions $\beta$, mean weights $\eta$ are Gamma distributions:

$$\begin{array}{cc}\hfill {\mathcal{Q}}_Z\left(Z\right)& =\prod _i{\mathcal{Q}}_{Z_i}\left(Z_i\right)=\prod _i\mathcal{N}\left(Z_i\right|{\mu }_{Z_i},{\Sigma }_{Z_i})\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_W\left(W\right)& =\mathcal{N}(vec\left(W\right)|{\mu }_{vec\left(W\right)},{\Sigma }_{vec\left(W\right)})\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\overline{Z}}\left(\overline{Z}\right)& =\mathcal{N}\left(\overline{Z}\right|{\mu }_{\overline{Z}},{\Sigma }_{\overline{Z}})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\sigma }\left(\sigma \right)& =\Gamma \left({\sigma }^{-2}\right|a_{\sigma },b_{\sigma })\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\alpha }\left(\alpha \right)& =\prod _j{\mathcal{Q}}_{{\alpha }_j}=\prod _j\Gamma \left({\alpha }_j\right|a_{{\alpha }_j},b_{{\alpha }_j})\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\beta }\left(\beta \right)& =\prod _k{\mathcal{Q}}_{{\beta }_k}=\prod _k\Gamma \left({\beta }_k\right|a_{{\beta }_k},b_{{\beta }_k})\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\eta }\left(\eta \right)& =\Gamma (\eta ,|a_{\eta },b_{\eta })\hfill \end{array}$$

(12)

3.1.1. Update Steps

In mean field approximation using the surrogate posterior ${\mathcal{Q}}_{\Theta }={\prod }_i{\mathcal{Q}}_{{\Theta }_i}$ conditioned on observations Y, the lower bound is maximized with respect to each unknown ${\Theta }_i$. With the conjugate prior, the optimal updates (denoted with "←") make the moments of ${\mathcal{Q}}_{{\Theta }_i}$ equal to the moments conditioned on the remaining parts of ${\mathcal{Q}}_{\Theta }$ [72]:

$$\begin{array}{c}\hfill {\mathcal{Q}}_{{\Theta }_i}\leftarrow {\displaystyle \frac{exp\left({\mathbb{E}}_{{\mathcal{Q}}_{/{\Theta }_i}}[ln(Pr[Y,\Theta ])]\right)}{\int exp\left({\mathbb{E}}_{{\mathcal{Q}}_{/{\Theta }_i}}[ln(Pr[Y,\Theta ])]\right)d{\Theta }_i}}\end{array}$$

(13)

From Equation (13), detailed update rules for each variable are presented subsequently, and the derivations of these formulas are in the supplementary material.

Updates for the parameters of the posterior for the precision of components ${\mathcal{Q}}_{{\alpha }_j},\forall j=1:J$:

$$\begin{array}{cc}\hfill a_{{\alpha }_j}& \leftarrow a_0+{\displaystyle \frac{K}{2}},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill b_{{\alpha }_j}& \leftarrow b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K{\mathbb{E}}_{{\mathcal{Q}}_{/{\alpha }_j}}\left[W_{jk}^2{\beta }_k\right]=b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right),\hfill \end{array}$$

(15)

where Equation (14) calculates the corrected degrees of freedom and Equation (15) calculates the corrected sum of squares. As $a_0$ and $b_0$ approach 0, the expectation of precision ${\alpha }_j$, which is ${\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]={\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}$, is exactly the inverse of the empirical or sample variance.

Updates for the parameters of the posterior of the precision of the mean weights ${\mathcal{Q}}_{\eta }$:

$$\begin{array}{cc}\hfill a_{\eta }& \leftarrow a_0+{\displaystyle \frac{K}{2}},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill b_{\eta }& \leftarrow b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K{\mathbb{E}}_{{\mathcal{Q}}_{/\eta }}\left[{\overline{Z}}_k^2{\beta }_k\right]=b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \end{array}$$

(17)

Updates for the parameters of the posterior of the precision of basis functions ${\mathcal{Q}}_{{\beta }_k},\forall k=1:K$:

$$\begin{array}{cc}\hfill a_{{\beta }_k}& \leftarrow a_0+{\displaystyle \frac{J+1}{2}},\hfill \\ \hfill b_{{\beta }_k}& \leftarrow b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/{\beta }_k}}[{\overline{Z}}_k^2\eta +\sum _{j=1}^J{W}_{jk}^2{\alpha }_j]\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & =b_0+{\displaystyle \frac{1}{2}}\left(\left({{\Sigma }_{\overline{Z}}}_{kk}+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{\eta }}{b_{\eta }}}+\sum _{j=1}^J\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\right)\hfill \end{array}$$

(19)

Updates for the parameters of the posterior of the mean weights ${\mathcal{Q}}_{\overline{Z}}$:

$$\begin{array}{cc}\hfill {\Sigma }_{\overline{Z}}& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\sum _{i=1}^P{\Psi }_i+\eta diag\left(\beta \right)\right]\right)}^{-1}={\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P{\Psi }_i+{\displaystyle \frac{a_{\eta }}{b_{\eta }}}diag\left({\displaystyle \frac{a}{b}}\right)\right)}^{-1},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\mu }_{\overline{Z}}& \leftarrow \left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\right]\sum _{i=1}^P(Y_i-{\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[Z_{i}W\right]{\Phi }_i){\Phi }_i^T\right){\Sigma }_{\overline{Z}}=\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P(Y_i-{\mu }_{Z_i}{\mu }_W{\Phi }_i){\Phi }_i^T\right){\Sigma }_{\overline{Z}}\hfill \end{array}$$

(21)

where $diag\left(\beta \right)$ denotes the diagonal matrix with diagonal entries given by $\beta$. Equation (20) indicates that the eigenvectors of ${\Sigma }_{\overline{Z}}$ are solely determined by the sum of Gram matrices ${\sum }_{i=1}^P{\Psi }_i$, while the eigenvalues of ${\Sigma }_{\overline{Z}}$ have a negative correlation with the scale of ${\sum }_{i=1}^P{\Psi }_i$, the prior $\eta diag\left(\beta \right)$ and data-dependent term ${\sigma }^{-2}$. It is sensible because, for instance, large noise would result in large uncertainty in $\overline{Z}$. In Equation (21), the data residuals, excluding component scores, are projected into the K-dimensional space through the inner product with ${\Phi }_i$ and summed over all sample functions to calculate the mean weights.

Updates for the parameters of the posterior of the weights ${\mathcal{Q}}_W$:

$$\begin{array}{cc}\hfill {\Sigma }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}{\left[{\sigma }^{-2}\sum _{i=1}^P\left({\Psi }_i^T\otimes \left(Z_i^T{Z}_i\right)\right)+diag\left(\beta \right)\otimes diag\left(\alpha \right)\right]}^{-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P\left({\Psi }_i^T\otimes ({{\mu }_{Z_i}}^T{\mu }_{Z_i}+{\Sigma }_{Z_i})\right)+diag\left({\displaystyle \frac{a}{b}}\right)\otimes diag\left({\displaystyle \frac{c}{d}}\right)\right)}^{-1},\hfill \\ \hfill {\mu }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[-{\sigma }^{-2}\sum _{i=1}^{P}vec{\left({\left({\Phi }_i({\Phi }_i^T{\overline{Z}}^T-Y_i^T)Z_i\right)}^T\right)}^T\right]{\Sigma }_{vec\left(W\right)}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^{P}vec{\left({\left({\Phi }_i({\Phi }_i^T{{\mu }_{\overline{Z}}}^T-Y_i^T){\mu }_{Z_i}\right)}^T\right)}^T{\Sigma }_{vec\left(W\right)}\hfill \end{array}$$

(23)

Equation (22) is similar to Equation (20), because it is correlated with ${\Phi }_i$, its prior $diag\left(\beta \right)\otimes diag\left(\alpha \right)$ and data-dependent terms ${\sigma }^{-2}$ and $Z_i$. In Equation (23), the data residual excluding the mean function is used to estimate the expectation of W.

Updates for the parameters of the posterior of the component scores ${\mathcal{Q}}_{Z_i}$:

$$\begin{array}{cc}\hfill H_{ijk}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_j{\Psi }_i{W}_k^T\right]=Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_k^T{W}_j\right]{\Psi }_i\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =Tr\left(\left({\Sigma }_{[W_k,W_j]}+{\mu }_{\left[W_j\right]}^T{\mu }_{\left[W_k\right]}\right){\Psi }_i\right),\forall j=1:K,k=1:K,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\Sigma }_{Z_i}& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}[{\sigma }^{-2}W{\Psi }_i{W}^T+I]\right)}^{-1}={[{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}{H}_i+I]}^{-1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\mu }_{Z_i}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[{\sigma }^{-2}(Y_i-\overline{Z}{\Phi }_i){\Phi }_i^T{W}^T\right]{\Sigma }_{Z_i}={\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}(Y_i-{\mu }_{\overline{Z}}{\Phi }_i){\Phi }_i^T{\left({\mu }_W\right)}^T{\Sigma }_{Z_i},\hfill \end{array}$$

(26)

where $H_i$ is a temporary variable denoting the Gram matrix of weighted kernel functions $W{\Phi }_i$ and ${\Sigma }_{[W_k,W_j]}$ denotes the covariance between $W_k^T$ and $W_j$ in $\mathcal{Q}$.

Updates for the parameters of the posterior of the noise ${\mathcal{Q}}_{\sigma }$:

$$\begin{array}{cc}\hfill a_{\sigma }& \leftarrow a_0+{\displaystyle \frac{1}{2}}\sum _i{N}_i,\hfill \\ \hfill b_{\sigma }& \leftarrow b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[\sum _i\left|\right|Y_i-(Z_{i}W+\overline{Z}){\Phi }_i{\left|\right|}_2^2\right]\hfill \\ \hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _i(Y_i{Y}_i^T-2Y_i{\left({\mu }_{Z_i}{\mu }_W{\Phi }_i\right)}^T-2Y_i{\left({\mu }_{\overline{Z}}{\Phi }_i\right)}^T+2{\mu }_{Z_i}{\mu }_W{\Psi }_i{\left({\mu }_{\overline{Z}}\right)}^T\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & +Tr\left(\left({\Sigma }_{\overline{Z}}+{\left({\mu }_{\overline{Z}}\right)}^T{\mu }_{\overline{Z}}\right){\Psi }_i\right))+{\displaystyle \frac{1}{2}}{vec\left(H^T\right)}^T\sum _{i}vec\left(vec\left({\Psi }_i\right)vec({\Sigma }_{Z_i}+{{\mu }_{Z_i}}^T{\mu }_{Z_i}{)}^T\right),\hfill \end{array}$$

(28)

where H is a temporary variable that is updated by

$$\begin{array}{cc}\hfill H_{j+kM}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[vec{\left(W_k{W_j}^T\right)}^T\right]=vec{({\Sigma }_{[W_k,W_j]}+{\mu }_{\left[W_j\right]}^T{\mu }_{\left[W_k\right]})}^T,\forall j=1:K,k=1:K\hfill \end{array}$$

(29)

Nearly noninformative (vagor) priors, i.e., with almost zero $a_0,b_0$, introduce an inherent identifiability ambiguity in our formulation, specifically, in the product of the precision parameters $\alpha ,\beta$ and $\eta$ (Equations 20 and 22). In our model, scaling $\alpha$ and $\eta$ by a specific factor while inversely scaling $\beta$ leaves the product (and hence the lower bound in Equation 5 ) unchanged. This inherent ambiguity can lead $\alpha$, $\beta$, and $\eta$ to converge to extreme values, thereby challenging numerical stability during optimization. To mitigate this issue, we adopt a heuristic constraint to ensure that the smallest values of $\alpha$ and $\beta$ remain within one order of magnitude of each other. Specifically, we enforce $\left|{log}_{10}^{\left({\displaystyle \frac{error}{min\left(\beta \right)}}\right)}\right|\le 1$. If an update to any ${\alpha }_j$ or ${\beta }_k$ would violate this constraint, that particular update is skipped while the rest of the parameters remain updated. This strategy does not alter the algorithm’s overall structure but stabilizes the optimization by curbing unnecessary flexibility in the precision parameters.

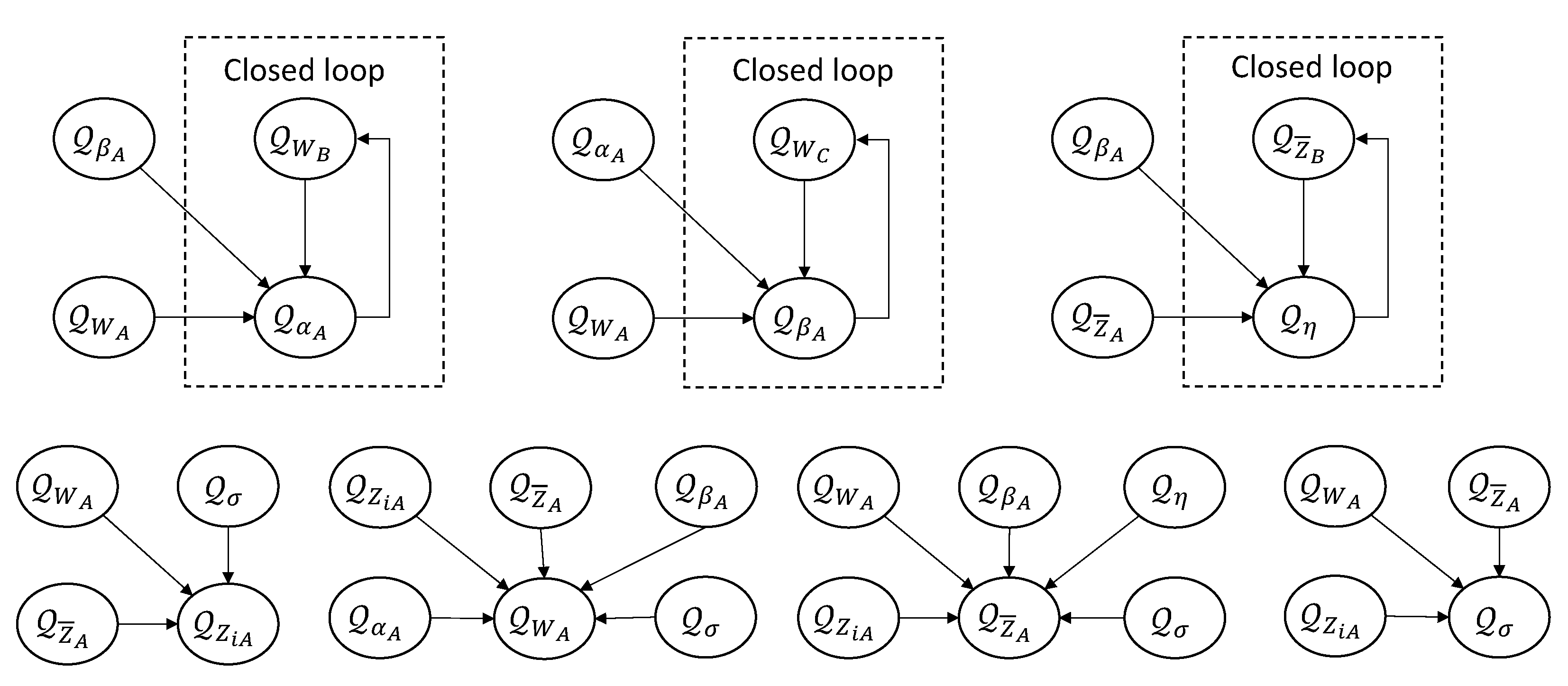
3.2. Scalable Update Strategy

The scalability of our algorithm so far is primarily challenged by the need to optimize the variational lower bound, $\mathcal{L}$ over K basis functions. As indicated by Equation (22), time complexity is $\mathcal{O}\left(K^6\right)$ (or, alternatively, $\mathcal{O}\left(K^{2}P{max}_i\left(N_i\right)\right)$, typically dominated by the former), which becomes prohibitive when K is large. In practice, however, only a small subset of these basis functions is necessary for an accurate representation–those with non-negligible weights under our sparse prior.

To address this, we focus the updates on the subspace of active basis functions, denoted as $K^{\left(a\right)}$, which comprises only those functions with non-negligible weights. The remaining basis functions, whose influence is minimal, are held fixed during optimization. Furthermore, the number of active principal components is noted as $J^{\left(\mathrm{a}\right)}$ and set equal to $K^{\left(a\right)}$, ensuring that the model spans the full range of possible ranks from 1 to $K^{\left(\mathrm{a}\right)}$. Consequently, we optimize ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$ using updates derived w.r.t. the objective $K^{\left(a\right)}$-dimensional lower bound ${\mathcal{L}}^{\left(a\right)}$ as an efficient surrogate of the full updates of $\mathcal{Q}$ w.r.t. the full lower bound $\mathcal{L}$, using only $K^{\left(a\right)}$ active basis functions. Meanwhile, the active dimensionality of the model is adjusted dynamically during optimization by activating or deactivating basis functions based on their precision parameters. For clarity, variables associated with the active subspace are annotated with the superscript $\left(a\right)$ (e.g., $a_{{\alpha }_j}^{\left(\mathrm{a}\right)}=a_0+{\displaystyle \frac{K^{\left(\mathrm{a}\right)}}{2}}$ versus $a_{{\alpha }_j}=a_0+{\displaystyle \frac{K}{2}}$).

3.2.1. Implicit Factorization

For notation clarity, we reorder the rows and columns of our parameter matrices to separate active components from inactive ones. Specifically, we partition as follows:

$$\begin{array}{cc}\hfill Z_i& =\left(\begin{array}{cc}{Z}_{iA}& Z_{iB}\end{array}\right),\overline{Z}=\left(\begin{array}{cc}{\overline{Z}}_A& {\overline{Z}}_B\end{array}\right),\alpha =\left(\begin{array}{cc}{\alpha }_A& {\alpha }_B\end{array}\right),\beta =\left(\begin{array}{cc}{\beta }_A& {\beta }_B\end{array}\right),\hfill \\ \hfill W& =\left(\begin{array}{cc}{W}_A& W_B\\ W_C& W_D\end{array}\right),{\Phi }_i=\left(\begin{array}{c}{\Phi }_{iA}\\ {\Phi }_{iB},\end{array}\right)\hfill \end{array}$$

(30)

Here, the subscript A denotes variables belonging to the active subspace (i.e., those corresponding to $K^{\left(a\right)}$ basis functions), while $B,C,$ and D denote the inactive components. Notably, the cross terms $W_B$ and $W_C$ involve both active and inactive components; these are updated implicitly, as proved in the supplements.

Following the strategy in [73], a basis function is deemed inactive if its precision exceeds a high threshold, i.e. ${\alpha }_j>{ϵ}^{-1}$ and ${\beta }_k>{ϵ}^{-1}$ as $ϵ\to 0$. In the limit, the inactive basis functions decouple from the active ones, leading to the following mean-field factorization:

$$\begin{array}{cc}\hfill {\mathcal{Q}}_W& ={\mathcal{Q}}_{W_A}{\mathcal{Q}}_{W_B}{\mathcal{Q}}_{W_C}{\mathcal{Q}}_{W_D}\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{\overline{Z}}& ={\mathcal{Q}}_{{\overline{Z}}_A}{\mathcal{Q}}_{{\overline{Z}}_B}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\mathcal{Q}}_{Z_i}& ={\mathcal{Q}}_{Z_{iA}}{\mathcal{Q}}_{Z_{iB}}.\hfill \end{array}$$

(33)

The factorization of $\alpha$ and $\beta$ was already obtained in Equations (10) and (11). These factorizations allow us to decouple the update for the active subspace with the proof provided in the supplementary material.

It implies that only updates for ${\mathcal{Q}}_{Z_{iA}},{\mathcal{Q}}_{W_A},{\mathcal{Q}}_{W_B},{\mathcal{Q}}_{W_C},{\mathcal{Q}}_{{\overline{Z}}_A},{\mathcal{Q}}_{{\alpha }_A},{\mathcal{Q}}_{{\beta }_A},{\mathcal{Q}}_{\sigma },{\mathcal{Q}}_{\eta }$ are required as shown in Figure 2. This strategy reduces the computational complexity from $\mathcal{O}\left(K^6\right)$ to $\mathcal{O}\left({K^{\left(a\right)}}^6\right)$. Moreover, the active dimensions $K^{\left(\mathrm{a}\right)}$ are initialized using a modified, multi-instance version of relevance vector machine [52], as detailed in Section 11 in the supplementary materials.

3.2.2. Low-Dimensional Lower Bound

This section shows how to optimize these active surrogates, e.g., ${\mathcal{Q}}_{{\overline{Z}}_A}$, using updates of ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$ w.r.t. the $K^{\left(a\right)}$-dimensional lower bound ${\mathcal{L}}^{\left(a\right)}$, which ultimately optimizes the full lower bound $\mathcal{L}$. To distinguish between the two, we denote the active surrogate posterior for the full model as ${\mathcal{Q}}_{{\overline{Z}}_A}$ and that for the reduced $K^{\left(a\right)}$-dimensional model as ${\mathcal{Q}}_{{\overline{Z}}_A}^{\left(\mathrm{a}\right)}$. The active Gaussian surrogate posteriors are shared, e.g., ${\mathcal{Q}}_{{\overline{Z}}_A}={\mathcal{Q}}_{{\overline{Z}}_A}^{\left(\mathrm{a}\right)}=\mathcal{N}\left({\overline{Z}}_A\right|{{\mu }_{\overline{Z}}}_A,{{\Sigma }_{\overline{Z}}}_A)$. This implies updating ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$ is equivalent to updating $\mathcal{Q}$, so we set the moments of the active distributions of the full model to match those of the reduced model. However, the surrogate posterior Gamma distributions differ between the two models. For example, the update of ${\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[{\alpha }_A\right]$ depends solely on ${\mathcal{Q}}_{W_A}$, whereas ${\mathbb{E}}_{\mathcal{Q}}\left[{\alpha }_A\right]$ also incorporates a cross term ${\mathcal{Q}}_{W_B}$ corresponding to the remaining $(K-K^{\left(a\right)})$ dimensions. This difference is reflected in how the scale parameters depend on the number of active versus total basis functions, as shown in Equations (14), (16) and (18). Nonetheless, we prove that in the limit $ϵ\to 0$, the fixed point of the $K^{\left(a\right)}$-dimensional updates of the complete surrogate $\mathcal{Q}$ equals that of the reduced surrogate ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$. Consequently, the updates for ${\mathcal{Q}}_{{\alpha }_A},{\mathcal{Q}}_{{\beta }_A}$, and ${\mathcal{Q}}_{\eta }$ are derived directly from the expectations of the reduced model ${\mathcal{Q}}_{{\alpha }_A}^{\left(\mathrm{a}\right)},{\mathcal{Q}}_{{\beta }_A}^{\left(\mathrm{a}\right)},{\mathcal{Q}}_{\eta }^{\left(\mathrm{a}\right)}$:

$$\begin{array}{cc}\hfill {\mathbb{E}}_{\mathcal{Q}}\left[{\alpha }_A\right]\leftarrow {\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[{\alpha }_A\right]& \iff b_{{\alpha }_j}\leftarrow {\displaystyle \frac{a_{{\alpha }_j}}{a_{{\alpha }_j}^{\left(\mathrm{a}\right)}}}{b}_{{\alpha }_j}^{\left(\mathrm{a}\right)},\forall j\le J^{\left(\mathrm{a}\right)},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\mathbb{E}}_{\mathcal{Q}}\left[{\beta }_A\right]\leftarrow {\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[{\beta }_A\right]& \iff b_{{\beta }_k}\leftarrow {\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}{b}_{{\beta }_k}^{\left(\mathrm{a}\right)},\forall k\le K^{\left(\mathrm{a}\right)},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\mathbb{E}}_{\mathcal{Q}}\left[\eta \right]\leftarrow {\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[\eta \right]& \iff b_{\eta }\leftarrow {\displaystyle \frac{b_{\eta }^{\left(\mathrm{a}\right)}}{a_{\eta }^{\left(\mathrm{a}\right)}}}{a}_{\eta }\hfill \end{array}$$

(36)

These update Equations (34), (35), (36) prove to optimize $\mathcal{L}$ in Theorem 1, 2 in the supplements.

3.2.3. Heuristic for Activating Basis Functions

The proposed method selects a relatively small set of basis functions from a potentially extensive set of possibilities. The computational costs are kept in check by recognizing that inactive basis functions do not interact with those active (with non-negligible weights). Due to computational constraints, we consider functions for activation sequentially rather than all at once. Thus, we propose Algorithm 1 to introduce unseen basis functions into the active set using a selective strategy akin to the heuristic approach described in [73].

The algorithm selects the top function, ${\varphi }_{Bk}$, from the inactive basis functions ${\left\{{\varphi }_{Bk}\right\}}_k$ by gauging their correlation with residuals and applying an angle-based threshold ${\tau }_{\mathrm{ang}}$ relative to the subspace of ${\varphi }_A$. The correlation with residuals for ${\varphi }_{Bk}$ is measured by ${\sum }_i{\left({\Phi }_{iBk}{(Y_i-{\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}[Z_{iA}{W}_A+{\overline{Z}}_A]{\Phi }_{iA})}^T\right)}^2$. The angle-based threshold ensures a meaningful distinction from active functions. Next, the current active surrogate posterior is expanded by a dimension for $\widetilde{{\varphi }_{Bk}}$, initiating optimization from the numerical maximum ${\tau }_{\max }$. Post optimization, the function gets retained if it falls below ${\tau }_{\max }$. Otherwise, the algorithm terminates. Efficiently, in trial optimization, the approach replaces one function with precision ${\tau }_{\max }$, if present.

Algorithm 1 Search for new basis functions to activate

Sort inactive basis functions ${\left\{{\varphi }_{Bk}\right\}}_k$ by correlation with residuals. Filter through ${\left\{{\varphi }_{Bk}\right\}}_k$, selecting the most correlated one as ${{\varphi }_B}_k$. Copy current active surrogate ${\mathcal{Q}}^{\left(\mathrm{a}\right)}(\Theta )$ posterior to ${{\mathcal{Q}}_k}^{{\left(a\right)}^{\prime }}(\Theta )$. Expand dimension in ${{\mathcal{Q}}_k}^{{\left(a\right)}^{\prime }}(\Theta )$ for ${{\varphi }_B}_k$. Optimize ${{\mathcal{Q}}_k}^{{\left(a\right)}^{\prime }}(\Theta )$ for 3 iterations using mean field approximation. if expected precision is within threshold then     ${\mathcal{Q}}^{\left(\mathrm{a}\right)}(\Theta )\leftarrow {{\mathcal{Q}}_k}^{{\left(a\right)}^{\prime }}(\Theta )$. end if

4. Faster Variant

To enhance the computational efficiency of our primary algorithm, we introduce a faster variant, denoted as ${\mathrm{BSFDA}}^{\mathrm{Fast}}$. This approach leverages conditional independence among the columns of W, enabling separate updates and thereby reducing computational complexity. Similar strategies have been described in [34,62]. The model is defined with an introduced variable ${\zeta }_i$ for the coefficient noise as follows:

$${\theta }_i=Z_{i}W+{\zeta }_i,$$

(37)

$${\zeta }_{ik}\sim \mathcal{N}(0,{\varsigma }_k^2{\beta }_k^{-1}).$$

(38)

Similar to before, we assign a conjugate Gamma prior to the precision:

$${\varsigma }_k^{-2}\sim \Gamma (a_0,b_0).$$

(39)

This formulation ensures that the columns of W are conditionally independent, allowing the variational distribution to factorize as: ${\mathcal{Q}}_{\mathcal{W}}={\prod }_k{\mathcal{Q}}_{W_{·k}}$, thereby facilitating separate updates for each column. Consequently, the time complexity is reduced from $\mathcal{O}\left({K^{\left(a\right)}}^6\right)$ to $\mathcal{O}\left({K^{\left(a\right)}}^3\right)$.

To align with the original model, it is necessary for $\zeta$ and the associated variance parameters $\varsigma$ to approach zero. Having $\varsigma$ too high would allow the coefficient noise to corrupt the signal, biasing the model toward underestimating the true signal levels, particularly because this noise operates in the coefficient space where it introduces smooth, correlated variation (low entropy, like signals) that is harder to eliminate than high-frequency white noise (maximum entropy). Injecting the same amount of noise leads to an unbiased estimation of the signals but increases the estimation variance. Conversely, as $\varsigma$ decreases, the columns of W become dependent, violating the independence assumption inherent in variational inference. This dependency degrades the approximation quality and slows down the optimization process. Such dependency issues are well documented in both variational inference and MCMC literature–with recent efforts addressing them via structured VI [72] or blocked/collapsed Gibbs sampling [74]. Empirical validations of this noise impact are conducted with both ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ in Section 5 and with Bayesian PCA [45,62] in Section 12.2 in the supplements.

To balance the trade-off between optimization speed and accuracy, we adopt a strategy of gradually decreasing the values of ${\varsigma }_k$ during the optimization iterations. Specifically, we initialize ${\varsigma }_k$ with a relatively large value and linearly decrease it from ${10}^{-2}$ to ${10}^{-5}$ over the first half of the iterations. After reaching ${10}^{-5}$, ${\varsigma }_k$ is fixed for the remaining iterations. This gradual reduction ensures that the algorithm initially maintains efficiency with benefits from minimizing interdependency among the columns of W to accelerate convergence while later preserving quality of the approximation by preventing the noise from obscuring signal components. We unify the scales by scaling the basis functions so that $Z_i$ is standard normal and W is an identity matrix in initialization. Empirical evaluations indicate the strategy above is effective in most applications.

By implementing these modifications, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ offers a practical solution that substantially accelerates the algorithm without significant loss in accuracy, making it well-suited for large-scale, high-dimensional functional data analysis.

5. Results

The proposed method proves its effectiveness through simulations and applications to observed data sets.

5.1. Simulation Results

In simulations, we evaluate functional data analysis performance in model selection, estimated covariance accuracy, and extendability to multi-dimensional domains.

The model selection metric is the accuracy in estimating the number of principal components, which is the dimension of the compact subspace of signal variations. The configuration of the simulations in this section aligns with that established in [37], covering various scenarios. Simulated data sets derive from a latent generative model with variables ${\mathcal{Z}}_i$ with dimension r for the i-th sample function and noise corruption with a standard deviation of $\sigma$: $Y_i={\sum }_{j=1}^r\left({\mathcal{Z}}_{ij}{f}_j\left(X_i\right)\right)+g\left(X_i\right)+E_i,{\mathcal{Z}}_{ij}\sim \mathcal{N}(0,v_j),E_j\sim \mathcal{N}(0,{\sigma }^{2}I),$ where ${\left\{f_j\right\}}_{j=1}^r$ represent eigenfunctions, ${\left\{v_j\right\}}_{j=1}^r$ are the eigenvalues, $g:R\mapsto R$ signifies the mean function. Here, we consider five scenarios.

Scenario 1: Data generated with $g=5{(x-0.6)}^2$, $r=3$, $v=(0.6,0.3,0.1)$, ${\sigma }^2=0.2$, $f_1\left(x\right)=1,f_2\left(x\right)=\sqrt{2}sin\left(2\pi x\right),f_3\left(x\right)=\sqrt{2}cos\left(2\pi x\right).$ Here $v_3<{\sigma }^2$, i.e., the noise has a larger variance than the smallest signal.

Scenario 2: Similar to Scenario 1, but the third eigenfunction is replaced by a function with higher frequencies $f_3\left(x\right)=\sqrt{2}cos\left(4\pi x\right)$, and the principal component scores follow a skewed Gaussian mixture model. Specifically, the j-th component score has 1/3 probability of following a $\mathcal{N}(2\sqrt{v_j/3},v_j/3)$ distribution, and 2/3 probability of following $\mathcal{N}(-\sqrt{v_j/3},v_j)$, for $j=1,2,3$.

Scenario 3: Data generated with $g=12.5{(x-0.5)}^2-1.25$, $r=3$, $v=(4,2,1)$, ${\sigma }^2=0.5$, $f_1\left(x\right)=1,f_2\left(x\right)=\sqrt{2}cos\left(2\pi x\right),f_3\left(x\right)=\sqrt{2}sin\left(4\pi x\right).$

Scenario 4: Same as Scenario 3, but the component scores are generated from a Gaussian mixture model as Scenario 2.

Scenario 5: Data from $g=12.5{(x-0.5)}^2-1.25$, $r=6$, $v=(4,3.5,3,2.5,2,1.5)$, ${\sigma }^2=0.5$, $f_1\left(x\right)=1,f_{2k}\left(x\right)=\sqrt{2}sin\left(2k\pi x\right)\mathrm{for}k=1,2,3,f_{2k+1}\left(x\right)=\sqrt{2}cos\left(2k\pi x\right)\mathrm{for}k=1,2$, j-th component score obeying $\mathcal{N}(0,v_j)$.

In each scenario, simulations produced 200 sample functions. We investigated 3 cases with sparse, medium, and dense sampling by assigning the number of observations per sample function $N_i=\{5,10,50\}$. Each case in each scenario is repeated 200 times. The method’s performance was compared to fpca from [22], AIC and BIC in the 2022 release of pace [20], modified AIC and BIC in [37], and all the competing methods in [37]. For fpca, we set the candidate numbers of basis functions as [8,10,15,20], and the candidate dimensions of the process as [2,3,4,5] for Scenario 1-4 and [4,5,6,7,8] for Scenario 5. The other parameters are all set to the defaults. Due to its consistent overestimation of the true number of components–likely resulting from interference by correlated noise and less sparse precision priors–we excluded LFRM[34] from further comparisons (see Section 12.1.1 in the supplements).

Each estimation chose ten length-scales of functions, which are selected using cross-validation and k-means clustering. This adaptive strategy allows the algorithm to choose distinct length-scales at different locations of the definition domain, thereby accommodating varying smoothness characteristics inherent in complex functional data–a flexibility that is not possible when using a regular grid that forces a single length-scale across the entire domain [34]. Sparse sampling in Scenario 5 used five length-scales to avoid over-fitting. Figure 3 shows the length-scales and centers of the selected kernel basis functions for three different numbers of sample points, $N_i$, in a random repetition of Scenario 5. The results reveal that the selected length-scales mainly concentrate around 0.07, with a few as high as 0.35–suggesting that the lower length-scales capture finer, high-frequency variations. The higher length-scales model the overall, lower-frequency quadratic mean structure and the constant baseline component. Furthermore, the estimated density functions of the selected length-scales exhibit consistent patterns across the three sampling densities, and the method selects 9, 11, and 12 basis functions respectively, demonstrating the algorithm’s adaptive fidelity and complexity based on the available observations. The supplements showcase the uncertainty evaluation in Figure 12.

Table 1, Table 2, Table 3, Table 4 and Table 5 show the results. Results for the first five methods are from [37]. Out of 15 cases, the proposed BSFDA exhibits the highest accuracy in 12. In the other 3 cases, the accuracy of BSFDA is comparable to the best result and is always above 0.950. ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ demonstrates performance comparable to BSFDA when applied to medium-density and dense datasets with significantly higher efficiency which we detail in Figure 5 later. However, its efficacy diminishes with sparse data. This limitation arises because the parameter $\varsigma$ can bias model estimation in scenarios with insufficient data evidence, leading to an underestimation of signal variance. Consequently, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ tends to underestimate the number of components, particularly those capturing nuanced variations, in the presence of sparse observations. Nonetheless, with adequate data, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ achieves performance on par with the original model.

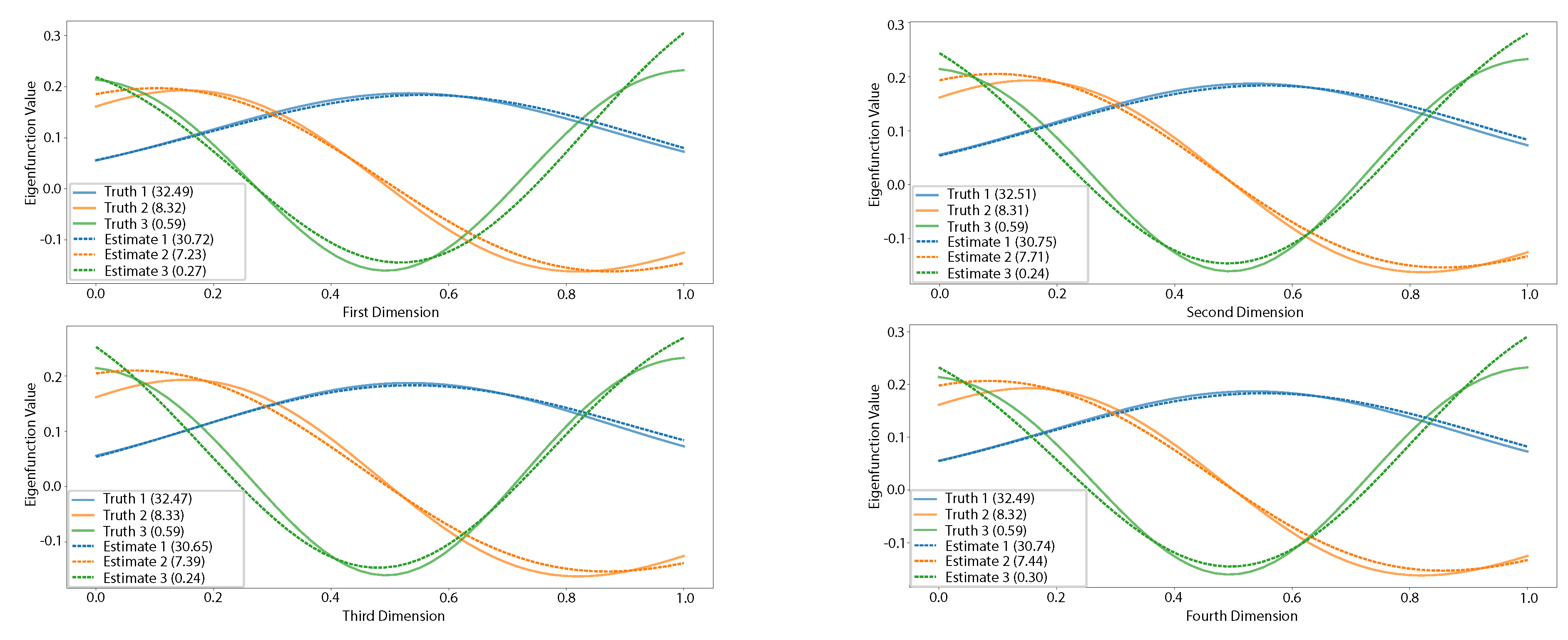
5.1.1. Mean Squared Error in Covariance Operator

The mean squared error across $X_{grid}$, a grid of 1000 index points:

$${\displaystyle \frac{\left|\right|cov(X_{grid},X_{grid})-\widehat{cov}(X_{grid},X_{grid}){\left|\right|}_F^2}{1000\times 1000}},$$

where $\left|\right|·{\left|\right|}_F$ is the Frobenius norm, measure the accuracy of the estimated covariance. The quadratic measure of error with Frobenius norm for covariance estimators has been used by [75]. Methods compared include fpca of [22], pace of [20] with AIC and BIC, refund-sc of [21]. Only cases in scenario 5 were used because of the time constraints (e.g., refund-sc takes 6 hours for 20 repetitions with 50 points in scenario 5). As the most challenging, scenario 5 should provide the most compelling comparison. The results in Table 6 demonstrate that the proposed method is comparable to the best work in terms of estimated covariance accuracy. Specifically, dense sampling becomes prohibitive for refund-sc. The results highlight the benefit of continuous formulations, as seen in both fpca and the proposed method, over the grid-based optimization in conventional methods. ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ again performed comparably well given data was adequate.

5.1.2. Multidimensional Functional Data Simulation

A simulation experiment with a four-dimensional index set reveals the proposed method’s advantages for high-dimensional data, where the gridding strategies of previous methods are impractical. The settings are as follows with a length-scale $l_{\mathrm{s}}=0.33$:

$$\begin{array}{cc}\hfill Z_i& \sim \mathcal{N}(0,I)\in R^{1\times 3}\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\varphi }_0\left(x\right)& ={\left(\pi l_{\mathrm{s}}^2\right)}^{-2}exp\left(-{\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{x-[0.5,0.5,0.5,0.5]}{l_{\mathrm{s}}}}∥}_2^2\right)\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill {\varphi }_1\left(x\right)& ={\left(\pi l_{\mathrm{s}}^2\right)}^{-2}exp\left(-{\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{x-[0.4,0.4,0.4,0.4]}{l_{\mathrm{s}}}}∥}_2^2\right)\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill {\varphi }_2\left(x\right)& ={\left(\pi l_{\mathrm{s}}^2\right)}^{-2}exp\left(-{\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{x-[0.6,0.6,0.6,0.6]}{l_{\mathrm{s}}}}∥}_2^2\right)\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill y_i\left(x\right)& =Z_{i0}*\sqrt{0.6}*({\varphi }_0\left(x\right)-{\varphi }_1\left(x\right))+Z_{i1}*\sqrt{0.3}*{\varphi }_1\left(x\right)+Z_{i2}*\sqrt{0.4}*{\varphi }_2\left(x\right)\hfill \end{array}$$

(44)

The observations include additive noise with a sigma of 4.472e-01. The cross-validation selects a length-scale of 0.405. The estimated noise sigma is 4.637e-01. The proposed method correctly estimates the number of principal components as 3 and selected 31 basis functions. As shown in Figure 4, the eigenfunctions are correctly estimated. In addition, the estimated mean function is zero, which is accurate.

Next, we present a convergence comparison between BSFDA and ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ under four different schedules for the coefficient noise ${\varsigma }_k$. Specifically, we compare the default diminishing schedule from ${10}^{-2}$ to ${10}^{-5}$ with three fixed settings: ${10}^{-2}$, ${10}^{-3}$, and ${10}^{-5}$. We evaluate the covariance error and the discrepancy between the estimated/true dimensionality in one replicate of each sample density in Scenario 5, and the 4D simulation. For the 4D, we adopt a default initial ${\varsigma }_k$ of ${10}^{-3}$. As illustrated in Figure 5, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ achieves comparable accuracy to BSFDA while converging significantly faster than BSFDA in terms of both covariance errors and component estimation for medium and densely sampled data. In the 4D case, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ converges in covariance estimation after approximately 10,000 seconds and in dimensionality after around 4,000 seconds, compared to roughly 100,000 seconds and 13,000 seconds, respectively, for BSFDA. However, for sparse data, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ exhibits reduced estimation accuracy and underestimates the number of components by one. A similar decline in accuracy is observed in the 4D simulation when data sparsity is high. This limitation arises because the introduction of coefficient noise $\varsigma$ biases the model towards eliminating signals that are deemed insignificant. Moreover, when comparing the three fixed-${\varsigma }_k$ variants of the fast algorithm, a clear trade-off emerges: smaller ${\varsigma }_k$ reduce overall error but slow down the optimization due to increased dependency among variables. These results collectively demonstrate the effectiveness of our chosen ${\varsigma }_k$ schedule in ${\mathrm{BSFDA}}^{\mathrm{Fast}}$, as it balances both efficiency and accuracy.

Figure 5. Convergence plots for Scenario 5 in Yehua and the 4D simulation. The upper row displays the covariance error against time, while the lower row illustrates the difference between the estimated and true number of components.

Figure 5. Convergence plots for Scenario 5 in Yehua and the 4D simulation. The upper row displays the covariance error against time, while the lower row illustrates the difference between the estimated and true number of components.

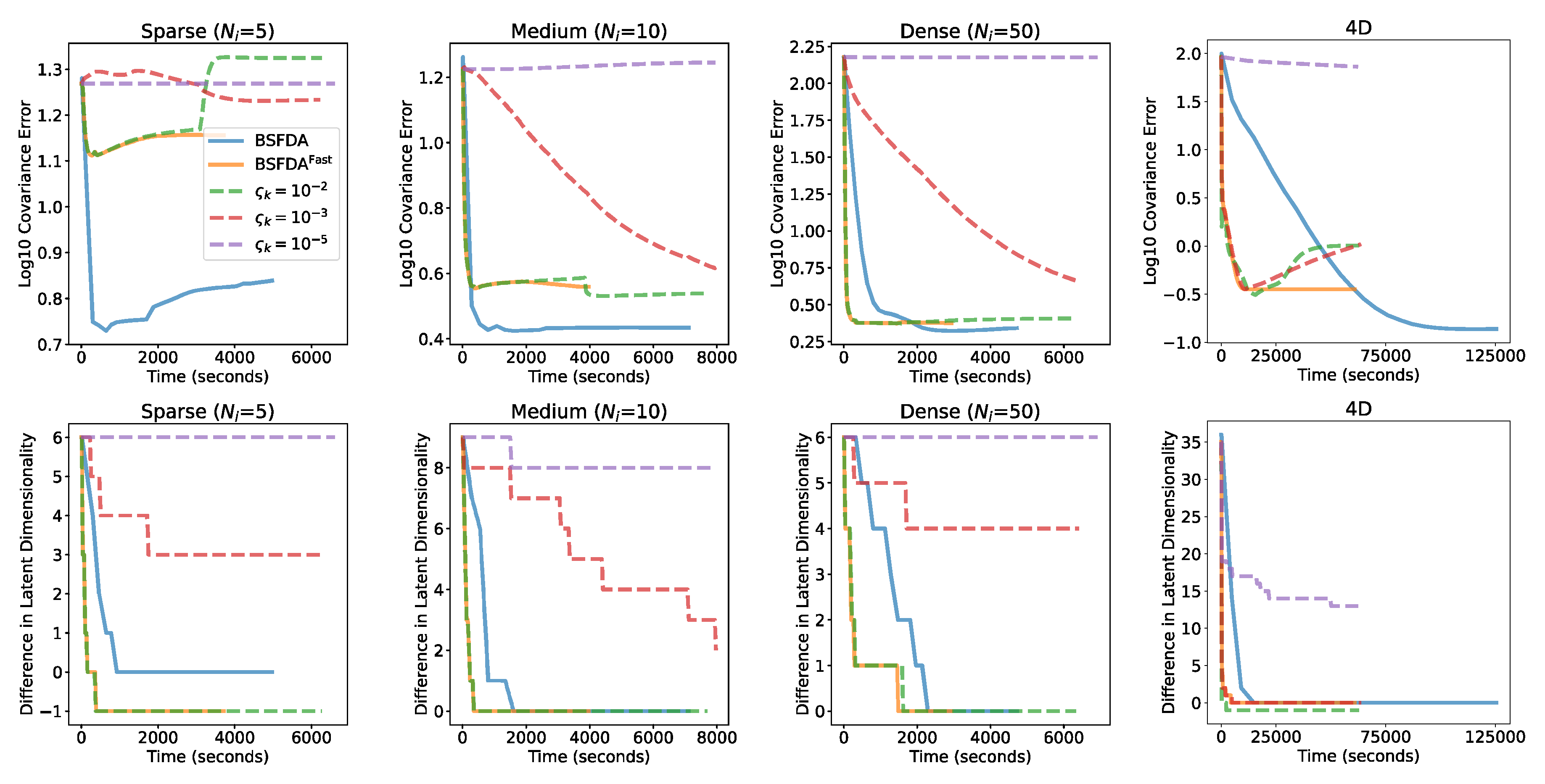
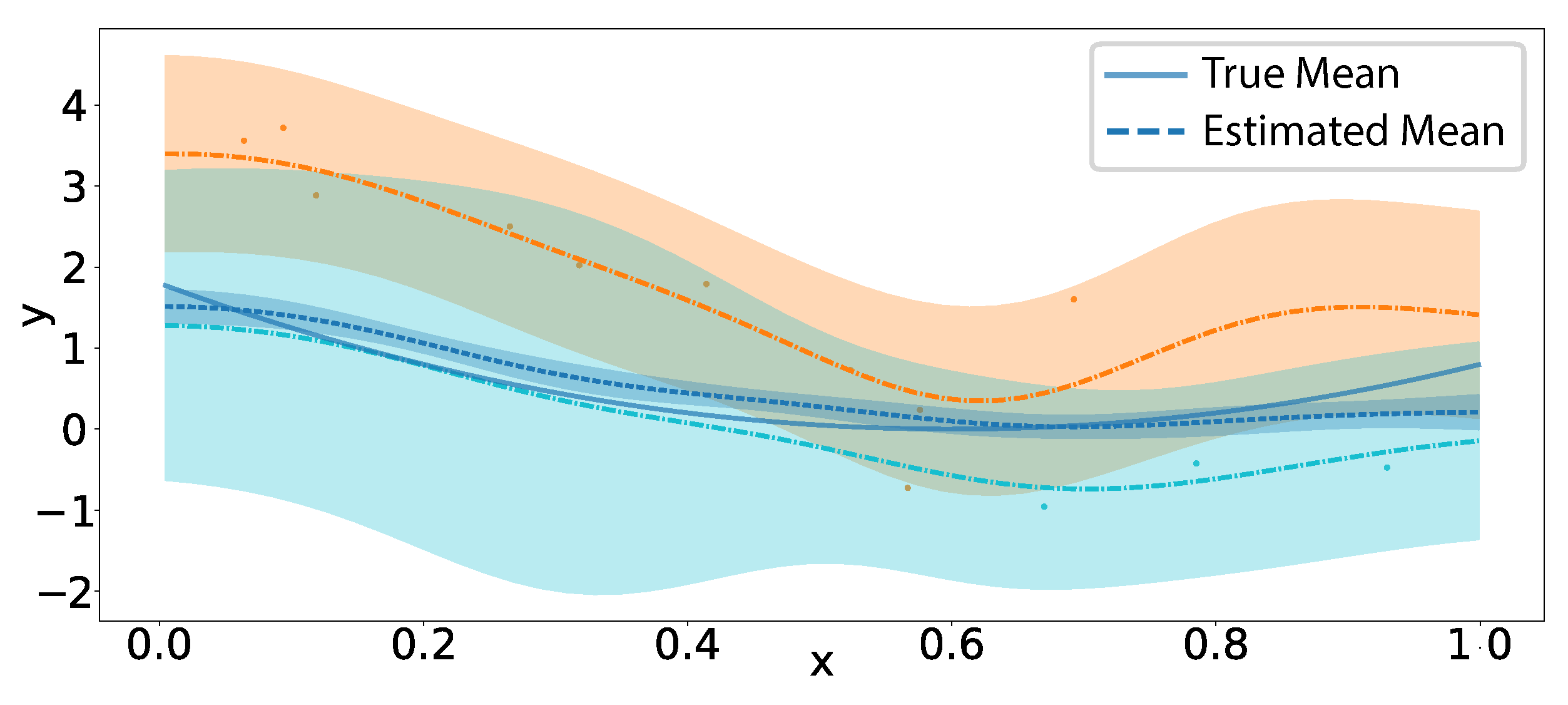
5.2. Results on Public Data Sets

The proposed method’s practicality was validated with 2 application data sets, CD4 and wind speed measurements.

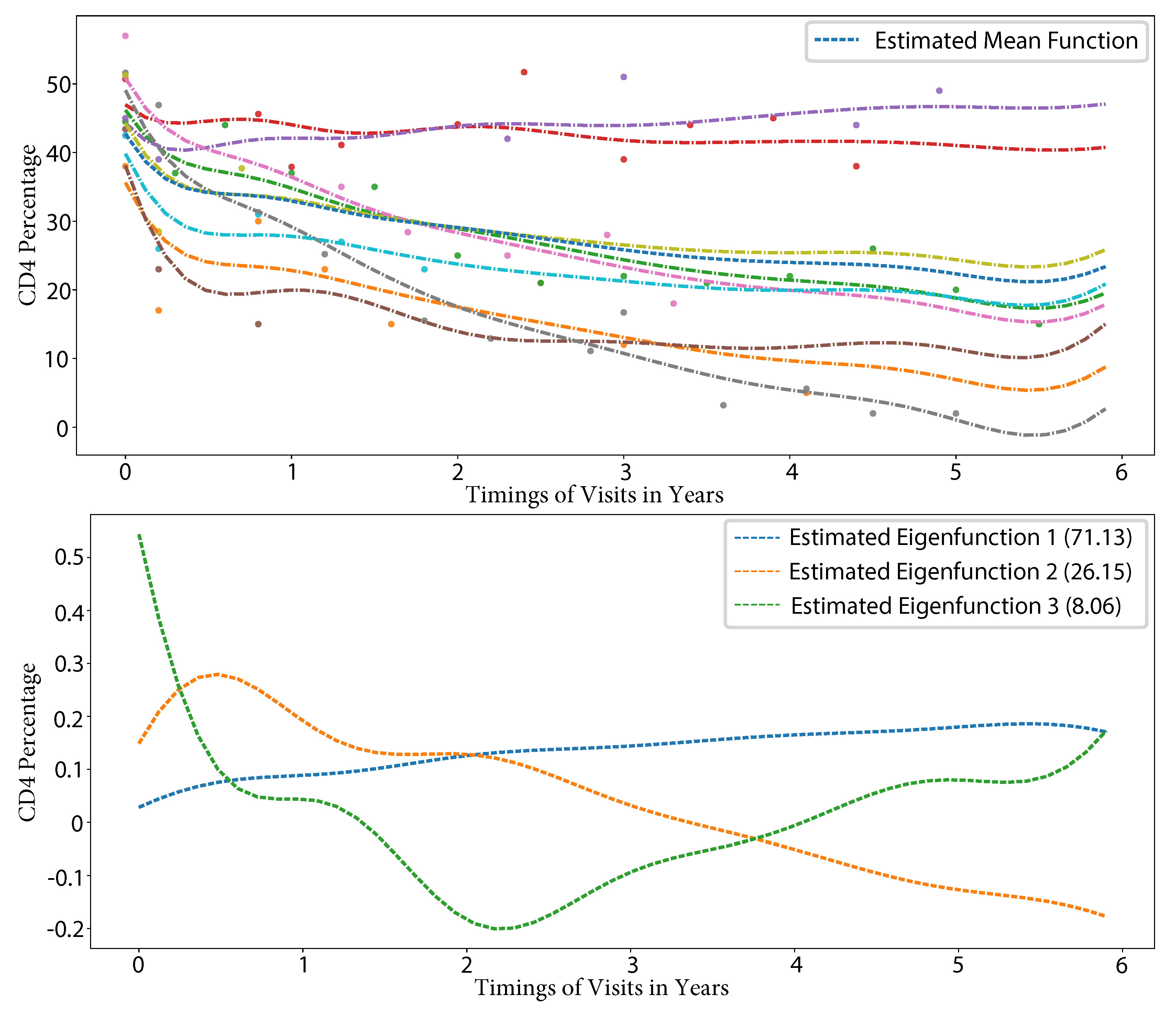
5.2.1. CD4

CD4 data, a classical form of functional data, received attention in [1,20,22]. CD4 cell counts gauge the immune system’s response to human immunodeficiency virus (HIV) infection, which leads to a progressive reduction in CD4 cell counts. The Multicenter AIDS Cohort Study (MACS) [76] provided the CD4 data. This dataset consists of CD4 percentages from 283 male human subjects that were HIV positive, each with 1 to 14 repeated measurements over time in years. Subjects were scheduled for reevaluation at least semiannually. However, missed visits caused a sparse and uneven distribution of measurements. The proposed method used five length-scales selected from cross-validation and k-means clustering. Finally, the model selected 9 basis functions. Figure 6 displays the estimated mean function, eigenfunctions, and curves of the observations. The mean function reflects the overall decreasing tendency with the progression of the disease. The eigenfunctions are obtained by applying singular value decomposition of the covariance operator that is discretized (for visualization purposes only) with a grid of 50 evenly spaced points over the whole timeline. The first eigenfunction is relatively flat and mainly captures the subject-specific average magnitude of the CD4 counts, consistent with the finding of [1,20,22]. The second eigenfunction captures the simple linear trend of the variations, as described in [22]. The third eigenfunction captures the piece-wise linear time trend with a breakpoint near 2.5 years since baseline. [1,20] found similar eigenfunctions.

5.2.2. Wind Speed

Wind-speed data, collected from 110 locations across Utah’s Salt Lake Valley, varies between 11 to 1440 measurements. The proposed method leverages ten length-scales selected from cross-validation and k-means clustering. Figure 7 illustrates the estimated mean function, curves of the observations, eigenfunctions, and covariance. The horizontal axis represents the seconds starting from 12:00 AM Greenwich Mean Time (GMT) on June 15, 2023, which corresponds to 6:00 PM in Salt Lake City. In Figure 7a, the estimated mean function depicts two pronounced peaks observed approximately at 8:00 PM and 6:00 AM, as well as two troughs around 12:00 AM and 12:00 PM. This pattern aligns with the diurnal cycle, particularly highlighting the thermal activities associated with sunset and sunrise. The peaks during sunset and sunrise are due to the interplay of topographical features, which result in specific breezes, such as the land breeze near the Great Salt Lake and the distinct mountain and valley breezes. The troughs, on the other hand, reflect moments when the atmosphere is at its most stable, with minimal thermal activities disrupting wind patterns. The complexity of the data is distilled and represented using 12 descriptors with 17 basis functions. As Figure 7b shows, the primary eigenfunction is relatively level, indicating that the most significant variation is the location-specific average magnitude. Its profile echoes the influence of sunrise and sunset observed in the mean function, with elevations around 7:00 PM and 5:00 AM and subdued patterns during other times, indicative of a similar atmospheric stability. The estimated covariance in Figure 7c highlights variance peaks around 8 PM and 5 AM, as well as a strong correlation between these periods. 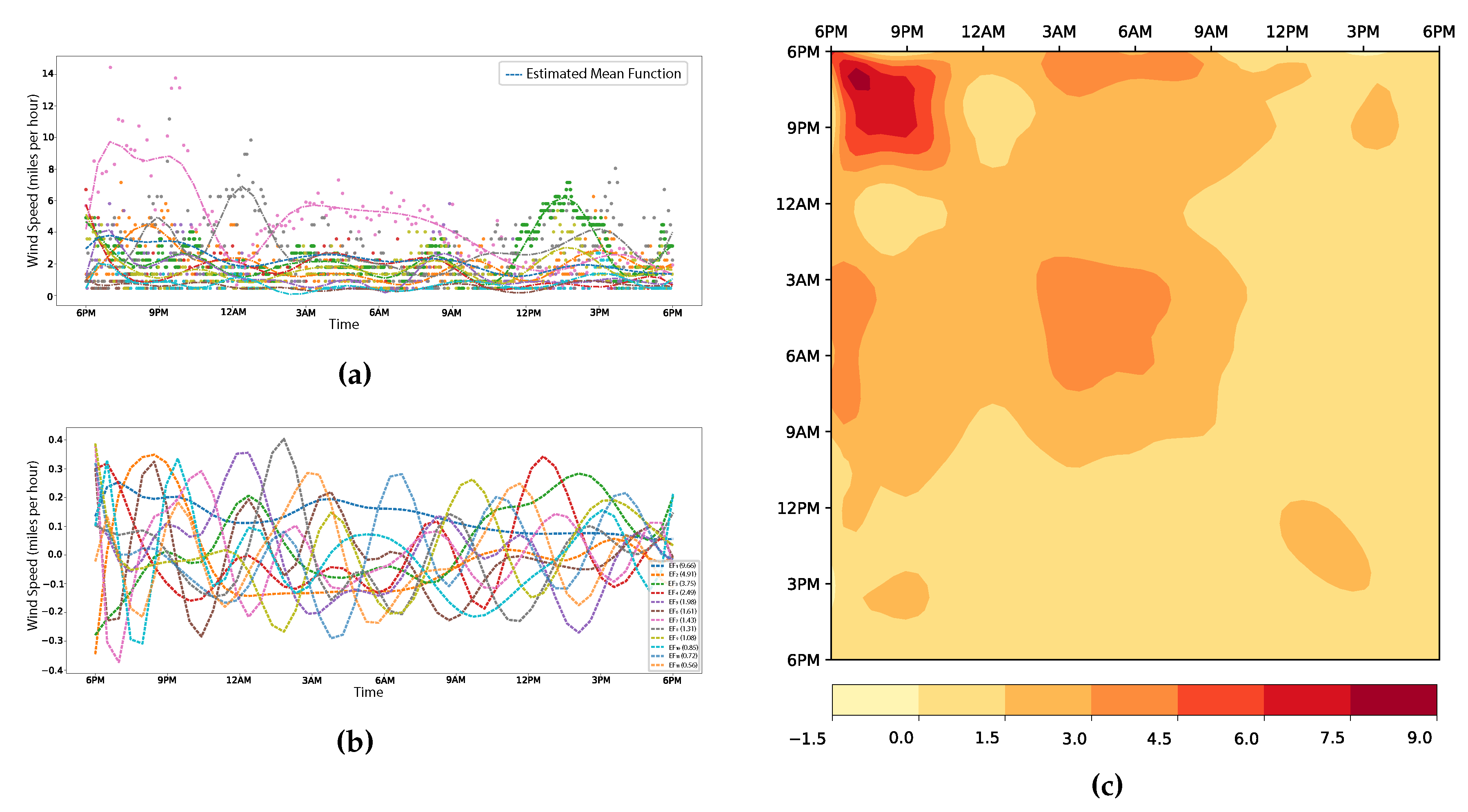This underscores the effects of location-specific topographic factors on wind speed.

5.2.3. Modeling Large-Scale, Dynamic, Geospatial Data

Here, we demonstrate the scalability on both the size of the measurements and the dimensionality of our framework. For this, we apply it to the ARGO dataset, which consists of ocean temperature measurements from more than 4,000 locations, at multiple depths, and time points [71]. ARGO is a nearly global observing system for ocean temperature, salinity, and other key variables via autonomous profiling floats. As of 2019, ARGO has generated over 338 gigabytes of data from 15,231 floats [71]. We focused on high-quality ("research" mode option in the database API) data from 1998 to 2024 for depths between 0–200 meters in the open-access snapshot of Argo GDAC of November 9, 2024 [77]. The number of measurement points per year varies widely–from 38,931 up to over 11 million, with 127 million in total. Figure 8 illustrates a global map of sea surface temperature measurements from February 2021, highlighting the dataset’s extensive spatial coverage.

In our modeling, each year’s data is treated as a single underlying function of four variables: latitude, longitude (on the spherical Earth), depth, and intra-annual time (modeled as a periodic variable). Note that the spatial data lies on a sphere and the time is a circle, assuming the periodicity of the time of the year. Our approach models these measurements holistically–without resorting to moving windows or sub-modeling–thereby preserving the continuous nature of the data and enabling the extraction of meaningful global, seasonal, and depth-dependent trends. Furthermore, the unique geospatial and temporal structure of Argo data, with spatial coordinates on a sphere and time exhibiting periodicity, necessitates specialized modeling techniques. Given that our model is 4 dimensional, the 4D kernel is defined as a product of the following kernels, following the design strategy for climatological data in [19]. The geospatial kernel on the sphere is a radial basis function (RBF) on geodesic distances. To ensure periodicity, the temporal kernel is an Exp-Sine-Squared $k(x,x^{\prime })=exp\left(-{\displaystyle \frac{2{sin}^2\left(\pi |x-x^{\prime }|\right)}{l_{\mathrm{s}}}}\right)$ where $l_{\mathrm{s}}$ is the length-scale. For depth, we use a Gaussian kernel.

The numeric data (excluding metadata) as input to the model was approximately 4 GB. For length-scale selection, we used Gaussian process regression on a small subset of 2,000 randomly selected data in 2016 (medium size of measurements) for a cross validated RMSE which we optimize with a grid search. The specific length scales were set as follows: geodesic length scale of $2\times {10}^3$ km, depth length scale of 70 m, time length scale of 3, and periodicity of 1. For evaluation, we held out 10% of the depth profiles (a single round trip of a buoy from surface to a depth at the same coordinate) from each year as testing data, following [78]. The total training set contained roughly 114 million points. Because the sample spacing is typically small relative to the selected length-scales, we apply agglomerative clustering to 10,000 randomly chosen index points, reducing them to 2,000 candidate basis functions. These candidate basis functions–precomputed for efficiency–took roughly 1.7 TB of memory. Computations were performed with 24 threads on a server equipped with 192 Intel^® Xeon^® Platinum 8360H CPUs @ 3.00GHz and 3TB RAM. Initialization was conducted using the modified RVM for 200 iterations for initial basis functions, using a stochastic optimization with a 1,000-batch size per year. Then ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ executed for 10,000 iterations, where the heuristic to include new bases also used a 1,000-batch size per year. With these computational strategies and heuristics, the entire modeling process was completed in 15 hours.

The proposed approach selected 163 effective basis functions and condensed them into 16 principle components. The final model occupies merely 50 MB of storage. The interpolation yielded a root mean square error (RMSE) of 1.95 and an $R^2$ of 94.2% on testing data, reflecting a reasonable balance between global dimension reduction and fidelity. The estimated white noise level was also 1.95, indicating that the training data adequately covers the underlying variability in the ARGO observations, and the final model is reasonably generalizable.

Figure 9 presents 2D visualizations of geospatial interpolations at three depths (in decibars, roughly meters) and a specific time (May 29, 2021) around 1°S and 30°W, each with three views. We have picked one measurement as the central point, denoted as the red circle, and selected a narrow window (±1 decibar, ±1 day) around this center. The cyan and fuchsia circles represent training and testing data, respectively, within this window. Their sizes indicate distance along the unplotted dimensions (depth and time here), reflecting variations in these dimensions. The visualizations show that temperatures are warmer near the equator and decrease with depth. The match between interpolated values and actual measurements demonstrates consistency in capturing broad spatial and vertical variations.

Figure 10 complements this by illustrating interpolation in the depth-time slices while holding the geospatial coordinates fixed, focusing on mixed layer characteristics. The "mixed layer" refers to a region of nearly uniform temperature, which is crucial for understanding thermodynamic potential and nutrient cycling [79]. Here, the plot uses a window of 50 km to include actual measurement, and the circle sizes denote geodesic distance from the chosen center. We plot every fifth measurement vertically to reduce overlap and improve clarity. Figure 10a uses the same center point, 1°S and 30°W, as in Figure 9, exhibiting a shallow mixed layer with pronounced vertical gradients. In contrast, Figure 10b adopts a center at a higher latitude, 49°N and 29°W, where the model reveals a deeper mixed layer. The temperature there remains relatively stable below the surface. The dominant variations are cyclic seasonal changes, which are warmer near the surface around September. As is shown, the vertical sequence of the center and the nearby testing sequence match the interpolation closely. These results confirm that the mid-latitudes exhibit a stronger seasonal cycle [79], and that ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ accurately approximates the actual measurements.

To our knowledge, this is the first time the ARGO dataset has been modeled in a full 4-dimensional principal component model, with the correct domain topology. We incorporate the entire period of 27 years rather than shorter spans (e.g., 2004-2008 or 2007-2016) [78,80,81]. Instead of segmenting the dataset into localized spatiotemporal windows, we process the entire 4D domain (latitude, longitude, depth, and intra-annual time) in a single holistic framework. Previous studies were typically tailored for ARGO datasets and handled each depth, month, or spatial region separately, restricting correlation estimates to limited windows (e.g., 1000 km and three months) while excluding data with large offsets [78,81]. In addition, they require repeated on-demand model fitting that can hinder scalability. Our kernel-based framework, by contrast, is broadly applicable to general functional data, only requiring kernel definitions for the domain. Although global dimension-reduction inevitably introduces some residual noise, the kernel-based design is extensible to finer spacing or multiple length scales if higher precision is needed. Furthermore, inference with our model is simply the evaluation of the active 163 active basis functions weighted by the 16 principal components. Interpolation over a 300×300 grid only takes about two seconds. By contrast, previous methods with Gaussian process regression require a weighted sum of all the measured data within a certain window. The parametric representations also facilitate straightforward derivative and integration calculations, which are essential for investigating ocean temperature stratification and heat content [78]. In summary, the Argo dataset provides an ideal testbed for our method, as it captures the dynamic behavior of high-dimensional geospatial data in a continuous framework. A more comprehensive study of ARGO is beyond this paper’s scope. Nonetheless, the results here confirm the clear advantages of the proposed method for large-scale, high-dimensional functional data.

6. Discussion

This paper proposed BSFDA, a novel framework for functional data analysis with irregular sampling, integrating model selection and scalability in one unique, coherent, and effective algorithm. Our extensive empirical studies, including both simulations and real world applications, show that BSFDA offer superior covariance estimation accuracy with remarkable efficiency.

In terms of accuracy, our method excels in model selection, consistently achieving top-tier performance. The accuracy of the covariance operator estimation also rivals that of the best existing methodologies in the field. This shows that our approach can not only handle large and complex datasets, but also ensures high accuracy and precision in the results it produces. Our method’s superiority compared to existing techniques is expected owing to the inherent iterative nature of data smoothing and covariance estimation in our approach.

In terms of scalability, our method demonstrates a linear growth of time complexity with the size of the dataset, and impressively, the computations are executed in a small, $K^{\left(a\right)}$-dimensional subspace. This ensures that as the datasets grow larger and more complex, the performance of our model remains robust and efficient. Additionally, we introduced a faster variant, ${\mathrm{BSFDA}}^{\mathrm{Fast}}$, which performs similarly to BSFDA on medium and dense datasets with significantly reduced computational cost. This leap in efficiency enabled a full 4-dimensional functional modeling, for the first time, of the large scale oceanic temperature dataset across 27 years (ARGO) [71]. Although ${\mathrm{BSFDA}}^{\mathrm{Fast}}$ can underestimate signal strength under very sparse sampling, the vanilla BSFDA effectively complements and alleviates this issue.

Looking ahead, it would be interesting to explore how extensions of regular PCA, such as simplified PCA and robust PCA [42], can be integrated within our proposed framework. These extensions will enhance the flexibility and robustness of our method, further improving its adaptability to various data conditions. In addition, we see potential in examining the extensions of functional PCA, such as time warping, dynamics, and manifold learning [1]. In particular, shape analysis emerges as a direct application of time warping. Such extensions would push the boundaries of what our proposed method could achieve, potentially enabling it to handle an even wider array of data structures and complexities.

In conclusion, our research findings affirm the proposed framework’s effectiveness and adaptability in advanced functional data analysis. Nonetheless, the method’s potential remains broad, and future work promises to widen its scope and refine its performance. By unifying sparse Bayesian learning, kernel-based expansions, and efficient variational inference, BSFDA offers a powerful foundation for large-scale, high-dimensional FDA challenges.

9.1. Implicit Factorization

We initialize the inactive precision parameters as:

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]& ={ϵ}^{-1},\forall j>J^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}}\left[{\beta }_k\right]& ={ϵ}^{-1},\forall k>K^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(79)

Under these settings and subsequent variational updates (using Equations (78) and (79)), in the limit as $ϵ\to 0$, the surrogate distributions satisfy:

$$\begin{array}{cc}\hfill {\mu }_{{Z_i}_B}& =0,{{\Sigma }_{Z_i}}_B=ϵI^{(J-J^{\left(\mathrm{a}\right)})},{{\Sigma }_{Z_i}}_{[A,B]}={\left({{\Sigma }_{Z_i}}_{[B,A]}\right)}^T=0\hfill \end{array}$$

(80)

$$\begin{array}{cc}\hfill {{\mu }_{\overline{Z}}}_B& =0,{{\Sigma }_{\overline{Z}}}_{[B,B]}=ϵI^{(K-K^{\left(\mathrm{a}\right)})},{{\Sigma }_{\overline{Z}}}_{[A,B]}={{\Sigma }_{\overline{Z}}}_{[B,A]}^T=0\hfill \\ \hfill {{\mu }_{vec\left(W\right)}}_B& =0,{{\mu }_{vec\left(W\right)}}_C=0,{{\mu }_{vec\left(W\right)}}_D=0,{{\Sigma }_{vec\left(W\right)}}_{[B,B]}=ϵI^{(K^{\left(\mathrm{a}\right)}J-K^{\left(\mathrm{a}\right)}{J}^{\left(\mathrm{a}\right)})},\hfill \\ \hfill {{\Sigma }_{vec\left(W\right)}}_{[C,C]}& =ϵI^{(J^{\left(\mathrm{a}\right)}K-J^{\left(\mathrm{a}\right)}{K}^{\left(\mathrm{a}\right)})},{{\Sigma }_{vec\left(W\right)}}_{[D,D]}=ϵI^{(JK+J^{\left(\mathrm{a}\right)}{K}^{\left(\mathrm{a}\right)}-J{K}^{\left(\mathrm{a}\right)}-J^{\left(\mathrm{a}\right)}K)},\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill {{\Sigma }_{vec\left(W\right)}}_{[x,y]}& =0,\forall (x,y)\notin \left\{\right(A,A),(B,B),(C,C),(D,D\left)\right\}\hfill \end{array}$$

(82)

For convenience, we initialize $\mathcal{Q}$ with the above properties.

Lemma 1.

If ${\mathcal{Q}}_{{\alpha }_j}\left[{\alpha }_j\right]=ϵ,\forall j\ge J^{\left(\mathrm{a}\right)}$ and ${\mathcal{Q}}_{{\beta }_k}\left[{\beta }_k\right]=ϵ,\forall k\ge K^{\left(\mathrm{a}\right)}$, then the variational distribution over W factorizes as ${\mathcal{Q}}_W={\mathcal{Q}}_{W_A}{\mathcal{Q}}_{W_B}{\mathcal{Q}}_{W_C}{\mathcal{Q}}_{W_D}$ in the limit as $ϵ\to 0$.

Proof. 

We express the distribution as

$$\begin{array}{cc}\hfill {\mathcal{Q}}_W& =\mathcal{N}(vec\left(W\right)|{\mu }_{vec\left(W\right)},{\Sigma }_{vec\left(W\right)})\hfill \\ \hfill & =exp\left(-{\displaystyle \frac{1}{2}}\left(ln|2\pi {\Sigma }_{vec\left(W\right)}|+{\mu }_{vec\left(W\right)}{{\Sigma }_{vec\left(W\right)}}^{-1}{{\mu }_{vec\left(W\right)}}^T\right)\right),\hfill \end{array}$$

The factorization holds if the off-diagonal block matrices in ${\Sigma }_{vec\left(W\right)}$, e.g. ${\Sigma }_{[W_A,W_B]}$, are all zero, i.e., the blocks are mutually independent. Initially, this is ensured by the definition for the initial status in Equation (82). Thus, we only need to show the statement remains true after ${\mathcal{Q}}_W$ is updated, i.e., after Equation (22) is applied with the inactive scale parameters ${\mathcal{Q}}_{{\alpha }_j}\left[{\alpha }_j\right]$ and ${\mathcal{Q}}_{{\beta }_k}\left[{\beta }_k\right]$ fixed at $ϵ$. First we regard ${\Sigma }_{\left[W_{ABC}\right]}$, i.e., the covariance of the union of $W_A,W_B,W_C$ after vectorization, as one block. By the block matrix inversion formula, we get ${\Sigma }_{[W_{ABC},W_D]}\propto {ϵ}^2\to 0$ and consequently ${\mathcal{Q}}_W={\mathcal{Q}}_{W_{ABC}}{\mathcal{Q}}_{W_D}$. Next, apply block matrix inversion formula to ${\Sigma }_{\left[W_{ABC}\right]}$ in Equation (22) and we get $({\Sigma }_{[W_B,W_A]},{\Sigma }_{[W_B,W_C]},{\Sigma }_{[W_C,W_A]},{\Sigma }_{[W_C,W_B]})\propto ϵ\to 0$, yielding the desired factorization.    □

Lemma 2.

If ${\mathcal{Q}}_{{\beta }_k}\left[{\beta }_k\right]=ϵ,\forall k\ge K^{\left(\mathrm{a}\right)}$, then the implicit factorization ${\mathcal{Q}}_{\overline{Z}}={\mathcal{Q}}_{{\overline{Z}}_A}{\mathcal{Q}}_{{\overline{Z}}_B}$ holds in the limit as $ϵ\to 0$.

Proof. 

It is similar to the proof for Lemma A1. Because ${\mathcal{Q}}_{\overline{Z}}=\mathcal{N}({\mu }_{\overline{Z}},{\Sigma }_{\overline{Z}})$, we only need the off-diagonal block is zero, i.e., ${{\Sigma }_{\overline{Z}}}_{[A,B]}=0$. Initially, it is ensured by definition for the initial status in Equation (81). ${\mathcal{Q}}_{\overline{Z}}$ is updated by Equation (20), Applying block matrix inversion formula with the inactive ${\mathcal{Q}}_{{\beta }_k}\left[{\beta }_k\right]$, we get ${{\Sigma }_{\overline{Z}}}_{[A,B]}\propto ϵ\to 0$, establishing the factorization.    □

Lemma 3.

If $j\ge J^{\left(\mathrm{a}\right)}$ or $k\ge K^{\left(\mathrm{a}\right)}$, then ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k{j}^{\prime }}{W}_{j{k}^{\prime }}\right]\propto \mathcal{O}\left(ϵ\right),\forall j^{\prime }=1:J,k^{\prime }=1:K$ in the limit as $ϵ\to 0$.

Proof. 

For initial status, apparently the largest ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k{j}^{\prime }}{W}_{j{k}^{\prime }}\right]$ is ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k{j}^{\prime }}^2\right]=ϵ$. Because either ${\mathcal{Q}}_{{\alpha }_j}\left[{\alpha }_j\right]=ϵ$ or ${\mathcal{Q}}_{{\beta }_k}\left[{\beta }_k\right]=ϵ$, after updates from Equations (22) and (23) are applied, ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k{j}^{\prime }}{W}_{j{k}^{\prime }}\right]={\Sigma }_{[W_{k{j}^{\prime }},W_{j{k}^{\prime }}]}+{{\mu }_{vec\left(W\right)}}_{k{j}^{\prime }}{{\mu }_{vec\left(W\right)}}_{j{k}^{\prime }}\propto \mathcal{O}\left(ϵ\right)$ by Woodbury matrix identity.    □

Lemma 4.

If ${\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]={\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}={ϵ}^{-1},\forall j\ge J^{\left(\mathrm{a}\right)}$, then the implicit factorization ${\mathcal{Q}}_{Z_i}={\mathcal{Q}}_{Z_{iA}}{\mathcal{Q}}_{Z_{iB}}$ holds in the limit as $ϵ\to 0$.

Proof. 

It is similar to the proof for Lemma 1. Because ${\mathcal{Q}}_{Z_i}=\mathcal{N}({\mu }_{Z_i},{\Sigma }_{Z_i})$, only ${{\Sigma }_{Z_i}}_{[A,B]}=0$ is needed. Initially, it is ensured by definition for the initial status Equation (80). ${\mathcal{Q}}_Z$ is updated by Equations (24) and (25). In Equation (24), when $j\ge J^{\left(\mathrm{a}\right)}$ or $k\ge K^{\left(\mathrm{a}\right)}$, $C_{ijk}=Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k·}^T{W}_{j·}\right]{\Psi }_i\right)={\sum }_{(j^{\prime },k^{\prime })}\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{k{j}^{\prime }}{W}_{j{k}^{\prime }}\right]{\left({\Psi }_i\right)}_{k^{\prime }{j}^{\prime }}\right)\propto \mathcal{O}\left(ϵ\right)\to 0$ applying Lemma 3. Applying block matrix inversion formula to Equation (25), ${{\Sigma }_{Z_i}}_{\left[AB\right]}\propto \mathcal{O}\left(ϵ\right)\to 0$, , thus proving the implicit factorization    □

9.2. Scale Parameters

Here we state the theorems that justify we can use updating rules for ${\mathcal{Q}}_{{\alpha }_j}^{\left(\mathrm{a}\right)}$ based on ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ to update ${\mathcal{Q}}_{{\alpha }_j}$ (and similarly, ${\mathcal{Q}}_{{\beta }_k}^{\left(\mathrm{a}\right)}$ for ${\mathcal{Q}}_{{\beta }_k}$, ${\mathcal{Q}}_{\eta }^{\left(\mathrm{a}\right)}$ for ${\mathcal{Q}}_{\eta }$) and it does maximize $\mathcal{L}$ ultimately.

Lemma 5.

$\forall W_{jk}\in W_B\cup W_C$, i.e., either $(j>J^{\left(\mathrm{a}\right)})$ or $(k>K^{\left(\mathrm{a}\right)})$, after updating ${\mathcal{Q}}_{W_B}$ and ${\mathcal{Q}}_{W_C}$ by Equations (22) and (23), ${\mathbb{E}}_{\mathcal{Q}}\left[W_{jk}^2\right]={\displaystyle \frac{b_{{\alpha }_j}{b}_{{\beta }_k}}{a_{{\alpha }_j}{a}_{{\beta }_k}}}$.

Proof. 

According to Equations (78) and (79), if $(j>J^{\left(\mathrm{a}\right)})$ or $(k>K^{\left(\mathrm{a}\right)})$, either ${\mathbb{E}}_{\mathcal{Q}}\left[{\alpha }_j\right]={ϵ}^{-1}$ or ${\mathbb{E}}_{\mathcal{Q}}\left[{\beta }_k\right]={ϵ}^{-1}$ respectively.

In the limit as $ϵ\to 0$, using Equation (22) and block matrix inversion formula we get

$$\begin{array}{cc}\hfill {\Sigma }_{W_{jk}}& \leftarrow \underset{ϵ\to 0}{lim}{\left({\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}[diag\left(\beta \right)\otimes diag\left(\alpha \right)+{\sigma }^{-2}\sum _i\left(\left({\Psi }_i\right)\otimes \left(Z_i^T{Z}_i\right)\right)]\right)}^{-1}\right)}_{[j+kM,j+kM]}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\left({\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[{\alpha }_j{\beta }_k\right]\right)}^{-1}+\mathcal{O}\left({ϵ}^2\right)\right)={\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[{\alpha }_j{\beta }_k\right]\right)}^{-1}={\displaystyle \frac{b_{{\alpha }_j}{b}_{{\beta }_k}}{a_{{\alpha }_j}{a}_{{\beta }_k}}}\hfill \end{array}$$

(83)

In the limit as $ϵ\to 0$ and using Equation (23)

$$\begin{array}{cc}\hfill {\mu }_{W_{jk}}& \leftarrow \underset{ϵ\to 0}{lim}{\left(-{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i}vec{\left({\left({\Phi }_i{({\mu }_{\overline{Z}}{\Phi }_i-Y_i)}^T{\mu }_{Z_i}\right)}^T\right)}^T{\Sigma }_{vec\left(W\right)}\right)}_{[1,j+kM]}\hfill \\ \hfill & =\left(-{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i}vec{\left({\left({\Phi }_i{({\mu }_{\overline{Z}}{\Phi }_i-Y_i)}^T{\mu }_{Z_i}\right)}^T\right)}^T\right){\left({\Sigma }_{vec\left(W\right)}\right)}_{·(j+kM)}\in \mathcal{O}\left(ϵ\right)\hfill \end{array}$$

(84)

Equation (84) uses the fact that elements in ${\left({\Sigma }_{vec\left(W\right)}\right)}_{·(j+kM)}$ are all $\mathcal{O}\left(ϵ\right)$ based on block matrix inversion formula. Thus,

$$\begin{array}{cc}\hfill \underset{ϵ\to 0}{lim}{\mathbb{E}}_{\mathcal{Q}}\left[W_{jk}^2\right]& =\underset{ϵ\to 0}{lim}\left({\Sigma }_{W_{jk}}+{\left({\mu }_{W_{jk}}\right)}^2\right)=\underset{ϵ\to 0}{lim}\left({\Sigma }_{W_{jk}}+\mathcal{O}\left({ϵ}^2\right)\right)\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\left({\displaystyle \frac{b_{{\alpha }_j}{b}_{{\beta }_k}}{a_{{\alpha }_j}{a}_{{\beta }_k}}}+\mathcal{O}\left({ϵ}^2\right)\right)={\displaystyle \frac{b_{{\alpha }_j}{b}_{{\beta }_k}}{a_{{\alpha }_j}{a}_{{\beta }_k}}}\hfill \end{array}$$

(85)

   □

Lemma 6.

$\forall k>K^{\left(\mathrm{a}\right)}$, after updating ${\mathcal{Q}}_{{\overline{Z}}_B}$ by Equations (20) and (21), ${\mathbb{E}}_{\mathcal{Q}}\left[{\overline{Z}}_k^2\right]={\displaystyle \frac{b_{\eta }}{a_{\eta }}}ϵ$.

Proof. 

If $k>K^{\left(\mathrm{a}\right)}$, ${\mathbb{E}}_{\mathcal{Q}}\left[{\beta }_k\right]={ϵ}^{-1}$.

Then using Equation (20) and block matrix inversion formula we get

$$\begin{array}{cc}\hfill {{\Sigma }_{\overline{Z}}}_{kk}& \leftarrow \underset{ϵ\to 0}{lim}{\left({\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[\sum _{i=1}^P\left({\sigma }^{-2}{\Psi }_i\right)+\eta diag\left(\beta \right)\right]\right)}^{-1}\right)}_{kk}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}{\left({\left(\sum _{i=1}^P\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}{\Psi }_i\right)+{\displaystyle \frac{a_{\eta }}{b_{\eta }}}diag\left({\displaystyle \frac{a}{b}}\right)\right)}^{-1}\right)}_{kk}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\left({\displaystyle \frac{b_{\eta }{b}_{{\beta }_k}}{a_{\eta }{a}_{{\beta }_k}}}+\mathcal{O}\left({ϵ}^2\right)\right)={\displaystyle \frac{b_{\eta }{b}_{{\beta }_k}}{a_{\eta }{a}_{{\beta }_k}}}\hfill \end{array}$$

(86)

Using Equation (21)

$$\begin{array}{cc}\hfill {{\mu }_{\overline{Z}}}_k& \leftarrow \underset{ϵ\to 0}{lim}{\left(\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\right]\sum _{i=1}^P(Y-{\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[Z_{i}W\right]{\Phi }_i){\Phi }_i^T\right){\Sigma }_{\overline{Z}}\right)}_{1k}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}{\left(\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P(Y-{\mu }_{Z_i}{\mu }_W{\Phi }_i){\Phi }_i^T\right){\Sigma }_{\overline{Z}}\right)}_{1k}\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P(Y-{\mu }_{Z_i}{\mu }_W{\Phi }_i){\Phi }_i^T\right){{\Sigma }_{\overline{Z}}}_{·k}\in \mathcal{O}\left(ϵ\right)\hfill \end{array}$$

(87)

Equation (87) uses the fact that elements in ${{\Sigma }_{\overline{Z}}}_{·k}$ are all $\in \mathcal{O}\left(ϵ\right)$.

$$\begin{array}{cc}\hfill {\mathbb{E}}_{\mathcal{Q}}\left[{\overline{Z}}_k^2\right]& =\underset{ϵ\to 0}{lim}\left({{\Sigma }_{\overline{Z}}}_{kk}+{{\mu }_{\overline{Z}}}_k^2\right)=\underset{ϵ\to 0}{lim}\left({{\Sigma }_{\overline{Z}}}_{kk}+\mathcal{O}\left({ϵ}^2\right)\right)\hfill \\ \hfill & =\underset{ϵ\to 0}{lim}\left({\displaystyle \frac{b_{\eta }{b}_{{\beta }_k}}{a_{\eta }{a}_{{\beta }_k}}}+\mathcal{O}\left({ϵ}^2\right)\right)=\underset{ϵ\to 0}{lim}\left({\displaystyle \frac{b_{\eta }}{a_{\eta }}}ϵ+\mathcal{O}\left({ϵ}^2\right)\right)={\displaystyle \frac{b_{\eta }}{a_{\eta }}}ϵ\hfill \end{array}$$

(88)

   □

Theorem 1.

$\forall j\le J^{\left(\mathrm{a}\right)}$, updates of ${\mathcal{Q}}_{{\alpha }_j}$ and ${\mathcal{Q}}_{W_B}$ will converge at ${\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]={\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}^{\left(\mathrm{a}\right)}}\left[{\alpha }_j\right]$ given ${\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}}\left[{\beta }_k\right]={\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}^{\left(\mathrm{a}\right)}}\left[{\beta }_k\right],\forall k\le K^{\left(\mathrm{a}\right)}$, $a_0=b_0=0$ and conditions in Equations (80)-(79) are satisfied in the limit as $ϵ\to 0$.

Proof. 

Assume ${\mathcal{Q}}_{{\alpha }_j}^{\left(\mathrm{a}\right)}$ has just been updated using Equations (14), (15), i.e., $\forall j\le J^{\left(\mathrm{a}\right)}$

$$\begin{array}{cc}\hfill a_{{\alpha }_j}^{\left(\mathrm{a}\right)}& =a_0+{\displaystyle \frac{K^{\left(\mathrm{a}\right)}}{2}}\hfill \\ \hfill b_{{\alpha }_j}^{\left(\mathrm{a}\right)}& =b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}{\mathbb{E}}_{{\mathcal{Q}}_{/{\alpha }_j}^{\left(\mathrm{a}\right)}}\left[W_{jk}^2{\beta }_k\right]\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}^{\left(\mathrm{a}\right)}}{b_{{\beta }_k}^{\left(\mathrm{a}\right)}}}\right)\hfill \end{array}$$

(90)

The updates for ${\mathcal{Q}}_{\alpha }$ derived from $\mathcal{L}$ are

$$\begin{array}{cc}\hfill b_{{\alpha }_j}& \leftarrow b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & =b_{{\alpha }_j}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \end{array}$$

(91)

It involves $W_{jk},k>K^{\left(\mathrm{a}\right)}$ and therefore they need to be kepted updated. Apply Theorem 5 for Equation (91) and we can get

$$\begin{array}{cc}\hfill b_{{\alpha }_j}& \leftarrow b_{{\alpha }_j}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({\displaystyle \frac{b_{{\alpha }_j}{b}_{{\beta }_k}}{a_{{\alpha }_j}{a}_{{\beta }_k}}}\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & =b_{{\alpha }_j}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{{\alpha }_j}}{a_{{\alpha }_j}}}\hfill \end{array}$$

(92)

Applying Equation (92) in an iterative manner, we will get a sequence of updates for $a_{{\alpha }_j}$. Solving

$$\begin{array}{cc}\hfill b_{{\alpha }_j}& =b_{{\alpha }_j}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{{\alpha }_j}}{\frac{K}{2}}}\hfill \end{array}$$

(93)

$$\begin{array}{cc}\hfill \Rightarrow b_{{\alpha }_j}& ={(1-{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{2}{K}})}^{-1}{b}_{{\alpha }_j}^{\left(\mathrm{a}\right)}={\displaystyle \frac{K}{K^{\left(\mathrm{a}\right)}}}{b}_{{\alpha }_j}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(94)

Thus, we can get that the sequence will converge at

$$\begin{array}{cc}\hfill b_{{\alpha }_j}& \leftarrow {\displaystyle \frac{K}{K^{\left(\mathrm{a}\right)}}}{b}_{{\alpha }_j}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(95)

As a result, ${\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]={\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}={\displaystyle \frac{a_{{\alpha }_j}^{\left(\mathrm{a}\right)}}{b_{{\alpha }_j}^{\left(\mathrm{a}\right)}}}={\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}^{\left(\mathrm{a}\right)}}\left[{\alpha }_j\right]$.    □

Theorem 2.

$\forall k\le K^{\left(\mathrm{a}\right)}$, updates of ${\mathcal{Q}}_{{\beta }_k}$ and ${\mathcal{Q}}_{W_C}$ will converge at ${\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}}\left[{\beta }_k\right]={\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}^{\left(\mathrm{a}\right)}}\left[{\beta }_k\right]$ given ${\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]={\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}^{\left(\mathrm{a}\right)}}\left[{\alpha }_j\right],\forall j\le J^{\left(\mathrm{a}\right)}$, $a_0=b_0=0$ and conditions in Equations (80)-(79) are satisfied in the limit as $ϵ\to 0$.

Proof. 

Assume ${\mathcal{Q}}_{{\beta }_k}^{\left(\mathrm{a}\right)}$ has just been updated using Equations (18) and (19), i.e.,

$$\begin{array}{cc}\hfill a_{{\beta }_k}^{\left(\mathrm{a}\right)}& =a_0+{\displaystyle \frac{K^{\left(\mathrm{a}\right)}+1}{2}}\hfill \\ \hfill b_{{\beta }_k}^{\left(\mathrm{a}\right)}& \leftarrow b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/{\beta }_k}^{\left(\mathrm{a}\right)}}[{\overline{Z}}_k^2+\sum _{j=1}^{J^{\left(\mathrm{a}\right)}}{W}_{jk}^2{\alpha }_j]\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill & =b_0+{\displaystyle \frac{1}{2}}\left(\left({{\Sigma }_{\overline{Z}}}_{kk}+{{\mu }_{\overline{Z}}}_k^2\right)+\sum _{j=1}^{J^{\left(\mathrm{a}\right)}}\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}^{\left(\mathrm{a}\right)}}{b_{{\alpha }_j}^{\left(\mathrm{a}\right)}}}\right)\right)\hfill \end{array}$$

(97)

The updates for ${\mathcal{Q}}_{{\beta }_k}$ derived from $\mathcal{L}$ is

$$\begin{array}{cc}\hfill b_{{\beta }_k}& \leftarrow b_0+{\displaystyle \frac{1}{2}}\left(\left({{\Sigma }_{\overline{Z}}}_{kk}+{{\mu }_{\overline{Z}}}_k^2\right)+\sum _{j=1}^J\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\right)\hfill \\ \hfill & =b_0+{\displaystyle \frac{1}{2}}\left(\left({{\Sigma }_{\overline{Z}}}_{kk}+{{\mu }_{\overline{Z}}}_k^2\right)+\sum _{j=1}^{J^{\left(\mathrm{a}\right)}}\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\left(\sum _{j=J^{\left(\mathrm{a}\right)}+1}^J\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\right)\hfill \\ \hfill & =b_{{\beta }_k}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\left(\sum _{j=J^{\left(\mathrm{a}\right)}+1}^J\left(\left({\Sigma }_{W_{jk}}+{\mu }_{W_{jk}}^2\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\right)\hfill \end{array}$$

(98)

It involves $W_{jk},j>J^{\left(\mathrm{a}\right)}$ and therefore they need to be kepted updated. Apply Theorem 5 for Equation (98) and we can get

$$\begin{array}{cc}\hfill b_{{\beta }_k}& \leftarrow b_{{\beta }_k}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\sum _{j=J^{\left(\mathrm{a}\right)}+1}^J\left(\left({\displaystyle \frac{b_{{\beta }_k}{b}_{{\alpha }_j}}{a_{{\beta }_k}{a}_{{\alpha }_j}}}\right){\displaystyle \frac{a_{{\alpha }_j}}{b_{{\alpha }_j}}}\right)\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill \Rightarrow & =b_{{\beta }_k}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{{\beta }_k}}{a_{{\beta }_k}}}\hfill \end{array}$$

(100)

Applying Equation (99) in an iterative manner, we will get a sequence of $b_{{\beta }_k}$. Solving

$$\begin{array}{cc}\hfill b_{{\beta }_k}& =b_{{\beta }_k}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{{\beta }_k}}{\frac{K+1}{2}}}\hfill \end{array}$$

(101)

$$\begin{array}{cc}\hfill b_{{\beta }_k}& ={(1-{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{2}{K+1}})}^{-1}{b}_{{\beta }_k}^{\left(\mathrm{a}\right)}={\displaystyle \frac{K+1}{K^{\left(\mathrm{a}\right)}+1}}{b}_{{\beta }_k}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(102)

Thus, we can get that the sequence will converge at

$$\begin{array}{cc}\hfill b_{{\beta }_k}& \leftarrow {\displaystyle \frac{K+1}{K^{\left(\mathrm{a}\right)}+1}}{b}_{{\beta }_k}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(103)

As a result, ${\mathbb{E}}_{\mathcal{Q}}\left[{\beta }_k\right]={\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}={\displaystyle \frac{a_{{\beta }_k}^{\left(\mathrm{a}\right)}}{b_{{\beta }_k}^{\left(\mathrm{a}\right)}}}={\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[{\beta }_k\right]$.    □

Theorem 3.

Updates of ${\mathcal{Q}}_{\eta }$ and ${\mathcal{Q}}_{{\overline{Z}}_B}$ will converge at ${\mathbb{E}}_{{\mathcal{Q}}_{\eta }}\left[\eta \right]={\mathbb{E}}_{{\mathcal{Q}}_{\eta }^{\left(\mathrm{a}\right)}}\left[\eta \right]$ given ${\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}}\left[{\beta }_k\right]={\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}^{\left(\mathrm{a}\right)}}\left[{\beta }_k\right],\forall k\le K^{\left(\mathrm{a}\right)}$, $a_0=b_0=0$ and conditions in Equations (80)-(79) are satisfied in the limit as $ϵ\to 0$.

Proof. 

Assume ${\mathcal{Q}}_{\eta }^{\left(\mathrm{a}\right)}$ has just been updated using Equations (16) and (17), i.e.,

$$\begin{array}{cc}\hfill a_{\eta }^{\left(\mathrm{a}\right)}& \leftarrow a_0+{\displaystyle \frac{K^{\left(\mathrm{a}\right)}}{2}}\hfill \\ \hfill {b_{\eta }}^{\left(\mathrm{a}\right)}& \leftarrow b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}{\mathbb{E}}_{{\mathcal{Q}}_{/\eta }}\left[{\overline{Z}}_k^2{\beta }_k\right]\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}^{\left(\mathrm{a}\right)}}{b_{{\beta }_k}^{\left(\mathrm{a}\right)}}}\right)\hfill \end{array}$$

(105)

The updates for ${\mathcal{Q}}_{\eta }$ derived from $\mathcal{L}$ is

$$\begin{array}{cc}\hfill b_{\eta }& \leftarrow b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^K\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _{k=1}^{K^{\left(\mathrm{a}\right)}}\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)+{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \\ \hfill & ={b_{\eta }}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({{\Sigma }_{\overline{Z}}}_k+{{\mu }_{\overline{Z}}}_k^2\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \end{array}$$

(106)

It involves ${\overline{Z}}_k,k>K^{\left(\mathrm{a}\right)}$ and therefore they need to be kept updated. Apply Lemma 6 for Equation (106) and we can get

$$\begin{array}{cc}\hfill b_{\eta }& \leftarrow {b_{\eta }}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}\sum _{k=K^{\left(\mathrm{a}\right)}+1}^K\left(\left({\displaystyle \frac{b_{\eta }{b}_{{\beta }_k}}{a_{\eta }{a}_{{\beta }_k}}}\right){\displaystyle \frac{a_{{\beta }_k}}{b_{{\beta }_k}}}\right)\hfill \end{array}$$

(107)

$$\begin{array}{cc}\hfill & ={b_{\eta }}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{\eta }}{a_{\eta }}}\hfill \end{array}$$

(108)

Applying Equation (108) in an iterative manner, we will get a sequence of updates for $b_{\eta }$. Solving

$$\begin{array}{cc}\hfill b_{\eta }& ={b_{\eta }}^{\left(\mathrm{a}\right)}+{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{b_{\eta }}{\frac{K}{2}}}\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill b_{\eta }& ={(1-{\displaystyle \frac{1}{2}}(K-K^{\left(\mathrm{a}\right)}){\displaystyle \frac{2}{K}})}^{-1}{b_{\eta }}^{\left(\mathrm{a}\right)}={\displaystyle \frac{K}{K^{\left(\mathrm{a}\right)}}}{b_{\eta }}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(110)

Thus, we can get that the sequence will converge at

$$\begin{array}{cc}\hfill b_{\eta }& \leftarrow {\displaystyle \frac{K}{K^{\left(\mathrm{a}\right)}}}{b_{\eta }}^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(111)

As a result, ${\mathbb{E}}_{\mathcal{Q}}\left[\eta \right]={\displaystyle \frac{b_{\eta }}{a_{\eta }}}={\displaystyle \frac{{b_{\eta }}^{\left(\mathrm{a}\right)}}{a_{\eta }^{\left(\mathrm{a}\right)}}}={\mathbb{E}}_{{\mathcal{Q}}^{\left(\mathrm{a}\right)}}\left[\eta \right]$.    □

In practice, due to limitations in numerical representation, we restrict values so that the active precision parameter estimates would not really go to infinity:

$$\begin{array}{c}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{{\alpha }_j}}\left[{\alpha }_j\right]\le {\tau }_{\max },\forall j\le J^{\left(\mathrm{a}\right)}\end{array}$$

(112)

$$\begin{array}{c}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{{\beta }_k}}\left[{\beta }_k\right]\le {\tau }_{\max },\forall k\le K^{\left(\mathrm{a}\right)}\end{array}$$

(113)

9.3. Weights and Noise

Here is how to update ${\mathcal{Q}}_{Z_A},{\mathcal{Q}}_{{\overline{Z}}_A},{\mathcal{Q}}_{W_A},{\mathcal{Q}}_{\sigma }$ in a scalable manner, using computation in the $K^{\left(\mathrm{a}\right)}$ dimension subspace only.

Theorem 4.

$\mathcal{L}$ and ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ share the same update rule for $Z_{iA}$, i.e.,

$$\begin{array}{cc}\hfill H_{iAjk}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{Aj}{\Phi }_{iA}{\Phi }_{iA}^T{W}_{Ak}^T\right]=Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[W_{Ak}^T{W}_{Aj}\right]{\Phi }_{iA}{\Phi }_{iA}^T\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =Tr\left(\left({\Sigma }_{[W_{Ak},W_{Aj}]}+{\mu }_{\left[W_{Aj}\right]}^T{\mu }_{\left[W_{Ak}\right]}\right){\Phi }_{iA}{\Phi }_{iA}^T\right),\forall j=1:J^{\left(\mathrm{a}\right)},k=1:K^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(114)

$$\begin{array}{cc}\hfill {{\Sigma }_{Z_i}}_A& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}[{\sigma }^{-2}{W}_A{\Phi }_{iA}{\Phi }_{iA}^T{W}_A^T+I]\right)}^{-1}={[{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}{H}_{iA}+I]}^{-1}\hfill \end{array}$$

(115)

$$\begin{array}{cc}\hfill {\mu }_{iA}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[{\sigma }^{-2}(Y_i-\overline{Z}{\Phi }_{iA}){\Phi }_{iA}^T{W}_A^T\right]{{\Sigma }_{Z_i}}_A={\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}(Y_i-{{\mu }_{\overline{Z}}}_A{\Phi }_{iA}){\Phi }_{iA}^T{\left({\mu }_{W_A}\right)}^T{{\Sigma }_{Z_i}}_A\hfill \end{array}$$

(116)

Proof. 

Apply Lemma 3 to Equation (24) we get

$$\begin{array}{cc}\hfill H_{iAjk}& \leftarrow Tr\left(\left({\Sigma }_{[W_{Ak},W_{Aj}]}+{\mu }_{\left[W_{Aj}\right]}^T{\mu }_{\left[W_{Ak}\right]}\right){\Phi }_{iA}{\Phi }_{iA}^T\right)+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to Tr\left(\left({\Sigma }_{[W_{Ak},W_{Aj}]}+{\mu }_{\left[W_{Aj}\right]}^T{\mu }_{\left[W_{Ak}\right]}\right){\Phi }_{iA}{\Phi }_{iA}^T\right),\forall j=1:J^{\left(\mathrm{a}\right)},k=1:K^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(117)

Apply block matrix inversion formula to Equation (25) we get

$$\begin{array}{cc}\hfill {{\Sigma }_{Z_i}}_A& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}[{\sigma }^{-2}{W}_A{\Phi }_{iA}{\Phi }_{iA}^T{W}_A^T+I]\right)}^{-1}+\mathcal{O}\left({ϵ}^2\right)\hfill \\ \hfill & \to {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}[{\sigma }^{-2}{W}_A{\Phi }_{iA}{\Phi }_{iA}^T{W}_A^T+I]\right)}^{-1}={[{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}{H}_{iA}+I]}^{-1}\hfill \end{array}$$

(118)

Apply block matrix multiplication and Theorem 5 to Equation (26) conditioned on Equation (81) we get

$$\begin{array}{cc}\hfill {\mu }_{iA}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_{Z_i}}}\left[{\sigma }^{-2}(Y_i-\overline{Z}{\Phi }_{iA}){\Phi }_{iA}^T{W}_A^T\right]{{\Sigma }_{Z_i}}_A+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to {\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}(Y_i-{{\mu }_{\overline{Z}}}_A{\Phi }_{iA}){\Phi }_{iA}^T{\left({\mu }_{W_A}\right)}^T{{\Sigma }_{Z_i}}_A\hfill \end{array}$$

(119)

   □

Theorem 5.

$\mathcal{L}$ and ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ share the same update rule for ${\overline{Z}}_A$, i.e.,

$$\begin{array}{cc}\hfill {{\Sigma }_{\overline{Z}}}_A& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[\sum _{i=1}^P\left({\sigma }^{-2}{\Phi }_{iA}{\Phi }_{iA}^T\right)+\eta diag\left({\beta }_A\right)\right]\right)}^{-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\left(\sum _{i=1}^P\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}{\Phi }_{iA}{\Phi }_{iA}^T\right)+{\displaystyle \frac{a_{\eta }}{b_{\eta }}}diag\left({\displaystyle \frac{a_A}{b_A}}\right)\right)}^{-1}\hfill \\ \hfill {{\mu }_{\overline{Z}}}_A& \leftarrow \left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\right]\sum _{i=1}^P(Y-{\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[Z_{iA}{W}_A\right]{\Phi }_{iA}){\Phi }_{iA}\right){{\Sigma }_{\overline{Z}}}_A\hfill \end{array}$$

(120)

$$\begin{array}{cc}\hfill & =\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P(Y-{\mu }_{iA}{\mu }_{W_A}{\Phi }_{iA}){\Phi }_{iA}\right){{\Sigma }_{\overline{Z}}}_A\hfill \end{array}$$

(121)

Proof. 

Apply block matrix inversion formula to Equation (20) conditioned on ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{\mathcal{Z}}}}}\left[{\beta }_k\right]={ϵ}^{-1},\forall k>K^{\left(\mathrm{a}\right)}$ and we get

$$\begin{array}{cc}\hfill {{\Sigma }_{\overline{Z}}}_A& \leftarrow {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[\sum _{i=1}^P\left({\sigma }^{-2}{\Phi }_{iA}{\Phi }_{iA}^T\right)+\eta diag\left({\beta }_A\right)\right]\right)}^{-1}+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to {\left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[\sum _{i=1}^P\left({\sigma }^{-2}{\Phi }_{iA}{\Phi }_{iA}^T\right)+\eta diag\left({\beta }_A\right)\right]\right)}^{-1}\hfill \end{array}$$

(122)

Apply block matrix multiplication and Theorem 5 to Equation (21) conditioned on Equation (80) we get

$$\begin{array}{cc}\hfill {{\mu }_{\overline{Z}}}_A& \leftarrow \left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\right]\sum _{i=1}^P(Y-{\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[Z_{iA}{W}_A\right]{\Phi }_{iA}){\Phi }_{iA}\right){{\Sigma }_{\overline{Z}}}_A+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to \left({\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[{\sigma }^{-2}\right]\sum _{i=1}^P(Y-{\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{Z}}}}\left[Z_{iA}{W}_A\right]{\Phi }_{iA}){\Phi }_{iA}\right){{\Sigma }_{\overline{Z}}}_A\hfill \end{array}$$

(123)

   □

Theorem 6.

$\mathcal{L}$ and ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ share the same update rule for $W_A$, i.e.,

$$\begin{array}{cc}\hfill {\Sigma }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}{\left[{\sigma }^{-2}\sum _{i=1}^P\left(\left({\Phi }_{iA}^T{\Phi }_{iA}\right)\otimes \left(Z_{iA}^T{Z}_{iA}\right)\right)+diag\left({\beta }_A\right)\otimes diag\left({\alpha }_A\right)\right]}^{-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & ={\left({\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^P\left(\left({\Phi }_{iA}^T{\Phi }_{iA}\right)\otimes ({\mu }_{iA}^T{\mu }_{iA}+{{\Sigma }_{Z_i}}_A)\right)+diag\left({\displaystyle \frac{a_A}{b_A}}\right)\otimes diag\left({\displaystyle \frac{c_A}{d_A}}\right)\right)}^{-1}\hfill \\ \hfill {\mu }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[-{\sigma }^{-2}\sum _{i=1}^{P}vec{\left({\left({\Phi }_{iA}({\Phi }_{iA}^T{\overline{Z}}_A^T-Y_i^T)Z_{iA}\right)}^T\right)}^T\right]{{\Sigma }_{vec\left(W\right)}}_A\hfill \end{array}$$

(124)

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{a_{\sigma }}{b_{\sigma }}}\sum _{i=1}^{P}vec{\left({\left({\Phi }_{iA}({\Phi }_{iA}^T{{\mu }_{\overline{Z}}}_A^T-Y_i^T){\mu }_{iA}\right)}^T\right)}^T{{\Sigma }_{vec\left(W\right)}}_A\hfill \end{array}$$

(125)

Proof. 

Apply block matrix inversion formula to Equation (22) conditioned on ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{\mathcal{Z}}}}}\left[{\beta }_k\right]={ϵ}^{-1},\forall k>K^{\left(\mathrm{a}\right)}$ and ${\mathbb{E}}_{{\mathcal{Q}}_{{/}_{\overline{\mathcal{Z}}}}}\left[{\alpha }_j\right]={ϵ}^{-1},\forall j>J^{\left(\mathrm{a}\right)}$, we get

$$\begin{array}{cc}\hfill {\Sigma }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}{\left[{\sigma }^{-2}\sum _{i=1}^P\left(\left({\Phi }_{iA}^T{\Phi }_{iA}\right)\otimes \left(Z_{iA}^T{Z}_{iA}\right)\right)+diag\left({\beta }_A\right)\otimes diag\left({\alpha }_A\right)\right]}^{-1}+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}{\left[{\sigma }^{-2}\sum _{i=1}^P\left(\left({\Phi }_{iA}^T{\Phi }_{iA}\right)\otimes \left(Z_{iA}^T{Z}_{iA}\right)\right)+diag\left({\beta }_A\right)\otimes diag\left({\alpha }_A\right)\right]}^{-1}\hfill \end{array}$$

(126)

Apply block matrix multiplication and Theorem 5 to Equation (23) conditioned on Equation (80) and Equation (81), we get

$$\begin{array}{cc}\hfill {\mu }_{vec\left(W\right)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[-{\sigma }^{-2}\sum _{i=1}^{P}vec{\left({\left({\Phi }_{iA}({\Phi }_{iA}^T{\overline{Z}}_A^T-Y_i^T)Z_{iA}\right)}^T\right)}^T\right]{{\Sigma }_{vec\left(W\right)}}_A+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to {\mathbb{E}}_{{\mathcal{Q}}_{{/}_W}}\left[-{\sigma }^{-2}\sum _{i=1}^{P}vec{\left({\left({\Phi }_{iA}({\Phi }_{iA}^T{\overline{Z}}_A^T-Y_i^T)Z_{iA}\right)}^T\right)}^T\right]{{\Sigma }_{vec\left(W\right)}}_A\hfill \end{array}$$

(127)

   □

Theorem 7.

$\mathcal{L}$ and ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ share the same update rule for σ, i.e.,

$$\begin{array}{cc}\hfill a_{\sigma }& \leftarrow a_0+{\displaystyle \frac{1}{2}}\sum _i{N}_i\hfill \\ \hfill b_{\sigma }& \leftarrow b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[\sum _i\left|\right|Y_i-(Z_{iA}{W}_A+{\overline{Z}}_A){\Phi }_{iA}{\left|\right|}_2^2\right]\hfill \\ \hfill & =b_0+{\displaystyle \frac{1}{2}}\sum _i(Y_i{Y}_i^T-2Y_i{\left({\mu }_{iA}{\mu }_{W_A}{\Phi }_{iA}\right)}^T-2Y_i{\left({{\mu }_{\overline{Z}}}_A{\Phi }_{iA}\right)}^T+2{\mu }_{iA}{\mu }_{W_A}{\Phi }_{iA}{\Phi }_{iA}^T{\left({{\mu }_{\overline{Z}}}_A\right)}^T\hfill \\ \hfill & +Tr\left(\left({{\Sigma }_{\overline{Z}}}_A+{\left({{\mu }_{\overline{Z}}}_A\right)}^T{{\mu }_{\overline{Z}}}_A\right){\Phi }_{iA}{\Phi }_{iA}^T\right))\hfill \end{array}$$

(128)

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{1}{2}}{vec\left(G_A^T\right)}^T\sum _{i}vec\left(vec\left({\Phi }_{iA}{\Phi }_{iA}^T\right)vec({{\Sigma }_{Z_i}}_A+{\mu }_{iA}^T{\mu }_{iA}{)}^T\right),\hfill \end{array}$$

(129)

where

$$\begin{array}{cc}\hfill G_{A(j+kM)}& \leftarrow {\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[vec{\left(W_{Ak}{W}_{Aj}^T\right)}^T\right]\hfill \\ \hfill & =vec{({\Sigma }_{[W_{Ak},W_{Aj}]}+{{\mu }_{vec\left(W\right)}}_{\left[W_{Aj}\right]}^T{{\mu }_{vec\left(W\right)}}_{\left[W_{Ak}\right]})}^T,\forall j=1:K^{\left(\mathrm{a}\right)},k=1:K^{\left(\mathrm{a}\right)}\hfill \end{array}$$

(130)

Proof. 

Apply block matrix multiplication and Theorem 5 to Equation (28) conditioned on Equations (80) and (81), we get

$$\begin{array}{cc}\hfill b_{\sigma }& \leftarrow b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[\sum _i\left|\right|Y_i-(Z_{iA}{W}_A+{\overline{Z}}_A){\Phi }_{iA}{\left|\right|}_2^2\right]+\mathcal{O}\left(ϵ\right)\hfill \\ \hfill & \to b_0+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{{\mathcal{Q}}_{/\sigma }}\left[\sum _i\left|\right|Y_i-(Z_{iA}{W}_A+{\overline{Z}}_A){\Phi }_{iA}{\left|\right|}_2^2\right]\hfill \end{array}$$

(131)

   □

We show ${\mathcal{Q}}_{Z_{iA}},{\mathcal{Q}}_{W_A},{\mathcal{Q}}_{{\overline{Z}}_{iA}},{\mathcal{Q}}_{\sigma }$ share the same update formulas as those derived from the low-dimensional lower bound: ${\mathcal{Q}}_{Z_{iA}}^{\left(\mathrm{a}\right)},{\mathcal{Q}}_{W_A}^{\left(\mathrm{a}\right)},{\mathcal{Q}}_{{\overline{Z}}_{iA}}^{\left(\mathrm{a}\right)},{\mathcal{Q}}_{\sigma }^{\left(\mathrm{a}\right)}$. Thus, in practice, if suffices to update ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$; we can then increase $K^{\left(\mathrm{a}\right)}$ by including new basis functions. This process proves to implicitly maximizes $\mathcal{L}$ with $\mathcal{Q}$.

9.4. Low-Dimensional Lower Bound

We now have updating formulas for the parameters in the active subspace. ${\mathcal{Q}}_{Z_{iA}}$ is updated by Equations (114), (115) and (116). ${\mathcal{Q}}_{W_A}$ is updated by Equations (124) and (125). ${\mathcal{Q}}_{{\overline{Z}}_A}$ is updated by Equations (120) and (121). ${\mathcal{Q}}_{{\alpha }_A},{\mathcal{Q}}_{{\beta }_A},{\mathcal{Q}}_{\eta }$ are updated by Theorem 1, 2 and 3, with the companion of implicit updates of ${\mathcal{Q}}_{W_B},{\mathcal{Q}}_{W_C}$. ${\mathcal{Q}}_{\sigma }$ is updated by Equations (130), (128) and (129). All the updating rules are identical to those derived from the low-dimensional lower bound ${\mathcal{L}}^{\left(\mathrm{a}\right)}$ with $K^{\left(\mathrm{a}\right)}$ basis functions. Therefore, in practice all we need is to optimize ${\mathcal{L}}^{\left(\mathrm{a}\right)}$, with time complexity of $\mathcal{O}\left({K^{\left(\mathrm{a}\right)}}^{2}max\left({K^{\left(\mathrm{a}\right)}}^4,P{max}_i\left(N_i\right)\right)\right)$, as described in Theorem 8, and then check if a new basis function should be included in the model.

For numerical stability, we scale $\varphi ,b$ such that ${min}_k\left({\mathbb{E}}_{Q_{\beta }}\left[{\beta }_k\right]\right)={min}_k\left({\displaystyle \frac{c_k}{d_k}}\right)=1$ at the beginning of Algorithm 2.

Theorem 8.

The lower bound $\mathcal{L}$ can be optimized using Algorithm 2 with time complexity of $\mathcal{O}\left({K^{\left(\mathrm{a}\right)}}^{2}max\left({K^{\left(\mathrm{a}\right)}}^4,P{max}_i\left(N_i\right)\right)\right)$.

Proof. 

It is a consequence of Theorems 1, 2, 3, 4, 5, 6, 7.    □

Algorithm 2 Variational inference

Require: ${\mu }_{Z_i},{\Sigma }_{Z_i},{\mu }_{vec\left(W\right)},{\Sigma }_{vec\left(W\right)},{\mu }_{\overline{Z}},{\Sigma }_{\overline{Z}},a_{\sigma },b_{\sigma },a_{{\alpha }_j},b_{{\alpha }_j},a_{{\beta }_k},b_{{\beta }_k},\forall i,j,k$▹ Multi sample RVM   while True do     ${\mathcal{L}}^{\left(\mathrm{a}\right)}\leftarrow lowerbound\left({\mathcal{Q}}^{\left(\mathrm{a}\right)}\right)$     Update ${\mathcal{Q}}^{\left(\mathrm{a}\right)}$ with respect to all parameters using mean field approximation     if $lowerbound\left({\mathcal{Q}}^{\left(\mathrm{a}\right)}\right)-{\mathcal{L}}^{\left(\mathrm{a}\right)}<{\tau }_{\mathrm{con}}$ then ▹ Insignificant increase         Search for new basis functions using Algorithm 1         if not found then ▹ Converged            break         end if     end if     Remove dimensions associated with the precision of the maximum values end while Get rid of dimensions associated with ${\alpha }_j\ge {min}_j\left({\alpha }_j\right){\tau }_{\mathrm{eff}}$ and ${\beta }_k\ge {min}_k\left({\beta }_k\right){\tau }_{\mathrm{eff}}$

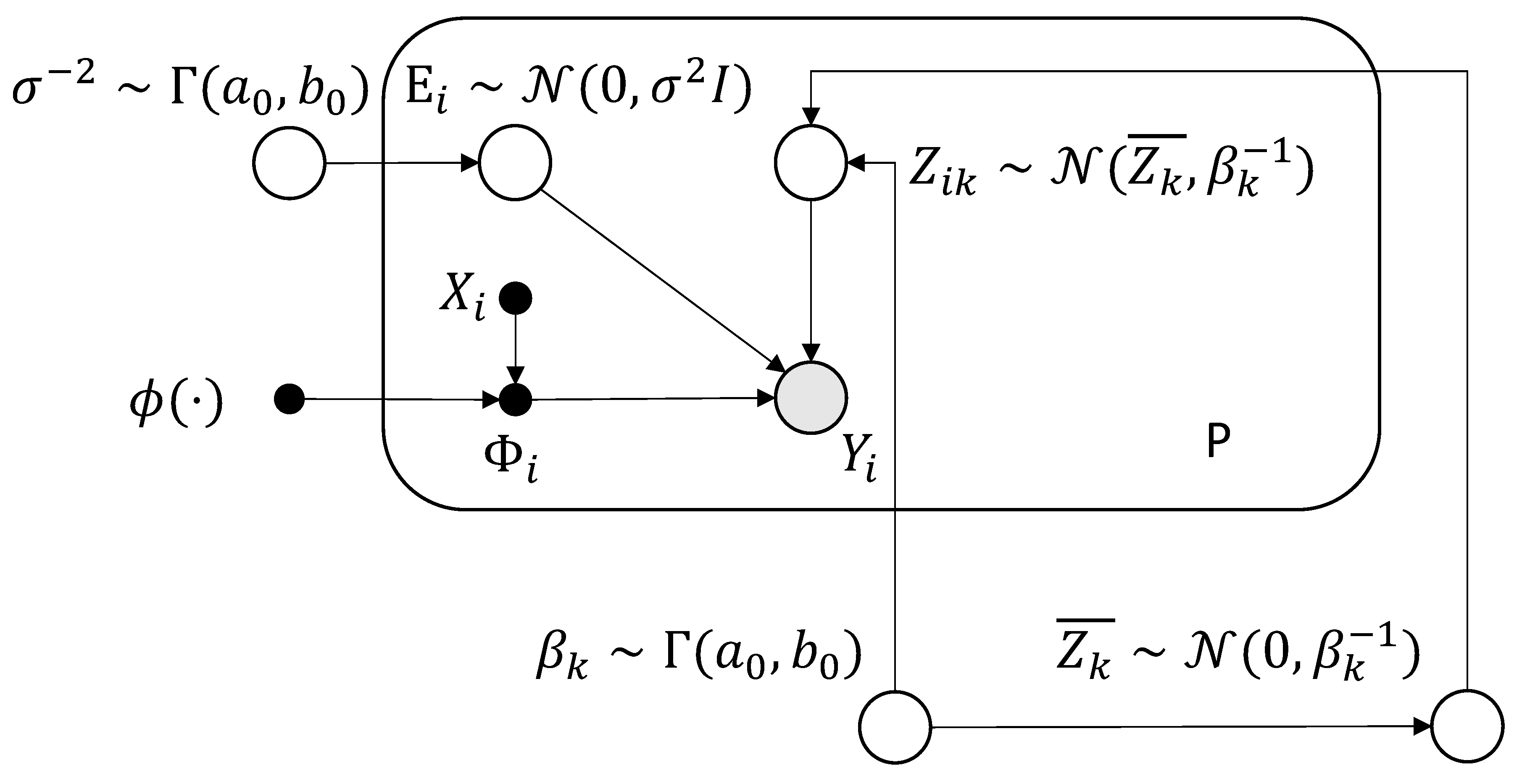
11.1. Maximum Likelihood Estimation

We apply maximum likelihood estimation for point estimates of $\overline{Z},\beta ,\sigma$.

$$\begin{array}{cc}\hfill {\overline{Z}}^{*},{\beta }^{*},{\sigma }^{*}& \leftarrow arg\underset{\overline{Z},\beta ,\sigma }{min}\mathcal{P},\hfill \end{array}$$

(151)

where $\mathcal{P}=-lnPr\left[Y\right|\overline{Z},\beta ,\sigma ]$. Conditioned on these estimates, we can calculate the expectation of Z.

Optimization of $\beta ,\overline{Z}$

We set the differentiation to zero, i.e., ${\displaystyle \frac{\partial \mathcal{P}}{\partial {\beta }_k}}=0$, and get:

$$\begin{array}{cc}\hfill {\beta }_k& \leftarrow \left\{\begin{array}{c}{\theta }_k,\mathrm{if}{\theta }_k>0\hfill \\ \infty ,\mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(152)

where

$$\begin{array}{cc}\hfill {\theta }_k& =\left({\displaystyle \frac{{\sum }_{i=1}^P{s}_{ik}^2}{{\sum }_{i=1}^P(q_{ik}^2-s_{ik})}}\right)\hfill \end{array}$$

(153)

$$\begin{array}{cc}\hfill q_{ik}& ={\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{(Y-\overline{Z}{\Phi }_i)}^T\hfill \end{array}$$

(154)

$$\begin{array}{cc}\hfill s_{ik}& ={\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}^T\hfill \end{array}$$

(155)

$$\begin{array}{cc}\hfill {\mathcal{C}}_{i_{{/}_k}}& ={\mathcal{C}}_i-{\Phi }_{ik}^T{\beta }_k^{-1}{\Phi }_{ik}\hfill \end{array}$$

(156)

$$\begin{array}{cc}\hfill {\mathcal{C}}_i& ={\Phi }_i^{T}diag\left({\beta }^{-1}\right){\Phi }_i+{\sigma }^{2}I=\sum _{k=1}^K{\Phi }_{ik}^T{\beta }_k^{-1}{\Phi }_{ik}+{\sigma }^{2}I\hfill \end{array}$$

(157)

We differentiate $\mathcal{P}$ with respect to $\overline{Z}$ and zero the derivative, i.e., ${\displaystyle \frac{\partial \mathcal{P}}{\overline{Z}}}=0$, to get:

$$\begin{array}{cc}\hfill \overline{Z}& \leftarrow \sum _{i=1}^P\left(Y_i{\mathcal{C}}_i^{-1}{\Phi }_i^T\right){\left(\sum _{i=1}^P\left({\Phi }_i{\mathcal{C}}_i^{-1}{\Phi }_i^T\right)\right)}^{-1}\hfill \end{array}$$

(158)

We approximate Equation (158) by ${\overline{Z}}_A\leftarrow {\sum }_{i=1}^P\left(Y_i{\mathcal{C}}_i^{-1}{\Phi }_{iA}^T\right){\left({\sum }_{i=1}^P\left({\Phi }_{iA}{\mathcal{C}}_i^{-1}{\Phi }_{iA}^T\right)\right)}^{-1}$ and ${\overline{Z}}_B\leftarrow 0$. This way we can apply the update with only the active basis functions.

Optimization of $\sigma$:

We use EM to optimize $\sigma$. In E step:

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i\right]& \leftarrow {\sigma }^{-2}(Y_i-\overline{Z}{\Phi }_i){\Phi }_i^T{\mathcal{S}}_i\hfill \end{array}$$

(159)

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i^T{\tilde{Z}}_i\right]& \leftarrow {\mathcal{S}}_i+{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_i\right]}^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i\right],\hfill \end{array}$$

(160)

where ${\mathcal{S}}_i={({\Psi }_i{\sigma }^{-2}+diag\left(\beta \right))}^{-1}$.

In M step

$$\begin{array}{cc}\hfill {\sigma }^{-2}& \leftarrow {\displaystyle \frac{{\sum }_{i=1}^P{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[\left|\right|Y_i-({\tilde{Z}}_i+\overline{Z}){\Phi }_i{\left|\right|}_2^2\right]}{{\sum }_{i=1}^P{N}_i}}\hfill \\ \hfill & ={\displaystyle \frac{{\sum }_{i=1}^P(Y_i-\overline{Z}{\Phi }_i){(Y_i-\overline{Z}{\Phi }_i-2{\Phi }_i^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_i\right]}^T)}^T+Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i^T{\tilde{Z}}_i\right]{\Psi }_i\right)}{{\sum }_{i=1}^P{N}_i}}\hfill \end{array}$$

(161)

The optimization iterates between the E-step Equations (159) and (160), and the M-step Equation (161).

In practice, we need only ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{\mathcal{Z}}}}\left[{\tilde{Z}}_{iA}\right],{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{\mathcal{Z}}}}\left[{\tilde{Z}}_{iA}^T{\tilde{Z}}_{iA}\right],{\mathcal{S}}_{iA}$, and they can be calculated using the $K^{\left(\mathrm{a}\right)}$ active basis functions. Thus, similar to [73], all the computations can be operated with only the active basis functions and thus it computationally efficient. This is described in Algorithm 3.

$$\begin{array}{cc}\hfill \mathcal{P}& =-lnPr\left[Y\right|\overline{Z},\beta ,\sigma ]=-\sum _{i=1}^{P}lnPr\left[Y_i\right|\overline{Z},\beta ,\sigma ]=\sum _{i=1}^P{\mathcal{P}}_i\hfill \end{array}$$

(162)

$$\begin{array}{cc}\hfill {\mathcal{P}}_i& =\int Pr\left[Y_i\right|{\tilde{Z}}_i,\overline{Z},\beta ,\sigma ]Pr\left[{\tilde{Z}}_i\right|\overline{Z},\beta ]d{\tilde{Z}}_i={\mathbb{E}}_{{\tilde{Z}}_i\sim \mathcal{N}(\overline{Z},\beta )}[Pr\left[Y_i\right|{\tilde{Z}}_i,\sigma ]]=\mathcal{N}\left(Y_i\right|\overline{Z}{\Phi }_i,{\mathcal{C}}_i)\hfill \end{array}$$

(163)

$$\begin{array}{cc}\hfill Pr& \left[Y_i\right|{\tilde{Z}}_i,\overline{Z},\beta ,\sigma ]=\mathcal{N}\left(Y_i\right|({\tilde{Z}}_i+\overline{Z}){\Phi }_i,{\sigma }^{2}I)\hfill \end{array}$$

(164)

Algorithm 3 Multi-sample relevance vector machine

while$\mathcal{P}$ is not converged do     $k\leftarrow \mathrm{a}\mathrm{random}\mathrm{number}\mathrm{that}\mathrm{satisfies}CosSim({\varphi }_k,{\varphi }_A)\le {\tau }_{\mathrm{sim}}$▹$\mathcal{O}\left({K^{\left(\mathrm{a}\right)}}^3\right)$     $s_{ik}\leftarrow {\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}^T,\forall i$ ▹ Sparsity factor. $\mathcal{O}\left(Pmax({K^{\left(\mathrm{a}\right)}}^3,{max}_i{\left(N_i\right)}^2)\right)$     $q_{ik}\leftarrow {\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{(Y-{\overline{Z}}_A{\Phi }_{iA})}^T,\forall i$ ▹ Quality factor. $\mathcal{O}\left(P{max}_i\left(N_i\right)max(K^{\left(\mathrm{a}\right)},{max}_i\left(N_i\right))\right)$     ${\theta }_k\leftarrow \left({\displaystyle \frac{{\sum }_{i=1}^P{s}_{ik}^2}{{\sum }_{i=1}^P(q_{ik}^2-s_{ik})}}\right)$     if $\theta >0$ then         ${\beta }_k\leftarrow {\theta }_k$ ▹ Precision is finite     else         ${\beta }_k\leftarrow \infty$ ▹ Precision is infinite and the dimension is removed     end if     ${\Phi }_{iA}\leftarrow \mathrm{All}{\Phi }_{ik}\mathrm{that}\mathrm{has}{\beta }_k<\infty ,\forall i$     ${\mathcal{C}}_i={\sum }_{{\beta }_k<\infty }{\Phi }_{ik}^T{\beta }_k^{-1}{\Phi }_{ik}+{\sigma }^{2}I,\forall i$     ${\overline{Z}}_A\leftarrow {\sum }_{i=1}^P\left(Y_i{\mathcal{C}}_i^{-1}{\Phi }_{iA}^T\right){\left({\sum }_{i=1}^P\left({\Phi }_{iA}{\mathcal{C}}_i^{-1}{\Phi }_{iA}^T\right)\right)}^{-1}$ ▹$\mathcal{O}\left(P{K}^{\left(\mathrm{a}\right)}max{\left(K^{\left(\mathrm{a}\right)},{max}_i\left(N_i\right)\right)}^2\right)$     ${\mathcal{S}}_{iA}\leftarrow {({\Phi }_{iA}{\Phi }_{iA}^T{\sigma }^{-2}+diag\left({\beta }_A\right))}^{-1},\forall i$     ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{\mathcal{Z}}}}\left[{\tilde{Z}}_{iA}\right]\leftarrow {\sigma }^{-2}(Y_i-{\overline{Z}}_A{\Phi }_{iA}){\Phi }_{iA}^T{\mathcal{S}}_{iA},\forall i$ ▹$\mathcal{O}\left(P{K^{\left(\mathrm{a}\right)}}^2{max}_i\left(N_i\right)\right)$     ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{\mathcal{Z}}}}\left[{\tilde{Z}}_{iA}^T{\tilde{Z}}_{iA}\right]\leftarrow {\mathcal{S}}_{iA}+{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_{iA}\right]}^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_{iA}\right],\forall i$     $\sigma \leftarrow {\displaystyle \frac{{\sum }_{i=1}^P(Y_i-{\overline{Z}}_A{\Phi }_{iA}){(Y_i-{\overline{Z}}_A{\Phi }_{iA}-2{\Phi }_{iA}^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_{iA}\right]}^T)}^T+Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_{iA}^T{\tilde{Z}}_{iA}\right]{\Phi }_{iA}{\Phi }_{iA}^T\right)}{{\sum }_{i=1}^P{N}_i}}$ end while

We apply Sylvester’s determinant theorem to Equation (157) and get

$$\begin{array}{cc}\hfill |{\mathcal{C}}_i|& =|{\mathcal{C}}_{i_{{/}_k}}\left|\right|I+{\beta }_k^{-1}{\Phi }_{ik}^T{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}|\hfill \end{array}$$

(165)

We apply Woodbury matrix identity to Equation (157) and get

$$\begin{array}{cc}\hfill {\mathcal{C}}_i^{-1}& ={\mathcal{C}}_{i_{{/}_k}}^{-1}-{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T{({\beta }_k+{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T)}^{-1}{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}\hfill \end{array}$$

(166)

We first expand ${\mathcal{P}}_i$

$$\begin{array}{cc}\hfill {\mathcal{P}}_i& =lnPr\left[Y_i\right|\overline{Z},\sigma ,\beta ]\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\sum _{i}ln\left|2\pi {\mathcal{C}}_i\right|+(Y_i-\overline{Z}{\Phi }_i){\mathcal{C}}_i^{-1}{(Y_i-\overline{Z}{\Phi }_i)}^T\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}(N_{i}ln\left(2\pi \right)+ln|{\mathcal{C}}_{i_{/k}}|+ln|I+{\beta }_k^{-1}{\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}^T|+(Y_i-\overline{Z}{\Phi }_i){\mathcal{C}}_i^{-1}{(Y_i-\overline{Z}{\Phi }_i)}^T\hfill \\ \hfill & -{({\beta }_k+{\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}^T)}^{-1}\left|\right|{\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{(Y-\overline{Z}{\Phi }_i)}^T{\left|\right|}_2^2)\hfill \\ \hfill & ={\mathcal{P}}_{i_{{/}_k}}+{\displaystyle \frac{1}{2}}(ln{\beta }_k-ln|{\beta }_k+s_{ik}|+{\displaystyle \frac{q_{ik}^2}{{\beta }_k+sik}})\hfill \end{array}$$

(167)

where we plug in Equations (165) and (166) and define $q_{ik},s_{ik}$ in a similar way to [73]. The sparsity factor $s_{ik}$ can be seen to be a measure of the extent that the basis function ${\varphi }_k$ overlaps those already present in the model under the measurements at index set $X_i$. The quality factor $q_{ik}$ is a measure of the alignment with the error of the model at $X_i$ with that basis function excluded. Because we are representing the mean functions using only the active basis functions, i.e., ${\overline{Z}}_k=0$ when ${\beta }_k=\infty$, Equation (154) only uses the K active basis functions. Similarly, Equation (155) only uses the K active basis functions.

For computational efficiency, we can compute $s_{ik},q_{ik}$ using $S_{ik}={\Phi }_{ik}{\mathcal{C}}_i^{-1}{\Phi }_{ik}^T,Q_{ik}={\Phi }_{ik}{\mathcal{C}}_i^{-1}{(Y-\overline{Z}{\Phi }_i)}^T$ in a similar way to [73] as follows

$$\begin{array}{cc}\hfill s_{ik}& ={\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{\Phi }_{ik}^T=S_{ik}+{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T{({\beta }_k+{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T)}^{-1}{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =S_{ik}+s_{ik}{({\beta }_k+s_{ik})}^{-1}{s}_{ik}\rightleftharpoons s_{ik}={\displaystyle \frac{{\beta }_k+s_{ik}}{{\beta }_k}}{S}_{ik}\hfill \end{array}$$

(168)

$$\begin{array}{cc}\hfill \Rightarrow s_{ik}& \leftarrow {(1-{\displaystyle \frac{1}{{\beta }_k}}{S}_{ik})}^{-1}{S}_{ik}={\displaystyle \frac{{\beta }_k{S}_{ik}}{{\beta }_k-S_{ik}}}\hfill \\ \hfill q_{ik}& ={\Phi }_{ik}{\mathcal{C}}_{i_{/k}}^{-1}{(Y-\overline{Z}{\Phi }_i)}^T\hfill \\ \hfill & =Q_{ik}+{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T{({\beta }_k+{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{\Phi }_{ik}^T)}^{-1}{\Phi }_{ik}{\mathcal{C}}_{i_{{/}_k}}^{-1}{(Y-\overline{Z}{\Phi }_i)}^T\hfill \end{array}$$

(169)

$$\begin{array}{cc}\hfill & =Q_{ik}+s_{ik}{({\beta }_k+s_{ik})}^{-1}{q}_{ik}\hfill \end{array}$$

(170)

$$\begin{array}{cc}\hfill \Rightarrow q_{ik}& \leftarrow {\displaystyle \frac{{\beta }_k+s_{ik}}{{\beta }_k}}{Q}_{ik}={\displaystyle \frac{{\beta }_k{Q}_{ik}}{{\beta }_k-S_{ik}}}\hfill \end{array}$$

(171)

11.2. Optimization of β,Z ¯

Derivation of Equation (152):

We differentiate $\mathcal{P}$ with respect to ${\beta }_k$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{P}}{\partial {\beta }_k}}& =\sum _{i=1}^P{\displaystyle \frac{1}{2}}\left({\beta }_k^{-1}-{|{\beta }_k+s_{ik}|}^{-1}-q_{ik}^2{({\beta }_k+s_{ik})}^2\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\beta }_k^{-1}\sum _{i=1}^P\left({({\beta }_k+s_{ik})}^{-2}({\beta }_k(s_{ik}-q_{ik}^2)+s_{ik}^2)\right)\hfill \end{array}$$

(172)

We further adopt the approximation $s_{1k}\approx s_{2k}\approx \dots \approx s_{Pk}$. Because $s_{ik}$ is a discrete measure of the overlapping between the basis functions, it should remain invariant with respect to different sampling grid $X_i$ given the number of measurements is adequate and similar. Alternatively, the Expectation maximization scheme can also be applied and is guaranteed to increase the likelihood $\mathcal{P}$ in each iteration until convergence. However, we opt for this gradient descent with approximations for its advantage in speed to obtain a reasonable initialization. This way we set the approximated differentiation to zero

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{P}}{\partial {\beta }_k}}& \approx {\displaystyle \frac{1}{2}}{\beta }_k^{-1}{({\beta }_k+s_{1k})}^{-2}\sum _{i=1}^P\left(({\beta }_k(s_{ik}-q_{ik}^2)+s_{ik}^2)\right)=0\hfill \end{array}$$

(173)

$$\begin{array}{cc}\hfill \Rightarrow {\beta }_k& \leftarrow {\theta }_k=\left({\displaystyle \frac{{\sum }_{i=1}^P{s}_{ik}^2}{{\sum }_{i=1}^P(q_{ik}^2-s_{ik})}}\right)\hfill \end{array}$$

(174)

Because ${\beta }_k$ is a scale parameter, we need ${\beta }_k>0$. Consequently, the optimal value for ${\beta }_k$ to maximize $\mathcal{P}$ dependents on the sign of ${\theta }_k$. When ${\theta }_k>0$, the maximum of $\mathcal{P}$ is achieved at ${\beta }_k={\theta }_k$.

On the other hand when ${\theta }_k\le 0$, $\mathcal{P}$ is monotonically increasing with respect to ${\beta }_k$ and therefore we should have ${\beta }_k\leftarrow \infty$ in order to maximize $\mathcal{P}$.

More intuitively, Equation (174) can be regarded as a weighted summation of the estimation of ${\beta }_k$ using each individual sample function and it automatically assigns more weights to those with more measurements. Therefore, this optimization strategy is supposed to provide reasonable estimates even when the sampled functions have different numbers of measurements.

Derivation of Equation (158):

We differentiate $\mathcal{P}$ with respect to $\overline{Z}$ and zero the derivative to get

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathcal{P}}{\overline{Z}}}& =-{\displaystyle \frac{1}{2}}\sum _{i=1}^P\left(-2Y_i{\mathcal{C}}_i{\Phi }_i^T+2\overline{Z}{\Phi }_i{\mathcal{C}}_i^{-1}{\Phi }_T\right)=0\hfill \end{array}$$

(175)

$$\begin{array}{cc}\hfill \Rightarrow \overline{Z}& \leftarrow \sum _{i=1}^P\left(Y_i{\mathcal{C}}_i^{-1}{\Phi }_i^T\right){\left(\sum _{i=1}^P\left({\Phi }_i{\mathcal{C}}_i^{-1}{\Phi }_i^T\right)\right)}^{-1}\hfill \end{array}$$

(176)

11.3. Optimization of σ

Derivation of Equations (159) and (160):

We use the Expectation maximization strategy with latent variables ${\tilde{Z}}_i$. It is similar to that used in [52]. It introduces a surrogate function, the log likelihood for the complete data ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\mathcal{P}}_{\tilde{Z}}\right]$, that is easier to optimize and in theory the process ultimately maximizes $\mathcal{P}$.

For the E-step, we calculate the posterior of ${\tilde{Z}}_i$.

$$\begin{array}{cc}\hfill lnPr\left[{\tilde{Z}}_i\right|Y_i,\overline{Z},\sigma ,\beta ]& =ln{\displaystyle \frac{Pr\left[Y_i\right|{\tilde{Z}}_i,\overline{Z},\sigma ,\beta ]Pr\left[{\tilde{Z}}_i\right|\beta ]}{Pr\left[Y_i\right|\overline{Z},\sigma ,\beta ]}}\hfill \end{array}$$

(177)

$$\begin{array}{cc}\hfill & \propto -{\displaystyle \frac{1}{2}}\left({\tilde{Z}}_i({\Psi }_i{\sigma }^{-2}+diag\left(\beta \right)){\tilde{Z}}_i^T-2{\sigma }^{-2}(Y_I-\overline{Z}{\Phi }_i){\Phi }_i^T{\tilde{Z}}_i^T\right)\hfill \end{array}$$

(178)

Therefore,

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i\right]& \leftarrow {\sigma }^{-2}(Y_i-\overline{Z}{\Phi }_i){\Phi }_i^T{\mathcal{S}}_i\hfill \end{array}$$

(179)

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i^T{\tilde{Z}}_i\right]& \leftarrow {\mathcal{S}}_i+{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_i\right]}^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i\right]\hfill \end{array}$$

(180)

where

$$\begin{array}{cc}\hfill {\mathcal{S}}_i& ={({\Psi }_i{\sigma }^{-2}+diag\left(\beta \right))}^{-1}\hfill \end{array}$$

(181)

Derivation of Equation (161):

In M-step, we need to maximum ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\mathcal{P}}_{\tilde{Z}}\right]$ conditioned on ${\mathcal{Q}}_{\tilde{Z}}$ with respect to ${\sigma }^{-2}$,

$$\begin{array}{cc}\hfill {\mathcal{P}}_{\tilde{Z}}& =\sum _{i=1}^{P}lnPr[Y_i,{\tilde{Z}}_i|\overline{Z},\sigma ,\beta ]=\sum _{i=1}^{P}ln(Pr\left[Y_i\right|{\tilde{Z}}_i,\overline{Z},\sigma ]Pr\left[{\tilde{Z}}_i\right|\beta ])\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\sum _{i=1}^P(N_{i}ln\left(2\pi {\sigma }^{-2}\right)+{\sigma }^{-2}\left|\right|Y_i-({\tilde{Z}}_i+\overline{Z}){\Phi }_i{\left|\right|}_2^2+\hfill \\ \hfill & \sum _{k=1}^{K}ln\left(2\pi {\beta }_k^{-1}\right)+Tr({\tilde{Z}}_{i}diag\left(\beta \right){\tilde{Z}}_i^T))\hfill \end{array}$$

(182)

We differentiate ${\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\mathcal{P}}_{\tilde{Z}}\right]$ with respect to ${\sigma }^{-2}$ and set to 0

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\mathcal{P}}_{\tilde{Z}}\right]}{\partial {\sigma }^{-2}}}& ={\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[-{\displaystyle \frac{1}{2}}\sum _{i=1}^P\left(N_i{\sigma }^{-2}-{\sigma }^{-4}\left|\right|Y_i-({\tilde{Z}}_i+\overline{Z}){\Phi }_i{\left|\right|}_2^2\right)\right]=0\hfill \\ \hfill \Rightarrow {\sigma }^{-2}& \leftarrow {\displaystyle \frac{{\sum }_{i=1}^P{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[\left|\right|Y_i-({\tilde{Z}}_i+\overline{Z}){\Phi }_i{\left|\right|}_2^2\right]}{{\sum }_{i=1}^P{N}_i}}\hfill \end{array}$$

(183)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{{\sum }_{i=1}^P(Y_i-\overline{Z}{\Phi }_i){(Y_i-\overline{Z}{\Phi }_i-2{\Phi }_i^T{\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}{\left[{\tilde{Z}}_i\right]}^T)}^T+Tr\left({\mathbb{E}}_{{\mathcal{Q}}_{\tilde{Z}}}\left[{\tilde{Z}}_i^T{\tilde{Z}}_i\right]{\Psi }_i\right)}{{\sum }_{i=1}^P{N}_i}}\hfill \end{array}$$

(184)

12.1. Benchmark Simulation

Figure 12 presents the application of the proposed BSFDA to the simulation benchmark (Scenario 1) outlined in [37]. While prior analyses have utilized this benchmark, the current experimental configuration is specifically adapted to highlight the method’s capacity for uncertainty quantification. The experimental design consists of 20 functional observations, each sampled at either 3 points (with a 20% probability) or 10 points (with an 80% probability), determined via random assignment. The number of sampled functions is decreased from 200 to 20 to underscore the effect and estimation of uncertainties. The actual white noise standard deviation is 0.4472, while the estimated standard deviation is 0.4839. The component number is also correctly estimated as 3. The figure depicts the true underlying function, the discrete observational data, and the corresponding functional estimates, accompanied by their respective 95% truncated uncertainty intervals.

Notably, the uncertainty associated with sparsely sampled functions exhibits substantial inflation in regions devoid of observations. In contrast, in sampled regions, the uncertainty aligns closely with that of densely sampled functions, approximating twice the standard deviation of the white noise. Additionally, the uncertainty bounds for the estimated mean function are presented, demonstrating reduced variability relative to individual function estimates.

Figure 12. Application of the proposed BSFDA to the simulation benchmark from [37], illustrating the true mean function (blue), observed measurements from two functions sampled at different densities (light blue for sparse, orange for dense), and the corresponding functional estimates with 95% truncated uncertainty intervals.

Figure 12. Application of the proposed BSFDA to the simulation benchmark from [37], illustrating the true mean function (blue), observed measurements from two functions sampled at different densities (light blue for sparse, orange for dense), and the corresponding functional estimates with 95% truncated uncertainty intervals.

Table 9. Distributions of the estimated component number $\widehat{r}$ for Scenario 1 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.155	0.005	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.008	0.405	0.335	0.565	0.215	0.000	0.000	0.000	0.000	0.985
	=3	0.000	0.580	0.380	0.410	0.735	0.650	0.880	0.645	0.995	0.015
	=4	0.121	0.010	0.115	0.010	0.045	0.335	0.120	0.235	0.005	0.000
	$\ge 5$	0.870	0.005	0.015	0.010	0.005	0.015	0.000	0.120	0.000	0.000
10	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.005	0.040	0.040	0.005	0.000	0.000	0.000	0.000	0.075
	=3	0.000	0.980	0.670	0.955	0.985	0.880	0.920	0.645	1.000	0.910
	=4	0.000	0.015	0.255	0.000	0.010	0.120	0.080	0.235	0.000	0.015
	$\ge 5$	1.000	0.000	0.035	0.005	0.000	0.000	0.000	0.120	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	1.000	0.830	1.000	1.000	1.000	1.000	0.890	0.980	0.945
	=4	0.000	0.000	0.150	0.000	0.000	0.000	0.000	0.060	0.020	0.050
	$\ge 5$	1.000	0.000	0.020	0.000	0.000	0.000	0.000	0.050	0.000	0.005

Table 9. Distributions of the estimated component number $\widehat{r}$ for Scenario 1 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.155	0.005	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.008	0.405	0.335	0.565	0.215	0.000	0.000	0.000	0.000	0.985
	=3	0.000	0.580	0.380	0.410	0.735	0.650	0.880	0.645	0.995	0.015
	=4	0.121	0.010	0.115	0.010	0.045	0.335	0.120	0.235	0.005	0.000
	$\ge 5$	0.870	0.005	0.015	0.010	0.005	0.015	0.000	0.120	0.000	0.000
10	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.005	0.040	0.040	0.005	0.000	0.000	0.000	0.000	0.075
	=3	0.000	0.980	0.670	0.955	0.985	0.880	0.920	0.645	1.000	0.910
	=4	0.000	0.015	0.255	0.000	0.010	0.120	0.080	0.235	0.000	0.015
	$\ge 5$	1.000	0.000	0.035	0.005	0.000	0.000	0.000	0.120	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	1.000	0.830	1.000	1.000	1.000	1.000	0.890	0.980	0.945
	=4	0.000	0.000	0.150	0.000	0.000	0.000	0.000	0.060	0.020	0.050
	$\ge 5$	1.000	0.000	0.020	0.000	0.000	0.000	0.000	0.050	0.000	0.005

Table 10. Distributions of the estimated component number $\widehat{r}$ for Scenario 2 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.230	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.205	0.395	0.000	0.140	0.050	0.075	0.000	0.000	0.960
	=3	0.005	0.630	0.245	0.375	0.605	0.570	0.620	0.475	1.000	0.040
	=4	0.125	0.155	0.110	0.440	0.210	0.345	0.275	0.350	0.000	0.000
	$\ge 5$	0.870	0.010	0.020	0.185	0.045	0.035	0.030	0.175	0.000	0.000
10	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.170	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.710	0.665	0.570	0.805	0.825	0.850	0.640	1.000	0.995
	=4	0.005	0.260	0.135	0.355	0.185	0.175	0.150	0.235	0.000	0.005
	$\ge 5$	0.995	0.030	0.030	0.075	0.010	0.000	0.000	0.125	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.630	0.795	0.955	0.945	1.000	1.000	0.950	1.000	0.950
	=4	0.000	0.320	0.185	0.045	0.055	0.000	0.000	0.020	0.000	0.050
	$\ge 5$	1.000	0.050	0.020	0.000	0.000	0.000	0.000	0.030	0.000	0.000

Table 10. Distributions of the estimated component number $\widehat{r}$ for Scenario 2 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.230	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.205	0.395	0.000	0.140	0.050	0.075	0.000	0.000	0.960
	=3	0.005	0.630	0.245	0.375	0.605	0.570	0.620	0.475	1.000	0.040
	=4	0.125	0.155	0.110	0.440	0.210	0.345	0.275	0.350	0.000	0.000
	$\ge 5$	0.870	0.010	0.020	0.185	0.045	0.035	0.030	0.175	0.000	0.000
10	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.170	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.710	0.665	0.570	0.805	0.825	0.850	0.640	1.000	0.995
	=4	0.005	0.260	0.135	0.355	0.185	0.175	0.150	0.235	0.000	0.005
	$\ge 5$	0.995	0.030	0.030	0.075	0.010	0.000	0.000	0.125	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.630	0.795	0.955	0.945	1.000	1.000	0.950	1.000	0.950
	=4	0.000	0.320	0.185	0.045	0.055	0.000	0.000	0.020	0.000	0.050
	$\ge 5$	1.000	0.050	0.020	0.000	0.000	0.000	0.000	0.030	0.000	0.000

Table 11. Distributions of the estimated component number $\widehat{r}$ for Scenario 3 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.335	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.025	0.035	0.260	0.220	0.005	0.000	0.005	0.000	0.000	0.025
	=3	0.005	0.720	0.325	0.640	0.590	0.320	0.400	0.450	0.995	0.945
	=4	0.130	0.170	0.080	0.075	0.280	0.640	0.565	0.360	0.005	0.030
	$\ge 5$	0.840	0.075	0.000	0.065	0.125	0.030	0.030	0.190	0.000	0.000
10	$\le 1$	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.015	0.000	0.035	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.580	0.770	0.965	0.665	0.740	0.755	0.440	0.995	1.000
	=4	0.000	0.400	0.145	0.030	0.320	0.260	0.245	0.380	0.005	0.000
	$\ge 5$	0.985	0.020	0.045	0.005	0.015	0.000	0.000	0.180	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.015	0.000
	=3	0.000	1.000	0.775	1.000	1.000	1.000	1.000	0.765	0.980	0.920
	=4	0.000	0.000	0.200	0.000	0.000	0.000	0.000	0.110	0.005	0.050
	$\ge 5$	1.000	0.000	0.025	0.000	0.000	0.000	0.000	0.125	0.000	0.030

Table 11. Distributions of the estimated component number $\widehat{r}$ for Scenario 3 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.335	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.025	0.035	0.260	0.220	0.005	0.000	0.005	0.000	0.000	0.025
	=3	0.005	0.720	0.325	0.640	0.590	0.320	0.400	0.450	0.995	0.945
	=4	0.130	0.170	0.080	0.075	0.280	0.640	0.565	0.360	0.005	0.030
	$\ge 5$	0.840	0.075	0.000	0.065	0.125	0.030	0.030	0.190	0.000	0.000
10	$\le 1$	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.015	0.000	0.035	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.580	0.770	0.965	0.665	0.740	0.755	0.440	0.995	1.000
	=4	0.000	0.400	0.145	0.030	0.320	0.260	0.245	0.380	0.005	0.000
	$\ge 5$	0.985	0.020	0.045	0.005	0.015	0.000	0.000	0.180	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.015	0.000
	=3	0.000	1.000	0.775	1.000	1.000	1.000	1.000	0.765	0.980	0.920
	=4	0.000	0.000	0.200	0.000	0.000	0.000	0.000	0.110	0.005	0.050
	$\ge 5$	1.000	0.000	0.025	0.000	0.000	0.000	0.000	0.125	0.000	0.030

Table 12. Distributions of the estimated component number $\widehat{r}$ for Scenario 4 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.315	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.015	0.020	0.180	0.160	0.015	0.000	0.000	0.000	0.000	0.000
	=3	0.015	0.710	0.410	0.640	0.560	0.515	0.575	0.370	1.000	0.975
	=4	0.145	0.185	0.070	0.095	0.260	0.450	0.390	0.515	0.000	0.025
	$\ge 5$	0.825	0.085	0.025	0.105	0.165	0.035	0.035	0.115	0.000	0.000
10	$\le 1$	0.000	0.000	0.010	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.830	0.775	0.920	0.900	0.750	0.760	0.350	0.995	0.990
	=4	0.000	0.150	0.190	0.045	0.085	0.250	0.240	0.380	0.005	0.010
	$\ge 5$	1.000	0.020	0.020	0.035	0.015	0.000	0.000	0.270	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.010	0.000
	=3	0.000	0.945	0.835	1.000	1.000	1.000	1.000	0.730	0.950	0.935
	=4	0.000	0.055	0.140	0.000	0.000	0.000	0.000	0.160	0.040	0.055
	$\ge 5$	1.000	0.000	0.025	0.000	0.000	0.000	0.000	0.110	0.000	0.010

Table 12. Distributions of the estimated component number $\widehat{r}$ for Scenario 4 (r=3).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 1$	0.000	0.000	0.315	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.015	0.020	0.180	0.160	0.015	0.000	0.000	0.000	0.000	0.000
	=3	0.015	0.710	0.410	0.640	0.560	0.515	0.575	0.370	1.000	0.975
	=4	0.145	0.185	0.070	0.095	0.260	0.450	0.390	0.515	0.000	0.025
	$\ge 5$	0.825	0.085	0.025	0.105	0.165	0.035	0.035	0.115	0.000	0.000
10	$\le 1$	0.000	0.000	0.010	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=3	0.000	0.830	0.775	0.920	0.900	0.750	0.760	0.350	0.995	0.990
	=4	0.000	0.150	0.190	0.045	0.085	0.250	0.240	0.380	0.005	0.010
	$\ge 5$	1.000	0.020	0.020	0.035	0.015	0.000	0.000	0.270	0.000	0.000
50	$\le 1$	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=2	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.010	0.000
	=3	0.000	0.945	0.835	1.000	1.000	1.000	1.000	0.730	0.950	0.935
	=4	0.000	0.055	0.140	0.000	0.000	0.000	0.000	0.160	0.040	0.055
	$\ge 5$	1.000	0.000	0.025	0.000	0.000	0.000	0.000	0.110	0.000	0.010

Table 13. Distributions of the estimated component number $\widehat{r}$ for Scenario 5 (r=6).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 4$	0.005	0.165	0.835	0.580	0.060	0.000	0.000	0.010	0.000	0.060
	=5	0.005	0.330	0.020	0.345	0.335	0.575	0.590	0.010	0.075	0.515
	=6	0.705	0.470	0.090	0.070	0.545	0.425	0.410	0.855	0.925	0.160
	=7	0.245	0.035	0.050	0.005	0.060	0.000	0.000	0.115	0.000	0.160
	$\ge 8$	0.040	0.000	0.005	0.000	0.000	0.000	0.000	0.010	0.000	0.105
10	$\le 4$	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=5	0.000	0.000	0.030	0.145	0.000	0.425	0.425	0.000	0.000	0.000
	=6	0.065	0.570	0.525	0.775	0.705	0.575	0.575	0.500	1.000	0.930
	=7	0.475	0.280	0.165	0.020	0.185	0.000	0.000	0.405	0.000	0.035
	$\ge 8$	0.455	0.150	0.030	0.060	0.110	0.000	0.000	0.095	0.000	0.035
50	$\le 4$	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=5	0.065	0.000	0.000	0.000	0.000	0.130	0.130	0.005	0.000	0.000
	=6	0.000	0.260	0.590	0.980	0.965	0.870	0.770	0.695	0.995	0.925
	=7	0.000	0.405	0.325	0.010	0.035	0.000	0.000	0.250	0.005	0.045
	$\ge 8$	0.935	0.335	0.080	0.010	0.000	0.000	0.000	0.050	0.000	0.030

Table 13. Distributions of the estimated component number $\widehat{r}$ for Scenario 5 (r=6).

$N_i$	$\widehat{r}$	${\mathrm{AIC}}_{\mathrm{PACE}}$	AIC	BIC	${\mathrm{PC}}_{p1}$	${\mathrm{IC}}_{p1}$	${\mathrm{AIC}}_{\mathrm{PACE}}^{2022}$	${\mathrm{BIC}}_{\mathrm{PACE}}^{2022}$	fpca	BSFDA	${\mathrm{BSFDA}}^{\mathrm{Fast}}$
5	$\le 4$	0.005	0.165	0.835	0.580	0.060	0.000	0.000	0.010	0.000	0.060
	=5	0.005	0.330	0.020	0.345	0.335	0.575	0.590	0.010	0.075	0.515
	=6	0.705	0.470	0.090	0.070	0.545	0.425	0.410	0.855	0.925	0.160
	=7	0.245	0.035	0.050	0.005	0.060	0.000	0.000	0.115	0.000	0.160
	$\ge 8$	0.040	0.000	0.005	0.000	0.000	0.000	0.000	0.010	0.000	0.105
10	$\le 4$	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=5	0.000	0.000	0.030	0.145	0.000	0.425	0.425	0.000	0.000	0.000
	=6	0.065	0.570	0.525	0.775	0.705	0.575	0.575	0.500	1.000	0.930
	=7	0.475	0.280	0.165	0.020	0.185	0.000	0.000	0.405	0.000	0.035
	$\ge 8$	0.455	0.150	0.030	0.060	0.110	0.000	0.000	0.095	0.000	0.035
50	$\le 4$	0.000	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000
	=5	0.065	0.000	0.000	0.000	0.000	0.130	0.130	0.005	0.000	0.000
	=6	0.000	0.260	0.590	0.980	0.965	0.870	0.770	0.695	0.995	0.925
	=7	0.000	0.405	0.325	0.010	0.035	0.000	0.000	0.250	0.005	0.045
	$\ge 8$	0.935	0.335	0.080	0.010	0.000	0.000	0.000	0.050	0.000	0.030

12.1.1. Performance of LFRM

To compare the latent factor regression model (LFRM) [34] as a dimension reduction model to ours, Bayesian scalable functional data analysis (BSFDA), we set the covariates in LFRM to zero, thus assigning standard Gaussian priors to the latent variables, analogous to our approach. We followed the simulation benchmark in [37] for selecting the number of components, focusing on Scenario 1 with 50 measurements per function (the densest data). Because LFRM does not estimate a mean function, we omitted the mean from the simulation run here.

The following hyperparameters of LFRM need to be determined:

• Gamma prior for white noise and correlated noise
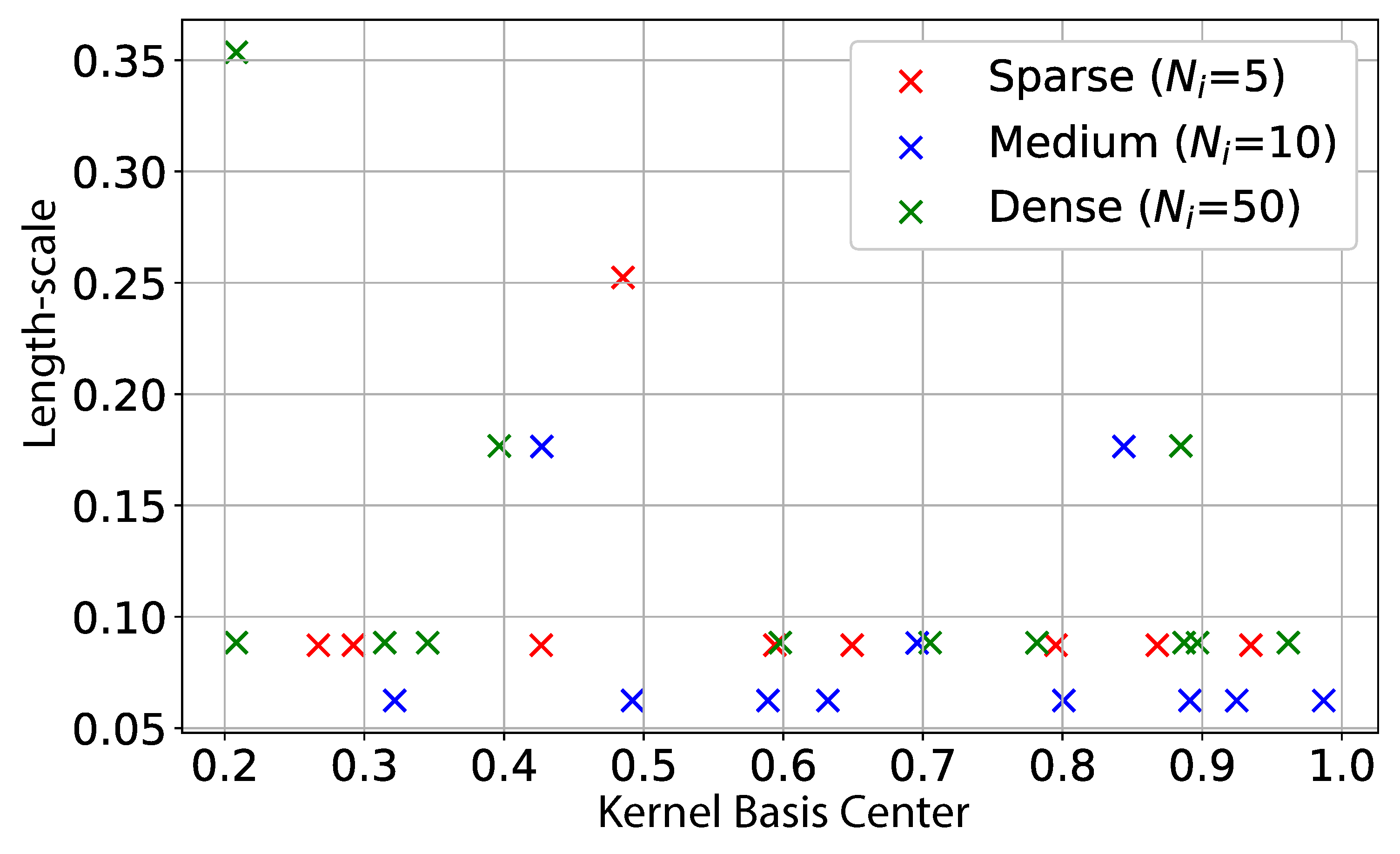
• Length-scale
• Number of basis functions
• Number of iterations

LFRM, with its default white-noise prior, correctly identified the white-noise variance (true value 0.2) in all tests. We thus retained that default. We tested different Gamma priors for correlated noise: the default prior, a noninformative-like (vagor) prior (same mean but 100 times the variance), and a low noise prior (same variance but 100 times the mean). We maintained the number of locations for basis functions at 10, which is the default setting. For length-scale in LFRM, we first used the best estimate from our cross-validation (CV). We then tried all 10 CV-selected length scales, producing 100 basis functions in total. However, this required substantial time, so we performed only two repeated runs for that setting. We kept LFRM’s default of 5000 burn-in iterations (25,000 total) with thinning at intervals of 5, verifying convergence through trace plots in line with [34]. Meanwhile, BSFDA was run 200 times as in Section 5, LFRM (10 length scales) 2 times, and all other settings 10 times.

Across repeated trials, LFRM consistently overestimated the true number of components (which is 3). Specifically:

• Standard LFRM estimated 10–14 components.
• LFRM with 10 length-scales estimated 6–8 components.
• LFRM with a low correlated-noise prior estimated 8–15 components.
• LFRM with a noninformative-like correlated-noise prior estimated 10–14 components.

In contrast, our method BSFDA produced a clear gap in the distribution of the precision parameters, effectively separating effective dimensions from redundant ones.

Several factors may explain LFRM’s performance:

• Correlated noise interference: The correlated noise can obscure the true signal.
• Prior specification: LFRM’s precision parameter prior are potentially less noninformative and not as sparse as those sparse Bayesian learning priors [52] in BSFDA.
• Element-wise vs. Column-wise Precision: The element-wise precision parameters in LFRM might compensate in a way that reduces overall sparsity.

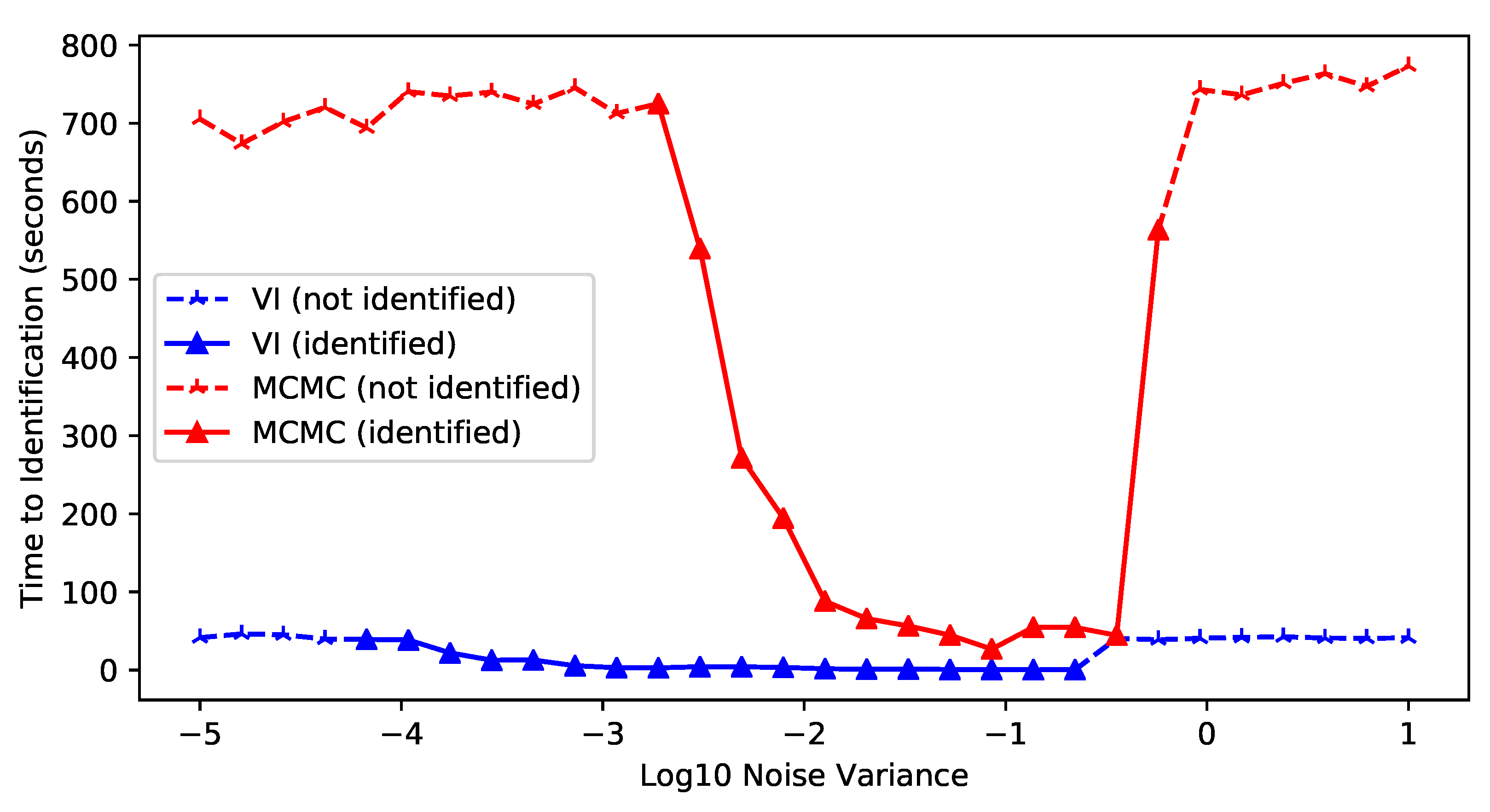
12.2. Variational Inference v.s. MCMC

We conducted experiments using both Gibbs sampling (MCMC) and mean-field approximation (Variational Inference) for the Bayesian PCA simulation [45,62] under varying noise levels. In our experiments, "satisfactory estimation" is defined as the point when the 4th smallest precision (i.e., the inverse of variance) is at least 100 times smaller than the 5th–indicating that the four true signal dimensions (with variances [5, 4, 3, 2]) have been correctly identified. For computational tractability, we capped VI at 200,000 iterations (approximately 200 seconds) and MCMC sampling at 20,000 iterations (about 20 minutes), with a burn-in period of 200 iterations and thinning set to 10.

Figure 13 illustrates the runtime for VI and MCMC to identify the correct components. Our key findings are as follows:

1.

When the noise level is close to the signal, neither MCMC or VI found the true dimension in the limited iterations (probably never will), because the data is heavily polluted.

2.

As the noise level decreases toward zero, the number of iterations (and runtime) required for satisfactory estimation increases dramatically; VI begins to fail around a noise level of $1\times {10}^{-4}$, and MCMC sampling around $1\times {10}^{-3}$, within the set time constraints.

3.

Across the 10 noise levels (about $3\times {10}^{-3}$ to $2\times {10}^{-1}$) where both successfully identified the correct dimensionality, VI consistently completes much faster than MCMC sampling. VI is approximately 20 times faster. 85.57 ± 50.24 in average, in the range of 32.46 to 189.12.

Figure 13. Time for variational inference and MCMC to identify the correct components in Bayesian PCA.

Figure 13. Time for variational inference and MCMC to identify the correct components in Bayesian PCA.

These results indicate that both MCMC sampling and VI become slower as noise decreases due to strong dependencies in the posterior. We hypothesize it is because both MCMC and VI suffer from the dependency introduced by low noise, which is a known long-standing issue with ongoing research methods, e.g., structured VI [72], or blocked/collapsed Gibbs sampler [74]. But both MCMC and VI work well provided there are sufficient iterations. This behavior suggests that the dependency induced by very low noise levels creates an optimization challenge rather than a fundamental modeling issue.

In summary: (1) VI is significantly faster than MCMC, (2) both methods slow down as the noise level decreases, and (3) both fail to recover the correct components when the noise is excessively high.