1. Introduction
Despite initial rejection of the Bachelier model [
6], its arithmetic Brownian motion dynamics have found acceptance in certain areas. To combine the strengths of both arithmetic and geometric Brownian motion models, the classical Black–Scholes–Merton (BSM) model [
7,
27] has been merged with a modernized Bachelier (MB) model [
31], producing a unified Bachelier–Black–Scholes–Merton (BBSM) model [
25]. Both the unified model and its MB limit allow for price trajectories taking values in
, while, under the BSM limit, price processes take values in
. Exploiting the more extensive price range of the MB model, [
31] developed a dynamic ESG-adjusted valuation (“ESG-adjusted pricing”) for assets, which allows for stocks with low ESG ratings to be given a negative ESG-adjusted value. A critical parameter of the adjusted valuation is the so-called ESG affinity, quantifying the market view of the “size” of the contribution of ESG ratings to asset values. [
5] explored fair valuation of options under the MB model using this ESG-adjusted asset valuation.
Consideration of ESG factors in financial modeling marks a paradigm shift in how asset values are assessed. As the world evolves toward a greener future, industry leaders must champion sustainability. (However, see [
15] for a study of how sustainability efforts have varied by market). Providing a solid quantitative use for ESG ratings is an important step in the effort to champion sustainability in the financial world. Consideration of ESG-adjusted prices alters the investment approach required for long-term investing, enabling ESG-conscious investors to more effectively measure, and (potentially) profit from, ESG strategies. Analyses based on such pricing must be woven into the investment processes of any discerning investor, as well as integrated into the corporate strategy of any company that is truly committed to increasing shareholder value [
21].
The first goal of this paper is to embed ESG asset valuation within the continuous-time BBSM model (
Section 2), placing ESG finance within the broader framework of a unified Bachelier and Black–Scholes–Merton theory. In
Section 3, we embed the ESG-adjusted asset valuation into the BBSM binomial option pricing model of [
25].
The second goal is to provide an empirical study of discrete option pricing under the ESG-BBSM binomial model of
Section 3. Our data set for 16 stocks selected from the Nasdaq-100 is described in
Section 4.1. Empirical examples of ESG-adjusted prices are presented in
Section 4.2. In
Section 4.3 we describe how to fit the required parameters of the binomial model to empirical data. In
Section 5, using published call option prices for 01/02/2024, we compute implied values of the ESG affinity parameter as functions of strike price and time to maturity. These can then be expressed in terms of an implied ESG valuation (as a function of strike price and time to maturity). Comparing the implied ESG valuation to financial spot prices provides insight into the views of option traders on the impact of ESG ratings on the underlying asset value.
The third goal of this study (
Section 6) focuses on a discrete-time, futures trading strategy that can be adopted by an option hedger (the trader taking a short position on an option) who may posses information regarding the future direction of movement of the ESG-adjusted valuation of the underlying stock. While the efficient market hypothesis argues that the direction of the asset price movement is unpredictable [
2,
3,
14,
17,
18,
19,
20,
23,
29], numerous studies challenge this view and indicate that price direction may, indeed, be predictable [
1,
4,
8,
9,
11,
12,
24,
26,
28,
30,
34,
35,
36,
38,
39]. As a result, [
10,
13,
37] and many others have worked on understanding informed trading markets and the strategies employed. We demonstrate that the trader can optimize this trading strategy to produce an effective dividend stream.
Section 7 concludes the paper with a discussion of future directions.
2. Embedding ESG pricing in the BBSM model
Consider the market
consisting of a risky asset
, a riskless asset
, and a European contingency claim (option)
. Under BBSM,
has the price dynamics of a continuous diffusion process determined by the stochastic differential equation
where
is a standard Brownian motion on a stochastic basis
of a complete probability space (
). The coefficients satisfy
,
,
,
, and are
-adapted processes. The
-adapted processes
and
are assumed to satisfy the usual regularity conditions.
1 [
25] define the appropriate price dynamics
2 of the riskless asset
in the BBSM market model as
Again,
and
are
-adapted processes. The
-adapted process
is also assumed to satisfy the usual regularity conditions.
3 The MB model is achieved as the limiting case
, while the classical BSM model is the limiting case
. For brevity, we adopt the notation
,
and
. We require
,
-almost surely (a.s.). A necessary condition for no-arbitrage is the requirement that
,
-a.s. Under the no-arbitrage assumption, the market price of risk is
which is strictly positive
-a.s. for all
providing
,
-.a.s.
The option
has the price dynamics
where
,
,
, has continuous partial derivatives
and
on
, and
T is the expiration (maturity) time of
. The option’s maturity payoff is
for some continuous function
. The risk-neutral valuation of
is [
25]
where
is the equivalent martingale measure and the asset price dynamics under
is
In (
6),
,
, is a standard Brownian motion on the stochastic basis
.
Consider a published ESG rating
4 (score)
for a company
X at time
t. argue that bounded scales for an ESG score do not differentiate adequately between the amount of effort that a company must undergo to raise their score above a current value.
5 They further argue that scores based upon a convex, monotonically increasing function better represent such effort, and that the choice of such a function should be based ultimately on an axiomatic approach. In the absence of such an approach, they proposed the relative ESG measure
where
is the ESG rating (score) of company
X and
is the ESG score of a relevant market index
I.
6 They further define the ESG-adjusted stock price of company
X at time
by
which incorporates ESG scores as part of an asset’s valuation. Here
represents the financial price of an asset, while
represents an ESG-adjusted valuation,
7 which refer to as the ESG-adjusted price. In (
8),
is referred to as the ESG affinity of the financial market.
8
The ESG-adjusted stock price (
8) can be negative.
9 This is not surprising as the relative score
is analogous to any financial `spread’. We note the following dependencies of
on
.
From (
9a) through (9d), we see that changing the value of
only affects the (additional) fractional financial price term
, which satisfies
.
3. Binomial Option Pricing under the BBSM Model
[
25], Section 7 developed a binomial option pricing model under the BBSM model. We briefly summarize that model here. Consider a BBSM market
) consisting of the risky asset (stock)
, the
and call option
. The stock price
evolves according to the binomial pricing tree
In (
10),
, is the stock price at time
,
where
T is the fixed maturity time and
. For every
,
,
, are independent, identically distributed Bernoulli random variables with
determining the filtration
of the stochastic basis
on the complete probability space
. The riskless asset
has the discrete price dynamics
where
is the instantaneous rate of (
2) at times
.
Under BBSM, price changes, rather than returns, are of primary interest. Let
Then,
In order that the càdlàg process on the Skorokhod space
generated by the binomial tree (
10) converge weakly to the continuous time process (
1), we require that the conditional mean and variance satisfy
where
and
are the instantaneous mean and variance of (
6) at time
. Then
and
are given by
The option
has the discrete price dynamics
,
. Consider a self-financing strategy,
replicating the option price process
:
The standard no-arbitrage arguments lead to
Thus, the risk-neutral valuation of the option is given by the recursion
where the risk-neutral probability
is
The limit
of (
18) and (
19) produces the option price recursion relation for the BSM model,
having risk-neutral probability
where
is the discrete form of the market price of risk,
, in the BSM model.
10 In this limit, the discrete price of the riskless asset obeys,
.
The limit
, produces the option price recursion relation for the [
31] Bachelier model,
The risk-neutral probability
is (see also [
22]),
In this limit, the discrete price of the riskless asset obeys
.
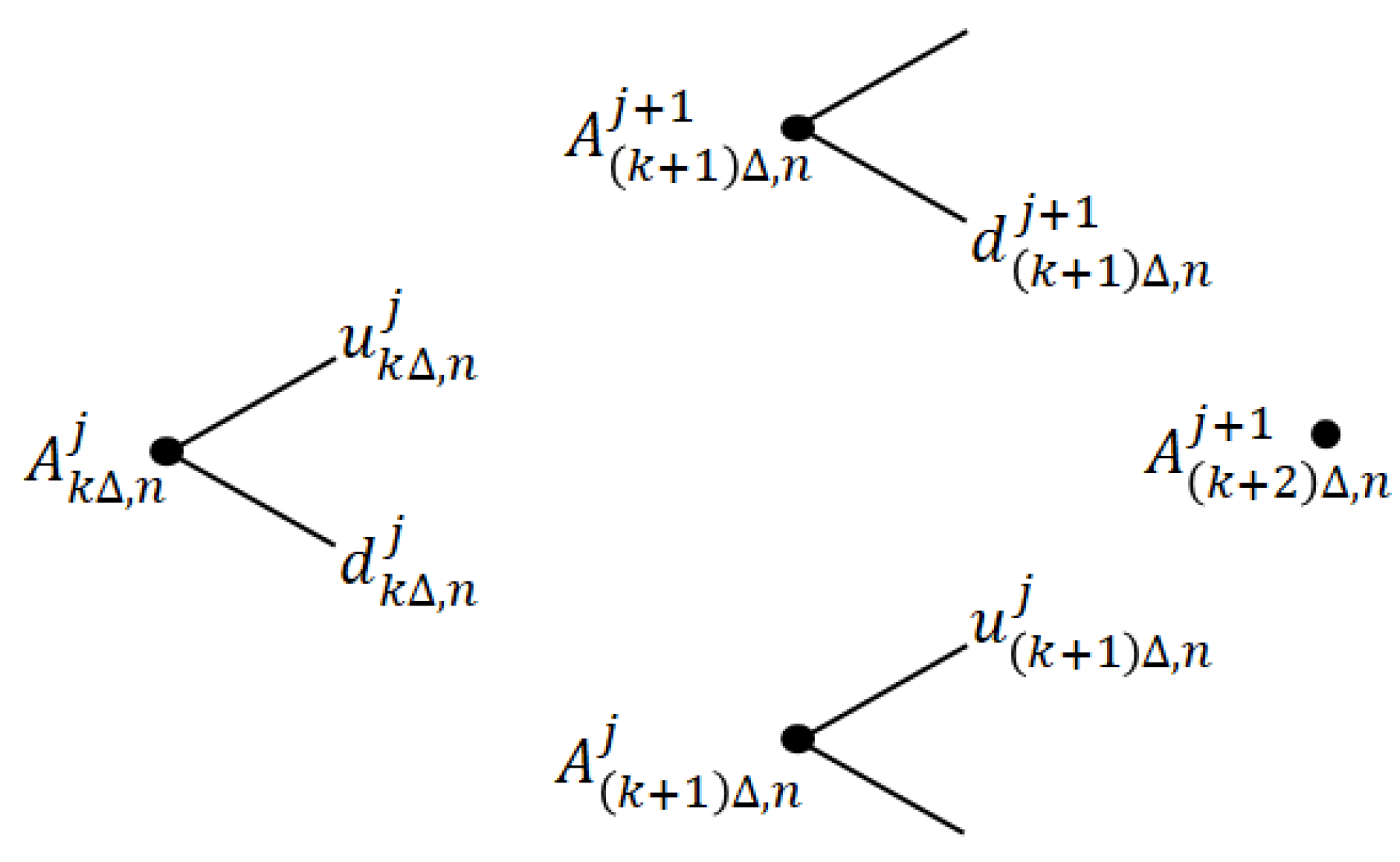
3.1. The Binomial Model is Not Recombining
A careful analysis shows that the risky-asset asset price process (
10) does not, in fact, form a recombining tree. For a fixed value of
k,
, the superscripts
and
determine node “level” values at time
. For a recombining binomial tree, at time
k, there are
level numbers Thus each node on the tree is indexed by a
pair,
,
. With the inclusion of level numbers, (
10) is written as
where, from (
16),
Figure 1 illustrates a price configuration on four nodes of the tree, with time and level values indicated. Substituting (
25) into (
24) gives
where
Note that , , , and are constants.
For the tree to be recombining, in
Figure 1 we must have
With some algebra, the difference
can be shown to be
independent of time or level number.
11 To ensure that the tree is numerically recombining in our empirical work in
Section 4, we define
We note that
vanishes more rapidly than
and
terms as
. However, theoretical work remains to be done to ascertain whether the càdlàg process on the Skorokhod space
generated by either (
10) or (
30) does indeed converge weakly to the continuous time process (
1). We leave this question open for further investigation. We do note that the BSM and MB limits of the price process (
10) are indeed recombining (binomial) trees whose generated càdlàg processes do converge weakly to the appropriate BSM and MB limits of the continuous time process (
1).
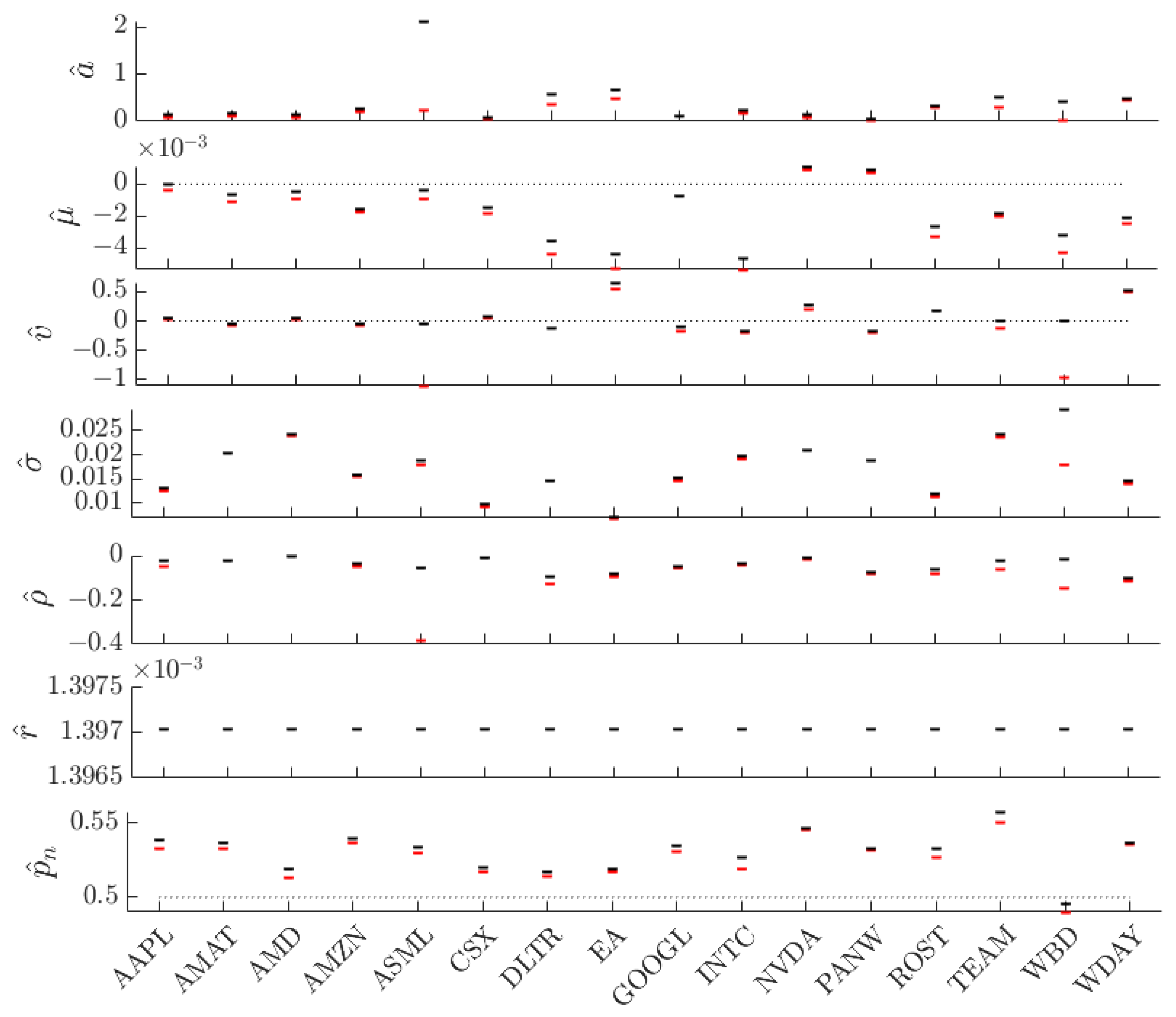
5. The Implied ESG Affinity
Let
denote published call option prices for an underlying stock having maturity date
,
, and strike price
,
. Let
denote the call option price computed from
Section 3 with constant parameters values. Let
denote the historical estimation of any parameter
. (Recall that, except for
, the parameters have dependence on the value of
.) Then implied values for
are computed via
Based upon call option prices published on 01/02/2024,
21 we computed theoretical call option prices for the same set of strike prices,
,
, and maturity times
,
. In (
39), the parameters
used in the theoretical option computation were fit from the historical data for each value of
tested in the minimization procedure. As the value of
is independent of the value of
and of the stock, theoretically it only needed to be calculated once. However, it is computed from the same regression (
36) that produces
, so it was recomputed for each value of
tested. The value
used to compute prices on the binomial tree was the smoothed value for 01/02/2024.
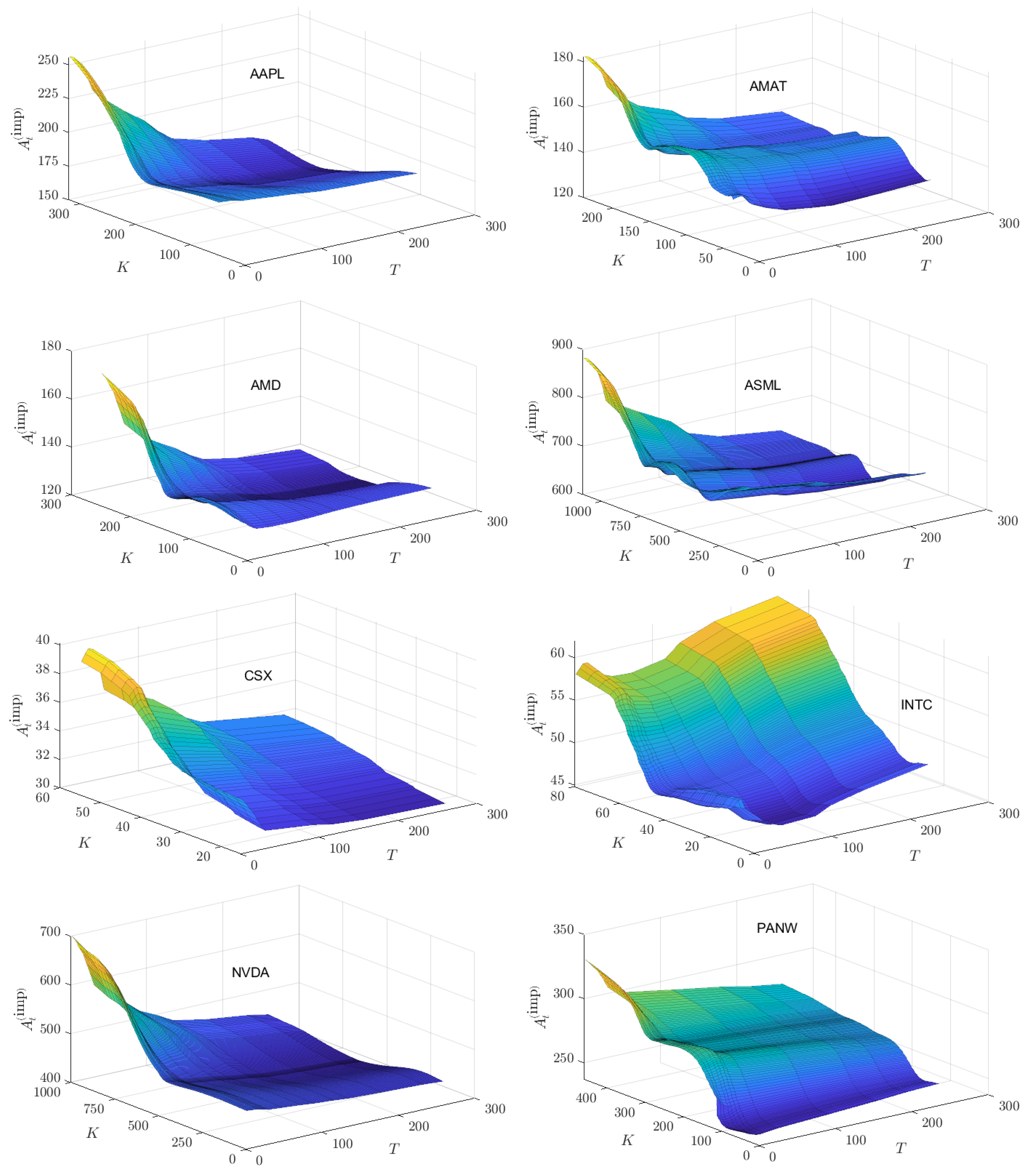
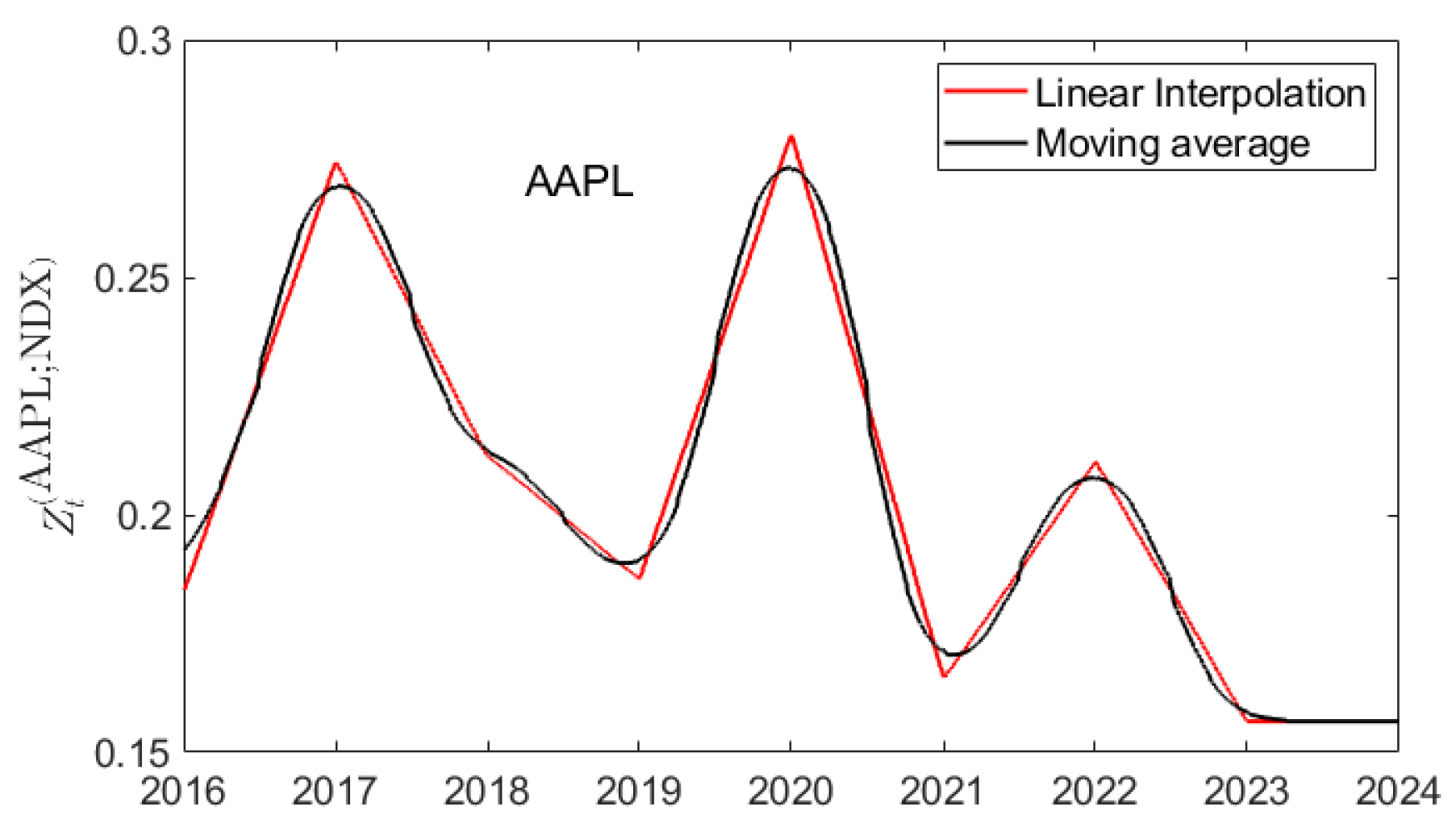
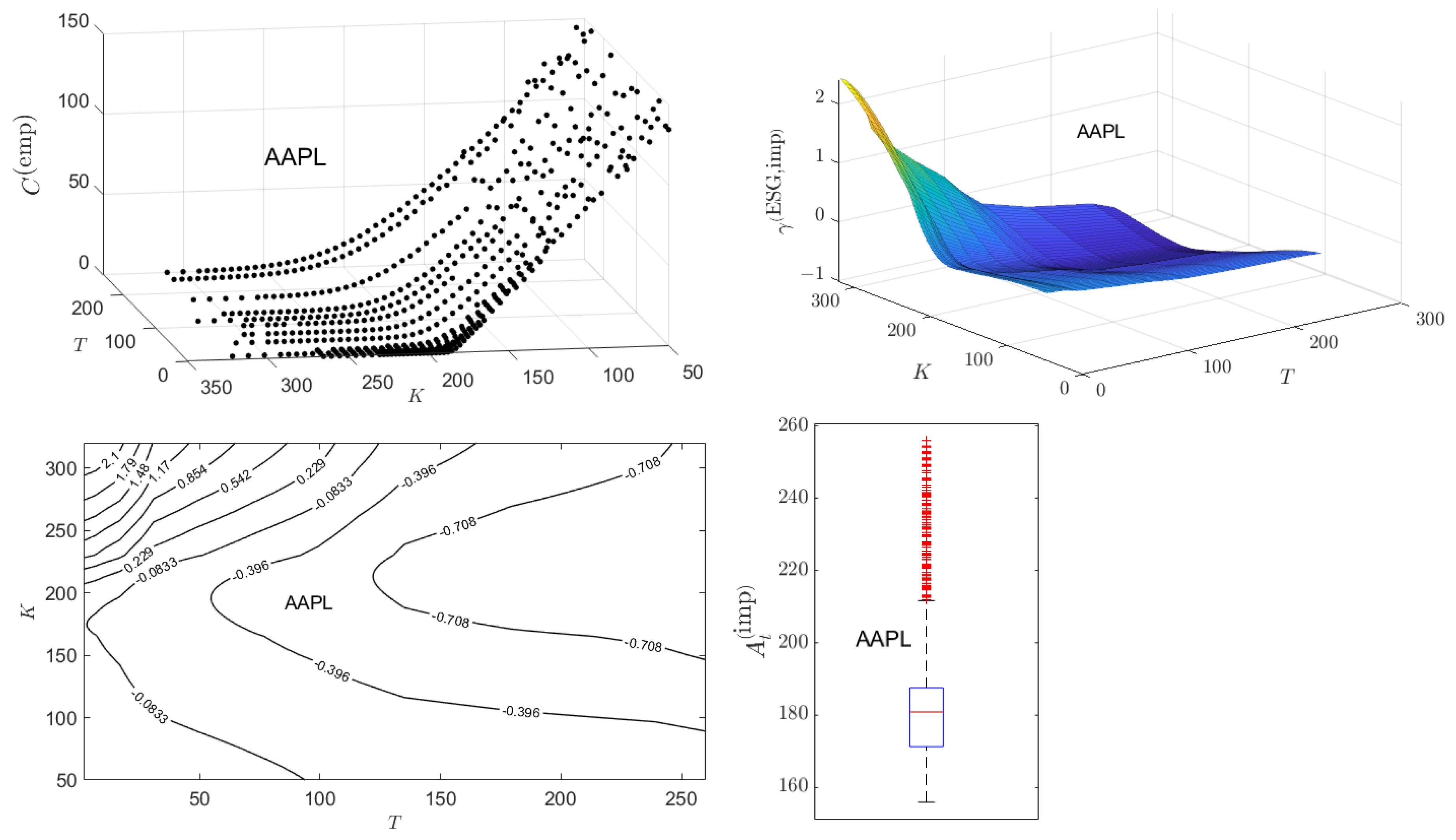
The published call option prices for AAPL on 01/02/2024 are presented in
Figure 8.
22 In contrast to some of the other stocks investigated, these option prices form a fairly “regular” surface over the published range of
,
, and maturity times
,
values. The values
computed from (
39) are plotted as a surface in
Figure 8.
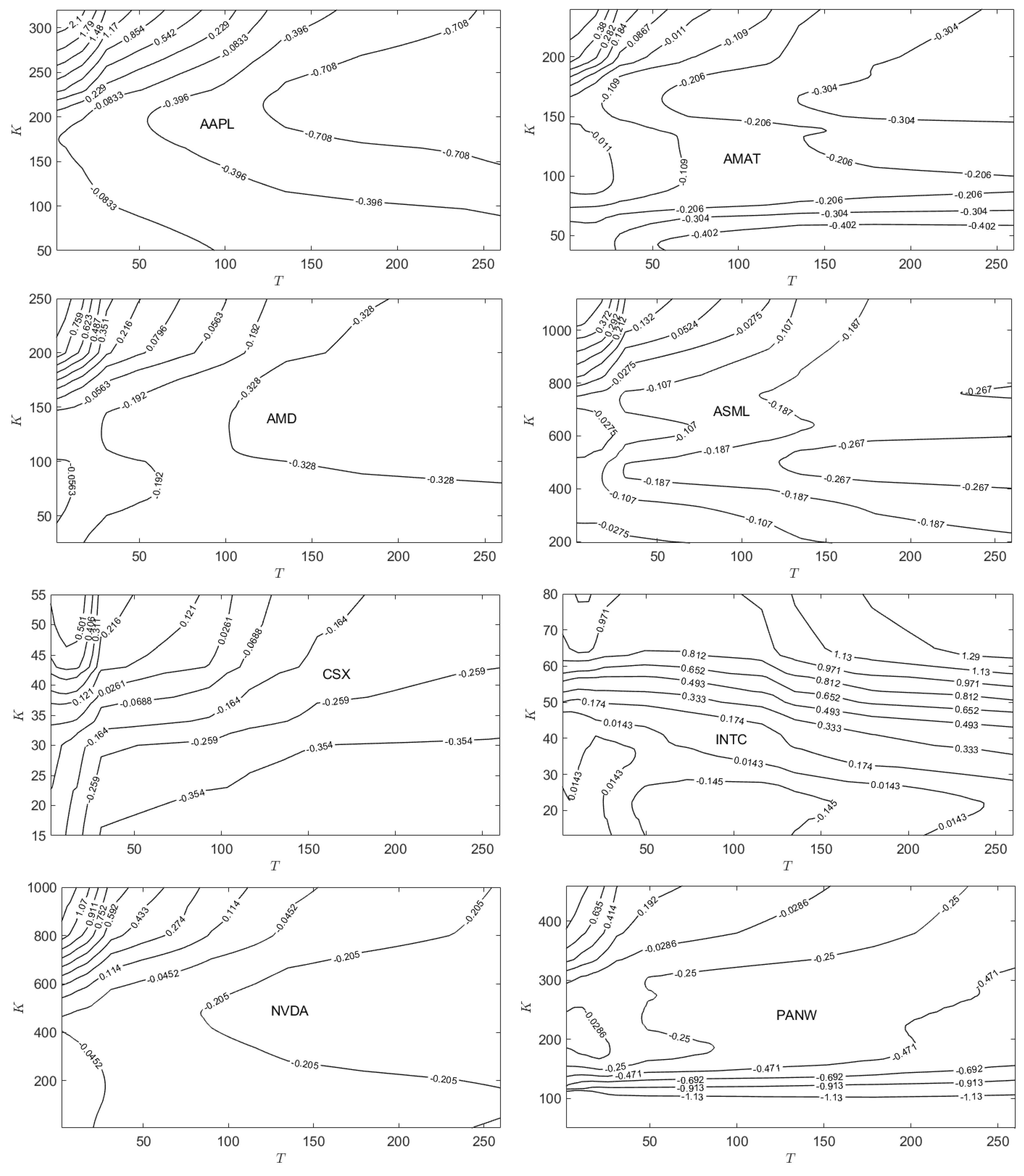
23 Analysis of the
surface is enhanced by consideration of surface contours as shown in the bottom left of the figure. The
contour lies between the contours
and
, indicating that option traders have a positive view (relative to ^NDX) of the ESG rating of AAPL in the upper left triangular region of out-of-the money (the adjusted closing price for AAPL on 01/02/2024 was
$185.64) strike prices and maturity dates not exceeding 110 trading days. However, over the majority of
values, the option traders have a negative view of the ESG rating of AAPL.
A further view of the
values is presented in
Figure 8 as a box-whisker summary of the distribution over the surface.
Table A1 in
Appendix A presents the numerical values of the minumum, maximum,
,
, and
percentiles of the
distribution for AAPL. This table also presents the
for AAPL based upon examination of historical adjusted ESG prices discussed in
Section 4.3. The overwhelming majority of
values lie within the
for AAPL, giving some confidence that the implied ESG affinity values being computed are consistent with semi-martingale behavior of the associated ESG-adjusted price.
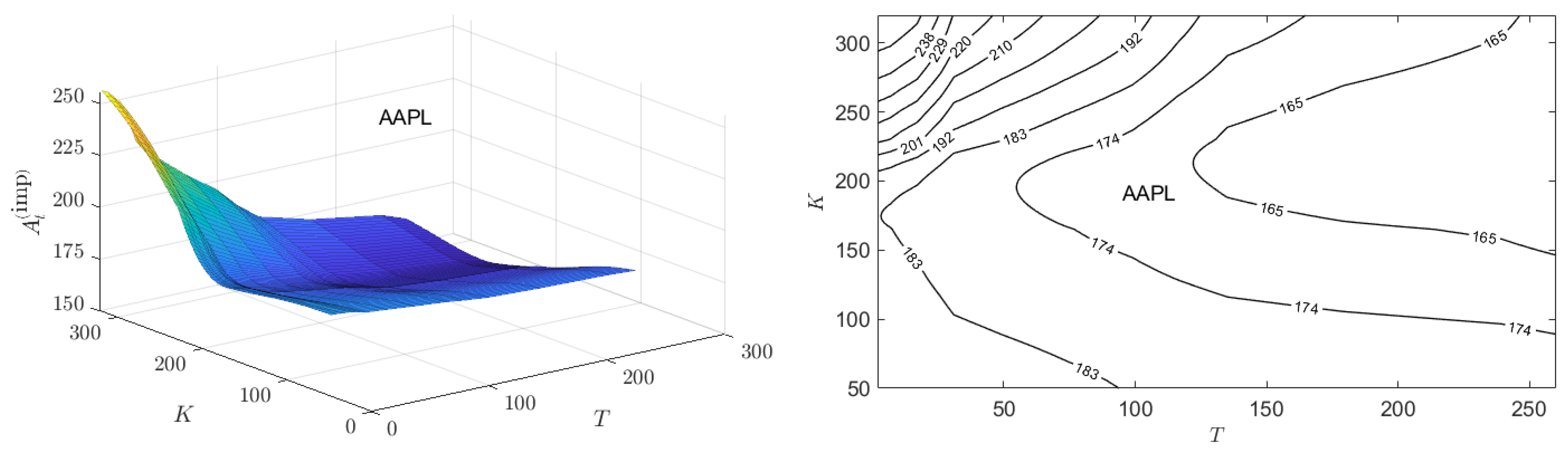
To appreciate the implication of this, we define from (
8) an implied ESG-adjusted price
where, for a given stock
X,
is a value from the implied ESG affinity surface, and
was the relative ESG score and
the spot price price used in computing the surface.
Figure 9 presents the surface of
values computed from the
values of
Figure 8. Also shown are contour levels of the
corresponding to the analogous contour levels of
shown in
Figure 8. Whether
is larger or smaller than
depends on the sign of the product
. If
is positive, then positive values of
correspond to an ESG valuation that exceeds
. However, if
is negative, then negative values of
correspond to an ESG valuation that exceeds
. Thus, consideration of the
surfaces rather than the
surfaces provides direct insight into the views of option traders on the ESG-valuation of stocks.
Since was positive on 01/02/2024, the surfaces of and are identical except for a rescaling of the z-axis. Similarly the contour plots for and are identical except for a rescaling of the value on the contour levels. The negative view of the option traders over most of the range for AAPL, results in implied, ESG-adjusted prices for 01/02/2024 that correspondingly fall below the financial price of AAPL on 01/02/2024.
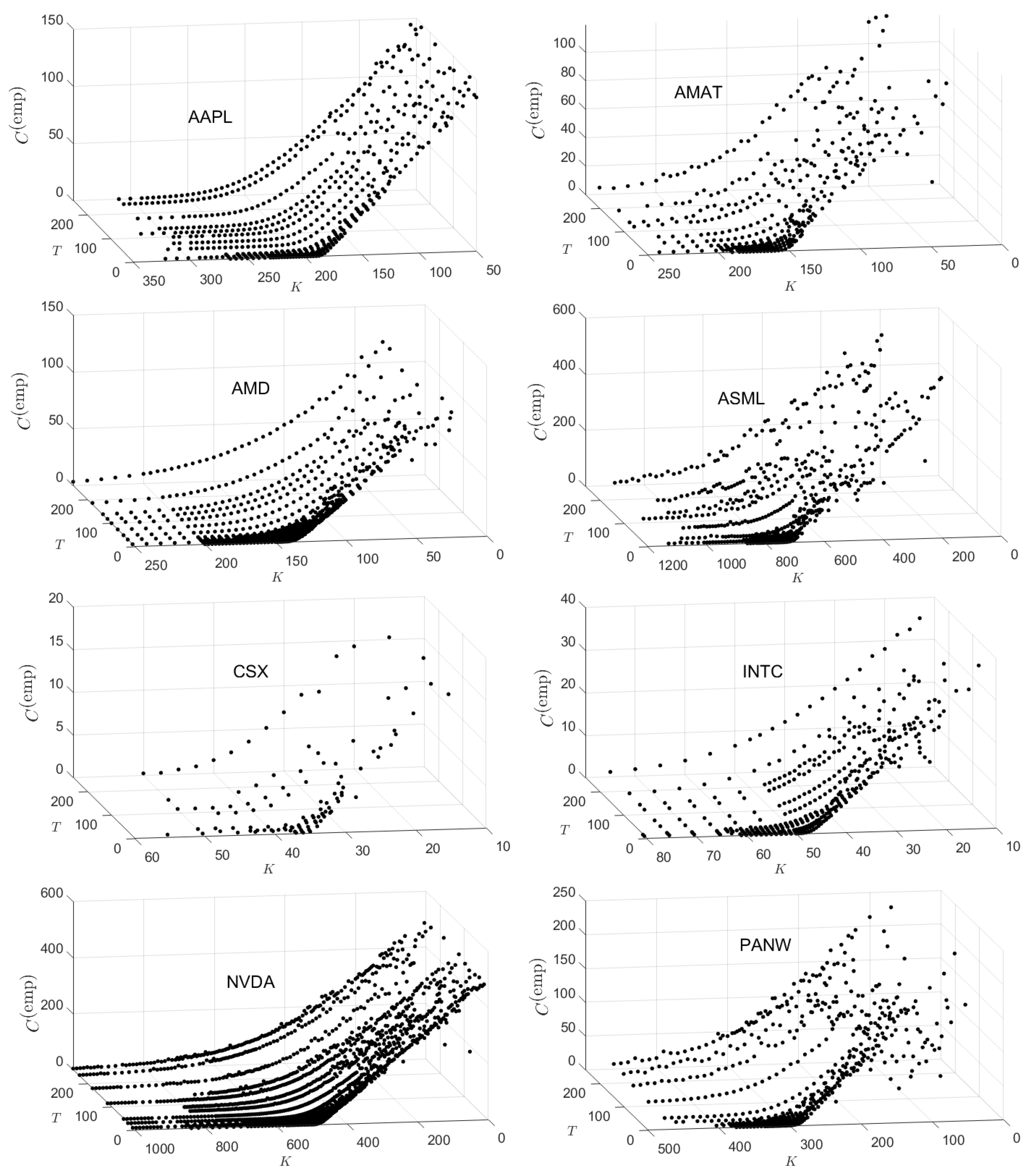
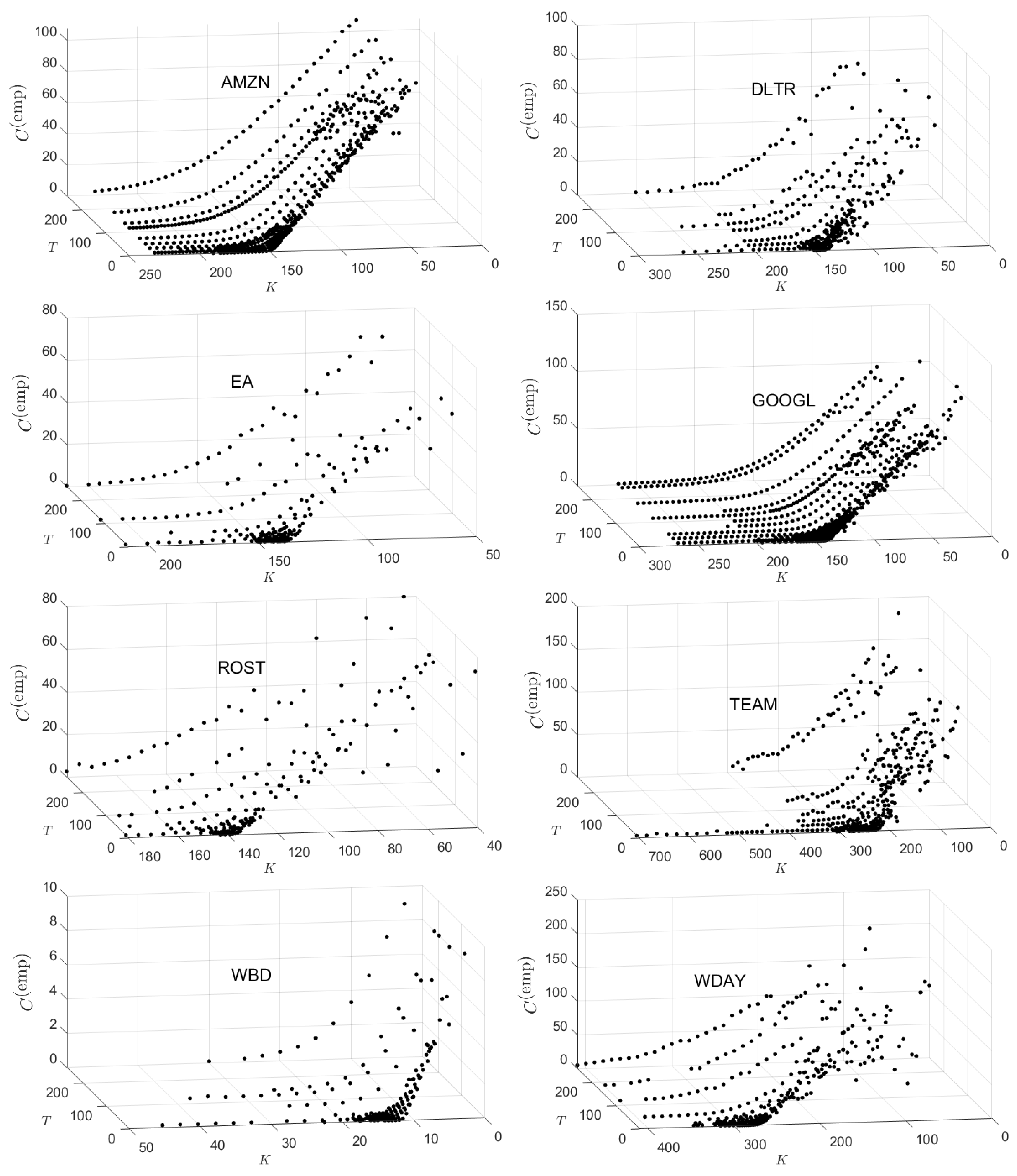
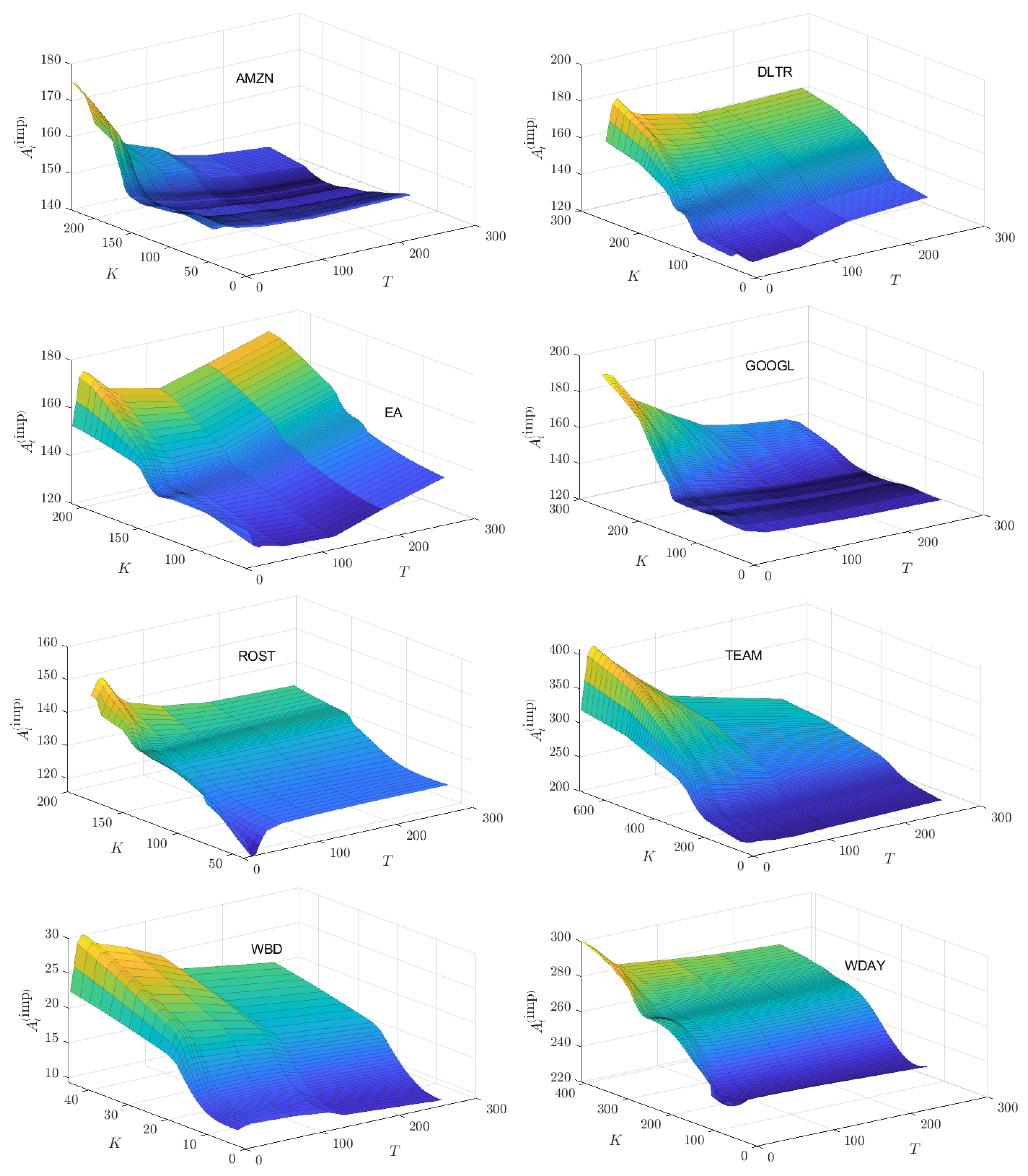
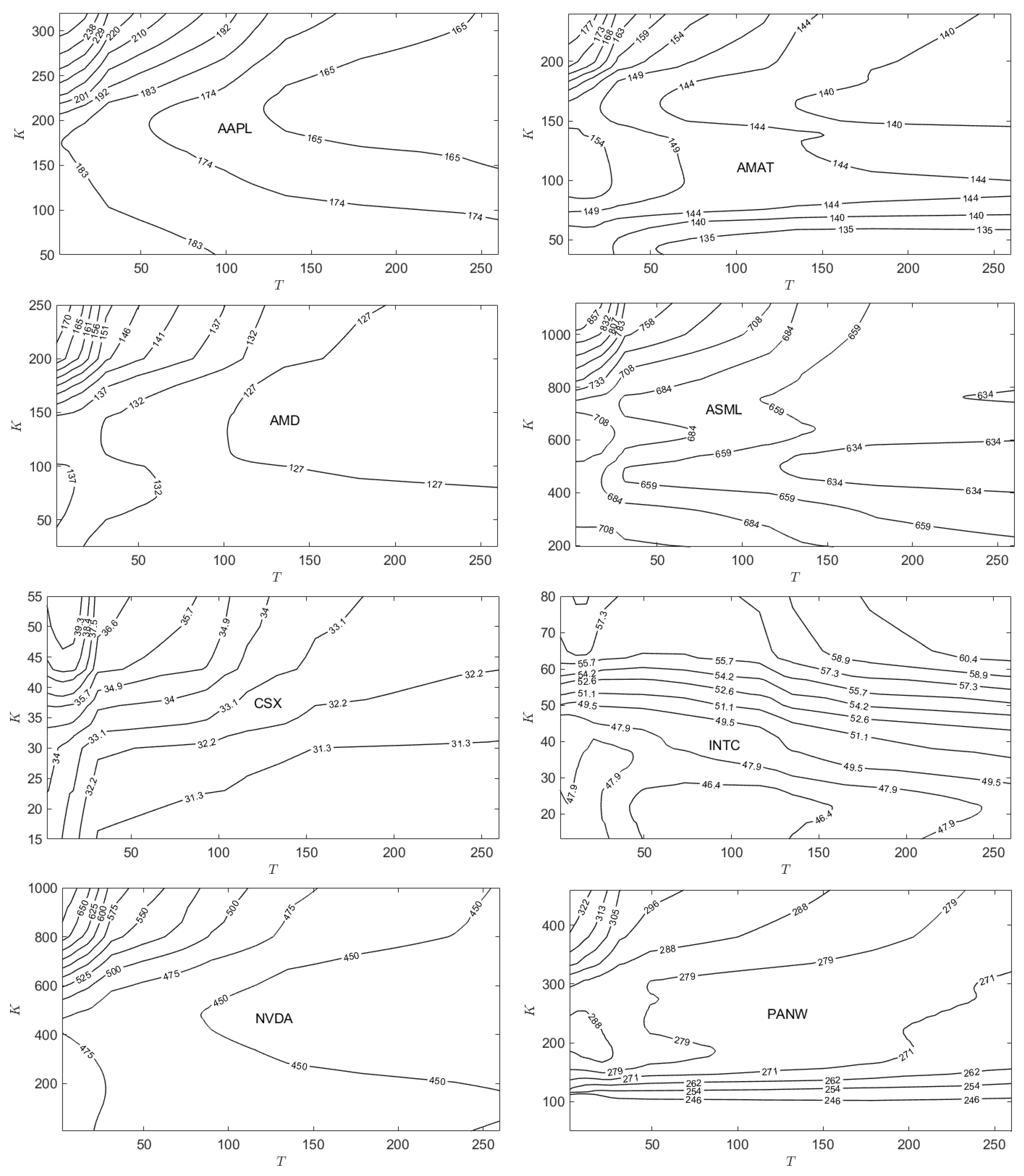
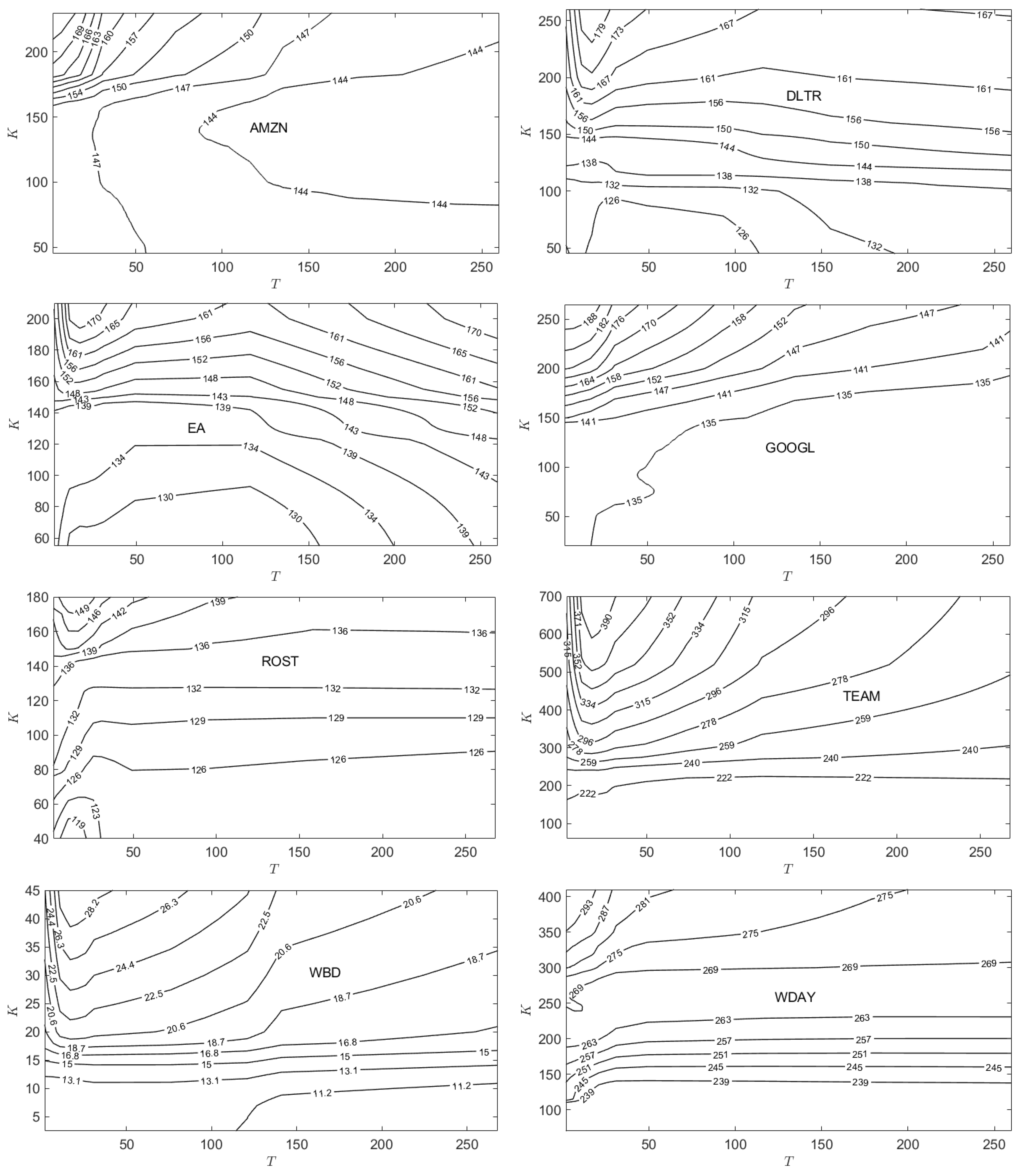
Figs.
Figure A1 and
Figure A2 in
Appendix B plot the published option prices on 01/02/2024 for all 16 stocks studied. The eight stocks for which
on
01/02/2024 are presented in
Figure A1, while the eight stocks for which
are presented in
Figure A2. This separation reflects the fact that when
, the corresponding surfaces for
and
will look like identical (rescaled) versions of each other. However, when
, the surface
will look like an inverted, rescaled version of the corresponding
surface. Examination of published option prices for PANW, TEAM, and WDAY show much greater irregularity over the range of
K and
T values than that shown for AAPL.
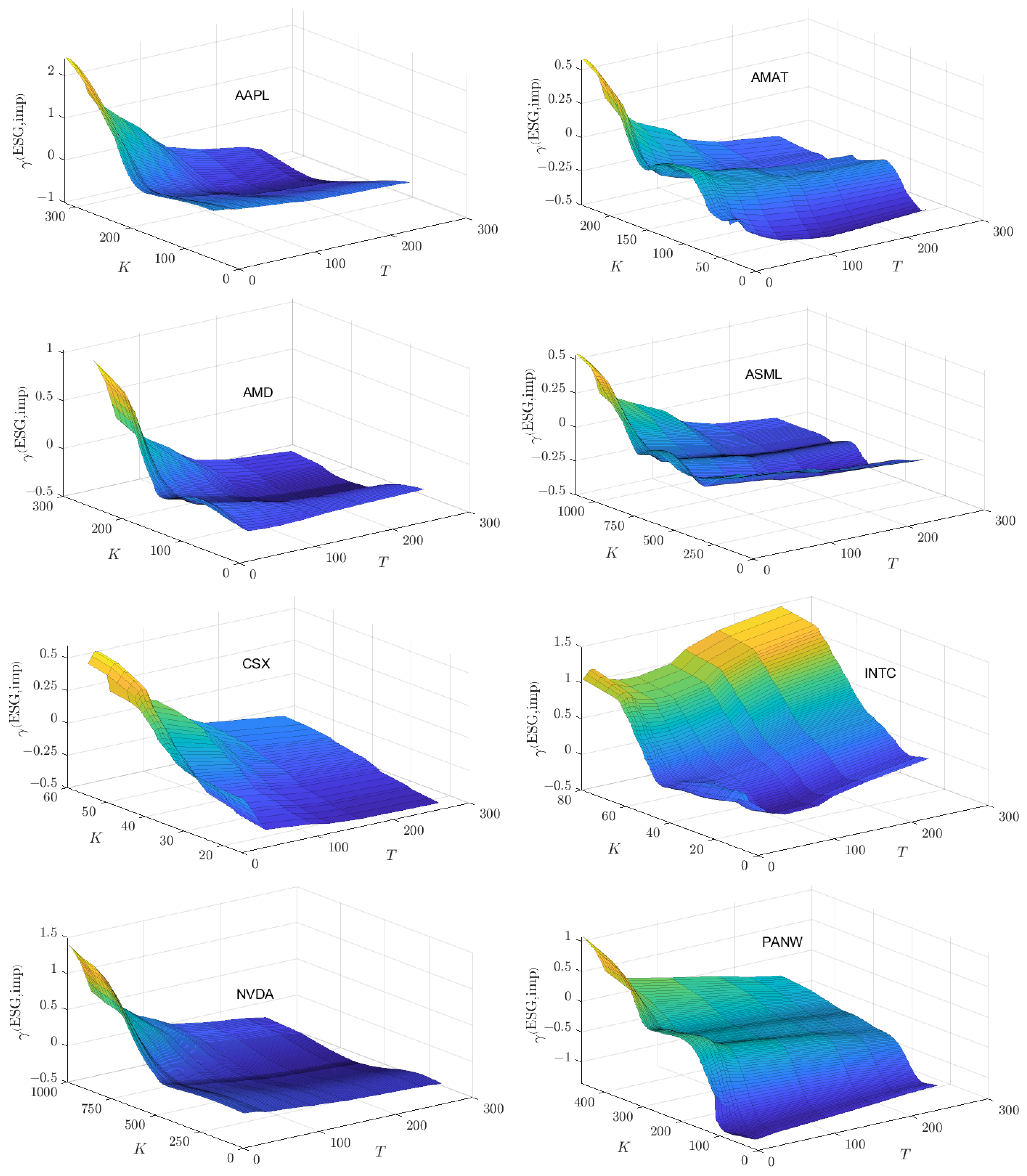
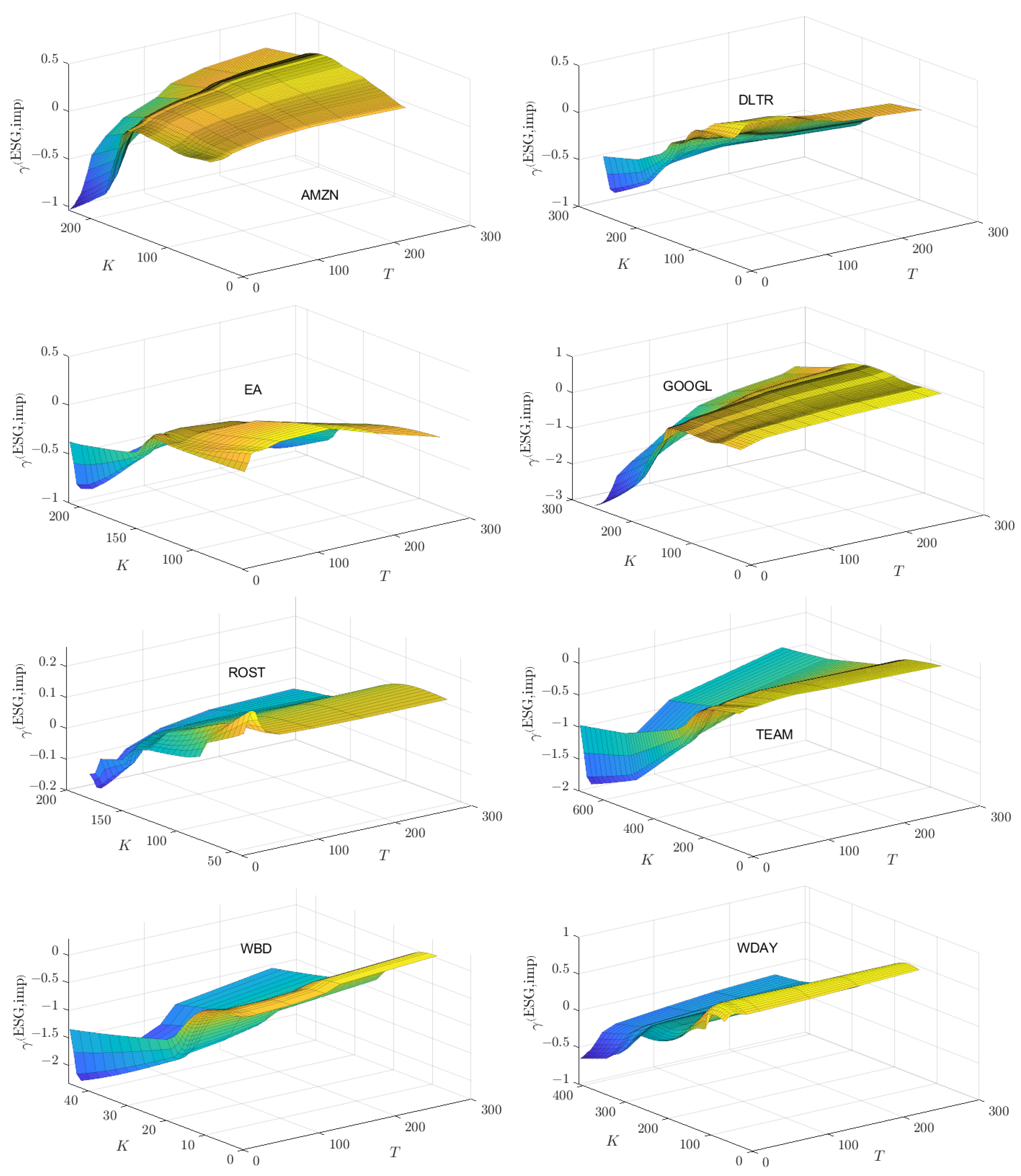
24
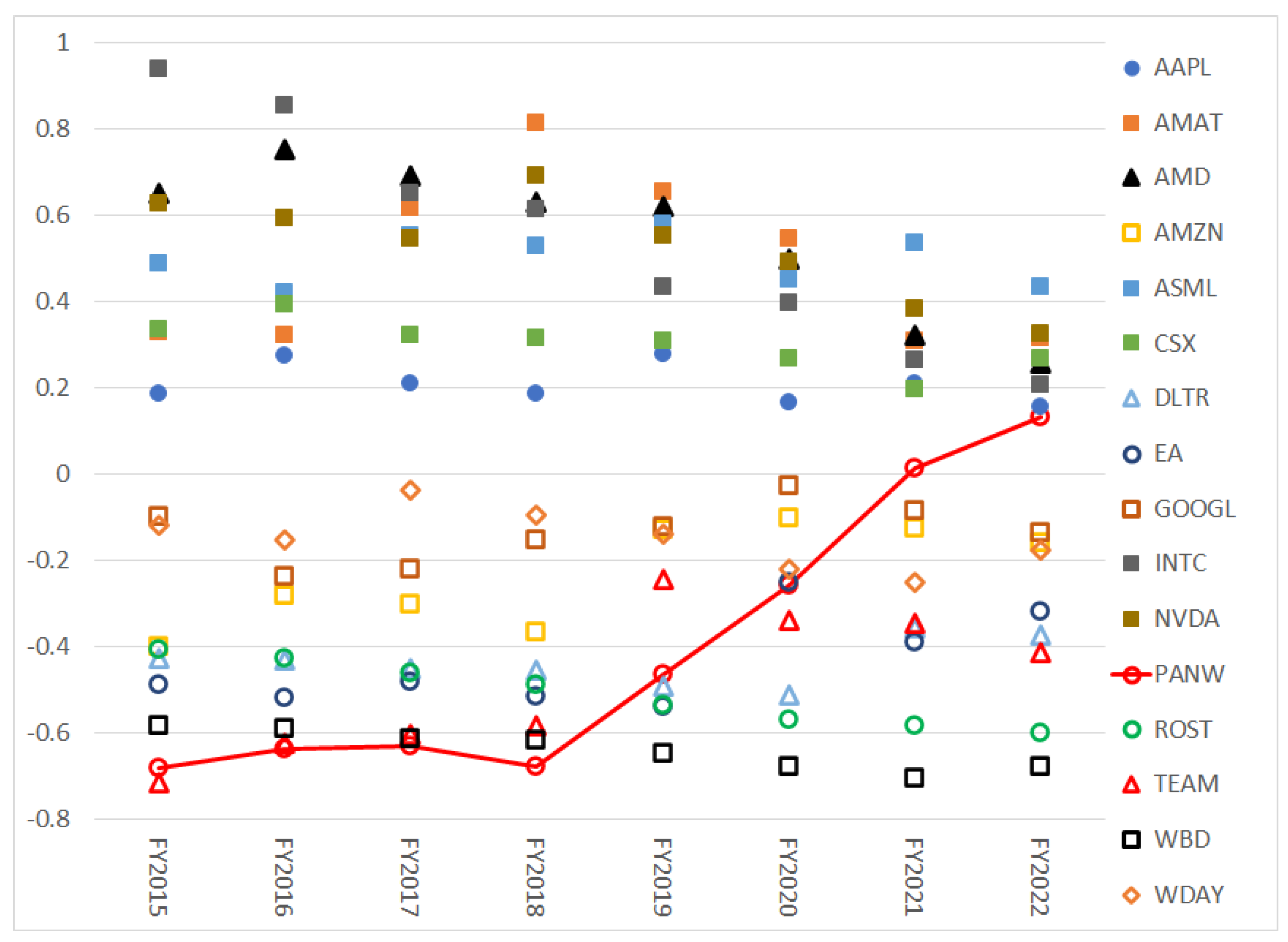
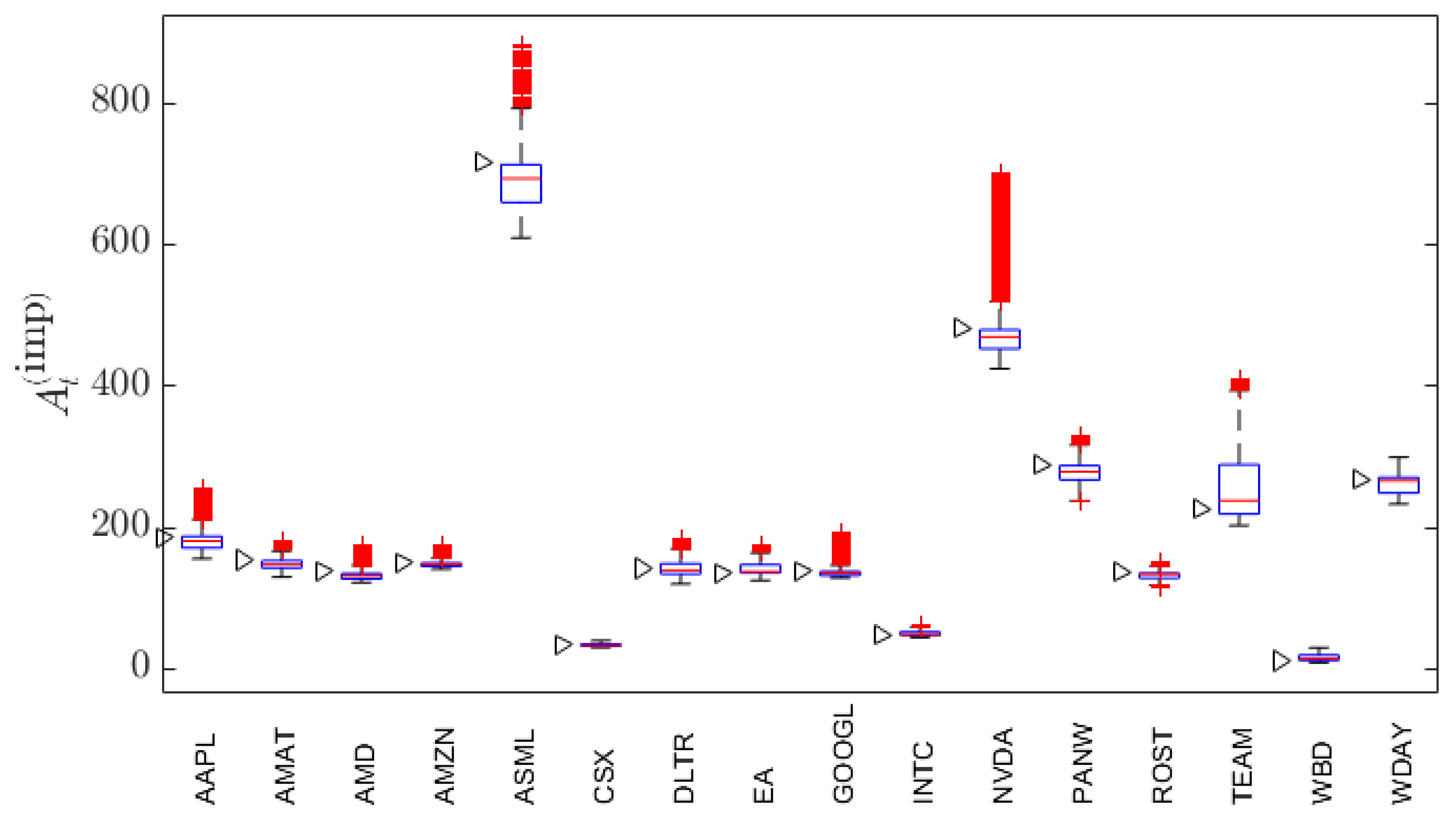
To summarize the information in
Appendix C and
Appendix D,
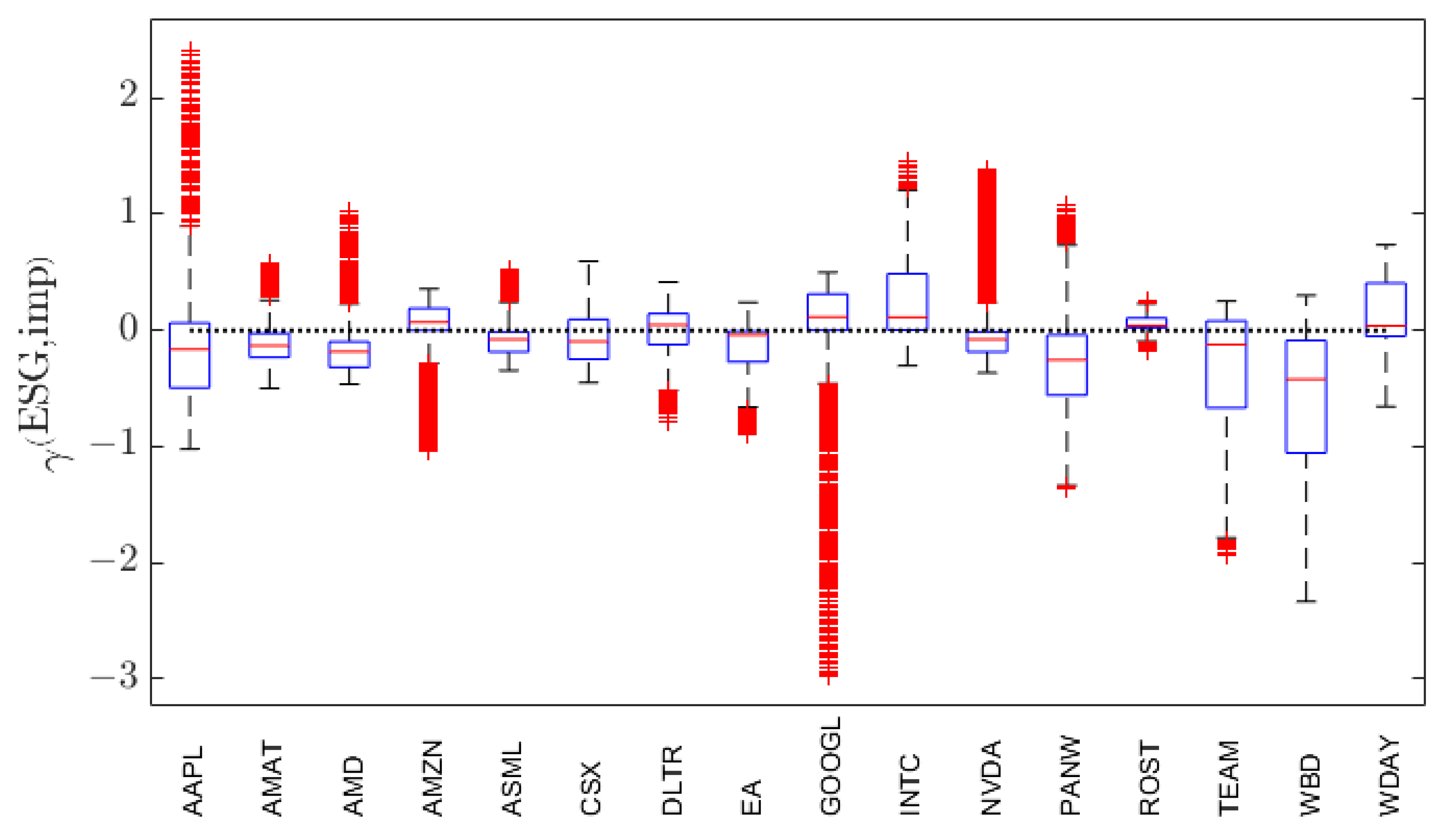
Figure 10 presents the box-whisker summaries of the distributions of
values for each of the 16 stocks. (The corresponding box-whisker summaries of the distributions of
values are given in
Figure A7.) Also indicated just to the left of each box-whisker summary is the financial spot price of the stock on 01/02/2024. For ease of reference, the financial spot prices on 01/02/2024 are listed in
Table A2. From the contour plots in
Figure A10 and
Figure A11, one can then ascertain over what region of
values option traders view the ESG valuation of the stock to be higher than its financial price. For EA, INTC, TEAM and WBD, spot traders have an implied ESG valuation that exceeds the spot price over most of the
region. For eight of the stocks (AAPL, AMAT, AMD, AMZN, ASML, CSX, NVDA, PANW), the implied ESG valuation exceeds the spot price over a triangular, out-of-the-money, shorter maturity time region as described above for AAPL. For the remaining four stocks, the implied ESG valuation exceeds the spot price over most of the out-of-the-money region. Thus, for 12 of the 16 stocks, option traders have in-the-money ESG valuations that are lower than the spot price.
6. Trading Forward Contracts Utilizing Information on Asset Price Direction
[
22] extended BSM-based binomial option pricing theory to complete markets containing traders that have information on the stock price direction. We further extend that theory using the BBSM-based binomial option pricing in complete markets of
Section 3. For simplicity, we assume the parameters in the BBSM binomial model are constant:
,
,
,
,
, and
,
. As earlier, we continue to assume
is constant.
Let ℵ denote the trader (hedger) holding the short position in the option contract. Let denote the probability that information held by ℵ at time , , on the direction of stock price movement within any interval is correct. If , ℵ is an informed trader; if , ℵ is misinformed; and if , we refer to ℵ as a noisy trader. We assume ℵ is the only informed trader in a market of noisy traders; consequently, ℵ’s informed trading actions do not influence market prices.
In [
22], Shannon’s entropy [see e.g., [
32,
33] is used to quantify the amount of information
ℵ possesses. As with the price movement probability
of
Section 3,
is the probability governing a Bernoulli random variable
such that
. Then Shannon’s entropy is
, having maximum value
. [
22] defined
ℵ’s level of information as
25
where
We address the question of
ℵ’s potential gain from trading with an information level
. At any time
,
,
ℵ makes independent bets,
,
. Thus, the filtration (
11) needs to be augmented with the sequence of
ℵ’s independent bets:
Specifically, relying on the information on stock-price direction,
ℵ adopts a trading strategy involving forward contracts. For convenience, we label the two scenarios given by (
10) for the price of
:
: , resulting in w.p. ,
: , resulting in w.p. ,
where
and
are given by (
16) with constant coefficients. If at
,
ℵ believes that
will happen,
ℵ takes a long position
26 in
-forward contracts, for some
.
27 The forward contracts mature at
. If at
,
ℵ believes that
will happen, then
ℵ takes a short position in
-forward contracts
26:oppparty having maturity
.
[
25] developed the price of a forward contract under the BBSM model. Assuming there is no initial cost to enter into the forward contract and constant coefficients, the
T-forward price of
is
where the constant coefficient solution to (
2) is [
25], (A3)]
Evaluating (
44) using (
45) gives
for all
. Discretizing (
46) over the time interval
and assuming
, (
46) becomes
For notational brevity, define
.
Using (
10), conditionally on
, the payoff possibilities of
ℵ’s forward contract positions can be written
The conditional expected payoff is
with
and
given by (
16).
We write
where,
, for any finite value of
.
is referred to as
ℵ’s information intensity. Again assuming
,
28 Under the same assumption, the conditional variance of
ℵ’s payoff is
The instantaneous information ratio is then
As
is positive, the information ratio on the payoff of
ℵ’s strategy increases: as
ℵ’s information intensity increases, and when
.
29
To hedge the short position in the option,
ℵ executes the positions (
17), while simultaneously running the futures trading strategy. This leads to an enhanced price process for
ℵ, the dynamics of which can be expressed as:
,
. The price change of the process (
54) is
Conditionally on
, and using (
16),
It is in
ℵ’s interest to find the value of
which maximizes the conditional Markowitz’ expected utility function,
where
is
ℵ’s risk-aversion parameter. Using (
56),
is maximized for
Under the optimal value,
and the instantaneous conditional market price of risk for
ℵ is
If
ℵ had not traded futures on the information possessed, the trader’s instantaneous conditional market price of risk would have been the same as a noisy trader:
Thus,
futures trading results in an (optimized) dividend
yield over the time interval
determined by the solution of
Thus,
We note that, relative to a noisy trader,
Equality between the first and last terms in (
64) is obtained for
or
since, under these limits, all traders become aware of the direction of the price movement.
We investigate the dividend payout
as a function of
and
. From (
59) we note that
is a monotonic function of
having the limits
and
. Under the limit
, which corresponds to sufficiently small values of
or sufficiently large values of
,
which is always positive, increasing with
and decreasing as
increases. Under the limit
, which corresponds to sufficiently large values of
or sufficiently small values of
,
In this limit, the dividend payout is essentially independent of
.
7. Conclusion
Dynamic asset pricing based upon geometric Brownian motion [
7,
27] has had a tremendous’ impact on finance theory. While having had difficulty gaining acceptance, dynamic pricing based upon arithmetic Brownian motion [
6] has certain attractive features. The unified BBSM model of [
25] encompasses the strengths of both models. By adapting the BBSM framework to a model of ESG-adjusted asset valuation, we put the full strength of the BBSM model to practical use. Using an empirical data set of 16 stocks taken from the Nasdaq-100, based on call option prices for 01/02/2024 we have shown that, generally, option traders were implying ESG-adjusted prices that exceed the spot price in the out-of-the-money region, while in-the-money, ESG-adjusted prices were lower that the spot price. A follow-up study is required to determine how universal an observation this may be. It would be interesting to investigate call option prices issued during periods of bull and bear markets, and during market disruptions.
We have further extended this ESG-BBSM model to consider futures trading strategy accessible to a trader ℵ holding information on the direction of ESG-adjusted prices. It would be of interest to evaluate ℵ’s optimal dividend payout by, for example, projecting it forward on the binomial tree and computing an expected dividend at time . While this could be evaluated for a specific asset, using historical estimated values , , , , , , , and a spot price (with ), there is no historical information available for , while the parameters and are trader-dependent. Thus, estimates of an expected averate dividend payout at require an investigation of a three dimensional phase space - a fairly daunting prospect best left for a separate study.