Temporal and Spatial Coupling Methods for the Efficient Modelling of Dynamic Solids

1. Introduction

The temporal and spatial discretisation of structural dynamic problems is directly related to the accuracy and computational cost of the explicit finite element method. Constrained by the Courant-Friedrichs-Lewy (CFL) condition, the critical time step, $\Delta t_C$ is proportional to the element size, and inversely to the dilatational wave speed [1]. This leads to simulations being restricted to $\min \{\Delta t\}$ of the element with the smallest size or highest wave speed. Initially referred to as subcycling, pioneering works allowed for the integration of multiple time steps in a single domain [2,3]. The coupling of various kinematic fields was explored, along with the stability of such algorithms [4,5]. Asynchronous variational integration is briefly mentioned as an alternative; that discretise the functional instead of the equations of motion, with varying time steps [6]. The main drawback being the high complexity of its implementation. The importance of varying, non-integer and large time step ratios was also extended to, with heterogeneous asynchronous time integration [7,8]. However, maintaining the continuity of kinematics at the interface remains a challenge, especially for all three fields [9]. In recent works, energy conserving methods have been developed, however they depart far from the CFL condition to resolve the interface conditions at consistent time steps [10]. Spatially, non-matching mesh algorithms facilitate more flexible geometric modelling [11]. Nitsche’s method has shown to weakly enforce conditions on the interfaces of non-matching meshes without additional unknowns, but commonly suffers from the sensitivity to parameters [12,13,14,15]. Following similar principles of weak continuity, Lagrange multipliers are called upon in the mortar-based methods [16,17,18,19,20]. These types of methods have proven to be very robust, however struggle to fulfil the inf-sup stability condition, and incur a large computational cost with mapping master and slave nodes [21]. In comparison, the use of localised Lagrange multipliers, introduces a frame that independently enforces compatibility constraints on each boundary [22,23,24,25,26,27]. However, as common with other methods that introduce an additional discretised interface, the construction of this interface is neither trivial or computationally cheap [28,29,30,31]. This brief review justifies the need for more efficient couplings; both temporally and spatially. Coupling algorithms that allow for varying time step ratios, whilst stepping close to the CFL condition, concertedly those that solve for non-matching meshes, without increasing the degrees of freedom, remain a hot topic of research.

2. Governing Equations of Dynamic Solids

The problem of a solid body subject to impact, is described through the partitioning of a domain as illustrated in Figure 1. The deformation is governed by the momentum balance equation acting on solid domain $\Omega$:

$$\begin{array}{c}\hfill \rho \ddot{\mathbf{u}}=\nabla ·\mathit{\sigma }+\rho \mathbf{b},\mathrm{in}\Omega \times [0,T]\end{array}$$

(1)

where $\rho$, $\ddot{\mathbf{u}}$, $\mathit{\sigma }$ and $\mathbf{b}$ denote the density, acceleration field, stress tensor and body forces. Deformation is described at time $t\in [0,T]$ for a specified constant $T>0$. Updated Lagrangian formulations of a single body are found in the following [32,33,34], here we extend this to a partitioned formulation to solve multiple solid subdomains.

Defining multiple subdomains, we state $\mathcal{B}$ is a solid body in an open region $\Omega \subset {\mathbb{R}}^3$, with its boundary denoted $𝜕\Omega$. $\Omega$ is partitioned into $\mathcal{S}$ non-overlapping subdomains:

$$\begin{array}{c}\hfill \Omega =\bigcup _{i=1}^S{\Omega }_i\mathrm{and}{\Omega }_i\cap {\Omega }_j=\varnothing \mathrm{for}i\ne j\end{array}$$

(2)

Starting from the simplest case, $\mathcal{S}=2$, for a two-subdomain partitioning, where ${\Omega }_L$ and ${\Omega }_s$ represent the large and small subdomains. The boundary between the two is defined $\Gamma$, where for matching conditions we enforce:

$$\begin{array}{c}\hfill {\ddot{\mathbf{u}}}_L={\ddot{\mathbf{u}}}_s\mathrm{on}\Gamma \end{array}$$

(3)

$$\begin{array}{c}\hfill {\mathbf{t}}_L={\mathbf{t}}_s\mathrm{on}\Gamma \end{array}$$

(4)

to ensure the continuity of acceleration $\ddot{\mathbf{u}}$ and tractions $\mathbf{t}$, as well as enforcing Dirichlet and Neumann boundary conditions. The variational formulation of the dynamic equilibrium in Equation 1 can be described for both ${\Omega }_L$ and ${\Omega }_s$ as the following:

$$\begin{array}{c}\hfill \underset{{\Omega }_L}{\int }{\rho }_L{\ddot{\mathbf{u}}}_L·\delta \dot{\mathbf{u}}d\Omega =\underset{{\Gamma }_L}{\int }{\mathbf{t}}_L·\delta \dot{\mathbf{u}}d\Gamma -\underset{{\Omega }_L}{\int }{\mathit{\sigma }}_L:\delta {\mathbf{D}}_{L}d\Omega +\underset{{\Omega }_L}{\int }{\rho }_L{\mathbf{b}}_L·\delta \dot{\mathbf{u}}d\Omega \end{array}$$

(5)

$$\begin{array}{c}\hfill \underset{{\Omega }_s}{\int }{\rho }_s{\ddot{\mathbf{u}}}_s·\delta \dot{\mathbf{u}}d\Omega =\underset{{\Gamma }_s}{\int }{\mathbf{t}}_s·\delta \dot{\mathbf{u}}d\Gamma -\underset{{\Omega }_s}{\int }{\mathit{\sigma }}_s:\delta {\mathbf{D}}_{s}d\Omega +\underset{{\Omega }_s}{\int }{\rho }_s{\mathbf{b}}_s·\delta \dot{\mathbf{u}}d\Omega \end{array}$$

(6)

where we denote a variational velocity $\delta \dot{\mathbf{u}}\in {\mathcal{V}}_0$, in a space ${\mathcal{V}}_0$ where $\forall \delta \dot{\mathbf{u}}\in H^1\left({\Omega }_i\right)$, and $\mathbf{D}$ as rate of deformation. A discrete approximation of the variational form can be reduced to the ordinary differential equations:

$$\begin{array}{c}\hfill {\mathbf{M}}_L{\ddot{\mathbf{u}}}_L={\mathbf{f}}_L^{\mathrm{ext}}-{\mathbf{f}}_L^{\mathrm{int}};{\mathbf{M}}_s{\ddot{\mathbf{u}}}_s={\mathbf{f}}_s^{\mathrm{ext}}-{\mathbf{f}}_s^{\mathrm{int}}\end{array}$$

(7)

where for subdomains ${\Omega }_L$ and ${\Omega }_s$, we sum over a number of finite elements, ${\mathcal{N}}_L$ and ${\mathcal{N}}_s$, in each subdomain:

$$\begin{array}{c}\hfill {\mathbf{M}}_L=\sum _{e=1}^{{\mathcal{N}}_L}{\int }_{{\Omega }_e}{\rho }_L{\mathbf{N}}^{\mathrm{T}}\mathbf{N}d{\Omega }_e;{\mathbf{M}}_s=\sum _{e=1}^{{\mathcal{N}}_s}{\int }_{{\Omega }_e}{\rho }_s{\mathbf{N}}^{\mathrm{T}}\mathbf{N}d{\Omega }_e\end{array}$$

(8)

$$\begin{array}{c}\hfill {\mathbf{f}}_L^{\mathrm{ext}}=\sum _{e=1}^{{\mathcal{N}}_L}{\int }_{{\Omega }_e}{\mathbf{N}}^{\mathrm{T}}{\mathbf{t}}_{L}d{\Omega }_e;{\mathbf{f}}_s^{\mathrm{ext}}=\sum _{e=1}^{{\mathcal{N}}_s}{\int }_{{\Omega }_e}{\mathbf{N}}^{\mathrm{T}}{\mathbf{t}}_{s}d{\Omega }_e\end{array}$$

(9)

$$\begin{array}{c}\hfill {\mathbf{f}}_L^{\mathrm{int}}=\sum _{e=1}^{{\mathcal{N}}_L}{\int }_{{\Omega }_e}{\mathbf{B}}^{\mathrm{T}}{\mathit{\sigma }}_{L}d{\Omega }_e{\mathbf{f}}_s^{\mathrm{int}}=\sum _{e=1}^{{\mathcal{N}}_s}{\int }_{{\Omega }_e}{\mathbf{B}}^{\mathrm{T}}{\mathit{\sigma }}_{s}d{\Omega }_e\end{array}$$

(10)

The Lagrangian shape functions are represented by $\mathbf{N}$, with their derivatives denoted $\mathbf{B}$. As common within the explicit finite element method, $\mathbf{M}$ is lumped for each subdomain, with ${\mathbf{f}}^{\mathrm{ext}}$ and ${\mathbf{f}}^{\mathrm{int}}$ both computed with vectors too. We elect to use the leapfrog time integration scheme to step through time, staggering the solution of each kinematic quantity such that:

$$\begin{array}{c}\hfill {\ddot{\mathbf{u}}}_L^n={\mathbf{M}}_L^{-1}({\mathbf{f}}_L^{\mathrm{ext}}-{\mathbf{f}}_L^{\mathrm{int}});{\ddot{\mathbf{u}}}_s^n={\mathbf{M}}_s^{-1}({\mathbf{f}}_s^{\mathrm{ext}}-{\mathbf{f}}_s^{\mathrm{int}})\end{array}$$

(11)

$$\begin{array}{c}\hfill {\dot{\mathbf{u}}}_L^{n+1/2}={\dot{\mathbf{u}}}_L^{n-1/2}+{\ddot{\mathbf{u}}}_L^n·\Delta t_L;{\dot{\mathbf{u}}}_s^{n+1/2}={\dot{\mathbf{u}}}_s^{n-1/2}+{\ddot{\mathbf{u}}}_s^n·\Delta t_s\end{array}$$

(12)

$$\begin{array}{c}\hfill {\mathbf{u}}_L^{n+1}={\mathbf{u}}_L^n+{\dot{\mathbf{u}}}_L^{n+1/2}·\Delta t_L;{\mathbf{u}}_s^{n+1}={\mathbf{u}}_s^n+{\dot{\mathbf{u}}}_s^{n+1/2}·\Delta t_s\end{array}$$

(13)

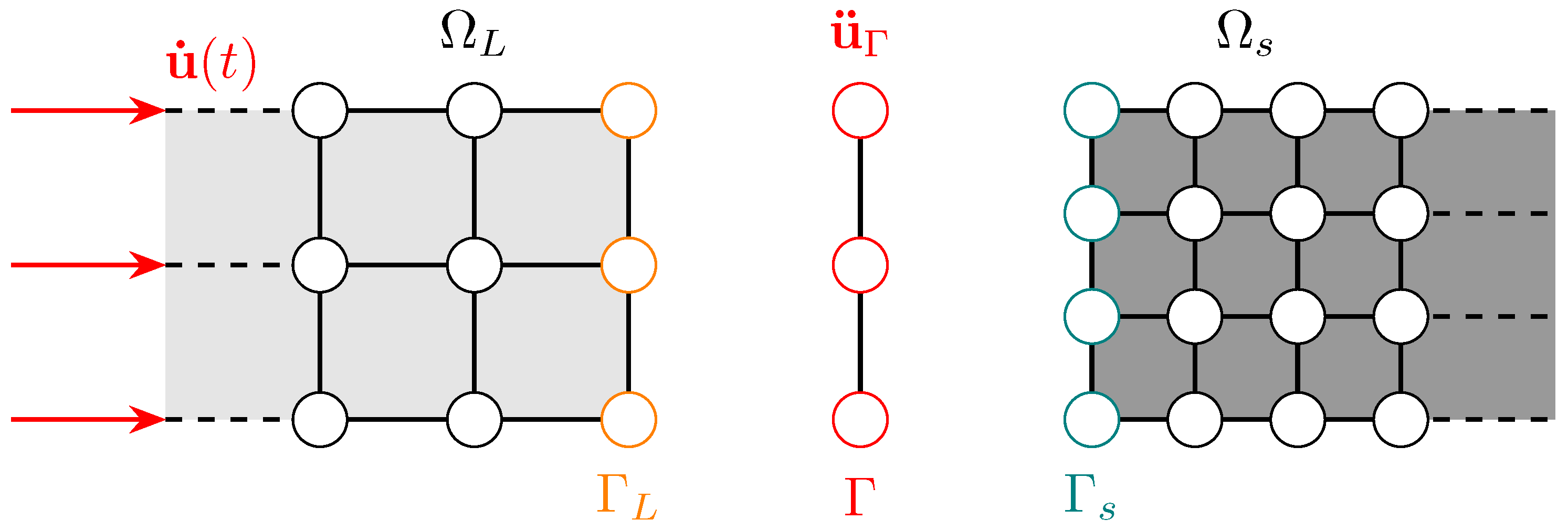
noting that a diagonal mass matrix allows for a direct computation of acceleration. Velocity $\dot{\mathbf{u}}$ is computed on the half time step, with displacement $\mathbf{u}$ found each full time step. Next we summarise the temporal coupling, enabled by multi-time step (MTS) integration.

3. Multi-Time Step Integration

Multi-time stepping enables partitioned subdomains ${\Omega }_L$ and ${\Omega }_s$ to integrate with $\Delta t_L$ and $\Delta t_s$, respectively. However, to allow for this difference in time steps, special attention must be given to the solution of the interface $\Gamma$. Crucially, the conditional stability of explicit methods require an element’s time step to obey the CFL condition for a linear undamped system:

$$\Delta t_C={\displaystyle \frac{2}{{\omega }_C}}\le \underset{e}{min}\left({\displaystyle \frac{h_e}{c_e}}\right)$$

(14)

Here we represent $\Delta t_C$ as the critical time step, ${\omega }_C$ as the maximum eigenfrequency, $h_e$ as the characteristic length of an element, and $c_e$ the dilatational (longitudinal) wave speed.

3.1. Salient Multi-Time Stepping Features

The asynchronous integration is enabled with three important groups of computations. The first being the explicit computation of the acceleration on the interface $\Gamma$:

$$\begin{array}{c}\hfill {\mathbf{M}}_{\Gamma }=\left({\mathbf{C}}_s^{\mathrm{T}}{\mathbf{M}}_s{\mathbf{C}}_s\right)+\left({\mathbf{C}}_L^{\mathrm{T}}{\mathbf{M}}_L{\mathbf{C}}_L\right)\end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathbf{f}}_{\Gamma }^{\mathrm{int}}={\mathbf{C}}_s^{\mathrm{T}}{\mathbf{f}}_s^{\mathrm{int}}+{\mathbf{C}}_L^{\mathrm{T}}{\mathbf{f}}_L^{\mathrm{int}};{\mathbf{f}}_{\Gamma }^{\mathrm{ext}}={\mathbf{C}}_s^{\mathrm{T}}{\mathbf{f}}_s^{\mathrm{ext}}+{\mathbf{C}}_L^{\mathrm{T}}{\mathbf{f}}_L^{\mathrm{ext}}\end{array}$$

(16)

We define indicator matrices (vectors in 1-D) for each subdomain $\mathbf{C}$ to identify the degrees of freedom on the interface of subdomains. These summations provide the ingredients for computing the interface acceleration as:

$$\begin{array}{c}\hfill {\ddot{\mathbf{u}}}_{\Gamma }={\mathbf{M}}_{\Gamma }^{-1}({\mathbf{f}}_{\Gamma }^{\mathrm{ext}}-{\mathbf{f}}_{\Gamma }^{\mathrm{int}})\end{array}$$

(17)

where we compute ${\ddot{\mathbf{u}}}_{\Gamma }$ at each large time step $\Delta t_L$. The integration of the subdomains is controlled by the definition of the time step ratios. Suppose the two subdomains begin at a similar point in time $t_L^N=t_s^n$ where N and n are the small and large steps respectively. The time after the maximum stable integration step on each subdomain is referred to as the trial time $t_T$, such that:

$$\begin{array}{c}\hfill t_{TL}^{N+1}=t_L+\Delta t_{CL};t_{Ts}^{n+k}=t_s+\Delta t_{Cs}\end{array}$$

(18)

where for every $\Delta t_L$, the number of small time steps k elapse since the last point in time where subdomains are equal in time. Now we can define the current time step ratio, $t_{ratio}^{n+k}$, and next time step ratio, $t_{ratio}^{n+k+1}$ for the advancement of ${\Omega }_s$ with:

$$\begin{array}{c}\hfill t_{ratio}^{n+k}={\displaystyle \frac{t_s^{n+k}-t_L^N}{t_{TL}^{N+1}-t_L^N}};t_{ratio}^{n+k+1}={\displaystyle \frac{(t_s^{n+k}+\Delta t_s^{n+k})-t_L^N}{t_{TL}^{N+1}-t_L^N}}\end{array}$$

(19)

Starting from each common time step with the integration of ${\Omega }_s$, the number of small time steps $\Delta t_s$ is determined by the evaluation of time step ratios $t_{ratio}^{n+k}$ and $t_{ratio}^{n+k+1}$. If the condition of $t_{ratio}^{n+k+1}\le 1$ or ($t_{ratio}^{n+k}\le 1$ and $t_{ratio}^{n+k+1}\le 1$) is satisfied, further steps on $\Delta t_s$ can proceed before integrating ${\Omega }_L$ over $\Delta t_L$. As a consequence of subdomains integrating over their own respective time step, we ensure that the proposed method still finds a common time between all subdomains. Following the small trial time $t_{Ts}$ exceeding the large trial time $t_{TL}$, the method proceeds to compute two additional ratios ${\alpha }_L$ and ${\alpha }_s$. These denote the reduction factors required to maintain the subdomains in synchronisation where $0\le \alpha \le 1$. We compute:

$$\begin{array}{c}\hfill {\alpha }_L=1-{\displaystyle \frac{(t_{TL}^N-t_s^{n+k})}{(t_{TL}^{N+1}-t_L^N)}};{\alpha }_s=1-{\displaystyle \frac{(t_{Ts}^{n+k}-t_{TL}^{N+1})}{(t_{Ts}^{n+k+1}-t_s^{n+k})}}\end{array}$$

(20)

Through computing $\alpha$ on both subdomains, we can compare reduction factors, such that:

$$\begin{array}{c}\hfill t_L^{N+1}=t_s^{n+k}=\left\{\begin{array}{c}{t}_s^n+\sum _{k=0}^{k-1}\Delta t_{Cs}^{n+k}+{\alpha }_s·\Delta t_{Cs}^{n+k},{\alpha }_s>{\alpha }_L\hfill \\ t_s^n+{\alpha }_L·\Delta t_{CL}^N,{\alpha }_L\ge {\alpha }_s\hfill \end{array}\right.\end{array}$$

(21)

where we look to reduce the time step of the subdomain closest to CFL condition. In the following section we summarise the multi-time stepping algorithm, with each of these key features, as well as its implementation.

3.2. Summary of Temporal Algorithm

We provide an overview of the method required to integrate ${\Omega }_L$ and ${\Omega }_s$ with $\Delta t_L$ and $\Delta t_s$. It shows a single large step N, exemplifying each of the features mentioned above. A note that $TOL=1$e-6 is used for when $\Delta t_L\approx \Delta t_s$, and computation of ${\mathbf{M}}_{\Gamma }$ in Equation 15 is only required at $t=0$ for a mass-conserving problem.

Algorithm 1 Summary of Algorithm for Coupling in Time from N to $N+1$

1: procedure a two-subdomain multi time integration step   2:     while $t_{ratio}^{n+k+1}\le 1$ or ($t_{ratio}^{n+k}\le 1$ and $t_{ratio}^{n+k+1}\le 1+$TOL ) do   3:         Integrate subdomain ${\Omega }_s$ with ${\ddot{\mathbf{u}}}_{\Gamma }$ and compute force vectors ${\mathbf{f}}_s^{\mathrm{int}},{\mathbf{f}}_s^{\mathrm{ext}}$ over $\Delta t_s$   4:         Compute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$   5:     Compute time step reduction factors ${\alpha }_L,{\alpha }_s$   6:     if ${\alpha }_L\ge {\alpha }_s$ then   7:         $\Delta t_L={\alpha }_L·\Delta t_L$   8:     else   9:         $\Delta t_s={\alpha }_s·\Delta t_s$ 10:         Integrate subdomain ${\Omega }_s$ with ${\ddot{\mathbf{u}}}_{\Gamma }$ and recompute force vectors ${\mathbf{f}}_s^{\mathrm{int}},{\mathbf{f}}_s^{\mathrm{ext}}$ over $\Delta t_s$ 11:         Recompute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$ 12:     Integrate subdomain ${\Omega }_L$ with ${\ddot{\mathbf{u}}}_{\Gamma }$ and compute force vectors ${\mathbf{f}}_L^{\mathrm{int}},{\mathbf{f}}_L^{\mathrm{ext}}$ over $\Delta t_L$ 13:     Compute interface acceleration ${\ddot{\mathbf{u}}}_{\Gamma }$ with Eqs. 15 - 17 for next time step 14:     Recompute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$

The proposed method is implemented in an open-source python code, found in the following repository https://github.com/kinfungchan/multi-time-step-integration. It contains re-implementations of methods from literature for the two-subdomain case [9,10]. Whilst we depict the case of just two subdomains, the algorithm can be extended to multiple by processing subdomains as pairs as shown in [35].

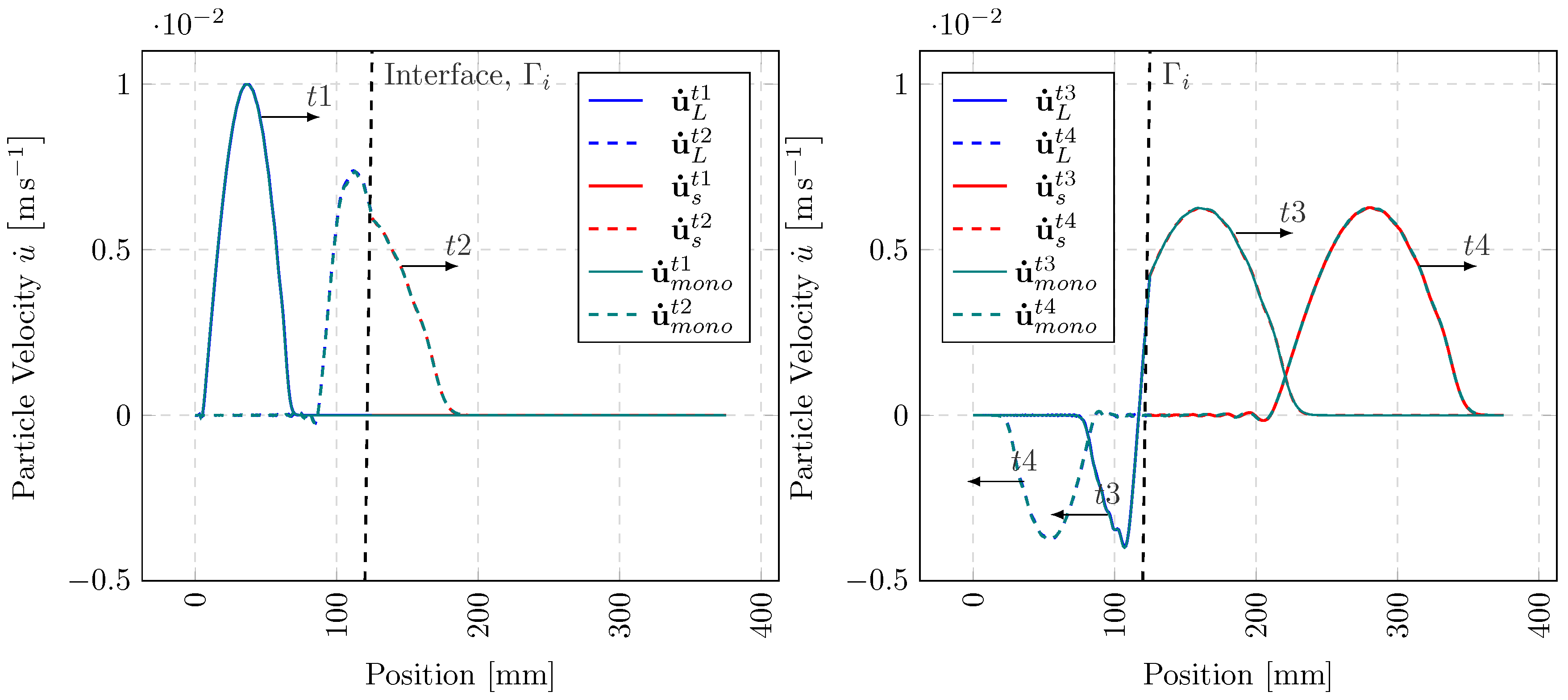
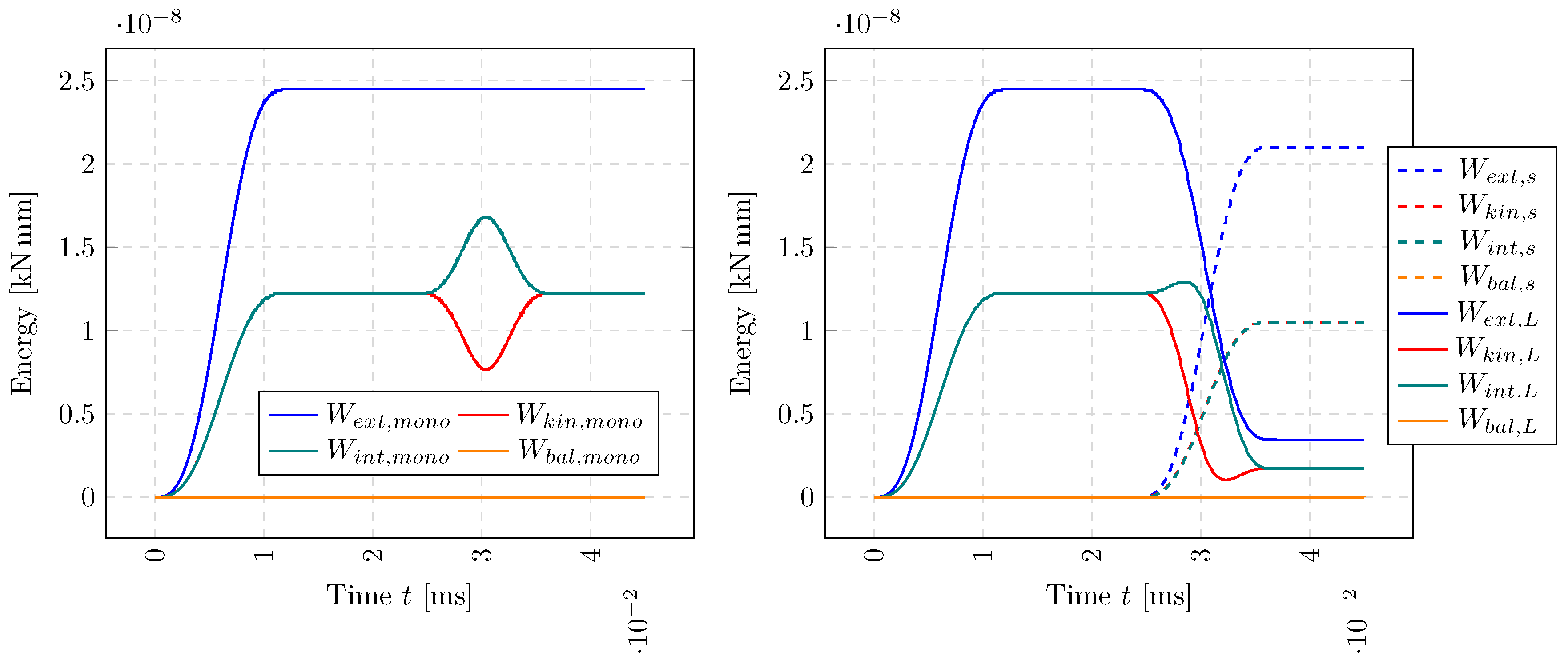
3.3. Numerical Examples in Time

We present a numerical example in 1-D, with the elastic wave propagation through a heterogeneous bar. Suppose the domain $\Omega$ is split into two subdomains ${\Omega }_L$ and ${\Omega }_s$ of similar discretisation, with isotropic elastic properties of $E_L=207$ GPa, $E_s=1000$ GPa and ${\rho }_L={\rho }_s=7.83\times {10}^{-6}$ ${\mathrm{kgmm}}^{-3}$. These material properties result in a non-integer $m=2.19$, where the time step ratio is solely driven by the dissimilar material properties. Figure 2 depicts the bar configuration. The velocity boundary condition is applied to ${\Omega }_L$ at $x=0$ with $\dot{u}\left(t\right)=0.01\sin \left(2\pi {\omega }_{L}t\right)$ ${\mathrm{ms}}^{-1}$ where we define a half sine wave with a frequency of ${\omega }_L={\left(125((7.83\times {10}^{-6})/207)\right)}^{-1}$ ${\mathrm{rads}}^{-1}$. The difference in material impedance results in a portion of the incident wave being transmitted and the remainder reflected in the opposite direction.

In Figure 3, a comparison between the coupled solution (${\Omega }_L$ with ${\Omega }_s$) and the monolithic (single time step) solution is presented at four separate time stamps. The multi-time step solution solves ${\dot{\mathbf{u}}}_L$ and ${\dot{\mathbf{u}}}_s$ over $\Delta t_L$ and $\Delta t_s$, whereas ${\dot{\mathbf{u}}}_{mono}$ is limited by $\Delta t_s$. Consequently, for $m=2.19$, our method reduces the number of integration steps on ${\Omega }_L$ by half. From prescription of the full wave at $t1$, through to the transmission and reflection of the wave at $t4$, the MTS solution aligns very well with the single time step solution, despite the halving the number of large time steps. This reduction in computational effort is even more prominent for highly heterogeneous configurations, as well as variance in spatial discretisation.

For the above simulation we also compute the energy components of each subdomain with the following:

$$\begin{array}{c}\hfill W_{\mathrm{ext}}^{n+1}=W_{\mathrm{ext}}^n+{\displaystyle \frac{\Delta t_i^{n+1/2}}{2}}{\left({\dot{\mathbf{u}}}_i^{n+1/2}\right)}^{\mathrm{T}}({\mathbf{f}}_{\mathrm{ext}}^n+{\mathbf{f}}_{\mathrm{ext}}^{n+1})=W_{\mathrm{ext}}^n+{\displaystyle \frac{1}{2}}\Delta {\mathbf{u}}_i^{\mathrm{T}}({\mathbf{f}}_{\mathrm{ext}}^n+{\mathbf{f}}_{\mathrm{ext}}^{n+1})\end{array}$$

(22)

$$\begin{array}{c}\hfill W_{\mathrm{int}}^{n+1}=W_{\mathrm{int}}^n+{\displaystyle \frac{\Delta t_i^{n+1/2}}{2}}{\left({\dot{\mathbf{u}}}_i^{n+1/2}\right)}^{\mathrm{T}}({\mathbf{f}}_{\mathrm{int}}^n+{\mathbf{f}}_{\mathrm{int}}^{n+1})=W_{\mathrm{int}}^n+{\displaystyle \frac{1}{2}}\Delta {\mathbf{u}}_i^{\mathrm{T}}({\mathbf{f}}_{\mathrm{int}}^n+{\mathbf{f}}_{\mathrm{int}}^{n+1})\end{array}$$

(23)

$$\begin{array}{c}\hfill W_{\mathrm{kin}}^n={\displaystyle \frac{1}{2}}{\left({\dot{\mathbf{u}}}_i^{n+1/2}\right)}^{\mathrm{T}}\mathbf{M}{\dot{\mathbf{u}}}_i^{n+1/2}\end{array}$$

(24)

where n can be interchanged with N when evaluating ${\Omega }_L$. The balance of energy can be evaluated in a similar way to the works of Neal and Belytschko [3], with the following:

$$\begin{array}{c}\hfill |W_{\mathrm{ext}}-W_{\mathrm{int}}+W_{\mathrm{kin}}|\le ||W_{bal}\left|\right|\end{array}$$

(25)

In Figure 4 we show each of the components of energy and its overall balance. For both monolithic and multi-time step solutions a smooth transition of energy is observed as the wave interacts with $\Gamma$. Remarkably, as the temporal coupling is enforced, the $W_{bal}$ for both ${\Omega }_L$ and ${\Omega }_s$ is of the order $1\times {10}^{-13}$ kNmm, significantly below each of the components at $1\times {10}^{-8}$ kNmm. This numerical example captures the propagation of a smooth pulse, however severe loading cases, as well as a 3-D problems, remain ongoing work.

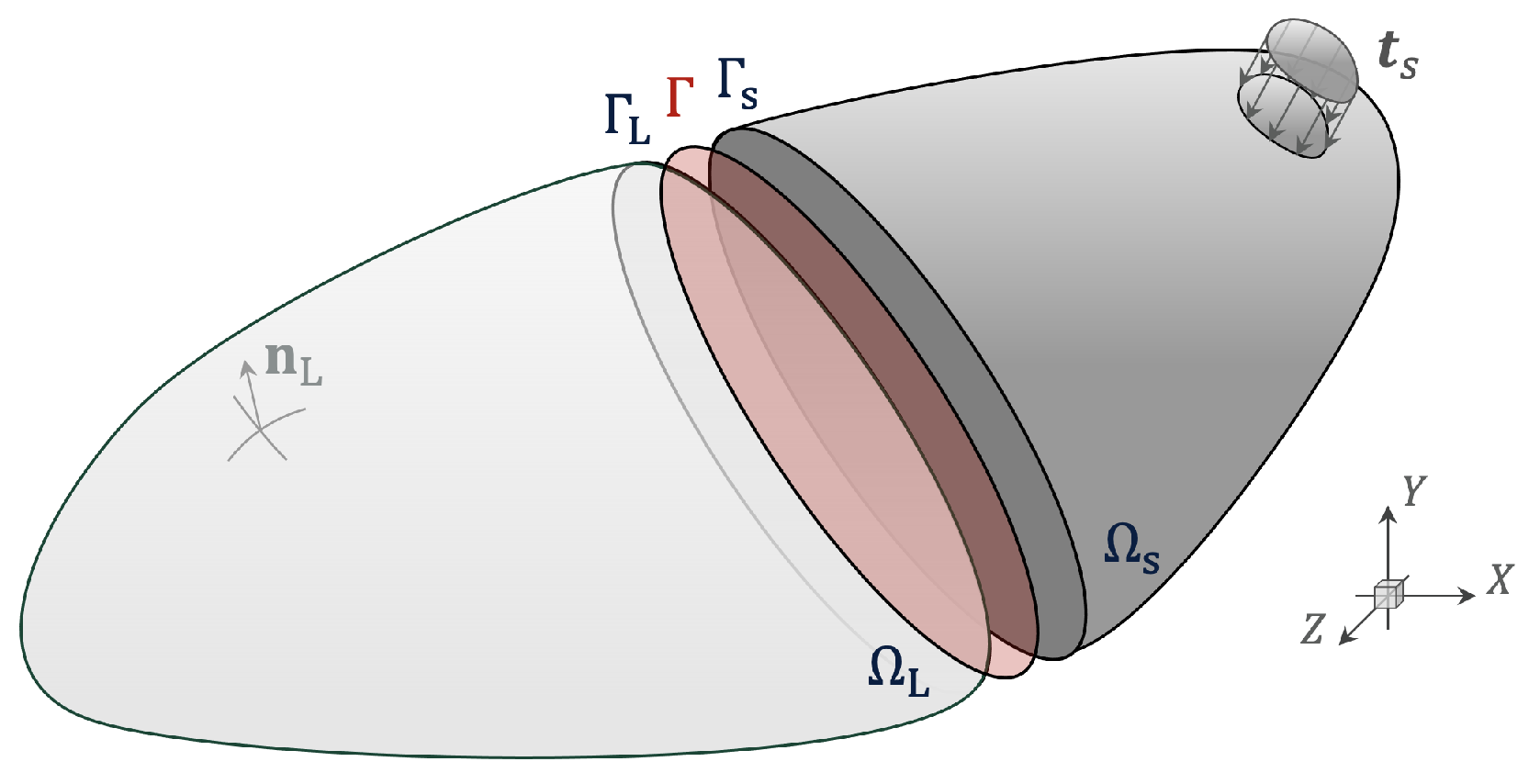
4. Solving Non-Matching Meshes

The problem of non-matching meshes is commonly found when simulating the dynamical behaviour of solids. We present an algorithm, combined with multi-time stepping, that relaxes the constraint of these conforming nodes, allowing for a coarser representation of a subdomain to be utilised; hence reducing the computational overhead.

4.1. Combined Spatial and Temporal Coupling

The following section follows on from governing equations defined in Section 2, however we now allow for the non-overlapping interface $\Gamma ={\Gamma }_L\cap {\Gamma }_s$ to consist of two separate spatial discretisations. Their compatibility is maintained such that:

$$\begin{array}{c}\hfill {\ddot{\mathbf{u}}}_{\Gamma L}\left({\mathbf{C}}_L{\mathbf{x}}_L\right)={\ddot{\mathbf{u}}}_{\Gamma s}\left({\mathbf{C}}_s{\mathbf{x}}_L\right)={\ddot{\mathbf{u}}}_{\Gamma }\left({\mathbf{x}}_{\Gamma }\right)\end{array}$$

(26)

$$\begin{array}{c}\hfill {\mathbf{t}}_{\Gamma L}\left({\mathbf{C}}_L{\mathbf{x}}_L\right)={\mathbf{t}}_{\Gamma s}\left({\mathbf{C}}_s{\mathbf{x}}_s\right)={\mathbf{t}}_{\Gamma }\left({\mathbf{x}}_{\Gamma }\right)\end{array}$$

(27)

where positions use incidence $\mathbf{C}$ matrix, such that ${\mathbf{C}}_L{\mathbf{x}}_L\in {\Gamma }_L$ and ${\mathbf{C}}_s{\mathbf{x}}_s\in {\Gamma }_s$ for each subdomain, and externally assembled interface contains ${\mathbf{x}}_{\Gamma }\in \Gamma$ to describe the common boundary between the subdomains. The total virtual power can be summated for two subdomains to give $\delta P=\delta P_L+\delta P_s+\delta P_{\Gamma }$, where a general form is obtained:

$$\begin{array}{c}\hfill \delta P=\delta {\dot{\mathbf{u}}}_L^{\mathrm{T}}\{{\mathbf{f}}_L^{\mathrm{int}}-{\mathbf{f}}_L^{\mathrm{ext}}+{\mathbf{M}}_L{\ddot{\mathbf{u}}}_L+{\mathbf{N}}_L^{\mathrm{T}}{\mathbf{f}}_{\Gamma L}\}+\delta {\dot{\mathbf{u}}}_s^{\mathrm{T}}\{{\mathbf{f}}_s^{\mathrm{int}}-{\mathbf{f}}_s^{\mathrm{ext}}+{\mathbf{M}}_s{\ddot{\mathbf{u}}}_s+{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{f}}_{\Gamma s}\}\\ \hfill +\delta {\mathbf{f}}_{\Gamma L}^{\mathrm{T}}\{{\mathbf{N}}_L^{\mathrm{T}}{\dot{\mathbf{u}}}_{\Gamma L}-{\mathbf{L}}_L^{\mathrm{T}}{\dot{\mathbf{u}}}_{\Gamma }\}+\delta {\mathbf{f}}_{\Gamma s}^{\mathrm{T}}\{{\mathbf{N}}_s^{\mathrm{T}}{\dot{\mathbf{u}}}_{\Gamma s}-{\mathbf{L}}_s^{\mathrm{T}}{\dot{\mathbf{u}}}_{\Gamma }\}-\delta {\dot{\mathbf{u}}}_{\Gamma }^{\mathrm{T}}\{{\mathbf{N}}_L^{\mathrm{T}}{\mathbf{f}}_{\Gamma L}+{\mathbf{N}}_s^{\mathrm{T}}{\mathbf{f}}_{\Gamma s}\}\end{array}$$

(28)

where variation in velocity coupling force on the interface $\dot{\mathbf{u}}$ and ${\mathbf{f}}_{\Gamma i}$ are accounted for. ${\mathbf{N}}_i^{\mathrm{T}}$ and ${\mathbf{L}}_i$ are interpolation (or prolongation), and incidence operators ($\Gamma$ to ${\Omega }_i$), respectively. To map to the interface we describe this spatial coupling operator ${\mathbf{N}}_i$ in more detail:

$$\begin{array}{c}\hfill {\mathbf{N}}_i\in {\mathbb{R}}^{{\mathcal{N}}_{\Gamma i}\times {\mathcal{N}}_{\Gamma }}\end{array}$$

(29)

with dimensions determined by ${\mathcal{N}}_{\Gamma i}$ and ${\mathcal{N}}_{\Gamma }$; as the number of nodes on the interface of the subdomain ${\Omega }_i$, and the number of nodes on the interface $\Gamma$, respectively. Therefore, ${\mathbf{N}}_{\Gamma }$ interpolates using Lagrangian shape functions for the two subdomains ${\Omega }_L$ and ${\Omega }_s$ as:

$$\begin{array}{c}\hfill {\mathbf{N}}_{\Gamma }\left(\mathbf{x}\right)=\delta ({\mathbf{x}}_{\Gamma }-{\mathbf{x}}_{\Gamma i}),\mathrm{for}i=L,s\end{array}$$

(30)

where $\delta$ is viewed as a dirac Delta function for coincident nodes. It is convenient to define a restriction operator ${\mathbf{R}}_i\in {\mathbb{R}}^{{\mathcal{N}}_{\Gamma }\times {\mathcal{N}}_{\Gamma i}}$ as the transpose of ${\mathbf{N}}_i$, to map both forces and mass from subdomain interfaces ${\Gamma }_L$ and ${\Gamma }_s$ onto $\Gamma$. The summation on the interfaces now become:

$$\begin{array}{c}\hfill {\mathbf{M}}_{\Gamma }={\mathbf{R}}_L{\mathbf{C}}_L^{\mathrm{T}}{\mathbf{M}}_L+{\mathbf{R}}_s{\mathbf{C}}_s^{\mathrm{T}}{\mathbf{M}}_s={\mathbf{R}}_L{\mathbf{M}}_{\Gamma L}+{\mathbf{R}}_s{\mathbf{M}}_{\Gamma s}\end{array}$$

(31)

$$\begin{array}{c}\hfill {\mathbf{f}}_{\Gamma }^{\mathrm{int}}={\mathbf{R}}_L{\mathbf{C}}_L^{\mathrm{T}}{\mathbf{f}}_L^{\mathrm{int}}+{\mathbf{R}}_s{\mathbf{C}}_s^{\mathrm{T}}{\mathbf{f}}_s^{\mathrm{int}}={\mathbf{R}}_L{\mathbf{f}}_{\Gamma L}^{\mathrm{int}}+{\mathbf{R}}_s{\mathbf{f}}_{\Gamma s}^{\mathrm{int}}\end{array}$$

(32)

$$\begin{array}{c}\hfill {\mathbf{f}}_{\Gamma }^{\mathrm{ext}}={\mathbf{R}}_L{\mathbf{C}}_L^{\mathrm{T}}{\mathbf{f}}_L^{\mathrm{ext}}+{\mathbf{R}}_s{\mathbf{C}}_s^{\mathrm{T}}{\mathbf{f}}_s^{\mathrm{ext}}={\mathbf{R}}_L{\mathbf{f}}_{\Gamma L}^{\mathrm{ext}}+{\mathbf{R}}_s{\mathbf{f}}_{\Gamma s}^{\mathrm{ext}}\end{array}$$

(33)

where we compute mass ${\mathbf{M}}_{\Gamma }$, internal force ${\mathbf{f}}_{\Gamma }^{\mathrm{int}}$ and external force ${\mathbf{f}}_{\Gamma }^{\mathrm{ext}}$ to allow for the explicit computation of ${\ddot{\mathbf{u}}}_{\Gamma }$ in Equation 17 to be recalled. These operators are analogous to concepts in multigrid methods and localised Lagrange multipliers (LLMs) [36,37]. Subsequently, we map ${\ddot{\mathbf{u}}}_{\Gamma }$ from $\Gamma$ back to the subdomains:

$$\begin{array}{c}\hfill {\ddot{\mathbf{u}}}_{\Gamma L}={\mathbf{N}}_L{\ddot{\mathbf{u}}}_{\Gamma };{\ddot{\mathbf{u}}}_{\Gamma s}={\mathbf{N}}_s{\ddot{\mathbf{u}}}_{\Gamma }\end{array}$$

(34)

We illustrate a non-matching mesh in Figure 5 and compute its operators through exemplifying a linear isoparametric mapping in 2-D, where $\Gamma$ is discretised with line elements to depict the simplicity of this coupling.

For the interpolation matrix, we elucidate that from $\Gamma$ to ${\Gamma }_L$ the mapping is simply one-to-one and ${\mathbf{N}}_L$ will always take the form of an identity matrix ${\Omega }_L$, whereas ${\mathbf{N}}_s$ requires computation of the shape functions:

$$\begin{array}{c}\hfill {\mathbf{N}}_L=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right];{\mathbf{N}}_s=\left[\begin{array}{ccc}1& 0& 0\\ 1/3& 2/3& 0\\ 0& 2/3& 1/3\\ 0& 0& 1\end{array}\right];{\mathbf{R}}_L={\mathbf{N}}_L^{\mathrm{T}};{\mathbf{R}}_s={\mathbf{N}}_s^{\mathrm{T}}\end{array}$$

(35)

where, for this simple case, it can also be shown that the restriction is the transpose of the interpolation. The interface $\Gamma$ is assumed to share the same geometrical description on both subdomain interfaces ${\Gamma }_L$ and ${\Gamma }_s$, without overlap or separation. The spatial and temporal methods are combined to give the following algorithm:

Algorithm 2 Summary of Non-Matching Mesh Algorithm with Multi-Time Stepping

1: procedure integrate a two-domain non-matching mesh with MTS   2:     while $t_{ratio}^{n+k+1}\le 1$ or ($t_{ratio}^{n+k}\le 1$ and $t_{ratio}^{n+k+1}\le 1+TOL$) do   3:         Compute ${\ddot{\mathbf{u}}}_{{\Gamma }_s}$ with operator ${\mathbf{N}}_s$ in Eq. 34 on ${\Gamma }_s$   4:         Integrate small domain ${\Omega }_s$ and compute vectors ${\mathbf{f}}_s^{\mathrm{int}},{\mathbf{f}}_s^{\mathrm{ext}}$   5:         Compute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$   6:     Compute time step reduction factors ${\alpha }_L,{\alpha }_s$   7:     if ${\alpha }_L\ge {\alpha }_s$ then   8:         $\Delta t_L={\alpha }_L·\Delta t_L$   9:     else 10:         $\Delta t_s={\alpha }_s·\Delta t_s$ 11:         Compute ${\ddot{\mathbf{u}}}_{{\Gamma }_s}$ with operator ${\mathbf{N}}_s$ in Eq. 34 on ${\Gamma }_s$ 12:         Integrate small domain ${\Omega }_s$ and compute vectors ${\mathbf{f}}_s^{\mathrm{int}},{\mathbf{f}}_s^{\mathrm{ext}}$ 13:         Recompute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$ 14:     Compute ${\ddot{\mathbf{u}}}_{{\Gamma }_L}$ with operator ${\mathbf{N}}_L$ in Eq. 34 on ${\Gamma }_L$ 15:     Integrate large domain ${\Omega }_L$ and compute vectors ${\mathbf{f}}_L^{\mathrm{int}},{\mathbf{f}}_L^{\mathrm{ext}}$ 16:     Summate kinetics with ${\mathbf{R}}_L,{\mathbf{R}}_s,{\mathbf{C}}_L,{\mathbf{C}}_s$ to find ${\mathbf{M}}_{\Gamma },{\mathbf{f}}_{\Gamma }^{\mathrm{int}}$ and ${\mathbf{f}}_{\Gamma }^{\mathrm{ext}}$ with Eq. 31 - 33 17:     Compute trial times $t_{Ts}^{n+k}$, $t_{TL}^{N+1}$ and time step ratios $t_{ratio}^{n+k}$, $t_{ratio}^{n+k+1}$

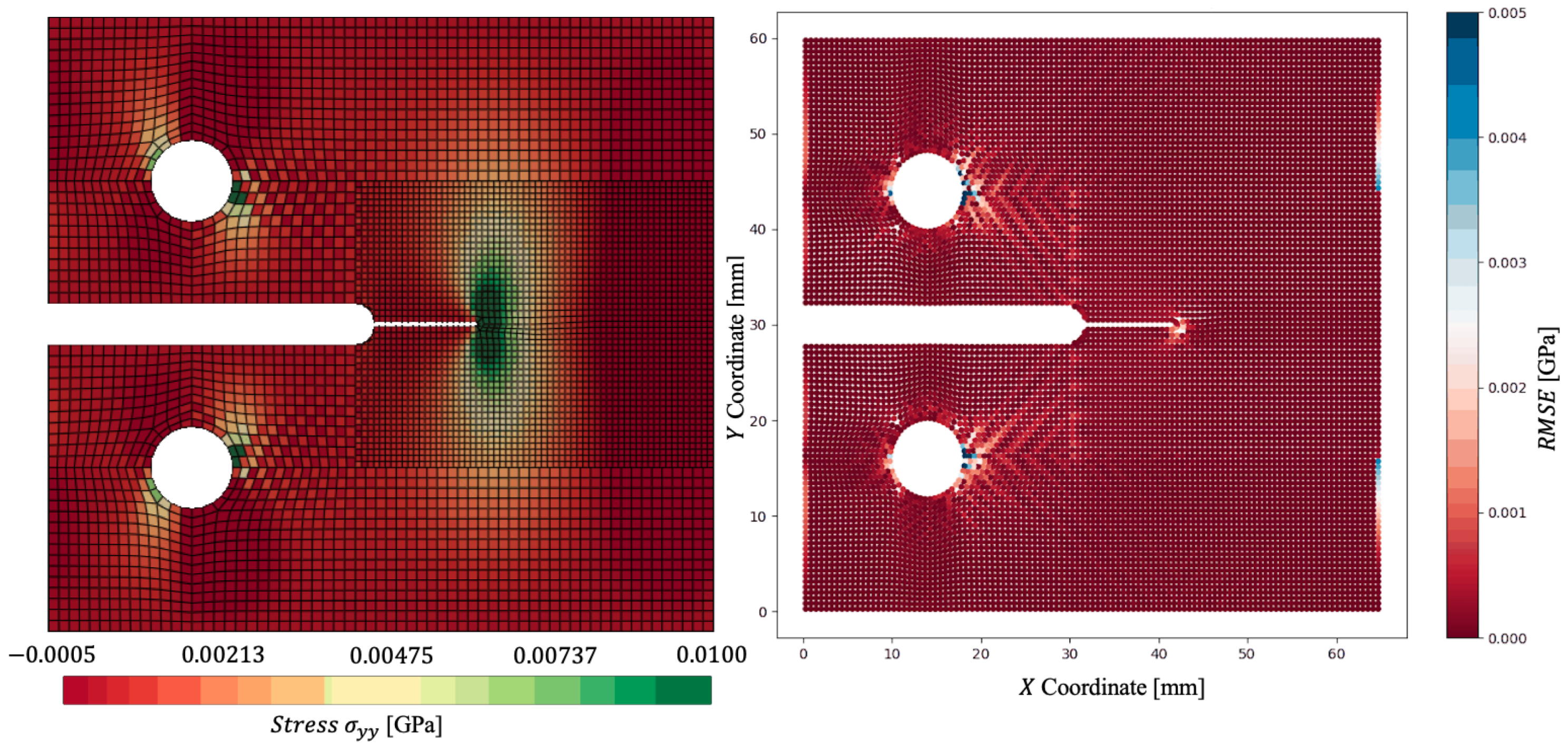
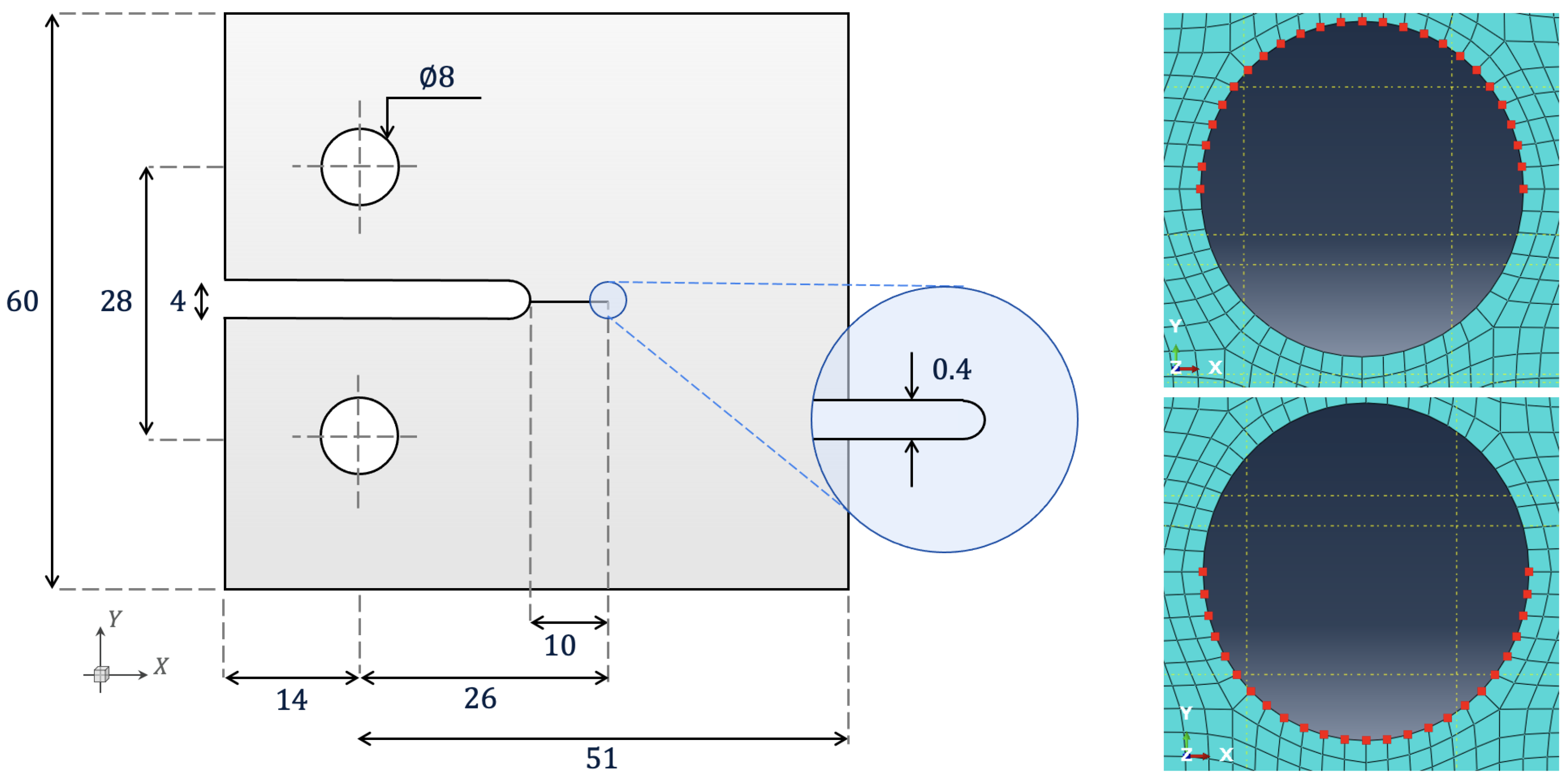
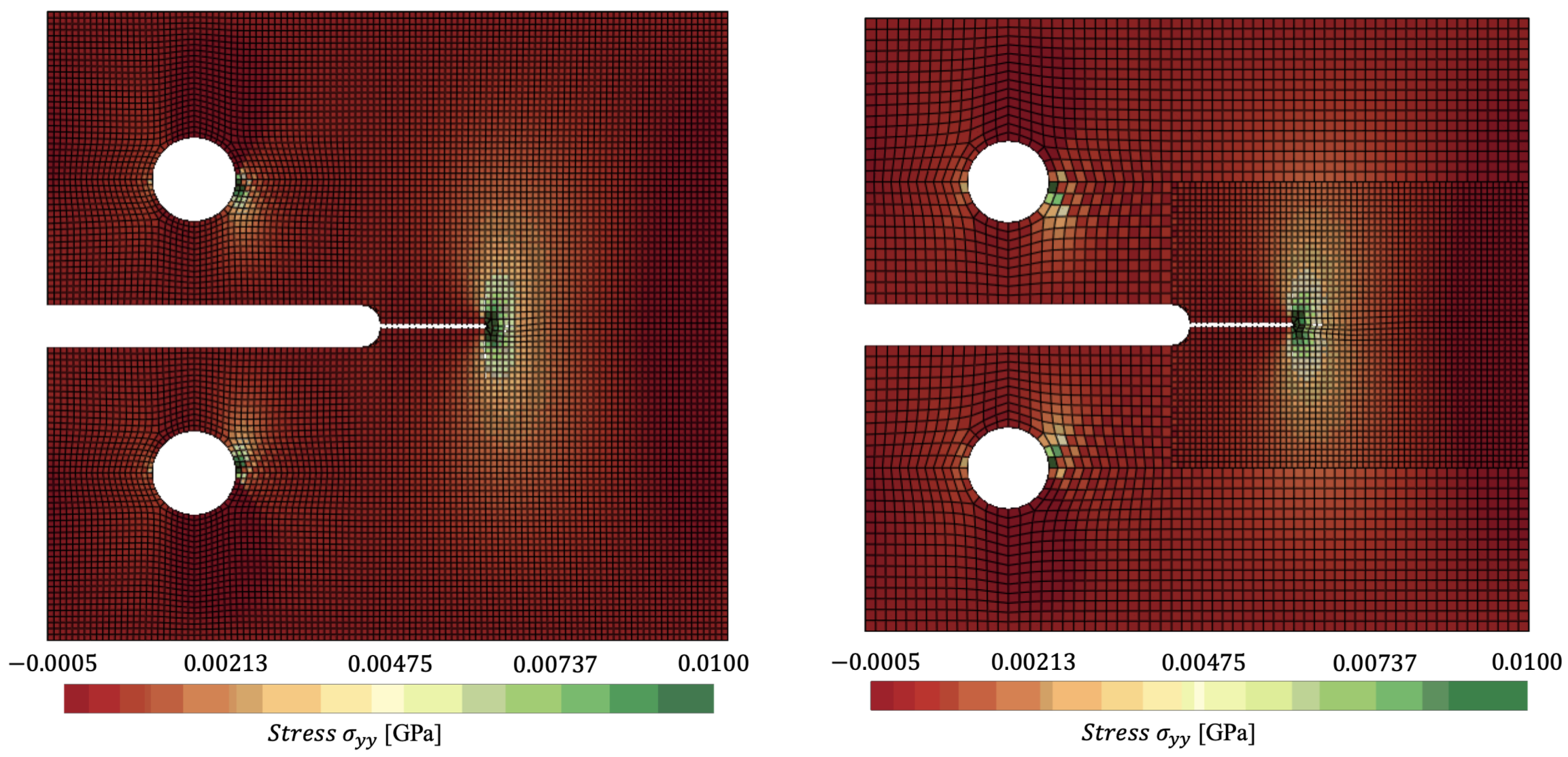
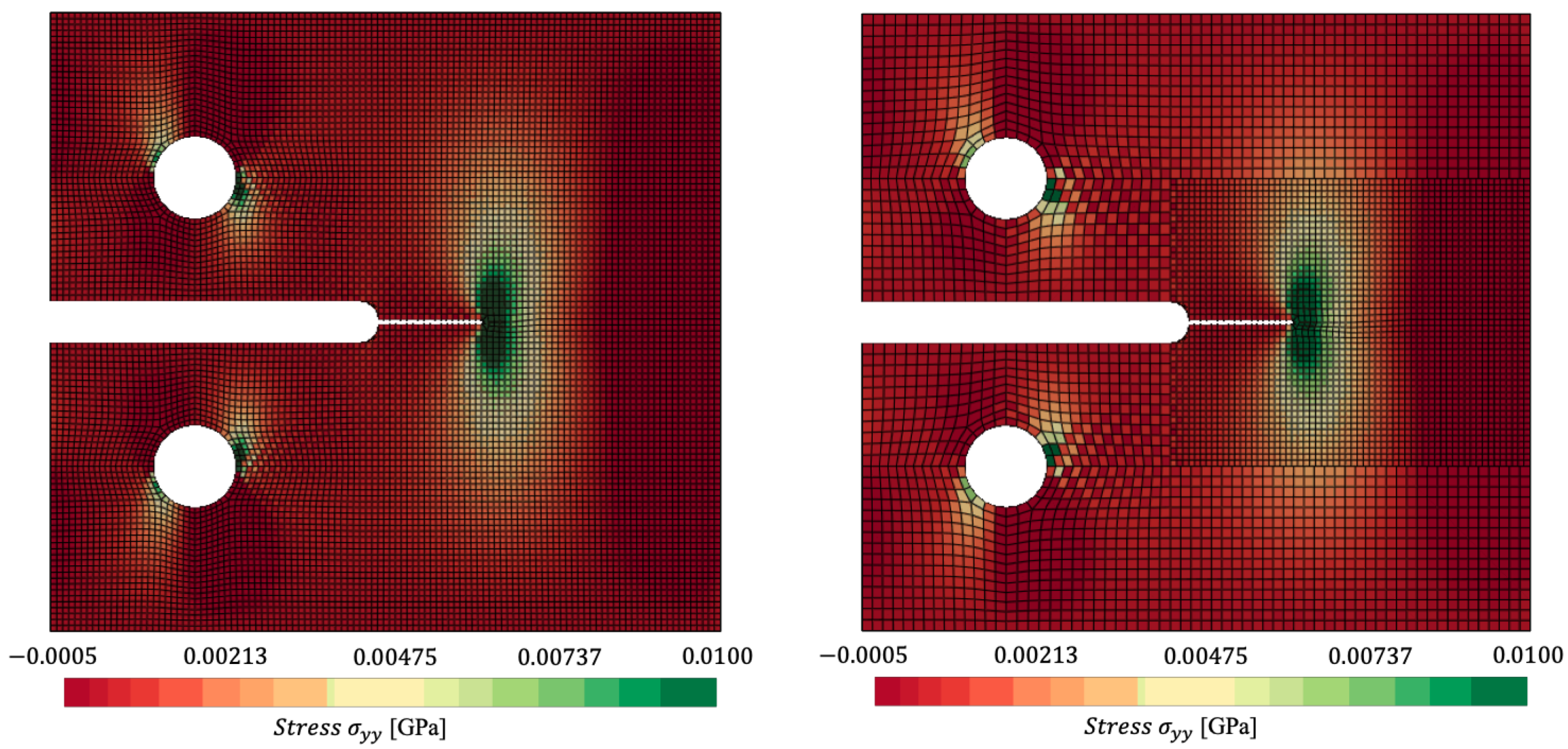
4.2. Numerical Examples in Space and Time

The following numerical study looks to represent the stress gradients prior to fracture in a compact-tension (CT) specimen test, utilising a similar geometry from literature [38,39]. Figure 6 (a) portrays the geometry modelled in the following example. As the specimen is loaded, stress concentrates about the specimen’s crack tip. We apply a ramped velocity $\dot{\mathbf{u}}\left(t\right)$ boundary condition on nodes that create a semicircle for upper and lower pins, as shown in Figure 6 (b), with a maximum magnitude of 0.2 ${\mathrm{ms}}^{-1}$. Whilst equivalent velocities are applied to each of the nodes in the pins, to replicate the contact pressure on the pins, methods such as those applied by Triclot et al. should be considered [40]. Material properties are similar to alumina with $E=370$ GPa, $\rho =3.9\times {10}^{-6}$ ${\mathrm{kgmm}}^{-3}$ and Poisson’s ratio $\nu =0.22$. We model the CT specimen with three simulations; one using a fine mesh throughout the entire domain, one coupling a coarse ${\Omega }_L$ and fine ${\Omega }_s$ mesh with a single $\Delta t$, and another with ${\Omega }_L$ and ${\Omega }_s$ integrating with multiple time steps $\Delta t_L$ and $\Delta t_s$, respectively. Structured meshes are used in all cases where an element size of $0.58$ mm for fine and 1 mm for coarse. All simulations use $Co=0.5$, running for a maximum $t_{final}=0.02$ ms.

In Figure 7 and Figure 8 we plot the stress contours ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ at $t=0.01408$ ms and $t=0.01966$ ms, respectively where the stress concentration can be visualised at the crack tip of the specimen. Figure 7 (a) and Figure 8 (a) capture the reference mesh, whilst Figure 7 (b) and Figure 8 (b) capture the spatially coupled mesh on a single time step $\Delta t_s$. Figure 8 accurately predicts maximum stresses of 0.0396 GPa vs 0.0410 GPa for reference against non-matching mesh.

Through combining spatial and temporal coupling, we observe similar ($<1\times {10}^{-6}$ GPa) results in ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ distribution, as seen in (a) of Figure 9. The difference in the coupled simulations is captured via the (b) of Figure 9, where the root mean square error (RMSE) is plotted. The stress ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ is linear interpolated for the non-matching mesh, to allow for comparison of stress on the coarse mesh’s Gauss points. The couplings capture nearly the entire specimen within a $<5$% error. Considerable error is located around the circumference of the pins, and the far right of the specimen, however these Gauss points reside far from the area of interest at the crack tip. To avoid such errors, a smaller element size would be required in ${\Omega }_L$, however this raises the trade-off between accuracy and computational efficiency. Considerable speedup is achieved, with both couplings, as presented in Table 9.

Figure 9. Comparison of ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ for: (a) - combined spatial and temporal coupling (multi-time stepping); (b) - RMSE Error of ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ for dynamically loaded compact-tension specimen at $t=0.01966$ ms.

Figure 9. Comparison of ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ for: (a) - combined spatial and temporal coupling (multi-time stepping); (b) - RMSE Error of ${\mathit{\sigma }}_{\mathit{y}\mathit{y}}$ for dynamically loaded compact-tension specimen at $t=0.01966$ ms.

Table 1. Computational runtime in seconds and speedup vs reference, of the dynamically loaded compact-tension specimen.

Simulation	Runtime [s]	Speedup
Reference (monolithic)	7428	-
Spatially Coupled	2267	3.27×
Spatially and Temporally Coupled	572	12.98×

Table 1. Computational runtime in seconds and speedup vs reference, of the dynamically loaded compact-tension specimen.

Simulation	Runtime [s]	Speedup
Reference (monolithic)	7428	-
Spatially Coupled	2267	3.27×
Spatially and Temporally Coupled	572	12.98×

5. Conclusions

We present coupling methods for the dynamic modelling of solids with explicit finite elements; temporally and spatially. When modelling composites, constituents have varying dilatational wave speeds, hence different time steps. Integrating over the smallest time step can prove highly inefficient, hence the need for multi-time stepping. Our method allows partitions of a domain to solve with their own respective time step, hence reducing computational overhead. Stability of the method is assessed through evaluation of the subdomains’ energies. The addition of the coupling in space solves the issue of non-matching meshes, so that small element sizes are only required in regions of interest. Coupling operators are easily implemented, without increasing the degrees of freedom on the interface. Ongoing work addresses the spatial coupling with a quadrilateral non-matching interfaces in 3-D domains [41]. Numerical examples capture an increase in efficiency with stress wave propagation in a heterogeneous bar, and the modelling of a compact-tension specimen. Both couplings in time and space reduce computational runtimes, when compared to their monolithic simulation, especially when combined. Future work looks at the coupling between macro and meso- scale meshes [42,43,44], with adaptivity a clear necessity for these multi-scale couplings [45]. Other coupling opportunities are plentiful when considering dynamic applications; the modelling of contact [14,16], composite fracture [38,39], fluid-structure interaction [13,27], and other impact engineering scenarios are just a few to mention.