Gravitational Waves and Higgs Field from Alena Tensor

1. Introduction

Gravitational waves are a well-understood and researched issue [1], and it seems that the area of this research will develop dynamically both in theoretical understanding [2] and methods of waves detection [3,4]. While there is much evidence that General Relativity is (so far) the best description of relativistic gravity, the analysis of gravitational waves provides further evidence and is an important area of research, providing significant information about physical systems. The ability to describe gravitational waves is also an important requirement for alternative to GR theories [5,6,7] and the theories of quantum gravity [8].

Alena Tensor is in the early stages of research. It is a recently discovered class of energy-momentum tensors that allows for equivalent description and analysis of physical systems in flat spacetime (with fields and forces) and in curved spacetime (using Einstein Field Equations) proposing the overall equivalence of the curved path and the geodesic. In this method it is assumed that the metric tensor is not a feature of spacetime, but only a method of its mathematical description. In previous publications [9,10,11] it was already shown that this approach allows for a unified description of a physical system (curvilinear, classical and quantum) ensuring compliance with GR and QM equations. Due to this property, the Alena Tensor seems to be a useful tool for studying unification problems, quantum gravity and many other applications in physics.

Many researchers try to reproduce GR equations in flat spacetime or vice versa [12,13] also many researchers try to incorporate electromagnetism into GR, connecting it in many ways with the geometry of spacetime [14,15,16,17,18,19,20,21]. There are known such approaches on the basis of differential geometry [22,23,23], based on field equations [24,25] as well as promising analyses of spinor fields [26] or helpful approximations for a weak field [27]. For this reason, the Alena Tensor should be viewed as a useful tool that can help in the development of many different approaches or, potentially, as an independent theory requiring theoretical and experimental verification. Therefore it seems worth checking whether the this approach ensures the existence of gravitational waves and what their interpretation is.

Another important reason for writing this article is the fact that although the Alena Tensor equations provide consistency with the Einstein Field Equations in curved spacetime, the description of curvilinear solutions provided by this approach has not been sufficiently discussed in the literature so far. The description of gravitational waves, due to the required mathematical apparatus, will allow to deepen knowledge of this approach and to narrow down the classes of GR solutions that are consistent with it. Such a description will not provide full knowledge about unification, because full unification is not a task for one article and will probably require many years of cooperation of the scientific community. However, this article has the potential to take another step towards unification using the Alena Tensor, providing theoretical tools and hints for further research on unification using this approach.

In this paper it will be analyzed the possibility of describing gravitational waves using the Alena Tensor. Due to the fact that research on this approach is a relatively young field, to facilitate the analysis of the article, the next section summarizes the results obtained so far and introduces the necessary notation. All computationally difficult equations and graphs can be found in the attached supplementary material as computational notebook.

In the Results section, at first it will be shown that the use of the Alena Tensor leads to the decomposition of the electromagnetic field stress-energy tensor into components dependent on two null vectors. Next, the general form of the metrics for curved spacetime described by the Alena Tensor will be obtained, the Riemann and Weyl tensors will be calculated and presented for an example field configuration. It will also be shown that the correct operation of the Alena Tensor requires the existence of the Higgs field. The article also presents tables and graphs illustrating the obtained results (Higgs field, Weyl tensor components, Newman-Penrose scalars) and it was shown, that the analysis of the equations lead to the conclusions contained in the abstract.

Although at the first moment the paradigm shift proposed by this approach may seem incomprehensible, the author hopes that the reader will trust the scientific method, which encourages us to calculate and check everything based on the correctness of the results obtained.

2. Short Introduction to Alena Tensor

The following chapter briefly explains the conclusions from the previous publications on Alena Tensor. The author uses the metric signature (+,-,-,-) which provides a positive value of the electromagnetic field tensor invariant. In previous publications it was treated as negative (reversal of the order of terms in the energy-momentum tensor of the electromagnetic field). The following equations remove this inconvenience while maintaining the correctness of the obtained results.

2.1. Transforming a curved path into a geodesic

To understand the Alena Tensor, it is easiest to recreate the reasoning that led to its creation [10] using the example of the electromagnetic field. One may consider the energy-momentum tensor in flat spacetime for a physical system with an electromagnetic field in the following form

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-{\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }$$

(1)

where $T^{\alpha \beta }$ is energy-momentum tensor for a physical system, $\varrho$ is density of matter, $U^{\alpha }$ is four-velocity, ${\mu }_r$ is relative permeability, ${{\rm Y}}^{\alpha \beta }$ is energy-momentum tensor for the electromagnetic field.

The density of four-forces acting in a physical system can be considered as a four-divergence. One may therefore denote the four-force densities occurring in the system:

• $f^{\beta }\equiv {\partial }_{\alpha }\varrho U^{\alpha }{U}^{\beta }$ is the density of the total four-force acting on matter
• ${\displaystyle \frac{1}{{\mu }_r}}{f}_{em}^{\beta }+f_{gr}^{\beta }\equiv {\partial }_{\alpha }{\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }$ are forces due to the field, where
• $f_{em}^{\beta }$ is the density of the electromagnetic four-force
• $f_{gr}^{\beta }={{\rm Y}}^{\alpha \beta }{\partial }_{\alpha }{\displaystyle \frac{1}{{\mu }_r}}$ was shown in [9] as related to the presence of gravity in the system.

One may assume that the forces balance, which will provide a vanishing four-divergence of the energy-momentum tensor for the entire system

$$0={\partial }_{\alpha }{T}^{\alpha \beta }=f^{\beta }-{\displaystyle \frac{1}{{\mu }_r}}{f}_{em}^{\beta }-f_{gr}^{\beta }$$

(2)

It may be noticed, that if one wanted to use $T^{\alpha \beta }$ for a curvilinear description, which would describe the same physical system but curvilinearly, then in curved spacetime the forces due to the field can be replaced with help of Christoffel symbols of the second kind. This means, that the entire field term can simply disappear from the equation in curved spacetime, because instead of a field and the forces associated with it, there will be corresponding curvature.

This would mean, that in curved spacetime ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }=0\to T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }$. As shown in [10], a minor amendment to continuum mechanics provides this property. Assuming ${\varrho }_o$ as rest mass density and $\varrho U^{\alpha }\equiv {\varrho }_o\gamma U^{\alpha }$ one gets mass density taking into account motion and Lorentz contraction of the volume and provides

$$\begin{array}{c}\hfill {\partial }_{\alpha }\varrho U^{\alpha }=0\to U_{,\alpha }^{\alpha }=-{\displaystyle \frac{d\gamma }{dt}}\to U_{;\alpha }^{\alpha }=0;U^{\alpha }{U}_{;\alpha }^{\beta }=0\end{array}$$

(3)

$$\begin{array}{c}\hfill \to {\displaystyle \frac{D{U}^{\beta }}{D\tau }}=0;{\left(\varrho U^{\alpha }{U}^{\beta }\right)}_{;\alpha }=0\end{array}$$

(4)

One may thus generalize ${{\rm Y}}^{\alpha \beta }$ making the following substitution

$${{\rm Y}}^{\alpha \beta }\equiv {\Lambda }_{\rho }\left({\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }-g^{\alpha \beta }\right)={\displaystyle \frac{1}{{\mu }_o}}{F}^{\alpha \delta }{g}_{\delta \gamma }{F}^{\beta \gamma }-{\Lambda }_{\rho }{g}^{\alpha \beta }$$

(5)

where $F^{\alpha \delta }$ is electromagnetic field strength tensor, ${\mu }_o$ is vacuum magnetic permeability, $g^{\alpha \beta }$ is metric tensor with the help of which the spacetime is considered, and

• ${\Lambda }_{\rho }={\displaystyle \frac{1}{4{\mu }_o}}{F}^{\alpha \mu }{g}_{\mu \gamma }{F}^{\beta \gamma }{g}_{\alpha \beta }$ is invariant of the electromagnetic field tensor,
• $\mathbb{k}=g_{\mu \nu }{\mathbb{k}}^{\mu \nu }$ is trace of ${\mathbb{k}}^{\alpha \beta }$,
• ${\mathbb{k}}^{\alpha \beta }$ is a metric tensor of a spacetime for which ${{\rm Y}}^{\alpha \beta }$ vanishes.

Tensor ${\mathbb{k}}^{\alpha \beta }$ may be calculated in flat spacetime and may be treated as fixed, since the value of ${\mathbb{k}}^{\alpha \beta }$ is independent of the $g^{\alpha \beta }$ adopted for analysis. In this way one obtains a generalized description of the tensor ${{\rm Y}}^{\alpha \beta }$, which has the following properties:

• in flat spacetime ${{\rm Y}}^{\alpha \beta }$ is the usual, classical energy-momentum tensor of the electromagnetic field
• its trace vanishes in any spacetime, regardless of the considered metric tensor $g^{\alpha \beta }$
• in spacetime for which $g^{\alpha \beta }={\mathbb{k}}^{\alpha \beta }$ the entire tensor ${{\rm Y}}^{\alpha \beta }$ vanishes
• ${\mathbb{k}}^{\alpha \beta }{\mathbb{k}}_{\alpha \beta }=4$ which is expected property of the metric tensor (it was already shown in [10] that ${\mathbb{k}}^{\alpha \beta }$ indeed may be considered as metric tensor for curved spacetime)

In the above manner one obtains the Alena Tensor $T^{\alpha \beta }$ in form of

$$T^{\alpha \beta }=\varrho U^{\alpha }{U}^{\beta }-{\displaystyle \frac{1}{{\mu }_r}}{\Lambda }_{\rho }\left({\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }-g^{\alpha \beta }\right)$$

(6)

with the yet unknown ${\displaystyle \frac{1}{{\mu }_r}}$ for which in curved spacetime ($g^{\alpha \beta }={\mathbb{k}}^{\alpha \beta }$) the energy-momentum tensor of the field ${{\rm Y}}^{\alpha \beta }$ vanishes.

The reasoning carried out above for electromagnetism is universal and allows to consider the Alena Tensor also for energy-momentum tensors associated with other fields. This leads to obtaining an energy-momentum tensor $T^{\alpha \beta }$ for the system that can be considered both in flat spacetime and in curved spacetime.

2.2. Connection with Continuum Mechanics, GR and QFT/QM

To make the Alena Tensor consistent with Continuum Mechanics in flat spacetime, it is enough to adopt the substitution ${\displaystyle \frac{1}{{\mu }_r}}\equiv {\displaystyle \frac{-p}{{\Lambda }_{\rho }}}$ where p is the negative pressure in the system and it is equal to $p\equiv \varrho c^2-{\Lambda }_{\rho }$ where c is the speed of light in a vacuum. Such substitution yields

$$\varrho U^{\alpha }{U}^{\beta }-T^{\alpha \beta }=p{\eta }^{\alpha \beta }-c^2\varrho {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }+{\Lambda }_{\rho }{\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }$$

(7)

where ${\eta }^{\alpha \beta }$ is the metric tensor of flat Minkowski spacetime. Introducing deviatoric stress tensor ${\Pi }^{\alpha \beta }\equiv -c^2\varrho {\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }$ one obtains relativistic equivalence of Cauchy momentum equation (convective form) in which only $f_{em}$ appears as a body force

$$f^{\alpha }={\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }+f_{em}^{\alpha }$$

(8)

The above substitution also provides a connection to General Relativity in curved spacetime. For this purpose, one may introduce the following tensors, which can be analyzed in both flat and curved spacetime

$$\begin{array}{c}\hfill R^{\alpha \beta }\equiv 2\varrho U^{\alpha }{U}^{\beta }-p{g}^{\alpha \beta };R\equiv R^{\alpha \beta }{g}_{\alpha \beta }=2{\Lambda }_{\rho }-2p\end{array}$$

(9)

$$\begin{array}{c}\hfill G^{\alpha \beta }\equiv R^{\alpha \beta }-{\displaystyle \frac{R}{2}}{\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }\end{array}$$

(10)

Above allows to rewrite Alena Tensor as

$$G^{\alpha \beta }+{\Lambda }_{\rho }{g}^{\alpha \beta }=2T^{\alpha \beta }+\varrho c^2\left(g^{\alpha \beta }-{\displaystyle \frac{4}{\mathbb{k}}}{\mathbb{k}}^{\alpha \beta }\right)$$

(11)

Analyzing the above equation in curved spacetime ($g^{\alpha \beta }={\mathbb{k}}^{\alpha \beta }$), one obtains simplifications

$$G^{\alpha \beta }+{\Lambda }_{\rho }{g}^{\alpha \beta }=2T^{\alpha \beta };G^{\alpha \beta }=R^{\alpha \beta }-{\displaystyle \frac{1}{2}}R{g}^{\alpha \beta }$$

(12)

thus above can be interpreted as the main equation of General Relativity up to the constant ${\displaystyle \frac{4\pi G}{c^4}}$ where $G^{\alpha \beta }$ and $R^{\alpha \beta }$ can be interpreted in curved spacetime, respectively, as Einstein curvature tensor and Ricci tensor both with an accuracy of ${\displaystyle \frac{4\pi G}{c^4}}$ constant.

Analyzing the $G^{\alpha \beta }$ tensor in flat spacetime ($g^{\alpha \beta }={\eta }^{\alpha \beta }$) one can also notice, that it is related to the non-body forces seen in the description of the Cauchy momentum equation

$${\partial }_{\beta }{G}^{\alpha \beta }={\partial }^{\alpha }p+{\partial }_{\beta }{\Pi }^{\alpha \beta }=f_{gr}^{\alpha }+f_{rr}^{\alpha }$$

(13)

which means that in the Alena Tensor analysis method gravity is not a body force, and as shown in [9] in above

• $f_{rr}^{\alpha }=\left({\displaystyle \frac{1}{{\mu }_r}}-1\right)f_{em}^{\alpha }$ is the density of the radiation reaction four-force
• $f_{gr}^{\alpha }=\varrho \left({\displaystyle \frac{d\varphi }{d\tau }}{U}^{\alpha }-c^2{\partial }^{\alpha }\varphi \right)$ is density of the four-force related to gravity, where
• $\varphi =-ln\left({\mu }_r\right)$ is related to the effective potential in the system with gravity.

It can be calculated that $f_{gr}^{\alpha }$ vanishes in two cases:

• $\overrightarrow{u}={\overrightarrow{u}}_{ff}\equiv -c{\displaystyle \frac{\nabla \varphi }{{\partial }^0\varphi }}$ - which turns out to be the case of free fall
• ${\partial }^{\alpha }\varphi =0$ which occurs in the case of circular orbits

Neglecting the electromagnetic force and the radiation reaction force, using the above equation one can reproduce the motion of bodies in the effective potential obtained from the solutions of General Relativity. Such a description has already been done for the Schwarzschild metric [9] for

$$\varphi +c_o\equiv \sqrt{{\displaystyle \frac{E^2}{m^2{c}^4}}-{\left({\displaystyle \frac{1}{c}}{\displaystyle \frac{dr}{d\tau }}\right)}^2}=\sqrt{\left(1-{\displaystyle \frac{r_s}{r}}\right)\left(1+{\displaystyle \frac{L^2}{r^2}}\right)}$$

(14)

where $c_o$ is a certain constant. The solutions obtained in this way enforce the existence of gravitational waves due to time-varying $\varphi$ (except for free fall and circular orbits).

In the above description, gravity itself is not a force, because the above description is based on an effective potential. However, one can see a similarity to Newton’s classical equations for the stationary case with a stationary observer, for which $f_{gr}^{\alpha }$ can be approximated by Newton’s gravitational force with the opposite sign. Thus for stationary observer $f_{gr}^{\alpha }$ represents a force that must exist to keep a stationary observer suspended above the source of gravity in fixed place.

The description of gravity obtained in this way is surprisingly consistent with current knowledge, despite the fact that gravity itself in this description is not a force, and the force $f_{gr}^{\alpha }$ is not a body force.

The Alena Tensor constructed in presented way according to [9,11] may be simplified in flat spacetime to

$$T^{\alpha \beta }={\Lambda }_{\rho }{\eta }^{\alpha \beta }-{\displaystyle \frac{1}{{\mu }_o}}{F}^{\alpha \gamma }{\partial }^{\beta }{A}_{\gamma };\mathcal{L}=T^{00}=-{\Lambda }_{\rho }=-{\displaystyle \frac{1}{4{\mu }_o}}{F}^{\alpha \beta }{F}_{\alpha \beta }$$

(15)

which allows its analysis in classical field theory and quantum theories. Obtained canonical four-momentum $H^{\alpha }\equiv -{\displaystyle \frac{1}{c}}\int T^{\alpha 0}{d}^{3}x$ provides $0=H_{,\alpha }^{\alpha }=H^{\alpha }{H}_{\alpha }$ and

$${\partial }^{\alpha }{H}^{\mu }{X}_{\mu }=H^{\alpha }={\mu }_r{P}^{\alpha }+q{\mathcal{E}}^{\alpha };-L={\displaystyle \frac{m{c}^2}{\gamma }}-W_{pv}$$

(16)

where $P^{\alpha }$ is four-momentum, $W_{pv}=-\int p{d}^{3}x$ is pressure-volume work, and where $q{\mathcal{E}}^{\alpha }$ and $-{\mu }_r{P}^{\alpha }$ are in fact two gauges of electromagnetic four-potential. In above $\left({\mu }_r-1\right)P^{\alpha }$ is responsible for the force associated with gravity and radiation reaction force. It was also shown that canonical four-momentum $H^{\mu }$ may be expressed as

$$H^{\mu }=P^{\mu }+W^{\mu }=-{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }+{\mathbb{S}}^{\mu }$$

(17)

where ${\mathbb{S}}^{\mu }$ due to its property ${\mathbb{S}}^{\mu }{U}_{\mu }=0$, seems to be some description of rotation or spin, and where $W^{\mu }$ describes the transport of energy due to the field.

The quantum picture obtained from the Alena Tensor [9,11] for the system with electromagnetic field leads to the conclusion that gravity and the radiation reaction force have always been present in Quantum Mechanics and Quantum Field Theory. This conclusion follows from the fact that the quantum equations obtained from the Alena Tensor for the system with electromagnetic field [9] are actually the three main quantum equations currently used:

• simplified Dirac equation for QED:
  ${\mathcal{L}}_{QED}={\displaystyle \frac{1}{4{\mu }_o}}{F}^{\alpha \beta }{F}_{\alpha \beta }={\displaystyle \frac{1}{2{\mu }_o}}{F}^{0\gamma }{\partial }^0{A}_{\gamma }={\displaystyle \frac{1}{2}}\overline{\Psi }\left(i\hslash c\neg D-m{c}^2\right)\Psi$
• Klein-Gordon equation,
• equivalent of the Schrödinger equation: $ic\hslash {\partial }^0\psi =-{\displaystyle \frac{{\hslash }^2}{m\left(\gamma +\frac{1}{\gamma }\right)}}{\nabla }^2\psi +cq{\widehat{A}}^0\psi$

where $A^{\alpha }$ and ${\widehat{A}}^{\alpha }$ are two gauges of electromagnetic four-potential, and where the last equation in the limit of small energies (Lorentz factor $\gamma \approx 1$) turns into the classical Schrödinger equation considered for charged particles.

The above results make the Alena Tensor a useful tool for the analysis of physical systems with fields, allowing modeling phenomena in flat spacetime, curved spacetime, and in the quantum image.

3. Results

Considering a flat spacetime with an electromagnetic field, described in a way provided by Alena Tensor using notation introduced in Section 2, one may reverse the reasoning presented in introduction and consider the field as a manifestation of a propagating perturbation of the curvature of spacetime which in flat spacetime is just interpreted as a field. For this purpose, one may define a certain perturbation $h^{\alpha \beta }$ of the metric tensor ${\mathbb{k}}^{\alpha \beta }$ that describes the deviation from flat spacetime, and also define its trace h as

$$h^{\alpha \beta }\equiv {\mathbb{k}}^{\alpha \beta }-{\eta }^{\alpha \beta };h=h^{\alpha \beta }{\eta }_{\alpha \beta }=\mathbb{k}-4$$

(18)

The stress-energy tensor of the electromagnetic field in flat spacetime can be thus represented as follows

$${\displaystyle \frac{\mathbb{k}}{4{\Lambda }_{\rho }}}{{\rm Y}}^{\alpha \beta }=h^{\alpha \beta }-{\displaystyle \frac{h}{4}}{\eta }^{\alpha \beta }$$

(19)

As one can see in the above, considering gravitational waves in the Alena Tensor is natural and does not require classical linearization. This would mean that gravitational waves in Alena Tensor approach are de facto a propagating disturbance of the energy-momentum tensor for the field (in the case analyzed, the electromagnetic field energy-momentum tensor).

Denoting the pressure amplitude ${\mathcal{P}}_o$ and ${\overline{h}}^{\alpha \beta }$ one obtains

$${\mathcal{P}}_o\equiv {\displaystyle \frac{4{\Lambda }_{\rho }}{\mathbb{k}}};{\overline{h}}^{\alpha \beta }\equiv h^{\alpha \beta }-{\displaystyle \frac{h}{4}}{\eta }^{\alpha \beta }\to {{\rm Y}}^{\alpha \beta }={\mathcal{P}}_o{\overline{h}}^{\alpha \beta }$$

(20)

which shows that the energy-momentum tensor of the field may be also interpreted as propagating vacuum pressure waves with tensor amplitude.

To provide an analysis of the above equation for gravitational waves and the analysis of the resulting classes of metrics, a representation using null-vectors will be useful. Therefore, in the next few steps it will be shown that Alena Tensor allows representing the energy-momentum tensor of the electromagnetic field with the use of two null-vectors.

3.1. Decomposition of the electromagnetic field using null vectors

At first step one may recall equation (17) and define new four-vector $B^{\mu }$ obtaining

$$B^{\mu }\equiv -{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }-{\mathbb{S}}^{\mu };H^{\mu }=-{\displaystyle \frac{\gamma L}{c^2}}{U}^{\mu }+{\mathbb{S}}^{\mu }$$

(21)

Since it is know from previous publications, that $H^{\mu }{H}_{\mu }=0$ and $U^{\mu }{\mathbb{S}}_{\mu }=0$, therefore above definition also yields $B^{\mu }{B}_{\mu }=0$. This property allows to represent $U^{\mu }$ and ${\mathbb{S}}^{\mu }$ using two null-vectors $H^{\mu }$ and $B^{\mu }$ as follows

$$H^{\alpha }-B^{\alpha }=2{\mathbb{S}}^{\mu };H^{\alpha }+B^{\alpha }=-{\displaystyle \frac{2\gamma L}{c^2}}{U}^{\alpha }\to H^{\alpha }{B}_{\alpha }={\displaystyle \frac{2{\gamma }^2{L}^2}{c^2}}$$

(22)

thus

$$H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }={\displaystyle \frac{2H^{\mu }{B}_{\mu }}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(H^{\alpha }{H}^{\beta }+B^{\alpha }{B}^{\beta }\right)$$

(23)

Next, one may define auxiliary parameter $\alpha$ as

$$\alpha \equiv {\displaystyle \frac{B^0}{H^0}}+{\displaystyle \frac{2H^{\mu }{B}_{\mu }}{H^{0}mc\gamma }}$$

(24)

and subtract the linear combination of $H^{\alpha }$ and $B^{\alpha }$ from both sides

$$\begin{array}{c}\hfill H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }-\alpha H^{\alpha }{H}^{\beta }-{\displaystyle \frac{H^0}{B^0}}{B}^{\alpha }{B}^{\beta }=\end{array}$$

(25)

$$\begin{array}{c}\hfill ={\displaystyle \frac{2H^{\mu }{B}_{\mu }}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)\end{array}$$

(26)

Next, using $H\equiv c{H}^0$ for simplicity, one may recall from [9] coefficients related to the electromagnetic field

• relative permeability ${\mu }_r={\displaystyle \frac{{\Lambda }_{\rho }}{-p}}={\displaystyle \frac{H}{W_{pv}}}=e^{-\varphi }$
• volume magnetic susceptibility $\chi ={\mu }_r-1={\displaystyle \frac{\varrho c^2}{-p}}={\displaystyle \frac{m{c}^2\gamma }{W_{pv}}}$
• relative permittivity ${\epsilon }_r={\displaystyle \frac{1}{{\mu }_r}}={\displaystyle \frac{-p}{{\Lambda }_{\rho }}}={\displaystyle \frac{W_{pv}}{H}}$
• electric susceptibility ${\chi }_e={\epsilon }_r-1=-{\displaystyle \frac{\varrho c^2}{{\Lambda }_{\rho }}}=-{\displaystyle \frac{m{c}^2\gamma }{H}}=-\chi {\epsilon }_r$

and notice, that one obtains Alena Tensor $T^{\alpha \beta }$ as

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mu }_r}{{\Lambda }_{\rho }}}{T}^{\alpha \beta }={\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(H^{\alpha }{B}^{\beta }+B^{\alpha }{H}^{\beta }-\alpha H^{\alpha }{H}^{\beta }-{\displaystyle \frac{H^0}{B^0}}{B}^{\alpha }{B}^{\beta }\right)=\end{array}$$

(27)

$$\begin{array}{c}\hfill ={\displaystyle \frac{\chi }{c^2}}{U}^{\alpha }{U}^{\beta }-{\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)\end{array}$$

(28)

where electromagnetic stress-energy tensor is equal to

$${\displaystyle \frac{1}{{\Lambda }_{\rho }}}{{\rm Y}}^{\alpha \beta }={\displaystyle \frac{\chi }{2H^{\mu }{B}_{\mu }}}\left(\left[1+\alpha \right]H^{\alpha }{H}^{\beta }+\left[1+{\displaystyle \frac{H^0}{B^0}}\right]B^{\alpha }{B}^{\beta }\right)$$

(29)

and where $T^{0\beta }$ actually simplifies, as shown in introduction, to

$${\displaystyle \frac{{\mu }_r}{{\Lambda }_{\rho }}}{T}^{0\beta }=-{\displaystyle \frac{{\mu }_r}{H^0}}{H}^{\beta }$$

(30)

Completing the definition of the first invariant of the electromagnetic field tensor ${\Lambda }_{\rho }$, one may define the second invariant $I_{\perp }$ by electric $\overrightarrow{E}$ and magnetic $\overrightarrow{B}$ fields as

$$I_{\perp }\equiv {\displaystyle \frac{1}{c{\mu }_o}}\overrightarrow{E}\overrightarrow{B}$$

(31)

where it is known [28], that

$${{\rm Y}}^{\alpha \beta }{{\rm Y}}_{\alpha \beta }=4\left({\Lambda }_{\rho }^2+I_{\perp }^2\right)=4\left({{\rm Y}}^{0\beta }{{\rm Y}}_{0\beta }\right)$$

(32)

Therefore from (29) one obtains simplifications

$$B^0={\displaystyle \frac{H^{\mu }{B}_{\mu }}{4H^0}}={\displaystyle \frac{{\gamma }^2{L}^2}{2cH}}\to \alpha ={\displaystyle \frac{B^0}{H^0}}\left(1-{\displaystyle \frac{8}{{\chi }_e}}\right)\to {\displaystyle \frac{1}{H^0}}+{\displaystyle \frac{1}{B^0}}={\displaystyle \frac{4c}{-L}}$$

(33)

and by defining a useful auxiliary variable $\phi$ one gets

$$e^{\phi }\equiv {\displaystyle \frac{-\gamma L}{\sqrt{2}H}}\to \gamma ={\displaystyle \frac{1}{\sqrt{2}}}cosh\left(\phi \right)\to e^{2\phi }={\displaystyle \frac{B^0}{H^0}}$$

(34)

Finally, defining for simplicity as below

$$e^{\theta }sinh\left(\theta \right)\equiv {\displaystyle \frac{-L}{m{c}^2\gamma }};I_o^2\equiv 1+{\displaystyle \frac{I_{\perp }^2}{{\Lambda }_{\rho }^2}}$$

(35)

then calculating from (29) and (32)

$$I_o^2={\chi }^2{\gamma }^2\left(1-{\displaystyle \frac{2L}{m{c}^2\gamma }}\right)={\chi }^2{\gamma }^2{e}^{2\theta }\to \sqrt{2}{\mu }_r{e}^{\phi }={\displaystyle \frac{-\gamma L}{W_{pv}}}=I_{o}sinh\left(\theta \right)$$

(36)

and expressing ${\mu }_r={\displaystyle \frac{H}{W_{pv}}}=e^{-\varphi }$, one gets further useful expressions

$${\displaystyle \frac{I_o}{\sqrt{2}}}={\displaystyle \frac{e^{\phi -\varphi }}{sinh\left(\theta \right)}};\chi \gamma =I_o{e}^{-\theta }$$

(37)

To simplify further analysis, one may also normalize four-vectors $H^{\mu }$ and $B^{\mu }$ using (33) as follows

$$a^{\mu }\equiv {\displaystyle \frac{1}{H^0}}{H}^{\mu };b^{\mu }\equiv {\displaystyle \frac{1}{B^0}}{B}^{\mu }\to a^{\mu }{b}_{\mu }=4$$

(38)

where $a^{\mu }$ (not $h^{\mu }$) was introduced to avoid confusion related to the previously defined perturbation $h^{\alpha \beta }$. After few calculations using previously derived relationships in (29)

$${\displaystyle \frac{\chi }{8H^0{B}^0}}[1+\alpha ]{\left(H^0\right)}^2={\displaystyle \frac{\chi }{8}}\left(-{\displaystyle \frac{4c{H}^0}{L}}-{\displaystyle \frac{8}{{\chi }_e}}\right)={\mu }_r\left(1-{\displaystyle \frac{m{c}^2\gamma }{2L}}\right)$$

(39)

$${\displaystyle \frac{\chi }{8H^0{B}^0}}\left[1+{\displaystyle \frac{H^0}{B^0}}\right]{\left(B^0\right)}^2=-{\displaystyle \frac{\chi c{B}^0}{2L}}=\chi {\gamma }^2+{\mu }_r{\displaystyle \frac{m{c}^2\gamma }{2L}}$$

(40)

one may now rewrite the electromagnetic field tensor ${{\rm Y}}^{\alpha \beta }$ as

$${{\rm Y}}^{\alpha \beta }={\mu }_r{\Lambda }_{\rho }\left(1+{\displaystyle \frac{1}{2e^{\theta }sinh\left(\theta \right)}}\right)a^{\alpha }{a}^{\beta }+{\Lambda }_{\rho }\left(\chi {\gamma }^2-{\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}\right)b^{\alpha }{b}^{\beta }$$

(41)

As shown in [9] element ${\mu }_r{\Lambda }_{\rho }$ is responsible for electric field energy density carried by light, where ${\Lambda }_{\rho }\chi {\gamma }^2$ was shown as describing energy density of magnetic moment and was linked to charged matter in motion. The element ${\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}$ is a new term and part of equation related to this term may be expressed as ${\mathbb{S}}^{\alpha \beta }$ with help of (37) as

$${\mathbb{S}}^{\alpha \beta }\equiv {\displaystyle \frac{{\mu }_r}{2e^{\theta }sinh\left(\theta \right)}}\left(a^{\alpha }{a}^{\beta }-b^{\alpha }{b}^{\beta }\right)={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-(\theta +\phi )}\left(a^{\alpha }{a}^{\beta }-b^{\alpha }{b}^{\beta }\right)$$

(42)

Since ${\mathbb{S}}^{\alpha \beta }$ does not actually carry energy but only momentum, it can be associated with some description of spin field effects by analogy to (22). Using (33), (34) (37) and (40), electromagnetic field tensor ${{\rm Y}}^{\alpha \beta }$ may be, however, expressed in more useful form. Since

$${\mu }_r\left(1+{\displaystyle \frac{1}{2e^{\theta }sinh\left(\theta \right)}}\right)={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi };-{\displaystyle \frac{\chi c{B}^0}{2L}}={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }$$

(43)

thus

$${\displaystyle \frac{1}{{\Lambda }_{\rho }}}{{\rm Y}}^{\alpha \beta }={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi }{a}^{\alpha }{a}^{\beta }+{\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }{b}^{\alpha }{b}^{\beta }$$

(44)

As one may notice, (38) also allows to simplify (21) by introducing $-e^{\phi }{s}^{\mu }\equiv {\displaystyle \frac{1}{H^0}}{\mathbb{S}}^{\mu }$

$$a^{\mu }=e^{\phi }\left({\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }-s^{\mu }\right);b^{\mu }=e^{-\phi }\left({\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }+s^{\mu }\right)$$

(45)

what using (34) yields

$$s^0=sinh\phi ;\overrightarrow{s}\overrightarrow{s}=1+{cosh}^2\phi ;s^{\mu }{s}_{\mu }=-2e^{2\phi }$$

(46)

and therefore allows to analyze the system using hyperbolic (and trigonometric) functions

$$\begin{array}{c}\hfill {\displaystyle \frac{a^{\mu }+b^{\mu }}{2}}={\displaystyle \frac{\sqrt{2}}{c}}cosh\phi U^{\mu }-sinh\phi s^{\mu }\end{array}$$

(47)

$$\begin{array}{c}\hfill {\displaystyle \frac{a^{\mu }-b^{\mu }}{2}}={\displaystyle \frac{\sqrt{2}}{c}}sinh\phi U^{\mu }-cosh\phi s^{\mu }\end{array}$$

(48)

$$\begin{array}{c}\hfill a^{\alpha }{a}^{\beta }=e^{2\phi }\left({\displaystyle \frac{2}{c^2}}{U}^{\alpha }{U}^{\beta }+s^{\alpha }{s}^{\beta }-{\displaystyle \frac{\sqrt{2}}{c}}\left[U^{\alpha }{s}^{\beta }+s^{\alpha }{U}^{\beta }\right]\right)\end{array}$$

(49)

$$\begin{array}{c}\hfill {\displaystyle \frac{\sqrt{2}}{c}}{U}^{\mu }={\displaystyle \frac{e^{-\phi }}{2}}{a}^{\mu }+{\displaystyle \frac{e^{\phi }}{2}}{b}^{\mu }\end{array}$$

(50)

One may thus denote normalized Alena Tensor in flat spacetime as $K^{\alpha \beta }$ with help of (27) and above as follows

$$K^{\mu \nu }\equiv {\displaystyle \frac{T^{\mu \nu }}{{\Lambda }_{\rho }}}={\displaystyle \frac{-{\chi }_e}{8}}\left(a^{\mu }{b}^{\nu }+b^{\mu }{a}^{\nu }-\left[1-{\displaystyle \frac{8}{{\chi }_e}}\right]a^{\mu }{a}^{\nu }-b^{\mu }{b}^{\nu }\right)$$

(51)

and notice, that it may be presented after simple calculations using (45) - (49) as

$$K^{\mu \nu }={\displaystyle \frac{-{\chi }_e}{c^2}}{U}^{\alpha }{U}^{\beta }-\left(\left[1-{\displaystyle \frac{{\chi }_e}{8}}(1+e^{-2\phi })\right]a^{\mu }{a}^{\nu }+\left[-{\displaystyle \frac{{\chi }_e}{8}}(1+e^{2\phi })\right]b^{\mu }{b}^{\nu }\right)$$

(52)

Since the expression in the brackets must be equal to ${\displaystyle \frac{1}{{\mu }_r}}{\displaystyle \frac{1}{{\Lambda }_{\rho }}}{{\rm Y}}^{\alpha \beta }$, thus

$${\displaystyle \frac{1}{{\Lambda }_{\rho }}}{{\rm Y}}^{\alpha \beta }=\left[{\mu }_r+{\displaystyle \frac{\chi }{8}}(1+e^{-2\phi })\right]a^{\mu }{a}^{\nu }+\left[{\displaystyle \frac{\chi }{8}}(1+e^{2\phi })\right]b^{\mu }{b}^{\nu }$$

(53)

Therefore, according to (41), (42) there must occur ${\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-(\theta +\phi )}={\displaystyle \frac{\chi }{8}}(1+e^{-2\phi })$. Indeed, with help of (34) and (37) one obtains

$${\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-\theta }={\displaystyle \frac{\chi }{8}}(e^{\phi }+e^{-\phi })={\displaystyle \frac{\chi }{4}}cosh\phi ={\displaystyle \frac{\chi }{2\sqrt{2}}}·{\displaystyle \frac{cosh\phi }{\sqrt{2}}}={\displaystyle \frac{1}{2\sqrt{2}}}·\chi \gamma ={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{-\theta }$$

(54)

and the same equality may be calculated for ${\displaystyle \frac{\chi }{8}}(1+e^{2\phi })={\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }$ what confirms compliance with (44). Since $\theta$ is merely auxiliary variable (used only to highlight certain relationships) and thanks to simple algebraic transformations may be expressed in terms of $\phi$

$$2\sqrt{2}H{e}^{\phi }=m{c}^2{e}^{\theta }sinh\left(\theta \right){cosh}^2\left(\phi \right)\to -{\displaystyle \frac{8}{{\chi }_e}}=\left(e^{2\theta }-1\right)\left(e^{-2\phi }+1\right)$$

(55)

one may thus further simplify the description of the system. This shows that further, in-depth analysis of the system is also possible, however, modeling and simplifying the description of the electromagnetic field or searching for elementary particles that provide stable solutions requires a separate article (probably several articles). From the perspective of describing gravitational waves, other elements of the description are crucial, which will be discussed next.

Finally, one may notice, that property $a^{\mu }{b}_{\mu }=4$ in (38) requires analysis in a complex basis. An example of such a basis are four-vectors

$$a^{\mu }\left(\sigma \right)\equiv \left(\begin{array}{c}1\\ isinh\left(i\sigma \right)\\ cosh\left(i\sigma \right)\\ 0\end{array}\right),b^{\mu }\left(\sigma \right)\equiv \left(\begin{array}{c}1\\ i\left(2\sqrt{2}cosh\left(i\sigma \right)-3sinh\left(i\sigma \right)\right)\\ -3cosh\left(i\sigma \right)+2\sqrt{2}sinh\left(i\sigma \right)\\ 0\end{array}\right)$$

(56)

where the angle $\sigma$ was introduced to facilitate further analysis. The null basis product is a simple consequence of equation (32) as a consequence of taking only the electromagnetic field into account in the analysis. Since reality requires other fields (e.g. electroweak), it can be assumed that changing ${{\rm Y}}^{\alpha \beta }\to {\overline{{\rm Y}}}^{\alpha \beta }$ into the field tensor corresponding to reality, would probably provide ${\overline{{\rm Y}}}^{\alpha \beta }{\overline{{\rm Y}}}_{\alpha \beta }=2\left({\overline{{\rm Y}}}^{0\beta }{\overline{{\rm Y}}}_{0\beta }\right)\to a^{\mu }{b}_{\mu }=2$, which then makes it possible to assume a basis in real numbers. However, since in this paper it is considered the Alena Tensor with the electromagnetic field only, the basis (56) will be retained for further analysis as an example, especially since the transition to the generalized field in the discussed approach is a fairly simple procedure.

A cursory examination shows that this basis describes the electromagnetic field very well indeed. It has a good representation in conformal geometry (null vectors correspond to points on the equator of the Penrose sphere), where the propagation directions are perpendicular to the time axis (purely spatial), ideal for describing a circularly or elliptically polarized wave in the direction of Poyting vector $\overrightarrow{z}\equiv (0,0,2i\sqrt{2})$, where $a^{\mu }{b}_{\mu }=4$ represents the constant phase relation between the electric and magnetic fields. The proposed basis naturally enters the Newman–Penrose formalism, allows for a full spinor representation of the electromagnetic field, where $\sigma$ is a typical massless wave, satisfies the wave equation $\square \sigma =0$, and since it provides a spin-helicity of +/- 1, it is well suited for further analysis in the QFT framework as a photon wave representation, describing a single-particle state. However, detailed analysis of these issues is beyond the scope of this article.

3.2. Covariant metric, Higgs field, Riemann tensor, Weyl tensor and gravitational waves

Substituting (41) into (19) using (37) and using Alena Tensor properties one gets expression for metric ${\mathbb{k}}^{\alpha \beta }$ describing the system in curved spacetime

$${\mathbb{k}}^{\alpha \beta }={\displaystyle \frac{\mathbb{k}}{4}}\left({\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\theta -\phi }{a}^{\alpha }{a}^{\beta }+{\displaystyle \frac{I_o}{2\sqrt{2}}}{e}^{\phi -\theta }{b}^{\alpha }{b}^{\beta }+{\eta }^{\alpha \beta }\right)$$

(57)

It turns out that using properties of metrics, one may find a general solution for the inverted metric ${\mathbb{k}}_{\alpha \beta }$. Summarizing the key properties one obtains

$${\mathbb{k}}^{\alpha \beta }{\eta }_{\alpha \beta }={\mathbb{k}}_{\alpha \beta }{\eta }^{\alpha \beta }=\mathbb{k};{\mathbb{k}}^{\alpha \beta }{\mathbb{k}}_{\alpha \beta }=4;det\left({\mathbb{k}}^{\alpha \beta }\right)det\left({\mathbb{k}}_{\alpha \beta }\right)=1;{\mathbb{k}}_{\alpha \mu }{\mathbb{k}}^{\mu \beta }={\delta }_{\alpha }^{\beta }$$

(58)

where in the last condition it is enough to check the index (0,0), because the null vectors are normalized ($a^0=1;b^0=1$). To simplify the calculations, it is easiest to define auxiliary variable q and start from anstaz with unknown $A,B,C,D$ in

$$e^{-q}\equiv {\displaystyle \frac{\mathbb{k}}{4}};{\mathbb{k}}_{\mu \nu }\equiv {\displaystyle \frac{A}{I_o}}{\displaystyle \frac{e^{\theta -\phi }}{\sqrt{2}}}{a}_{\mu }{a}_{\nu }+{\displaystyle \frac{B}{I_o}}{\displaystyle \frac{e^{\phi -\theta }}{\sqrt{2}}}{b}_{\mu }{b}_{\nu }-C\left(a_{\mu }{b}_{\nu }+b_{\mu }{a}_{\nu }\right)+D{\eta }_{\mu \nu }$$

(59)

By eliminating the subsequent variables to provide equations (58), one obtains covariant metric in the form

$${\mathbb{k}}_{\mu \nu }\equiv {\displaystyle \frac{sinh\left(q\right)}{I_o}}{\displaystyle \frac{e^{\theta -\phi }}{\sqrt{2}}}{a}_{\mu }{a}_{\nu }+{\displaystyle \frac{sinh\left(q\right)}{I_o}}{\displaystyle \frac{e^{\phi -\theta }}{\sqrt{2}}}{b}_{\mu }{b}_{\nu }-sinh\left(q\right)\left(a_{\mu }{b}_{\nu }+b_{\mu }{a}_{\nu }\right)+e^q{\eta }_{\mu \nu }$$

(60)

where invariants of electromagnetic field turns out to be related to the trace

$${\displaystyle \frac{I_{\perp }^2}{{\Lambda }_{\rho }^2}}={\displaystyle \frac{1}{e^{2q}-2}}\to I_o=\sqrt{{\displaystyle \frac{e^{2q}-1}{e^{2q}-2}}};det\left({\mathbb{k}}_{\alpha \beta }\right)=e^{2q}\left(e^{2q}-2\right)$$

(61)

which means that the trace $\mathbb{k}$ is also invariant. The supplementary material contains equations confirming the correctness of the derivation.

Using arc ⌢ for simplicity, to emphasize the change to curvilinear description (since values in curvilinear description may be different), one may notice, that considered in curved spacetime trace $\stackrel{⌢}{\mathbb{k}}=4$ yields $\stackrel{⌢}{q}=0$. Therefore, the transition to curved spacetime can be understood as solutions with imaginary magnetic field $\overrightarrow{B}\to i\overrightarrow{B}$. It is also worth notice, that for the null basis example (56), the above metric seems to describe a gravitational wave in conformal geometry, where ${\displaystyle \frac{\mathbb{k}}{4}}=e^{-q}$ plays the role of a conformal factor ${\Omega }^{-2}$. Further analysis in this direction should allow to isolate both the polarization and the relation of $\mathbb{k}$ to the Ricci scalar by classical relation $R={\Omega }^{-2}\left(\tilde{R}-6\tilde{\square }log\Omega \right)$.

Expressing $U^{\mu }$ by null-vectors as in (49) and requesting $U^{\alpha }{U}^{\beta }{\mathbb{k}}_{\alpha \beta }=c^2$ one obtains ugly expression linking $cosh(\phi +\theta )$ and q (due to the complexity of the calculations and the result, it is shown in the attached supplementary material with calculations).

$$cosh(\theta +\phi )={\displaystyle \frac{cosh\left(q\right)-3sinh\left(q\right)-1}{2\sqrt{-\frac{1}{coth\left(q\right)-3}}(cosh\left(q\right)-3sinh\left(q\right))}}$$

(62)

However, substituting q as the $I_o$ function according to (61)

$$q=log\sqrt{2-{\displaystyle \frac{1}{1-I_o^2}}}$$

(63)

and denoting $V\equiv 1+2I_o^4-3I_o^2$, it appears that this ugly expression (62) actually expresses following dependence

$$cosh(\theta +\phi )={\displaystyle \frac{1+\sqrt{V}}{\sqrt{2}{I}_o}}\to V=1+2I_o^2{cosh}^2(\theta +\phi )-2\sqrt{2}{I}_{o}cosh(\theta +\phi )$$

(64)

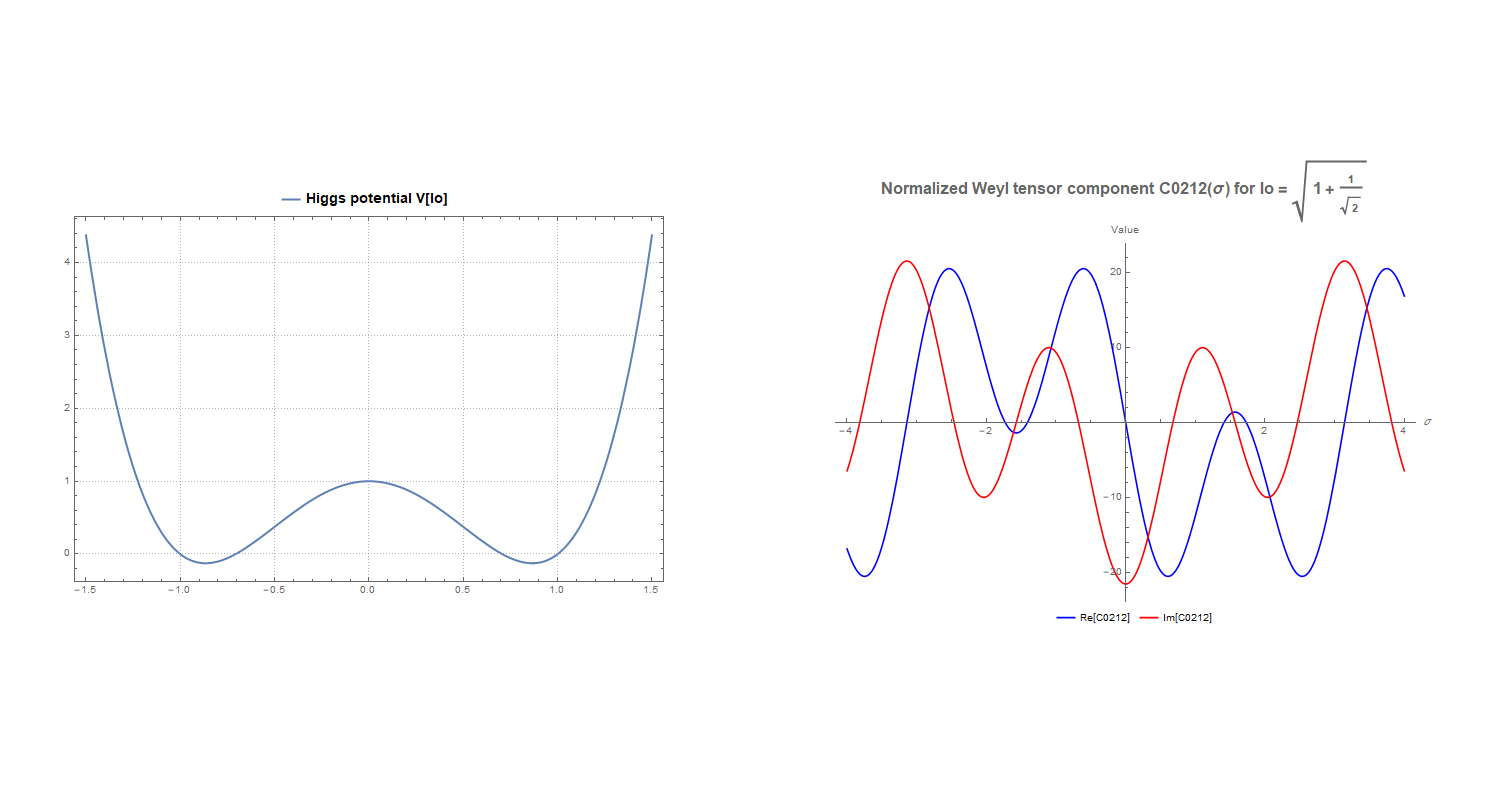
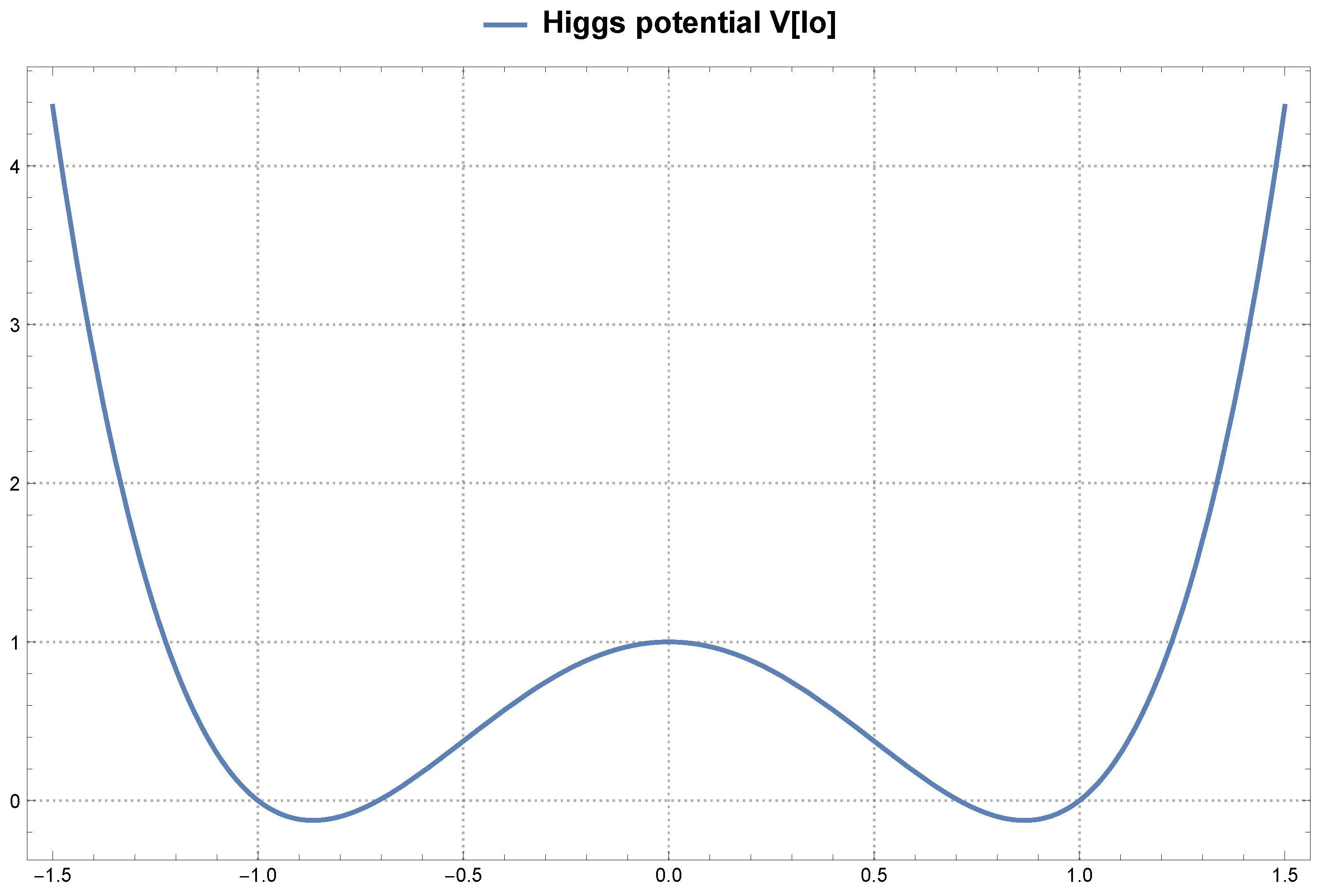
where V is the classical Higgs potential and the broken symmetry in the system can be interpreted as an apparent mismatch of coefficients related to $cosh(\phi +\theta )$. The Figure 1 shows the classic "Mexican sombrero" potential $V\left(I_o\right)$. Since $cosh(\phi +\theta )$ is related in equation (42) to the angle describing the spin, this means that in this solution the spin effect of the field is described by invariant angle (depends only on $I_o$) and, according to (61) it is closely related to the trace of the metric and, consequently, to the Ricci scalar in the curvilinear description and thus to spacetime curvature. This also at least means that to obtain correct results in curved spacetime in the Alena Tensor model, the Higgs-like potential is needed.

Since this paper considers a system with only electromagnetic field, the above described broken symmetry should be considered more as a consequence of the Higgs field in electromagnetism (equivalent to the Abelian mechanism and broken U(1) symmetry) visible in the curvilinear description within GR. However, the above result may contribute to a better understanding of the description of the Higgs field action within the GR containing electromagnetism and connections of the Higgs potential with curvature and spin seen in obtained result. Perhaps it will also help to extend Alena Tensor description to the electroweak field, which will allow to compare the quantum and curvilinear images, which, however, deserves a separate article.

For $I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}$ the whole metric becomes significantly simplified and symmetric

$$I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}\to V=I_o^2\to q=ln\left(\sqrt{2}{I}_o\right)\to {\displaystyle \frac{sinh\left(q\right)}{\sqrt{2}{I}_o}}={\displaystyle \frac{I_o}{2\sqrt{2}}}$$

(65)

which means that it may be assumed that adopting the above value leads to some significant and physically important solution of the equations for the system.

Using hyperbolic identities and expressing

$$cosh(\theta +\phi )=cosh\left(\theta \right)cosh\left(\phi \right)+sinh\left(\theta \right)sinh\left(\phi \right)=e^{-\theta }cosh\left(\phi \right)+e^{\phi }sinh\left(\theta \right)$$

(66)

then using (37) one obtains

$$\chi {\gamma }^2+{\mu }_r{e}^{2\phi }={\displaystyle \frac{1+\sqrt{V}}{2}}\to V={\left(2{\gamma }^2\chi +2{\mu }_r{e}^{2\phi }-1\right)}^2$$

(67)

which allows for further analysis of the Higgs potential. For example, using (41) and (46), the relation between electromagnetic energy density ${{\rm Y}}^{00}$, angle $\phi$ and spin four-vector ${\mathbb{S}}^{\mu }$ zero component is therefore

$${\displaystyle \frac{1}{{\Lambda }_{\rho }}}{{\rm Y}}^{00}={\mu }_r+\chi {\gamma }^2={\displaystyle \frac{1+\sqrt{V}}{2}}-2{\mu }_r{e}^{\phi }sinh\left(\phi \right)={\displaystyle \frac{1+\sqrt{V}}{2}}+{\displaystyle \frac{2c{\mathbb{S}}^0}{W_{pv}}}$$

(68)

Above also explains the origin of $\phi$ and the connection of spin and Lagrangian with the energy density of the electromagnetic field. Since, according to the considered Alena Tensor approach, in curved spacetime the energy density expressed by ${{\rm Y}}^{00}$ must vanish (the entire stress-energy tensor of the electromagnetic field vanishes), this means, that $\phi$ and thus $\gamma$ in curved spacetime becomes invariant, which allows to analyze the transition to curved spacetime.

One may now consider what value the Alena Tensor takes in curved spacetime. To do this, it is easiest to analyze the behavior of $K^{\mu \nu }$. As one may calculate, the determinant of this tensor is 0 and the matrix rank is 2, but, as described in the introduction, it degenerates to $\stackrel{⌢}{K^{\mu \nu }}={\displaystyle \frac{-\stackrel{⌢}{{\chi }_e}}{c^2}}{U}^{\alpha }{U}^{\beta }$ in curved spacetime. It can be seen that in the Alena Tensor approach the metric follows from propagation. However, in curved spacetime the electromagnetic field according to this approach should vanish, remaining present only in the metric and determining geodetic. This can be achieved by degenerating vectors $a^{\mu }$ and $b^{\mu }$ to a single vector in curved spacetime $\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}$. However, in such situation the equation (49) forces this vector to be the four-velocity, divided by the Lorenz factor

$$\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}\to U^{\mu }={\displaystyle \frac{c}{\sqrt{2}}}\left({\displaystyle \frac{e^{-\phi }}{2}}\stackrel{⌢}{a^{\mu }}+{\displaystyle \frac{e^{\phi }}{2}}\stackrel{⌢}{a^{\mu }}\right)=c\gamma \stackrel{⌢}{a^{\mu }}\to \stackrel{⌢}{a^{\mu }}={\displaystyle \frac{1}{c\gamma }}{U}^{\mu }$$

(69)

which degenerates $\stackrel{⌢}{K^{\mu \nu }}$ from (51) to the form

$$\stackrel{⌢}{a^{\mu }}=\stackrel{⌢}{b^{\mu }}={\displaystyle \frac{1}{c\gamma }}{U}^{\mu }\to \stackrel{⌢}{K^{\mu \nu }}=-\stackrel{⌢}{a^{\mu }}\stackrel{⌢}{a^{\nu }}=-{\displaystyle \frac{1}{c^2{\gamma }^2}}{U}^{\mu }{U}^{\nu }\to \stackrel{⌢}{{\chi }_e}={\displaystyle \frac{1}{{\gamma }^2}}$$

(70)

As can be easily verified, the exact above relation of variables leads to the vanishing field stress-energy tensor in (53) upon transition to curved spacetime.

Since the metric is known and $U^{\mu }$ may be expressed by values of $a^{\mu }$, $b^{\mu }$ in flat spacetime thanks to (49) this allows to easy obtain the normalized Einstein tensor and Ricci tensor (normalized by ${\Lambda }_{\rho }$) using the equation (12). According to the notation used in (12) one obtains

$${\displaystyle \frac{1}{{\Lambda }_{\rho }}}{R}^{\mu \nu }=2\stackrel{⌢}{K^{\mu \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\mu \nu };{\displaystyle \frac{1}{{\Lambda }_{\rho }}}{G}^{\mu \nu }=2\stackrel{⌢}{K^{\mu \nu }}-{\mathbb{k}}^{\mu \nu }$$

(71)

where Ricci scalar R (normalized according to notation used) may be calculated as ${\displaystyle \frac{1}{{\Lambda }_{\rho }}}R=4+{\displaystyle \frac{2}{{\gamma }^2}}$.

The described system seems to be Petrov type D or II [29], although to be sure, the Weyl tensor should be calculated. This does not seem possible for the general case (without auxiliary assumptions about symmetries), but one could simplify the obtained description considerably, based on the following observation. One may notice, that the vanishing Lorentz factor $\gamma$ in $\stackrel{⌢}{K^{\alpha \beta }}$ can be interpreted as an important suggestion for the description of motion in curved spacetime. Such motion would correspond to a stream of particles moving without dilation, a strictly ordered flow without local perturbations, resembling a perfect, infinitely stiff fluid. This means that $\stackrel{⌢}{K^{\alpha \beta }}$ should be the Killing tensor and the system should have hidden symmetry (similar to the Carter constant in Kerr solutions).

As shown previously, product of the basis is in considered case $a^{\mu }{b}_{\mu }=4$, which means that null vectors have global significance for spacetime geometry, thus Killing tensor should have a strong connection with propagation along null vectors (it is not a random symmetry, but a deep feature of spacetime) and this would mean the existence of special wave surfaces, e.g. electromagnetic waves and/or gravitational radiation. This would be also a clear indication that spacetime belongs to the Petrov D or II class and is associated with wave propagation solutions.

Also, the analysis of obtained equations drive to conclusion, that energy (energy density) is not something external to geometry in Alena Tensor approach, but energy is defined by the geometry of spacetime itself. This is a result in the spirit of General Relativity, but it goes even deeper: metric ${\mathbb{k}}^{\mu \nu }$ depends on $e^{\phi }$, but at the same time ${\displaystyle \frac{1}{\gamma \left(\phi \right)}}$ depends on the metric because it is trace of $\stackrel{⌢}{K^{\alpha \beta }}$ in this metric. The system itself defines its own energy through the structure of the field, which is similar to the idea of Self-consistent Field [30] - where the field and the source are inseparable, or Emergent Gravity [31,32] - where energy, gravity and geometry arise from a common structure, or Induced Geometry [33] - where energy comes from deformation of spacetime itself, as e.g. in Sakharov’s theory [34]. It seems impossible to "decree" energy in Alena Tensor, but it must be calculated from geometry and the system works as a closed causal cycle.

The dependence for $\stackrel{⌢}{K^{\alpha \beta }}$ of its norm and trace in curved spacetime (the norm is the square of the trace) is a key property for null space and suggests that $\stackrel{⌢}{K^{\alpha \beta }}$ describes isometries related to null wave propagation, similar to pp-wave [35] and Robinson-Trautman solutions [36], what is actually expected in considered approach based on electromagnetic stress-energy tensor and result (57). This would also mean that the Killing tensor is directly related to the energy distribution in spacetime as expected, similar to other GR solutions (eg. Kerr solution), and lead to a rather groundbreaking but also expected result in the context of the discussed approach, that the Killing tensor directly determines the Einstein tensor in main GR equation.

Since $\stackrel{⌢}{K^{\alpha \beta }}$ is simply the Alena Tensor (stress-energy tensor for the system) divided by ${\Lambda }_{\rho }$, it gives correct conserved values in the Noether formalism (conserved density of energy and momentum). From the definition of the Alena Tensor as the energy-momentum tensor for the system it also follows that $\stackrel{⌢}{K^{\mu \nu }}$ is symmetric and ${\nabla }_{\mu }\stackrel{⌢}{K^{\mu \nu }}$ vanishes.

Since ${\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }=-{\displaystyle \frac{c^2}{{\gamma }^2}}$ this implies that along a geodesic parametrized by proper time $\tau$, its total derivative vanishes.

$${\displaystyle \frac{d}{d\tau }}\left({\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }\right)=0=U^{\lambda }{\nabla }_{\lambda }{\stackrel{⌢}{K}}_{\alpha \beta }{U}^{\alpha }{U}^{\beta }$$

(72)

Using the symmetry of ${\stackrel{⌢}{K}}_{\mu \nu }$ one may note that

$$U^{\alpha }{U}^{\mu }{U}^{\nu }{\nabla }_{\alpha }{\stackrel{⌢}{K}}_{\mu \nu }=U^{\alpha }{U}^{\mu }{U}^{\nu }{\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}$$

(73)

Therefore, the condition

$$\left({\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}\right)U^{\alpha }{U}^{\mu }{U}^{\nu }=0\to {\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}=0$$

(74)

holds for arbitrary tangent vectors $U^{\mu }$, and it indeed follows that ${\nabla }_{(\alpha }{\stackrel{⌢}{K}}_{\mu \nu )}=0$. Therefore normalized Alena Tensor is Killing tensor for considered system.

In this way Alena Tensor theory, in curved spacetime, becomes equivalent to some specific case of General Relativity equation expressed in the following form

$${\nabla }_{(\mu }{\stackrel{⌢}{K}}_{\alpha \beta )}=0\to {\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }+\Lambda {\mathbb{k}}_{\alpha \beta }=2\Lambda {\stackrel{⌢}{K}}_{\alpha \beta }$$

(75)

where according to (12) in the above equation ${\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }$ is the classical Einstein tensor in commonly used notation ${\displaystyle \frac{4\pi G}{c^4}}{G}_{\alpha \beta }=G_{\alpha \beta }^{*}$ (classical Einstein tensor).

Thanks to the above, since the Weyl tensor is defined as the part of the Riemann tensor that does not depend on the Ricci tensor, this implies that since Killing tensor determines the Einstein tensor, and the Einstein tensor determines the Ricci tensor, then one could calculate the Weyl tensor by extracting the part of the curvature that does not contain the Ricci tensor. This would also mean that the Christoffel symbols can be expressed as a function of the Killing and Einstein tensors, and the Riemann tensor can be written directly as a function of the Ricci and Killing tensors.

For the system under consideration, one may therefore construct a general Weyl tensor ansatz $C^{\mu \nu \alpha \beta }$, which must contain only components that do not become zero when the trace part is subtracted from the Riemann tensor. It should be of the form

$$C^{\mu \nu \alpha \beta }\equiv c_1{\Sigma }^{\mu \nu \alpha \beta }+c_2{P}^{\mu \nu \alpha \beta }+c_3{Q}^{\mu \nu \alpha \beta }$$

(76)

where

$$\begin{array}{ccc}\hfill {\Sigma }^{\mu \nu \alpha \beta }& =& a^{\mu }{b}^{\nu }{a}^{\alpha }{b}^{\beta }-a^{\mu }{b}^{\nu }{b}^{\alpha }{a}^{\beta }-b^{\mu }{a}^{\nu }{a}^{\alpha }{b}^{\beta }+b^{\mu }{a}^{\nu }{b}^{\alpha }{a}^{\beta }\hfill \end{array}$$

(77)

$$\begin{array}{ccc}\hfill P^{\mu \nu \alpha \beta }& =& a^{\mu }{a}^{\nu }{b}^{\alpha }{b}^{\beta }-b^{\mu }{b}^{\nu }{a}^{\alpha }{a}^{\beta }\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill Q^{\mu \nu \alpha \beta }& =& a^{\mu }{b}^{\nu }{\eta }^{\alpha \beta }-a^{\alpha }{b}^{\beta }{\eta }^{\mu \nu }\hfill \end{array}$$

(79)

It is easy to check that the above tensors are linearly independent and form the basis for the representation of any Weyl tensor in the system under consideration. Analysis of their behavior indicates that

• ${\Sigma }^{\mu \nu \alpha \beta }$ is responsible for "pure" directional propagation, e.g. a gravitational wave propagating along null directions (purely conformal part of the Weyl tensor, described solely by null geometry),
• $P^{\mu \nu \alpha \beta }$ describes non-radiating, "axial" deformation of space, e.g. tidal sequences, consistent with mass motion without undulations,
• $Q^{\mu \nu \alpha \beta }$ describes conformal distortion of the background metric itself.

The coefficients $c_1$, $c_2$, $c_3$ are not known a priori, but one may determine them with help of Riemann tensor. To obtain Riemann tensor $R^{\mu \nu \alpha \beta }$ in the system under consideration, it is enough to assume the following ansatz

$$\begin{array}{c}\hfill R^{\mu \nu \alpha \beta }\equiv A_1\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)+\end{array}$$

(80)

$$\begin{array}{c}\hfill +A_2\left(\stackrel{⌢}{K^{\mu \alpha }}{\mathbb{k}}^{\nu \beta }-\stackrel{⌢}{K^{\mu \beta }}{\mathbb{k}}^{\nu \alpha }-\stackrel{⌢}{K^{\nu \alpha }}{\mathbb{k}}^{\mu \beta }+\stackrel{⌢}{K^{\nu \beta }}{\mathbb{k}}^{\mu \alpha }\right)\end{array}$$

(81)

t has the following justification

• The Riemann tensor satisfies the known algebraic symmetries: $R_{\mu \nu \alpha \beta }=-R_{\nu \mu \alpha \beta }=-R_{\mu \nu \beta \alpha },R_{\mu \nu \alpha \beta }=R_{\alpha \beta \mu \nu },R_{\mu \left[\nu \alpha \beta \right]}=0$. The above ansatz satisfies them automatically.
• There are only two tensor objects available in the system: the metric ${\mathbb{k}}_{\mu \nu }$ and the Killing tensor ${\stackrel{⌢}{K}}_{\mu \nu }=-{\displaystyle \frac{1}{c^2{\gamma }^2}}{U}_{\mu }{U}_{\nu }$. The Riemann tensor must be constructed exclusively from them.
• The first term with $A_1$ corresponds to the geometry of a spacetime with constant curvature, as in de Sitter spacetime: $R_{\left(\mathrm{constant}\mathrm{curvature}\right)}^{\mu \nu \alpha \beta }\sim {\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }$
• The second term with $A_2$ is the minimal geometrically correct extension that takes into account the presence of non-null energy (represented by $\stackrel{⌢}{K^{\mu \nu }}$). Its construction provides correct symmetries and enables the reproduction of a non-null Ricci tensor $R^{\nu \beta }=R_{\mu }^{\mu \nu \beta }$
• Other possible combinations (e.g. $\stackrel{⌢}{K}\otimes \stackrel{⌢}{K}$) are linearly dependent or asymmetric with respect to the required properties of the Riemann tensor, and do not provide new information in the case under consideration.
• The whole creates the most general fourth-order tensor with Riemann symmetries, which can be constructed from available geometric objects.

Computing the contraction of the above Riemann tensor anstaz with ${\mathbb{k}}_{\mu \alpha }$ one gets

$${\mathbb{k}}_{\mu \alpha }{R}^{\mu \nu \alpha \beta }=3A_1{\mathbb{k}}^{\nu \beta }+A_2\left(2\stackrel{⌢}{K^{\nu \beta }}-{\displaystyle \frac{1}{{\gamma }^2}}{\mathbb{k}}^{\nu \beta }\right)$$

(82)

Since normalized Ricci tensor $R^{\alpha \beta }$ is known (71), therefore considering for simplicity above Riemann tensor anstaz as normalized, one gets

$$A_1={\displaystyle \frac{1}{3}}\left(1+{\displaystyle \frac{2}{{\gamma }^2}}\right);A_2=1$$

(83)

Such normalized form is convenient to use because it allows one to easily obtain both: classical tensors (multiplication by the cosmological constant $\Lambda$) and tensors in the Alena Tensor notation (multiplication by field invariant ${\Lambda }_{\rho }$).

Next, one may consider normalized trace part of the Riemann tensor $S^{\mu \nu \alpha \beta }$, which provides the necessary symmetries and the vanishing trace in the Weyl tensor. For this to be satisfied, trace part must have the following, classical [37] form (where Ricci tensor $R^{\nu \beta }$ is considered for simplicity also as normalized):

$$\begin{array}{c}\hfill S^{\mu \nu \alpha \beta }={\displaystyle \frac{1}{2}}\left({\mathbb{k}}^{\mu \alpha }{R}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{R}^{\nu \alpha }-{\mathbb{k}}^{\nu \alpha }{R}^{\mu \beta }+{\mathbb{k}}^{\nu \beta }{R}^{\mu \alpha }\right)\end{array}$$

(84)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{6}}R\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)=\end{array}$$

(85)

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}[{\mathbb{k}}^{\mu \alpha }\left(2\stackrel{⌢}{K^{\beta \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\beta \nu }\right)-{\mathbb{k}}^{\mu \beta }\left(2\stackrel{⌢}{K^{\alpha \nu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\alpha \nu }\right)\end{array}$$

(86)

$$\begin{array}{c}\hfill -{\mathbb{k}}^{\nu \alpha }\left(2\stackrel{⌢}{K^{\beta \mu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\beta \mu }\right)+{\mathbb{k}}^{\nu \beta }\left(2\stackrel{⌢}{K^{\alpha \mu }}+\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\mathbb{k}}^{\alpha \mu }\right)]\end{array}$$

(87)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{3}}\left(2+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)\end{array}$$

(88)

Since all terms related to $\stackrel{⌢}{K^{\mu \nu }}$ reduce after grouping the components in $C^{\mu \nu \alpha \beta }=R^{\mu \nu \alpha \beta }-S^{\mu \nu \alpha \beta }$, one obtains normalized Weyl tensor in generalized form for the system under consideration

$$\begin{array}{c}\hfill C^{\mu \nu \alpha \beta }=R^{\mu \nu \alpha \beta }-S^{\mu \nu \alpha \beta }=\end{array}$$

(89)

$$\begin{array}{c}\hfill \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\nu \beta }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\nu \alpha }\right)\end{array}$$

(90)

$$\begin{array}{c}\hfill -{\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right)\left({\mathbb{k}}^{\mu \alpha }{\mathbb{k}}^{\beta \nu }-{\mathbb{k}}^{\mu \beta }{\mathbb{k}}^{\alpha \nu }+{\mathbb{k}}^{\nu \alpha }{\mathbb{k}}^{\beta \mu }-{\mathbb{k}}^{\nu \beta }{\mathbb{k}}^{\alpha \mu }\right)\end{array}$$

(91)

Trace of above Weyl tensor disappears and it has all the expected symmetries. Substituting the metric known from (57), one obtains the coefficients postulated in the anstaz (76) and as one may notice from non-zero coefficient $c_1$, gravitational waves exist in the system.

$$\begin{array}{ccc}\hfill c_1& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o^2}{8}}{e}^{-2q}\hfill \end{array}$$

(92)

$$\begin{array}{ccc}\hfill c_2& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o^2}{4}}{e}^{-2q}sinh\left(2\theta -2\phi \right)\hfill \end{array}$$

(93)

$$\begin{array}{ccc}\hfill c_3& =& \left(1+{\displaystyle \frac{1}{{\gamma }^2}}\right){\displaystyle \frac{I_o}{\sqrt{2}}}{e}^{-2q}sinh\left(\theta -\phi \right)\hfill \end{array}$$

(94)

One can also demonstrate the existence of gravitational waves using classical analysis using the Weyl tensor components and Newman-Penrose formalism [38]. Having calculated the above-mentioned tensors and sample basis (56), one may notice, that four-vector $a^{\mu }\left(\sigma \right)$ is purely real. One may thus construct a Newman-Penrose tetrad around it, fitting to the geometry of the system, as follows

$$\begin{array}{ccc}\hfill l^{\mu }& \equiv & a^{\mu }\left(\sigma \right)\hfill \end{array}$$

(95)

$$\begin{array}{ccc}\hfill n^{\mu }& \equiv & {\displaystyle \frac{1-sin\sigma }{{cos}^2\sigma }}\left(1,1,0,0\right)\hfill \end{array}$$

(96)

$$\begin{array}{ccc}\hfill m^{\mu }& \equiv & {\displaystyle \frac{1}{\sqrt{2}\left(cos\frac{\sigma }{2}+sin\frac{\sigma }{2}\right)}}\left(-{\displaystyle \frac{icos\sigma }{1+sin\sigma }},-{\displaystyle \frac{icos\sigma }{1+sin\sigma }},-i,1\right)\hfill \end{array}$$

(97)

$$\begin{array}{ccc}\hfill {\overline{m}}^{\mu }& \equiv & {\displaystyle \frac{cos\frac{\sigma }{2}+sin\frac{\sigma }{2}}{\sqrt{2}}}\left({\displaystyle \frac{icos\sigma }{1+sin\sigma }},{\displaystyle \frac{icos\sigma }{1+sin\sigma }},i,1\right)\hfill \end{array}$$

(98)

The above four-vectors satisfy all the tetrad requirements and lead to only two non-zero NP scalars

$$\begin{array}{ccc}\hfill {\Psi }_3& =& 8C_1\left[(i\sqrt{2}-1)sin\left({\displaystyle \frac{\sigma }{2}}\right)-(i\sqrt{2}+1)cos\left({\displaystyle \frac{\sigma }{2}}\right)\right]\hfill \end{array}$$

(99)

$$\begin{array}{ccc}\hfill {\Psi }_4& =& 4C_1\left[1-2i\sqrt{2}cos\left(\sigma \right)-3sin\left(\sigma \right)\right]\hfill \end{array}$$

(100)

what is confirmed in the supplementary materials. Scalar ${\Psi }_3$ can be zeroed by a rotation around $n^{\mu }$ without modifying ${\Psi }_4$ and the system under consideration is thus Petrov type III or N. However, taking into account the non-zero Ricci tensor and the Bel criteria, considered spacetime must be Petrov type III, since due $C^{\mu \nu \alpha \beta }$ is built from reversible metric (89), thus there does not exist any vector ${\xi }_{\beta }$ satisfying $C^{\mu \nu \alpha \beta }{\xi }_{\beta }=0$.

Therefore, finally, spacetime described by Alena Tensor with only electromagnetic field may be interpreted as a certain form of the Kundt solution with dust [39] of Petrov type III, similar to described in [40,41]. One may also notice, that additional fields added to the Alena Tensor depending on the new null directions should break the obtained degeneracy leading to the general Petrov type I case.

One may also substitute an example basis (56) into Weyl tensor to analyze its values. Table 1 presents the values of the key components of the Weyl tensor in this basis.

Table 1. Component values of the Weyl tensor.

Component	Value
$C^{0212}$	${\displaystyle \frac{i(16C_1-5C_2)cos\left(\sigma \right)-7i{C}_{2}cos\left(3\sigma \right)}{\sqrt{2}}}+8C_{1}sin\left(\sigma \right)-20C_2{cos}^2\sigma sin\left(\sigma \right)$
$C^{1313}$	0
$C^{0202}$	$4C_1\left(1+3cos\left(2\sigma \right)-2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{1010}$	$4C_1\left(1-3cos\left(2\sigma \right)+2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{2323}$	0
$C^{1213}$	0
$C^{1323}$	0

Table 1. Component values of the Weyl tensor.

Component	Value
$C^{0212}$	${\displaystyle \frac{i(16C_1-5C_2)cos\left(\sigma \right)-7i{C}_{2}cos\left(3\sigma \right)}{\sqrt{2}}}+8C_{1}sin\left(\sigma \right)-20C_2{cos}^2\sigma sin\left(\sigma \right)$
$C^{1313}$	0
$C^{0202}$	$4C_1\left(1+3cos\left(2\sigma \right)-2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{1010}$	$4C_1\left(1-3cos\left(2\sigma \right)+2i\sqrt{2}sin\left(2\sigma \right)\right)$
$C^{2323}$	0
$C^{1213}$	0
$C^{1323}$	0

One may then solve the system of equations (37, 55, 64) presenting the results only as a function of $I_o$ and $\sigma$. Due to the complex relationships between variables, analytical solution and obtained results are presented in supplementary file. Weyl tensor component values were calculated for the value $I_o=\sqrt{1+{\displaystyle \frac{1}{\sqrt{2}}}}$ adopted for the analysis (65) and for chosen solution $\phi \left(I_o\right),\theta \left(I_o\right)$. 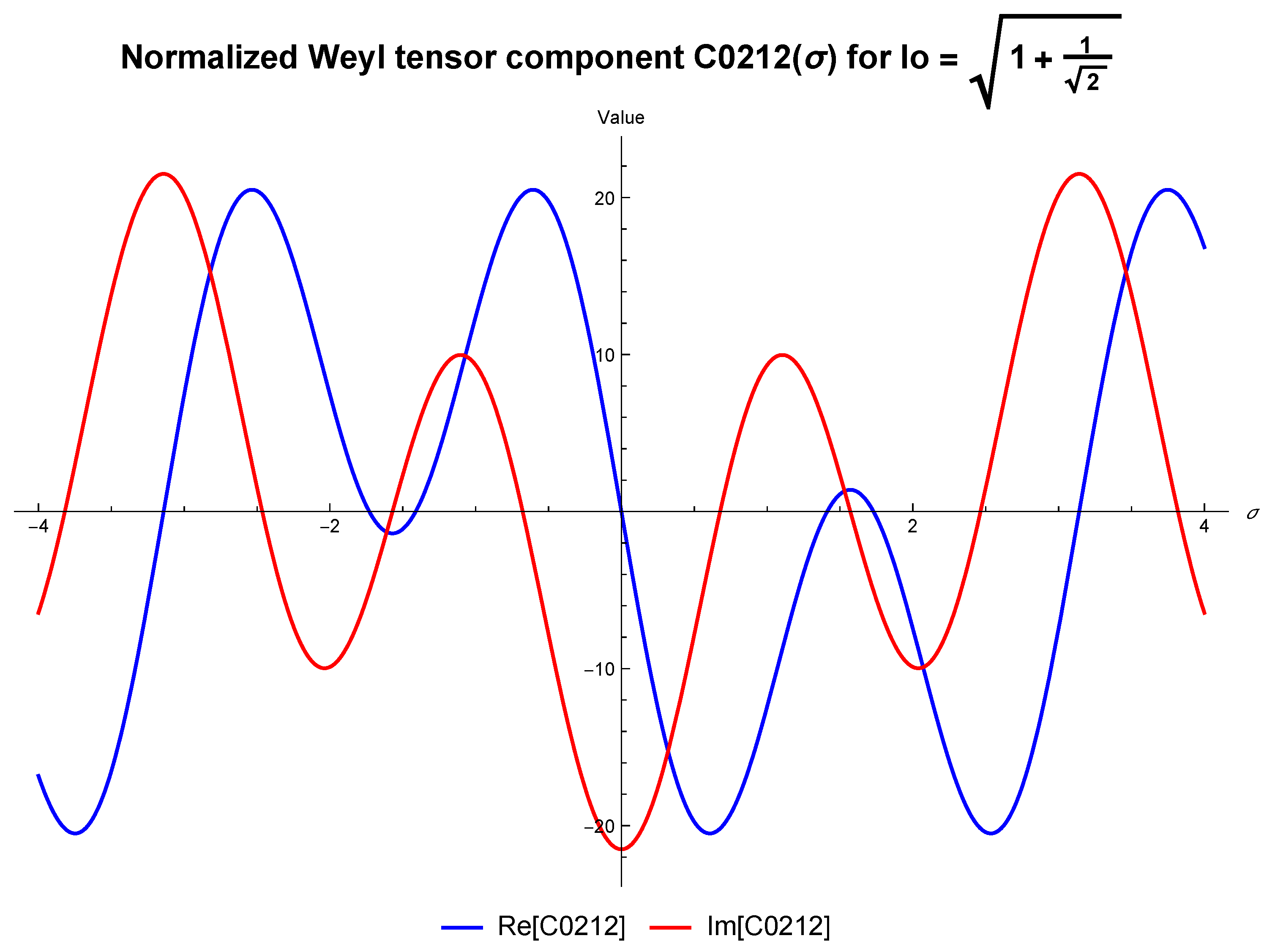The Figure 2 below clearly shows the wave nature of the $C^{0212}$ component of the Weyl tensor, presenting the result of the calculations performed. Obtained Weyl tensor component $C^{0212}$ seems to encode the variation of some curvature field along the propagating direction $\sigma$.

Gravitational waves are often modeled using Gaussian impulse as in [42], but this can also be done using the dependence of ${\Psi }_4$ on $\sigma$. One may therefore show the deformation effects for an example arrangement of test particles on a circle. In the supplementary materials there are calculations and a gif file presenting animation of this distortion. This animation reveals the typical quadrupolar nature of spacetime distortions induced by gravitational waves (characteristic twisting and stretching).

Figure 3. Deformation visualization for particles on a circle.

Figure 3. Deformation visualization for particles on a circle.

The above Weyl tensor components are actually normalized. One may thus present the main GR equation in the Alena Tensor notation (12) and represent it using the vacuum pressure $2p_{\Lambda }\equiv {\displaystyle \frac{\Lambda c^4}{4\pi G}}={\Lambda }_{\rho }$ as follows

$$G^{\alpha \beta }+2p_{\Lambda }{\mathbb{k}}^{\alpha \beta }=2T^{\alpha \beta }=2{\Lambda }_{\rho }\stackrel{⌢}{K^{\alpha \beta }}=4p_{\Lambda }\stackrel{⌢}{K^{\alpha \beta }}$$

(101)

Since the obtained Weyl tensor is normalized (by $\Lambda$ - classical notation or by ${\Lambda }_{\rho }$ - Alena Tensor notation) this means that the interpretation from (20) that gravitational waves in the Alena Tensor approach are in fact propagating vacuum pressure disturbances also seems to be correct.

It is also worth noting that the obtained metric term $e^{-q}{\eta }^{\alpha \beta }={\displaystyle \frac{\mathbb{k}}{4}}{\eta }^{\alpha \beta }$ can in principle be interpreted as a vacuum energy contribution (effective cosmological constant) as in [43,44] playing the role of a metric scaling factor, as e.g. described in [45].

Additionally, one may invoke the scalar field $\varphi$ associated with the presence of matter, where $e^{\varphi }={\displaystyle \frac{1}{{\mu }_r}}$. It is known from Section 2.2 that $e^{\varphi }$ is responsible for the presence of sources and in their absence ${\mu }_r=1$. Therefore, interpreting whole ${{\rm Y}}^{\alpha \beta }$ as the wave amplitude tensor one would get representation ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha \beta }={\mathcal{P}}_o{\overline{h}}^{\alpha \beta }{e}^{\varphi }$ which would also allow to search for $e^{\varphi }$ as a certain wave function.

This approach allows for two simplifications related to the analysis of gravitational waves. Considering the force $f_{gr}^{\alpha }$ responsible for effects related to gravity as shown in (14) and extracting the acceleration ${\mathcal{A}}^{\alpha }$ from it, one gets

$$\varrho {\mathcal{A}}^{\alpha }\equiv f_{gr}^{\alpha }=\varrho \left({\displaystyle \frac{d\varphi }{d\tau }}{U}^{\alpha }-c^2{\partial }^{\alpha }\varphi \right)\to c^2\square \varphi ={\gamma }^2{\displaystyle \frac{d^2\varphi }{d{t}^2}}-{\partial }_{\alpha }{\mathcal{A}}^{\alpha }$$

(102)

since according amendment from [10] ${\partial }_{\alpha }\gamma U^{\alpha }=0$.

As shown in [9], $\varphi$ is directly related to the effective potential in gravitational systems which can be calculated from the GR equations. This would allow searching for propagating changes of the effective potential itself ($\square \varphi =0$) similarly as was postulated in [46]. It would significantly simplify both the calculations and perhaps the methods of detecting gravitational waves, for example, using the approach discussed in [47].

The second potential simplification results from the possibility of analyzing only the Poynting four-vector ${{\rm Y}}^{\alpha 0}$ as ${\displaystyle \frac{1}{{\mu }_r}}{{\rm Y}}^{\alpha 0}={\mathcal{P}}_o{\overline{h}}^{\alpha 0}{e}^{\varphi }$ which might also help simplify the calculations and search for experimental proof for the Alena Tensor approach.

4. Conclusion and Discussion

As shown in the above article, the Alena Tensor ensures the existence of gravitational waves and allows their physical interpretation, providing key tools for their further analysis including the ability to calculate and visualize Weyl tensor components. The obtained decomposition of the electromagnetic field stress-energy tensor (57) allows for further analysis of metrics for curved spacetimes (e.g. extending obtained solution for other fields) and also to use the proposed null basis for further Alena Tensor development in the framework of conformal geometry, the NP formalism and the description of photons in QFT. It also seems reasonable to generalize above results for more fields or non-linear electromagnetism using e.g. approach presented in [48] and search for a description of elementary particles that will provide relatively stable solutions to the obtained equations, perhaps also taking into account new approaches, such as those proposed in [49].

It remains an open question whether the Alena Tensor is a correct way to describe physical systems, but this paper shows that it exhibits many properties that are expected from such a description, including the existence of gravitational waves whose behavior and description agrees with GR. The obtained picture of Kundt spacetime with dust of Petrov III type would suggest, that in gravitational waves for sources that can be treated simplistically as the result of the existence of an electromagnetic field alone, one should be able to observe effects related to non-zero ${\Psi }_3$ (visible twisted components). Perhaps, however, generalization of the Alena Tensor to other fields (e.g. electroweak) will correct the above conclusion, providing the possibility of experimental verification of the obtained result for more realistic sources.

It is worth noting that the obtained non-zero form of the Weyl tensor (89) constructed from the metric ${\mathbb{k}}^{\mu \nu }$ will not change regardless of the fields considered and no matter how many null vectors the metric consists of (assuming more complex fields than electromagnetism). This Weyl tensor has also an important property: for any tetrad considered in curved spacetime, all NP scalars become zero, and they remain non-zero only for tetrads constructed on the background Minkowski metric. This means that gravitational waves derived from Alena Tensor do not exist in curved spacetime and can be detected only against the background of the Minkowski metric. Therefore, according to the postulate (19), gravitational waves are not "local fluctuations" of curvature but global effects of the difference of geometry with respect to a flat background. This result has a rather intuitive interpretation and means that, according to the equivalence principle, observers in curved spacetime do not experience gravity in any form, including gravitational waves, because their tetrad "co-curves" with the geometry.

The above form of the Weyl tensor can thus be treated as a formal geometry of the equivalence principle and as a requirement for every physically possible solution of GR, which would, however, require a separate proof. This direction of further research also seems very important, because it would provide a formal justification for the fact that the measurability of gravity is relational, not absolute, and also offers a new way of considering quantum gravity: not so much as field fluctuations, but as fluctuations of the geometric background with respect to the algebraically defined Weyl tensor.

Additionally, quite surprisingly, this approach naturally forces the existence of the Higgs field and this field turns out to be necessary to even consider curved spacetime, leading to symmetry breaking in the described case of GR with electromagnetism. The spontaneously appearing faithful reproduction of the Higgs potential may of course be a completely coincidental result, but it may also be an indication that the proposed approach is worth further investigation and development for other fields (electroweak or more general solutions), to obtain complete picture of unification. This direction of research seems to be particularly important. The unification of gravity with electroweak interactions has been analyzed so far, among others, in the context of symmetry breaking and gauge geometry [50,51], through the prism of the influence of gravity on the global properties of quantum vacuum [52,53], analogies between spin-gravity coupling and the Higgs mechanism [54] or analysis of chiral fermions and CPT symmetry in the presence of curvature [55,56]. It seems that the approach considered in the article best fits into the last of these research directions, due to the possibility of analyzing the structure of the Weyl curvature, the potential asymmetry of gravitational waves (related to ${\Psi }_3$) and because it actually touches upon chirality in the spatial and propagation sense, although not directly in the fermion sense.

The connection between Alena Tensor and the Killing tensor obtained in this paper reveals a deep, nonlinear connection between the matter distribution and the geometry and symmetries of spacetime. These results show that the matter distribution in this approach is not arbitrary, but precisely tuned to the geometry and hidden symmetries of spacetime, which allows for their further analysis in the language of Killing tensors and conformal Weyl curvature.

As indicated in the introduction, the Alena Tensor is a new approach and certainly requires a lot of work and further research. For example, one may consider modifications and extensions, adapting it to e.g. non-conserved energy-momentum frameworks as presented in [57] or to the generalizations of GR [58] and other known gravity models [59]. This would open up additional possibilities for analyzing non-classical solutions and new directions of reasoning contained in these publications, which could also increase the unification potential of the Alena Tensor. An equally interesting research direction seems to be the use of the smooth transition between classical, quantum and curvilinear descriptions provided by the Alena Tensor to reanalyze existing studies, such as [60].

The author hopes that the results obtained in this article will facilitate further use of discussed approach as a tool that can help develop many different concepts. It seems that its further analysis may provide useful descriptions of the transformation between curved and flat spacetime and bring new insights that will contribute to a better understanding of issues related to the broadly understood unification of physical theories.

5. Statements

All data that support the findings of this study are included within the article (and any supplementary files).

During the preparation of this work the author did not use generative AI or AI-assisted technologies.

Author did not receive support from any organization for the submitted work.

Author have no relevant financial or non-financial interests to disclose.