Submitted:
03 February 2025
Posted:
04 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Brief Review of the Eringen’s Constitutive Elasticity
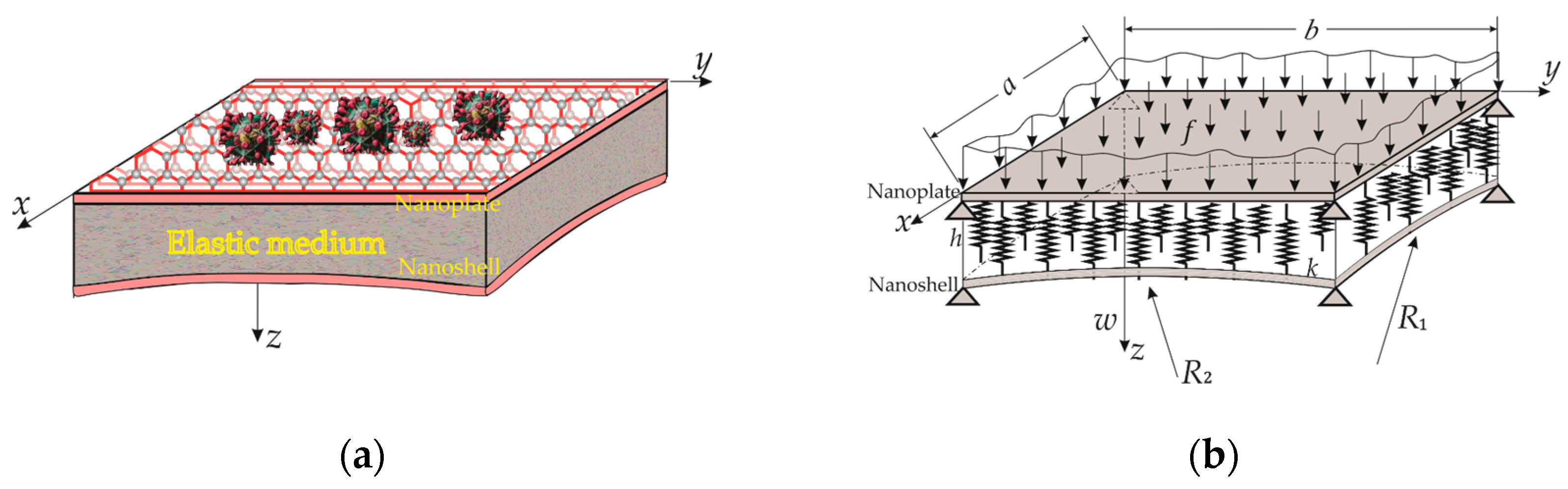
3. Mathematical Formulations of the Equations of Motion for an Orthotropic Nano-Plate
4. Mathematical Formulation of the Equations of Motion for an Orthotropic Doubly Curved Shallow Nano-Shell
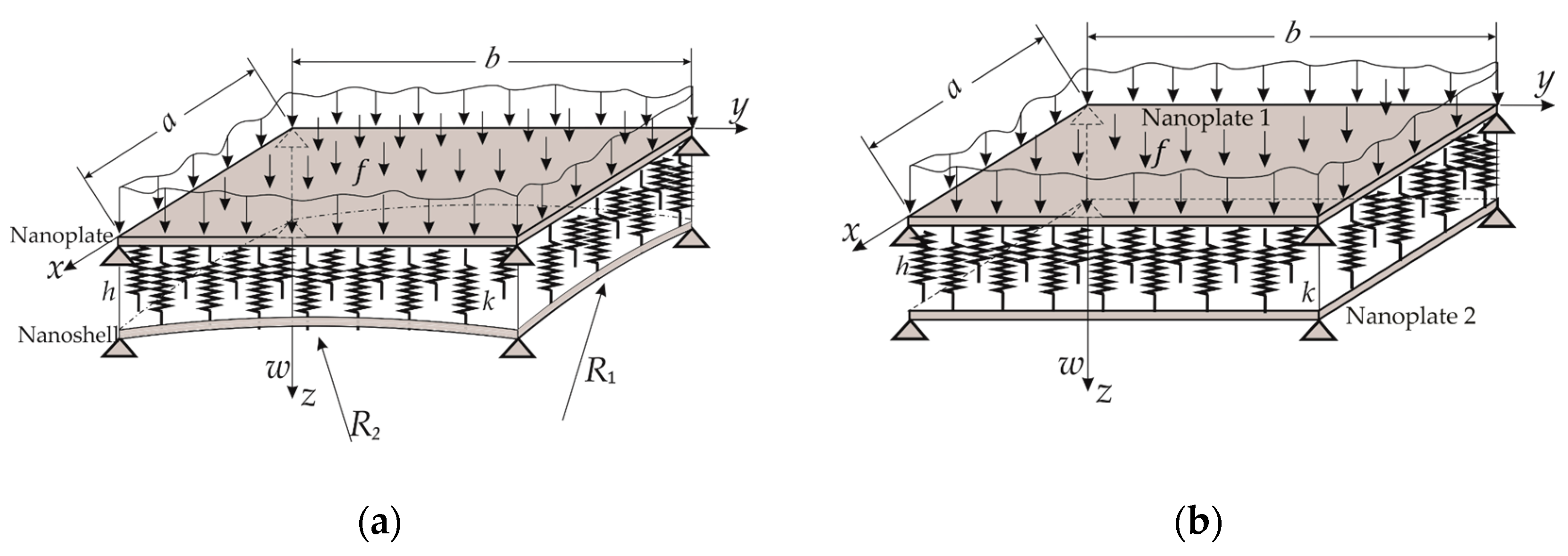
5. Formulation of Model ECSNPS
6. Solution Methodology for Determining the Natural Frequencies of ECSNPS
7. Forced Vibration of the Damped ECSNPS
8. Results and Discussion
8.1. Natural Frequencies Analysis
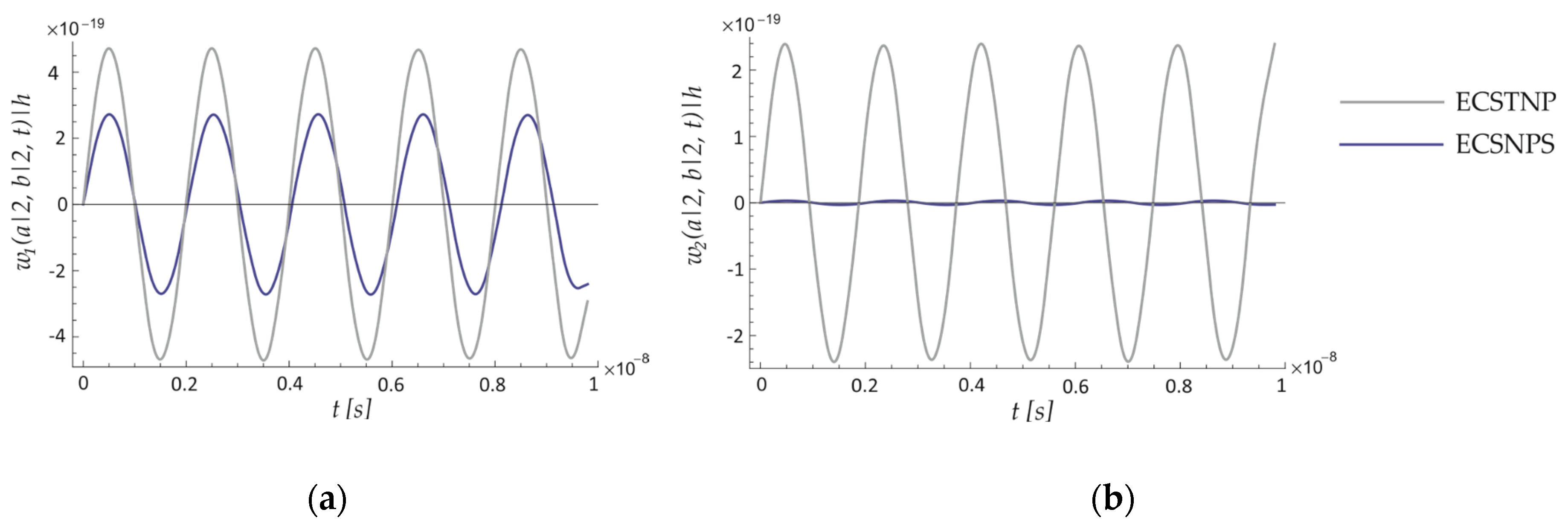
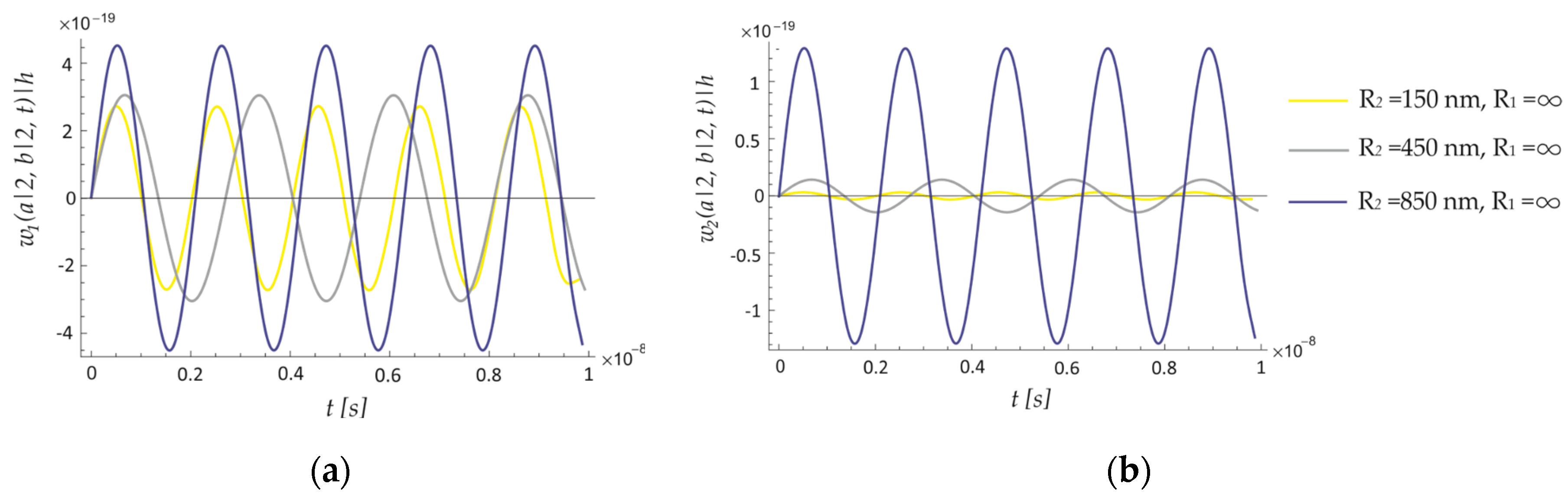
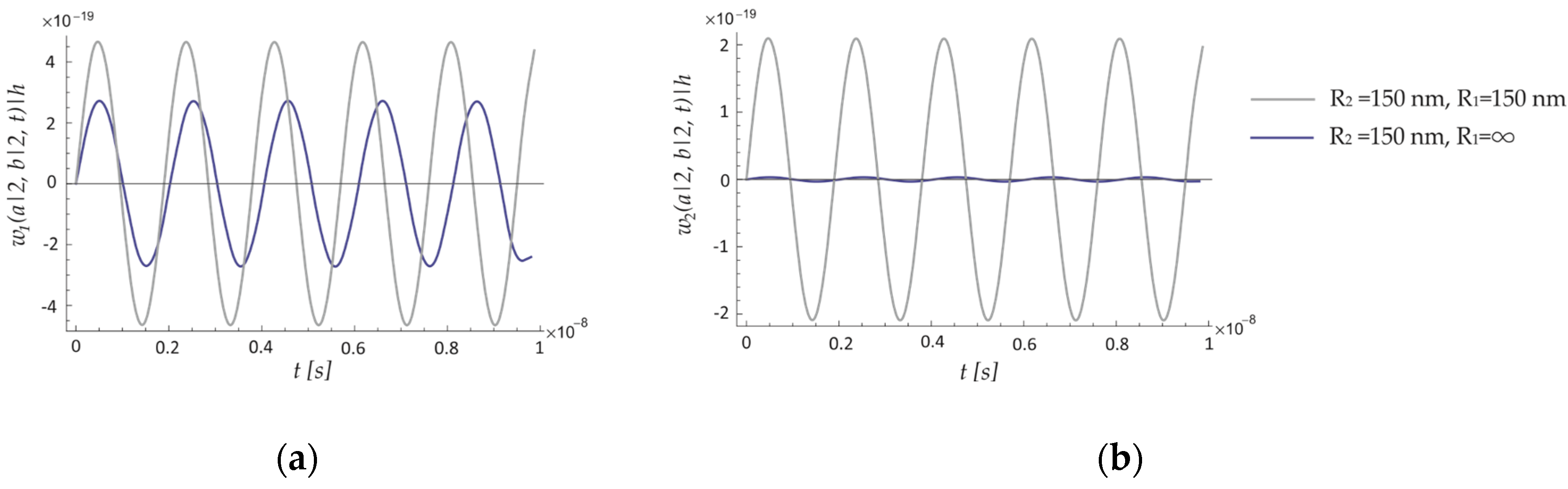
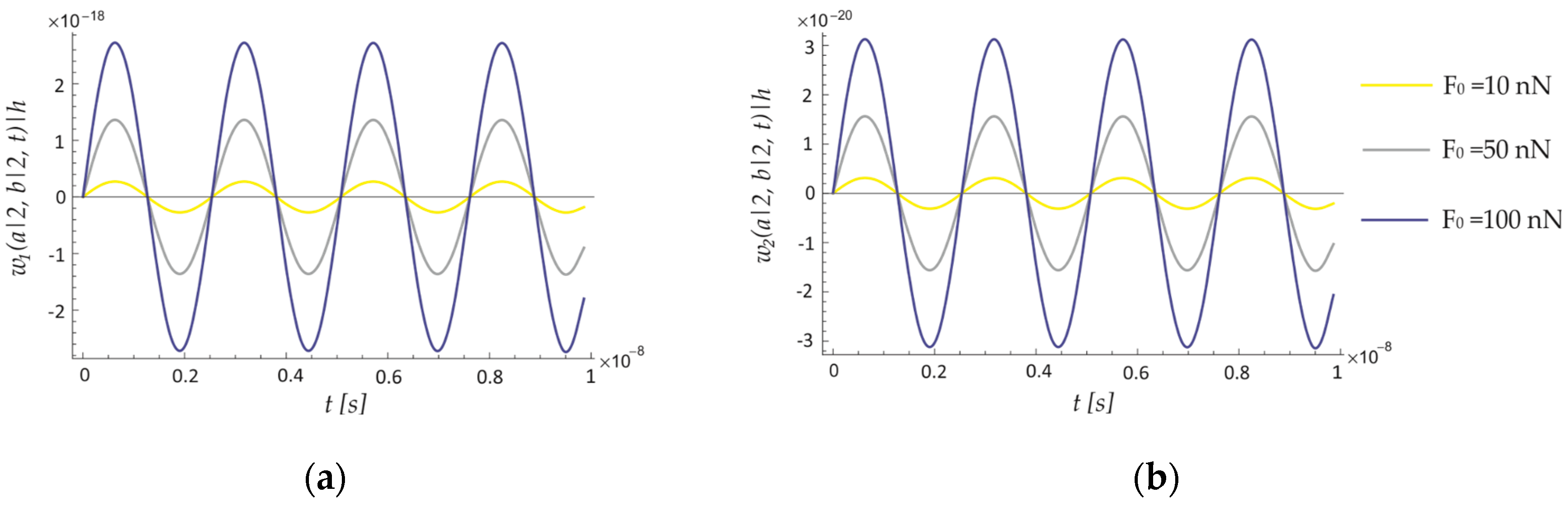
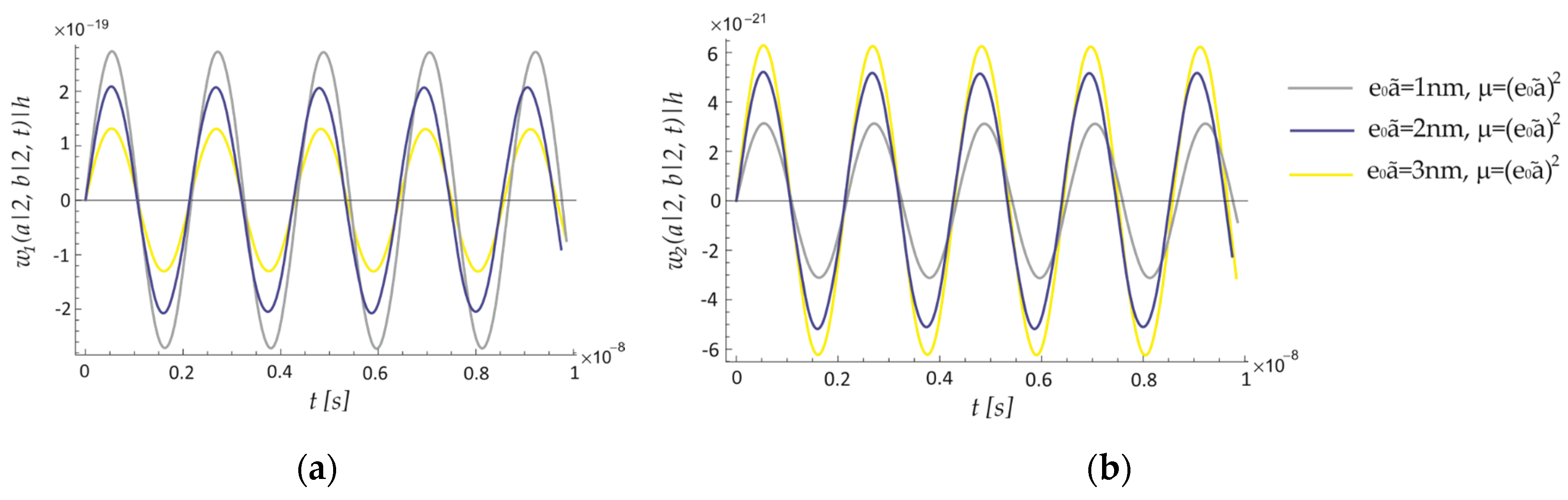
8.2. Forced Vibration of the ECSNPS
9. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECSNPS | Elastically Connected System of Nano-Plate and nano-Shell |
| ECSTNP | Elastically Connected System of Two Nano-Plates |
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equations |
Appendix A
References
- Li, X.; Warzywoda, J.; McKenna, G.B. Mechanical responses of a polymer graphene-sheet nano-sandwich. Polymer 2014, 55, 4976–4982. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yao, L. Analysis of the vibration behaviors of rotating composite nano-annular plates based on nonlocal theory and different plate theories. Appl. Sci. 2021, 12, 230. [Google Scholar] [CrossRef]
- Lam, D. C.; Yang, F.; Chong, A. C. M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids. 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Eringen, A. C.; Edelen, D. G. B. On nonlocal elasticity. Int. Jour. of Eng. Scie. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Jour. of Appl. Physics. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A. C. Nonlocal continuum field theories; Springer Science & Business, 2002. [Google Scholar]
- Cheng, N.; Juntian, T.A.N.G.; Peng, F.E.N.G.; Zhihao, H.A.O.; Zhang, Y.; Chang, M. Experimental and theoretical study on flexural performance of lightweight sandwich panels using FRP connectors. Case Studies in Const. Materials 2024, 21, e03947. [Google Scholar] [CrossRef]
- Zhou, S.; Qi, L.; Zhang, R.; Li, A.; Ren, F.; Zheng, Z.; Qiao, J.; Sun, Y.; Zhou, S. Analysis of the electromechanical responses of sandwich circular nano-plate based on flexoelectric nano-ultrasonic transducer. Appl. Math. Mod 2025, 137, 115697. [Google Scholar] [CrossRef]
- Marchetti, F.; Ege, K.; Leclere, Q.; Roozen, N.B. On the structural dynamics of laminated composite plates and sandwich structures; a new perspective on damping identification. Jour. of Sound and Vib 2020, 474, 115256. [Google Scholar] [CrossRef]
- Di Sciuva, M.; Sorrenti, M. Bending, free vibration and buckling of functionally graded carbon nanotube-reinforced sandwich plates, using the extended Refined Zigzag Theory. Comp. Struct 2019, 227, 111324. [Google Scholar] [CrossRef]
- Atanasov, M. S.; Karličić, D.; Kozić, P. Forced transverse vibrations of an elastically connected nonlocal orthotropic double-nanoplate system subjected to an in-plane magnetic field. Acta Mech. 2017, 228, 2165–2185. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Noormohammadi A., O.; Rabczuk, T. Frequency characteristics of multiscale hybrid nanocomposite annular plate based on a Halpin–Tsai homogenization model with the aid of GDQM. Appl. Sci 2020, 10, 1412. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Zhang, J. Dynamic response of double-layer rectangular sandwich plates with graded foam cores under blast loading. Intern. Jour. of Impact Eng 2025, 195, 105141. [Google Scholar] [CrossRef]
- Fu, T.; Wang, X.; Hu, X.; Rabczuk, T. Impact dynamic response of stiffened porous functionally graded materials sandwich doubly-curved shells with Arc-type auxetic core. Intern. Jour. of Impact Eng. 2024, 191, 105000. [Google Scholar] [CrossRef]
- Atanasov, M. S. Stability and forced vibration of coupled nano-structures. Doctoral dissertation. 2023. [Google Scholar]
- Pavlovic I., R.; Pavlovic, R.; Janevski, G.; Despenic, N.; Pajkovic, V. Dynamic behavior of two elastically connected nanobeams under a white noise process. Facta Univ., series: Mech. Eng. 2020, 18, 219–227. [Google Scholar] [CrossRef]
- Leissa, A. W.; Kadi, A. S. Curvature effects on shallow shell vibrations. Jour. of Sound and Vib. 1971, 16, 173–187. [Google Scholar] [CrossRef]
- Bhimaraddi, A. Free vibration analysis of doubly curved shallow shells on rectangular planform using three-dimensional elasticity theory. Inter. Jour. of Sol. and Struct. 1991, 27, 897–913. [Google Scholar] [CrossRef]
- Dereli, E.; Mbendou II, J.; Patel, V.; Mittelstedt, C. Analytical and numerical analysis of composite sandwich structures with additively manufactured lattice cores. Comp. Part C: Open Access 2024, 14, 100484. [Google Scholar] [CrossRef]
- Arefi, M. Analysis of a doubly curved piezoelectric nano shell: nonlocal electro-elastic bending solution. Eur. Jour. of Mech-A/Solids. 2018, 70, 226–237. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D. On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comp. Meth. in Appl. Mech. and Eng. 2020, 359, 112767. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S. A. Free vibration analysis of orthotropic doubly-curved shallow shells based on the gradient elasticity. Comp. Part B: Eng. 2013, 45, 1448–1457. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano-spherical shell based on the modified couple stress theory. Inter. Jour. of Mech. Sci. 2016, 115, 501–515. [Google Scholar] [CrossRef]
- Turan, F.; Karadeniz, M.; Zeren, E. Free vibration and buckling behavior of porous orthotropic doubly-curved shallow shells subjected to non-uniform edge compression using higher-order shear deformation theory. Thin-Wall. Struct. 2024, 205, 112522. [Google Scholar] [CrossRef]
- Hwu, C.; Hsu, H. W.; Lin, Y. H. Free vibration of composite sandwich plates and cylindrical shells. Comp. Struct, 2017, 171, 528–537. [Google Scholar] [CrossRef]
- Reddy, J. N. Mechanics of laminated composite plates and shells: theory and analysis; CRC press, 2004. [Google Scholar]
- Reddy, J. N. Theory and analysis of elastic plates and shells; CRC press, 2006. [Google Scholar]
- Karličić, D.; Murmu, T.; Adhikari, S.; McCarthy, M. Non-local Structural Mechanics; John Wiley and Sons, 2015. [Google Scholar]
- Amabili, M. Nonlinear vibrations and stability of shells and plates; Cambridge Univ. Press: New York, 2008. [Google Scholar]
- Pouresmaeeli, S.; Ghavanloo, E.; Fazelzadeh, S. A. Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Comp. Struct. 2013, 96, 405–410. [Google Scholar] [CrossRef]
- Radić, N.; Jeremić, D.; Mijatović, B. Vibration analysis of orthotropic double-nanoplate system subjected to unidirectional in-plane magnetic field with various boundary conditions. Jour. of Mech. and Civil Eng. 2018, 15, 59–76. [Google Scholar]
- Kelly, S. G. Mechanical vibrations: theory and applications. Cengage learning. 2012. [Google Scholar]
- Oniszczuk, Z. Free transverse vibrations of an elastically connected rectangular simply supported double-plate complex system. Jour. of Sound and Vib. 2000, 236, 595–608. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Forced transverse vibrations of an elastically connected complex rectangular simply supported double-plate system. Jour. of Sound and Vib. 2004, 270, 997–1011. [Google Scholar] [CrossRef]

| a b h | ||
| TPa TPa TPa | kg/m3 nm | nm nm GPa/nm |
| 2.434 2.473 1.039 | 0.197 6316 0.129 | 10 4.5 0.075 |
| n=1 n=2 n=3 |
4.61953×1011 | 2.99085×1012 | 7.38604×1012 | 1.21507×1013 | |
| m=1 | 9.31595×1011 | 2.30851×1012 | 1.03814×1013 | 1.64871×1013 | |
| 1.46995×1012 | 2.15757×1012 | 1.15336×1013 | 1.82203×1013 | ||
| n=1 n=2 n=3 |
5.70087×1011 | 5.67846×1012 | 6.99782×1012 | 1.36309×1013 | |
| m=2 | 1.01025×1012 1.52519×1012 |
4.20984×1012 3.45108×1012 |
1.01672×1013 1.13942×1013 |
1.67344×1013 1.82509×1013 |
|
| n=1 n=2 n=3 |
7.34647×1011 | 6.85678×1012 | 7.19172×1012 | 1.51839×1013 | |
| m=3 | 1.13034×1012 1.61201×1012 |
5.94912×1012 4.78913×1012 |
9.69245×1012 1.11226×1013 |
1.71264×1013 1.83239×1013 |
|
| n=1 n=2 n=3 |
3.84471×1011 | 2.07360×1012 | 5.08588×1012 | 8.36769×1012 | |
| m=1 | 5.86577×1011 | 1.35492×1012 | 5.97785×1012 | 9.49374×1012 | |
| 8.24879×1011 | 1.19378×1012 | 6.20668×1012 | 9.80507×1012 | ||
| n=1 n=2 n=3 |
4.33619×1011 | 3.68099×1012 | 4.50109×1012 | 8.78749×1012 | |
| m=2 | 6.24265×1011 8.54911×1011 |
2.40523×1012 1.86919×1012 |
5.77111×1012 6.10670×1012 |
9.49987×1012 9.78197×1012 |
|
| n=1 n=2 n=3 |
5.04771×1011 | 4.25083×1012 | 4.25083×1012 | 9.17758×1012 | |
| m=3 | 6.77858×1011 8.95666×1011 |
3.33059×1012 2.56714×1012 |
5.40006×1012 5.92601×1012 |
9.54656×1012 9.76398×1012 |
|
| n=1 n=2 n=3 |
3.44521×1011 | 1.53112×1012 | 3.71222×1012 | 6.10881×1012 | |
| m=1 | 4.49233×1011 | 9.63276×1011 | 4.11125×1012 | 6.52950×1012 | |
| 5.85347×1011 | 8.49677×1011 | 4.19978×1012 | 6.63473×1012 | ||
| n=1 n=2 n=3 |
3.73072×1011 | 2.64494×1012 | 3.19060×1012 | 6.25442×1012 | |
| m=2 | 4.78425×1011 6.15194×1011 |
1.66611×1012 1.28667×1012 |
3.95389×1012 4.12822×1012 |
6.50982×1012 6.61318×1012 |
|
| n=1 n=2 n=3 |
4.11932×1011 | 2.96932×1012 | 2.96932×1012 | 6.39772×1012 | |
| m=3 | 5.11162×1011 6.42609×1011 |
2.28870×1012 1.75086×1012 |
3.68065×1012 4.00041×1012 |
6.51242×1012 6.59264×1012 |
|
| Oniszczuk [33,34] | Present study | ||||
| n=1 n=2 n=3 |
52.8 | 72.0 | 52.7975095047 | 72.0248360629 | |
| m=1 | 84.5 | 97.7 | 84.4760152075 | 97.6534543441 | |
| 137.3 | 145.8 | 137.2735247122 | 145.7532867105 | ||
| n=1 n=2 n=3 |
179.5 | 186.1 | 179.5115323161 | 186.0763021839 | |
| m=2 | 211.2 264.0 |
216.8 268.5 |
211.1900380189 263.9875475236 |
216.7976756296 268.4947397018 |
|
| n=1 n=2 n=3 |
390.7 | 393.8 | 390.7015703349 | 393.7609897669 | |
| m=3 | 422.4 475.2 |
425.2 477.7 |
422.3800760378 475.1775855425 |
425.2116280556 477.6962819637 |
| Ghavanloo E. et al. [22] | Presented study | |
| Ω1 | 5.0843 | |
| Ω2 | 12.2689 | |
| Ω3 | 13.4459 | |
| Ω4 | 20.1542 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





