Two-Band Superconductivity and Transition Temperature Limited by Thermal Fluctuations in Ambient Pressure La_3-xPr_xNi2O_7-d (x = 0.0, 0.15, 1.0) Thin Films

1. Introduction

High-temperature superconductivity in nickelates had predicted by first principles calculations [4] in 1999 and experimentally discovered in several nanometers thick Nd_1-xSr_xNiO₂ films [5] twenty years later. Recently, high-temperature superconductivity in highly compressed bulk nickelate phase La₃Ni₂O_7-δ (LNO-327) has been reported [6]. Despite a fact that this phase had been synthesized more than four decades ago [7], and it had been intensively studied [8,9,10,11] since then (including studies at high pressure [12]), only experiments at pressures above 10 GPa allowed to detect the high-temperature superconductivity in bulk La₃Ni₂O_7-δ samples. Very recently two research groups [1]^, [2] reported on the observation of ambient pressure superconducting state with $T_{c,onset}\cong 40K$ and $T_{c,zero}=2-9K$ in a few nanometers thick epitaxial La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15) films. It should be noted that nearly two decades ago [13], epitaxial La_n+1Ni_nO_3n+1 (n = 1,2,3,∞) films with thickness 130-200 nm had been fabricated and studied; however, temperature dependent resistivity $\rho \left(T\right)$ in these films was measured in the range of $300K\lesssim T\lesssim 900K$ [13] only.

Here from an analysis of temperature dependent self-field critical current density, $J_c\left(sf,T\right)$, reported for La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15, 1.0) films [1,2,3] we extracted the ground state in-plane London penetration depth, ${\lambda }_{ab}\left(0\right)$, the Ginzburg-Landau parameter, ${\kappa }_c\left(0\right)$, BCS ratios (the gap-to-transition temperature ratio, ${\displaystyle \frac{2\mathsf{\Delta }\left(0\right)}{k_B{T}_c}}$, and relative jump in electronic specific heat at the transition temperature, ${\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}$), and explained a large width of the resistive transition as manifestation of low superfluid density in these films. We also found that two-band s-wave superconductivity is a preferable model for the order parameter in the La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15, 1.0) films [1,2,3] for existing experimental $J_c\left(sf,T\right)$ data.

2. Fundamental Parameters for La_3-xPr_xNi₂O_7-δ (x = 0.0; 0.15; 1.0) Films

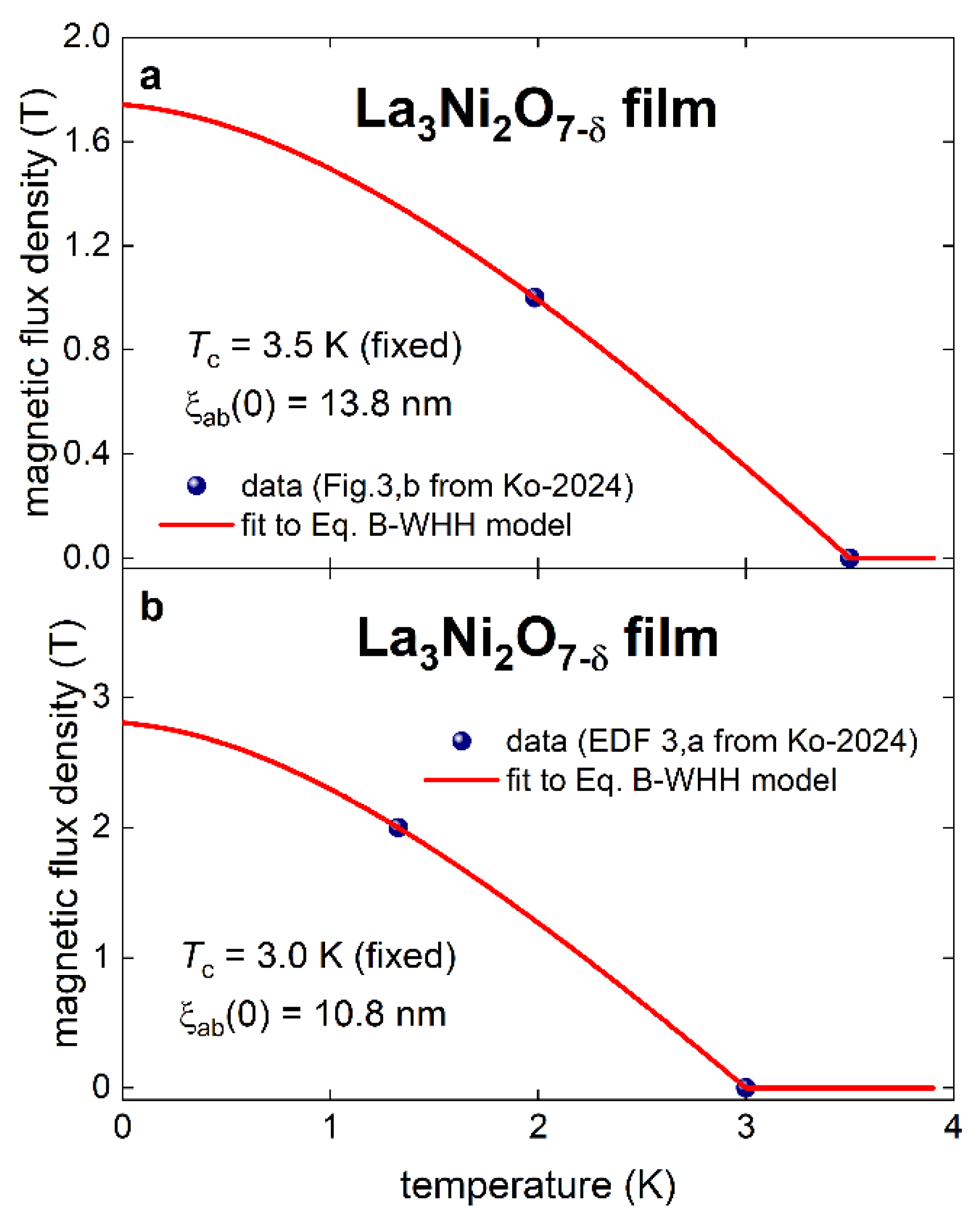
2.1. Transition Temperature and Coherence Length Definitions

Superconducting coherence length, $\xi \left(T\right)$, is one of two fundamental lengths of any superconductor. Commonly accepted simple approach to determine the ground state coherence length, $\xi \left(0\right)$, is to fit the upper critical field data, $B_{c2}\left(T\right)$, to the Ginzburg-Landau expression:

$$B_{c2}\left(T\right)={\displaystyle \frac{{\varphi }_0}{2\pi {\xi }^2\left(T\right)}}$$

(1)

where ${\varphi }_0={\displaystyle \frac{h}{2e}}$ is the superconducting flux quantum, $h$ is the Planck’s constant, $e$ is the electron charge. From several available analytical approximations of Eq. 1 within frames of the Werthamer-Helfand-Hohenberg (WHH) theory [14,15], here we used two expressions [16,17]:

$$B_{c2,c}\left(T\right)={\displaystyle \frac{1}{0.693}}\times {\displaystyle \frac{{\varphi }_0}{2\pi {\xi }_{ab}^2\left(0\right)}}\times \left(\left(1-{\displaystyle \frac{T}{T_c}}\right)-0.153\times {\left(1-{\displaystyle \frac{T}{T_c}}\right)}^2-0.152\times {\left(1-{\displaystyle \frac{T}{T_c}}\right)}^4\right)$$

(2)

$$B_{c2,c}\left(T\right)={\displaystyle \frac{{\varphi }_0}{2\pi {\xi }_{ab}^2\left(0\right)}}\times \left({\displaystyle \frac{1-{\left(\frac{T}{T_c}\right)}^2}{1+0.42\times {\left(\frac{T}{T_c}\right)}^{1.47}}}\right)$$

(3)

where $B_{c2,c}\left(T\right)$ is the out-of-plane upper critical field, ${\xi }_{ab}\left(0\right)$ is the ground state in-plane coherence length, and ${\xi }_{ab}\left(0\right)$ and $T_c$ are free fitting parameters. Eq. 2 will be designated as B-WHH model [16], and Eq.3 will be designated as PK-WHH [17] model below. From our experience, data fits to Eqs. 2,3 results in very close $\xi \left(0\right)$ and $T_c$ values (but for the purpose of verification of the deduced free fitting parameters we used both fits).

The crucial issue here is the criterion of the upper critical field definition, $B_{c2}\left(T\right)$, which can be applied to available experimental data. Theoreticians rarely discuss this key issue, and experimentalists tend to overestimate (sometimes by manifold) the $B_{c2}\left(T\right)$ values by chosen high resistive criteria [1,2,5,6,18,19,20,21,22]:

$${\displaystyle \frac{R\left(T=T_{c,0.50}\right)}{R\left(T=T_{c,onset}\right)}}=0.50$$

(4)

where $R\left(T=T_{c,onset}\right)$ is the resistance at temperature, where $R\left(T\right)$ starts to drop.

It should be also noted that several research groups [22,23] demonstrated the consequences of applying different resistive criteria, ${\displaystyle \frac{R\left(T=T_c\right)}{R\left(T=T_{c,onset}\right)}}$, for the $B_{c2}\left(T\right)$ definition for infinite-layer nickelate superconductor Nd_1-xSr_xNiO₂. For instance, Wang et al [22] showed that applying different criteria for $R\left(T\right)$ data for Nd_0.775Sr_0.225NiO₂ film results in manifold difference in the $B_{c2}\left(T\right)$ values (and at some temperatures, the difference is more than 20 times). Moreover, different criteria result in different shapes of the temperature dependent $B_{c2}\left(T\right)$. Because the $B_{c2}\left(T\right)$ shape is a primary property which is analyzed by the WHH theory [14,15], this implies that fundamental superconducting parameters deduced by this theory [14,15] depend not from fundamental intrinsic properties of the superconductor, but they determined by the chosen criterion for the upper critical field definition.

In regard of highly compressed La₃Ni₂O₇ phase, the large difference between extrapolated ground state upper critical field value $B_{c2}\left(0\right)$ when different resistive criteria was applied has been demonstrated by Zhang et al. [24].

These issues demonstrate a large uncertainty associated with the one of two fundamental fields of any type-II superconductor, which is unusual for any fundamental property of material.

To resolve this issue, from our view, the criterion should be as strict as it is practically possible:

$${\displaystyle \frac{R\left(T=T_{c,zero}\right)}{R\left(T=T_{c,onset}\right)}}\to 0$$

(5)

because the superconducting state has several unique properties, and one of them is the entire zero resistivity. And because of this, it is incorrect to designate the superconducting coherence length to the state at which the material [25,26,27] (including, nickelates [1,2,5,18,21,28,29,30]) exhibits the resistivity of:

$$\rho \left(T\cong 15K\right)=\left(3-10\right)\times {10}^{-5}\mathsf{\Omega }\times \mathrm{c}\mathrm{m}$$

(6)

which is the respective resistivity value to Eq. 4. The level of resistivity described by Eq. 6 is by several orders of magnitude exceeds the resistivity of noble normal metals at the same temperatures. In term of resistance, Eqs. 4,6 often imply that the $T_c$ is defined [25,26,27] at $R\left(T=T_{c,0.50}\right)\cong \mathrm{5,000}\mathsf{\Omega }$, which cannot be accepted to be the resistance of the superconducting state by any standards.

It should be stressed that initial drop in resistance at $T_{c,onset}$ originates from thermodynamic fluctuations [22,31,32,33] “occurring at temperatures above the superconducting transition temperature” [34], which is $T_{c,zero}$. The strength of these fluctuations can be quantified by two characteristic temperatures, which we calculated for the La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15, 1.0) films below (see Section 4).

Despite strict criterion (Eq. 5) is in a rare use, there are several research groups who implemented this criterion to define the $T_c$ and $B_{c2}\left(T\right)$ [24,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. It should be noted that there are several other strict criteria for the $T_c$ and $B_{c2}\left(T\right)$ definitions (for instance, these criteria are based on the onset of the diamagnetic response [40,49,50,51,52,53,54,55], the peak of the jump in the specific electronic heat [56,57,58,59,60,61,62], or on the onset of the spontaneous Nernst effect [48], or superconducting gap closing [63]). Some research groups use several techniques and criteria [48,64,65,66,67,68,69] to define the $T_c$ and $B_{c2}\left(T\right)$.

However, the majority of reports on thin film superconductors utilize the manifold overestimated criterion (Eq. 4) [1,2,3,5,21,25,26,30,70,71]. In a particular case of the La₃Ni₂O_7-δ films [1], the difference between $T_{c,0.90}=38K$ and $T_{c,zero}\cong 3K$ (see Figures 1,3 in Ref. [1]) is remarkable. Based on that, the difference between the $B_{c2,c}\left(T\right)$ and ${\xi }_{ab}\left(0\right)$ defined by different criteria are enormous. Similar problem is for La_2.85Pr_0.15Ni₂O_7-δ films [2], for which the $T_{c,0.90}=32K$ and $T_{c,zero}\cong 9K$ (see Figure 2 in Ref. [2]).

Additional reason for defining the transition temperature by Eq. 5 is the request to harmonize parameters of another genuine phenomenon of superconductors, which is dissipative-free electric current flow. The current becomes dissipative at some value, known as critical current, $I_c$, and material resistivity at this state [72] is:

$$\rho \left(I=I_c\right)={10}^{-13}\mathsf{\Omega }\times \mathrm{c}\mathrm{m}$$

(7)

which is by eight-nine orders of magnitude lower than the half of normal state resistivity in nickelate films [1,2,3,5,18,21,28,29,30] (Eq. 4).

Considering that the critical current density (which is $J_c={\displaystyle \frac{I_c}{A}}$, where $A$ is cross-section of the conductor) in the absence of external magnetic field, which is designated as the self-field critical current density, $J_c\left(sf,T\right)$, in thin-film superconductors describes by universal equation [73]:

$$J_c\left(sf,T\right)={\displaystyle \frac{{\varphi }_0}{4\pi {\mu }_0}}{\displaystyle \frac{ln\left(\frac{{\lambda }_{ab}\left(T\right)}{{\xi }_{ab}\left(T\right)}\right)+0.5}{{\lambda }_{ab}^3\left(T\right)}}$$

(8)

where ${\mu }_0=4\pi {10}^{-7}{\displaystyle \frac{N}{A^2}}$ is the permeability of free space, and ${\lambda }_{ab}\left(T\right)$ is London penetration depth, there is a request that ${\lambda }_{ab}\left(T\right)$ and ${\xi }_{ab}\left(T\right)$ should be harmonized.

Otherwise, if ${\xi }_{ab}\left(T\right)$ will be defined by Eq. 4, and ${\lambda }_{ab}\left(T\right)$ will be defined by Eq. 7, then the Ginzburg-Landau parameter, ${\kappa }_c\left(T\right)={\displaystyle \frac{{\lambda }_{ab}\left(T\right)}{{\xi }_{ab}\left(T\right)}}$, and the lower critical field:

$$B_{c1}\left(T\right)={\displaystyle \frac{{\varphi }_0}{4\pi }}{\displaystyle \frac{ln\left({\kappa }_c\left(T\right)\right)+0.5}{{\lambda }_{ab}^2\left(T\right)}}$$

(9)

would be undefined for a large temperature range between $T_{c,0.90}=38K$ and $T_{c,zero}=3K$ (see Figures 1,3 in Ref. [1]).

This implies that $T_c$ should be defined by a condition at which both characteristic lengths, ${\lambda }_{ab}\left(T\right)$ and ${\xi }_{ab}\left(T\right)$, as well as, other related fundamental parameters, do exist:

$$\left\{\begin{array}{c}\lambda \left(T\to T_c\right)\to \infty \\ \xi \left(T\to T_c\right)\to \infty \\ \kappa \exists \left(T\le T_c\right)\\ J_c\left(sf,T=T_c\right)=0\\ B_{c1}\left(T=T_c\right)=0\\ B_{c2}\left(T=T_c\right)=0\end{array}\right.$$

(10)

For instance, the La₃Ni₂O_7-δ film [1] exhibits (Figure 3,a [1], insert):

$$J_c\left(sf,T\to 3K\right)\to 0$$

(11)

and this implies that:

$$\left\{\begin{array}{c}{\lambda }_{ab}\left(T\to 3.0K\right)\to \infty \\ {\xi }_{ab}\left(T\to 3.0K\right)\to \infty \\ T_c=3.0K\end{array}\right.$$

(12)

All $J_c\left(sf,T\right)$ data fits were performed with homemade software freely available online [74].

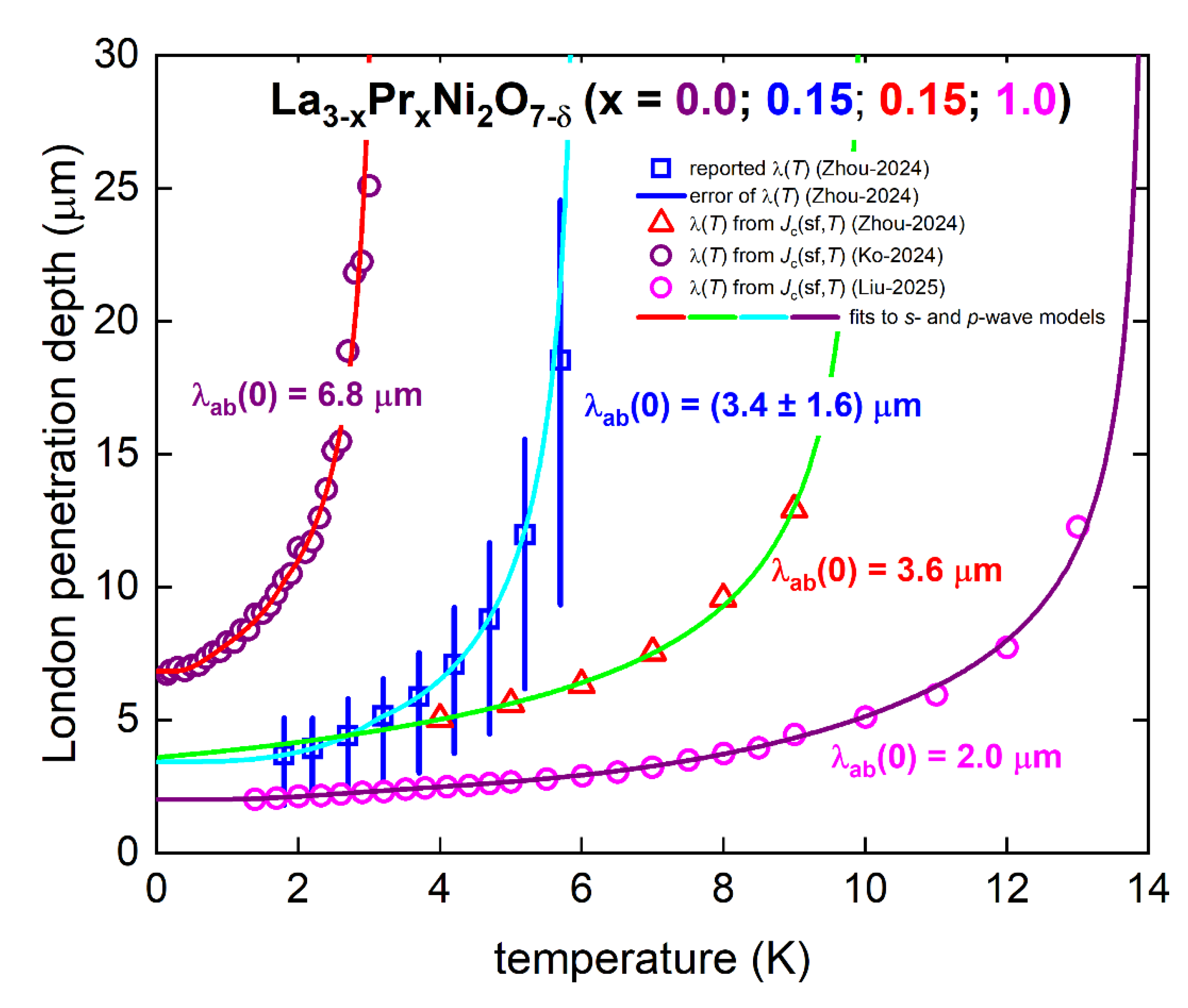
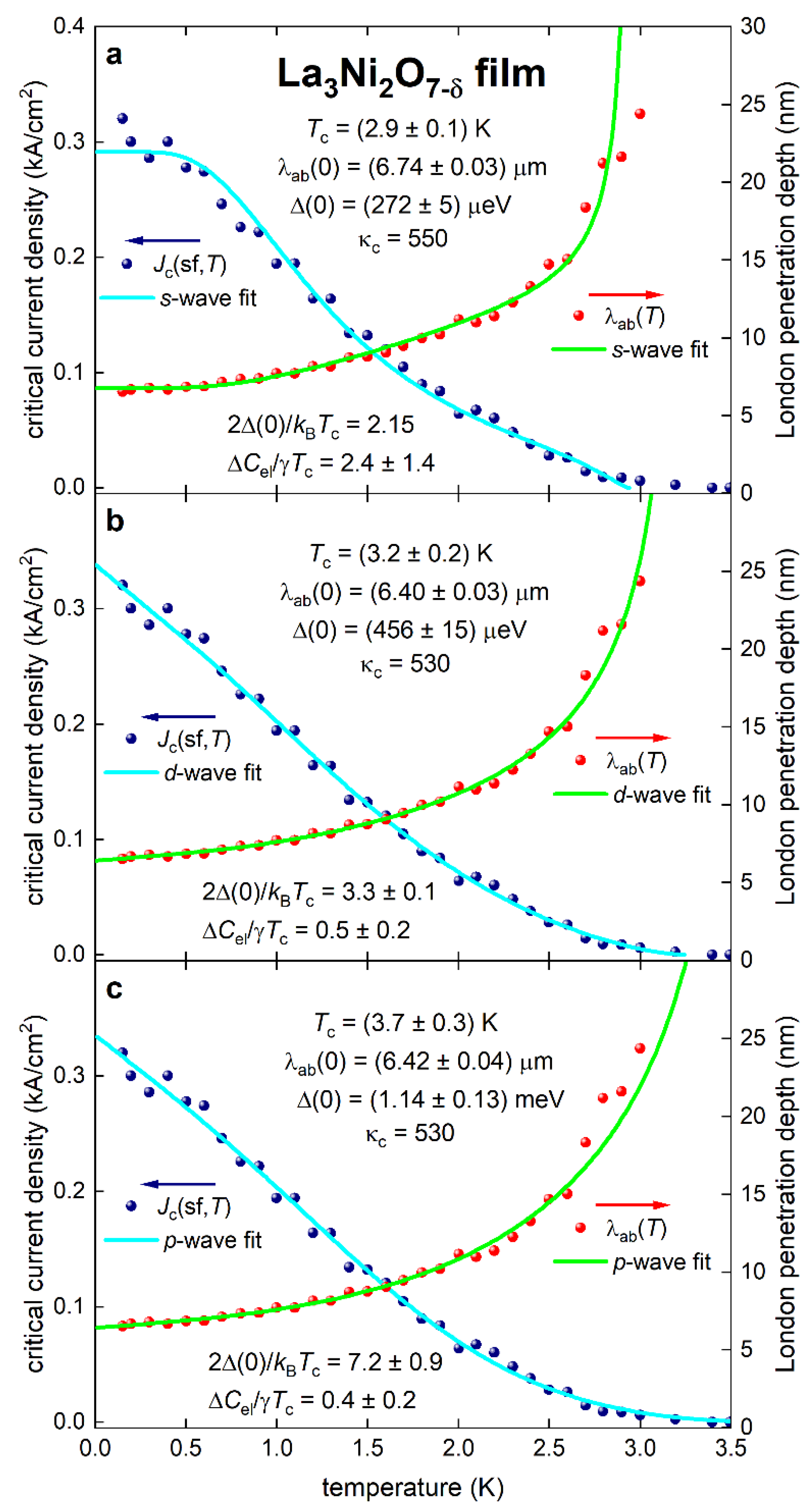
2.2. London Penetration Depth and Other Fundamental Parameters

There are two available R(T,B) datasets for the La₃Ni₂O_7-δ films reported by Ko et al [1], for which we applied the resistive criteria discussed above:

• For Figure 3,b [1]:

  $${\displaystyle \frac{\rho \left(T=T_c\right)}{\rho \left(T=T_{c,onset}\right)}}={\displaystyle \frac{\rho \left(T=T_c=3.5K\right)}{\rho \left(T=40K\right)}}\cong {\displaystyle \frac{0.014m\mathsf{\Omega }\times \mathrm{c}\mathrm{m}}{0.23m\mathsf{\Omega }\times \mathrm{c}\mathrm{m}}}=0.06$$

  (13)
• For the Extended Data Figure 3,a [1]:

  $${\displaystyle \frac{R\left(T=T_c\right)}{R\left(T=T_{c,onset}\right)}}={\displaystyle \frac{R\left(T=T_c=3K\right)}{R\left(T=10K\right)}}\cong {\displaystyle \frac{6\mathsf{\Omega }}{30\mathsf{\Omega }}}=0.2$$

  (14)

Despite both R(T,B) datasets (i.e. Figure 3,b [1] and Extended Data Figure 3,a [1]) consists of only two curves which satisfy the condition (Eqs. 13,14), it is still possible to estimate the ${\xi }_{ab}\left(0\right)$ value in the La₃Ni₂O_7-δ films [1], from the data fits to Eqs. 2,3 (Figure 1).

As a result, we estimated the ground state coherence length in the La₃Ni₂O_7-δ films [1] as the average value of:

$${\xi }_{ab}\left(0\right)=12nm$$

(15)

However, detailed experimental $R\left(T,B\right)$ data in the temperature range of $0<T\le 4K$ and field range of $0\le B\le 3T$ range is required to determine the ${\xi }_{ab}\left(0\right)$ value more accurately.

Because the self-field critical current density, $J_c\left(sf,T\right)$, has a very weak dependence (Eq. 6) from temperature dependent Ginsburg-Landau parameter, ${\kappa }_c\left(T\right)={\displaystyle \frac{{\lambda }_{ab}\left(T\right)}{{\xi }_{ab}\left(T\right)}}$, we simplify Eq. 6 to the form [73]:

$$J_c\left(sf,T\right)={\displaystyle \frac{{\varphi }_0}{4\pi {\mu }_0}}{\displaystyle \frac{ln\left(\frac{{\lambda }_{ab}\left(0\right)}{{\xi }_{ab}\left(0\right)}\right)+0.5}{{\lambda }_{ab}^3\left(T\right)}}$$

(16)

where ${\xi }_{ab}\left(0\right)=12nm$ (Eq. 12) is fixed parameter.

Temperature dependent London penetration depth for s-wave superconductors is given by the following equation [75,76]:

$${\lambda }_{ab}\left(T\right)={\displaystyle \frac{{\lambda }_{ab}\left(0\right)}{\sqrt{1-\frac{1}{2k_{B}T}\times \underset{0}{\overset{\infty }{\int }}\frac{d\epsilon }{{\cos \mathrm{h}}^2\left(\frac{\sqrt{{\epsilon }^2+{\mathsf{\Delta }}^2\left(T\right)}}{2k_{B}T}\right)}}}}$$

(17)

where $k_B$ is the Boltzmann constant. Temperature dependent superconducting gap amplitude, $\mathsf{\Delta }\left(T\right)$, can be described by analytical expression [75,76]:

$$\mathsf{\Delta }\left(T\right)=\mathsf{\Delta }\left(0\right)\times tanh\left[{\displaystyle \frac{\pi k_B{T}_c}{\mathsf{\Delta }\left(0\right)}}\times \sqrt{\eta \times {\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\times \left({\displaystyle \frac{T_c}{T}}-1\right)}\right]$$

(18)

where $\eta \equiv {\displaystyle \frac{2}{3}}$ for s-wave superconductors [75,76], and ${\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}$ is the relative jump in the electronic heat at $T_c$, and $\gamma$ is the Sommerfeld parameter. Direct measurements of superconducting gap in highly compressed elemental sulfur [63] confirmed temperature dependent shape of the $\mathsf{\Delta }\left(T\right)$ described by Eq. 18.

For d-wave superconductors, London penetration depth is given by [75,76]:

$${\lambda }_{ab}\left(T\right)={\displaystyle \frac{{\lambda }_{ab}\left(0\right)}{\sqrt{1-\frac{1}{2\pi k_{B}T}\times \underset{0}{\overset{2\pi }{\int }}{cos}^2\left(\theta \right)\times \left(\underset{0}{\overset{\infty }{\int }}\frac{d\epsilon }{{cosh}^2\left(\frac{\sqrt{{\epsilon }^2+{\mathsf{\Delta }}^2\left(T,\theta \right)}}{2k_{B}T}\right)}\right)d\theta }}}$$

(19)

where the superconducting energy gap, $\mathsf{\Delta }\left(T,\theta \right)$, is given by [75,76]:

$$\mathsf{\Delta }\left(T,\theta \right)={\mathsf{\Delta }}_m\left(T\right)\times cos\left(2\theta \right)$$

(20)

where ${\mathsf{\Delta }}_m\left(T\right)$ is the maximum amplitude of the k-dependent d-wave gap given by Eq. 15, $\theta$ is the angle around the Fermi surface subtended at (π, π) in the Brillouin zone (details can be found elsewhere [75,76]), and $\eta \equiv {\displaystyle \frac{7}{5}}$ in accordance with Refs. [75,76,77,78].

p-wave superconductors have the gap function given by [75,76,79]:

$$\mathsf{\Delta }\left(\overrightarrow{\mathit{k}},\overrightarrow{\mathit{l}},T\right)=\mathsf{\Delta }\left(T\right)\times f\left(\overrightarrow{\mathit{k}},\overrightarrow{\mathit{l}}\right)$$

(21)

where $\mathsf{\Delta }$ is the superconducting gap, $\overrightarrow{\mathit{k}}$ is the wave vector, and $\overrightarrow{\mathit{l}}$ is the gap axis. The electromagnetic response depends [80] on the mutual orientation of the vector potential $\overrightarrow{\mathit{A}}$ and the gap axis $\overrightarrow{\mathit{l}}$. At experimental conditions during the self-field critical current measurements in epitaxial thin films this is the orientation of the crystallographic axes compared with the direction of the electric current [80]. In addition, from four different p-wave pairing states (which are two “axial” states, where there are two point nodes, and two “polar” states, where there is an equatorial line node), previous analysis [80] showed that the only p-wave case that is distinguishable from dirty s- and d-wave is the p-wave polar $\overrightarrow{\mathit{A}}\perp \overrightarrow{\mathit{l}}$ case. Details can be found in Ref. [80]. For this polar $\overrightarrow{\mathit{A}}\perp \overrightarrow{\mathit{l}}$ p-wave case the London penetration depth is given by [75,76,80]:

$${\lambda }_{ab}\left(T\right)={\displaystyle \frac{{\lambda }_{ab}\left(0\right)}{\sqrt{1-\frac{3}{4k_{B}T}\times \underset{0}{\overset{1}{\int }}\frac{\left(1-x^2\right)}{2}\times \left(\underset{0}{\overset{\infty }{\int }}\frac{d\epsilon }{{cosh}^2\left(\frac{\sqrt{{\epsilon }^2+{\mathsf{\Delta }}^2\left(T\right)\times f^2\left(x\right)}}{2k_{B}T}\right)}\right)dx}}}$$

(22)

where the superconducting energy gap, is given by Eq. 21, where [75,76,80]:

$$\mathsf{\Delta }\left(T\right)=\mathsf{\Delta }\left(0\right)\times tanh\left[{\displaystyle \frac{\pi k_B{T}_c}{\mathsf{\Delta }\left(0\right)}}\times \sqrt{\eta \times {\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\times \left({\displaystyle \frac{T_c}{T}}-1\right)}\right]$$

(23)

$$\eta ={\displaystyle \frac{2}{3}}{\displaystyle \frac{1}{\underset{0}{\overset{1}{\int }}{f}^2\left(x\right)dx}}$$

(24)

$$f\left(x\right)=x$$

(25)

Ko et al [1] reported the $J_c\left(sf,T\right)$ data for the La₃Ni₂O_7-δ film in Figure 3,a [1], which we fitted to single s-, d-, and polar $\overrightarrow{\mathit{A}}\perp \overrightarrow{\mathit{l}}$ p-wave gap symmetry models (Eqs. 16-25) in Figure 2.

Deduced unitless BCS ratios (Figure 2) are in large difference from the weak-coupling limits for s-, d-, and polar $\overrightarrow{\mathit{A}}\perp \overrightarrow{\mathit{l}}$ p-wave symmetries [75,76,77,80,81,82]:

$${\displaystyle \frac{2\mathsf{\Delta }\left(0\right)}{k_B{T}_c}}=3.53;{\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}=1.43 (\mathrm{weak-coupling} \mathrm{limits} \mathrm{for} s-\mathrm{wave} \mathrm{symmetry})$$

(26)

$${\displaystyle \frac{2{\mathsf{\Delta }}_m\left(0\right)}{k_B{T}_c}}=4.28;{\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}=0.995 (\mathrm{weak-coupling} \mathrm{limit} \mathrm{for} d-\mathrm{wave} \mathrm{symmetry})$$

(27)

$${\displaystyle \frac{2{\mathsf{\Delta }}_m\left(0\right)}{k_B{T}_c}}=4.92;{\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}=0.792 (\mathrm{weak-coupling} \mathrm{limit} \mathrm{for} \mathrm{polar} \overrightarrow{\mathit{A}}\perp \overrightarrow{\mathit{l}} p-\mathrm{wave} \mathrm{symmetry})$$

(28)

Thus, we concluded that ambient pressure La₃Ni₂O_7-δ films are multiple-band superconductor.

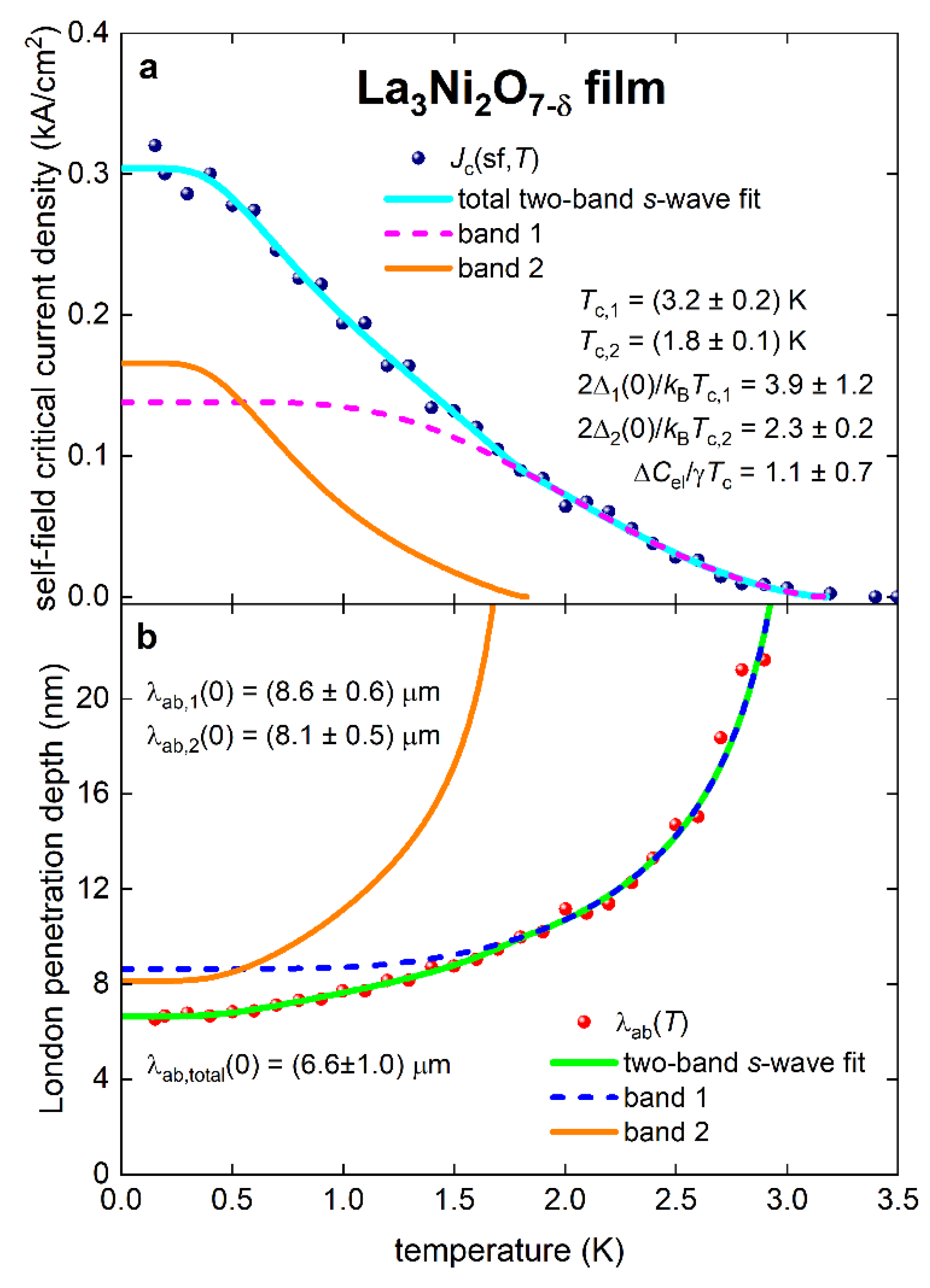
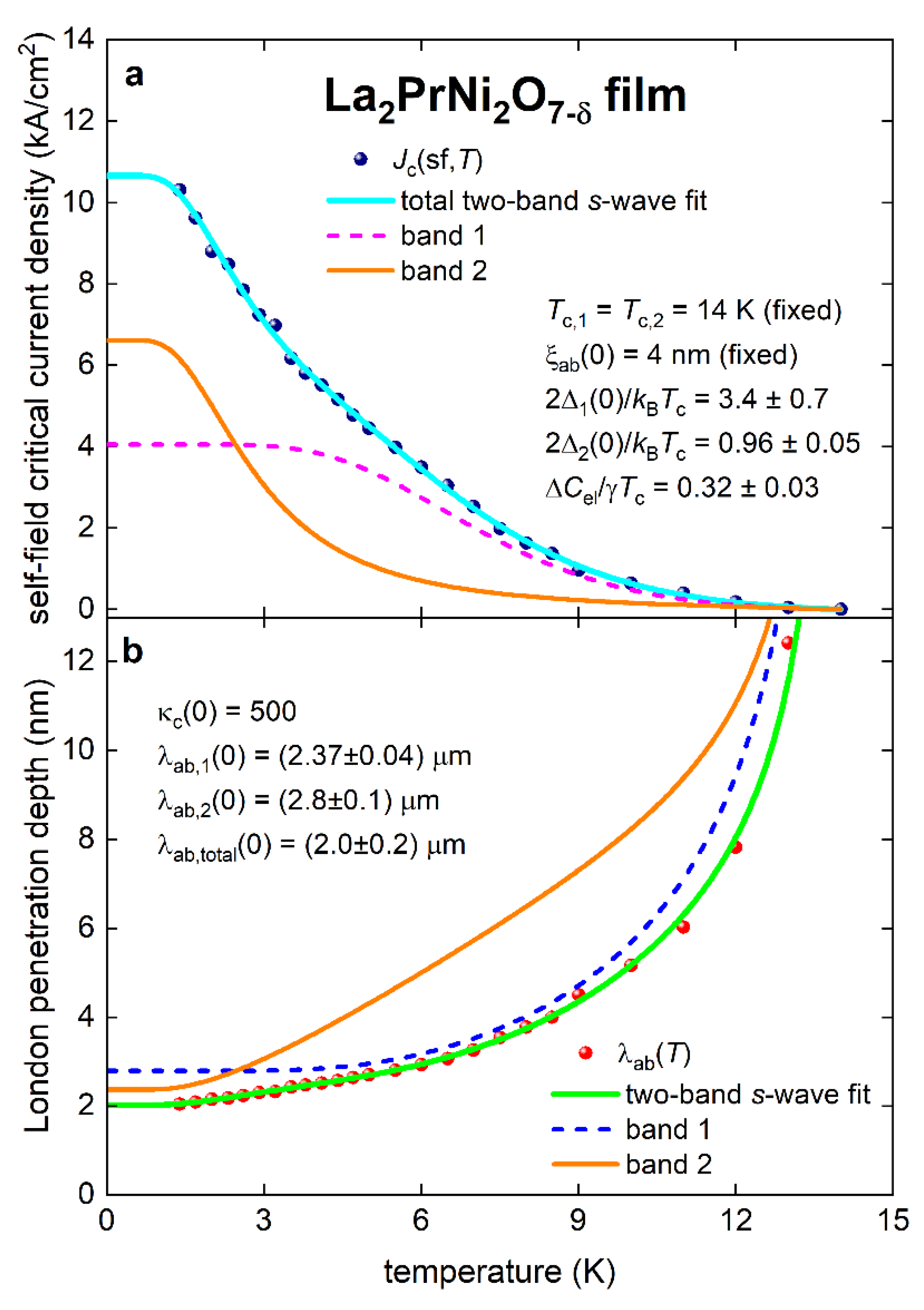
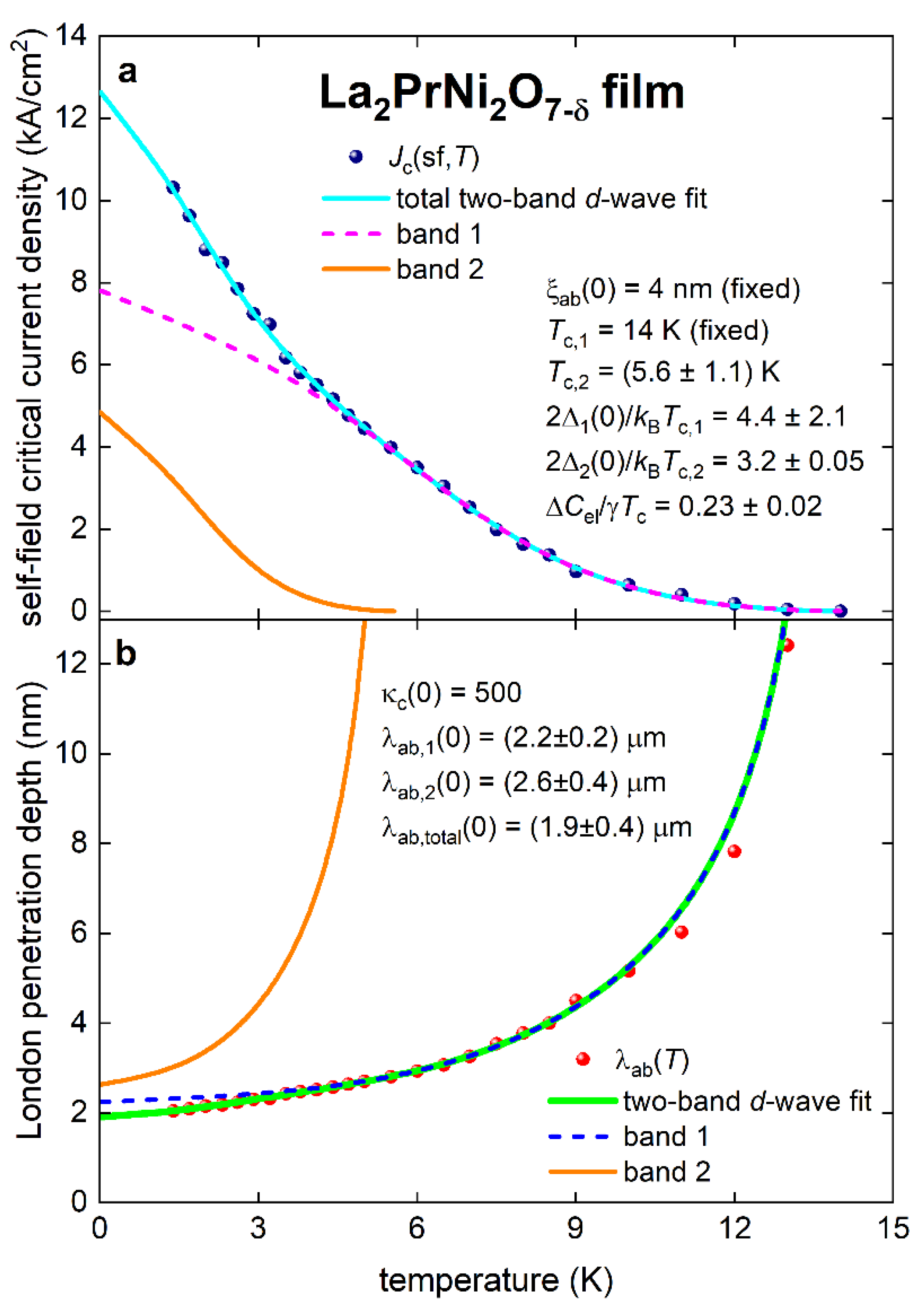
2.3. Two-Band Superconductivity

Thus, we tested six possible two-band cases (i.e. s- + s-; s- + d-; …, p- + p-) of superconductivity in these films. To do this, we used two-band model [77,83]:

$$J_{c,total}\left(sf,T\right)=J_{c,band1}\left(sf,T\right)+J_{c,band2}\left(sf,T\right)$$

(29)

where $band1$ and $band2$ designate critical current density originated from respectful band; each band has its independent ${\mathsf{\Delta }}_i\left(0\right)$, ${\lambda }_{ab,i}\left(0\right)$, ${\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)}_i$, and $T_{c,i}$ (Eqs. 16-25). We used fixed ${\xi }_{ab}\left(0\right)=12nm$ value for both bands.

From performed fits of the $J_c\left(sf,T\right)$ data to six possible two-band models, we found that deduced parameters for two-band s-wave model are in reasonable proximity to the values reported for MgB₂ superconductor [84,85,86] (Figure 3). It should be noted, that in this fit we assumed the condition [77,83] of:

$${\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)}_{band1}={\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)}_{band2}$$

(30)

by keeping this joint parameter to be free. Without this restriction, several deduced parameters have large uncertainties. Denser raw $J_c\left(sf,T\right)$ dataset with measurements performed with a smaller temperature step ($\mathsf{\Delta }T\cong {\displaystyle \frac{T_c}{200}}$) would make it possible to deduce separate values for $\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)$ for each band.

Fits to other two-band models (Eq. 29) are either diverged, either the deduced parameters are in times different from respectful weak coupling limiting values (Eqs. 26-28). Fits to three-band models are possible in principle, but to do this, the experimental $J_c\left(sf,T\right)$ dataset should be very dense with $\mathsf{\Delta }T\cong {\displaystyle \frac{T_c}{1000}}$ and covers as lower as possible temperature range.

It should be stressed that independent from assumed pairing symmetry and/or multiple-band superconductivity, the absolute values of ${\lambda }_{ab}\left(0\right)\cong 6.5\mu m$ and ${\kappa }_c\left(0\right)\cong 550$ are remaining the same. The former value is in close proximity to the ${\lambda }_{ab}\left(0,P=16.6GPa\right)\cong 6.0\mu m$ determined [87] from the $J_c\left(sf,T\right)$ data reported for highly compressed bulk La₃Ni₂O_7-δ sample [24]. Both these ${\lambda }_{ab}\left(0\right)$ values are in the same ballpark with the upper limit of ${\lambda }_{ab}\left(T=1.8K\right)=3.7{\pm }_{1.9}^{1.4}\mu m$ recently reported for La_2.85Pr_0.15Ni₂O_7-δ thin film by independent research group [2].

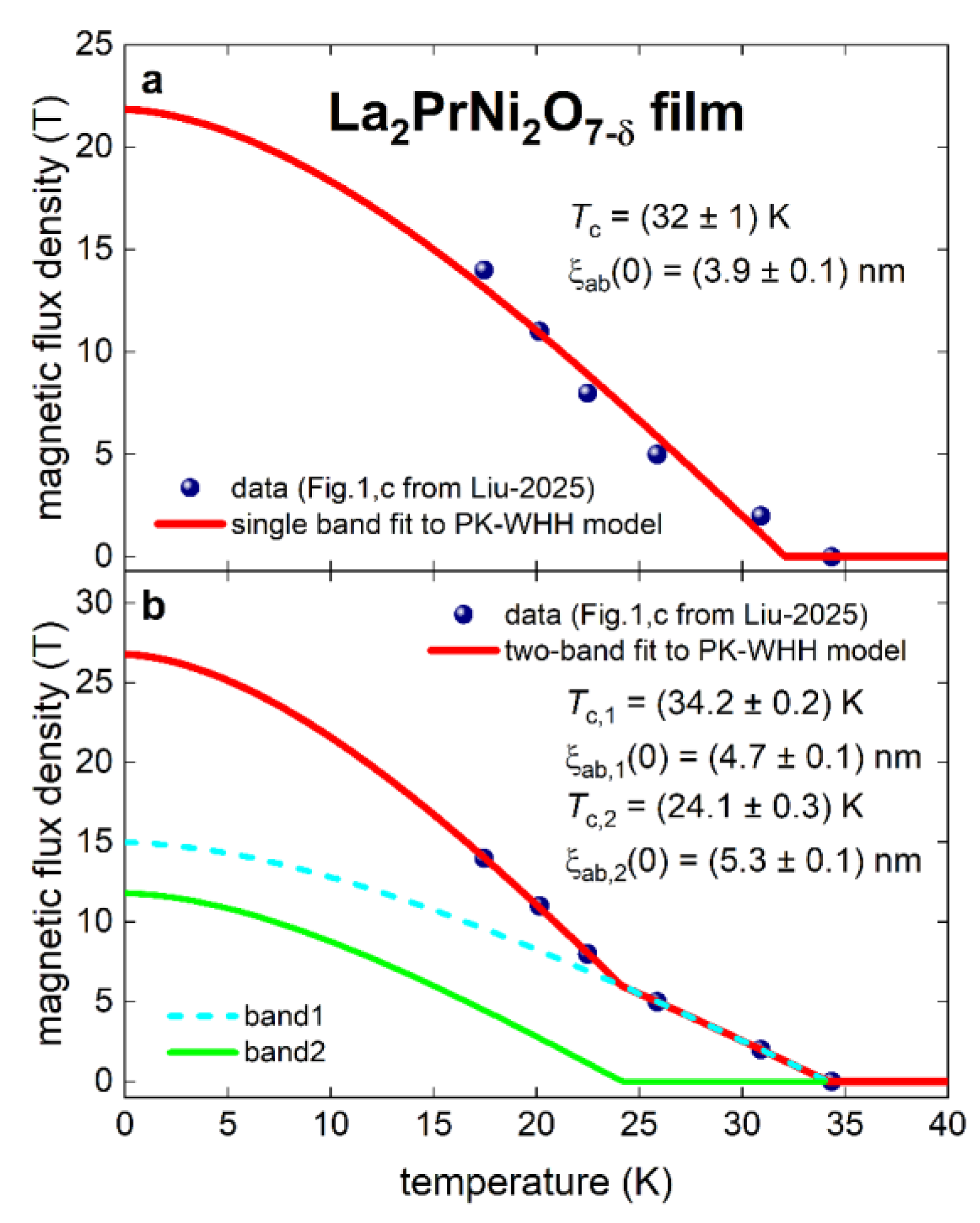
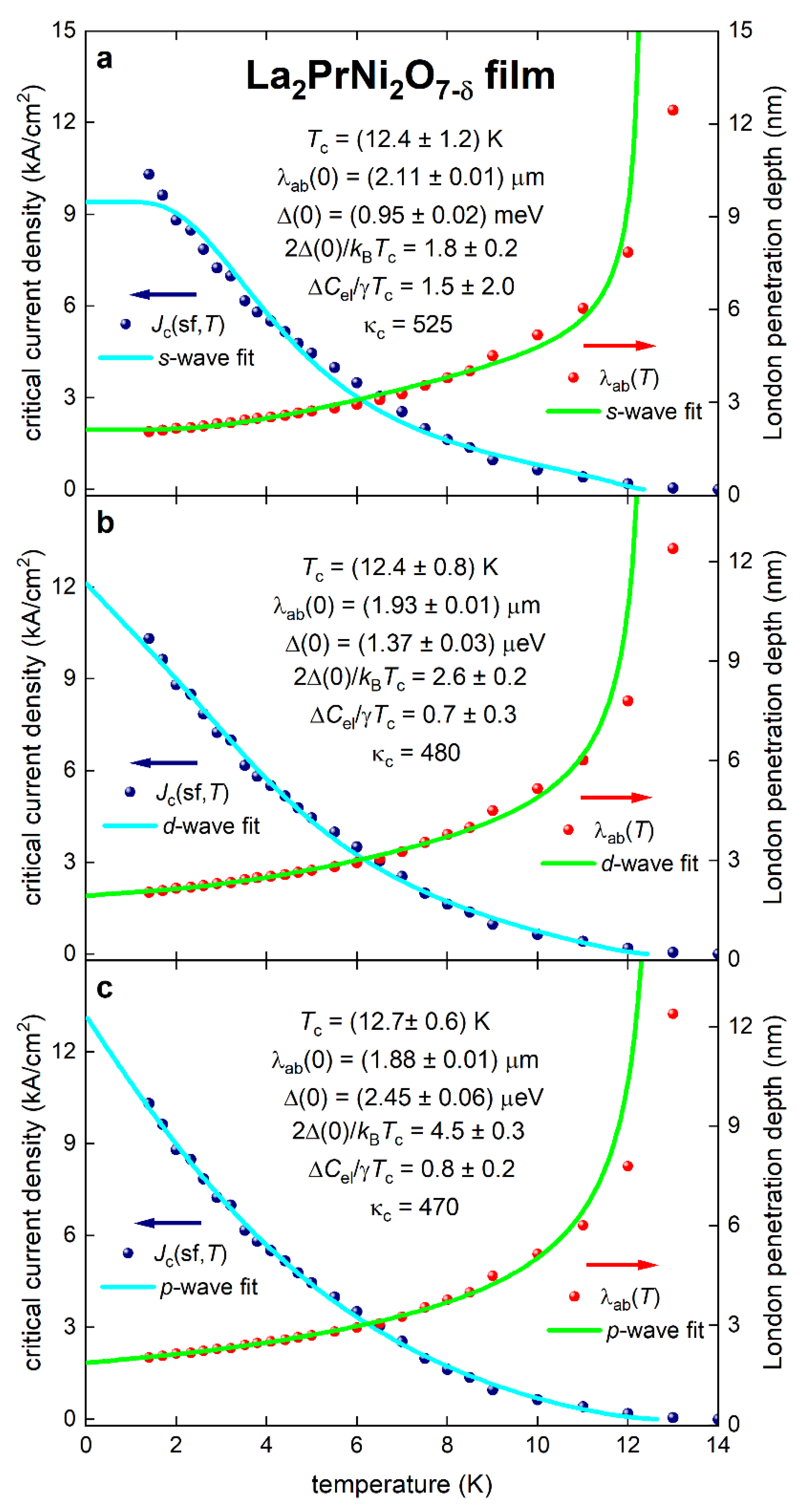
3. Fundamental Parameters in La₂PrNi₂O_7-δ Films

To deduce in-plane ground state coherence length ${\xi }_{ab}\left(0\right)$ in La₂PrNi₂O_7-δ films [3] we applied strict resistive criterion:

$${\displaystyle \frac{\rho \left(T=T_{c,0.01}\right)}{\rho \left(T=40K\right)}}=0.01$$

(31)

to the $\rho \left(T,B\right)$ data reported by Liu et al [3] in their Figure 1,c [3]. Obtained $B_{c2}\left(T\right)$ dataset and data fit to Eq. 3 are shown in Figure 4,a. Better fit quality was obtained for two-band model [88,89,90]:

$$B_{c2,total}\left(T\right)=B_{c2,band1}\left(T\right)+B_{c2,band2}\left(T\right)$$

(32)

where $band1$ and $band2$ designate upper critical field originated from the respectful band; each band has its independent ${\xi }_{ab,i}\left(0\right)$ and $T_{c,i}$ values, and where $B_{c2,band1}\left(T\right)$ and $B_{c2,band2}\left(T\right)$ can be described by one of two equations (Eqs. 2,3). The result of $B_{c2}\left(T\right)$ data fit to two-band PK-WHH model (Eqs. 3,32) is shown in Figure 4,b.

For the $J_c\left(sf,T\right)$ analysis in the La₂PrNi₂O_7-δ film [3], we rounded in-plane ground state coherence length to ${\xi }_{ab}\left(0\right)=4.0nm$.

Liu et al [3] measured E-J curves in zero applied field for the La₂PrNi₂O_7-δ film [3] and reported the $J_c\left(sf,T\right)$ dataset obtained by application of the E_c = 5 μV/cm criterion which is in the same ballpark with commonly used E_c = 1 μV/cm criterion in applied superconductivity [91,92,93].

In Figure 5 we showed the $J_c\left(sf,T\right)$ reported by Liu et al in their Figure 1,b [3] together with fits to single band models (Eqs. 16-25). One can see that deduced parameters for s- and d-wave are significantly different from the weak-coupling limits (Eqs. 26,27). Deduced parameters for p-wave symmetry fit within their uncertainties are within the weak-coupling limiting values for this symmetry. The confirmation for this gap symmetry is required denser $J_c\left(sf,T\right)$ dataset, which span on as wide as it is experimentally possible temperature range, because the $J_c\left(sf,T\right)$ temperature dependence at $T<{0.3\times T}_c$ demonstrates unique distinct features of s-, d-, p-wave symmetry. It should be noted that deduced the Ginsburg-Landau parameter remains its large value ${\kappa }_c\cong 500$, similar to the one in the La₃Ni₂O_7-δ film [1] (Figures 2,3).

We further analyzed the $J_c\left(sf,T\right)$ data within two-band models. In Figure 6 we showed the $J_c\left(sf,T\right)$ data fit to two-band s-wave model (Eq. 29), where (because two-band fit requires denser $J_c\left(sf,T\right)$ dataset that all parameters will be free) we reduced the number of free-fitting parameters by assuming that: (a) both bands have transition temperature equals to the experimental value $T_{c,band1}=T_{c,band2}=14K$; (b) accepting the restriction described by Eq. 30; (c) and fixing the Ginzburg-Landau parameter to ${\kappa }_c=500$.

The fit (Figure 6) shows that the gap-to-transition temperature ratios, ${\displaystyle \frac{2{\mathsf{\Delta }}_i\left(0\right)}{k_B{T}_c}}$, for two bands are, within their uncertainties, in reasonable agreement with the value reported for MgB₂ superconductor [86].

In Figure 7 we showed the $J_c\left(sf,T\right)$ data fit to (d-+d-)-wave model (Eq. 29), where we reduced the number of free-fitting parameters assuming that: (a) one band has $T_{c,band1}$ equals to the experimental value $T_{c,band1}=14K$; (b) ${\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)}_{band1}={\left({\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}\right)}_{band2}$, and (c) ${\kappa }_c=500$.

We showed that there is a variety of gap symmetry models which can with good accuracy describe currently available experimental $J_c\left(sf,T\right)$ dataset [3] measured in ambient pressure La₂PrNi₂O_7-δ film. Thus, denser $J_c\left(sf,T\right)$ data which is measured at, as wide as it is experimentally possible, temperature range is required to reveal the gap symmetry in the ambient pressure La₂PrNi₂O_7-δ films. However, we are confident that ambient pressure La_3-xPr_xNi₂O_7-δ (x = 0.0; 1.0) films are high-κ type-II superconductors with large London penetration depth ${\lambda }_{ab}\left(0\right)=1.9-6.5nm$, and these films are more likely multiple-band superconductors.

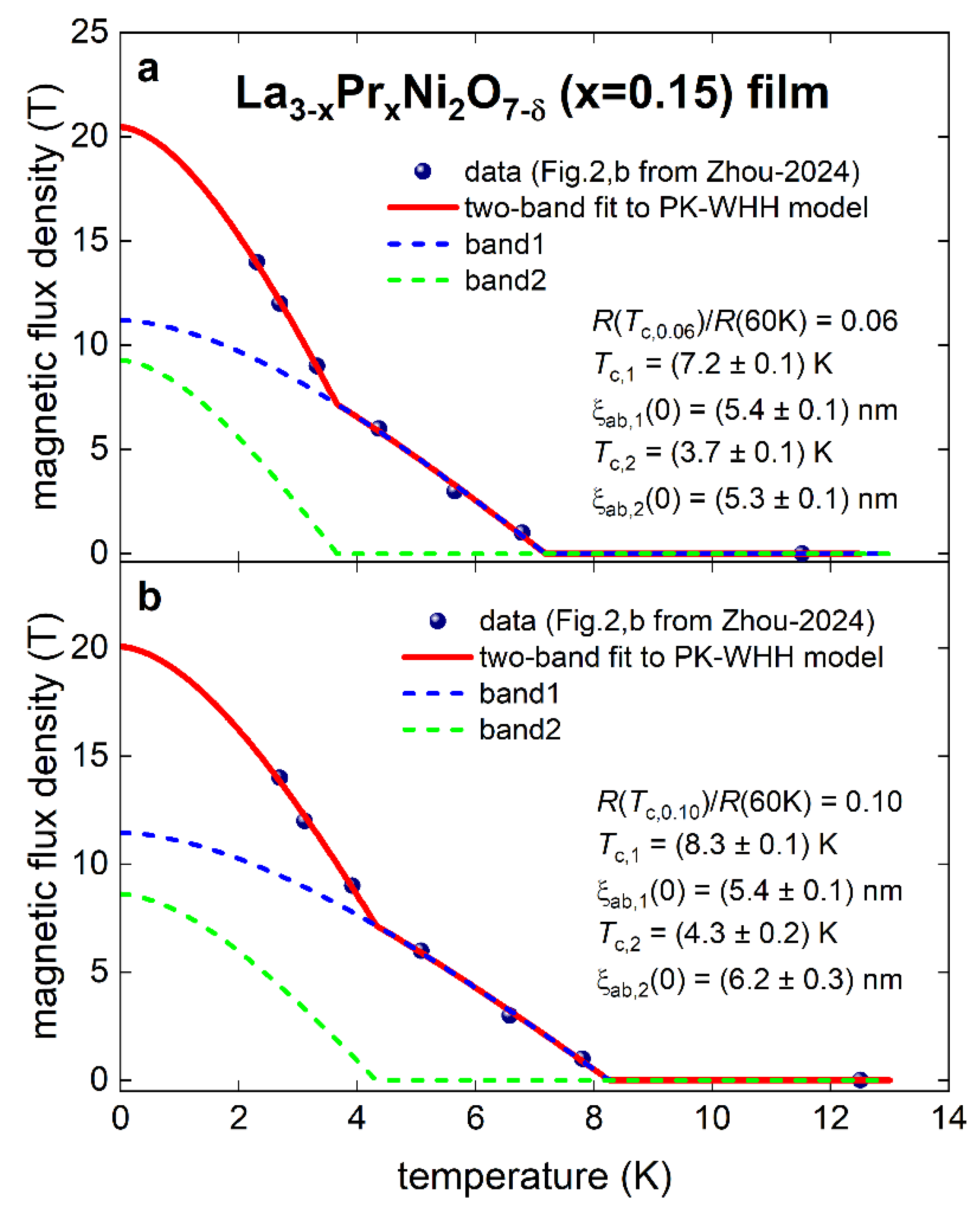
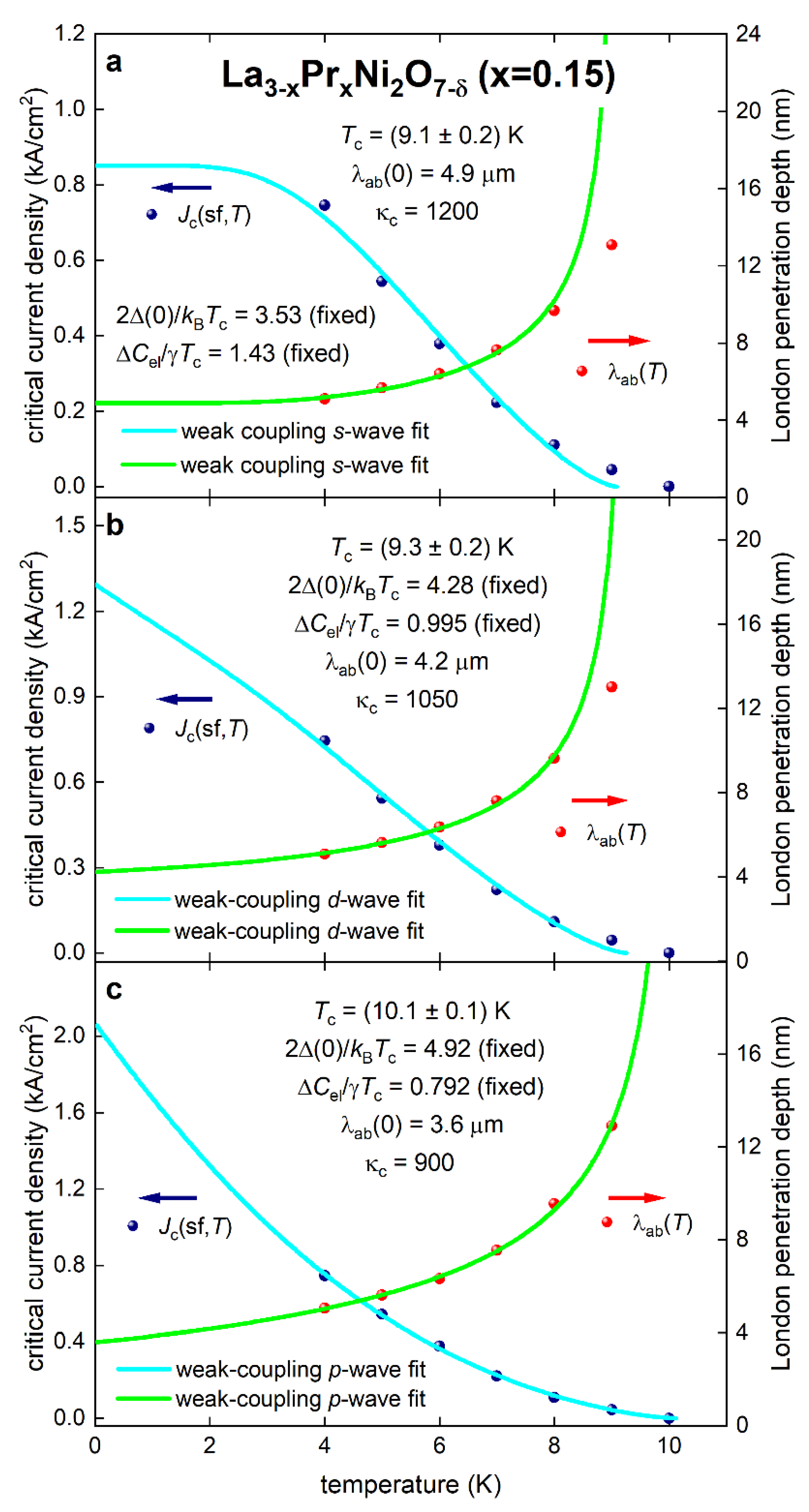
4. Fundamental Parameters in La_3-xPr_xNi₂O_7-δ (x = 0.15) Films

Zhou et al. [2] reported V-I curves for 6 nm thick La_3-xPr_xNi₂O_7-δ (x = 0.15) film [2] which exhibits the $T_{c,onset}\cong 40K$. Despite the authors [2] noted “…that, due to the significant heating effect caused by the applied current (a result of the high critical current associated with the elevated TC), the actual sample temperatures are higher than the recorded values”, there is still an interest to estimate the $J_c\left(sf,T\right)$ dataset and ${\lambda }_{ab}\left(0\right)$, because Zhou et al. [2] reported ${\lambda }_{ab}\left(T=1.8K\right)=3.7{\pm }_{1.9}^{1.4}\mu m$ measured by mutual inductance technique, and, thus, even estimated ${\lambda }_{ab}\left(0\right)$ value deduced from $J_c\left(sf,T\right)$ can shed a light on the absolute value of the London penetration depth in ambient pressure La_3-xPr_xNi₂O_7-δ films.

In Figure 8 we showed the out-of-plane upper critical field data, $B_{c,c}\left(T\right)$, deduced from $R\left(T,B\right)$ dataset showed in Figure 2,b [2] for which we used resistive criteria of ${\displaystyle \frac{R\left(T=T_{c,0.06}\right)}{R\left(T=60K\right)}}=0.06$ (in Figure 8,a) and ${\displaystyle \frac{R\left(T=T_{c,0.10}\right)}{R\left(T=60K\right)}}=0.10$ (in Figure 8,b).

It can be seen that two-band fit to PK-WHH model (Eqs. 3,32) have a good quality, and deduced ${\xi }_{ab,total}\left(0\right)=4.0nm$ is close proximity to the value deduced in La₂PrNi₂O_7-δ film [3] (Figure 4). Also, Figure 8 demonstrate two-band feature of the superconducting state in La_3-xPr_xNi₂O_7-δ (x = 0.15) film [2].

We estimated $J_c\left(sf,T\right)$ dataset in the La_3-xPr_xNi₂O_7-δ (x = 0.15) film [2] from V-I curves showed in Extended Data Figure 7 [2] by assuming transport current bridge lateral dimensions of 5x5 mm and by applying electric field criterion of E_c = 25 μV/cm which is manifold larger than commonly used criterion of E_c = 1 μV/cm, but raw experimental data have noise level at about E = 20 μV/cm (it should be also taking into account a note about sample heating mentioned above).

Derived $J_c\left(sf,T\right)$ dataset and fits to single band models are shown in Figure 9, where because of small number of raw data points we reduced as much as it is practically possible the number of free-fitting parameters by fixing ${\displaystyle \frac{2\mathsf{\Delta }\left(0\right)}{k_B{T}_c}}$ and ${\displaystyle \frac{\mathsf{\Delta }{C}_{el}}{\gamma T_c}}$ values to their weak-coupling limits for respectful gap symmetry (Eqs. 26-28).

In the result, deduced ${\lambda }_{ab}\left(0\right)=3.6-4.9\mu m$ values are within uncertainty range for the value reported by Zhou et al. [2] ${\lambda }_{ab}\left(T=1.8K\right)=3.7{\pm }_{1.9}^{1.4}\mu m$ measured by mutual inductance technique.

5. More Evidences for Multiple-Band Superconductivity in Ruddlesden–Popper Nickelates

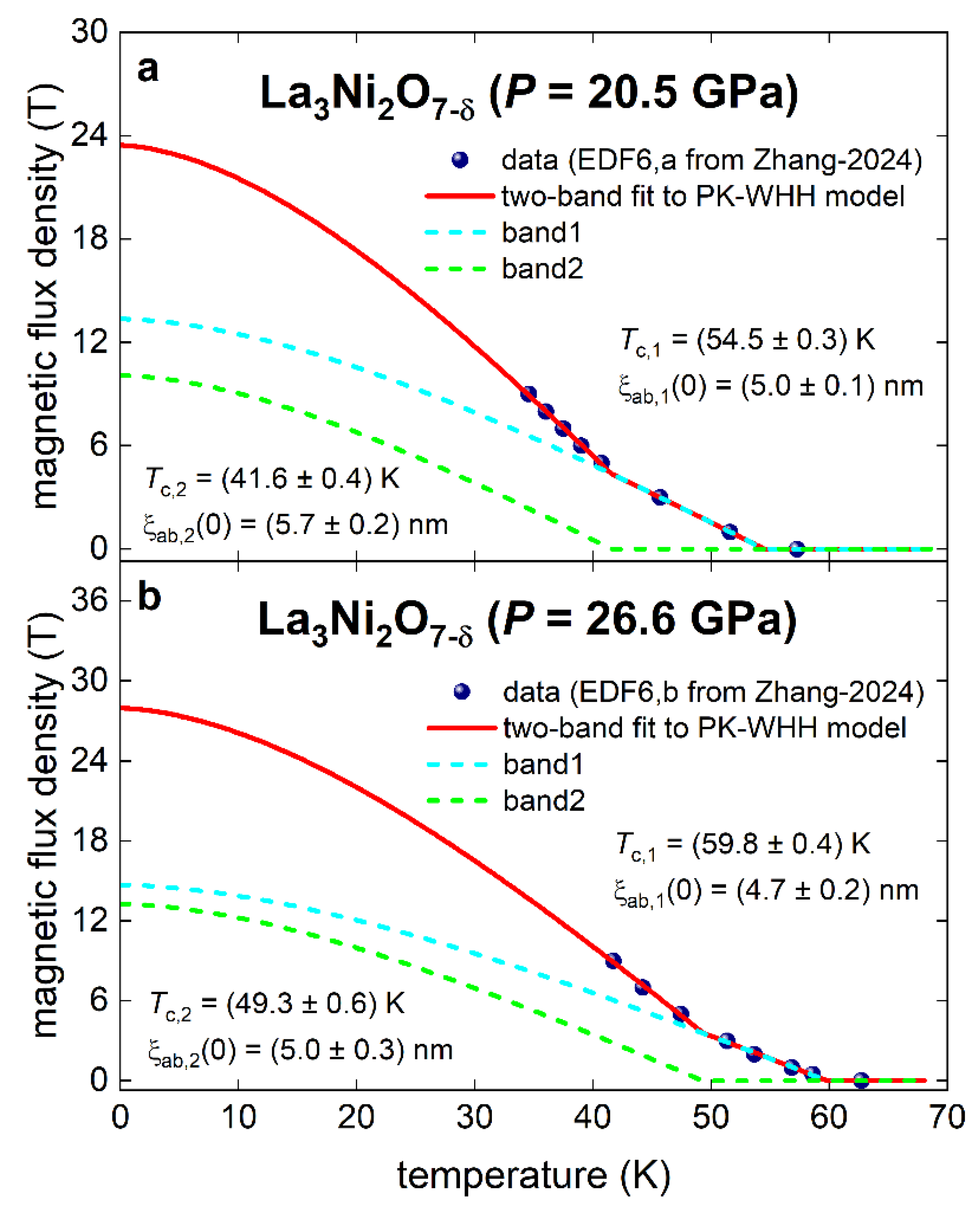
5.1. Highly Compressed Single Crystals La₃Ni₂O_7-δ

Zhang et al [24] reported on zero-resistance state in highly compressed La₃Ni₂O_7-δ single crystals at temperature with highest $T_{c,zero}=40K$. For one of these crystals, raw experimental dataset for $B_{c2}\left(T\right)$ defined by the strictest criterion:

$$R\left(T,B_{appl}\right)=0.0$$

(33)

compressed at pressure P = 20.5 GPa and P = 26.6 GPa has been reported in Extended Data Figure 6 [24]. In Figure 10 we fitted these two $B_{c2}\left(T\right)$ datasets to the two-band model (Eqs. 3, 32), from which two-band superconductivity in highly compressed La₃Ni₂O_7-δ single crystals can be seen.

We can express a request for experimentalists to measure the $R\left(T,B\right)$ data at low applied magnetic field in Ruddlesden–Popper and infinite layer nickelates [1,2,3,18,22,23,94,95]. Indeed, at the low applied fields, $0T\le B_{appl}\le 2T$, the ${\xi }_{ab}\left(0\right)$ for the band which exhibits higher transition temperature, $T_c$, can be determined. However, commonly accepted approach is different, and it is related to the applying as high as possible magnetic field, $B_{appl}$, with practically no any experimental data for an applied field in the range of $0T\le B_{appl}<2T$, except at $B_{appl}=1T$.

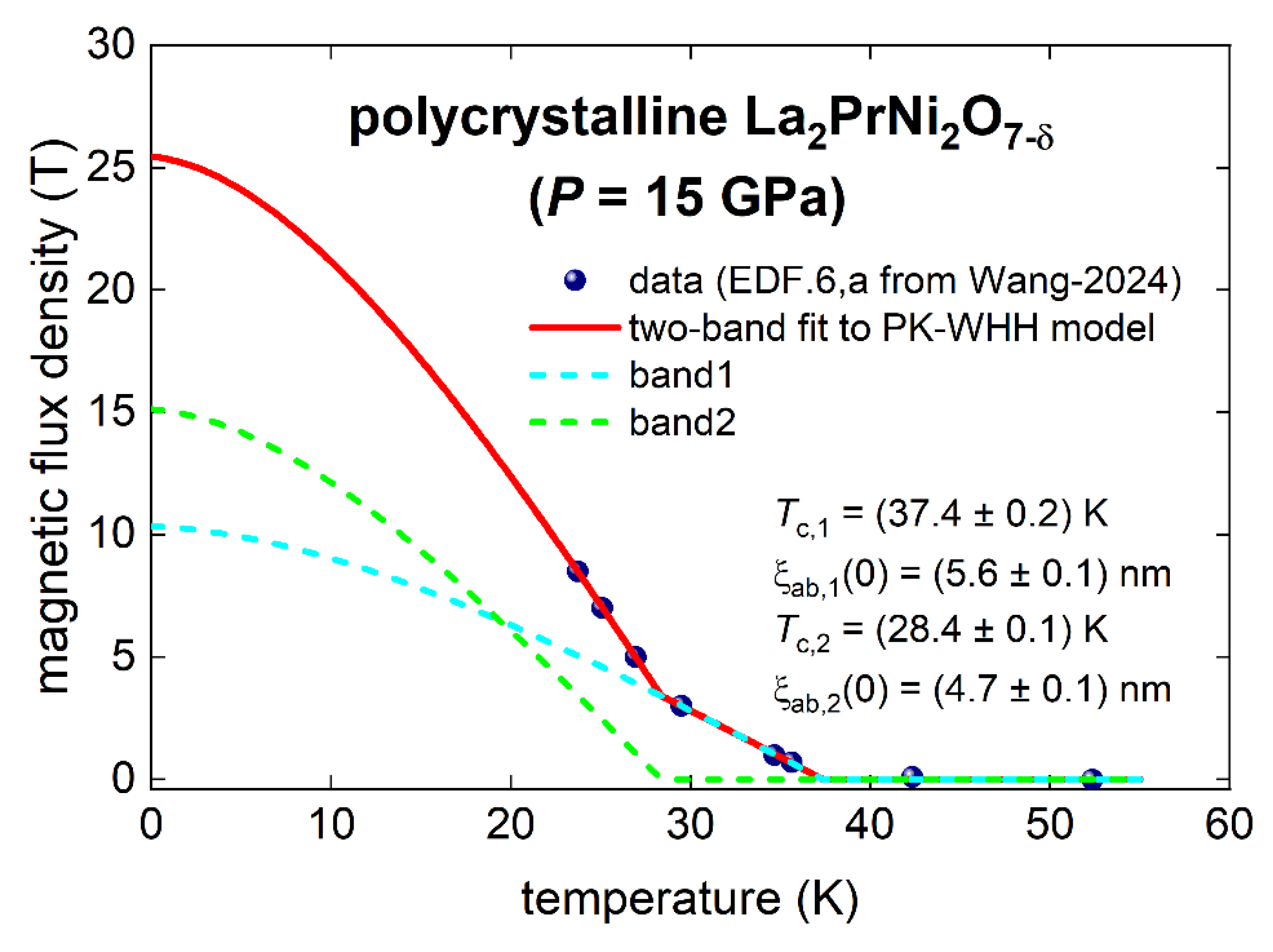
5.2. Highly Compressed Polycrystalline La₂PrNi₂O_7-δ

Wang et al [96] reported on zero-resistance state in highly compressed La₃PrNi₂O_7-δ polycrystalline samples with highest $T_{c,zero}=60K$. We digitized the $R\left(T,B_{appl}\right)$ data from Extended Data Figure 6,a [96] and applied the criterion of:

$${\displaystyle \frac{R\left(T_{c,0.20}\right)}{R\left(T=80K\right)}}=0.20$$

(34)

Determined $B_{c2}\left(T,P=15GPa\right)$ dataset and the fit to the two-band model are shown in Figure 11.

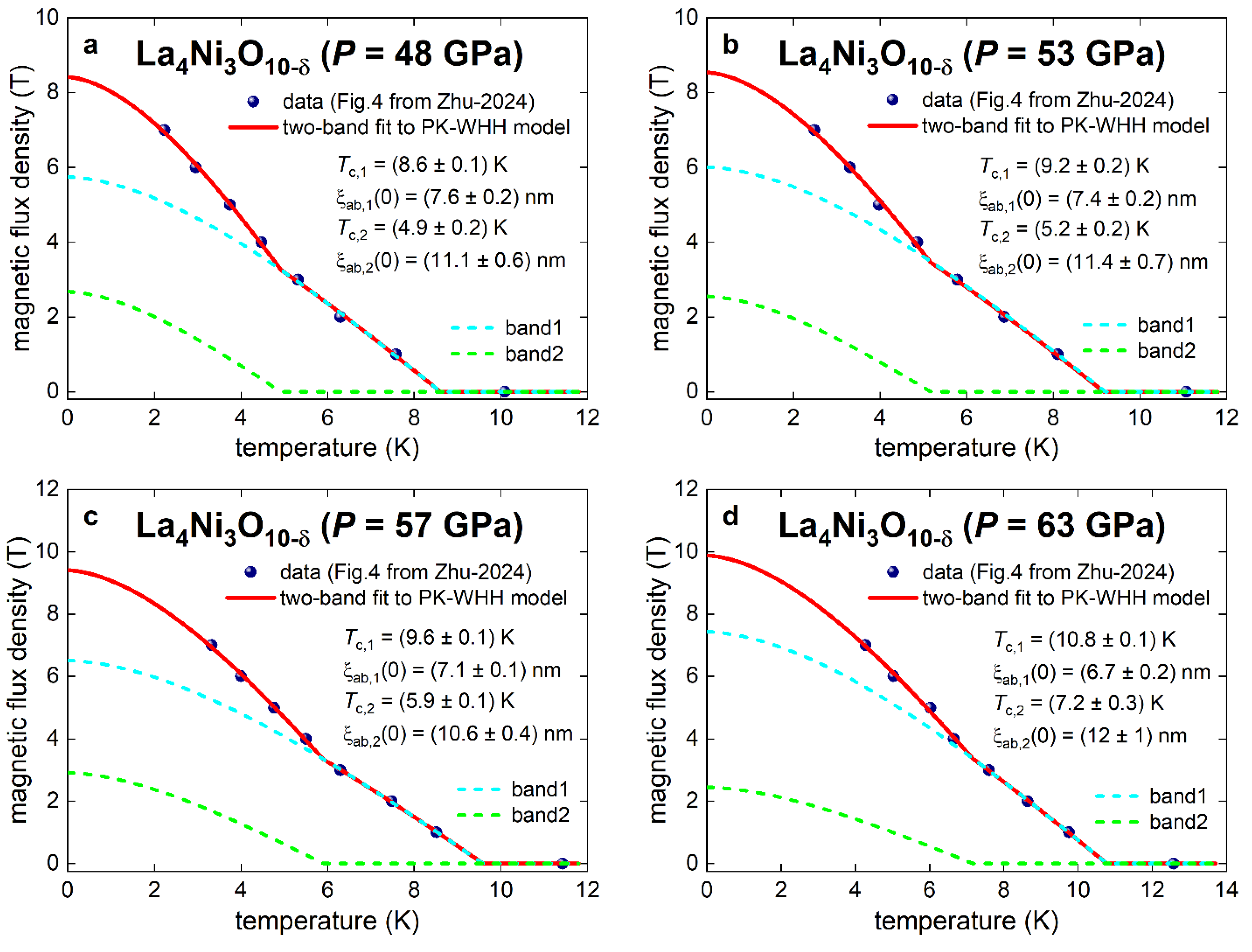
5.3. Highly Compressed Single Crystals La₄Ni₃O_10-δ

Zhu et al [97] reported on zero-resistance state in highly compressed La₄Ni₃O_10-δ single crystals with the highest $T_{c,zero}\cong 12K$. Raw experimental $R\left(T,B_{appl}\right)$ data is available for this study [97]. We applied the lowest possible criterion for each $R\left(T,B_{appl},P\right)$ dataset in the range of:

$$0.01\le {\displaystyle \frac{R\left(T_c\right)}{R\left(T=50K\right)}}\le 0.07$$

(35)

to determine the $B_{c2}\left(T,P\right)$. Data fit to two-band model for La₄Ni₃O_10-δ single crystal compressed at four pressures are shown in Figure 12, from which two-band superconductivity in highly compressed La₄Ni₃O_10-δ is evident.

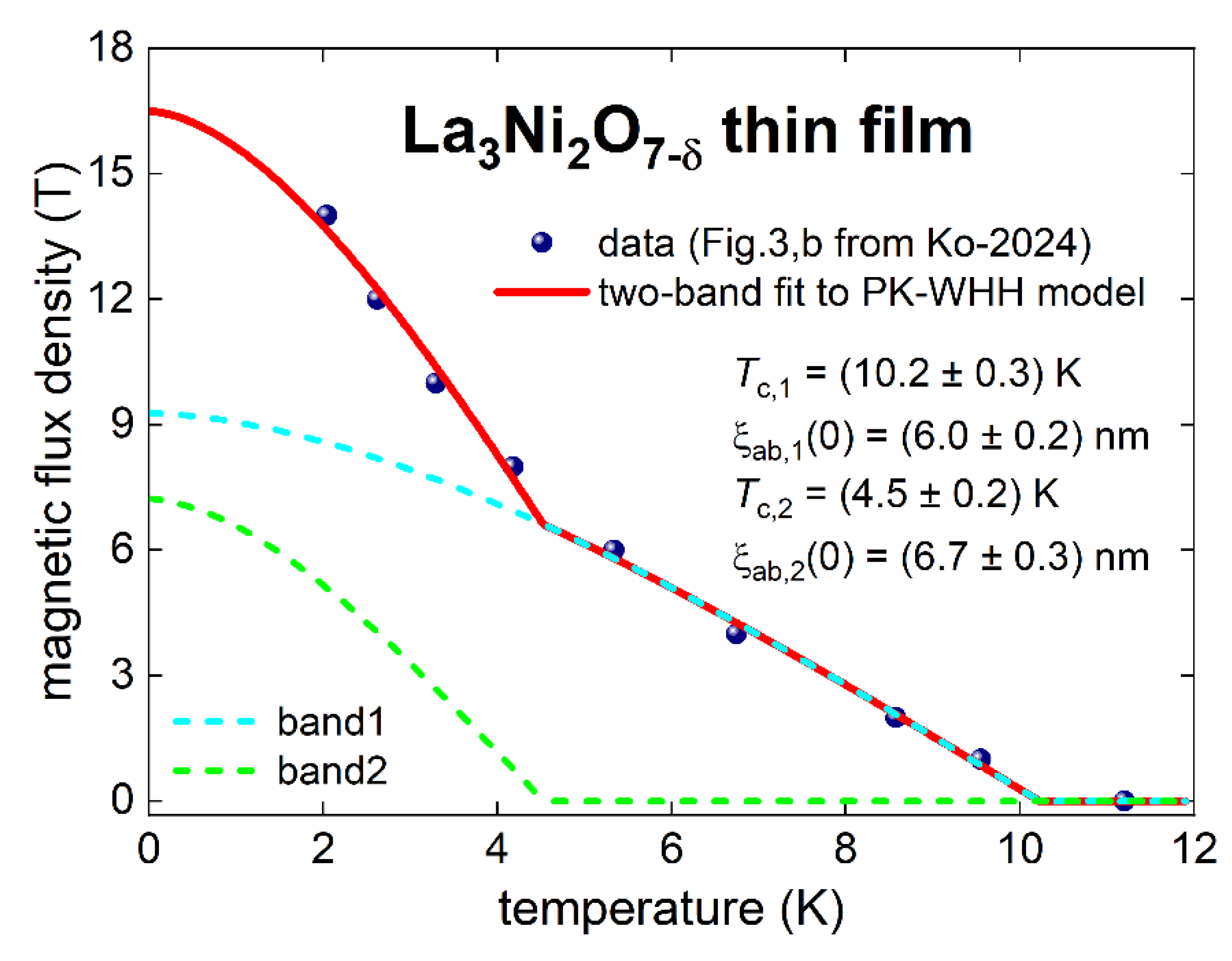
5.4. Ambient Pressure La₃Ni₂O_7-δ Thin Film

For the completeness, in Figure 13 we showed the $B_{c2}\left(T\right)$ dataset for La₃Ni₂O_7-δ thin film [1] defined by non-strict criterion, which allows to cover the high-field range of the $R\left(T,B\right)$ data, reported by Ko et al [1] in their Figure 3,b [1]:

$${\displaystyle \frac{R\left(T=T_c\right)}{\rho \left(T_{c,onset}=40K\right)}}=0.29$$

(36)

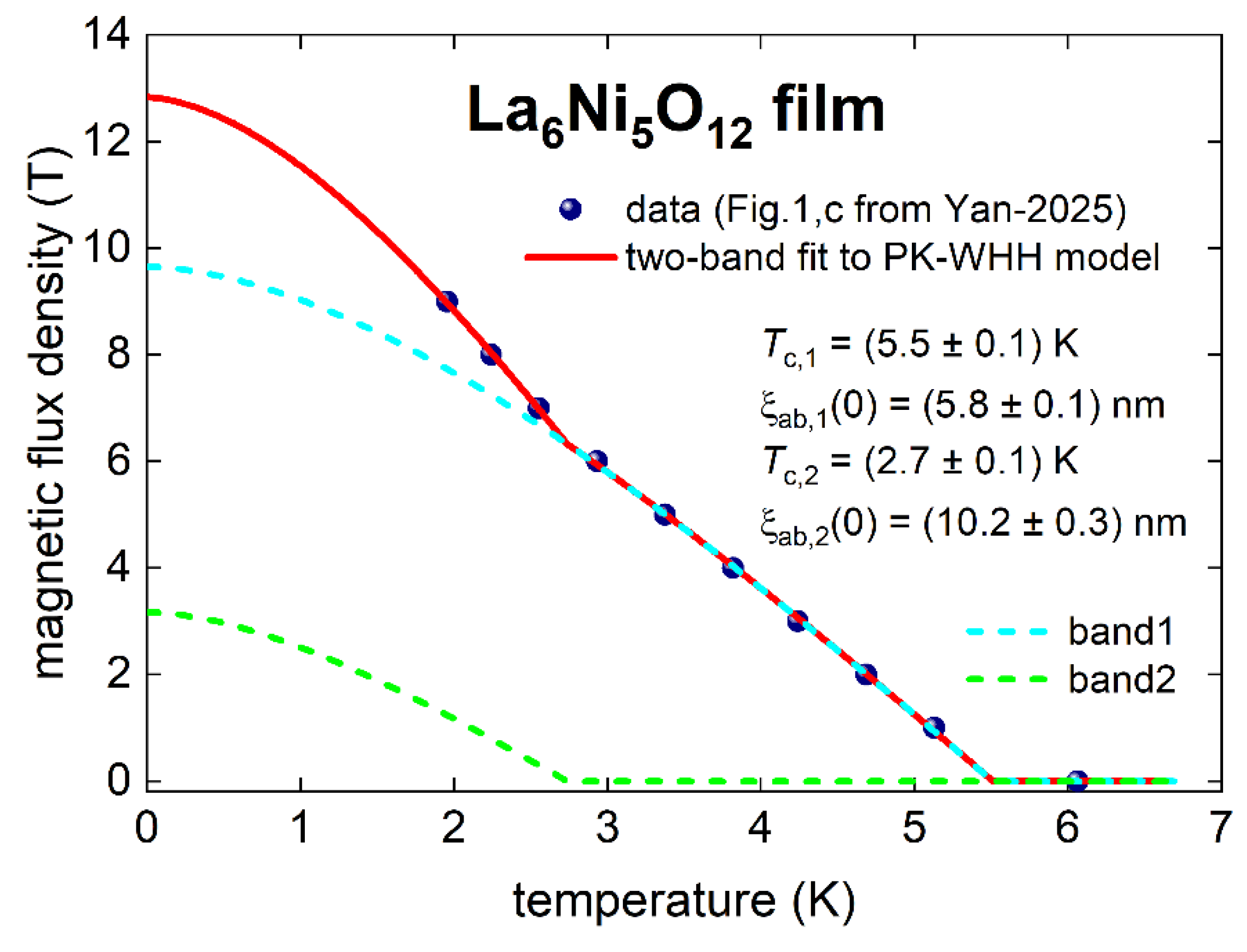
5.5. Ambient Pressure La₆Ni₅O₁₂ Thin Film

Recently, Yan et al. [98] reported on observation of significant drop in resistivity in ambient pressure single-unit-cell Nd₆Ni₅O₁₂ film at temperatures $T\lesssim 10K$. Despite the zero resistance was not observed in the film (down to $T=1.8K$), typical for superconductors suppression of the $T_c^{onset}$ in applied magnetic field was observed. We assumed that the single-unit-cell Nd₆Ni₅O₁₂ film is a superconductor and applied resistive criterion:

$${\displaystyle \frac{R\left(T=T_{c,0.50}\right)}{\rho \left(T_{c,onset}=30K\right)}}=0.50$$

(37)

to determine the $B_{c2}\left(T\right)$ dataset for Nd₆Ni₅O₁₂ film. In Figure 14 we showed the obtained $B_{c2}\left(T\right)$ dataset and data fit to two-band model (Eqs. 3, 32). Evidence for two-band superconductivity can be seen in Figure 14. We should note that the emergence of the second band is completely missed if the $B_{c2}\left(T\right)$ will be defined by overwhelmingly large criterion of ${\displaystyle \frac{R\left(T=T_{c,0.90}\right)}{\rho \left(T_{c,onset}=30K\right)}}=0.90$, as the one implemented by Yan et al. [98] in their Figure 1,d.

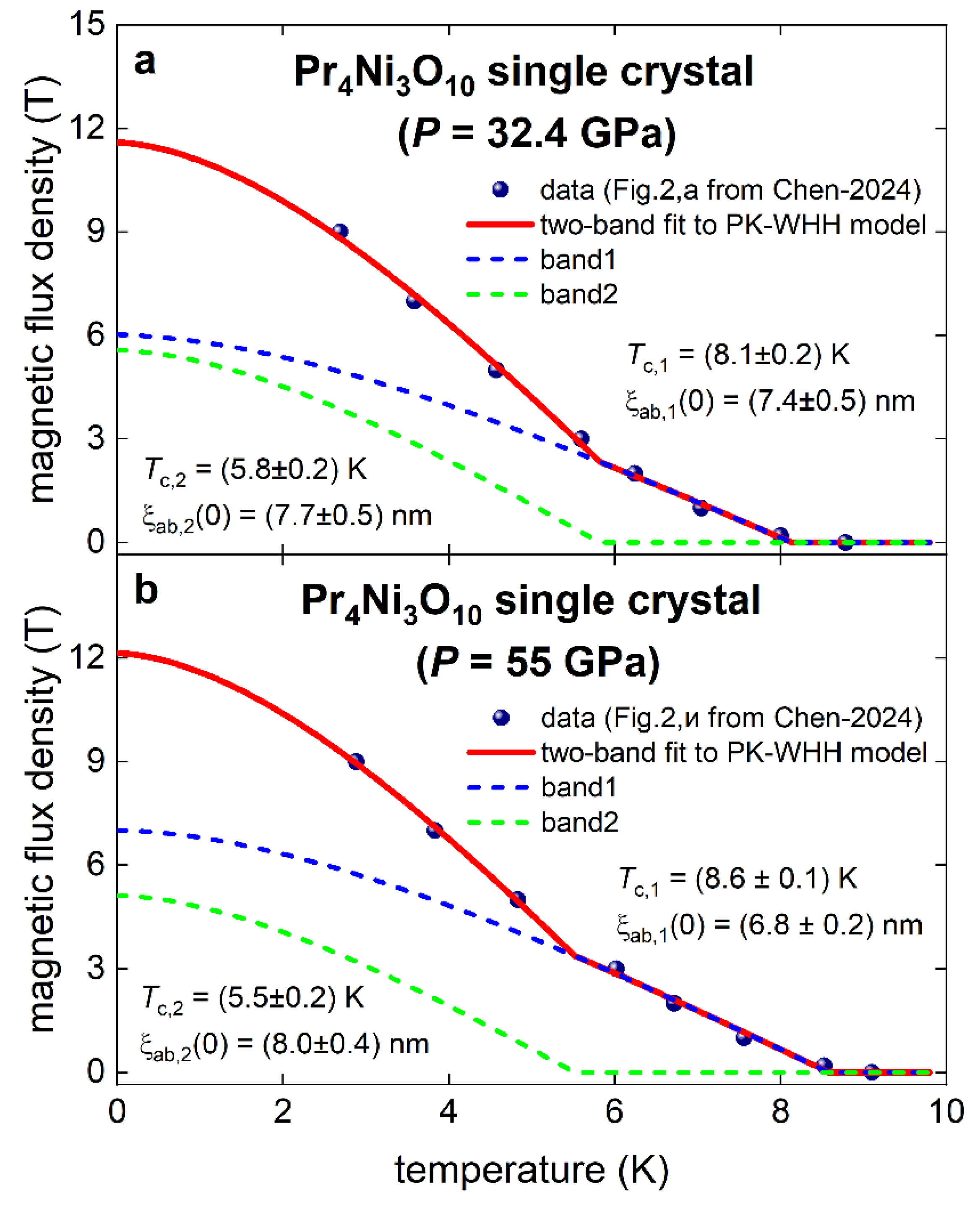
5.6. Highly Compressed Pr₄Ni₃O₁₀ Single Crystal

To demonstrate that the Ruddlesden-Popper nickelates exhibit two-band superconductivity in Figure 15 we showed the $B_{c2}\left(T\right)$ datasets deduced from the $R\left(T,B\right)$ dataset measured in highly compressed Nd₆Ni₅O₁₂ single crystal by Chen et al. [99]. It should be noted, that recently Zhang et al. [100] reported on observation of the zero-resistance state with $T_{c,zero}\left(P=70.5GPa\right)=18K$ in the single crystal of the same phase Nd₆Ni₅O₁₂, however, the $R\left(T,B\right)$ dataset is unavailable to date.

In Figure 15,a we applied the criterion of ${\displaystyle \frac{R\left(T=T_{c,0.56}\right)}{\rho \left(T_{c,onset}=30K\right)}}=0.56$ to define the $B_{c2}\left(T,P=32.4GPa\right)$ dataset reported in Figure 2,a [99], and in Figure 15,b we applied the criterion of ${\displaystyle \frac{R\left(T=T_{c,0.50}\right)}{\rho \left(T_{c,onset}=30K\right)}}=0.84$ to define $B_{c2}\left(T,P=55GPa\right)$ in the Nd₆Ni₅O₁₂ single crystal.

Data fits to Eqs. 3,32 (Figure 15) confirms two-band nature of the superconducting state in highly compressed Nd₆Ni₅O₁₂ single crystal.

6. The limitation of T_c in nickelates by thermal fluctuations

Thermal fluctuations are expected to break Cooper pairs and suppress superconductivity for materials with low superfluid density [32]. For HTS cuprates strong thermal fluctuations reduce the observed transition temperature, T_c, below its meanfield value, by up to 30%, and similar feature have been understood in iron-based superconductors [101,102,103,104], however, the transition temperatures in near-room-temperature hydride superconductors [105,106,107,108,109,110,111] based on their 3D nature and short London penetration depth λ(0) [112,113,114] are not affected by thermal fluctuations [33,115].

However, large London penetration depth λ(T) in ambient pressure La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15, 1.0) films deduced herein and reported in Ref. [2] opened a question about the impact of thermal fluctuations on T_c in these films.

By considering unit cells of the Ruddlesden-Popper nickelate family phases, La_n+1Ni_nO_3n+1 (n = 2,3) considering herein, one can conclude that main structural element where high-temperature superconductivity is originated from is the 3D Ni-O octahedron. Thus, in opposite to HTS cuprates, the superconductivity in La_n+1Ni_nO_3n+1 can be classified to exhibit 3D nature, despite the superconductivity observed in very thin films of La_n+1Ni_nO_3n+1.

Based on this, we can calculate the phase fluctuation temperature for 3D superconductors in accordance with Emery and Kivelson approach [32]:

$$T_{fluc,phase}[K]={\displaystyle \frac{2.2\times {\varphi }_0^2\sqrt{\pi }\xi \left(0\right)}{{{4{\pi }^2\mu }_{0}k}_B{\lambda }^2\left(0\right)}}={\displaystyle \frac{0.55\times {\varphi }_0^2}{{\pi }^{1.5}{{\mu }_{0}k}_B}}\times {\displaystyle \frac{1}{{\lambda }_{ab}\left(0\right)\times {\kappa }_c\left(0\right)}}={\displaystyle \frac{0.0243\left[m^{2}K\right]}{{\lambda }_{ab}\left(0\right)\times {\kappa }_c\left(0\right)\left[m^2\right]}}$$

(38)

The substitution of the deduced values for the La₃Ni₂O_7-δ film [1] in Eq. 38 returns:

$$T_{fluc,phase}\left({\lambda }_{ab}\left(0\right)=6.4\mu m;{\kappa }_c\left(0\right)=500\right)=7.6K$$

(39)

Defined by us (Eq. 13) $T_{c,0.06}=3.0-3.5K$ in this film is about half of the $T_{fluc,phase}=7.6K$, which is expected value, if we take into account that thermal fluctuations cause ~ 30-50% suppression for T_c.

The substitution of the deduced values for the La₂PrNi₂O_7-δ film [3] in Eq. 38 returns:

$$T_{fluc,phase}\left({\lambda }_{ab}\left(0\right)=2.0\mu m;{\kappa }_c\left(0\right)=500\right)=24K$$

(40)

which is again about twice higher than the observed $T_{c,zero}=14K$.

For the for the La_3-xPr_xNi₂O_7-δ film [2], the substitution of the lower limit for the reported ${\lambda }_{ab}\left(T=1.8K\right)=3.7{\pm }_{1.9}^{1.4}\mu m$ value and ${\kappa }_c\left(0\right)=500$, returns:

$$T_{fluc,phase}\left({\lambda }_{ab}\left(0\right)=1.8\mu m;{\kappa }_c\left(0\right)=500\right)=27K$$

(41)

We need to mention, that the authors [2] pointed out that reported $J_c\left(sf,T\right)$ (from which we extracted ${\lambda }_{ab}\left(0\right)=4.0\mu m$) was measured at conditions of large heat realize. Thus, the shortest London penetration depth ${\lambda }_{ab}\left(0\right)=3.6\mu m$ (Figure 9) which we deduced from the $J_c\left(sf,T\right)$ represents the upper-limiting value for the London penetration depth, for which we calculate:

$$T_{fluc,phase}\left({\lambda }_{ab}\left(0\right)=3.6\mu m;{\kappa }_c\left(0\right)=900\right)=7.5K$$

(42)

Thus, the La_3-xPr_xNi₂O_7-δ film [2] exhibits the phase fluctuation temperature in the range:

$$7.5K\le T_{fluc,phase}\le 27K$$

(43)

And thus, observed in experiment diamagnetic $T_{c,diamag}=8.5K$ and resistive $T_{c,zero}=\cong 9.0K$ are in the range described by Eq. 43.

In Figure 16, we summarized the London penetration depth data ${\lambda }_{ab}\left(T\right)$ for La_3-xPr_xNi₂O_7-δ (x = 0.0, 0.15, 1.0) films.