Submitted:
26 January 2025
Posted:
27 January 2025
You are already at the latest version
Abstract
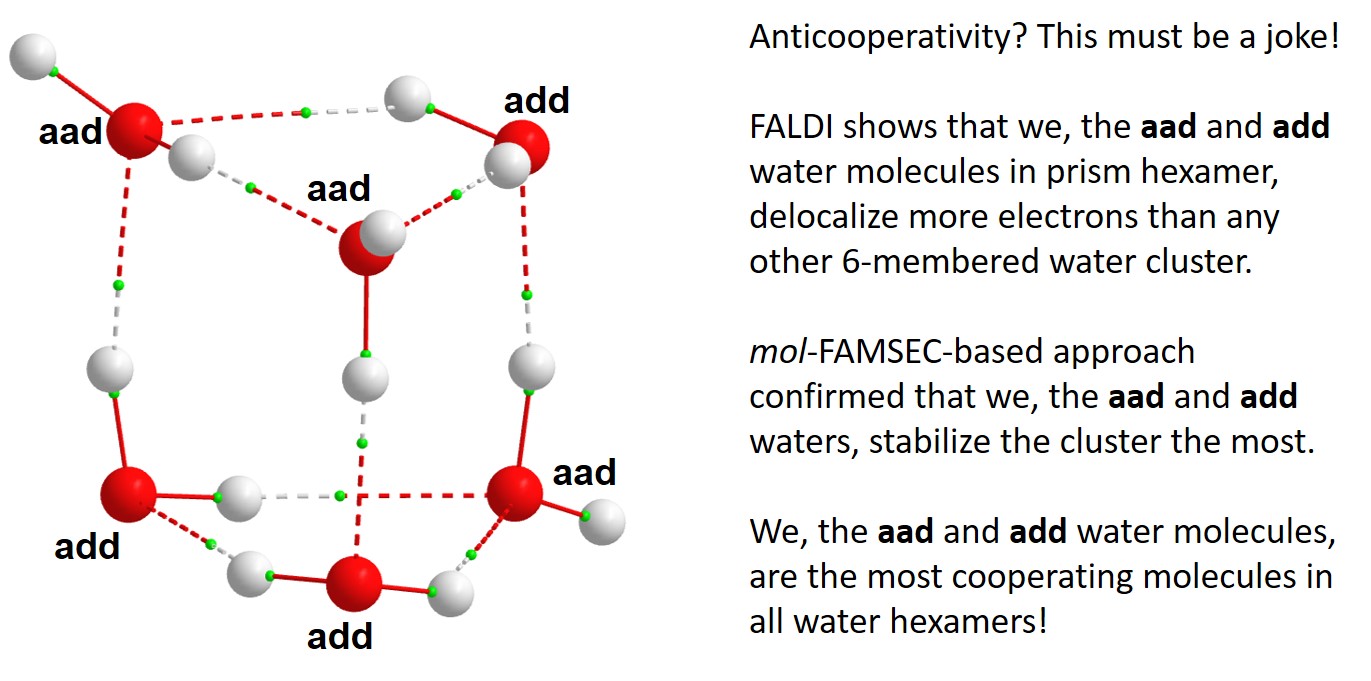
Keywords:
1. Introduction
- (a)
- Intermolecular e-delocalization by water molecules in a cluster can be interpreted as equivalent to doing something together or working together with others from Oxford dictionary definition of cooperativity, and
- (b)
- Reaching the lowest e-energy of a water cluster through intermolecular e-delocalization (from our definition) compares well with Cooperative activity is essential to effective community work to achieve a shared aim as per Oxford dictionary definition.
- 1. 3D 6-water clusters discussed in this work are more stable than 2D cyclic homodromic water hexamer and the latter is restricted to ad configurations showing only positive, non-additivity in the strength of H-bonds, i.e., classical cooperativity, and
- 2. Prism, being the most stable 3D 6-water hexamer, does not have water molecules of ad configurations (there are 3 aad and 3 add waters)
- i.
- Are more stable than the 6-water cyclic hexamer; notably, they are the smallest 3D clusters that are more stable than their cyclic counterparts, and
- i.
- ii. Have water molecules with aad and add configurations and these motifs are observed in each of the ice polymorphs [2].
- i.
- i.
- ii. The Fragment Attributed Molecular System Energy Change (FAMSEC) family of methods [53,54] is used to identify molecular fragments that either drive or obstruct a chemical change the most. FAMSEC also meets the all-body requirements as the quantified energy contributions made by fragments are harvested from entire space occupied by a system.
2. Computational Methods
3. Theoretical Background
3.1. The FALDI Density Decomposition Scheme
3.2. A Fragment Attributed Molecular System Energy Change (FAMSEC) Protocol
4. Results and Discussion
4.1. Validation of B3LYP-Computed Relative Stabilities of Water Hexamers
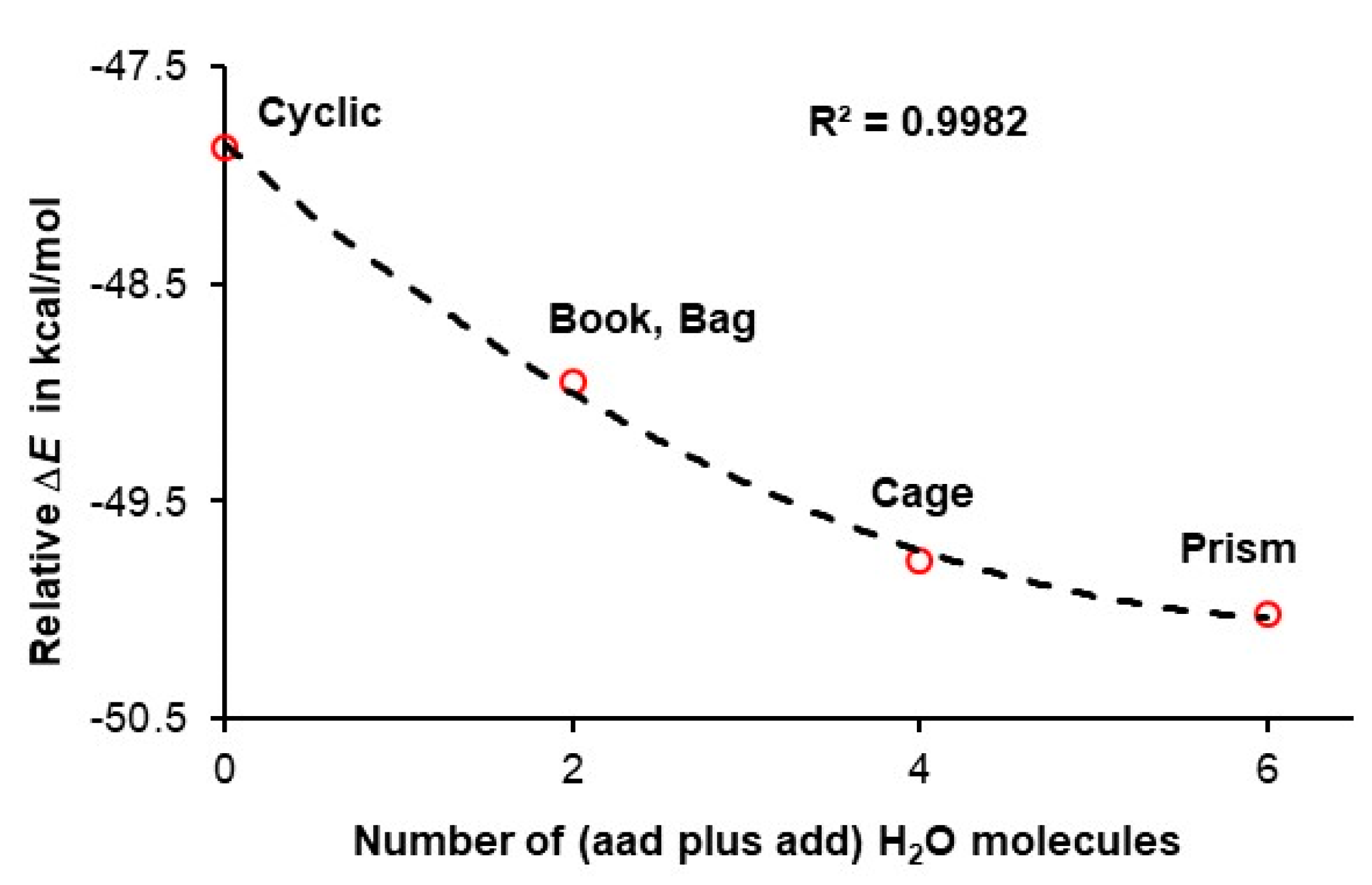
4.2. A Cooperativity-Driven Decrease in E(hexamer) Relative to E(6H2O)
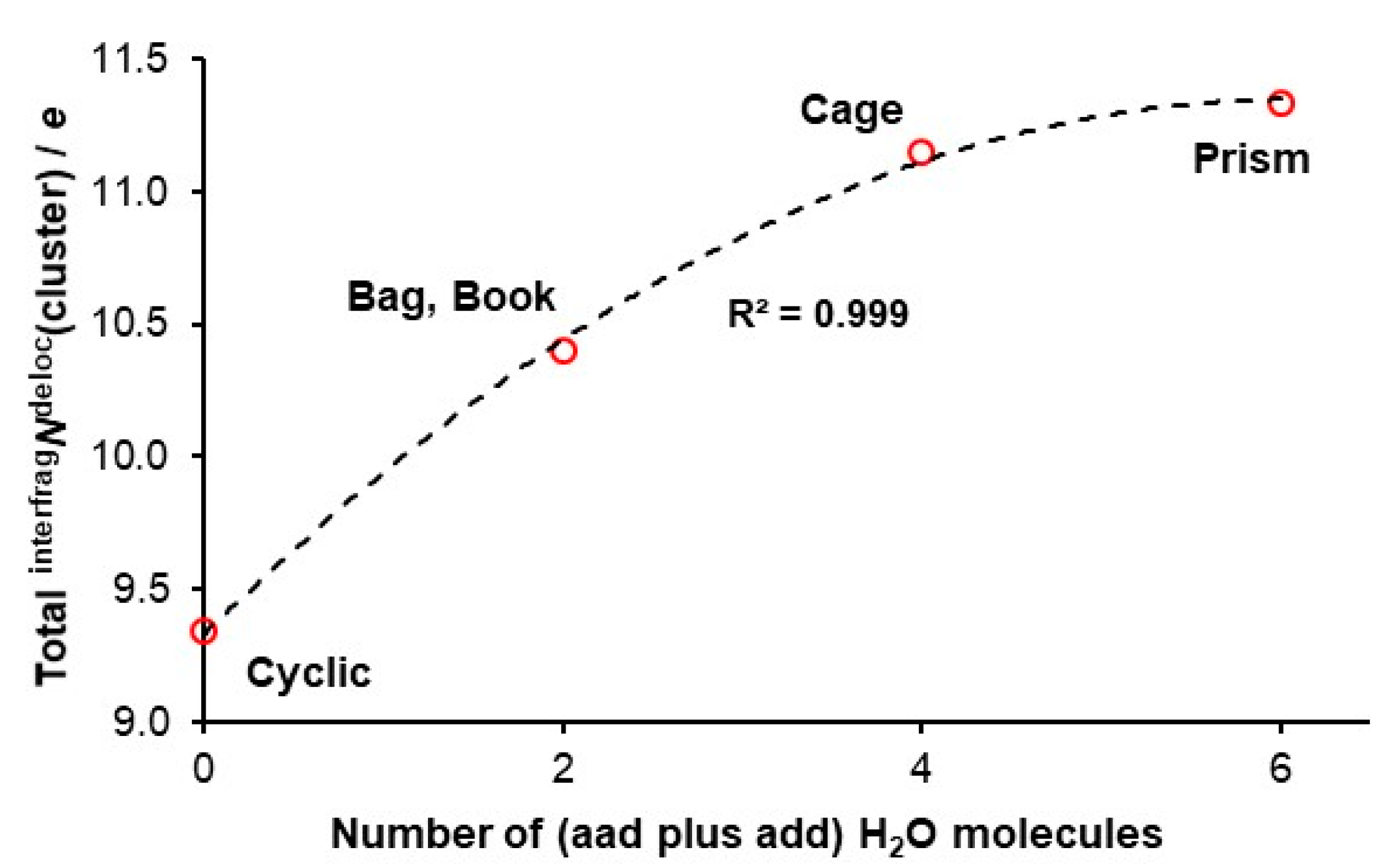
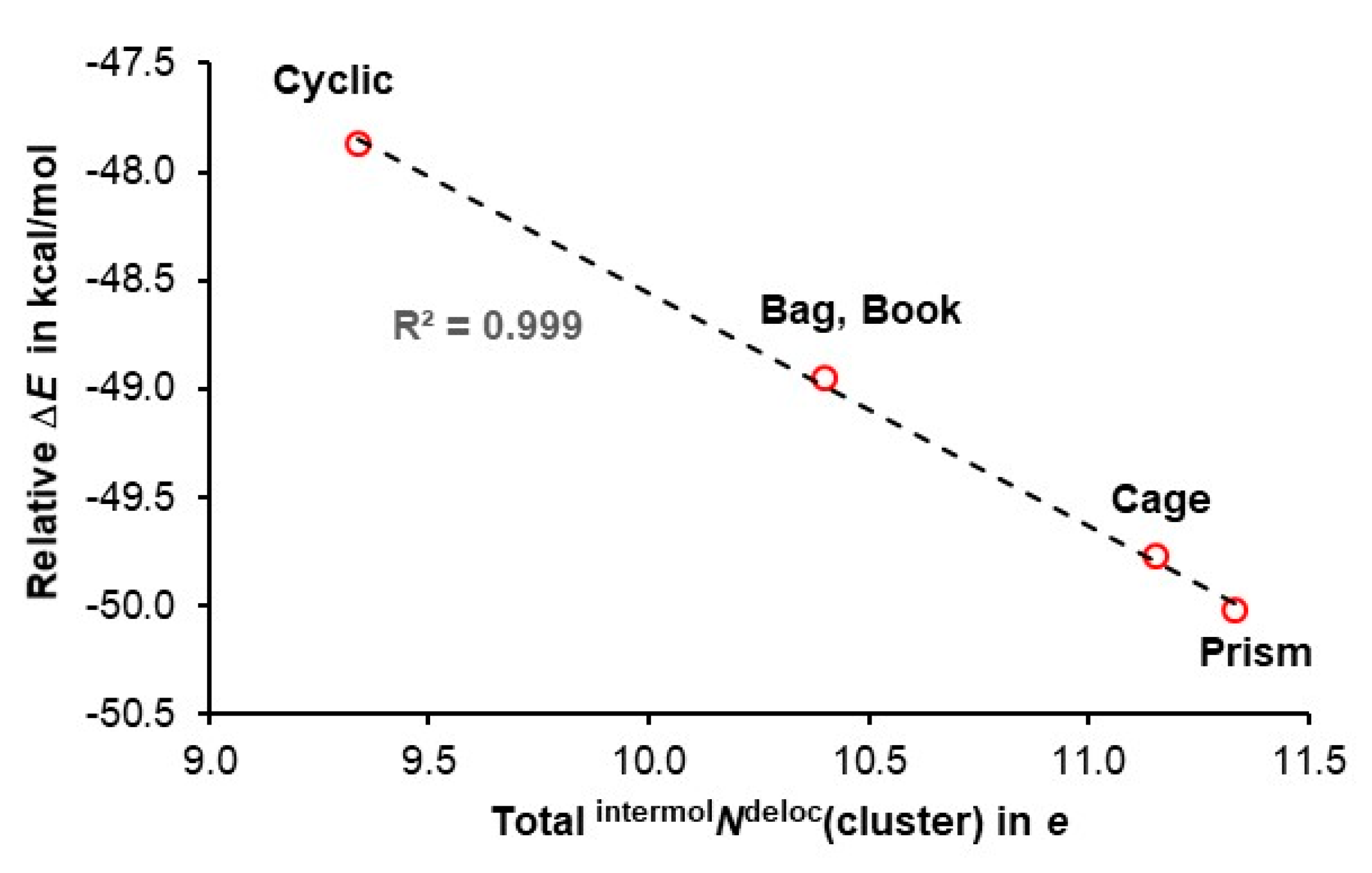
4.3. Quantifying Cooperativity
- (i)
- The number of delocalized electrons by ad waters in 3D hexamers examined is the same as found for cyclic hexamer for which intermolNdeloc = 1.557±0.001e [47],
- (ii)
- The difference in intermolNdeloc between aad and add waters in 3D hexamers is insignificant and, the most importantly,
- (iii)
- There is a very significant difference in the number of delocalized electrons between ad and double-acceptor aad and double-donor add waters with ad delocalizing about 0.45e less.
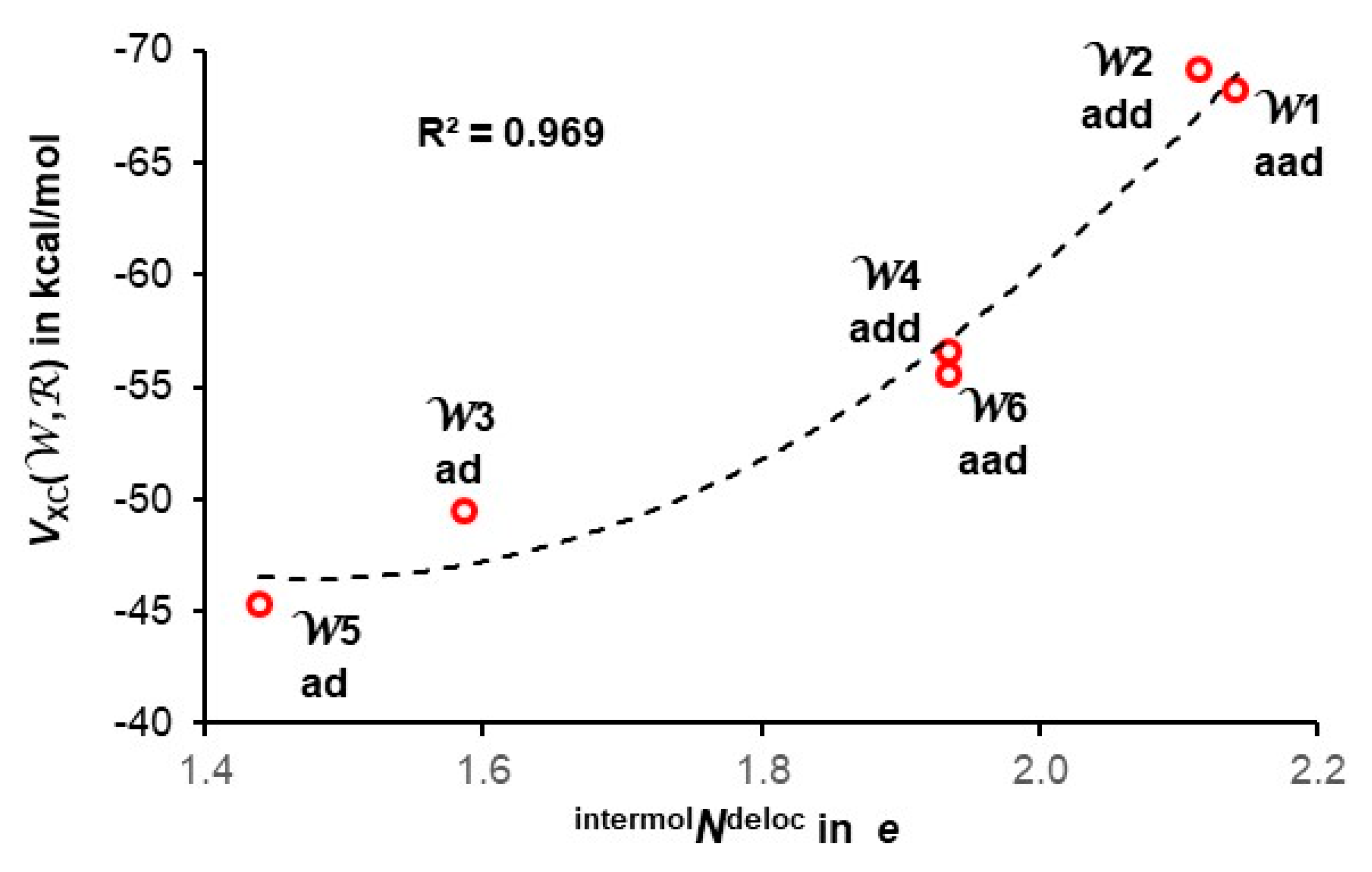
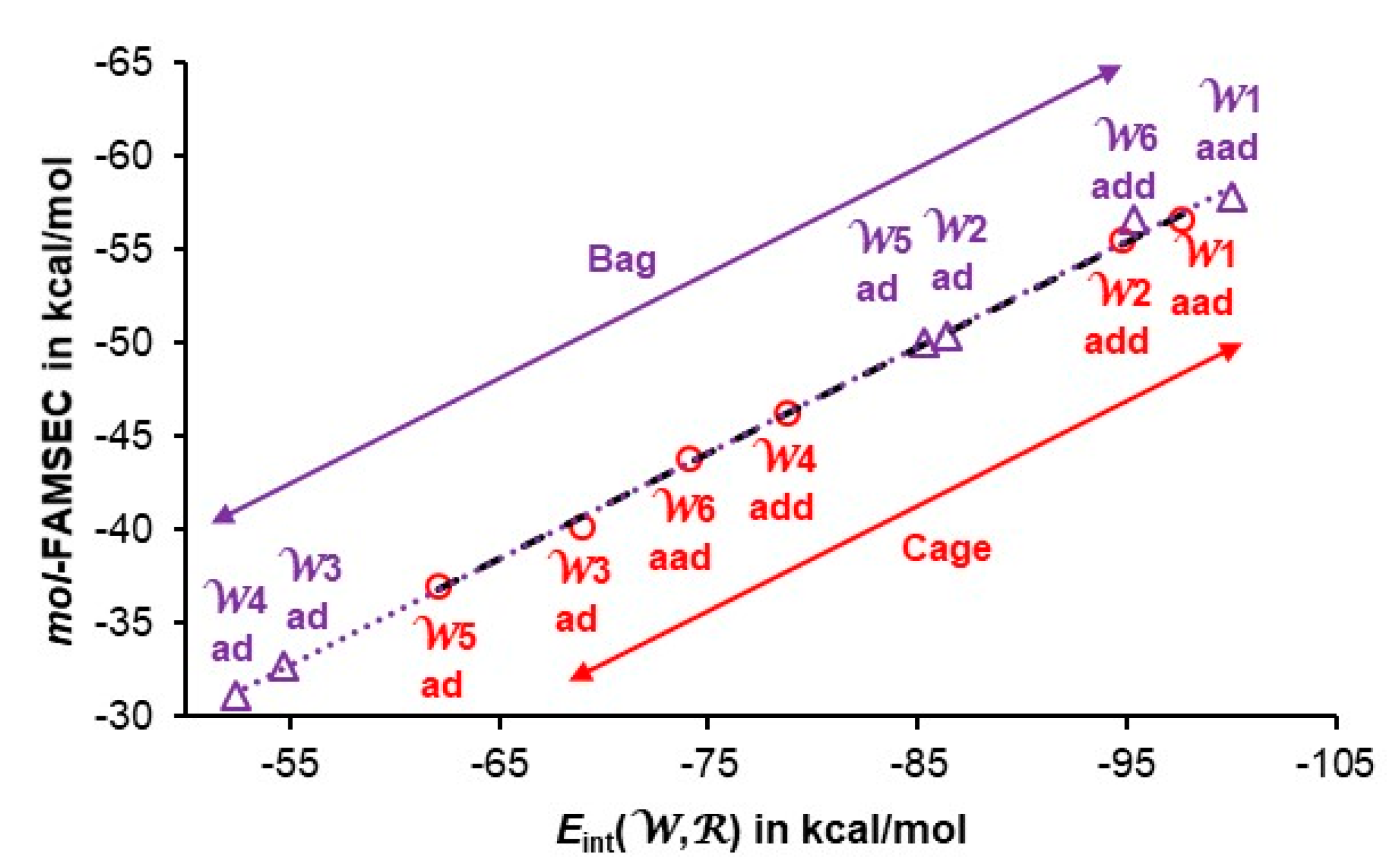
4.4. Quantifying Individual Water’s Contribution to the Cluster’s Stability
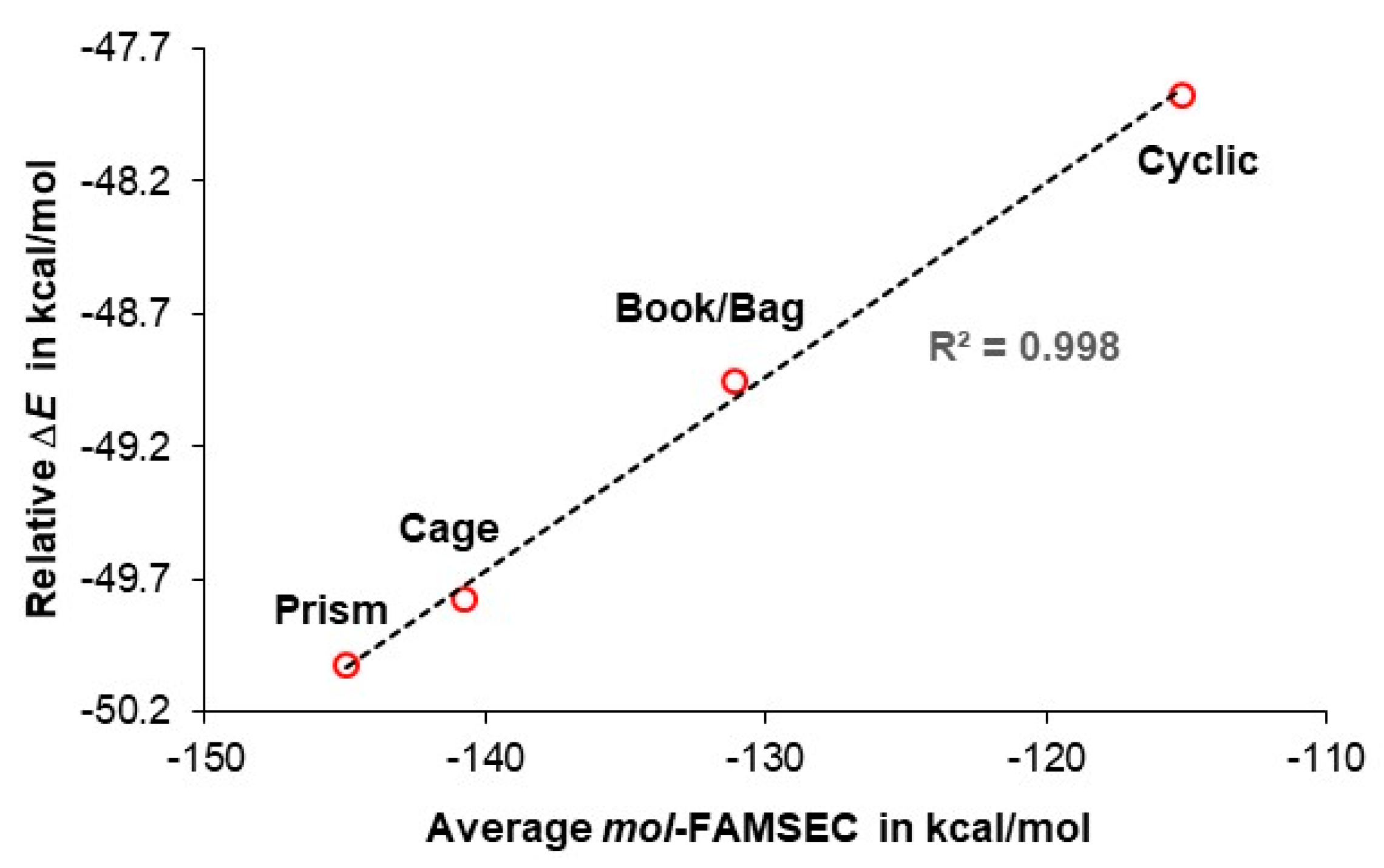
4.5. Quantifying Individual Intermolecular H-bonds’ Contribution to the Cluster’s Stability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- H. S. Frank, W-Y. Wen, III. Ion-Solvent Interaction. Structural Aspects of Ion-Solvent Interaction in Aaqueous Solutions: A Suggested Picture of Water Structure. Discuss. Faraday Soc. 1957, 24, 133–140. [Google Scholar] [CrossRef]
- D. Hankins, J. W. Moskowitz, F. H. Stillinger, Water Molecule Interactions. J. Chem. Phys. 1970, 53, 4544–4554. [Google Scholar] [CrossRef]
- J. C. White, E. R. Davidson, An Analysis of the Hydrogen Bond in Ice. J. Chem. Phys. 1990, 93, 8029–8035. [Google Scholar] [CrossRef]
- S. S. Xantheas, T. H. Dunning, Jr. The Structure of the Water Trimer From ab Initio Calculations. J. Chem. Phys. 1993, 98, 8037–8040. [Google Scholar] [CrossRef]
- S. S. Xantheas, T. H. Dunning, Jr. Ab Initio Studies of Cyclic Water Clusters (H2O)n, n = 1–6. I. Optimal Structures and Vibrational Spectra. J. Chem. Phys. 1993, 99, 8774–8792. [Google Scholar] [CrossRef]
- S. S. Xantheas Ab Initio Studies of Cyclic Water Clusters (H2O)n, n = 1–6. II. Analysis of Many-Body Interactions. J. Chem. Phys. 1994, 100, 7523–7534. [Google Scholar] [CrossRef]
- W. A.P. Luck, The importance of cooperativity for the properties of liquid water. J. Mol. Struct. 1998, 448, 131–14. [Google Scholar] [CrossRef]
- J. M. Ugalde, I. Alkorta and J. Elguero, Water Clusters: Towards an Understanding Based on First Principles of Their Static and Dynamic Properties. Angew. Chem. Int. Ed., 2000, 39, 717–721. [Google Scholar] [CrossRef]
- R. Ludwig, Water: From Clusters to the Bulk. Angew. Chem. Int. Ed. 2001, 40, 1808–1827. [Google Scholar] [CrossRef]
- F. N. Keutsch, J. D. Cruzan and R. J. Saykally, The Water Trimer. Chem. Rev., 2003, 103, 2533–2577. [Google Scholar]
- K. Ohno, M. Okimura, N. Akaib, Y. Katsumotoa, The effect of cooperative hydrogen bonding on the OH stretching-band shift for water clusters studied by matrix-isolation infrared spectroscopy and density functional theory. Phys. Chem. Chem. Phys. 2005, 7, 3005–3014. [Google Scholar] [CrossRef] [PubMed]
- Y. I. Neela, A. S. Y. I. Neela, A. S. Mahadevi, G. N. Sastry, Hydrogen Bonding in Water Clusters and Their Ionized Counterparts. J. Phys. Chem. B 2010, 114, 17162–17171. [Google Scholar] [CrossRef] [PubMed]
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel, B. H. Pate, Structures of Cage, Prism, and Book Isomers of Water Hexamer from Broadband Rotational Spectroscopy. Science, 2012, 336, 897–901. [Google Scholar] [CrossRef] [PubMed]
- L. Albrecht and R. J. Boyd, Visualizing Internal Stabilization in Weakly Bound Systems Using Atomic Energies: Hydrogen Bonding in Small Water Clusters. J. Phys. Chem. A, 2012, 116, 3946–3951. [Google Scholar] [CrossRef]
- J. M. Guevara-Vela, R. Chávez-Calvillo, M. García-Revilla, J. Hernández-Trujillo, O. Christiansen, E. Francisco, Á. Martín Pendás, and T. Rocha-Rinza, Hydrogen-Bond Cooperative Effects in Small Cyclic Water Clusters as Revealed by the Interacting Quantum Atoms Approach. Chem. Eur. J., 2013, 19, 14304–14315. [Google Scholar]
- L. Albrecht, S. Chowdhury, R. J. Boyd, Hydrogen Bond Cooperativity in Water Hexamers: Atomic Energy Perspective of Local Stabilities. J. Phys. Chem. A, 2013, 117, 10790–10799. [Google Scholar] [CrossRef] [PubMed]
- J. C. Howard and G. S. Tschumper, WIREs Comput. Mol. Sci. Wavefunction Methods for the Accurate Characterization of Water Clusters. 2014, 4, 199–224.
- B. D. Marshall, A Second Order Thermodynamic Perturbation Theory for Hydrogen Bond Cooperativity in Water. J. Chem. Phys. 2017, 146, 174104. [Google Scholar] [CrossRef]
- A. Rakshit, P. Bandyopadhyay, J. P. Heindel and S. S. Xantheas, Atlas of Putative Minima and Low-Lying Energy Networks of Water Clusters n = 3–25. J. Chem. Phys. 2019, 151, 214307. [Google Scholar] [CrossRef] [PubMed]
- Simon, M. Rapacioli, E. Michoulier, L. Zheng, K. Korchagina and J. Cuny, Contribution of the Density-Functional-Based Tight-Binding Scheme to the Description of Water Clusters: Methods, Applications and Extension to Bulk Systems. Mol. Sim. 2019, 45, 249–268. [Google Scholar] [CrossRef]
- M. B. Ahirwar, S. R. Gadre and M. M. Deshmukh, Direct and Reliable Method for Estimating the Hydrogen Bond Energies and Cooperativity in Water Clusters, Wn, n = 3 to 8. J. Phys. Chem. A, 2020, 124, 6699–6706. [Google Scholar] [CrossRef] [PubMed]
- J. A. Bilbrey, J. P. Heindel, M. Schram, P. Bandyopadhyay, S. S. Xantheas, S. Choudhury, A Look Inside the Black Box: Using Graph Theoretical Descriptors to Interpret a Continuous-Filter Convolutional Neural Network (CF-CNN) Trained on the Global and Local Minimum Energy Structures of Neutral Water Clusters. J. Chem. Phys. 2020, 153, 024302. [Google Scholar]
- D. Ben-Amotz, Electric Buzz in a Glass of Pure Water. Hydrogen Bond Charge Transfer in Water May Have Far-Reaching Chemical Iimplications. Science, 2022, 376, 800–801. [Google Scholar]
- L. E. Seijas, C. H. Zambrano, R. Almeida, J. Alí-Torres, L. Rincón, F. J. Torres, Exploring the Non-Covalent Bonding in Water Clusters. Int. J. Mol. Sci. 2023, 24, 5271. [Google Scholar] [CrossRef] [PubMed]
- G. D. Santis, K. M. Herman, J. P. Heindel, S. S. Xantheas, Descriptors of Water Aggregation. J. Chem. Phys., 2024, 160, 054306. [Google Scholar]
- L. Ojamäe, K. Hermansson, Ab Initio Study of Cooperativity in Water Chains: Binding Energies and Anharmonic Frequencies. J. Phys. Chem. 1994, 98, 4271–4282. [Google Scholar] [CrossRef]
- W. A. P. Luck, D. Klein, K. Rangsriwatananon, Anti-Cooperativity of the Two Water OH Groups. J. Mol. Struct. 1997, 416, 287–296. [Google Scholar] [CrossRef]
- M. Huš, T. Urbic, Strength of Hydrogen Bonds of Water Depends on Local Environment. J. Chem. Phys. 2012, 136, 144305. [Google Scholar] [CrossRef]
- L. Albrecht, R. J. Boyd, Atomic energy analysis of cooperativity, anti-cooperativity, and non-cooperativity in small clusters of methanol, water, and formaldehyde. Comput. Theoret. Chem. 2015, 1053, 328–336. [Google Scholar] [CrossRef]
- S. Saha, G. N. Sastry, Quantifying cooperativity in water clusters: an attempt towards obtaining a generalised equation. Mol. Phys. 2015, 113, 3031–3041. [Google Scholar] [CrossRef]
- J.M. Guevara-Vela, E. Romero-Montalvo, V. A. M. Gómez, R. Chávez-Calvillo, M. García-Revilla, E. Francisco, Á. Martín Pendás, and T. Rocha-Rinza, Hydrogen Bond Cooperativity and Anticooperativity Within the Water Hexamer. Phys. Chem. Chem. Phys. 2016, 18, 19557–19566.
- A. S. Mahadevi and G. N. Sastry, Cooperativity in Noncovalent Interactions. Chem. Rev., 2016, 116, 2775–2825. [Google Scholar] [CrossRef]
- P. L. Silvestrelli, Hydrogen bonding characterization in water and small molecules. J. Chem. Phys. 2017, 146, 244315. [Google Scholar] [CrossRef]
- V. M. Castor-Villegas, J. M. Guevara-Vela, W. E. Vallejo Narváez, Á. Martín Pendás, T. Rocha-Rinza, A. Fernández-Alarcón, On the Strength of Hydrogen Bonding Within Water Clusters on the Coordination Limit. J. Comput. Chem. 2020, 41, 2266–2277. [Google Scholar]
- A. Sauza-de la Vega, T. Rocha-Rinza, J. M. Guevara-Vela, Cooperativity and Anticooperativity in Ion-Water Interactions: Implications for the Aqueous Solvation of Ions. Chem. Phys. Chem. 2021, 22, 1269–1285. [Google Scholar] [CrossRef] [PubMed]
- T. Steiner, The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- M. Hakala, K. Nygård, S. Manninen, L. G. M. Pettersson, K. Hämäläinen, Intra- and Intermolecular Effects in the Compton Profile of Water. Phys. Rev. B. 2006, 73, 035432. [CrossRef]
- Ignatov, O. Mosin, Mathematical Models Describing Water Clusters as Interaction Among Water Molecules. Distributions of Energies of Hydrogen Bonds. J. Med. Physiol. Biophys. 2014, 3, 48–70. [Google Scholar]
- M. Weimann, M. Fárník, M. A. Suhm, M. E. Alikhani, J. Sadlej, Cooperative and Anticooperative Mixed Trimers of HCl and Methanol. J Mol. Struct. 2006, 790, 18–26. [Google Scholar] [CrossRef]
- A. Zabardasti, A. Kakanejadi, F. Ghenaatian, Z. Bigleri, A Theoretical Study of Cooperative and Anticooperative Effects on Hydrogen-Bonded Clusters of Water and the Cyanuric Acid. Mol. Sim. 2010, 36, 960–968. [Google Scholar] [CrossRef]
- Zabardasti, A. Kakanejadi, S. Moosavi, Z. Bigleri, M. Solimannejad, Anticooperativity in Dihydrogen Bonded Clusters of Ammonia and BeH42–. J. Mol. Struct: THEOCHEM 2010, 945, 97–100. [Google Scholar] [CrossRef]
- G. Han, Y. Ding, P. Qian, C. Zhang, and W. Song, Theoretical Investigation of Gas Phase Ethanol–(Water)n (n = 1–5) Clusters and Comparison with Gas Phase Pure Water Clusters (Water)n (n = 2–6). Int. J. Quantum Chem., 2013, 113, 1511–1521. [Google Scholar] [CrossRef]
- E. Romero-Montalvo, J. M. Guevara-Vela, A. Costales, Á. Martín Pendás and T. Rocha-Rinza, Cooperative and Aticooperative Effects in Resonance Assisted Hydrogen Bonds in Merged Structures of Malondialdehyde. Phys. Chem. Chem. Phys., 2017, 19, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Monu, B. K. Oram, B. Bandyopadhyay, Simultaneous Exhibition of Positive and Negative Cooperativity by Purely C H⋅⋅⋅O H-bonded (1,3-cyclohexanedione)n (n = 2–6) Clusters: A Density Functional Theoretical Investigation. Int. J. Quantum Chem. 2021, 121, 26581. [Google Scholar] [CrossRef]
- S. Guo, C. Zhu, G, Chen, J. Gu, C. Ma, H. Gao, L. Li, Y. Zhang,·X. Li, Z. Wang, Y. Wei, G. Wang, J. Shen, A Theoretical Study on Intermolecular Hydrogen Bonds of Isopropanol-Water Clusters. Theoret. Chem. Acc. 2022, 141, 6. [Google Scholar]
- D. Patkar, M. B. Ahirwar, M. M. Deshmukh, Energetic Ordering of Hydrogen Bond Strengths in Methanol-Water Clusters: Insights via Molecular Tailoring Approach. Chem. Phys. Chem. 2022, 23, 202200143. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, S. Zaaiman, S. Hussain, J. H. de Lange, All-Body Concept and Quantified Limits of Cooperativity and Related Effects in Homodromic Cyclic Water Clusters From a Molecular-Wide and Electron Density (MOWeD)-Based Approach. J. Comput. Chem. 2024, 45, 2812–2824. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, A Unified Molecular-Wide and Electron Density Based Concept of Chemical Bonding. WIREs Comput Mol Sci. 2022, 12, 1579. [CrossRef]
- R. F. W. Bader, Bond Paths are not Chemical Bonds. J. Phys. Chem. A, 2009, 113, 10391–10396. [Google Scholar] [CrossRef]
- H. de Lange, I. Cukrowski, Toward Deformation Densities for Intramolecular Interactions without Radical Reference States Using the Fragment, Atom, Localized, Delocalized, and Interatomic (FALDI) Charge Density Decomposition Scheme. J. Comput. Chem. 2017, 38, 981–997. [CrossRef]
- H. de Lange, D. M. van Niekerk, I. Cukrowski, FALDI-Based Decomposition of an Atomic Interaction Line Leads to 3D Representation of the Multicenter Nature of Interactions. J. Comput. Chem. 2018, 39, 973–985. [Google Scholar] [CrossRef] [PubMed]
- H. de Lange, I. Cukrowski, Exact and Exclusive Electron Localization Indices Within QTAIM Atomic Basins. J. Comput. Chem. 2018, 39, 1517–1530. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, IQA-Embedded Fragment Attributed Molecular System Energy Change in Exploring Intramolecular Interactions. Comput. Theoret. Chem. 2015, 1066, 62–75. [CrossRef]
- Cukrowski, G. Dhimba and D. L. Riley, A Reaction Energy Profile and Fragment Attributed Molecular System Energy Change (FAMSEC)-Based Protocol Designed to Uncover Reaction Mechanisms: a Case Study of the Proline-Catalysed Aldol Reaction. Phys. Chem. Chem. Phys., 2019, 21, 16694–16705. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990.
- A. Blanco, Á. Martín Pendás, E. Francisco, Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef]
- E. Francisco, Á. Martín Pendás, M. A. Blanco, A Molecular Energy Decomposition Scheme for Atoms in Molecules. J. Chem. Theory Comput. 2006, 2, 90–102. [Google Scholar] [CrossRef]
- T. A. Keith, AIMAll (Version 19.02.13); TK Gristmill Software: Overland Park, KS, USA, 2019. [Google Scholar]
- Cukrowski, Reliability of HF/IQA, B3LYP/IQA, and MP2/IQA data in interpreting the nature and strength of interactions. Phys. Chem. Chem. Phys., 2019, 21, 10244–10260. [CrossRef]
- W. Humphrey, A. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics. J. Molec. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Cukrowski, J. H. de Lange and S. Hussain, MOWeD-LAC (Molecular-wide electron (de)localization atomic counts) and MOWeD-LFC (Molecular-wide electron (de)localization fragment counts) software applications, 2023. Available at https://bit.ly/link-to-mowed-software.
- H. de Lange, D. M. E. van Niekerk, I. Cukrowski, FALDI-Based Criterion for and the Origin of an Electron Density Bridge with an Associated (3,–1) Critical Point on Bader’s Molecular Graph. J. Comput. Chem. 2018, 39, 2283–2299. [Google Scholar] [CrossRef]
- S. de Beer, I. Cukrowski, J. H. de Lange, Characterization of bonding modes in metal complexes through electron density cross-sections. J Comput Chem. 2020, 41, 2695–2706. [Google Scholar] [CrossRef] [PubMed]
- D. L. Cooper, J. H. de Lange, R. Ponec, Comparison of DAFH and FALDI-like approaches. Theoret. Chem. Acc. 2020, 139, 179. [Google Scholar] [CrossRef]
- T. G. Bates, J. H. de Lange, I. Cukrowski, The CH⋅⋅⋅HC interaction in biphenyl is a delocalized, molecular-wide and entirely non-classical interaction: Results from FALDI analysis. J Comput Chem. 2021, 42, 706–718. [Google Scholar] [CrossRef] [PubMed]
- K. Mdhluli, W. Nxumalo, I. Cukrowski, A REP-FAMSEC Method as a Tool in Explaining Reaction Mechanisms: A Nucleophilic Substitution of 2-Phenylquinoxaline as a DFT Case Study. Molecules, 2021, 26, 1570. [Google Scholar] [CrossRef]
- Cukrowski, G. Dhimba, D. L. Riley, A Molecular-Wide and Electron Density-Based Approach in Exploring Chemical Reactivity and Explicit Dimethyl Sulfoxide (DMSO) Solvent Molecule Effects in the Proline Catalyzed Aldol Reaction. Molecules 2022, 27, 962. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, P. Mangondo, Interacting Quantum Fragments-Rooted Preorganized-Interacting Fragments Attributed Relative Molecular Stability of the BeII Complexes of Nitrilotriacetic Acid and Nitrilotri-3-Propionic Acid. J Comput Chem. 2016, 37, 1373–1387. [Google Scholar] [CrossRef]
- P. Mangondo, I. Cukrowski, On the Origin of the Relative Stability of ZnIINTA and ZnIINTPA Metal Complexes. An Insight From the IQA, IQF, and -FARMS methods. Int. J. Quantum Chem. 2017, 117, 25321. [Google Scholar] [CrossRef]
- Cukrowski, F. Sagan and M. P. Mitoraj, On the Stability of Cis- and Trans-2-Butene Isomers. An Insight Based on the FAMSEC, IQA, and ETS-NOCV Schemes. J. Comput. Chem. 2016, 37, 2783–2798. [Google Scholar] [CrossRef]
- P. Mitoraj, F. Sagan, D. W. Szczepanik, J. H. de Lange, A. L. Ptaszek, D. M. E. van Niekerk and I. Cukrowski, Origin of Hydrocarbons Stability from a Computational Perspective: A Case Study of Ortho-Xylene Isomers. Chem. Phys. Chem, 2020, 21, 494–502. [Google Scholar] [CrossRef] [PubMed]
- M. Bates, G. S. Tschumper, CCSD(T) Complete Basis Set Limit Relative Energies for Low-Lying Water Hexamer Structures. J. Phys. Chem. A, 2009, 113, 3555–3559. [Google Scholar] [CrossRef] [PubMed]
- S. Kryachko, Ab Initio Studies of the Conformations of Water Hexamer: Modelling the Penta-Coordinated Hydrogen-Bonded Pattern in liquid water. Chem. Phys. Lett. 1999, 314, 353–363. [CrossRef]
- R. M. Olson, J. L. Bentz, R. A. Kendall, M. W. Schmidt, M. S. Gordon, A Novel Approach to Parallel Coupled Cluster Calculations: Combining Distributed and Shared Memory Techniques for Modern Cluster Based Systems. J. Chem. Theory Comput., 2007, 3, 1312–1328. [Google Scholar] [CrossRef]
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [CrossRef]
- Koch, M. Pavanello, X. Shao, M. Ihara, P. W. Ayers, C. F. Matta, S. Jenkins, S. Manzhos, The Analysis of Electron Densities: From Basics to Emergent Applications. Chem. Rev. 2024, 124, 12661–12737. [Google Scholar] [CrossRef] [PubMed]
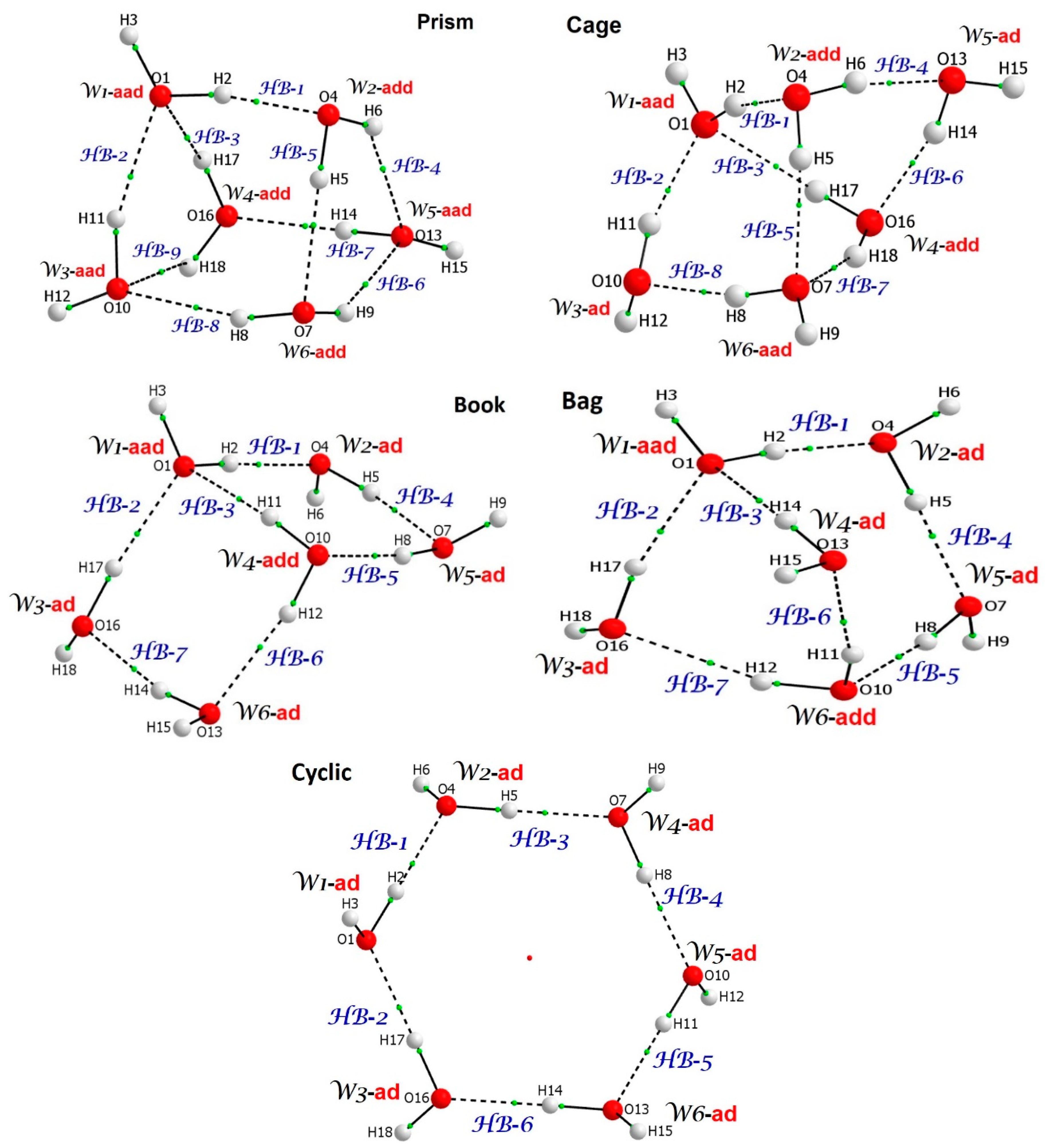
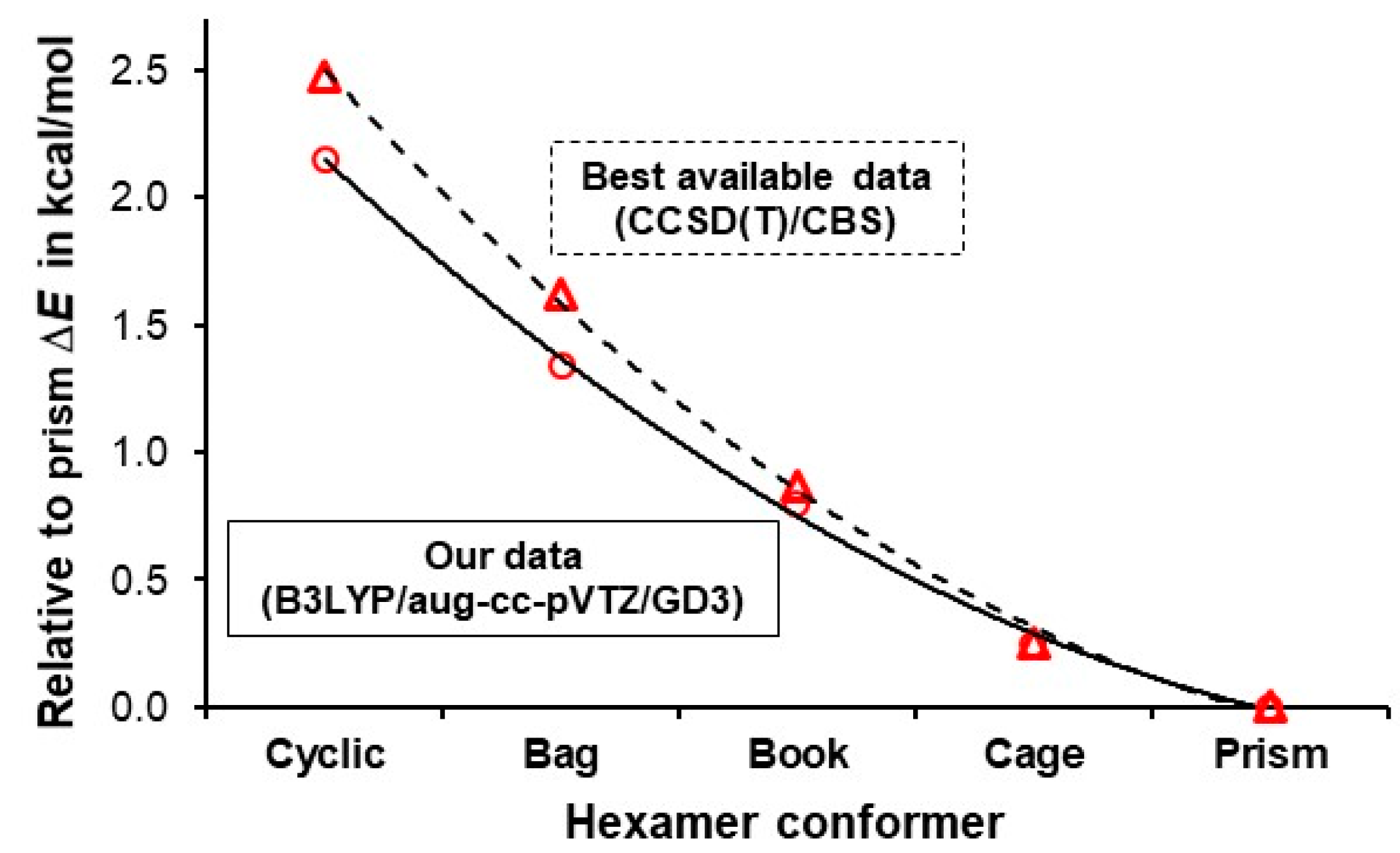
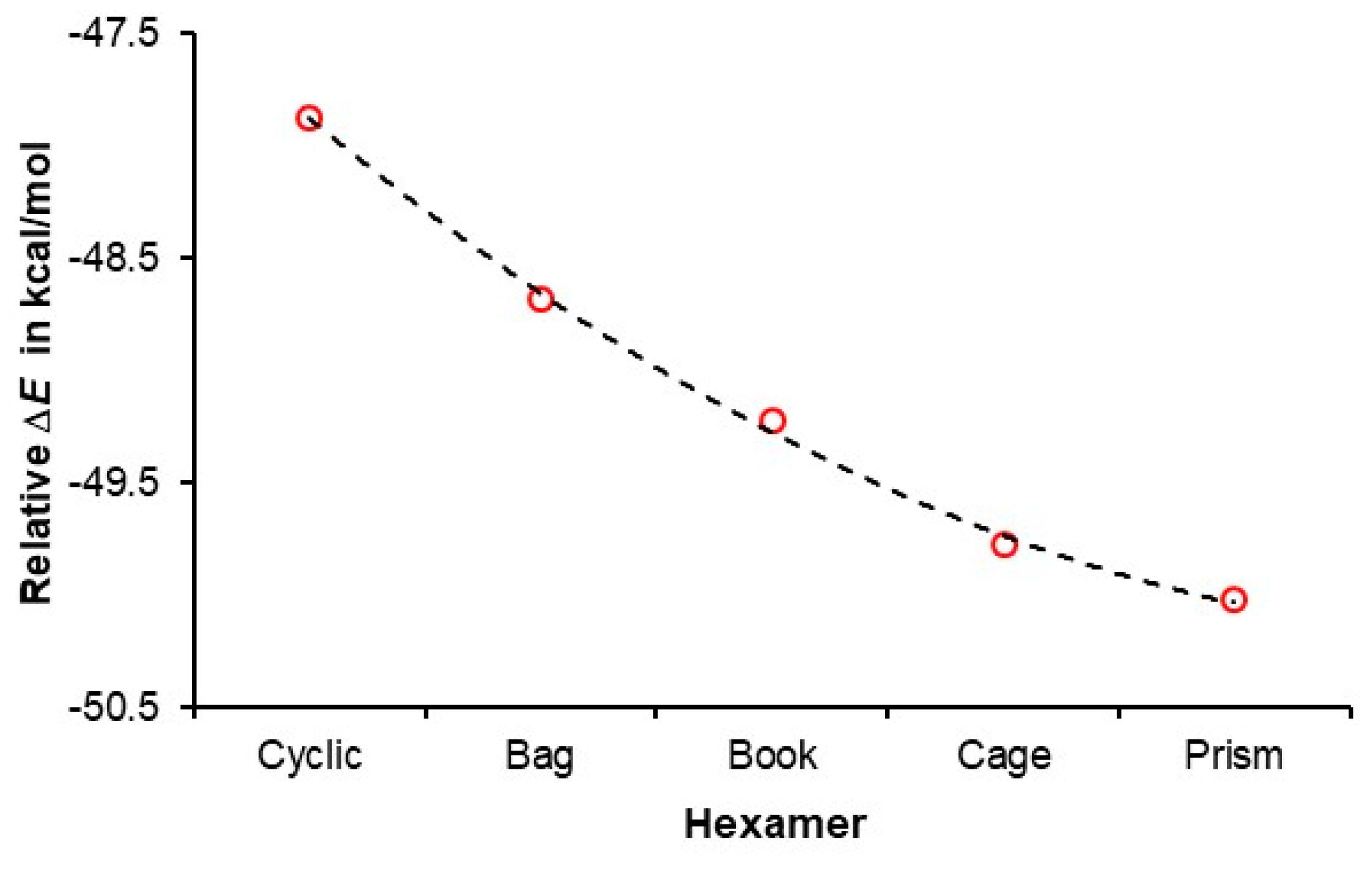
| ΔE = E(hexamer) – E(prism) in kcal/mol | ||||||
| Source | Level of theory | Cyclic | Bag | Book | Cage | Prism |
| Our data | B3LYP/aug-cc-pVTZ/GD3 | 2.15 | 1.34 | 0.80 | 0.25 | 0 |
| Bates et al [74] | CCSD(T)/CBS | 2.48 | 1.62 | 0.87 | 0.25 | 0 |
| Kryachko [75] | MP2(full)/aug-cc-pVDZ | 2.06 | N/A | 1.16 | 0.25 | 0 |
| Olson et al [76] | CCSD(T)/aug-cc-pVTZ | 2.10 | N/A | 1.20 | 0.30 | 0 |
| Prism | Cage | Book | Bag | ||||
| Water | Ndeloc | Water | Ndeloc | Water | Ndeloc | Water | Ndeloc |
| aad W1 | 2.112 | aad W1 | 2.142 | aad W1 | 2.100 | aad W1 | 2.188 |
| add W2 | 2.027 | add W2 | 2.116 | add W4 | 2.048 | add W6 | 2.074 |
| aad W3 | 1.771 | add W4 | 1.935 | ad W2 | 1.647 | ad W2 | 1.719 |
| add W4 | 1.861 | aad W6 | 1.935 | ad W3 | 1.484 | ad W3 | 1.433 |
| aad W5 | 1.778 | ad W3 | 1.587 | ad W5 | 1.603 | ad W4 | 1.411 |
| add W6 | 1.786 | ad W5 | 1.439 | ad W6 | 1.412 | ad W5 | 1.677 |
| Energy terms in kcal/mol | |||
| Water | Eint(W,R) | VXC(W,R) | mol-FAMSEC |
| aad W1 | -100.03 | -70.22 | -57.81 |
| add W6 | -95.36 | -69.20 | -56.58 |
| ad W2 | -86.34 | -59.52 | -50.39 |
| ad W5 | -85.31 | -59.23 | -50.07 |
| ad W3 | -54.68 | -40.56 | -32.69 |
| ad W4 | -52.42 | -39.20 | -31.12 |
| Average: | -79.0 | -56.3 | -46.4 |
| St. Dev.: | 20.5 | 13.6 | 11.7 |
| Water cluster | |||||
| Prism | Cage | Book | Bag | Cyclic | |
| H-bond | mol-FAMSEC in kcal/mol | ||||
| HB-1 | –141.0 | –139.3 | –139.5 | –142.1 | –115.2 |
| HB-2 | –157.3 | –145.1 | –167.7 | –142.7 | |
| HB-3 | –163.0 | –161.0 | –143.4 | –143.7 | |
| HB-4 | –126.4 | –133.0 | –119.4 | –121.8 | |
| HB-5 | –156.9 | –161.5 | –118.8 | –119.2 | |
| HB-6 | –139.1 | –150.1 | –119.4 | –122.4 | |
| HB-7 | –124.4 | –109.8 | –109.2 | –125.5 | – |
| HB-8 | –138.1 | –126.3 | – | – | – |
| HB-9 | –158.5 | – | – | – | – |
| Average: | –145.0 | –140.8 | –131.1 | –131.1 | –115.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





