Submitted:
22 December 2024
Posted:
23 December 2024
You are already at the latest version
Abstract
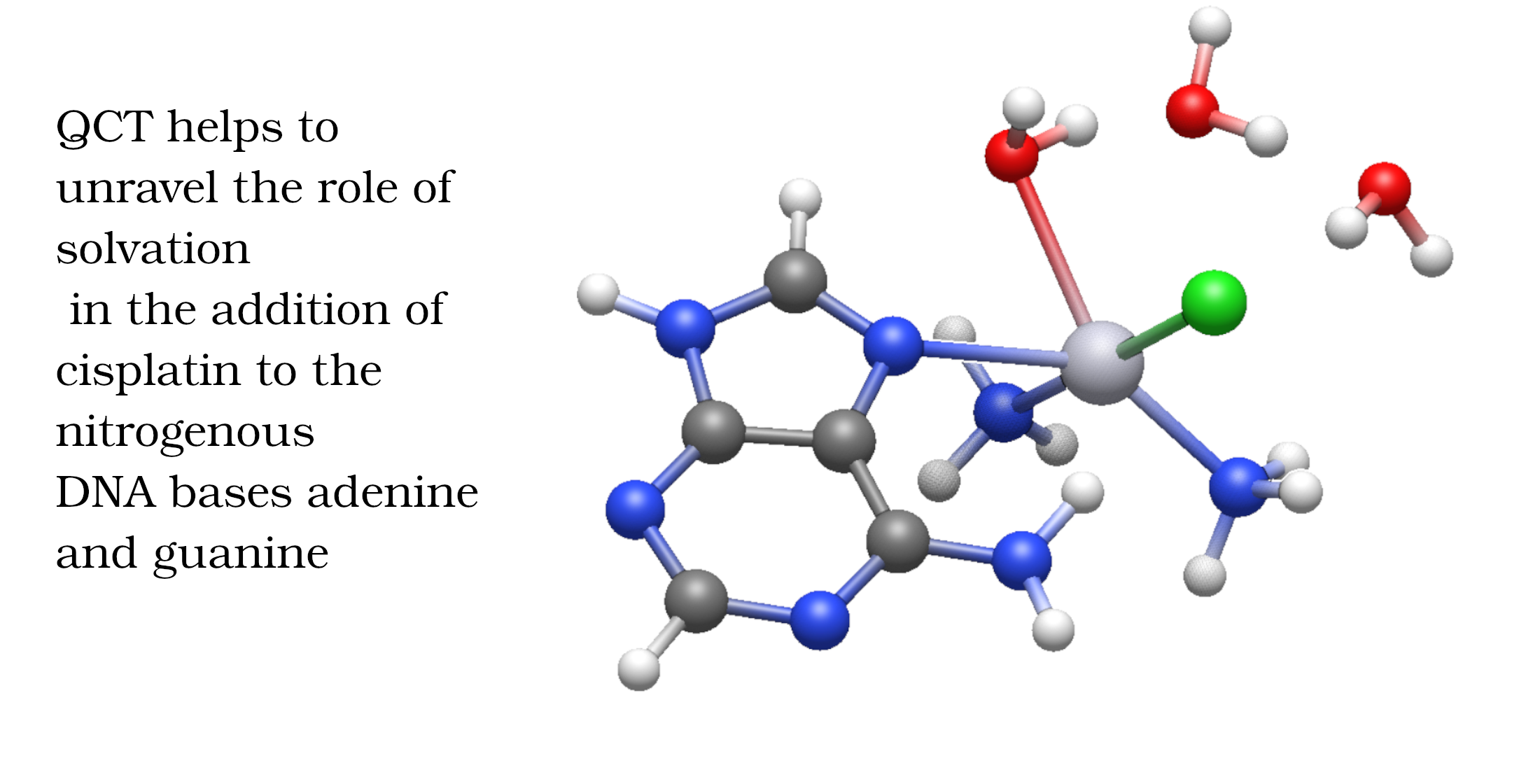
Keywords:
1. Introduction
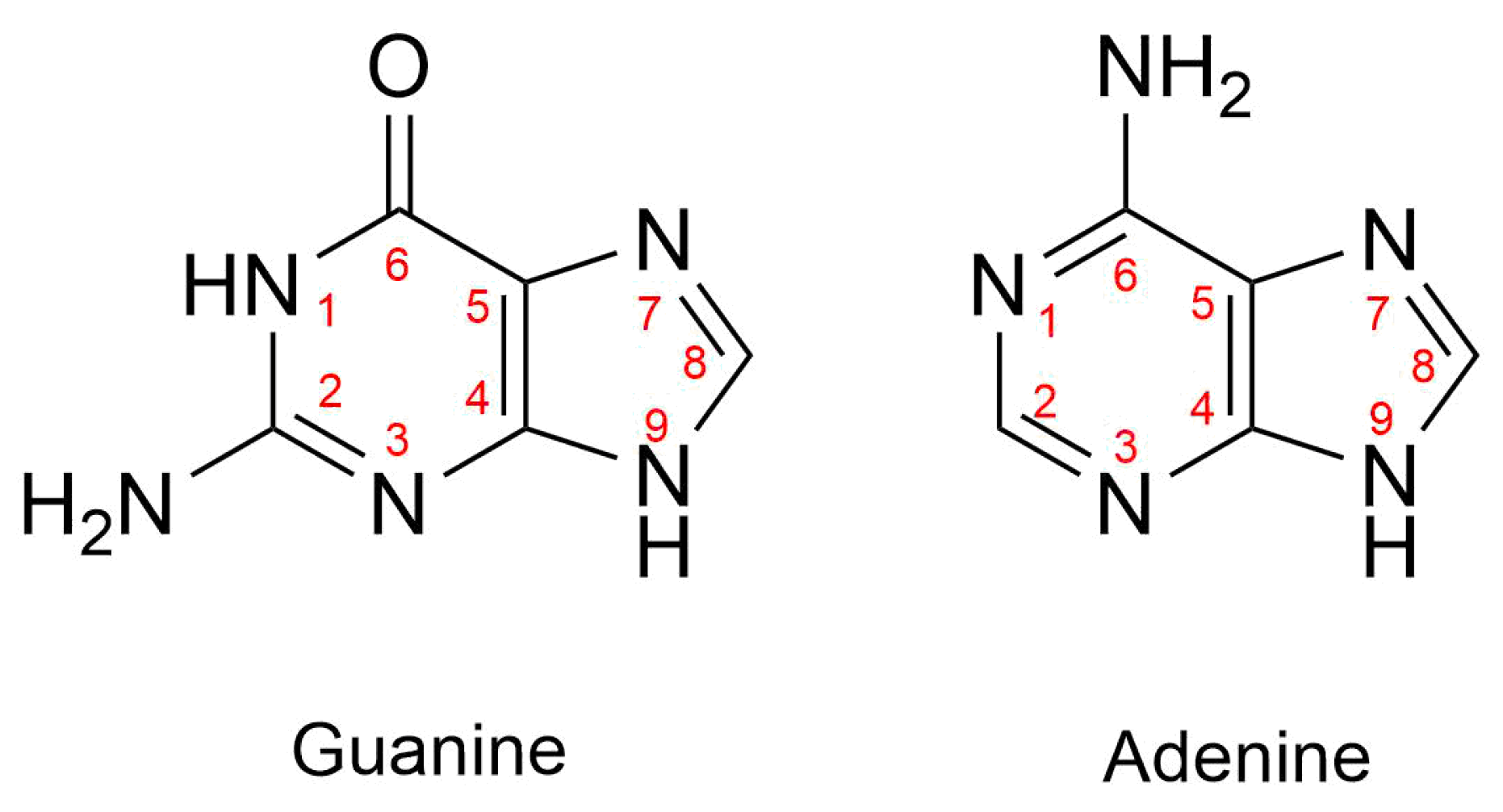
2. Theoretical Framework
3. Computational Details
4. Results and Discussion
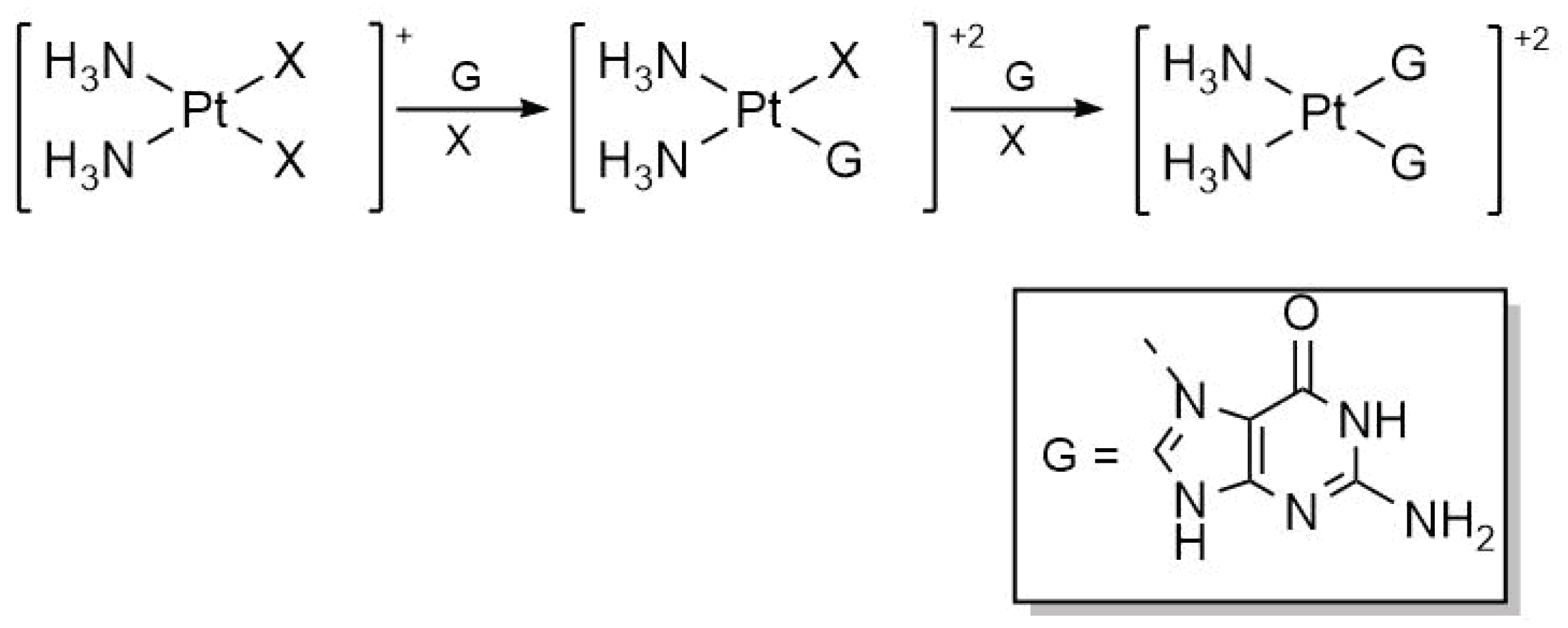
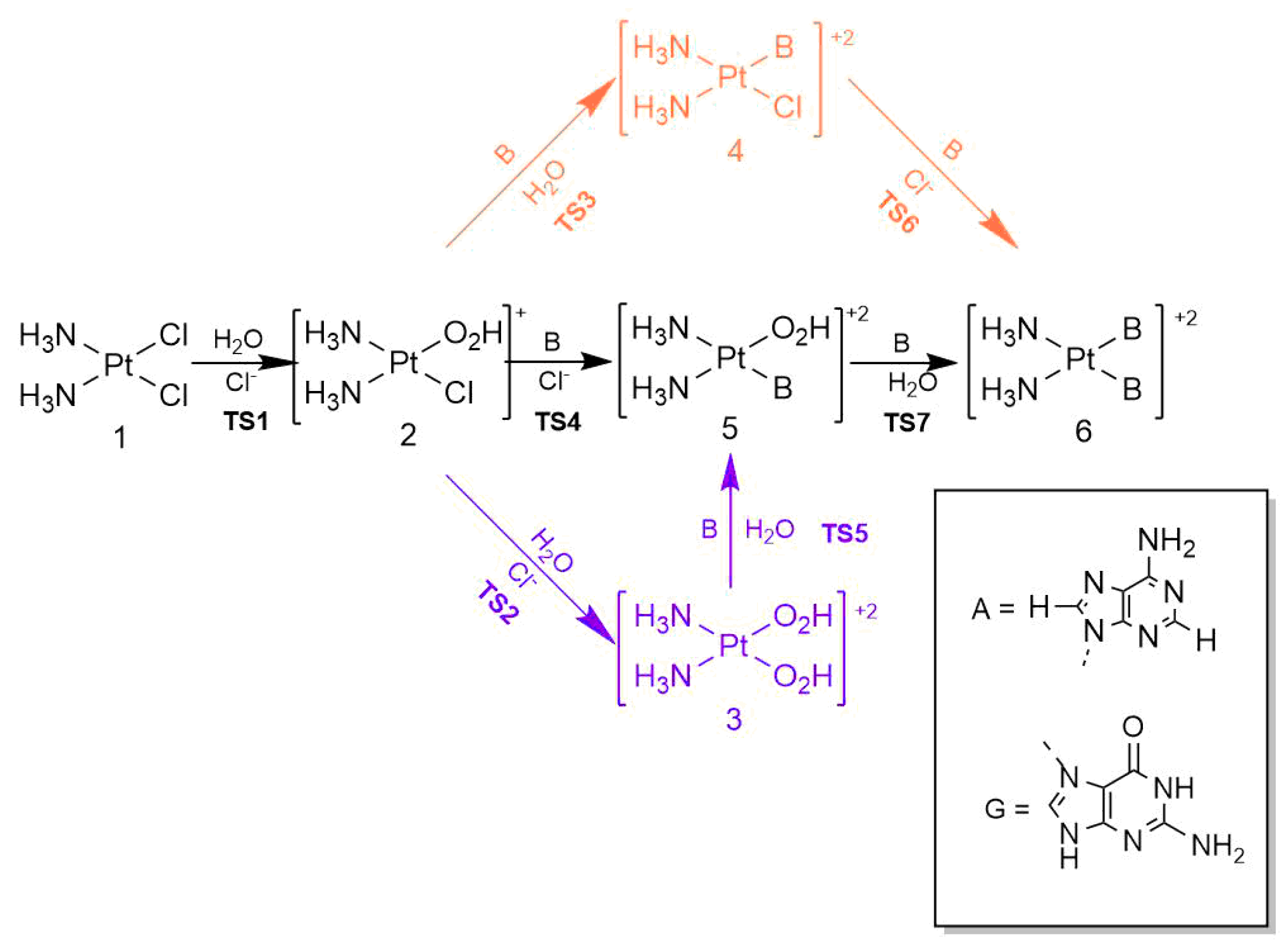
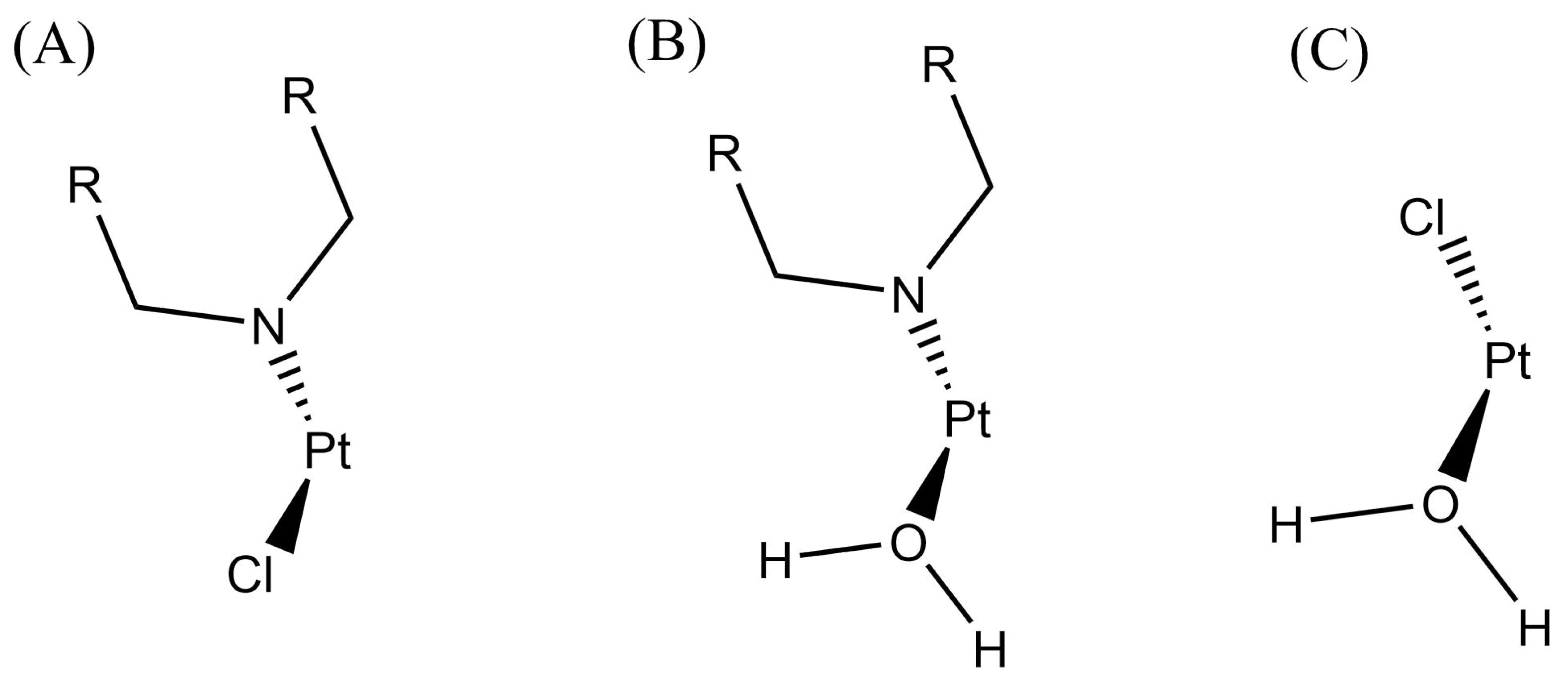
4.1. Monofunctional and Bifunctional Addition of DNA Bases to Cisplatin
4.2. Energetics for the Reaction of Cisplatin with Bases Adenine and Guanine
4.3. QTAIM and IQA Wave Function Analyses
- the breaking of chemical bonds involves an energy cost, while the formation of these interactions release energy to the surroundings and,
- the energy of the transition states is higher than those of the reactants in every case (all values of in Table 3),
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Romani, A.M. Cisplatin in cancer treatment. Biochem. Pharmacol. 2022, 206, 115323. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, B.; Van Camp, L.; Krigas, T. Inhibition of Cell Division in Escherichia coli by Electrolysis Products from a Platinum Electrode. Nature 1965, 205, 698–699. [Google Scholar] [CrossRef]
- de Vries, G.; Rosas-Plaza, X.; van Vugt, M.A.; Gietema, J.A.; de Jong, S. Testicular cancer: Determinants of cisplatin sensitivity and novel therapeutic opportunities. Cancer Treatment Reviews 2020, 88, 102054. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Sun, G.; Zhong, M.; Yu, Y.; Brewer, M. Anticancer efficacy of cisplatin and trichostatin A or 5-aza-2′-deoxycytidine on ovarian cancer. Br. J. Cancer 2013, 108, 579–586. [Google Scholar] [CrossRef]
- Go, R.S.; Adjei, A.A. Review of the Comparative Pharmacology and Clinical Activity of Cisplatin and Carboplatin. J. Clin. Oncol. 1999, 17, 409–409. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Chen, X.; Wang, X.; Wei, X.; Wang, D.; Liu, X.; Xu, L.; Batu, W.; Li, Y.; Guo, B.; others. RSL3 enhances the antitumor effect of cisplatin on prostate cancer cells via causing glycolysis dysfunction. Biochem. Pharmacol. 2021, 192, 114741. [Google Scholar] [CrossRef] [PubMed]
- Makovec, T. Cisplatin and beyond: molecular mechanisms of action and drug resistance development in cancer chemotherapy. J. Radiol. Oncol. 2019, 53, 148–158. [Google Scholar] [CrossRef]
- Mantri, Y.; Baik, M. Computational Studies: Cisplatin, 2005. [CrossRef]
- Goodsell, D.S. The Molecular Perspective: Cisplatin. Stem Cells 2006, 24, 514–515, [https://academic.oup.com/stmcls/article-pdf/24/3/514/41878088/stmcls_24_3_514.pdf]. [Google Scholar] [CrossRef]
- Martin Jr, D.S. Anomalies in ligand exchange reactions for platinum (II) complexes. Inorg. Chim. Acta Rev. 1967, 1, 87–97. [Google Scholar] [CrossRef]
- Atkins, P. Shriver and Atkins’ inorganic chemistry; Oxford University Press, USA, 2010.
- Tullius, T.D.; Ushay, H.M.; Merkel, C.M.; Cardonna, J.P.; Lippard, S.J., Structural Chemistry of Platinum—DNA Adducts. In Platinum, Gold, and Other Metal Chemotherapeutic Agents; chapter 3, pp. 51–74. [https://pubs.acs.org/doi/pdf/10.1021/bk-1983-0209.ch003]. [CrossRef]
- Fichtinger-Schepman, A.M.J.; Van der Veer, J.L.; Den Hartog, J.H.J.; Lohman, P.H.M.; Reedijk, J. Adducts of the antitumor drug cis-diamminedichloroplatinum(II) with DNA: formation, identification, and quantitation. Biochemistry 1985, 24, 707–713. [Google Scholar] [CrossRef] [PubMed]
- Baik, M.H.; Friesner, R.A.; Lippard, S.J. Theoretical study of cisplatin binding to purine bases: why does cisplatin prefer guanine over adenine? J. Am. Chem. Soc. 2003, 125, 14082–14092. [Google Scholar] [CrossRef] [PubMed]
- Lakbaibi, Z.; Jaafar, A.; EL Aatiaoui, A.; Tabyaoui, M. Effect of the explicit solvation of 2-propanol on the Darzens reaction mechanism: A computational study. Comput. Theor. Chem. 2022, 1209, 113628. [Google Scholar] [CrossRef]
- Wang, B.; Cao, Z. How water molecules modulate the hydration of CO2 in water solution: Insight from the cluster-continuum model calculations. J. Comput. Chem. 2012, 34, 372–378. [Google Scholar] [CrossRef] [PubMed]
- Alberto, M.E.; Lucas, M.F.A.; Pavelka, M.; Russo, N. The Second-Generation Anticancer Drug Nedaplatin: A Theoretical Investigation on the Hydrolysis Mechanism. J. Phys. Chem. B 2009, 113, 14473–14479. [Google Scholar] [CrossRef]
- Lebwohl, D.; Canetta, R. Clinical development of platinum complexes in cancer therapy: an historical perspective and an update. Eur. J. Cancer 1998, 34, 1522–1534. [Google Scholar] [CrossRef] [PubMed]
- de Cózar, A.; Larrañaga, O.; Bickelhaupt, F.M.; San Sebastián, E.; Ortega-Carrasco, E.; Maréchal, J.D.; Lledós, A.; Cossío, F.P. New insights into the reactivity of cisplatin with free and restrained nucleophiles: microsolvation effects and base selectivity in cisplatin–DNA interactions. ChemPhysChem 2016, 17, 3932–3947. [Google Scholar] [CrossRef] [PubMed]
- Huque, F.T.; Platts, J.A. The effect of intramolecular interactions on hydrogen bond acidity. Org. Biomol. Chem. 2003, 1, 1419–1424. [Google Scholar] [CrossRef] [PubMed]
- Romero-Montalvo, E.; Guevara-Vela, J.M.; Narváez, W.E.V.; Costales, A.; Pendás, Á.M.; Hernández-Rodríguez, M.; Rocha-Rinza, T. The bifunctional catalytic role of water clusters in the formation of acid rain. Chem. Commun. 2017, 53, 3516–3519. [Google Scholar] [CrossRef] [PubMed]
- Sauza-de la Vega, A.; Salazar-Lozas, H.; Narváez, W.E.V.; Hernández-Rodríguez, M.; Rocha-Rinza, T. Water clusters as bifunctional catalysts in organic chemistry: the hydrolysis of oxirane and its methyl derivatives. Org. Biomol. Chem. 2021, 19, 6776–6780. [Google Scholar] [CrossRef]
- Robertazzi, A.; Platts, J.A. Hydrogen bonding, solvation, and hydrolysis of cisplatin: A theoretical study. J. Comput. Chem. 2004, 25, 1060–1067. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Francisco, E. Real space bond orders are energetic descriptors. Phys. Chem. Chem. Phys. 2018, 20, 16231–16237. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef]
- Figgen, D.; Peterson, K.A.; Dolg, M.; Stoll, H. Energy-consistent pseudopotentials and correlation consistent basis sets for the 5d elements Hf–Pt. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Vetere, V.; Adamo, C.; Maldivi, P. Performance of the `parameter free’ PBE0 functional for the modeling of molecular properties of heavy metals. Chem. Phys. Lett. 2000, 325, 99–105. [Google Scholar] [CrossRef]
- Bancroft, D.P.; Lepre, C.A.; Lippard, S.J. Platinum-195 NMR kinetic and mechanistic studies of cis-and trans-diamminedichloroplatinum (II) binding to DNA. J. Am. Chem. Soc. 1990, 112, 6860–6871. [Google Scholar] [CrossRef]
- Repta, A.J.; Long, D.F. Reactions of cisplatin with human plasma and plasma fractions. In Cisplatin; Elsevier, 1980; pp. 285–304.
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- York, D.M.; Karplus, M. A smooth solvation potential based on the conductor-like screening model. J. Phys. Chem. A 1999, 103, 11060–11079. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef] [PubMed]
- Keith, T.A. AIMAll (Version 19.10. 12). TK Gristmill Software: Overland Park, KS, USA 2019, p. 23.
- Clayden, J.; Greeves, N.; Warren, S. Organic Chemistry; OUP Oxford, 2012.

| Level of Theory | (kcal/mol) | (kcal/mol) | (kcal/mol) |
|---|---|---|---|
| PBE0-D3BJ implicit solv. | 24.20 | 24.25 | 6.95 |
| PBE0-D3BJ explicit solv. | 26.02 | 26.77 | 5.12 |
| M06-2X implicit solv. | 20.57 | 19.81 | 5.98 |
| M06-2X explicit solv. | 22.04 | 23.28 | 3.51 |
| M06-2X implicit solv.* | 21.56 | 19.85 | 20.28 |
| Monofunctionalisation of cisplatin with guanine | |||
|---|---|---|---|
| Level of Theory | Solvation Type | (kcal/mol) | (kcal/mol) |
| PBE0-D3BJ | Implicit Solv. | 24.17 | 18 ± 1 |
| PBE0-D3BJ | Explicit Solv. | 23.91 | 18 ± 1 |
| M06-2X | Implicit Solv. | 19.17 | 18 ± 1 |
| M06-2X | Explicit Solv. | 18.07 | 18 ± 1 |
| Bifunctionalisation of cisplatin with guanine | |||
| Level of Theory | Solvation Type | (kcal/mol) | (kcal/mol) |
| PBE0-D3BJ | Implicit Solv. | 16.97 | 21 ± 2 |
| PBE0-D3BJ | Explicit Solv. | 21.01 | 21 ± 2 |
| M06-2X | Implicit Solv. | 10.20 | 21 ± 2 |
| M06-2X | Explicit Solv. | 24.30 | 21 ± 2 |
| Transition State | Implicit (kcal/mol) | Explicit (kcal/mol) | (kcal/mol) |
|---|---|---|---|
| TS1 | 19.81 | 23.28 | 3.46 |
| TS2 | 18.89 | 18.79 | −0.10 |
| TS3A | 16.70 | 12.12 | −4.58 |
| TS4A | 20.66 | 32.24 | 11.58 |
| TS5A | 17.28 | 16.51 | −0.77 |
| TS6A | 16.11 | 17.86 | 1.75 |
| TS7A | 16.21 | 16.40 | 0.20 |
| TS3G | 14.95 | 21.08 | 6.13 |
| TS4G | 20.00 | 18.40 | −1.60 |
| TS5G | 14.55 | 12.17 | −2.38 |
| TS6G | 10.10 | 25.17 | 15.07 |
| TS7G | 16.71 | 18.89 | 2.18 |
| Reaction Step | (au) | (kcal/mol) |
|---|---|---|
| TS1 | −0.0283 | −17.76 |
| TS3A | −0.0811 | −50.87 |
| TS3G | 0.0740 | 46.40 |
| TS4A | 0.6122 | 384.13 |
| TS6G | 0.2314 | 145.16 |
| (A) | (B) | (C) | ||||||
|---|---|---|---|---|---|---|---|---|
| TS | (expl) | (impl) | TS | (expl) | (impl) | TS | (expl) | (impl) |
| 0.27 | 0.31 | 0.27 | 0.27 | 0.26 | 0.24 | |||
| −0.31 | −0.31 | −0.32 | −0.30 | −0.45 | −0.46 | |||
| 0.33 | 0.29 | 0.29 | 0.27 | |||||
| −0.45 | −0.38 | −0.33 | −0.32 | |||||
| Reaction Step | |||
|---|---|---|---|
| TS1 | −0.19 | −0.22 | 0.03 |
| TS3A | −0.04 | −0.05 | 0.01 |
| TS3G | −0.05 | −0.03 | −0.02 |
| TS4A | −0.12 | −0.09 | −0.03 |
| TS6G | −0.04 | 0.00 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





