A POD-Based Reduced-Dimension Method of Solution Coefficient Vectors in Crank-Nicolson Mixed Finite Element Method for the Fourth-Order Parabolic Equation

1. Introduction

The research focuses on exploring the fourth-order variable coefficient parabolic equation with the initial-boundary value

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{u}_t+\epsilon \nabla ·(b(\mathit{x},t)\nabla (\nabla ·(a(t)\nabla u)))=f(u),\hfill & (\mathit{x},t)\in \Omega \times J,\hfill \\ u(\mathit{x},t)=\Delta u(\mathit{x},t)=0,\hfill & (\mathit{x},t)\in \partial \Omega \times \overline{J},\hfill \\ u(\mathit{x},0)=u_0(\mathit{x}),\hfill & \mathit{x}\in \Omega .\hfill \end{array}\right.\end{array}$$

(1)

$\Omega \subset {\mathbb{R}}^d(d=1,2,3)$ is a bounded convex polygonal domain. $\partial \Omega$ is boundary of $\Omega$. $J=(0,T],0<T<\infty$. $u_0(\mathit{x})$ is known initial function. $a=a(t)$, $b=b(\mathit{x},t)$ satisfying

$$\begin{array}{c}{\mathbf{H}}_1:0<a_0⩽a(t)⩽a_1<+\infty ,\hfill \\ {\mathbf{H}}_2:0<b_0⩽b(\mathit{x},t)⩽b_1<+\infty ,\hfill \\ {\mathbf{H}}_3:|a_t(t)|+|b_t(\mathit{x},t)|⩽d_0,\hfill \end{array}$$

(2)

for some positive constants $a_0$, $a_1$, $b_0$, $b_1$ and $d_0$. $\epsilon$ is a positive constant. $f(u)=u^3-u$ adheres to the properties of Lipschitz continuity, implying the existence of a positive constant $\mathcal{L}$ satisfying

$$|f(u_1)-f(u_2)|⩽\mathcal{L}|u_1-u_2|.$$

(3)

For simplicity, we assume that $u_0(\mathit{x})=0$ in the following theoretical analysis.

The fourth-order parabolic equations are commonly used to describe higher-order physical behaviors, such as considering the internal damping or viscoelastic properties of materials. Within the category of fourth-order parabolic equations, models such as the Cahn-Hilliard equation [1,2], fourth-order reaction-diffusion equation [3,4], and the Swift-Hohenberg equation [5] are included. Due to the inclusion of higher-order derivatives, solving and analyzing these kinds of equations is usually more complex and often requires the use of numerical methods. Currently, various numerical methods have been employed to solve fourth-order parabolic equations. For example, finite element (FE) method [1,6,7], mixed finite element method (MFE) [3,8,9,10], discontinuous space-time MFE method [11,12], two-grid MFE method [13,14], weak galerkin FE method [2,15], finite difference method [16], implicit compact difference method [17,18,19,20], cubic spline method [21], blow-up [22,23,24,25] and so on. In the paper, the MFE method is employed to study the fourth-order variable coefficient parabolic equation for spatial analysis. The method of time discretization is the Crank-Nicolson (CN) scheme.

A prevalent challenge in addressing high-order partial differential equations (PDEs) through the MFE method is the rapid escalation of unknown dimensions when dealing with coupled equations, often resulting in a doubling of the data volume processed. Such significantly elevated dimensions not only heighten memory requirements but also substantially escalate computational costs. In practical scenarios, this increased computational burden can pose a significant barrier to solving complex PDE problems. An effective strategy to mitigate these challenges involves the implementation of order reduction techniques. The primary objective of these techniques is to minimize the number of variables considered during the solution process using mathematical methods, thereby alleviating computational demands while preserving as much as possible a good approximation quality. Currently, several effective numerical reduced-order methods have gained widespread application, including the POD method [26,27], the spectral element method [28] , the sparse grid method [29], and the balanced truncation method [30] .

Certainly, integrating POD technology with diverse numerical methods can effectively address a range of PDEs. It is the most widely utilized method for dimensionality reduction and has been attracting increasing attention. [31] and [32] combined the compact difference method and POD technique to study the fourth-order parabolic equation. Zhao and Piao [33] studied the KDV-RLW-Rosenau equation using the POD method in conjunction with B-spline Galerkin FE formulations. In [34], the heat equation was addressed using the POD reduced-order methods and the two-step backward differentiation formula (BDF2). Janes and Singler [35] solved the damped wave equation by the POD method and the second difference quotients (DDQs). He et al. [36] employed a space-time FE method that integrates a POD-based extrapolation with DG time stepping to analyze the parabolic equation. Lu et al. [37] merged the POD method with a collocation approach using local radial basis functions (RBFs) to address time-dependent nonlocal diffusion problems.

For the POD-based FE and MFE reduced-dimension models, there are two existing methods. The first involves establishing optimized models which reduce the dimensions of the FE or the MFE subspaces. For further references, please consult [38,39,40,41,42,43,44]. The second, introduced by Luo et al. in 2020, presented an innovative strategy for dimension reduction of CNFE [45,46] and CNMFE [47,48,49,50,51] solution coefficient vectors. To our understanding, no existing literature has documented simplifying the solution coefficient vectors of CNMFE scheme used POD technology in solving fourth-order variable coefficient parabolic equations. The paper primary objective presents a rapid algorithm capable of solving fourth-order variable coefficient parabolic equations.

The research is organized as follows: Section 2 discusses the CNMFE scheme, detailing its uniqueness, stability, and convergence. Section 3 dedicates to construct a POD-based RDCNMFE matrix model, while also analyze its uniqueness, stability, and error estimates. In Section 4, we perform numerical simulations on 2D fourth-order variable coefficient parabolic equations. Finally, Section 5 summarizes the key results and conclusions of the research.

2. The CNMFE Method for the Fourth-Order Variable Coefficient Parabolic Equation

2.1. The CNMFE Scheme

In this paper, the Sobolev spaces and the associated norms adhere to the conventional definitions commonly found in existing literature [52]. To construct the CNMFE scheme for the fourth-order variable coefficient parabolic equation (1), we begin by introducing a diffusion term defined as $q=-\nabla ·(a(t)\nabla u)$. This introduces a pair of lower-order equations

$$\left\{\begin{array}{c}{u}_t-\epsilon \nabla ·(b(\mathit{x},t)\nabla q)=f(u),(\mathit{x},t)\in \Omega \times J,\hfill \\ q+\nabla ·(a(t)\nabla u)=0,(\mathit{x},t)\in \Omega \times J,\hfill \\ u(\mathit{x},t)=q(\mathit{x},t)=0,(\mathit{x},t)\in \partial \Omega \times \overline{J}.\hfill \end{array}\right.$$

(4)

Applying Green’s formula, we obtain the mixed weak form of (4) as provided below.

Problem 1. 

Find $\{u,q\}$: $[0,T]\mapsto H_0^1\times H_0^1$, such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}(u_t,\upsilon )+\epsilon (b\nabla q,\nabla \upsilon )=(f(u),\upsilon ),\forall \upsilon \in H_0^1,\hfill \\ (q,\chi )-(a\nabla u,\nabla \chi )=0,\forall \chi \in H_0^1,\hfill \end{array}\right.\end{array}$$

(5)

Let ${\Im }_h$ represent the quasi-uniform triangulation on $\overline{\Omega }$. The FE subspace ${\mathbb{S}}_h$ is defined as the following span of the orthonormal basis ${\left\{{\zeta }_j(x)\right\}}_{j=1}^M$

$$\begin{array}{c}{\mathbb{S}}_h=\{{\upsilon }_h\in H_0^1\cap C(\Omega );{\upsilon }_h{\mid }_K\in {\mathbb{P}}_{M-1}(K),K\in \Im \}=\mathrm{span}\{{\zeta }_j(\mathit{x}):1⩽j⩽M\},\hfill \end{array}$$

(6)

where ${\mathbb{P}}_{M-1}(K)$ is a polynomial space of $(M-1)$ degree.

For a positive integer N, define $\Delta t=T/N$, ${\psi }^n=\psi (t_n)$, ${\overline{\partial }}_t{\psi }^n=({\psi }^n-{\psi }^{n-1})/\Delta t$ and ${\psi }^{n-{\displaystyle \frac{1}{2}}}=({\psi }^n+{\psi }^{n-1})/2$. Hence, Problem 1 can be reformulated at time $t=t_{n-{\displaystyle \frac{1}{2}}}$ as follows.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}(u_t(t_{n-{\displaystyle \frac{1}{2}}}),\upsilon )+\epsilon (b(t_{n-{\displaystyle \frac{1}{2}}})\nabla q(t_{n-{\displaystyle \frac{1}{2}}}),\nabla \upsilon )=(f(u(t_{n-{\displaystyle \frac{1}{2}}})),\upsilon ),\forall \upsilon \in H_0^1,\hfill \\ (q(t_{n-{\displaystyle \frac{1}{2}}}),\chi )-(a(t_{n-{\displaystyle \frac{1}{2}}})\nabla u(t_{n-{\displaystyle \frac{1}{2}}}),\nabla \chi )=0,\forall \chi \in H_0^1.\hfill \end{array}\right.\end{array}$$

(7)

The equivalent equation is that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \left(\frac{u^n-u^{n-1}}{\Delta t},\upsilon \right)+\epsilon (b(t_{n-\frac{1}{2}})\nabla q^{n-\frac{1}{2}},\nabla \upsilon )=(f({\widehat{\widehat{u}}}^{n-\frac{1}{2}}),\upsilon )+(R_1^{n-\frac{1}{2}},\upsilon )+(R_2^{n-\frac{1}{2}},\upsilon ),\forall \upsilon \in H_0^1,}\hfill \\ (q^{n-{\displaystyle \frac{1}{2}}},\chi )-(a(t_{n-{\displaystyle \frac{1}{2}}})\nabla u^{n-{\displaystyle \frac{1}{2}}},\nabla \chi )=0,\forall \chi \in H_0^1,\hfill \end{array}\right.\end{array}$$

(8)

where

$$f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})={\displaystyle \frac{3}{2}}f(u^{n-1})-{\displaystyle \frac{1}{2}}f(u^{n-2}),$$

(9)

$$R_1^{n-{\displaystyle \frac{1}{2}}}={\displaystyle \frac{u^n-u^{n-1}}{\Delta t}}-u_t(t_{n-{\displaystyle \frac{1}{2}}}),$$

(10)

$$R_2^{n-{\displaystyle \frac{1}{2}}}=f(u(t_{n-{\displaystyle \frac{1}{2}}}))-f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}}).$$

(11)

When $t_n=n\Delta t$, define the CNMFE approximations of $\{u,q\}$ as $\{u_h^n,q_h^n\}$. Therefore, we can formulate the CNMFE scheme of Problem 1 using the form below.

Problem 2. 

For $1⩽n⩽N$, find $\{u_h^n,q_h^n\}\in {\mathbb{S}}_h\times {\mathbb{S}}_h$, such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle ({\overline{\partial }}_t{u}_h^n,{\upsilon }_h)+\epsilon (b^{n-\frac{1}{2}}\nabla q_h^{n-\frac{1}{2}},\nabla {\upsilon }_h)=(f({\widehat{\widehat{u}}}_h^{n-\frac{1}{2}}),{\upsilon }_h),\forall {\upsilon }_h\in {\mathbb{S}}_h,}\hfill \\ (q_h^{n-{\displaystyle \frac{1}{2}}},{\chi }_h)-(a^{n-{\displaystyle \frac{1}{2}}}\nabla u_h^{n-{\displaystyle \frac{1}{2}}},\nabla {\chi }_h)=0,\forall {\chi }_h\in {\mathbb{S}}_h,\hfill \end{array}\right.\end{array}$$

(12)

Remark 1. 

[50], Formula (12) Using the linearized term

$$f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}})={\displaystyle \frac{3}{2}}f(u_h^{n-1})-{\displaystyle \frac{1}{2}}f(u_h^{n-2})={\displaystyle \frac{3}{2}}{(u_h^{n-1})}^3-{\displaystyle \frac{1}{2}}{(u_h^{n-2})}^3-{\displaystyle \frac{3}{2}}{u}_h^{n-1}+{\displaystyle \frac{1}{2}}{u}_h^{n-2},$$

(13)

it is evident that equation (12) structured as a linear scheme.

2.2. The Uniqueness, Stability and Error Estimates of the CNMFE Solutions

Utilizing the orthonormal basis of the FE space ${\mathbb{S}}_h$, the CNMFE approximations $\{u_h^n,q_h^n\}$ to Problem 2 can be expressed as

$$\begin{array}{c}{\displaystyle u_h^n=\sum _{j=1}^M{U}_{hj}^n{\zeta }_j=\zeta ·{\mathit{U}}_h^n,q_h^n=\sum _{j=1}^M{Q}_{hj}^n{\zeta }_j=\zeta ·{\mathit{Q}}_h^n,}\hfill \end{array}$$

(14)

in which $\zeta =({\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_M)$ is the orthonormal basis function vector. ${\mathit{U}}_h^n=(U_{h1}^n,U_{h2}^n,\cdots ,$

$U_{hM}^n{)}^T$ and ${\mathit{Q}}_h^n={(Q_{h1}^n,Q_{h2}^n,\cdots ,Q_{hM}^n)}^T$ represent the unknown CNMFE solution coefficient vectors. With the solutions $\{u_h^n,q_h^n\}$ defined in (14), the matrix-form of Problem 2 is as follows.

Problem 3. 

For $1⩽n⩽N$, find $\{{\mathit{U}}_h^n,{\mathit{Q}}_h^n\}\in {\mathbb{R}}^M\times {\mathbb{R}}^M$ and $\{u_h^n,q_h^n\}\in {\mathbb{S}}_h\times {\mathbb{S}}_h$ that satisfy

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\overline{\partial }}_t{\mathit{U}}_h^n+\epsilon {\mathit{B}}^{n-\frac{1}{2}}{\mathit{Q}}_h^{n-\frac{1}{2}}=\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}}),}\hfill \\ {\mathit{Q}}_h^{n-{\displaystyle \frac{1}{2}}}-{\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}{\mathit{U}}_h^{n-{\displaystyle \frac{1}{2}}}=0,\hfill \\ {\displaystyle u_h^n=\sum _{j=1}^M{U}_{hj}^n{\zeta }_j={\mathit{U}}_h^n·\zeta ,q_h^n=\sum _{j=1}^M{Q}_{hj}^n{\zeta }_j={\mathit{Q}}_h^n·\zeta ,}\hfill \end{array}\right.\end{array}$$

(15)

where

$${\mathit{B}}^{n-{\displaystyle \frac{1}{2}}}={(b_{ij}(t_{n-{\displaystyle \frac{1}{2}}}))}_{1⩽i,j⩽M},b_{ij}(t_{n-{\displaystyle \frac{1}{2}}})=(b(\mathit{x},t_{n-{\displaystyle \frac{1}{2}}})\nabla {\zeta }_j,\nabla {\zeta }_i),$$

$${\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}={(a_{ij}(t_{n-{\displaystyle \frac{1}{2}}}))}_{1⩽i,j⩽M},a_{ij}(t_{n-{\displaystyle \frac{1}{2}}})=(a(t_{n-{\displaystyle \frac{1}{2}}})\nabla {\zeta }_j,\nabla {\zeta }_i),$$

and

$${\displaystyle \mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}})=\frac{3}{2}\mathit{F}({\mathit{U}}_h^{n-1})-\frac{1}{2}\mathit{F}({\mathit{U}}_h^{n-2})={(\frac{3}{2}(f(\sum _{j=1}^M{U}_{hj}^{n-1}{\zeta }_j),{\zeta }_i)-\frac{1}{2}(f(\sum _{j=1}^M{U}_{hj}^{n-2}{\zeta }_j),{\zeta }_i))}_{1⩽i⩽M}.}$$

Theorem 1. 

Given that $\Delta t$ is small enough, the Problem 3 has the unique CNMFE solutions $\{u_h^n,q_h^n\}\in {\mathbb{S}}_h\times {\mathbb{S}}_h$.

Proof of Theorem 1. 

Problem 3 can alternatively be expressed as

$$\left(\begin{array}{cc}\mathit{I}& {\displaystyle \frac{\epsilon \Delta t}{2}{\mathit{B}}^n}\\ -{\mathit{S}}^n& \mathit{I}\end{array}\right)\left(\begin{array}{c}{\mathit{U}}_h^n\\ {\mathit{Q}}_h^n\end{array}\right)=\left(\begin{array}{cc}\mathit{I}& {\displaystyle -\frac{\epsilon \Delta t}{2}{\mathit{B}}^{n-1}}\\ {\mathit{S}}^{n-1}& -\mathit{I}\end{array}\right)\left(\begin{array}{c}{\mathit{U}}_h^{n-1}\\ {\mathit{Q}}_h^{n-1}\end{array}\right)+\Delta t\left(\begin{array}{c}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})\\ \tilde{\mathit{O}}\end{array}\right),$$

(16)

where $\mathit{I}$ denotes the $M\times M$ identity matrix, and $\tilde{\mathit{O}}$ stands for a zero column vector of $M\times 1$.

Due to

$$\left(\begin{array}{cc}\mathit{I}& \mathit{O}\\ {\mathit{S}}^n& \mathit{I}\end{array}\right)\left(\begin{array}{cc}\mathit{I}& {\displaystyle \frac{\epsilon \Delta t}{2}{\mathit{B}}^n}\\ -{\mathit{S}}^n& \mathit{I}\end{array}\right)=\left(\begin{array}{cc}\mathit{I}& {\displaystyle \frac{\epsilon \Delta t}{2}{\mathit{B}}^n}\\ \mathit{O}& {\displaystyle \frac{\epsilon \Delta t}{2}{\mathit{S}}^n{\mathit{B}}^n+\mathit{I}}\end{array}\right),$$

(17)

where $\mathit{O}$ represents the $M\times M$ zero matrix. Because $\Delta t$ is small enough, ${\displaystyle \frac{\epsilon \Delta t}{2}{\mathit{S}}^n{\mathit{B}}^n+\mathit{I}}$ is invertible. Hence, the coefficient matrix of (16) is invertible, then there exists the unique solutions $(u_h^n,q_h^n)\in {\mathbb{S}}_h\times {\mathbb{S}}_h$ for Problem 3. □

It is necessary to discuss the characteristics of $\mathit{B}$ and $\mathit{S}$ in Problem 3 for establishing the stability of the CNMFE solutions.

Lemma 1. 

[53], Lemma 1.19 Matrices $\mathit{B}$ and $\mathit{S}$ are positive definite and satisfy the following properties

$${\parallel \mathit{B}\parallel }_{\infty }⩽C,\parallel {\mathit{B}}^{-1}{\parallel }_{\infty }⩽{C,\parallel \mathit{S}\parallel }_{\infty }⩽C,{\parallel {\mathit{S}}^{-1}\parallel }_{\infty }⩽C.$$

(18)

Theorem 2. 

The CNMFE solutions $\{u_h^n,q_h^n\}$ have unconditional stability.

Proof of Theorem 2. 

We represent (15) as

$$\left\{\begin{array}{c}{\displaystyle {({\mathit{B}}^{n-\frac{1}{2}})}^{-1}{\overline{\partial }}_t{\mathit{U}}_h^n+\epsilon {\mathit{Q}}_h^{n-\frac{1}{2}}={({\mathit{B}}^{n-\frac{1}{2}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}}),}\hfill \\ {\mathit{Q}}_h^{n-{\displaystyle \frac{1}{2}}}={\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}{\mathit{U}}_h^{n-{\displaystyle \frac{1}{2}}}.\hfill \end{array}\right.$$

(19)

Inserting the second equation of (19) into the first, and considering that $\mathit{S}$ is positive definite, we obtain

$${\displaystyle {({\mathit{S}}^{n-\frac{1}{2}})}^{-1}{({\mathit{B}}^{n-\frac{1}{2}})}^{-1}{\overline{\partial }}_t{\mathit{U}}_h^n+\epsilon {\mathit{U}}_h^{n-\frac{1}{2}}={({\mathit{S}}^{n-\frac{1}{2}})}^{-1}{({\mathit{B}}^{n-\frac{1}{2}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}}).}$$

(20)

Letting ${\mathit{D}}^{n-{\displaystyle \frac{1}{2}}}={({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}$, and taking the inner product of (20) and ${\overline{\partial }}_t{\mathit{U}}_h^n$, we have

$${\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_h^n,{\overline{\partial }}_t{\mathit{U}}_h^n)+\epsilon ({\mathit{U}}_h^{n-\frac{1}{2}},{\overline{\partial }}_t{\mathit{U}}_h^n)=({\mathit{D}}^{n-\frac{1}{2}}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}}),{\overline{\partial }}_t{\mathit{U}}_h^n).}$$

(21)

Then, two sides of (21) are that

$$\begin{array}{c}{\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_h^n,{\overline{\partial }}_t{\mathit{U}}_h^n)+\epsilon ({\mathit{U}}_h^{n-\frac{1}{2}},{\overline{\partial }}_t{\mathit{U}}_h^n)=\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_h^n{\parallel }^2+\frac{\epsilon }{2\Delta t}(\parallel {\mathit{U}}_h^n{\parallel }^2-\parallel {\mathit{U}}_h^{n-1}{\parallel }^2),}\hfill \end{array}$$

(22)

and

$${\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}}),{\overline{\partial }}_t{\mathit{U}}_h^n)⩽C\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\parallel }_{\infty }^2\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}})\parallel +\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_h^n{\parallel }^2.}$$

(23)

Combining lemma 1 with (3), and considering that $\parallel {\mathit{U}}_h^0\parallel$ and $\parallel \mathit{F}({\mathit{U}}_h^0)\parallel$ are bounded, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\parallel }_{\infty }^2{\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}})\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C\left(\parallel \frac{1}{2}\mathit{F}({\mathit{U}}_h^{n-1})-\frac{1}{2}\mathit{F}({\mathit{U}}_h^{n-2}){\parallel }^2+\parallel \mathit{F}({\mathit{U}}_h^{n-1})-\mathit{F}({\mathit{U}}_h^0){\parallel }^2+{\parallel \mathit{F}({\mathit{U}}_h^0)\parallel }^2\right)}\hfill \\ ⩽\hfill & {\displaystyle C(\parallel {\mathit{U}}_h^{n-1}-{\mathit{U}}_h^{n-2}{\parallel }^2+\parallel {\mathit{U}}_h^{n-1}-{\mathit{U}}_h^0{\parallel }^2+\parallel \mathit{F}({\mathit{U}}_h^0){\parallel }^2)}\hfill \\ ⩽\hfill & {\displaystyle C+C(\parallel {\mathit{U}}_h^{n-1}{\parallel }^2+\parallel {\mathit{U}}_h^{n-2}{\parallel }^2),2⩽n⩽N,}\hfill \end{array}$$

(24)

Combining (22), (23) and (24), we have

$$\begin{array}{c}{\displaystyle \frac{\epsilon }{2\Delta t}(\parallel {\mathit{U}}_h^n{\parallel }^2-\parallel {\mathit{U}}_h^{n-1}{\parallel }^2)⩽C+C(\parallel {\mathit{U}}_h^{n-1}{\parallel }^2+\parallel {\mathit{U}}_h^{n-2}{\parallel }^2),2⩽n⩽N.}\hfill \end{array}$$

(25)

Multiplying (25) by $2\Delta t$ , summating from 2 to n and noting that $\parallel {\mathit{U}}_h^1\parallel ⩽C$, we have

$$\begin{array}{cc}\parallel {\mathit{U}}_h^n{\parallel }^2\hfill & {\displaystyle ⩽\parallel {\mathit{U}}_h^1{\parallel }^2+\frac{2\Delta t}{\epsilon }\sum _{i=2}^{n}C+\frac{C\Delta t}{\epsilon }\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_h^i\parallel }^2}\hfill \\ \hfill & {\displaystyle ⩽\parallel {\mathit{U}}_h^1{\parallel }^2+CT+C\Delta t\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_h^i\parallel }^2,}\hfill \\ \hfill & {\displaystyle ⩽C+C\Delta t\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_h^i\parallel }^2,2⩽n⩽N.}\hfill \end{array}$$

(26)

We apply the Gronwall inequality to (26) to obtain

$$\parallel {\mathit{U}}_h^n{\parallel }^2⩽C{e}^{Cn\Delta t}⩽C,1⩽n⩽N.$$

(27)

And because

$$\parallel {\mathit{Q}}_h^n\parallel =\parallel {\mathit{S}}^n{\mathit{U}}_h^n\parallel ⩽\parallel {\mathit{S}}^n{\parallel }_{\infty }\parallel {\mathit{U}}_h^n\parallel ⩽C\parallel {\mathit{U}}_h^n\parallel ⩽C,1⩽n⩽N.$$

(28)

From (27) and (28), we get

$$\parallel {\mathit{U}}_h^n\parallel +\parallel {\mathit{Q}}_h^n\parallel ⩽C,1⩽n⩽N.$$

(29)

Given that $\parallel \zeta \parallel ⩽C$, it easily follows

$$\parallel u_h^n\parallel +\parallel q_h^n\parallel =\parallel {\mathit{U}}_h^n·\zeta \parallel +\parallel {\mathit{Q}}_h^n·\zeta \parallel ⩽C\parallel {\mathit{U}}_h^n\parallel \parallel \zeta \parallel +C\parallel {\mathit{Q}}_h^n\parallel \parallel \zeta \parallel ⩽C,1⩽n⩽N.$$

(30)

As indicated by (29) and (30), the CNMFE solution coefficient vectors $\{U_h^n,Q_h^n\}$ are bounded, implying that the CNMFE solutions $\{u_h^n,q_h^n\}$ retain unconditional stability.

□

It is essential to define the projection operators $R_h$ and $P_h$ for analyzing the convergence of the CNMFE solutions.

Lemma 2. 

The projection $R_h:H_0^1\to {\mathbb{S}}_h$, defined by

$$(\nabla (u-R_{h}u),\nabla {\chi }_h)=0,\forall {\chi }_h\in {\mathbb{S}}_h,$$

(31)

with the following estimates

$$\parallel u-R_h{u\parallel }_{L^2(\Omega )}+h\parallel u-R_h{u\parallel }_{H^1(\Omega )}⩽C{h}^2{\parallel u\parallel }_{H^2(\Omega )},$$

(32)

$$\parallel u_t-R_h{u}_t{\parallel }_{L^2(\Omega )}⩽C{h}^2{(\parallel u\parallel }_{H^2(\Omega )}+\parallel u_t{\parallel }_{H^2(\Omega )}).$$

(33)

Lemma 3. 

The projection $P_h:H_0^1\to {\mathbb{S}}_h$, defined by

$$(b\nabla (q-P_{h}q),\nabla {\upsilon }_h)=0,\forall {\upsilon }_h\in {\mathbb{S}}_h,$$

(34)

with the following estimates

$$\parallel q-P_h{q\parallel }_{L^2(\Omega )}+h\parallel q-P_h{q\parallel }_{H^1(\Omega )}⩽C{h}^2{\parallel q\parallel }_{H^2(\Omega )},$$

(35)

$$\parallel q_t-P_h{q}_t{\parallel }_{L^2(\Omega )}⩽C{h}^2{(\parallel q\parallel }_{H^2(\Omega )}+\parallel q_t{\parallel }_{H^2(\Omega )}).$$

(36)

Errors can be divided for simplifying theoretical analysis as follows

$$u(t_n)-u_h^n=u(t_n)-R_{h}u(t_n)+R_{h}u(t_n)-u_h^n={\eta }^n+{\xi }^n,$$

(37)

$$q(t_n)-q_h^n=q(t_n)-P_{h}q(t_n)+P_{h}q(t_n)-q_h^n={\psi }^n+{\theta }^n.$$

(38)

Subtracting (12) from (8) and using (31) and (34) at $t=t_{n-{\displaystyle \frac{1}{2}}}$, the error equations are derived as

$$\begin{array}{cc}\hfill & {\displaystyle \left(\frac{{\xi }^n-{\xi }^{n-1}}{\Delta t},{\upsilon }_h\right)+\epsilon (b^{n-\frac{1}{2}}\nabla {\theta }^{n-\frac{1}{2}},\nabla {\upsilon }_h)}\hfill \\ =\hfill & {\displaystyle -\left(\frac{{\eta }^n-{\eta }^{n-1}}{\Delta t},{\upsilon }_h\right)+(f({\widehat{\widehat{u}}}^{n-\frac{1}{2}})-f({\widehat{\widehat{u}}}_h^{n-\frac{1}{2}}),{\upsilon }_h)+(R_1^{n-\frac{1}{2}},{\upsilon }_h)+(R_2^{n-\frac{1}{2}},{\upsilon }_h),\forall {\upsilon }_h\in {\mathbb{S}}_h,}\hfill \end{array}$$

(39)

$$({\theta }^{n-{\displaystyle \frac{1}{2}}},{\chi }_h)-(a^{n-{\displaystyle \frac{1}{2}}}\nabla {\xi }^{n-{\displaystyle \frac{1}{2}}},\nabla {\chi }_h)=-({\psi }^{n-{\displaystyle \frac{1}{2}}},{\chi }_h),\forall {\chi }_h\in {\mathbb{S}}_h.$$

(40)

The following lemma is presented for deriving error estimates. The lemma can be straightforwardly obtained through Taylor expansion.

Lemma 4. 

[54] $R_1^{n-{\displaystyle \frac{1}{2}}}$ and $R_2^{n-{\displaystyle \frac{1}{2}}}$ satisfy the following estimates

$$\parallel R_1^{n-{\displaystyle \frac{1}{2}}}\parallel ⩽C\Delta t^2{\parallel u_{ttt}\parallel }_{L^{\infty }(L^2)},$$

(41)

$$\parallel R_2^{n-{\displaystyle \frac{1}{2}}}\parallel ⩽C(u)\Delta t^2{\parallel u_{ttt}\parallel }_{L^{\infty }(L^2)}.$$

(42)

Based on Lemmas 2, 3 and 4, we can establish the theorems that concern the fully discrete error estimates for the Crank-Nicolson method.

Theorem 3. 

Given that the solutions to (5) adhere to regularity conditions with $u_t\in L^2(H^2)$, $u_{ttt}\in L^{\infty }(L^2)$, $u\in L^{\infty }(H^2)$. It follows that a positive constant C exists, which does not depend on h and $\Delta t$, satisfying

$$\begin{array}{c}\parallel u(t_J)-u_h^J\parallel ⩽C(h^2\parallel |•|\parallel +{(\Delta t)}^2\parallel u_{ttt}{\parallel }_{L^{\infty }(L^2)}),\hfill \end{array}$$

(43)

in which $\parallel |•|\parallel \triangleq {\parallel u\parallel }_{H^2}+\parallel u_t{\parallel }_{L^2(H^2)}+{\parallel q\parallel }_{H^2}+\parallel q_t{\parallel }_{L^2(H^2)}+{\parallel u\parallel }_{L^{\infty }(H^2)}$.

Proof of Theorem 3. 

Taking ${\upsilon }_h={\theta }^{n-{\displaystyle \frac{1}{2}}}$ and ${\displaystyle {\chi }_h=\frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}$ in (39) and (40), respectively, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \epsilon \parallel {(b^{n-\frac{1}{2}})}^{\frac{1}{2}}\nabla {\theta }^{n-\frac{1}{2}}{\parallel }^2}\hfill \\ =\hfill & {\displaystyle -(\frac{{\eta }^n-{\eta }^{n-1}}{\Delta t},{\theta }^{n-\frac{1}{2}})-(\frac{{\xi }^n-{\xi }^{n-1}}{\Delta t},{\theta }^{n-\frac{1}{2}})+(f({\widehat{\widehat{u}}}^{n-\frac{1}{2}})-f({\widehat{\widehat{u}}}_h^{n-\frac{1}{2}}),{\theta }^{n-\frac{1}{2}})}\hfill \\ \hfill & +(R_1^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}})+(R_2^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}}),\hfill \end{array}$$

(44)

$$({\theta }^{n-{\displaystyle \frac{1}{2}}},{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}})-(a^{n-{\displaystyle \frac{1}{2}}}\nabla {\xi }^{n-{\displaystyle \frac{1}{2}}},{\displaystyle \frac{\nabla {\xi }^n-\nabla {\xi }^{n-1}}{\Delta t}})=-({\psi }^{n-{\displaystyle \frac{1}{2}}},{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}).$$

(45)

Subtracting (45) from (44), we have

$$\begin{array}{cc}\hfill & {\displaystyle \epsilon \parallel {(b^{n-\frac{1}{2}})}^{\frac{1}{2}}\nabla {\theta }^{n-\frac{1}{2}}{\parallel }^2}\hfill \\ =\hfill & {\displaystyle -(\frac{{\eta }^n-{\eta }^{n-1}}{\Delta t},{\theta }^{n-\frac{1}{2}})-(a^{n-\frac{1}{2}}\nabla {\xi }^{n-\frac{1}{2}},\frac{\nabla {\xi }^n-\nabla {\xi }^{n-1}}{\Delta t})+({\psi }^{n-\frac{1}{2}},\frac{{\xi }^n-{\xi }^{n-1}}{\Delta t})}\hfill \\ \hfill & +(f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}),{\theta }^{n-{\displaystyle \frac{1}{2}}})+(R_1^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}})+(R_2^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}}),\hfill \\ =\hfill & {\displaystyle -(\frac{{\eta }^n-{\eta }^{n-1}}{\Delta t},{\theta }^{n-\frac{1}{2}})-\frac{1}{2\Delta t}(\parallel {(a^{n-\frac{1}{2}})}^{\frac{1}{2}}\nabla {\xi }^n{\parallel }^2-\parallel {(a^{n-\frac{1}{2}})}^{\frac{1}{2}}\nabla {\xi }^{n-1}{\parallel }^2)}\hfill \\ \hfill & {\displaystyle +\frac{({\psi }^n,{\xi }^n)-({\psi }^{n-1},{\xi }^{n-1})}{\Delta t}-({\xi }^{n-\frac{1}{2}},\frac{{\psi }^n-{\psi }^{n-1}}{\Delta t})}\hfill \\ \hfill & +(f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}),{\theta }^{n-{\displaystyle \frac{1}{2}}})+(R_1^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}})+(R_2^{n-{\displaystyle \frac{1}{2}}},{\theta }^{n-{\displaystyle \frac{1}{2}}}).\hfill \end{array}$$

(46)

Multiplying (46) by $2\Delta t$, summating from $n=1,\cdots ,J$, and considering that $\parallel \xi \parallel ⩽C_1\parallel \nabla \xi \parallel$ and $\parallel \theta \parallel ⩽C_2\parallel \nabla \theta \parallel$, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle a_0\parallel \nabla {\xi }^J{\parallel }^2+C\epsilon b_0\Delta t\sum _{n=1}^J{\parallel \nabla {\theta }^{n-\frac{1}{2}}\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C\Delta t\sum _{n=1}^J(\parallel \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}{\parallel }^2+\parallel f({\widehat{\widehat{u}}}^{n-\frac{1}{2}})-f({\widehat{\widehat{u}}}_h^{n-\frac{1}{2}}){\parallel }^2+\parallel R_1^{n-\frac{1}{2}}{\parallel }^2+\parallel R_2^{n-\frac{1}{2}}{\parallel }^2)}\hfill \\ \hfill & {\displaystyle +C\parallel {\psi }^J{\parallel }^2+C\Delta t\sum _{n=1}^J(\parallel \nabla {\xi }^{n-\frac{1}{2}}{\parallel }^2+\parallel \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}{\parallel }^2)+\frac{a_0}{2}{\parallel \nabla {\xi }^J\parallel }^2.}\hfill \end{array}$$

(47)

For the nonlinear term $\parallel f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2$, from reference [50], we have

$$\begin{array}{c}\parallel f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2⩽C(\parallel {\eta }^{n-1}{\parallel }^2+\parallel {\eta }^{n-2}{\parallel }^2+\parallel {\xi }^{n-1}{\parallel }^2+\parallel {\xi }^{n-2}{\parallel }^2).\hfill \end{array}$$

(48)

Substituting (48) into (47), and using the Gronwall lemma and $\parallel \xi \parallel ⩽C_1\parallel \nabla \xi \parallel$, we get

$$\begin{array}{cc}\hfill & {\displaystyle \parallel \nabla {\xi }^J{\parallel }^2+C\Delta t\sum _{n=1}^J{\parallel \nabla {\theta }^{n-\frac{1}{2}}\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C\Delta t\sum _{n=1}^J(\parallel \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}{\parallel }^2+\parallel \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}{\parallel }^2+\parallel R_1^{n-\frac{1}{2}}{\parallel }^2+\parallel R_2^{n-\frac{1}{2}}{\parallel }^2)}\hfill \\ \hfill & {\displaystyle +C\Delta t\sum _{n=0}^{J-1}\parallel {\eta }^n{\parallel }^2+C{\parallel {\psi }^J\parallel }^2.}\hfill \end{array}$$

(49)

Noting that

$$\parallel {\displaystyle \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}}{\parallel }^2⩽{\displaystyle \frac{1}{\Delta t}}{\int }_{t_{n-1}}^{t_n}{\parallel {\eta }_t(s)\parallel }^{2}ds,$$

(50)

$$\parallel {\displaystyle \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}}{\parallel }^2⩽{\displaystyle \frac{1}{\Delta t}}{\int }_{t_{n-1}}^{t_n}{\parallel {\psi }_t(s)\parallel }^{2}ds.$$

(51)

Substituting (50) and (51) into (49) and combining Lemma 4, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \parallel {\xi }^J{\parallel }^2+C\Delta t\sum _{n=1}^J{\parallel \nabla {\theta }^{n-\frac{1}{2}}\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C({\int }_{t_0}^{t_J}(\parallel {\eta }_t{(s)\parallel }^2+\parallel {\psi }_t{(s)\parallel }^2{)ds+(\Delta t)}^4\parallel u_{ttt}{\parallel }_{L^{\infty }(L^2)}^2+\Delta t\sum _{n=0}^{J-1}\parallel {\eta }^n{\parallel }^2+\parallel {\psi }^J{\parallel }^2).}\hfill \end{array}$$

(52)

The proof of (43) is effectively completed combining Lemma 2, 3, (52), and the triangle inequality.

□

Theorem 4. 

With $u_h^0=R_{h}u(t_0)$ and $q_h^0=R_{h}q(t_0)$, given that the solutions to (5) adhere to regularity conditions with $u_t,q_t\in L^2(H^2)$, $u_{ttt}\in L^{\infty }(L^2)$, $u\in L^{\infty }(H^2)$. It follows that a positive constant C exists, which does not depend on h and $\Delta t$, satisfying

$$\begin{array}{c}\parallel q(t_J)-q_h^J\parallel ⩽C(h^2\parallel |•|\parallel +{(\Delta t)}^2\parallel u_{ttt}{\parallel }_{L^{\infty }(L^2)}),\hfill \end{array}$$

(53)

Proof of Theorem 4. 

From (40) we can get

$${\displaystyle \left(\frac{{\theta }^n-{\theta }^{n-1}}{\Delta t},{\chi }_h\right)-\left(a^{n-\frac{1}{2}}\nabla \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t},\nabla {\chi }_h\right)=-\left(\frac{{\psi }^n-{\psi }^{n-1}}{\Delta t},{\chi }_h\right),\forall {\chi }_h\in {\mathbb{S}}_h.}$$

(54)

Taking ${\displaystyle {\upsilon }_h=\frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}$ and ${\displaystyle {\chi }_h={\theta }^{n-\frac{1}{2}}}$ in (39) and (54), respectively, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \parallel {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}{\parallel }^2+\epsilon \left(b^{n-\frac{1}{2}}\nabla {\theta }^{n-\frac{1}{2}},\nabla {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)}\hfill \\ =\hfill & -\left({\displaystyle \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}},{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)+\left(f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}),{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)\hfill \\ \hfill & +\left(R_1^{n-{\displaystyle \frac{1}{2}}},{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)+\left(R_2^{n-{\displaystyle \frac{1}{2}}},{\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right),\hfill \end{array}$$

(55)

$$\begin{array}{cc}{\displaystyle \frac{1}{2\Delta t}(\parallel {\theta }^n{\parallel }^2-\parallel {\theta }^{n-1}{\parallel }^2)}\hfill & =(a^{n-{\displaystyle \frac{1}{2}}}\nabla {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}},\nabla {\theta }^{n-{\displaystyle \frac{1}{2}}})-({\displaystyle \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}},{\theta }^{n-{\displaystyle \frac{1}{2}}})\hfill \\ \hfill & ⩽a_1(\nabla {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}},\nabla {\theta }^{n-{\displaystyle \frac{1}{2}}})+C(\parallel {\displaystyle \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}}{\parallel }^2+\parallel {\theta }^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2).\hfill \end{array}$$

(56)

From (55), we have

$$\begin{array}{cc}\hfill & {\displaystyle \parallel {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}{\parallel }^2+\epsilon b_0\left(\nabla {\theta }^{n-\frac{1}{2}},\nabla {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)}\hfill \\ ⩽\hfill & C(\parallel {\displaystyle \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}}{\parallel }^2+\parallel f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2+\parallel R_1^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel R_2^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2)+{\displaystyle \frac{1}{2}}{\parallel {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\parallel }^2,\hfill \end{array}$$

(57)

so

$$\begin{array}{cc}{\displaystyle \left(\nabla {\theta }^{n-\frac{1}{2}},\nabla {\displaystyle \frac{{\xi }^n-{\xi }^{n-1}}{\Delta t}}\right)⩽}\hfill & C(\parallel {\displaystyle \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}}{\parallel }^2+\parallel f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2\hfill \\ \hfill & +\parallel R_1^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel R_2^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2),\hfill \end{array}$$

(58)

Substituting (58) into (56) yields

$$\begin{array}{cc}{\displaystyle \frac{1}{2\Delta t}(\parallel {\theta }^n{\parallel }^2-\parallel {\theta }^{n-1}{\parallel }^2)⩽}\hfill & C(\parallel {\displaystyle \frac{{\eta }^n-{\eta }^{n-1}}{\Delta t}}{\parallel }^2+\parallel {\displaystyle \frac{{\psi }^n-{\psi }^{n-1}}{\Delta t}}{\parallel }^2+\parallel f({\widehat{\widehat{u}}}^{n-{\displaystyle \frac{1}{2}}})-f({\widehat{\widehat{u}}}_h^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2\hfill \\ \hfill & +\parallel R_1^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel R_2^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2+\parallel {\theta }^{n-{\displaystyle \frac{1}{2}}}{\parallel }^2).\hfill \end{array}$$

(59)

Multiplying (59) by $2\Delta t$, summating from $n=1,\cdots ,J$ and employing (50) and (51), we get

$$\begin{array}{cc}{\displaystyle \parallel {\theta }^J{\parallel }^2⩽}\hfill & {\displaystyle \parallel {\theta }^0{\parallel }^2+C\Delta t\sum _{n=1}^J(\parallel f({\widehat{\widehat{u}}}^{n-\frac{1}{2}})-f({\widehat{\widehat{u}}}_h^{n-\frac{1}{2}}){\parallel }^2+\parallel R_1^{n-\frac{1}{2}}{\parallel }^2+\parallel R_2^{n-\frac{1}{2}}{\parallel }^2)}\hfill \\ \hfill & {\displaystyle +C{\int }_0^{t_J}(\parallel {\eta }_t{(s)\parallel }^2+\parallel {\psi }_t{(s)\parallel }^2)ds+C\Delta t\sum _{n=1}^J{\parallel {\theta }^{n-\frac{1}{2}}\parallel }^2.}\hfill \end{array}$$

(60)

Using the Gronwall Lemma and (48),we have

$$\begin{array}{cc}{\displaystyle \parallel {\theta }^J{\parallel }^2⩽}\hfill & {\displaystyle \parallel {\theta }^0{\parallel }^2+C\Delta t\sum _{n=0}^{J-1}(\parallel {\eta }^n{\parallel }^2+\parallel {\xi }^n{\parallel }^2)+C\Delta t\sum _{n=1}^J(\parallel R_1^{n-\frac{1}{2}}{\parallel }^2+\parallel R_2^{n-\frac{1}{2}}{\parallel }^2)}\hfill \\ \hfill & {\displaystyle +C{\int }_0^{t_J}(\parallel {\eta }_t{(s)\parallel }^2+\parallel {\psi }_t(s){\parallel }^2)ds.}\hfill \end{array}$$

(61)

Substitute (52) and Lemma 4 into (61), we get

$$\begin{array}{cc}{\displaystyle \parallel {\theta }^J{\parallel }^2⩽}\hfill & {\displaystyle \parallel {\theta }^0{\parallel }^2+C{\int }_0^{t_J}(\parallel {\eta }_t{(s)\parallel }^2+\parallel {\psi }_t{(s)\parallel }^2)ds+C(\parallel {\eta }^n{\parallel }_{L^{\infty }(L^2)}^2+\parallel {\psi }^J{\parallel }^2)}\hfill \\ \hfill & +C{(\Delta t)}^4{\parallel u_{ttt}\parallel }_{L^{\infty }(L^2)}^2\hfill \end{array}$$

(62)

We complete the proof combining Lemma 2, 3, (62) and the triangle inequality. □

3. The POD-Based RDCNMFE Method for the Fourth-Order Variable Coefficient Parabolic Equation

3.1. Structure of POD Bases

Initially, computing the first $\mathcal{K}$-step coefficient vectors ${\{{\mathit{U}}_h^n,{\mathit{Q}}_h^n\}}_{n=1}^{\mathcal{K}}$ by Problem 3, the snapshot matrices ${\mathit{Z}}_1={({\mathit{U}}_h^1,{\mathit{U}}_h^2,\cdots ,{\mathit{U}}_h^{\mathcal{K}})}_{M\times \mathcal{K}}$ and ${\mathit{Z}}_2={({\mathit{Q}}_h^1,{\mathit{Q}}_h^2,\cdots ,{\mathit{Q}}_h^{\mathcal{K}})}_{M\times \mathcal{K}}$ are generated. Next, we compute the eigenvalues and eigenvectors of matrices ${\mathit{Z}}_i{\mathit{Z}}_i^T(i=1,2)$. Organize the eigenvalues as ${\mu }_{i,1}⩾{\mu }_{i,2}⩾\cdots ⩾{\mu }_{i,r_i}>0(r_i=\mathrm{rank}({\mathit{Z}}_i))$. The eigenvectors form the eigenmatrix ${\tilde{\Phi }}_i=({\phi }_{i,1},{\phi }_{i,2},\cdots ,{\phi }_{i,r_i})\in {\mathbb{R}}^{M\times r_i}$. Lastly, the initial d vectors of ${\tilde{\Phi }}_i$ are selected as POD bases ${\Phi }_i=({\phi }_{i,1},{\phi }_{i,2},\cdots ,{\phi }_{i,d})(d⩽r_i)$, such that

$$\parallel {\mathit{Z}}_i-{\Phi }_i{\Phi }_i^T{\mathit{Z}}_i{\parallel }_2=\sqrt{{\mu }_{i,d+1}},i=1,2,$$

(63)

in which ${\displaystyle {\parallel \mathit{Z}\parallel }_2=\underset{\mathit{v}\in {\mathbb{R}}^M}{sup}\frac{\parallel \mathit{Z}\mathit{v}\parallel }{\parallel \mathit{v}\parallel }}$ and ${\displaystyle \parallel \mathit{v}\parallel =\sqrt{\sum _{i=1}^M{\left|v_i\right|}^2}}$ for vector $\mathit{v}={(v_1,v_2,\cdots ,v_M)}^T$. For $n=1,2,\cdots ,\mathcal{K}$, it follows that

$$\parallel {\mathit{U}}_h^n-{\Phi }_1{\Phi }_1^T{\mathit{U}}_h^n\parallel =\parallel ({\mathit{Z}}_1-{\Phi }_1{\Phi }_1^T{\mathit{Z}}_1){\mathit{e}}^n\parallel ⩽\parallel ({\mathit{Z}}_1-{\Phi }_1{\Phi }_1^T{\mathit{Z}}_1){\parallel }_2\parallel {\mathit{e}}^n\parallel ⩽\sqrt{{\mu }_{1,d+1}},$$

(64)

$$\parallel {\mathit{Q}}_h^n-{\Phi }_2{\Phi }_2^T{\mathit{Q}}_h^n\parallel =\parallel ({\mathit{Z}}_2-{\Phi }_2{\Phi }_2^T{\mathit{Z}}_2){\mathit{e}}^n\parallel ⩽\parallel ({\mathit{Z}}_2-{\Phi }_2{\Phi }_2^T{\mathit{Z}}_2){\parallel }_2\parallel {\mathit{e}}^n\parallel ⩽\sqrt{{\mu }_{2,d+1}}.$$

(65)

${\mathit{e}}^n(1⩽n⩽\mathcal{K})$, the nth component being 1, named unit vectors. Consequently, ${\Phi }_i=({\phi }_{i,1},{\phi }_{i,2},\cdots ,{\phi }_{i,d})$$(d⩽r_i,i=1,2)$ are optimal POD bases.

Remark 2. 

It is obvious that the order $M\times M$ of the matrices ${\mathit{Z}}_i{\mathit{Z}}_i^T$ is significantly greater than the order $\mathcal{K}\times \mathcal{K}$ of the matrices ${\mathit{Z}}_i^T{\mathit{Z}}_i$. However, their positive eigenvalues are same, we can compute the first d eigenvalues ${\mu }_{i,j}$ and eigenvectors ${\varphi }_{i,j}$ of the matrices ${\mathit{Z}}_i^T{\mathit{Z}}_i$. Then, we can derive the eigenvectors for ${\mathit{Z}}_i{\mathit{Z}}_i^T$ through the relationships ${\phi }_{i,j}={\mathit{Z}}_i{\varphi }_{i,j}/\sqrt{{\mu }_{i,j}}$. This approach facilitates the creation of POD bases ${\Phi }_i$. $(1⩽j⩽d,i=1,2)$

3.2. The RDCNMFE Scheme

Initially, we let ${\alpha }_d^n={({\alpha }_1^n,{\alpha }_2^n,\dots ,{\alpha }_d^n)}^T$ and ${\beta }_d^n={({\beta }_1^n,{\beta }_2^n,\dots ,{\beta }_d^n)}^T$, and define the RDCNMFE solution coefficient vectors as follows: ${\mathit{U}}_d^n={(U_{d1}^n,U_{d2}^n,\dots ,U_{dM}^n)}^T$ and ${\mathit{Q}}_d^n={(Q_{d1}^n,Q_{d2}^n,\dots ,Q_{dM}^n)}^T$. Next, the first $\mathcal{K}$ RDCNMFE solution coefficient vectors are promptly derived using ${\mathit{U}}_d^n={\Phi }_1{\Phi }_1^T{\mathit{U}}_h^n=:{\Phi }_1{\alpha }_d^n$ and ${\mathit{Q}}_d^n={\Phi }_2{\Phi }_2^T{\mathit{Q}}_h^n=:{\Phi }_2{\beta }_d^n$, for $1⩽n⩽\mathcal{K}$, as outlined in section 3.1. Finally, for subsequent time steps $\mathcal{K}+1⩽n⩽N$, we employ ${\mathit{U}}_d^n={\Phi }_1{\alpha }_d^n$ and ${\mathit{Q}}_d^n={\Phi }_2{\beta }_d^n$, replacing the original CNMFE solution vectors $\{{\mathit{U}}_h^n,{\mathit{Q}}_h^n\}$ in Problem 3. This allows us to develop the following RDCNMFE matrix scheme.

Problem 4. 

Find $\{{\mathit{U}}_d^n,{\mathit{Q}}_d^n\}\in {\mathbb{R}}^M\times {\mathbb{R}}^M$ and $\{u_d^n,{\omega }_d^n\}\in {\mathbb{S}}_h\times {\mathbb{S}}_h(1⩽n⩽N)$, such that

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill & {\alpha }_d^n={\Phi }_1^T{\mathit{U}}_h^n,{\beta }_d^n={\Phi }_2^T{\mathit{Q}}_h^n,1⩽n⩽\mathcal{K},\hfill \\ \hfill & {\Phi }_1{\overline{\partial }}_t{\alpha }_d^n+\epsilon {\mathit{B}}^{n-{\displaystyle \frac{1}{2}}}{\Phi }_2{\beta }_d^{n-{\displaystyle \frac{1}{2}}}=\mathit{F}({\Phi }_1{\widehat{\widehat{\alpha }}}_d^{n-{\displaystyle \frac{1}{2}}}),\mathcal{K}+1⩽n⩽N,\hfill \\ \hfill & {\Phi }_2{\beta }_d^{n-{\displaystyle \frac{1}{2}}}-{\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}{\Phi }_1{\alpha }_d^{n-{\displaystyle \frac{1}{2}}}=0,\mathcal{K}+1⩽n⩽N,\hfill \\ \hfill & {\displaystyle u_d^n=\sum _{j=1}^M{U}_{dj}^n{\zeta }_j={\mathit{U}}_d^n·\zeta ={\Phi }_1{\alpha }_d^n·\zeta ,q_d^n=\sum _{j=1}^M{Q}_{dj}^n{\zeta }_j={\mathit{Q}}_d^n·\zeta ={\Phi }_2{\beta }_d^n·\zeta ,1⩽n⩽N.}\hfill \end{array}\hfill \end{array}\right.$$

(66)

Here, $\{{\mathit{U}}_h^n,{\mathit{Q}}_h^n\}(n=1,2,\cdots ,\mathcal{K})$ denotes the first $\mathcal{K}$ solution vectors of Problem 3. The definitions of matrix ${\mathit{B}}^{n-{\displaystyle \frac{1}{2}}}$, ${\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}$, and vector $\mathit{F}$, along with the FE basis vectors $\zeta =({\zeta }_1(x),{\zeta }_2(x),\cdots ,{\zeta }_M(x))$ are detailed in section 2.2.

3.3. The Uniqueness, Stability and Error Estimate of the RDCNMFE Solutions

Theorem 5. 

With the assumptions laid out in Theorem 3 and 4, we consider $\{u^n,q^n\}\in H_0^1\times H_0^1$ as the solutions of Problem 1, and $\{u_d^n,q_d^n\}\in {\mathbb{S}}_h\times {\mathbb{S}}_h$ as reduced-dimension solutions of Problem 4. Then the RDCNMFE solutions are both unique and unconditionally stable for $1⩽n⩽N$, and have the error estimate as follows.

$$\begin{array}{c}\hfill \parallel u^n-u_d^n\parallel +\parallel q^n-q_d^n\parallel ⩽C(h^2+\Delta t^2+\sqrt{{\mu }_{1,d+1}}+\sqrt{{\mu }_{2,d+1}}).\end{array}$$

(67)

Proof of Theorem 5. 

(1)

Demonstrate the uniqueness.

For $1⩽n⩽\mathcal{K}$, Theorem 1 ensures that the solutions $\{u_h^n,q_h^n\}$ in problem 3 are unique. Consequently, the corresponding solutions $\{u_d^n,q_d^n\}$, derived from the first and fourth expressions of problem 4, also have uniqueness.

For $\mathcal{K}+1⩽n⩽N$, by applying ${\mathit{U}}_d^n={\Phi }_1{\alpha }_d^n$ and ${\mathit{Q}}_d^n={\Phi }_2{\beta }_d^n$, the last three equations of Problem 4 are reformulated as

$${\overline{\partial }}_t{\mathit{U}}_d^n+\epsilon {\mathit{B}}^{n-{\displaystyle \frac{1}{2}}}{\mathit{Q}}_d^{n-{\displaystyle \frac{1}{2}}}=\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}),\mathcal{K}+1⩽n⩽N,$$

(68)

$${\mathit{Q}}_d^{n-{\displaystyle \frac{1}{2}}}-{\mathit{S}}^{n-{\displaystyle \frac{1}{2}}}{\mathit{U}}_d^{n-{\displaystyle \frac{1}{2}}}=0,\mathcal{K}+1⩽n⩽N,$$

(69)

$${\displaystyle u_d^n=\sum _{j=1}^M{U}_{dj}^n{\zeta }_j={\mathit{U}}_d^n·\zeta ,q_d^n=\sum _{j=1}^M{Q}_{dj}^n{\zeta }_j={\mathit{Q}}_d^n·\zeta ,\mathcal{K}+1⩽n⩽N.}$$

(70)

For $\mathcal{K}+1⩽n⩽N$, the solutions ${\{u_h^n,q_h^n\}}_{n=\mathcal{K}+1}^N$ in Problem 3 are unique. Because $(68)-(70)$ adhere to the identical structure as problem 3, the solutions ${\{u_d^n,q_d^n\}}_{n=\mathcal{K}+1}^N$ for $(68)-(70)$ also have uniqueness.

(2)

Analyse the stability.

(i) When $1⩽n⩽\mathcal{K}$.

Applying Theorem 2 and considering the orthonormality of the vectors in ${\Phi }_1$ and ${\Phi }_2$, it follows that

$$\begin{array}{cc}\parallel u_d^n\parallel +\parallel q_d^n\parallel \hfill & =\parallel {\mathit{U}}_d^n·\zeta \parallel +\parallel {\mathit{Q}}_d^n·\zeta \parallel \hfill \\ \hfill & =\parallel {\Phi }_1{\Phi }_1^T{\mathit{U}}_h^n·\zeta \parallel +\parallel {\Phi }_2{\Phi }_2^T{\mathit{Q}}_h^n·\zeta \parallel \hfill \\ \hfill & ⩽C(\parallel u_h^n\parallel +\parallel q_h^n\parallel )\hfill \\ \hfill & ⩽C,1⩽n⩽\mathcal{K}.\hfill \end{array}$$

(71)

(ii) When $\mathcal{K}+1⩽n⩽N$.

From the positive definite symmetry of matrix $\mathit{B}$, (68) can be reformulated as

$$\begin{array}{c}{\displaystyle {({\mathit{B}}^{n-\frac{1}{2}})}^{-1}{\overline{\partial }}_t{\mathit{U}}_d^n+\epsilon {\mathit{Q}}_d^{n-\frac{1}{2}}={({\mathit{B}}^{n-\frac{1}{2}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}}).}\hfill \end{array}$$

(72)

Substituting (69) into (72), and since $\mathit{S}$ is positive definite, we obtain

$${\displaystyle {({\mathit{S}}^{n-\frac{1}{2}})}^{-1}{({\mathit{B}}^{n-\frac{1}{2}})}^{-1}{\overline{\partial }}_t{\mathit{U}}_d^n+\epsilon {\mathit{U}}_d^{n-\frac{1}{2}}={({\mathit{S}}^{n-\frac{1}{2}})}^{-1}{({\mathit{B}}^{n-\frac{1}{2}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}}).}$$

(73)

Letting ${\mathit{D}}^{n-{\displaystyle \frac{1}{2}}}={({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}$, and taking the inner product of (73) and ${\overline{\partial }}_t{\mathit{U}}_d^n$, we have

$${\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_d^n,{\overline{\partial }}_t{\mathit{U}}_d^n)+\epsilon ({\mathit{U}}_d^{n-\frac{1}{2}},{\overline{\partial }}_t{\mathit{U}}_d^n)=({\mathit{D}}^{n-\frac{1}{2}}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}}),{\overline{\partial }}_t{\mathit{U}}_d^n).}$$

(74)

Then, two sides of (74) are that

$$\begin{array}{c}{\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_d^n,{\overline{\partial }}_t{\mathit{U}}_d^n)+\epsilon ({\mathit{U}}_d^{n-\frac{1}{2}},{\overline{\partial }}_t{\mathit{U}}_d^n)=\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_d^n{\parallel }^2+\frac{\epsilon }{2\Delta t}(\parallel {\mathit{U}}_d^n{\parallel }^2-\parallel {\mathit{U}}_d^{n-1}{\parallel }^2),}\hfill \end{array}$$

(75)

and

$${\displaystyle ({\mathit{D}}^{n-\frac{1}{2}}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}}),{\overline{\partial }}_t{\mathit{U}}_d^n)⩽C\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\parallel }_{\infty }^2\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}})\parallel +\parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{\frac{1}{2}}{\overline{\partial }}_t{\mathit{U}}_d^n{\parallel }^2.}$$

(76)

Similar to (24), we obtain

$$\parallel {({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{{\displaystyle \frac{1}{2}}}{\parallel }_{\infty }^2\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2⩽C+C(\parallel {\mathit{U}}_d^{n-1}{\parallel }^2+\parallel {\mathit{U}}_d^{n-2}{\parallel }^2).$$

(77)

Combining (75), (76) and (77), we have

$$\begin{array}{c}{\displaystyle \frac{\epsilon }{2\Delta t}(\parallel {\mathit{U}}_d^n{\parallel }^2-\parallel {\mathit{U}}_d^{n-1}{\parallel }^2)⩽C+C(\parallel {\mathit{U}}_d^{n-1}{\parallel }^2+\parallel {\mathit{U}}_d^{n-2}{\parallel }^2).}\hfill \end{array}$$

(78)

Multiplying (78) by $2\Delta t$ and summating from 2 to n, it follows that

$$\begin{array}{cc}\parallel {\mathit{U}}_d^n{\parallel }^2\hfill & {\displaystyle ⩽\parallel {\mathit{U}}_d^1{\parallel }^2+\frac{2\Delta t}{\epsilon }\sum _{i=2}^{n}C+\frac{C\Delta t}{\epsilon }\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_d^i\parallel }^2}\hfill \\ \hfill & {\displaystyle ⩽\parallel {\mathit{U}}_d^1{\parallel }^2+CT+C\Delta t\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_d^i\parallel }^2.}\hfill \end{array}$$

(79)

Noting that

$$\parallel {\mathit{U}}_d^1{\parallel }^2=\parallel {\Phi }_1{\Phi }_1^T{\mathit{U}}_h^1{\parallel }^2⩽C{\parallel {\mathit{U}}_h^1\parallel }^2⩽C,$$

(80)

putting (80) into (79), we have

$$\parallel {\mathit{U}}_d^n{\parallel }^2⩽C+C\Delta t\sum _{i=0}^{n-1}{\parallel {\mathit{U}}_d^i\parallel }^2.$$

(81)

Using the Gronwall inequality for (81),

$$\parallel {\mathit{U}}_d^n{\parallel }^2⩽C{e}^{Cn\Delta t}⩽C.$$

(82)

And

$$\parallel {\mathit{Q}}_d^n\parallel =\parallel {\mathit{S}}^n{\mathit{U}}_d^n\parallel ⩽\parallel {\mathit{S}}^n{\parallel }_{\infty }\parallel {\mathit{U}}_d^n\parallel ⩽C\parallel {\mathit{U}}_d^n\parallel ⩽C.$$

(83)

So we get

$$\parallel {\mathit{U}}_d^n\parallel +\parallel {\mathit{Q}}_d^n\parallel ⩽C.$$

(84)

Because of $\parallel \zeta \parallel ⩽C$, we get

$$\parallel u_d^n\parallel +\parallel q_d^n\parallel =\parallel {\mathit{U}}_d^n·\zeta \parallel +\parallel {\mathit{Q}}_d^n·\zeta \parallel ⩽C\parallel {\mathit{U}}_d^n\parallel ·\parallel \zeta \parallel +C\parallel {\mathit{Q}}_d^n\parallel ·\parallel \zeta \parallel ⩽C,\mathcal{K}+1⩽n⩽N.$$

(85)

Based on (71) and (85), we can conclude that the solutions $\{u_d^n,q_d^n\}(1⩽n⩽N)$ exhibit unconditional stability.

(3)

Discuss the error estimates.

(i) For $1⩽n⩽\mathcal{K}$.

According to (64) and (65), and considering $\parallel \zeta \parallel ⩽C$, we obtain

$$\begin{array}{cc}\parallel u_h^n-u_d^n\parallel +\parallel q_h^n-q_d^n\parallel \hfill & ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_d^n{\parallel }_{\infty }\parallel \zeta \parallel +\parallel {\mathit{Q}}_h^n-{\mathit{Q}}_d^n{\parallel }_{\infty }\parallel \zeta \parallel \hfill \\ \hfill & ⩽C\parallel {\mathit{U}}_h^n-{\Phi }_1{\Phi }_1^T{\mathit{U}}_h^n\parallel +\parallel {\mathit{Q}}_h^n-{\Phi }_2{\Phi }_2^T{\mathit{Q}}_h^n\parallel \hfill \\ \hfill & ⩽C(\sqrt{{\mu }_{1,d+1}}+\sqrt{{\mu }_{2,d+1}}),1⩽n⩽\mathcal{K}.\hfill \end{array}$$

(86)

(ii) For $\mathcal{K}+1⩽n⩽N$.

Defining ${\delta }^n={\mathit{U}}_h^n-{\mathit{U}}_d^n$ and ${\rho }^n={\mathit{Q}}_h^n-{\mathit{Q}}_d^n$, and combining (19), (72) and (69), we obtain

$${({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{\overline{\partial }}_t{\delta }^n+\epsilon {\rho }^{n-{\displaystyle \frac{1}{2}}}={({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}),$$

(87)

$${\rho }^{n-{\displaystyle \frac{1}{2}}}={({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{\delta }^{n-{\displaystyle \frac{1}{2}}}.$$

(88)

Putting (88) into (87), and since $\mathit{S}$ is positive definite, we have

$$\begin{array}{cc}\hfill & {({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{\overline{\partial }}_t{\delta }^n+\epsilon {\delta }^{n-{\displaystyle \frac{1}{2}}}\hfill \\ =\hfill & {({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-{({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}).\hfill \end{array}$$

(89)

Letting ${\mathit{D}}^{n-{\displaystyle \frac{1}{2}}}={({\mathit{S}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{({\mathit{B}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}$, we obtain

$${({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{\overline{\partial }}_t{\delta }^n+\epsilon {\delta }^{n-{\displaystyle \frac{1}{2}}}={({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-{({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}).$$

(90)

Taking the inner product of (90) and ${\overline{\partial }}_t{\delta }^n$,

$$\begin{array}{cc}\hfill & ({({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}{\overline{\partial }}_t{\delta }^n,{\overline{\partial }}_t{\delta }^n)+\epsilon ({\delta }^{n-{\displaystyle \frac{1}{2}}},{\overline{\partial }}_t{\delta }^n)\hfill \\ =\hfill & ({({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-{({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}),{\overline{\partial }}_t{\delta }^n).\hfill \end{array}$$

(91)

Then, two sides of (91) are that

$$\begin{array}{cc}\hfill & {\displaystyle ({({\mathit{D}}^{n-\frac{1}{2}})}^{-1}{\overline{\partial }}_t{\delta }^n,{\overline{\partial }}_t{\delta }^n)+\epsilon ({\delta }^{n-\frac{1}{2}},{\overline{\partial }}_t{\delta }^n)}\hfill \\ =\hfill & {\displaystyle \parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{-\frac{1}{2}}{\overline{\partial }}_t{\delta }^n{\parallel }^2+\frac{\epsilon }{2\Delta t}(\parallel {\delta }^n{\parallel }^2-\parallel {\delta }^{n-1}{\parallel }^2),}\hfill \end{array}$$

(92)

and

$$\begin{array}{cc}\hfill & ({({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-{({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-1}\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}),{\overline{\partial }}_t{\delta }^n)\hfill \\ ⩽\hfill & C\parallel {({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-{\displaystyle \frac{1}{2}}}{\parallel }_{\infty }^2\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-{\displaystyle \frac{1}{2}}})-\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-{\displaystyle \frac{1}{2}}}){\parallel }^2+{\parallel {({\mathit{D}}^{n-{\displaystyle \frac{1}{2}}})}^{-{\displaystyle \frac{1}{2}}}{\overline{\partial }}_t{\delta }^n\parallel }^2.\hfill \end{array}$$

(93)

Using Lemma 1 and (3), we can estimate the first term of (93) as follows

$$\begin{array}{cc}\hfill & {\displaystyle \parallel {({\mathit{D}}^{n-\frac{1}{2}})}^{-\frac{1}{2}}{\parallel }_{\infty }^2{\parallel \mathit{F}({\widehat{\widehat{\mathit{U}}}}_h^{n-\frac{1}{2}})-\mathit{F}({\widehat{\widehat{\mathit{U}}}}_d^{n-\frac{1}{2}})\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C\parallel \left(\frac{3}{2}\mathit{F}({\mathit{U}}_h^{n-1})-\frac{1}{2}\mathit{F}({\mathit{U}}_h^{n-2})\right)-\left(\frac{3}{2}\mathit{F}({\mathit{U}}_d^{n-1})-\frac{1}{2}\mathit{F}({\mathit{U}}_d^{n-2})\right){\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C\parallel \frac{3}{2}({\mathit{U}}_h^{n-1}-{\mathit{U}}_d^{n-1}){\parallel }^2+\parallel \frac{1}{2}({\mathit{U}}_h^{n-2}-{\mathit{U}}_d^{n-2}){\parallel }^2}\hfill \\ ⩽\hfill & {\displaystyle C(\parallel {\delta }^{n-1}{\parallel }^2+\parallel {\delta }^{n-2}{\parallel }^2).}\hfill \end{array}$$

(94)

Combining (92), (93) and (94), we have

$${\displaystyle \frac{\epsilon }{2\Delta t}}(\parallel {\delta }^n{\parallel }^2-\parallel {\delta }^{n-1}{\parallel }^2)⩽C(\parallel {\delta }^{n-1}{\parallel }^2+\parallel {\delta }^{n-2}{\parallel }^2).$$

(95)

Multiplying (95) by $2\Delta t$ and summating from $\mathcal{K}+1$ to $n(n⩽N)$, it follows that

$$\begin{array}{c}{\displaystyle \parallel {\delta }^n{\parallel }^2⩽\parallel {\delta }^K{\parallel }^2+\frac{C\Delta t}{\epsilon }\sum _{i=K-1}^{n-1}{\parallel {\delta }^i\parallel }^2.}\hfill \end{array}$$

(96)

Noting that

$$\parallel {\delta }^K{\parallel }^2=\parallel {\mathit{U}}_h^K-{\mathit{U}}_d^K{\parallel }^2={\parallel {\mathit{U}}_h^K-{\Phi }_1{\Phi }_1^T{\mathit{U}}_h^K\parallel }^2,$$

(97)

Putting (97) into (96), from (64) and (65), we have

$${\displaystyle \parallel {\delta }^n{\parallel }^2⩽C{\mu }_{1,d+1}+C\Delta t\sum _{i=K-1}^{n-1}{\parallel {\delta }^i\parallel }^2.}$$

(98)

Applying the Gronwall’s inequality for (98),

$$\parallel {\delta }^n{\parallel }^2⩽C{\mu }_{1,d+1}{e}^{Cn\Delta t}⩽C{\mu }_{1,d+1}.$$

(99)

And

$$\parallel {\rho }^n\parallel =\parallel {\mathit{S}}^n{\delta }^n\parallel ⩽C\parallel {\mathit{S}}^n{\parallel }_{\infty }\parallel {\delta }^n\parallel ⩽C\parallel {\delta }^n\parallel ,$$

(100)

thus, we get

$$\parallel {\delta }^n\parallel +\parallel {\rho }^n\parallel ⩽C(\sqrt{{\mu }_{1,d+1}}+\sqrt{{\mu }_{2,d+1}}).$$

(101)

Because of $\parallel \zeta \parallel ⩽C$, we have

$$\begin{array}{cc}\parallel u_h^n-u_d^n\parallel +\parallel q_h^n-q_d^n\parallel \hfill & ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_d^n{\parallel }_{\infty }·\parallel \zeta \parallel +\parallel {\mathit{Q}}_h^n-{\mathit{Q}}_d^n{\parallel }_{\infty }·\parallel \zeta \parallel \hfill \\ \hfill & ⩽\parallel {\mathit{U}}_h^n-{\mathit{U}}_d^n\parallel ·\parallel \zeta \parallel +\parallel {\mathit{Q}}_h^n-{\mathit{Q}}_d^n\parallel ·\parallel \zeta \parallel \hfill \\ \hfill & ⩽C(\sqrt{{\mu }_{1,d+1}}+\sqrt{{\mu }_{2,d+1}}).\hfill \end{array}$$

(102)

Combining the triangle inequality, with Theorem 3 and 4, (86) and (102), we obtain

$$\begin{array}{cc}\parallel u^n-u_d^n\parallel +\parallel q^n-q_d^n\parallel \hfill & ⩽\parallel u^n-u_h^n\parallel +\parallel u_h^n-u_d^n\parallel +\parallel q^n-q_h^n\parallel +\parallel q_h^n-q_d^n\parallel \hfill \\ \hfill & ⩽C(h^2+\Delta t^2+\sqrt{{\mu }_{1,d+1}}+\sqrt{{\mu }_{2,d+1}}),1⩽n⩽N.\hfill \end{array}$$

(103)

□

4. The Numerical Experiments for the Fourth-Order Parabolic Equations

The efficiency of the proposed method is validated by two numerical examples. We compare the reduced-dimension scheme with the standard CNMFE scheme in terms of errors, convergence orders, and CPU runtime. For the purpose of analysis, we conduct experiments on the specified fourth-order parabolic equation.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{u}_t+\epsilon \nabla ·(b\nabla (\nabla ·(a(t)\nabla u)))-u^3+u=g(x,y,t),\hfill & (x,y,t)\in \Omega \times (0,T],\hfill \\ u(x,y,t)=\Delta u(x,y,t)=0,\hfill & (x,y,t)\in \partial \Omega \times [0,T],\hfill \\ u(x,y,0)=u_0(x,y),\hfill & (x,y)\in \Omega ,\hfill \end{array}\right.\end{array}$$

(104)

Solving Problem 3 gets the standard CNMFE solutions $\{u_h^n,q_h^n\}$. In order to get the RDCNMFE solutions $\{u_d^n,q_d^n\}$, the four steps are as follows.

Step 1:

In order to generate the snapshot matrices ${\mathit{Z}}_1=({\mathit{U}}_h^1,{\mathit{U}}_h^2,\cdots ,{\mathit{U}}_h^{20})$ and ${\mathit{Z}}_2=({\mathit{Q}}_h^1,{\mathit{Q}}_h^2,\cdots ,{\mathit{Q}}_h^{20})$, the initial $\mathcal{K}=20$ CNMFE solution vectors $\{{\mathit{U}}_h^n,{\mathit{Q}}_h^n\}(n=1,2,\cdots ,20)$ are calculated out by Problem 3.

Step 2:

Calculate the eigenvalues ${\mu }_{i,j}(i=1,2,j=1,2,\cdots ,20)$ of the matrix ${\mathit{Z}}_i^T{\mathit{Z}}_i$ and arrange them in descending order, along with their corresponding eigenvectors ${\varphi }_{i,j}$.

Step 3:

By calculating, it is observed that $\sqrt{{\mu }_{i,7}}⩽h^2+\Delta t^2(i=1,2)$. From the matrix ${\mathit{Z}}_i^T{\mathit{Z}}_i$, the first 6 eigenvectors ${\varphi }_{i,j}(j=1,2,\cdots ,6)$ can be selected. Applying the formula ${\phi }_{i,j}={\mathit{Z}}_i{\varphi }_{i,j}/\sqrt{{\mu }_{i,j}}$, we construct the POD bases ${\Phi }_i=({\phi }_{i,1},{\phi }_{i,2},\cdots ,{\phi }_{i,6})$.

Step 4:

Inserting the result into Problem 4 and calculating the RDCNMFE solutions.

Example 1. 

We consider the model $(104)$ in $\Omega ={[0,1]}^2\subset {\mathbb{R}}^2$ with the exact solution $u(x,y,t)={\mathrm{e}}^{-t}\sin (\pi x)\sin (\pi y)$. Choosing $a(t)=t^2+1$, $b=1$, the source term is

$$g(x,y,t)={\mathrm{e}}^{-t}(t^2+1)4\epsilon {\pi }^4\sin (\pi x)\sin (\pi y)-{\mathrm{e}}^{-3t}{\sin }^3(\pi x){\sin }^3(\pi y).$$

(105)

Since $q=-\nabla ·(a(t)\nabla u)$, the exact solution of q is $q(x,y,t)=2{\pi }^2{\mathrm{e}}^{-t}(t^2+1)\sin (\pi x)\sin (\pi y)$.

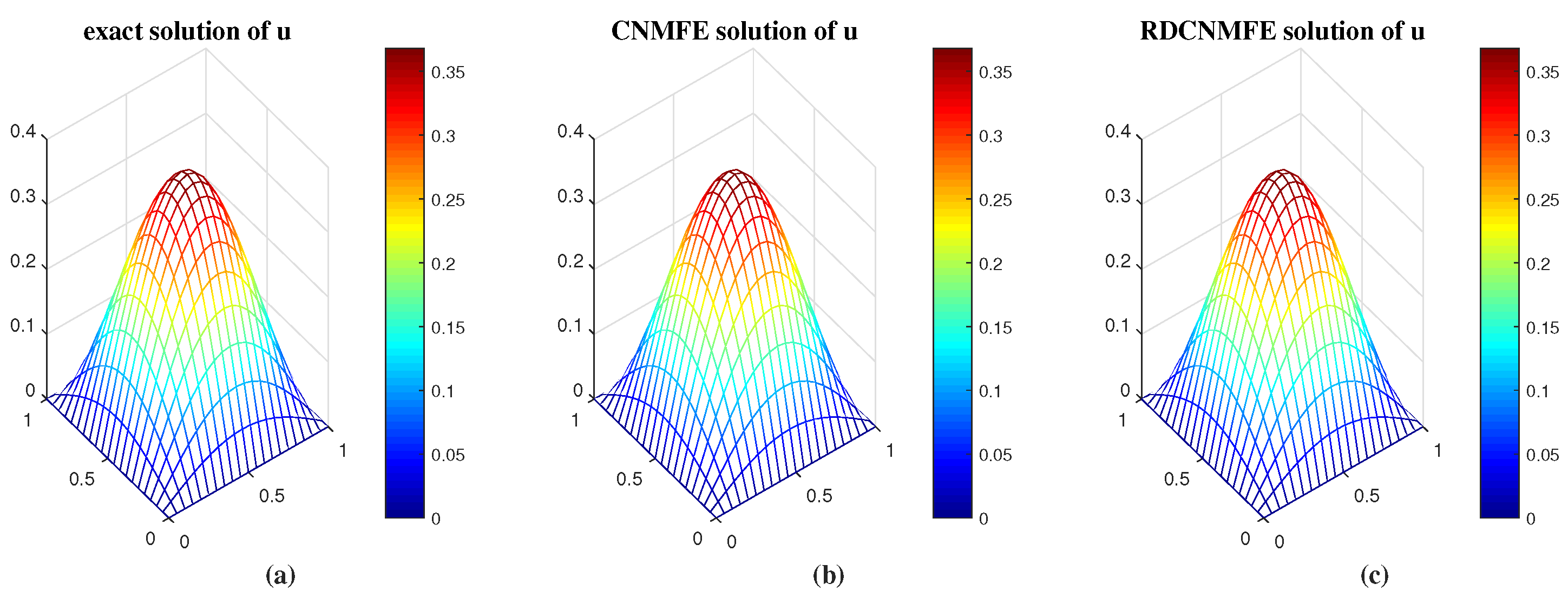
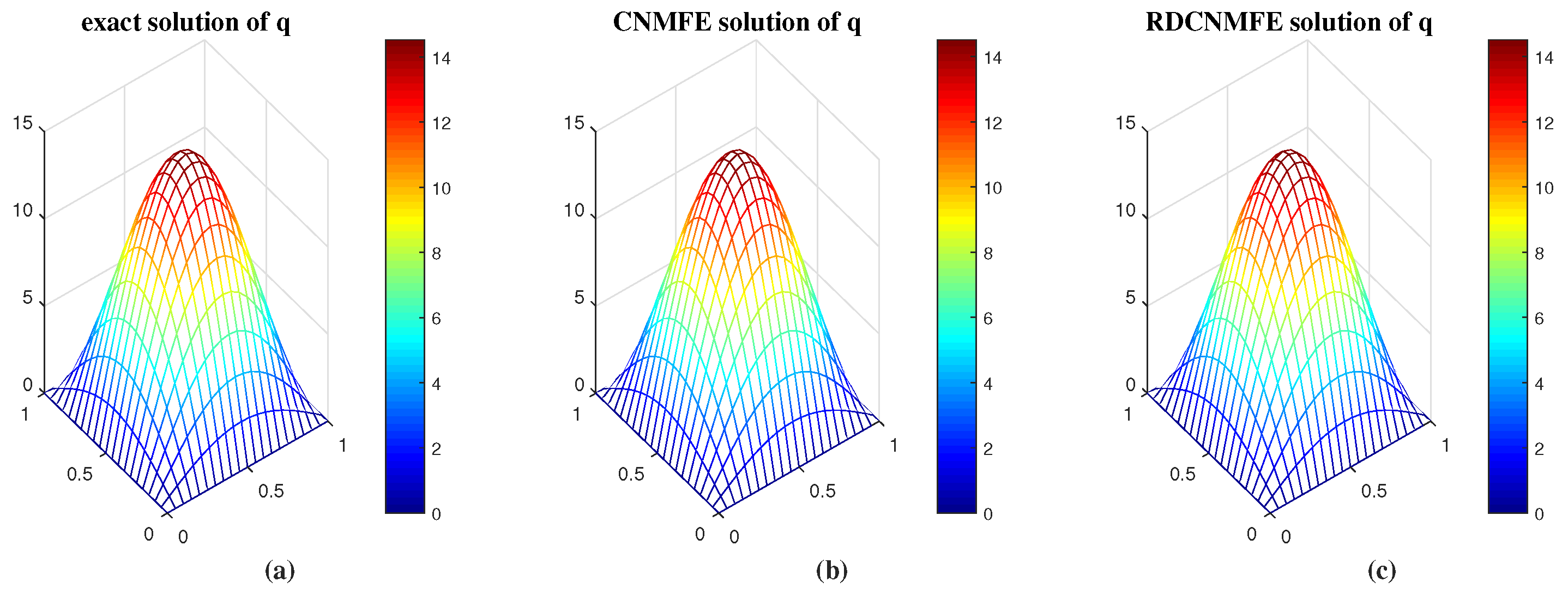
When $T=1$, with $h=\sqrt{2}/20$ and $\Delta t=1/100$, we get the standard CNMFE solutions and RDCNMFE solutions. They are compared with the exact solutions, as shown in Figure 1 and Figure 2. Obviously, both methods simulate the exact solutions very well.

When $T=1$ and $\Delta t=1/100$, so as to enable easier comparison, we use both methods to compute the $L^2$ error and convergence order of $\{u,q\}$, as shown in Table 1 and Table 2.

When $T=1.0,2.0,3.0$, with $h=\sqrt{2}/40$ and $\Delta t=1/100$, we record the $L^2$ error obtained and the CPU runtime required using both methods to further examing the efficacy of the POD-based RDCNMFE method, as shown in Table 3. The data indicates that both methods obtain the same $L^2$ errors. With each incremental second, the conventional CNMFE method increases by approximately 260 seconds, whereas the RDCNMFE method only increases just over 10 seconds.

Example 2. 

We explore the model $(104)$ in $\Omega ={[0,1]}^2\subset {\mathbb{R}}^2$ with the exact solution $u(x,y,t)={\mathrm{e}}^{-t}\sin (2\pi x)\sin (2\pi y)$. Letting $a(t)=t^2+1$, $b=1$, the source term is

$$g(x,y,t)={\mathrm{e}}^{-t}(t^2+1)16\epsilon {\pi }^4\sin (2\pi x)\sin (2\pi y)-{\mathrm{e}}^{-3t}{\sin }^3(2\pi x){\sin }^3(2\pi y).$$

(106)

The exact solution of q is $q(x,y,t)=8{\pi }^2{\mathrm{e}}^{-t}(t^2+1)\sin (2\pi x)\sin (2\pi y)$.

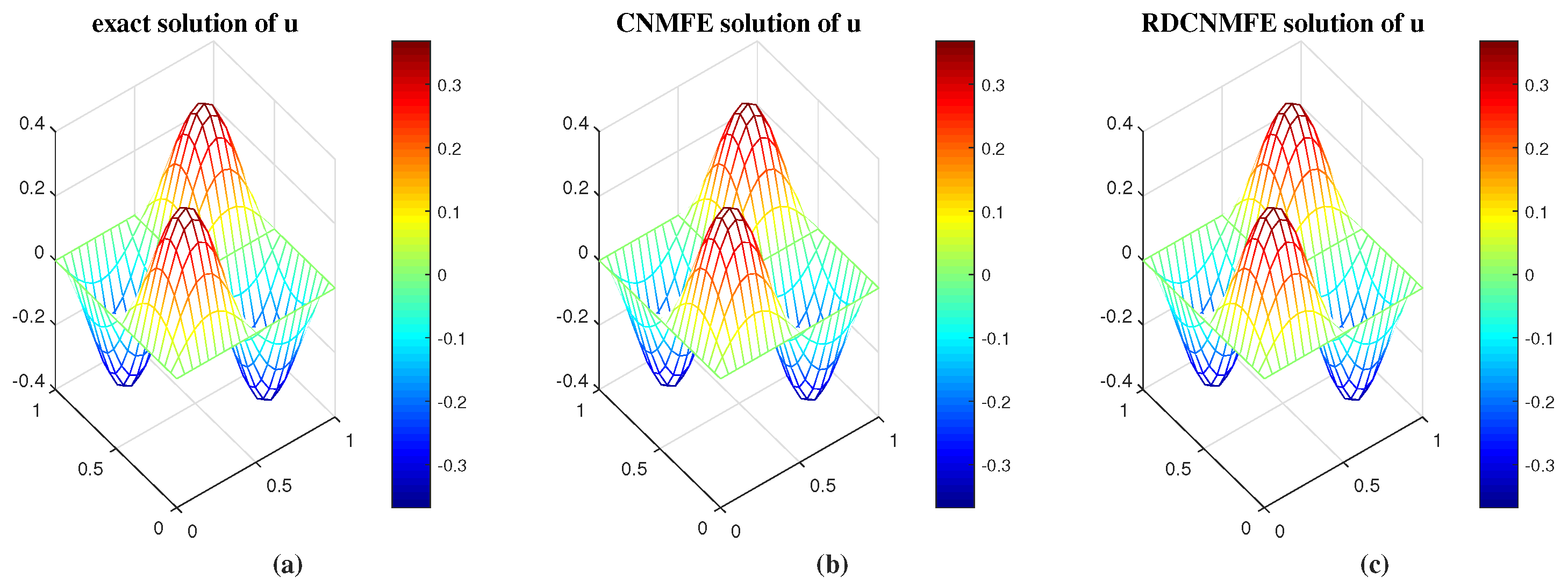
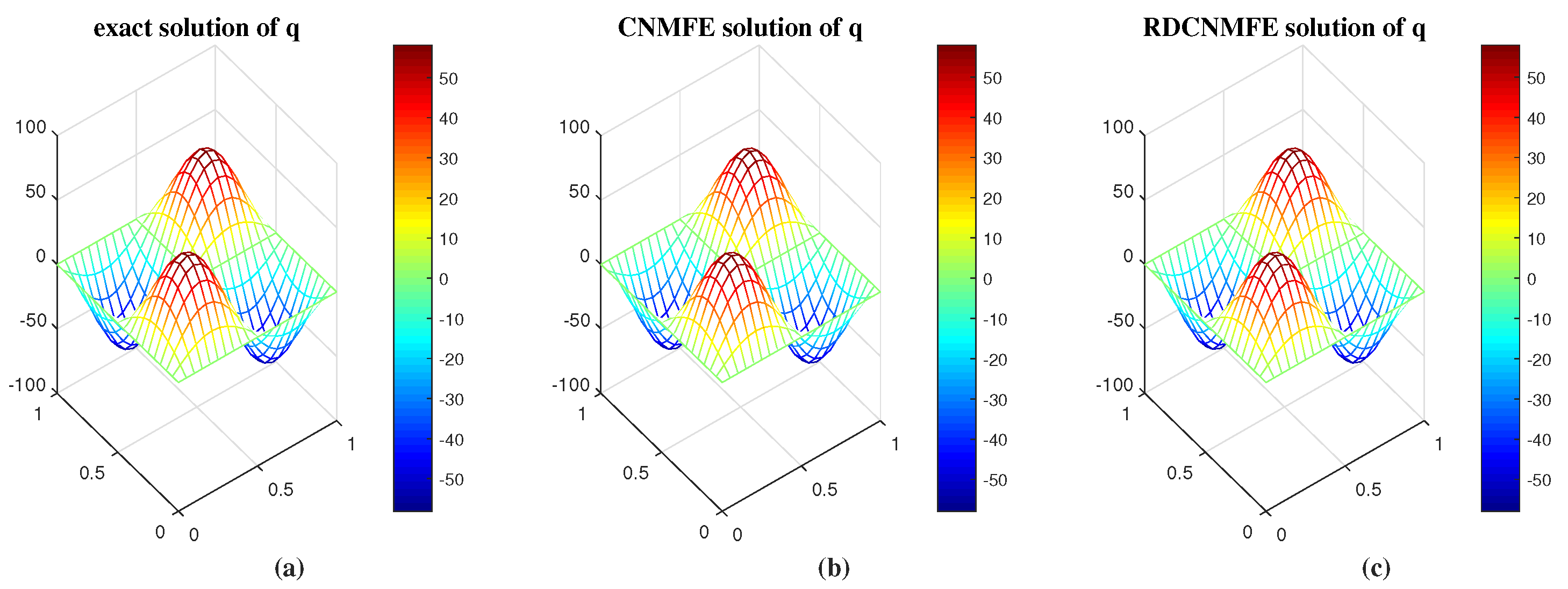
When $T=1$, setting $h=\sqrt{2}/20$ and $\Delta t=1/100$, we employ the CNMFE and RDCNMFE methods to obtain the numerical solutions for equation $(104)$ that has the noted source term $(106)$. Both solutions of $\{u,q\}$ are compared with the exact solutions. It can be seen clearly from Figure 3 and Figure 4 that both solutions closely approximate the exact solutions.

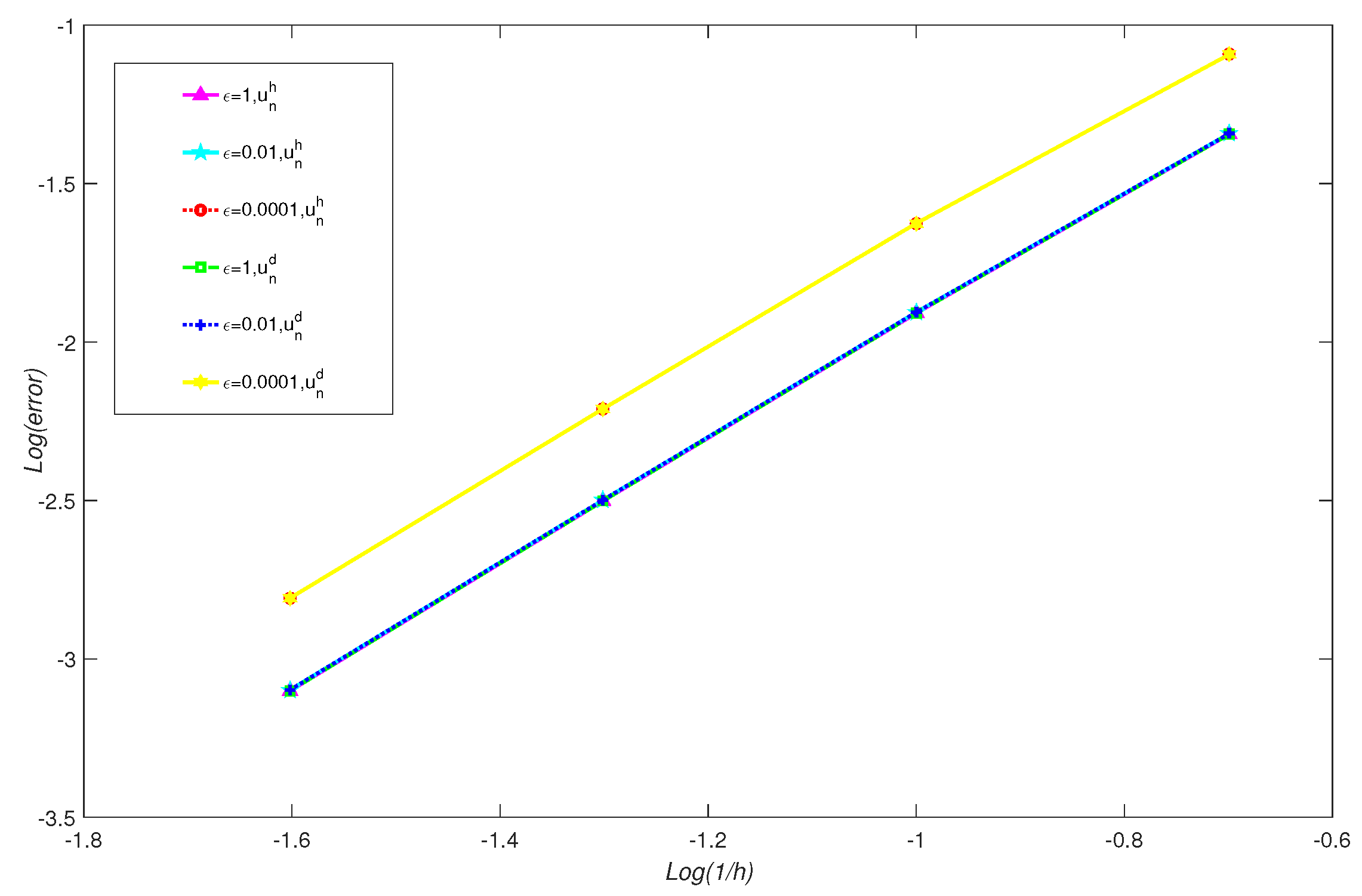
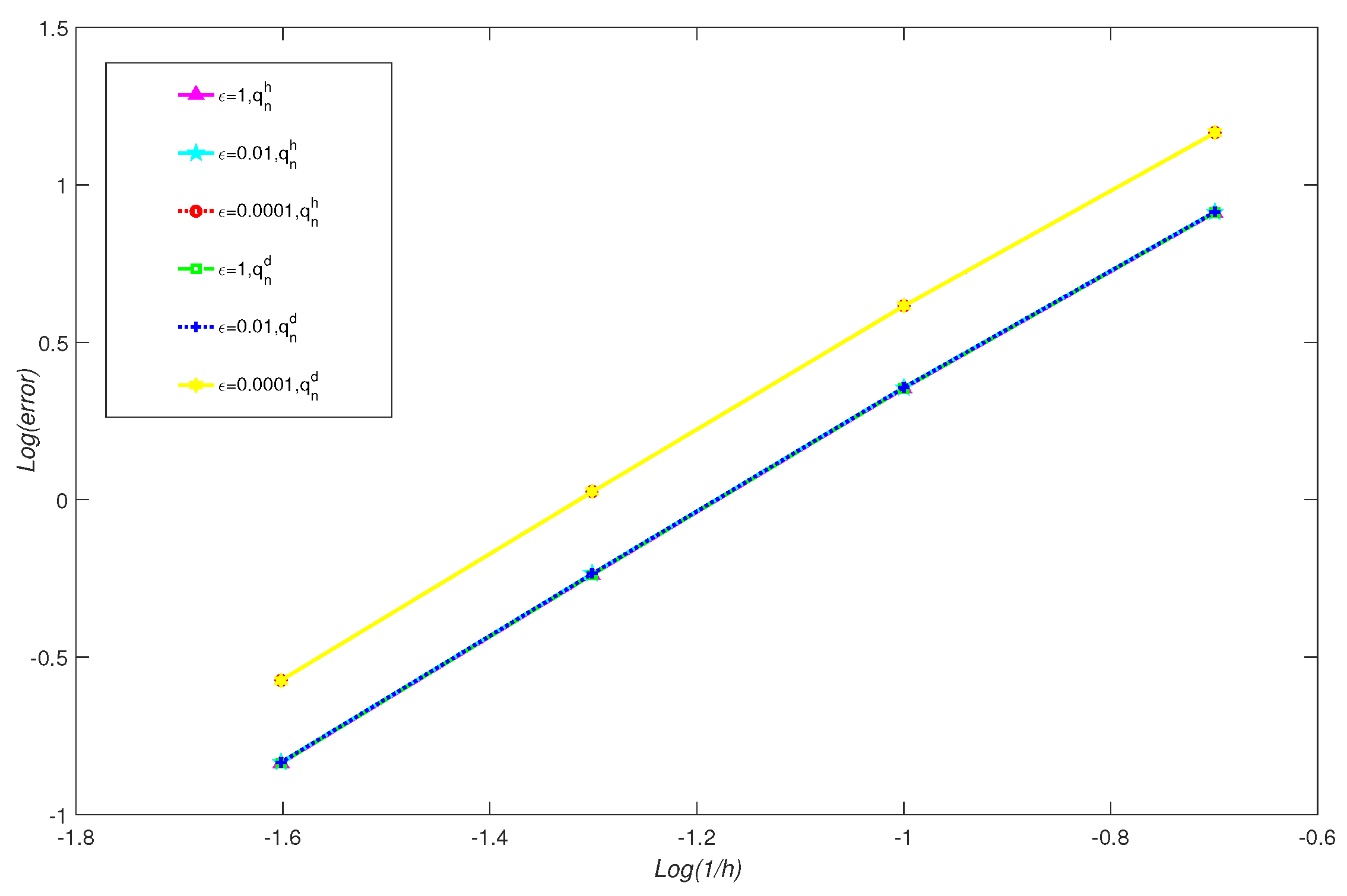
When $T=1$, setting $\Delta t=1/100$ and $\epsilon =1,0.01,0.0001$, we compute the CNMFE and RDCNMFE solutions of $\{u,q\}$. Then we get the $L^2$ errors and convergence orders of both methods, as shown in Table 4 and Table 5. Figure 5 and Figure 6 provide the comparison of error results of $\{u,q\}$ when $\epsilon =1,0.01,0.0001$. The figures demonstrates that when $\epsilon$ is set to a very small value, such as $\epsilon =0.0001$, although the solutions obtained by both methods are convergent, their associated errors tend to increase.

For purpose of demonstrating the effectiveness of the POD-based reduce-dimension method, we need to compare the CPU runtime of both methods. When $T=0.5,1.0,1.5,2.0,$

$2.5,3.0$, with $h=\sqrt{2}/40$ and $\Delta t=1/100$, we calculate the CNMFE and RDCNMFE solutions. Then we recorded the CPU runtime required using both methods in Table 6. Evidenced in Table 6, using the CNMFE method, the CPU runtime increases by about 130 seconds for every additional $0.5$ second. However, applying the RDCNMFE method, it takes just a few seconds for every added $0.5$ second. The significant reduction in CPU runtime using the reduced-dimension method can be attributed to the difference in degrees of freedom at each time node. Specifically, the standard CNMFE method is calculated with $2\times {41}^2$ degrees of freedom, while the RDCNMFE method just has $2\times 6$ degrees of freedom.

From the numerical results obtained from the above provided examples, it is evident that the RDCNMFE method based on POD serves as an efficient numerical technique for addressing the fourth-order variable coefficient parabolic equations.

5. Conclusions

In this research, our focus was on reducing dimension of solution coefficient vectors employing the CNMFE method combined with POD technique for the nonlinear variable coefficient fourth-order parabolic equation. Firstly, we developed a CNMFE scheme for the equations. We extensively analyzed the uniqueness, stability, and error estimates of the CNMFE solutions. Subsequently, the POD bases was derived from the initial $\mathcal{K}$ CNMFE solution coefficient vectors. We constructed a reduced-dimension matrix model and applied conventional FE analysis techniques in order to study the uniqueness, stability and convergence of the RDCNMFE solutions. Furthermore, we conducted detailed numerical experiments to compare the efficacy of both methods. The RDCNMFE method exhibited a reduced number of degrees of freedom at each time nodes compared to the conventional CNMFE method. This feature significantly reduces the computational load of the RDCNMFE method, thereby decreasing the runtime. Notably, this study has streamlined the calculations by linearizing the nonlinear terms, thereby eliminating repetitive numerical iterations. Thus, the RDCNMFE method emerges as an innovative and efficient numerical approach for addressing complex nonlinear PDEs.

In the following study, the method will be extended to more high-order PDEs, such as the fractional fourth-order PDEs, the Schrödinger equation with fourth-order disturbance term and so on. Additionally, we believe this method can be adapted to more complex problems.