Submitted:
28 August 2024
Posted:
29 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Crank-Nicolson Mixed Finite Element Method of the EFK Equation
2.1. The CNMFE Schemes
2.2. The Uniqueness, Stability and Convergence of the CNMFE Solutions
3. The reduced-dimension method of the Crank-Nicolson mixed finite element solution coefficient vectors of the EFK equation
3.1. Construction of POD basis vectors
3.2. Formulation of the RDCNMFE scheme
3.3. The uniqueness, stability and error estimate of the RDCNMFE solutions
-
For , Theorem 1 guarantees the uniqueness of solutions to problem 3. Therefore, the solutions generated from first and fourth formulas in problem 4 must also be unique.For , using , , the last three formulas of Problem 4 can be converted toFor , the set of solutions for Problem 3 is unique. Since (62) – (64) follow the same formats as problem 3, the set of solutions for (62) – (64) is also unique.
- (2)
-
Demonstrate the stability of the RDCNMFE solutions.When , since the vectors in and are orthonormal, using Theorem 2, we haveWhen , since is a positive definite symmetric matrix, we can rewrite (62) asPutting (63) into (66), we haveTaking the inner product of (67) and ,Then the left side of (68) is thatand the right side of (68) is thatUsing the same technique as (22), we haveCombining (69), (70) and (71), we haveMultiplying both sides of (72) by , and summating from 2 to n, we obtainNoting thatputting (74) into (73), we haveUsing the Gronwall Lemma for (75),AndSo we haveThus, noting that , we getFrom (65) and (79), the RDCNMFE solutions are unconditional stable.
- (3)
-
Analyse the error estimate of the RDCNMFE solutions.When , from , (58) and (59), we haveWhen , letting and , and combining (17), (66) and (63), we obtainPutting (82) into(81), we haveTaking the inner product of (83) and ,Then the left side of (84) is thatand the right side of (84) is thatCombining Lemma 1 with the global Lipschitz-continuity of , the first term of (86) can be estimated asCombining (85), (86) and (87), we haveMultiplying both sides of (88) by , and summating from to , we obtainNoting thatPutting (90) into (89), from (58) and (59), we haveApplying the Gronwall Lemma for (91),Andthus, we getFurther, from , we obtainUsing the triangle inequality, Theorem 3 and 4, (80) and (95), we obtain
4. The Numerical Examples for the EFK Equations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| POD | proper orthogonal decomposition |
| CNMFE | Crank-Nicolson mixed finite element |
| RDCNMFE | reduced-dimension Crank-Nicolson mixed finite element |
| EFK | extended Fisher-Kolmogorov |
References
- Adams, R.A. Sobolev Spaces; Academic Press: New York, USA, 1975. [Google Scholar]
- Coullet, P.; Elphick, C.; Repaux, D. Nature of spatial chaos. Phys. Rev. Lett. 1987, 58, 431–434. [Google Scholar] [CrossRef] [PubMed]
- Ilati, M.; Dehghan, M. Direct local boundary integral equation method for numerical solution of extended Fisher-Kolmogorov equation. Eng. Comput-Germany. 2018, 34, 203–213. [Google Scholar] [CrossRef]
- Liu,F.N.; Zhao, X.P.; Liu, B. Fourier pseudo-spectral method for the extended Fisher-Kolmogorov equation in two dimensions. Adv. Differ. Equ-Ny. 2017, 2017, 1–17.
- Bashan, A.; Ucar, Y.; Yagmurlu, N.M.; Esen, A. Numerical solutions for the fourth order extended Fisher-Kolmogorov equation with high accuracy by differential quadrature method. Sigma. J. Eng. Nat. Sci. 2018, 9, 273–284. [Google Scholar]
- Awasthi, A. Polynomial based differential quadrature methods for the numerical solution of fisher and extended Fisher-Kolmogorov equations. Int. J. Appl. Comput. Math. 2017, 3, 665–677. [Google Scholar]
- Li, S.G.; Xu, D.; Zhang, J.; Sun, C.J. A new three-level fourth-order compact finite difference scheme for the extended Fisher-Kolmogorov equation. Appl. Numer. Math. 2022, 178, 41–51. [Google Scholar] [CrossRef]
- Qiao, L.; Nikan, O.; Avazzadeh, Z. Some efficient numerical schemes for approximating the nonlinear two-space dimensional extended Fisher-Kolmogorov equation. Appl. Numer. Math. 2023, 185, 466–482. [Google Scholar] [CrossRef]
- Kadri, T.; Omrani, K. A fourth-order accurate finite difference scheme for the extended-Fisher-Kolmogorov equation. Bull. Korean Math. Soc. 2018, 55, 297–310. [Google Scholar]
- Ismail, K.; Atouani, N.; Omrani, K. A three-level linearized high-order accuracy difference scheme for the extended Fisher-Kolmogorov equation. Eng. Comput-Germany. 2021, 2, 1–11. [Google Scholar] [CrossRef]
- He, D.D. On the L∞-norm convergence of a three-level linearly implicit finite difference method for the extended Fisher-Kolmogorov equation in both 1D and 2D, Comput. Math. Appl., 2016, 71, 2594–2607. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Elsakout, D.M.; Muttardi, M.M. Numerical solution for stochastic extended Fisher-Kolmogorov equation. Chaos, Solitons and Fractals. 2021, 151, 111213.
- Danumjaya, P.; Pani, A.K. Mixed finite element methods for a fourth order reaction diffusion equation. Numer. Meth. Part. D. E. 2012, 28, 1227–1251. [Google Scholar] [CrossRef]
- Doss, L.J.T.; Nandini, A.P. An H1-Galerkin mixed finite element method for the extended Fisher-Kolmogorov equation. Int. J. Numer. Anal. Model. Ser. B. 2012, 3, 460–485. [Google Scholar]
- Wang, J.F.; Li, H.; He, S.; Gao, W.; Liu, Y. A new linearized Crank-Nicolson mixed element scheme for the extended Fisher-Kolmogorov equation. The Scientific World Journal. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.Z.; Zhang, X.H. A reduced fourth-order compact difference scheme based on a proper orthogonal decomposition technique for parabolic equations. Bound. Value. Probl. 2019, 130. [Google Scholar] [CrossRef]
- Xu, B.Z.; Zhang, X.H.; Ji, D.B. A reduced high-order compact finite difference scheme based on POD technique for the two dimensional extended Fisher-Kolmogorov equation. IAENG Int. J. Appl. Math. 2020, 50. [Google Scholar]
- Luo, Z.D.; Teng, F. A reduced-order extrapolated finite difference iterative scheme based on POD method for 2D Sobolev equation. Appl. Math. Comput. 2018, 329, 374–383. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. A reduced-order Schwarz domain decomposition method based on POD for the convection-diffusion equation. Comput. Math. Appl. 2024, 160, 60–69. [Google Scholar] [CrossRef]
- Luo, Z.D.; Teng, F.; Xia, H. A reduced-order extrapolated Crank-Nicolson finite spectral element method based on POD for the 2D non-stationary Boussinesq equations. J. Math. Anal. Appl. 2019, 471, 564–583. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jiang, W.R. A reduced-order extrapolated Crank-Nicolson finite spectral element method for the 2D non-stationary Navier-Stokes equations about vorticity-stream functions. Appl. Numer. Math. 2020, 147, 161–173. [Google Scholar] [CrossRef]
- Luo, Z.D.; Li, L.; Sun, P. A reduced-order MFE formulation based on POD method for parabolic equations. Acta. Math. Sci. 2013, 33B, 1471–1484. [Google Scholar] [CrossRef]
- Liu, Q.; Teng, F.; Luo, Z. A reduced-order extrapolation algorithm based on CNLSMFE formulation and POD technique for two-dimensional Sobolev equations. Appl. Math. J. Chinese Univ. 2014, 29, 171–182. [Google Scholar] [CrossRef]
- Luo, Z.D.; Zhou, Y.J.; Yang, X.Z. A reduced finite element formulation based on proper orthogonal decomposition for Burgers equation. Appl. Numer. Math. 2009, 59, 1933–1946. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. A reduced-order characteristic finite element method based on POD for optimal control problem governed by convection-diffusion equation. Comput. Meth. Appl. M. 2022, 391, 114538. [Google Scholar] [CrossRef]
- Song, J.P.; Rui, H.X. Reduced-order finite element approximation based on POD for the parabolic optimal control problem. Numer. Algorithms. 2024, 95, 1189–1211. [Google Scholar] [CrossRef]
- Luo, Z.D. A POD-based reduced-order stabilized Crank-Nicolson MFE formulation for the Non-Stationary parabolized Navier-Stokes equations. Math. Model. Anal. 2015, 20, 346–368. [Google Scholar] [CrossRef]
- Luo, Z.D. A POD-based reduced-order TSCFE extrapolation iterative format for two-dimensional heat equations. Bound. Value Probl. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Luo, Z.D. The reduced-order extrapolating method about the Crank-Nicolson finite element solution coefficient vectors for parabolic type equation. Mathematics. 2020, 8, 1261. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Luo, Z.D. The reduced-dimension technique for the unknown solution coefficient vectors in the Crank-Nicolson finite element method for the Sobolev equation. J. Math. Anal. Appl. 2022, 513, 126207. [Google Scholar] [CrossRef]
- Teng, F.; Luo, Z.D. A reduced-order extrapolation technique for solution coefficient vectors in the mixed finite element method for the 2D nonlinear Rosenau equation. J. Math. Anal. Appl. 2020, 485, 123761. [Google Scholar] [CrossRef]
- Luo, Z.D. The dimensionality reduction of Crank-Nicolson mixed finite element solution coefficient vectors for the unsteady Stokes equation. Mathematics. 2022, 10, 2273. [Google Scholar] [CrossRef]
- Li, Y.J.; Teng, F.; Zeng, Y.H.; Luo, Z.D. Two-grid dimension reduction method of Crank-Nicolson mixed finite element solution coefficient vectors for the fourth-order extended Fisher-Kolmogorov equation. J. Math. Anal. Appl. 2024, 536, 128168. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Li, Y.J.; Zeng, Y.T.; Cai, Y.H.; Luo, Z.D. The dimension reduction method of two-grid Crank-Nicolson mixed finite element solution coefficient vectors for nonlinear fourth-order reaction diffusion equation with temporal fractional derivative. Commun. Nonlinear Sci. 2024, 133, 107962. [Google Scholar] [CrossRef]
- Luo, Z.D.; Yang, J. The reduced-order method of continuous space-time finite element scheme for the non-stationary incompressible flows. J. Comput. Phys. 2022, 456, 111044. [Google Scholar] [CrossRef]
- Luo, Z.D. The founfations and applications of mixed finite element methods; Chinese Science Press: Beijing, China, 2006(in Chinese).
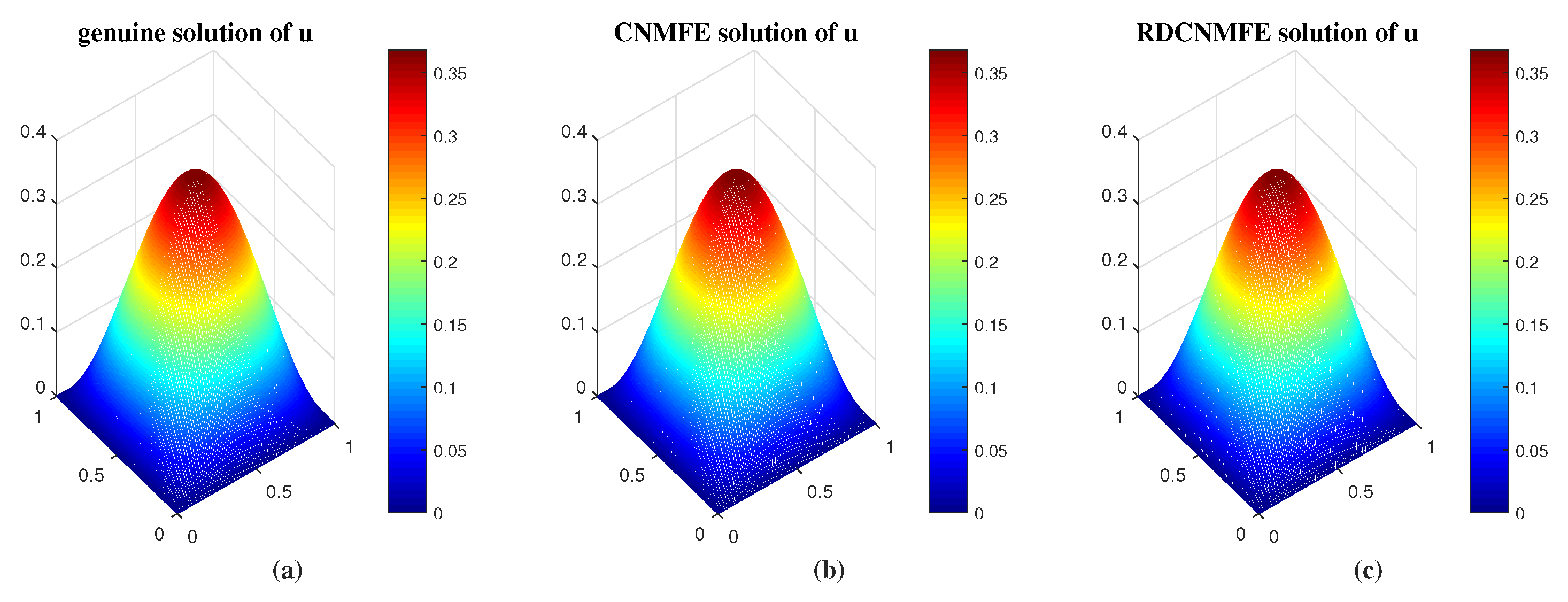
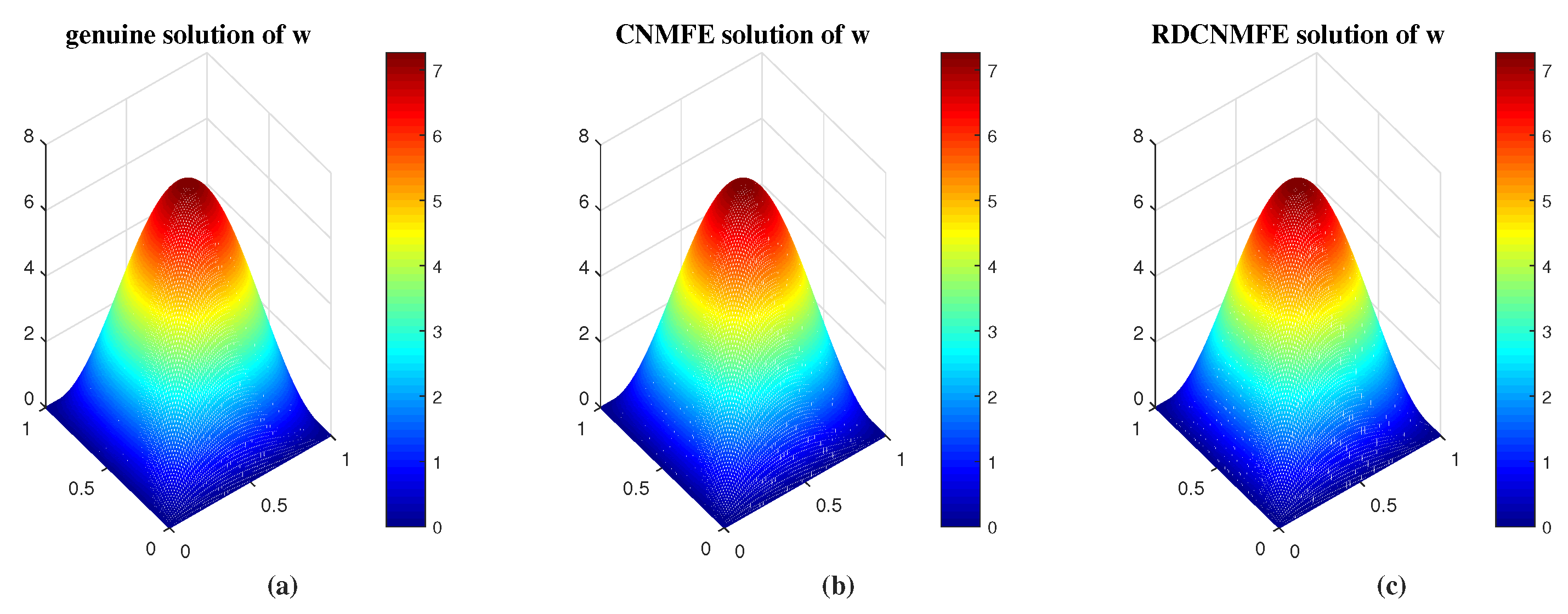

| CNMFE Method | RDCNMFE Method | |||
|---|---|---|---|---|
| Grid | Order | Order | ||
| 3.0742e-03 | – | 3.0742e-03 | – | |
| 7.5577e-04 | 2.0242 | 7.5577e-04 | 2.0242 | |
| 1.7251e-04 | 2.1313 | 1.7251e-04 | 2.1313 | |
| 2.7256e-05 | 2.6620 | 2.7274e-05 | 2.6611 | |
| CNMFE Method | RDCNMFE Method | |||
|---|---|---|---|---|
| Grid | Order | Order | ||
| 1.0990e-01 | – | 1.0990e-01 | – | |
| 2.7344e-02 | 2.0068 | 2.7344e-02 | 2.0068 | |
| 6.5061e-03 | 2.0714 | 6.5069e-03 | 2.0712 | |
| 1.2863e-03 | 2.3385 | 1.2901e-03 | 2.3345 | |
| CNMFE Method | RDCNMFE Method | |||||
|---|---|---|---|---|---|---|
| Real time | CPU runtime(s) | CPU runtime(s) | ||||
| 2.7256e-05 | 1.2863e-03 | 224.368 | 2.7274e-05 | 1.2901e-03 | 4.410 | |
| 2.5421e-05 | 1.4650e-03 | 260.357 | 4.7928e-05 | 1.4653e-03 | 4.545 | |
| 1.7506e-05 | 1.4287e-03 | 285.453 | 1.7724e-05 | 1.4523e-03 | 4.635 | |
| 1.1089e-05 | 1.3743e-03 | 311.536 | 1.5943e-05 | 1.6888e-03 | 4.678 | |
| 6.8308e-06 | 1.3343e-03 | 342.801 | 6.8312e-06 | 1.3403e-03 | 4.919 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





