1. Introduction
Relaxation phenomena in a electrolytic cell submitted to a step-like electric field are usually investigated using the Poisson-Nernst-Planck model, which is based on the continuity equations and Poisson’s equation that relates the electric field to the electric charge of ionic origin. The generation-recombination term [
1] in the continuity equations is usually considered in the determination of the impedance spectroscopy of cells subjected to periodic excitations of small amplitude [
2,
3,
4,
5]. However, it is neglected in the analysis of relaxation phenomena in electrolytic cells subjected to a step-like external electric field. The goal of the present paper is to investigate the role of the generation-recombination term in the dielectric relaxation phenomenon of an electrolytic cell limited by blocking electrodes. We assume that ions are generated through the decomposition of neutral particles via the reaction mechanism
, with dissociation and recombination coefficients as described in standard kinetic models. The reaction could be optically induced, as in semiconductors, or driven by another external energy source. Our focus is on the relaxation of the electric current in the circuit, which is the quantity experimentally observable. The paper is organized as follows: In Sect.II the time dependence of the bulk ion density generated by the dissociation of neutral particles is determined. In Sect.III, the time dependence of the Debye length, Debye time and dielectric relaxation time are investigated. Moreover, the validity of the adiabatic approximation is discussed. Section IV is devoted on the analysis of current relaxation in a circuit containing the electrolytic cell limited by blocking electrodes. Finally, the conclusions are reported in Sect.V.
2. Model
Let us consider an insulating liquid containing, at
a uniform distribution of neutral impurities that can produce ions by means of the reaction
. The reaction could be initiated for instance through exposure to light or heat or interaction with another external source of energy. The evolution of the bulk density of the neutral
, positive,
and negative,
, particles is described by the continuity equations [
1]
where
and
are the dissociation and association coefficients respectively. The dissociation coefficient is expected to depend on the energy of the source that induces the decomposition of the neutral particles. In (
1,2,3) the current densities
,
and
are given by
In (
4)
,
,
are the diffusion coefficients of the particles in the insulating liquid,
and
the mobilities of the positive and negative ions respectively, and
the local electric field, related to the bulk densities of ions by the Poisson equation
where
is the dielectric constant of the solvent in which the ions are dispersed. For a thick cell in the shape of a slab, limiting our analysis to an infinite medium in equilibrium, the drift diffusion phenomena can be neglected. In this case the medium is globally and locally electrically neutral. Therefore, assuming
and writing
, (
1,2,3), are cast in the form
We assume that for
the impurities have an initial bulk density
, and that the system evolves towards an equilibrium state as
, under the effect of the external source inducing the decomposition of the neutral particles. This implies that
From (
6,7) it follows that
Consequently, from (7) we get
By substituting (
10) into (
6) we obtain
from the latter it follows that the quantity
is time independent. Hence, for (
8), the integration constant
c can be expressed in terms of the equilibrium value of
p, denoted by
P. We have
and the ordinary differential equation (
12) becomes
Integrating (
14) with the initial condition
, we obtain
where the relaxation time
is given by
The bulk densities of the neutral particles and ions in the equilibrium state,
N and
P respectively, are given by (
6,7). Taking into account the condition
, these equations can be rewritten as
with the solution
The relaxation time (
16), in terms of the dissociation and association coefficients
and
is expressed as
In the framework of the present model, the dissociation parameter, defined by
, is
It is possible to express
and
in terms of
and
. A simple calculation gives
In term of
and
the time evolution of the ionic density is
The time evolution of the neutral particles (not dissociated) is given by
, and by means of (
23) it is found to be
It could be of some interest the time
for which
. A simple calculation gives
from which it follows that
exists only if
, as expected. In
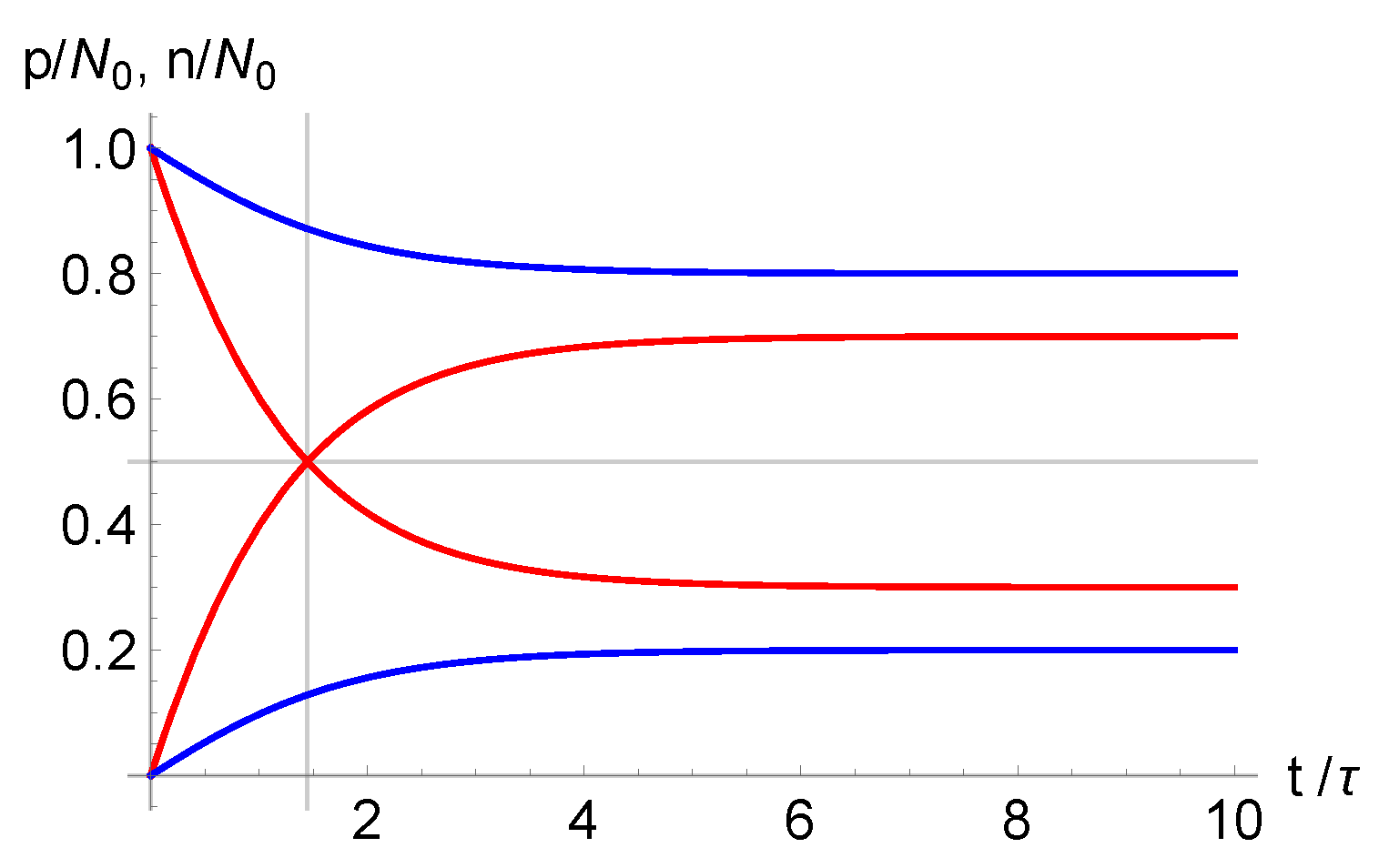
Figure 1 it is shown the time dependence of
and
for
and
, and the same
.
3. Debye Length and Dielectric Relaxation Time
The Debye length [
6] for the simple case of a single type of mobile ions with bulk density,
p, is defined as
, where
is the thermal voltage. In standard problems,
is of the order of the thickness of the layer where the ions are confined when the cell is subjected to a small external potential difference, of the order of
. The Debye relaxation time is defined by
and the dielectric relaxation time [
7] by
. The quantity
is related to the relaxation of the initial distribution of ions, under the effect of the external field, and it is rather important for applications. In the case under consideration, since
these quantities are time dependent. We indicate by
and rewrite (
23) as
. The quantities of interest are
where
are the usual quantities evaluated for the equilibrium density of mobile ions at equilibrium,
P.
The bulk density of mobile ions,
, changes with time
t with a characteristic time
, and their confinement with
[
8,
9,
10]. If
, the system follows adiabatically the variation of
. This implies that
p can be treated as time-independent in the analysis. This assumption is valid for
where
In the case in which
,
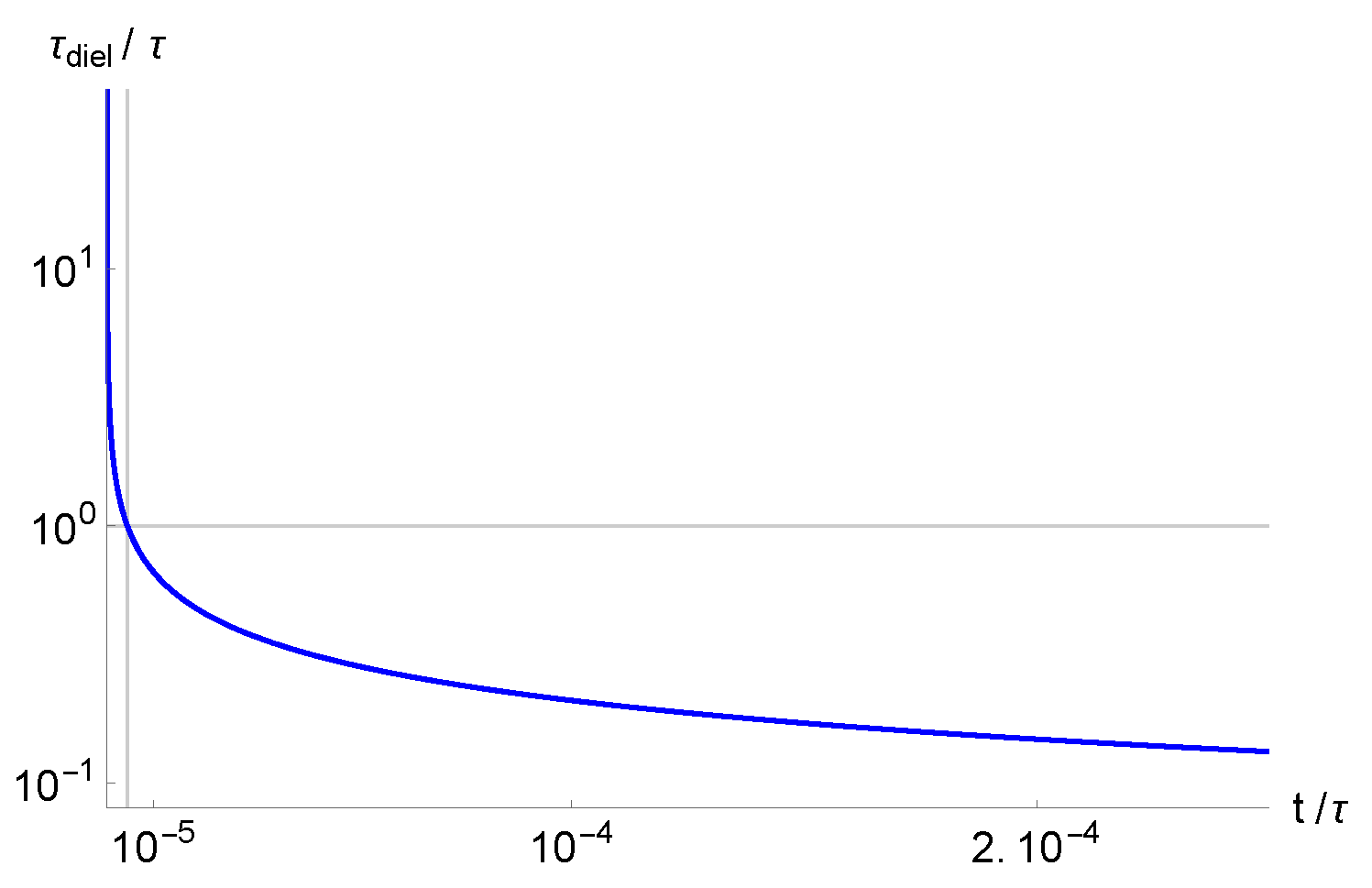
is very small, and the adiabatic approximation can be used for the analysis of the relaxation phenomena in a real system. In
Figure 2 is shown the time dependence of the dielectric relaxation time in the presence of the considered generation-recombination term.
4. Electric Current Relaxation in a Cell Limited by Blocking Electrodes
We recently investigated the dielectric relaxation in an electrolytic cell limited by blocking electrodes [
11] containing a bulk density of impurities that are completely dissociated. According to the analysis presented in [
11], when the cell is subjected to a small dc external potential difference of amplitude
, the equations of the Poisson-Nernst-Planck model can be linearized. The equilibrium distributions are practically reached after a few relaxation times,
. In particular, the electric potential profiles tends to
For
, the time dependence of the potential profile is well described by
In the adiabatic approximation, (
30) and (
31) remain valid, but it is necessary to replace
and
with
and
given by (
27). It follows that
depends on
t directly, and via the quantities
and
. In the external circuit, if the electrodes are blocking, the electric current is just a displacement current, related to the time variation of the surface electric field
. From (
30) the profile of the electric field is given by
In particular the surface electric field is
The related displacement current is then
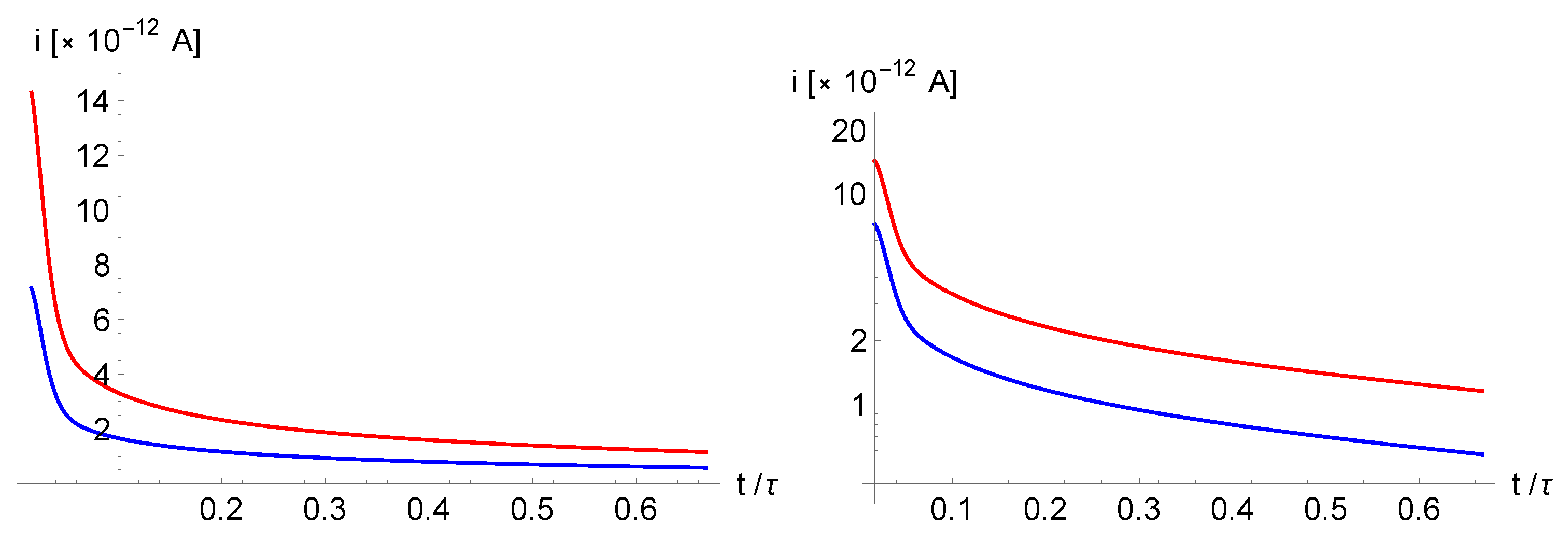
In
Figure 3a is shown the time dependence of the electric current in the external circuit containing the electrolytic cell. As evident from
Figure 3a, the current dependence is characterized by a short relaxation time associated with dielectric relaxation and a long relaxation time related to the generation-recombination term
. For
, an apparent plateau is observed. The values of the corresponding currents are proportional to the applied potential difference, as evident from Eq.s(
33,
34).
5. Conclusions
We have investigated the role of the generation-recombination term in the dielectric relaxation of an electrolytic cell with blocking electrodes. In our analysis, we assumed that the characteristic time of the chemical reaction, which describes the decomposition of the neutral particles that generate the ions, is much longer than the dielectric relaxation time corresponding to the equilibrium state. Within this framework, the adiabatic approximation, in which the system is always considered to be very close to equilibrium for a given ion density, we have evaluated the electric field profile and the corresponding displacement current. This current originates from the time variation of both the bulk ion density and the dielectric relaxation time. According to our results, the time relaxation of the electric current in the external circuit is characterized by two relaxation times, which are significantly different from each other and are related to the two different sources of the current.
References
- J. Ross Macdonald, Phys. Rev. 92, 4 (1953).
- G. Barbero and I. Lelidis, J. Phys. Chem. B 115, 3496 (2011).
- J. Bisquert, J. Phys. Chem. B 106, 325 (2002).
- F. Fabregat-Santiago, G. Garcia-Belmonte, J. Bisquert, A. Zaban, and P. Salvador, J. Phys. Chem. B 106, 334 (2002).
- I. Lelidis, G. Barbero, A. Sfarna, J. Chem. Phys. 137, 154104 (2012).
- P. W. Atkins, "Physical Chemistry" 5th. ed. (Oxford University Press, Oxford, U.K., 1994).
- M. Z. Bazant, K. Thorton, A. Adjadari, Phys. Rev. E 70, 021506 (2004).
- R. J. Hunter, "Foundations of Colloidal Science", 2nd. ed. (Oxford University Press, Oxford, U.K., 2000).
- W. B. Russel, D. Saville, and W. R. Schowalter, "Colloidal Dispersions" (Cambridge University Press, Cambridge, England, 1989).
- J. Lyklema, "Fundamentals of Interface and Colloid Science" (Academic, New York, 1995), Vol. 2.
- I. Lelidis, A. L. Alexe-Ionescu, G. Barbero, J. Phys. Chem. C 128, 949 (2024).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).