Higgs Physics at Muon Collider

1. Introduction

The discovery of the Higgs boson at the Large Hadron Collider (LHC) confirmed the mechanism of electroweak symmetry breaking and mass generation in the Standard Model (SM). While the measured properties of the Higgs boson are consistent with SM predictions, significant open questions remain. These include the exact nature of the Higgs potential, the strength of its self-couplings, and the potential presence of new physics beyond the SM. The couplings of the Higgs boson with SM particles have been measured at the LHC, but achieving sub-percent precision is essential to explore potential deviations from the SM [1]. Furthermore, the trilinear (${\lambda }_3$) and quadrilinear (${\lambda }_4$) Higgs self-couplings, which are critical for probing the Higgs potential, cannot be observed in current experiments due to the low cross section of multi-Higgs processes [2]. At a multi-TeV Muon Collider, a significant number of Higgs bosons, summarized in Table 1, could be produced through $WW$ fusion in the process $\mu \mu \to H\nu \nu$ enabling detailed studies of their couplings. Moreover processes such as $\mu \mu \to HH\nu \nu$ and $\mu \mu \to HHH\nu \nu$ could be observed to measure ${\lambda }_3$ and ${\lambda }_4$ [3].

Thus, the Muon Collider provides a unique opportunity to meet the physics requirements for next generation particle accelerators. It combines the clean environment of a lepton machine with the capability of reaching very high collision energies as a hadron machine, thanks to the low synchrotron radiation losses of muon beams. However, the unstable nature of the muon introduces several technical challenges that must be addressed for both the machine and detectors to establish the feasibility of such a collider.

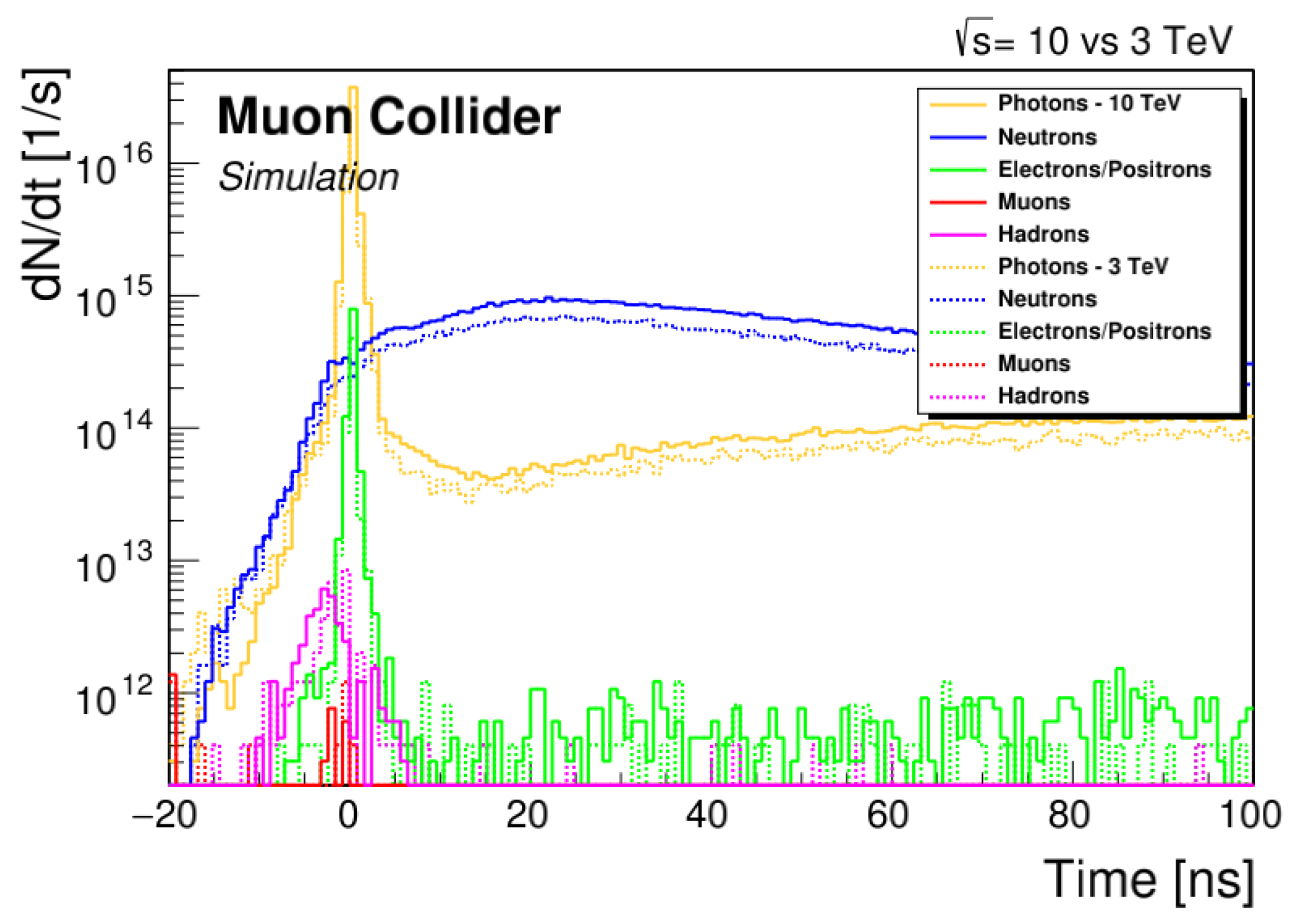
2. Beam-Induced Background (BIB)

One of the primary challenges associated with the Muon Collider arises from the intrinsic instability of muons. They decay in the beam pipe, and the resulting decay products interact with the collider components, generating a flux of photons, neutrons, and charged particles that reach the detector, known as Beam-Induced Background (BIB) [4]. Effective mitigation strategies are essential to reduce BIB and ensure the desired detector performance and measurement accuracy. These include both hardware and software approaches. In particular in the Machine-Detector Interface (MDI) design includes two tungsten, cone-shaped shielding (nozzles) located along the beamline inside the detector area to minimize the number and the energy of the incoming particles. Moreover, the reconstruction algorithm will be tuned to handle the combinatorial noise coming from the BIB, exploiting advanced 5D sensors, which are capable of measuring energy, position, and timing with very high resolution. In particular, the time of arrival in the detector is a crucial information since a large fraction of BIB is asynchronous to the bunch crossing, as shown in Figure 1. A prototype detector design, along with specialized reconstruction algorithms, has already been developed for a Muon Collider at $3TeV$[5,6]. The detector and MDI optimization for the $10TeV$ case is in progress [7].

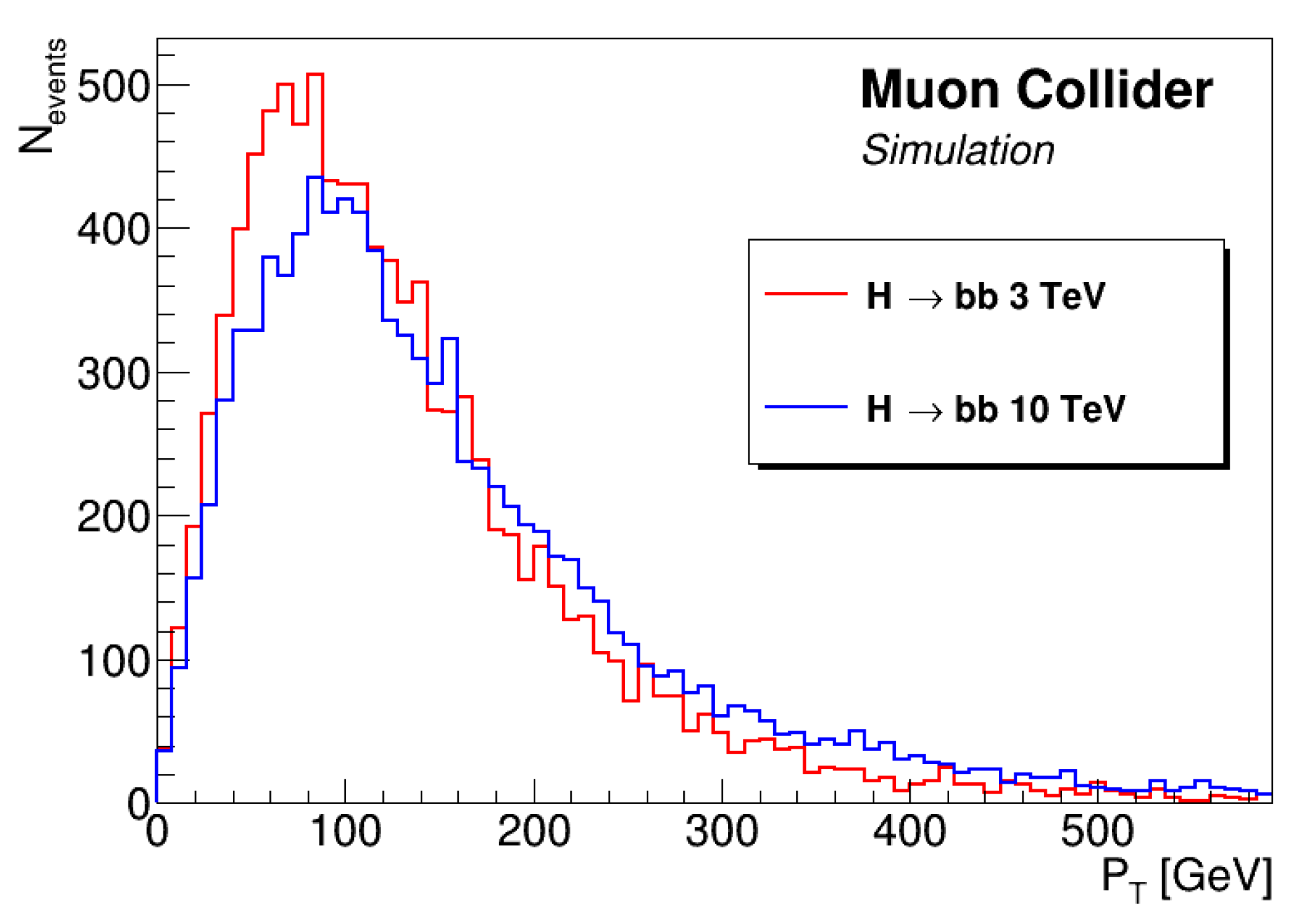
3. Higgs Cross Section

This section presents the sensitivity estimates for measuring the cross-sections of Higgs boson decays into various channels at a center-of-mass energy of $\sqrt{s}=3TeV$ at a Muon Collider. The analysis was conducted following these steps:

• Monte Carlo Event Generation: The Higgs decay modes considered in this study include:

  -

  $H\to b\overline{b}$,

  -

  $H\to W{W}^{*}$,

  -

  $H\to Z{Z}^{*}$,

  -

  $H\to {\mu }^{+}{\mu }^{-}$,

  -

  $H\to \gamma \gamma$.

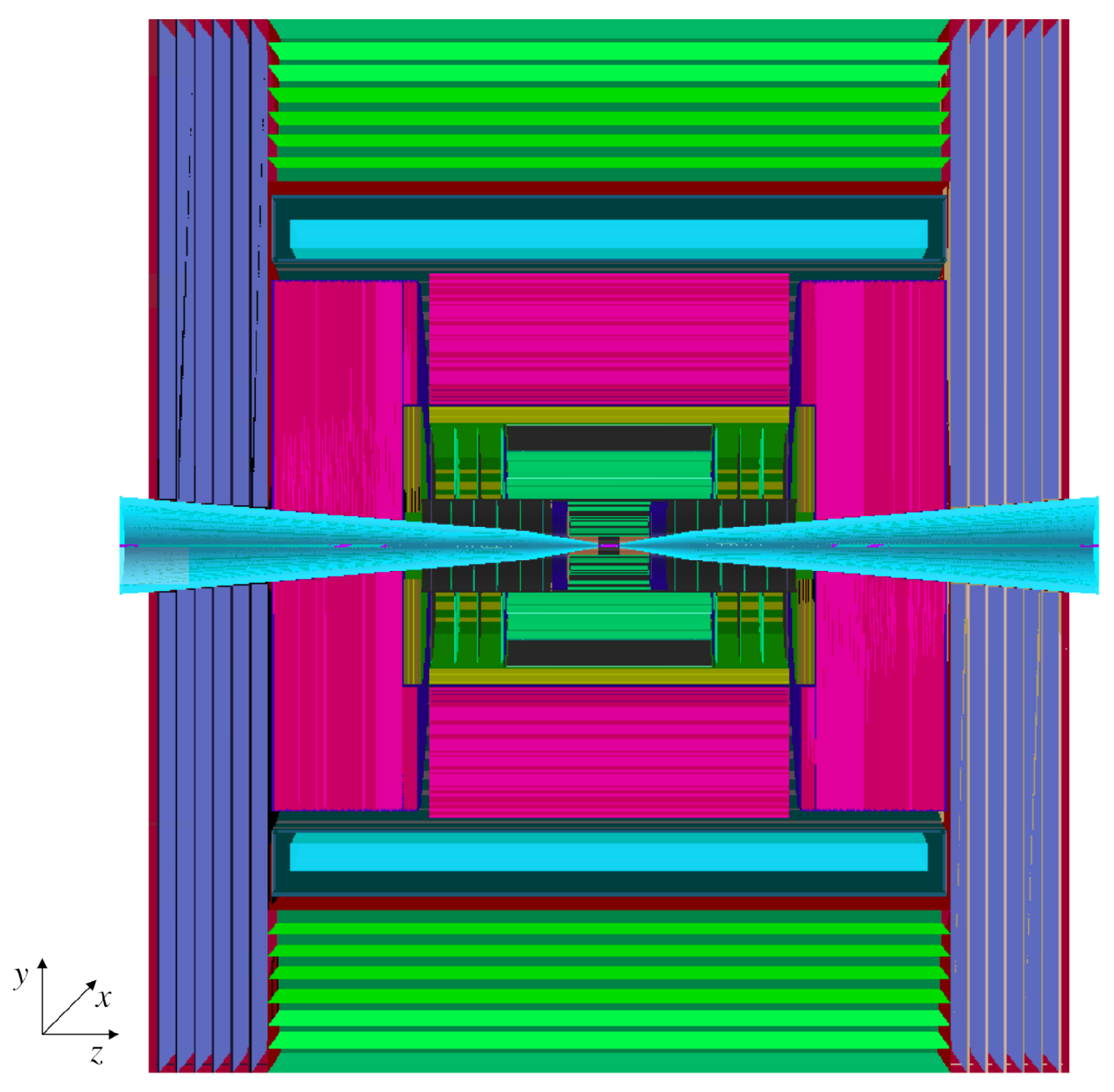
  Signal events were generated at leading order using the Monte Carlo event generators MadGraph5_aMC@NLO [8] (referred to hereafter as MadGraph) and WHIZARD2[9]. Particle showering and hadronization were handled with PYTHIA version 8.200. For each decay mode, the corresponding background processes were also simulated. The complete list of generated samples is provided in Appendix A.
• Detector Simulation: A detailed detector simulation was carried out using GEANT4[10]. The detector incorporates advanced silicon-based tracking systems, electromagnetic and hadronic calorimeters, and operates within a 3.57 T magnetic field. Beam-Induced Background (BIB) was overlaid at the hit level, and digitization was applied to simulate sensor responses with realistic timing and spatial resolutions. The detector model is shown in Figure 2.
• Full Event Reconstruction: Physics objects were reconstructed using algorithms adapted from the iLCSoft framework[11], including the PandoraPFA package[12] for particle flow techniques. The reconstruction algorithms were optimized to mitigate BIB effects. Additional details can be found in [13].
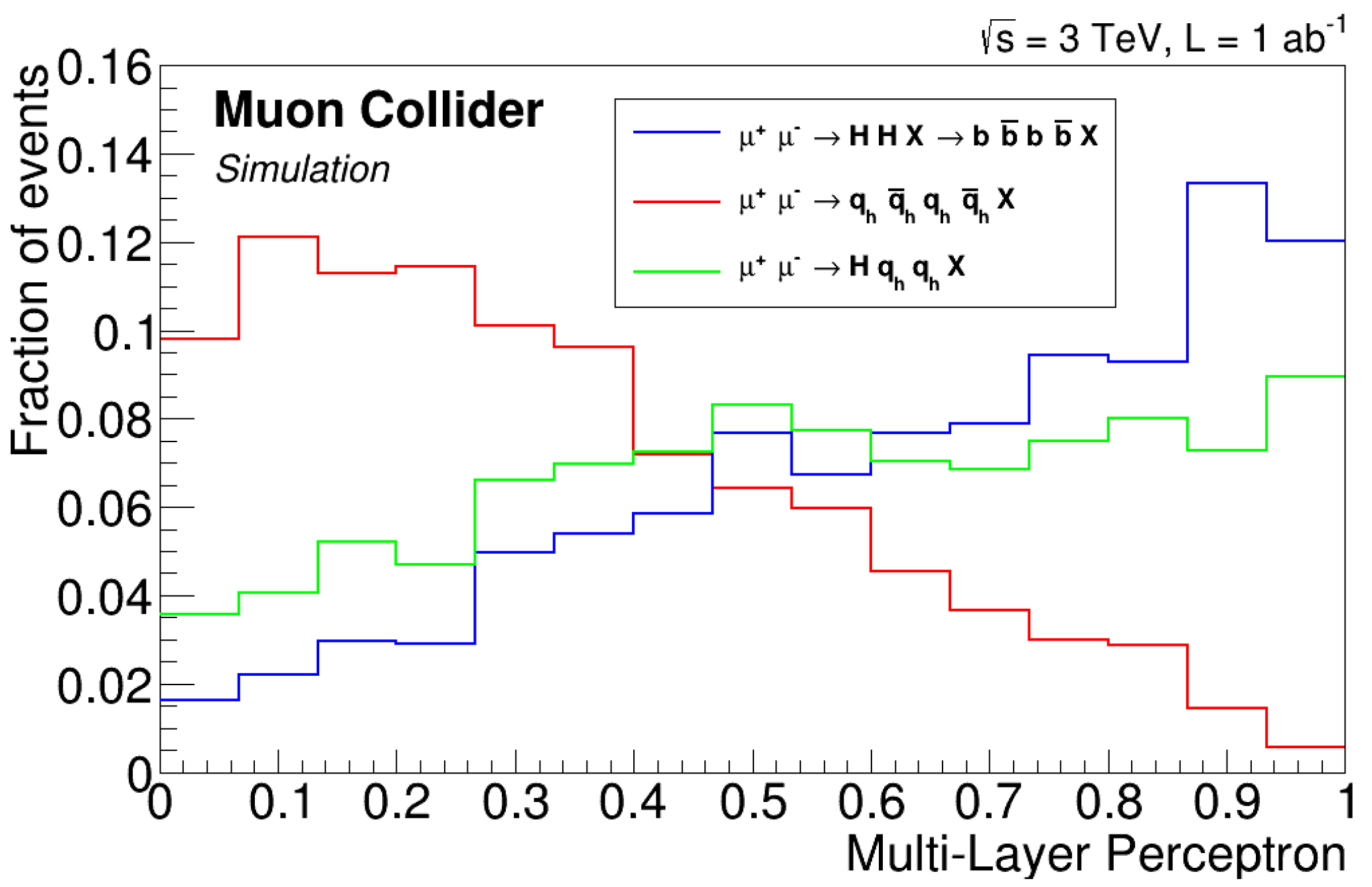
• Determination of the Sensitivity: The sensitivity on the cross-section for each Higgs decay mode was derived from the sensitivity on the number of events using the relation:

  $$N_{\mathrm{events}}=\mathcal{L}·ϵ·\sigma$$

  (1)

  where $\mathcal{L}$ is the luminosity, $ϵ$ is the efficiency, and $\sigma$ is the cross-section. The sensitivity on $\sigma$ was determined by propagating the sensitivity on the number of events, assuming negligible uncertainties on the luminosity and efficiency.
  For $H\to b\overline{b}$, the cross-section was determined by fitting the di-jet invariant mass distributions of signal and background using double-Gaussian functions to model the signal and background. A likelihood function was constructed with these models, and an unbinned maximum-likelihood fit was performed on pseudo-data. The signal and background yields were allowed to float to extract the $H\to b\overline{b}$ yield and its uncertainty. The uncertainty on the cross-section was estimated by averaging over several pseudo-experiments. The result is shown in Table 2.
  For the other signals considered in this study, the statistical sensitivity on the cross-section was determined using a counting experiment. Assuming negligible uncertainties on the efficiency and integrated luminosity, the relative error on $\sigma$ is given by:

  $${\displaystyle \frac{\Delta \sigma }{\sigma }}={\displaystyle \frac{\sqrt{S+B}}{S}}$$

  (2)

  where S and B are the expected numbers of signal and background events, respectively. To maximize the signal-to-background ratio, machine learning algorithms such as Boosted Decision Trees (BDTs)[14] and Multi-Layer Perceptrons (MLPs)[15] were trained on physical observables specific to each signal process and used as discriminators. The results are presented in Table 2. The table also includes results obtained with fast simulation performed with Delphes cards[16] without incorporating BIB[17]. The two estimates are in very good agreement, indicating that BIB effects on physics performance are manageable.

4. Double Higgs Cross Section

Double Higgs events will be produced at a Muon Collider through processes reported in Figure 3.

Following the procedure outlined in Section 3, the expected precision on the measurement of the double Higgs boson production cross section has been estimated. For this analysis, only the $H\to b\overline{b}$ decay channel has been considered for both Higgs bosons, given the limited contribution from other decay modes [18,19]. However, further studies will include additional channels such as $HH\to b\overline{b}{W}^{+}{W}^{-}$ and $HH\to b\overline{b}{\tau }^{+}{\tau }^{-}$.

The reconstruction of $HH$ events begins by forming all possible two-jet combinations, requiring at least one jet in each pair to be tagged as a b-jet. Higgs boson candidates are identified by selecting the jet pairs whose invariant masses, $m_{12}$ and $m_{34}$, minimize the figure of merit:

$$F=\sqrt{{(m_{12}-m_H)}^2+{(m_{34}-m_H)}^2},$$

(3)

where $m_H$ is the known Higgs boson mass.

The primary background in this analysis arises from processes that produce four heavy-quark jets ($q_h{\overline{q}}_h{q}_h{\overline{q}}_h$), predominantly through the decay of intermediate electroweak gauge bosons. Another significant background stems from ${\mu }^{+}{\mu }^{-}\to H{q}_h{\overline{q}}_{h}X\to b\overline{b}{q}_h{\overline{q}}_{h}X$, where single Higgs production mimics the signal but lacks the trilinear Higgs coupling.

To suppress these backgrounds, advanced tagging algorithms are used, and light-quark jets or fake jets are assumed to be negligible due to effective vetoing techniques based on jet substructure and machine learning methods. To enhance the separation of the $HH$ signal from the background, a MLP is trained using the following observables:

• The invariant masses of the two jet pairs;
• The magnitude of the vector sum of the four jet momenta;
• The total energy of the four jets;
• The angle between the two jet pairs relative to the leading candidate;
• The maximum separation angle between jets in the event;
• The angles between the highest-$p_{\mathrm{T}}$ jet in the pair and the leading and sub-leading candidates with respect to the z-axis;
• The transverse momenta of the four jets.

The output of the MLP is shown in Figure 4, demonstrating clear separation between the $HH$ signal and the dominant $q_h{\overline{q}}_h{q}_h{\overline{q}}_{h}X$ background.

Using the MLP output, pseudo-datasets were generated based on the expected event yields. The $HH$ signal yield was extracted by fitting the MLP distribution. Averaging over pseudo-experiments yielded an uncertainty of $33\%$.

Since the cross section is directly proportional to the signal yield as described in Eq. 1, and uncertainties in efficiency and luminosity are considered negligible, the sensitivity to the cross section is given by:

$${\displaystyle \frac{\Delta \sigma (HH\to b\overline{b}b\overline{b})}{\sigma (HH\to b\overline{b}b\overline{b})}}=33\%.$$

(4)

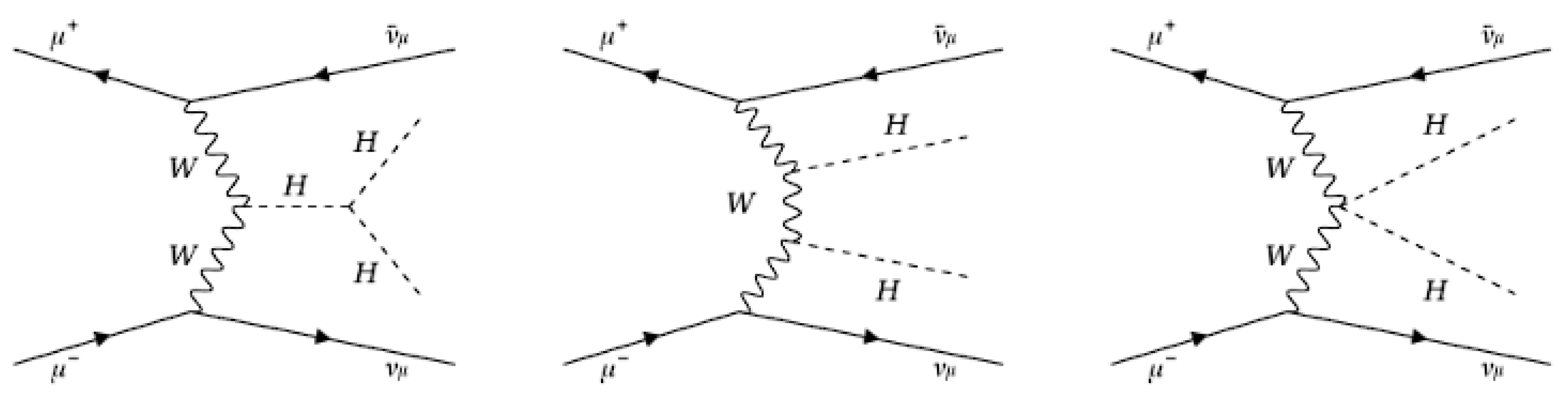
5. Trilinear Higgs Coupling

The double Higgs cross section is sensitive to the ${\lambda }_3$ parameter of the Higgs potential when the production occurs via off-shell Higgs ($H^{*}$). The Feynman diagram of the processes is reported on the left in Figure 3.

In order to estimate the sensitivity on the measurement of ${\lambda }_3$ the following procedure has been adopted:

• Different set of double Higgs events has been generated with WHIZARD varying ${\kappa }_{{\lambda }_3}={\displaystyle \frac{{\lambda }_3}{{\lambda }_3^{SM}}}$ from 0.2 to 1.8 with 0.2 steps.
• The same MLP used in Section 4 has been exploited to separated the SM signal, corresponding to ${\kappa }_{{\lambda }_3}=1$, from physical background.
• A second MLP has been trained to separate the double Higgs processes via $H^{*}$ from the other two. The observables considered to perform the discrimination were: the angle between the two Higgs boson momenta in the laboratory frame, the angle between the highest-$p_T$ jet momenta of each pair with respect to the z axis, and the helicity angle of the two Higgs boson candidates.
• The scores of the two MLPs for the considered samples have been arranged in 2-dimensional histograms. To obtain the expected data distribution, 2-dimensional templates of the signal and background components are built for each ${\kappa }_{{\lambda }_3}$ hypothesis.
• Pseudo-datasets are generated with the total 2D template for the ${\kappa }_{{\lambda }_3}=1$ hypothesis. For each pseudo-experiment, the likelihood difference $-\Delta \log \left(L\right)$ is calculated as a function of ${\kappa }_{{\lambda }_3}$ by comparing the pseudo-data distribution to the ${\kappa }_{{\lambda }_3}$ templates.
• The log-likelihood profile has been fitted with a polynomial function of fourth degree. The uncertainty on ${\kappa }_{{\lambda }_3}$ at 68% Confidence Level (C.L.) is estimated as the interval around ${\kappa }_{{\lambda }_3}=1$ where the fitted polynomial has a value below 0.5.

The result obtained with the current algorithms, does not provide an adequate representation of the true potential of Muon Collider for this measurement. However, realistic assumption has been made on the jet tagging efficiency and energy resolution to estimate the uncertainty on the trilinear Higgs self-coupling ${\lambda }_3$. Considering a $76\%$b-tagging efficiency, a $20\%c$-mistag rate and a $10\%$ jet momentum resolution the likelihood scan reported in Figure 5 has been obtained, resulting in sensitivity on ${\kappa }_{{\lambda }_3}$ of

$$0.81<{\kappa }_{{\lambda }_3}<1.44,68\%C.L.$$

(5)

Further details about the assumption of the reconstruction algorithm can be found in [13]. This result is compatible with previous studies performed with fast simulation[20]:

$$0.73<{\kappa }_{{\lambda }_3}<1.35,68\%C.L.$$

(6)

6. Conclusions

The results presented in this study demonstrate the potential of the Muon Collider operating at a center-of-mass energy of $\sqrt{s}=3TeV$ to probe the Higgs sector of the Standard Model with high precision. The agreement between the results obtained using full detector simulations, which account for realistic Beam-Induced Backgrounds, and those derived from fast simulations at $\sqrt{s}=3TeV$ supports the validity of the fast simulation methodology.

This consistency allows us to assume that the results from fast simulations for the $\sqrt{s}=10TeV$ Muon Collider, shown in Figure 6, provide a realistic representation of its potential. In particular, the $\sqrt{s}=3TeV$ case has been considered as a proof of concept for multi-TeV stages. At $\sqrt{s}=10TeV$, objects are more boosted towards the forward region, however, the transverse momentum distribution of objects such as the Higgs boson remains rather similar between $\sqrt{s}=3TeV$ and $\sqrt{s}=10TeV$, as shown in Figure 7. This similarity further supports the reliability of fast simulation results for the 10 TeV Muon Collider. The $\sqrt{s}=10TeV$ machine emerges as one of the most promising facilities for advancing Higgs boson studies and achieving precision measurements of its properties.

Ongoing efforts are focused on optimizing the detector design and the MDI for the $10TeV$ machine. These optimizations will ensure enhanced performance, and detailed results are anticipated to be published by 2025.