2. Equations
These laws want to explain the results of the final derivation process of this research and what this research wants to prove.
(1)
Where Gµν represents the Einstein tensor, G is the universal gravitational constant, Tµν is the energy-momentum tensor, is the wavelength is (nm), is the photon energy is in electron volt, n is the energy level.
Where k represents the wave vector.
Where
represents the reduced Planck constant, rn is the Bohr radius, En is the photon energy is in joules, is the Planck time, is the Planck length. This law explains the final result of the derivation. This law proves the creation of a relationship that links the photon energy and curvature of space-time.
Where
represents the Planck energy.
(5)
The precise structure constant links the speed of the electron to the speed of light through this law.
Likewise, it affects energy in relativity and makes it the total energy of the photon.
(6)
Where E represents the energy, h( a) is the atomic constant, KE is the kinetic energy, P is the momentum, is the angular velocity, C is the speed of light, is the Phase Velocity, and is the fine-structure constant. This law explains the final result of the derivation. This law proves the creation of a relationship that links energy and kinetic energy. That the lost kinetic energy comes out in the form of radiant energy.
(7)
Where
represents the Planck acceleration,
is the Planck energy. This law explains the final result of the derivation. This law proves the creation of a relationship that links the Planck energy and curvature of space-time.
(8)
Where ε0 represents the vacuum permittivity, is the Vacuum permeability, is the electron charge. This law works to link the constants ( gravity, electron charge and Planck constant ) into one law.
(9)
This is a law that links the constants ( gravity, electron charge and speed ) into one law.
(10)
Where represents the multiverse constant,
is the fine-structure constant. This law wants to prove is the creation of a relationship that links the curvature of space-time and the energy of the total photon.
This law affects the Planck constant and the charge of the electron.
Where Vacuum permeability, is the Planck length, is the .
(13)
Where represents the Planck constant,
is the frequency.
(14)
Where represents the Planck mass.
(15)
These equations represent the energy of a photon in electron volts.
These equations represent the modification of Bragg’s law.
k is the wave vector, is the momentum
is the Phase Velocity
k is the wave vector
These equations represent some of the laws that can represent the energy of a photon in relativity in joules.
These equations represent some laws that can represent the Bohr energy, wavelength laws, and Rydberg constant, where the electron energy is in volts and the wavelength is in nanometers.
4. Derivation of Equations
Completing the derivation of the laws resulting from quantum relativity ( quantum world )
This is derivation number 1
This is derivation number 2
k is the wave vector
is the Phase Velocity
This is derivation number 3
This is derivation number 4
This is derivation number 5
k is the wave vector
is the Phase Velocity, General quantitative relativity
This is derivation number 6
k is the wave vector
This is derivation number 7
is the wavelength is (nm), is the photon energy is in electron volt
This is derivation number 8
This is derivation number 9
This is derivation number 10
kE
This is derivation number 11
k is the wave vector
This is derivation number 12
This is derivation number 13
Where represents the Planck mass.
This is derivation number 14
This is derivation number 15
Dirac equation
Ratio of electron mass to Planck mass (David mass )
Where
represents the affine derivative,
is the connection coefficients,
is the partial derivative
This is derivation number 16
This is derivation number 17
This is derivation number 18
This is derivation number 19
Where
represents the Planck force
This is derivation number 20
This is derivation number 21
This is derivation number 22
This is derivation number 23
This is derivation number 24
This is derivation number 25
This is derivation number 26
This is derivation number 27
This is derivation number 28
This is derivation number 29
This is derivation number 30
This is derivation number 31
This is derivation number 32
This is derivation number 33
Bragg’s law
This is derivation number 34
This is derivation number 35
This is derivation number 36
This is derivation number 37
This is derivation number 38
This is derivation number 39
is the Phase Velocity
This is derivation number 40
is the Phase Velocity
This is derivation number 41
These are some equations after removing the speed of light and putting in the phase speed. The phase velocity was included because it became clear from the derivation, I made that from Einstein's perspective on the speed of light he was focusing on the speed of light in a vacuum and did not consider other media such as water which affect the speed of light as Christian Huygens explained it and therefore this had to be into account in the calculations.
6. Results Obtained
This scientific research aims to prove a theory by comparing the practical results of this theory with the original results and making the comparison in a table. We will discuss that here .
My theory is based on introducing the curvature of spacetime into the equation, but quantum mechanics shows that it is not affected by gravity. How to interact with the curvature of spacetime has not yet been proven. As a result, my equations show a way to conduct an experiment that enables direct interaction with the curvature of spacetime. Therefore, this experiment practically proves that quantum mechanics made a mistake in its concept when it showed gravity does not interact with it. How to conduct an experimental experiment to prove the validity of my equations
Steps to conduct the experiment
1) The place where the experiment will take place must be chosen, and it must be at a high altitude, such as Mount Everest because the higher the altitude, the less gravity.
2) The experiment is about creating a quantum leap for the electron so that we can know the emission lines that represent the fingerprint of the element and compare them at different heights. Let us take the example of the hydrogen atom. After knowing the choice of the element, the device that will measure the spectral lines of the element must be taken to Mount Everest, where the experiment will be conducted.
3) We will excite the element keeping all elements constant as energy and the comparison will be between wavelength and curvature of spacetime. The first measurement is at the bottom of the mountain, that is, before climbing the mountain first. Then we measure in the middle of the mountain, then we test at the top of the mountain and compare the atomic spectra. If my theoretical results are correct, there will be skewing of the spectral lines at different heights due to distortion of the fabric of space-time.
4) If we measure atomic spectra, we also measure the Zeeman, Stark, and magneto-stark effects separately.
The reason they were not previously able to measure the curvature of space-time is because my equations show that the effect of energy and wavelength when measured as two variables will cancel each other out, so space-time will not be affected.
Gravitational Effect on Atomic Energy Levels
Objective: Measure the effect of gravity on atomic energy levels
Equipment:
A gas sample (e.g., hydrogen or cesium) in a vacuum chamber.
A laser to excite electrons at specific energy levels.
A high-precision spectrometer.• A variable gravitational field (e.g., using aircraft simulating microgravity).
Procedure:
.1 Measure the atomic spectrum in a normal gravitational environment.
.2 Measure the spectrum in a reduced-gravity environment (e.g., during parabolic flights).
.3 Compare the energy levels and emission lines.
Expected Outcome:
If the spectrum shifts at different gravitational strengths, it indicates that gravity affects atomic energy levels
My equations clearly show that if proven in practical experiments, it indicates that the gravitational constant G is not a cosmic constant in quantum mechanics, but is affected by the wavelength and the energy difference, that is, it is variable. In other words, gravity is not an absolute quantity, but rather the quantum state is influenced by me. For this reason, quantum mechanics is not related to general relativity.
My equations explain the effect (magnetic attraction) and Bayfield-Brown effect My equations confirm the effect of electromagnetism on gravity.
Well, with these experiments, the Pound-Rebecca experiments, also known as gravitational redshift, will prove what the equation tells you.
Photon energy equation.
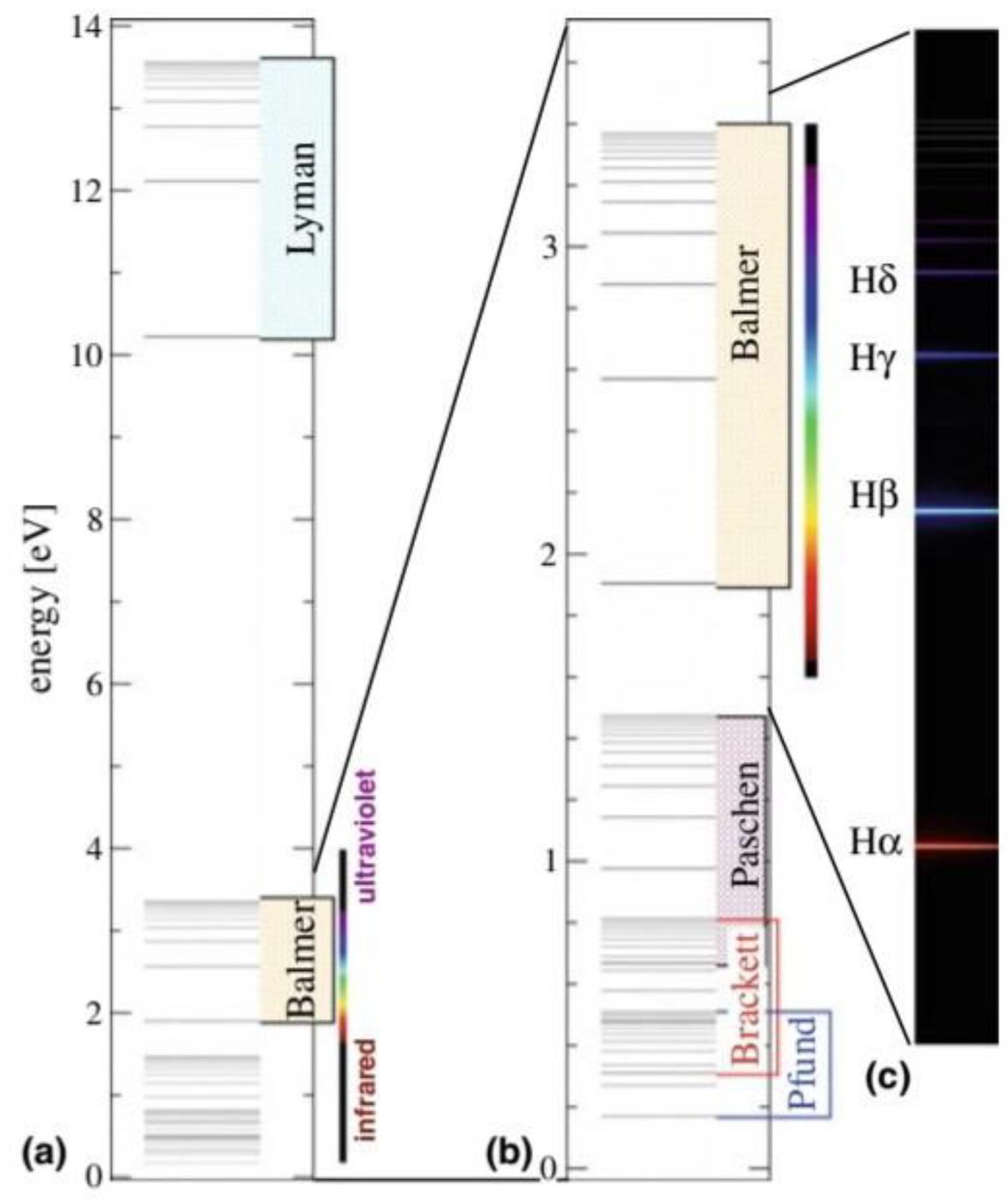
Example of a hydrogen atom.
We remove the energy level
1
The unit of measurement for photon energy is electron volt (eV), the wavelength is (nm)
The unit of measurement for photon energy is electron volt (eV)
Space-time represents in the equation the force of attraction of the nucleus for the electron. Where we take the hydrogen atom compared to the sodium atom. We find after comparison that the undulations that occur in the sodium atom are higher than those that occur in the hydrogen atom. That is, during the occurrence of the quantum jump of the electron, the higher energy level than the level occupied by the electron undulates. So the number of ripples (ripple amplitude) is higher than that of the hydrogen atom during the occurrence of the quantum jump, and this is consistent with the de Broglie equation. n × λ is represented by a ratio to space-time. It is the number of ripples that occur in the energy level higher than the level occupied by the electron until interference occurs between the two levels, the higher energy level and the level occupied by the electron. In other words, as the number of orbitals occupied by the electron increases, the number of ripples that occur at the higher energy levels increases, causing the curvature (contraction) of the fabric of space-time. The interference between the two levels occurs in a wave form so that the quantum jump of the electron occurs. The photon's energy is represented by a ratio to the fabric of space-time, the force that causes the fabric of space-time to bend (contract). The more energy increases, the more space-time contracts through the occurrence of quantum disturbances at the highest energy level, which makes the highest energy level generate waves similar to the orbital number occupied by the electron. Because of these disturbances that occur at the highest energy level, the two levels interfere with each other, the highest energy level, and the level occupied by the electron. A quantum leap occurs, and this is consistent with the quantum Zeno effect, where the electron will remain fixed in its position. This is what my equation indicates, as I explain that these quantum fluctuations occur through a contraction in the fabric of space-time. This contraction occurs as a result of this tissue absorbing energy. Because of this, contraction affects the energy levels in the atom. This contraction works to contract the energy level higher than the level occupied by the electron. Wave interference occurs between the highest energy level and the level occupied by the electron, and a quantum jump occurs from the observer’s perspective. But from the electron's perspective, it remains fixed in its position.
The Casimir effect is according to a law that states that after all the objects acting on the plates disappear until imaginary particles are detected. My equation proves that there is one thing that was not included in the calculations, which is the effect of space-time. Since the plates have a static mass that works to curve space-time, and the presence of imaginary particles works when they collide with each other, they disappear. But according to the law of conservation of energy, the energy will not disappear and will affect the fabric of space-time, making it turbulent like a water wave, and these disturbances that occur on it form waves. This wave works to impact the panels from moving in and out, and because the external disturbances are higher than the internal ones, they cause the panels to move towards each other.
This relationship shows that although we cannot measure what happens when an electronic quantum jump occurs. This law also shows that there is a relationship between the energy of the photon and the fabric of space-time, even if it is not measured by measuring devices. Because measuring devices are considered primitive devices when making the process of measuring the quantitative world. What is being measured are the spectra of the elements being measured, not what happens to the electron when the quantum jump of the electron to the higher level. Second, Maxwell told Rutherford that the electron changes direction as it orbits the nucleus, so it must lose energy to cause a collision with the nucleus, which it does not. My equation tells me the electron moves in a large circle around the nucleus. A body moving in a large circle whose direction of motion is in a straight line. Thus, the electron moves in a straight line. Newton's law states that an object at rest remains at rest unless acted upon by an external or internal force. Likewise, an object in motion stays in motion unless an external or internal force affects its movement, the electron does not lose energy.
The results of the experimental value were obtained by using the results of previous research on the hydrogen atom. I prove in table 7 that the results of the equations are identical to their original results in table 5, which indicates the validity of this law
Photon energy equation.
These are the results of a relationship between energy and wavelength. The observed results show that whenever the energy increases, the wavelength decreases, as shown by this equation in the hydrogen atom.