Submitted:
14 January 2025
Posted:
16 January 2025
You are already at the latest version
Abstract
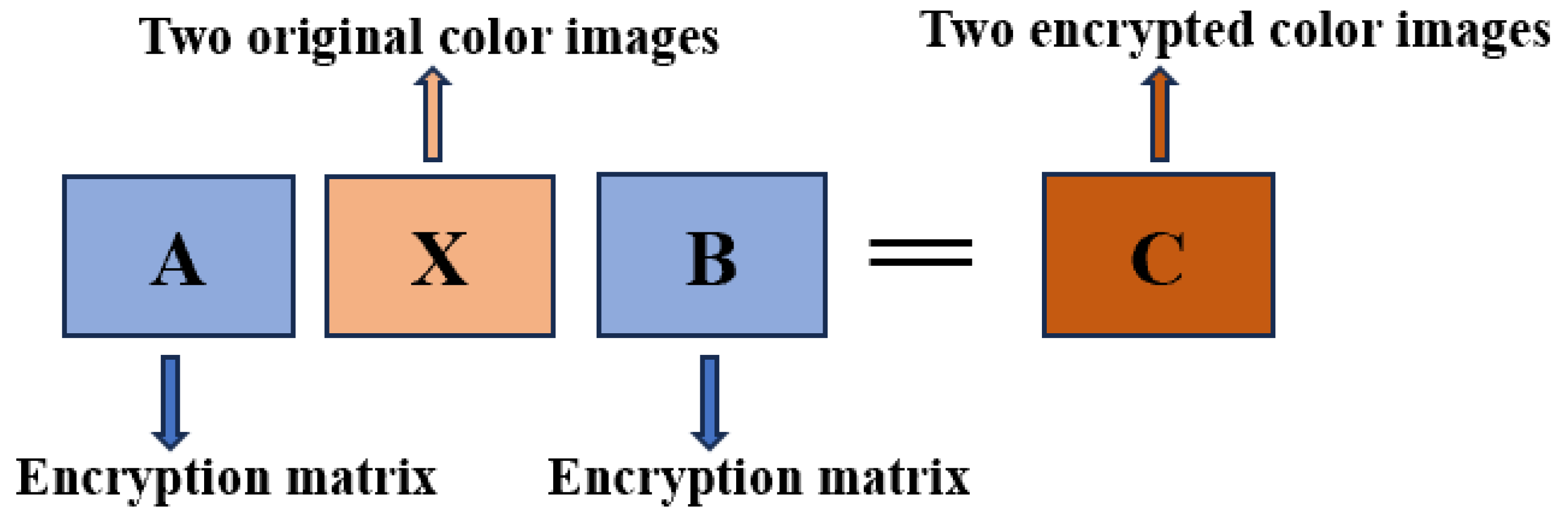
This survey provides a comprehensive overview of the solutions to the matrix equation AXB=C over real numbers, complex numbers, quaternions, dual quaternions, dual split quaternions, and dual generalized commutative quaternions, including various special solutions. Additionally, we summarize the numerical algorithms for these special solutions. This matrix equation plays an important role in solving linear systems and control theory. We specifically explore the application of this matrix equation in color image processing, highlighting its unique value in this field. Taking the dual quaternion matrix equation AXB=C as an example, we design a scheme for simultaneously encrypting and decrypting two color images. Experimental results demonstrate that this scheme is highly feasible.
Keywords:
MSC: 15A03, 15A09, 15A24, 15B33, 15B57, 65F10, 65F45
1. Introduction
2. Preliminaries
2.1. Real Matrix
2.2. Complex Matrix
2.2.1. Hermitian,Positive Semidefinite And Positive Definite Matrices
2.2.2. Moore-Penrose Inverses Of Matrices
2.2.3. Reflexive, Reflexive, Generalized Reflexive, And ()-symmetric Matrices
2.2.4. Generalized Singular Value Decomposition
2.3. Semi-Tensor Product Of Matrices
- (1)
- Set , , denote
- (2)
- Set , , denote
2.4. Quaternion Matrix And Dual Quaternion Matrix
2.4.1. Quaternions
2.4.2. Quaternion Matrix
- , A is called Hermitian.
- , A is called Persymmetric.
- and , A is called Bisymmetric (bihermitian).
- and , A is called a quaternion skew bihermitian matrix.
- , and , B is called a ()-symmetric (()-skew symmetric) matrix, where and .
- .
- .
- .
- .
- .
- .
- .
- .
- ;
- ;
- ;
- ;
- commutes with and with respect to multiplication.
2.4.3. Dual Quaternion Matrix
- .
- .
- .
2.5. Dual Split Quaternion Matrix
2.5.1. Split Quaternion Matrix
- .
- (i)
- (ii)
- (i)
- (ii)
- ,
2.5.2. Dual Split Quaternion Matrix
2.6. Dual Generalized Commutative Quaternion Matrix
2.6.1. Generalized Commutative Quaternion Matrix
- .
- .
- .
- (a)
- .
- (b)
- .
- (c)
- .
- (a)
- .
- (b)
- .
- (c)
- .
2.6.2. Dual Generalized Commutative Quaternion Matrix
2.7. Tensor
- (1)
- ,
- (2)
- ,
- (3)
- ,
- (4)
- ,
3. Various Solutions Of Matrix Equation
- In 1976, Khatri and Mitra [17] studied the solvability conditions and general solution expressions for the matrix Equation (1) with Hermitian and nonnegative definite solutions. Subsequently, in 2004, Zhang [28] investigated Hermitian nonnegative-definite and positive-definite solutions of this equation. Later, Wang et al. [29] and Cvetković-ilić [30] explored Re-nonnegative definite solutions of the same equation. Since *congruence encompasses Hermitian, positive definite, and positive semidefinite matrices, Zheng et al. [44] studied the *congruence class of the solutions to this matrix equation in 2009.
- Employing the GSVD, Hua [32] and Liao [33] investigated the symmetric solutions and symmetric positive semidefinite least-squares solutions of matrix Equation (1) over . Additionally, in 2022, Hu et al. [34] studied the symmetric solutions of this matrix equation within a specific subspace over the real number field. The quaternion is an extension of real and complex numbers with broad applications. Accordingly, Liu [38] explored the -Hermitian solution of this matrix equation. In addition, Wang et al. [35] and Zhang et al. [36] studied the least squares bisymmetric solutions and the skew bihermitian solutions of matrix Equation (1) over .
- In 2006, D.S. Cvetković-ilić [39] studied the reflexive and anti-reflexive solutions of the matrix Equation (1) over the complex field. In 2011, Herrero et al. [41] investigated the reflexive and anti-reflexive solutions of the same equation over . Building on these efforts, Liu et al. [42] explored the minimum norm least squares Hermitian (anti-)reflexive solutions of this equation in 2017. Subsequently, Yuan et al. [40] examined generalized reflexive solutions of this matrix equation over the complex field. In 2024, Liao et al. [43] extended this line of research by studying the -symmetric solutions of this matrix equation over , which encompass generalized reflexive solutions.
- In 2018, Yang et al. [45] studied the Hankel solutions and various Toeplitz solutions of matrix Equation (1) over . In 2022, Zhang et al. [46] investigated the orthogonal solutions of this matrix equation in the complex field. Moreover, since tensors are higher-dimensional matrices with broader applications, Xie et al. [12] studied the K-reducible solutions of this matrix equation in quaternion tensors.
- Previous studies on various specific solutions to matrix Equation (1) have mostly been based on the assumption that and C are matrices. We know that matrices can be viewed as a special type of operator. Thus, in 2010, Arias et al. [47] explored the existence of positive solutions to this operator equation without this additional assumption. Building on this work, Cvetković-Ilić et al. [48] further investigated the positive solutions of this operator equation in 2019.
- In addition, some scholars have employed matrix rank to investigate various aspects of matrix Equation (1). For example, Porter et al. (1979) [51] studied the number of solutions to this matrix equation over a given finite field. In 2007, Liu [52] explored the problems of maximal and minimal ranks for the least-squares solutions of this equation over the complex field. Subsequently, Zhang et al. [54] extended the study to the maximal and minimal ranks of submatrices of the least-squares solutions over . In 2010, Wang et al. [53] investigated the maximal and minimal ranks of the four real matrices involved in the quaternion solution of this equation.
- The traditional matrix product imposes requirements on the dimensions of the two matrices involved, while the semi-tensor product removes these restrictions and has broad applications. Consequently, in 2019, Ji et al. [13] studied matrix Equation (1) over the field of real numbers under the semi-tensor product. In 2020, Prokip [56] investigated this matrix equation over a principal ideal domain. , and are extensions of , and , respectively. Therefore, in 2024, Chen et al. [8] investigated this matrix equation over , while Si et al. [11] explored it over , and Shi et al. [98] concentrated on .
- The matrix Equation (1) has a Hermitian solution iffis Hermitian. In this case, the general Hermitian solution can be expressed aswhere W is an arbitrary Hermitian matrix with appropriate sizes, and are arbitrary Hermitian solutions of the matrix equations
- The matrix Equation (1) is consistent if and only ifIn this case, the general solution can be expressed aswhere are arbitrary matrices with appropriate sizes over .
- The matrix Equation (1) has a Re-nnd solution if and only ifIn this case, the general Re-nnd solution can be expressed aswhereandwith , are all arbitrary matrices.
- The least square skew bihermitian solutions of matrix Equation (1) is given bywhere y is an arbitrary real vector with appropriate size and the minimal norm least square skew bihermitian solution of this matrix equation can be expressed as
-
The matrix Equation (1) has a reflexive solution iff one of the following conditions is satisfied
- 1)
- ,
- 2)
- .
In this case, the general reflexive solution can be expressed aswhere can be obtained by rearranging , and . Herewith y an arbitrary vector. - The matrix Equation (1) has a reflexive solution iff or . In this case, the general reflexive solution can be expressed aswhere can be reconstructed from and , respectively. Herewith z an arbitrary vector.
- the least-squares Hermitian reflexive solution is expressed aswhere can be obtained byand y is an arbitrary real vector. In this case, the solution X with the minimum-norm is provided bywhere are presented by
- the least-squares Hermitian antireflexive solution is expressed aswhereand z is an arbitrary real vector. In this case, the solution X with the minimum-norm is derived bywhere is presented by
- Its general Toeplitz solution is given by , whereand w is an arbitrary real vector. Here,Specifically, when , we can obtain the upper triangular Toeplitz solution of this matrix equation. Similarly, when , we can also obtain the lower triangular Toeplitz solution.
- Its symmetric Toeplitz solution is exoressed as , whereand the method for finding is the same as for Equation (15), except that .
- Its Hankel solution is provided by , whereand the procedure to determine is similar to that in Equation (15), except that p and q range from 1 to .
- The equation is consistent.
- There exists a positive operator such that .
- There exists a positive operator such that .
- The operator is non-negative, and .
-
The following statements are equivalent.
- (a)
- The operator equation has a positive solution.
- (b)
- There exist a real number and such that, for every ,
- (c)
-
There exists a positive operator such that and the equationis consistent.
- (d)
- There exists and a real number such that
-
Specifically, if is closed, we have the following equivalent descriptions.
- (a)
- The operator equation is consistent,
- (b)
- ,
- (c)
- ,
- (d)
- ,
where and . In this case, the general positive solution is expressed aswhereHere, and satisfy the conditionsandrespectively.
- The extreme ranks of are provided bywhere
- The extreme ranks of are presented bywhere
- The dual split quaternion matrix Equation (1) is solvable.
-
The systemis solvable.
- The dual generalized commutative quaternion matrix Equation (1) is solvable.
-
The systemis solvable.
- (1)
- When ,
- (2)
- When ,
- (3)
- When ,
4. Various Algorithms For Solving The Matrix Equation
5. An Application
6. Conclusions
- The exploration of special solutions to matrix Equation (1) over dual quaternions, dual split quaternions, or dual generalized commutative quaternions could be a valuable direction for future research. This includes solutions such as (anti-)symmetric solutions, (anti-)reflexive solutions, (R, S)-(skew)symmetric solutions, bisymmetric solutions, reducible solutions, and so on. Furthermore, it would be interesting to investigate whether these solutions can be considered over dual quaternion tensors, dual split quaternion tensors, or dual generalized commutative quaternion tensors.
- The study of corresponding numerical algorithms over quaternions, dual quaternions, dual split quaternions, or dual generalized commutative quaternions is another promising direction for future research. Furthermore, it would be worth exploring whether these algorithms can be extended to tensors (over the complex field), dual quaternion tensors, dual split quaternion tensors, or dual generalized commutative quaternion tensors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, F.Z.; Hu, X.Y.; Zhang, L. The solvability conditions for the inverse eigenvalue problems of centro-symmetric matrices. Linear Algebra Appl. 2003, 364, 147–160. [Google Scholar] [CrossRef]
- Liang, M.L.; You, C.H.; Dai, L.F. An efficient algorithm for the generalized centro-symmetric solution of matrix equation AXB=C. Numer. Algorithms. 2007, 44, 173–184. [Google Scholar] [CrossRef]
- Chen, H.C. Generalized reflexive matrices: Special properties and applications. SIAM J. Matrix Anal. Appl. 1998, 19, 140–153. [Google Scholar] [CrossRef]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Cambridge Philos. Soc. Cambridge University Press, 1955, 51, 406–413. [Google Scholar] [CrossRef]
- He, Z.H.; Wang, Q.W. A real quaternion matrix equation with applications. Linear Multilinear Algebra. 2013, 61, 725–740. [Google Scholar] [CrossRef]
- Wei, M.S.; Li, Y.; Zhang, F.X. Quaternion matrix computations. Beijing: Nova Science Publisher. 2018.
- Rodman, L. Topics in quaternion linear algebra; Princeton University Press, 2014. [Google Scholar]
- Chen, Y.; Wang, Q.W.; Xie, L.M. Dual quaternion matrix equation AXB=C with applications. Symmetry. 2024, 16, 287. [Google Scholar] [CrossRef]
- Zhang, F.X.; Wei, M.S.; Li, Y.; Zhao, J.L. An efficient method for least squares problem of the quaternion matrix equation X-AX^B=C. Linear Multilinear Algebra. 2020, 70, 2569–2581. [Google Scholar] [CrossRef]
- Trench, W.F. Minimization problems for (R,S)-symmetric and (R,S)-skew symmetric matrices. Linear Algebra Appl. 2004, 389, 23–31. [Google Scholar] [CrossRef]
- Si, K.W.; Wang, Q.W. The general solution to a classical matrix equation AXB=C over the dual split quaternion algebra. Symmetry. 2024, 16, 491. [Google Scholar] [CrossRef]
- Xie, M.Y.; Wang, Q.W. Reducible solution to a quaternion tensor equation. Front. Math. China. 2020, 15, 1047–1070. [Google Scholar] [CrossRef]
- Ji, Z.D.; Li, J.F.; Zhou, X.L.; Duan, F.J.; Li, T. On solutions of matrix equation AXB=C under semi-tensor product. Linear Multilinear Algebra. 2021, 69, 1935–1963. [Google Scholar] [CrossRef]
- Liu, X.C.; Li, Y.; Ding, W.X.; Tao, R.Y. A real method for solving octonion matrix equation AXB=C based on semi-tensor product of matrices. Adv. Appl. Clifford Algebr. 2024, 34, 12. [Google Scholar] [CrossRef]
- He, Z.H. The general solution to a system of coupled Sylvester-type quaternion tensor equations involving η-Hermicity. B. Iran. Math. Soc. 2019, 45, 1407–1430. [Google Scholar] [CrossRef]
- Wu, L.; Cain, B. The Re-nonnegative definite solutions to the matrix inverse problem AX=B. Linear Algebra Appl. 1996, 236, 137–146. [Google Scholar] [CrossRef]
- Khatri, C.G.; Mitra, S.K. Hermitian and nonnegative definite solutions of linear matrix equations. SIAM J. Appl. Math. 1976, 31, 579–585. [Google Scholar] [CrossRef]
- Rao, C.R. Estimation of variance and covariance components in linear models. J. Am. Stat. Assoc. 1972, 67, 112–115. [Google Scholar] [CrossRef]
- Stagg, G.W.; El-Abaid, A.H. Computer methods in power system analysis. McGraw- Hill, New York, 1968.
- Took, C.C.; Mandic, D.P. Augmented second-order statistics of quaternion random signals. Signal Process. 2011, 91, 214–224. [Google Scholar] [CrossRef]
- Li, J.F.; Hu, X.Y.; Duan, X.F.; Zhang, L. Numerical solutions of AXB=C for mirrorsymmetric matrix X under a specified submatrix constraint. Computing. 2010, 90, 39–56. [Google Scholar] [CrossRef]
- Kirkland, S.J.; Neumann, M.; Xu, J.H. Transition matrices for well-conditioned Markov chains. Linear Algebra Appl. 2007, 424, 118–131. [Google Scholar] [CrossRef]
- Lei, J.Z.; Wang, C.Y. On the reducibility of compartmental matrices. Comput Biol Med. 2008, 38, 881–885. [Google Scholar] [CrossRef] [PubMed]
- Santesso, P.; Valcher, M.E. On the zero pattern properties and asymptotic behavior of continuous-time positive system trajectories. Linear Algebra Appl. 2007, 425, 283–302. [Google Scholar] [CrossRef]
- Hsieh, C.; Skelton, R.E. All covariance controllers for linear discrete-time systems. IEEE Trans. Autom. Control. 1990, 35, 908–915. [Google Scholar] [CrossRef]
- Chu, M.T.; Trendafilov, N.T. On a differential equation approach to the weighted orthogonal procrustes problem. Stat. Comput. 1998, 8, 125–133. [Google Scholar] [CrossRef]
- Chu, M.T.; Trendafilov, N.T. The orthogonally constrained regression revisited. J. Comput. Graph. Stat. 2001, 10, 746–771. [Google Scholar] [CrossRef]
- Zhang, X. Hermitian nonnegative-definite and positive-definite solutions of the matrix equation AXB=C. Appl Math E-Notes 2004, 4, 40–47. [Google Scholar]
- Wang, Q.W.; Yang, C.L. The Re-nonnegative definite solutions to the matrix equation AXB=C. Comment. Math. Univ. Carolin. 1998, 39, 7–13. [Google Scholar]
- Cvetković-ilić, D.S. Re-nnd solutions of the matrix equation AXB=C. J. Aust. Math. Soc. 2008, 84, 63–72. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. Towards a generalized singular value decomposition. SIAM J. Numer. Anal. 1981, 18, 398–405. [Google Scholar] [CrossRef]
- Hua, D. On the symmetric solutions of linear matrix equations. Linear Algebra Appl. 1990, 131, 1–7. [Google Scholar] [CrossRef]
- Liao, A.P. Least-squares solution of AXB=D over symmetric positive semidefinite matrices. J. Comput. Math. 2003, 21, 175–182. [Google Scholar]
- Hu, S.S.; Yuan, Y.X. The symmetric solution of the matrix equation AXB=D on subspace. Comput. Appl. Math. 2022, 41, 373. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Ding, W.X. The least squares Bisymmetric solution of quaternion matrix equation AXB=C. AIMS Math. 2021, 6, 13247–13257. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Li, Y.; Zhao, H.; Zhao, J.L.; Wang, G. Least-squares bihermitian and skew bihermitian solutions of the quaternion matrix equation AXB=C. Linear Multilinear Algebra. 2022, 70, 1081–1095. [Google Scholar] [CrossRef]
- Yuan, S.F.; Liao, A.P.; Wang, P. Least squares η-bi-Hermitian problems of the quaternion matrix equation (AXB,CXD)=(E,F). Linear Multilinear Algebra. 2015, 63, 1849–1863. [Google Scholar] [CrossRef]
- Liu, X. The η-anti-Hermitian solution to some classic matrix equations. Appl. Math. Comput. 2018, 320, 264–270. [Google Scholar] [CrossRef]
- Cvetković-ilić, D.S. The reflexive solutions of the matrix equation AXB=C. Comput. Math. Appl. 2006, 51, 897–902. [Google Scholar] [CrossRef]
- Yuan, Y.X.; Dai, H. Generalized reflexive solutions of the matrix equation AXB=D and an associated optimal approximation problem. Comput. Math. Appl. 2008, 56, 1643–1649. [Google Scholar] [CrossRef]
- Herrero, A.; Thome, N. Using the GSVD and the lifting technique to find {P,k+1} reflexive and anti-reflexive solutions of AXB=C. Appl. Math. Lett. 2011, 24, 1130–1141. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.W. The least squares Hermitian (anti)reflexive solution with the least norm to matrix equation AXB=C. Math. Probl. Eng. 2017, 2017, 9756035. [Google Scholar] [CrossRef]
- Liao, R.P.; Liu, X.; Long, S.J.; Zhang, Y. (R,S)-(skew) symmetric solutions to matrix equation AXB=C over quaternions. Mathematics 2024, 12, 323. [Google Scholar] [CrossRef]
- Zheng, B.; Ye, L.J.; Cvetković-ilić, D.S. The *congruence class of the solutions of some matrix equations. Comput. Math. Appl. 2009, 57, 540–549. [Google Scholar] [CrossRef]
- Yang, J.; Deng, Y.B. On the solutions of the equation AXB=C under Toeplitz-like and Hankel matrices constraint. Math. Methods Appl. Sci. 2018, 41, 2074–2094. [Google Scholar] [CrossRef]
- Zhang, H.T.; Liu, L.N.; Liu, H.; Yuan, Y.X. The solution of the matrix equation AXB=D and the system of matrix equations AX=C,XB=D with X*X=Ip. Appl. Math. Comput. 2022, 418, 126789. [Google Scholar] [CrossRef]
- Arias, M.L.; Gonzalez, M.C. Positive solutions to operator equations AXB=C. Linear Algebra Appl. 2010, 433, 1194–1202. [Google Scholar] [CrossRef]
- Cvetković-Ilić, D.; Wang, Q.W.; Xu, Q.X. Douglas’ +Sebestyén’s lemmas =a tool for solving an operator equation problem. J. Math. Anal. Appl. 2020, 482, 123599. [Google Scholar] [CrossRef]
- Douglas, R.G. On majorization, factorization and range inclusion of operators in Hilbert spaces. Proc. Amer. Math. Soc. 1966, 17, 413–416. [Google Scholar] [CrossRef]
- Sebestyén, Z. Restriction of positive operators. Acta Sci. Math. 1983, 46, 299–301. [Google Scholar]
- Porter, A.D.; Mousouris, N. Ranked solutions of AXC=B and AX=B. Linear Algebra Appl. 1979, 24, 217–224. [Google Scholar] [CrossRef]
- Liu, Y.H. Ranks of least squares solutions of the matrix equation AXB=C. Comput. Math. Appl. 2008, 55, 1270–1278. [Google Scholar] [CrossRef]
- Wang, Q.W.; Yu, S.W.; Xie, W. Extreme ranks of real matrices in solution of the quaternion matrix equation AXB=C with applications. Algebra Colloq. 2010, 17, 345–360. [Google Scholar] [CrossRef]
- Zhang, F.X.; Li, Y.; Guo, W.B.; Zhao, J.L. Least squares solutions with special structure to the linear matrix equation AXB=C. Appl. Math. Comput. 2011, 217, 10049–10057. [Google Scholar] [CrossRef]
- Marsaglia, G.; Styan, G.P. Equalities and inequalities for ranks of matrices. Linear Multilinear Algebra. 1974, 2, 269–292. [Google Scholar] [CrossRef]
- Prokip, V.M. On solvability of the matrix equation AXB=C over a principal ideal domain. Modeling, control and information technologies: Proceedings of International scientific and practical conference. 2020, 4, 47–50. [Google Scholar] [CrossRef]
- Cheng, D.Z.; Xu, T.T.; Qi, H.S. Evolutionarily stable strategy of networked evolutionary games. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1335–1345. [Google Scholar] [CrossRef]
- Cheng, D.Z.; Zhao, Y.; Mu, Y.F. Strategy optimization with its application to dynamic games. 49th IEEE Conference on Decision and Control. 2010; 5822–5827. [Google Scholar] [CrossRef]
- Cheng, D.Z. Input-state approach to Boolean networks. IEEE Trans. Neural Netw. Learn. Syst. 2009, 20, 512–521. [Google Scholar] [CrossRef]
- Cheng, D.Z.; Qi, H.S. A linear representation of dynamics of Boolean networks. IEEE Trans. Automat. Control. 2010, 55, 2251–2258. [Google Scholar] [CrossRef]
- Deng, Y.B.; Bai, Z.Z.; Gao, Y.H. Iterative orthogonal direction methods for Hermitian minimum norm solutions of two consistent matrix equations. Numer. Linear Algebra Appl. 2006, 13, 801–823. [Google Scholar] [CrossRef]
- Peng, Y.X.; Hu, X.Y.; Zhang, L. An iteration method for the symmetric solutions and the optimal approximation solution of the matrix equation AXB=C. Appl. Math. Comput. 2005, 160, 763–777. [Google Scholar] [CrossRef]
- Peng, Z.Y. An iterative method for the least squares symmetric solution of the linear matrix equation AXB=C. Appl. Math. Comput. 2005, 170, 711–723. [Google Scholar] [CrossRef]
- Hou, J.J.; Peng, Z.Y.; Zhang, Z.L. An iterative method for the least squares symmetric solution of matrix equation AXB=C. Numer. Algorithms. 2006, 42, 181–192. [Google Scholar] [CrossRef]
- Lei, Y.; Liao, A.P. A minimal residual algorithm for the inconsistent matrix equation AXB=C over symmetric matrices. Appl. Math. Comput. 2007, 188, 499–513. [Google Scholar] [CrossRef]
- Liao, A.P.; Lei, Y. Optimal approxomate solution of the matrix equation AXB=C over symmetric matrices. J. Comput. Math. 2007, 25, 543–552. [Google Scholar]
- Peng, Y.X.; Hu, X.Y.; Zhang, L. An Iterative Method for Bisymmetric Solutions and Optimal Approximation Solution of AXB=C. Third International Conference on Natural Computation(ICNC 2007), 2007; 829–832. [Google Scholar]
- Ding, F.; Liu, P.X.; Ding, J. Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle. Appl. Math. Comput. 2008, 197, 41–50. [Google Scholar] [CrossRef]
- Peng, Z.Y. A matrix LSQR iterative method to solve matrix equation AXB=C. Int. J. Comput. Math. 2010, 87(8), 1820–1830. [Google Scholar] [CrossRef]
- Peng, Z.Y. New matrix iterative methods for constraint solutions of the matrix equation AXB=C. J. Comput. Appl. Math. 2010, 235, 726–735. [Google Scholar] [CrossRef]
- Li, J.F.; Hu, X.Y.; Zhang, L. Numerical solutions of AXB=C for centrosymmetric matrix X under a specified submatrix constraint. Numer. Linear Algebra Appl. 2011, 18(5), 857–873. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Dai, L. On Hermitian and skew-Hermitian splitting iteration methods for the linear matrix equation AXB=C. Comput. Math. Appl. 2013, 65, 657–664. [Google Scholar] [CrossRef]
- Khorsand Zak, M.; Toutounian, F. Nested splitting conjugate gradient method for matrix equation AXB=C and preconditioning. Comput. Math. Appl. 2013, 66, 269–278. [Google Scholar] [CrossRef]
- Sarduvan, M.; Si̇maek, S.; Özdemi̇r, H. On the best approximate (P,Q)-orthogonal symmetric and skew-symmetric solution of the matrix equation AXB=C. J. Numer. Math. 2014, 22(3), 255–269. [Google Scholar] [CrossRef]
- Xie, D.X.; Xu, A.B.; Peng, Z.Y. Least-squares symmetric solution to the matrix equation AXB=C with the norm inequality constraint. Int. J. Comput. Math. 2016, 93(9), 1564–1578. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, X.; Zhou, P. A modified HSS iteration method for solving the complex linear matrix equation AXB=C. J. Comput. Math. 2016; 34, 437–450. [Google Scholar]
- Tian, Z.L.; Tian, M.Y.; Liu, Z.Y.; Xu, T.Y. The Jacobi and Gauss–Seidel-type iteration methods for the matrix equation AXB=C. Appl. Math. Comput. 2017, 292, 63–75. [Google Scholar] [CrossRef]
- Wang, X.; Tang, X.B.; Gao, X.G.; Wu, W.H. Finite iterative algorithms for the generalized reflexive and anti-reflexive solutions of the linear matrix equation AXB=C. Filomat. 2017; 31, 2151–2162. [Google Scholar]
- Li, C.M.; Duan, X.F.; Li, J.; Yu, S.T. A new algorithm for the symmetric solution of the matrix equation AXB=E and CXD+F. Ann. Funct. Anal. 2018, 9, 8–16. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhou, Y.; Zhang, Y.L.; Lin, L.; Xie, D.X. Some remarks on Jacobi and Gauss–Seidel-type iteration methods for the matrix equation AXB=C. Appl. Math. Comput. 2019, 354, 305–307. [Google Scholar] [CrossRef]
- Wang, Q.W.; Xu, X.J. Iterative algorithms for solving some tensor equations. Linear Multilinear Algebra. 2019, 67(7), 1325–1349. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Li, Z.; Ferreira, C.; Zhang, Y.L. Stationary splitting iterative methods for the matrix equation AXB=C. Appl. Math. Comput. 2020, 378, 125195. [Google Scholar] [CrossRef]
- Yu, D.M.; Chen, C.R.; Han, D.R. ADMM-based methods for nearness skew-symmetric and symmetric solutions of matrix equation AXB=C. East Asian J. Appl. Math. 2020, 10, 698–716. [Google Scholar] [CrossRef]
- Chen, F.; Li, T.Y. Two-step AOR iteration method for the linear matrix equation AXB=C. Comp. Appl. Math. 2021, 40, 89. [Google Scholar] [CrossRef]
- Tian, Z.L.; Li, X.J.; Dong, Y.H.; Liu, Z.Y. Some relaxed iteration methods for solving matrix equation AXB=C. Appl. Math. Comput. 2021, 403, 126189. [Google Scholar] [CrossRef]
- Wu, N.C.; Liu, C.Z.; Zuo, Q. On the Kaczmarz methods based on relaxed greedy selection for solving matrix equation AXB=C. J. Comput. Appl. Math. 2022, 413, 114374. [Google Scholar] [CrossRef]
- Duan, X.F.; Zhang, Y.S.; Wang, Q.W.; Li, C.M. Paige’s Algorithm for solving a class of tensor least squares problem. BIT. 2023, 63, 48. [Google Scholar] [CrossRef]
- Tian, Z.L.; Duan, X.F.; Wu, N.C.; Liu, Z.Y. The parameterized accelerated iteration method for solving the matrix equation AXB=C. Numer. Algorithms. 2023, 97, 843–867. [Google Scholar] [CrossRef]
- Duan, X.F.; Zhang, Y.S.; Wang, Q.W. An efficient iterative method for solving a class of constrained tensor least squares problem. Appl. Numer. Math. 2024, 196, 104–117. [Google Scholar] [CrossRef]
- Tian, Z.L.; Wang, Y.D.; Wu, N.C.; Liu, Z.Y. On the parameterized two-step iteration method for solving the matrix equation AXB=C. Appl. Math. Comput. 2024, 464, 128401. [Google Scholar] [CrossRef]
- Daniilidis, K. Hand-eye calibration using dual quaternions. Int. J. Robot. Res. 1999, 18, 286–298. [Google Scholar] [CrossRef]
- Wang, X.; Yu, C.; Lin, Z. A dual quaternion solution to attitude and position control for rigid body coordination. IEEE Trans. Rob. 2012, 28, 1162–1170. [Google Scholar] [CrossRef]
- da Cruz Figueredo, L.F.; Adorno, B.V.; Ishihara, J.Y. Robust H∞ kinematic control of manipulator robots using dual quaternion algebra. Automatica. 2021, 132, 109817. [Google Scholar] [CrossRef]
- Kenright, B. A beginners guide to dual-quaternions. 20th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, 5: 2012. https://api.semanticscholar.org/CorpusID, 2012. [Google Scholar]
- Kula, L.; Yayli, Y. Dual split quaternions and screw motion in Minkowski 3-space. Iran. J. Sci. Technol. Trans. 2006, 30, 245–258. [Google Scholar]
- Özkaldi, S.; Gündoğan, H. Dual split quaternions and screw motion in 3-dimensional Lorentzian space. Adv. Appl. Clifford Algebr. 2011, 21, 193–202. [Google Scholar] [CrossRef]
- Huang, G.X.; Yin, F.; Guo, K. An iterative method for the skew-symmetric solution and the optimal approximate solution of the matrix equation AXB=C. J. Comput Appl. Math 2008, 212, 231–244. [Google Scholar] [CrossRef]
- Shi, L.; Wang, Q.W.; Xie, L.M.; Zhang, X.F. Solving the dual generalized commutative quaternion matrix equation AXB=C. Symmetry. 2024, 16, 1359. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Software. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Peng, Z.Y.; Fang, Y.Z.; Xiao, X.W.; Du, D.D. New algorithms to compute the nearness symmetric solution of the matrix equation. SpringerPlus. 2016, 5, 1005. [Google Scholar] [CrossRef]
- van der Woude, J.W. Almost non-interacting control by measurement feedback. Systems Control Lett. 1987, 9, 7–16. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, X.; Zhang, Y. Least-squares solutions of the generalized reduced biquaternion matrix equations. Filomat. 2023, 37, 863–870. [Google Scholar] [CrossRef]



| Proposed by | Type of solution | Algorithm type | Number Field |
|---|---|---|---|
| Ding, 2008 [68] | general solution | GBI | |
| Khorsand Zak, 2013 [73] | NSCG | ||
| Wang, 2013 [72] | HSS | ||
| Zhou, 2016 [76] | MHSS | ||
| Tian, 2017 [77] | Jacobi and GS | ||
| Liu, 2020 [82] | stationary splitting iteration | ||
| Tian, 2021 [85] | relaxed Jacobi and RGS | ||
| Chen, 2021 [84] | TS-AOR | ||
| Wu, 2022 [86] | ME-RGRK and ME-MWRK | ||
| Tian, 2023 [88] | PAI | ||
| Tian, 2024 [90] | PTSI | ||
| Wang, 2019 [81] | general solution (tensor) | iteration |
| Proposed by | Type of solution | Algorithm type | Number Field |
|---|---|---|---|
| Peng, 2005 [62] | symmetric, optimal approximation | iteration | |
| Peng, 2005 [63] | least squares symmetric | iteration | |
| Deng, 2006 [61] | Hermitian minimum norm | IOD | |
| Hou, 2006 [64] | least squares symmetric | iteration | |
| Liao, 2007 [66] | optimal approximate least-squares symmetric | GSVD,CCD | |
| Lei, 2007 [65] | optimal approximate least-squares symmetric | minimal residual algorithm | |
| Huang, 2008 [97] | skew-symmetric, optimal approximation | iteration | |
| Peng, 2010 [69] | symmetric, symmetric R-symmetric, ()-symmetric | LSQR | |
| Peng, 2010 [70] | symmetric, symmetric R-symmetric, ()-symmetric | Paige’s algorithm | |
| Xie, 2016 [75] | least-squares symmetric | GLTR | |
| Peng, 2016 [100] | nearness symmetric | AVMM | |
| Yu, 2020 [83] | nearness skew-symmetric and symmetric | ADMM | |
| Duan, 2024 [89] | least-squares symmetric (tensor) | ADMM |
| Proposed by | Type of solution | Algorithm type | Number Field |
|---|---|---|---|
| Liang, 2007 [2] | generalized centro-symmetric | iteration | |
| Peng, 2007 [67] | bisymmetric, optimal approximation | iteration | |
| Li, 2010 [21] | mirrorsymmetric | conjugate gradient least squares method (CGLS) | |
| Li, 2011 [71] | centrosymmetric | CGLS | |
| Sarduvan, 2014 [74] | -orthogonal (skew-) symmetric | spectral decomposition | |
| Wang, 2017 [78] | Generalized reflexive and anti-reflexive | iteration | |
| Duan, 2023 [87] | least squares solution (tensor) | Paige’s algorithm |
| Color image name | SSIM |
|---|---|
| Apple | 1 |
| Kettle | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




