1. Introduction
Artificial intelligence (AI) has many branches according to the tasks to be performed, with machine learning (ML) being one of the most well-known branches that has gained prominence alongside the development of computer science. It focuses on developing systems and algorithms that automatically learn from data without explicit programming [
1,
2,
3]. However, two main types of ML are categorized according to the problem to be solved: supervised learning and unsupervised learning. Supervised learning relies on having pre-labeled input data (denoted
X) and the desired output (denoted
y). This type of learning aims to understand the hidden relationship between inputs and outputs to predict new outcomes based on unseen (new) input data [
4,
5,
6]. On the other hand, unsupervised learning uses input data that is not pre-labeled (does not contain output y). Instead, an unsupervised learning model is applied to discover patterns and hidden relationships in the data autonomously based on the input data only [
7,
8]. Furthermore, there are other types of ML such as reinforcement learning (RL), which interact directly with the problem’s environment to build policies that guide decision-making based on rewards and penalties obtained through trial and error [
9,
10,
11,
12].
In the early stages of AI, researchers focused on building systems (with minimal intelligence) capable of performing specific tasks using fixed rules (conditional and logical operations). As the field evolved, scientists realized that intelligent systems needed methods to learn from data, rather than relying on rigid rule-based methods with minimal capabilities [
13,
14]. As a result, supervised learning algorithms, specifically classifiers, emerged as tools for learning systems to make predictions or decisions based on the available experiences. However, one of the most preeminent algorithms in supervised learning is artificial neural network (ANN), inspired by the fundamental concept of neurons in the human brain and how they are interconnected [
15]. These networks are based on the concept of neurons, which are basic units in the brain that communicate with each other to perform processes such as thinking and learning [
16]. The algorithm simulates the functions of brain cells by proposing multiple layers of artificial neurons (an input layer and an output layer). These neurons interact with each other using weights assigned to each connection, and the role of the algorithm is to optimize these weights to minimize the error resulting from interactions with the input data, thereby producing accurate outputs [
17]. Moreover, an older algorithm inspired by mathematics is the logistic regression (LR), which aims to find a perfect line that best fits the data points, minimizing the error between actual and predicted labels. These methods were used in statistical analyses before being adopted in ML [
18]. The complexity of linear operations increased, leading to more sophisticated methods, such as support vector machine (SVM), where the main idea is to create clear boundaries between different data classes by maximizing the margin between them [
19]. Comprehensively, most of ML classifiers have drawn their inspirations from mathematical operations or nature (e.g., simulating the functioning of human brain cells) to create robust systems (classifiers) for solving complex problems. Current ML classifiers face multiple challenges related to performance, accuracy or loss, overfitting, and handling data with complex and nonlinear patterns [
20,
21].
In this context, this paper proposes a new classifier called artificial liver classifier (ALC), inspired by the human liver’s biological functions. Specifically, it draws on the detoxification function, highlighting its ability to process toxins and convert them into removable forms. Additionally, improvements have been made to FOX optimization algorithm (FOX), a state-of-the-art optimization algorithm, to enhance its performance and ensure compatibility with the proposed ALC. The research aims to bridge the gap in current ML’s algorithms by combining the simplicity of mathematical design with solid performance by simulating the detoxification function in the human liver. Furthermore, the proposed classifier aims to improve classification performance by processing data dynamically, simulating the human liver’s adaptive ability, enabling its application in fields requiring high-precision solutions and flexibility in dealing with different data patterns. The main challenge lies in transforming the liver’s detoxification function into a simplified mathematical model that effectively incorporates properties such as repetition, interaction, and adaptation to the data [
22]. By comparing the proposed classifier with established ML classifiers, the study expects to improve the performance of ML, including increased computation speed, better handling of overfitting problems, and avoidance of excessive computational complexity. Additionally, this paper introduces a new concept for drawing inspiration from biological systems, opening up extensive opportunities for researchers to develop mathematical models based on other biological functions of the liver, such as filtering blood or amino acid regulation [
23]. Moreover, it represents a starting point for interdisciplinary applications combining biology, mathematics, and AI, enhancing our understanding of incorporating natural processes into ML techniques to create efficient, reliable, and intelligent systems.
The proposed ALC has been evaluated using a variety of commonly used ML datasets, including Wine, Breast Cancer Wisconsin, Iris Flower, MNIST, and Voice Gender [
24], which are explained in detail in
Section 4.1. This diversity in the datasets ensures extensive coverage of different data types, including text, images, and audio, and enables handling binary and multi-class classification problems [
25,
26,
27]. The purpose of using these datasets is to conduct comprehensive tests to assess the performance of the proposed ALC and compare it with the established classifiers. The originality and contributions that distinguish this research are as follows:
Introducing a new classifier inspired by the liver’s biological functions, specifically detoxification, highlighting new possibilities in designing effective classification algorithms based on biological behaviour.
Enhancing the FOX to improve its performance, address existing limitations, and ensure better compatibility with the proposed ALC.
Relying on simple mathematical models that simulate the liver’s biological interactions, ensuring a balance between design simplicity and high performance.
Opening new avenues for researchers to draw inspiration from human organ functions, such as the liver, and simulate them in computational ways to contribute innovative solutions for real-world challenges.
Testing the proposed ALC on diverse datasets demonstrates its effectiveness through experimental results and comparisons with established classifiers.
This paper is structured as follows:
Section 2 reviews the literature that has attempted to address classification issues across various data types.
Section 3 provides an analytical overview of the human liver, focusing on detoxification function and the study’s motivation.
Section 4 present the used materials and the proposed methodology, including the improvement of classifier design and FOX training algorithm.
Section 5 and
Section 6 cover the presentation and analysis of results, including comparisons with previous works. Finally, the study concludes with findings, recommendations, limitations, and future research directions in
Section 7.
2. Related Works
This section reviews the standard algorithms used in ML classification, with their practical applications across various datasets highlighted [
28]. Additionally, recent studies in the field are discussed to identify existing challenges and to shed light on research gaps requiring further attention [
29]. Accordingly, the extent to which the proposed classifier can offer practical solutions to these gaps and contribute to the future advancement of the field will be investigated. However, Xiao et al. utilized 12 standard ML classifiers on the MNIST dataset, demonstrating its suitability as a benchmark for evaluating the proposed ALC. Their results identified the Support Vector Classifier (SVC) with a polynomial kernel (C=100) as the best-performing model, achieving an accuracy of 0.978 [
30]. This comparable result poses a challenge for the proposed ALC to surpass. Furthermore, the study [
31] employed online pseudo-inverse update method (OPIUM) to classify the MNIST dataset, achieving an accuracy of 0.9590. However, the author noted that these results do not represent cutting-edge methods but rather serve as an instructive baseline and a means of validating the dataset. This makes it feasible to compare the performance of the proposed ALC against OPIUM, as surpassing this baseline would demonstrate an improvement over existing methods. On the other hand, in a comparative study by Cortez et al., three classifiers—SVM, multiple regression (MR), and ANN—were evaluated on the Wine dataset. The SVM model demonstrated superior performance, achieving accuracies of 0.8900 for red wine and 0.8600 for white wine, outperforming the other methods with an average accuracy of 0.8790 [
32]. Hence, the findings of Cortez et al. serve as a foundation for further advancements in ML applications, providing a basis for evaluating the proposed ALC.
Another study utilized a recursive recurrent neural network (RRNN) on Breast Cancer Wisconsin dataset. The results demonstrated that the proposed model achieved an accuracy of 0.9950 [
33]. Despite its outstanding performance, the computational demands of RRNN require substantial resources, which may limit their applicability in resource-constrained environments. Moreover, the study [
34] presents a new classification model called CS3W-IFLMC. This model incorporates intuitionistic fuzzy (IF) and cost-sensitive three-way decisions (CS3WD) approaches, contributing to improved classification accuracy and reduced costs associated with incorrect decisions. The proposed model has been evaluated using 12 benchmark datasets, demonstrating superior performance compared to large margin distribution machine (LDM), FSVM, and SVM. However, the study remains limited in scope, as it focuses solely on binary classification tasks and does not extend to multi-class classification problems [
34]. Furthermore, in another study, the researchers examined gender classification (male or female) based on voice data using multi-layer perceptron (MLP). The findings showed that the MLP model outperformed several other methods, including LR, classification and regression tree (CART), random forest (RF), and SVM. The MLP achieved a classification accuracy of 0.9675. This study concluded that the proposed model demonstrates strong discriminative power between genders, which enhances its applicability in auditory data classification tasks [
35].
The reviewed literature, highlights significant advancements in classification models, primarily focusing on improving performance and addressing computational challenges. However, several limitations and research gaps remain. One major issue is the reliance on computationally intensive methods, which can hinder applicability in resource-constrained environments. The absence of practical hyperparameter tuning or reduction mechanisms may also contribute to overfitting and computational inefficiencies. These limitations underscore the need for a new classifier to address such challenges. Hence, the proposed ALC should emphasize simplicity in design to ensure faster training time with lower cost.
3. Detoxification in Liver and Motivation
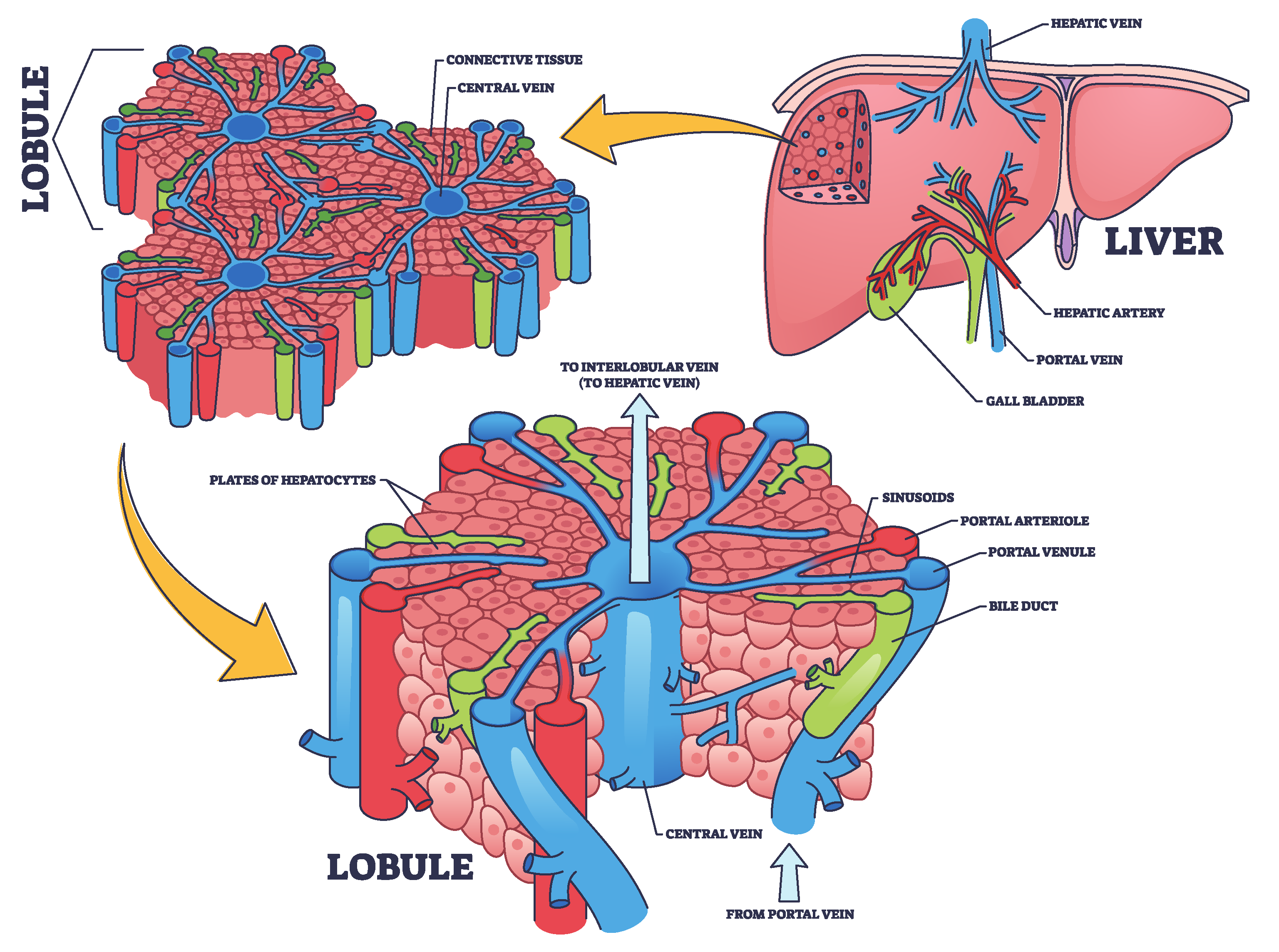
The liver, as illustrated in
Figure 1, is the largest internal organ in the human body and is vital in numerous complex physiological processes. It is located in the right upper quadrant of the abdominal cavity and consists of two primary lobes, the right and left, surrounded by a thin membrane known as the hepatic capsule [
36]. Internally, the liver is composed of microscopic units called hepatic lobules. These hexagonal structures contain hepatic cells organized around a central vein. The lobules are permeated by a network of hepatic sinusoids, which are small channels through which blood flows, facilitating the exchange of oxygen and nutrients between the blood and hepatic cells [
37]. Furthermore, the liver receives blood from two sources, each contributing different functions. The oxygenated blood enters via the hepatic artery from the aorta, meeting the liver’s energy demands. While, the portal vein delivers nutrient-rich and toxin-rich blood from the gastrointestinal tract and spleen [
38]. The blood from both sources mixes in the hepatic sinusoids, allowing the hepatic cells to perform metabolic and regulatory functions efficiently [
39].
However, detoxification is one of the most important liver’s functions, which removes toxins from the bloodstream [
40]. Detoxification occurs in two phases. In the phase I, hepatic enzymes known as cytochrome P450 chemically modify toxins through oxidation and reduction reactions, altering their structures to make them more reactive [
41]. In the phase II, the modified compounds are conjugated with water-soluble molecules such as sulfates or glucuronic acid, making them easier to excrete [
42]. Finally, the toxins are either excreted via bile into the digestive tract or removed from the bloodstream by the kidneys [
43].
Figure 1.
Structural and functional organization of the liver: hepatic lobule and blood flow pathways, concept inspired by [
44].
Figure 1.
Structural and functional organization of the liver: hepatic lobule and blood flow pathways, concept inspired by [
44].
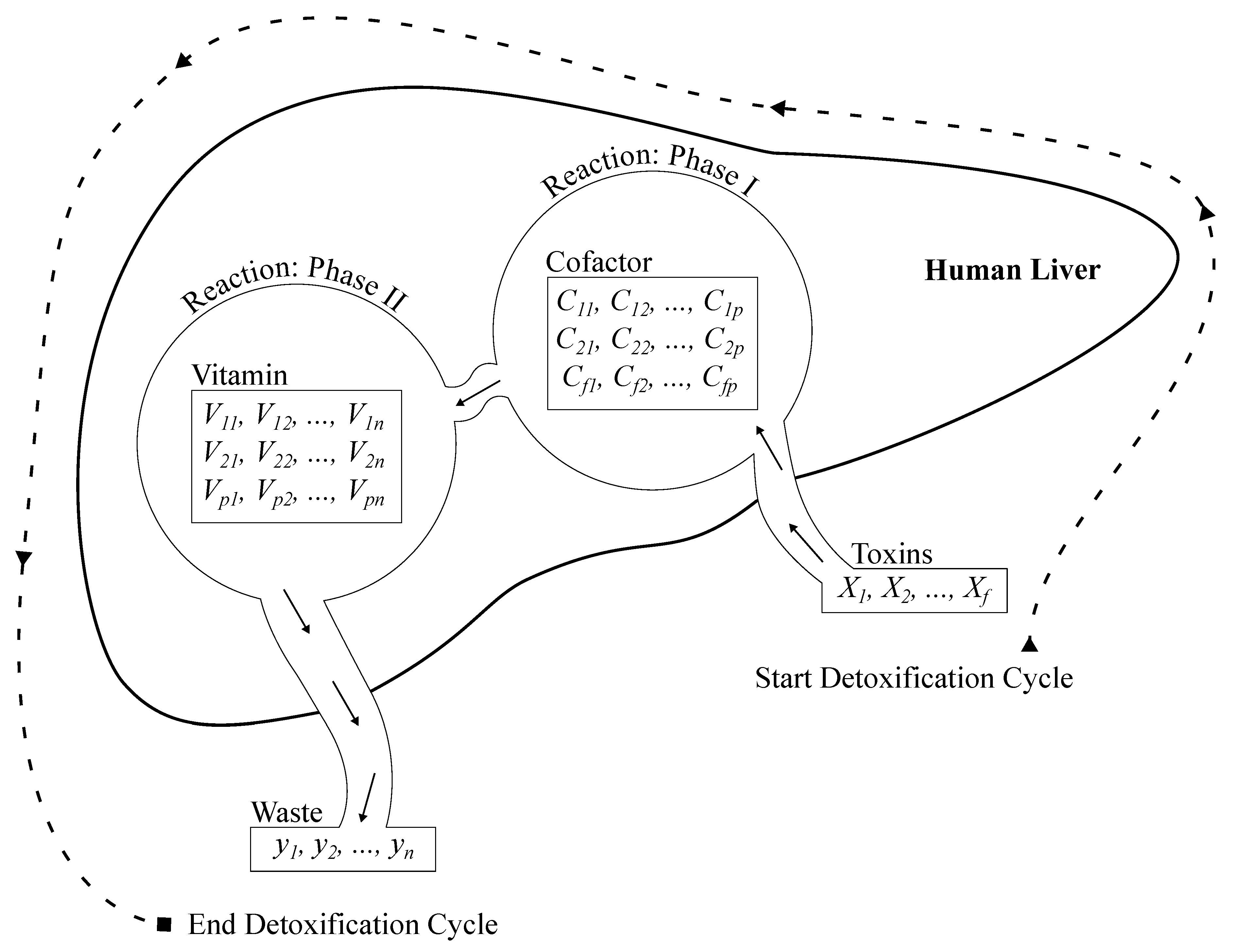
The complex biochemical system of the liver has inspired us to develop a new ML classifier known as ALC, modeled after the liver’s detoxification mechanisms. The design of the proposed ALC was guided by an in-depth understanding of the liver’s two primary detoxification phases—Cytochrome P450 enzymes and Conjugation pathways—where toxins are transformed into excretable compounds. The proposed ALC classify feature vectors effectively with minimum training time by simulating these phases using simple ML and optimization methods. This innovation marks a significant step forward, demonstrating how biological systems can inspire advanced computational models. It particularly encourages researchers in computer science to explore biological processes for developing intelligent ML models.
4. Materials and Methods
This section presents the standard datasets employed for evaluating the proposed ALC in the conducted experiments. Additionally, the architecture of the proposed ALC is provided, including mathematical equations, algorithms, and flowcharts. Furthermore, the section elaborates on the FOX, which serves as the learning algorithm for the proposed ALC, highlighting its improvements.
4.1. Materials
The following datasets are widely used by ML researchers to evaluate their work, making these benchmark datasets suitable for this paper. The MNIST dataset comprises 70,000 grayscale images of handwritten digits (0–9), each of size
pixels. It is widely used for multi-class classification tasks due to its diversity and large size [
45]. As this dataset is image-based, feature vectors were extracted using the linear discriminant analysis (LDA) method, which effectively reduces data dimensionality while emphasizing significant features. This process yielded nine features per image to construct the feature vectors [
46]. Additionally, the Iris dataset, a small-scale collection containing 150 instances across three classes with four features per instance, was included in the proposed ALC evaluation [
47,
48,
49]. The Breast Cancer Wisconsin dataset, a binary dataset containing 569 samples with 30 features each, was employed to assess the proposed ALC’s performance on high-dimensional data [
33,
50]. Furthermore, the Wine dataset, consisting of 178 samples across three classes with 13 features per instance, was selected for its multi-class nature [
48,
51]. Finally, the Voice Gender dataset was employed to ensure feature diversity. This dataset comprises 3,168 samples, each defined by 21 acoustic features, aimed at distinguishing gender (male or female) by leveraging unique vocal characteristics [
35]. These datasets collectively provided a diverse range of classification challenges, enabling a comprehensive evaluation of the proposed ALC’s performance.
4.2. Methods
This section begins with a detailed introduction to the architecture of the proposed ALC. Moreover, it delves into the improvements made to the FOX as a learning algorithm, highlighting its key modifications.
4.2.1. Artificial Liver Classifier
As explained earlier in
Section 3, the detoxification process involves the liver’s ability to process toxins. Oxygenated blood enters the liver via the hepatic artery, while nutrient-rich blood flows through the portal vein. These sources mix within the hepatic sinusoids, enabling hepatic cells to perform essential functions, including a detoxification function that comprises two phases.
Phase I: toxins are chemically modified to become more reactive. This phase is mathematically simulated by the following equation:
where
is the matrix of reactive toxins,
X is the input toxins matrix (feature vector) and
n is the number of outputs (labels). The cofactor matrix is is initialized randomly within the range
and has dimensions
, where
f corresponds to the number of features in the input feature vector, and
p is the number of lobules. The human liver containing many lobules, with approximately 100,000 [
52]. The
p play a crucial role in the phase I and should be tuned appropriately based on the problem. Thus, selecting
p with the range
is typically sufficient and can often be determined through trial and error. Additionally, the term
represents the mean of all elements in the cofactor matrix that used to balance the reaction.
However, the reactive toxins (
A) must be activated to enhance their reactivity before progressing to phase II. This activation involves eliminating all negative values, effectively transforming them to zero while retaining only the positive values. This process is mathematically expressed by the following equation:
where
is the activated toxins matrix.
Phase II: involves the conjugation of modified compounds from phase I with water-soluble molecules to make them excretable. This phase reduces the toxicity of compounds and facilitates their elimination from the body. this phase can be mathematically modeled using Equation
1, but with key differences. Instead of toxins, the matrix
is used as input, representing the modified compounds (activated toxins) generated in phase I. Additionally, a matrix referred to as the vitamin matrix is employed in place of the cofactor matrix. This vitamin matrix is initialized randomly within the range
and has dimensions
.
where
represents the conjugated compounds and
represents the mean of all elements in the vitamin matrix.
Finally, after completing the reactions in both phase I and phase II, the detoxification process is concluded. The result is a set of less harmful and water-soluble wastes that can be excreted through bile, urine, stool, and other pathways. The elimination process is modeled using the softmax activation function, which provides probabilistic outputs for each class [
53,
54,
55]. These probabilities represent the confidence scores for the likelihood of different detoxified compounds being excreted.
where
represents the normalized probability for output class
i.
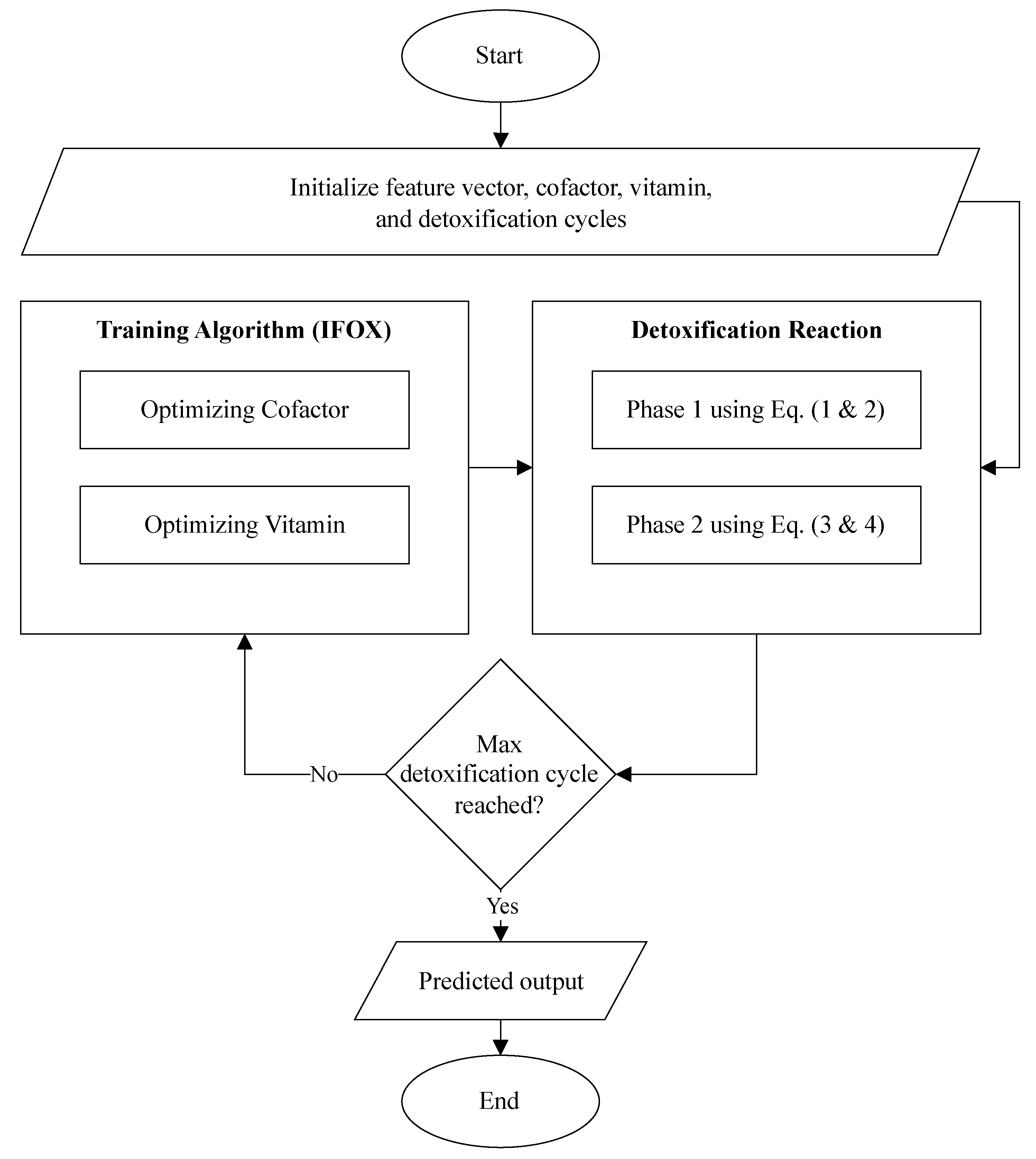
The Algorithm 1 and
Figure 2 describes the architecture of the proposed ALC. First, the cofactor and vitamin matrices are initialized randomly, where these matrices are defined based on the dimensions corresponding to the number of features (
f), number of lobules (
p), and number of output classes (
n). Next, the IFOX, as presented in Algorithm 2, is configured, specifying the number of detoxification cycles (maximum number of epochs) and detoxification power (maximum number of fox agents). The target objective function for optimization is the
REACTION procedure in Algorithm 1, where the IFOX optimizes the cofactor and vitamin matrices by minimizing the reaction error (i.e., loss). The optimized cofactor and vitamin matrices, resulting from the optimization process, are subsequently applied within the
REACTION along with the toxins (feature vector) to predict the output classes.
|
Algorithm 1 Artificial Liver Classifier (ALC) |
Input: toxins, number of features, number of lobules, number of outputs, detoxification cycles, and detoxification power.
Output: predicted classes. |
| 1: Initialize cofactor and vitamin matrices randomly. |
|
| 2: Initialize the training algorithm (IFOX). |
▹ Algorithm 2 |
| 3: Optimize cofactor and vitamin matrices using IFOX. |
|
| 4: Reaction(toxins, optimized cofactor, optimized vitamin) to compute final predictions. |
|
| 5: return predicted classes. |
|
| 6: procedure Reaction(toxins, cofactor, vitamin) |
|
| 7: Compute the reactive toxins. |
▹ using Equation 1
|
| 8: Activate reactive toxins. |
▹ using Equation 2
|
| 9: Perform conjugation to make toxins less harmful. |
▹ using Equation 3
|
| 10: Normalize outputs to obtain predicted classes. |
▹ using Equation 4
|
| 11: return predicted classes. |
|
| 12: end procedure
|
|
Furthermore, the flowchart visualized the proposed ALC is presented in
Figure 3. Additionally, the source code for the implementation of the proposed ALC can be accessed at the following repository:
https://github.com/mwdx93/alc.
4.2.2. Training Algorithm
The FOX, developed by Mohammed and Rashid in 2022, mimics the hunting behavior of red foxes by incorporating physics-based principles. These include prey detection based on sound and distance, agent’s jumping during the attack governed by gravity, and direction, as well as additional computations such as timing and walking [
17,
56]. These features make FOX a competitive optimization algorithm, outperformed several methods such as particle swarm optimization (PSO) and fitness dependent optimizer (FDO). The FOX is works as follows: Initially, the ground is covered with snow, requiring the fox agent to search randomly for its prey. During this random search, the fox agent uses the Doppler effect to detect and gradually approach the source of the sound. This process takes time and enables the fox agent to estimate the prey’s location by calculating the distance. Once the prey’s position is determined, the fox agent computes the required jump to catch it. Additionally, the search process is facilitated through controlled random walks, ensuring the fox agent progresses toward the prey while maintaining an element of randomness. The FOX balances exploitation and exploration phases statically, with a 50% probability for each [
57]. Thus, the FOX operates as follows:
However, the FOX has some limitations in its design. These limitations were acknowledged by the author of FOX [
56], while others have been identified through further analysis. For instance, one notable drawback is its static approach to balancing exploration and exploitation. This paper aims to address these limitations by proposing a new variation of the FOX called IFOX to make it integrable with the proposed ALC as a training algorithm to optimize the cofactor and vitamin matrices. For reference, the implementation of the FOX can be accessed at
https://github.com/hardi-mohammed/fox.
|
Algorithm 2 IFOX: new variation of FOX optimization algorithm |
Input: Maximum number of epochs , maximum number of fox agents
Output: and
- 1:
Initialize the fox agents population
- 2:
Initialize
- 3:
while do
- 4:
for all do
- 5:
- 6:
if then
- 7:
- 8:
- 9:
end if
- 10:
end for
- 11:
- 12:
- 13:
- 14:
- 15:
for all do
- 16:
- 17:
if then
- 18:
- 19:
else
- 20:
- 21:
end if
- 22:
end for
- 23:
- 24:
end while
|
The IFOX, as visualized in Algorithm 2, incorporates several improvements over the FOX. First, it transforms the balance between exploitation and exploration into a dynamic process using the
-greedy method, rather than a static approach [
58,
59]. This dynamic adjustment is controlled by the parameter
, which decreases progressively as the optimization process iterate. Second, the computation of distances is eliminated in favor of directly using the best position, facilitated by the parameter
, derived from
. This modification simplifies the FOX by removing Equations
5 and
6, and simplifying Equation
8 by eliminating the probability parameter
p and the directional variables (
and
). Third, in Equation
9, the variables
a and
are excluded. Finally, the results shown in
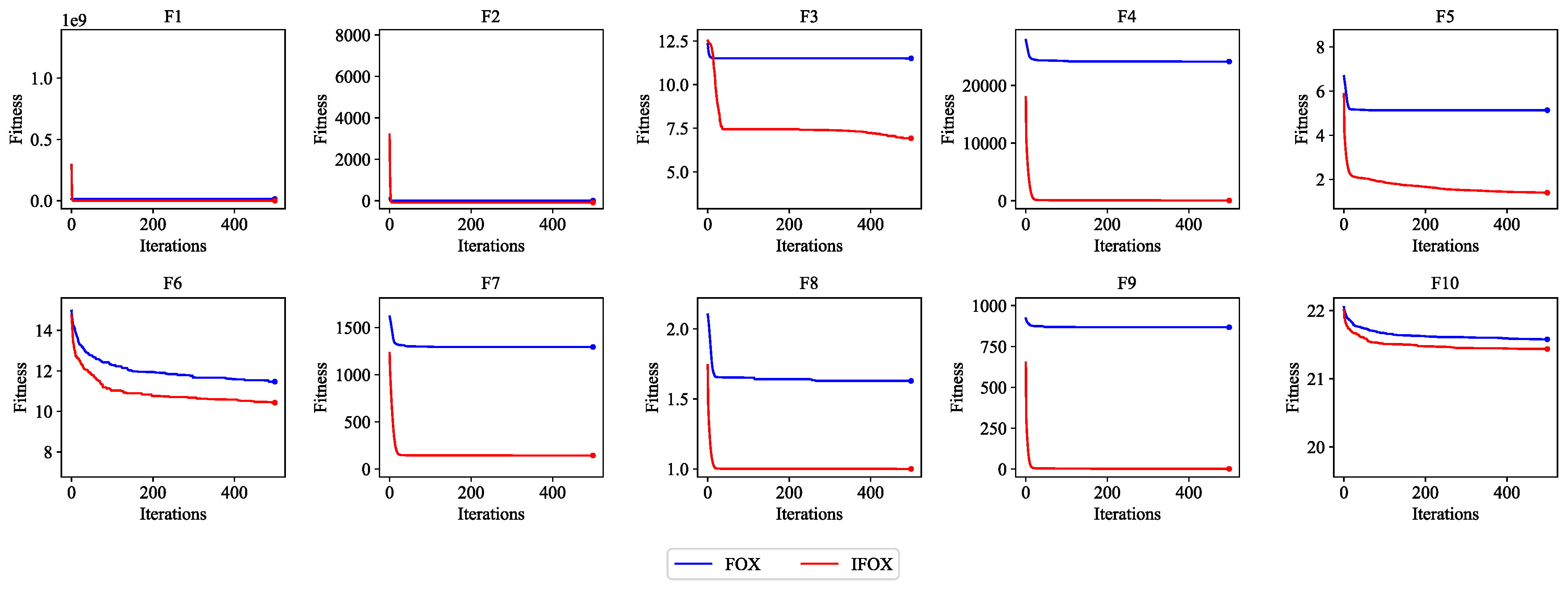
Figure 4 demonstrate that IFOX outperforms the FOX on the CEC2019 benchmark test functions, establishing it as a suitable training algorithm to integrate it with the proposed ALC.
5. Results
This section presents the performance results of the proposed ALC on multiple benchmark datasets, as described in
Section 4.1. The experimental parameter settings were configured for each dataset as follows: 500 detoxification cycles, a detoxification power of 10, and dataset-specific numbers of lobules. Specifically, the number of lobules was set to 10 for Iris Flower and Breast Cancer Wisconsin, 15 for Wine and Voice Gender, and 50 for MNIST. These values were adjusted based on several trials and errors. Moreover, each dataset has been split into a training set comprising 80% of the entire dataset and a validation set comprising 20%. To facilitate later comparison and analysis, additional classifiers, including MLP, SVM, LR, and XGBoost (XGB), were executed on the same datasets. However, all experiments were conducted on an MSI GL63 8RD laptop equipped with an Intel® Core™ i7-8750H × 12 processor and 32 GB of memory. This consistent setup ensured a robust evaluation of the proposed ALC alongside the other classifiers under the same conditions.
5.1. Performance Metrics
To evaluate the performance of the proposed ALC, several metrics were employed, including log loss (cross-entropy loss), accuracy, precision, recall, F1-score, and training time. Initially, Log loss (Equation
10) quantifies the divergence between predicted probabilities and actual labels, where lower values indicate better predictive performance [
60]. The accuracy (Equation
11) measures the proportion of correctly classified instances, serving as a straightforward indicator of overall correctness. Moreover, precision (Equation
12) evaluates the proportion of true positives among all positive predictions, emphasizing the model’s ability to reduce false positives. In contrast, recall (Equation
13) focuses on the proportion of true positives among all actual positive instances, highlighting the importance of minimizing false negatives. Furthermore, the F1-score (Equation
14), as the harmonic mean of precision and recall, provides a balanced assessment when class distributions are imbalanced [
61]. Moreover, the overfitting gap defined as the difference between training and validation accuracy, provides insights into generalization. A smaller value indicate better generalization, while a larger value indicates overfitting, where the model excels on the training set but struggles with unseen data. Finally, the training time reflects the duration required to train the model, offering insight into its computational efficiency.
where TP, TN, FP, and FN represent the true positive, true negative, false positive, and false negative counts, respectively. Additionally,
y denotes the actual labels, while
represents the predicted labels.
5.2. Experimental Results
The performance results of the proposed ALC are presents through this subsection, summarized in the figures and tables. Additionally, comparisons with other classifiers, including MLP, SVM, LR, and XGB, have been conducted on the five datasets described in
Section 4.1.
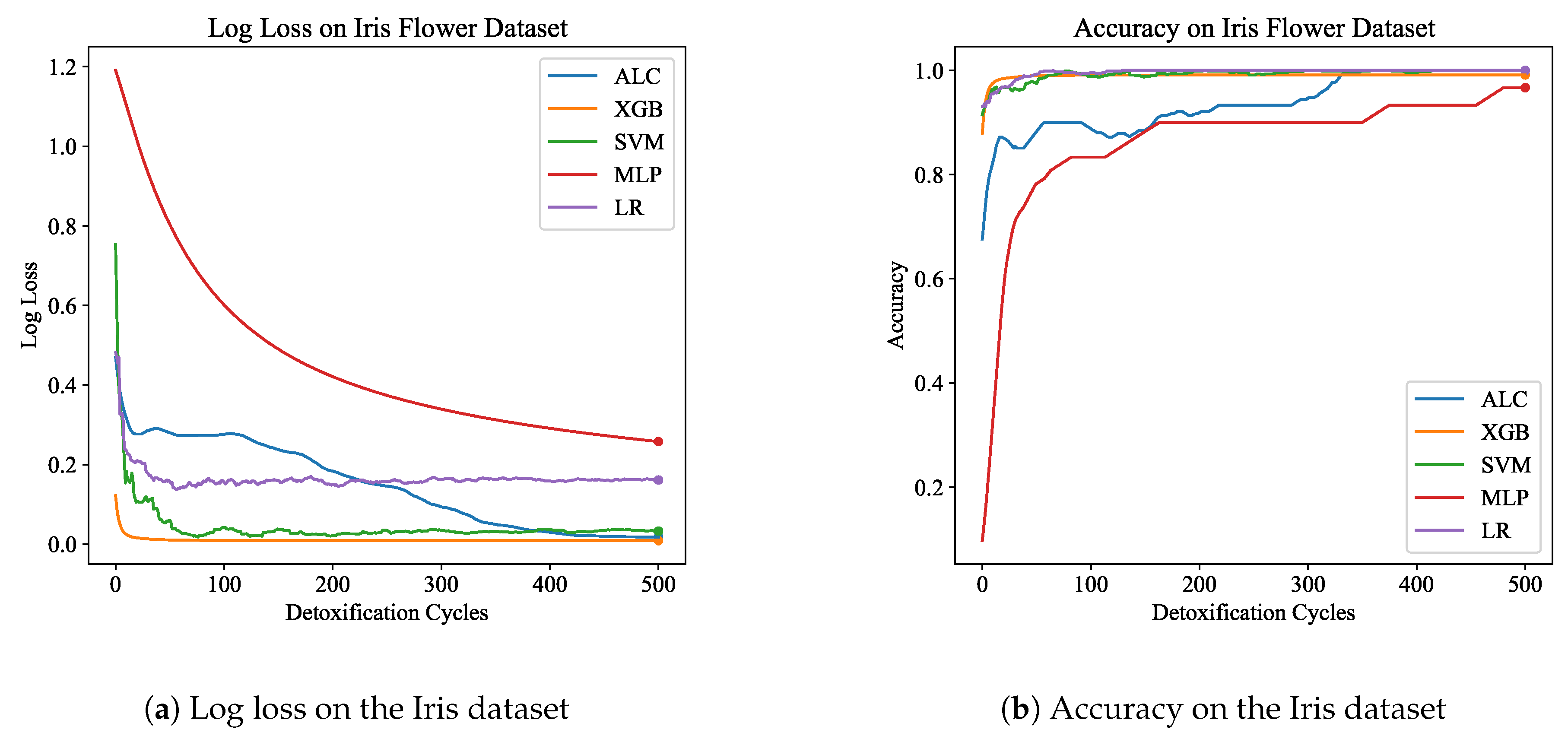
Table 1 presents the performance results of the proposed ALC and other classifiers on the Iris Flower dataset, for both the training and validation set. Additionally,
Figure 5a and
Figure 5b display the loss and accuracy, respectively, on the validation set. The proposed ALC achieved 100% accuracy on the validation set, with a loss of 0.0176 and an overfitting gap of -0.0241%, with a training time of 2.18 seconds. The XGB achieved 100% accuracy, with a loss of 0.0087 and an overfitting gap of -0.0121%, with a training time of 0.96 seconds. The SVM reached 100% accuracy, with a loss of 0.0704 and an overfitting gap of -0.0342%, with a training time of 4.13 seconds. The MLP achieved 96.67% accuracy, with a loss of 0.2543 and an overfitting gap of -0.0714%, with a training time of 4.28 seconds. Lastly, the LR reached 100% accuracy, with a loss of 0.0539 and an overfitting gap of -0.0438%, with a training time of 4.33 seconds.
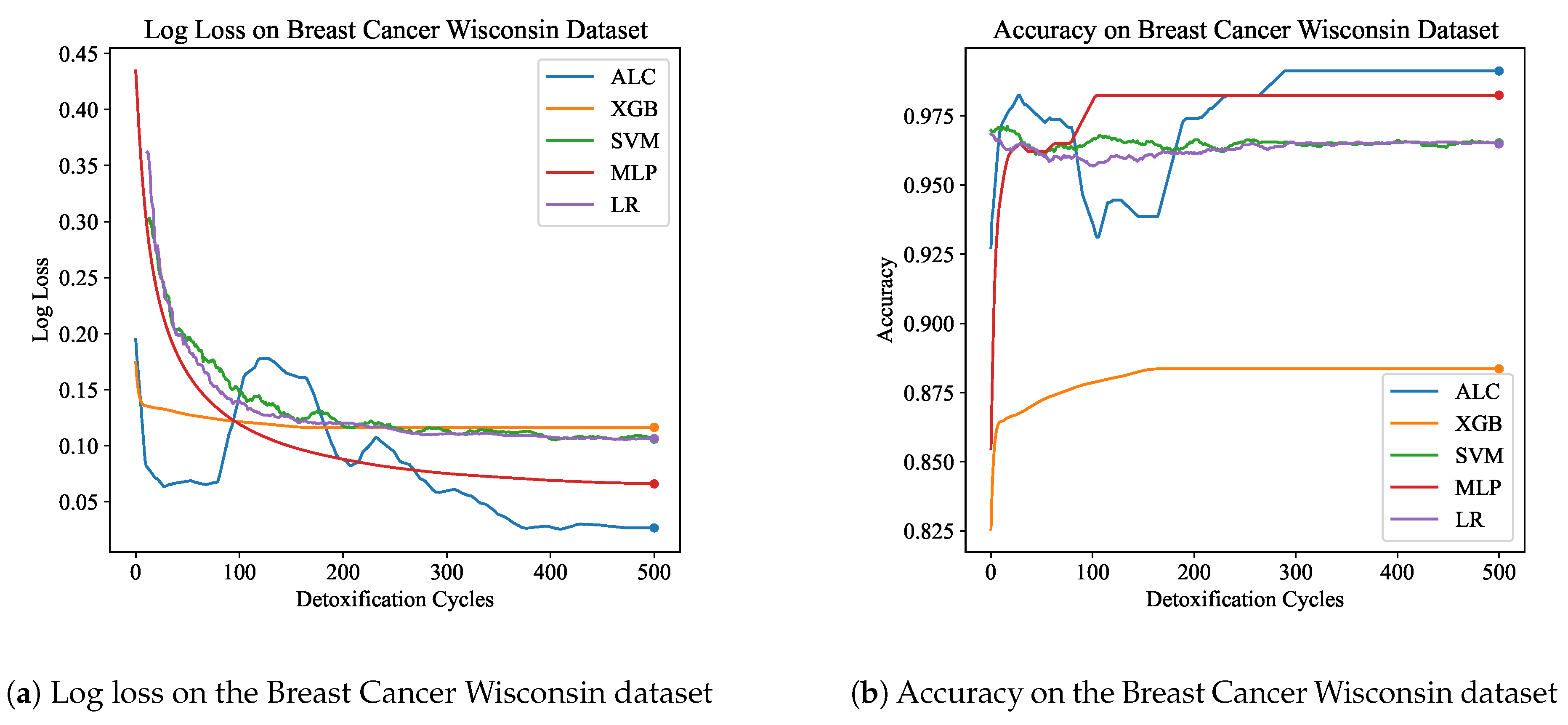
Table 2 presents the performance results of the proposed ALC and other classifiers on the Breast Cancer Wisconsin dataset, for both the training and validation sets.
Figure 6a and
Figure 6b display the loss and accuracy, respectively, on the validation set. The proposed ALC achieved 99.12% accuracy on the validation set, with a loss of 0.0267 and an overfitting gap of -0.0022%, with a training time of 3.27 seconds. The XGB achieved 88.36% accuracy, with a loss of 0.1164 and an overfitting gap of 0.1118%, with a training time of 1.14 seconds. The SVM reached 98.25% accuracy, with a loss of 0.1105 and an overfitting gap of 0.0263%, with a training time of 3.72 seconds. The MLP achieved 98.25% accuracy, with a loss of 0.0656 and an overfitting gap of 0.0066%, with a training time of 4.65 seconds. Lastly, the LR achieved 96.49% accuracy, with a loss of 0.1067 and an overfitting gap of 0.0241%, with a training time of 3.78 seconds.
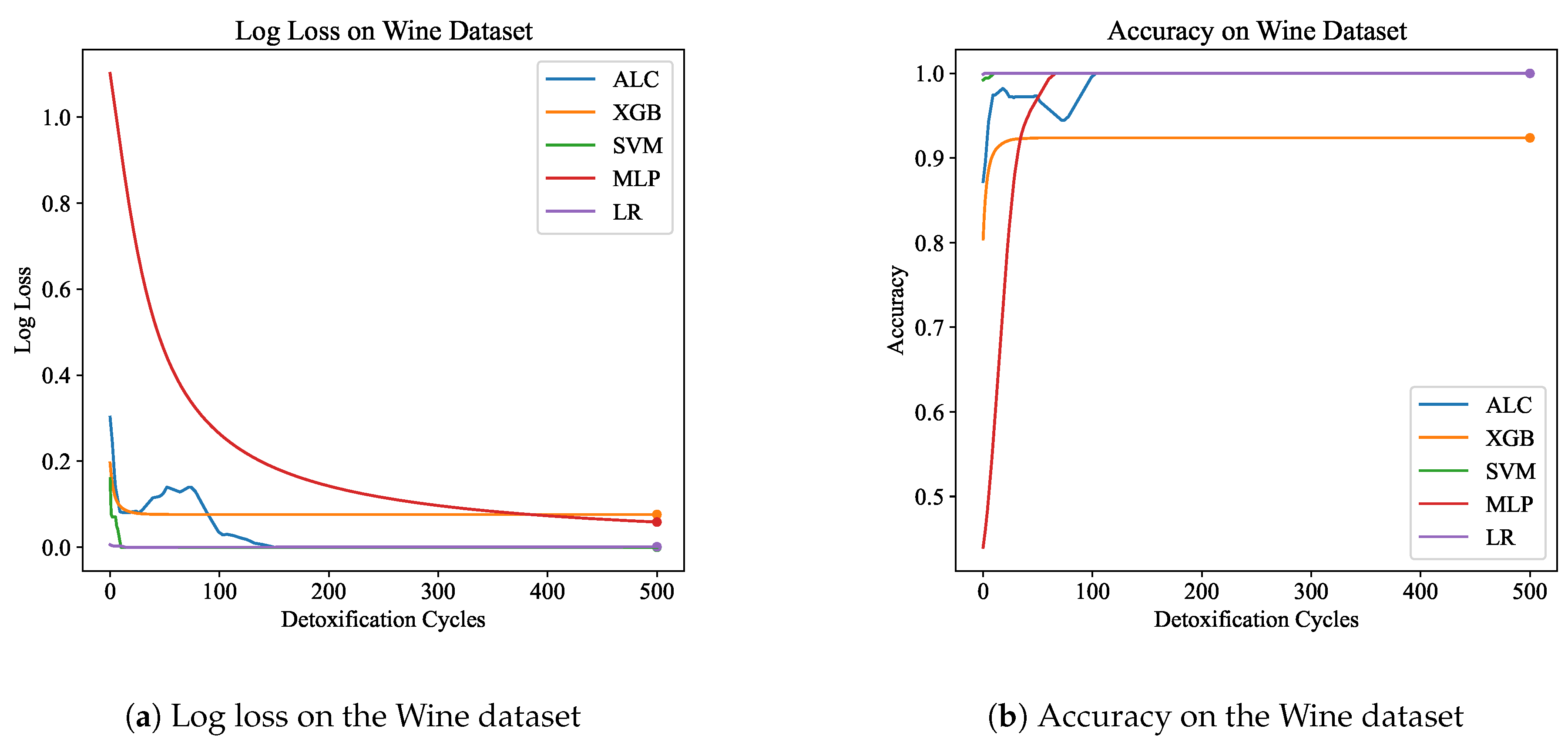
Table 3 presents the performance results of the proposed ALC and other classifiers on the Wine dataset.
Figure 7a and
Figure 7b display the loss and accuracy, respectively, on the validation set. The proposed ALC achieved 100% accuracy on the validation set, with a loss of 0.0002 and an overfitting gap of 0.0000%, with a training time of 2.41 seconds. The XGB achieved 92.38% accuracy, with a loss of 0.0762 and an overfitting gap of 0.0666%, with a training time of 1.15 seconds. The SVM achieved 100% accuracy, with a loss of 0.0001 and an overfitting gap of 0.0000%, with a training time of 3.94 seconds. The MLP achieved 100% accuracy, with a loss of 0.0572 and an overfitting gap of -0.0070%, with a training time of 3.84 seconds. Lastly, the LR achieved 100% accuracy, with a loss of 0.0012 and an overfitting gap of 0.0000%, with a training time of 3.84 seconds.
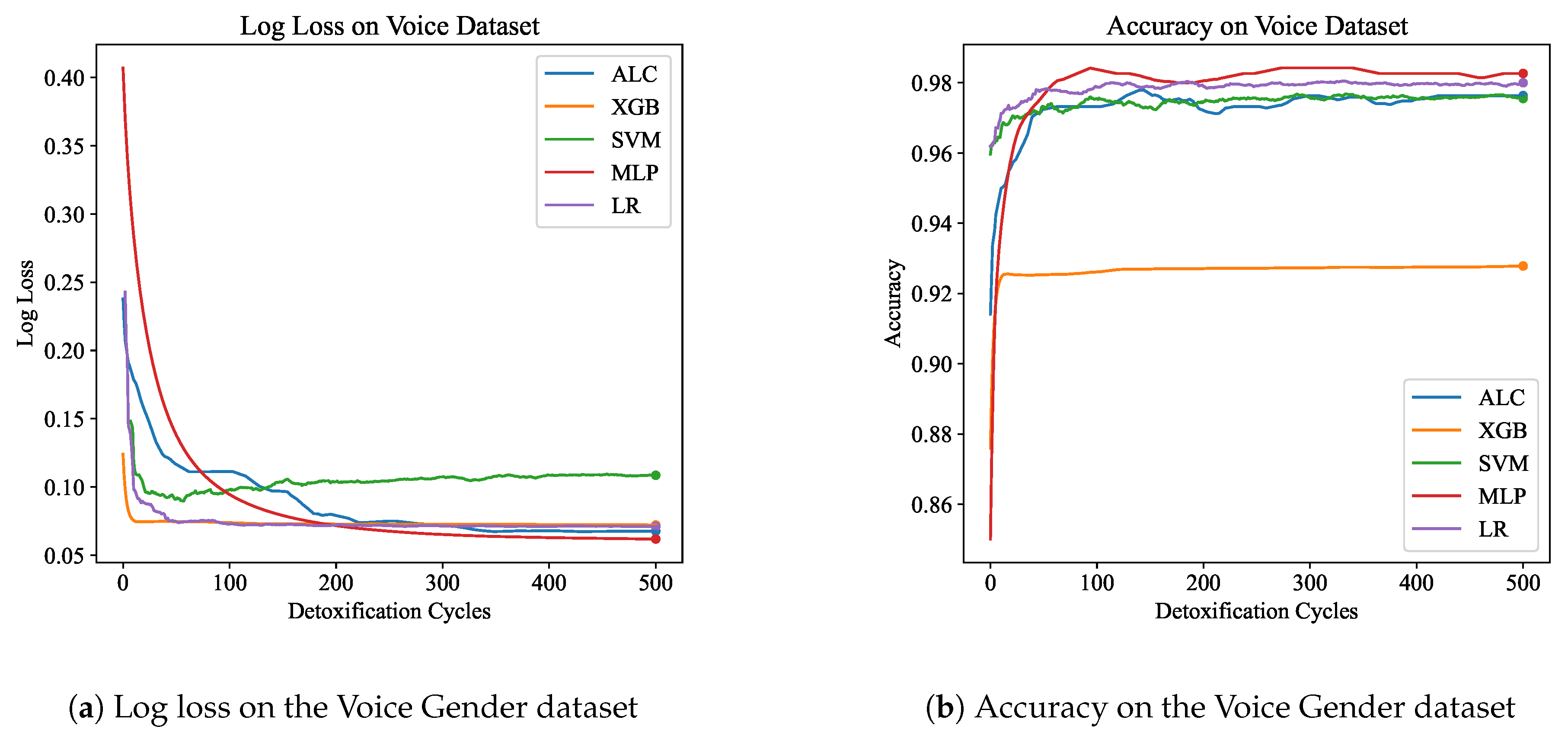
Table 4 presents the performance results of the proposed ALC and other classifiers on the Voice Gender dataset.
Figure 8a and
Figure 8b display the log loss and accuracy, respectively, on the validation set. The proposed ALC achieved 97.63% accuracy on the validation set, with a loss of 0.0677 and an overfitting gap of 0.0004%, with a training time of 3.17 seconds. The XGB achieved 92.79% accuracy, with a loss of 0.0721 and an overfitting gap of 0.0709%, with a training time of 1.24 seconds. The SVM achieved 97.32% accuracy, with a loss of 0.1136 and an overfitting gap of 0.0043%, with a training time of 4.24 seconds. The MLP achieved 98.26% accuracy, with a loss of 0.0618 and an overfitting gap of -0.0036%, with a training time of 12.70 seconds. Lastly, the LR achieved 98.11% accuracy, with a loss of 0.0709 and an overfitting gap of -0.0063%, with a training time of 4.44 seconds.
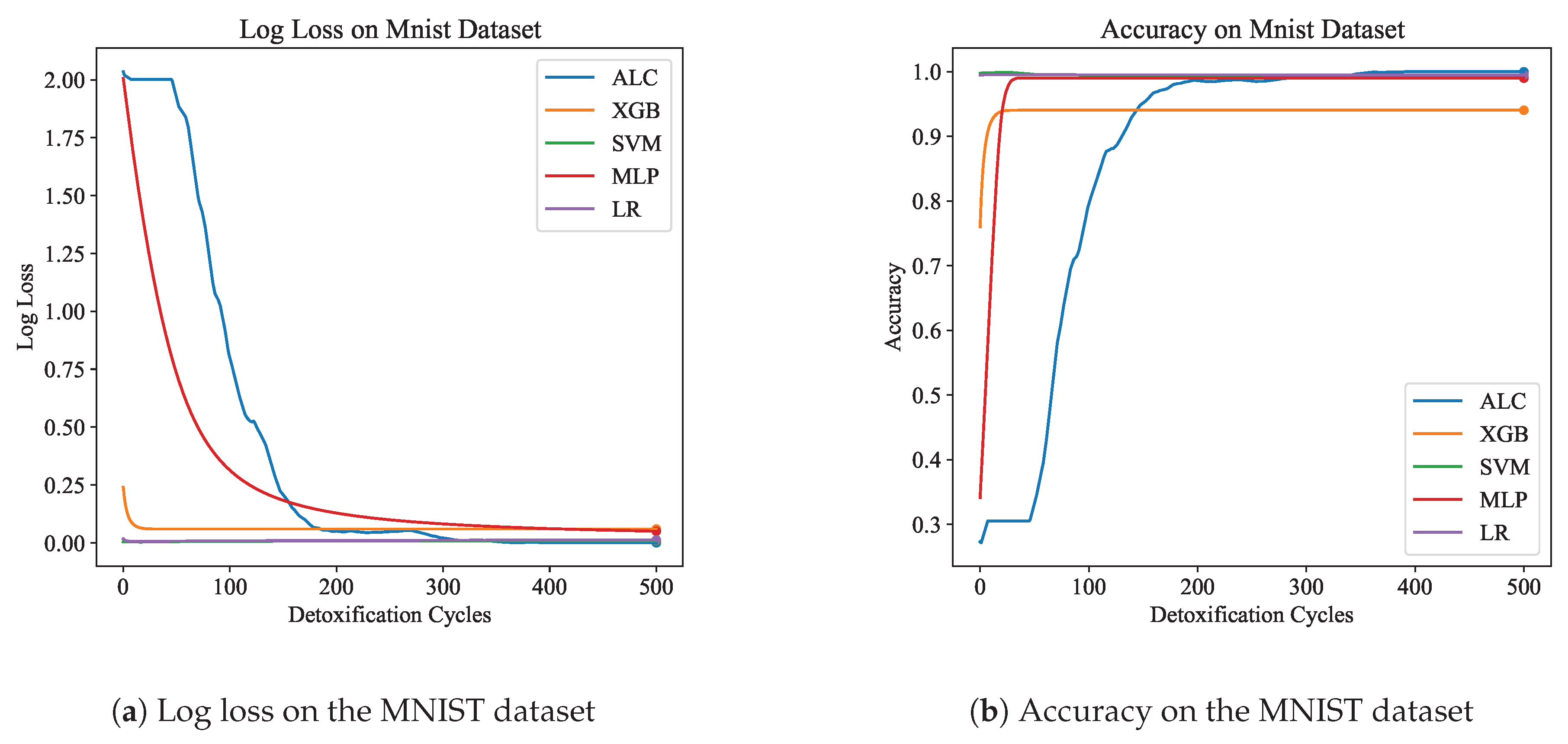
Table 5 presents the performance results of the proposed ALC and other classifiers on the MNIST dataset.
Figure 9a and
Figure 9b display the log loss and accuracy, respectively, on the validation set. The proposed ALC achieved 99.75% accuracy on the validation set, with a loss of 0.0000 and an overfitting gap of 0.0025%, with a training time of 6.04 seconds. The XGB achieved 94.05% accuracy, with a loss of 0.0595 and an overfitting gap of 0.0535%, with a training time of 2.40 seconds. The SVM achieved 99.50% accuracy, with a loss of 0.0082 and an overfitting gap of 0.0050%, with a training time of 5.46 seconds. The MLP achieved 99.00% accuracy, with a loss of 0.0489 and an overfitting gap of 0.0100%, with a training time of 5.27 seconds. Lastly, the LR achieved 99.50% accuracy, with a loss of 0.0123 and an overfitting gap of 0.0050%, with a training time of 5.56 seconds.
In summary, the proposed ALC outperformed or matched other classifiers across the datasets tested, including Iris, Breast Cancer Wisconsin, Wine, Voice Gender, and MNIST. The results demonstrated superior loss, accuracy, precision, recall, and F1-scores, highlighting the reliability and generalization of the proposed ALC in achieving high classification performance. Furthermore, the proposed ALC exhibited minimal overfitting and efficient training times compared to other classifiers. However, the next section will provide a detailed analysis and interpretation of these results, and shedding light on limitations and imperfections of the proposed ALC.
6. Discussion
The results presented in
Section 5.2, derived from experiments conducted on the datasets described in
Section 4.1, highlight the superior performance of the proposed ALC compared to other classifiers. However, a more in-depth statistical analysis is necessary, particularly of the validation set results, as they are considered more reliable indicators of classifier performance due to being obtained from unseen data. The statistical analysis presented in
Table 6 compare the performance of the proposed ALC with four classifiers—XGB, SVM, MLP, and LR—across the five datasets described in
Section 4.1. The analysis focuses on four metrics: loss, accuracy, overfitting gap, and training time, with statistical significance determined using the Wilcoxon signed-rank test at a threshold of
. The Wilcoxon signed-rank test is used to compare paired samples, particularly when data may not follow a normal distribution. It assesses whether the differences between paired observations are statistically significant [
62]. Hence, this analysis results provide insights into the strengths of the proposed ALC in terms of its generalization, accuracy, and computational efficiency.
The loss metric, which is a primary indicator of classifier generalizability, demonstrates that the proposed ALC outperforms other classifiers in several datasets. Specifically, in the Iris Flower dataset, the proposed ALC showed statistically significant improvements in loss compared to SVM (), MLP (), and LR (), while its performance was comparable to XGB (), indicating XGB outperforms the proposed ALC. Similarly, in the Breast Cancer Wisconsin dataset, the proposed ALC showed significant improvements over XGB (), SVM (), MLP (), and LR (). In the Wine dataset, the proposed ALC demonstrated significant improvements compared to XGB (), MLP (), and LR (), but did not show statistically significant with SVM (). These trends were consistent in more complex datasets like Voice Gender and MNIST, where the proposed ALC achieved lower loss values compared to other classifiers in most cases (). The findings indicate that the proposed ALC offers better generalization across these datasets of varying complexity.
In terms of accuracy, the differences between the proposed ALC and other classifiers were generally less pronounced, as reflected by
P-values exceeding 0.05 in most datasets. Notable exceptions include the Voice Gender dataset, where the proposed ALC significantly outperformed SVM (
), and the Breast Cancer Wisconsin dataset, where the proposed ALC showed an advantage over XGB (
). Furthermore, additional accuracy comparisons were conducted with other models discussed in the related work
Section 2, as presented in
Table 7, demonstrating the superiority of the proposed ALC. These results suggest that while accuracy remains an important metric, it may not always effectively differentiate the performance of classifiers, particularly when accuracy levels are already high across classifiers [
63].
The overfitting gap metric, which measures the difference in performance between the training and validation sets, disclose that the proposed ALC achieves better generalization. Significant improvements were observed across most datasets, including Breast Cancer Wisconsin and MNIST, where P-values were consistently below 0.05. However, in the Wine dataset, the differences in the overfitting gap were less consistent, with P-values often exceeding the significance threshold (). These findings underline the ability of the proposed ALC to reducing the risk of overfitting.
The training time metric, which evaluates the computational efficiency of the classifiers, indicates that the proposed ALC maintains competitive performance while being efficient. Significant differences in training time were observed in smaller datasets, such as Iris Flower, Breast Cancer Wisconsin, Wine, and Voice Gender. However, for larger and more complex datasets like MNIST, the training time of the proposed ALC was comparable to that of other classifiers (). The proposed ALC showed a lack of significant differences compared to XGB due to it’s use of tree-based models, which generally demonstrate faster processing times.
The proposed ALC did not employ mini-batch training methods, such as stochastic gradient descent (SDG), which are commonly used to reduce computational costs compared to full-batch training [
64]. While this limitation may result in longer training times for large datasets, the focus of this work was to demonstrate the performance of the proposed classifier rather than to optimize computational efficiency. Future research could explore integrating mini-batch training, parallelism, or other efficiency-enhancing techniques to address this limitation. Additionally, the proposed ALC exhibits slower convergence due to its reliance on a stochastic optimizer that does not directly utilize the training error for parameter optimization, particularly for the cofactor and vitamin metrics. Improving convergence rates could be achieved through the adoption of guided optimization algorithms, enhancements to IFOX, or the development of alternative methods, presenting promising avenues for future advancements.
7. Conclusions
In conclusion, this paper suggests a novel supervised learning classifier, termed the artificial liver classifier (ALC), inspired by the human liver’s detoxification function. The ALC is easy to implement, fast, and capable of reducing overfitting by simulating the detoxification function through straightforward mathematical operations. Furthermore, it introduces an improvement to the FOX optimization algorithm, referred to as IFOX, which is integrated with the ALC as training algorithm to optimize parameters effectively. Furthermore, the ALC was evaluated on five benchmark machine learning datasets: Iris Flower, Breast Cancer Wisconsin, Wine, Voice Gender, and MNIST. The empirical results demonstrated its superior performance compared to support vector machines, multilayer perceptrons, logistic regression, XGBoost and other established classifiers. Despite these superiority, the ALC has limitations, such as longer training times on large datasets and slower convergence rates, which could be addressed in future work using methods like mini-batch training or parallel processing. Finally, this paper underscores the potential of biologically inspired models and encourages researchers to simulate natural functions to develop more efficient and powerful machine learning models.
Author Contributions
Conceptualization, M.A.J and T.A.R; methodology, M.A.J and T.A.R; software, M.A.J; validation, M.A.J, Y.H.A and T.A.R; formal analysis, M.A.J; investigation, M.A.J, Y.H.A and T.A.R; resources, M.A.J; data curation, M.A.J; writing—original draft, M.A.J; writing—review and editing, M.A.J, Y.H.A and T.A.R; visualization, M.A.J; supervision, Y.H.A and T.A.R; project administration, M.A.J, Y.H.A and T.A.R; funding acquisition, M.A.J and T.A.R. All authors have read and agreed to the published version of the manuscript.
Funding
The authors received no funding for this study.
Data Availability Statement
The data used in this paper is publicly available. Detailed descriptions, including links and sources for each dataset, are provided within the respective sections of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kolides, A.; Nawaz, A.; Rathor, A.; Beeman, D.; Hashmi, M.; Fatima, S.; Berdik, D.; Al-Ayyoub, M.; Jararweh, Y. Artificial intelligence foundation and pre-trained models: Fundamentals, applications, opportunities, and social impacts. Simulation Modelling Practice and Theory 2023, 126, 102754. [CrossRef]
- Dwivedi, Y.K.; Hughes, L.; Ismagilova, E.; Aarts, G.; Coombs, C.; Crick, T.; Duan, Y.; Dwivedi, R.; Edwards, J.; Eirug, A.; et al. Artificial Intelligence (AI): Multidisciplinary perspectives on emerging challenges, opportunities, and agenda for research, practice and policy. International Journal of Information Management 2021, 57, 101994. [CrossRef]
- Khudhair, A.T.; Maolood, A.T.; Gbashi, E.K. Symmetry Analysis in Construction Two Dynamic Lightweight S-Boxes Based on the 2D Tinkerbell Map and the 2D Duffing Map. Symmetry 2024, 16, 872. [CrossRef]
- Jiang, T.; Gradus, J.L.; Rosellini, A.J. Supervised Machine Learning: A Brief Primer. Behavior Therapy 2020, 51, 675–687. [CrossRef]
- Beam, K.S.; Zupancic, J.A.F. Machine learning: remember the fundamentals. Pediatric Research 2022, 93, 291–292. [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A comparison review of transfer learning and self-supervised learning: Definitions, applications, advantages and limitations. Expert Systems with Applications 2024, 242, 122807. [CrossRef]
- Watson, D.S. On the Philosophy of Unsupervised Learning. Philosophy & Technology 2023, 36. [CrossRef]
- Molnar, C.; Casalicchio, G.; Bischl, B., Interpretable Machine Learning – A Brief History, State-of-the-Art and Challenges. In ECML PKDD 2020 Workshops; Springer International Publishing, 2020; p. 417–431. [CrossRef]
- Gao, Q.; Schweidtmann, A.M. Deep reinforcement learning for process design: Review and perspective. Current Opinion in Chemical Engineering 2024, 44, 101012. [CrossRef]
- Mutar, H.; Jawad, M. Analytical Study for Optimization Techniques to Prolong WSNs Life. IRAQI JOURNAL OF COMPUTERS, COMMUNICATIONS, CONTROL AND SYSTEMS ENGINEERING 2023, 23, 13–23. [CrossRef]
- Ismael, M.H.; Maolood, A.T. WITHDRAWN: Developing modern system in healthcare to detect COVID 19 based on Internet of Things. Materials Today: Proceedings 2021. [CrossRef]
- Khudhair, A.T.; Maolood, A.T.; Gbashi, E.K. Symmetric Keys for Lightweight Encryption Algorithms Using a Pre–Trained VGG16 Model. Telecom 2024, 5, 892–906. [CrossRef]
- Grzybowski, A.; Pawlikowska–Łagód, K.; Lambert, W.C. A History of Artificial Intelligence. Clinics in Dermatology 2024, 42, 221–229. [CrossRef]
- Jabber, S.; Hashem, S.; Jafer, S. Analytical and Comparative Study for Optimization Problems. IRAQI JOURNAL OF COMPUTERS, COMMUNICATIONS, CONTROL AND SYSTEMS ENGINEERING 2023, 23, 46–57. [CrossRef]
- Palanivinayagam, A.; El-Bayeh, C.Z.; Damaševičius, R. Twenty Years of Machine-Learning-Based Text Classification: A Systematic Review. Algorithms 2023, 16, 236. [CrossRef]
- Schmidgall, S.; Ziaei, R.; Achterberg, J.; Kirsch, L.; Hajiseyedrazi, S.P.; Eshraghian, J. Brain-inspired learning in artificial neural networks: A review. APL Machine Learning 2024, 2. [CrossRef]
- Jumaah, M.A.; Ali, Y.H.; Rashid, T.A.; Vimal, S. FOXANN: A Method for Boosting Neural Network Performance. Journal of Soft Computing and Computer Applications 2024, 1. [CrossRef]
- Jumin, E.; Zaini, N.; Ahmed, A.N.; Abdullah, S.; Ismail, M.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Machine learning versus linear regression modelling approach for accurate ozone concentrations prediction. Engineering Applications of Computational Fluid Mechanics 2020, 14, 713–725. [CrossRef]
- Quan, Z.; Pu, L. An improved accurate classification method for online education resources based on support vector machine (SVM): Algorithm and experiment. Education and Information Technologies 2022, 28, 8097–8111. [CrossRef]
- Tufail, S.; Riggs, H.; Tariq, M.; Sarwat, A.I. Advancements and Challenges in Machine Learning: A Comprehensive Review of Models, Libraries, Applications, and Algorithms. Electronics 2023, 12, 1789. [CrossRef]
- Khudhair, A.T.; Maolood, A.T.; Gbashi, E.K. A Novel Approach to Generate Dynamic S-Box for Lightweight Cryptography Based on the 3D Hindmarsh Rose Model. Journal of Soft Computing and Computer Applications 2024, 1. [CrossRef]
- Tan, Y.; An, K.; Su, J. Review: Mechanism of herbivores synergistically metabolizing toxic plants through liver and intestinal microbiota. Comparative Biochemistry and Physiology Part C: Toxicology & Pharmacology 2024, 281, 109925. [CrossRef]
- Ishibashi, H.; Nakamura, M.; Komori, A.; Migita, K.; Shimoda, S. Liver architecture, cell function, and disease. Seminars in Immunopathology 2009, 31, 399–409. [CrossRef]
- Hoffmann, F.; Bertram, T.; Mikut, R.; Reischl, M.; Nelles, O. Benchmarking in classification and regression. WIREs Data Mining and Knowledge Discovery 2019, 9. [CrossRef]
- Seliya, N.; Abdollah Zadeh, A.; Khoshgoftaar, T.M. A literature review on one-class classification and its potential applications in big data. Journal of Big Data 2021, 8. [CrossRef]
- N, P.; G, M. A Review: Binary Classification and Hybrid Segmentation of Brain Stroke using Transfer Learning-Based Approach. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT). IEEE, 2023, p. 1–6. [CrossRef]
- Sidumo, B.; Sonono, E.; Takaidza, I. An approach to multi-class imbalanced problem in ecology using machine learning. Ecological Informatics 2022, 71, 101822. [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Computer Science 2021, 2. [CrossRef]
- Azevedo, B.F.; Rocha, A.M.A.C.; Pereira, A.I. Hybrid approaches to optimization and machine learning methods: a systematic literature review. Machine Learning 2024, 113, 4055–4097. [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: a Novel Image Dataset for Benchmarking Machine Learning Algorithms, 2017. [CrossRef]
- Cohen, G.; Afshar, S.; Tapson, J.; van Schaik, A. EMNIST: an extension of MNIST to handwritten letters, 2017. [CrossRef]
- Cortez, P.; Cerdeira, A.; Almeida, F.; Matos, T.; Reis, J. Modeling wine preferences by data mining from physicochemical properties. Decision Support Systems 2009, 47, 547–553. [CrossRef]
- Rajeswari, V.; Sakthi Priya, K. Ontological modeling with recursive recurrent neural network and crayfish optimization for reliable breast cancer prediction. Biomedical Signal Processing and Control 2025, 99, 106810. [CrossRef]
- Fan, S.; Li, H.; Guo, C.; Liu, D.; Zhang, L. A novel cost-sensitive three-way intuitionistic fuzzy large margin classifier. Information Sciences 2024, 674, 120726. [CrossRef]
- Buyukyilmaz, M.; Cibikdiken, A.O. Voice Gender Recognition Using Deep Learning. In Proceedings of the Proceedings of 2016 International Conference on Modeling, Simulation and Optimization Technologies and Applications (MSOTA2016). Atlantis Press, 2016, msota-16. [CrossRef]
- Moradi, E.; Jalili-Firoozinezhad, S.; Solati-Hashjin, M. Microfluidic organ-on-a-chip models of human liver tissue. Acta Biomaterialia 2020, 116, 67–83. [CrossRef]
- Kennedy, C.C.; Brown, E.E.; Abutaleb, N.O.; Truskey, G.A. Development and Application of Endothelial Cells Derived From Pluripotent Stem Cells in Microphysiological Systems Models. Frontiers in Cardiovascular Medicine 2021, 8. [CrossRef]
- Schlegel, A.; Mergental, H.; Fondevila, C.; Porte, R.J.; Friend, P.J.; Dutkowski, P. Machine perfusion of the liver and bioengineering. Journal of Hepatology 2023, 78, 1181–1198. [CrossRef]
- Gibert-Ramos, A.; Sanfeliu-Redondo, D.; Aristu-Zabalza, P.; Martínez-Alcocer, A.; Gracia-Sancho, J.; Guixé-Muntet, S.; Fernández-Iglesias, A. The Hepatic Sinusoid in Chronic Liver Disease: The Optimal Milieu for Cancer. Cancers 2021, 13, 5719. [CrossRef]
- Donati, G.; Angeletti, A.; Gasperoni, L.; Piscaglia, F.; Croci Chiocchini, A.L.; Scrivo, A.; Natali, T.; Ullo, I.; Guglielmo, C.; Simoni, P.; et al. Detoxification of bilirubin and bile acids with intermittent coupled plasmafiltration and adsorption in liver failure (HERCOLE study). Journal of Nephrology 2020, 34, 77–88. [CrossRef]
- Guengerich, F.P. A history of the roles of cytochrome P450 enzymes in the toxicity of drugs. Toxicological Research 2020, 37, 1–23. [CrossRef]
- Sun, H.; Schanze, K.S. Functionalization of Water-Soluble Conjugated Polymers for Bioapplications. ACS Applied Materials &; Interfaces 2022, 14, 20506–20519. [CrossRef]
- Zhang, A.; Meng, K.; Liu, Y.; Pan, Y.; Qu, W.; Chen, D.; Xie, S. Absorption, distribution, metabolism, and excretion of nanocarriers in vivo and their influences. Advances in Colloid and Interface Science 2020, 284, 102261. [CrossRef]
- Nikmaneshi, M.R.; Firoozabadi, B.; Munn, L.L. A mechanobiological mathematical model of liver metabolism. Biotechnology and Bioengineering 2020, 117, 2861–2874. [CrossRef]
- G, E.R.; M, S.; G, A.R.; D, S.; Keerthi, T.; R, R.S. MNIST Handwritten Digit Recognition using Machine Learning. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE). IEEE, 2022, p. 768–772. [CrossRef]
- Lasalvia, M.; Capozzi, V.; Perna, G. A Comparison of PCA-LDA and PLS-DA Techniques for Classification of Vibrational Spectra. Applied Sciences 2022, 12, 5345. [CrossRef]
- Goyal, S.; Sharma, A.; Gupta, P.; Chandi, P., Assessment of Iris Flower Classification Using Machine Learning Algorithms. In Soft Computing for Intelligent Systems; Springer Singapore, 2021; p. 641–649. [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Ajibare, A.T.; Akinyemi, L.A.; Mirjalili, S., Tuning SVMs’ hyperparameters using the whale optimization algorithm. In Handbook of Whale Optimization Algorithm; Elsevier, 2024; p. 495–521. [CrossRef]
- Kumar, M.; Mehta, U.; Cirrincione, G. Enhancing neural network classification using fractional-order activation functions. AI Open 2024, 5, 10–22. [CrossRef]
- Alshayeji, M.H.; Ellethy, H.; Abed, S.; Gupta, R. Computer-aided detection of breast cancer on the Wisconsin dataset: An artificial neural networks approach. Biomedical Signal Processing and Control 2022, 71, 103141. [CrossRef]
- Waheed, Z.; Humaidi, A. Whale Optimization Algorithm Enhances the Performance of Knee-Exoskeleton System Controlled by SMC. IRAQI JOURNAL OF COMPUTERS, COMMUNICATIONS, CONTROL AND SYSTEMS ENGINEERING 2023, 23, 125–135. [CrossRef]
- Krebs, N.J.; Neville, C.; Vacanti, J.P., Cellular Transplants for Liver Diseases. In Cellular Transplantation; Elsevier, 2007; p. 215–240. [CrossRef]
- Bridle, J.S., Probabilistic Interpretation of Feedforward Classification Network Outputs, with Relationships to Statistical Pattern Recognition. In Neurocomputing; Springer Berlin Heidelberg, 1990; p. 227–236. [CrossRef]
- Arora, A.; Alsadoon, O.H.; Khairi, T.W.A.; Rashid, T.A. A Novel Softmax Regression Enhancement for Handwritten Digits Recognition using Tensor Flow Library. In Proceedings of the 2020 5th International Conference on Innovative Technologies in Intelligent Systems and Industrial Applications (CITISIA). IEEE, 2020, p. 1–9. [CrossRef]
- Maharjan, S.; Alsadoon, A.; Prasad, P.; Al-Dalain, T.; Alsadoon, O.H. A novel enhanced softmax loss function for brain tumour detection using deep learning. Journal of Neuroscience Methods 2020, 330, 108520. [CrossRef]
- Mohammed, H.; Rashid, T. FOX: a FOX-inspired optimization algorithm. Applied Intelligence 2022, 53, 1030–1050. [CrossRef]
- Aula, S.A.; Rashid, T.A. FOX-TSA: Navigating Complex Search Spaces and Superior Performance in Benchmark and Real-World Optimization Problems. Ain Shams Engineering Journal 2025, 16, 103185. [CrossRef]
- Liu, Y.; Cao, B.; Li, H. Improving ant colony optimization algorithm with epsilon greedy and Levy flight. Complex &; Intelligent Systems 2020, 7, 1711–1722. [CrossRef]
- Abdalrdha, Z.K.; Al-Bakry, A.M.; Farhan, A.K. CNN Hyper-Parameter Optimizer based on Evolutionary Selection and GOW Approach for Crimes Tweet Detection. In Proceedings of the 2023 16th International Conference on Developments in eSystems Engineering (DeSE). IEEE, 2023. [CrossRef]
- XUE, Y.; JIN, G.; SHEN, T.; TAN, L.; WANG, L. Template-guided frequency attention and adaptive cross-entropy loss for UAV visual tracking. Chinese Journal of Aeronautics 2023, 36, 299–312. [CrossRef]
- Naidu, G.; Zuva, T.; Sibanda, E.M., A Review of Evaluation Metrics in Machine Learning Algorithms. In Artificial Intelligence Application in Networks and Systems; Springer International Publishing, 2023; p. 15–25. [CrossRef]
- Hodges, C.B.; Stone, B.M.; Johnson, P.K.; Carter, J.H.; Sawyers, C.K.; Roby, P.R.; Lindsey, H.M. Researcher degrees of freedom in statistical software contribute to unreliable results: A comparison of nonparametric analyses conducted in SPSS, SAS, Stata, and R. Behavior Research Methods 2022, 55, 2813–2837. [CrossRef]
- Qu, Y.; Roitero, K.; Barbera, D.L.; Spina, D.; Mizzaro, S.; Demartini, G. Combining Human and Machine Confidence in Truthfulness Assessment. Journal of Data and Information Quality 2022, 15, 1–17. [CrossRef]
- Wojtowytsch, S. Stochastic Gradient Descent with Noise of Machine Learning Type Part I: Discrete Time Analysis. Journal of Nonlinear Science 2023, 33. [CrossRef]
Figure 2.
Architecture of the proposed ALC.
Figure 2.
Architecture of the proposed ALC.
Figure 3.
Flowchart of the proposed ALC.
Figure 3.
Flowchart of the proposed ALC.
Figure 4.
Convergence performance curve of the FOX (blue) and IFOX (red) on the CEC2019 benchmark test functions. Lower fitness values indicate better convergence performance.
Figure 4.
Convergence performance curve of the FOX (blue) and IFOX (red) on the CEC2019 benchmark test functions. Lower fitness values indicate better convergence performance.
Figure 5.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Iris dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 5.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Iris dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 6.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Breast Cancer Wisconsin dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 6.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Breast Cancer Wisconsin dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 7.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Wine dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 7.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Wine dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 8.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Voice Gender dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 8.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the Voice Gender dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 9.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the MNIST dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Figure 9.
Performance results comparison of the proposed ALC (blue) with other classifiers on the validation set of the MNIST dataset. Subfigure (a) shows the log loss values, and subfigure (b) shows accuracy.
Table 1.
Performance results of the proposed ALC and other classifiers on the Iris Flower dataset.
Table 1.
Performance results of the proposed ALC and other classifiers on the Iris Flower dataset.
| Classifier |
ALC |
XGB |
SVM |
MLP |
LR |
| Training set results |
| Loss |
0.0514 |
0.0151 |
0.0668 |
0.3129 |
0.1034 |
| Accuracy |
0.9917 |
1.0000 |
0.9750 |
0.9000 |
0.9750 |
| Precision |
0.9919 |
1.0000 |
0.9767 |
0.9057 |
0.9768 |
| Recall |
0.9917 |
1.0000 |
0.9750 |
0.9000 |
0.9750 |
| F1-Score |
0.9917 |
1.0000 |
0.9750 |
0.8996 |
0.9750 |
| Validation set results |
| Loss |
0.0176 |
0.0087 |
0.0704 |
0.2543 |
0.0539 |
| Accuracy |
1.0000 |
1.0000 |
1.0000 |
0.9667 |
1.0000 |
| Precision |
1.0000 |
1.0000 |
1.0000 |
0.9694 |
1.0000 |
| Recall |
1.0000 |
1.0000 |
1.0000 |
0.9667 |
1.0000 |
| F1-Score |
1.0000 |
1.0000 |
1.0000 |
0.9664 |
1.0000 |
| Overfitting |
-0.0241% |
-0.0121% |
-0.0342% |
-0.0714% |
-0.0438% |
| Time (sec.) |
2.18 |
0.96 |
4.13 |
4.28 |
4.33 |
Table 2.
Performance results of the proposed ALC and other classifiers on the Breast Cancer Wisconsin dataset.
Table 2.
Performance results of the proposed ALC and other classifiers on the Breast Cancer Wisconsin dataset.
| Classifier |
ALC |
XGB |
SVM |
MLP |
LR |
| Training set results |
| Loss |
0.0200 |
0.0047 |
0.0388 |
0.0657 |
0.0296 |
| Accuracy |
0.9890 |
0.9953 |
0.9912 |
0.9890 |
0.9890 |
| Precision |
0.9893 |
1.0000 |
0.9912 |
0.9891 |
0.9890 |
| Recall |
0.9890 |
1.0000 |
0.9912 |
0.9890 |
0.9890 |
| F1-Score |
0.9890 |
1.0000 |
0.9912 |
0.9890 |
0.9890 |
| Validation set results |
| Loss |
0.0267 |
0.1164 |
0.1105 |
0.0656 |
0.1067 |
| Accuracy |
0.9912 |
0.8836 |
0.9825 |
0.9825 |
0.9649 |
| Precision |
0.9913 |
0.9561 |
0.9825 |
0.9825 |
0.9658 |
| Recall |
0.9912 |
0.9561 |
0.9825 |
0.9825 |
0.9649 |
| F1-Score |
0.9912 |
0.9560 |
0.9825 |
0.9825 |
0.9651 |
| Overfitting |
-0.0022% |
0.1118% |
0.0263% |
0.0066% |
0.0241% |
| Time (sec.) |
3.27 |
1.14 |
3.72 |
4.65 |
3.78 |
Table 3.
Performance results of the proposed ALC and other classifiers on the Wine dataset.
Table 3.
Performance results of the proposed ALC and other classifiers on the Wine dataset.
| Classifier |
ALC |
XGB |
SVM |
MLP |
LR |
| Training set results |
| Loss |
0.0000 |
0.0096 |
0.0006 |
0.0783 |
0.0026 |
| Accuracy |
1.0000 |
0.9904 |
1.0000 |
0.9930 |
1.0000 |
| Precision |
1.0000 |
1.0000 |
1.0000 |
0.9931 |
1.0000 |
| Recall |
1.0000 |
1.0000 |
1.0000 |
0.9930 |
1.0000 |
| F1-Score |
1.0000 |
1.0000 |
1.0000 |
0.9930 |
1.0000 |
| Validation set results |
| Loss |
0.0002 |
0.0762 |
0.0001 |
0.0572 |
0.0012 |
| Accuracy |
1.0000 |
0.9238 |
1.0000 |
1.0000 |
1.0000 |
| Precision |
1.0000 |
0.9514 |
1.0000 |
1.0000 |
1.0000 |
| Recall |
1.0000 |
0.9444 |
1.0000 |
1.0000 |
1.0000 |
| F1-Score |
1.0000 |
0.9449 |
1.0000 |
1.0000 |
1.0000 |
| Overfitting |
0.0000% |
0.0666% |
0.0000% |
-0.0070% |
0.0000% |
| Time (sec.) |
2.41 |
1.15 |
3.94 |
3.84 |
3.84 |
Table 4.
Performance results of the proposed ALC and other classifiers on the Voice dataset.
Table 4.
Performance results of the proposed ALC and other classifiers on the Voice dataset.
| Classifier |
ALC |
XGB |
SVM |
MLP |
LR |
| Training set results |
| Loss |
0.0892 |
0.0012 |
0.1235 |
0.0627 |
0.0928 |
| Accuracy |
0.9767 |
0.9988 |
0.9775 |
0.9791 |
0.9747 |
| Precision |
0.9767 |
1.0000 |
0.9775 |
0.9791 |
0.9748 |
| Recall |
0.9767 |
1.0000 |
0.9775 |
0.9791 |
0.9747 |
| F1-Score |
0.9767 |
1.0000 |
0.9775 |
0.9791 |
0.9747 |
| Validation set results |
| Loss |
0.0677 |
0.0721 |
0.1136 |
0.0618 |
0.0709 |
| Accuracy |
0.9763 |
0.9279 |
0.9732 |
0.9826 |
0.9811 |
| Precision |
0.9766 |
0.9813 |
0.9736 |
0.9827 |
0.9811 |
| Recall |
0.9763 |
0.9811 |
0.9732 |
0.9826 |
0.9811 |
| F1-Score |
0.9764 |
0.9811 |
0.9732 |
0.9827 |
0.9811 |
| Overfitting |
0.0004% |
0.0709% |
0.0043% |
-0.0036% |
-0.0063% |
| Time (sec.) |
3.17 |
1.24 |
4.24 |
12.70 |
4.44 |
Table 5.
Performance results of the proposed ALC and other classifiers on the MNIST dataset.
Table 5.
Performance results of the proposed ALC and other classifiers on the MNIST dataset.
| Classifier |
ALC |
XGB |
SVM |
MLP |
LR |
| Training set results |
| Loss |
0.0000 |
0.0060 |
0.0010 |
0.0404 |
0.0048 |
| Accuracy |
1.0000 |
0.9940 |
1.0000 |
1.0000 |
1.0000 |
| Precision |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
| Recall |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
| F1-Score |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
| Validation set results |
| Loss |
0.0000 |
0.0595 |
0.0082 |
0.0489 |
0.0123 |
| Accuracy |
0.9975 |
0.9405 |
0.9950 |
0.9900 |
0.9950 |
| Precision |
0.9981 |
0.9818 |
0.9953 |
0.9906 |
0.9953 |
| Recall |
0.9976 |
0.9800 |
0.9950 |
0.9900 |
0.9950 |
| F1-Score |
0.9978 |
0.9801 |
0.9950 |
0.9900 |
0.9950 |
| Overfitting |
0.0025% |
0.0535% |
0.0050% |
0.0100% |
0.0050% |
| Time (sec.) |
6.04 |
2.40 |
5.46 |
5.27 |
5.56 |
Table 6.
Wilcoxon signed-rank test results comparing classifier pairs on validation set metrics across all datasets.
Table 6.
Wilcoxon signed-rank test results comparing classifier pairs on validation set metrics across all datasets.
| Classifier pair |
Dataset |
P-value |
| |
|
Loss |
Accuracy |
Overfitting |
Time |
| ALC vs. XGB |
Iris Flower |
0.998 |
0.500 |
0.995 |
0.995 |
| ALC vs. SVM |
Iris Flower |
0.003 |
0.500 |
0.002 |
0.007 |
| ALC vs. MLP |
Iris Flower |
0.002 |
0.500 |
0.014 |
0.000 |
| ALC vs. LR |
Iris Flower |
0.012 |
0.008 |
0.013 |
0.006 |
| ALC vs. XGB |
Breast Cancer |
0.008 |
0.019 |
0.006 |
0.999 |
| ALC vs. SVM |
Breast Cancer |
0.003 |
0.022 |
0.013 |
0.078 |
| ALC vs. MLP |
Breast Cancer |
0.024 |
0.022 |
0.011 |
0.002 |
| ALC vs. LR |
Breast Cancer |
0.000 |
0.036 |
0.000 |
0.010 |
| ALC vs. XGB |
Wine |
0.035 |
0.500 |
0.003 |
0.996 |
| ALC vs. SVM |
Wine |
0.944 |
0.001 |
0.500 |
0.003 |
| ALC vs. MLP |
Wine |
0.002 |
0.500 |
0.017 |
0.002 |
| ALC vs. LR |
Wine |
0.013 |
0.500 |
0.500 |
0.002 |
| ALC vs. XGB |
Voice Gender |
0.038 |
0.033 |
0.002 |
0.992 |
| ALC vs. SVM |
Voice Gender |
0.000 |
0.005 |
0.008 |
0.001 |
| ALC vs. MLP |
Voice Gender |
0.990 |
0.941 |
0.023 |
0.001 |
| ALC vs. LR |
Voice Gender |
0.027 |
0.937 |
0.005 |
0.001 |
| ALC vs. XGB |
MNIST |
0.002 |
0.032 |
0.009 |
1.000 |
| ALC vs. SVM |
MNIST |
0.006 |
0.102 |
0.029 |
0.983 |
| ALC vs. MLP |
MNIST |
0.002 |
0.038 |
0.016 |
0.987 |
| ALC vs. LR |
MNIST |
0.004 |
0.101 |
0.028 |
0.942 |
Table 7.
Performance comparison (accuracy metric) of the proposed ALC with models discussed in the related work.
Table 7.
Performance comparison (accuracy metric) of the proposed ALC with models discussed in the related work.
| Classifier |
Dataset |
Accuracy |
| ALC |
Iris Flower |
1.0000 |
| SVM [34] |
|
0.9600 |
| ALC |
Breast Cancer |
0.9912 |
| RRNN [33] |
|
0.9951 |
| ALC |
Wine |
1.0000 |
| SVM [32] |
|
0.8790 |
| MR [32] |
|
0.8645 |
| ANN [32] |
|
0.8675 |
| SVM [34] |
|
0.9830 |
| ALC |
Voice Gender |
0.9763 |
| MLP [35] |
|
0.9674 |
| ALC |
MNIST |
0.9975 |
| SVC [30] |
|
0.9780 |
| DT [30] |
|
0.8860 |
| KNN [30] |
|
0.9590 |
| MLP [30] |
|
0.9720 |
| OPIUM [31] |
|
0.9590 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).