1. Introduction
In recent years, the demand for point cloud processing techniques has surged, driven by their increasing application in emerging fields such as augmented and virtual reality (AR/VR), autonomous driving and robotics. These applications often rely on the storage and transmission of large point clouds, which typically consist of millions of individual points. Consequently, the development of efficient point cloud compression methods has become critical to addressing the substantial data demands inherent in these systems. Unlike the structured nature of 2D image and video data, 3D point clouds are inherently unstructured, presenting unique challenges in compression. This complexity highlights the need for specialised algorithms and has driven extensive research efforts aimed at optimizing point cloud compression techniques.
Nearly all point cloud compression methods in literature begin by voxelising the input point cloud, converting it into a grid of discrete, integer-coordinated voxels. This voxelisation process not only imposes structure on the otherwise unstructured point cloud but also makes the data more amenable to compression techniques, such as convolution-based approaches and octree partitioning schemes. By introducing a structured representation, voxelisation enables compression algorithms to more effectively exploit spatial redundancies and patterns within the data.
The most established point cloud compression codecs are being developed by the Moving Picture Experts Group (MPEG), the organisation responsible for widely adopted video coding standards such as AVC [
1], HEVC [
2], and VVC [
3]. They are maintaining two distinct point cloud compression standards: the geometry-based point cloud compression standard (G-PCC) [
4] and the video-based point cloud compression standard (V-PCC) [
5]. The V-PCC standard leverages the power of established video codecs by projecting the 3D point cloud onto 2D planes and then compressing these projections as video streams. This approach benefits from the maturity and optimisation of existing video compression technologies. The G-PCC standard, on the other hand, works purely in 3D and has two variants. The first option is an octree-based codec, which recursively splits the bounding box around the voxelised point cloud into eight subnodes until the nodes are voxel-sized; at this point, the octree leaves are all the occupied voxels. The only information to be encoded are the occupancy bits, which indicate which subnodes are occupied. So, most active research investigates how to efficiently entropy code these using predictions from recently coded or neighbouring nodes. The octree-based codec recursively divides the bounding box of the voxelised point cloud into eight subnodes, continuing until the nodes become voxel-sized. At this point, the octree leaves represent the occupied voxels, and the compression task is reduced to encoding the occupancy bits, which indicate for each node what subnodes are occupied. Active research in this area focuses on enhancing the efficiency of entropy coding these occupancy bits by leveraging predictions from previously coded or spatially neighboring nodes.
The second approach, which performs predictive geometry coding, is designed for scenarios requiring low-complexity decoding and minimal latency, such as streaming applications. This method uses a prediction graph to model the point cloud, where each point’s geometry is estimated based on its predecessors in the graph. This predictive framework enables streamlined compression while maintaining efficient decoding.
Most point cloud compression research can also be classified into geometry-based [
6] and video-based codecs [
7,
8]. The focus of this paper is on voxelisation which is used in geometry-based codecs. Recent geometry-based point cloud compression research has increasingly focused on learning-based approaches, which can typically be grouped into four main categories. Voxel-based methods process voxelised point clouds directly using 3D convolutions, either in dense [
9,
10,
11] or sparse forms [
12,
13,
14], with the latter accounting for the inherent sparsity of point clouds. Octree-based methods build upon the octree structure used in the G-PCC standard but enhance it with machine learning to improve entropy coding of occupancy information. For instance, VoxelContext [
15] employs convolutional neural networks to predict occupancy probabilities, while transformer-based techniques such as Octattention [
16], Octformer [
17], and EHEM [
18] model complex dependencies between octree nodes to boost compression efficiency. Hybrid methods combine elements of voxel-based and octree-based approaches. For instance, VoxelDNN [
19,
20] employs a pruned octree structure and encodes its leaves using a voxel-based approach. Finally, some methods operate directly on the unvoxelised version of the point cloud. Examples include approaches based on PointNet++ [
21], such as those proposed in [
22,
23], or methods employing recurrent neural networks [
24]. However, these techniques often struggle to scale effectively to higher bitrates and larger point clouds [
12,
25].
To the best of our knowledge, all existing point cloud compression methods operating on voxelised data rely on uniform voxelisation. However, this approach fails to consider the spatial distribution of points within the input data. As a result, bitrate is often misallocated—excessively spent in sparse regions while insufficiently invested in dense, detail-rich areas. To address these shortcomings, we propose a novel non-uniform voxelisation method that adapts to the specific point distribution of the input cloud, optimizing the allocation of resources to minimise Euclidean coding error. Our approach is compatible with any point cloud codec designed for voxelised data. By demonstrating the substantial benefits of non-uniform voxelisation compared to the traditional uniform approach, this work highlights the need to reconsider voxelisation strategies for advancing the state of point cloud compression.
The remainder is structured as follows: first, the necessary basics of quantisation are explained in
Section 2. Then the proposed methodology is explained in detail in
Section 3. The experimental setups and their results are summarised in
Section 4. Finally, conclusions are drawn in
Section 5.
2. Background Knowledge
Voxelisation of a point cloud is quantising the positions of the points along the three spatial axes. Quantisation is the process of mapping a continuous range of values to a discrete set of symbols. Formally, a quantiser is characterised by its decision boundaries
, where
and
, with consecutive pairs of boundaries defining bins that are associated with reconstruction values
. So, the quantisation function can be expressed as
The goal of designing a quantiser is to minimise bitrate while also minimising the distortion introduced in the process. This goal is often formalised by using a lagrangian multiplier
and minimising
. Where the distortion is usually given by the mean squared error
While the rate is given by
where
is the codeword that is assigned to quantisation bin
k. For a sufficiently efficient entropy codec, the cost of each codeword approaches the information content
, so the total rate approaches the entropy,
.
In this work, we look at two quantisers:
3. Proposed Methodology
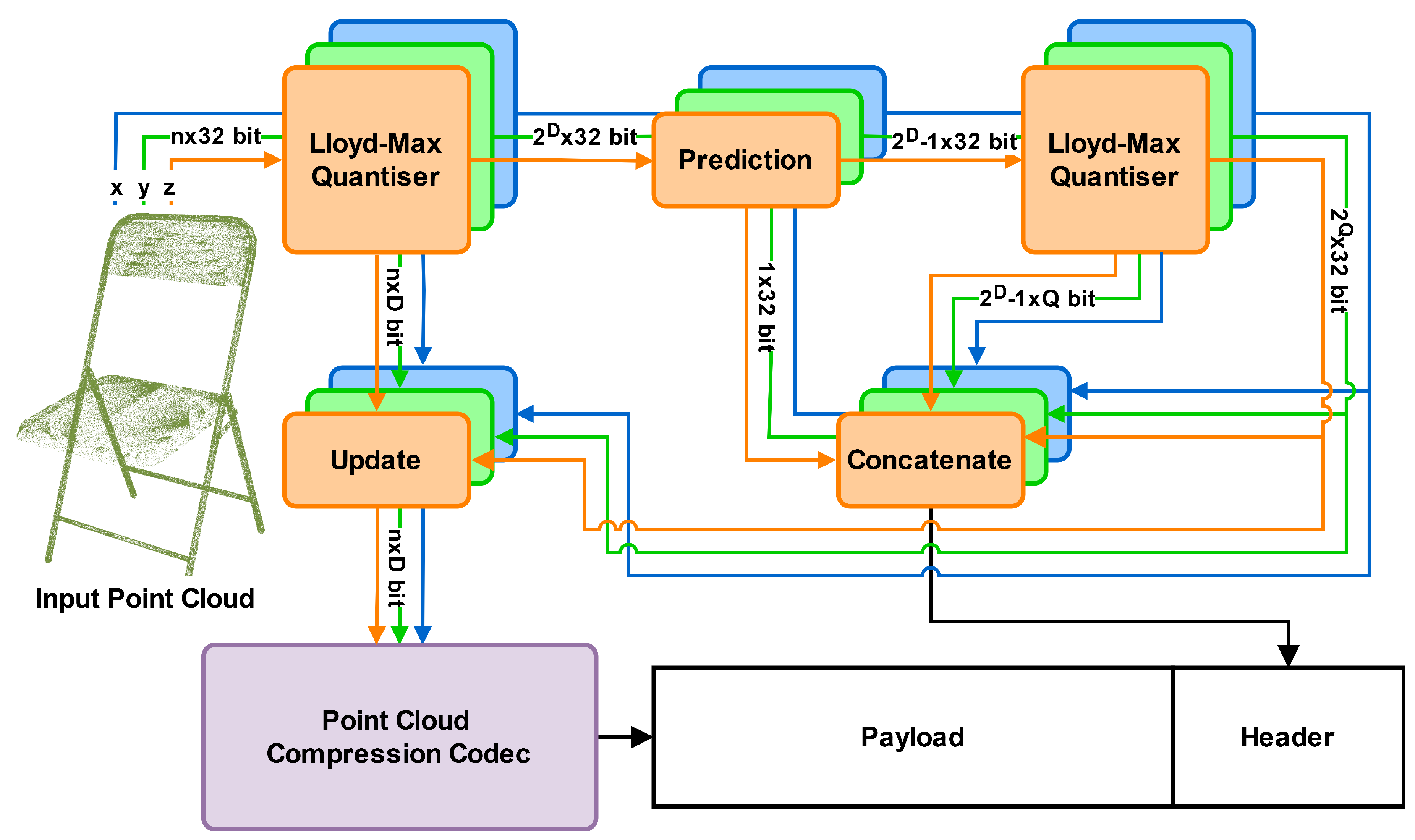
We propose a novel non-uniform voxelisation method designed to minimise Euclidean distortion, as illustrated in
Figure 1. Our approach extends the traditional Lloyd-Max algorithm to efficiently compress point cloud data by applying it independently to the distribution of points across each of the three dimensions. This allows the resulting voxels to take on generalised cuboid shapes, rather than being constrained to cubes. It can be shown that minimising Euclidean error in three-dimensional space reduces to minimising squared error along each dimension independently, assuming decision boundary planes that are orthogonal to the axes.
While these assumptions may appear restrictive, they are crucial for the practical application of non-uniform quantisation to point clouds. Although a vector quantisation approach might initially appear more suitable due to its ability to perform generalised multi-dimensional quantisation, voxelisation necessitates the creation of an
grid, which vector quantisation is not designed for. Additionally, the reconstruction values must be included in the geometry header to ensure accurate point cloud reconstruction on the decoder side. Making the quantisers interdependent introduces a size complexity of
for the header overhead, which is impractical for real-world applications. As we will demonstrate, even the
complexity of independent quantisers poses significant challenges. Finally, optimising and encoding non-planar quantisation boundaries is beyond the scope of this work.
Another important consideration is the execution time of the voxelisation process. While extracting the point distribution and determining an appropriate quantiser along each axis is straightforward and efficient, directly processing the points in three-dimensional space is far more complex. These complexities are a key reason why most existing approaches incorporate a voxelisation step in the first place.
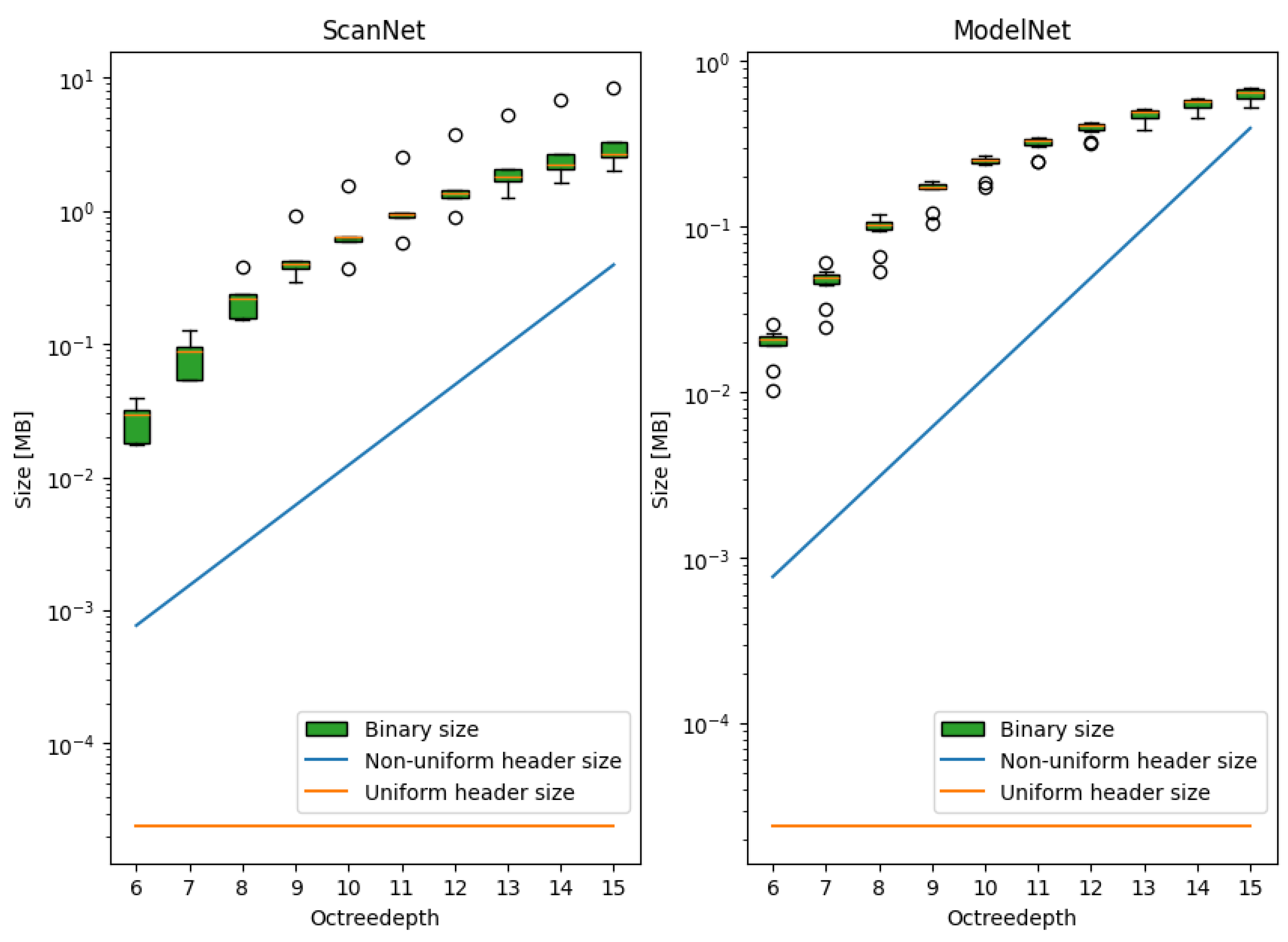
To accurately reconstruct the point cloud at the decoder, it is necessary to encode the mapping between the internal integer coordinate system and the actual point cloud coordinates. However, the bitrate required is very substantial due to the large number of voxels along each dimension, making it impractical to transmit this data directly. As the octree depth increases, the number of reconstruction levels grows exponentially, with each level requiring a 32-bit float representation. At higher quality levels, the overhead of transmitting this information becomes prohibitive.
Figure 2 illustrates the considerable overhead introduced by communicating the reconstruction levels compared to just the outer boundaries of a uniform approach. The impact of header overhead on the efficiency of the proposed method will be further explored in
Section 4.3.
To address the overhead, our approach applies an additional Lloyd-Max quantiser to the reconstruction levels in order to reduce the introduced overhead. By quantising the output reconstruction levels of the Lloyd-Max quantiser, we obtain an approximate version of the original quantiser. The primary goal is to minimise the additional distortion, denoted as
, introduced by this approximation, relative to the optimal distortion achieved by the original quantiser. It is important to note that only the reconstruction values need to be communicated and approximated, meaning both quantisers share the same boundaries.
where
is the probability or importance of a certain interval. We apply quantisation on the reconstruction levels only after a prediction step to more efficiently spend the quantisation bits. Thus, the distortion to be minimised by the second Lloyd-Max quantiser is a discrete version of equation
2:
where
are the reconstruction values of the second quantiser and
.
4. Results
4.1. Datasets
The efficiency of the proposed method is demonstrated through performance evaluation on two widely used public datasets. ScanNet [
26] is a popular 3D indoor scene point cloud dataset commonly used for tasks such as segmentation, compression, and other point cloud processing applications. We evaluate the proposed method using 20 scenes from this dataset. The second dataset, ModelNet [
28], consists of synthetic meshes representing various object categories. For evaluation, we selected two meshes from each of the ten categories, sampling 1,000,000 points and their associated normals from each mesh.
4.2. Experimental Details
All voxelisation in the state-of-the-art point cloud compression research is uniform, which thus serves as the baseline for comparison for our proposed non-uniform voxelisation approach. To measure the effect of the proposed method on bitrate, we encode the voxelised point cloud using the G-PCC standard [
4], which is a state-of-the-art point cloud compression codec that is widely used as a benchmark in the point cloud compression field. Rate-distortion tuning is achieved by adjusting the octree depth parameter, which in our experiments varies between 6 and 16. To evaluate performance, we use four key metrics. The bitrate is measured in bits per point (bpp). Reconstruction quality is assessed by calculating the PSNR of the point-to-point and point-to-plane distortions, as defined in [
29], with
. Additionally, the Bjontegaard Delta rate (BD-rate) is employed to quantify overall gains in rate and quality. All experiments are performed on a desktop system with an Intel Core i9-9900K CPU and 64 GB of memory. A new parameter introduced by the proposed method is the number of bits used for the reconstruction values in the second quantisation, referred to as Q-bits. Lower values result in significant rate savings, while higher values yield higher-quality reconstructions. Empirical results indicate that setting this parameter to four provides the optimal performance, as detailed in
Section 4.3.
4.3. Q-Bits Tuning
In addition to the octree depth, which defines the number of quantisation bits for the first quantiser, the proposed approach introduces a second tunable parameter: the number of quantisation bits for the second quantiser, referred to as Q-bits. We investigated the effects of tuning this parameter and identified optimal values for performance. The results are shown in
Table 1. The first notable observation is the importance of the second quantisation, as the method performs significantly worse at 12 bits per reconstruction value compared to the uniform approach. Furthermore, the method exhibits robust performance across a range of smaller Q-bit values, suggesting that fine-tuning this parameter is not required to achieve good results.
4.4. Comparison to SOTA
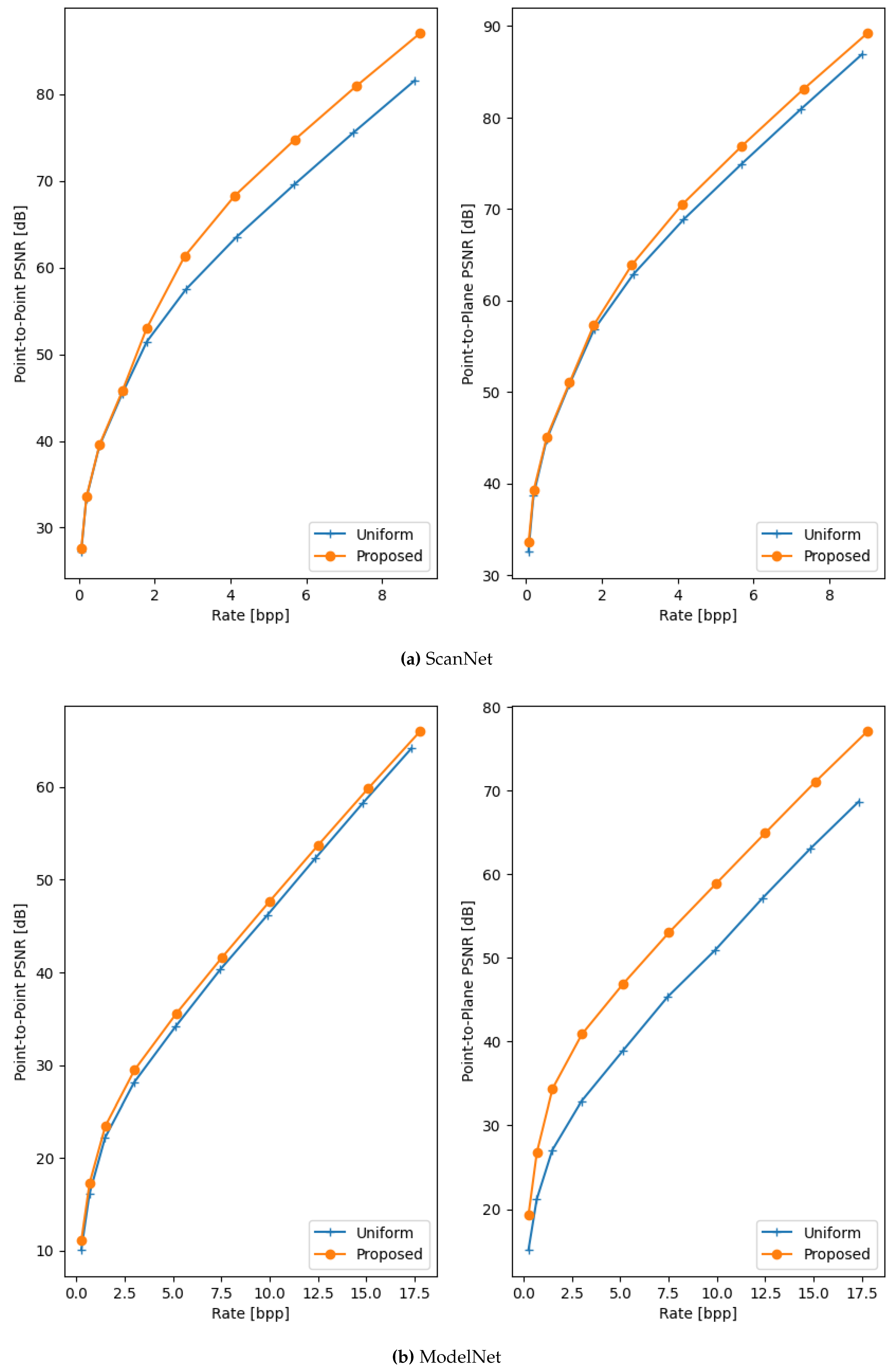
The results of the comparison between the proposed method and uniform voxelisation are presented in
Table 2 and
Figure 3. These results demonstrate the efficacy of the proposed method, with average BD-rate gains of 10.41% and 22.34% for point-to-point and point-to-plane distortion, respectively. The proposed method consistently achieves significantly higher PSNRs while incurring only a slight increase in rate. A qualitative comparison between the proposed method and the baseline is shown in
Figure 4. The strength of the non-uniform approach lies in its ability to adapt to the point distribution within the input point cloud, such as aligning the reconstruction values with dense regions like the seat of the ModelNet chair or the floor and walls in the ScanNet scene. In contrast, the uniform approach fails to account for point distribution, often resulting in large errors in these critical regions.
4.5. Impact of Density
Point cloud compression methods are designed to handle a wide range of densities, from sparse point clouds captured by real-time depth sensors to highly dense point clouds used in applications such as heritage preservation. To assess the impact of point cloud density on the performance of the proposed method, we conducted experiments using the ModelNet dataset. Since ModelNet provides mesh data, we sampled it to generate point clouds with varying densities, allowing for controlled experimentation across a broad range of point counts. Specifically, we sampled point clouds containing between 50,000 and 4,000,000 points, which reflects the typical density variations encountered in real-world datasets, as summarised in
Table 3.
The results of the density experiment are presented in
Table 4. The findings indicate that the proposed method performs better for denser point clouds. This can be attributed to the reduced relative overhead of communicating reconstruction values, which does not scale proportionally with the number of points. The proposed method consistently outperforms the uniform voxelisation approach across all density levels. Additionally, as the density increases, the rate allocated to quantisation becomes a smaller fraction of the total rate, enabling higher Q-bits values without a significant increase in cost. These results highlight the robustness and scalability of the proposed method, making it particularly well-suited for applications that involve high-density point clouds.
4.6. Execution Time
The final aspect of the proposed method to evaluate is its execution time. While the method’s adaptability to the input point cloud enhances its performance, it also introduces additional computational complexity. The execution times are provided in
Table 5. Despite this increased complexity, the rise in execution time is relatively small compared to the overall processing time of the G-PCC codec. Therefore, the trade-off in execution time is modest when weighed against the significant improvements in coding efficiency offered by the proposed method.
5. Conclusions
This paper presents a novel approach to point cloud compression by introducing non-uniform, distortion-minimizing voxelisation—representing the first exploration of non-uniform quantisation in this domain. Unlike traditional methods that rely on uniform voxelisation, the proposed technique adapts voxel sizes to the local distribution of points, thereby optimizing compression performance. The method’s efficiency and robustness were thoroughly validated through extensive experiments on the well-established public datasets, ScanNet and ModelNet. The results highlight the potential for further exploration of innovative non-uniform voxelisation techniques to advance the field of point cloud compression.
Author Contributions
Conceptualization, B.V. and A.M.; methodology, B.V.; software, B.V.; validation, B.V. and A.M.; formal analysis, B.V.; investigation, B.V.; resources, A.M.; data curation, B.V.; writing—original draft preparation, B.V.; writing—review and editing, L.D and A.M.; visualization, B.V.; supervision, A.M.; project administration, X.X.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by Innoviris within the research project MUSCLES.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wiegand, T.; Sullivan, G.; Bjontegaard, G.; Luthra, A. Overview of the H.264/AVC video coding standard. IEEE Transactions on Circuits and Systems for Video Technology 2003, 13, 560–576, Conference Name: IEEE Transactions on Circuits and Systems for Video Technology. [Google Scholar] [CrossRef]
- Sullivan, G.J.; Ohm, J.R.; Han, W.J.; Wiegand, T. Overview of the High Efficiency Video Coding (HEVC) Standard. IEEE Transactions on Circuits and Systems for Video Technology 2012, 22, 1649–1668, Conference Name: IEEE Transactions on Circuits and Systems for Video Technology. [Google Scholar] [CrossRef]
- Bross, B.; Wang, Y.K.; Ye, Y.; Liu, S.; Chen, J.; Sullivan, G.J.; Ohm, J.R. Overview of the Versatile Video Coding (VVC) Standard and its Applications. IEEE Transactions on Circuits and Systems for Video Technology 2021, 31, 3736–3764, Conference Name: IEEE Transactions on Circuits and Systems for Video Technology. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, F.; Xu, Y.; Preda, M. Standardization Status of MPEG Geometry-Based Point Cloud Compression (G-PCC) Edition 2. In Proceedings of the 2024 Picture Coding Symposium (PCS); 2024; pp. 1–5, ISSN 2472-7822. [Google Scholar] [CrossRef]
- Mammou, K.; Kim, J.; Tourapis, A.M.; Podborski, D.; Flynn, D. Video and Subdivision based Mesh Coding. In Proceedings of the 2022 10th European Workshop on Visual Information Processing (EUVIP); 2022; pp. 1–6, ISSN 2471-8963. [Google Scholar] [CrossRef]
- Shao, Y.; Gao, W.; Liu, S.; Li, G. Advanced Patch-Based Affine Motion Estimation for Dynamic Point Cloud Geometry Compression. Sensors 2024, 24, 3142, Number: 10 Publisher: Multidisciplinary Digital Publishing Institute. [Google Scholar] [CrossRef]
- Tohidi, F.; Paul, M.; Ulhaq, A.; Chakraborty, S. Improved Video-Based Point Cloud Compression via Segmentation. Sensors 2024, 24, 4285, Number: 13 Publisher: Multidisciplinary Digital Publishing Institute. [Google Scholar] [CrossRef] [PubMed]
- Dumic, E.; Bjelopera, A.; Nüchter, A. Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression. Sensors 2022, 22, 197, Number: 1 Publisher: Multidisciplinary Digital Publishing Institute. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.; Liu, H.; Ma, Z. Lossy Point Cloud Geometry Compression via End-to-End Learning. IEEE Transactions on Circuits and Systems for Video Technology 2021, 31, 4909–4923, Conference Name: IEEE Transactions on Circuits and Systems for Video Technology. [Google Scholar] [CrossRef]
- Quach, M.; Valenzise, G.; Dufaux, F. Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP); 2019; pp. 4320–4324, arXiv:1903.08548 [cs, eess, stat]. [Google Scholar] [CrossRef]
- Zhuang, L.; Tian, J.; Zhang, Y.; Fang, Z. Variable Rate Point Cloud Geometry Compression Method. Sensors 2023, 23, 5474, Number: 12 Publisher: Multidisciplinary Digital Publishing Institute. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Feng, X.; Cao, C.; Ma, Z. Sparse Tensor-Based Multiscale Representation for Point Cloud Geometry Compression. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 9055–9071, Conference Name: IEEE Transactions on Pattern Analysis and Machine Intelligence. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; An, Y.; Li, T.H.; Liu, S.; Li, G. ScanPCGC: Learning-Based Lossless Point Cloud Geometry Compression using Sequential Slice Representation. In Proceedings of the ICASSP 2024 - 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2024; pp. 8386–8390, ISSN 2379-190X. [Google Scholar] [CrossRef]
- Akhtar, A.; Li, Z.; Van der Auwera, G. Inter-Frame Compression for Dynamic Point Cloud Geometry Coding. IEEE Transactions on Image Processing 2024, 33, 584–594, Conference Name: IEEE Transactions on Image Processing. [Google Scholar] [CrossRef] [PubMed]
- Que, Z.; Lu, G.; Xu, D. VoxelContext-Net: An Octree Based Framework for Point Cloud Compression. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2021, pp.
- Fu, C.; Li, G.; Song, R.; Gao, W.; Liu, S. OctAttention: Octree-Based Large-Scale Contexts Model for Point Cloud Compression. Proceedings of the AAAI Conference on Artificial Intelligence 2022, 36, 625–633, Number: 1. [Google Scholar] [CrossRef]
- Cui, M.; Long, J.; Feng, M.; Li, B.; Kai, H. OctFormer: Efficient Octree-Based Transformer for Point Cloud Compression with Local Enhancement. Proceedings of the AAAI Conference on Artificial Intelligence 2023, 37, 470–478, Number: 1. [Google Scholar] [CrossRef]
- Song, R.; Fu, C.; Liu, S.; Li, G. Efficient Hierarchical Entropy Model for Learned Point Cloud Compression. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada; 2023; pp. 14368–14377. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Learning-Based Lossless Compression of 3D Point Cloud Geometry. In Proceedings of the ICASSP 2021 - 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2021; pp. 4220–4224, ISSN 2379-190X. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Lossless Coding of Point Cloud Geometry Using a Deep Generative Model. IEEE Transactions on Circuits and Systems for Video Technology 2021, 31, 4617–4629, Conference Name: IEEE Transactions on Circuits and Systems for Video Technology. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 652–660. [Google Scholar]
- You, K.; Gao, P. Patch-Based Deep Autoencoder for Point Cloud Geometry Compression. In Proceedings of the ACM Multimedia Asia; 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y. 3D Point Cloud Geometry Compression on Deep Learning. In Proceedings of the Proceedings of the 27th ACM International Conference on Multimedia; New York, NY, USA, 2019; MM ’19; pp. 890–898. [Google Scholar] [CrossRef]
- Tu, C.; Takeuchi, E.; Carballo, A.; Takeda, K. Point Cloud Compression for 3D LiDAR Sensor using Recurrent Neural Network with Residual Blocks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA); 2019; pp. 3274–3280, ISSN 2577-087X. [Google Scholar] [CrossRef]
- Quach, M.; Pang, J.; Tian, D.; Valenzise, G.; Dufaux, F. Survey on Deep Learning-Based Point Cloud Compression. Frontiers in Signal Processing 2022, 2. Publisher: Frontiers. [Google Scholar] [CrossRef]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Niessner, M. ScanNet: Richly-Annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI; 2017; pp. 2432–2443. [Google Scholar] [CrossRef]
- Zhirong, Wu.; Song, S.; Khosla, A.; Fisher, Yu.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 2015; pp. 1912–1920. [Google Scholar] [CrossRef]
- Maglo, A.; Lavoué, G.; Dupont, F.; Hudelot, C. 3D Mesh Compression: Survey, Comparisons, and Emerging Trends. ACM Computing Surveys 2015, 47, 44–1. [Google Scholar] [CrossRef]
- Tian, D.; Ochimizu, H.; Feng, C.; Cohen, R.; Vetro, A. Geometric distortion metrics for point cloud compression. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP); 2017; pp. 3460–3464, ISSN 2381-8549. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition; 2012; pp. 3354–3361, ISSN 1063-6919. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A Multimodal Dataset for Autonomous Driving. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA; 2020; pp. 11618–11628. [Google Scholar] [CrossRef]
- Sun, P.; Kretzschmar, H.; Dotiwalla, X.; Chouard, A.; Patnaik, V.; Tsui, P.; Guo, J.; Zhou, Y.; Chai, Y.; Caine, B.; et al. Scalability in Perception for Autonomous Driving: Waymo Open Dataset, 2020. arXiv:1912.04838 [cs].
- Armeni, I.; Sax, S.; Zamir, A.R.; Savarese, S. Joint 2D-3D-Semantic Data for Indoor Scene Understanding. 2017, arXiv:1702.01105 [cs]. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).