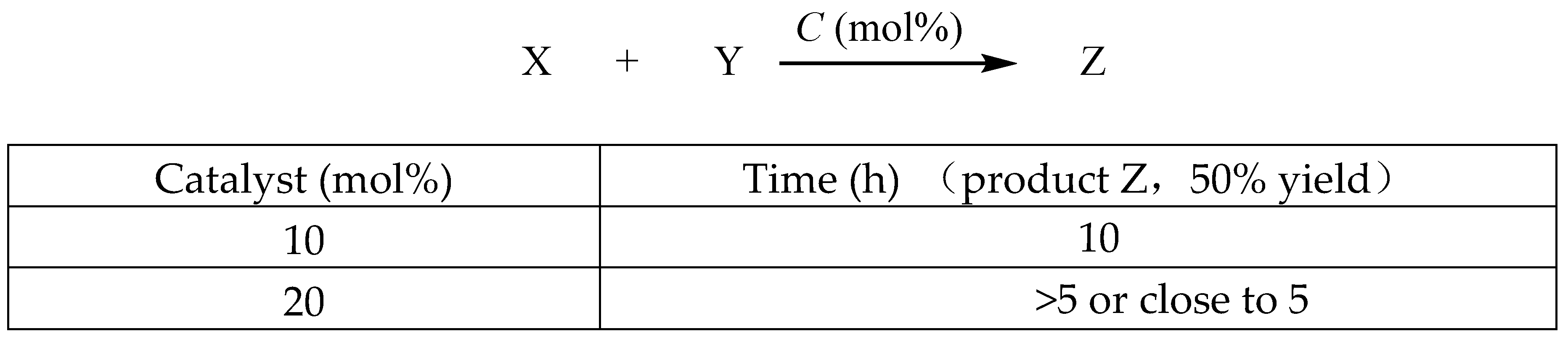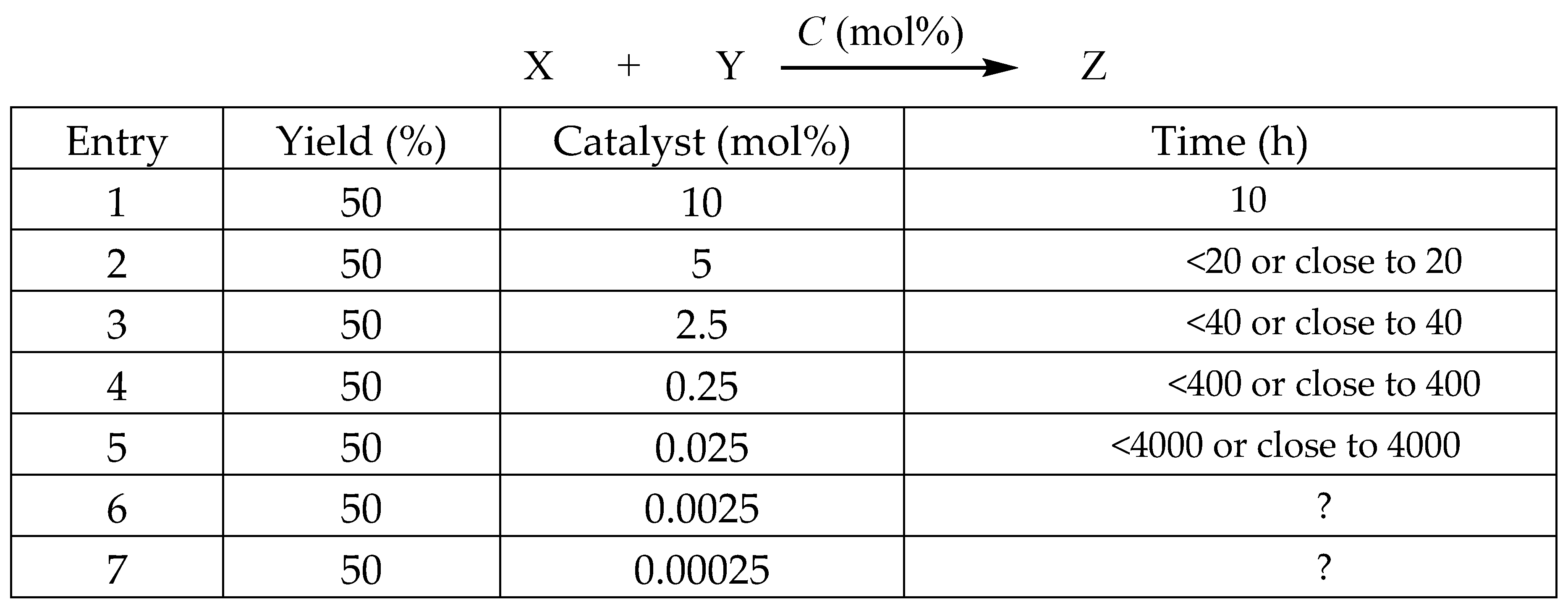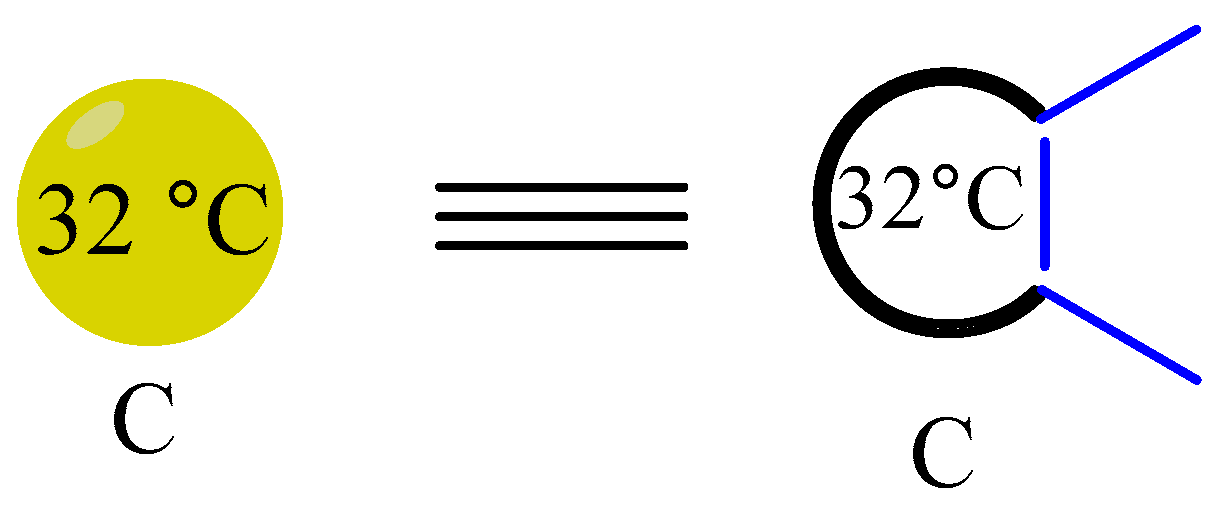1. The Relationship Between the Second Law of Thermodynamics and Life
There are many differences between living matter and non-living matter, which we can easily judge and distinguish.[
1] The most significant aspect of living matter is its ability to undergo metabolism, which differs from that of non-living matter. But what is life?[
2] What does metabolism mean?[
3] We still don’t have a complete understanding of the nature of life. Here, we aim to establish the simplest model of life by understanding the second law of thermodynamics.[
4] The cell is regarded as the smallest unit of life, and a single cell is a form of life. Therefore, our model of life is considered the simplest model of cellular metabolism.
The second law of thermodynamics states that in isolated systems in a spontaneous state, thermal energy is always transferred from the high-temperature part to the low-temperature part, resulting in thermodynamic equilibrium. The thermodynamic equilibrium state has the highest entropy value as it approaches the equilibrium state.[
5] Life can be viewed as a system that stands in opposition to the second law of thermodynamics. First, life is a system that has not yet reached thermodynamic equilibrium. Second, life activities, or metabolism, essentially aim to maintain this thermodynamic imbalance or continue to evolve away from equilibrium. Third, once it reaches thermodynamic equilibrium, life will come to an end.
Our aim is to develop a model that has a thermodynamically unbalanced initial state. If this model is moving towards thermodynamic equilibrium, it indicates that the system is coming close to death. On the contrary, if the system moves away from thermodynamic equilibrium, or in a direction of entropy decrease, it indicates that the system has obvious life characteristics and is currently in an alive state, and this evolution is called metabolism.
We first create a model of a high energy bloc based on volatilization before constructing a model of life.
2. Volatilization Assumption: Building a High-Energy Bloc Model
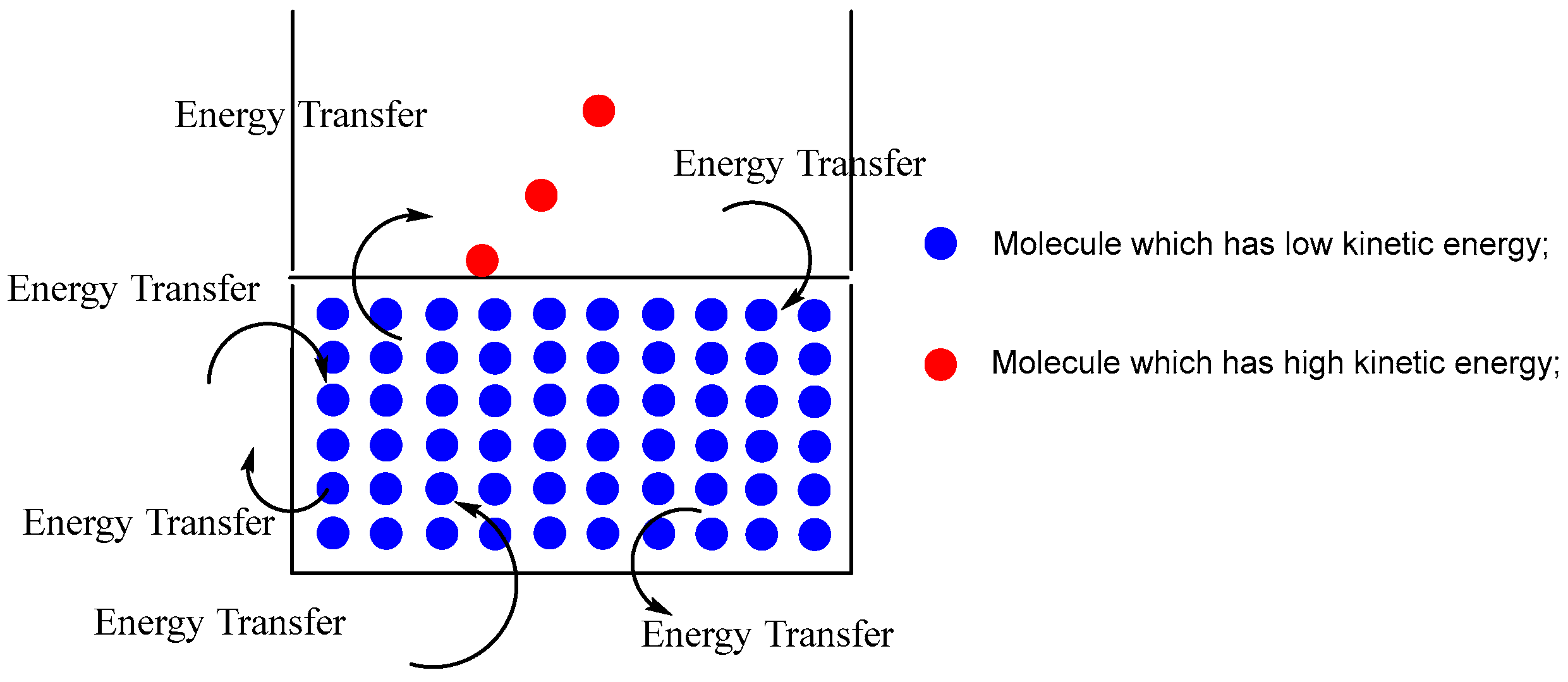
There are many amazing creatures and phenomena in nature; the only thing missing is discovery. The phenomenon of liquids evaporating is truly remarkable. Even when the temperature is at room level (25 ºC) or lower, water molecules in a glass of water still manage to evaporate from the water’s surface into the air occasionally. It is anticipated that the kinetic energy of the water molecules that evaporate from the surface into the air will be greater than the average kinetic energy of the water molecules presents in the glass. The collision of water molecules with varying kinetic energy levels occurs constantly, leading to the exchange of energy with the surroundings. As a result, water molecules with greater kinetic energy are consistently generated and subsequently evaporate into the atmosphere.
Objects with high temperatures will transfer heat to objects with low temperatures as per the second law of thermodynamics. The law of conservation of energy states that objects with high kinetic energy will lose kinetic energy over time during collisions, whereas objects with low kinetic energy will gain kinetic energy during collisions, and their kinetic energy will eventually equalize. As a result, we can deduce that the water molecules in this glass of water with the higher kinetic energy will gradually lose kinetic energy due to collisions with other water molecules that have lower kinetic energy. But the opposite phenomenon is called volatilization.[
6] This glass of water will perpetually generate water molecules possessing kinetic energy significantly exceeding the average kinetic energy of the molecules contained within the glass, as illustrated in
Figure 1. Eventually, these molecules will escape from the water's surface into the surrounding atmosphere. Stated differently, volatilization is nonexistent in accordance with the second law of thermodynamics.
Regretfully, the volatilization phenomenon mentioned above has not yet been explained in any literature. We are trying to establish a model that will account for the phenomenon of volatilization. We assume that the water volatilization system can be thought as a chaotic system.[
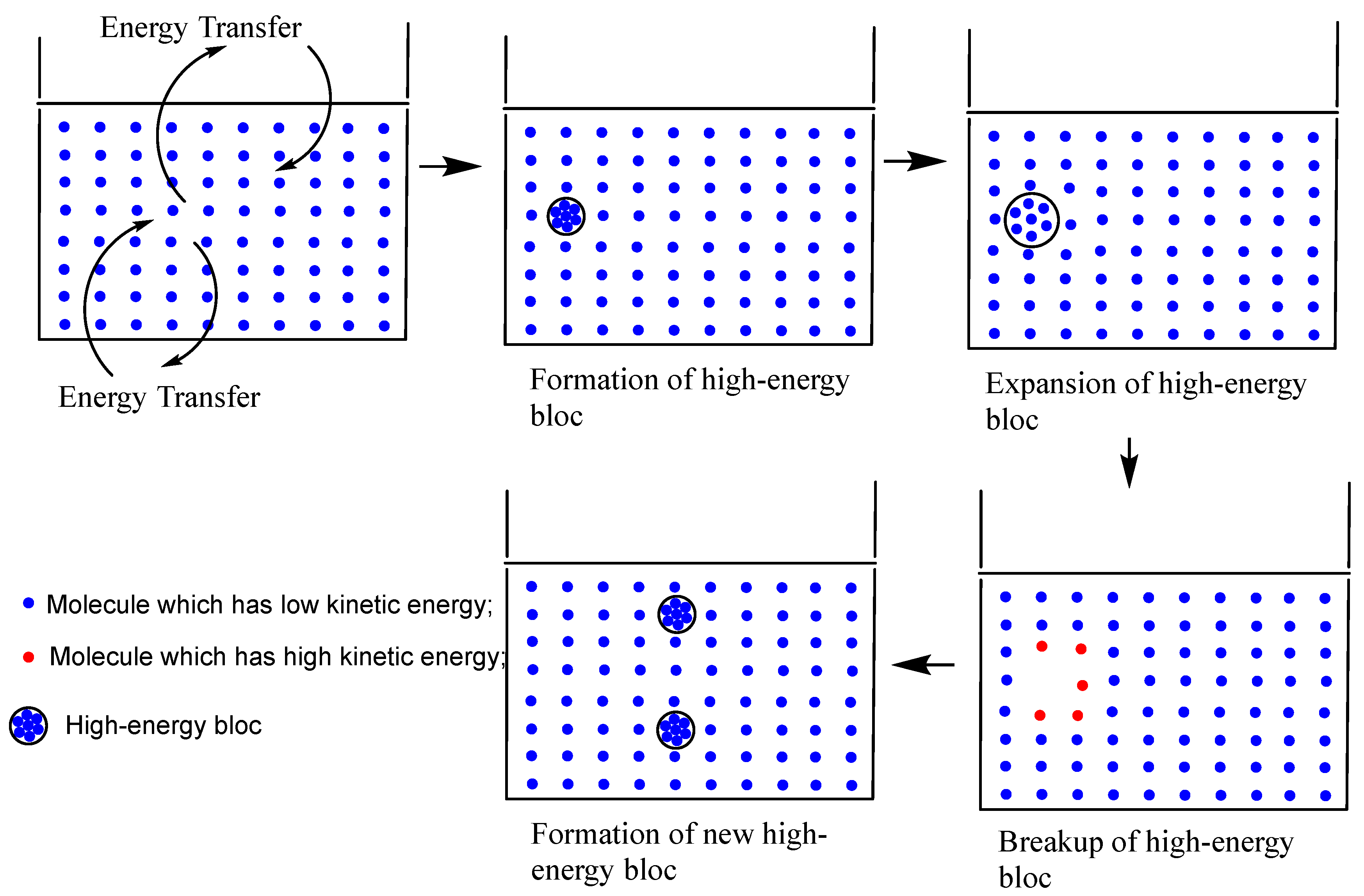
7] Uneven heat transfer causes the liquid’s internal energy to fluctuate when it exchanges energy with the outside environment, which can have chaotic consequences. After then, the energy transfer within the liquid appears chaotic and disorderly. However, at the next uncertain time, energy will become ordered, leading to the generation of a high-energy bloc, or compressed solvent group made up of several solvent molecules. Then, because of the uneven energy exchange with the outside world, this high-energy bloc can be viewed as an embodiment of the chaotic system of liquid, where the energy transmitted internally transforms from disorder to order. The following are the traits of the high-energy bloc:
A group of several solvent molecules (10, 20, or more) is created inside the solution when it exchanges energy with the external environment. This group is most likely created by molecular resonance. This group of solvent molecule’s number is determined by factors such as temperature, pressure, the size, shape, and intermolecular forces of the solvent molecules. Additionally, it pertains to the velocity and uniformity of energy interaction with the surrounding environment.
Because the solvent molecules in this group are closer together than they are to one another in a typical solvent system, this system is compressed and stores energy as potential energy as a result of absorbing energy from its surroundings. So, it is referred to as a high-energy bloc.
Before disintegrating, the kinetic energy of this high-energy system is not significantly different from the average kinetic energy of other molecules in the solvent. This is because the high-energy bloc stores the energy from its surroundings mainly through compressed potential energy.
The next instant, the high-energy bloc will enlarge, break apart, and collide with the nearby solvent molecules, sharply increasing the kinetic energy of the affected solvent molecules. When these high kinetic energy solvent molecules collide with other solvent molecules, they will eventually form new compressed high energy groups made of solvent molecules for a variety of reasons, including molecular resonance. In this way, thermal energy in the solution oscillates and transfers. The entire procedure is depicted in
Figure 2.
We now attempt to utilize the high-energy bloc model to explain volatilization. Taking a glass of water as a case in point, there will be uneven energy exchange between the glass’s surface, walls, bottom, and the surrounding air. The water inside the glass will oscillate in energy because of the energy transfer, creating compressed high-energy groups made up of several water molecules. In the following instant, the high-energy groups will spread out and break apart as they collide with nearby water molecules, greatly enhancing their kinetic energy. These high-energy water molecules will continue to collide with other water molecules to exchange energy, and eventually, following a few collisions, they will form new high-energy groups. Volatilization of liquid water occurs when high-energy water molecules generated on or near the water surface are deprived of the opportunity to collide with other water molecules to form new high-energy groups. As a result, the high-energy molecules may separate from the water’s surface and enter the atmosphere.
Essentially, we think that the high-energy blocs and the high kinetic energy solution molecules transformed one another to propagate the thermal energy throughout the liquid. In the meantime, let's generalize that energy transfer causes solute molecules in a solution to form high-energy groups in addition to solvent molecules.
In the subsequent discussion, we will utilize homogeneous catalytic systems as a case study to thoroughly examine the principles of catalysis. Our aim is to critically assess the existing theories of catalysis and to introduce our own theoretical framework. It is our assertion that the inability of scientists to comprehend the phenomena of life through the lens of the second law of thermodynamics stems from inaccuracies in their theory of catalysis. Consequently, the theory of catalysis presented in the following sections constitutes the fundamental focus of this article.
3. A Comprehension of the Established Principles of Homogeneous Catalysis
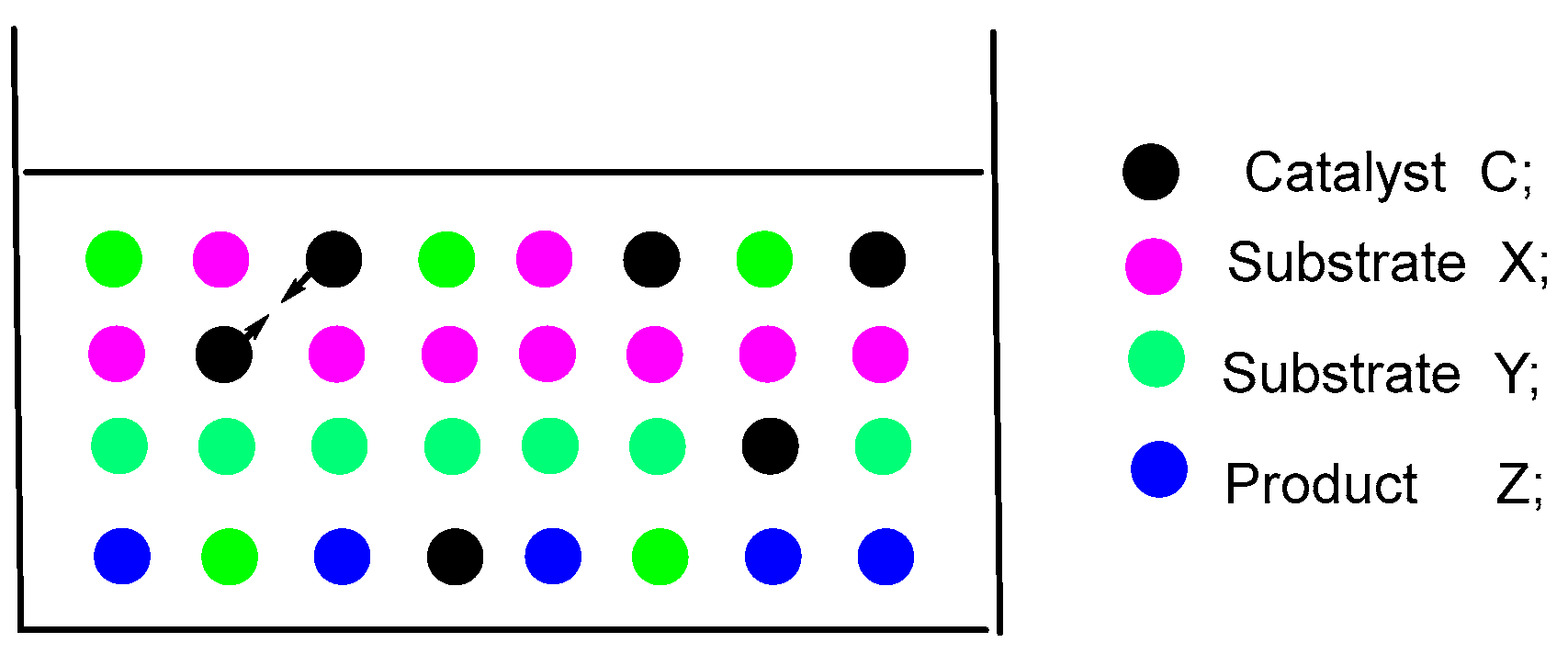
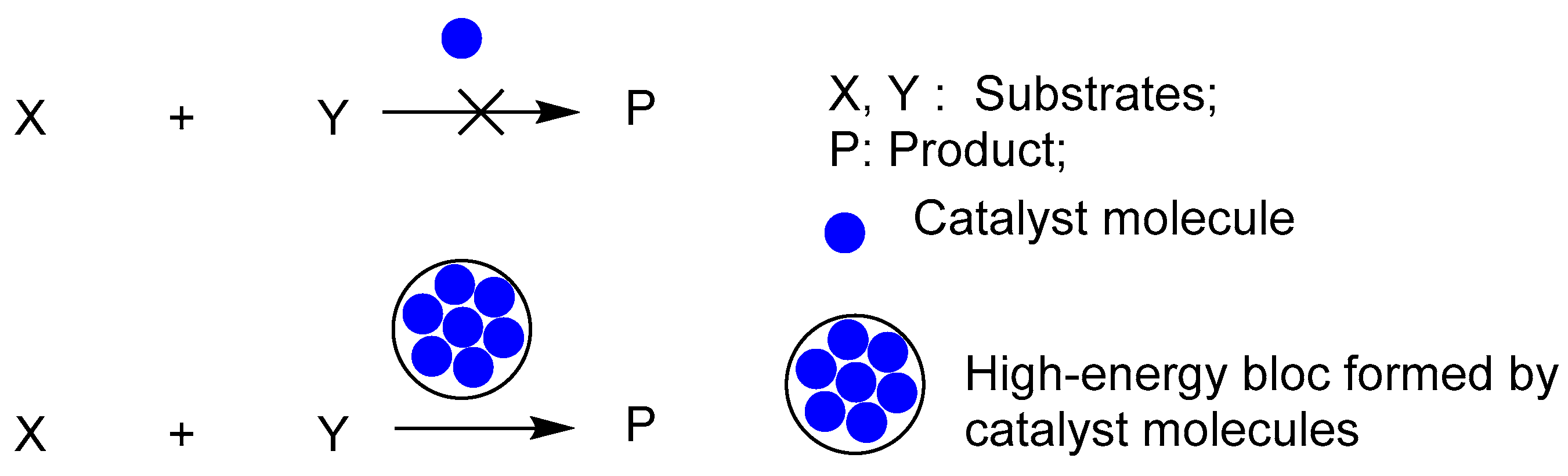
The widely recognized theory of homogeneous catalysis can be derived from the collision theory.[
8] According to this theory, in a solution, the catalyst C initially collides with the substrate X, resulting in their binding and the activation of substrate X to produce XC. Subsequently, XC interacts with substrate Y, leading to the formation of the complex XYC. X and Y establish a new bond to produce CZ. Subsequently, C is isolated from Z to yield the product Z along with the regenerated catalyst C. This process is illustrated in
Figure 3.
This catalytic process provides us with the following insights.
The completion of the catalytic process occurs when the catalyst molecule C engages in successive collisions with substrates X and Y. If the external conditions, such as temperature, solvent, and other parameters, are held constant, the probability of catalyst C colliding with substrates X and Y will significantly influence the rate of the catalytic reaction.
Each catalytic cycle is executed autonomously by an individual catalyst molecule, indicating that every catalyst molecule possesses catalytic activity. In a mixture of substrates X and Y, the presence of even a trace amount of catalyst C, or just one molecule of catalyst C, can facilitate a catalytic reaction, leading to the generation of product Z. However, it is likely that the resulting quantity of product Z will be too small to be observed.
If it is believed that the reasoning does not present an issue, we shall proceed with our contemplation. Based on the above catalytic theory, it can be inferred that an increase in the concentration of the catalyst will significantly influence the catalytic rate. An increase in the quantity or concentration of the catalyst leads to a heightened likelihood of collisions occurring between the catalyst and the substrates X and Y. Concurrently, the likelihood of collisions among the catalyst molecules themselves also rises. The interaction between catalyst molecules effectively consumes the potential for collisions between catalyst molecules and substrate molecules X and Y. Each time two catalyst molecules collide, it results in the loss of two opportunities for catalyst molecules to engage with substrates, as illustrated in
Figure 4.
To put it differently, as we progressively augment the quantity of catalyst (loading), both the rate of the catalytic reaction and the speed of product formation rise. However, it is important to note that the effectiveness of the catalyst may still decline. The increase in the quantity of catalyst leads to a higher likelihood of collisions among catalyst molecules. This, in turn, diminishes the probability of collisions between the catalyst molecules and the substrates, resulting in a decrease in the overall activity of the catalyst.
Assume, for instance in
Figure 5, that a homogeneous catalytic process is employing 10 mol% loading to catalyze substrates X and Y to obtain 50% product Z in 10 hours while maintaining constant solvent, temperature, and other parameters. Increasing the catalyst amount to 20 mol%, with the volume of the catalytic system remaining unchanged, is expected to result in a reaction time for achieving 50% of product Z that exceeds 5 hours, likely falling between 5.1 and 5.5 hours. This assessment seems reasonable and could correspond to real-world scenarios.
Certainly, that is not the subject of our discussion. Our primary focus will be on the duration required to achieve 50% conversion of product Z from the catalytic reaction as the quantity of catalyst is progressively diminished. In the previously mentioned example of homogeneous catalysis, let us consider that the duration required to catalyze substrates X and Y using a 10 mol% catalyst to achieve 50% conversion to product Z is 10 hours, as illustrated in
Figure 6. Assuming all other conditions remain constant, a reduction of the catalyst amount to 5 mol% will result in the catalytic reaction time required to achieve 50% of product Z being slightly under 20 hours. Maintain a reduction of the catalyst to 2.5 mol%. Following this adjustment, the time required for the catalytic reaction to achieve 50% of product Z should be slightly below 40 hours. In a similar manner, if the catalyst loading is decreased to 0.25 mol% and the duration is increased tenfold to 400 hours, it is possible to achieve a yield of 50% of product Z, correct? Is it possible for us to further decrease the quantity of catalyst while simultaneously prolonging the duration of the catalytic reaction, potentially allowing it to continue indefinitely?
However, to the dismay of all, the actual circumstances do not align with the aforementioned depiction. The ultimate conclusion is that in any homogeneous catalytic reaction, it is not possible to continuously decrease the quantity of catalyst.[9-11] When the quantity of catalyst is consistently decreased, a specific threshold, such as 1 mol%, results in the reaction taking 10 hours to reach completion. However, if the catalyst amount is further reduced to 0.5 mol%, the reaction may persist for 20 hours or even extend to 40 or 160 hours without achieving completion. This indicates a significant loss of catalytic activity or a drastic reduction in its effectiveness. Consequently, this phenomenon, which indicates that the catalyst cannot be reduced indefinitely, is referred to as the concentration-dependent effect on catalyst activity.[
12]
4. A Novel Concept Has Been Introduced: The Catalyst Activity's Concentration-Dependent Effect
In any homogeneous catalytic reaction, maintaining constant conditions such as solvent, substrate concentration, and temperature, a reduction in the catalyst amount will yield specific results. When the catalyst quantity is decreased to a certain threshold, for instance, 1 mol%, further reductions to levels like 0.5 mol% or 0.1 mol%-essentially reflecting a decrease in catalyst concentration-will lead to a situation where extending the reaction time does not result in the completion of the catalytic process. This indicates that as the catalyst amount diminishes, there exists a critical point at which the catalyst's activity significantly declines or is entirely lost. This phenomenon is referred to as the concentration-dependent effect on catalyst activity. This observation indicates that the catalytic theory, which posits that a single catalyst molecule can complete the entire catalytic cycle, is incorrect. Below, we present our own theory of homogeneous catalysis.
5. Catalysis Assumption: Single Catalyst Molecule Exhibits no Catalytic Activity
We are going to explain homogeneous catalytic reaction using the high-energy bloc model. Catalysis is the process of increasing the rate of a chemical reaction by adding a substance known as a catalyst, which is not consumed in the reaction and remains unchanged after the reaction.[
8] In this instance, we assert that a single catalyst molecule exhibits no catalytic activity. In homogeneous catalytic reactions, multiple catalyst molecules exchange energy with the surrounding environment to form compressed high-energy groups that catalyze the substrates and accomplish catalytic cycling. Solvent molecules, catalyst molecules, and substrate molecules make up a homogeneous catalytic system. Solvent molecules will compress into high-energy groups when external heat is introduced. These groups will then expand, break apart, and collide with other solvent molecules to produce high kinetic energy solvent molecules, which will create new high-energy groups in subsequent collisions. Then, we assume that catalyst molecules in the solution, like solvent molecules, will form compressed high-energy clusters during the process of exchanging energy with the outside world (of course, substrate molecules also form high-energy groups, which is temporarily not considered contributing to catalysis). High-energy solvent or catalyst molecules will be produced when they expand, fracture, and collide with other solvent or catalyst molecules. Subsequently, they will collide once more, creating new high-energy clusters made of catalyst molecules.
Numerous homogeneous catalytic reactions are dependent on catalyst loading, according to the literature.[9-11] There is a critical concentration for each catalyst in a particular catalytic reaction. When the solvent volume and substrate molar amount remain unchanged, there is a critical value for catalyst loading, such as 5 mol% or 1 mol%, The catalytic activity will drastically drop if the catalyst loading is less than this specified amount. It is assumed that a single catalyst molecule cannot catalyze a reaction on its own. If not, the catalyst activity’s concentration-dependent effect cannot occur. The real catalyst, which exhibit catalytic activity, are thought to be the high-energy blocs made up of catalyst molecules. Those individual catalyst molecules are unable to activate the substrates (as seen in
Figure 7) due to their lower energy compared to the compressed high-energy groups made up of catalyst molecules. This is because high-energy groups store more energy than other molecules in the system, primarily potential energy.
In conclusion, it is thought that a single catalyst molecule lacks catalytic activity for all homogeneous catalytic reactions. When catalyst molecules in solution receive external energy, they compress into high-energy blocs made up of multiple catalyst molecules; these high-energy clusters are what act as catalyst. At the next instant, the high-energy group will expand, releasing energy to activate the substrate and finish catalysis. Simultaneously, the high-energy group will burst and break apart, distributing the leftover energy to nearby molecules before coming together again in subsequent collisions to form a new high-energy group made up of catalyst molecules.
6. Understand How Concentration Affects Catalyst Activity
We now understand that the genuine, active catalyst in homogeneous catalytic processes is the high-energy bloc made up of many catalyst molecules. The concentration of the catalyst markedly impacts the formation of high-energy blocs made up of catalyst molecules. The likelihood that several catalyst molecules may collide to form a high energy group may be significantly decreased if the catalyst's concentration is continuously decreased. There must be a requirement for the catalyst concentration because the creation of high-energy blocs requires multiple catalyst molecules to collide quickly. Thus, the production of a high energy group made up of catalyst molecules has a concentration dependent effect, which is basically the concentration dependent effect of catalyst activity. There won't be any catalytic reaction if the concentration of the catalyst is very low, which is why we say the catalyst abruptly lost activity. This is because the high energy group made up of catalyst molecules might not form at all. In contrast, if a single catalyst molecule is capable of catalyzing the reaction, the catalytic activity will increase as the catalyst concentration decreases. In other words, the catalytic reaction will always be finished as long as the reaction time is extended.
It is now understood that the high-energy clusters created by the catalyst molecules serve as the genuine, active catalysts, and this finding will be utilized to construct the model of life.
7. Create the Life Model by Deriving it From the Second Law of Thermodynamics
Life is invariable connected to entropy and the second law of thermodynamics. When a system reaches thermodynamic equilibrium, the entropy value gets to maximum. On the other hand, the system’s entropy value decreases with increasing system disequilibrium. In addition to indicating how far the system has deviated from its equilibrium state, entropy also shows how chaotic the system is. Here, we start with the second law of thermodynamics and represent the thermodynamic state of the system with the population standard deviation σ.[
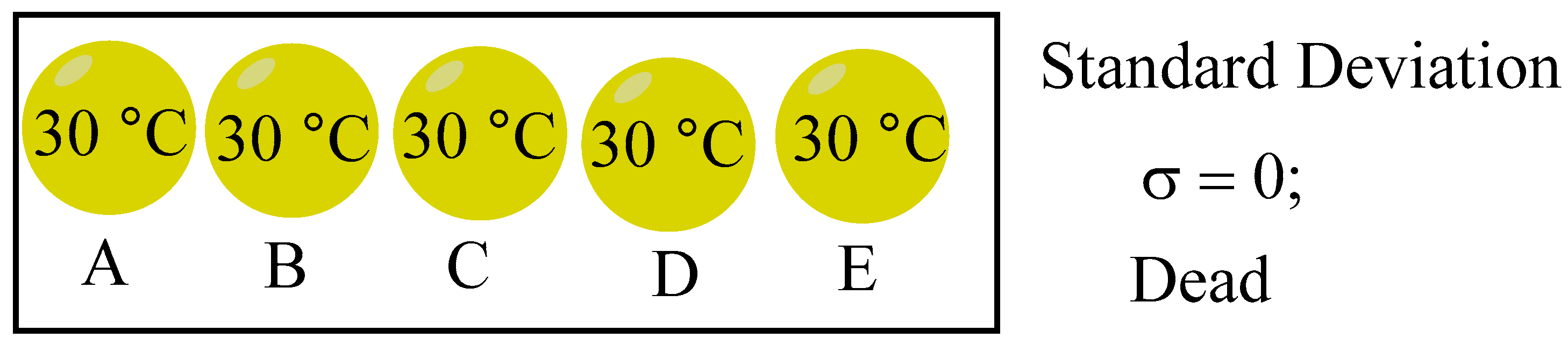
13] We also employ the idea of entropy, but we don’t compute it; rather, it just denotes how far the system is from its equilibrium. To calculate, we will use the standard deviation σ. When the system reaches equilibrium and its standard deviation σ is zero, its entropy is at its maximum. The entropy of the system diminishes as the system moves further away from its equilibrium state, a phenomenon evidenced by an increased standard deviation. Five spheres make up this system: A, B, C, D and E. The standard deviation σ is computed using the temperature within each of the five spheres. The system has reached equilibrium (σ = 0), and the entropy is maximum. The system’s entropy decreases and its distance from equilibrium increases with a larger σ.
Living organisms are thought to be systems that have not attained thermodynamic equilibrium, in accordance with the second law of thermodynamics. As seen in
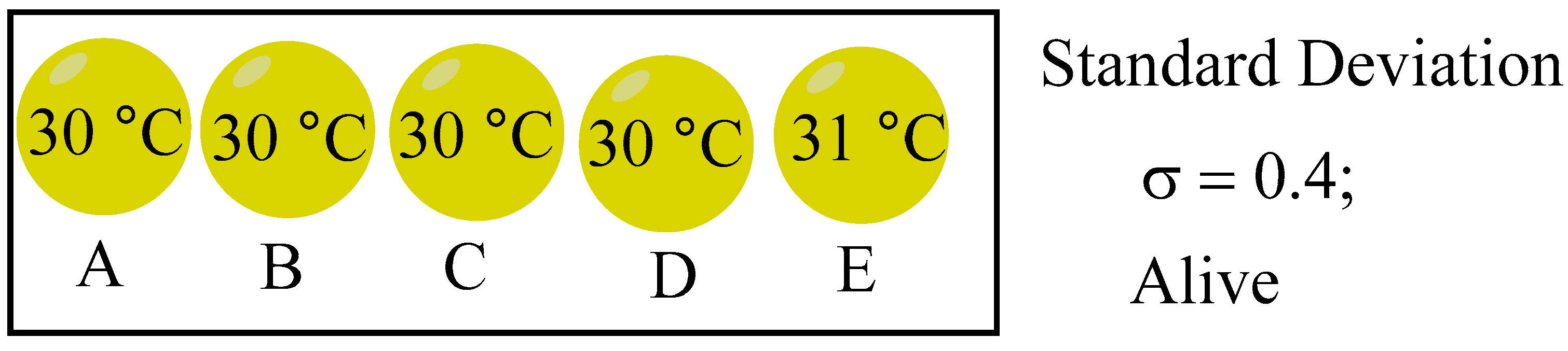
Figure 8 below, the system composed of five spheres is dead with an interior temperature of 30 ºC; this is balanced thermodynamically.
With σ = 0.4 in
Figure 9, the following alive system has different ball temperatures and has not attained thermodynamic equilibrium.
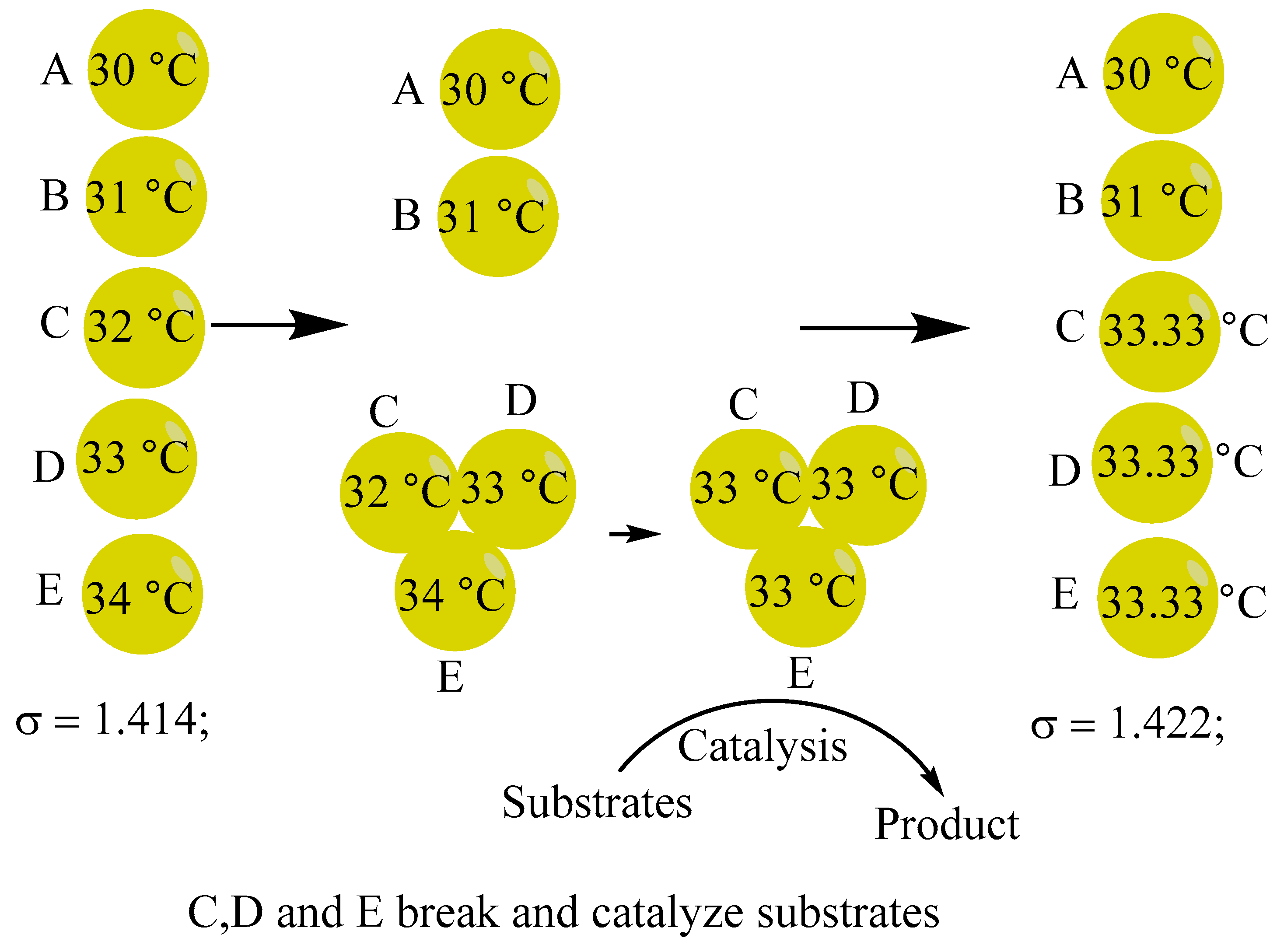
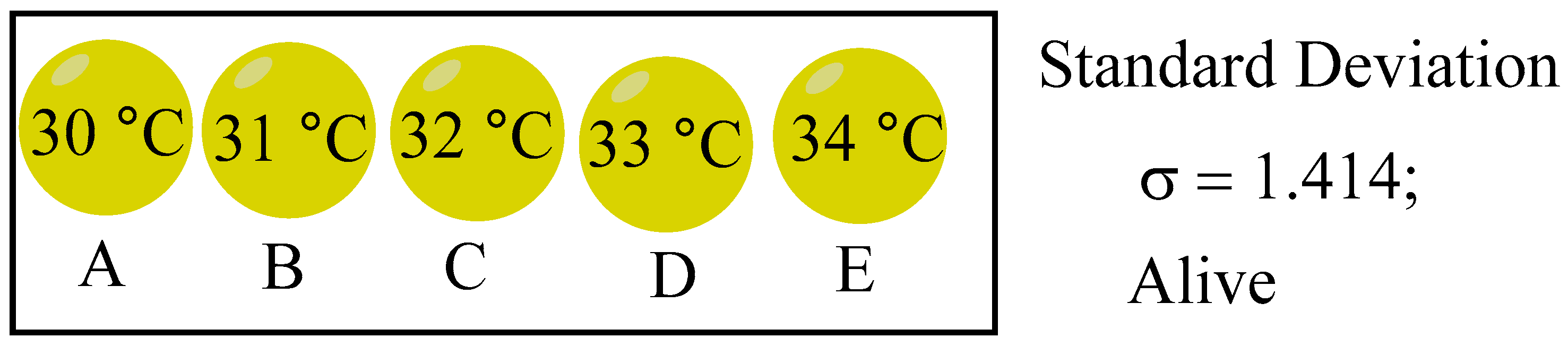
The following living systems are considered as initial states of life: A (30 ºC), B (31 ºC), C (32 ºC), D (33 ºC), and E (34 ºC), as illustrated in
Figure 10, with σ calculated to be 1.414. A decrease in σ suggests that the system is progressing towards thermodynamic equilibrium and nearing a state of death. Conversely, if σ remains constant or increases, it signifies that the system has sustained itself and is in a viable living state. Let's now consider the qualities that the system below must possess in order to resist the second law of thermodynamics.
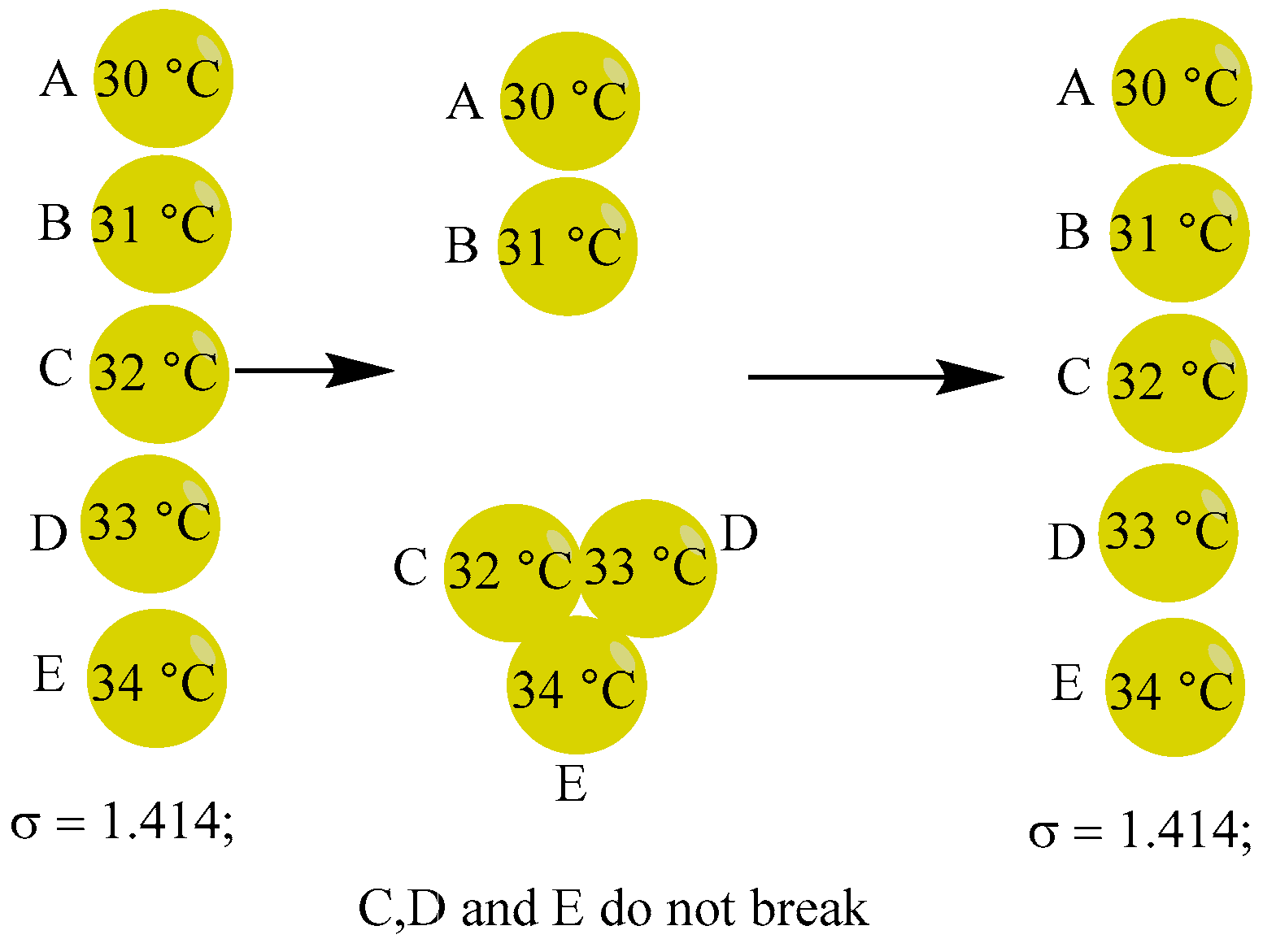
The interior temperatures of the five spheres in the system above vary, and the ball with higher temperature will transfer heat to the ball with lower temperature. After heat transfer occurs, σ will drop. When, for instance, ball A and ball B’s heat transmission reaches equilibrium, the system states are as follows: A (30.5 ºC), B (30.5 ºC), C (32 ºC), D (33 ºC) and E (34 ºC); σ = 1.378. Let’s assume the following scenarios in order to keep this system from reaching thermodynamic equilibrium.
Condition 1. We consider the five spheres (A, B, C, D and E) to be insulated bags with insulated interiors and exteriors. It is not possible for the heat inside the ball to escape if they are not opened. The five balls’ internal energy won’t interact with outer world even if they crash with one another if they are not opened.
In this scenario, there will be no heat exchange (or energy exchange) between the five balls and the external environment. Thus, σ in this system won’t change.
Under some circumstances, the spheres must be opened to exchange heat with the outside since the five balls are insulated bags and the spheres’ interior, and exterior are both insulated. The system’s σ could go up or down once the sphere opens. Put another way, this life now confronts the prospect of dying as well as the hope of surviving when the spheres are opened.
In the homogeneous catalysis, the system catalyzes the substrate to complete the catalytic cycle by exchanging energy with the outside world through compressed high-energy blocs composed of catalyst molecules. Catalytic processes, in our opinion, are fundamental to biological metabolism.[3a] We would like to add or change the following for condition 1.
Condition 2. We consider that A, B, C, D and E are five biomolecules with the potential to be catalytically active, meaning they can be employed as catalysts to speed up reactions.
Although the five biomacromolecules A, B, C, D and E have identical structures, their internal energies differ. In this case, we are using temperature to indicate their internal energy levels. When the system exchanges energy with the outside world, a compressed high-energy bloc will be formed at random by three of the five spheres. Thus, three options exist.
- 1)
Three random balls collide to produce a compacted high-energy bloc If the surrounding temperature is too low (such as -100 ºC). As illustrated in
Figure 11 below, the energy stored in the bloc itself is insufficient, preventing the opening of three randomly selected balls and preventing any energy exchange inside the three balls.
As it happens,
Table 1 has five additional combinations of the five balls that have equal probability.
- 2)
The surrounding temperature (for example, 50 ºC) is appropriate, and the compressed high-energy bloc (made up of random three spheres) itself has sufficient energy stored in it to open the spheres and exchange energy to bring the internal energy of the three spheres into balance. As seen in
Figure 12, spheres C, D and E form a high energy bloc and open for energy exchange to establish equilibrium. This is expressed as follows: σ=1.265; CDE(33 ºC), A(30 ºC), B(31 ºC);
Table 2 has five additional combinations of the five balls that have identical odds
.
Any of these six combinations will lower σ, as the data in
Table 2 show. The system progresses both in the direction of thermodynamic equilibrium and death.
- 3)
It serves as an addition to the second circumstance. The resulting high-energy bloc is catalytically active. It can spontaneously catalyze the substrate and accomplish catalytic cycling if there are substrates around. The energy in these three spheres may aid in the catalysis of the substrates during this process. It’s also possible for these three balls to get energy by catalyzing the substrates, which would raise their internal temperatures.
As seen above, this living organism confronts both life and death when it opens the three spheres. In the absence of any substrates, these five spheres will spontaneously organize into a high-energy cluster consisting of three spheres dedicated to energy exchange repeatedly, leading to rapid attainment of thermodynamic equilibrium (σ=0). At this juncture, the living organism will die.
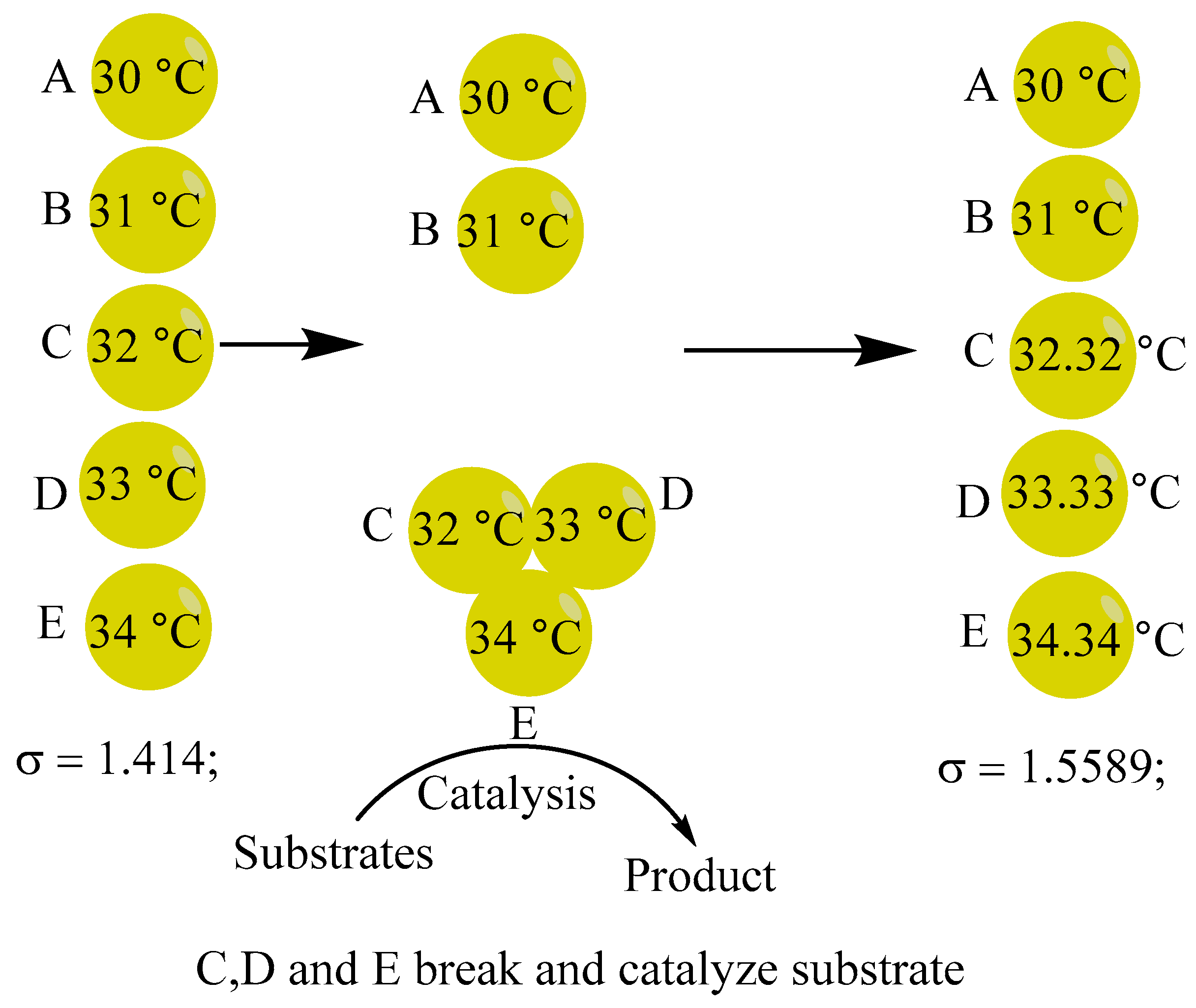
Because of the energy produced by catalysis, the three spheres that made up the compacted high-energy group may see an increase in internal temperature. Assuming that the temperature increase within the spheres is one hundredth of the initial temperature, this value solely depicts the trend of energy acquisition within the biomolecules during the catalytic process. There is no practical meaning to the value by itself. When the internal temperature of sphere C is measured at 33 ºC prior to catalysis, one percent of this temperature corresponds to 0.33 ºC. After the catalysis process, the temperature increases to 33.33 ºC (33.33 ºC = 33 ºC + 0.33 ºC) as sphere C absorbs energy through the formation of substrate chemical bonds. This could enhance σ, enabling living organisms to endure. Subsequently, a thorough analysis is required, which can be separated into two cases: 3A and 3B.
3A. In the compact high-energy bloc comprising three spheres, each sphere facilitates internal heat exchange to achieve thermal equilibrium, subsequently catalyzing a reaction. This process ensures that each sphere acquires an equivalent of energy from the catalysis of substrates, represented as follows: CDE(33.33 ºC), A(30 ºC), B(31 ºC); with a standard deviation of σ = 1.422;
Figure 13.
Collision of biomolecules and the acquisition of equivalent energy in catalysis.
Figure 13.
Collision of biomolecules and the acquisition of equivalent energy in catalysis.
There exist five additional combinations of the five balls that have equal probabilities, as illustrated in
Table 3.
Based on the analysis presented in
Table 3, it is evident that only the compressed high-energy bloc, which comprises spheres C, D and E as catalyst, will result in an increase in the value of σ and drive the system to evolve away from equilibrium. Conversely, some compressed high-energy blocs cause a rise in entropy, or a drop in the value of σ. Thus, the activity of living organisms and the catalytic functions of internal biomolecules are inherently distinct. The distance from the thermodynamic equilibrium is represented by the activity of living things. Living things are more active when they are further from the equilibrium condition. The catalytic activity of biomolecules within living organisms has persisted, even after the organism’s death.
3B. Prior to each sphere opening for internal heat exchange, the compressed high-energy bloc catalyzes the reaction. Before there is an energy exchange, each sphere receives a distinct amount of energy from the substrates, splits, and the balls close. As seen in
Figure 14, the ball with a high energy or high internal temperature contributes more to the catalysis. The energy obtained is as follows, which we think does not go against the second law of thermodynamics: σ = 1.5589; CDE(32.32, 33.33, 34.34 ºC), A(30 ºC), B(31 ºC);
There are five additional combinations of the five spheres that have equal probabilities, as presented in
Table 4.
The analysis presented above (
Table 4) indicates the existence of three categories of compressed high-energy blocs for catalysis, namely BCD, BCE, and CDE, which serve to enhance σ and drive the system away from equilibrium.
Considering the system of five spheres as a model of living creature, the preceding analysis indicates that in the absence of catalytic reactions, the system will eventually approach equilibrium (σ=0). The system may evolve in a direction that is more thermodynamically imbalanced direction (σ increase) under catalysis, as demonstrated in 3A and 3B. This could be the nature of biological metabolism.
The results indicate that not every compressed high-energy bloc will lead to an increase in the value of σ; however, there exists a possibility among these combinations that may enhance σ. Compressed high-energy groups BCE and CDE serve as catalysts that exhibit greater catalytic activity compared to other combinations, such as ABC and ABD, owing to their enhanced internal energy.
Not all high-energy groups consisting of three biomolecules have the ability to finish the catalytic process, and not all high-energy groups consisting of three biomolecules will cause the σ value to rise after the catalytic reaction is finished. This relates to the likelihood of successful catalysis, which is contingent upon the concentration of biomolecules (acting as catalyst), the kind and concentration of substrates, and the ambient temperature. And they are all connected to the state of activity, rest, or sleep of the living organisms.[
14]
8. Considering Biomolecules Through the Lens of the Second Law of Thermodynamics
Let us now examine what we have learned about living organism thus far using the second law of thermodynamics.
Different internal energy in biomolecules with the same structure indicate that life is a thermodynamically imbalanced system. When the system achieves thermodynamic equilibrium and the internal energy are equal, the live thing dies.
Biological macromolecules that possess identical structures can exhibit varying internal energies due to the fact that these macromolecules function as insulated containers, resulting in adiabatic conditions both internally and externally. If these containers remain sealed, they will not interact with the external environment, and consequently, the entropy (or σ value) of the living system will remain unchanged. As a result, there won’t be any heat exchange between these biological macromolecules and the external environment, and the entropy of the system remain unchanged. At extremely low temperatures or in highly dilute concentrations, interactions among these biomolecules do not result in the opening of the molecules, there is no exchange of internal energy, and the entropy (or σ value) of the living system is unchanged.
These biomolecules with the same structure but varying internal energies will form high-energy clusters made up of several biomolecules (3, 4, 5, or more) by exchanging energy with the surrounding environment at the right temperatures and concentrations. These high-energy clusters may potentially open these biomolecules, enabling them to trade internal energy and raise the biological system’s entropy (or lower its σ value). These high-energy groups, which are made up of many biomolecules, can also act as a catalyst to catalyze substrates. The outcome of this catalytic process may lead to an increase, a stabilization, or a decrease in the entropy of the living system. The sole method identified to decrease the entropy (or increase standard deviation σ) of living systems thus far has been via catalytic reactions, commonly referred to as metabolism.
Biomacromolecules with various structures can also compress into high-energy groups, which will raise the system’s entropy through internal energy exchange. Since it is very intricate, we won’t get into it here.
Based on the second law of thermodynamics, that's what we now understand about life. We must have a deeper understanding of the mechanisms by which several biomacromolecules combine to produce high-energy bloc before moving on to the topic of what life is.
To address the problems of catalysis and system entropy, we treat the biomolecules A, B, C, D and E above as spheres, as previously mentioned. However, to address the question of what life is, we must reevaluate the structures of A, B, C, D and E, and determine the distinctions between biological macromolecules, or insulated bags, and regular molecules. Additionally, we will investigate the self-opening mechanism of high-energy blocs made up of several biological macromolecules.
Numerous macromolecules in biology possess three-dimensional spatial structures, resembling containers. We are confident that, although these containers may be insufficient in size to accommodate small molecules like water, they are capable of retaining energy, or heat, a phenomenon we refer to as the insulation effect. The temperature is used to signify the high and low states of energy, or thermal energy, for example, the inside of a biological molecule is 35 ºC and the exterior is 30 ºC. As long as the biological molecule doesn’t form a high-energy bloc, it won’t transfer internal energy to the exterior even if it collides with other molecules. When the biological molecule, serving as a container, is opened (by forming a high-energy bloc at appropriate temperature), other small molecules may either enter or exit. This process facilitates the transfer of internal energy, allowing for an exchange of energy with external environment. Ultimately, this results in the equalization of internal and external temperatures.
9. Biological Macromolecules as Insulated Bags and Their Insulated Bag Upgrading Process
It is important to state that our previous assumptions are founded on our analysis of specific phenomena. For instance, we have developed a compressed high-energy bloc model made up of solvent molecules based on volatilization. Similarly, we presented a high-energy group model composed of catalyst molecules to describe the concentration-dependent effect of catalysts in homogeneous catalytic reactions. The subsequent assumptions and rationale are solely founded on imagination. Therefore, the significance of the following concepts is in offering a perspective on the issue, not in the accuracy of the outcomes.
To begin, let's imagine that biomacromolecules with an insulating function have two antennas, as shown in
Figure 15.
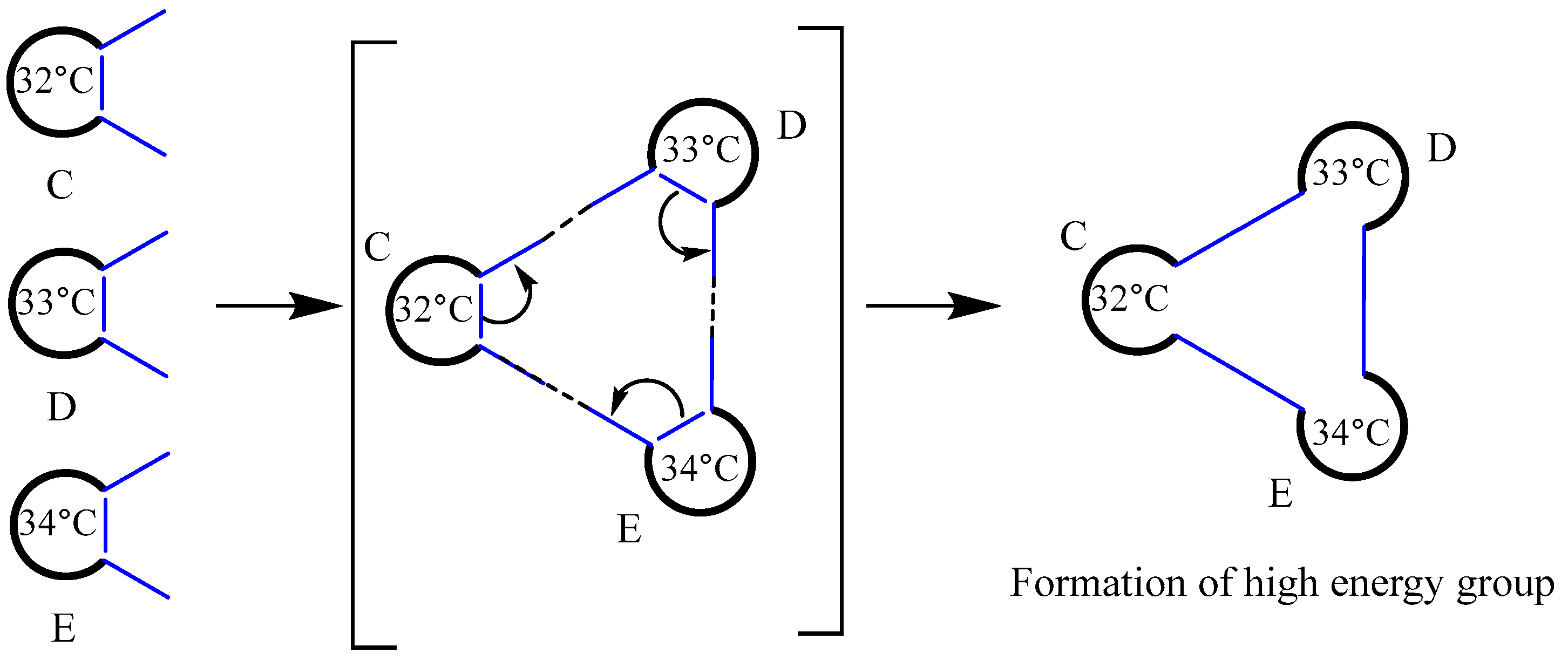
Bonds are created between the antennas of several biomolecules, C, D, and E, when they form a high-energy bloc. Next, as seen in
Figure 16, open the molecules. The mechanism may be regarded as a rearrangement of chemical bonds.
After the formation of this high-energy group consisting of biomolecules and their complete opening, the biomolecules either opt to catalyze the substrates, which could possibly lead to an increase in σ, or they exchange energy within the group to lower the system's σ. Consequently, two additional questions have emerged as follows:
All biomolecules are insulated bags with three-dimensional spatial configurations. What distinguishes them from one another?
A living organism is a system that is far from thermodynamic equilibrium, as evidenced by variations in the internal energy of the biomacromolecules that comprise it. The larger this disparity in internal energy, the lower the entropy value of the organism. As biomacromolecules with organisms persist in catalyzing substrates, the internal energy differentials may progressively increase. Concurrently, the σ value of biological system is on the rise. What implications does this have for future developments?
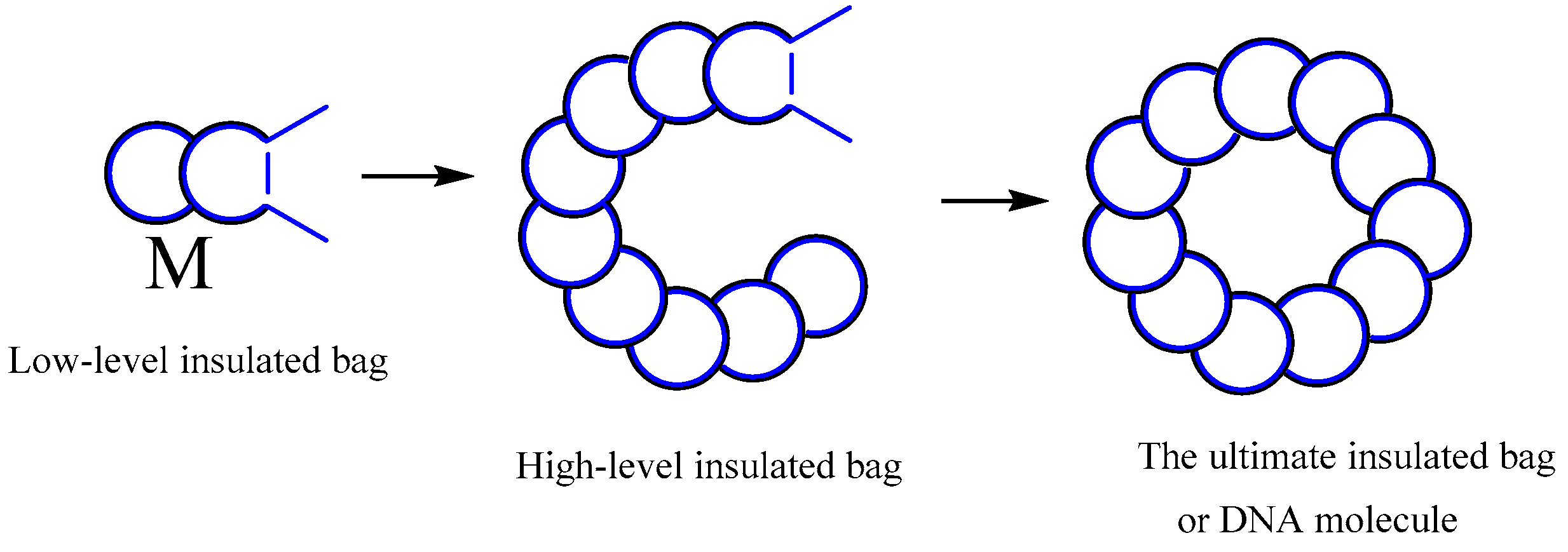
In order to answer the aforementioned concerns, we presume that the biomacromolecules employed as insulated bags are categorized into distinct grades. Even the tiniest living cells contain thousands of different biomolecules. Here, we just suppose that the five biomolecules that make up living things are A, B, C, D, and E. In reality, there exist thousands of A, B, C, D, and E in living organism. Molecules with high internal energy (or temperature) combined to create high-energy blocs, like CDE, have a higher chance of catalyzing the substrates successfully than molecules with low internal energy, like ABC. The difference in internal energy of these biomolecules increases as a result of their continued catalysis of substrates. At a pivotal moment, three or more biomolecules possessing significantly different internal energies may interact to generate a high-energy complex. These molecules will undergo chemical reactions, establish new chemical bonds, and produce novel biomolecules. We refer to this as the insulated bag’s escalation reaction. If the biomacromolecule served as a primary insulated bag prior to the upgrading reaction, the resultant biomacromolecule produced following the upgrading reaction will function as a secondary insulated bag or a higher-level insulated bag. For instance, three biomolecules, L1 (30 ºC), L2 (55 ºC), and L3 (60 ºC), create a high-energy bloc. Subsequently, the energy from L2 and L3 will transfer to L1, a phenomenon that can be described as a domino effect. Consequently, this process may disrupt certain chemical bonds and form new ones, leading to the production of novel biomolecular M and fragment molecule N, as shown in
Figure 17 below.
According to our hypothesis, biomolecules catalyze substrates continually to gain energy, resulting in an increase in internal energy differences and a drop in entropy values (i.e., an increase in σ). All of this is done to enable biomolecules to develop into more advanced insulated bags. Therefore, biomolecules (apart from DNA molecules) have a tendency to become more efficient at insulating, and the upgrading reaction of the insulated bag is actually driven by the negative entropy that is acquired by catalysis (or metabolism).
The most important question we now need to consider is: What is life?
It is evident that molecule M is a secondary insulated bag, but it still possesses two tentacles that allow it to form high-energy blocs with other molecules, catalyze substrates, and eventually develop into a more sophisticated insulated bag like M2 (
Figure 18). What will occur subsequently? Is there a maximum level of insulation available?
The purported highest level insulated bag lacks the two antennas, or these two antennas may be folded within the molecule structure, preventing the formation of high-energy blocs with other molecules. Furthermore, even if high-energy blocs are formed with other molecules, they are unable to open the molecules, which prevents them from catalyzing the substrates. It is believed that one example of this type of molecule is DNA. The insulated bag depicted in
Figure 19, which represent the highest level of insulation, do not feature external antennae, or, to put it another way, their antennas are concealed inside the molecules. Molecules with such structures will not open to exchange energy with other molecules, regardless of whether they form high-energy groups.
10. Classification of Organic Molecules
According to our comprehension of the second law of thermodynamics, we can now attempt to categorize natural or organic molecules into three distinct groups.
Non-insulated bags of molecules. These molecules, which include water molecules, amino acids, and non-folding peptide chains, only have primary and secondary structures.
Insulated bag of molecules. These molecules have an 'inner' or 'outer' tertiary structure, which resembles a container. For instance, under specific circumstances, biological macromolecules having tertiary structures, such as proteins and enzyme molecules, might collide with one another to generate high-energy clusters. These molecules have two antennas, and they readily open up for internal energy exchange when they form high-energy blocs at appropriate temperature. These high-energy groups may simultaneously function as catalysts, facilitating the transformation of substrates, altering, or augmenting their internal energy, and ultimately initiating the thermal bag upgrade reaction, which results in the formation of new biological macromolecules with improved thermal insulation efficiency.
The ultimate insulated bag of molecules. This category of molecules bears similarities to the second category. They curl their antennas inside the molecules, or they don’t have any, which is the difference. Even when the molecules collide with one another, they do not become available for internal energy exchange. Furthermore, they do not form high-energy blocs for catalysis, nor do they progress into more advanced insulated bags. We refer to these molecules as the “the ultimate insulated bags”, and we assume that the DNA molecule is one of them.
Figure 20.
Classification of molecules in nature.
Figure 20.
Classification of molecules in nature.
11. What Is Life?
We think that life is a system created by the ultimate insulated bag (like DNA molecules). The system’s job is to exchange materials and energy with the external environment by harnessing the energy that the ultimate insulated bag releases. Normally, we refer to this process as metabolism. In this procedure, the energy that was previously released is restored to the ultimate insulated bag, thereby concluding a thermodynamic cycle. Life can be understood as a system constructed by the ultimate insulated bag, capable of executing at least one thermodynamic cycle. This means that the instructions (or energy) from the ultimate insulated bag are what propel the biological system to interchange materials and energy with the outside world. The restoration of the ultimate thermal bag is the most crucial outcome of the exchange of materials and energy between the organism and its external environment; without it, the organism will die.
Too much detail can mislead us when it comes to studying life. In order to infer the logic of life from the second law of thermodynamics, we must make assumptions and overlook the majority of the facts. Most biological discoveries may not be helpful in explaining what life is because they are unable to explain the distinction between an organism’s moments of life and death. Stated differently, most findings in biology primarily inform us about the composition of current life forms rather than providing insights into the essence of life itself.
As we have mentioned, the DNA molecule is the ultimate thermal bag or the highest-level insulated bag. It does not acquire internal energy via the catalysis of substrates. As a result, both the energy inside and the energy outside of the DNA molecule have difficulty moving through each other. It is our assumption that the energy contained in a DNA molecule is digital and ordered. For instance, messenger RNA uses information from DNA to make protein. We suppose that DNA is releasing digital energy, and its internal temperature or energy continuously lowers with the ongoing translation of messenger RNA.[
15] The structure of the protein is determined by DNA, which serves as a homolog to DNA molecules. Likewise, messenger RNA is regarded as a homolog of DNA molecules and can enter their interiors to acquire energy for coding. Stated differently, the synthesis of the organism’s ordered structure is fundamentally driven by the release of internal energy from the ultimate insulated DNA molecule. Additionally, it is not necessary to worry about whether there will always be structural variations when DNA releases digital energy to build these biomolecules. These biomacromolecules upgrade their own insulation levels by catalyzing substrates, while simultaneously charging DNA. However, the macromolecular structure of the constituent organism may undergo certain structural alterations each time it completes a thermodynamic cycle. Subtle variations in their structure may significantly influence the charging of DNA molecules, and the energy required for recharging must also be ordered energy, or digital energy. It is our belief that minor variations in these homologous structures diminish their effectiveness in the process of charging DNA molecule. Additionally, the way that fully charged and 90% charged DNA release energy to synthesis other homologous biomolecules may also change slightly. This cycle, whether it pertains to the nuanced variations in the structure of synthetic homologues resulting from the differing energy levels with DNA as the initial factor, or the slight structural differences in homologues induced by external influences during the synthesis of biomolecular homologues, will ultimately accumulate to a significant extent that cannot be overlooked as DNA molecules repeatedly undergo the thermodynamic cycles. This could be the result of the organism aging, which is primarily shown in the gradual reduction of the charging efficiency of the organism’s DNA molecules as the organism ages due to structural changes in homologues of the DNA molecules that make up the organism.[
16] The alteration within the organism is frequently referred to as the entropy of the organism, which is characterized by a continual increase without any decrease. Additionally, the aging process of the organism can be associated with the growing disorder within the living system. This should not be mistaken for the entropy previously utilized to illustrate the extent to which the biological system deviated from equilibrium, as this concept is unrelated to the level of disorder, or so it is believed.
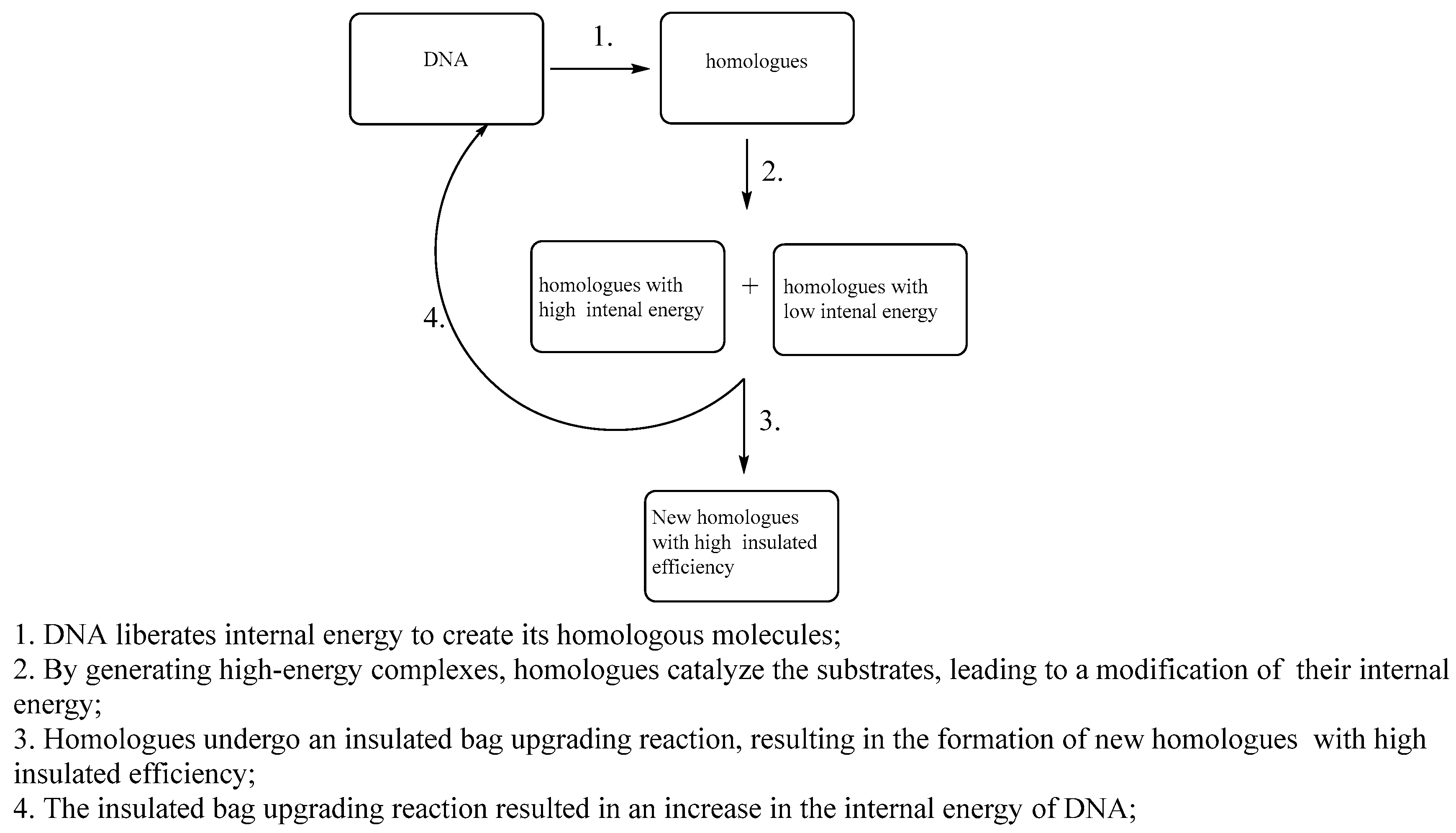
12. The Greatest Challenge Lies in Charging the Ultimate Insulated Bag
So how does DNA acquire its energy? We assume that orderly bioelectricity is the only energy that can be restored with DNA. Since, from a catalytic perspective, molecular collisions make it extremely difficult to open DNA molecules, and even when they do, the molecules only release energy or digital energy externally rather than regenerating energy in this way. Direct interaction with other molecules can solely cause the DNA molecule to release energy, but it cannot restore energy to the DNA molecule. DNA molecules, as previously mentioned, release energy to synthesize homologous biomacromolecules, which function as insulated bags. These molecules serve as catalysts that facilitate the eventual occurrence of upgrading reaction of the insulated bags. We believe that when homologous macromolecules generated by DNA molecules upgrade their own insulation efficiency, they will produce an ordered bioelectric field. DNA slowly restores its internal energy via interaction within this bioelectric field, reverting to its condition prior to energy release (
Figure 21) [
17].
In conclusion, two essential steps are required to charge a DNA molecule. First, homologous macromolecules must be generated from the DNA molecules. Second, these homologous macromolecules must participate in the insulated bag upgrading reactions.
13. What Is Death?
The condition in which the ultimate thermal bag is unable to acquire energy is considered to be its demise.[
18] We will refrain from addressing the topics of ageing and age-related mortality at this moment. Life can be characterized as a system that arises from the releases of energy by the ultimate thermal bag. This system is capable of replenishing energy through metabolic processes, thereby facilitating the completion of the thermodynamic cycle. As we previously stated, metabolism, or biomacromolecule catalysis, raises the standard division σ of biological systems. The increase in the standard division σ of biological systems leads to the initiation of the thermal bag upgrading reaction within biological macromolecules. The biological macromolecules, which serve as homologues to DNA molecules, will charge the DNA molecules during the thermal bag upgrading reactions. Nevertheless, not every biological macromolecule’s catalysis can result in a rise in the biological system’s standard division σ. If specific conditions are met whereby the catalysis of biological macromolecules fails to enhance the standard division σ of biological system, the biological macromolecules will be unable to participate in the thermal bag upgrading reaction. Consequently, the DNA molecules will remain uncharged, leading to the demise of the organism.
14. The Assumption About the Soul - The Soul Cannot Exist Independently of the Body [19]
Our comprehension of the essence of life leads us to conclude that the soul cannot exit independently in the tangible world. Life can be conceptualized as a system in which the ultimate insulated bag successfully undergoes a minimum of one thermodynamic cycle. The charging process of the ultimate insulated bag (DNA molecule) is inherently linked to the bioelectric field, and the essence of the soul must be connected to the presence of this bioelectric field. For instance, the majority, approximately 80%, of bioelectricity is utilized to charge DNA, while the remaining 20% is regarded as excess bioelectricity, which is ultimately associated with consciousness or the soul. Should the efficiency of charging the ultimate insulated bag diminish, the residual bioelectric energy of the living organism in the subsequent thermodynamic cycle will likewise be reduced. For example, as individuals age, their ability to charge DNA molecules diminishes, leading to a corresponding reduction in their available external bioelectric energy, which is expressed as consciousness. Upon their passing, the bioelectric energy contained within their bodies will inevitably dissipate, leading to the natural cessation of their consciousness or soul.
Furthermore, we define a living creature as an imbalanced system in thermodynamics (standard division σ>0). Its increase of σ can only be maintained by constant catalysis, or metabolism. The soul itself should be life if it can exist outside of the body, but it cannot increase or alter its σ. As a result, the soul is unable to exist outside of the body.[
20]
15. How Did Life Begin on Earth?
Let us now consider the formation of the first life. Miller's experiment,[
21] indicates that when lightning strikes, the primordial atmosphere can transform water, carbon dioxide, and nitrogen into small molecules like amino acids. These amino acids can indeed aggregate into dimers under specific conditions, eventually leading to the formation of extended chains made up of numerous amino acids. For millions of years, Earth has had the capacity to produce extensive chains of amino acids and other molecules, including fragments of nucleic acids. The inception of life can be traced back to the initial insulated bag. As molecular chains, including amino acids and nucleic acids, extend in length, they undergo folding to create a three-dimensional configuration, representing the most basic form of an insulated bag. As insulated bags, these biological molecules will then generate high-energy blocs, which will act as catalysts to catalyze reactions, alter their own internal energy states, and ultimately result in the production of high-level insulated bags through insulation upgrading reactions. The catalysis was basically metabolism, even if life had not yet developed. Therefore, metabolism existed before life.[
22] Biological macromolecules will eventually approach the ultimate insulated bags as long as the thermal bag upgrading reaction continues unabated. It is challenging to envision the process of achieving the ultimate insulated bag, as this may entail certain unforeseen reactions or influences, or it could simply result from an incidental alteration. The process of life formation officially commences with the creation of the ultimate insulated bag, even though this initial bag may not necessarily be a DNA molecule. Before a fully developed organism is formed, the primary challenge lies in charging the ultimate insulated bag. This prompts an inquiry into the source of the initial internal energy for the ultimate thermal bag. The ultimate thermal bag utilizes this energy to create its homologous system. We hold the view that the sun plays a vital role. It is our belief that, due to the incomplete establishment of the living system, the energy derived from sunlight influences the homologues, which collectively undertake the responsibility of replenishing the ultimate insulating bag until a fully developed life form emerges.
It is often stated that life originates from pre-existing life, and to date, we have not succeeded in synthesizing life artificially. This is due to the fact that the emergence of life was a prolonged process that involved numerous simultaneous steps. Our current understanding suggests that the emergence of life generally proceeds through the following stages:
Organic compounds are produced from inorganic substances.
Organic compounds progressively undergo polymerization or condensation, resulting in the formation of elongated one-dimensional chains.
Organic molecules' one-dimensional chains are long enough to fold into three-dimensional structures, which serve as primary insulated bags.
Several molecules exhibiting the characteristics of insulated bags assemble into a high-energy bloc that acts as a catalyst, facilitating the transformation of substrates while altering their internal energy states. Subsequently, a thermal bag upgrading reaction takes place, resulting in the production of enhanced insulated bags. The catalysis and insulated bag upgrading reactions will keep happening until the thermal insulation level reaches its maximum potential for improvement.
The advanced insulated bags described above are clearly more than mere DNA fragments; they also encompass various other insulated bags made up of distinct small molecule aggregates. The insulated bags created from fragments of DNA molecules possess benefits that remain to be fully understood. Following an extended phase of competition, the advanced insulated bags produced from DNA fragments undergo uncharted reactions or transformations, ultimately evolving into the ultimate insulated bag composed of the complete DNA molecule.
As the ultimate insulated bag, the DNA creates a system of homologues with the aid of sunlight that can self-recharge in the absence of light. Therefore, life, or a cell, is the system made up of the DNA ultimate insulated bag and its homologues [
23].
16. Mutual Validation of Biological Homochirality and Thermal Bag Upgrading Reaction
Homochirality,[
24] has been a challenging issue in the origin of life, as evidenced by the selection of only one chiral molecule (such as D-sugar or L-chiral amino acid) by living organisms. Utilizing the upgrading reaction of an insulated bag to explore the origins of life could potentially elucidate the phenomenon of homochirality.[
25] It is reasonable to deduce that chemical reactions in nature could take place in left-handed or right-handed chiral environments, respectively, corresponding to the existence of left-handed and right-handed quartz crystals.[
26] If achiral macromolecules used as low-level insulated bags carry out catalytic reactions in such a chiral container to enhance their own internal energy, the upgrading reaction of insulated bags will eventually take place and evolve into new chiral macromolecules with higher thermal insulation efficiency. Racemic biomolecules, for instance, may be able to remove right-handed small molecules from a container of left-handed quartz crystals while keeping left-handed ones during the upgrading reaction of the insulated bag. This is because right-handed small molecules may have a stronger interaction force with left-handed quartz crystals [
27].
If this hypothesis holds true, it prompts an additional inquiry: the left-handed quartz pool is expected to generate biomacromolecules composed of left-handed small molecules, while the corresponding right-handed quartz pool will similarly yield biomacromolecules formed from right-handed small molecules. However, this leads to the question of why life itself is constituted of left-handed small molecules. Let's revisit the birth of the first life. The emergence of life originates from a group of biomacromolecules that function as primary insulated bags. These molecules continuously catalyze substrates to facilitate upgrading reactions of insulated bags, resulting in the formation of larger biomolecules with improved insulation efficiency. Low-efficiency thermal insulation molecules may eventually disintegrate into smaller molecules or become a component of other high-efficiency thermal insulation bags. The origin of life can be described as the evolution of a molecule from a basic insulated bag to an ultimate insulated bag, where numerous molecules engage in a multitude of reactions, ultimately resulting in the success of a single molecule. In the competition for the upgrading reaction of thermal bags in the future, only one type of biomacromolecule, either left-handed or right-handed, derived from various chiral pools, will ultimately prevail. The homochirality observed in organisms provides additional evidence for the occurrence of the upgrading reaction of insulated bags within living systems.
17. Conclusions
A high-energy bloc model was developed, grounded in the phenomenon of volatilization, and we put forth the hypothesis that a solitary catalyst molecule in homogeneous catalysis has no catalytic activity. The concentration dependence of catalysts in homogeneous catalysis has been addressed through the application of the high-energy bloc model. An alternative interpretation of entropy is put forth, which holds that all biomolecules are insulated bags. We have offered a good explanation for the fundamentals of biological metabolism based on our knowledge of homogeneous catalysis. We have redefined the classification of organic molecules found in nature, proposed a hypothesis regarding the essence of life, and investigated the origins of life.
Acknowledgements
We extend our gratitude to the Merck library for offering a valuable literature search platform. Additionally, we appreciate the assistance of Mr. Steven Xu, a senior student at Wesleyan University, for his contributions in revising the article and fostering engaging discussions.
References
- Kevin, K. Living Things and Nonliving Things: A Compare and Contrast Book. Mt. Pleasant, SC, Arbordale Publishing, 2017.
- Schrödinger, E. What is life? And mind and matter. Cambridge University Press; 1944; b) Benner, S. A. Astrobiology. 2010, 10, 1021–1030; c) Gómez-Márquez, J. Mol Biol Rep. 2021, 48, 6223–6230.
- Judge, A., Dodd, M.S. Essays in Biochemistry 2020, 64, 607–647; b).
- Butler, J.A.V. Nature 1946, 158, 153-154; b) Schneider E.D., Kay, J. J. Mathl. Comput. Modelling 1994, 19, 25-48; c) England, J. L. J. Chem. Phys., 2013, 139, 121923-121928.
- Mortimer, R. G. (2008). Physical Chemistry. Elsevier Science.
- Silberberg, M. A. (2006). Chemistry (4th ed). New York: McGraw-Hill.
- Lorenz, E. (1993). The Essence of Chaos. University of Washington Press. P. 181-206.
- Masel, RI. (2001). Chemical Kinetics and Catalysis. New York: Wiley-Interscience.
- Hierso, J. -C., Fihri, A., Amardeil, R., Meunier, P., Doucet, H., Santelli, M. Tetrahedron 2005, 61, 9759-9766; b) Enguehard-Gueiffier, C., Thery, I., Gueiffier, A., Buchwald, S. L. Tetrahedron 2006, 62, 6042-6049; c) Huang, W., Guo, J., Xiao, Y., Zhu, M., Zou, G., Tang, J. Tetrahedron 2005, 61, 9783-9790; d) Raminelli, C., Gargalaka, J., Silveira, C. C., Comasseto, J. V. Tetrahedron 2007, 63, 8801-8809.
- Kim, T.-J., Lee, H.-Y., Ryu, E.-S., Park, D.-K., Cho, C. S., Shim, S. C., Jeong, J. H. J. Organomet. Chem. 2002, 649, 258-267; b) Omote, M., Nishimura, Y., Sato, K., Ando, A., Kumadaki, I. Tetrahedron 2006, 62, 1886-1894; c) Gao, B., Fu, Z., Yu, Z., Yu, L., Huang, Y., Feng, X. Tetrahedron 2005, 61, 5822-5830; d) Sweetman, B. A., Guiry, P. J. Tetrahedron 2018, 74, 5567-5581; e) Zong, H., Huang, H., Bian, G., Song, L. Tetrahedron Lett. 2013, 54, 2722-2725; f) Aga, M. A., Kumar, B., Rouf, A., Shah, B. A., Taneja, S. C. Tetrahedron Lett.2014, 55, 2639-2641; g) Wu, X., Liu, X., Zhao, G. Tetrahedron Asymmetry 2005, 16, 2299-2305; h) Lu, Y.-N., Guo, Q.-S., Jiang, F.-Y., Li, J.-S. Tetrahedron Asymmetry 2006, 17, 1842-1845; i) Dabiri, M., Salehi, P., Kozehgary, G., Heydari, S., Heydari, A., Esfandyari, M. Tetrahedron Asymmetry 2008, 19, 1970-1972; j) Salehi, P., Dabiri, M., Kozehgary, G., Baghbanzadeh, M. Tetrahedron Asymmetry 2009, 20, 2609-2611; k) Qi, G., Judeh, M. A. Tetrahedron Asymmetry 2010, 21, 429-436; l) Yue, H., Huang, H., Bian, G., Zong, H., Li, F., Song, L. Tetrahedron Asymmetry 2014, 25, 170-180; m) Liu, B., Dong, Z.-B., Fang, C., Song, H.-B., Li, J.-S. Chirality 2008, 20, 828-832; n) Shen, B., Huang, H., Bian, G., Zong, H., Song, L. Chirality 2013, 25, 561-566.
- Takahashi, H., Kawakita, T., Ohno, M., Yoshioka, M., Kobayashi, S. Tetrahedron 1992, 48, 5691-5700; b) Yoshioka, M., Kawakita, T., Ohno, M. Tetrahedron Lett. 1989, 30, 1657-1660.
- It should be acknowledged that most reaction times cited in the literature focus on the completion of reactions instead of reaching a 50% yield. Although the scientific validity of these findings may not be robust, the information they provide is significant, and the conclusions we formulate are logical.
- Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education.
- Siegel, J.M. Trends in Neurosciences 2008, 31, 208-213; b) Freiberg, A. S. Journal of Circadian Rhythms 2020, 18, 1-5.
- Chapeville, F., et al. Proceedings of the National Academy of Sciences 1962, 48, 1086–1092; b) Crick, F. Symposia of the Society for Experimental Biology 1958, 12, 138–163.
- Viña, J., Borrás, C., Miquel, J. IUBMB life. 2007, 59,249-54; b) Weinert, B. T., Timiras, P. S. Appl Physiol. 2003, 95, 1706-1716.
- The fundamental structure of the life cycle, as depicted in Figure 21, serves merely as a basic representation of our proposed model of life. Our responsibility is confined to the completion of a single thermodynamic cycle by living organisms. Further assumptions cannot be made at this stage, as doing so would lead to potential misconceptions among scientists.
- Nirmala, J. G., Lopus, M. Cell Biology and Toxicology. 2020, 36, 145–164.
- Santoro, G., Wood, MD., Merlo, L., Anastasi, GP., Tomasello, F., Germanò, A. Neurosurgery. 2009, 65, 633–43; b) Musolino, J. (2015). The Soul Fallacy: What Science Shows We Gain from Letting Go of Our Soul Beliefs. Amherst, New York: Prometheus Books. pp. 21–38; c) Squire, L. et al. "Fundamental Neuroscience, 4th edition" (2012). Chapter 43.
- Reaching this conclusion is, undoubtedly, futile. The soul must be a system that has not attained thermodynamic equilibrium if it is to be considered a separate life. How can we articulate this thermodynamic imbalance? What methods can we employ to determine its standard deviation σ? We currently lack any insights.
- Miller, SL. Science. 1953, 117, 528-529.
- Wächtershäuser, G. Microbiological Reviews. 1988, 52, 452-484.
- Undoubtedly, the sun may have had an essential influence in the initial five stages of life's formation; however, for the sake of clarity, we will refrain from addressing it in this discussion.
- Nelson, L. et al. (2008). Lehninger Principles of Biochemistry. Macmillan.
- Oparin AI. The Origin of Life. Izd. Moskovshii, Rabochii; 1924; b) Haldane JB. The origin of life. Rationalist Annu. 1929, 148, 3-10.
- Donnay, J.D.H. & Le Page, Y. Acta Cryst., 1978, A34, 584-594; b) Glazer, A.M. J. Appl. Cryst. 2018, 51, 915-918.
- It is indeed uncertain whether the interaction between right-handed small molecules and left-handed quartz crystals is inherently stronger. However, it is certain that the force exerted between a left-handed quartz crystal and a left-handed small molecule differs from the force between a left-handed quartz crystal and a right-handed small molecule.
Figure 1.
Volatilization of water.
Figure 1.
Volatilization of water.
Figure 2.
Formation, decomposition, and regeneration of high-energy blocs.
Figure 2.
Formation, decomposition, and regeneration of high-energy blocs.
Figure 3.
The classical mechanism of homogeneous catalysis.
Figure 3.
The classical mechanism of homogeneous catalysis.
Figure 4.
Homogeneous catalytic system.
Figure 4.
Homogeneous catalytic system.
Figure 5.
Case 1: Investigation into Homogeneous Catalysis.
Figure 5.
Case 1: Investigation into Homogeneous Catalysis.
Figure 6.
Case 2: Investigation into Homogeneous Catalysis.
Figure 6.
Case 2: Investigation into Homogeneous Catalysis.
Figure 7.
Chemical reaction catalyzed by high-energy bloc.
Figure 7.
Chemical reaction catalyzed by high-energy bloc.
Figure 8.
Life in a state of thermodynamic equilibrium.
Figure 8.
Life in a state of thermodynamic equilibrium.
Figure 9.
Life in a state of thermodynamic imbalance.
Figure 9.
Life in a state of thermodynamic imbalance.
Figure 10.
Initial state of life.
Figure 10.
Initial state of life.
Figure 11.
Collision of biomolecules at very low temperature.
Figure 11.
Collision of biomolecules at very low temperature.
Figure 12.
Collision of biomolecules at ambient temperature.
Figure 12.
Collision of biomolecules at ambient temperature.
Figure 14.
Collision of biomolecules and gaining different energies in catalysis.
Figure 14.
Collision of biomolecules and gaining different energies in catalysis.
Figure 15.
Biomacromolecules with two antennas.
Figure 15.
Biomacromolecules with two antennas.
Figure 16.
Mechanism of energy exchange with biomacromolecules.
Figure 16.
Mechanism of energy exchange with biomacromolecules.
Figure 17.
Upgrading reaction of insulated bag.
Figure 17.
Upgrading reaction of insulated bag.
Figure 18.
Insulated bags with different insulation levels.
Figure 18.
Insulated bags with different insulation levels.
Figure 19.
The formation of the ultimate insulated bag.
Figure 19.
The formation of the ultimate insulated bag.
Figure 21.
The fundamental framework of life cycle.
Figure 21.
The fundamental framework of life cycle.
Table 1.
σ of biomolecule collisions at very low temperature.
Table 1.
σ of biomolecule collisions at very low temperature.
| Collison (three spheres) |
The state of system after collision |
standard deviation |
| ABC |
A(30 ºC), B(31 ºC), C(32 ºC), D(33 ºC), E(34 ºC) |
σ=1.414 |
| ABD |
A(30 ºC), B(31 ºC), C(32 ºC), D(33 ºC), E(34 ºC) |
σ=1.414 |
| ABE |
A(30 ºC), B(31 ºC), C(32 ºC), D(33 ºC), E(34 ºC) |
σ=1.414 |
| BCD |
A(30 ºC), B(31 ºC), C(32 ºC), D(33 ºC), E(34 ºC) |
σ=1.414 |
| BCE |
A(30 ºC), B(31 ºC), C(32 ºC), D(33 ºC), E(34 ºC) |
σ=1.414 |
Table 2.
σ of biomolecule collisions at ambient temperature without catalysis.
Table 2.
σ of biomolecule collisions at ambient temperature without catalysis.
| Collison (three spheres) |
The state of system after collision |
standard deviation |
| ABC |
ABC(31 ºC), D(33 ºC), E(34 ºC) |
σ=1.265 |
| ABD |
ABD(31.33 ºC), C(32 ºC), E(34 ºC) |
σ=1.034 |
| ABE |
ABE(31.67 ºC), C(32 ºC), D(33 ºC) |
σ=0.515 |
| BCD |
BCD(32 ºC), A(30 ºC), E(34 ºC) |
σ=1.265 |
| BCE |
BCE(32.33 ºC), A(30 ºC), D(33 ºC) |
σ=1.032 |
Table 3.
σ of biomolecule collisions and catalysis in 3A model.
Table 3.
σ of biomolecule collisions and catalysis in 3A model.
| Collison (three spheres) |
The state of system after collision |
standard deviation |
| ABC |
ABC(31.31 ºC), D(33 ºC), E(34 ºC) |
σ=1.1185 |
| ABD |
ABD(31.643 ºC), C(32 ºC), E(34 ºC) |
σ=0.9176 |
| ABE |
ABE(31.987 ºC), C(32 ºC), D(33 ºC) |
σ=0.4039 |
| BCD |
BCD(32.32 ºC), A(30 ºC), E(34 ºC) |
σ=1.0302 |
| BCE |
BCE(32.653 ºC), A(30 ºC), D(33 ºC) |
σ=1.1041 |
Table 4.
σ of biomolecule collisions with catalysis in 3B model .
Table 4.
σ of biomolecule collisions with catalysis in 3B model .
| Collison (three spheres) |
The state of system after collision |
standard deviation |
| ABC |
ABC(30.30, 31.31, 32.32 ºC), D(33 ºC), E(34 ºC) |
σ=1.2880 |
| ABD |
ABD(30.30, 31.31, 33.33 ºC), C(32 ºC), E(34 ºC) |
σ=1.3385 |
| ABE |
ABE(30.30, 31.31, 34.34 ºC), C(32 ºC), D(33 ºC) |
σ=1.3900 |
| BCD |
BCD(31.31, 32.32, 33.33 ºC), A(30 ºC), E(34 ºC) |
σ=1.4257 |
| BCE |
BCE(31.31, 33.33, 34.34 ºC), A(30 ºC), D(33 ºC) |
σ=1.5451 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).