Submitted:
08 January 2025
Posted:
09 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
- Real-time UAV Geolocation framework: We propose a framework for real-time UAV geolocation that enables autonomous navigation and positioning at reduced cost, which has the ability to adapt to downward-tilted camera configurations.
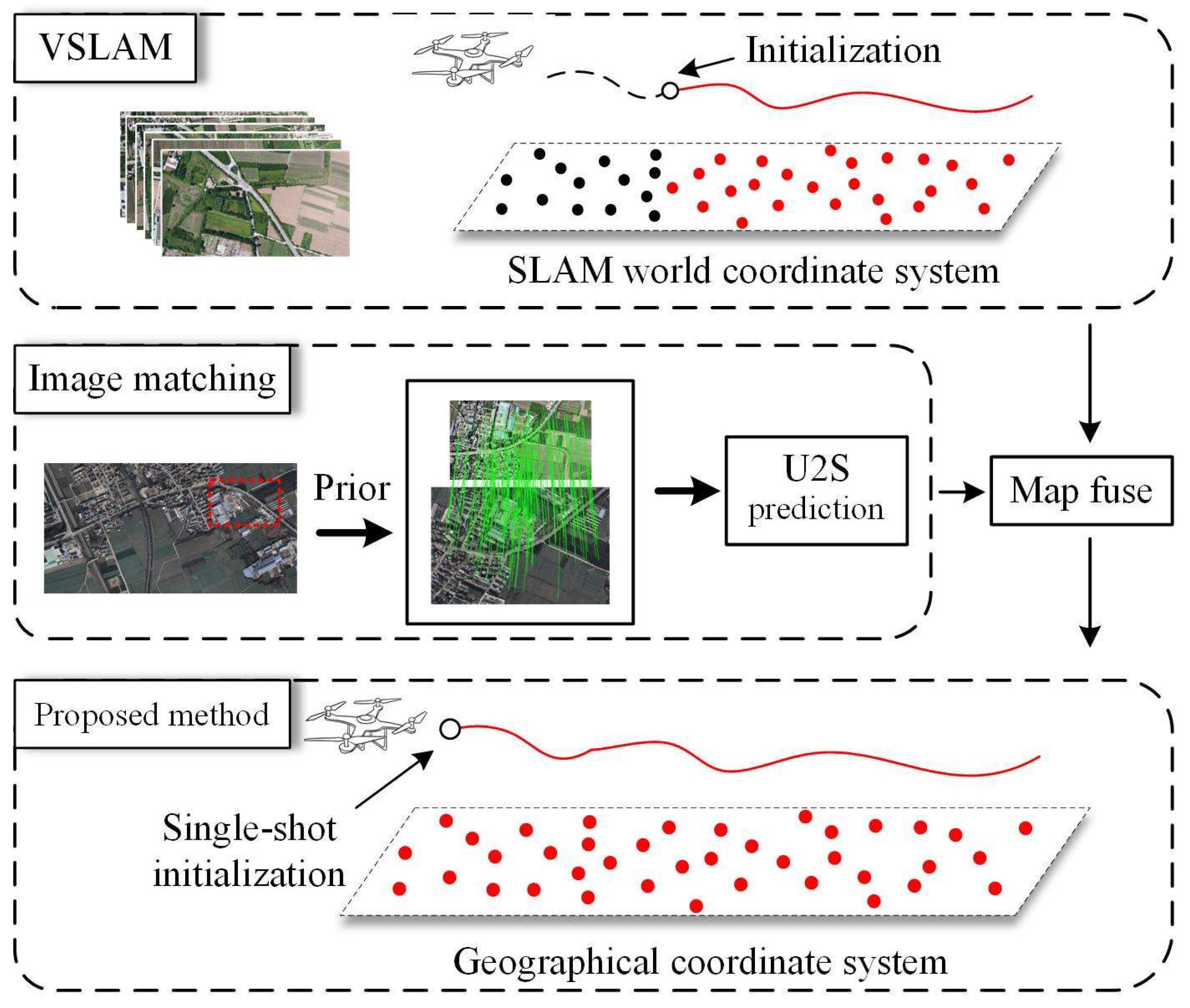
- Similarity-Based Heterogeneous Image Matching: This method aligns satellite images with UAV images within a unified coordinate system by employing a homography matrix. Subsequently, it performs image matching between the aligned satellite and UAV images. Ultimately, similarity transformations are utilized to constrain the degrees of freedom in pose estimation. This comprehensive process enables precise U2S prediction for UAVs.
- Global Map Fusion Method: This method leverages U2S predictions derived from heterologous image matching and visual information sourced from vSLAM to rapidly construct and refine a global map that is precisely aligned with the geographic coordinate system. This method enables real-time estimation of UAVs' geographic poses.
2. Methodology
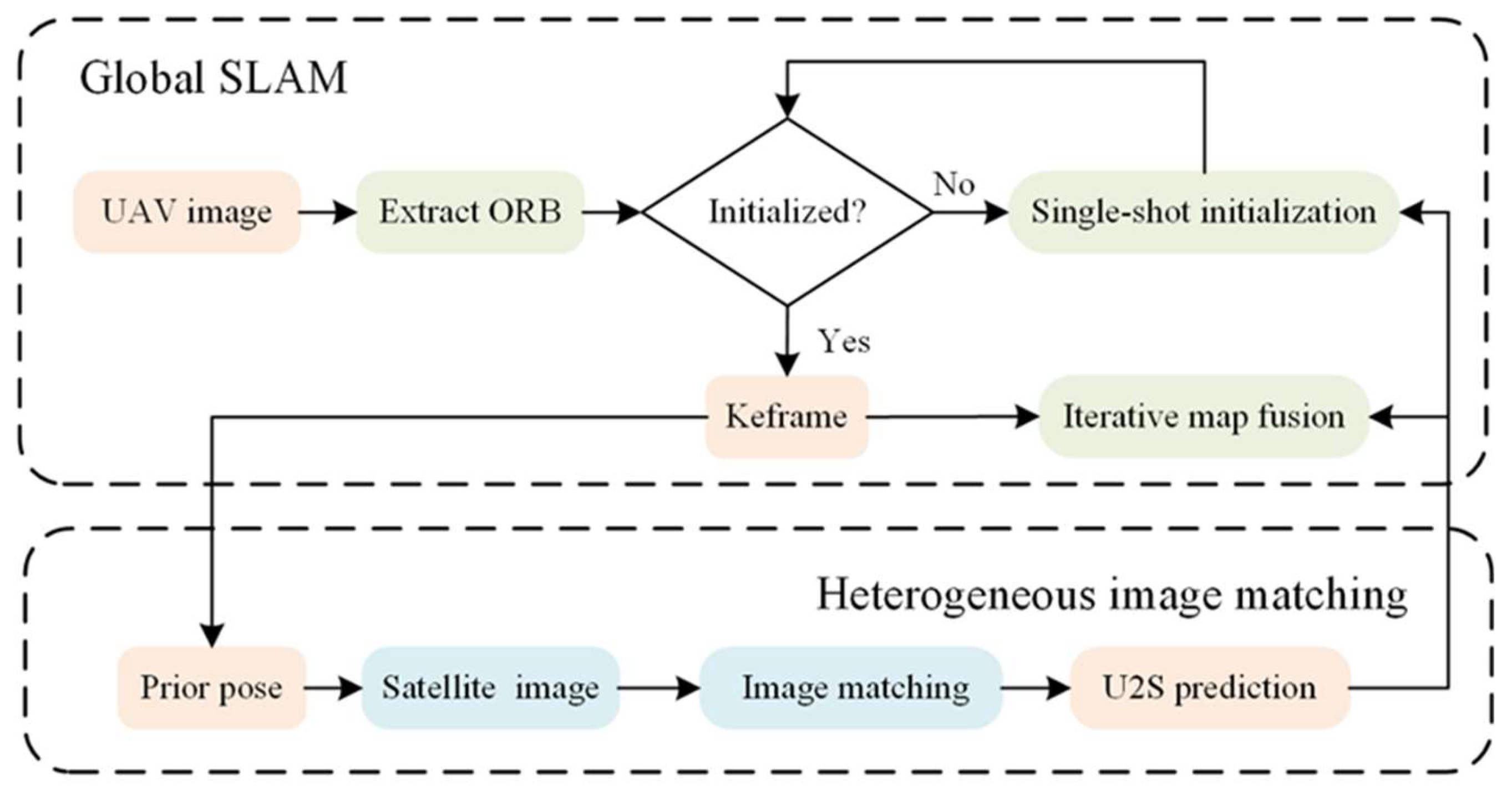
2.1. Similarity-Based Heterogeneous Image Matching

2.1.1. Offline Preprocessing
2.1.2. Extraction and Transformation of Satellite Images
2.1.3. Computing U2S Prediction
2.1.4. Consistency Check of U2S Prediction
2.2. Global Map Fusion Method

2.2.1. Single-Shot Global Initialization
2.2.2. Iterative Global Map Fusion
3. Experimental Setups and Results
3.1. Experimental Setup
3.2. Evaluation Metrics
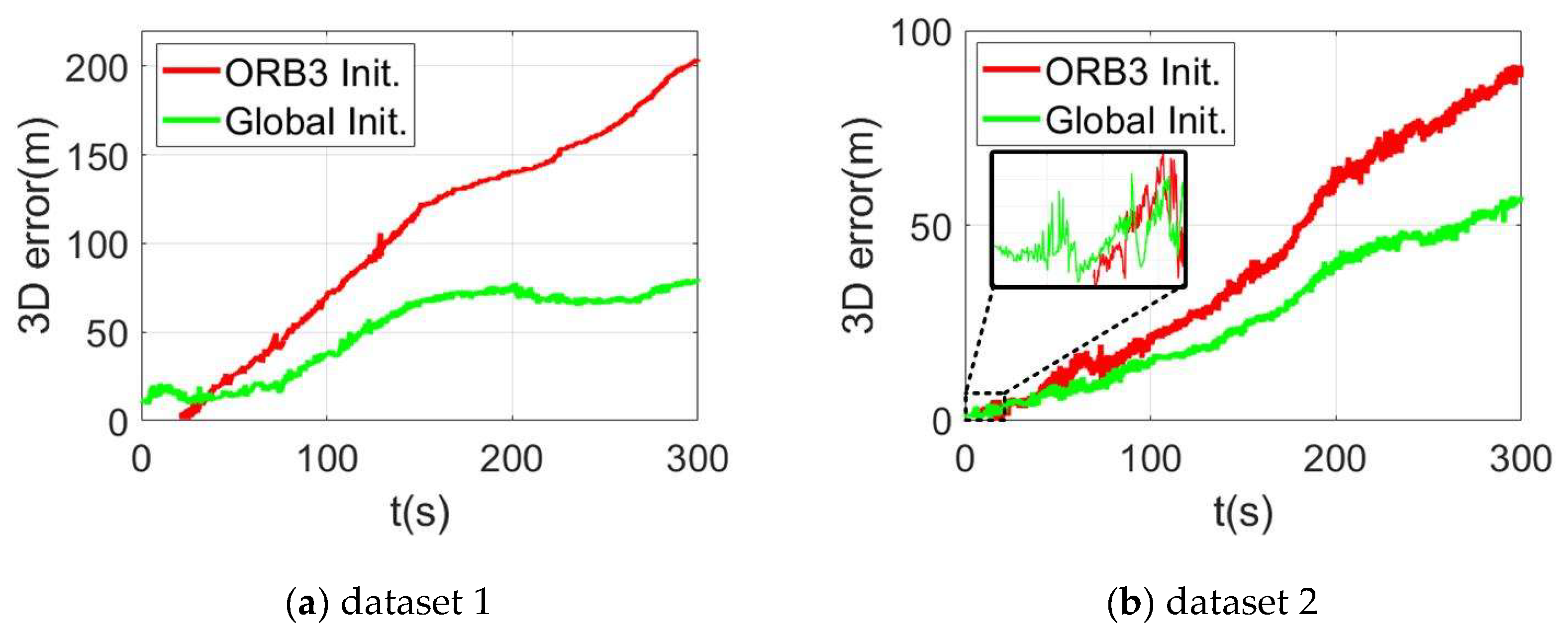
3.3. Global Initialization Experiment
3.4. UAV Localization Experiment
3.5. Ablation Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scherer, J.; Yahyanejad, S.; Hayat, S.; Yanmaz, E.; Andre, T.; Khan, A.; Vukadinovic, V.; Bettstetter, C.; Hellwagner, H.; Rinner, B. An Autonomous Multi-UAV System for Search and Rescue. In Proceedings of the MobiSys'15: The 13th Annual International Conference on Mobile Systems, Applications, and Services, Florence Italy, 18 May 2015. [CrossRef]
- Messinger, M.; Silman, M. Unmanned aerial vehicles for the assessment and monitoring of environmental contamination: An example from coal ash spills. Environ. Pollut. 2016, 218, 889-894. [CrossRef]
- Liu, Y.; Meng, Z.; Zou, Y.; Cao, M. Visual Object Tracking and Servoing Control of a Nano-Scale Quadrotor: System, Algorithms, and Experiments. IEEE/CAA J. Autom. Sin. 2021, 8, 344-360. [CrossRef]
- Ganesan, R.; Raajini, X.M.; Nayyar, A.; Sanjeevikumar, P.; Hossain, E.; Ertas, A.H. BOLD: Bio-Inspired Optimized Leader Election for Multiple Drones. Sensors 2020, 20, 3134. [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE T. Pattern. Ansl. 2007, 29, 1052-1067. [CrossRef]
- Civera, J.; Davison, A.J.; Montiel, J.M.M. Inverse Depth Parametrization for Monocular SLAM. IEEE T. Robot. 2008, 24, 932-945. [CrossRef]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the 2007 6th IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Nara, Japan, 13 - 16 November 2007. [CrossRef]
- A, H.S.; B, J.M.M.M.; A, A.J.D. Visual SLAM: Why filter? Image. Vision. Comput. 2012, 30, 65-77. [CrossRef]
- Strasdat, H.M.; Montiel, J.M.M.; Davison, A.J. Scale Drift-Aware Large Scale Monocular SLAM. In Proceedings of the Robotics: Science and Systems, 27 June 2010. [CrossRef]
- Strasdat, H.; Davison, A.J.; Montiel, J.M.M.; Konolige, K. Double window optimisation for constant time visual SLAM. In Proceedings of the 2011 International Conference on Computer Vision, 6-13 November 2011. [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE T. Robot. 2015, 31, 1147-1163. [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE T. Robot. 2017, 33, 1255-1262. [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE T. Robot. 2021, 37, 1874-1890. [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G.R. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, 6 November 2011. [CrossRef]
- Galvez-López, D.; Tardos, J.D. Bags of Binary Words for Fast Place Recognition in Image Sequences. IEEE T. Robot. 2012, 28, 1188-1197. [CrossRef]
- Engel, J.J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the European Conference on Computer Vision, 6 September 2014. [CrossRef]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems. IEEE T. Robot. 2017, 33, 249-265. [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE. T. Pattern. Anal. 2018, 40, 611-625. [CrossRef]
- Wang, R.; Schwörer, M.; Cremers, D. Stereo DSO: Large-Scale Direct Sparse Visual Odometry with Stereo Cameras. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), 22-29 October 2017.
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct Sparse Odometry with Loop Closure. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 01-05 October 2018. [CrossRef]
- Lee, S.H.; Civera, J. Loosely-Coupled Semi-Direct Monocular SLAM. IEEE Robot. Autom. Let. 2019, 4, 399-406. [CrossRef]
- Stumberg, L.V.; Usenko, V.; Cremers, D. Direct Sparse Visual-Inertial Odometry Using Dynamic Marginalization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), 21-25 May 2018. [CrossRef]
- Zubizarreta, J.; Aguinaga, I.; Montiel, J.M.M. Direct Sparse Mapping. IEEE T. Robot. 2020, 36, 1363-1370. [CrossRef]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [CrossRef]
- Nassar, A.; Amer, K.; ElHakim, R.; ElHelw, M. A Deep CNN-Based Framework For Enhanced Aerial Imagery Registration with Applications to UAV Geolocalization. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 18-22 June 2018.
- Choi, J.; Myung, H. BRM Localization: UAV Localization in GNSS-Denied Environments Based on Matching of Numerical Map and UAV Images. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 24 Oct.-24 Jan. 2021, 2020. [CrossRef]
- Li, Y.; Yang, D.; Wang, S.; He, H.; Hu, J.; Liu, H. Road-Network-Based Fast Geolocalization. IEEE T. Geosci. Remote. 2021, 59, 6065-6076. [CrossRef]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-Free Local Feature Matching with Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 20-25 June 2021.
- Goforth, H.; Lucey, S. GPS-Denied UAV Localization using Pre-existing Satellite Imagery. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), 20-24 May 2019. [CrossRef]
- Chen, S.; Wu, X.; Mueller, M.W.; Sreenath, K. Real-time Geo-localization Using Satellite Imagery and Topography for Unmanned Aerial Vehicles. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 27 September - 01 October 2021. [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 18-23 June 2018.
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 18-22 June 2018.
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching With Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 13-19 June 2020.
- Kinnari, J.; Verdoja, F.; Kyrki, V. GNSS-denied geolocalization of UAVs by visual matching of onboard camera images with orthophotos. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), 06-10 December 2021. [CrossRef]
- Hao, Y.; He, M.; Liu, Y.; Liu, J.; Meng, Z. Range–Visual–Inertial Odometry with Coarse-to-Fine Image Registration Fusion for UAV Localization. Drones 2023, 7, 540. [CrossRef]
- Patel, B.; Barfoot, T.D.; Schoellig, A.P. Visual Localization with Google Earth Images for Robust Global Pose Estimation of UAVs. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), 31 May 2020 - 31 August 2020. [CrossRef]
- Yao, F.; Lan, C.; Wang, L.; Wan, H.; Gao, T.; Wei, Z. GNSS-denied geolocalization of UAVs using terrain-weighted constraint optimization. Int. J. Appl. Earth. Obs. 2024, 135, 104277. [CrossRef]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. Int. J. Comput. Vision. 2009, 81, 155-166. [CrossRef]
- Sarlin, P.-E.; DeTone, D.; Yang, T.-Y.; Avetisyan, A.; Straub, J.; Malisiewicz, T.; Bulò, S.R.; Newcombe, R.A.; Kontschieder, P.; Balntas, V. OrienterNet: Visual Localization in 2D Public Maps with Neural Matching. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 17-24 June 2023.
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 7-12 October 2012. [CrossRef]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A. 1987, 4, 629-642. [CrossRef]


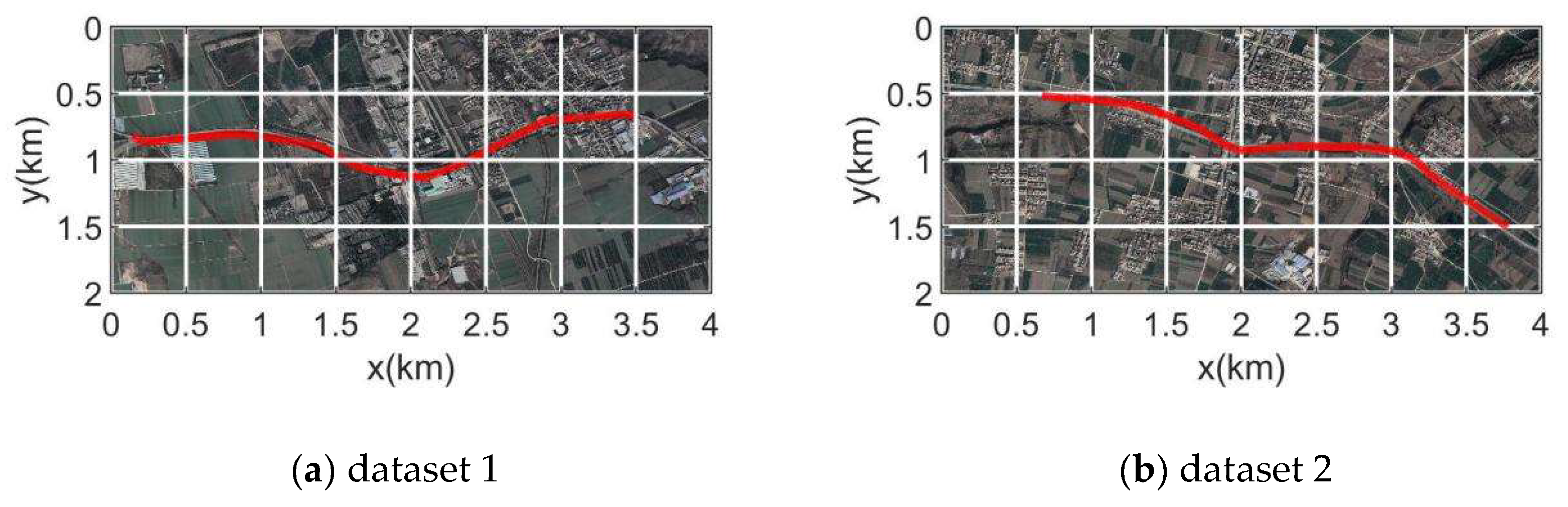
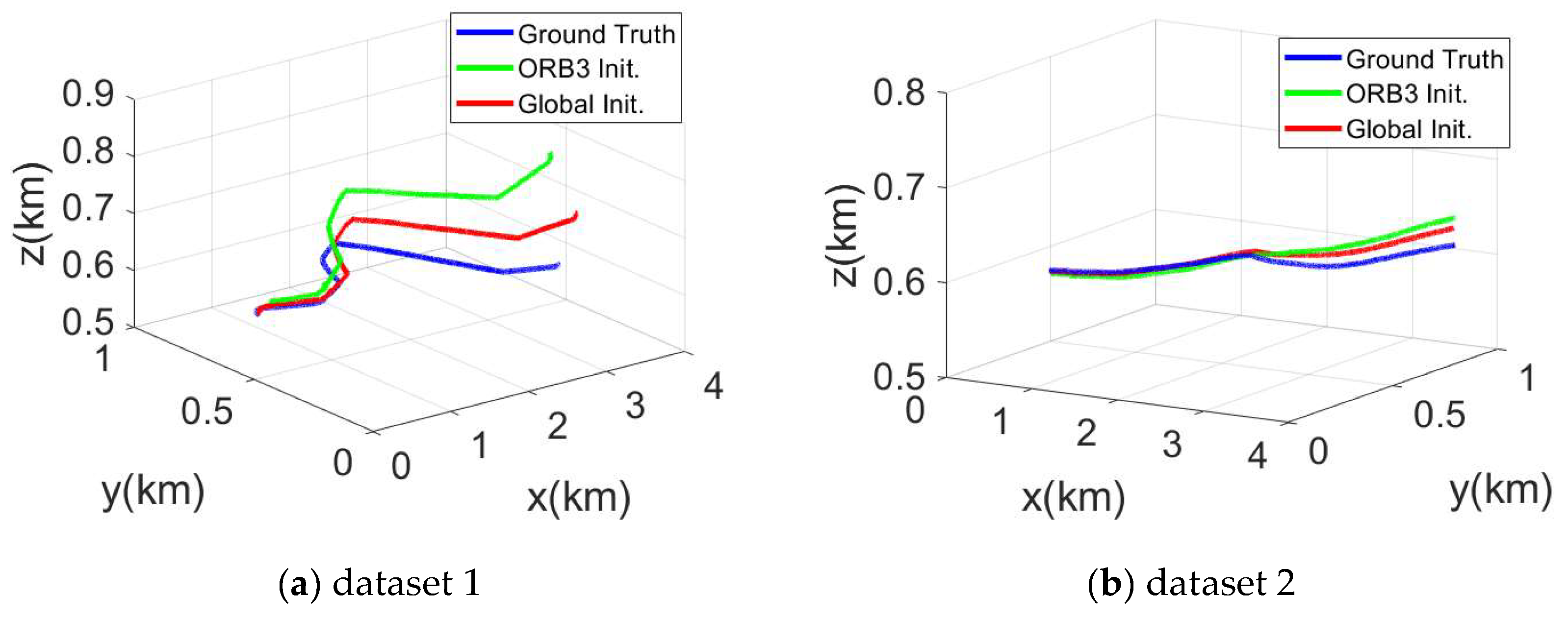
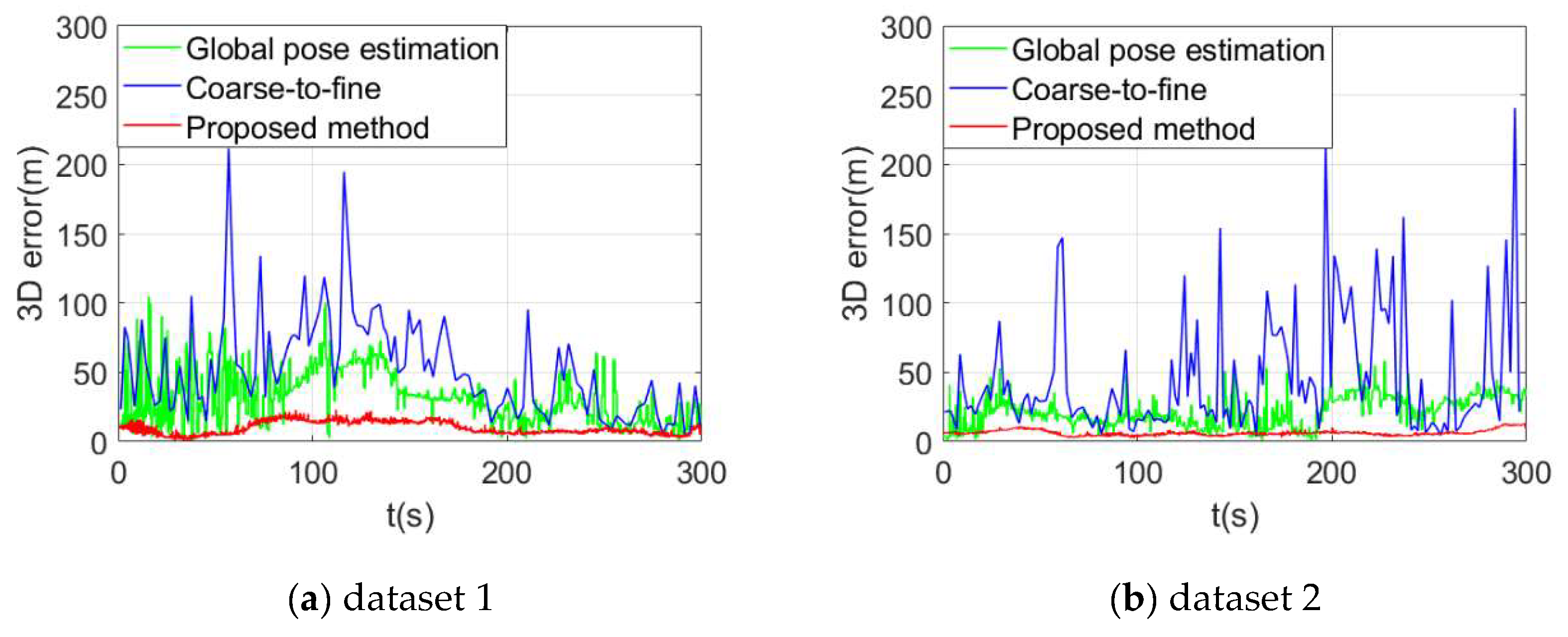
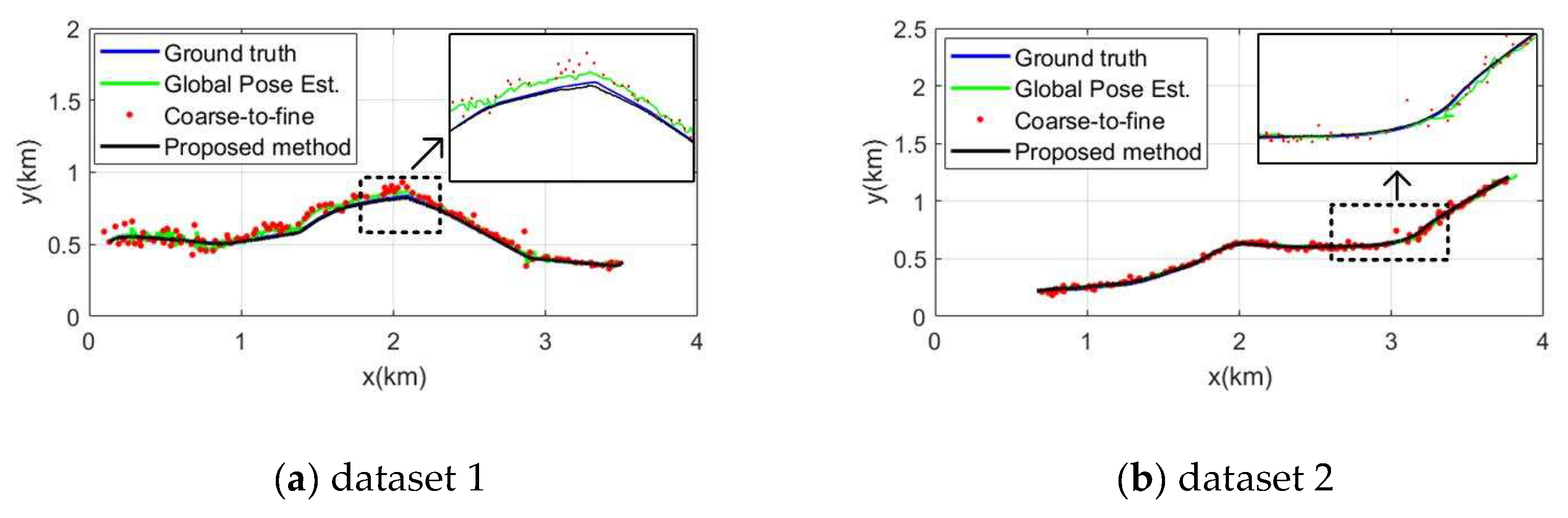
| Dataset | Length (km) | Altitude (m) | Duration (s) | Pitch (◦) | Frame rate (fps) |
|---|---|---|---|---|---|
| 1 | 3.56 | 600 | 300 | 60~80 | 20 |
| 2 | 3.40 | 520 | 300 | 90 | 20 |
| Dataset | Method | Max (m) | Mean (m) | RMSE (m) | Time cost (s) |
|---|---|---|---|---|---|
| 1 | ORB3 Init. | 103.94 | 50.25 | 64.01 | 11.70 |
| Global Init. | 40.07 | 30.89 | 28.25 | 0.65 | |
| 2 | ORB3 Init. | 91.22 | 41.99 | 50.65 | 4.85 |
| Global Init. | 57.53 | 27.13 | 32.30 | 0.65 |
| Dataset | Method | Max (m) | Mean (m) |
|---|---|---|---|
| 1 | Global pose estimation | 31.03 | 36.52 |
| Coarse-to-fine | 51.79 | 64.51 | |
| Proposed Method | 9.81 | 10.85 | |
| 2 | Global pose estimation | 21.46 | 24.10 |
| Coarse-to-fine | 31.29 | 46.83 | |
| Proposed Method | 6.32 | 6.63 |
| Dataset | Metric | Single-init | EPnP-U2S | Aff-U2S | Conc-U2S | Traj-fusion | Full |
|---|---|---|---|---|---|---|---|
| 1 | Mean | 50.89 | 20.34 | 13.03 | 12.83 | 13.37 | 9.81 |
| RMSE | 56.25 | 21.88 | 13.36 | 13.98 | 14.63 | 10.85 | |
| 2 | Mean | 27.13 | 15.76 | 7.93 | 7.27 | 7.36 | 6.32 |
| RMSE | 32.30 | 16.13 | 8.31 | 7.95 | 8.02 | 6.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





