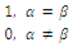Principles of Economic Inequality Dynamics the Economic Dynamics and (Beyond) Standard Model (IV)

1. Curved Spacetime in Economics and Why

This chapter applies insight from the general theory of relativity to economic modeling. It is appropriate to first mention, without comments, two popular books published in the last few years. One is by Tomas L. Friedman (2005/2007), The World Is Flat: A Brief History of the Twenty-First Century. The other is by David M. Smick (2008), The World Is Curved: Hidden Dangers to the Global Economy. We discussed the flat Minkowski space-time employed by the special theory of relativity (Yang, Y., 2022). In this chapter, we will discuss the curved space-time that is used to characterize the general theory of relativity.

As Wilczek (2008) states, in the general theory of relativity, Einstein used the concept of curved space-time in order to construct a theory of gravity. We can describe the general theory of relativity by using two mathematically equivalent ideas: geometrically curved space-time or a metric field. On the geometric view, in curved space-time, one can imagine that the vector changes its direction and length from point to point; thus, the notion of vector has to be extended to the idea of tensor. For a field view, an example given by Feynman (1997) is a heated board with temperature varying at different points. Field theory is widely used in physics. There are three key concepts to the notion of a field. First, it contains something physical, economic, monetary, or mental everywhere in a continuous sense. Second, the distribution of the “thing” is in general not isotropic, but is instead aeolotropic. Wilczek argues that it also requires the aeolotropism to be spontaneous in nature (2008). Third, it has a metric because according to Einstein, space without metrics is unthinkable (1920). Based on this idea, Wilczek extends the notion of a metric field to his investigation of a metric grid (2008). The example he used to explain is a map with information of locations in terms of their aeolotropism.

So far, we have by analogy referred to the quasi-light-ness of money in terms of its masslessness, energy, and speed. By the same token, one may also imagine a field of money in terms of its luminosity, whose distribution is in general aeolotropic. By this, we mean individuals view economic events differently, or they pay different degrees of attention to economic events, from one to another and from an event to another event. We reported how commonly shared cognition makes it possible for money to travel with the highest and constant speed. The present chapter will focus more on how individual differences make the economic space-time curved. Indeed, it cannot be wrong to say that the broader the freedom to be shared, the deeper the individual differences that can be allowed, as Simmel stated (1900). This is common sense, given the notion of the free market in monetary economics.

We may now consider a general economic system, or an economic space, in which each point stands for an economic event. In the market economy, an event involves a group of individual participants. The economics textbooks always remind us that everything is related to everything else; it should be equally true to say that everyone is related to everyone else. Recall that in our earlier work, the human economy is treated as experimental—probably the greatest experiment mankind has ever conducted (Yang, Y. 2002). In economics, when we talk about decision making, it is always about individual decision making. This is because that decision making always involves mental activities, and the human mind is individually oriented. We propose that the economic system is always accompanied by a field of human thinking. The economic space is filled out with what we would call the “mental ethers.” For a given economic event, these mental ethers involve a local neighborhood of individual economic cognitions. Let me modify Wilczek’s (2008) words: the new theory sees an economic world based on a multiplicity of space-filling mental ethers. I would call this totality the cognitive grid.

In the present chapter, we will explain why tensor analysis (Section 3) and curvilinear coordinates (Section 4) are necessary from a modeling perspective when a field of mental ethers is attached to the economic system. Section 5 will characterize the notion of Pareto efficiency in economics by the notion of geodesics in the general theory of relativity. There, we will also enjoy an economic and everyday life version of the “happiest moment” that Einstein experienced. We will characterize what we would call the economic gravity in terms of economic curvature. Some mathematical tools are not avoidable, but we will try to make the context as descriptive as possible. Before we turn to Section 3, it seems necessary to insert Section 2 below because we have another concern with current theories in economics.

2. Macro-Externality and Full-Dimensional Individual Differences

Our concern is with the notion of externality. In economics, an externality (or transaction spillover) is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit. A benefit in this case is called a positive externality or external benefit, while a cost is called a negative externality or external cost. By this definition, one can see that externality is a notion in microeconomics; it is defined in terms of trading and pricing and in terms of the buyer and the seller. The third party is affected either monetarily or non-monetarily. We may refer to this traditional definition as micro-externality. We will argue that it is necessary to modify this traditional notion of externality to a macroeconomic version.

One among the most significant economic phenomena is about the fiscal policy. For example, the U.S. issued a bailout consisting of $700 billion in response to the 2008 financial crisis. It is in essence a “trade” between the U.S. government and big companies such as banks or automobile manufacturers. It is indeed a trade, though it is not treated as such, because it seems too big (say, too macro). The third party affected by this trade is every individual tax payer (collectively called the public.) The monetary costs to the third parties here are self-indexing; it is the whole price of $700 billion plus operational costs. We refer to this phenomenon as an example of macro-externality, which also has significant nonmonetary effects on the third party, which in this case we will call the “state of mentality,” or the “collective mental economic state.” The notion of the state of economic mentality is sensitive because it is directly related to what people used to call the potential market, which is exactly what the bailout money aims to stimulate.

It is worth noting that there have been two rounds of significant macroeconomic mentality build-ups since the 1990s. The first round happened during the “dot-com” bubble years, which is still fresh in the minds of those affected. Given the advancement of the Internet, the entry barrier to the stock market was nearly eliminated. This was unthinkable to old generations. Suddenly, almost every individual became a market participant. People began to dreams of ways to quickly gain fortune. Every individual participant in the market felt like an authority and told others how to invest. This is a kind of economic mental state built up globally and universally. When the financial market crashed, this universal mentality remained.

The second round happened from the recent world financial crisis in 2008. This time, ordinary people started to feel that no one in the world, including national or world leaders, bankers, and economists knew any better than they did about the inner workings of the global economy. This has been a very embarrassing situation as the public came to believe that all the authorities in economics were suddenly lost. And while the economy has continued to slowly recover, this global economic mentality remains.

As a result, from the micro-perspective, the bailout has achieved the unprecedented individual divergence in economic thinking. People no longer ask what your country can do for you but instead ask what you can do for yourself. This is based on the personal endowment of economic resources. From a macro-perspective, each country or region has become more self-oriented and this makes the global economy a more curved place. To mathematically characterize this phenomenon, in the next two sections, we will show that tensor analysis and the local frame of curved coordinates are necessary mathematical tools to apply.

3. Economic Polarizability: The Invisible Hand as a Tensor

We assume, as our working hypothesis, that people have different views toward any given economic event, and that they pay different degrees of attention or spend different amounts of mental energy on any given economic event. We further assume that for any given individual, one may have inconsistent views toward different economic events, and one pays different degrees of attention or spends different amounts of mental energy on them. In this sense, we say that the mental ethers are the economic space-filling item (in Wilczek’s terms, 2008). Mental ethers are in general not isotropic or uniformly distributed, but are aeolotropic everywhere. To analyze the aeolotropism of mental ethers, we can utilize tensor analysis. Tensor analysis is a mathematical tool which can be introduced through examples either in terms of geometry or physics.

To introduce the notion of a tensor, we may first consider electric polarizability in physics (which can be referenced from any textbook or by utilizing the internet) as an example, and then analogously introduce the notion of economic polarizability. Economic polarizability is a new concept being formally introduced in this volume. We need to distinguish between two cases: when the electric medium is treated as isotropic and when it is treated as aeolotropic. polarizability is a property of matter. Polarizability determines the dynamical response of a bound system to external fields, and provides insight into its internal structure. In case of the electric medium that is isotropic, the electric polarizability α is defined as the ratio of the induced dipole moment P of an atom to the electric field E,

P= αE

Two points are worth noting here. First, for any given unit area or for a point in a three-dimensional space, the electric dipole moment P and electric field intensity E are two vectors (namely, tensors of rank 1.) Second, the dielectric is isotropic, vectors P and E share the same direction and the polarizability α is defined as a scalar quantity. The fact that it is a scalar quantity does not affect the shared direction of P and E, but rather only determines the proportional relation between the corresponding components P_i and E_i (i = 1, 2, 3) in P and E.

Given the above insight, conceptually, we may generalize the notion of economic polarizability. The above case can be seen as corresponding to the various multiplier effects in economics including the money multiplier, fiscal multipliers, and Keynesian multiplier effects. In this case, the distribution of mental ethers, which are assumed as the economic medium, is isotropic. In monetary macroeconomics and banking, the money multiplier is used to measure how much the money supply increases in response to a change in the monetary base. The fiscal multiplier is used to analyze the effect of either fiscal policy, exogenous changes in spending, or aggregate output. Keynesian multipliers are used to measure the effect on aggregate demand in response to an exogenous change in spending. A monetary or a fiscal policy is used to simulate a particular economic state, and that will form some expected field in which at each point will be exemplified as a vector with a degree of certain intensity and with an intended direction. At this point, we suppose the response vector in the economy shares the same direction as predicted with the polarization and that this is in accord with the expected effect by the economic multiplier theories. This way, the relation between the stimuli vector (written as S) and response vector (written as R) shall be treated as a kind of economic polarizability, characterized by the corresponding multiplier α. For example, in the dynamic case, Keynesian polarizability can be calculated by a single multiplier equation, which contains a time variable t. Notice again that the above analogy is based on the assumption that mental ethers as the economic medium in economic space are isotropic, which can be seen as a special case.

When the electric medium is isotropic, the polarizability α is a scalar quantity, which implies that the applied electric field can only produce polarization components parallel to the field. However, when the electric medium is aeolotropic, an electric field in the x-direction may produce a y or z component in vector P. In this case, the (linear) polarizability has to be characterized by a tensor. Let us try to introduce the notion of rank 2 tensor in the three-dimensional space as an example. Consider two vectors (rank 1 tensors) P = (P_x, P_y, P_z) and E= (E_x, E_y, E_z). It is more convenient to understand the tensor relating the two vectors in terms of their components, and rewrite P = (P_x, P_y, P_z) by P = (P₁, P₂, P₃) and E= (E_x, E_y, E_z) by E= (E₁, E₂, E₃). When the electric medium is aeolotropic, the linear relation between P and E can be represented in terms of their components in three linear equations:

P₁ =  α₁₁E₁ + α₁₂E₂ + α₁₃E₃

P₂ =  α₂₁E₁ + α₂₂E₂ + α₂₃E₃

P₃ =  α₃₁E₁ + α₃₂E₂ + α₃₃E₃

Or write as

$${\mathit{P}}_{\mathit{i}}={\displaystyle {\sum }_{j=1}^3} {\mathit{\alpha }}_{\mathit{ij}}{\mathit{E}}_j (i=1,2,3)$$

Here, α_ij has two subscripts, so it is of rank 2; in the case above, it is a three-by-three matrix containing nine elements (n²).

In economics, it is not too hard to accept the concept of a stimuli vector. For any monetary or fiscal policy, say hundreds of billions of dollars in bailout money, the policy will have a predicted direction, a quantity component, and an expected time component. Usually, there are a few other components that need to be taken into account. For the time being, if one would feel more comfortable dealing with traditional multiplier effects, you may neglect other components by taking them as null components. It is now easier to accept the concept of the response vector. Given our assumption that the mental ethers as an economic medium are aeolotropic, the response vector in general is not parallel to the direction of the stimuli vector, and it may yield different component values that are not proportional to their corresponding components in the stimuli vector. This view is also consistent with the rational expectation theory and its falsifications. Thus, in case that the mental ether medium is aeolotropic, α_ij (i, j = 1, . . . , n) should be used to characterize the relation between the stimuli vector and its corresponding response vector for a chosen number n of dimensions.

However, α_ij alone does not accomplish a tensor of rank 2. Actually, a_ij is only one part of a tensor. By definition, a rank 2 tensor must have another part, which is the transformation rule from one coordinate basis to another. In other words, a tensor should be invariant, despite any particular coordinate basis. This is particularly important to us. As we mentioned in Chapter 5, each coordinate basis represents an admissible observer. We want to observe that all the individual market participants are symmetric to the same economic polarizability.

Consider any given economic stimuli vector S=(S₁, S₂, S₃) and a corresponding response vector R=(R₁, R₂, R₃). Write R_i (i =1, 2, 3) to denote the three numbers for the three components in the current basis {e_i}. Now, consider a new basis {e_i’}. We know, through the basis transformation rule, the basis component e_i’ can be represented in the current basis as:

$$e_j={\sum }_{i=1}^3{A}_{i`i}{e}_i$$

If it follows the same transformation, and becomes

$$R_j={\sum }_{i=1}^3{A}_{i`i}{R}_i,$$

we say R_i (i=1, 2, 3) is a tensor of rank 1. Likewise, S_i (i =1, 2, 3) can be treated as another rank 1 tensor, with transformation rule represented by

$$S_j={{\sum }_{j=1}^3{A}_{j`j}R}_j$$

Thus, the transformation rule for representing α_ijin a new basis {e_i’} can be given as follows:

$$a_{i`j`}={\sum }_{i=1}^3{\sum }_{j=1}^3{A_{i`i}A}_{j`j}{a}_j$$

Together with this transformation rule, a_ij becomes a tensor of rank 2 (as it has two subscripts), which is an invariant, independent of any particular frame of coordinates. This completes our introduction to the very basic idea of tensor analysis. As we introduced earlier, the economic polarizability must be characterized as a tensor but not a scalar quantity, where the mental medium is aeolotropic. In this case, the economic response vector may go in unpredicted directions and can yield unexpected components.

In this section, one can see that at the level of economic analysis we can treat the mental medium as isotropic. Prima facie, the multiplier effects support monetary or fiscal policies in a limited sense. At the deeper levels, taking the aeolotropism of the mental medium into account, the invisible hand works like a tensor. This invisible hand does not favor any specific individual market participant but instead makes them symmetric. The transformation rule promises that the polarization is an objective economic phenomenon, which is independent of any observers though they may view it differently. The rank of a tensor can be higher than 2, if one is interested in looking into more complex economic issues.

Another theoretical issue, which should not be taken as an accident, is worth mentioning here: tensor analysis is related to probability theory. As Lucien Hardy elegantly characterized (2004), the degree of freedom K is defined as the minimum number of measure probabilities to determine a state, and the dimension number N is defined as the number of states that can be distinguished by one measuring test. In this way, both classical mechanics and quantum mechanics can be viewed as probability theories. For classical Newtonian mechanics, K = N; for quantum mechanics, K = N². Hence, when the economic polarization is characterized by a tensor of rank 2, the degree of freedom may achieve a quantum theoretic level. In turn, as we explained in Chapters 1 and 2, the degree of disturbance to the permissible observers becomes higher, and accordingly, the economic world they can observe becomes smaller. In other words, many economic quantum fluctuations occur beyond the observational power of individual market participants. This reflects the experimental nature of human economy. Thus, each policy vector can be treated as a measurement vector.

When a global economic polarization results in national or regional economic polarizations, the possible transformations would make the degree of freedom increase exponentially. This can yield a new compound polarization, which may achieve the degree of freedom of K². If this process continues, like an economic nuclear process, it would cause the grip of the invisible hand to quiver, which in turn would cause the “monetary light” to curve, demand further administrative disturbance, and contribute more energy to political or even military events. This means the permissible observers or individual market participants change their straight way to think through or lose their straight vision to view through the economic space-time. There is probably too heavy of a fog as each nation or each individual is concerned with her own safety. Given the experimental nature of human economy, as the experimenters, the individual participants may feel overloaded by the living data. From a mathematical perspective, it implies that the observers have lost their frame of universal straight coordinates and turned to form their own local coordinates. Einstein introduced tensor analysis using examples in geometry, such as quadratic surfaces. The next section will elaborate on this concept.

4. Economic Space with Local Curvilinear Coordinates

It is not hard to imagine that huge economic events make the economic space curved. Since the global financial crisis began in 2008, each country or region has initiated all kinds of monetary or fiscal policies to protect its own economy. During the economic downturn, each individual has become more concerned about personal or family welfares instead of general social needs. Our working hypothesis is that people may have different views toward an economic event, and each individual may have different views toward different events. We want to speculate when the Cartesian frame of straight coordinates collapses, how the individual constructs a local curvilinear coordinate system.

Consider an affine space, in which each point represents an economic event. (This is different from Minkowski space-time where each point represents an admissible observer.) For a given event E, the individual needs to first determine the number of features to be taken into account. Let us say, three, for the time being, write @1, @2, @3. Now consider a small connected neighborhood of E; for any neighboring events, every individual takes the same three features into account. This way, the individuals has turned the three features into three variables, written as X₁, X₂, X₃. Now, we can connect three features by a linear function x_α. Because three variables are involved here, three such functions are needed in order to secure a solution. Write them as:

x_α = x_α (X₁, X₂, X₃) (α = 1, 2, 3)

Here, x_α are continuous, differentiable, and single-value functions. If the inverse functions

X_i = X_i (x₁, x₂, x₃) (i = 1, 2, 3)

are also continuous, differentiable, and single-valued, we say x_α (α = 1, 2, 3) sets up a local curvilinear coordinate system in the neighborhood of E. By the same token, X_i (i = 1, 2, 3) can be seen as another local curvilinear coordinates in the neighborhood of E, and the transformation between the two is self-obtained by the definition. Likewise, because any other curvilinear coordinate systems are linearly dependent on x_α, the general transformation rules hold.

For any given point M in the connected neighborhood, it yields a tangent direction along each curved coordinate. Because the point has direction, we can calculate the corresponding partial derivative. We also have the useful property that states that:

$$\text{∂} x_{\alpha }/ \text{∂}{x}_{\alpha } ={\displaystyle {\sum }_{j=1}^3}(\text{∂}{x}_a / \text{∂}{X}_i) (\text{∂}{X}_i / \text{∂}{X}_{\beta }),$$

where δ_αβ = {

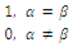
This property enables us to construct the coordinate’s basis and form the so-called local frame of curved coordinates.

Given the basic ideas briefly introduced above, we have shown the rough picture about the so-called manifold in differential geometry. An individual’s knowledge about space structures can go deeper and deeper with each step. For any given point in a manifold, one can define a tensor. For any two given points, we may also define the connection between the two corresponding tensors. The connection is called affine connection space. Furthermore, if a non-degenerative metric tensor is introduced, we will obtain Riemann space, which is the space that Einstein used in his general theory of relativity.

Given the insights and tools that we may use from the general theory of relativity, we can look at economic space. With a cognitive field being attached to economic space, there are predictably going to be many interesting stories. These stories would go beyond the scope of this volume, and we leave the possibilities open here for more careful thinking in the future. Nevertheless, one story is essential, which will be described and reviewed in the next section. We will characterize the concept of Pareto efficiency in economics in terms of the notion of geodesics. From the general theory of relativity, geodesics can be used to describe economic curvature and economic gravity.

5. Pareto Efficiency, Geodesics, and Economic Gravity

Both the notions of Pareto efficiency and geodesics are extreme cases, which are essential concepts in their home disciplines. If they can be matched analogically, it will serve as a bridge between economics and the general theory of relativity. Let us first examine the concept of geodesics.

In the general theory of relativity, geodesics are defined by a second order differential equation with a connection as a coefficient, which we are not going to be getting into. Instead, the notion of geodesics can be viewed in a much more intuitive way. In a flat space, the geodesic is the straight line connecting two points with the shortest distance. In a curved space, the geodesic curve between two points can be seen as an arc. Here, the geodesic curve is not characterized best in terms of the distance, but instead, in terms of the tangent vector. Similar to the case for a straight line from another perspective, the geodesic curve is best characterized when all the tangent vectors along the curve are parallel. Between any two points, the geodesic curve is unique.

We now turn to review the notion of Pareto efficiency in economics. Its formal definitions can be found in any textbook or easily referenced online. Pareto efficiency, also known as Pareto optimality, is mathematically characterized in terms of allocations of goods or resources and individual utility. In a more behavioral manner, it is defined in terms of so-called Pareto frontiers, along which all consumers are assumed to share the same marginal rate of substitution. In a perfect competitive market, given the initial allocation of goods, a change to a different allocation that makes at least one individual better off without making any other individual worse off is called a Pareto improvement. A market state, namely, an allocation, is defined as Pareto-efficient when no further Pareto improvement can be made. Being in a Pareto-efficient state implies that the equilibrium condition for market clearance exists. We can characterize the notion of Pareto efficiency in terms of geodesics in two ways.

One way is to treat the Pareto-efficient state as a singularity point in the market space. Though it is not connected to any other state points, it can be seen as being connected to itself. The arc line from the Pareto-efficient point to itself has a length of zero. In tensor analysis, it is called an isotropic geodesic, meaning that a geodesic that has lost its direction.

Another way is to line up all the individual market participants. Since Pareto efficiency does not make any statement about equality or overall well-being of a society, given the general individual differences in personal endowments, we can assume the line of individual utilities is a curve. Let us call this curve a Pareto path within the Pareto-efficient state. Under this state, we can reasonably assume that individuals think in different directions in order to become better off or at least earn a fair share. This supposition allows us to yield a tangent vector at each utility point along the Pareto path. However, since no one can make a move without breaking the Pareto-efficient state, the length of each tangent vector here can only be zero. In this way, every tangent vector on the Pareto path is degenerated to an isovector (null vector); therefore, they are all parallel. In this sense, by the characterization of geodesics given earlier, we say the Pareto-efficient state can be characterized as the economic geodesic.

Both ways above seem counterintuitive, if not confusing. But let us think of situations in our daily life. When a friend or a colleague asks someone, “How are you doing?” you often hear the response “Same old, same old.” What would that mean if one is in a three-dimensional space, where time is passing by? Every day is a new day. If one is in a four-dimensional space-time, as we mentioned earlier, because time no longer moves, everything must always be in motion. What that conversation means in terms of common sense is that the semester is moving very fast. We are too busy in our day-to-day lives, so we feel as if they are merging into one day, the same old days. In other words, our feelings do not distinguish between these days.

Consider one more example in our ordinary life. Someone used to work from nine to five every working day. It is your dream profession, and you greatly enjoy the job. If people say that you just work for money, you might reply that “This is my career.” What is the difference between the call of duty and your willingness (or desire) to work? They are different matters, but often, we simply do not distinguish them.

In the history of science, there is a well-known story called the Einstein’s “happiest moment.” Einstein was puzzled over the Newtonian notion of inertial frames for quite a while. In solving this puzzle, he first derived the following equation:

$$\ddot{a}={\displaystyle \frac{G_m}{I_m}}\times \mathrm{K} \left(\text{curvature}\right)$$

The meaning of this formula is as follows:

$$\mathrm{Acceleration}={\displaystyle \frac{Grativationmass}{Inertialmass}}\times \left(\mathit{intensity}\mathit{of}\mathit{the}\mathit{gravitational}\mathit{field}\right)$$

Einstein then made the following analysis (1916): “If now, as we find from experience, the acceleration is to be independent of the nature and the condition of body and always the same for a given gravitational field, then the ratio of the gravitational to the inertial mass must likewise be the same for all bodies. By a suitable choice of units we can thus make this ratio equal to unity. We then have the following law: The gravitational mass of a body is equal to its inertial law.” This is called Einstein’s equivalence principle in his general theory of relativity.

I, myself, am convinced that what confused Einstein is analogically similar to what would make us feel counterintuitive in treating Pareto efficiencies as economic geodesics. We will discuss this further in a later chapter, which is about what I call ordinary rationality and Wittgenstein’s idea about subjective certainty. Here, I leave readers to get a glimpse at the comparisons and analogies above. From the above formula and what Einstein concluded, we may read out in economic terms that the acceleration in our economic life is equivalent to the intensity of some “economic gravitational field.” But what is an “economic gravitational field?”

In the general theory of relativity, the intensity of the gravitational field is defined in terms of the notion of curvature, which involves massive mathematics. For our purpose here, the intuitive description by Feynman (1997/2004) should be enough: Curvature is the difference between measured results and the geodesics. As we all know, a Pareto-efficient state is an ideal economic state. One of the reasons why it is theoretically useful is that the notion of Pareto efficiency tells us what is economically inefficient and why we need to make Pareto improvements. Allow and Debreu mathematically demonstrated that a free-market system will lead to a Pareto-efficient outcome, which is called the first welfare theorem. The theorem assumes a number of strong conditions, which can hardly be satisfied in any actual economy or by any real market. In this sense, we say the difference between a measurable economic or market state and the ideal Pareto-efficient state (which one may call a Pareto economic geodesic) is the curvature for that measured state. Because we assume any real, sufficiently active free market can never achieve the Pareto-efficient state, economic curvatures exist everywhere. This, in turn, forms what we shall call the economic gravitational field. This also means that the economic space-time is curved everywhere.

Before ending this paper, one may ask: what about the “same old, same old” experiences? Unfortunately, that is counted as the sunk cost in our economic life (Yang, Y. 2022, 2024). Keep in mind that the current economics is about new opportunities or something additional, specifically additional per unit to be accelerated; that is the core idea of marginal analysis. Given what we have lectured so far, all individual market participants are non-inertial systems that should be governed by the same economic law: the intensity of economic gravity accelerates people’s extra economic efforts. In turn, it holds what we may call the economic version of Einstein’s equivalence principle: within a small economic space, the mental measurements of what one is used to doing constantly and what one is demanded to do are not distinguishable, so they can be treated as equivalent to each other from a cognitive perspective.

6. Conclusion Remarks

Inequality is always a serious concern of political economics. Nevertheless, the mainstream economics mostly focus on efficiency. The present paper postulates a new model of inequality and pareto efficiency. The general relativity theory is used as referential framework from a modeling perspectives. The economic inequality is characterized in a curved space and the Pareto efficiency is modeled as the geodesics.

We have provided certain details for constructing such a model mathematically. The logic of this structure is as follows.

Remark 1. Inequality is an unavoidable issue for political economics. In the political and socio dimension, the mathematical analyses at the global level must be based on a curved space but not a flat space from modeling perspectives.

Remark 2. In the economic dimension, the pareto efficiency serves as a geodesic of the curved space. The differences between individual intentions for improvements and the geodesic are curvatures. This curvature is the geometric characterization of the economic gravity.

Remark 3. By the Einstein Equivalence Principle, the curvature determines how hard one needs to work. The greater the curvature, the harder one has to work. The acceleration of working is the algebraic characterization of economic gravity. In physics, there is a saying that the curvature tells the material how to move, and the materials tell the space how to curve.

Remark 4. At the local level of mathematical modeling, each individual establishes a local frame, as the differential geometry taught us. Individual local frames must be connected by the invisible hand. This connection is a tensor.