1. Introduction
The emergence of thin nano-atomic layers in 2D semiconductor materials has revolutionized the development of modern semiconductor devices, owing to their unique properties, such as high flexibility, tunable band gaps, and enhanced light-matter interactions. These characteristics make 2D materials ideal candidates for applications in next-generation electronic, optoelectronic, and photonic devices. With the increasing demand for new magnetic and thermoelectric devices, it has become crucial to accurately predict and evaluate the physical properties of semiconductors that can fulfill these requirements. Researchers are especially focused on non-toxic 2D semiconductors, synthesized from abundant elements, to ensure their environmental sustainability and efficiency. Materials like KAlTe2 and KInTe2, which belong to the A-B-X2 family of compounds, are of significant interest due to their promising properties for use in optoelectronics, photovoltaics, and nonlinear optics [
1,
2,
3]. The A-B-X2 structure consists of an alkali metal (A), a group III element (B), and a chalcogen (X), forming a stable and versatile framework. In KAlTe2 and KInTe2, potassium (K) serves as the alkali metal with a valency of +1, aluminum (Al) or indium (In) have a valency of +3, and tellurium (Te) is a chalcogen with a valency of -2. This stoichiometry ensures stability and is integral to the materials' desirable properties. Both KAlTe2 and KInTe2 crystallize in a tetragonal structure, where the lattice constants a and b are equal, and the c-axis differs, giving rise to unique electronic and structural characteristics. While earlier research has provided insights into the crystallography of these materials, some structural aspects, such as detailed bonding characteristics and thermodynamic behavior, remain underexplored. Previous studies have mainly focused on the atomic positions and bond lengths in single crystals of KAlTe2 and KInTe2. Still, further investigation into the bonding and interaction of atoms is necessary to fully understand their behavior. Mulliken population analysis has revealed that the Aluminum-Tellurium (Al-Te) and Indium-Tellurium (In-Te) bonds are predominantly covalent, while the Potassium-Tellurium (K-Te) bond is ionic. This is consistent with the general trend observed in A-B-X2 compounds, where the B-X bonds tend to be covalent, and the A-X bonds are ionic. These findings are aligned with experimental observations and provide a deeper understanding of the materials' atomic-level behavior. Given the intriguing properties of KAlTe2 and KInTe2, there is a growing interest in exploring their thermoelectric and magnetic characteristics, especially at different temperatures, to unlock their potential in energy conversion and storage applications. Additionally, investigating their thermodynamic properties, which have yet to be fully explored, could further enhance the understanding of these materials and expand their applications in advanced technological devices [
4,
5,
6,
7,
8,
9].
2. Method of Calculations
Material properties can be investigated using both experimental and theoretical approaches. Experimentally, properties are often studied by analyzing wave functions derived from the Schrödinger Wave Equation. Theoretically, Density Functional Theory (DFT) provides a powerful framework for material analysis, grounded in the Kohn-Sham Equation. DFT-based tools play a crucial role in exploring various material properties, including electronic, structural, and mechanical characteristics. Among the DFT methods, the Full-Potential Linearized Augmented Plane Wave (FP-LAPW) approach, implemented in computational packages like WIEN2k and CASTEP, is widely used for analyzing complex materials such as KAlTe₂ and KInTe₂. This method is particularly effective in providing accurate calculations of the electronic structure and bonding characteristics of materials. In structural studies, the exchange-correlation energy is commonly described using the Generalized Gradient Approximation (GGA), specifically the GGA-PBEsol functional, as formulated by Perdew et al. [
10,
11,
12,
13,
14]. The GGA-PBEsol functional is well-regarded for its ability to provide reliable results for the structural properties of materials. When investigating the electronic properties, the band gap is a critical parameter. For conductors, semiconductors, insulators, and superconductors, the band gap is often calculated using standard GGA functionals. While GGA provides reasonable estimates of band gaps, it is known to underestimate them in certain materials, particularly semiconductors and insulators. This limitation has led to the development of more advanced functionals within the GGA framework, which aim to provide a more accurate representation of electronic structures across different types of materials. These advancements help overcome challenges in modeling and predicting material properties more effectively. Other DFT methods, such as the Local Density Approximation (LDA), meta-GGA, and hybrid functionals, are also used to calculate the mechanical properties of materials, each offering unique strengths in addressing the mechanical and electronic behaviors of complex systems [
15,
16,
17].
3. Results and Discussion
In this section we are investigating the structural, bandgap and Bonding properties of ternary telluride.
3.1. Structural Properties:
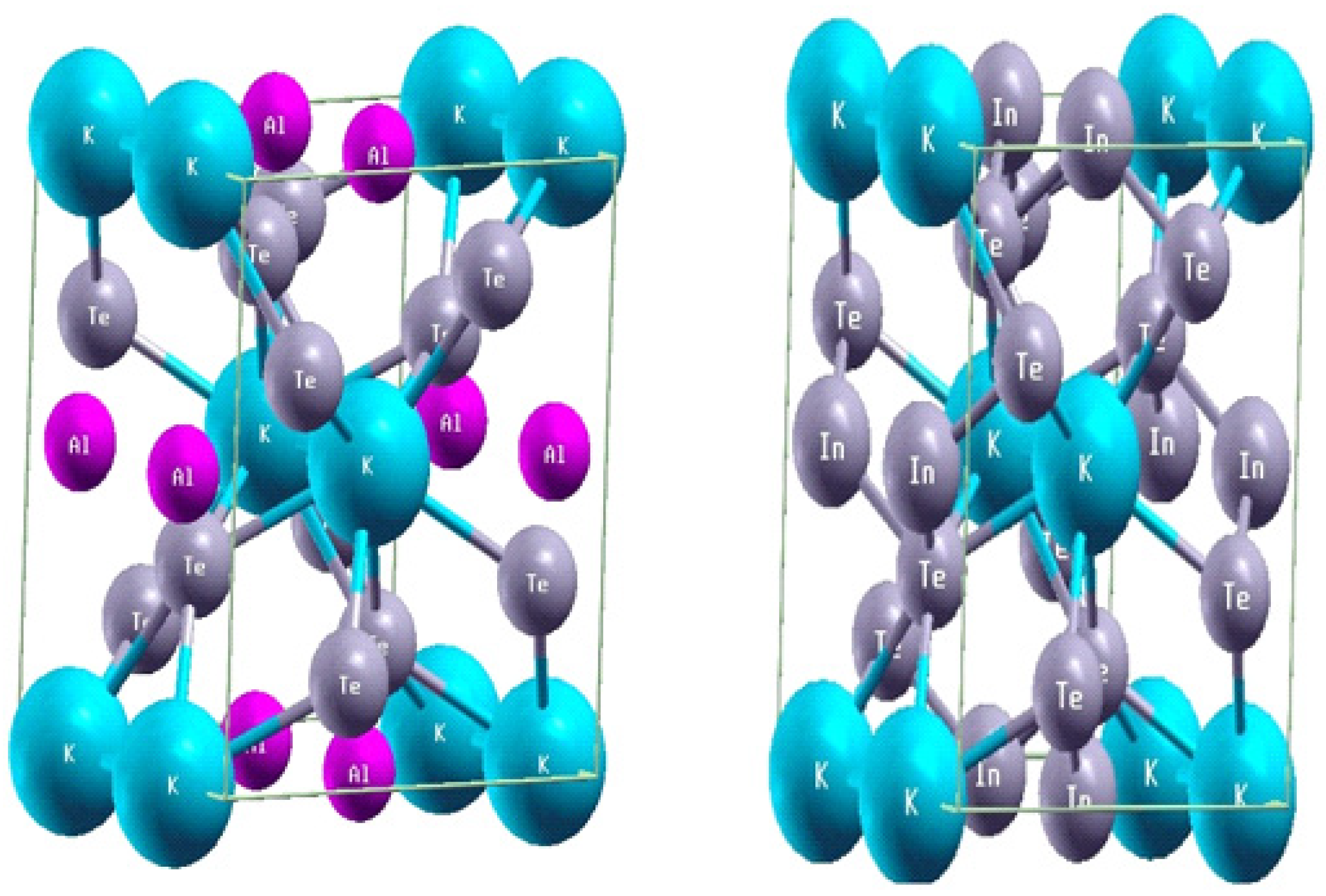
The structural features of tetragonal materials were investigated using the full-potential Linearized Augmented Plane Wave (FP-LAPW) method, a well-established technique in density functional theory (DFT). This approach employed the Generalized Gradient Approximation (GGA) to analyze the DFT volume of unit cell structures and examine the chemical compositions. Specifically, the ternary tellurides KAlTe₂ and KInTe₂ were studied, both of which crystallize in the tetragonal space group I4/mcm (No. 140). The unit cell arrangements of these materials are shown in the accompanying
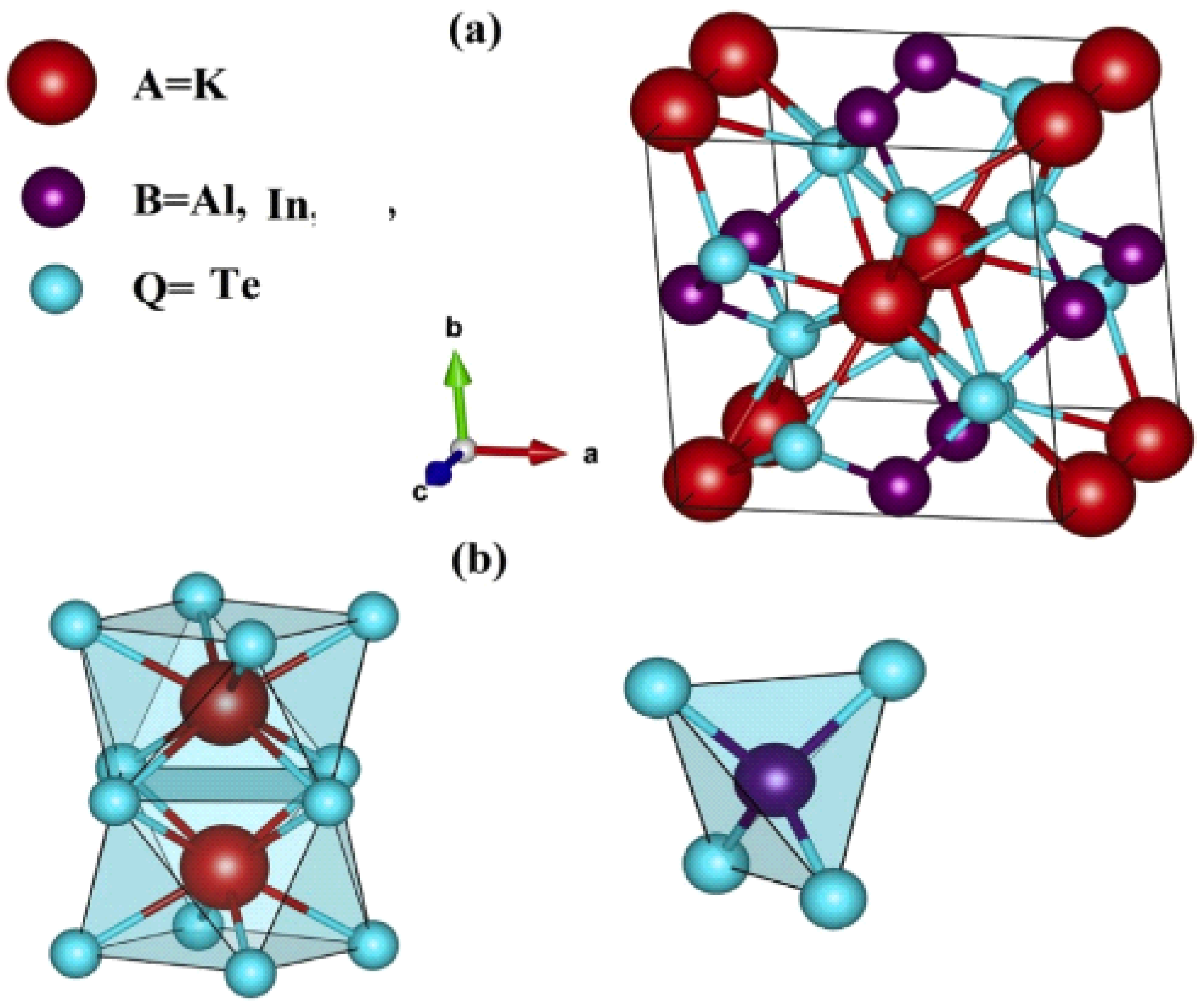
Figure 3.1.(1)(2). In these structures, the Wyckoff positions of the atoms are defined as follows: Te atoms occupy the 8h sites with coordinates (0.1645, 0.6645, 0), K atoms are situated at the 4a sites with coordinates (0, 0, 0.25), and the atoms (Al or In) are located at the 4b sites with coordinates (0, 0.50, 0.25). These arrangements form distinctive structural units. The XTe₄ tetrahedral units consist of Al or In cations surrounded by four Te atoms in a slightly distorted tetrahedral geometry [
1,
18,
19,
20,
21]. Meanwhile, the K cations are positioned at the center of quadratic antiprisms composed of eight Te anions, resulting in KTe₈ octahedral units. These unique geometries are illustrated in
Figure 3.1.2(a) and 2(b). The coordination behavior of these structures provides further insight into their crystallography. In a body-centered cubic (BCC) lattice, the coordination number (CN) is 8, as each atom has eight nearest neighbors. In contrast, the face-centered cubic (FCC) lattice has a CN of 12 due to its denser packing and 12 nearest neighbors. The body-centered tetragonal (BCT) structure emerges as a transitional phase when the cubic lattice is distorted in one direction. This intermediate structure bridges the characteristics of BCC and FCC lattices, theoretically resulting in a coordination number that lies between 8 and 12, depending on the degree of distortion and specific atomic arrangement. The structural complexity of KAlTe₂ and KInTe₂, including their tetrahedral and octahedral configurations, reflects the interplay of symmetry, bonding, and atomic packing within the tetragonal system. These features not only define their unique electronic and structural properties but also highlight the versatility of the FP-LAPW method and GGA in exploring the detailed crystallographic and chemical characteristics of advanced materials.
3.2. Optimization Plots:
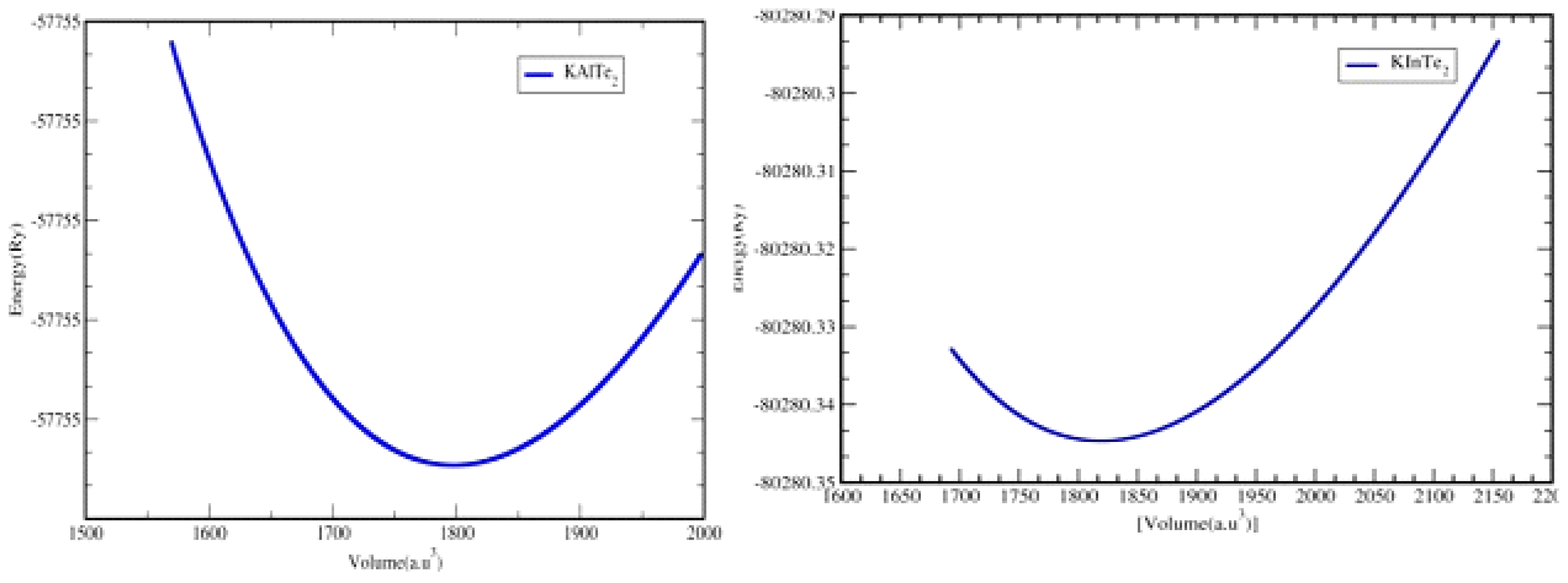
Optimization plays a pivotal role in theoretical calculations as it establishes a material's ground-state structural properties, which are essential for understanding its stability and behavior. This process involves minimizing the energy of a compound to its lowest possible level, thereby identifying the most stable configuration. During optimization, various structural files are generated, each representing a potential configuration of the material. These configurations are evaluated iteratively until the ground-state energy is achieved. For materials like KAlTe₂ and KInTe₂, optimization is conducted using the WIEN2k package, which employs the percent c/a ratio from the initial structural file to refine the lattice parameters as shown in
Figure 3.2.1. By systematically adjusting the c/a ratio, the method pinpoints the structural configuration with the minimum energy. The energy variation as a function of the percent c/a ratio reveals key insights into the relative stability of the compounds. Specifically, the optimization data show that in the tetragonal structure, KAlTe₂ is more stable than KInTe₂, as evidenced by its lower ground-state energy. The structural parameters derived from this process are presented in the accompanying existed values, which highlights their accuracy by comparing them to previous experimental and theoretical findings [
22,
23,
24]. The comparison demonstrates strong agreement, validating the reliability of the optimization methodology. These results not only affirm the stability of KAlTe₂ in the tetragonal structure but also underscore the broader significance of optimization in theoretical studies. By providing a detailed understanding of structural properties, optimization serves as a foundation for further investigations into the electronic, optical, and mechanical behavior of materials. This iterative and precise approach is indispensable for accurately modeling and predicting the properties of advanced materials, ensuring consistency with experimental and theoretical benchmarks.
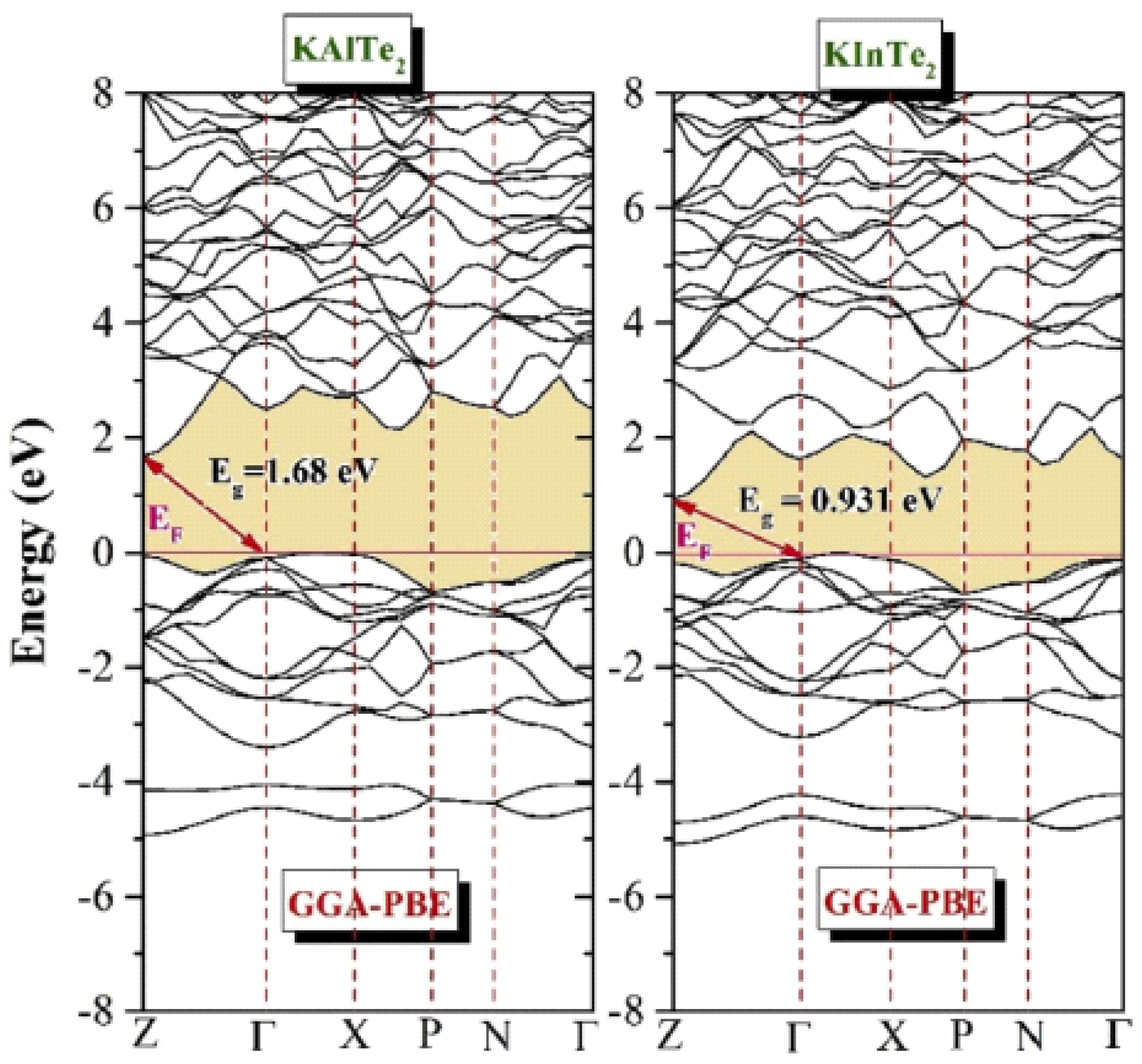
3.3. Band Structure:
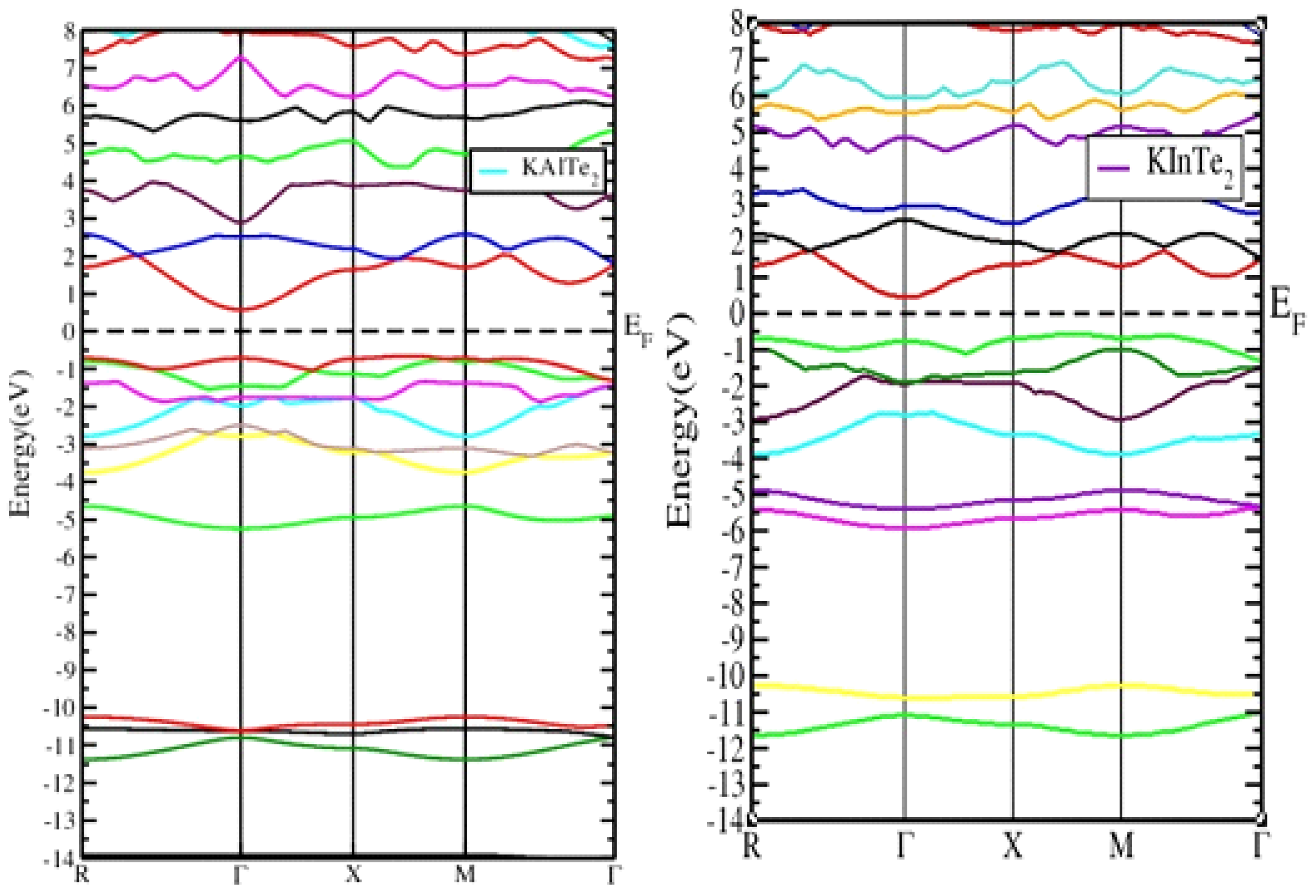
Tellurides are naturally intrinsic semiconductors, but doping with potassium and aluminum/indium transforms them into extrinsic semiconductors with tailored electronic properties. The band gap, a critical parameter for semiconductors, can be roughly estimated from density of states (DOS) plots. However, DOS analysis alone does not reveal whether the band gap is direct or indirect. Determining the band gap's nature requires examining the band structure at various symmetry points. If the energy states form curves at different symmetry points, the band gap is indirect. Conversely, a direct band gap is identified when the conduction band minima and valence band maxima align at the same symmetry point.
Figure 3.3.1 and
Figure 3.3.2 demonstrates the band structures of KAlTe₂ and KInTe₂, calculated using the Generalized Gradient Approximation (GGA) method within the DFT framework. The analysis reveals that both materials are direct band gap semiconductors, as the conduction band minima and valence band maxima are aligned at the Γ symmetry point. Further confirms these results, showing the Fermi energy level set at 0.0 eV. For KAlTe₂, the conduction band minima and valence band maxima are located within the first Brillouin zone, affirming its direct band gap nature. Similarly, KInTe₂ exhibits direct band gap characteristics, supported by contributions from critical symmetry points like R, Γ, X, and M. The calculated band gaps for KAlTe₂ and KInTe₂ using the GGA approach are 1.68 eV and 0.931 eV, respectively [
3,
25,
26,
27]. These values align with earlier studies based on DFT. When recalculated using the HSEO6 functional, the band gaps were refined to 2.178 eV for KAlTe₂ and 1.858 eV for KInTe₂, providing further accuracy. The agreement between theoretical predictions and experimental findings underscores the reliability of the computational models used. The semiconducting nature of KAlTe₂ and KInTe₂, combined with their direct band gap properties, makes them highly suitable for various optoelectronic applications. These include photovoltaic devices, light-emitting diodes (LEDs), and other technologies requiring materials with high transparency or controlled absorption. Their band gap values indicate potential for use in devices operating within specific energy ranges, ensuring efficient performance and broad applicability. These findings emphasize the potential of doped tellurides in advancing next-generation electronic and optoelectronic technologies.
3.4. Bonding Nature/Electron charge density:
The electron density plots provided in the following
Figure 3.4 offer valuable insights into the bonding nature and charge transfer within the crystal structures of KAlTe₂ and KInTe₂. These plots visually represent the distribution of electron density across the material, helping to elucidate the types of bonds between the various ions and providing a clearer understanding of the material’s overall electronic characteristics. In KAlTe₂, the electron density around the potassium ion is nearly spherical, which suggests that the potassium bonds are more ionic in nature compared to covalent. This indicates that potassium primarily forms ionic interactions with other atoms in the structure. On the other hand, the electron density reveals a strong covalent bond between aluminum and tellurium atoms. The electron cloud distribution around aluminum and tellurium shows a more directional bonding nature, characteristic of covalent bonds. This trend is similarly observed in KInTe₂, where indium and tellurium also exhibit a strong covalent bond. However, the potassium-tellurium bond in KInTe₂, like in KAlTe₂, remains predominantly ionic. This ionic-covalent bonding pattern aligns with what has been observed in other A-B-X₂ structures, where A represents an alkali metal and B and X are other elements. In these structures, the B-X bonds (such as aluminum-tellurium or indium-tellurium) tend to be primarily covalent, while the A-X bonds (such as potassium-tellurium) are predominantly ionic. These bonding characteristics are consistent with experimental observations and theoretical predictions in similar materials [
1,
3,
28]. The unique bonding nature in KAlTe₂ and KInTe₂ plays a crucial role in their electronic properties. The ionic and covalent interactions contribute to the material's overall stability and electronic behavior, making them suitable candidates for various applications. Their distinctive charge transfer properties and bonding types make these materials particularly important for use in photovoltaic devices, optoelectronic applications, and nonlinear optical devices. As the demand for advanced materials in these technologies grows, KAlTe₂ and KInTe₂ are emerging as promising candidates due to their unique structural and electronic characteristics.
3.5. Mechanical Nature:
The mechanical properties of the investigated materials, KAlTe₂ and KInTe₂, have been rigorously analyzed through advanced computational methods, with the results systematically presented in
Table 3.1 and
Table 3.2. These analyses were performed using the Generalized Gradient Approximation (GGA) framework within the renowned WIEN2k and CASTEP computational codes. Both methods are widely acknowledged for their precision in simulating the electronic and structural properties of complex materials, making them suitable for accurate mechanical property calculations. The study focuses on key mechanical parameters, including elastic constants, bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio. These parameters are essential for understanding the materials' structural rigidity, mechanical stability, and their potential for practical applications in various technological fields [
29,
30]. The application of the GGA approach ensures improved accuracy in the computations by incorporating corrections to the exchange-correlation energy, providing a more realistic representation of the materials' mechanical responses under various conditions. This approach also offers a good balance between computational efficiency and the precision required for the analysis of mechanical properties. In addition, the use of WIEN2k and CASTEP codes allows for a detailed exploration of the intricate relationship between the crystallographic structure and the mechanical properties of these materials. DFT calculations are typically performed at various temperature values to assess the temperature dependence of the mechanical properties. Several DFT methods, including Local Density Approximation (LDA), meta-GGA, hybrid functionals, and Full-Potential Linearized Augmented Plane Wave (FP-LAPW), are employed to calculate the mechanical properties of materials. While GGA is widely used due to its balance between accuracy and computational cost, the FP-LAPW method provides higher precision, particularly for more complex systems, by treating both core and valence electrons separately. The findings from this study contribute to a deeper understanding of KAlTe₂ and KInTe₂, supporting their potential for innovative technological applications.
Conclusion
In summary, the physical properties of KAlTe₂ and KInTe₂, including their structural, band gap, and bonding characteristics, were analyzed using first-principles methods. The computed crystal structure properties are in excellent agreement with existing experimental data, confirming the tetragonal crystal structure of both materials. The analysis reveals that these materials exhibit strong covalent bonding between aluminum/indium and tellurium, while the potassium-tellurium bond is predominantly ionic, highlighting their anisotropic and stable nature. Density functional theory (DFT) calculations also predict that these materials are ductile, indicating mechanical flexibility. The band gap analysis, based on the Generalized Gradient Approximation (GGA) technique, reveals that KAlTe₂ is a direct band gap semiconductor with a band gap of 1.68 eV, while KInTe₂ is an indirect band gap semiconductor with a band gap of 0.931 eV. The findings suggest that replacing aluminum with indium in KAlTe₂ reduces the band gap numerically, making KInTe₂ more suited for applications requiring different band gap properties. These results confirm the significant potential of KAlTe₂ and KInTe₂ in material science, particularly for optoelectronic applications such as photovoltaic devices, light-emitting diodes, and other technologies requiring specific electronic properties. The comparison with previous experimental and theoretical data demonstrates the reliability of the first-principles approach in predicting the behavior of these materials.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
References
- Bouchenafa, M.; Benmakhlouf, A.; Sidoumou, M.; Bouhemadou, A.; Maabed, S.; Halit, M.; Al-Douri, Y. Theoretical investigation of the structural, elastic, electronic, and optical properties of the ternary tetragonal tellurides KBTe2 (B= Al, In). Materials Science in Semiconductor Processing 2020, 114, 105085–105088. [Google Scholar] [CrossRef]
- Benmakhlouf, A.; Bentabet, A.; Bouhemadou, A.; Maabed, S.; Khenata, R.; Bin-Omran, S. Structural, elastic, electronic and optical properties of KAlQ2 (Q= Se,Te): A DFT study. Solid State Sciences 2015, 48, 72–81. [Google Scholar] [CrossRef]
- Ullah, Z.; Amir, M.; Bazilla, A.; Ullah, S.; Shahzad, U.; Ullah, N.; Khan, J.; Gul, S. Electronic, Thermoelectric and Magnetic properties of Ternary Telluride KAlTe2 and KInTe2 from Theoretical Perspective. Next Research 2024, 1, 100077. [Google Scholar] [CrossRef]
- Belgoumri, G.; Bentabet, A.; Khenata, R.; Bouhadda, Y.; Benmakhlouf, A.; Rai, D.P.; Bounab, S. Insight into the structural, electronic and elastic properties of AInQ2 (A: K, Rb and Q: S, Se, Te) layered structures from first-principles calculations. Chinese Journal of Physics 2018, 56, 1074–1088. [Google Scholar] [CrossRef]
- Benmakhlouf, A. Structural, elastic, electronic and optical properties of KAlQ2 (Q¼ Se, Te): a DFT study. Solid State Sci 2015, 48, 72–81. [Google Scholar] [CrossRef]
- Feng, K.K. Synthesis structure, physical properties, and electronic structure of KGaSe2. Solid State Sci 2012, 14, 1152–1156. [Google Scholar] [CrossRef]
- Kim, J.; Hughbanks, T. Synthesis and structures of ternary chalcogenides of aluminum and gallium w ith stacking faults: KMQ2 (M= Al, Ga; Q= Se, Te). Journal of Solid-State Chemistry 2000, 149, 242–251. [Google Scholar] [CrossRef]
- Witt, C.W.; Shires, W.B.; Tan, W.C.; Jankowski, J.W.; Pickard, J.C. Random Structure Searching with Orbital-Free Density Functional Theory. The Journal of Physical Chemistry A 2021, 125, 1650–1660. [Google Scholar] [CrossRef]
- Trani, F.; Ninno, D.; Cantele, G.; Iadonisi, G.; Hameeuw, K.; Degoli, E.; Ossicini, S. Screening in semiconductor nanocrystals: Ab initio results and Thomas-Fermi theory. Physical Review B—Condensed Matter and Materials Physics 2006, 73, 245430. [Google Scholar] [CrossRef]
- Xie, Q.X.; Wu, J.; Zhao, Y. Accurate correlation energy functional for uniform electron gas from an interpolation ansatz without fitting parameters. Physical Review B 2021, 103, 045130. [Google Scholar] [CrossRef]
- Claeys, C.; Hsu, P.C.; Mols, Y.; Han, H.; Bender, H.; Seidel, F. . Simoen, E. Electrical Activity of Extended Defects in Relaxed InxGa1− xAs Hetero-Epitaxial Layers. ECS Journal of Solid State Science and Technology 2020, 9, 033001. [Google Scholar] [CrossRef]
- Ikeda, A.; Koibuchi, S.; Kitao, S.; Oudah, M.; Yonezawa, S.; Seto, M.; Maeno, Y. Negative ionic states of tin in the oxide superconductor Sr 3− x SnO revealed by Mössbauer spectroscopy. Physical Review B 2019, 100, 245145. [Google Scholar] [CrossRef]
- Tran, F. (2018). WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties.
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Wu, C.S.; Lee, P.Y.; Chai, J.D. Electronic properties of cyclacenes from TAO-DFT. Scientific reports 2016, 6, 37249. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Francis, S.; Roldan, A. The influence of support materials on the structural and electronic properties of gold nanoparticles–a DFT study. Physical Chemistry Chemical Physics 2019, 21, 19011–19025. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Wang, N.; Li, M.; Xiao, H.; Liu, Z.; Zu, X.; Qiao, L. The thermal and electrical transport properties of layered LaCuOSe under high pressure. Journal of Alloys and Compounds 2021, 861, 157984. [Google Scholar] [CrossRef]
- Wiebeler, H. (2020). A linear scaling DFT-Method and high-throughput calculations for p-type transparent semiconductors (Doctoral dissertation, Universitätsbibliothek).
- Schwarz, K.; Blaha, P. Solid state calculations using WIEN2k. Computational Materials Science 2003, 28, 259–273. [Google Scholar] [CrossRef]
- Schwarz, K. DFT calculations of solids with LAPW and WIEN2k. Journal of Solid State Chemistry 2003, 176, 319–328. [Google Scholar] [CrossRef]
- Labrim, H.; Jabar, A.; Laanab, L.; Jaber, B.; Bahmad, L.; Selmani, Y.; Benyoussef, S. Optoelectronic and thermoelectric properties of the perovskites: NaSnX3 (X= Br or I)—a DFT study. Journal of Inorganic and Organometallic Polymers and Materials 2023, 33, 3049–3059. [Google Scholar] [CrossRef]
- Selmani, Y.; Labrim, H.; Mouatassime, M.; Bahmad, L. Structural, optoelectronic and thermoelectric properties of Cs-based fluoroperovskites CsMF3 (M= Ge, Sn or Pb). Materials Science in Semiconductor Processing 2022, 152, 107053. [Google Scholar] [CrossRef]
- Bouhmaidi, S.; Marjaoui, A.; Talbi, A.; Zanouni, M.; Nouneh, K.; Setti, L. A DFT study of electronic, optical and thermoelectric properties of Ge-halide perovskites CsGeX3 (X= F, Cl and Br). Computational Condensed Matter 2022, 31, e00663. [Google Scholar] [CrossRef]
- Prihadi, H.L.; Zen, F.P.; Ariwahjoedi, S.; Dwiputra, D. (Replica trick calculation for entanglement entropy of static black hole spacetimes. International Journal of Geometric Methods in Modern Physics 2023, 20, 2350132. [Google Scholar] [CrossRef]
- Madsen, H.K.G.; Singh, J.D. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Kaur, T.; Sinha, M.M. (2021). Probing thermoelectric properties of high potential Ca3PbO: An Ab Initio Study. In IOP Conference Series: Materials Science and Engineering (Vol. 1033, No. 1, p. 012080). IOP Publishing.
- Mahmood, Q.; Hassan, M.; Ahmad SH, A.; Bhamu, K.C.; Mahmood, A.; Ramay, S.M. Study of electronic, magnetic and thermoelectric properties of AV2O4 (A= Zn, Cd, Hg) by using DFT approach. Journal of Physics and Chemistry of Solids 2019, 128, 283–290. [Google Scholar] [CrossRef]
- Feng, S.; Wang, N.; Li, M.; Xiao, H.; Liu, Z.; Zu, X.; Qiao, L. The thermal and electrical transport properties of layered LaCuOSe under high pressure. Journal of Alloys and Materials 2021, 861, 157984–157989. [Google Scholar] [CrossRef]
- Ribeiro, R.A.; Andres, J.; Longo, E.; Lazaro, S.R. Magnetism and multiferroic properties at MnTiO3 surfaces: A DFT study. Applied Surface Science 2018, 452, 463–472. [Google Scholar] [CrossRef]
- Benmekideche, N.; Bentabet, A.; Bouhadda, Y.; Boubatra, D.; Belgoumri, G.; Fetah, S.; Benyelloul, K. DFT study of structural, electronic and elastic properties of two polymorphs of monoclinic CsGaQ2 (Q= S, Se). Chinese Journal of Physics 2019, 56, 1345–1352. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).