1. Introduction
The rapid advancements in information and communication technologies, coupled with the increasing capabilities of computing resources, have enabled significant progress in the domains of artificial intelligence and machine learning. Among these advances, convolutional neural networks (CNN) have emerged as essential tools for the processing and classification of images [
1]. The ability of these networks to autonomously identify and extract salient features from visual data [
2] makes them valuable allies in various fields, including medical image classification [
3]. Beyond medical applications, CNN are widely used in areas such as autonomous driving [
4], where they assist in object detection and scene segmentation; security [
5], where they enhance facial recognition and surveillance systems; and in the field of agriculture, where they aid in crop and livestock monitoring by analyzing aerial images captured by drones [
6]. These diverse applications underscore the versatility and significance of CNN in solving complex, real-world problems across multiple domains.
Magnetic resonance imaging (MRI) is a powerful, non-invasive tool frequently used in diagnosing and monitoring brain tumors. Brain tumors refer to abnormal growths of cells within the brain that can be either benign or malignant, with various types such as gliomas, meningiomas, and pituitary tumors [
7]. MRI produces high-resolution, detailed images of the brain, enabling precise visualization of tumor characteristics, including their location, size, and structure [
8]. However, the complex and heterogeneous nature of brain tumors makes manual interpretation of MRI images challenging [
9]. CNN offer a promising solution by automating the extraction of relevant features from visual data, thereby assisting clinicians in brain tumor classification and diagnosis.
Designing an optimal CNN architecture for MRI-based brain tumor classification presents substantial challenges [
10]. This task requires an optimal configuration across a large parameter space that includes network depth, filter counts, convolutional layer dimensions, and numerous other hyperparameters. Crafting these architectures manually to achieve peak performance is often labor-intensive and can lead to suboptimal outcomes. To streamline this process, evolutionary algorithms (EA) [
11,
12] have been employed. By simulating natural selection, EA generate a population of candidate solutions and improves them over successive generations using mechanisms like selection, crossover, and mutation [
13]. EA have proven effective across various complex optimization problems, given their capacity to navigate large search spaces and yield high-quality solutions. A widely used EA is the Particle Swarm Optimization (PSO) which models collective behaviors observed in bird flocks or fish schools. PSO facilitates the efficient, iterative search for an optimal CNN architecture by treating each particle as a candidate solution. These particles refine their positions by balancing their individual learning with insights from their neighbors, progressively converging toward an optimal design [
10,
14,
15]. Besides PSO, other evolutionary techniques, such as genetic algorithms (GA), have been utilized to optimize CNN architectures [
16,
17].
The present study proposed enhancements to the psoCNN algorithm [
18] to optimize CNN architectures for MRI-based brain tumor classification. By combining CNN’s feature extraction abilities with PSO’s optimization power, the model aimed to achieve reliable diagnostic accuracy.
The key contributions of this work are outlined as follows:
A suitable brain MRI dataset containing different tumor types is selected.
An initialization strategy is developed to predominantly configure particles with convolutional and pooling layers, ensuring that pooling layers are implicitly positioned after each convolutional layer.
The search space is refined to focus on determining the optimal number of convolutional layers, their kernel sizes, as well as the ideal number of fully connected layers and their respective neuron counts.
Incremental training is applied, allowing particles to undergo progressively deeper learning over time.
The optimal CNN architecture is rigorously evaluated using a holdout validation approach, with classification performance assessed through a detailed analysis of the confusion matrix.
2. Related Work
Recent advancements in brain tumor classification using MRI have explored a range of methods, including manually designed CNN architectures, state-of-the-art pre-trained models, and approaches based on evolutionary algorithms. For instance, one study employed a genetic algorithm to evolve CNN architectures tailored to identify different glioma grades, achieving 90.9% accuracy in one case study and 94.2% accuracy in distinguishing between glioma, meningioma, and pituitary tumors [
19]. However, the method faced challenges due to its expansive search space, which resulted in complex models. Another approach integrated a novel CNN model for feature extraction with classical machine learning algorithms, using Bayesian optimization to fine-tune hyperparameters [
20] . This hybrid model outperformed nine state-of-the-art CNN models, achieving an impressive mean classification accuracy of 97.15%. Similarly, a different study combined a CNN with an SVM classifier and tested it on two datasets, yielding 99% accuracy for binary classification and 98% for multi-classification [
21]. A comparative analysis [
22], a generic CNN model and six pre-trained models were evaluated with various preprocessing techniques. Among these, InceptionV3 stood out as the most accurate, achieving an average accuracy of 97.12%, surpassing other models. However, these custom and state-of-the-art models raise questions about the optimality of their architectures. Additionally, they may be overly complex for MRI-based brain tumor classification, particularly when using pre-trained models designed for broader applications. The present study focuses on identifying the optimal CNN architecture, ensuring it is well-suited for the task while striking a balance between model complexity and performance.
3. Convolutional Neural Networks (CNN)
CNN have emerged as indispensable tool in the field of medical imaging, owing to their exceptional ability to identify intricate patterns, particularly in brain tumor classification tasks. The substantial applicability of these models, demonstrating their superiority over alternative methods and highlight their potential to significantly improve diagnostic accuracy [
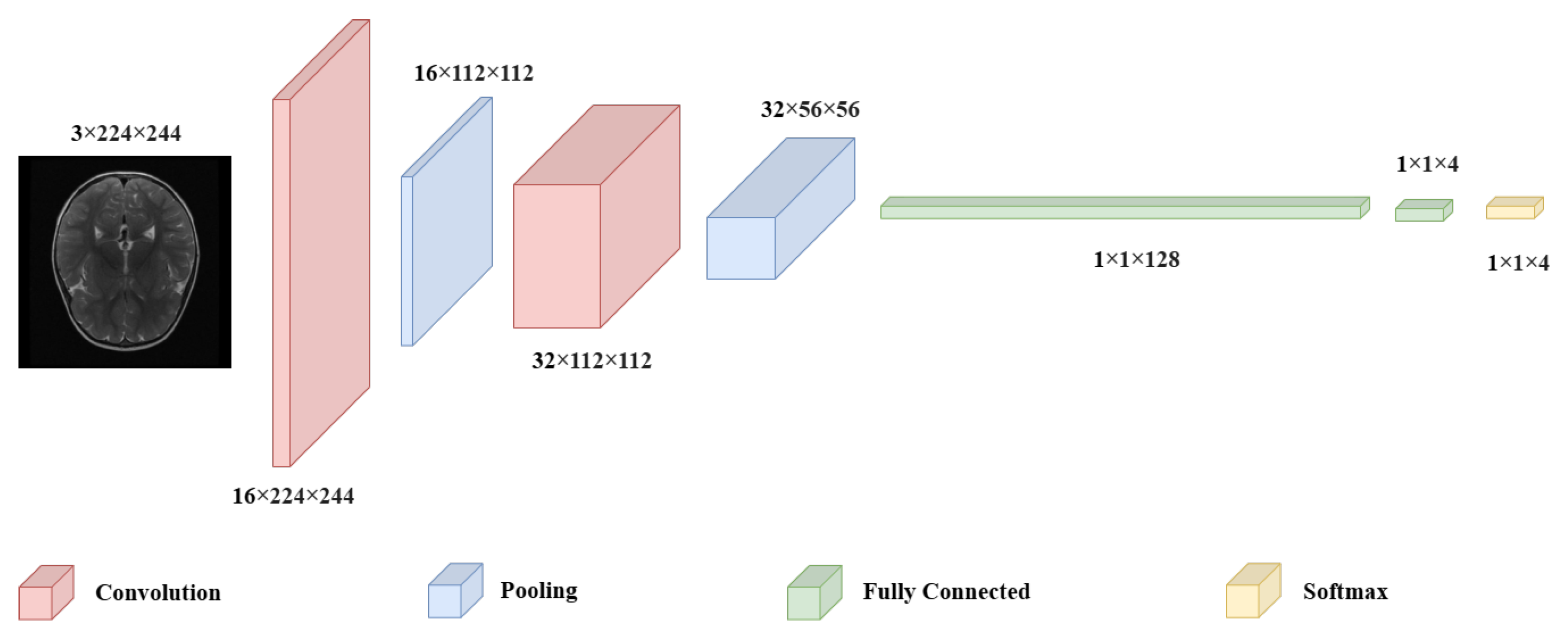
23]. CNN utilize a layered approach, where convolutional layers extract spatial features by applying filters. Pooling layers reduce dimensionality while retaining essential information, and fully connected layers at the end aggregate these features for classification. In this design, convolution and pooling operations sequentially capture intricate image details, which the fully connected layers at the model’s tail use to make final predictions (
Figure 1).
A CNN consists of interconnected neurons, each with specific weights and biases. These neurons take inputs from prior layers and perform calculations that combine the input values with the respective weights. CNN are designed with the assumption that the input data are images, which allows the model architecture to incorporate certain image-related features. The main types of layers within CNN include convolutional (C), pooling (P), and fully-connected (FC) layers [
24]. These layers are organized sequentially, such as each layer’s output serves as the input for the next. Mathematically, a CNN can be defined as follows:
Here, X represents the input image, which can be represented as a tensor encoding the color channels and spatial size of the image, is the activation function at the j-th layer, represents the operation using weights at the j-th layer, is the result from applying weights before activation, denotes the weights at the j-th layer, and is the output of the j-th layer.
3.1. Convolutional Layer (C)
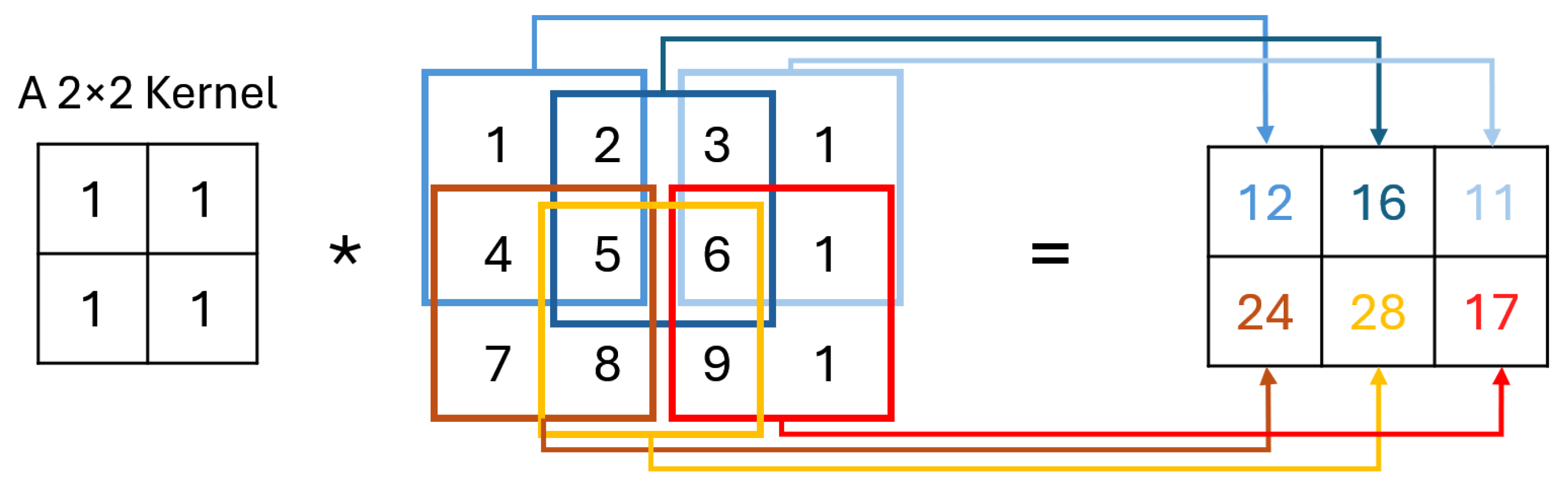
The C layer operates using small learnable filters which extend through the entire depth of the input but are narrow in spatial dimensions. As these filters traverse the input, they generate activation maps by calculating scalar products at each position, capturing important features [
25], as shown in
Figure 2. These activation maps, unique to each filter, stack together to form the output volume, allowing the network to learn specific spatial features. By training, CNN develop filters that detect patterns within localized areas, known as receptive fields, connecting only to limited input regions. Key hyperparameters— “number of filters”, “stride”, and “padding”—help control the model’s complexity and output dimensions. Adjusting stride, for instance, impacts the receptive field overlap, with smaller strides increasing overlap and larger strides reducing it, thereby affecting the spatial resolution of activations. Similarly, zero-padding around the input’s borders provides additional control over the output dimensions, enabling CNN to achieve greater flexibility in capturing spatial patterns [
26].
3.2. Pooling Layer (P)
Pooling layers [
27], reduce the spatial dimensions of feature maps, lowering computational demands and helping to prevent overfitting by downsampling. By transforming input data into a condensed representation, pooling layers focus on essential features while discarding less relevant information, thus reducing memory and computation requirements. Two main pooling types, local and global, offer distinct benefits: local pooling captures details within small regions, whereas global pooling compresses information into a scalar that summarizes features over the entire feature map. Among popular techniques, max pooling selects the maximum value within a region, preserving sharp and prominent features, while average pooling smooths the data by computing an average, capturing broader patterns but sometimes losing contrast. These pooling methods have core hyperparameters, such as those associated with the C layer.
3.3. Fully Connected Layer (FC)
FC layers play a critical role in combining the features extracted from C and P layers, transforming them into a final output suitable for classification or regression tasks. These layers are typically positioned towards the end of the network, where each neuron is connected to every neuron in the preceding layer, forming dense connections. This arrangement allows FC layers to capture complex relationships among features, but it also significantly increases the number of parameters, potentially leading to high computational costs and a tendency to overfit on small datasets. The number of neurons in each layer is a crucial hyperparameter in tuning fully connected layers, as it directly influences the model’s capacity to learn complex patterns.
3.4. Activation Function
To fully unlock the representational power of the previous layers, activation functions are introduced between them. Without activation functions, these layers would only perform linear transformations, limiting the network’s ability to capture intricate relationships in the data. They add the necessary nonlinearity, allowing the network to model more sophisticated patterns and interactions. Placed after each layer, they transform the output before it passes to the next, which directly impacts how well the network learns from data.
Historically, functions like Sigmoid and Tanh were commonly used; however, they often led to vanishing gradients in deep networks. This limitation prompted the introduction of ReLU, defined as
, a simple yet powerful function that addresses the vanishing gradient issue for positive values, while requiring minimal computation. To address ReLU’s limitations, particularly for negative input values, researchers have developed several variations, including Leaky ReLU, PReLU, and other advanced functions, each designed to handle gradient issues more effectively and to improve overall network performance [
28].
3.5. Softmax Cross-Entropy Loss
The softmax cross-entropy loss function is central to image classification, especially when handling multiclass problems [
29]. As CNN generate predictions over multiple classes, this loss function quantifies the difference between the predicted probability distribution and the true distribution of the classes. It operates by applying the softmax function to convert output logits into probabilities across multiple classes, with the loss calculated based on the negative log likelihood of the correct class. By doing so, it ensures that each output probability lies between 0 and 1 and that the total sums to 1. Mathematically, if we denote the true label vector by y and the predicted probabilities by p, the cross-entropy loss L is given by:
where C represents the total number of classes,
is 1 for the correct class and 0 otherwise, and
is the predicted probability for class i.
3.6. Training CNN
Optimizing CNN architectures requires careful integration of effective layer configurations, regularization strategies, and efficient training processes to create models that perform well and generalize effectively. Regularization is a key component in this optimization process, addressing the challenge of overfitting and improving model robustness [
30]. Techniques like batch normalization stabilize the training process by normalizing the inputs within each layer, which minimizes the internal covariate shift that often slows down training. By maintaining a consistent input distribution, batch normalization allows for faster and more stable convergence and supports the use of higher learning rates, further accelerating the learning process. Dropout, another important regularization technique, reduces overfitting by randomly deactivating a percentage of neurons during each training iteration. This discourages the network from depending heavily on specific neurons, encouraging it to develop a more distributed, resilient representation of the data, especially within FC layers. Training CNN effectively also requires robust optimization algorithms alongside backpropagation which the processs of calculating the gradient of the loss function relative to each parameter. Optimizers such as Stochastic Gradient Descent (SGD) and adaptive methods like Adam and RMSprop are essential for efficiently updating weights and achieving convergence, as they balance learning rate adjustments and momentum to navigate complex parameter spaces effectively [
31].
4. Particle Swarm Optimization
PSO is a nature-inspired, population-based algorithm that simulates the collective behavior observed in groups of animals, such as flocks of birds, schools of fish, and insect swarms. Introduced by Eberhart and Kennedy in 1995 [
32,
33], PSO models how these groups coordinate to find resources, with each individual adjusting its movement by learning from both its own experience and the collective insights of the swarm. The algorithm has since evolved to address a wide range of complex optimization challenges. Researchers have developed numerous PSO variants and adaptations, targeting specific application needs and exploring different parameter settings, topology configurations, and multi-objective capabilities [
34]. This algorithm remains popular in engineering, machine learning, and other fields for its adaptability, efficiency in parallel computing, and quick convergence to optimal solutions. However, current research tends to emphasize application and enhancement, with foundational theoretical studies lacking, restricting its full potential.
In PSO, each particle within the swarm represents a possible solution, with its movement through the solution space governed by iterative updates to both its position and velocity. The particle’s velocity at each iteration reflects a balance between the particle’s own historical experience and the collective experience of the swarm. The velocity update for a particle at a given iteration is calculated by combining its current velocity with adjustments based on two influences: the particle’s best-known position, referred to as the personal best (pBest), and the best-known position found by any particle in the swarm, known as the global best (gBest). This velocity update can be expressed mathematically as:
Where
represents the inertia weight, which determines the influence of the particle’s prior velocity, encouraging continuity in its motion. The parameters
and
, often called the cognitive and social coefficients, control the particle’s tendency to be guided by its own previous successes (cognitive factor) or by the success of the swarm as a whole (social factor). Random variables
and
, uniformly distributed between 0 and 1, introduce stochasticity, allowing for a broader exploration of the solution space. After updating the velocity, the particle’s position is then recalculated by adding this velocity to its current position:
This process continues iteratively, with particles refining their search paths based on ongoing updates from both individual and collective feedback. This cycle repeats until a stopping condition, such as reaching an optimal solution threshold or achieving a predefined number of iterations, is satisfied.
5. Application of PSO to the Optimization of CNN Architecture
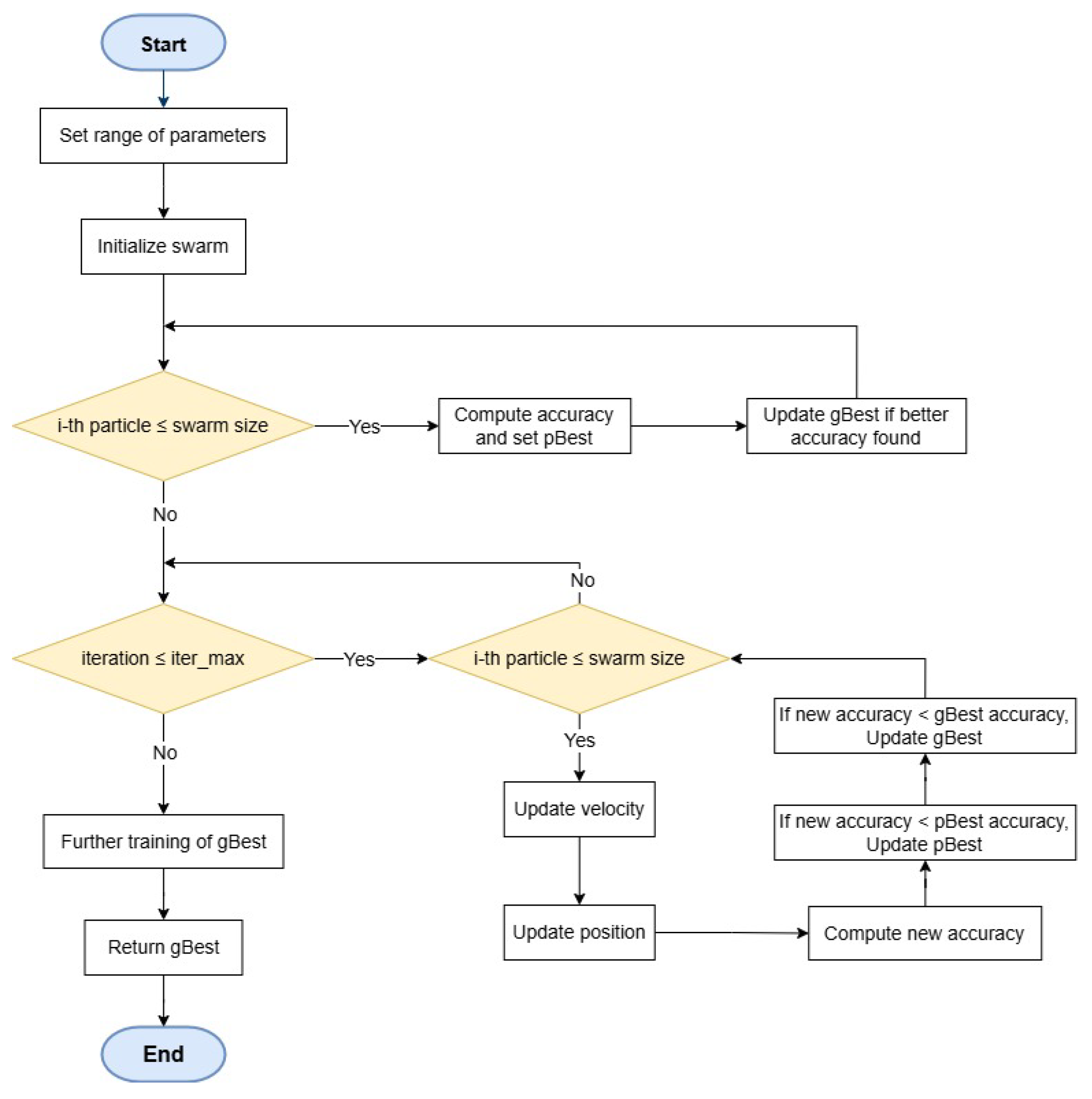
The core structure of the algorithm is illustrated in
Figure 3. This framework accepts input data related to the specific task, including the training dataset and hyperparameters for CNN architecture generation, such as the maximum allowable number of layers at initialization. The algorithm determines the global best particle (gBest) by using PSO to select the most effective layers within the swarm, eliminating the need for manual fine-tuning of each layer’s hyperparameters. This approach ensures that high-quality layers from prior generations are retained in the optimization process, rather than being reinitialized with every iteration. Although particles undergo reassessment during each iteration, well-performing layers are preserved, enabling valuable features to carry over from one generation to the next.
This algorithm adheres to the PSO structure and consists of six core steps: efficient CNN encoding, initializing the swarm, assessing each particle’s fitness, evaluating differences between particles, calculating velocities, and updating particles. The following sub-sections will describe these steps in more detail, emphasizing the initialization and fitness evaluation improvements that contribute to enhanced performance.
5.1. Particle-Based Encoding Scheme
One of the key challenges in adapting a PSO algorithm to identify optimal CNN architectures lies in designing an encoding strategy that enables effective velocity updates for each particle. In this encoding format, each particle directly represents CNN layers without the need for numerical transformation, using a straightforward structure. The encoding is organized as a list of lists, where each sub-list corresponds to one specific layer, with details on its hyperparameters. In this framework, convolutional and max pooling layers are integrated, treated as a single combined operation rather than independent layers. Each convolutional layer (C) is paired with a max pooling operation, consistently using a kernel size of 2×2 and a stride of 2×2. This ensures a simplified and uniform structure for layer encoding. The attributes for convolutional layers include the number of filters, filter size, and stride, while the pooling operation is implicitly applied as part of the convolutional layer. Fully connected (FC) layers are also represented in the encoding, specifying the number of neurons. Illustrated in
Figure 4, this encoding scheme constructs the CNN by interpreting each particle component sequentially from left to right, adding each layer as specified. Importantly, this encoding does not store weight values, so a brief retraining phase is required to compute the accuracy of each particle.
5.2. Initiating the Swarm
The swarm initialization process begins by generating N particles, where each particle represents a CNN architecture with a randomly configured set of layers. The architectures can have between three and a maximum number of layers, with the first layer always set to a C layer and the final layer to a FC layer. To preserve the structural integrity of the CNN, FC layers are restricted to the end of the architecture, avoiding their placement between C layers. The C layers are initialized with randomly selected numbers of kernels and kernel sizes, and every C layer is immediately followed by a max pooling layer with predefined window sizes and stride values. The FC layers at the end of the network are assigned a random number of neurons. All layers employ the ReLU as the activation function. To ensure functional CNN architectures, the process also manages the placement of pooling layers to avoid reducing the output dimensions below 7×7. Additionally, particles are initialized with a balanced structure, where approximately two-thirds of the layers are either convolutional or pooling layers, and one-third are fully connected layers, allowing for both effective feature extraction and classification capabilities.
5.3. Fitness Evaluation
In the fitness evaluation stage, each particle’s configuration is converted into a CNN model and trained for an initial number of epochs. The accuracy of each CNN is then evaluated on a validation set, aiming to identify the architecture with the highest performance. This process utilizes the Adam optimizer for efficient convergence, applies a dropout rate of 20% just before the final FC layer to prevent overfitting. Weight initialization follows the standard configuration in PyTorch [
35]. However, a significant bottleneck arises because every particle must be trained on the full dataset, making this evaluation phase time intensive. The algorithm is designed specifically to discover the most effective CNN architecture rather than focusing on fine-tuning its weights. Initially, each particle undergoes training for a preset number of epochs, and with each iteration, the training duration is increased by one epoch to refine accuracy measurements. For a comprehensive evaluation of the gBest obtained, a final retraining phase is conducted using an extended number of epochs to solidify the performance assessment.
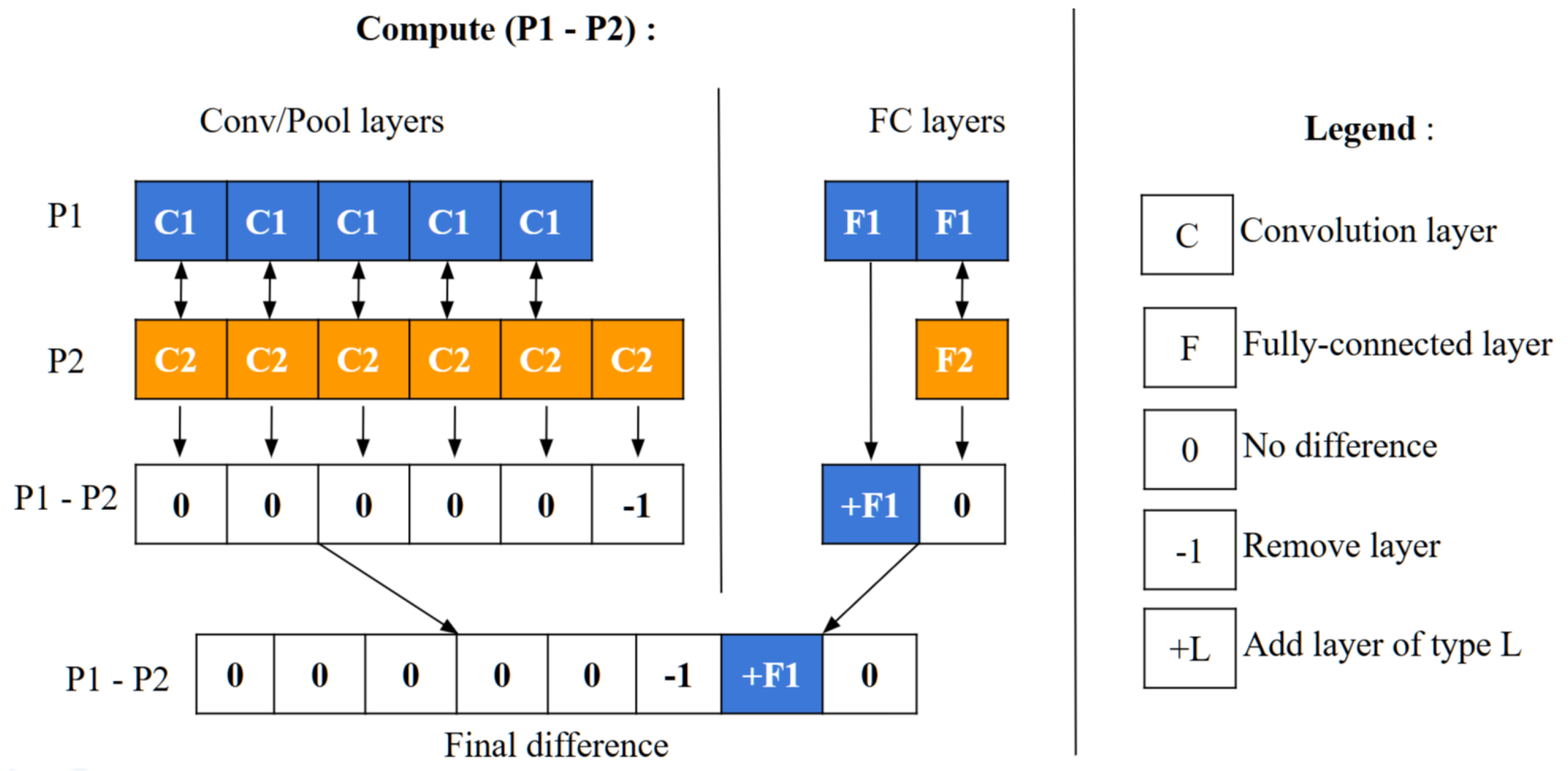
5.4. Calculation of Difference Between Particles
To compute a particle’s velocity and subsequently update its position, a specific operator is employed to measure the symbolic difference between two particles. This process, depicted in
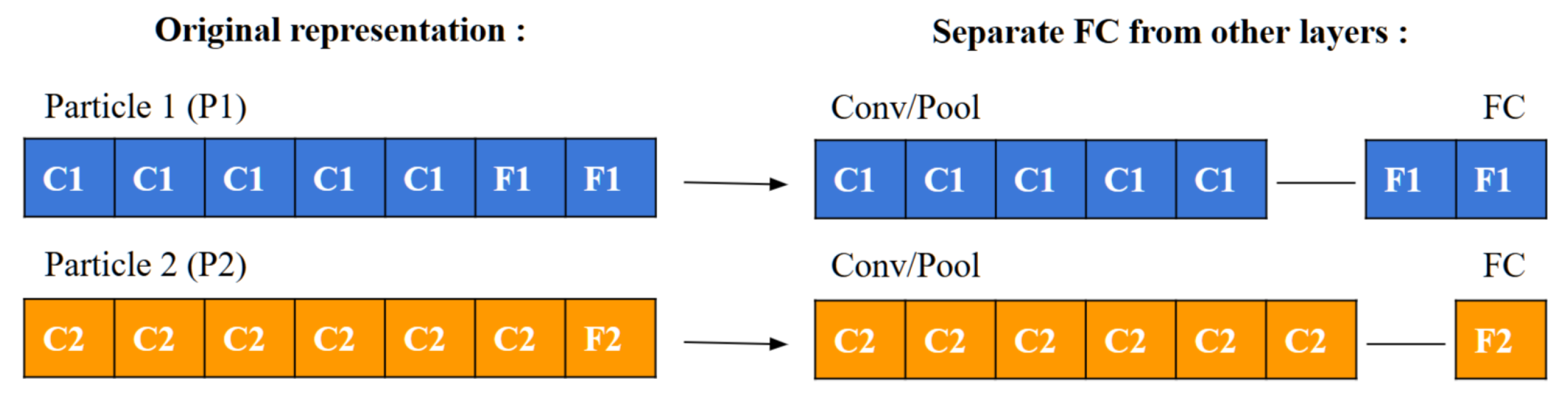
Figure 5, involves a detailed comparison between particles labeled as P1 and P2. Initially, the layers of each particle are separated into two categories: convolutional/pooling (C/P) layers and fully connected (FC) layers, as demonstrated in
Figure 6.
These two categories of layers are then assessed individually to identify any structural differences. The comparison is made relative to P1 by examining the C/P and FC layer groups independently. For C/P layers, differences are assessed from left to right, whereas for FC layers, the comparison proceeds from right to left. If the layer types match between P1 and P2, the difference is zero. If they differ, the difference is determined by P1’s layer type. When P1 contains fewer layers than P2, a difference of -1 is assigned, suggesting the removal of a layer from P2. Conversely, if P1 has more layers, a difference of +L is indicated, where L represents P1’s layer type, suggesting the addition of a layer to P2.
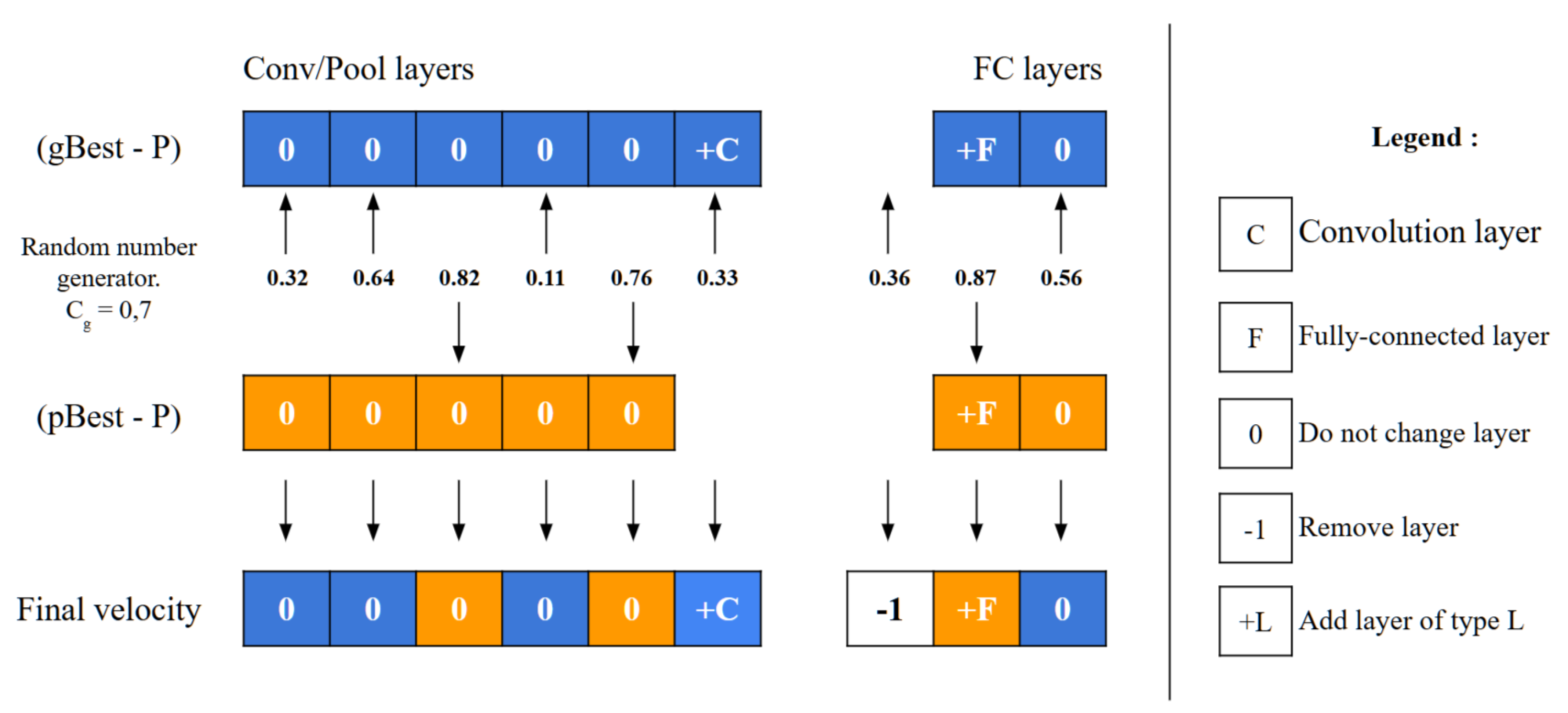
5.5. Particle Velocity Calculation
The velocity operator calculates two main differences: (gBest-P) and (pBest-P). To decide which difference to apply to each layer, the operator employs a threshold value,
along with a random number generator. For each layer, it compares the random number to
; if the number is below
, the layer difference from (gBest-P) is chosen, whereas if the number is above
, the layer difference from (pBest-P) is selected instead, as depicted in
Figure 7. This decision process repeats for every layer, allowing
to control the particle’s resemblance to either gBest or pBest. As
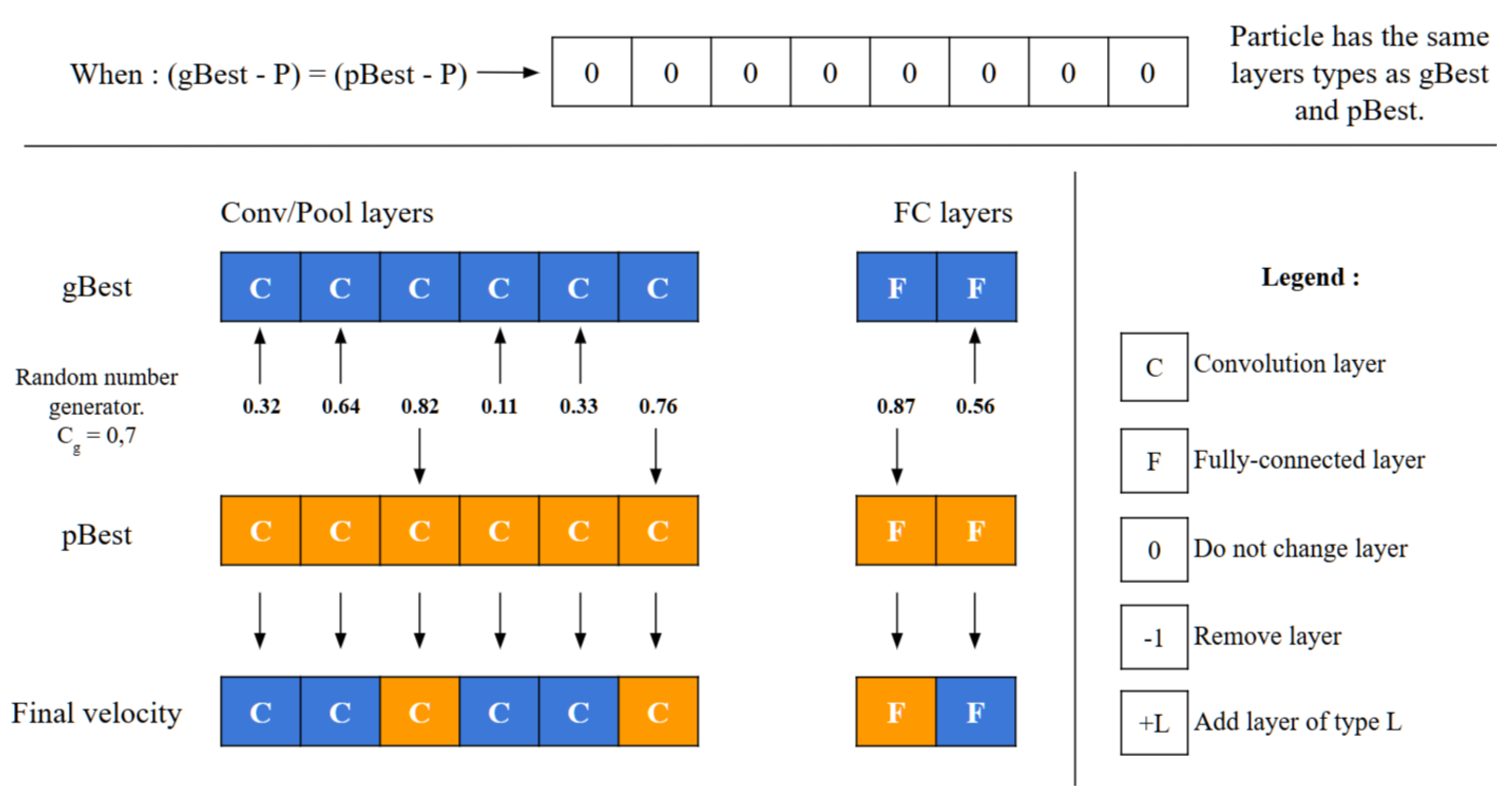
approaches 1, the particle’s structure aligns more closely with gBest. A unique scenario arises during the final iterations if (gBest-P) equals (pBest-P). In this, the operator decides between adopting gBest or pBest directly, based on the value of
, as shown in
Figure 8.
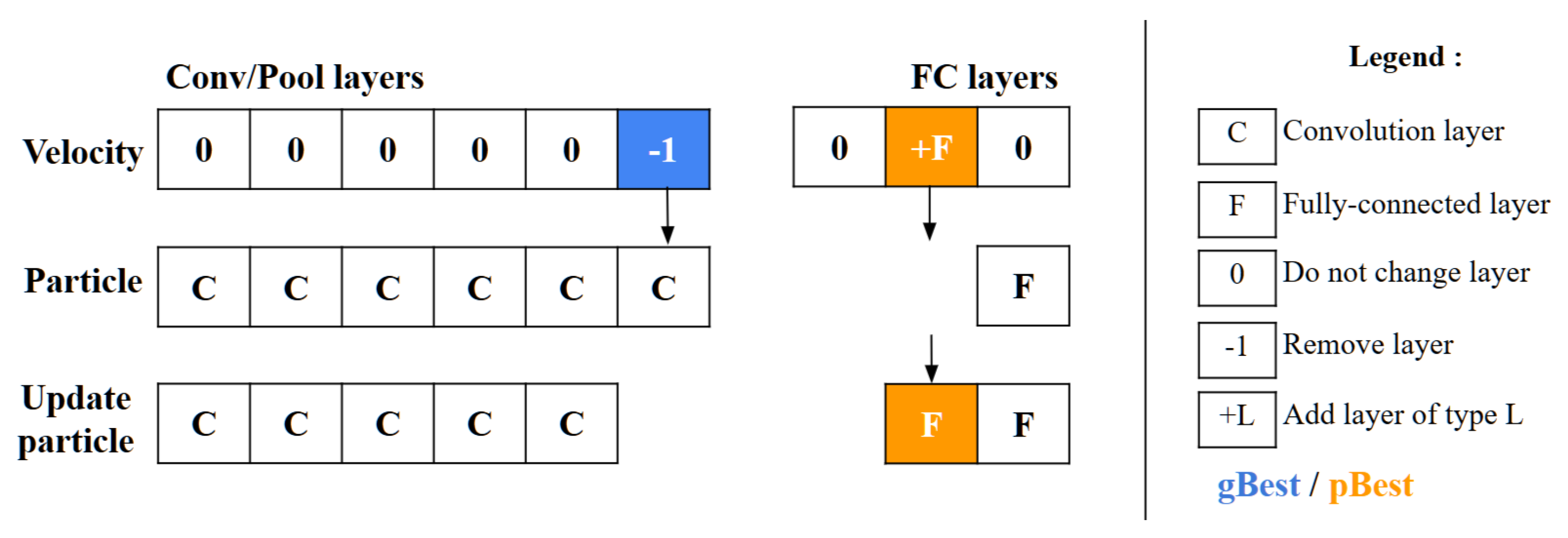
5.6. Particle Position Adjustment
After calculating a particle’s velocity, the update particle operator is then applied to modify the particle’s configuration. This adjustment process, shown in
Figure 9 entails a comparison between the particle’s current velocity and its existing position. The operator handles the C/P and FC layer blocks individually, ensuring that updates are made only to the position components where velocity is non-zero. Through this mechanism, particles have the flexibility to evolve over time—either contracting by removing layers or expanding by adding layers to the particle’s architectural structure.
6. Experimental Results
6.1. Dataset
For this study, we utilized a publicly available MRI dataset from Kaggle [
36], comprising 7,023 brain MRI images sorted into four categories: glioma, meningioma, pituitary, and no tumor. This dataset integrates images from several sources, including figshare [
37], the SARTAJ dataset [
38], and Br35H [
39], with non-tumor images primarily sourced from Br35H.
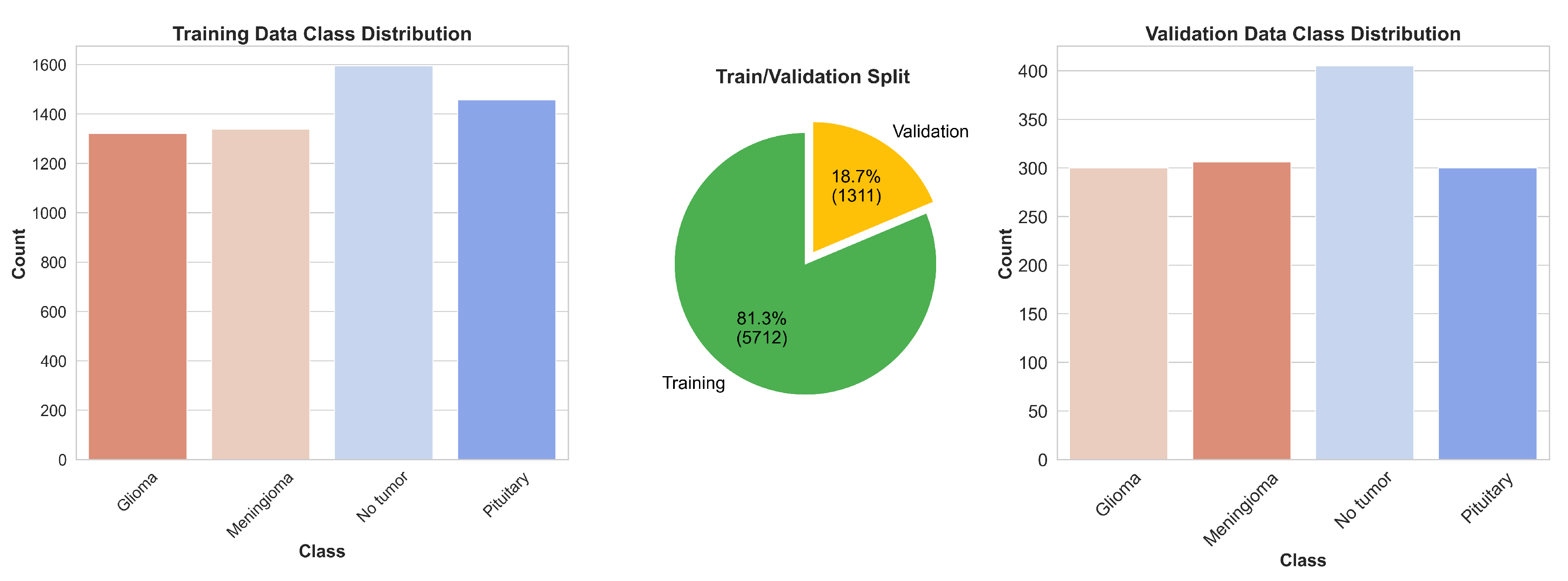
Figure 10 illustrates the distribution of these images across each category, while
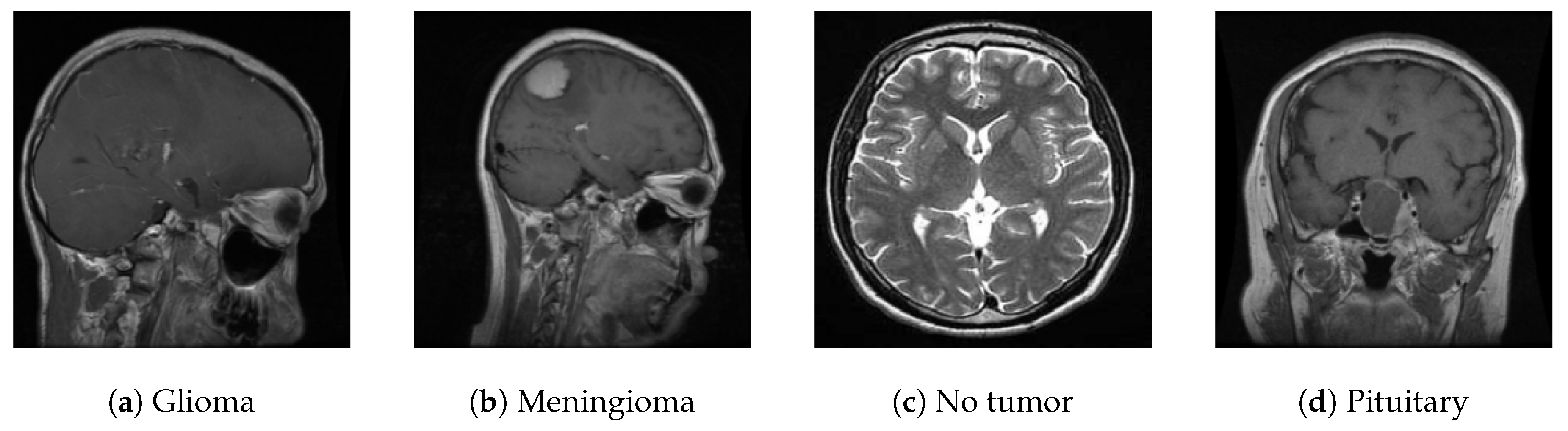
Figure 11 presents sample images from each class.
6.2. Algorithm Parameters
The parameters utilized in this study fall into three main categories: those associated with PSO configuration, those related to the initialization of CNN architectures and those governing the evaluation process for individual particles. The parameters specific to the PSO process, summarized in
Table 1, define essential aspects such as the termination criteria, the size of the swarm, and the rate (
) at which particles converge towards the global best (gBest). A larger swarm or increased iteration count improves the probability of achieving optimal solutions, albeit at a higher computational cost.
The CNN initialization parameters are presented in
Table 2. These parameters specify the range of configurations possible for the CNN architectures generated within the swarm. Each particle’s architecture is initialized by randomly selecting values within these predefined limits.
Finally, the parameters for particle evaluation and final best particle training are detailed in
Table 3. These parameters include the starting number of epochs used during the evaluation phase of individual particles and the extended training of the best-performing architecture after optimization concludes.
6.3. Results
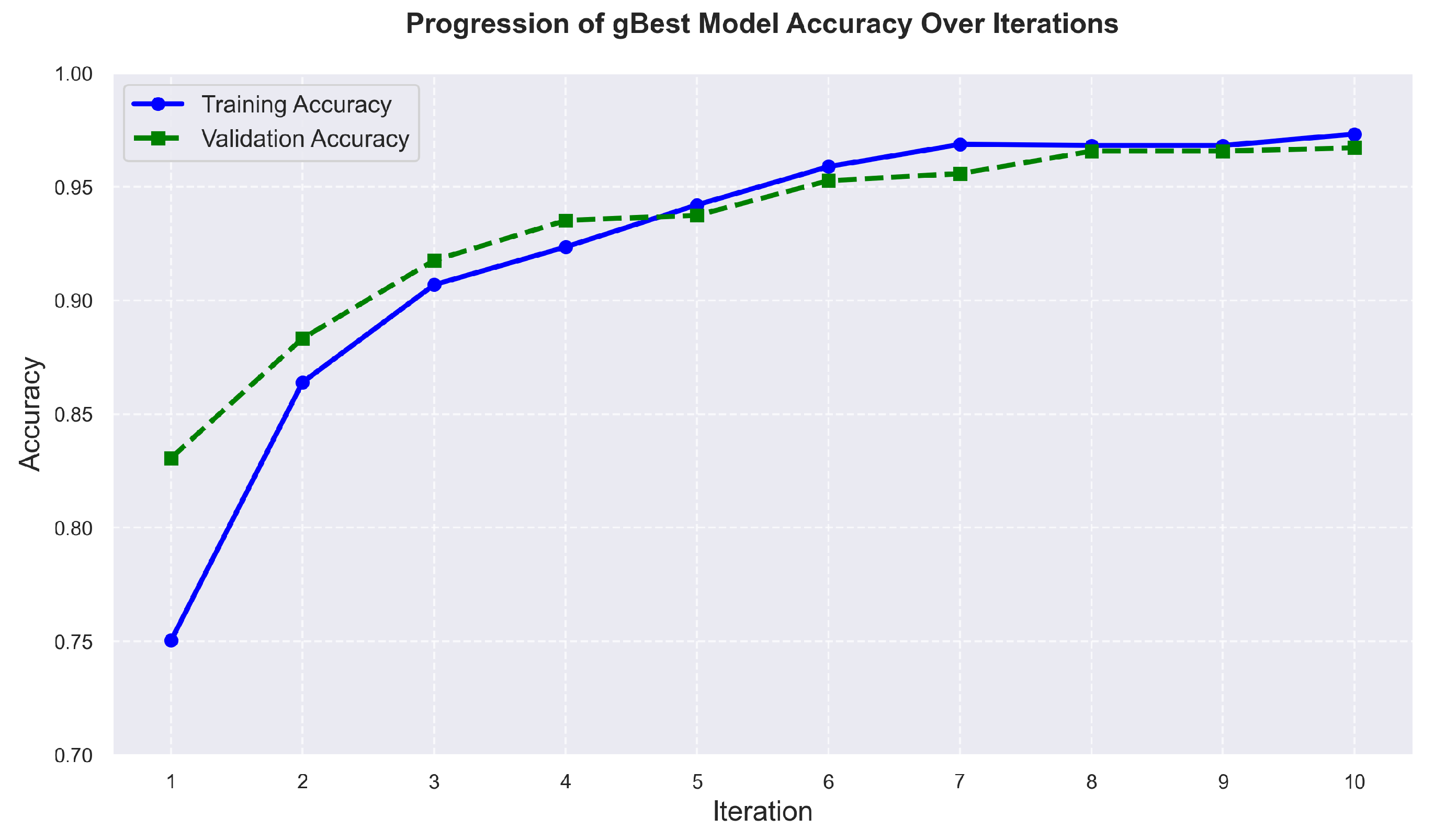
The algorithm’s results are presented in this sub-section, highlighting the progression of the gBest model’s accuracy over iterations. As shown in
Figure 12, the training accuracy increases from 75,04% in the initial iteration to 97,32% by the tenth iteration. Similarly, the validation accuracy improves from 83,07% to 96,72% over the same period. This progression reflects the algorithm’s effectiveness in exploring and optimizing architectural configurations. The architecture founded by the algorithm, detailed in
Table 4, utilizes a first convolutional layer with 5×5 kernels and a second layer with 3×3 kernels. This architecture comprises a total of 12,851,556 trainable parameters, enabling effective feature extraction and classification. The training process was carried out using a mini-batch of 32 images.
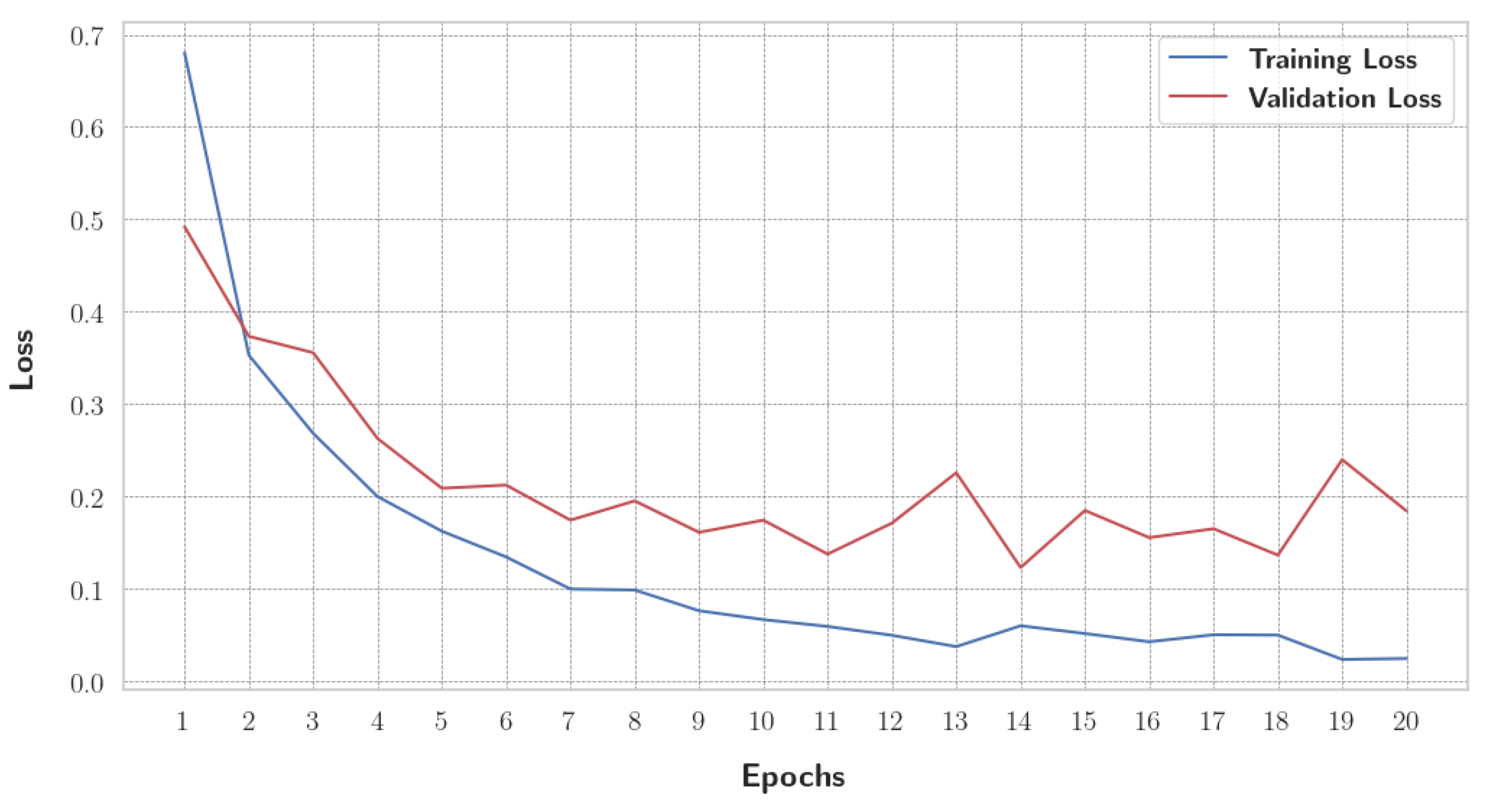
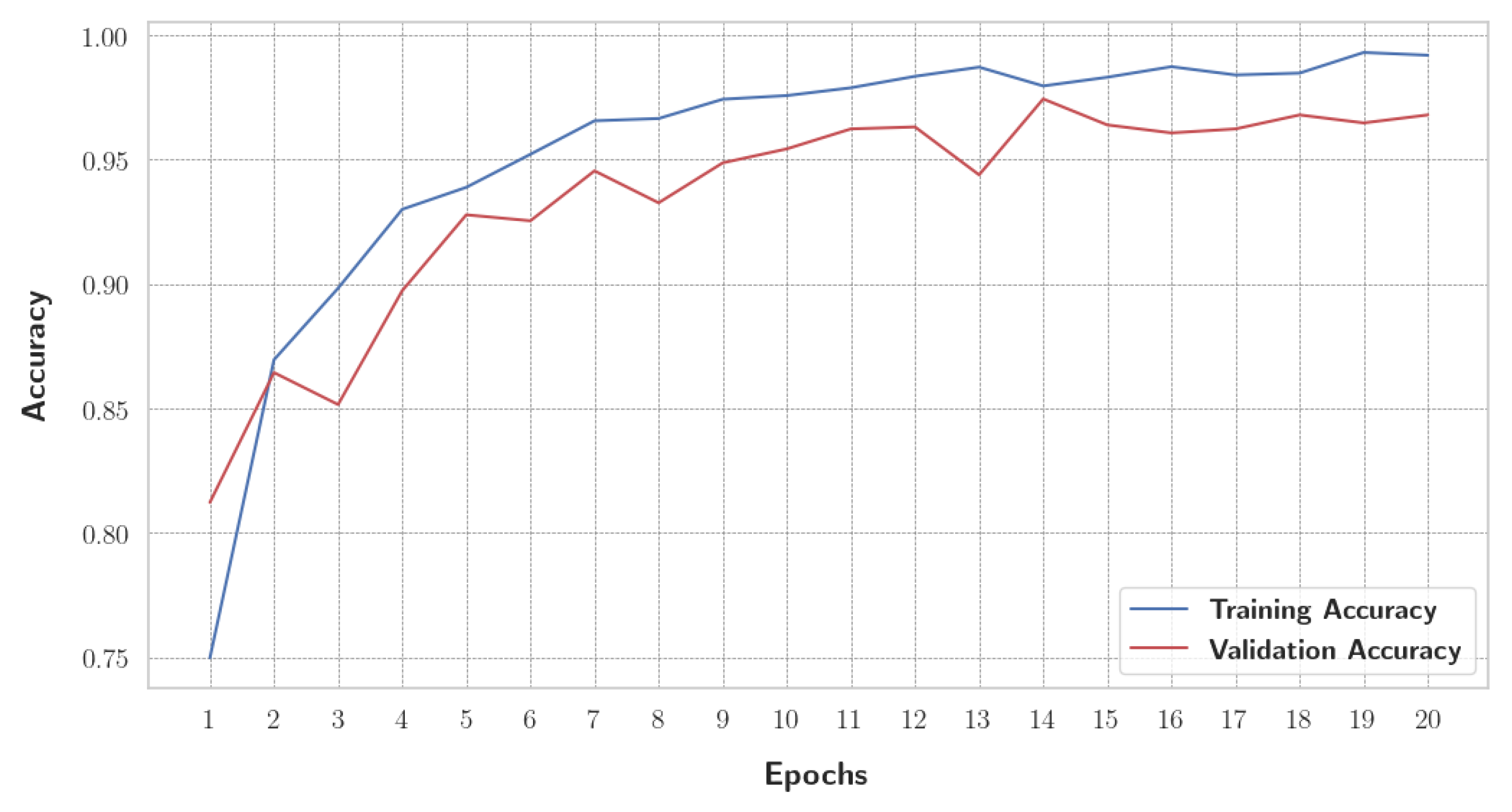
Before initiating the training of the final gBest particle, 5% of the dataset was set aside for testing and prediction purposes. This testing set was created by sampling 81.3% of the 5% from the training data and 18.7% from the validation data. This procedure ensured that the class distribution in the testing subset aligned with the original proportions of the training and validation data. The gBest particle model completed its training within 20 epochs. The training process resulted in a steady reduction in training loss, starting from 0.68 and decreasing to 0.024 by the final epoch. Correspondingly, the training accuracy improved from 74.97% at the beginning to 99.18% at the end. The validation loss exhibited an initial value of 0.492, fluctuating throughout the epochs, and concluded at 0.184. Similarly, the validation accuracy increased from 81.2% to 96.8%. These trends are illustrated in
Figure 13, which shows the progression of loss over the epochs, and
Figure 14, which displays the accuracy trends for both training and validation data.
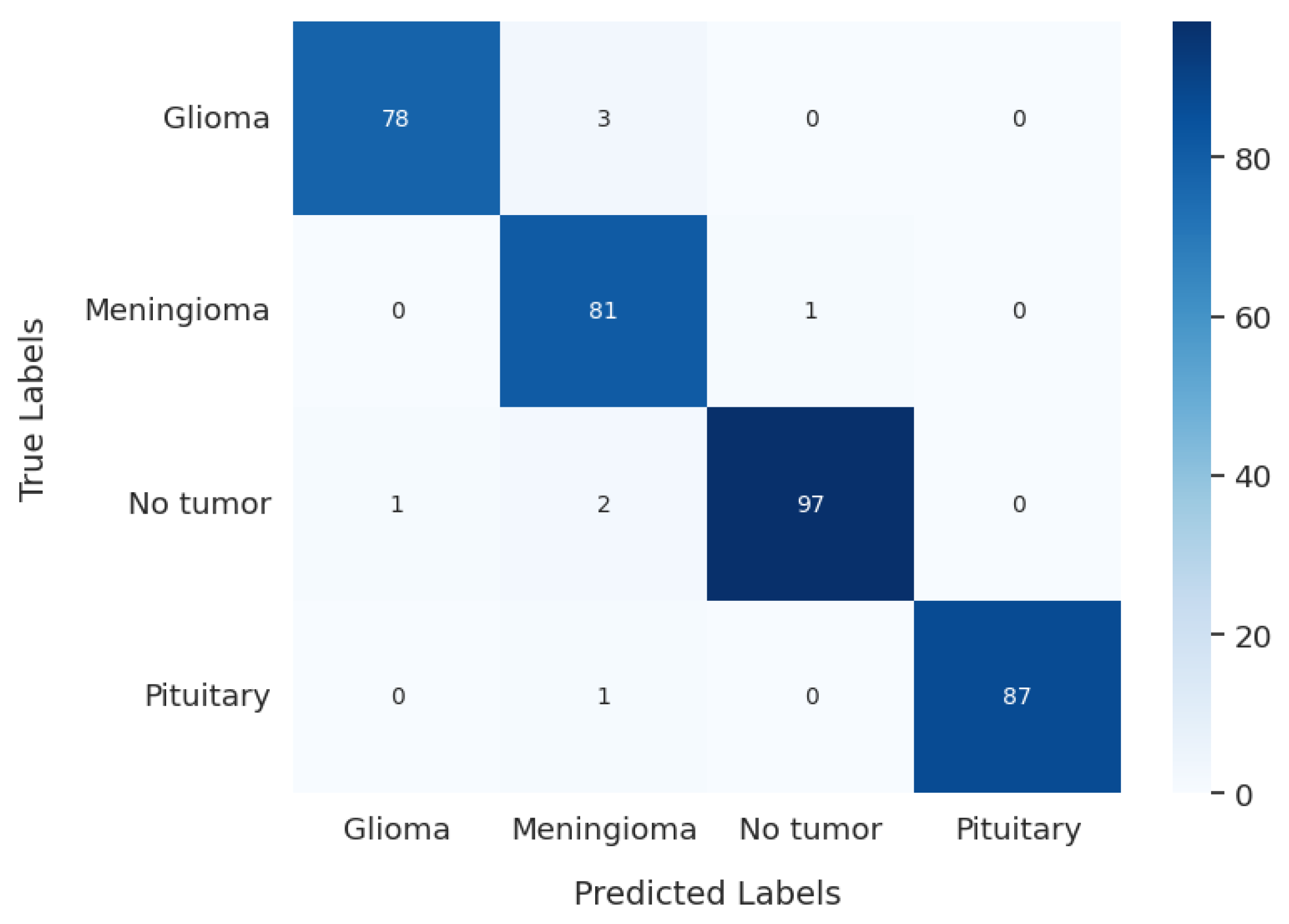
After training, the model was evaluated using the test data, yielding a test loss of 0.137 and a test accuracy of 97.72%. The model’s classification performance was further analyzed using a confusion matrix, presented in
Figure 15. The confusion matrix offers a comprehensive understanding of a model’s classification performance by illustrating the correspondence between actual and predicted labels. It emphasizes essential components of classification results and serves as the basis for evaluating metrics such as precision, recall, and F1 score, which are summarized in
Table 5 for each class.
6.4. Discussion
The gBest confusion matrix provides a detailed insight into the classification of different tumor types. For Glioma, the model correctly identified 78 cases, with 3 false negatives and 1 false positive, suggesting a strong ability to detect this type of tumor. Meningioma classification was slightly less precise, with 81 correct identifications, 1 false negative, and 6 false positives, indicating a minor trade-off in precision. The model excelled in identifying No Tumor cases, with 97 correct classifications, only 3 false negatives, and 1 false positive, reflecting its high reliability in this category. Pituitary tumor classification was nearly flawless, with 87 correct identifications and only 1 false negative.
The model’s performance metrics, including precision, recall, and F1 scores, demonstrate its robust capabilities. The Glioma classification exhibits high precision and recall, signifying a low rate of errors in identifying this tumor type. The Meningioma classification shows a high recall but slightly lower precision, suggesting the model effectively identifies most Meningiomas while producing a few additional false positives. The No Tumor classification boasts near-flawless precision and recall, underscoring the model’s robust ability to accurately detect the absence of tumors. The Pituitary tumor classification is virtually perfect, with 100% precision and high recall, indicating exceptional accuracy in this specific category. These results underscore the success of using PSO in searching for the optimal architecture, leading to a highly successful and generalizable model. This method proved to be efficient in identifying a well-suited configuration, thereby yielding acceptable performance in our context. The integration of automated optimization techniques not only streamlines the architecture selection process but also ensures that the model is tailored effectively to the task at hand.
Table 6 provides a comparative analysis of the classification performance with a related method that employs a genetic algorithm (GA) combined with CNN for MRI brain tumor classification [
19]. The proposed method consistently achieves higher accuracy across all tumor types. For glioma classification, the proposed approach achieves an accuracy outperforming the GA-based approach (
Table 6). Similarly, the accuracy for meningioma classification improves in the proposed approach. The most significant improvement is observed in pituitary tumor classification, where the proposed method exceeded the GA-based approach.
In addition to these performance improvements, independent trials and observations on the dataset revealed that the characteristics of MRI brain tumor images do not require overly complex models for effective classification. This insight prompted a reduction in the range of hyperparameters explored during the algorithm optimization process. By focusing on identifying simpler models, the proposed method was able to achieve a balance between complexity and performance, resulting in a model that not only outperformed the GA-based approach in terms of accuracy but also offered a streamlined design. This indicates that leveraging PSO for architecture optimization is an effective strategy for identifying optimal solutions with reduced complexity, particularly in cases where the image data does not demand intricate models for accurate classification.
7. Conclusions
The main findings of the present study indicate that PSO can successfully automate the CNN design process, achieving improved performance in classifying MRI images of brain tumors. These results suggest that PSO has potential applications in optimizing CNN architectures for various medical imaging tasks.
Nevertheless, the approach has certain limitations. The used algorithm relies on hyperparameters of the initialized architectures, which may restrict the exploration of alternative solutions. Addressing this limitation by incorporating mechanisms to adjust hyperparameters dynamically during optimization and adhering to established architectural conventions during initialization may improve the algorithm’s flexibility and performance.
Future research could build upon this study by incorporating additional computational resources to facilitate broader evaluations and testing on diverse datasets and tumor types to assess generalizability. Investigating hybrid optimization techniques that combine PSO with other algorithms could further enhance performance. Additionally, extending the PSO framework to optimize other neural network types, such as Recurrent Neural Networks (RNNs) or Long Short-Term Memory (LSTM) networks, may provide insights into its applicability beyond CNN architectures.
Author Contributions
Conceptualization, S.E.A. and Y.S.; methodology, S.E.A. and Y.S.; software, S.E.A. and Y.S.; validation, Y.F.; formal analysis, S.E.A. and Y.S.; investigation, S.E.A. and Y.S.; resources, Y.F. ; data curation, S.E.A. and Y.S.; writing—original draft preparation, Y.S. and S.E.A.; writing—review and editing, S.E.A. and Y.S.; visualization, S.E.A. and Y.S.; supervision, Y.F.; project administration, Y.F. and S.E.A.; funding acquisition, Y.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Conflicts of Interest
The authors declare no conflicts of interest.
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Pathak, K.; Pavthawala, M.; Patel, N.; Malek, D.; Shah, V.; Vaidya, B. Classification of Brain Tumor Using Convolutional Neural Network. In Proceedings of the 2019 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA); 2019; pp. 128–132. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.; Setio, A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.; van Ginneken, B.; Sánchez, C. A survey on deep learning in medical image analysis. Medical Image Analysis 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Adaji, P.O.; Mazadu, J.I. Image Segmentation and Object Detection for Automobile using OpenCV and CNN. Journal of Network and Information Security 2024, 12, 7–23. [Google Scholar]
- Singh, A.; Bhatt, S.; Nayak, V.; Shah, M. Automation of surveillance systems using deep learning and facial recognition. International Journal of System Assurance Engineering and Management 2023, 14, 236–245. [Google Scholar] [CrossRef]
- Gao, J.; Bambrah, C.; Parihar, N.; Kshirsagar, S.; Mallarapu, S.; Yu, H.; Wu, J.; Yang, Y. Analysis of Various Machine Learning Algorithms for Using Drone Images in Livestock Farms. Agriculture 2024, 14, 522. [Google Scholar] [CrossRef]
- Al-Galal, S.A.Y.; Alshaikhli, I.F.T.; Abdulrazzaq, M.; Hassan, R.; Abdulrazzaq, M.; Moustafa, H. Brain Tumor MRI Medical Images Classification Model Based on CNN (BTMIC-CNN). J. Eng. Sci. Technol 2022, 17, 4410–4432. [Google Scholar]
- Villanueva-Meyer, J.E.; Mabray, M.C.; Cha, S. Current clinical brain tumor imaging. Neurosurgery 2017, 81, 397–415. [Google Scholar] [CrossRef]
- Bauer, S.; Wiest, R.; Nolte, L.P.; Reyes, M. A survey of MRI-based medical image analysis for brain tumor studies. Physics in Medicine & Biology 2013, 58, R97. [Google Scholar]
- Lawrence, T.; Zhang, L.; Lim, C.P.; Phillips, E.J. Particle swarm optimization for automatically evolving convolutional neural networks for image classification. IEEE access 2021, 9, 14369–14386. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to evolutionary computing; Springer, 2015.
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Information sciences 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion wesley 1989, 1989, 36. [Google Scholar]
- Wang, B.; Sun, Y.; Xue, B.; Zhang, M. Evolving deep convolutional neural networks by variable-length particle swarm optimization for image classification. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC). IEEE; 2018; pp. 1–8. [Google Scholar]
- Nistor, S.C.; Czibula, G. IntelliSwAS: Optimizing deep neural network architectures using a particle swarm-based approach. Expert Systems with Applications 2022, 187, 115945. [Google Scholar] [CrossRef]
- Yuan, G.; Xue, B.; Zhang, M. An evolutionary neural architecture search method based on performance prediction and weight inheritance. Information Sciences 2024, 667, 120466. [Google Scholar] [CrossRef]
- Berrajaa, A.; Merras, M.; Berrajaa, I. Advanced CNN based on genetic algorithm to automated femoral neck fracture classification. Signal, Image and Video Processing 2024, pp. 1–10.
- Junior, F.E.F.; Yen, G.G. Particle swarm optimization of deep neural networks architectures for image classification. Swarm and Evolutionary Computation 2019, 49, 62–74. [Google Scholar] [CrossRef]
- Anaraki, A.K.; Ayati, M.; Kazemi, F. Magnetic resonance imaging-based brain tumor grades classification and grading via convolutional neural networks and genetic algorithms. biocybernetics and biomedical engineering 2019, 39, 63–74. [Google Scholar] [CrossRef]
- Celik, M.; Inik, O. Development of hybrid models based on deep learning and optimized machine learning algorithms for brain tumor Multi-Classification. Expert Systems with Applications 2024, 238, 122159. [Google Scholar] [CrossRef]
- Bansal, S.; Jadon, R.S.; Gupta, S.K. A Robust Hybrid Convolutional Network for Tumor Classification Using Brain MRI Image Datasets. International Journal of Advanced Computer Science and Applications 2024, 15. [Google Scholar] [CrossRef]
- Gómez-Guzmán, M.A.; Jiménez-Beristaín, L.; García-Guerrero, E.E.; López-Bonilla, O.R.; Tamayo-Perez, U.J.; Esqueda-Elizondo, J.J.; Palomino-Vizcaino, K.; Inzunza-González, E. Classifying Brain Tumors on Magnetic Resonance Imaging by Using Convolutional Neural Networks. Electronics 2023, 12. [Google Scholar] [CrossRef]
- Singh, G.; Chhabra, A.; Mittal, A. Evaluating Deep Learning Algorithms for MRI-Based Brain Tumor Classification. In Proceedings of the 2024 International Conference on Emerging Innovations and Advanced Computing (INNOCOMP). IEEE; 2024; pp. 428–434. [Google Scholar]
- LeCun, Y.; Bengio, Y.; et al. Convolutional networks for images, speech, and time series. The handbook of brain theory and neural networks 1995, 3361, 1995. [Google Scholar]
- Wu, J. Introduction to convolutional neural networks. National Key Lab for Novel Software Technology. Nanjing University. China 2017, 5, 495. [Google Scholar]
- O’Shea, K. An introduction to convolutional neural networks. arXiv preprint, arXiv:1511.08458 2015.
- Zafar, A.; Aamir, M.; Mohd Nawi, N.; Arshad, A.; Riaz, S.; Alruban, A.; Dutta, A.K.; Almotairi, S. A comparison of pooling methods for convolutional neural networks. Applied Sciences 2022, 12, 8643. [Google Scholar] [CrossRef]
- Hao, W.; Yizhou, W.; Yaqin, L.; Zhili, S. The role of activation function in CNN. In Proceedings of the 2020 2nd International Conference on Information Technology and Computer Application (ITCA). IEEE; 2020; pp. 429–432. [Google Scholar]
- Wang, Q.; Ma, Y.; Zhao, K.; Tian, Y. A comprehensive survey of loss functions in machine learning. Annals of Data Science 2020, pp. 1–26.
- Moradi, R.; Berangi, R.; Minaei, B. A survey of regularization strategies for deep models. Artificial Intelligence Review 2020, 53, 3947–3986. [Google Scholar] [CrossRef]
- Goodfellow, I. Deep learning; MIT press, 2016.
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the Proceedings of the IEEE international conference on neural networks. Citeseer, 1995, Vol. 4, pp. 1942–1948.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95-international conference on neural networks. ieee, 1995, Vol. 4, pp. 1942–1948.
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: an overview. Soft computing 2018, 22, 387–408. [Google Scholar] [CrossRef]
- PyTorch. PyTorch Documentation: Default Weights Initialization. https://pytorch.org/docs/stable/nn.init.html.
- Nickparvar, M. Brain Tumor MRI Dataset, Kaggle, 2021. [CrossRef]
- Cheng, J. brain tumor dataset, 2017. [CrossRef]
- Bhuvaji, S.; Kadam, A.; Bhumkar, P.; Dedge, S.; Kanchan, S. Brain Tumor Classification (MRI), Kaggle, 2020. [CrossRef]
- Hamada, A. Br35H :: Brain Tumor Detection, Kaggle, 2020.
Figure 1.
Architecture of a CNN.
Figure 1.
Architecture of a CNN.
Figure 2.
Convolution operation.
Figure 2.
Convolution operation.
Figure 3.
Algorithm Flowchart.
Figure 3.
Algorithm Flowchart.
Figure 4.
Particle-based encoding scheme.
Figure 4.
Particle-based encoding scheme.
Figure 5.
Calculation of the difference between two particles.
Figure 5.
Calculation of the difference between two particles.
Figure 6.
Separating FC layers from other layers.
Figure 6.
Separating FC layers from other layers.
Figure 7.
Velocity calculation of a single particle.
Figure 7.
Velocity calculation of a single particle.
Figure 8.
Particle velocity calculation when gBest and pBest are the same.
Figure 8.
Particle velocity calculation when gBest and pBest are the same.
Figure 9.
Updating the architecture of a particle.
Figure 9.
Updating the architecture of a particle.
Figure 10.
Data distribution.
Figure 10.
Data distribution.
Figure 11.
Samples from the dataset.
Figure 11.
Samples from the dataset.
Figure 12.
Progression of the gBest model’s accuracy through iterations.
Figure 12.
Progression of the gBest model’s accuracy through iterations.
Figure 13.
Progression of gBest training and test loss.
Figure 13.
Progression of gBest training and test loss.
Figure 14.
Progression of gBest training and test accuracy.
Figure 14.
Progression of gBest training and test accuracy.
Figure 15.
The gBest confusion matrix.
Figure 15.
The gBest confusion matrix.
Table 1.
PSO Parameters.
| Description |
Value |
| Number of iterations |
10 |
| Swarm size |
15 |
|
0.5 |
Table 2.
CNN Architecture Initialization Parameters.
Table 2.
CNN Architecture Initialization Parameters.
| Description |
Value |
| Max number of filters |
40 |
| Max filter size |
|
| Max neurons in FC layer |
140 |
| Max number of layers |
9 |
Table 3.
Particle Training Parameters.
Table 3.
Particle Training Parameters.
| Description |
Value |
| Starting epochs for particle evaluation |
1 |
| Epochs for final best particle training |
40 |
Table 4.
The optimal CNN architecture identified through the algorithm.
Table 4.
The optimal CNN architecture identified through the algorithm.
| Layer (Type) |
Output Shape |
Param # |
| ZeroPad2d-1 |
[32, 3, 228, 228] |
0 |
| Conv2d-2 |
[32, 16, 224, 224] |
1,216 |
| ReLU-3 |
[32, 16, 224, 224] |
0 |
| MaxPool2d-4 |
[32, 16, 112, 112] |
0 |
| ZeroPad2d-5 |
[32, 16, 114, 114] |
0 |
| Conv2d-6 |
[32, 32, 112, 112] |
4,640 |
| ReLU-7 |
[32, 32, 112, 112] |
0 |
| MaxPool2d-8 |
[32, 32, 56, 56] |
0 |
| Linear-9 |
[32, 128] |
12,845,184 |
| ReLU-10 |
[32, 128] |
0 |
| Dropout-11 |
[32, 128] |
0 |
| Linear-12 |
[32, 4] |
516 |
Table 5.
Evaluation metrics calculated from the confusion matrix for each class.
Table 5.
Evaluation metrics calculated from the confusion matrix for each class.
| Class |
TP |
FP |
FN |
TN |
Precision |
Recall |
F1 Score |
Accuracy |
| Glioma |
78 |
1 |
3 |
269 |
0.9873 |
0.9629 |
0.9750 |
0.9886 |
| Meningioma |
81 |
6 |
1 |
263 |
0.9310 |
0.9878 |
0.9585 |
0.9800 |
| No Tumor |
97 |
1 |
3 |
250 |
0.9897 |
0.9700 |
0.9798 |
0.9886 |
| Pituitary |
87 |
0 |
1 |
263 |
1.0000 |
0.9886 |
0.9943 |
0.9971 |
Table 6.
Comparison of Test Classification Accuracy: PSO-Optimized versus GA-Optimized Approaches.
Table 6.
Comparison of Test Classification Accuracy: PSO-Optimized versus GA-Optimized Approaches.
| Approach |
Class |
Accuracy |
| GA + CNN [19] |
Glioma |
0.965 |
| |
Meningioma |
0.945 |
| |
Pituitary |
0.974 |
| Proposed Method |
Glioma |
0.9886 |
| |
Meningioma |
0.980 |
| |
Pituitary |
0.9971 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).