Effectiveness of Self-Learning Module Developed on the Enhancement of Student’ Academic Performance in Basic Calculus Amidst COVID-19

Cherry Rose Malgapo

doi:10.20944/preprints202412.2255.v1

Submitted:

25 December 2024

Posted:

26 December 2024

You are already at the latest version

Part of the Following Collection

Preprints on COVID-19 and SARS-CoV-2

Abstract

Self-learning Modules plays a vital role in the development of student progress wherein the necessary knowledge, theory, concept and formulas where written and explained. The researcher aimed to the determine the effectiveness of personally developed self-learning module on the enhancement of students’ academic performance in accordance to the compliance standards by the Department of Education on guidelines in the evaluation of layout and design of DepEd-developed ADM modules. The researcher used the descriptive and experimental type of research to collect and analyze data using one-shot pre-test and post-test in two groups of student-participants - control and experimental. The participants were purposively selected and group using matching technique based on their previous grade in Pre-Calculus. With regards to the findings of the study, the pretest scores of the two groups of student-participants in Basic Calculus were evidently shows almost the same. Whereas, the posttest scores revealed that the average posttest weighted mean scores of three sets of posttests on the same competencies, experimental group have an outstanding performance while controlled group have performed very satisfactory. The findings imply that those in experimental group were improved their posttest scores compare to those in controlled group. The findings concluded that the used of developed self-learning module in Basic Calculus helped student-participants in experimental group to have a better improved academic performance.

Keywords:

Academic Performance

;

Basic Calculus

;

Effectiveness

;

Self –Developed Learning Module

Subject:

Computer Science and Mathematics - Mathematics

Introduction

Self-learning Modules plays a vital role in the development of student progress wherein the necessary knowledge, theory, concept and formulas where written and explained. As teachers we always wanted the best for our dear students to ensure learning in the safest and easiest ways amidst COVID-19 pandemic. Development of self-learning modules is one of the important factors to ensure that learners achieve specific goals or educational outcomes reflected in the curriculum in easiest way or suitable for different individuals.

Not all learning materials like books are available in bookstores and in online library even in DepEd learning resources portal. Despite that there are available and provided Self-Learning Modules (SLMs) by the Department, but still there is huge factors affecting the learning development of the students such that the available SLMs/module are not suited to the learning individual differences, environment settings and localized diversity of learning.

Some students were getting bored and experiences difficulties in understanding the content knowledge and pedagogy, course design, complexity of activities and exercises and many more that really affects to their academic performance.

And we all know that Basic Calculus is one the subjects in Senior High School particularly in grade 11 Science and Technology, Engineering and Mathematics (STEM) that needs to be focus on to learning the competencies and to achieve learning goals of each lesson/ topics. This includes basic concepts of limit and continuity of a function, basic concepts of derivations, and anti-derivatives and Rieman Intergral.

This subject need to have mastery of the lessons because it has a big role for their future courses and career they want to be in their tertiary level. Thus, the basic knowledge they gained will help them to enlighten their mind and knowledge in future as to boost their analytical, problem solving and higher order thinking skills.

As teacher, for almost four years in Senior High School, even in face-to-face learning students experience challenges and difficulties to learn the subject, so how much more this trying times of COVID-19 pandemic. We cannot say there is a lot of learning resources available to help learners to achieved mastery of the subject matter. Teachers plays a more powerful role to identify his/her students’ need so he/she need to be more careful, creative and innovative in helping our students in consideration for their strength and weakness to learn the lesson/ topics in Basic Calculus.

With all this challenges and difficulties facing by the students, teachers will always find different appropriate and alternative ways on how the learning progress of the students will continue to better academic performance in satisfaction to the diversity of learning. Some teachers are developed their teaching instructional materials, activity sheets, exercises in the most simple and easiest way achieve learning goals and competencies and to help learners in their greater capabilities to learn in the context of distance learning amidst COVID-19. And are adopted others work but the teachers itself is one what his/her learners needs to cope up and continuously to learn at their own paced.

One of the important educational innovations is the development of self-learning materials that suited to the individual differences and help provide variations of ways and strategies to make easy and comfortable toward teaching and learning process especially in this trying time of pandemic, that can be a great use. It consists of pretest, introductory concepts, exercises, activities, chapter quiz, chapter summary and reflections in easy, simplified and understandable manner to catch the interest of the learners and improve their critical and problem solving and academic performance. Basically, the principles of learning modules involve the DepEd Most Essential Learning Competencies (MELCs) into limited units or chapters for the learners building up learning.

Onyedikachi (2011) as cited in the study of Oden (n.d), teaching without tools is impossible to attain the teaching and learning goals and competency. The instructional tools spice up the teaching and learning process to make possible on better understanding and make students learn from themselves.

In line with this, the proponent proposed the use of developed self-learning module in Basic Calculus that will be use as their learning materials wherein all activities and discussion of the topics aligned to curriculum guide in more simplest form in order to motivate the students to learn and enhance their academic performance. The study also seeks answer to the determine the effectiveness of personally developed self-learning module in terms of physical attributes, design and layouts, typographical organization and visuals in accordance to the compliance standards by the Department of Education on guidelines in the evaluation of layout and design of DepEd-developed ADM modules.

Review of the Related Literature

According to Portana et.al (2021), the developed instructional materials can be classified as primary and secondary aids and outlines used in effective teaching and learning. Hence, it is the ability of the teachers to identify the quality and appropriateness upon utilizing the developed instruction materials. And on students’ part, instructional materials may guide them to acquire more information so as to bring the learners much appreciation on the topics under consideration.

Additionally, Malgapo (2021), revealed in her study the scores of the same sets of student-participants in the same competencies were evidently improving using developed instructional module in Physics. The post-test of the same groups had f-value of 14.976 with significant value of .000 and interpreted as “Significant”. The students can easily understand the topics in the personally developed instructional module than other available instructional materials in Physics. She concluded that personally developed instructional module in Physics is “very effective” for the students to have a better understanding on the lessons/topics. The students can easily finish the learning task provided in the module.

Jogan (2016), confirmed self-learning modules give the opportunity to develop a good work ethics. The knowledge through Self Learning Modules also helps to inculcate self-study habits and self-confidence among students which are very much essential to enhance learning.

According to the study conducted by Torrefranca, E.C. (2017) the findings brought about implications for both theory and practice regarding the usefulness of modules in classroom instruction and the teacher devising the modules.

The integration of SLMs with the alternative learning delivery modalities (modular, television-based, radio-based instruction, blended and online) will help DepED ensure learners have access to quality basic education with face-to-face classes is still prohibited due to public health situation, (Department of Education, 2020).

Furthermore, instructional tools like developed materials is one of the tools that can help teachers convey knowledge in a very natural way leading to good teaching and learning process (Koko, 2016).

Moreover, Onasanwa and Omosewo (2011), discussed instructional materials as a key component that may use in teaching and learning process that can disseminate information, data, ideas and messages that could help learners enhance their academic achievements.

Self-learning modules may prove to be a boon for students due to enrich features. SLMs also can perform the role of teacher, making the students become independent thinkers or learn at their own-paced. They gain free to learn without any restriction (Kanchan, 2016).

As cited in the study of Tety (2016), instructional materials have been observed as a powerful strategy to bring about effective teaching and learning. It can be used to make learning more interesting and memorable, which can have positive effects on students’ academic performance.

Instructional materials are preeminent factors toward academic performance. It is a remarkable for teacher to develop instructional materials to guide the students to improve their academic achievement and also to designed materials to enrich students learning (Quisumbing,2017).

Synthesis of Review of Related Literature

Based on the review of related literature and studies Portana et.al (2021); Malgapo (2021), Jogan (2016); Torrefranca, E.C. (2017); (Department of Education, 2020); and Koko (2015), confirmed that self-learning module are leading to better teaching and learning process while other studies of can help students’ academic achievement, Kanchan, (2016).

Quisumbing,2017; Tety (2016); Onasanwa and Omosewo (2011), discussed that SLMs help the students to improve their academic performance and enhance students’ learning.

The reviewed literatures and studies are similar the current study based on the effects of personally developed SLMs. On other hand some factors are dissimilar in terms of the contributing factors and parameters in the personally developed self-learning module to help students’ improved academic performance based on the DepEd ADM guidelines and standards wherein the researcher push through to conduct the study and also to determine the effectiveness on the enhancement of learners’ academic achievement in Basic Calculus.

Conceptual Framework

The conceptual framework of the study was anchored on the utilization of self-develop learning module in Basic Calculus. The self-developed learning module in Basic Calculus was designed to cater the learning needs of the learners for additional learning resources and references in more easy, simple, fun motivating and engaging activities that suited to the individual learning difference during distance learning modality. The self-learning modules has complete inclusion from the discussion of terms and concepts, illustration of examples, activities and exercises, reminders, summary and reflections. According to Gagne (2005), instructional materials is the direct link between the materials that the teachers use, and the students’ learning outcomes. These outcomes include higher abilities to learn, quality strategies to learn and active participation and positive attitude towards learning. Further, the theory assume that instructional materials have the capacity to development into students the highest order of intellectual skills as they illustrate clearly, step by step ho to follow rules/principles and elaborate on the concepts, which have positive impact to solving new problems by analyzing the situations and formulating a plan. Moreover, instructional materials can be used to developed higher learning abilities to the learners through self-teaching or guided learning that implies to mainly comprise eliciting performance and proving feedback on performance correctness.

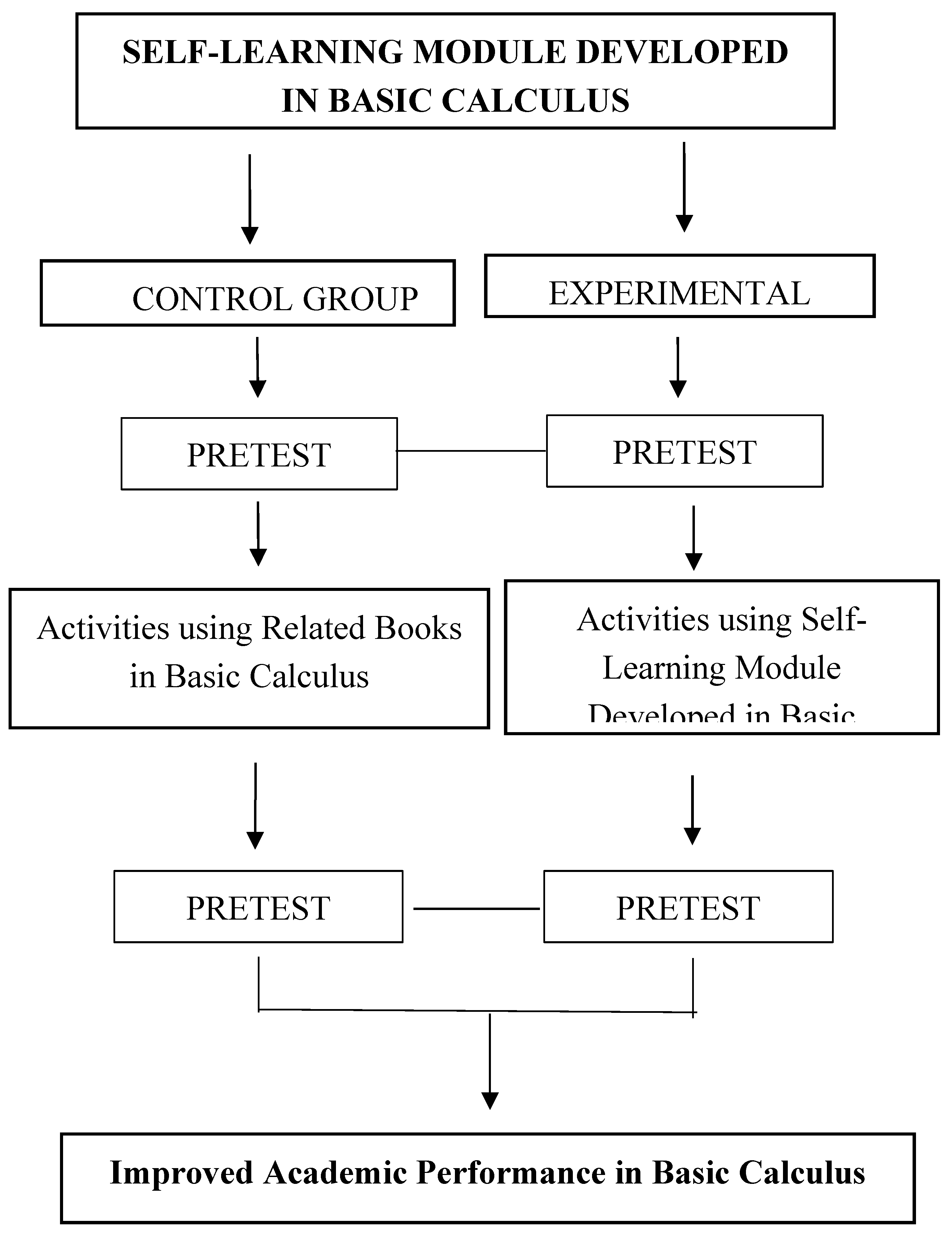
Guided with the conceptual framework of the study Figure 1 shows the flow and concepts. At the top is the self-learning module developed in Basic Calculus. The two groups of participants/respondents will be taken same set of pre-test in each topic in the above mentioned subject. After the pre-test they will be using different learning materials, the controlled group will be use available or provided learning materials by DepED while experimental group will be use developed self-learning module by the proponent herself teaching Basic Calculus. Thirdly, the learner will take the posttest to test the learning progress of the two groups of respondents with the used of different learning tools. Fourth, the after completion of the learning competencies of the subject, a survey questionnaire will also give to experimental group only to rate their experiences and challenges facing during the used of developed self-learning module in Basic Calculus. And finally, all data gathered will be tested, analyze and organize using statistical tools or SPSS data analysis to determine the effectiveness towards students’ academic performance.

Research Questions

The following questions are the main focused of the study entitled “Effectiveness of Self-Learning Module developed in Basic Calculus”, would determine:

How may the present status of the students in Basic Calculus?
How may the pretest in Basic Calculus of Control group and Experimental group be described?
How may the posttest in Basic Calculus Control group and Experimental group be described?
Is there a significant difference between the result of the pretest of Control group and Experimental group?
Is there a significant difference between the result of the post test of Control group and Experimental group?
What action plan may propose based on the findings of the study?

Hypotheses

This study tested the hypothesis below:

There is no significant difference between the result of the pretest of Control group and Experimental group.
There is no significant difference between the result of the post test of Control group and Experimental group.

Significance of the Study

The main objective of this study was to determine the effectiveness of the self-learning module developed in Basic Calculus on the enhancement of students’ academic performance particularly grade 11 STEM students at Aliaga National High School.

The study was significant to the following:

Students. The findings of this study helped the students in mastery of basic concepts and helped them to improved scholastic performance in Basic Calculus in more safe, simple and easiest way at their own paced.

Teachers. The findings of the study served as motivation to teachers to continuously develop self-learning module in teaching as to help diverse teaching strategies and motivation to help satisfied individual differences and enhance students’ academic performance.

Administrators. The findings of the study helped the administrators in policy making in developing and using the self-learning modules in teaching.

Department of Education. The findings may help to realize the positive sides of developing self-learning materials as to satisfy the needs of locality especially the students as the benefactor.

Scope and Limitation

The scope of the study was limited to the use of self-learning module developed in Basic Calculus based on DepEd MELCs and the used of other available learning materials to test the effectiveness on the enhancement of students’ academic performance. The module covered and was limited to the introductory concepts, sample activity, exercises, pre-test and posttest to measure the effectiveness as to improve students’ academic performance. The pretest and posttest were the main instruments and tools to gather the needed data and could be used to measure the differences in academic performance between controlled and experimental group.

The sample respondents of the study are limited to 50 grade 11 STEM students and since there is only one section of grade 11 STEM, the proponent decided to group into two using matching technique and each group was composed of 25 students each. The sample size of 25 each group were considered by the researcher so that biases in choosing respondent were eliminated. Since grade 11 STEM students are only one section and the only Strands/Tracks with Basic Calculus subject in the curriculum, the proponent used purposive sampling technique wherein all students in STEM are considered respondents of the study in accordance to satisfy the objectives of the study.

Furthermore, with the used of purposive sampling method, the researcher believed that this type of sampling method is based on own judgement, selective and subjective sampling. According to Alchemer (2021), purposive sampling is a form of non-probability sampling in which researchers rely on their own judgement when choosing members of the population to participate in the study.

All data collected and gathered, were statistically treated using data analysis such as frequency count, percentage and weighted mean.

METHODS

Type of Research

This study used the descriptive and experimental type of research to collect and analyze data using one-shot pre-test and post-test design in two groups-control and experimental for the student-participants. The developed self-learning module were the main tools used by the experimental groups while the control group was used DepEd learning resources or any related books in basic calculus.

Pre-test and post-test were conducted on each topic/lesson as indicated in the MELCs. Likewise, posttest of the two groups compared and analyzed to determine the effectiveness of the developed self-learning module in Basic Calculus.

According to Upen (2018), descriptive research and experimental research are used to facilitate to gain maximum outcomes. Descriptive research use in the study to investigate the effectiveness of developed self-learning module in Basic Calculus and the experimental part is to measure on the extent of developed self-learning module on the enhancement of students’ academic performance.

Participants

The respondents were composed of 50 Grade 11 STEM students at Aliaga National High School, Senior High School department for the S.Y. 2020-2021. These are the students under blended learning delivery modality in Science, Technology, Engineering and Mathematics (STEM) strand. The 50 respondents were group into two and composed of 25 students in each group -controlled and experimental groups. The selection of the respondents in groupings were based on their previous grade in Pre-Calculus using matching technique. The students-participants were selected because they were the only strand had the subject of Basic Calculus. Table 1 shows the respondents of the study.

In the controlled all lessons about Basic Calculus were delivered based on available learning materials coming from DepEd or any related learning resources wherein Experimental groups lessons were delivered using the personally developed self-learning module in Basic Calculus.

Sampling Technique

The respondents of the study are chosen using purposive sampling technique in order to determine the effectiveness of self-learning module developed on the enhancement of students’ academic performance in Basic Calculus amidst COVID-19 and to satisfy the objectives of the study. The researcher decided to utilized purposive sampling because this sampling method is a non-probability sampling wherein the researcher had her own judgement on selecting the participants in appropriate to the objective of the study. The respondents are the 50 grade 11 STEM students for the S.Y. 2020-2021 and were group into two-controlled and experimental. The selection of the respondents, the proponent used matching technique based on their previous grade in Pre-Calculus. All students who have matched in their grade are considered the respondents of the study.

Instrumentations

The instrument used in the study were the pretest, posttest and self-learning module developed personally made by the proponent based on the most learning competencies (MELCs) in Basic Calculus. The pretest is design to test the prior knowledge of the student-participants regarding the topic/lesson while the posttest is design to measure the mastery on the lessons/topics of the student-respondents. The pre-test and posttest were composed of 10 to 20 items depending the learning competencies of the lessons and scored based on the rubric provided.

The pretest and posttest will be given through online, on the scheduled date session per week of the students in Basic Calculus and they are given 30minutes to 1 hour and or depend on the level of difficulties of the topics. The scores in the pretest and posttest were statistically treated using mean score.

For the reliability of the instruments, the pre-test and posttest were subjected to content validation and evaluated by some experts in the field-Master Teacher, Department and Mathematics Teachers.

And for the validity of the instruments, the data gathered will be tested using reliability and validity test analysis- weighted mean for the content validation of pretest and posttest.

Sources of Data

The main sources of the data of the study are the pretest and posttest scores of the student-garnered based on the recorded activities and performances.

Data Collection Procedure

To collect the needed data, the researcher asked permission to conduct the study from the School Principal at Aliaga National High School at Division of Nueva Ecija.

After approval, from the School Principal, the researcher asked parents’ consent to notify and understand the importance and flow of the study. The proponent was responsible for the confidentiality of data gathered that is why the personal data and information would be kept confidential and use only for the purpose of research.

And finally, the data from pretest and posttest scores of the respondents got from personal class record of the researcher wherein she was the subject teacher in Basic Calculus.

Therefore, upon completion of the study the proponent assured that no personal data/ information revealed.

Ethical Considerations

Protocols

To ensure safety of all, the researcher decided to send the pretest and posttest, developed self-learning module in Basic Calculus via online plat forms thru google classroom, messenger and emails to ensure safety of all involved in the study.

Distance Learning Class Activities

For the pre-test and posttest and the lesson discussion schedule depends on the class schedule of the students. The pretest/posttests will be done on the availability of the students to participate as long as they will pass their output on given time required.

Personally- Developed Self-Learning Module in Basic Calculus

The developed Self-learning module in Basic Calculus was developed using several researches and different references based on the DepEd Most Essential Learning Competencies (MELCs). The development of the self-learning module were carefully designed based on the diversity of learning considering the minimum level of students’ understanding of the topics in Basic Calculus.

The researcher also follows the guidelines and procedures and protocols regarding plagiarism. If there is part of the developed self-learning module are same with the other materials, she will assure it is properly cited and use as references.

A set of evaluation were utilized in data gathering. These are:

Pre-Test was used to measure the degree of dependent variable before the treatment. It is composed of 10 to 15 items of test questions and the items will defend on the level of difficulty of the topic in Basic Calculus.
Post Test was used to measure the degree of change after the treatment. It was based on the pretest.
Self-Learning Module Developed in Basic Calculus is personally developed by the researcher and it will used in teaching-learning process for the experimental group amid COVID-19 pandemic in simplex and easiest term measuring the effectiveness and help improved students’ academic performance even in this trying times of pandemic and distance learning educational system.
Survey Questionnaire is personally made by the researcher based on the DepEd AMD guideline for design and layouts and for the effectiveness parameters will based on several references towards teaching and learning preferences.

The module consists of cover page, preliminary page, pre-test, introductory concepts, sample exercises, activities, summary and students’ reflection dealing with the topics/lessons. And designed self-learning module will developed into simple and easy to understand at different level of student’s knowledge and understanding with creativity and passion.

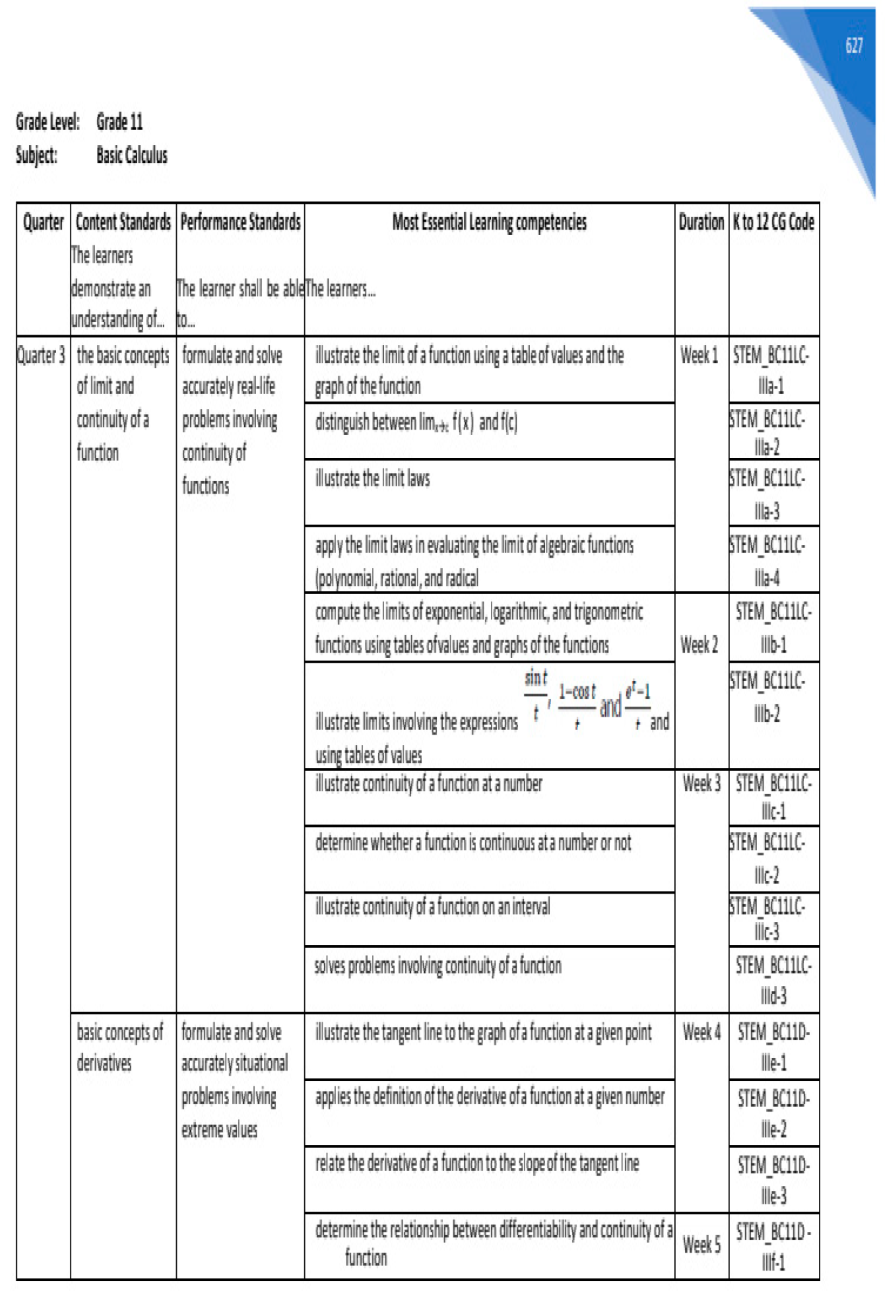
Table 2 shows the DepEd Most Essential Learning Competencies in Basic Calculus.

Data Privacy

In this study, all data collected from the respondents was used only for the purpose of research and the confidentiality will be kept to the public. The proponent asked permission to the principal and parents of the participants before the study will be conducted.

Data Analysis

The to determine the effectiveness of self-developed learning module in Basic Calculus on the enhancement of students’ academic performance amidst COVID-19, all data obtained were process, analyze and interpret using Microsoft excel as follows:

To describe the pretest in Basic Calculus of experimental and controlled group, mean was used.
To describe the posttest in Basic Calculus of experimental and controlled group, mean was also used.
To determine the significant difference between the result of the pretest of control and experimental group, weighted mean difference was utilized.
And to determine the significant difference between the result of the posttest of control and experimental group, weighted mean difference was also utilized.

RESULTS AND DISCUSSION

1. Present status of the students in Basic Calculus

Based on the data gathered from the series of post-test and pre-test as well as observations of subject teacher in Basic Calculus, students have experiences difficulties in learning specifically when it comes to analysis, solving situational problems, and complex problems included in the Basic Calculus module most specially under controlled group. While those in experimental group, they experience little bit challenged to them in solving problem but they were still answered correctly the given situational problems with the use of Self-learning module developed. This was the main reason why the researcher came up to developed and utilized Self-Learning Module in Basic Calculus.

Furthermore, the claimed by the researcher based on the difficulties of the students in solving problems were considered valid and reliable because all data were based on the scores of controlled in the series of tests and activities with the used of other learning materials and module in Basic Calculus.

The claims by the researcher on the present status of the students in Basic Calculus were supported by the statement came from the students in controlled group:

Student A:“Isa sa pinaka nahihirapan po ako ay topic po o lesson about problem solving, di ko po maintindihan gagawin. Lalo na po pag iba-iba na un given at equation dami po kasi sinosolve bago makuha un sagot kahirap pong intindihin.”.

Student B:“One of the most difficult topics I encountered in Basic Calculus is solving situational problems. I cannot understand the equations so I cannot answer the questions/problems correctly.”

2. Pretest of the Control and Experimental Group

Table 3 present the data of the pretest scores of the students-participants in Basic Calculus. As shown, the pretest mean score of the experimental group got 15.28 and a little bit greater than the pretest mean score of 14.48 obtained by the control group both interpreted as “Fair”.

Figure 2 shows the actual pretest scores of the student-participants in Basic Calculus. As shown in figure, the scores of the three sample participants have the same scores of 4 gained from their pretest number 1 with 10 items.

With regards to overall total scores, out of 45 items the highest scored obtained by the controlled group got 19 points while the experimental got 22.

The findings meant that the pretest scores of the students in Basic Calculus on the same competencies were evidently almost the same. The students have same level of prior knowledge regarding the topics.

3. Posttest of the Control and Experimental Group

Table 4 presents the data on the posttest of two groups of student-participants on Basic Calculus. As presented in the table, the posttest weighted mean scores of experimental group got 37.28 which was interpreted as “Outstanding” while the controlled group got 33.48 and interpreted as “Very Satisfactory”.

Figure 3 shows the actual posttest scores of the students in posttest number 1 in 10 items. As shown, the students got almost perfect scores of 9 and 10 in posttest number 1.

The findings revealed that the average posttest weighted mean scores of three sets of posttests on the same competencies, experimental group have an outstanding performance while controlled group have performed very satisfactory. The results imply that experimental group were evidently improving their achievements in Basic Calculus using developed self-learning module.

4. Difference between the result of the pretest of control and experimental group

Table 5 shows the difference of between the results of pretest of the two groups of respondents. As shown, in pre-test number one there was 0.52 on the performance of experimental group to control while there was no difference on pretest scores on the second test. On the other hand, there was .28 difference on the third pretest scores of the two groups of respondents.

The findings imply that 0.52 and .28 differences does not matter on the level of students’ prior knowledge about the topics. The student-respondents have same level of learning competencies and knowledge and understanding on the topics, before it would be discussed by the teacher

Furthermore, the students rely on what they know or based on their knowledge obtained on the previous mathematics subjects.

5. Difference between the result of the Posttest of Control and Experimental group

Table 6, presents the data on difference between posttest scores of two groups of student-respondents. As shown, posttest scores of experimental group had difference of 1.20, 2.24 and 0.76 respectively to the controlled group on the three posttest given in Basic Calculus.

The findings imply that those in experimental group were improved their posttest scores compare to those in controlled group. The findings concluded that the used of developed self-learning module in Basic Calculus helped student-participants in experimental group to have a better improved academic performance.

Conclusions

The present status of the students in Basic Calculus have experienced learning difficulties specifically in solving problems.
The pretest scores of the students in Basic Calculus concluded that both controlled and experimental group have the same level of prior knowledge regarding the topics.
With regards to the posttest, controlled group were performed very satisfactory while experimental group were outstandingly performed. Therefore, it is concluded that experimental group were evidently improved their academic achievements using developed self-learning module.
There is no significant influence on the pretest scores of two groups of respondents, it is therefore concluded that the students have the level of understanding and prior knowledge on the topic/lesson in Basic Calculus.
There is a significant difference on the posttest of two groups of respondents, therefore findings concluded that the used of self-learning module developed in Basic Calculus was found effective to enhance and improved students’ academic performance and reduce their learning difficulties.
Based on the findings of the study, the researcher may propose to continuously use and develop self-learning module that could help learners to improved students’ academic performance. And the self-learning module can also help students to effectively learn at their own pace especially during distance learning.

Recommendations

The proponent recommends to use other data to continuously enhance the designs, layouts, organization of the developed self-learning module in Basic Calculus. Continuous development of modules in all learning areas suited to diversity of learners is recommended.

Teachers may assist students and better identify their learning needs and individual differences especially during distance learning. The teacher may continuously develop and create self-learning modules based on the locality and level of students to understand the subject matter at their own paced in more fun, enjoyable and simple form.

For the School Heads and DepEd Officials may continue to supports teachers in developing learning modules in accordance to satisfy and meet the learning needs of the students in all areas.

Electronic Resources

http://www.sparknotes.com/math/calcab/ functions limits continuity

http://www.zweigmedia.com/

http://tutorial.math.lamar.edu/Classes/CalcI/ComputingIndefiniteIntegrals.aspx

www.zweigmedia.com/RealWorld/trig/trig4.html

https://maths.mq.edu.au/numeracy/web_mums/module4/Worksheet43/module4.pdf

https://portal.uea.ac.uk/documents/6207125/8199685/

http://tutorial.math.lamar.edu/Classes/CalcI/SubstitutionRuleIndefinite.aspx

https://www.khanacademy.org

Appendices

Appendix A

Research Instrument-Pre-tests and Post-tests

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRE-TEST

Limit of a Functions

(Logarithmic, Exponential and Trigonometric)

Evaluate the following limits of a function.

$\lim_{x \to 1} \ln x$
$\lim_{X \to 1} e^{x}$
$\lim_{X \to 1} e^{x}$
$\lim_{x \to 1} \log x$
$\lim_{x \to - 3} e^{2 x}$
$\lim_{x \to 1} \frac{\sin x}{x}$
$\lim_{x \to 0} \frac{\sin 3 x}{x}$
$\lim_{x \to 1} \frac{\cos x}{x^{2}}$
$\lim_{x \to 1} \frac{3 \sin 3 x}{2 x}$
$\lim_{x \to 1} \frac{x^{2}}{\tan x^{3}}$

Table A1. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

Limit of a Functions

(Logarithmic, Exponential and Trigonometric)

Evaluate the following limits of a function.

$\lim_{x \to 2} \log x$
$\lim_{x \to - 2} e^{x}$
$\lim_{x \to - 3} e^{2 x}$
$\lim_{x \to 1} {\log 5}^{2 x}$
$\lim_{x \to - 1} {\ln 2}^{x}$
$\lim_{x \to 0} \frac{1 - \cos x}{x^{2}}$
2. $\lim_{x \to 0} \frac{{s i n}^{3} x}{sin x - \tan x}$
$\underset{x \to 3}{3 . \lim} (x - 3) \csc π x$
$\underset{x \to 2}{4 . \lim} \frac{3 \sin 3 x}{x}$
5. $\lim_{y \to π} \frac{{s i n}^{2} y}{1 + \cos y}$

Table A2. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

CONTINUOUS AND DISCONTINUOUS FUNCTION

Answer the following, tell whether the following function is continuous or not. Write C if continuous function and D if discontinuous function.
- $f (x) = \frac{x - 1}{x}, a t x = 1$
- $f (x) = \frac{x}{x}, a t x = 2$
- $f (x) = \frac{3 x}{x + 2}, a t x = - 1$
- $f (x) = \frac{x^{2} - 4}{x + 3}, a t x = 0$
- $f (x) = \frac{x - 1}{x}, a t x = - 2$
- $f (x) = \frac{3 x + 2}{x 2 - 6 + 9}, a t x = 3$
- $f (x) = \frac{x - 4}{x + 2}, a t x = \pm 4$
- $f (x) = \frac{x - 1}{3 x}, a t x = \infty$
- $f (x) = \frac{\sin x}{x}, a t x = π$
- $f (x) = \tan x, a t x = n$
- $f (x) = 3 x^{2} + 2 x - 6, a t x = - 3$
- $f (x) = \cos 3 x, a t x = 1$
- $f (x) = 3 x, a t x = - 2$
- $f (x) = \frac{x}{x - 2}, a t x = 2$
- $f (x) = \csc θ, a t x =$ 1

Table A3. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POSTEST

CONTINUOUS AND DISCONTINUOUS FUNCTION

Examine the following limits whether continuous or not. Prove your answer using three conditions of continuity of a function.
- $f (x) = \frac{x - 1}{x}, a t x = 1$
- $f (x) = \frac{x}{x}, a t x = 2$
- $f (x) = \frac{3 x}{x + 2}, a t x = - 1$
- $f (x) = \frac{x^{2} - 4}{x + 3}, a t x = 0$
- $f (x) = \frac{x - 1}{x}, a t x = - 2$
- $f (x) = \frac{3 x + 2}{x 2 - 6 + 9}, a t x = 3$
- $f (x) = \frac{x - 4}{x + 2}, a t x = \pm 4$
- $f (x) = \frac{x - 1}{3 x}, a t x = \infty$
- $f (x) = \frac{\sin x}{x}, a t x = π$
- $f (x) = \tan x, a t x = n$
- $f (x) = 3 x^{2} + 2 x - 6, a t x = - 3$
- $f (x) = \cos 3 x, a t x = 1$
- $f (x) = 3 x, a t x = - 2$
- $f (x) = \frac{x}{x - 2}, a t x = 2$
- $f (x) = \csc θ, a t x = n π$

Table A4. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

DIFFERENTIATION RULES USING FOUR STEPS RULE

Find the derivatives of the following functions using differentiation rules.

y = 2x + 3
$y = x^{2} - x$
$y = x + 12$
$y = - 10$
$y = 3 x^{2} - x - 5$
$y = - x^{2} - 2$

Table A5. Table A5. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

DIFFERENTIATION RULES USING FOUR STEPS RULE

Find the derivatives of the following functions using differentiation rules.

y = 8x + 3
$y = {4 x}^{2} - 5 x - 3$
$y = 3 x + 12$
$y = 10 x - 2$
$y = 8 x^{3} - 3 x - 5$
$y = 4 x^{2} + 10 x - 3$

Table A6. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

DERIVATIVE OF TRANSCENDENTAL FUNCTION

Find the derivative of the following transcendental function. Write your answer on your notebook.
- $y = 4^{x}$ 6. $y = 6^{2 x - 4}$
- $y = e^{3 x}$ 7. $y = x^{2} e^{- 3 x}$
- $y = {l o g}_{7} x$ 8. $y = {l o g}_{2} x^{3}$
- $y = 3 s i n 2 x 9 .$ y = sin x
- $y = s e c \frac{1}{2} x$ 10.y = tan x

Table A7. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

DERIVATIVE OF TRANSCENDENTAL FUNCTION

$y = 2^{x}$
$y = e^{2 x + 1}$
$y = {l o g}_{5}$
$y = \ln z$
$y = {l o g}_{3} x^{2}$
x = cos 5h
$y = c s c 8 x$
$y = {c o s}^{2} t - {s i n}^{2} t$
$y = s i n \frac{x}{2}$
$h = c o t 2 θ$

Table A8. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

IMPLICIT DERIVATIVE

Find the implicit derivatives of the following.

$4 x^{2} + 6 y^{2} = 64$
$x y^{2} - 2 x + 16 = 0$
$x^{2} + y^{2} = r^{2}$
$(x + y)^{3} + (x - y)^{3} = x^{4} + y^{4}$
If x = $\frac{1}{3} y^{3} + y, f i n d \frac{d y}{d x}$

Table A9. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

IMPLICIT DERIVATIVES

EVALUATE the following functions.

Given $f (x) = 4 x^{2} - 3 x + 7, f i n d f^{'} (x), f^{''} (x) a n d f^{'''} (x)$
If ${2 x}^{2} + 3 x y + y^{2} = 5; f i n d \frac{d y}{d x}$
Given $y = u^{3} a n d u = 3 x + 1, f i n d \frac{d y}{d x}$
If $y = \frac{6}{(1 - u)^{2}} a n d x = \frac{6}{1 - u^{2}} f i n d \frac{d y}{d x}$
If $I f y = \frac{x^{4}}{\sqrt{1 - 2 x}} f i n d \frac{d y}{d x}$

Table A10. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:_____________ _

PRE TEST

APPLICATIONS of DERIVATIVES

I.

Solve all problems neatly and completely.

Find two numbers whose sum is a, if the product of one by the cube of the other is to be maximum.
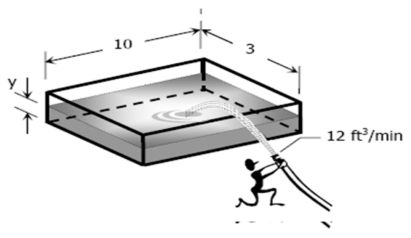
A rectangular trough is 10 ft long and 3 ft wide. Find how fast the surface rises, if water flows in at the rate of12 ft³/min.
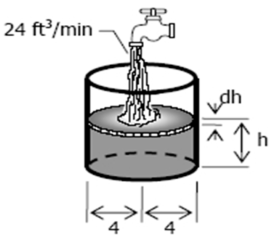
Water flows into a vertical cylindrical tank at the rate of 24 cu. ft. per minute. If the radius of the tank is 4 ft, how fast is the surface rising?
A box is to be made from a piece of cardboard 9 in. square by cutting equal squares out of the corners and then turning up the sides. Find the volume of the largest box that can be made in this way.

Table A11. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

APPLICATIONS OF DERIVATIVES

Solve all problems neatly and completely.
- A ladder 20 ft. long leans against a vertical wall. If the top slides downward at the rate of 2 ft. /sec, find how fast the lower end is moving when it is 16 ft. from the wall.
- Locate the critical points & find its maximum/minimum points of the function $y = x^{3} - 9 x^{2} + 15 x - 5 .$
- Find the volume of the largest box that can be made by cutting equal squares out of the corners of a piece of cardboard of dimensions 15 inches by 24 inches, and then turning up the sides.
- Water flows into a vertical cylindrical tank at 12 ft³ per min, the surface rises 6 in/min. Find the radius of the tank.

Table A12. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRE-TEST

ANTIDERIVATIVE

Evaluate the following
- ∫x⁷ dx
- ∫ (6x² - 4x + 3) dx
- ∫ (4x³ -7x² + 3x - 5) dx
- ∫ ( ${5 x}^{\frac{3}{2}}$ + ${2 x}^{\frac{1}{2}}$ - 7x + 3) dx
- ∫ (7x^-3 + ${3 x}^{\frac{1}{2}}$ - ${5 x}^{\frac{- 3}{2}}$ - 6) dx
- ∫ $\sqrt{x}$ + 4 dx
- $\frac{1}{2} \sqrt[3]{x}$ + $5 \sqrt[4]{x^{3}}$ dx
- ∫(4 $\sqrt{x} + 3 \sqrt[3]{x^{2}}$ - $\frac{4}{x^{2}}$ - $\frac{3}{x}$ +2) dx
- ∫ cos x dx
- ∫sec² dx

Table A13. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

ANTIDERIVATIVE

FIND THE ANTIDERIVATIVE OF THE FOLLOWING FUNCTIONS

f(x)= 7 $\sqrt{x}$
f(x)= (-7x³)²
f(x)= $\frac{2 x + 1}{x^{2} + x + 1}$
∫(5t³) − 10t⁻⁶ + 4 dt
∫x⁸ + x⁻⁸ dx
∫ $3^{4} \sqrt{x^{3}} \frac{7}{x^{5}} + \frac{1}{6 \sqrt{x}}$ dx
∫sin x − cos x)dx
∫tan x + cos x)dx
∫cosec(2x − 3)Dx
∫sec(2x − 3)tan(2x − 3)dx

Table A14. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

INDEFIITE INTEGRAL

Evaluate the following indefinite integrals
- $\int \sqrt[4]{x}$ dx
- $\int \frac{1}{t^{3}} d t$
- $\int c o s w d w$
- $\int \frac{{2 t}^{3} + 1}{{(t^{4} + 2 t)}^{3}} d t$
- $\int (1 - \frac{1}{w}) c o s (w - \ln w) d w$
- $\int (8 y - 1) e^{{4 y}^{2} - y} d y$
- $\int \sqrt{7 x + 6} d x$
- $\int \frac{x^{3}}{\sqrt{x^{2} + 1}} d x$

Table A15. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POST TEST

INDEFINITE INTEGRAL

II.: Evaluate the following indefinite integrals

$\int \frac{x^{3}}{x^{3} + 1} d x$
$\int \frac{1}{{\sqrt{x e}}^{\sqrt{x}}} d x$
$\int \frac{\sqrt[3]{x}}{5^{\sqrt[3]{4} - 2}} d x$
$\int (1 - \frac{1}{w}) c o s (w - \ln w) d w$
2. $\int 3 (8 y - 1) e^{{4 y}^{2} - y} d y$
3. ∫ x²(3 − 10x³)⁴ dx
4.∫ $\frac{x}{\sqrt{1 - 4 x^{2}}}$ dx
∫ (6x − 20)¹⁰ dx

Table A16. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

SUBSTITUTION RULE OF INTEGRATION

Evaluate the following function using substitution of integration.

Determine f(x) given that $f (x) = 34 x^{4} + 23 x^{3}$ what is $f (2)$ and f (-2)
Determine $h (z)$ given that $h^{'} (z) = 12 z^{3} - 14 z^{2} + 10$ find $h (- 1)$
Determine $g (v)$ given that $g^{'} (v) = \frac{1}{2} v^{- \frac{1}{2}} - \frac{1}{4} v^{- \frac{3}{4}}$ find $g (16)$ and $g (1 / 2)$
Determine $P (t)$ given that $P^{'} (t) = 6 e^{t} - 4 - 10 t$ what is P(0)
Determine $g (x)$ given that $g^{'} (x) = 12 x^{2} - 30 x + 4$ , $g (- 1)$ and $g (2)$

Table A18. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

POSTTEST

SUBSTITUTION RULE OF INTEGRATION

Evaluate the following function using substitution of integration.

Determine f(x) given that $f (x) = 12 x^{5} + 30 x^{4}$ find $f (4)$ , f(2), f (-2)
Determine $h (z)$ given that $h^{'} (z) = 10 z^{3} - 4 z^{2} + 8$ determine $h (- 1)$ , h (0) and h (1)
Determine $g (v)$ given that $g^{'} (v) = \frac{1}{2} v^{- \frac{1}{2}} - \frac{1}{4} v^{- \frac{3}{4}}$ find g (2/3) and $g (- 3)$
Determine $P (t)$ given that $P^{'} (t) = e^{t} - 4 - 10 t$ find P(0) and P (1/2)
Determine $g (x)$ given that $g^{'} (x) = 22 x^{3} - 3 x + 4$ , waht $g (- 12)$ and $g (3)$ .

Table A19. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

PRETEST

APPLICATIONS

I.: Solve the following problems
1.: A spring has a natural length of 25 cm and a force of 3.5 N is required to stretch and hold the spring to a length of 32 cm. What is the work required to stretch the spring from a length of 30 cm to a length of 45 cm?
2.: A cable that weighs 2 kg/meter is lifting a load of 50 kg that is initially at the bottom of a 75 meter shaft. How much work is required to lift the load 40 meters?
3.: A cable that weighs 1.5 kg/meter and is attached to a bucket that weighs 75 kg. Initially there are 500 kg of grain in the bucket and as the bucket is raised 2 kg of grain leaks out of a hole in the bucket for every meter the bucket is raised. The bucket is 200 meters below a bridge. How much work is required to raise the bucket to the top of the bridge?
4.: A tank of water is in the shape of a cylinder of height 25 meters and radius of 7 meters. If the tank is completely filled with water how much work is required to pump all of the water to the top of the tank. Assume that the density of water is 1000 kg/m³.

Table A20. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

APPLICATIONS OF DERIVATIVE

POSTTEST

I.: Solve the following problems
1.: A spring has a natural length of 9 inches and a force of 7 lbs is required to stretch and hold the spring to a length of 21 inches. What is the work required to stretch the spring from a length of 12 inches to a length of 30 inches?
2.: A cable that weighs 1.5 kg/meter and is attached to a bucket that weighs 75 kg. Initially there are 500 kg of grain in the bucket and as the bucket is raised 2 kg of grain leaks out of a hole in the bucket for every meter the bucket is raised. The bucket is 200 meters below a bridge. How much work is required to raise the bucket to the top of the bridge?
3.: A tank of water is in the shape of a cylinder of height 25 meters and radius of 7 meters. If the tank is completely filled with water how much work is required to pump all of the water to the top of the tank. Assume that the density of water is 1000 kg/m³.
4.: A cable that weighs 12 kg/meter is lifting a load of 250 kg that is initially at the bottom of a 175 meter shaft. How much work is required to lift the load 400 meters?

Table A21. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

Name: _________________________________ Score: _____________

Grade & Section:_________________________ Date:______________

FORMATIVE TEST

Prove the following mathematical induction:

Prove that mathematical induction that 7²ⁿ + 3^{n – 1} + (2^{3n – 3}) is divisible by 25, for n=1
P(n) is the statement ‘n² – n + 41 is prime’ number? Verify it. For n=1, n=2 and n=41
Prove 3n – n + 7 is divisible by 3 for all real numbers

Table A22. Rubric for Equations Solved

Descriptors	SCORE
All data, given, solutions and answers were completely presented.	5 points
Data, given, solution and answers were not completely presented.	4 points
Data, given, solution and answers were completely presented but incorrect answer	3 points
Data, given , solution and answers were not presented.	2 points
No answer at all	1 point

References

Alchemer (2021). What is Purposive Sampling? Retrieved from: https://www.alchemer.com/resources/blog/purposive-sampling-101/.
Alice, O. (2012). Challenges facing the teachers and students in the of instructional technologies: A case of selected secondary schools in KISII Country, Kenya. Retrieved from:https://ir-library.ku.ac.ke/bitstream/handle/123456789/6532/Omariba%20Alice.pdf?sequence=3\.
Department of Education (2020). DepEd prepares Self-Learning Modules for education’s new normal. Retrieved from: DepEd prepares Self-Learning Modules for education’s new normal Department of Education.
Encyclopedia Britannica. (n.d.). Rene Descartes. Retrieved from http://www.britannica.com/EBchecked/topic/158787/Rene-Descartes/images-videos.
Ezekoka, M. A. (2008). Teaching Materials and Students Academic Achievements. Proceedings of the 43^rd Annual Conference of STA 7-416-419. Ibadan:Heinemann.
Felipe L. Comandante, J. (2011). Analytic Geometry with Solid Mensuration (Made Easy). Mandaluyong City: National Book Store.
Fuller, G. (n.d.). Analytic Geometry (4th Editiion). Massachusetts Addison: Wesley Publishing Co.
Jogan, S.N. (2016). Self-Learning Modules in the Achievement and Retension of Highere Secondary Students in English. JRF Scholar, Department of Education, Gulbarga University, Kalaburagi-585106. Retrieved from: Self learning modules for students and teachers (slideshare.net).
Kanchan (2016). Effectiveness of self learning modules on the achievement and retention of undergraduate students in commerce. Semantic SCHOLAR.ID:39051021.
Koko, M.N. (2016). The Effective Use of School Instructional Materials. Retrieved from: file:///C:/Users/ITZ%20SHAR/Downloads/THEEFFECTIVEUSEOFSCHOOLINSTRUCTIONALMATERIALSAutosaved.pdf.
Koko, M.N. (2015). Teaching Business. Port Harcourt, Nigeria: Harvey Publication Company.
Kuhfittig, P. F. (1983). Technical Calculus with Analytic Geometry. Monterey, California: Brooks/Cole Publishing Company.
Luis, E., Malgapo C.R.T., Daracan J. ; Santiago, J & Sanglay, F.E.( 2015) Caculus with Analytic Geometry.
Malgapo, C.R.T. (2021). Effectiveness of Developed Instructional Module on the Enhancement of Learners Academic Achievements in Physics. Preprint. Physical Science, Acoustic. [CrossRef]
Marcelo, G. G. (2009). Basic Calculus. Sta. Mesa Heights, Quezon City: REX Book Store.
Mateo, R. A., & Sergio E. Ymas, J. (2002). Differential Calculus. Sampaloc, Manila: Ymas Publishing House.
Nocon, F. P., & al, e. (2007). Differential Calculus. Mandaluyong City: Nationl Bookstore.
Oden, C. (n.d). The Effectiveness of Instructional Materials in Teaching and Learning of Biology in Senior Secondary School. Retrieved from: https://www.projecttopics.org/effectiveness-instructional-materials-teaching-learning-biology-senior-secondary-school.html.
Onasanya, S.A. and Omosewo, E.O. (2011). Effect of improvised and standard instructional materials on Secondary School Students’ Academic Performance in Physics in Ilorin, Nigeria. Retrieved from: https://scialert.net/fulltext/?doi=sjsres.2011.68.
Portana, H. V., Fronda, J.G., Policarpio, D.G.T., Rome, C. R., & Lllames, G.A. (2020). Effectiveness and Acceptability of Instructional Materials in the Enhancement of Students’ Academic Achievement. International Journal of Advanced Engineering Management and Science, 7(1),12-15-2021. [CrossRef]
Quisumbing, L.A, Caluza, D.G.D., Funcion, D.G.; Gotardo, M.A., Verecio, R.L. and Cinco, J.C. (2117). Views and Preferences in the Development of Instructioal Materials fo IT Courses: The Case of BSIT Students. Research Article, Leyte Normal University, Philippnes. International Journal of Recent Advances in Multidisciplinaty Research. Vol. 04. Retrieved from: (5) (PDF) VIEWS AND PREFERENCES IN THE DEVELOPMENT OF INSTRUCTIONAL MATERIALS FOR IT COURSES: THE CASE OF BSIT STUDENTS (researchgate.net).
Soetan, A.K., Iwokwagh, N.S., R.A. Shehu, and Onasanya, S.A. (2010). Creating engaging 3-D animation digitization for instructional media and communication. Inform.Technol. J., 9: 89-97.
Tety, J.L. (2016). Role of Instructional Materials in Academic Performance in Community Secondary Schools in Rombo District. Dissertation. University of Tanzania. Retrieved from: DISSERTATION_-_JOHN_LAWRENCE_TETY_-_FINAL.pdf (out.ac.tz).
Upen (2018). Difference Between Descriptive and Experimental Research. PEDIAA. Retrieved from: Difference Between Descriptive and Experimental Research - Pediaa.Com.

Figure 1. Conceptual Framework of the study.

Figure 2. Actual Pretest of the Student-Participants.

Figure 3. Actual Posttest Scores.

Table 1. Respondents of the Study.

Table 2. Most Essential Learning Competencies in Basic Calculus.

Table 3. Pretest Scores of Control and Experimental Group.

	PRETEST SCORES
Participant	Control Group				Experimental Group
	PrT1 10 items	PrT2 15 items	PrT3 20 items	Total (45) Pretest Scores	PrT1 10 items	PrT2 15 items	PrT3 20 items	Total (45) Pretest Scores
1	2	7	8	17	3	5	8	16
2	3	6	6	15	3	7	7	17
3	4	3	5	12	4	2	5	11
4	2	4	9	15	5	6	9	20
5	3	5	2	10	6	7	3	16
6	3	4	4	11	3	5	4	12
7	2	4	6	12	3	6	6	15
8	6	4	5	15	3	3	6	12
9	7	4	7	18	4	4	7	15
10	3	6	13	22	2	4	10	16
11	5	4	12	21	3	4	9	16
12	3	7	2	12	4	3	2	9
13	4	4	3	11	3	3	3	9
14	2	3	2	7	4	6	12	22
15	2	5	5	12	5	6	5	16
16	2	6	6	14	7	7	6	20
17	3	7	7	17	4	8	7	19
18	3	8	8	19	3	9	8	20
19	3	5	5	13	3	5	5	13
20	3	7	4	14	3	6	4	13
21	4	5	6	15	4	7	7	18
22	2	7	7	16	5	8	7	20
23	3	6	3	12	3	3	3	9
24	4	8	4	16	3	5	5	13
25	3	5	8	16	4	5	6	15

Pretest Mean Score	14.48				15.28

Legend: 36.01 - 45.00 Outstanding; 27.01 - 36.00 Very Satisfactory; 18.01 - 27.00 Satisfactory; 9.01 - 18.00 Fair; 0 - 9.00 Did not meet expectation

Table 4. Post Test Scores of Controlled and Experimental Group.

	POSTTEST SCORES (20Items)
Participant	Control Group				Experimental Group
	PsT1 10 items	PsT2 15 items	PsT3 20 items	Total (45) Posttest Scores	PsT1 10 items	PsT2 15 items	PsT3 20 items	Total (45) Posttest Scores
1	8	9	17	34	10	15	16	16
2	8	11	16	35	10	14	18	17
3	10	12	13	35	9	15	12	11
4	9	9	18	36	10	10	14	20
5	9	10	14	33	10	11	18	16
6	8	8	11	27	9	15	13	12
7	9	14	12	35	9	14	9	15
8	7	13	11	31	9	15	12	12
9	6	11	11	28	9	14	18	15
10	6	10	18	34	10	15	16	16
11	5	10	12	27	10	14	16	16
12	8	12	15	35	8	13	11	9
13	9	13	8	30	8	14	18	9
14	9	10	9	28	9	15	17	22
15	9	11	15	35	10	13	16	16
16	10	9	16	35	10	13	9	20
17	10	11	13	34	9	14	10	19
18	9	12	12	33	9	15	15	20
19	8	12	15	35	10	14	16	13
20	9	15	16	40	10	14	15	13
21	7	12	16	35	10	15	14	18
22	6	13	13	32	9	12	13	20
23	8	11	14	33	10	11	10	9
24	9	14	15	38	9	14	14	13
25	9	14	16	39	9	13	15	15

Posttest Mean Score	33.48				37.28

Legend: 36.01 - 45.00 Outstanding; 27.01 - 36.00 Very Satisfactory; 18.01 - 27.00 Satisfactory; 9.01 - 18.00 Fair 0 - 9.00 Did not meet expectation.

Table 5. Difference between the Results of Pretest.

Group	Pretest	1	2	3
	Items	10	15	20
	N	Mean	Mean	Mean
Controlled	25	3.24	5.36	5.88

Experimental	25	3.76	5.36	6.16

Mean Difference		.52	0	.28

Table 6. Difference between the Results of Posttest.

Group	Pretest	1	2	3
	Items	10	15	20
	N	Mean	Mean	Mean
Controlled	25	8.20	11.44	13.44

Experimental	25	9.40	13.68	14.20

Mean Difference		1.20	2.24	0.76

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Effectiveness of Self-Learning Module Developed on the Enhancement of Student’ Academic Performance in Basic Calculus Amidst COVID-19

Abstract

Keywords:

Subject:

Introduction

Review of the Related Literature

Synthesis of Review of Related Literature

Conceptual Framework

Research Questions

Hypotheses

Significance of the Study

Scope and Limitation

METHODS

Type of Research

Participants

Sampling Technique

Instrumentations

Sources of Data

Data Collection Procedure

Ethical Considerations

Protocols

Distance Learning Class Activities

Personally- Developed Self-Learning Module in Basic Calculus

Data Analysis

RESULTS AND DISCUSSION

1. Present status of the students in Basic Calculus

2. Pretest of the Control and Experimental Group

3. Posttest of the Control and Experimental Group

4. Difference between the result of the pretest of control and experimental group

5. Difference between the result of the Posttest of Control and Experimental group

Conclusions

Recommendations

Electronic Resources

Appendices

Appendix A

References

MDPI Initiatives

Important Links

Subscribe