Photon-Field Interactions: A Relativistic and Quantum Approach

1. Introduction

Maxwell’s equations have long been the foundation for describing electromagnetic phenomena, providing a comprehensive framework for understanding the dynamics of electric and magnetic fields in the presence of charges and currents. These equations are traditionally written as:

$$\begin{array}{cc}\hfill \nabla ·\mathbf{E}& ={\displaystyle \frac{\rho \left(\mathbf{r}\right)}{{ϵ}_0}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \nabla \times \mathbf{E}& =-{\displaystyle \frac{\partial \mathbf{B}}{\partial t}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \nabla ·\mathbf{B}& =0,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \nabla \times \mathbf{B}& ={\mu }_0\mathbf{J}+{\displaystyle \frac{\partial \mathbf{D}}{\partial t}}.\hfill \end{array}$$

(4)

In classical electromagnetism, the energy and momentum of fields are described without explicitly considering the quantum properties of light. However, photons, the quanta of the electromagnetic field, carry energy (E) and momentum (p) are inherently linked to their wave-like properties. From relativistic and quantum perspectives, these relationships can be expressed as follows:

$$\begin{array}{cc}\hfill E& =pc,p={\displaystyle \frac{E}{c}}=\hslash k={\displaystyle \frac{h}{\lambda }},\hfill \end{array}$$

(5)

where $k=2\pi /\lambda$ is the wave vector, ℏ is the reduced Planck’s constant, and h is Planck’s constant.

These relationships highlight the dual nature of photons as both particles and waves. However, integrating photon effects into classical field equations requires a novel approach, particularly to address how the photon’s momentum (p) interacts with the electric and magnetic fields. In this work, we propose an extension of Maxwell’s equations by incorporating an effective potential associated with photon momentum. This is achieved by redefining the electric field as:

$$\begin{array}{c}\hfill \mathbf{E}=-\nabla \left(pc\right)\end{array}$$

(6)

which leads to a fourth-order differential equation when coupled with relativistic and quantum considerations. By bridging these ideas with the kinetic energy operator in the Hamiltonian, we derive a generalized framework for photon-field interactions. Furthermore, the boundary conditions for the system we re defined using the Lorenz system, enabling us to explore the quasi-stability and chaotic dynamics of these interactions.

The integration of relativistic, quantum, and chaotic perspectives offers new insights into the behavior of electromagnetic fields in the presence of photons, providing a unified approach to understanding photon-field coupling. This study not only extends the applicability of Maxwell’s equations but also contributes to the broader understanding of the interplay between quantum mechanics, relativity, and nonlinear dynamics.

2. Modified Maxwell Equations and Effective Potential

We introduce the concept of an effective potential to incorporate photon effects into an electromagnetic framework. This potential reflects the contribution of photons to the electric field, bridging the quantum nature of photons with the classical dynamics of fields.

2.1. Effective Potential and Field Definitions

In the traditional formulation, the electric field is derived from a scalar potential $\Phi$ as:

$$\begin{array}{c}\hfill \mathbf{E}=-\nabla \Phi .\end{array}$$

(7)

In the presence of photons, we redefine the scalar potential to include the photon’s energy-momentum relation. The effective potential is given by:

$$\begin{array}{c}\hfill \Phi =pc,\end{array}$$

(8)

where p is the photon momentum and c is the speed of light. Substituting this into the electric field equation yields:

$$\begin{array}{c}\hfill \mathbf{E}=-\nabla \left(pc\right).\end{array}$$

(9)

This modification integrates the photon’s energy directly into the field dynamics. For the magnetic field $\overrightarrow{B}$ , we retain its standard definition in terms of the vector potential $\overrightarrow{A}$:

$$\begin{array}{c}\hfill \mathbf{B}=\nabla \times \mathbf{A}\end{array}$$

(10)

2.2. Modifications to Maxwell’s Equations

Using these definitions, Maxwell’s equations are reformulated to include photon effects:

1. Modified Gauss’s Law

Incorporating $\Phi =pc$ , Gauss’s law becomes:

$$\begin{array}{c}\hfill \nabla ·\mathbf{E}={\displaystyle \frac{\rho \left(\mathbf{r}\right)}{{\epsilon }_0}}\end{array}$$

(11)

Substituting $\overrightarrow{E}=-\nabla \left(pc\right)$ , we obtain:

$$\begin{array}{c}\hfill {\nabla }^{2}p={\displaystyle \frac{\rho \left(\mathbf{r}\right)\sqrt{{\mu }_0{\epsilon }_0}}{{\epsilon }_0}}\end{array}$$

(12)

2. Faraday’s Law

The time-dependent magnetic field remains governed by Faraday’s law:

$$\begin{array}{c}\hfill \nabla \times \mathbf{E}=-{\displaystyle \frac{\partial \mathbf{B}}{\partial t}}\end{array}$$

(13)

Substituting $\overrightarrow{E}=-\nabla \left(pc\right)$:

$$\begin{array}{c}\hfill \nabla \times (-\nabla \left(pc\right))=-{\displaystyle \frac{\partial (\nabla \times \mathbf{A})}{\partial t}}\end{array}$$

(14)

And finally:

$$\begin{array}{c}\hfill \nabla \times \mathbf{p}=-\sqrt{{\mu }_0{\epsilon }_0}{\displaystyle \frac{\partial }{\partial t}}(\nabla \times \mathbf{A})\end{array}$$

(15)

3. Gauss’s Law for Magnetism

This law remains unchanged as:

$$\begin{array}{c}\hfill \nabla ·\mathbf{B}=0\end{array}$$

(16)

4. Ampere’s Law with Maxwell’s Correction

Incorporating photon effects, Ampere’s law becomes:

$$\begin{array}{c}\hfill \nabla \times (\nabla \times \mathbf{A})={\displaystyle \frac{1}{\sqrt{{\mu }_0{\epsilon }_0}}}\left(\nabla \mathbf{p}(\sigma +{\epsilon }_0{\displaystyle \frac{\partial }{\partial t}})\right)\end{array}$$

(17)

2.3. Fourth-Order Field Equation

Combining the modified Gauss’s law with the Hamiltonian operator, where the kinetic energy term is expressed as:

$$\begin{array}{c}\hfill \widehat{T}=-{\displaystyle \frac{{\hslash }^2}{2m_e}}{\nabla }^2,\end{array}$$

(18)

we derive a fourth-order field equation:

$$\begin{array}{c}\hfill {\nabla }^4\left({\alpha }^2\psi (\mathbf{r},t)\right)={\displaystyle \frac{\rho (\mathbf{r},t)\sqrt{{\mu }_0{ϵ}_0}}{ϵ(\mathbf{r},t)}},\end{array}$$

(19)

and $\psi (\mathbf{r},t)$ is Quantum electric field potential.

To ensure the Lorentz invariance of the proposed framework, we redefine the fourth-order operator as ${\square }^2={\left({\partial }_{\mu }{\partial }^{\mu }\right)}^2$ , where ${\partial }_{\mu }$ represents the four-gradient. This guarantees that the modified equations maintain consistency under relativistic transformations. For example, the scalar potential $\psi$ and the dielectric permittivity $\epsilon (\overrightarrow{r},t)$ are treated as Lorentz scalars. This ensures that the proposed equation:

This formulation encapsulates photon-field interactions within a relativistic and quantum framework, providing a unified description that connects classical and quantum perspectives. is invariant under Lorentz transformations when reformulated in terms of ${\square }^2$.

3. Boundary Conditions and Stability Analysis

The dynamics of the modified fourth-order equation derived in Section 2 necessitate the establishment of appropriate boundary conditions to ensure consistency and predictability. In this section, we introduce boundary conditions using the Lorenz system, highlighting its role in defining quasi-stable solutions.

3.1. Lorenz System and Boundary Conditions

The Lorenz system, a classic model in chaotic dynamics, is utilized here to impose constraints on the modified Maxwell equations. The governing equations of the Lorenz system are:

$$\begin{array}{cc}\hfill \dot{x}& =\sigma (y-x),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \dot{y}& =x(\rho -z)-y,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \dot{z}& =xy-\beta z,\hfill \end{array}$$

(22)

where $\alpha$, $\beta$ and $\rho$ are system parameters. To link these equations to the modified fourth-order equation, we redefine the parameters in terms of the physical variables of the field:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\sigma ={\displaystyle \frac{1}{2(y-x)}}\hfill \\ \beta ={\displaystyle \frac{xy}{z}}\hfill \\ \rho =z+{\displaystyle \frac{y}{x}}\hfill \end{array}\right.\end{array}$$

(23)

3.2. Stability Conditions for Quasi-Stable Solutions

For the fourth-order equation:

$$\begin{array}{c}\hfill {\nabla }^4\left({\alpha }^2\varphi (\mathbf{r},t)\right)={\displaystyle \frac{\rho (\mathbf{r},t)\sqrt{{\mu }_0{\epsilon }_0}}{\epsilon (\mathbf{r},t)}},\end{array}$$

(24)

to exhibit quasi-stability, the following conditions must be satisfied:

1. $(\dot{x},\dot{y},\dot{z})=(0,0,0)$ ensuring no dynamic changes in the Lorenz variables.

2. Approximate equality of variables:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\sigma :x\approx y\hfill \\ \beta :z\approx 0\hfill \\ \rho :x\approx 0,z\to \infty \hfill \end{array}\right.\end{array}$$

(25)

Under these conditions, the Lorenz system reduces to a steady-state configuration, providing consistent boundary constraints for the modified Maxwell equations.

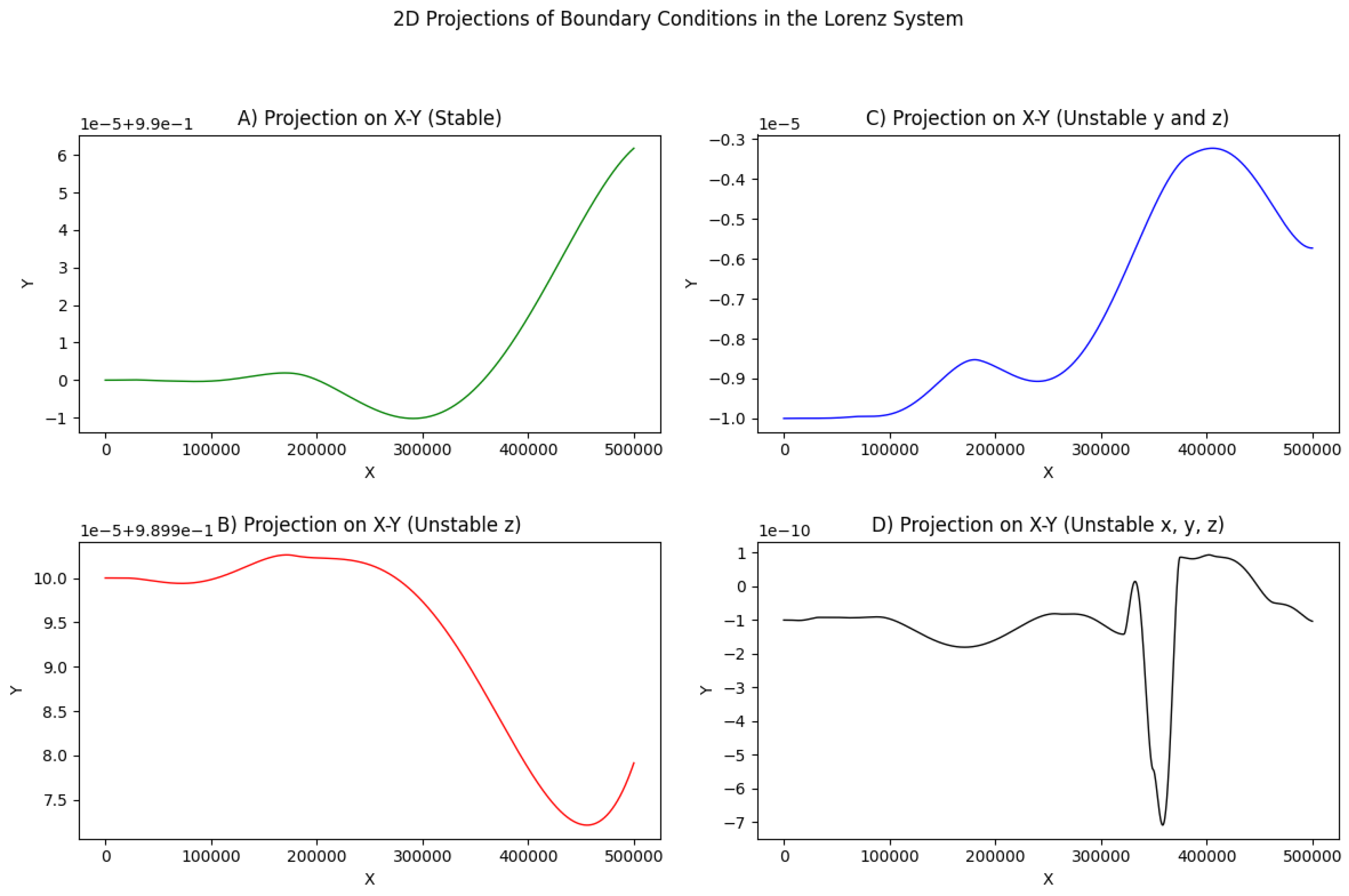
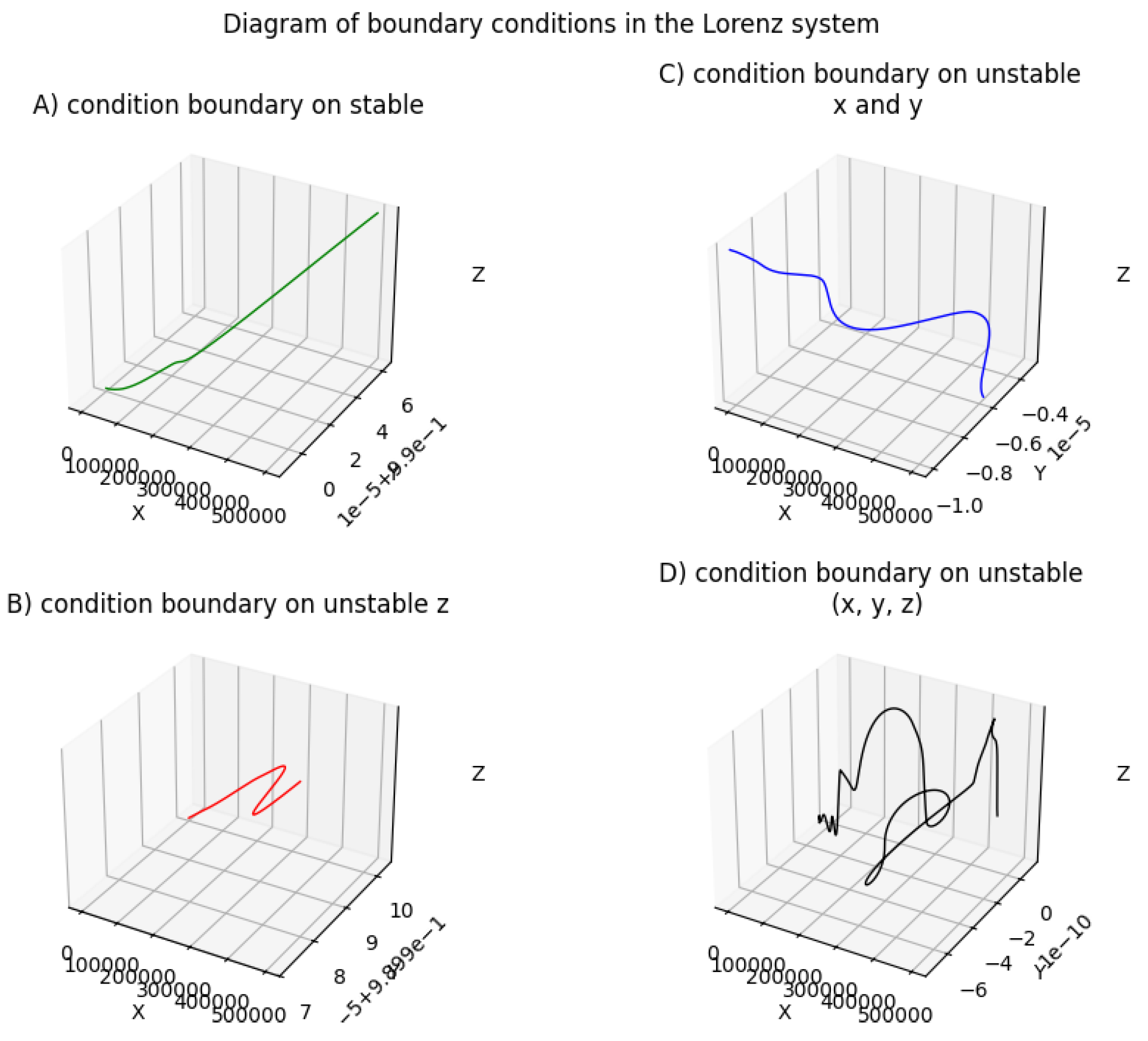
Figure 1. The figure presents the 2D projections of the 3D trajectories shown in the Figure 2, focusing on the X–Y plane for various boundary conditions in the Lorenz system. Each subplot corresponds to one of the cases depicted earlier.

Figure 1. The figure presents the 2D projections of the 3D trajectories shown in the Figure 2, focusing on the X–Y plane for various boundary conditions in the Lorenz system. Each subplot corresponds to one of the cases depicted earlier.

3.3. Implications of Boundary Conditions

The application of the Lorenz system as a basis for boundary conditions introduces a novel perspective on the interplay between chaotic dynamics and relativistic quantum fields. By linking chaotic variables to the behavior of the photon-field system, the analysis highlights the sensitivity of stability to parameter relationships and initial conditions. The resulting quasi-stable solutions offer a bridge between deterministic higher-order equations and the inherent unpredictability of chaotic systems, enriching our understanding of non-linear and relativistic effects in photon-field interactions.

Figure 2. Two-dimensional projections of the boundary conditions in the Lorenz system under various scenarios of stability and instability. Panel (A) shows the stable behavior, while panels (B), (C), and (D) highlight different forms of instability in the boundary conditions

Figure 2. Two-dimensional projections of the boundary conditions in the Lorenz system under various scenarios of stability and instability. Panel (A) shows the stable behavior, while panels (B), (C), and (D) highlight different forms of instability in the boundary conditions

4. Comparison with QED

The fourth-order differential equation developed in this study finds conceptual parallels with Quantum Electrodynamics (QED), which rigorously describes the interaction of photons with charged particles. The foundation of QED lies in its action, expressed as:

$$\begin{array}{c}\hfill S_{QED}=\int d^{4}x{\mathcal{L}}_{QED}\end{array}$$

(26)

where the Lagrangian density is given by:

$$\begin{array}{c}\hfill {\mathcal{L}}_{QED}=-{\displaystyle \frac{1}{4}}{F}^{\mu \nu }{F}_{\mu \nu }+{\psi }^{*}(i{\gamma }^{\mu }{D}_{\mu }-m)\psi \end{array}$$

(27)

Here:

• $F_{\mu \nu }={\partial }_{\mu }{A}_{\mu }-{\partial }_{\nu }{A}_{\mu }$: Electromagnetic field strength tensor, describing the field’s dynamics.
• $A_{\mu }$: Electromagnetic four-potential.
• $\psi$: Dirac spinor for charged particles.
• : Mass of the charged particle.
• $D_{\mu }={\partial }_{\mu }+ie{A}_{\mu }$: Covariant derivative coupling the particle to the electromagnetic field.
• ${\gamma }^{\mu }$: Gamma matrices used in relativistic quantum mechanics.

The QED action combines the dynamics of electromagnetic fields with the quantum behavior of particles, illustrating how photons mediate interactions.

Comparison with the Fourth-Order Framework

• 1. Photon Dynamics
  In QED, photons serve as the quantum mediators of the electromagnetic interaction, encapsulating both wave-like and particle-like properties. The fourth-order equation introduced in this work incorporates photon effects directly into the electric field through the effective potential $\Phi =-{\displaystyle \frac{{\hslash }^2}{2m_e}}{\nabla }^2$, bridging photon dynamics with quantum mechanical operators.
  2. Effective Potential
  The concept of effective potential in this study resembles the interaction terms in the QED Lagrangian. While QED uses interaction terms like $ie{A}_{\mu }\psi$ , this study introduces higher-order spatial derivatives (${\nabla }^4$) to encapsulate non-local or intense-field effects, providing an alternative formulation of photon-field coupling.
  3. Higher-Order Dynamics
  QED traditionally employs first-order field equations derived from Maxwell’s equations. The introduction of a fourth-order framework expands the scope, potentially capturing effects such as photon-photon interactions or nonlinearities in high-intensity regimes. These extensions may reflect higher-order corrections to the QED action in strong-field approximations.
  4. Boundary Conditions and Chaos
  QED action primarily deals with linear boundary conditions, determined by charge distributions or external fields. In contrast, the chaotic Lorenz system as a boundary condition in this study introduces a novel dynamic, allowing the modeling of fluctuating or non-uniform charge distributions, which could provide insights into non-equilibrium QED systems.
  5. Relativistic and Quantum Structure
  Both QED and the proposed fourth-order equation integrate relativistic momentum (p) and quantum operators ($\widehat{p}$). However, the explicit inclusion of time-dependent dielectric properties and chaotic constraints in this framework provides a unique lens through which photon-field interactions can be explored.

Summary of Comparison

The proposed framework aligns conceptually with QED’s principles by maintaining the photon-field coupling’s quantum and relativistic nature. However, it extends these principles by integrating chaotic systems and higher-order derivatives, which are not traditionally addressed in QED. This study serves as a complementary perspective, potentially useful in understanding non-linear, non-equilibrium, or intense-field phenomena. Further exploration of its implications within the QED action framework could enhance the theoretical underpinnings of both models.

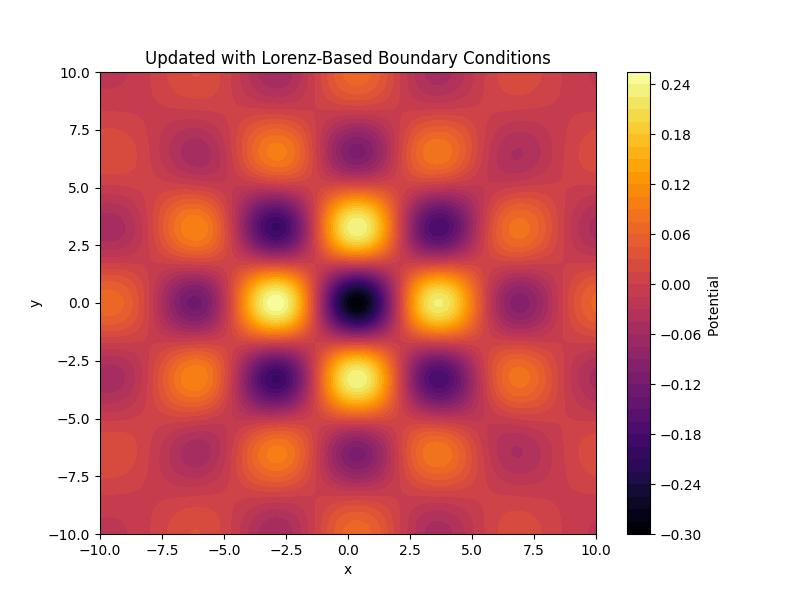
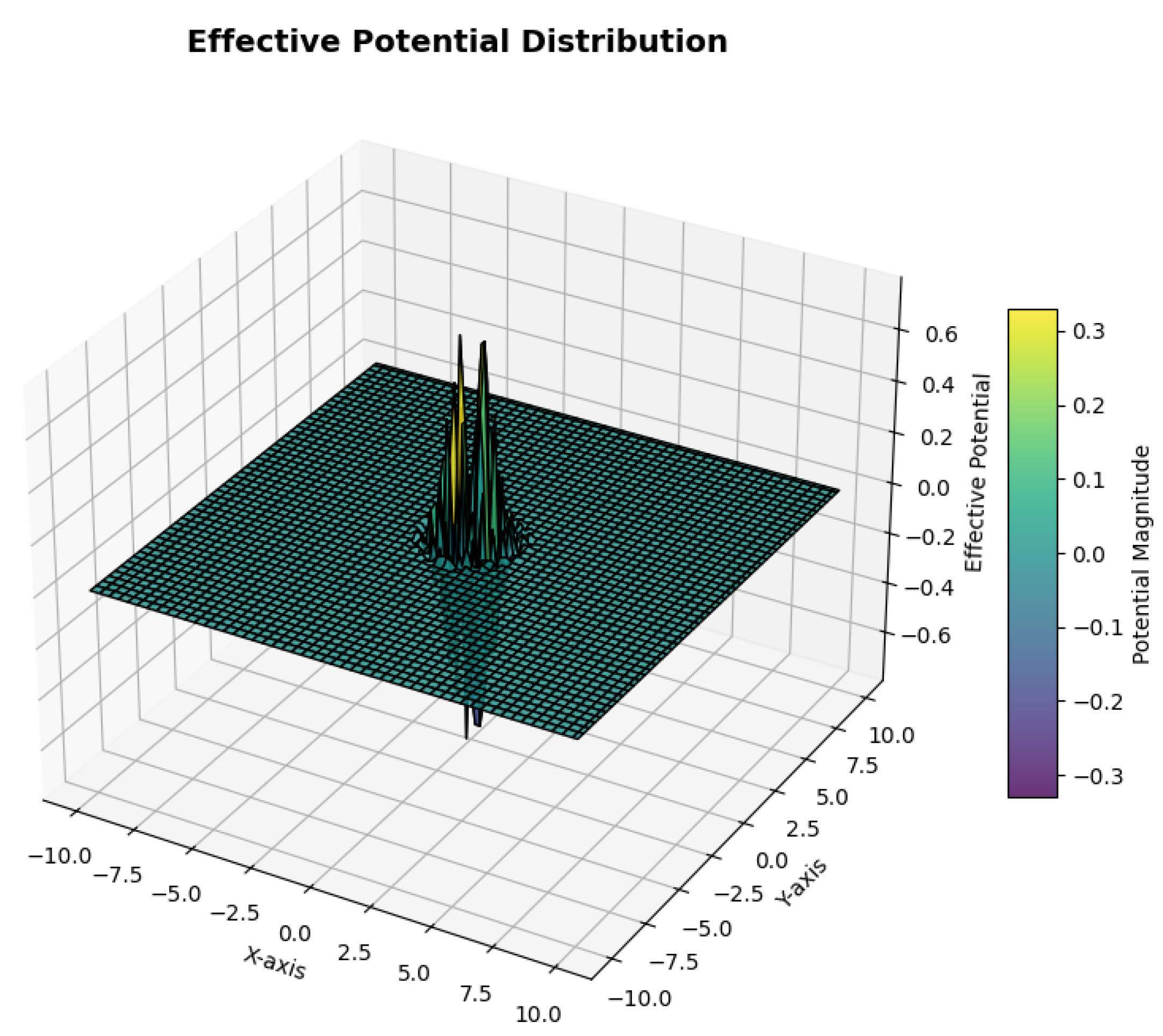
Figure 3. Here is a 3D visualization of the effective potential distribution, modeled as a Gaussian function to reflect localized field interactions with radial symmetry. The spatial coordinates illustrate how the potential decays smoothly from the center, indicating diminishing interaction strength at larger distances. This representation highlights the interplay between localized field behavior and stability conditions under the imposed Lorenz-system-based boundary constraints.

Figure 3. Here is a 3D visualization of the effective potential distribution, modeled as a Gaussian function to reflect localized field interactions with radial symmetry. The spatial coordinates illustrate how the potential decays smoothly from the center, indicating diminishing interaction strength at larger distances. This representation highlights the interplay between localized field behavior and stability conditions under the imposed Lorenz-system-based boundary constraints.

5. Conclusion and Applications

Based on the derived equations and simulations, it is evident that if a photon interacts with a charge density, it alters the stability of the system. This interaction highlights the coupling between photons and fields, offering a deeper understanding of photon-field dynamics. These insights pave the way for further exploration into the interplay of quantum effects and field behavior under relativistic and chaotic conditions. The implications of this study extend to various fields:

1. Quantum Optics:

Enhancing the understanding of photon interactions in complex media, contributing to advancements in light-matter interaction models.

2. Photonics and Nano-Technology:

Informing the design of highly sensitive photonic devices, such as quantum sensors and optical circuits, that leverage photon-field dynamics.

3. Astrophysics and Cosmology:

Providing theoretical frameworks for understanding radiation interactions in high-energy astrophysical phenomena, such as pulsars and black hole accretion disks.

4. Fundamental Physics:

Offering a new perspective on stability and chaos in relativistic quantum systems, which could influence further developments in quantum electrodynamics (QED). This multifaceted approach underscores the importance of understanding photon-field interactions, opening new avenues for both theoretical research and practical applications.

The proposed modifications to Maxwell’s equations integrate quantum and relativistic considerations, offering a novel framework to understand electromagnetic field dynamics in the presence of photons. By incorporating the effective potential and deriving a fourth-order differential equation, this study bridges classical electromagnetism with quantum mechanics, capturing phenomena that extend beyond the limitations of traditional Maxwellian theory. The higher-order derivatives encapsulate rapid and nonlinear variations in field behavior, while the inclusion of chaotic boundary conditions provides a robust mechanism to explore stability and quasi-stability in complex electromagnetic systems. These advancements allow for the examination of photon-field interactions under intense and non-equilibrium conditions, addressing scenarios where conventional approaches fail to provide accurate predictions. This extended framework enhances our ability to analyze photon-mediated interactions, offering deeper insights into phenomena such as photon-photon interactions, field instabilities, and high-frequency electromagnetic modes. Furthermore, the synergy between chaotic dynamics and quantum field theory opens avenues for novel applications in photonics, quantum optics, and high-energy astrophysical phenomena. By uniting quantum, relativistic, and chaotic perspectives, this work enriches the theoretical foundation of field interactions, contributing significantly to the understanding of nonlinear and high-intensity electromagnetic fields. Future explorations may leverage this framework to advance both fundamental physics and practical applications in cutting-edge technologies.