1. Introduction
Within the calibration of material models, the numerical results of a simulation model are compared with the experimental measurements. One common approach is to minimize the squared errors between the simulation response and the measurements, the so-called least squares approach [
1]. This minimization task can be solved by a single-objective optimization algorithm to obtain the optimal parameter set. The optimization procedure requires special attention, if the optimization task is not convex and contains several local minima, as discussed in [
2]. A recent overview of optimization techniques applied to solve a calibration task is given in [
3,
4]. Often a maximum likelihood approach [
1] is used to formulate the optimization goal. To ensure a successful identification with optimization techniques, the sensitivity of the model parameters with respect to the considered model outputs should be investigated initially, as discussed in [
5].
Additionally to the parameter values itself, the estimation of the parameter uncertainty due to scatter in the experimental measurements and inherent randomness of the material properties requires further investigations. Generally, probabilistic and non-probabilistic techniques have been developed to estimate the parameter uncertainty [
6]. A well-known probabilistic method is the maximum likelihood approach [
1,
7], which uses a straight-forward linearization to represent the parameter scatter as a multi-variate normal distribution. A generalization of this method is the Bayesian updating technique [
1], where the joint distribution function of the model parameters could also be non-normally, but can be obtained only implicitly from the model input-output dependencies in the general case. A good overview and recent developments of this technique are given e.g. in [
8,
9,
10,
11]. Since the parameter distribution function can be obtained in closed form only for special cases, inverse sampling procedures such as Markov Chain Monte Carlo methods (MCMC) are usually applied to generate discrete samples of the unknown multidimensional parameter distribution [
12]. Most of these methods rely on the original Metropolis-Hastings algorithm [
13]. However, the MCMC methods usually require a large number of model evaluations and surrogate models are often applied to reduce the numerical burden of the identification procedure [
2,
14]. Recent developments utilize Bayesian neural networks to represent the forward simulation model including the corresponding parameter and responses uncertainty in a probabilistic approximation model [
15,
16,
17]. Alternatively to the ordinary least squares formulation, Kalman filter identification has been introduced [
18] and recently applied for material parameter identification in [
19,
20]. This technique is a Bayesian estimator using prior information to identify the parameters. However, all the mentioned probabilistic methods require an accurate estimate of the measurement covariance matrix, which is often not available.
Additionally to probabilistic methods, interval approaches have been developed which model the uncertainty of the model inputs and outputs as interval numbers [
21,
22] or confidence sets [
23]. Based on this assumption, interval predictor models have been used for model parameter identification [
24]. The unknown model parameter bounds can be obtained for inverse problems from the given model output bounds by interval optimization methods [
25,
26]. In [
27] interval optimization was introduced for fuzzy numbers to obtain a quasi-density of unknown model outputs in forward problems. However, this method can also be applied to inverse problems, which usually results in minimum and maximum values for each parameter considered in the model calibration. In [
28,
29] bounding boxes have been used to represent the multidimensional domain of the feasible input parameter space. This idea has been extended quite recently to consider correlations between the model parameters [
30,
31].
In the following paper, we will investigate different methods to estimate the uncertainty of the calibrated parameters from given measurement uncertainty. Using the classical probabilistic approaches as the maximum likelihood estimator and the Bayesian updating procedure as benchmark methods, the scatter of the identified parameters will be estimated as a multi-variate probability density function. Furthermore, we present an interval-based approach by assuming the scatter of the measurements not as correlated random numbers but as individual intervals with known minimum and maximum values. The corresponding possible minimum and maximum values for each input parameter will be obtained using a constrained optimization procedure. Furthermore, the identification of the whole feasible parameter domain for the given measurement bounds is obtained by a novel radial line-search method, which is extended for more than two model parameters using Fekete point sets on a unit hypersphere. With help of this approach, a uniform discretization of the feasible parameter domain boundary is obtained. Furthermore, we put emphasis on the initial sensitivity analysis, which should be considered for all approaches to neglect unimportant parameters in the calibration procedure. As numerical examples, we identify first the material parameters of a bilinear elasto-plasticity model and second the fracture parameters of plain concrete with respect to a wedge splitting test.
2. Materials and Methods
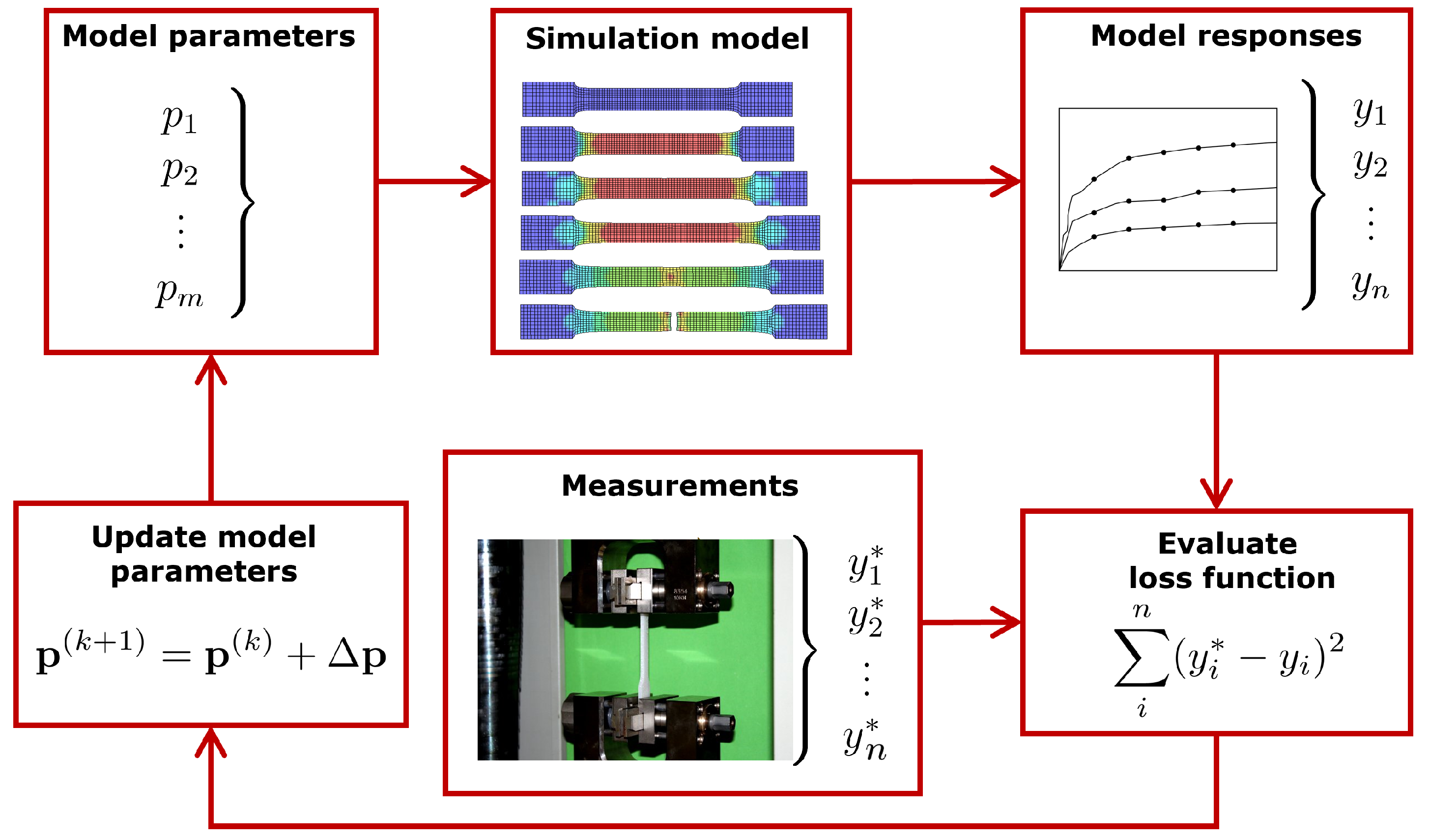
Within the calibration of material models, the numerical results of a simulation model
are compared with the experimental measurements
as illustrated in
Figure 1. One common approach is to minimize the squared errors between the simulation response and the measurements, the so-called least squares approach [
1]:
This minimization task can be solved by a single-objective optimization algorithm to obtain the optimal parameter set
. The optimization procedure requires special attention, if the optimization task is not convex and contains several local minima, as discussed in [
2].
2.1. Sensitivity Analysis of the Forward Problem
In order to obtain a sufficient accuracy of the calibrated model parameters, a certain sensitivity of these parameters with respect to the model responses is necessary. If all model responses are not sensitive with respect to a specific parameter, this parameter can not be identified within an inverse approach. In such a case, a non-sensitive parameter should be kept fixed and not considered in the calibration process.
A quite common approach for a sensitivity analysis is the global variance-based method using Sobol indicices [
32,
33]. In this method, the contribution of the variation of the input parameters with respect to the variation of a certain model output can be analyzed. Originally, this method was introduced for sensitivity analysis in the context of uncertainty quantification, but it can similarly apply for optimization problems as discussed in [
34]. If we define lower and upper bounds for the
m unknown model parameters
we can assume a uniform distribution for each parameter
The variance contribution of the parameter
with respect to a model output
can be quantified with the first order sensitivity measure introduced by [
32]
where
is the unconditional variance of
and
is called the
variance of conditional expectation with
denoting the set of all parameters but
.
measures the first order effect of
on the model output. Since first order sensitivity indices quantify only the decoupled influence of each parameter, the total effect sensitivity indices have been introduced by [
33] as follows
where
measures the first order effect of
on the model output which does not contain any effect corresponding to
.
Generally, the computation of
and
requires special estimators with a large number of model evaluations [
34]. In [
35] regression based estimators have been introduced, which require only a single sample set of the model input parameters and the corresponding model outputs. One very simply estimator for the first order index is the squared Pearson correlation coefficient
The Pearson correlation assumes a linear dependence between model input and output. If this is fulfilled, the sum of the first order indices should be close to one. However, if the model output is a strongly nonlinear function of the parameters, the sum is smaller than one and a reliable estimate is not possible with this approach.
With the Metamodel of Optimal Prognosis (MOP) [
35] a more accurate meta-model based approach for variance-based sensitivity analysis was introduced, where the quality of the meta-model is estimated with the Coefficient of Prognosis (CoP) by means of a sample cross-validation. If the CoP is close to one, the meta-model can represent the main part of the model output variation and thus the sensitivity estimates are sufficiently accurate. In the MOP approach, different types of meta-models such as classical polynomial response surface models [
36,
37], Kriging [
38], Moving Least Squares [
39] as well as artificial neural networks [
40] are tested automatically for a specific model output and evaluated by means of the CoP measure. This approach is available with the Ansys optiSLang software package [
41]. Further information on the CoP measure can be found in [
42]. The samples for the regression based estimators can be generated pure randomly within the defined parameter bounds. However, in order to increase the accuracy of the sensitivity estimates, we apply an improved Latin Hypercube sampling (LHS) [
43], which reduces the spurious correlations between the inputs parameters.
2.2. Maximum Likelihood Approach
In the maximum likelihood approach [
1,
7] the likelihood of the parameters is defined to be proportional to the conditional probability of the measurements
for a given parameter set
By assuming, that the chosen model can represent the material behavior perfectly, the remaining gap between model responses and experimental observations
can be explained only by measurement errors. In this case,
is equivalent to the probability of reproducing the measurement errors. Assuming a multivariate normal distribution for the measurement errors yields [
7]
where
is the covariance matrix of the measurement uncertainty. Maximizing the likelihood
L is equivalent to minimize
and yields to the following objective function
If the measurement errors
are assumed to be independent, the objective function equals a weighted least squares formulation
where the weight factor
for each measurement value is the inverse of its variance
. For constant measurement errors this objective simplifies to the well-known least squares formulation introduced in Eq.
1. In this case the optimal parameter set
can be obtained by the maximum likelihood approach with standard optimization procedures without exact knowledge of the measurement covariance matrix.
The objective function in Eq.
9 can be linearized as follows [
7]
where
is a sensitivity matrix, which contains the partial derivatives of the model responses with respect to the parameters
Assuming, that the optimal parameter set
has been found by minimizing the objective function, we can estimate the sensitivity matrix at the optimal parameter set e.g. by a central differences method.
Assuming a linear relation between the model parameters and responses, the covariance matrix of the parameters can be estimated with the so-called Markov estimator [
1,
7]
This covariance matrix
contains the necessary information about the scatter of the individual parameters, as well as possible pairwise correlations. The distribution of the parameters is Gaussian as assumed for the measurements. The estimated scatter and correlations are a very useful information to judge about the accuracy and uniqueness of the identified parameters in a calibration process. This method can be interpreted as an inverse first order second moment method: assuming a linear relation between parameters and measurements and a joint normal distribution of the measurements, we can directly estimate the joint normal covariance of the parameters. However, the application of this linearization scheme requires an accurate estimate of the optimal parameter set
by a previous least squares minimization. Furthermore, the inversion of the matrix in Eq.
13 requires, that every parameter is sensitive w.r.t. the model output. This should be investigated with an initial sensitivity analysis, as explained in
Section 2.1.
The linearization in Eq.
11 is of course a simplification of the general nonlinear case and contains only the first term of the Taylor series expansion of the non-linear model responses. We will investigate the influence of this linearization by means of the second example in this paper. Further discussion on applicability of this approach for nonlinear models can be found in [
7] and [
2].
The evaluation of Eq.
13 requires an estimate of the measurement covariance matrix
. If a measurement procedure is repeated very often, this matrix can be estimated directly from measurement statistics. However, this is often not possible. A valid estimate could be to assume independent measurement errors. The resulting covariance matrix is then diagonal, where at least the scatter of the individual measurement points has to be estimated. From a few measurement repetitions only, this can be estimated straight forward. If even such information is not available, the measurement scatter can be assumed to be constant
for each output value
In this case, the estimated covariances of the parameters are directly scaled by the assumed measurement scatter
If only a single measurement curve is available for the investigated responses, the misfit of the calibration process can be used for a rough estimate. Assuming the measurement errors to be constant and independent, we obtained the following estimate
where
n is the number of measurement points.
The sensitivity matrix in Eq.
12 can be visualized as shown in the result section by normalizing the partial derivatives with respect to the parameter ranges
By using the variance formula for a sum of linear factors, we can estimate local variance-based first order sensitivity indices from this partial derivatives by assuming again a uniform distribution of the parameters within the defined bounds
2.3. Bayesian Updating
Another probabilistic method is the Bayesian updating approach [
1], which can represent non-linear relations between the parameters and the responses but requires much more numerical effort to obtain the statistical estimates. In this approach, the unknown conditional distribution of the parameters is formulated with respect to the given measurements by using the Bayes’ theorem as follows
The likelihood function
can be formulated as probability density function, whereby often a multi-normal distribution function is utilized similarly as by Markov estimator
The so-called prior distribution
can be assumed either from previous information or as a uniform distribution within initially defined parameter bounds. Since the normalization term
is usually not known, the posterior parameter distribution
could not be obtained in closed form. However, in such a case, Markov Chain Monte Carlo methods could be used to generate discrete samples of the posterior distribution. A recent overview of these methods is given in [
12]. For further details on Bayesian updating, the interested reader is referred to [
6]. In our study, the well-known Metropolis-Hastings algorithm [
13] is applied, which considers only the forward evaluation of the likelihood function to generate samples of the posterior distribution. Detailed benchmark investigations on the Metropolis-Hastings algorithm as well as an efficient approximation of the likelihood function can be found in [
2].
2.4. Interval Optimization
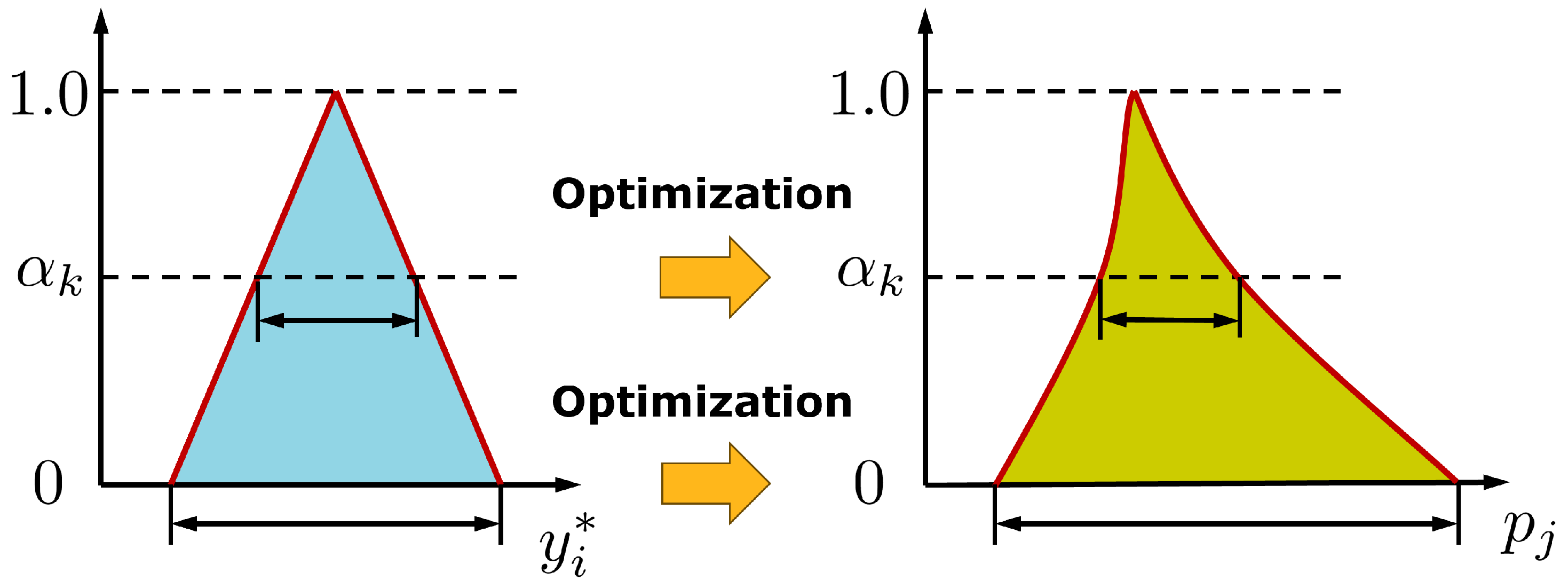
Instead of modeling the measurement points as correlated random numbers, which requires the estimate of the full covariance matrix, we can assume, that each measurement point is an interval number with known minimum and maximum bounds as shown in
Figure 2. For such a given interval of each measurement point, we want to obtain the corresponding range of the model parameters which fulfill
In the classical interval optimization approach, usually the interval of an uncertain response is obtained from the known interval of the input parameters by several forward optimization runs. A specific approach for this purpose, the
-level optimization [
27], as shown in principle in
Figure 2, where the most probable value is assumed for each input parameter with the maximum
-level and a linear descent to zero is defined between the maximum and the lower and upper bounds. The
-level optimization will detect the shape of the corresponding
-levels of the unknown outputs. In an inverse approach, we need to search for the possible minimum and maximum values of the input parameters
for a given level, while each response value
is constrained to the corresponding interval as defined in Eq.
21. The corresponding constraint optimization task can be formulated for each input parameter
as an individual minimization and maximization task as follows
where the specific
-level defines the lower and upper bounds
and
of each response value. This approach detects the lower and upper parameter bounds only and will not investigate possible interactions in the multidimensional parameters space. Therefore, we present a new radial line-search approach in the next section, which investigates the whole feasible domain of the possible model parameter values.
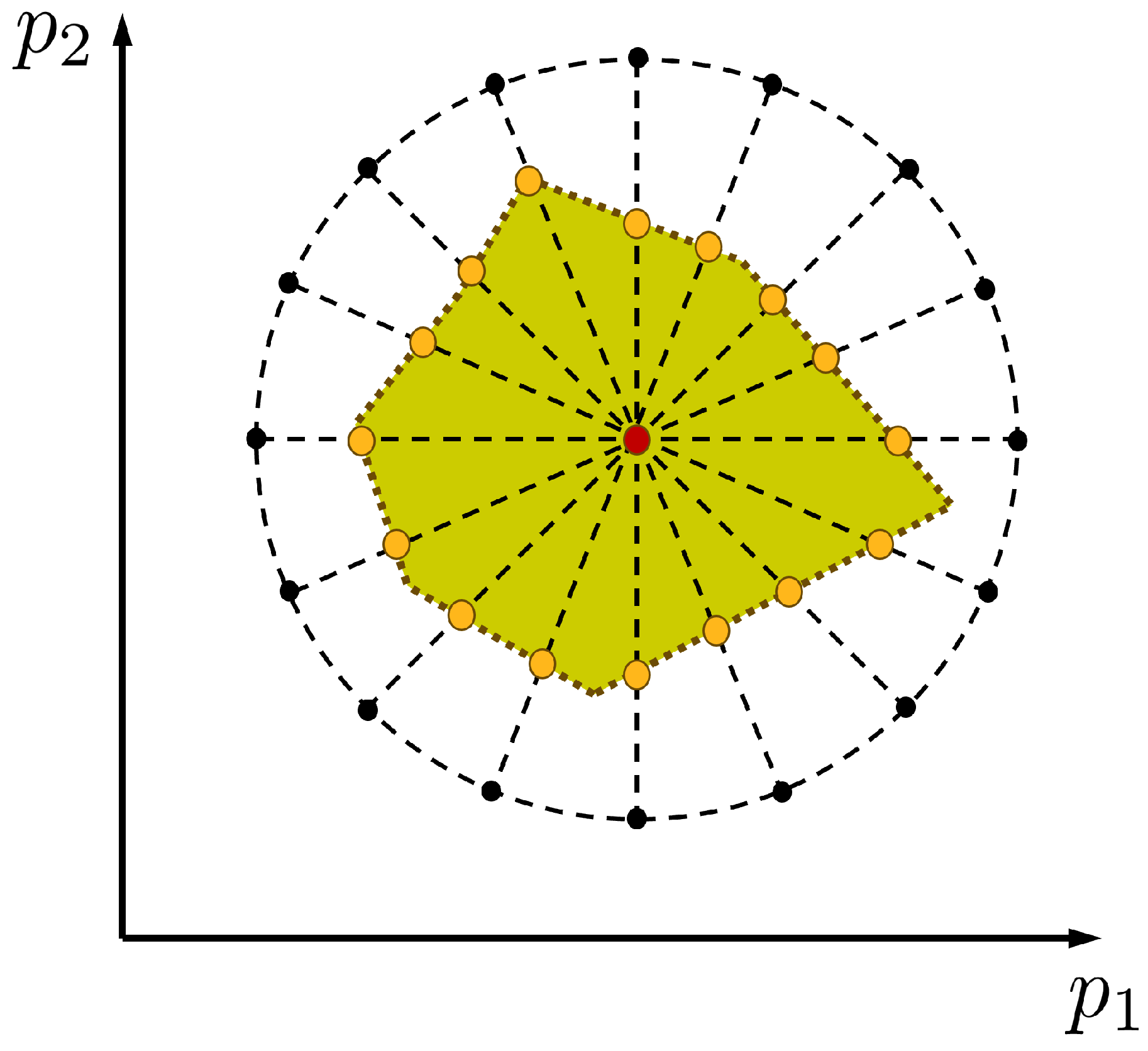
2.5. Radial Line-Search Approach
Assuming interval constrains for each response value
according to Eq.
21, the corresponding domain of the feasible input parameter domain
is defined as
This domain of feasible parameter sets
could be analyzed in case of two input parameters with a line-search approach as illustrated in
Figure 3: starting from the optimal parameter set
, we search in every direction for the maximum radius of the feasible parameter domain
where
is a direction vector of unit length
The direction vectors
can be chosen randomly or uniformly distributed as shown in
Figure 3 for two input parameters. For each direction a line-search is performed in order to obtain the maximum possible radius
for this direction. This search can be realized by bisection or other methods. The obtained boundary points
result in a uniform discretization of the feasible parameter domain
. This approach is similar to the directional sampling method developed for probability integration in reliability analysis [
44,
45].
In order to extend this method to more than two input parameters, the search directions
have to be discretized on a 3D- or higher dimensional (hyper-) sphere. One very efficient discretization method to obtain almost equally distributed points on the hyper-sphere are the Fekete point sets [
46], which are generated using a minimum potential energy criterion
where
is the number of points on the unit hyper-sphere. The minimization of the potential energy results in equally distributed point sets and will require a significant smaller number of model evaluations to obtain a suitable representation of the parameter domain boundary. An efficient optimization procedure to solve Eq.
26 is proposed in [
46]. Once the initial points have been generated, a line-search is performed for each of the search directions
similarly as in two dimensions. This search procedure is performed in our study by using a simple bisection method [
47]. However, since every direction can be evaluated independently, a parallel computing of the required model evaluations is possible. The obtained points on the boundary can be used to visualize a discretized shape of the feasible parameter domain. If more than two or three parameters are investigated, this visualization could be displayed in 2D or 3D subspaces.
3. Results
3.1. Bilinear Elasto-Plasticity Model
As a first example, we will investigate a uniaxial bilinear elasto-plasticity model defined as follows
where
is the uniaxial stress depending on the uniaxial strain
. The model parameters are the Young’s modulus
E, the yield stress
and the hardening modulus
H.
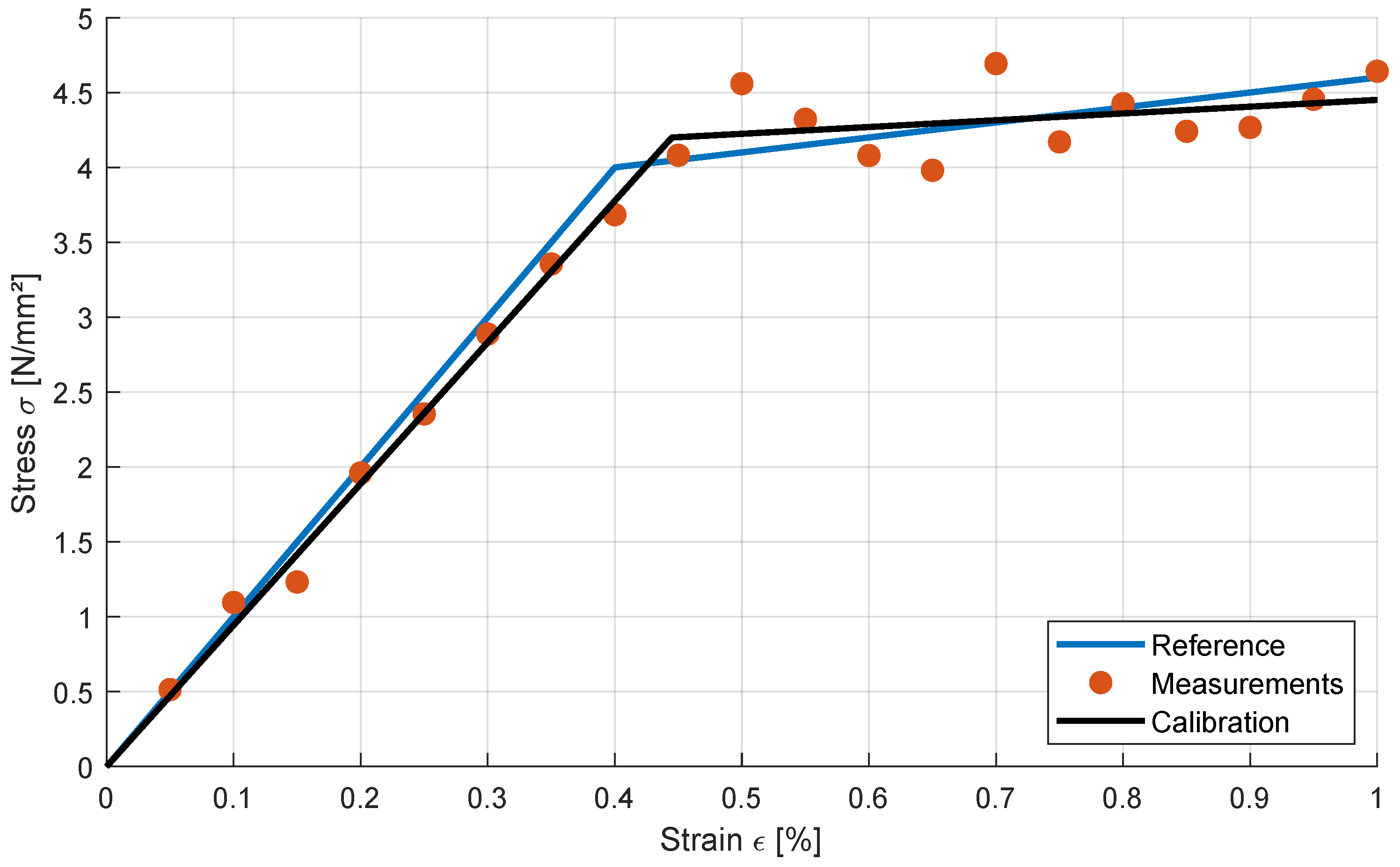
Figure 4 shows a reference curve for a selected parameter set
,
and
, which is used in the following investigations.
3.1.1. Deterministic Calibration with Noisy Measurements
By assuming additional uncertainties in the measurement points
, the obtained optimal parameter set could significantly deviate from the reference parameters as shown in
Figure 4, where an additional Gaussian noise term is used to generate synthetic measurement points
where
is a normally distributed random number with zero mean and unit variance. If we repeat the calibration of the model with different samples of the noise term, the calibrated optimal parameters will show a certain scatter, which depends on the size of the noise term. 1000 samples of the calibrated parameters are shown exemplarily in
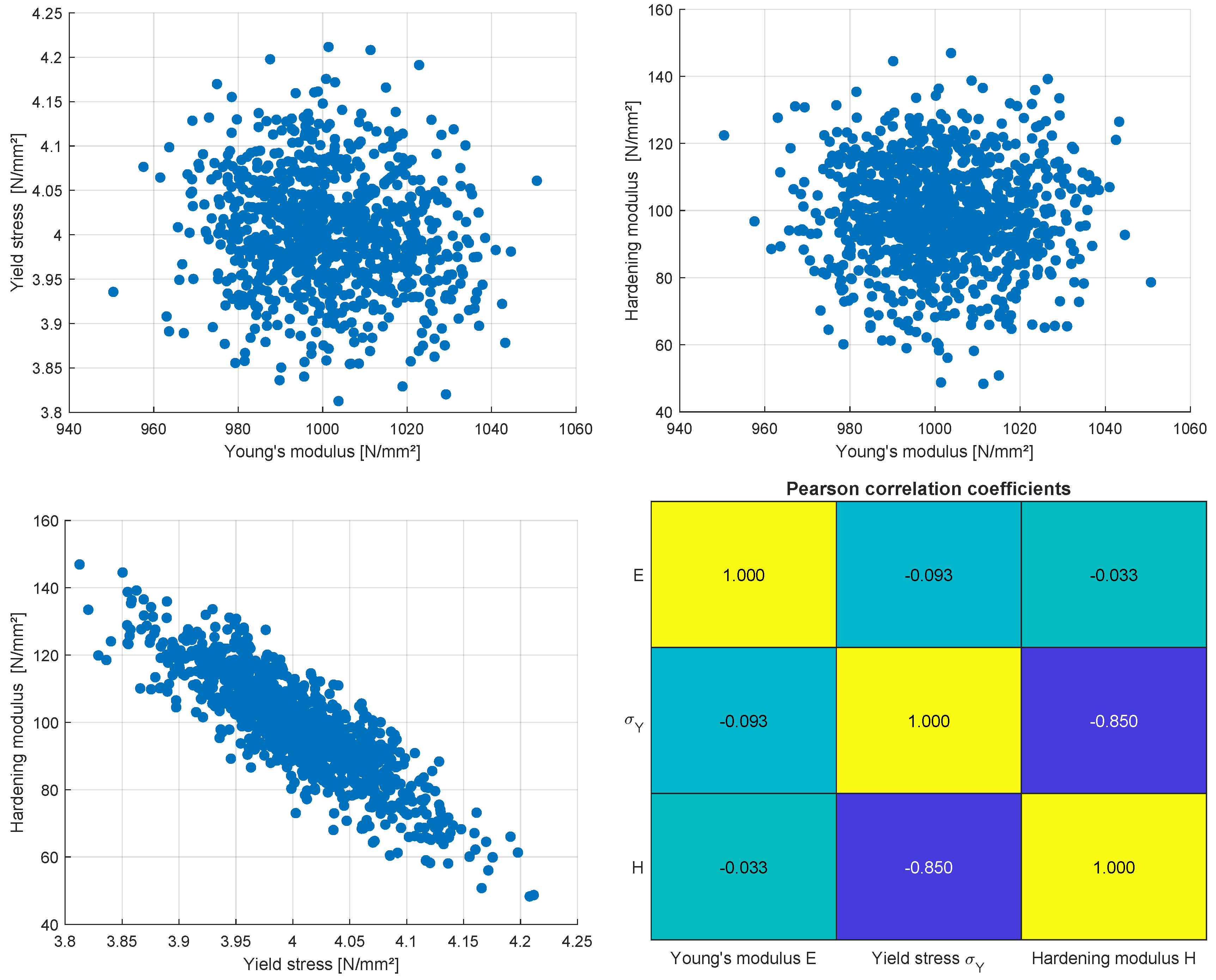
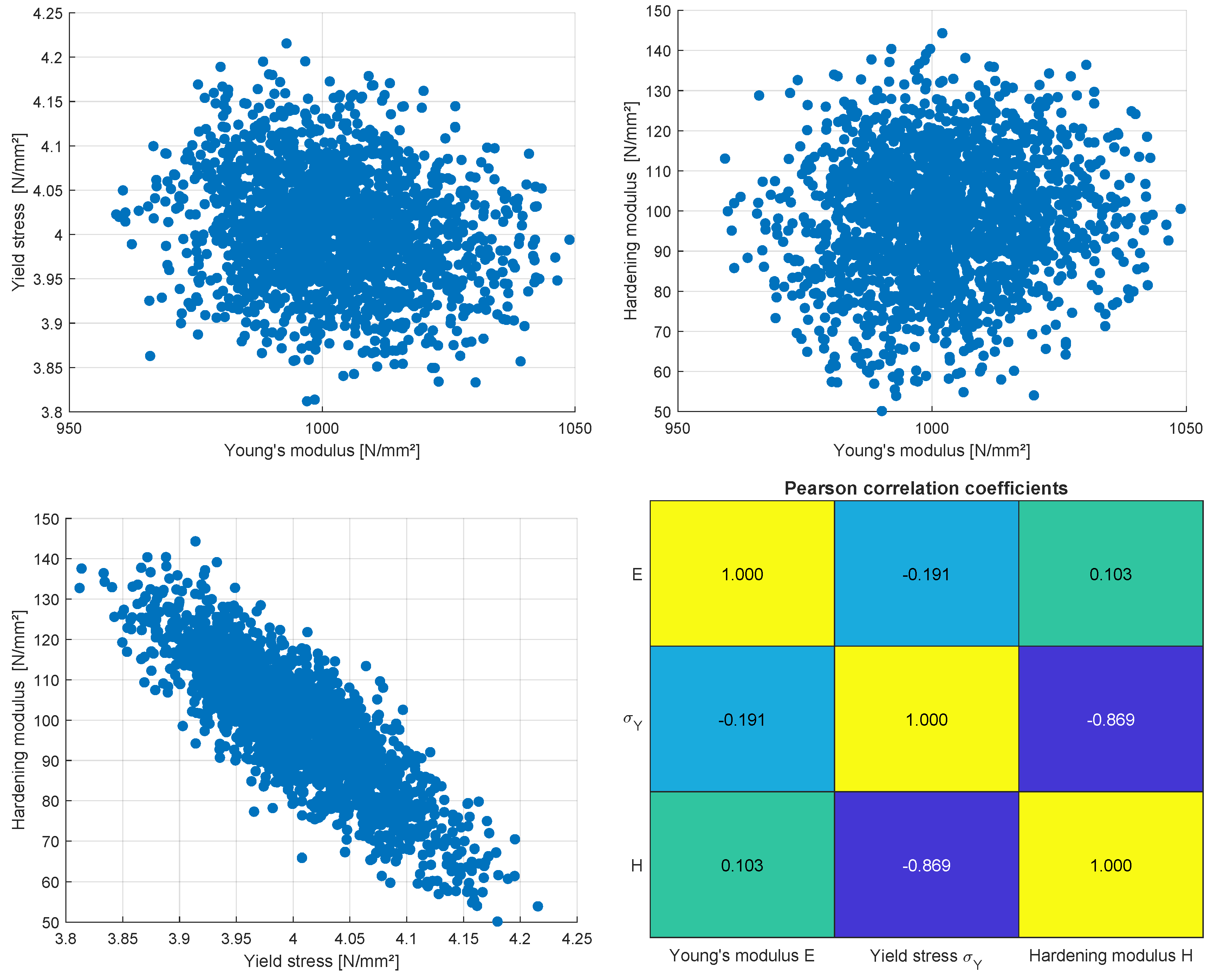
Figure 5 for a noise term of
by considering 20 measurement points as shown in
Figure 4. The figure indicates, that all three identified parameters show significant scatter and the yield stress and the hardening modulus show a significant correlation to each other.
3.1.2. Sensitivity Analysis
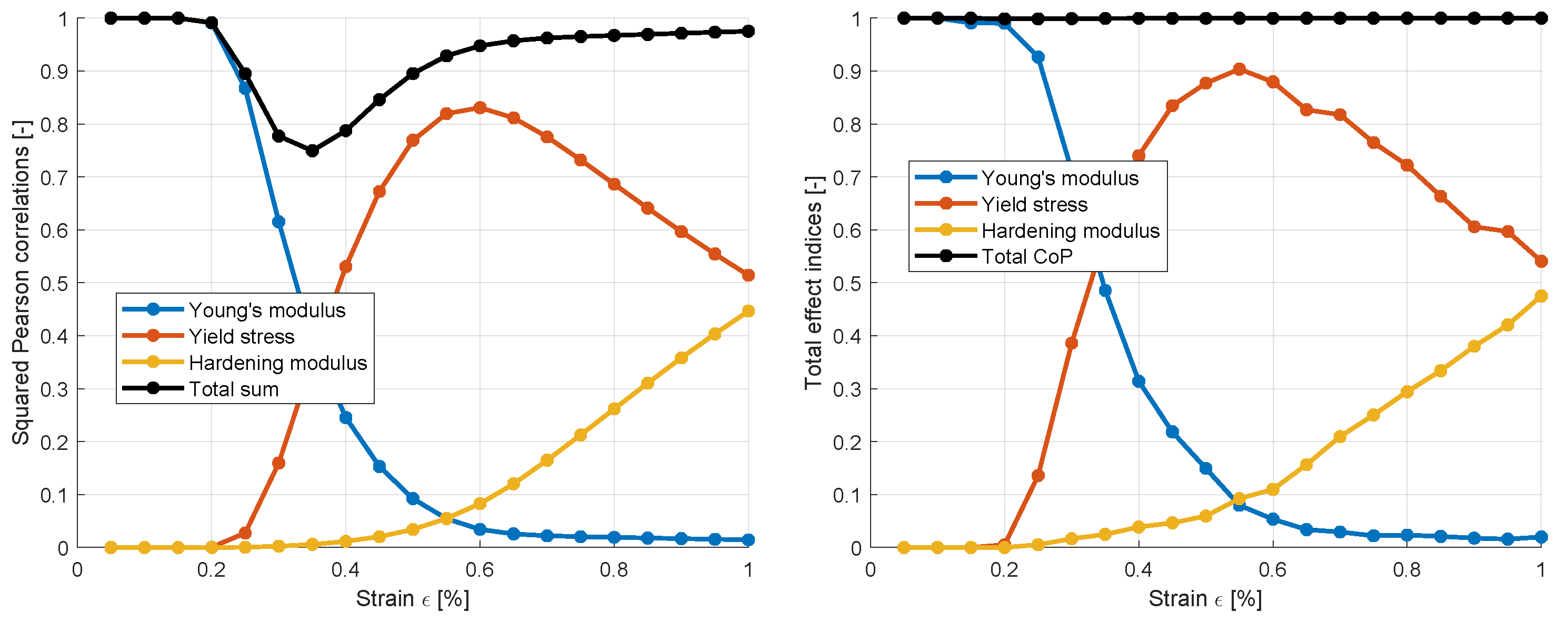
By means of the bilinear example, we will apply the presented probabilistic approaches and the interval optimization methods. Initially, we perform a sensitivity analysis to investigate the different estimators discussed in
Section 2.1. For this purpose, we calculate the sensitivity indices from the squared Pearson correlations by evaluating 20 points on the stress-strain curve. 1000 Latin Hypercube samples have been generated by considering the parameter bounds of
,
and
. The obtained sensitivity indices shown in
Figure 6 indicate, that the Young’s modulus has a significant influence for smaller strain values whereas the yield stress and the hardening modulus become more important with increasing strains. However, the sum of the individual sensitivity indices is not close to one for strain values between 0.2 and 0.6 % which is caused be the non-linear relation between these stress values with respect to the model parameters. The sensitivity indices by using the MOP approach are evaluated in a second step using the same 1000 samples. As indicated in figure, these estimates show a similar behavior as the correlation based estimates. However, the approximation quality of the underlying meta-model is almost excellent for all stress values. Thus, the estimated total effect indices are more reliable measures to judge on the sensitivity of the model parameters for this example.
3.1.3. Maximum Likelihood Approach
In a next step, the Markov estimator is applied using Eq.
13 to estimate the parameter covariance matrix from the measurement covariance matrix. Again, 20 measurement points are considered on the hardening curve with a constant measurement error of
. The covariance matrix is assembled according to Eq.
14. The required sensitivity matrix in Eq.
12 is estimated by using central difference at the optimal parameter set, which requires only 6 additional model evaluations. In
Figure 7 the estimated scatter of the parameters is visualized by generating 1000 samples of the estimated parameter covariances. The figure indicates a similar scatter and correlation of the parameters as obtained with the 1000 calibration runs in
Figure 5.
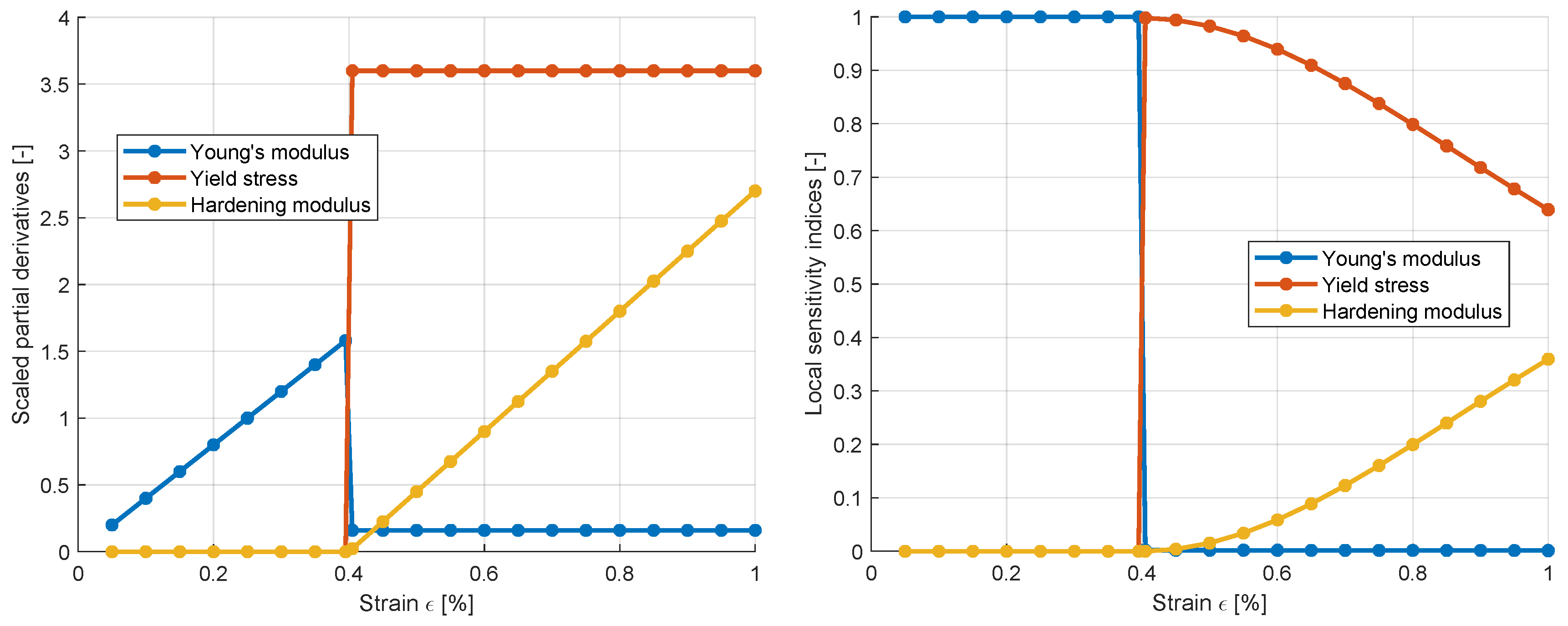
Figure 8 shows the normalized derivatives of the sensitivity matrix.
In a next step, the influence of the assumed measurement error
and the number of measurement points
is investigated.
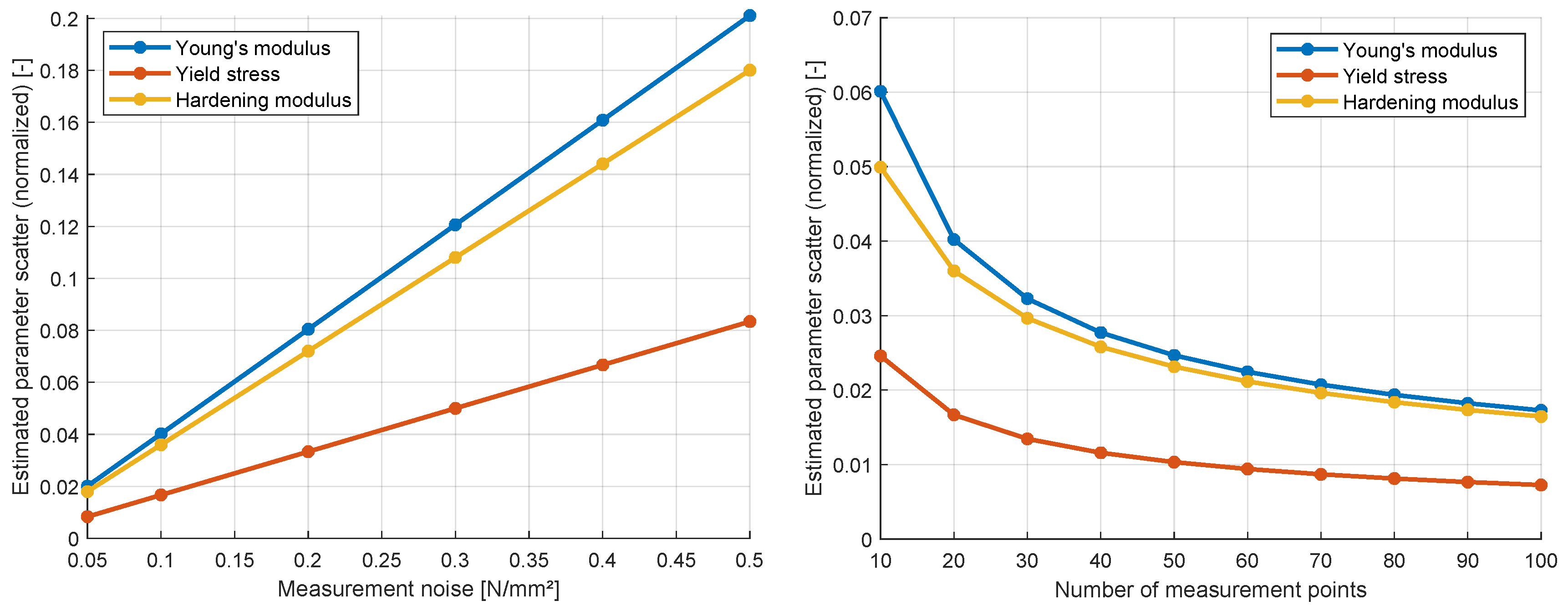
Figure 9 shows the estimated parameter scatter normalized with the parameter ranges depending on the size of an independent measurement error according to Eq.
14 for 20 measurement points. The figure indicates a linear relation of the standard deviation for all three parameters, as expected from the formulation in Eq.
15. The normalized parameter scatter of the yield stress is significantly smaller compared to the scatter of the Young’s and hardening moduli. This is caused by the fact, that sensitivity of the yield stress is on average larger as observed in the normalized partial derivatives in
Figure 8. Additionally, the influence of the number of measurement points is shown in
Figure 9 for a constant
. This figure clearly indicates, that with an increasing number of independent measurement points, the estimated scatter and thus the uncertainty decreases. This problem is investigated in detail in [
48] and could be resolved only, if a realistic correlation between the measurement points is assumed in the covariance matrix.
3.1.4. Bayesian Updating
The Bayesian updating approach is investigated next by using a constant measurement error
and a diagonal covariance matrix as within the previous investigations with Markov estimator. The posterior distribution in Eq.
19 is evaluated for the bilinear model using the Metropolis-Hastings algorithm with 20.000 samples, whereby the first 2.000 samples of the so-called burn-in phase are neglected in the statistical analysis. In
Figure 10 the estimated parameter scatter is shown. The pair-wise anthill plots and the correlation matrix indicate a good agreement with the results of the Markov estimator shown in
Figure 7. This may be explained by an approximately linear behavior of the model for small parameter variations.
In
Figure 11 the estimated mean values and the variation of the model response values are visualized for the generated samples. The figure indicates a good agreement of the mean response values with the deterministic reference curve. Around a deterministic yield strain of
a larger deviation could be observed. More interesting is the standard deviation of the individual stress responses. In contrast to the assumption of a constant measurement error of
, the variation of all stress values is smaller caused by the inherent correlations of the model responses.
3.1.5. Interval Optimization and Radial Line-Search
Next, the presented interval approaches are applied for the bilinear model by considering a constant measurement interval size of
. First, the minimum and maximum parameter values are obtained with 2 optimization runs for each model parameter by using an evolutionary algorithm from the Ansys optiSLang software package [
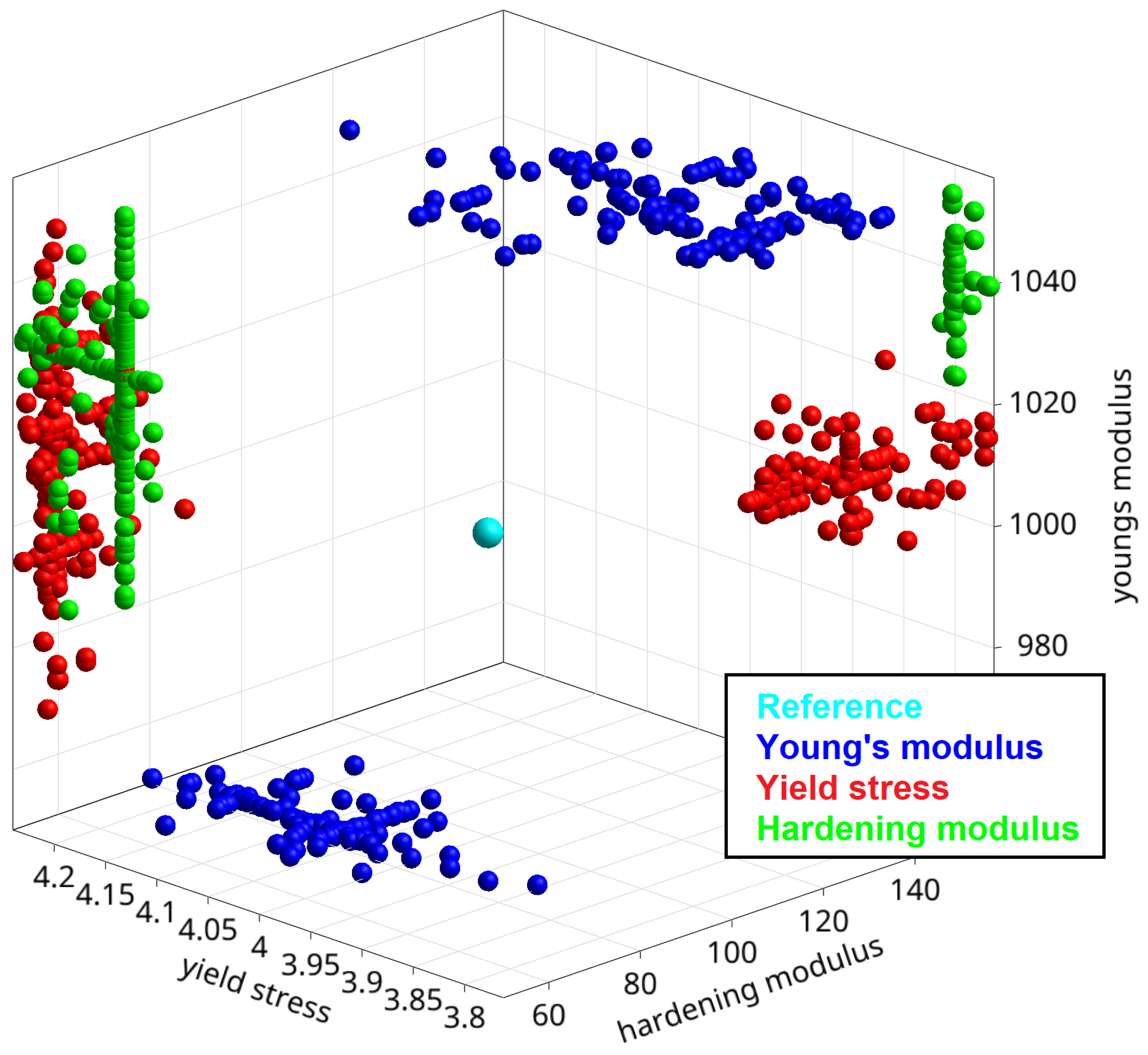
41] with 25 generations and a population size of 20. The obtained best parameter sets of each optimization run are shown in
Figure 12, which span a three-dimensional box around the reference parameter set.
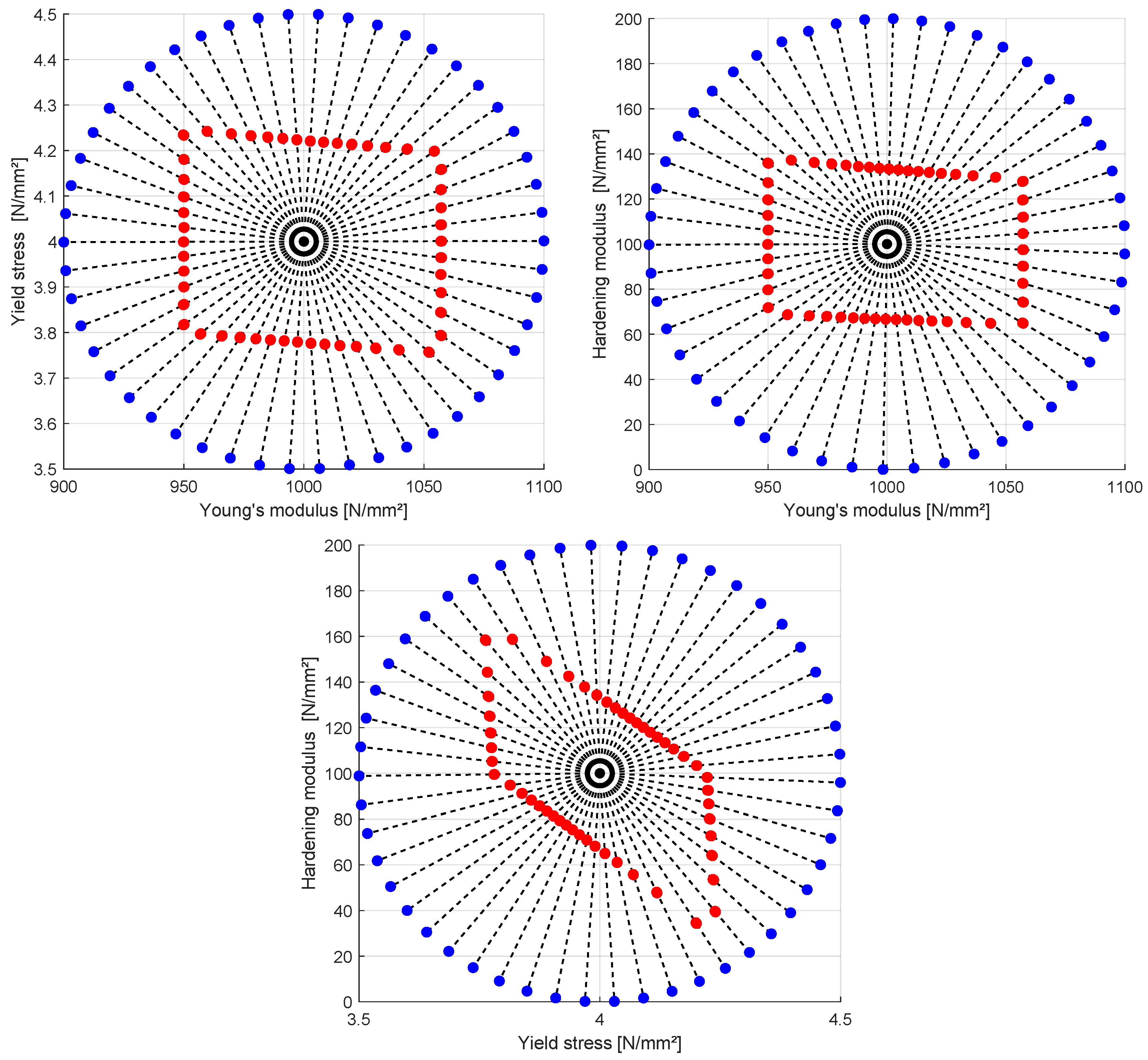
Second, the radial line-search approach is applied for different 2D subspaces by considering two model parameters as optimization variables while the third is kept at the reference value. In
Figure 13 the initial radial search points and the finally obtained boundary points are shown for all 2D subspaces. The initial parameter bounds have been chosen from the previous optimization results as
,
, and
and 50 uniformly distributed search directions are considered for each subspace. The subspace plots in
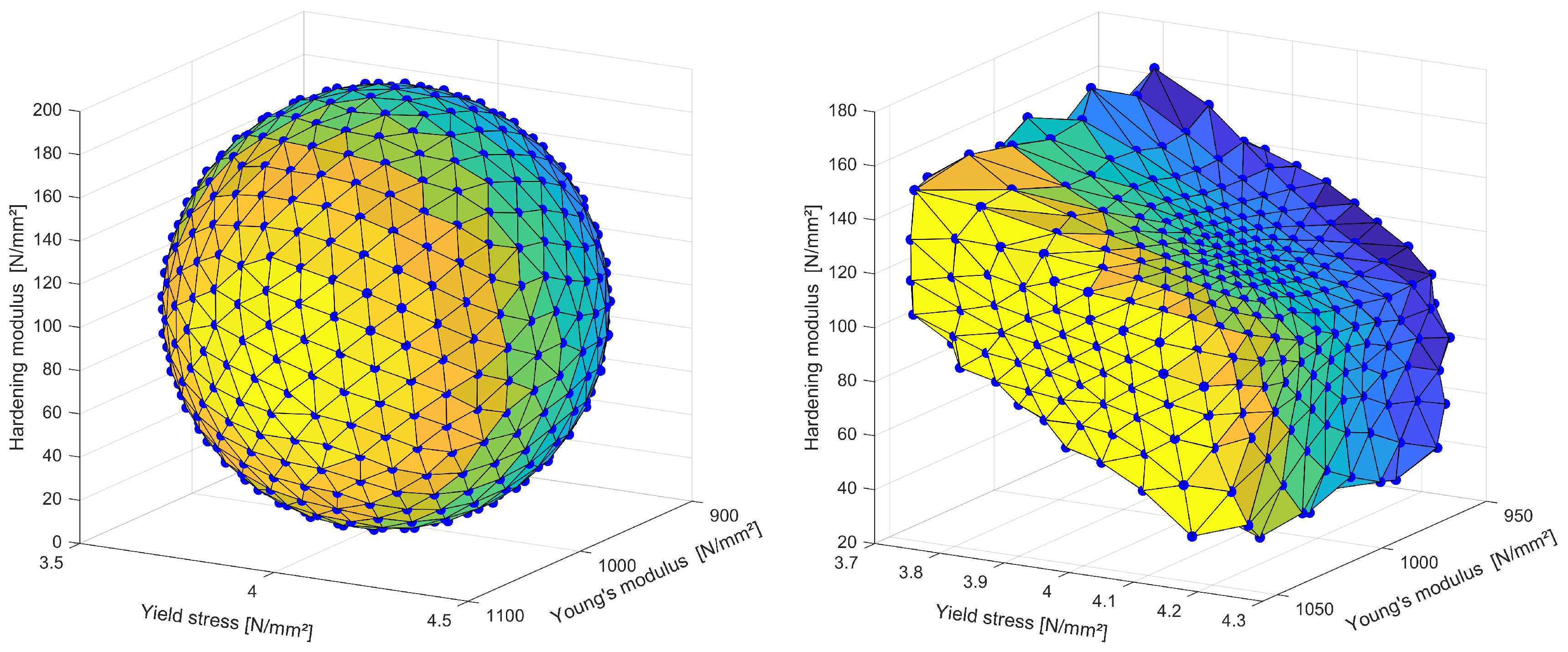
Figure 13 indicate an almost rectangular boundary of the feasible Young’modulus-yield stress subspace and of the Young’s modulus - hardening modulus subspace, meanwhile in the third subspace, the yield stress - hardening modulus subspace, the boundary indicates a significant dependence of the feasible parameter values.
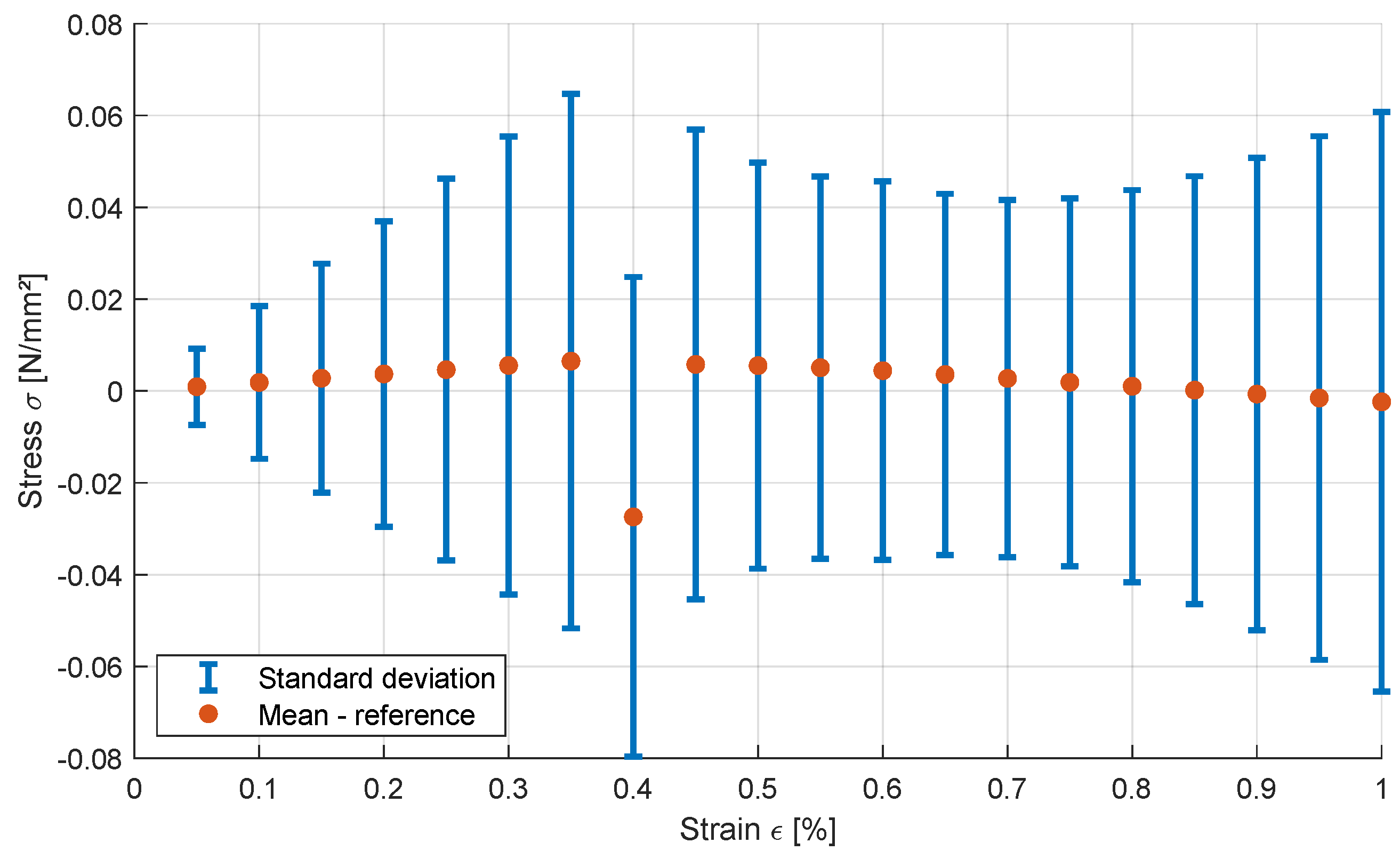
Finally, the bilinear example is investigated with the radial line-search with all three parameters. For this purpose, 500 uniformly distributed Fekete points are generated on the unit sphere by considering the parameter bounds of the 2D analysis. The line-search is performed for each direction individually with a bisection with 10 refinement steps. In
Figure 14 the initial search points are shown together with the obtained boundary points for all 500 directions. In the figure, a Delaunay triangulation of the convex hull of boundary points is used for better visualization purposes by utilizing the MATLAB plotting library [
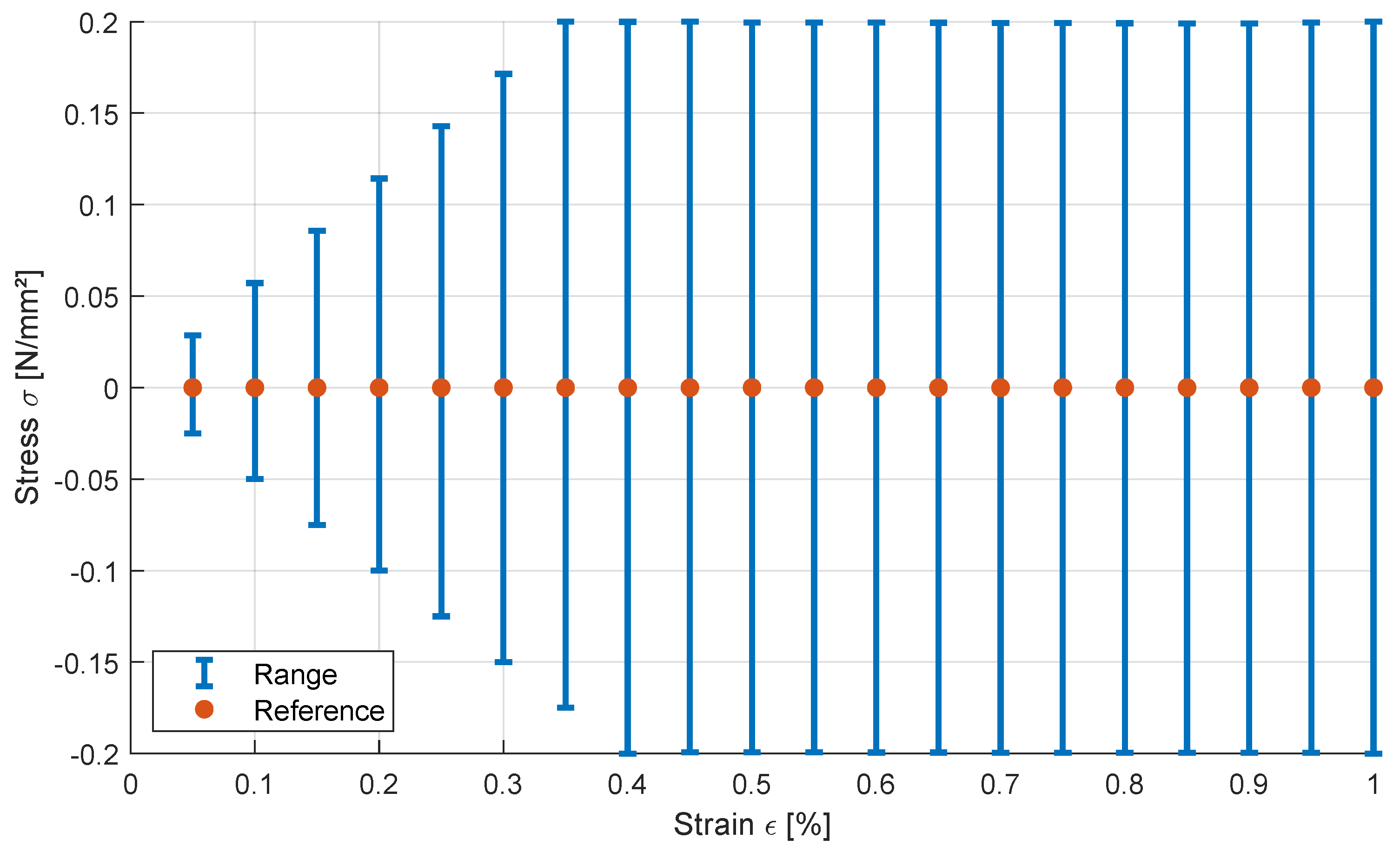
49]. The obtained feasible parameter domain indicates a dependence between yield stress and hardening modulus similar to the 2D analyses. The ranges of the response values of the obtained boundary points are given in
Figure 15, where the most values approach to the
interval. For strain values below
the maximum and minimum response values decrease linearly due to the pure elastic behavior and the resulting perfect correlation of the stress-strain curves.
3.2. Tension Softening Model for Concrete Cracking
3.2.1. Sensitivity Analysis and Deterministic Parameter Optimization
By means of the second numerical example, the material parameters of plain concrete are identified using the measurement results of a wedge splitting test published in [
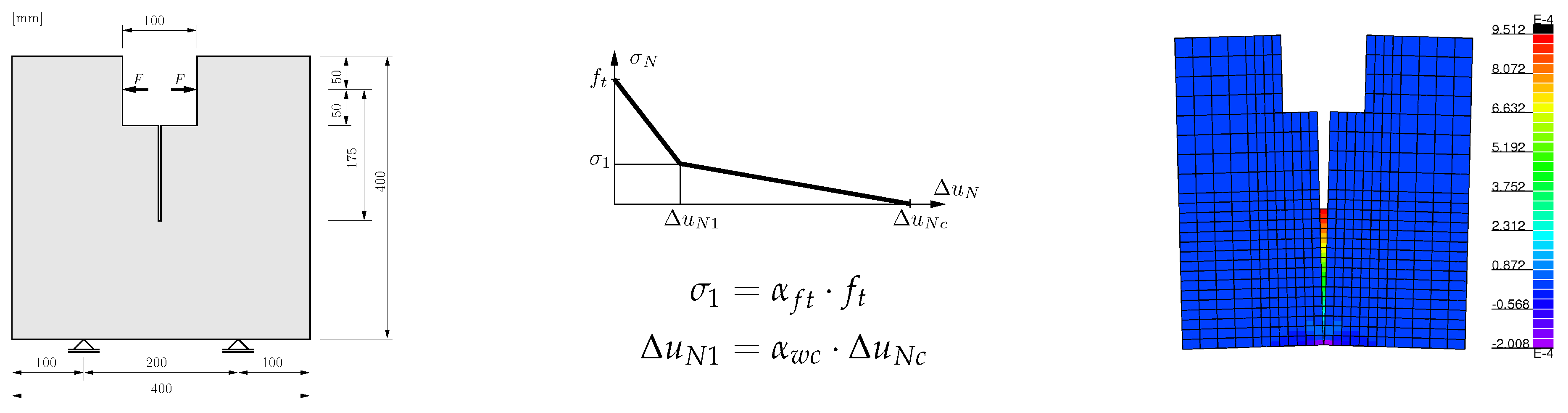
50]. The geometry of the investigated concrete specimen is shown in
Figure 16. The softening curve is obtained by a displacement-controlled simulation. The simulation model is discretized by 2D finite elements and considers an elastic base material and a predefined crack with bilinear softening law. The displacements are measured as the relative displacements between the load application points. Further details about the simulation model can be found in [
51].
Six unknown parameters are identified with the presented methods: the Young’s modulus
E, the Poisson’s ratio
, the tensile strength
, the Mode-I fracture energy
and the two shape parameters
and
, which define the kink of the bilinear softening law in terms of the tensile stress
and the relative displacements normal to the crack surface
. In
Table 1 the reference parameters according to [
50] and the defined parameter bounds for the calibration are given.
In a first step, the sensitivity of the material parameters with respect to the simulated force values is investigated by generating 200 samples within the defined bounds by using an improved Latin-Hypercube Sampling according to [
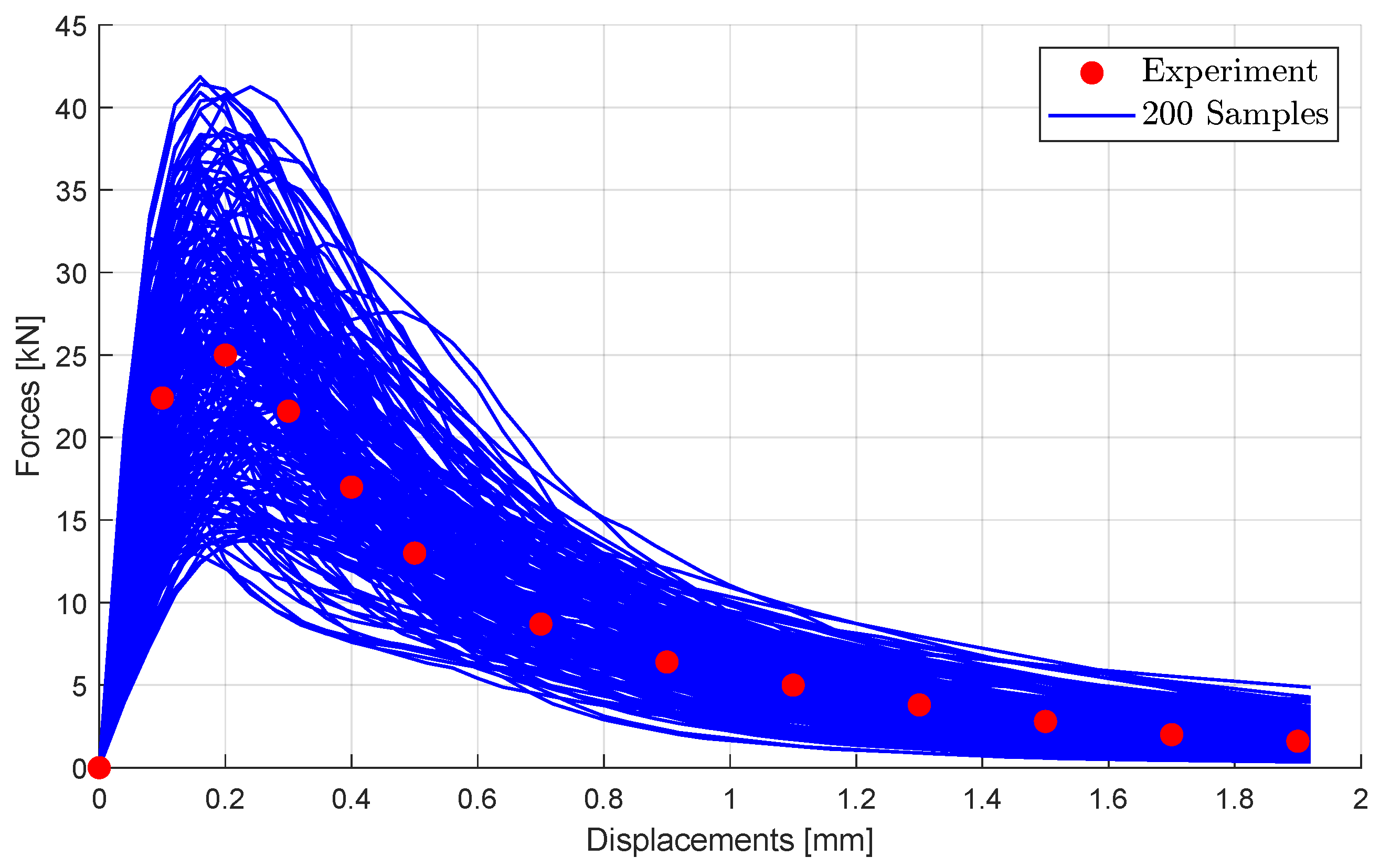
43]. The corresponding force-displacement curves of these samples are given in
Figure 17 additionally to the experimental values according to [
50]. The total effect sensitivity indices of the model parameters are estimated for each force value on the load-displacement curve by using the Metamodel of Optimal Prognosis [
35] approach, as discussed in
Section 2.1. These sensitivity indices are shown in
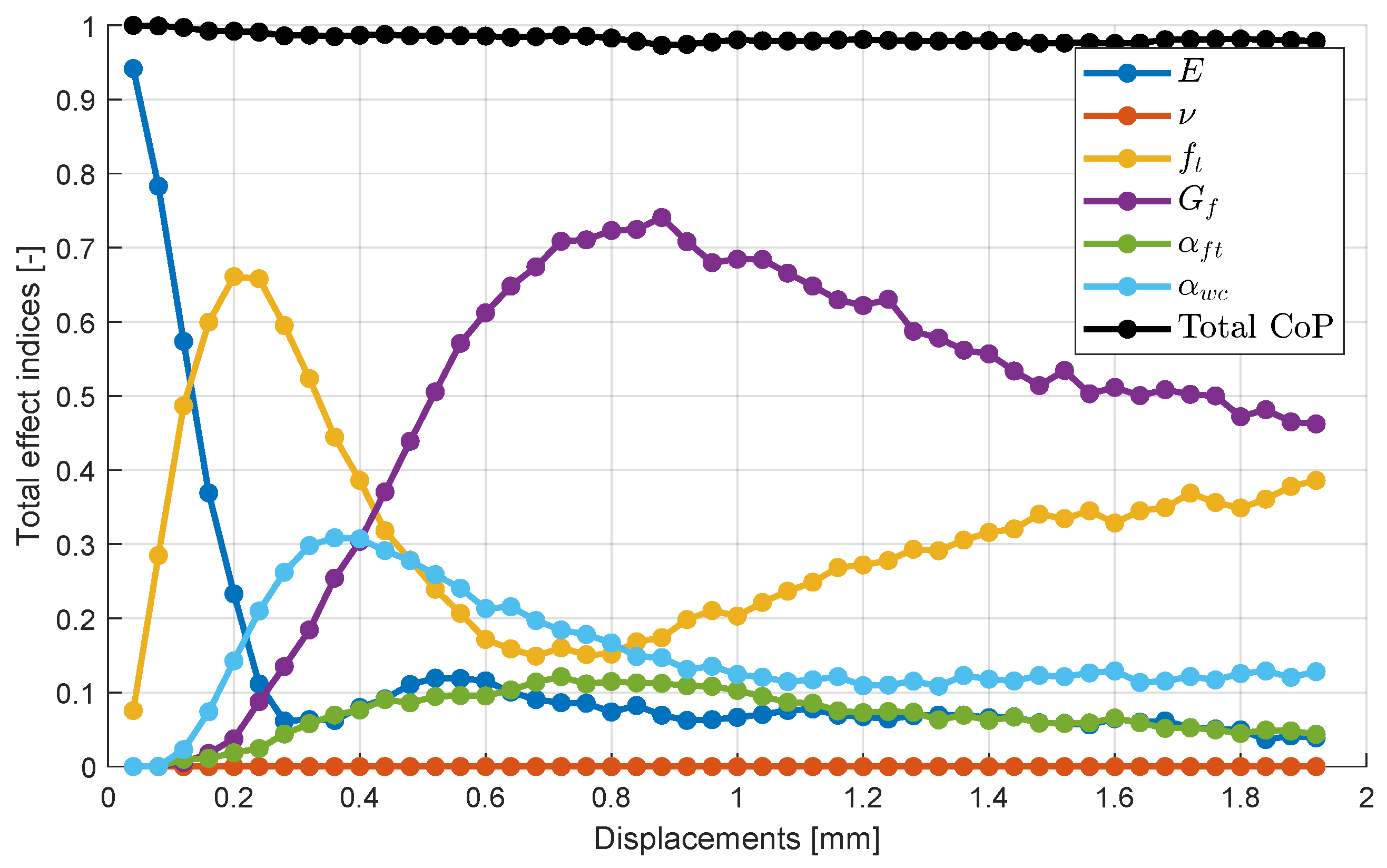
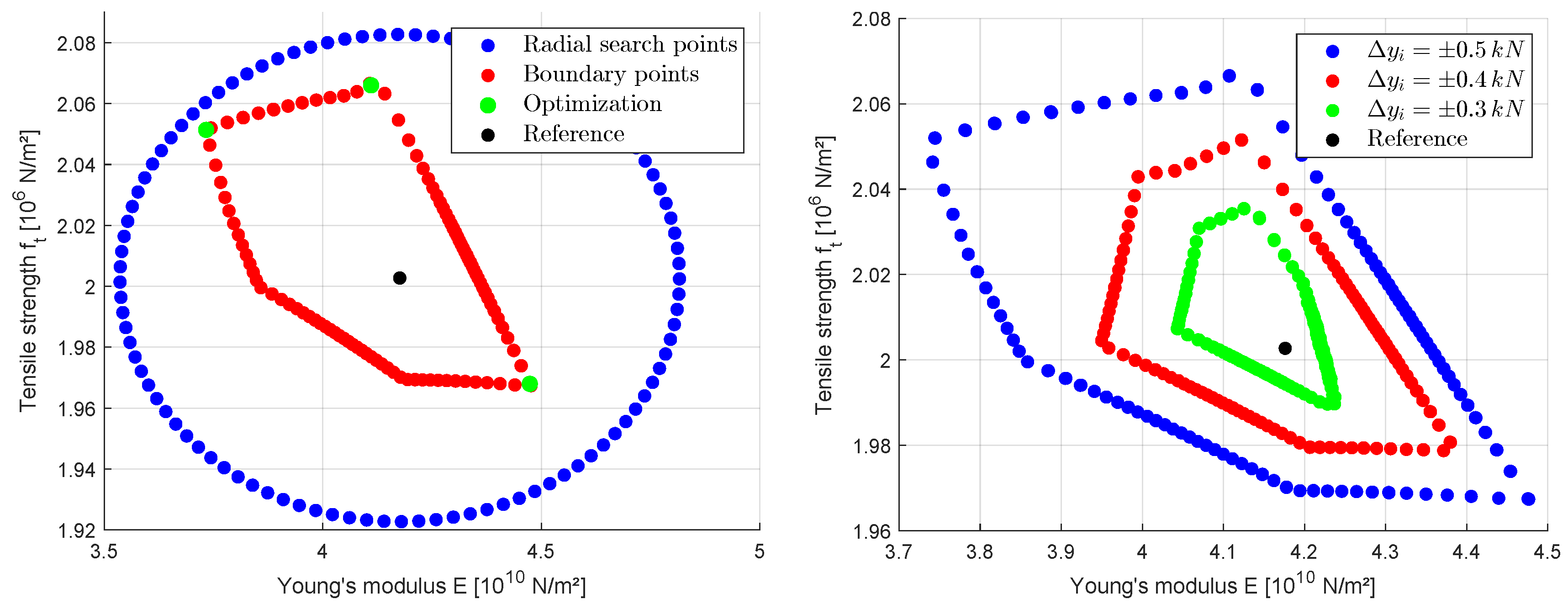
Figure 18 depending on the displacement values. The figure indicates, that the Poisson’ ratio is not sensitive to any of the simulation results. Because of this finding, we do not consider it in the following parameter calibration and uncertainty estimation. The other parameters show a certain influence whereby the Young’s modulus, the tensile strength and the fracture energy are most important.
The optimal parameter set is determined by a least-squares minimization using Eq.
1, whereby the deviation of the response values is evaluated at the 13 displacement values of the experimental measurement points. As optimization approach, an Adaptive Response Surface Method of the Ansys optiSLang software package [
41] is utilized, which required 220 model evaluations. The obtained optimal parameter values are given in
Table 1 and the corresponding load-displacement curve is shown in
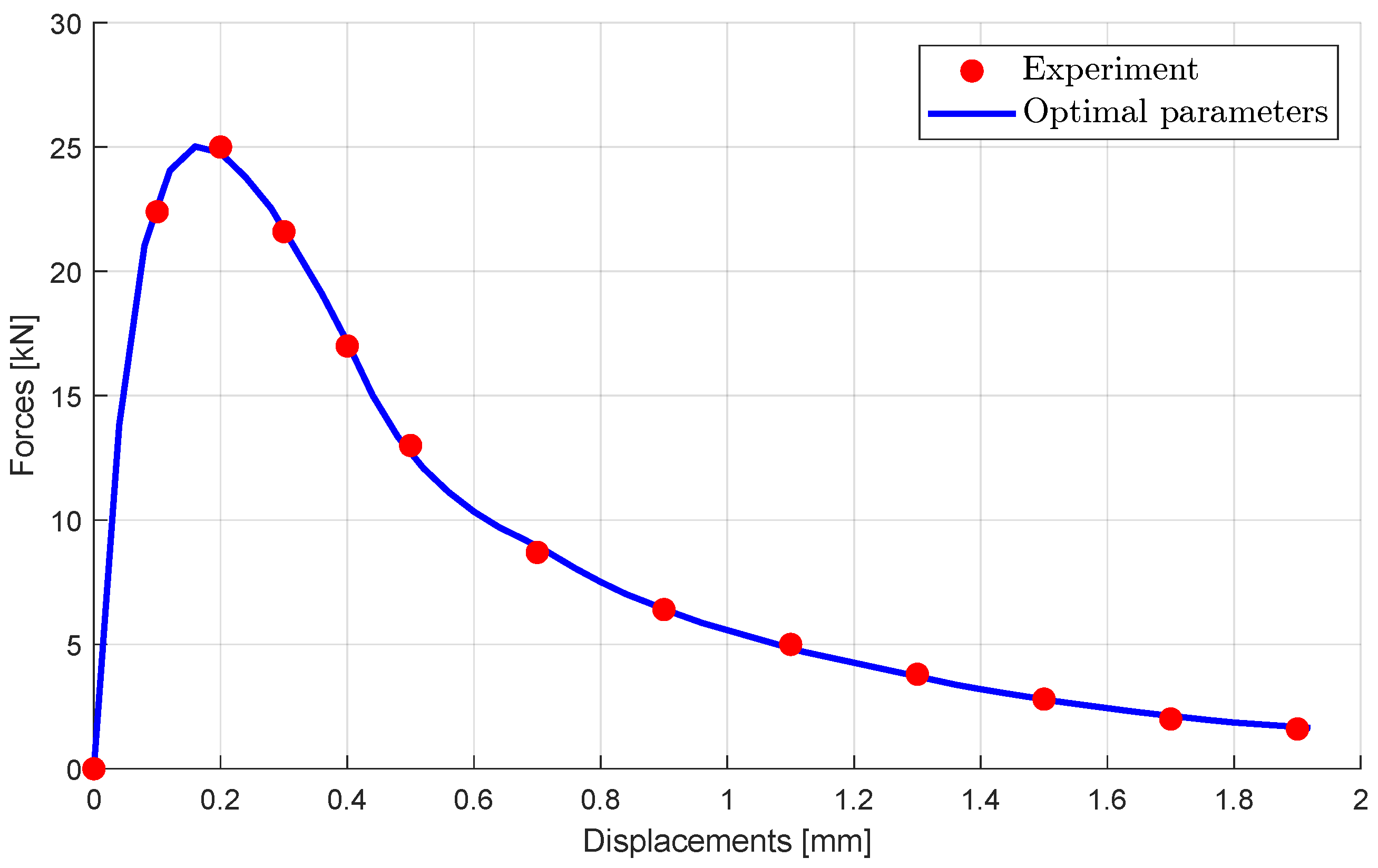
Figure 19, which indicates almost perfect agreement with the experimental values.
3.2.2. Probabilistic Uncertainty Estimation
In a next step, the Markov estimator and the Bayesian updating approaches are applied to estimate the parameter uncertainties. The covariance matrix of the 13 measurement points are defined accordingly to Eq.
14 as a diagonal matrix, whereby a constant standard deviation is assumed as the root mean squared error of the deterministic calibration as
The estimated parameter uncertainty using the Markov estimator are given in
Table 2. The mean values are the optimal parameter values from the previous deterministic optimization. The standard deviation and the parameter correlation matrix are obtained from the estimated covariance matrix by using Eq.
15. The partial derivatives required in Eq.
12 are estimated using a central differences approach with an interval of
of the initial parameter ranges. Thus, only 10 additional model evaluations were necessary to perform the Markov estimator for this example.
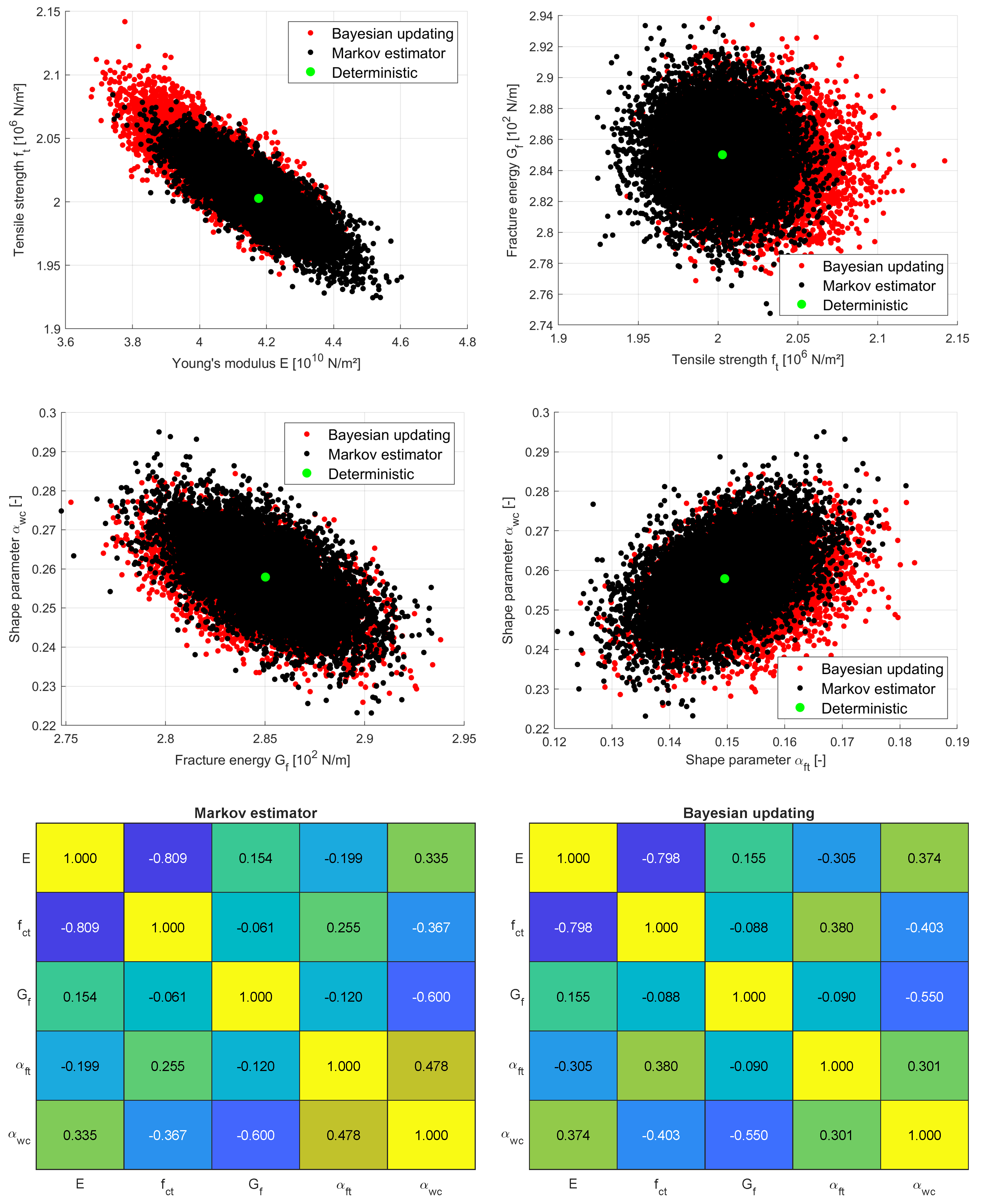
The results in
Table 2 indicate, that the shape parameters and the Young’s modulus have a significantly larger coefficient of variation (CoV) as the tensile strength and the fracture energy. This can be explained, if we compare the sensitivity indices of the parameters given in
Figure 18, where the fracture energy and the tensile strength have in average the largest values. The estimated parameter correlation matrix is given in
Figure 20, which indicate a significant correlation between the Young’s modulus and the tensile strength. Further dependencies could be observed between the fracture energy and one of the shape parameters. Additionally, the figure shows some interesting pair-wise anthill plots with 10.000 samples generated with the multi-variate normal distribution considering the estimated parameter covariance matrix of the Markov estimator.
Next, the Bayesian updating is performed with the same diagonal measurement covariance matrix used for the Markov estimator. 50.000 samples are generated with the Metropolis-Hastings algorithm, whereby 5.000 samples of the burn-in phase are neglected in the statistical analysis. The remaining 45.000 samples are shown additionally in
Figure 20. In
Table 2 the corresponding statistical estimates are given. The table and the pair-wise anthill plots indicate, that the mean values differ significantly from the Markov estimator results for the Young’s modulus and the tensile strength. Good agreement of the statistical properties is obtained for the fracture energy and the shape parameters. Even the estimated parameter correlations are quite close to the Markov estimator results.
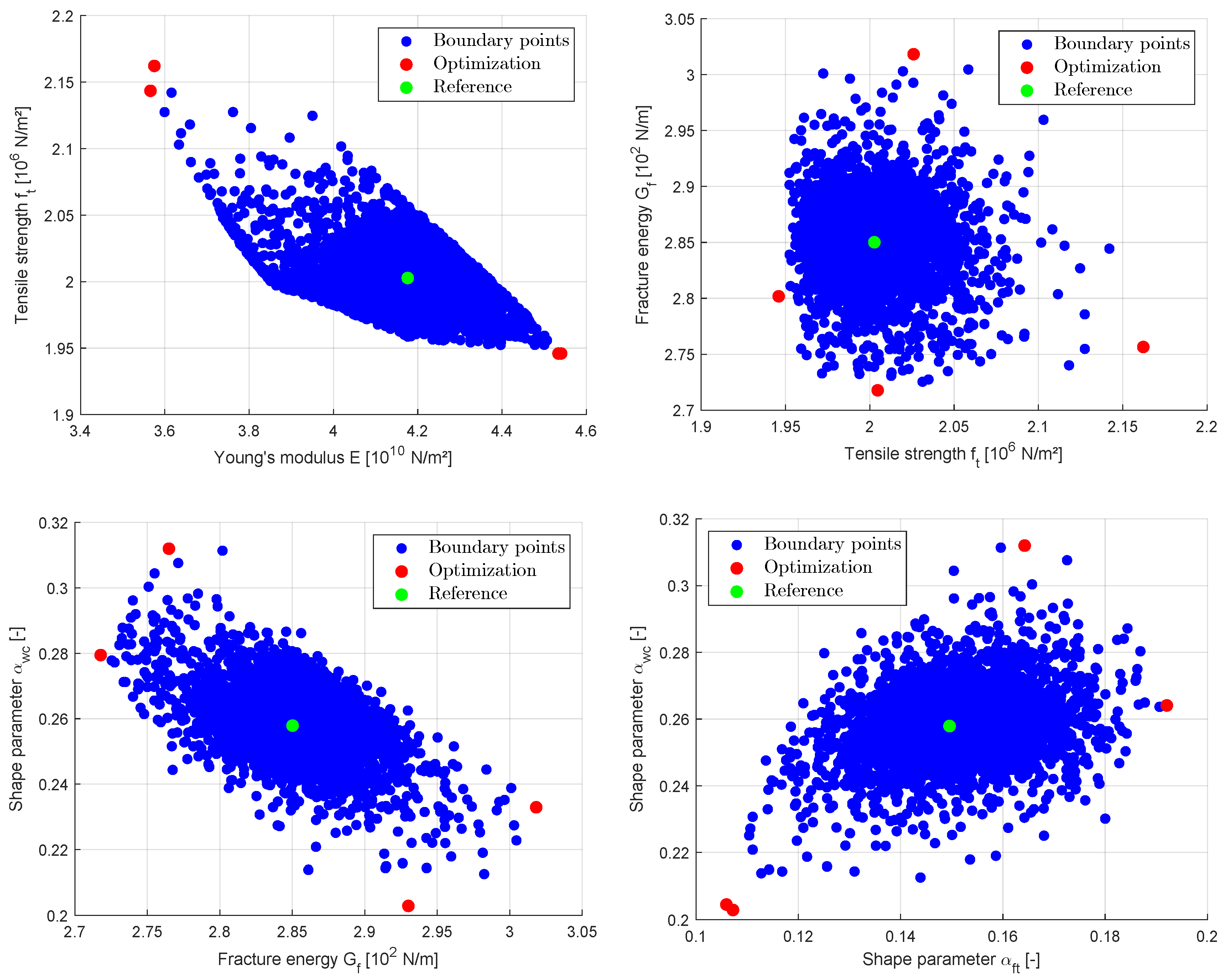
3.2.3. Interval Approaches
Finally, the proposed radial line-search algorithm is demonstrated by means of this example. In a first step, only the Young’s modulus and the tensile strength are considered as uncertain parameters, meanwhile the remaining parameters are kept constant. The resulting two-dimensional search points are shown in
Figure 21 for an assumed measurement interval of
, which corresponds to 3.3 times the RMSE. This interval is equivalent to the
confidence interval of the previously assumed measurement uncertainty. The figure clearly indicates, that the feasible 2D parameter domain is non-symmetric and bounded by different linear and non-linear segments. Different
-levels could be investigated, if the measurement interval is modified in the analysis.
Figure 21 shows additionally the domain boundary for different values of
, where a non-linear shrinkage of the domain boundary could be observed. The figure clearly indicates, that the obtained parameter domain boundary is not symmetric as assumed by the Markov estimator.
In a second step, all five sensitive parameters are considered in the radial line-search. 5.000 directions have been investigated in this analysis, where the ranges of the hyper-sphere are given in
Table 3. The table shows additionally the minimum and maximum possible parameters bounds obtained by the interval optimization approach by assuming the measurement interval as
. For each minimization and maximization task, again the evolutionary algorithm from the Ansys optiSLang software package [
41] with 25 generations and a population size of 20 was applied. The minimum and maximum parameter values are shown together with the obtained 5.000 boundary points of the radial line-search approach in
Figure 22 for some selected parameter subspaces. The figure indicates for the Young’s modulus and tensile strength a non-symmetric dependence. The dependence between the other parameters seems to be similar as the results obtained with the Bayesian updating.
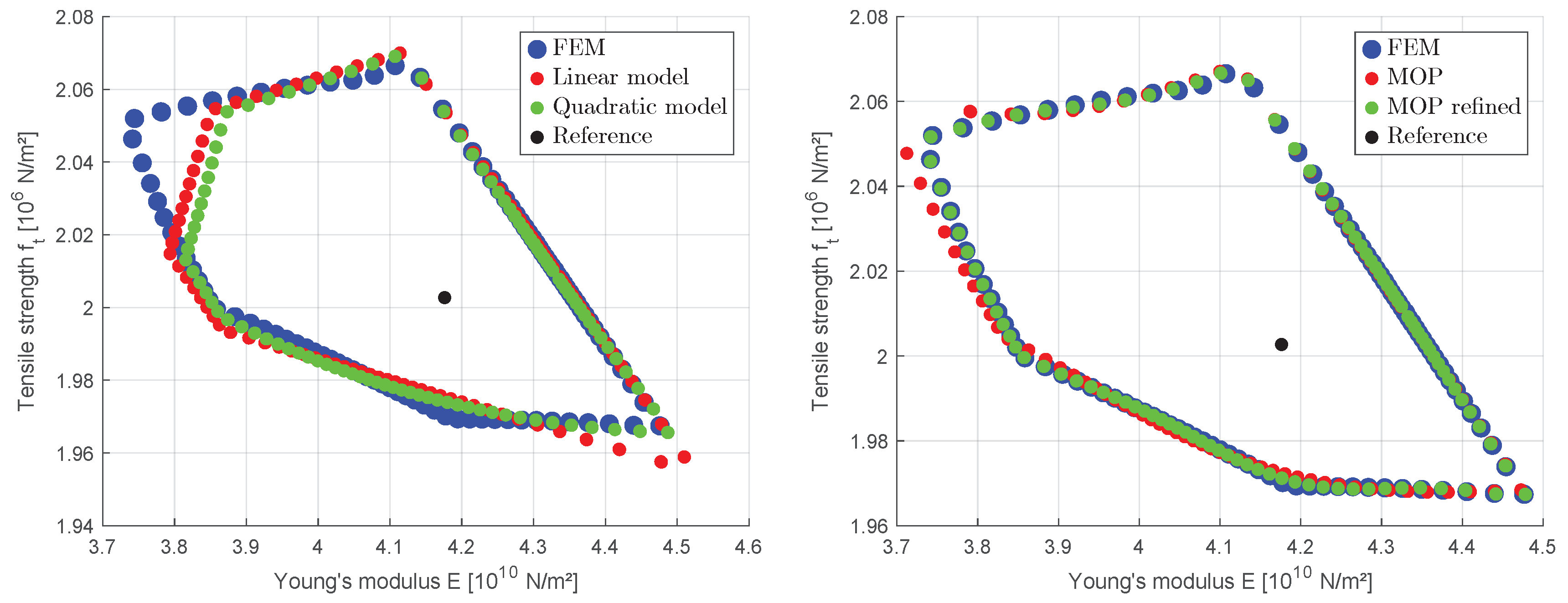
Since the evaluation of the radial line search requires a huge number of model evaluations, we will investigate the accuracy of different approximation methods by means of this example. First a linear approximation model from the 10 samples of the central differences approach within an interval of
of the initial parameter ranges is investigated. We apply the radial line-search on this 5D approximation model as investigated previously only in the 2D subspace of the Young’s modulus and the tensile strength as uncertain parameters, meanwhile the remaining parameters are kept constant. In
Figure 23 the results by using the original FEM model are compared to results obtained with the linear approximation model. The figure indicates already a sufficient accuracy, which represents the main characteristics of the feasible parameter domain. The 2D analysis has been chosen to enable a more clear visualization of the approximation errors.
Additionally, we apply a full quadratic approximation model based on 100 Latin-Hypercube samples generated within the
domain of all 5 parameters around the optimal parameter values
. The results of the 2D line-search shown in
Figure 23 are quite similar as obtained with the linear model, but still show a certain deviation from the FEM solutions. In order to get a better representation of the non-linear dependencies of the model responses and the model parameters in the range of the parameter scatter, we apply the Metamodel of Optimal Prognosis as a more sophisticated surrogate on the response values obtained from the 100 LHS samples within the
parameter ranges. As indicated additionally in
Figure 23, the straight forward application of the MOP already yields to quite accurate results. An additional improvement of the surrogate model could be achieved by considering the obtained 100 boundary points of the line-search procedure as additional support points within the surrogate model, which results in an almost perfect agreement of the line-search results.
4. Conclusions
In the presented paper we have investigated well-known probabilistic approaches as benchmark methods for the uncertainty quantification of calibrated material parameters. The applied Markov estimator and the Bayesian updating require the knowledge of the measurement covariances to estimate the multi-variate probability density function of the calibrated model parameters. Often this matrix can be estimated quite roughly based on few measurement curves. If the covariance matrix is assumed as a diagonal matrix this implies independent measurement errors and the estimated parameter scatter directly depends on the number of considered points on the measurement curve. As a consequence, the obtained results might be difficult to interpret and a successful application of the probabilistic approaches would require a more accurate estimate of the measurement covariance matrix.
In order to overcome this limitation, an interval optimization approach which assumes only the maximum and minimum values of the measurement points was extended in the presented paper. With help of this approach, the full feasible parameter domain fulfilling the defined measurement intervals could be determined by a novel radial line-search procedure, which will search for the boundary of the feasible parameter space based on the underlying simulation model. The boundary domain is discretized with uniformly distributed Fekete points, which define the radial directions based on the optimal parameter set obtained in the previous deterministic calibration. For each direction, the boundary point was obtained by a one-dimensional line-search procedure. Compared to previous interval search procedures as published in [
26,
30,
31], the presented approach does not require any assumption on the parameter correlation.
However, the computation requires numerous model evaluations but can be computed in parallel for each independent search direction. The computational burden could be reduced significantly by using either low order approximation schemes or by applying more sophisticated surrogate models on support points around the optimal parameter set. Here is place for further research in order to determine a fully automatic adaptive scheme based on surrogate models.
As a result of the presented approach, we obtain the boundary of the feasible parameter domain by means of a given number of discretization points in the parameter input space. The transfer to a closed description of the parameter uncertainty e.g. with correlated interval numbers is an open question which would motivate further research.
Author Contributions
All contributions by T. Most.
Funding
This research received no external funding.
Data Availability Statement
Datasets available on request from the author.
Acknowledgments
We acknowledge support for the publication costs by the Open Access Publication Fund of Bauhaus Universität Weimar and the Deutsche Forschungsgemeinschaft (DFG).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MCMC |
Markov Chain Monte Carlo |
| CoP |
Coefficient of Prognosis |
| CoV |
Coefficient of Variation |
| LHS |
Latin Hypercube Sampling |
| MOP |
Metamodel of Optimal Prognosis |
References
- Beck, J.V.; Arnold, K.J. Parameter estimation in engineering and science; Wiley Interscience: New York, 1977.
- Most, T. Identification of the parameters of complex constitutive models: Least squares minimization vs. Bayesian updating. In 15th working conference IFIP Working Group 7.5 on Reliability and Optimization of Structural Systems, Munich, April 7-10, 2010; 2010.
- Ereiz, S.; Duvnjak, I.; Fernando Jiménez-Alonso, J. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723.
- Machaček, J.; Staubach, P.; Tavera, C.E.G.; Wichtmann, T.; Zachert, H. On the automatic parameter calibration of a hypoplastic soil model. Acta Geotechnica 2022, 17, 5253–5273.
- Scholz, B. Application of a micropolar model to the localization phenomena in granular materials: general model, sensitivity analysis and parameter optimization. Phd thesis, Universität Stuttgart, Germany, 2007.
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mechanical Systems and Signal Processing 2015, 56, 123–149.
- Ledesma, A.; Gens, A.; Alonso, E. Estimation of parameters in geotechnical backanalysis — I. Maximum likelihood approach. Computers and Geotechnics 1996, 18, 1–27.
- Rappel, H.; Beex, L.A.; Noels, L.; Bordas, S. Identifying elastoplastic parameters with Bayes’ theorem considering output error, input error and model uncertainty. Probabilistic Engineering Mechanics 2019, 55, 28–41.
- Rappel, H.; Beex, L.A.; Hale, J.S.; Noels, L.; Bordas, S. A tutorial on Bayesian inference to identify material parameters in solid mechanics. Archives of Computational Methods in Engineering 2020, 27, 361–385.
- Bi, S.; Beer, M.; Cogan, S.; Mottershead, J. Stochastic model updating with uncertainty quantification: an overview and tutorial. Mechanical Systems and Signal Processing 2023, 204, 110784.
- Tang, X.S.; Huang, H.B.; Liu, X.F.; Li, D.Q.; Liu, Y. Efficient Bayesian method for characterizing multiple soil parameters using parametric bootstrap. Computers and Geotechnics 2023, 156, 105296.
- Lye, A.; Cicirello, A.; Patelli, E. Sampling methods for solving Bayesian model updating problems: A tutorial. Mechanical Systems and Signal Processing 2021, 159, 107760.
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109.
- de Pablos, J.L.; Menga, E.; Romero, I. A methodology for the statistical calibration of complex constitutive material models: Application to temperature-dependent elasto-visco-plastic materials. Materials 2020, 13, 4402.
- Unger, J.F.; Könke, C. An inverse parameter identification procedure assessing the quality of the estimates using Bayesian neural networks. Applied soft computing 2011, 11, 3357–3367.
- Lucas, A.; Iliadis, M.; Molina, R.; Katsaggelos, A.K. Using deep neural networks for inverse problems in imaging: beyond analytical methods. IEEE Signal Processing Magazine 2018, 35, 20–36.
- Mohammad-Djafari, A. Regularization, Bayesian inference, and machine learning methods for inverse problems. Entropy 2021, 23, 1673.
- Cividini, A.; Maier, G.; Nappi, A. Parameter estimation of a static geotechnical model using a Bayes’ approach. In Proceedings of the International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Elsevier, 1983, Vol. 20, pp. 215–226.
- Bolzon, G.; Fedele, R.; Maier, G. Parameter identification of a cohesive crack model by Kalman filter. Computer Methods in Applied Mechanics and Engineering 2002, 191, 2847–2871.
- Furukawa, T.; Pan, J.W. Stochastic identification of elastic constants for anisotropic materials. International Journal for Numerical Methods in Engineering 2010, 81, 429–452.
- Beer, M.; Ferson, S.; Kreinovich, V. Imprecise probabilities in engineering analyses. Mechanical systems and signal processing 2013, 37, 4–29.
- Faes, M.; Moens, D. Recent trends in the modeling and quantification of non-probabilistic uncertainty. Archives of Computational Methods in Engineering 2020, 27, 633–671.
- Kolumban, S.; Vajk, I.; Schoukens, J. Approximation of confidence sets for output error systems using interval analysis. Journal of Control Engineering and Applied Informatics 2012, 14, 73–79.
- Crespo, L.G.; Kenny, S.P.; Colbert, B.K.; Slagel, T. Interval predictor models for robust system identification. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC). IEEE, 2021, pp. 872–879.
- van Kampen, E.; Chu, Q.; Mulder, J. Interval analysis as a system identification tool. In Proceedings of the Advances in Aerospace Guidance, Navigation and Control: Selected Papers of the 1st CEAS Specialist Conference on Guidance, Navigation and Control. Springer, 2011, pp. 333–343.
- Fang, S.E.; Zhang, Q.H.; Ren, W.X. An interval model updating strategy using interval response surface models. Mechanical Systems and Signal Processing 2015, 60, 909–927.
- Möller, B.; Graf, W.; Beer, M. Fuzzy structural analysis using α-level optimization. Computational mechanics 2000, 26, 547–565.
- Gabriele, S.; Valente, C. An interval-based technique for FE model updating. International Journal of Reliability and Safety 2009, 3, 79–103.
- Khodaparast, H.H.; Mottershead, J.; Badcock, K. Interval model updating: method and application. In Proceedings of the Proc. of the ISMA, University of Leuven, Belgium, 2010.
- Liao, B.; Zhao, R.; Yu, K.; Liu, C. A novel interval model updating framework based on correlation propagation and matrix-similarity method. Mechanical Systems and Signal Processing 2022, 162, 108039.
- Mo, J.; Yan, W.J.; Yuen, K.V.; Beer, M. Efficient non-probabilistic parallel model updating based on analytical correlation propagation formula and derivative-aware deep neural network metamodel. Computer Methods in Applied Mechanics and Engineering 2025, 433, 117490.
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Mathematical Modelling and Computational Experiment 1993, 1, 407–414.
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliability Engineering and System Safety 1996, 52, 1–17.
- Saltelli, A.; et al. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd: Chichester, England, 2008.
- Most, T.; Will, J. Sensitivity analysis using the Metamodel of Optimal Prognosis. In Proceedings of the 8th Optimization and Stochastic Days, Weimar, Germany, 24-25 November, 2011, 2011. [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response surface methodology: process and product optimization using designed experiments; John Wiley & Sons, 2002.
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, third ed.; John Wiley & Sons, 2003.
- Krige, D. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South Africa 1951, 52, 119–139.
- Lancaster, P.; Salkauskas, K. Surface generated by moving least squares methods. Mathematics of Computation 1981, 37, 141–158.
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; PWS Publishing Company, 1996.
- Ansys Germany GmbH. Ansys optiSLang user documentation. Weimar, Germany, 2023R1 ed., 2023. https://www.ansys.com/products/connect/ansys-optislang Accessed: 2024-04-18.
- Most, T.; Gräning, L.; Wolff, S. Robustness investigation of cross-validation based quality measures for model assessment. Engineering Modelling, Analysis and Simulation 2025, 2. [CrossRef]
- Huntington, D.; Lyrintzis, C. Improvements to and limitations of Latin hypercube sampling. Probabilistic engineering mechanics 1998, 13, 245–253.
- Bucher, C. Computational analysis of randomness in structural mechanics; CRC Press, Taylor & Francis Group: London, 2009.
- Nie, J.; Ellingwood, B.R. Directional methods for structural reliability analysis. Structural Safety 2000, 22, 233–249.
- Nie, J.; Ellingwood, B.R. A new directional simulation method for system reliability. Part I: application of deterministic point sets. Probabilistic Engineering Mechanics 2004, 19, 425–436.
- Estep, D. Practical Analysis in One Variable; Springer: New York, NY, 2002.
- Most, T. Assessment of structural simulation models by estimating uncertainties due to model selection and model simplification. Computers and Structures 2011, 89, 1664–1672. [CrossRef]
- The MathWorks Inc.. MATLAB user documentation. Natick, Massachusetts, United States, R2022b ed., 2022. https://www.mathworks.com.
- Trunk, B.G. Einfluss der Bauteilgrösse auf die Bruchenergie von Beton. Phd thesis, ETH Zurich, 1999.
- Most, T. Stochastic crack growth simulation in reinforced concrete structures by means of coupled finite element and meshless methods. Phd thesis, Bauhaus-Universität Weimar, 2005.
Figure 1.
The principle of model calibration by using the results of an analytical or simulation model with a given parameter set with respect to measurement observations .
Figure 1.
The principle of model calibration by using the results of an analytical or simulation model with a given parameter set with respect to measurement observations .
Figure 2.
Interval optimization as inverse identification of minimum and maximum parameter bounds based on given measurement intervals.
Figure 2.
Interval optimization as inverse identification of minimum and maximum parameter bounds based on given measurement intervals.
Figure 3.
Identification of the feasible input parameter domain of a two-dimensional parameter space by a radial line-search approach.
Figure 3.
Identification of the feasible input parameter domain of a two-dimensional parameter space by a radial line-search approach.
Figure 4.
Bilinear elasto-plasticity model: reference stress-strain curve, synthetic measurements and calibrated model.
Figure 4.
Bilinear elasto-plasticity model: reference stress-strain curve, synthetic measurements and calibrated model.
Figure 5.
Bilinear model: scatter and correlations of the calibrated optimal parameters from 1000 samples of noisy measurement points.
Figure 5.
Bilinear model: scatter and correlations of the calibrated optimal parameters from 1000 samples of noisy measurement points.
Figure 6.
Bilinear model: approximated first order sensitivity indices using squared correlation coefficients (left) and total effect sensitivity indices using the Metamodel of Optimal Prognosis [
35] (right) from 1000 Latin Hypercube samples.
Figure 6.
Bilinear model: approximated first order sensitivity indices using squared correlation coefficients (left) and total effect sensitivity indices using the Metamodel of Optimal Prognosis [
35] (right) from 1000 Latin Hypercube samples.
Figure 7.
Bilinear model: estimated parameter scatter using Markov estimator with 20 measurement points on the stress-strain curve and independent measurement errors .
Figure 7.
Bilinear model: estimated parameter scatter using Markov estimator with 20 measurement points on the stress-strain curve and independent measurement errors .
Figure 8.
Bilinear model: normalized partial derivatives at the optimal parameter set (left) and corresponding local first order sensitivity indices (right).
Figure 8.
Bilinear model: normalized partial derivatives at the optimal parameter set (left) and corresponding local first order sensitivity indices (right).
Figure 9.
Bilinear model: estimated parameter scatter using Markov estimator normalized with the parameter ranges dependent on the measurement error (left) and dependent on the number of measurement points (right).
Figure 9.
Bilinear model: estimated parameter scatter using Markov estimator normalized with the parameter ranges dependent on the measurement error (left) and dependent on the number of measurement points (right).
Figure 10.
Bilinear model: estimated parameter scatter by using Bayesian updating with 20 measurement points on the stress-strain curve and independent measurement errors .
Figure 10.
Bilinear model: estimated parameter scatter by using Bayesian updating with 20 measurement points on the stress-strain curve and independent measurement errors .
Figure 11.
Bilinear model: Estimated response statistics of Bayesian parameter samples by assuming independent measurement errors with .
Figure 11.
Bilinear model: Estimated response statistics of Bayesian parameter samples by assuming independent measurement errors with .
Figure 12.
Bilinear model: obtained parameter sets for the minimization and maximization of the Young’s modulus (blue), the yield stress (red) and the hardening modulus (green) considering a measurement interval of .
Figure 12.
Bilinear model: obtained parameter sets for the minimization and maximization of the Young’s modulus (blue), the yield stress (red) and the hardening modulus (green) considering a measurement interval of .
Figure 13.
Bilinear model: obtained parameter bounds from the radial line-search approach in the 2D subspaces of the Young’s modulus, yield stress and hardening modulus considering a measurement interval of .
Figure 13.
Bilinear model: obtained parameter bounds from the radial line-search approach in the 2D subspaces of the Young’s modulus, yield stress and hardening modulus considering a measurement interval of .
Figure 14.
Bilinear model: 500 initial Fekete points (left) and final line-search points on the boundary of the feasible parameter domain (right) by considering .
Figure 14.
Bilinear model: 500 initial Fekete points (left) and final line-search points on the boundary of the feasible parameter domain (right) by considering .
Figure 15.
Bilinear model: obtained response ranges of the three parameter line-search considering a measurement interval of .
Figure 15.
Bilinear model: obtained response ranges of the three parameter line-search considering a measurement interval of .
Figure 16.
Wedge splitting test: geometry, bi-linear softening law and finite element model with 2D plane-stress elements and interface elements as predefined crack
Figure 16.
Wedge splitting test: geometry, bi-linear softening law and finite element model with 2D plane-stress elements and interface elements as predefined crack
Figure 17.
Wedge splitting, test: experimental measurement valutes and 200 Latin Hybercube samples of thesimulated load-displacement curve using the initial parameter bounds.
Figure 17.
Wedge splitting, test: experimental measurement valutes and 200 Latin Hybercube samples of thesimulated load-displacement curve using the initial parameter bounds.
Figure 18.
Wedge splitting test: estimated total effect sensitivity estimates using the Metamodel of Optimal Prognosis.
Figure 18.
Wedge splitting test: estimated total effect sensitivity estimates using the Metamodel of Optimal Prognosis.
Figure 19.
Wedge splitting test: experimental measurement values compared to the simulated load-displacement curve with optimal parameter values.
Figure 19.
Wedge splitting test: experimental measurement values compared to the simulated load-displacement curve with optimal parameter values.
Figure 20.
Wedge splitting test: estimated parameter scatter and correlations using the Markov estimator and Bayesian updating.
Figure 20.
Wedge splitting test: estimated parameter scatter and correlations using the Markov estimator and Bayesian updating.
Figure 21.
Wedge splitting test: radial search directions and obtained boundary points for the 2D analysis with (left) and boundary points for different interval sizes (right).
Figure 21.
Wedge splitting test: radial search directions and obtained boundary points for the 2D analysis with (left) and boundary points for different interval sizes (right).
Figure 22.
Wedge spliting, test:, minimum and maximum parameter values determined by interval optimizationand the obtained boundary points from the 5l radial line-search approach by using 5.000 directions with .
Figure 22.
Wedge spliting, test:, minimum and maximum parameter values determined by interval optimizationand the obtained boundary points from the 5l radial line-search approach by using 5.000 directions with .
Figure 23.
Wedge splitting test: 2D radial line-search considering linear and quadratic approximation models (left) and by using the MOP approximation based on 100 LHS samples and additional refinement samples (right).
Figure 23.
Wedge splitting test: 2D radial line-search considering linear and quadratic approximation models (left) and by using the MOP approximation based on 100 LHS samples and additional refinement samples (right).
Table 1.
Wedge splitting test: initial material parameter bounds and optimal values.
Table 1.
Wedge splitting test: initial material parameter bounds and optimal values.
| Parameter |
Unit |
Reference value |
Bounds |
Deterministic optimization |
| Young’s modulus E
|
|
2.830 |
1.00 - 6.00 |
4.176 |
| Poisson’s ratio
|
− |
0.180 |
0.10 - 0.40 |
- |
| Tensile strength
|
|
2.270 |
1.00 - 4.00 |
2.003 |
| Fracture energy
|
|
2.850 |
2.00 - 4.00 |
2.850 |
| Shape parameter
|
− |
0.163 |
0.05 - 0.50 |
0.150 |
| Shape parameter
|
− |
0.242 |
0.05 - 0.50 |
0.258 |
Table 2.
Wedge splitting test: estimated statistical properties of the identified parameters using the Markov estimator and Bayesian updating.
Table 2.
Wedge splitting test: estimated statistical properties of the identified parameters using the Markov estimator and Bayesian updating.
| Parameter |
Unit |
Markov estimator |
Bayesian updating |
| |
|
|
Mean |
Stddev |
CoV |
Mean |
Stddev |
CoV |
| Young’s modulus E
|
|
4.176 |
0.116 |
0.028 |
4.065 |
0.136 |
0.033 |
| Tensile strength
|
|
2.003 |
0.023 |
0.011 |
2.025 |
0.030 |
0.015 |
| Fracture energy
|
|
2.850 |
0.024 |
0.008 |
2.847 |
0.026 |
0.009 |
| Shape parameter
|
− |
0.150 |
0.008 |
0.051 |
0.153 |
0.008 |
0.055 |
| Shape parameter
|
− |
0.258 |
0.009 |
0.034 |
0.256 |
0.009 |
0.035 |
Table 3.
Wedge splitting test: parameter bounds in the 5D parameter space obtained with the interval optimization and defined ranges for the radial line-search approach.
Table 3.
Wedge splitting test: parameter bounds in the 5D parameter space obtained with the interval optimization and defined ranges for the radial line-search approach.
| Parameter |
Unit |
Reference |
Optimization |
Line-search ranges |
| |
|
|
|
Min |
Max |
|
|
| Young’s modulus E
|
|
4.176 |
3.566 |
4.540 |
± 1.200 |
| Tensile strength
|
|
2.003 |
1.946 |
2.162 |
± 0.176 |
| Fracture energy
|
|
2.850 |
2.718 |
3.018 |
± 0.240 |
| Shape parameter
|
− |
0.150 |
0.106 |
0.192 |
± 0.080 |
| Shape parameter
|
− |
0.258 |
0.203 |
0.312 |
± 0.080 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).