Submitted:
23 December 2024
Posted:
25 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Lie Point Symmetry Analysis
2.1. Determination of Lie point symmetries of (4)
2.2. One-parameter Lie group transformation using
2.3. Optimal system of sub-algebras
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 |
2.4. Lie Group-Invariants and Similarity Solutions of (4)
2.4.1. Invariant Solutions Using Subalgebra Component
2.4.2. Invariant Solutions Using Subalgebra Component
2.4.3. Invariant Solutions Using Subalgebra Component
2.4.4. Invariant Solutions Using Subalgebra Component
2.4.5. Invariant Solutions Using Subalgebra Component
2.4.6. Invariant Solutions Using Subalgebra Component
2.4.7. Invariant Solutions Using Subalgebra Component
2.4.8. Invariant Solutions Using Subalgebra Component
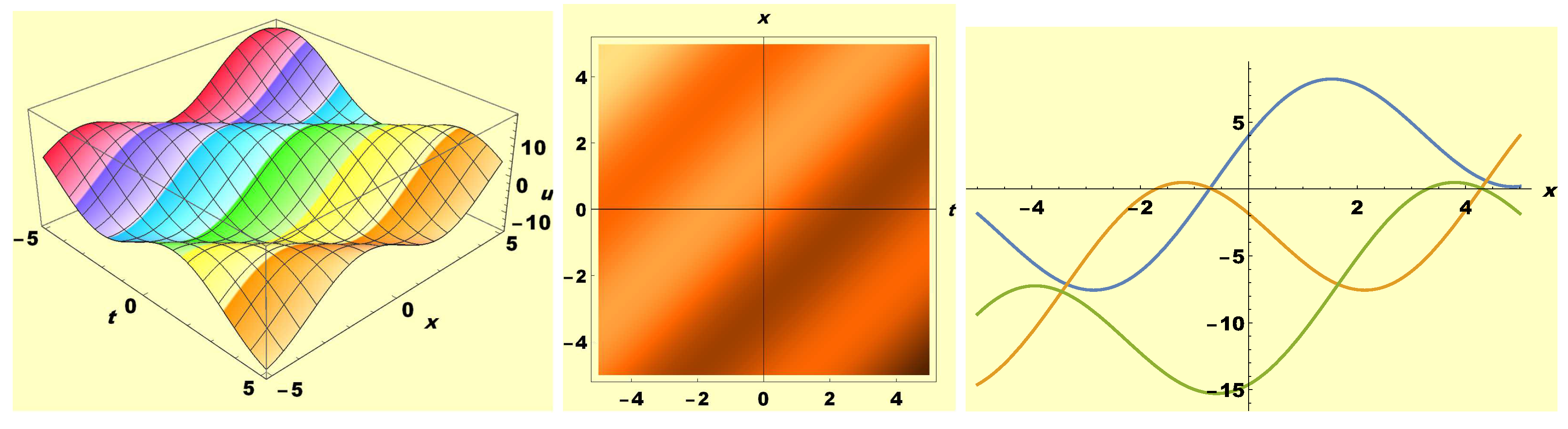
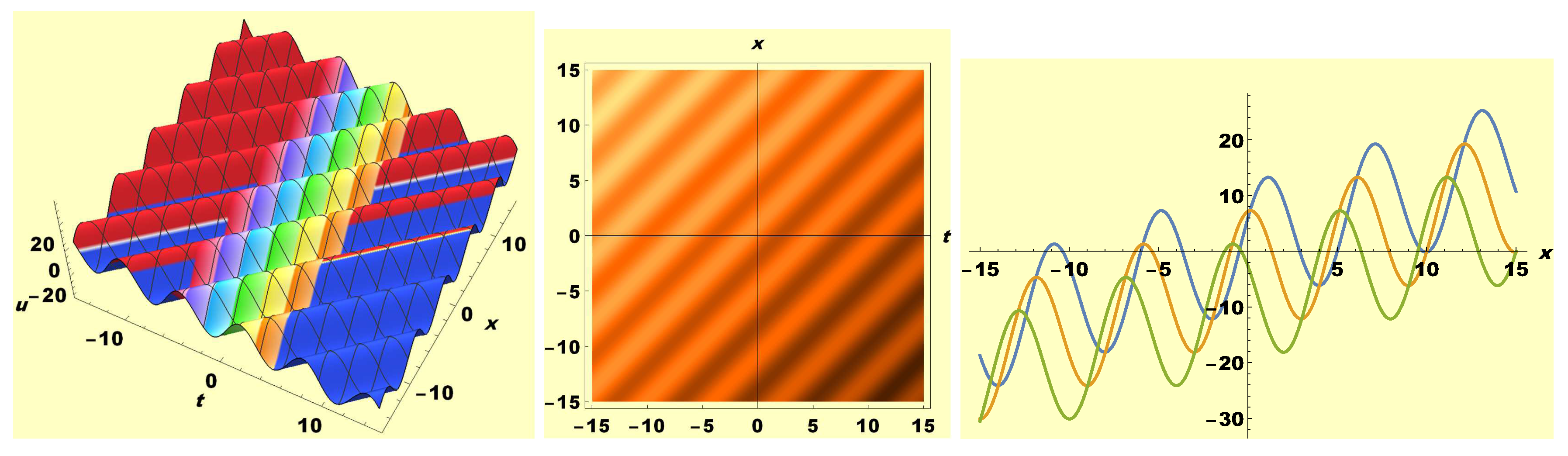
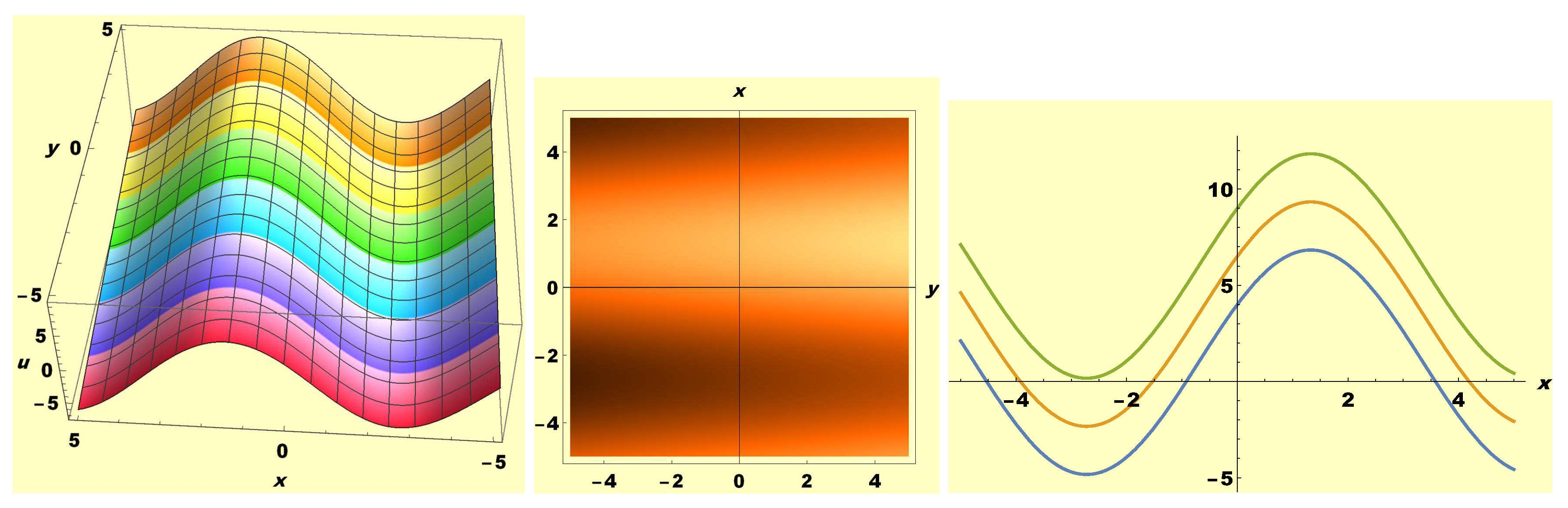
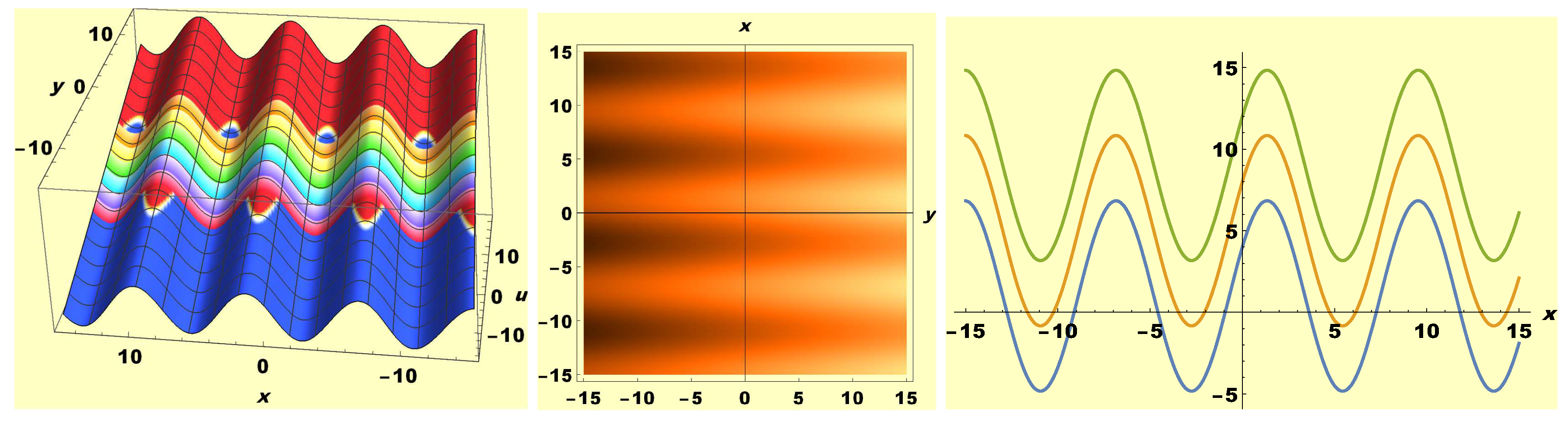
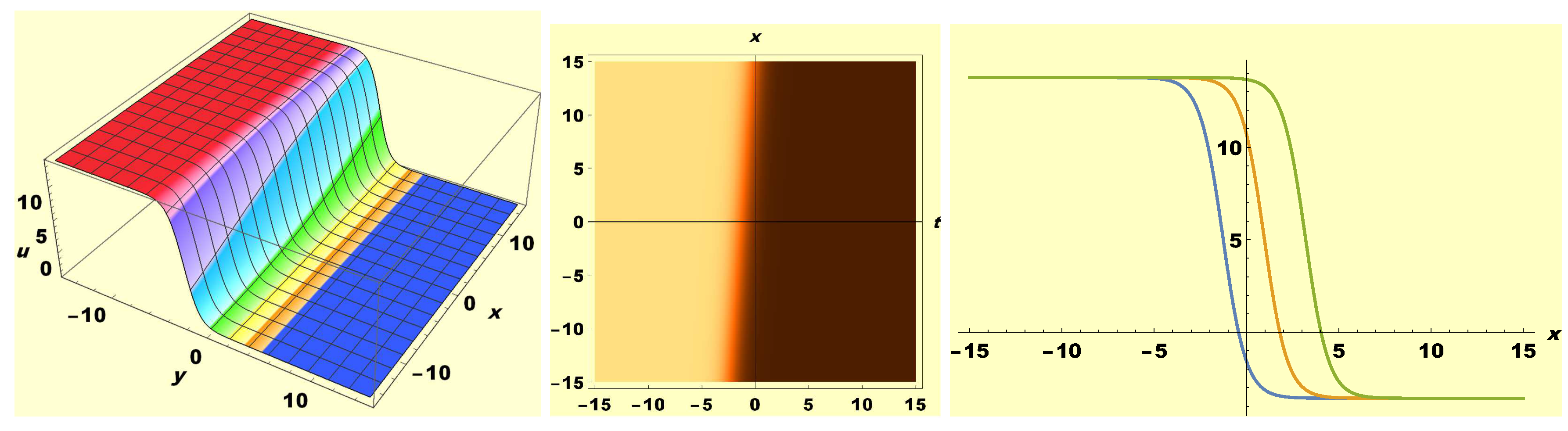
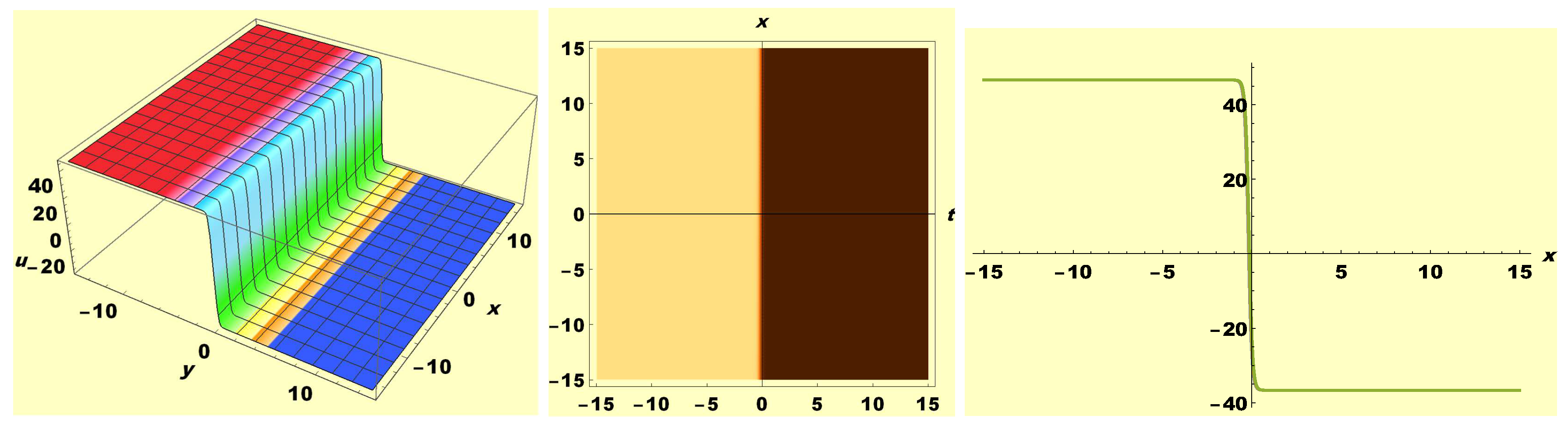
3. Graphical Appraisal of Solutions and Discussion
4. Conservation Laws of 2D-gnrAKNSe (4)
4.1. The technique’s overview
4.2. Formal Lagrangian and Conserved Currents
4.3. Derivation of Conservation Laws via Ibragimov’s Theorem
5. Concluding Remarks
References
- V. Zaitsev, A.D. Polyanin, Handbook of Nonlinear Partial Differential Equations, CRC Press, Boca Raton, (2004).
- O.D. Adeyemo, C.M. Khalique, Y.S. Gasimov, F. Villecco, Variational and non-variational approaches with Lie algebra of a generalized (3+1)-dimensional nonlinear potential Yu-Toda-Sasa-Fukuyama equation in Engineering and Physics, Alex. Eng. J., 63 (2023) 17–43. [CrossRef]
- O.D. Adeyemo, T. Motsepa, C.M. Khalique, A study of the generalized nonlinear advection-diffusion equation arising in engineering sciences, Alex. Eng. J., 61 (2022) 185–194. [CrossRef]
- C.M. Khalique, O.D. Adeyemo, A study of (3+1)-dimensional generalized Korteweg-de Vries-Zakharov-Kuznetsov equation via Lie symmetry approach, Results Phys., 18 (2020) 103197. [CrossRef]
- X.X. Du, B. Tian, Q.X. Qu, Y.Q. Yuan, X.H. Zhao, Lie group analysis, solitons, self-adjointness and conservation laws of the modified Zakharov-Kuznetsov equation in an electron-positron-ion magnetoplasma, Chaos Solitons Fract., 134 (2020) 109709.
- C.R. Zhang, B. Tian, Q.X. Qu, L. Liu, H.Y. Tian, Vector bright solitons and their interactions of the couple Fokas–Lenells system in a birefringent optical fiber, Z. Angew. Math. Phys., 71 (2020) 1–19. [CrossRef]
- X.Y. Gao, Y.J. Guo, W.R. Shan, Water-wave symbolic computation for the Earth, Enceladus and Titan: The higher-order Boussinesq-Burgers system, auto-and non-auto-Bäcklund transformations, Appl. Math. Lett., 104 (2020) 106170. [CrossRef]
- O.D. Adeyemo, L. Zhang, C.M. Khalique, Optimal solutions of Lie subalgebra, dynamical system, travelling wave solutions and conserved currents of (3+1)-dimensional generalized Zakharov–Kuznetsov equation type I, Eur. Phys. J. Plus, 137 (2022) 954. https://doi.org/10.1140/epjp/s13360-022-03100-z. [CrossRef]
- O.D. Adeyemo, C.M. Khalique, Shock waves, periodic, topological kink and singular soliton solutions of a new generalized two dimensional nonlinear wave equation of engineering physics with applications in signal processing, electromagnetism and complex media, Alex. Eng. J., 73 (2023) 751–769.. [CrossRef]
- O.D. Adeyemo, C.M. Khalique, An optimal system of Lie subalgebras and group-invariant solutions with conserved currents of a (3+1)-D fifth-order nonlinear model with applications in electrical electronics, chemical engineering and pharmacy, J. Nonlinear Math. Phys., 30 (2023) 843–916. https://doi.org/10.1007/s44198-022-00101-5. [CrossRef]
- U. Al Khawajaa, H. Eleuchb, H. Bahloulid, Analytical analysis of soliton propagation in microcavity wires, Results Phys. 12 (2019) 471–474. [CrossRef]
- O.D. Adeyemo, L. Zhang, C.M. Khalique, Bifurcation theory, Lie group-invariant solutions of subalgebras and conservation laws of a generalized (2+1)-dimensional BK equation Type II in plasma physics and fluid mechanics, Mathematics, 10 (2022) 2391. [CrossRef]
- A.M. Wazwaz, Exact soliton and kink solutions for new (3+1)-dimensional nonlinear modified equations of wave propagation, Open Eng., 7 (2017) 169–174. [CrossRef]
- O.D. Adeyemo, C.M. Khalique, Lie group theory, stability analysis with dispersion property, new soliton solutions and conserved quantities of 3D generalized nonlinear wave equation in liquid containing gas bubbles with applications in mechanics of fluids, biomedical sciences and cell biology, Commun. Nonlinear Sci. Numer. Simul., 123 (2023) 107261. [CrossRef]
- M.J. Ablowitz, P.A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering, Cambridge University Press, Cambridge, UK, 1991.
- O.D. Adeyemo, Applications of cnoidal and snoidal wave solutions via an optimal system of subalgebras for a generalized extended (2+1)-D quantum Zakharov-Kuznetsov equation with power-law nonlinearity in oceanography and ocean engineering, J. Ocean Eng. Sci., 9 (2024) 126–153. [CrossRef]
- N.A. Kudryashov, N.B. Loguinova, Extended simplest equation method for nonlinear differential equations, Appl. Math. Comput., 205 (2008) 396-402.
- N. K. Vitanov, Application of simplest equations of Bernoulli and Riccati kind for obtaining exact traveling-wave solutions for a class of PDEs with polynomial nonlinearity, Commun. Nonlinear Sci. Numer. Simul., 15 (2010) 2050–2060. [CrossRef]
- Y. Chen, Z Yan, New exact solutions of (2+1)-dimensional Gardner equation via the new sine-Gordon equation expansion method, Chaos Solitons Fract., 26 (2005) 399–406. [CrossRef]
- L. Li, C. Duan, F. Yu, An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (mKdV) equation, Phys. Lett. A, 383 (2019) 1578–1582. [CrossRef]
- M. Wang, X. Li, J. Zhang, The (G′/G) expansion method and travelling wave solutions for linear evolution equations in mathematical physics, Phys. Lett. A, 24 (2005) 1257–1268. [CrossRef]
- L. Feng, S. Tian, T. Zhang, J. Zhou, Lie symmetries, conservation laws and analytical solutions for two-component integrable equations, Chinese J. Phys., 55 (2017) 996–1010.
- Y. Zhang, R. Ye, W.X. Ma, Binary Darboux transformation and soliton solutions for the coupled complex modified Korteweg-de Vries equations, Math. Meth. Appl. Sci., 43 (2020) 613–627. [CrossRef]
- J. Weiss, M. Tabor, G. Carnevale, The Painlevé property and a partial differential equations with an essential singularity, Phys. Lett. A, 109 (1985) 205–208. [CrossRef]
- L. Zhang, C.M. Khalique, Classification and bifurcation of a class of second-order ODEs and its application to nonlinear PDEs, Discrete and Continuous dynamical systems Series S, 11 (2018) 777–790.
- C. Chun, R. Sakthivel, Homotopy perturbation technique for solving two point boundary value problems-comparison with other methods, Comput. Phys. Commun., 181 (2010) 1021–1024. [CrossRef]
- M.T. Darvishi, M. Najafi, A modification of extended homoclinic test approach to solve the (3+1)-dimensional potential-YTSF equation, Chin. Phys. Lett., 28 (2011) 040202. [CrossRef]
- A.M. Wazwaz, Traveling wave solution to (2+1)-dimensional nonlinear evolution equations, J. Nat. Sci. Math., 1 (2007) 1–13. [CrossRef]
- A.M. Wazwaz, Partial Differential Equations, CRC Press, Boca Raton, Florida, USA, 2002.
- L.V. Ovsiannikov, Group Analysis of Differential Equations, Academic Press, New York, USA, 1982.
- P.J. Olver, Applications of Lie Groups to Differential Equations, second ed., Springer-Verlag, Berlin, Germany, 1993.
- Y. Zhou, M. Wang, Y. Wang, Periodic wave solutions to a coupled KdV equations with variable coefficients, Phys. Lett. A, 308 (2003) 31–36.
- C.H. Gu, Soliton Theory and Its Application, Zhejiang Science and Technology Press, Zhejiang, China, 1990.
- A.H. Salas, C.A. Gomez, Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation, Math. Probl. Eng., (2010) 2010.
- X. Zeng, D.S. Wang, A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation, Appl. Math. Comput., 212 (2009) 296–304. [CrossRef]
- M. Date, M. Jimbo, M. Kashiwara, T. Miwa, Operator apporach of the Kadomtsev-Petviashvili equation - Transformation groups for soliton equations III, JPSJ., 50 (1981) 3806–3812.
- C.K. Kuo, W.X. Ma, An effective approach to constructing novel KP-like equations, Waves Random Complex Media, 32 (2020) 629–640. [CrossRef]
- W.X. Ma, E. Fan, Linear superposition principle applying to Hirota bilinear equations, Comput. Math. Appl., 61 (2011) 950–959.
- A.M. Wazwaz, Multiple-soliton solutions for a (3+1)-dimensional generalized KP equation, Commun. Nonlinear Sci. Numer. Simul., 17 (2012) 491–495.
- W.X. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 379 (2015) 1975–1978. [CrossRef]
- Z. Zhao, B. Han, Lump solutions of a (3+1)-dimensional B-type KP equation and its dimensionally reduced equations, Anal. Math. Phys., 9 (2017) 119–130.
- C.M. Khalique, O.D. Adeyemo, I. Mohapi, Exact solutions and conservation laws of a new fourth-order nonlinear (3+1)-dimensional Kadomtsev-Petviashvili-like equation, Appl. Math. Inf. Sci., 18 (2024) 1–25. [CrossRef]
- S.C. Anco, G.W. Bluman, Direct construction method for conservation laws of partial differential equations. Part I: Examples of conservation law classifications, Eur. J. Appl. Math., 13 (2002) 545–566.
- M.L. Gandarias, M.S. Bruzón, M. Rosa, Symmetries and conservation laws for some compacton equation, Math. Probl. Eng. 2015 (2015). [CrossRef]
- S.C. Anco, Generalization of Noether’s Theorem in Modern Form to Non-variational Partial Differential Equations; Recent progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science. Springer, New York, NY, (2017) 119–182.
- L.D. Moleleki, B. Muatjetjeja, A.R. Adem, Solutions and conservation laws of a (3+1)-dimensional Zakharov-Kuznetsov equation, Nonlinear Dyn., 87 (2017) 2187–2192. [CrossRef]
- M.S. Bruzón, E. Recio, R. de la Rose, Local conservation laws, symmetries, and exact solutions for a Kudryashov-Sinelshchikov equation, Math. Method Appl. Sci., 41 (2018) 1631–1641.
- M.S. Bruzón, M.L. Gandarias, Traveling wave solutions of the K(m, n) equation with generalized evolution, Math. Meth. Appl. Sci. 41 (2018) 5851–5857.
- C.M. Khalique, L.D. Moleleki, A (3+1)-dimensional generalized BKP-Boussinesq equation: Lie group approach, Results Phys., 13 (2019) 2211–3797. [CrossRef]
- S. Arbabi, M. Najafi, M. Najafi, New soliton solutions of dissipative (2+1)-dimensional AKNS equation, IJAMS 1 (2013) 98–103. [CrossRef]
- Z. Cheng, X. Hao, The periodic wave solutions for a (2+1)-dimensional AKNS equation, Appl. Math. Comput., 234 (2014) 118–126. [CrossRef]
- A.M. Wazwaz, N-soliton solutions for shallow water waves equations in (1+1) and (2+1) dimensions, Appl. math. comput. 217 (2011) 8840–8845.
- W. Hereman, A. Nuseir, Symbolic methods to construct exact solutions of nonlinear partial differential equations, Math. Comput. Simulat., 43 (1997) 13–27. [CrossRef]
- T. Özer, New traveling wave solutions to AKNS and SKdV equations, Chaos Soliton Fract., 42 (2009) 577–583. [CrossRef]
- N. Liu, X.Q. Liu, Application of the binary Bell polynomials method to the dissipative (2+1)-dimensional AKNS equation, Chin. Phys. Lett., 29 (2012) 120201.
- M.S. Bruźon, M.L. Gandarias, C. Muriel, J. Ramírez, F.R. Romero, Traveling-wave solutions of the Schwarz-Korteweg-de Vries equation in (2+1)-dimensions and the Ablowitz-Kaup-Newell-Segur equation through symmetry reductions, Theoret. math. Phys. 137 (2003) 1378–1389. [CrossRef]
- D.M. Mothibi, Conservation laws for Ablowitz-Kaup-Newell-Segur equation." AIP Conference Proceedings. Vol. 1738. No. 1. AIP Publishing LLC, 2016.
- H. Wang, Y.H. Wang, CRE solvability and soliton-cnoidal wave interaction solutions of the dissipative (2+1)-dimensional AKNS equation, Appl. Math. Lett., 69 (2017) 161–167.
- M. Najafi, M. Najafi, M.T. Darvishi, New exact solutions to the (2+1)-Dimensional Ablowitz-Kaup-Newell-Segur equation: modification of the extended homoclinic test approach, Chin. Phys. Lett., 29 (2012) 040202.
- Z.Y. Ma, H.L. Wu, Q.Y. Zhu, Lie Symmetry, full symmetry group and exact solutions to the (2+1)-dimensional dissipative AKNS equation, Rom. J. Phys., 62 (2017) 114.
- Z. Zhao, B. Han, On symmetry analysis and conservation laws of the AKNS system, Z. Naturforsch. A, 71 (2016) 741–750.
- W. Ma, W. Strampp, An explicit symmetry constraint for the Lax pairs and the adjoint Lax pairs of AKNS systems, Phys. Lett. A, 185 (1994) 277–286. [CrossRef]
- W. Ma, M. Chen, Direct search for exact solutions to the nonlinear Schrödinger equation, Appl. Math. Comput. 215 (2009) 2835–2842. [CrossRef]
- Y. Li, J.E. Zhang, Bidirectional soliton solutions of the classical Boussinesq system and AKNS system, Chaos Solitons Fract., 16 (2003) 271–277. [CrossRef]
- L. Wang, Y.T. Gao, D.X. Meng, X.L. Gai, P.B. Xu, Soliton-shape-preserving and soliton-complex interactions for a (1+1)-dimensional nonlinear dispersive-wave system in shallow water, Nonlinear Dyn., 66 (2011) 161–168. [CrossRef]
- A. Ali, A.R. Seadawy, D. Lu, Computational methods and traveling wave solutions for the fourth-order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications, Open Phys., 16 (2018) 219–226. [CrossRef]
- M.A. Helal, A.R. Seadawy, M.H. Zekry, Stability analysis solutions for the fourth-order nonlinear ablowitz-kaup-newell-segur water wave equation, Appl. Math. Sci., 7 (2013) 3355–3365.
- A. Ali, A.R. Seadawy, D. Lu, New solitary wave solutions of some nonlinear models and their applications, Adv. Differ. Equ-NY, 2018 (2018) 232. [CrossRef]
- V.B. Matveev, A.O. Smirnov, Solutions of the Ablowitz-Kaup-Newell-Segur hierarchy equations of the “rogue wave” type: aunified approach, Theor. Math. Phys., 186 (2016) 156–182.
- P.J. Olver, Applications of Lie Groups to Differential Equations, New York, Springer-Verlag, (1986).
- P.J. Olver, Equivalence, invariants and symmetry, Cambridge University Press, 1995.
- X. Hu, Y. Li, Y. Chen, A direct algorithm of one-dimensional optimal system for the group invariant solutions, J. Math. Phys., 56 (2015) 053504.
- N.H. Ibragimov, Integrating factors, adjoint equations and Lagrangians, J. Math. Anal. Appl. 318 (2006) 742–757. [CrossRef]
- N.H. Ibragimov, A new conservation theorem, J. Math. Anal. Appl., 333 (2007) 311–328.








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




