Evaluation of Machine Learning Models for Enhancing Sustainability in Additive Manufacturing

1. Introduction

Manufacturing is a cornerstone of industrial development and economic growth, playing a pivotal role in producing goods to meet societal demands [1]. However, traditional manufacturing methods often entail significant resource consumption and waste generation, raising concerns about their environmental impact. The manufacturing sector accounts for a substantial share of global greenhouse gas emissions, energy consumption (15%), and material consumption (35-40%) [2]. Consequently, the quest for more sustainable manufacturing practices has become increasingly urgent in the face of climate change and resource depletion for a circular economy.

Additive Manufacturing (AM) or 3D Printing has emerged as a revolutionary approach characterized by its layer-by-layer construction of parts from digital models. This innovative method contrasts sharply with conventional manufacturing (CM) which typically relies on subtractive processes to remove material from a larger block [3]. AM offers numerous advantages, including design flexibility, ability to create complex geometries, and reduced material waste. AM can minimize waste and optimize resource utilization. Furthermore, AM enables the production of products close to end users, reducing transportation emissions and enhancing supply chain efficiency [4].

The AM sustainability potential can be further amplified by its capability to fabricate lightweight structures that meet stringent performance requirements, making it particularly attractive for industries such as aerospace, automotive, and healthcare [5], where material efficiency and performance are paramount [6]. Additionally, AM facilitates the use of alternative and recycled materials, contributing to a more sustainable lifecycle for products [7]. However, despite its inherent advantages, the widespread adoption of AM faces challenges such as variability in material properties, process parameters, and complexities of optimizing designs.

Sustainability in AM integrates environmental, social, and economic considerations. It emphasizes the optimization of material usage, energy efficiency, and innovative production techniques to meet current manufacturing demands while ensuring that future generations can sustain production capabilities without exhausting resources or inflicting harm on the environment [8]. Specifically, the sustainability metrics considered in this research include energy consumption, part weight, scrap weight, and printing time, which directly relates to the economic and environmental goals of sustainability. Energy consumption and production time drive the operational efficiency, influence both energy usage and carbon emissions. Reducing material usage, reflected in part and scrap weights, conserves resources and minimizes waste. By optimizing these parameters, AM can achieve material savings, which in turn reduces energy consumption, emissions, printing time, and overall costs. These interconnected improvements address both economic and environmental sustainability and highlight the importance of parameter optimization for efficient and sustainable AM processes.

Machine learning (ML) has emerged as a promising approach to address the above challenges and offer a powerful tool for analyzing complex datasets and uncovering relationships between parameters and performance outcomes. Integrating ML into the AM process enables users to predict mechanical properties and assess AM parameters impact on sustainability metrics [9]. By employing advanced algorithms, ML can analyze vast amounts of data generated during the AM process [10], and facilitate the optimization of parameters like the layer thickness, infill type and build orientation. This data-driven approach enhances the process efficiency while supporting informed decision-making to achieve sustainability objectives.

Hyperparameter optimization methods are essential for enhancing ML models in the context of AM. Techniques such as grid search [11] and random search [12] systematically and randomly navigate parameter spaces, respectively. However, these methods can be computationally intensive and may lack the desired precision. In contrast, Bayesian optimization offers a probabilistic framework that effectively balances exploration and exploitation, although its implementation can be intricate [13]. The Limited-memory Broyden-Fletcher-Goldfarb-Shanno with Box constraints (L-BFGS-B) optimizer, a gradient-based approach, excels in managing bounded continuous optimization, yielding results that are both faster and more computationally efficient [14]. This study employs L-BFGS-B to overcome limitations of the traditional methods, thereby advancing the parameter optimization for the AM sustainability.

The contribution of this research lies in its direct focus on sustainability outcomes by considering both environmental and economic dimensions. By relating specific parameter choices to measurable sustainability metrics, such as energy efficiency and material conservation. The result demonstrates that parameter optimization can advance efficient and sustainable AM processes. It provides a scalable solution to enhance AM sustainability, which addresses the gap in the existing research to offer valuable insights for AM development.

2. Literature Review

AM builds parts layer by layer, guided by digital models, which significantly reduces the material waste and energy consumption compared to CM [3]. Due to these advantages, AM is often considered a more sustainable option than CM [8].

Sustainability of manufacturing processes including AM is commonly assessed by three primary approaches: cradle-to-grave [15], cradle-to-gate [16], and gate-to-gate [17]. The cradle-to-grave approach evaluates sustainability metrics like energy consumption and material usage from raw material extraction to product’s disposal after its useful life. Cradle-to-gate focuses on these metrics from the raw material extraction to production stage, while gate-to-gate examines only the production process. Analysis methods employed in these approaches include Life Cycle Costing (LCC) which focuses on the total economic cost, and Life Cycle Assessment (LCA) which evaluates environmental impacts over the product’s lifecycle [18].

Various approaches have been proposed to investigate AM sustainability. Some studies have focused on energy consumption and material usage as key indicators of AM sustainability [19]. Energy consumption in AM encompasses multiple stages, including warm-up time, printing time, post-processing, and material processing, all of them contribute to the overall energy demand. Additionally, factors such as machine’s efficiency and its rate of utilization play a crucial role in determining energy use. A machine running at the optimal capacity with high utilization rates tends to be more energy-efficient, as downtime and idle energy consumption are minimized. In contrast, low utilization or inefficient operation can lead to wasted energy [20]. Moreover, the quantity and type of material processed, whether metals, polymers or composites, can influence the energy required for both material handling and post-processing stages. Insightfully managing these aspects is the key to enhancing AM sustainability by optimizing the energy use while maintaining production quality [21]. Others have examined relationships between electrical energy consumption and emissions to assess AM sustainability [22]. In the context of metal AM, energy [23] and exergy [24] metrics have been used to evaluate sustainability. Additionally, some studies have explored the recyclability of PET filaments to assess sustainability for the material usage [25]. Design plays a pivotal role in achieving AM sustainability. By leveraging the AM flexibility, designers can optimize part geometries to reduce material usage, create lightweight structures, and minimize waste. Features such as topology optimization and lattice structures allow for efficient designs that maintain strength while using less material [26]. Furthermore, design for recyclability and modular components can extend product life cycles, facilitate remanufacturing, and enhance material recovery, contributing to a circular economy. Thoughtful design choices in AM can not only improve resource efficiency but also reduce energy consumption in the manufacturing process [27]. Traditionally, the Taguchi method, a well-established approach for optimizing parameters in manufacturing and engineering processes, is applied. It provides a systematic framework aimed at enhancing performance while minimizing variability. By employing orthogonal arrays and signal-to-noise ratios, this method effectively reduces the number of experimental trials needed to identify optimal process parameters. Its robust statistical foundation has made it a preferred choice in quality control and process optimization, as it can identify resilient settings with minimal experimental effort [19].

However, the Taguchi method has notable limitations. Its signal-to-noise ratios often fail to accurately determine optimal factor levels, and its application requires substantial statistical expertise, limiting accessibility for non-experts. The method’s effectiveness depends on interactions between controllable and noise factors. When these interactions are weak, its reliability diminishes, while strong interactions among controllable factors can obscure the true optimum. Additionally, its offline nature makes it unsuitable for real-time process adjustments, and its assumption of linear, additive effects may not hold in complex manufacturing systems with nonlinear interactions. These constraints underscore the need for more flexible, data-driven optimization techniques [28]. Although these studies have made significant contributions to understanding AM sustainability, approaches they used are often time-consuming, labor-intensive, and resource-intensive, requiring extensive experiments and data collection to draw meaningful conclusions.

To address the challenges of AM sustainability, ML tools have been increasingly studied for their potential to predict and optimize various processes [29]. By focusing on key mechanical properties such as tensile strength, compressive strength, and Young’s modulus, researchers have harnessed ML techniques to enhance the efficiency of AM. While specific models like Regression [30], Classification [31], and Neural Networks (NN) [26,27] have been employed, the overarching goal remains the same: optimizing AM processes to reduce waste and energy consumption. For instance, the prediction of tensile strength through ML allows for the identification of optimal processing parameters, which improves the part quality and minimizes defects [29,30]. It is crucial as defects in printed parts often lead to increased material waste and longer production times. Similarly, by accurately predicting the compressive strength [34] and Young’s modulus [35], ML can facilitate the design of components to meet performance specifications without the excess material usage including geometrical feature identification and segmentation [36]. Printing temperature, layer height and printing speed significantly impact the tensile strength. Temperature has a positive impact while the layer height and printing speed negatively impact the tensile strength [37]. Printing temperature has a similar effect on Young’s modulus [38]. Layer height and infill percentage dominantly impact Young’s modulus, and infill patterns can significantly influence the strength, stiffness, and weight of a 3D printed part [39]. Therefore, optimizing printing parameters is essential to ensure desired mechanical performance and prevent defects, as slight variations can affect strength, stiffness, and durability [40]. Moreover, the integration of ML into parameter optimization strategies [32,33], such as adjusting layer thickness, infill type and build orientation, contributes significantly to sustainability efforts [19]. These efforts can reduce the need for trial-and-error methods traditionally used in AM, thereby decreasing production time and energy consumption.

Hyperparameter tuning is an essential process to enhance the performance of ML models by identifying the most effective parameter configurations. The grid search method systematically evaluates all possible combinations of predefined hyperparameters for a thorough assessment, but it incurs significant computational costs [11]. In contrast, the hybrid grid search improves efficiency by combining systematic exploration of critical parameters with random sampling of less influential ones [43]. Bayesian optimization utilizes a probabilistic framework with a surrogate function to iteratively refine optimal parameter settings, leading to the enhanced computational efficiency [13]. The L-BFGS method, employed with support vector regressors [44], is a gradient-based optimization technique specifically tailored for continuous and differentiable functions. It iteratively adjusts parameters within established constraints, promoting the faster convergence and reducing computational expense [45]. These methods highlight the crucial role of hyperparameter tuning in enhancing the ML model performance while ensuring efficiency, particularly in the AM field, where accurate and sustainable predictions are paramount.

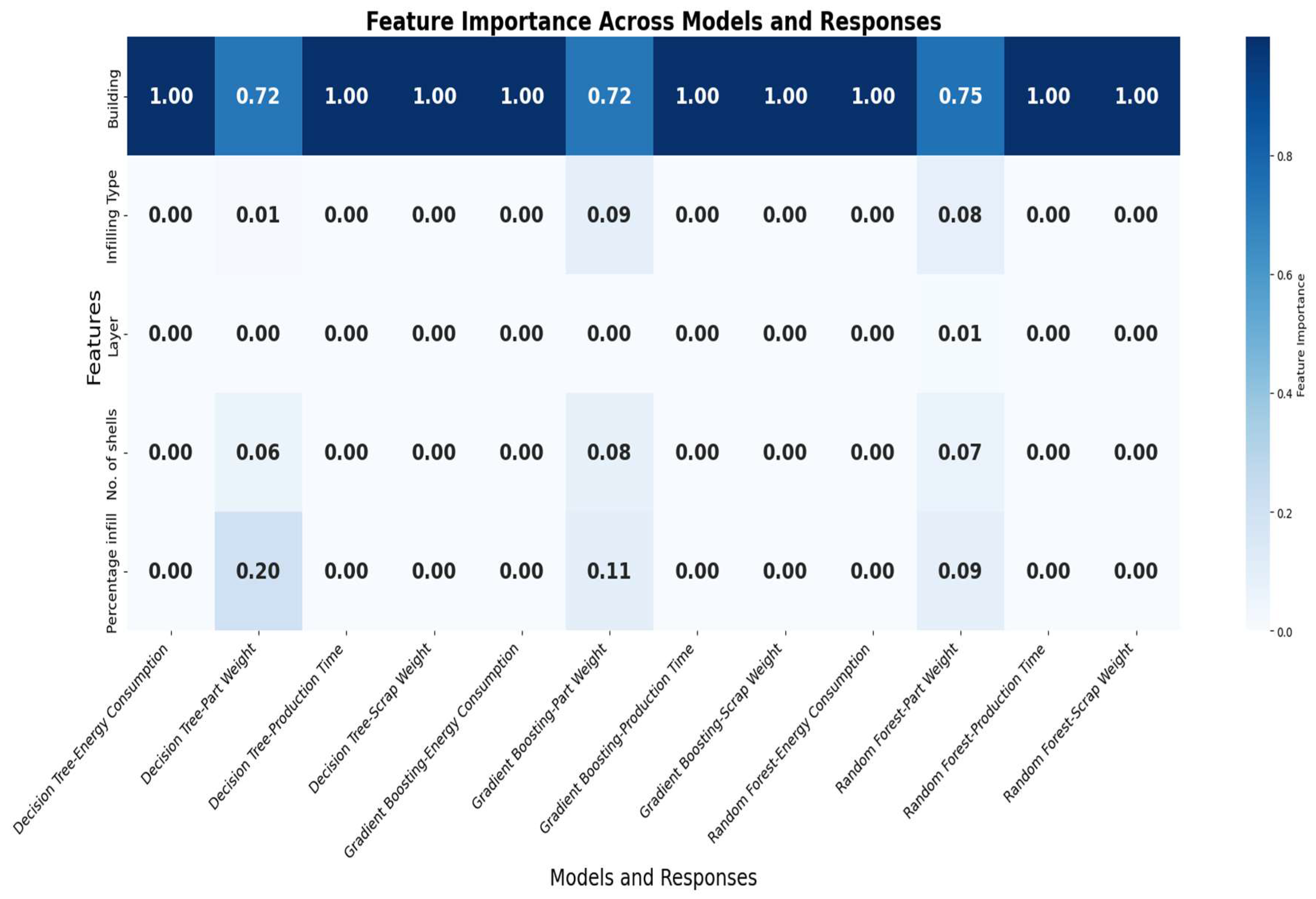
Despite advancements in utilizing ML for predicting mechanical properties, a significant gap remains in directly correlating AM parameters with sustainability metrics. While the indirect benefits of enhancing mechanical properties and reducing defects are evident, further research is essential to establish clear connections between specific ML applications and sustainability outcomes in AM. Understanding the specific AM parameters to impact sustainability metrics is crucial for improving the overall efficiency and environmental performance of the AM process. This research aims to directly analyze the relationship by evaluating different ML models and presenting optimized parameters, which offers a substantial advancement over the traditional time-consuming and resource-intensive approaches for AM sustainability. To achieve this, we select Linear Regression, Decision Trees, Random Forest, and Gradient Boosting models that are widely recognized for their robustness and effectiveness in regression tasks and commonly used in literature. This selection helps evaluation of the L-BFGS-B optimization method in the computational efficiency and effectiveness for an alternative to traditional hyperparameter tuning methods such as the grid search. Although other ML methods such as Neural Networks, k-Nearest Neighbors, Gaussian Process Regression and Support Vector Regression have their merits, they are not included in this research due to their limitations in the dataset size, relevance to continuous data, and less frequent use in the AM context. By integrating sustainability assessments into the ML process, our research introduces a novel data-driven method that examines key parameters such as the layer thickness, number of shells, build orientation, infill type and infill percentage. Impacts of these parameters are evaluated in energy consumption, part weight, scrap weight and printing time to form a comprehensive framework for AM sustainability. Our research solution could ultimately lead to the development of sustainable AM practices that align with industry goals and environmental standards.

3. Methodology

In this section, we discuss the evaluation of ML models, hyperparameter optimization, evaluation metrics, data collection, and sustainability metrics.

3.1. ML Models

ML models employed in this research are Random Forest, Decision Trees, Gradient Boosting, and Linear Regression. These models are selected for their robustness and effectiveness in handling regression tasks, and widespread use in related applications, making them ideal for evaluating sustainability metrics in AM. Random Forest and Gradient Boosting, as ensemble-based models, excel in capturing complex interactions between features while reducing overfitting through their inherent aggregation mechanisms [46]. Decision Trees provide clear interpretability, enabling insights into the relative importance of process parameters [32] Linear Regression offers a baseline for the comparison due to its simplicity and efficiency [35] Each model configuration is carefully chosen to align with our objectives to ensure reliable predictions across sustainability metrics in the energy consumption, part weight, scrap weight and production time. This combination of models provides a comprehensive framework to assess the impact of AM process parameters on sustainability outcomes.

3.1.1. Linear Regression (LinReg)

Linear regression is a technique used in statistics and Machine Learning to model the relationship between dependent and independent variables, assuming a linear relationship. Changes in the dependent variable occur proportionally with changes in the independent variables, as shown in the equation below:

$$Y=\beta o+\beta X+\epsilon$$

(1)

where Y is the dependent variable, X is the independent variable, $\mathsf{\beta }\mathsf{o}$ is the intercept, $\mathsf{\beta }$ is the slope of the line, and ε represents the error between the predicted and actual values [35].

By minimizing the sum of squared differences between the true and predicted values, linear regression identifies the best-fit line, a process known as the least squares method. It is most effective for linear data with the minimal noise.

3.1.2. Decision Tree (DT)

Decision Trees are simple yet powerful regression models that split the data recursively into regions with minimal target variance. They are particularly intuitive, as they create a flowchart-like structure where each internal node represents a decision rule, and leaf nodes correspond to predictions. However, DTs are prone to overfitting due to their tendency to memorize training data [32].

Mathematically, the decision at each split minimizes the Mean Squared Error (MSE):

$$MSE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-y^{*}\right)}^2$$

(2)

where ${\mathrm{y}}_{\mathrm{i}}$ is the actual value, ${\mathrm{y}}^{\mathrm{*}}$ is the mean of the target values in a region, n is the number of data points in the region.

The tree grows until a stopping criterion, such as the maximum depth or minimum samples per leaf, is met. Predictions are made by taking the mean of target values in the corresponding region.

3.1.3. Random Forest (RF)

Random Forest enhances the performance of Decision Trees by using an ensemble of trees trained on bootstrapped subsets of the data. Each tree randomly selects a subset of features for splitting, introducing randomness that reduces overfitting and improves generalization. RF is robust to noise and highly effective in predicting complex patterns [46].

For regression, RF predicts by averaging the outputs of all the T trees:

$$y^{*}RF={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T{y^{*}}^{\left(t\right)}$$

(3)

where ${{\mathrm{y}}^{\mathrm{*}}}^{\left(\mathrm{t}\right)}$ is the prediction of the t-th tree.

By combining the strengths of multiple weak learners, RF provides accurate and stable predictions while remaining resistant to overfitting.

3.1.4. Gradient Boosting (GB)

Gradient Boosting is an advanced ensemble technique that builds trees sequentially, where each tree corrects the residuals of the previous trees. Unlike RF, which trains trees independently, GB uses a gradient descent approach to optimize a loss function, typically the MSE for regression tasks. This iterative refinement allows GB to capture complex relationships effectively [47].

The residuals at iteration t are computed as:

$$r_i^{\left(t\right)}=y_i-{y_i^{*}}^{(t-1)}$$

(4)

where ${\mathrm{y}}_{\mathrm{i}}$ is the actual value, and ${{\mathrm{y}}_{\mathrm{i}}^{\mathrm{*}}}^{(\mathrm{t}-1)}$is the prediction from the previous iteration.

The updated prediction is:

$${y_i^{*}}^{\left(t\right)}={y_i^{*}}^{(t-1)}+ŋ.f^{\left(t\right)}\left(x_i\right)$$

(5)

where η is the learning rate, and ${\mathrm{f}}^{\left(\mathrm{t}\right)}\left({\mathrm{x}}_{\mathrm{i}}\right)$ is the prediction from the t-th tree.

GB’s iterative error minimization makes it highly accurate, but it requires careful tuning of hyperparameters to prevent overfitting or underfitting.

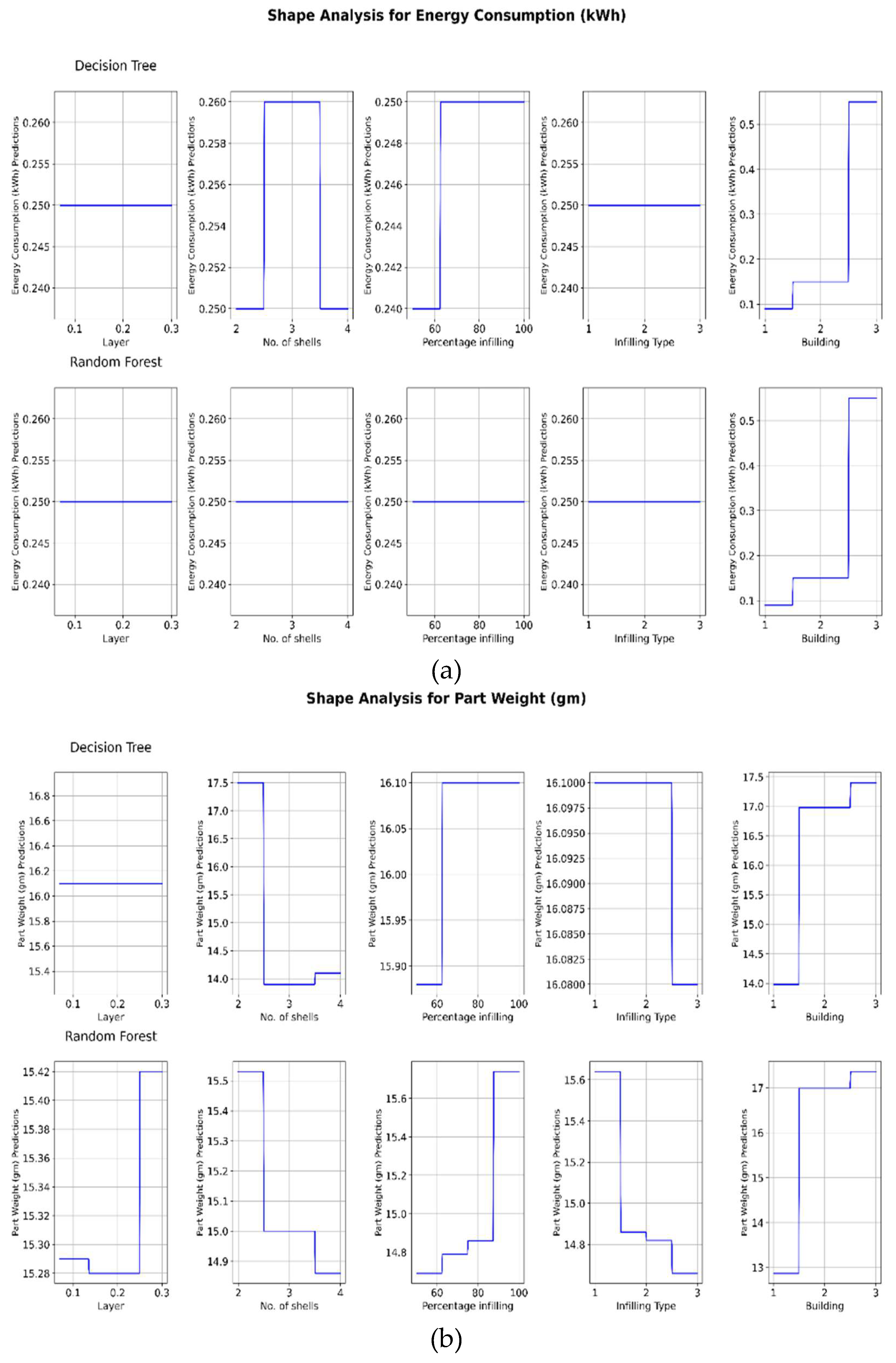
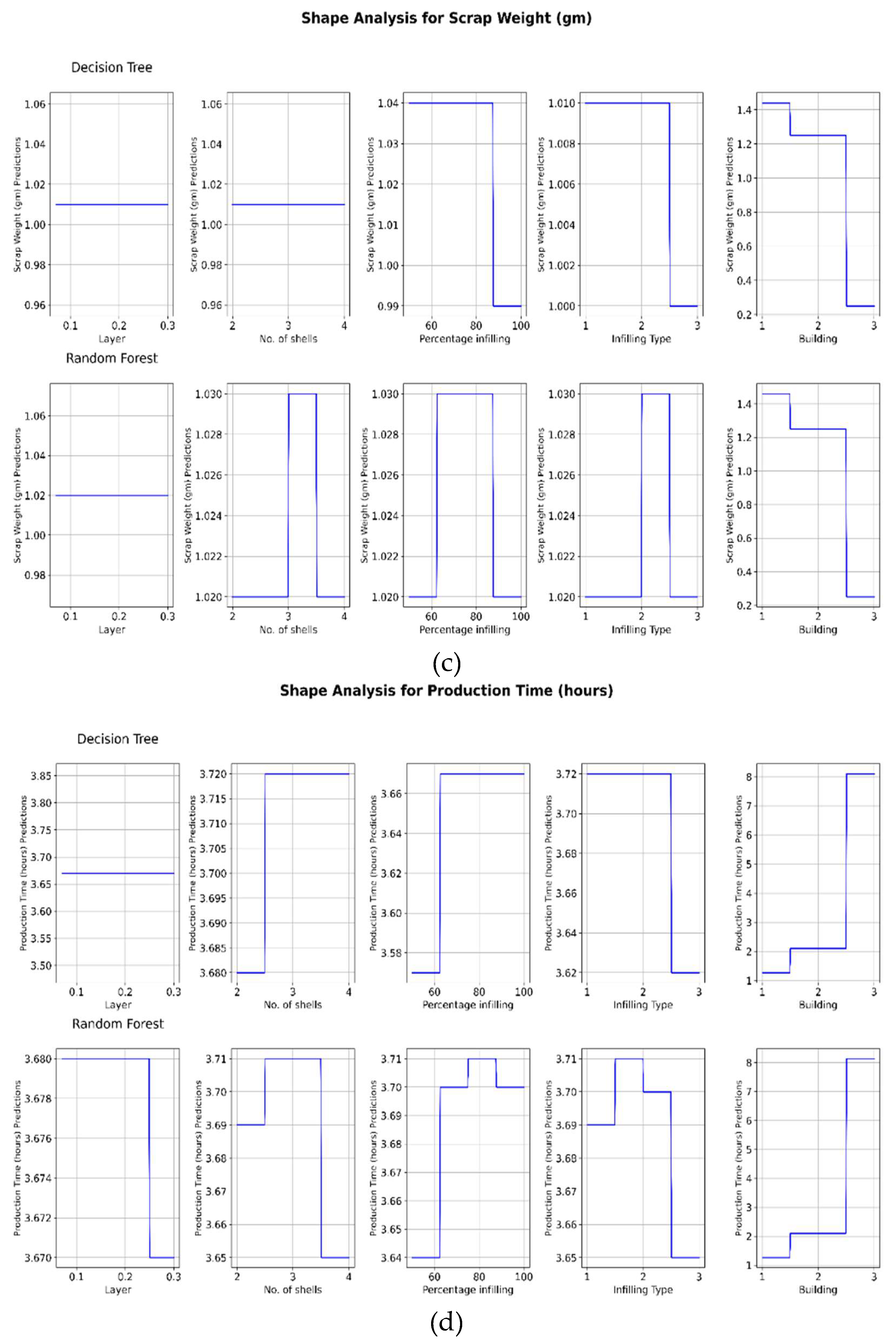
3.2. Hyperparameter Optimization

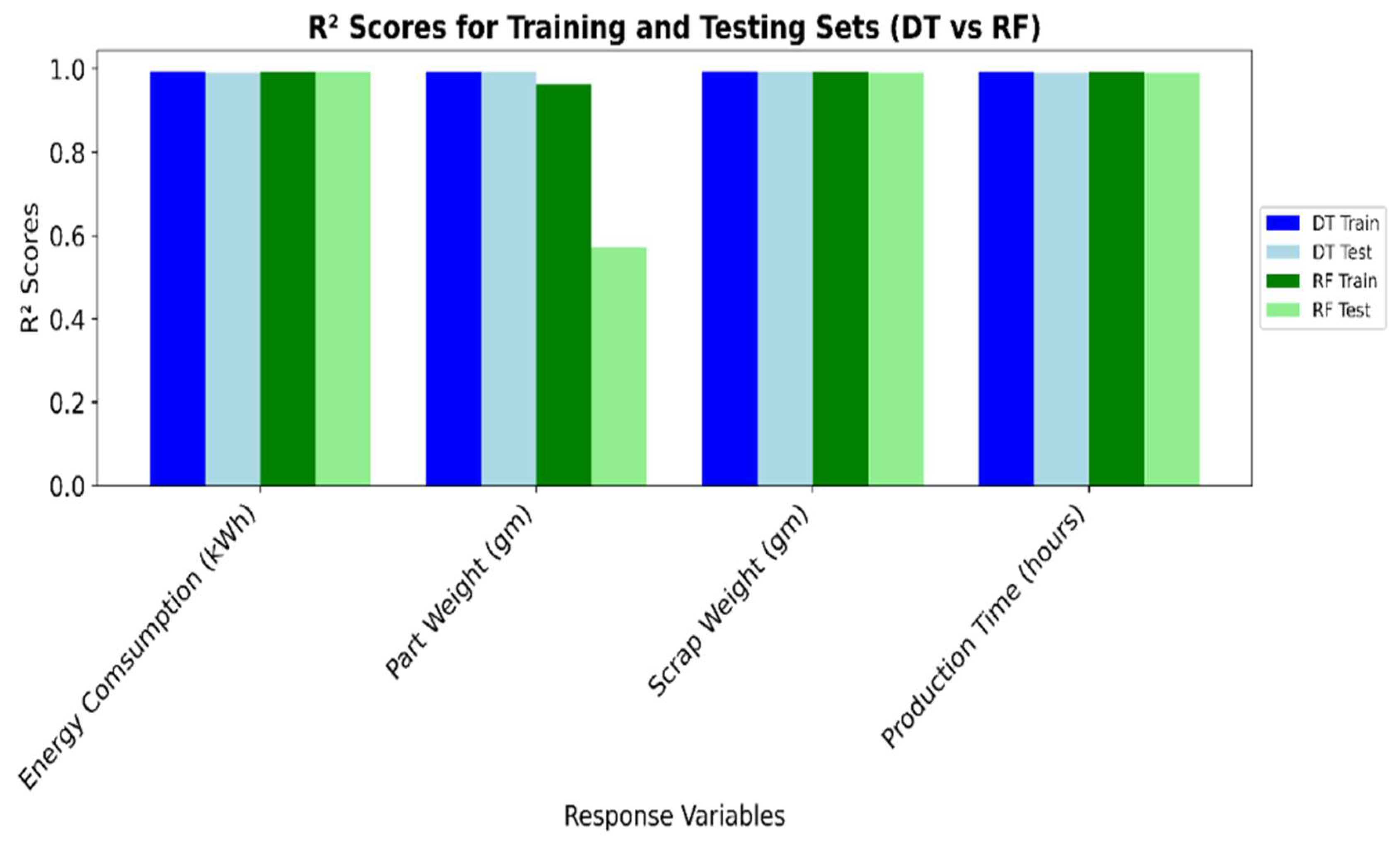
For the parameter optimization and response variable prediction, the model is initialized by importing Python libraries and defining a dataset with various parameters related to AM. ML models such as Decision Tree (DT) and Random Forest (RF) regressors are used to predict multiple response variables, including the energy consumption, part weight, scrap weight, and production time. Both models utilize the ‘random_state’ parameter to ensure reproducibility of results, the RF model also incorporates the ‘n_estimators’ parameter to define the number of trees in the forest, which is set to 100. The data are split into training and test sets, with 20% reserved for testing, and a consistent random state is used for reproducibility across different runs [47]. To enhance the model performance, the ‘StandardScaler’ is applied to normalize the feature scales.

For the hyperparameter optimization, the minimize function from the ‘scipy.optimize’ library is utilized to leverage the L-BFGS-B method. Unlike the grid search or random search that are computationally expensive and time-intensive, L-BFGS-B is chosen for its efficiency in optimizing continuous and smooth functions within bounded constraints. The considered hyperparameters include ‘n_estimators’ for RF and ‘max_depth’ for both DT and RF. Other hyperparameters, such as ‘min_samples_split’ and ‘min_samples_leaf’, are not included for the computational efficiency and focus on parameters with the most significant impact on the model performance. This setup aims to fine-tune the models and optimize AM parameters to minimize costs and improve efficiency. Table 1 highlights the hyperparameter configurations for the models used in the parameter optimization.

This approach ensures a balance between the computational efficiency and predictive accuracy to demonstrate the practical application of advanced ML techniques in improvement of the AM sustainability.

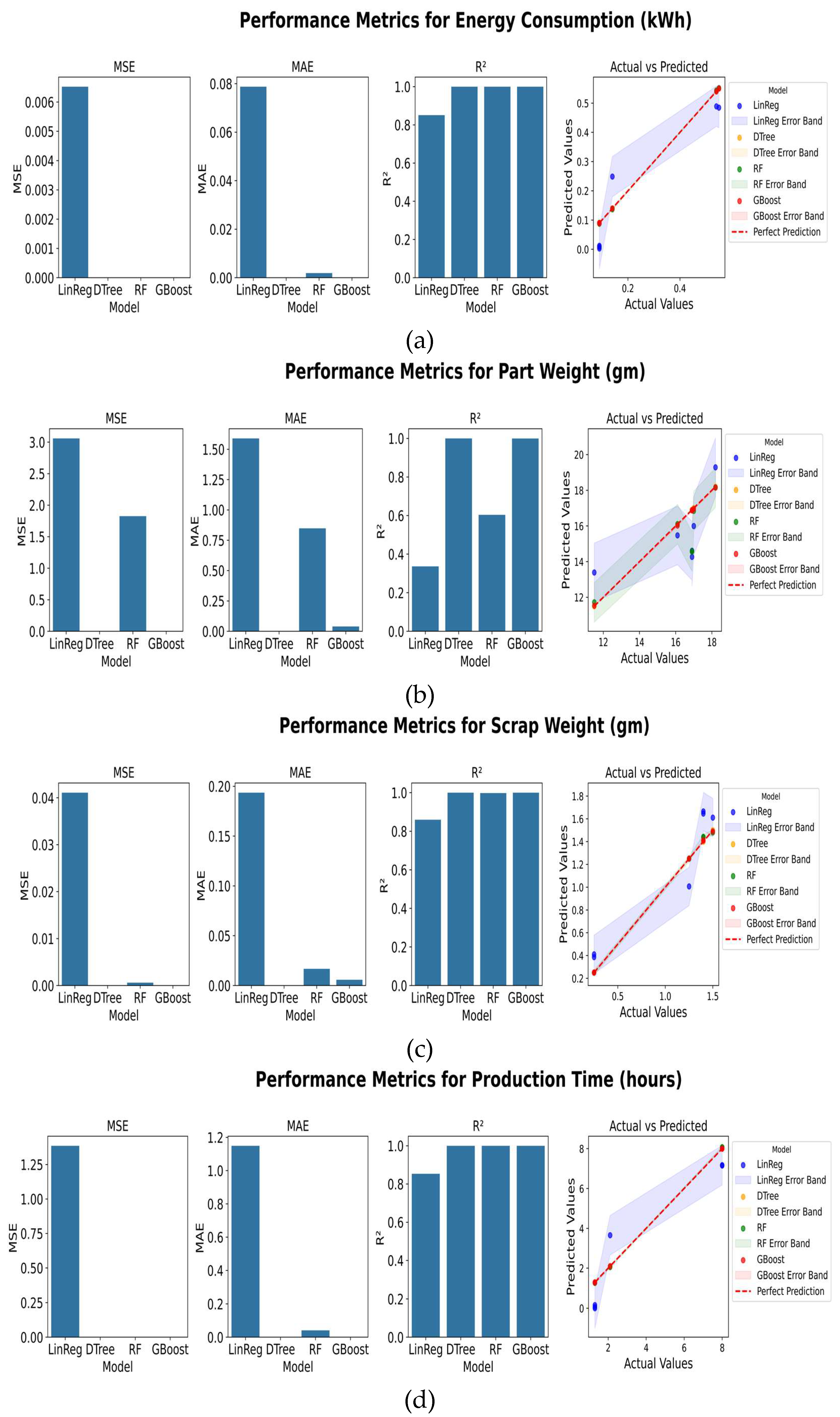
3.3. Evaluation Metrics

The models’ performance is assessed using the Coefficient of Determination (R²), Mean Absolute Error (MAE) and Mean Squared Error (MSE) [34].

R², MAE, and MSE are fundamental metrics used to evaluate the accuracy of regression models. R², or the coefficient of determination, quantifies the percentage of the variance in the dependent variable that is predictable from the independent variables, with values closer to 1 indicating a better fit of the model [32], mathematically represented as:

$$R^2=1-{\displaystyle \frac{S{S}_{res}}{S{S}_{tot}}}$$

(6)

where $S{S}_{res}$ (Sum of Squares of Residuals) = ${\sum }_{i=1}^n{\left(y_i-y_i^{*}\right)}^2$, $S{S}_{tot}$ (Total sum of squares) = ${\sum }_{i=1}^n{\left(y_i-y_i^{-}\right)}^2$, $y_i$= actual values, $y_i^{*}$=predicted values, and $y_i^{-}$= mean of actual values.

Mean Absolute Error (MAE) measures the average magnitude of errors in predictions, giving a straightforward indication of prediction accuracy with a perfect score of 0, mathematically represented as:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n|y_i-y_i^{*}|$$

(7)

where $|y_i-y_i^{\mathrm{*}}|$ is the absolute error between the actual and predicted values.

Meanwhile, Mean Squared Error (MSE) calculates the average of the squares of the errors, heavily penalizing larger errors, which makes it sensitive to outliers in the data set, mathematically represented as:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-y_i^{*}\right)}^2$$

(8)

These metrics together provide a comprehensive overview of a model’s predictive performance, helping in both the diagnostics of model behavior and the comparison of different models under consideration [48]. To evaluate the model performance comprehensively, we incorporate multiple techniques beyond the traditional metrics like R², MAE, and MSE.

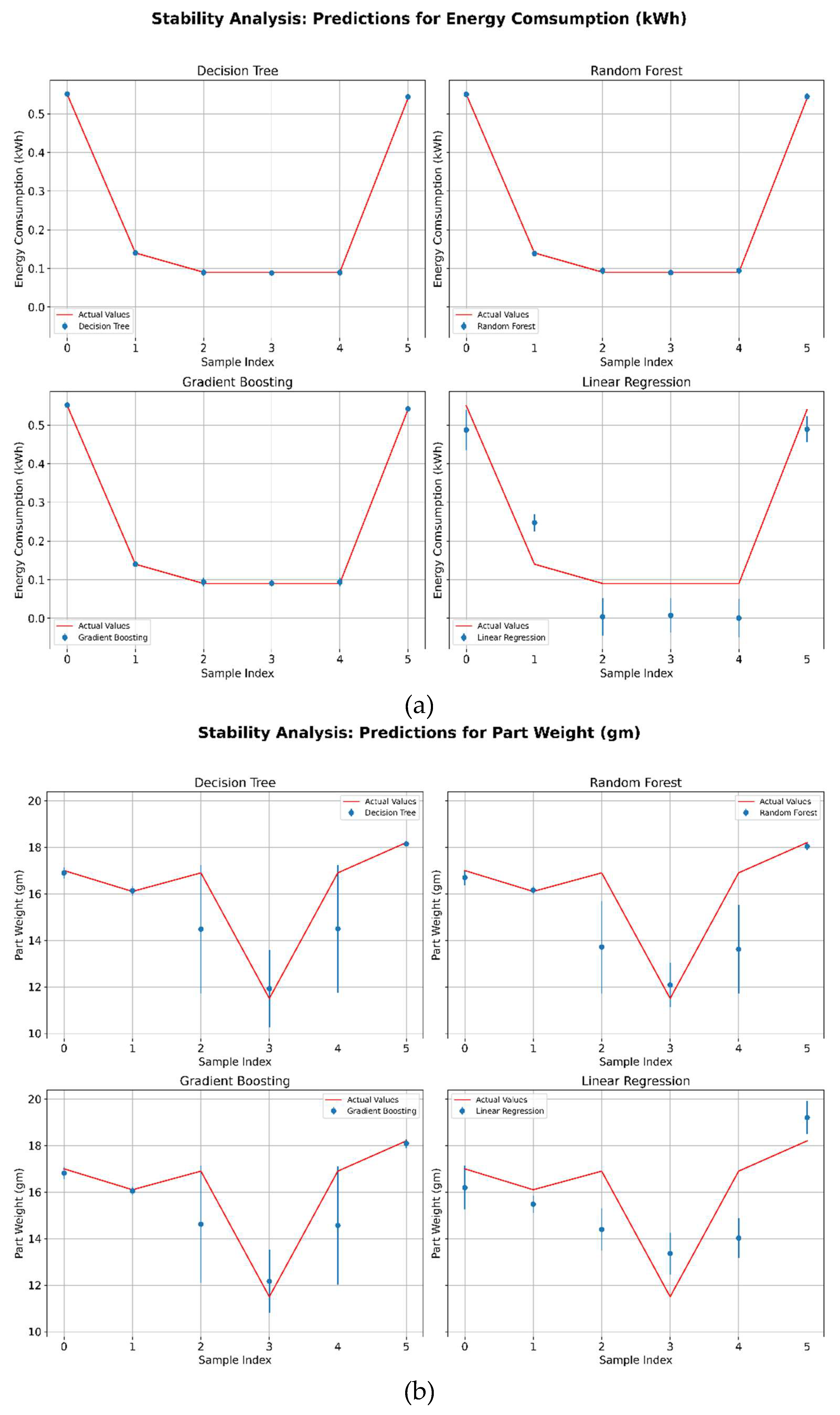
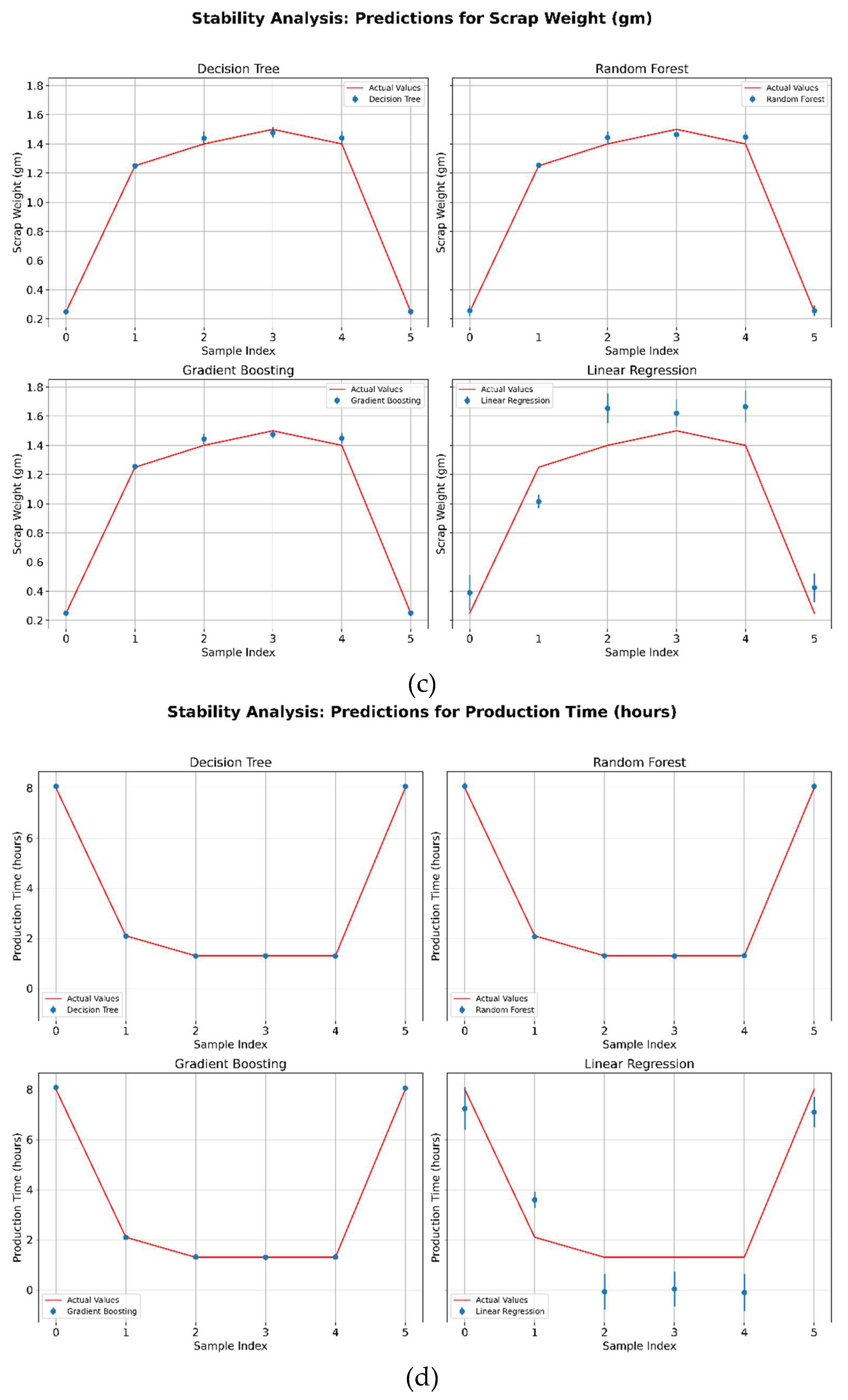
Model Stability Analysis: Stability analysis assesses the consistency of model predictions by calculating the mean and standard deviation of predictions across multiple bootstrap samples. This method highlights the reliability of each model under varying training conditions to offer deeper insights into model robustness.

True vs. Predicted Values with Error Bands: The actual vs. predicted values plots provide a visual representation of model accuracy. To enhance interpretability, error bands are added to these plots, representing the standard deviation of errors. Residuals ($e_i$) are calculated as follows.

$$e_i=y_i-y_i^{*}$$

(9)

where $y_i$ and $y_i^{*}$ are the true and predicted values, respectively. The standard deviation of residuals (${\delta }_e$) quantifies the error spread:

$${\delta }_e=\sqrt{{\displaystyle \frac{1}{m}}}{\sum }_{i=1}^m{e}_i^2$$

(10)

where ‘m’ is the total number of samples. The error bands are then defined as:

$$\mathrm{Upper}\mathrm{Bound}=y_i+{\delta }_e\mathrm{and}\mathrm{Lower}\mathrm{Bound}=y_i-{\delta }_e.$$

(11)

Selecting appropriate evaluation metrics is crucial for ensuring the reliability, robustness, and interpretability of machine learning models, especially with experimental datasets. This study employs a comprehensive assessment framework combining prediction accuracy metrics, uncertainty quantification, and visual validation methods. Bootstrap-based stability analysis evaluates prediction variability across response variables, ensuring model consistency.

Additionally, true vs. predicted values plots visually assess bias, variance, and predictive performance, providing deeper insights into model reliability and generalizability. This integrated approach strengthens model evaluation, ensuring the selected models are statistically sound and practically applicable.

3.4. Dataset Description, Preprocessing and Datasplitting

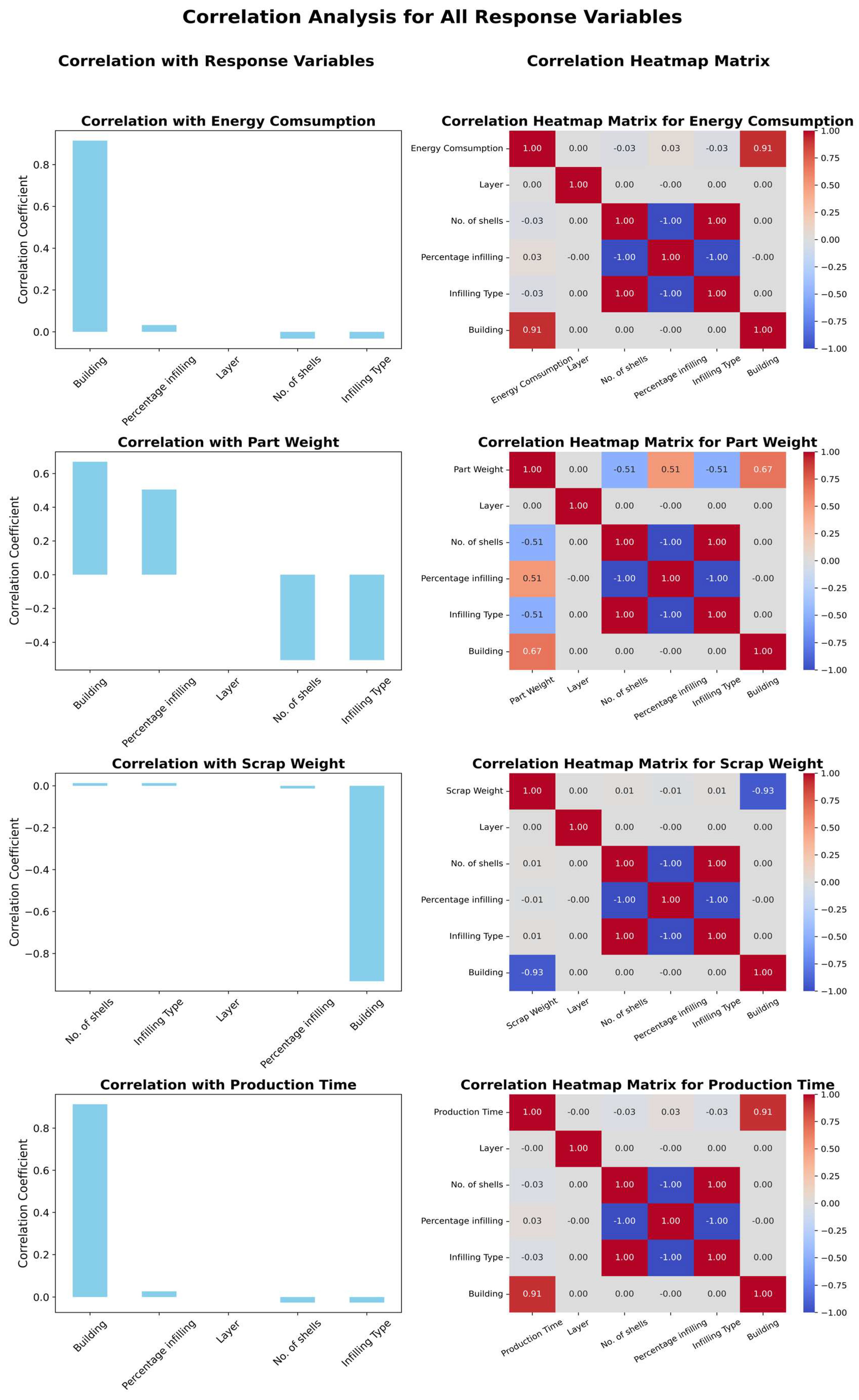
To evaluate the AM sustainability, four key metrics, energy consumption, part weight, scrap weight, and printing time, are analyzed using five process parameters at three levels, as shown in Table 2. The Taguchi Orthogonal Arrays (OA) approach is employed to optimize experimental design, reducing the number of experiments from 243 (full factorial design) to 27, as per the L27 OA design [19]. The dataset is provided by the corresponding author who is also the author of the referenced paper [19]. This ensures that the dataset structure, including process parameters and response variables, aligns with the objectives of this research.

Numerical features, such as the layer thickness and infill percentage, are standardized using the ‘StandardScaler’ to enhance the model performance and ensure consistent training. Categorical variables, including the infill type (Cross, Diamond, Honeycomb) and build orientation (Flat, On-edge, Upright), are encoded using ‘pd.Categorical’. The choice of ‘pd.Categorical’ over methods like One-Hot Encoding is driven by its compactness, as it avoids the feature expansion and minimizes dimensionality. This results in the lower memory usage and computational overhead for its high efficiency. Additionally, the distinct categories in the dataset are effectively represented with direct numerical encoding to eliminate the need for binary columns required by One-Hot Encoding. This approach ensures efficient preprocessing while maintaining clarity and interpretability, aligning seamlessly with our goals.

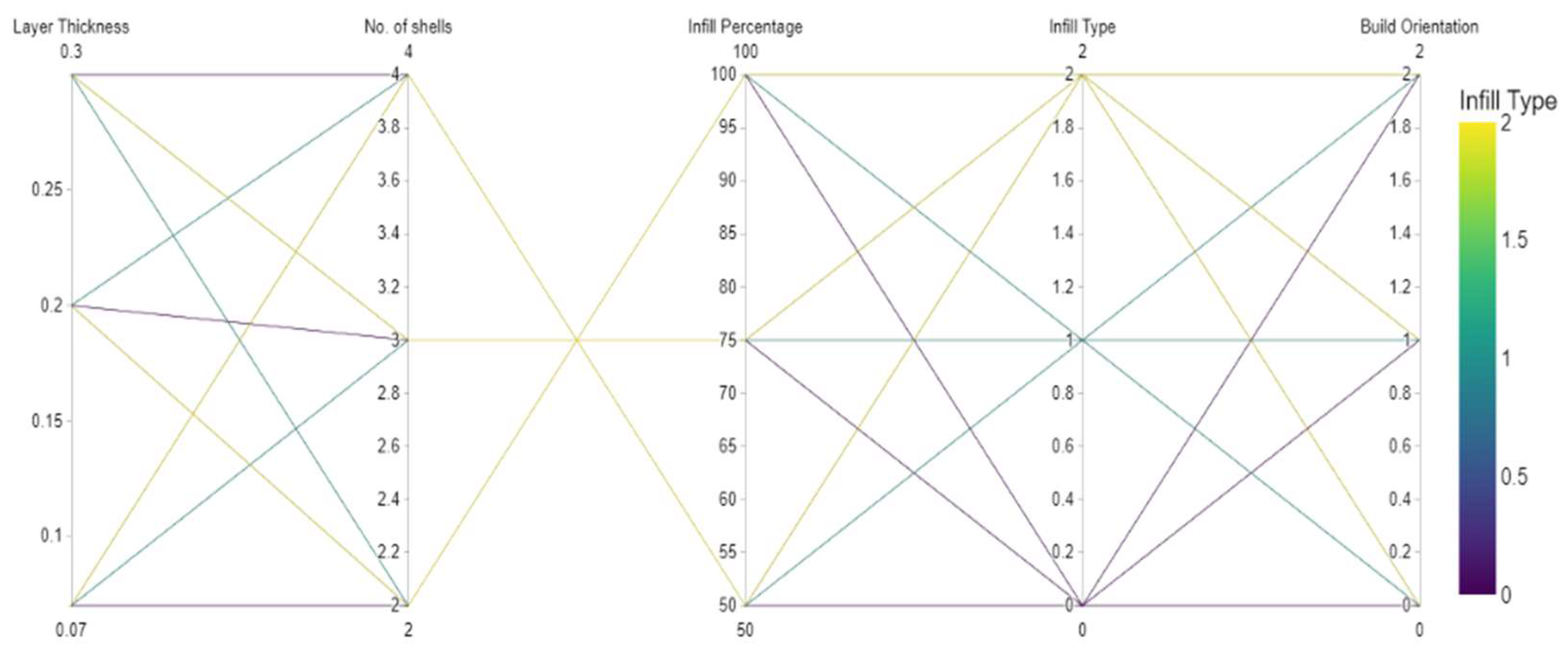
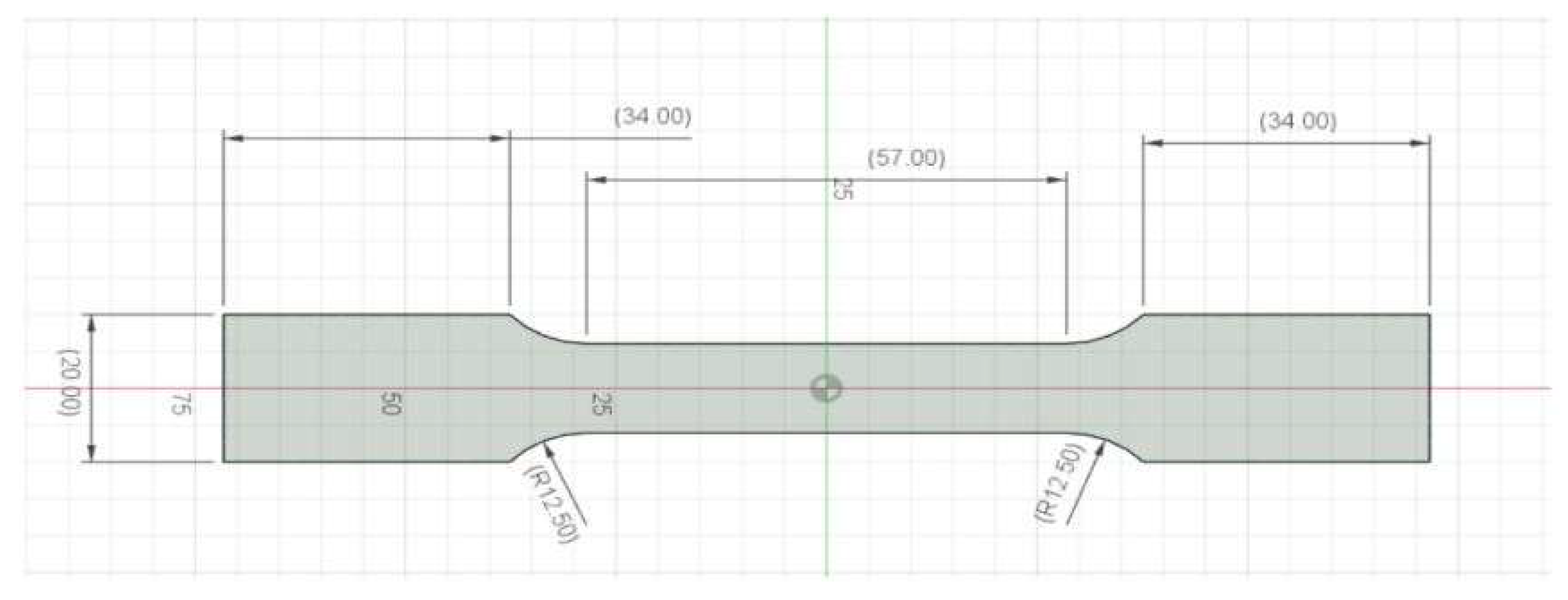
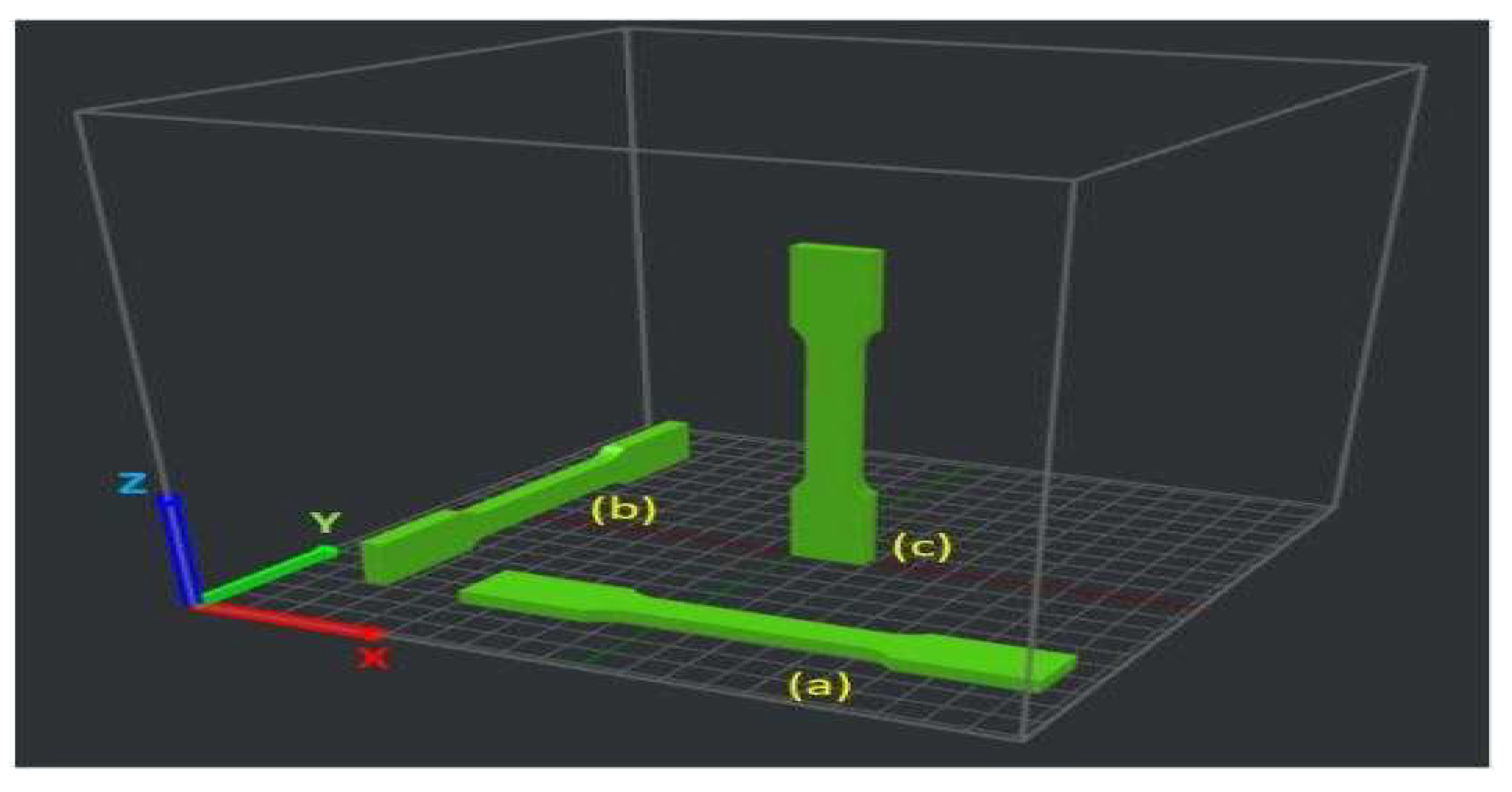
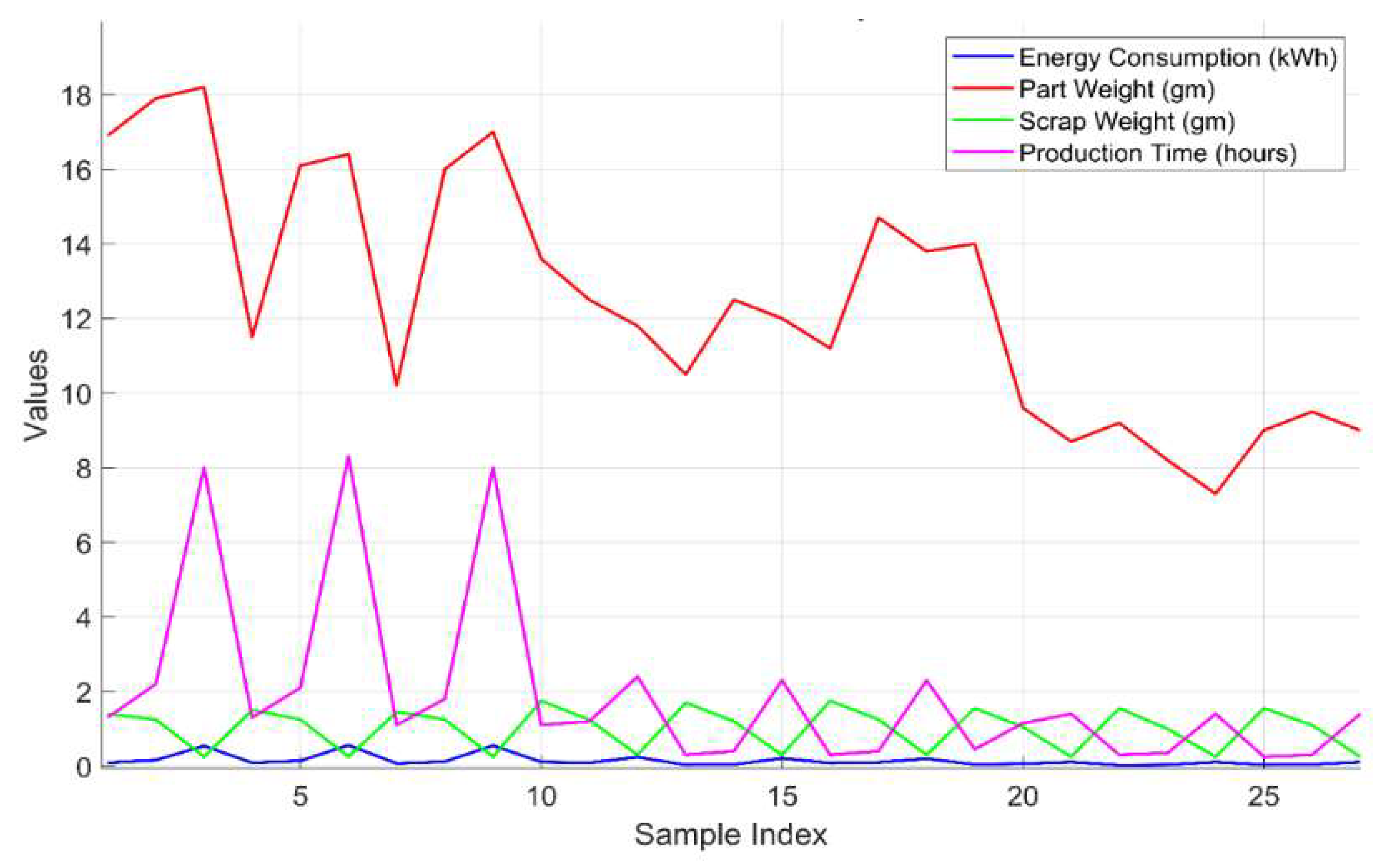
Figure 1 displays the parameter combinations used in the study for 3D Printing specimens. Figure 2 shows dimensions of the experimental specimen. Polylactic Acid (PLA) material with a 1.75 mm diameter is used to fabricate ASTM-standard specimen. Figure 3 displays 3 building orientations. Figure 4 presents the experimental data collected for the four-sustainability metrics. The x-axis represents the sample index, while the y-axis displays the corresponding values for each metric, allowing for a clear comparison across the different samples in terms of energy consumption, part weight, scrap weight, and production time. The energy consumed is determined by multiplying the 3D printer’s power consumption by the sum of the warm-up and printing times. Part weight and scrap weight are measured by weighing the printed part and any additional materials such as support structures, respectively. Production time encompasses both set-up and printing durations.

To ensure the reliable model evaluation, the dataset is split into training and testing sets using an 80:20 ratio. This split allows much of the data to be used for training the models, while a representative portion is reserved for testing their performance. A fixed random seed is applied during the splitting process to maintain consistency and reproducibility of results across different runs. This approach ensures that the training and testing sets remain representative of the overall dataset for a robust evaluation of the model ability.

3.5. Sustainability Metrics

Among the three aspects of sustainability, economic, environmental and social sustainability [49], this research focuses on the economic and environmental aspects. Energy efficiency, material efficiency, and process efficiency are identified as key factors contributing to both environmental and economic sustainability[2,37]. Energy efficiency reduces the energy consumption, lowers operational costs while minimizing the carbon footprint. Material efficiency involves optimizing the resource utilization, reducing waste, conserving natural resources, and decreasing pollution [20]. Economically, it leads to significant cost savings by minimizing the material usage. Processing efficiency enhances production rates, reduces energy use and operational costs, thereby improves profitability and environmental outcomes.

In the context of AM, sustainability metrics in energy consumption, part weight, scrap weight, and production time quantitatively represent the environmental impact and efficiency of the printing process. These metrics facilitate informed decisions to balance sustainability goals with operational performance. Mathematical representations of these metrics are as follows.

3.5.1. Energy Consumption (EC)

It can be represented as the total kilowatt-hours (kWh) used during the production of a single part and the warm-up time [15].

$$EC=Px(T_{warm-up}+T_{printing})$$

(12)

where $\mathrm{P}$ is the power rating of the 3D printer (in kilowatts), $T_{\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{m}-\mathrm{u}\mathrm{p}}$ is the time the printer takes to warm-up, and ${\mathrm{T}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}}$ is time taken to print the part (in hours).

3.5.2. Part Weight (PW)

The total mass of the final product, usually measured in grams or kilograms [51] is represented as:

$$PW={\sum }_{i=1}^n{m}_i$$

(13)

where ${\mathrm{m}}_{\mathrm{i}}$ is the mass of each component of the part if the part consists of multiple components.

3.5.3. Scrap Weight (SW)

The total mass of waste material generated during the printing process [51] is represented as:

$$SW={\sum }_{j=1}^k{w}_j$$

(14)

where $w_j$ is the weight of the waste material for each print job.

3.5.4. Production Time (PT)

The total time required to produce a part, which includes setup time, printing time, and post-processing time [51] is represented as:

$$PT=t_{setup}+t_{print}+t_{post}$$

(15)

where ${\mathrm{t}}_{\mathrm{s}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{p}}$ is the time for setting up the printer, ${\mathrm{t}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{t}}$ is the actual printing time, and ${\mathrm{t}}_{\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}}$ is the time required for any post-processing steps.

4. Results and Discussion

This section presents results and discussions of the ML models performance and the relationship analysis of parameters to the response variables.

4.1. ML Models Evaluation

We evaluate the performance and stability of four ML models, LinReg, DT, RF, and GB, in predicting the sustainability metrics of energy consumed, material used, scrap weight, and printing time in AM. The performance metric plots (e.g., R² and MSE) and model stability plots are applied in a comprehensive evaluation.

4.1.1. Performance Evaluation

The performance metric plots in Figure 5 clearly highlight the superiority of the RF model across all response variables. In Figure 5(a) for MSE and MAE, RF consistently achieves the lowest values, indicating its ability to minimize prediction errors effectively. Similarly, in Figure 5(c), RF secures the highest R² values, nearing 1, signifying exceptional alignment between predicted and actual values. This performance underscores RF’s robustness and accuracy, which stems from its ensemble structure that combines predictions from multiple decision trees. DT, shown alongside RF in Figure 5 (a) and (c) for part weight and scrap weight respectively, achieves competitive R² values and low MSE and MAE, making it a strong secondary choice despite slightly lower precision.

Figure 5 (b) and (c) further demonstrate the limitations of LinReg and GB. LinReg, as evident in its high MSE in Figure 5(a) and lower R² values in Figure 5(c), struggles with the non-linear relationships present in the dataset. GB performs moderately but is less consistent than RF and DT, with higher variability as seen in Figure 5(a).

The “Actual vs. Predicted” performance in Figure 5 highlights RF’s strong predictive accuracy across all metrics (energy consumption, printing time, part weight, and scrap weight). RF’s predictions closely align with the red diagonal line, supported by narrow and consistent error bands, indicating minimal prediction uncertainty. In Figure 5(a), RF’s tight error bands demonstrate its stability, while LinReg shows wider bands, reflecting inconsistent predictions for lower energy consumption values. In Figure 5(b), RF again outperforms with the minimal variability, while LinReg and GB exhibit broader error bands at higher printing time, suggesting reduced reliability.

In Figure 5(c), RF maintains the superior performance with narrow error bands for the part weight, while DT shows slightly wider bands, indicating moderate deviations. LinReg displays irregular error bands, especially for lighter parts, highlighting its challenges in capturing data complexity. In Figure 5(d) for the scrap weight, RF shows consistently narrow error bands, while GB and LinReg exhibit broader bands, particularly for higher scrap weights, reflecting greater prediction uncertainty in these models.

Overall, the error bands provide a clear depiction of the model stability and reliability, reinforcing RF’s superior performance and DT’s moderate reliability, while highlighting limitations of LinReg and GB in capturing complex relationships in AM parameters.

4.1.2. Model Stability Analysis

The stability plots in Figure 6 provide a detailed visualization of the consistency of predictions for different models across various parameter combinations, helping us draw key conclusions about their performance. For RF, the narrow confidence intervals displayed in the plots in Figure 6 (a–d) demonstrate its minimal prediction variability, as seen by the blue points closely aligning with the red lines (actual values). This consistent alignment across all parameter combinations highlights RF’s robustness and reliability, making it particularly well-suited for applications in AM, where prediction stability is critical. The lack of large deviations in RF’s plots indicates its ability to generalize effectively, regardless of the parameter complexity.

In comparison, the DT model also shows relatively consistent predictions in its plot, with blue points closely following the red lines. However, the confidence intervals for DT are slightly wider than those of RF, particularly in regions where parameters are more variable, such as in Figure 6 (a) and (d). This indicates moderate variability in DT’s predictions, suggesting that while it remains reliable, it is not as robust as RF for scenarios requiring high precision.

The LinReg model, on the other hand, exhibits significant instability in its predictions, as evident from the wide confidence intervals and inconsistent alignment of blue points with the red lines. For instance, in nonlinear regions such as in Figure 6 (a) and (d), LinReg fails to follow the trend of actual values, leading to erratic predictions. These deviations in the plot indicate that LinReg struggles to handle nonlinear interactions, making it unsuitable for complex AM parameter optimization tasks.

GB demonstrates moderate stability in its predictions, as observed in its plot where the blue points align reasonably well with the red lines in Figure 6 (a) and (d), energy consumption and printing time respectively. However, occasional spikes in variability can be seen, such as around in Figure 6 (b) and (c) for part weight and scrap weight respectively, where confidence intervals widen significantly. These spikes suggest that GB is sensitive to certain parameter changes, which can limit its effectiveness in scenarios requiring highly consistent predictions.

By examining plots in Figure 6, findings can be related to the observed trends and prediction patterns. For instance, RF’s narrow confidence intervals and tight clustering of blue points around the red lines clearly showcase its stability and reliability. In contrast, LinReg’s wide intervals and scattered blue points highlight its instability, while GB’s occasional deviations and moderate alignment reflect its sensitivity to parameter changes. The DT plot shows stable predictions overall, with slightly more variability than RF but far better alignment than LinReg. These visual patterns directly support the conclusion that RF is the most robust and reliable model for AM applications, with DT as a secondary choice, while LinReg and GB exhibit limitations in handling complex parameter spaces.

4.1.3. Model Selection and Parameter Optimization

The selection of RF and DT ML models for detailed evaluation is based on a balance between performance and stability. RF, with its superior accuracy and low variability, is ideal for precise and consistent predictions. DT, while less accurate, offers stability and interpretability, making it a valuable complementary model. LinReg and GB, due to their higher variability and weaker performance metrics, are less suitable for this application.

Figure 7 illustrates the high performance of the DT and RF models on the test set, as evidenced by consistently high R² scores across all response variables. RF demonstrates superior generalization with test set R² scores close to 1, indicating exceptional accuracy in capturing the underlying patterns of energy consumption, production time, part weight, and scrap weight. DT also performs well, though with slightly lower R² scores compared to RF, reflecting minor variability in prediction accuracy. This strong alignment between predicted and observed values highlights the robustness of both models, particularly RF, in parameter optimization and predictive reliability.

Table 3 lists the optimized parameters derived from the models, highlighting key combinations of AM parameters that contribute to minimizing energy consumption, reducing production time, and ensuring consistent part weight and scrap weight. These results demonstrate the practical utility of ML models in guiding AM practices.

4.2. Relationship Analysis between Process Parameters and Response Variables

The correlation analysis is presented in Figure 8 using both bar plots (left) of correlation coefficients and heatmaps (right) of pairwise correlations, which provides a comprehensive understanding of the relationships between features and response variables [39]. The bar plots Figure 8(left) highlight building orientation as the most influential feature across all response variables, showing a strong positive correlation with energy consumption (0.91) and production time (0.91), while displaying a strong negative correlation with scrap weight (-0.93). This indicates that building orientation directly impacts energy usage and time requirements, while inversely affecting material waste. For the part weight, building orientation shows a positive correlation (0.67), further emphasizing its critical role. Secondary features, such as percentage infilling and the number of shells, exhibit moderate correlations in specific cases; for instance, percentage infilling moderately correlates with part weight (0.51), reflecting its influence on material usage and density.

The heatmaps Figure 8 (right) complement these findings by illustrating pairwise correlations between all features and response variables. Building orientation maintains consistently high correlations across all response variables, reaffirming its dominant influence. In contrast, other features such as layer thickness, number of shells, and infilling type show negligible correlations, indicating their limited direct impact on energy consumed, printing time, and scrap weight. Moreover, the heatmaps reveal minimal interdependencies between features, suggesting that the response variables are predominantly influenced by building orientation rather than complex interactions among features. Together, the bar plots and heatmaps confirm the models’ ability to accurately identify and quantify the impact of critical parameters, highlighting building orientation as the primary driver of AM outcomes, with secondary factors like percentage infilling playing a supporting role.

Figure 9 illustrates the feature importance values across the most effective ML models and response variables, highlighting the influence of key AM parameters. Building orientation is identified as the most critical feature, consistently showing the highest importance across all models and response variables, including the energy consumption, production time, part weight, and scrap weight. Infill type demonstrates the moderate importance in specific cases, such as the production time and part weight, while other features like the layer thickness, number of shells, and percentage infill exhibit minimal influence across the models. The results suggest that the building orientation significantly impacts the sustainability metrics, making it a priority for the AM process optimization. This analysis provides valuable insights into the relative contributions of different parameters for informed decision-making to improve AM efficiency and sustainability.

Partial dependence plots in Figure 10 are a visualization technique to interpret ML models by illustrating the marginal effect of a selected feature (or set of features) on the predicted outcome. These plots help isolate and understand the relationship between specific input features and response variables while averaging out effects of other features [34].

In Figure 10, the partial dependence plots reveal a predictable and interpretable relationship between building orientation and the response variables, including energy consumption, printing time, material used, and scrap weight. For energy consumption and production time in Figure 10 (a) and (d), the plots exhibit a steady and smooth upward trend as building orientation becomes more complex. This highlights a direct relationship, where increasing orientation complexity demands longer printing times and higher energy usage. In contrast, other parameters, such as layer thickness and the number of shells, show negligible effects on these response variables, as evidenced by their nearly flat trends. This suggests that energy consumption and production time are primarily dictated by building orientation.

For part weight and scrap weight shown in Figure 10 (b) and (c), the influence of building orientation is more nuanced yet significant. The plots indicate a positive trend for part weight, where increasing orientation complexity results in greater part weights due to changes in material distribution patterns. Conversely, the scrap weight demonstrates a consistent decline as the building orientation becomes more optimized, reflecting the ability of certain orientations to reduce waste. While interactions with other parameters, such as percentage infilling, are minimal, they are slightly more pronounced for part weight, where infilling marginally contributes to observed variations. The consistent and smooth gradients observed in the plots across all response variables underscore the robustness of the models in capturing both linear and non-linear dependencies, validating their ability to generalize effectively to complex parameter spaces.

The shape analysis presented in Figure 11, DT (top) and RF (bottom) highlights the robustness of the models by illustrating the relationship between predicted and observed values for energy usage, printing time, material used, and scrap weight [34]. For the energy consumption plots in Figure 11(a), the predicted distributions display smooth and consistent trends that align closely with the observed values, especially as building orientation changes. This alignment demonstrates the models’ ability to accurately capture the impact of building orientation on energy requirements, with significant shifts in predictions observed as orientation becomes more complex. Similarly, for the production time plots in Figure 11(d), the models show a steady increase in predicted values with varying orientation, mirroring the observed trends. This further validates their precision in reflecting dependencies driven by orientation changes.

For the part weight, plots in Figure 11(b) reveal a stable relationship between predicted and observed values, capturing dependencies influenced by building orientation. The slight variations introduced by secondary parameters like percentage infilling are evident but minimal, reinforcing the models’ focus on the primary contributor i.e. orientation. For the scrap weight plots in Figure 11(c), the predicted values show a clear alignment with observed trends, with consistent decreases in scrap weight as the building orientation optimizes. This reflects the models’ capability to minimize material waste effectively through accurate predictions.

Overall, the smooth transitions and alignment in Figure 11 demonstrate that both the models, DT and RF, are well-calibrated and capable of generalizing across different parameter combinations. This further supports their reliability in predicting and optimizing AM processes, contributing to improved efficiency and sustainability.

The results demonstrate the exceptional performance of the DT and RF models in predicting and optimizing response variables for AM. Building orientation consistently emerges as the dominant factor influencing energy usage, printing time, material used, and scrap weight, as highlighted by feature importance rankings and partial dependence plots. The models capture clear, interpretable relationships, showing that increasing orientation complexity leads to higher energy usage and production time, increased part weight, and reduced scrap. Secondary features, such as percentage infilling and the number of shells, play minor roles, contributing only marginally in specific cases. The smooth gradients and alignment between predicted and observed distributions validate the robustness and generalizability of DT and RF as dominant ML models. Together, these findings underscore the models’ capability in both prediction and optimization, reinforcing their utility in enhancing AM processes for improved efficiency and sustainability.

5. Conclusions

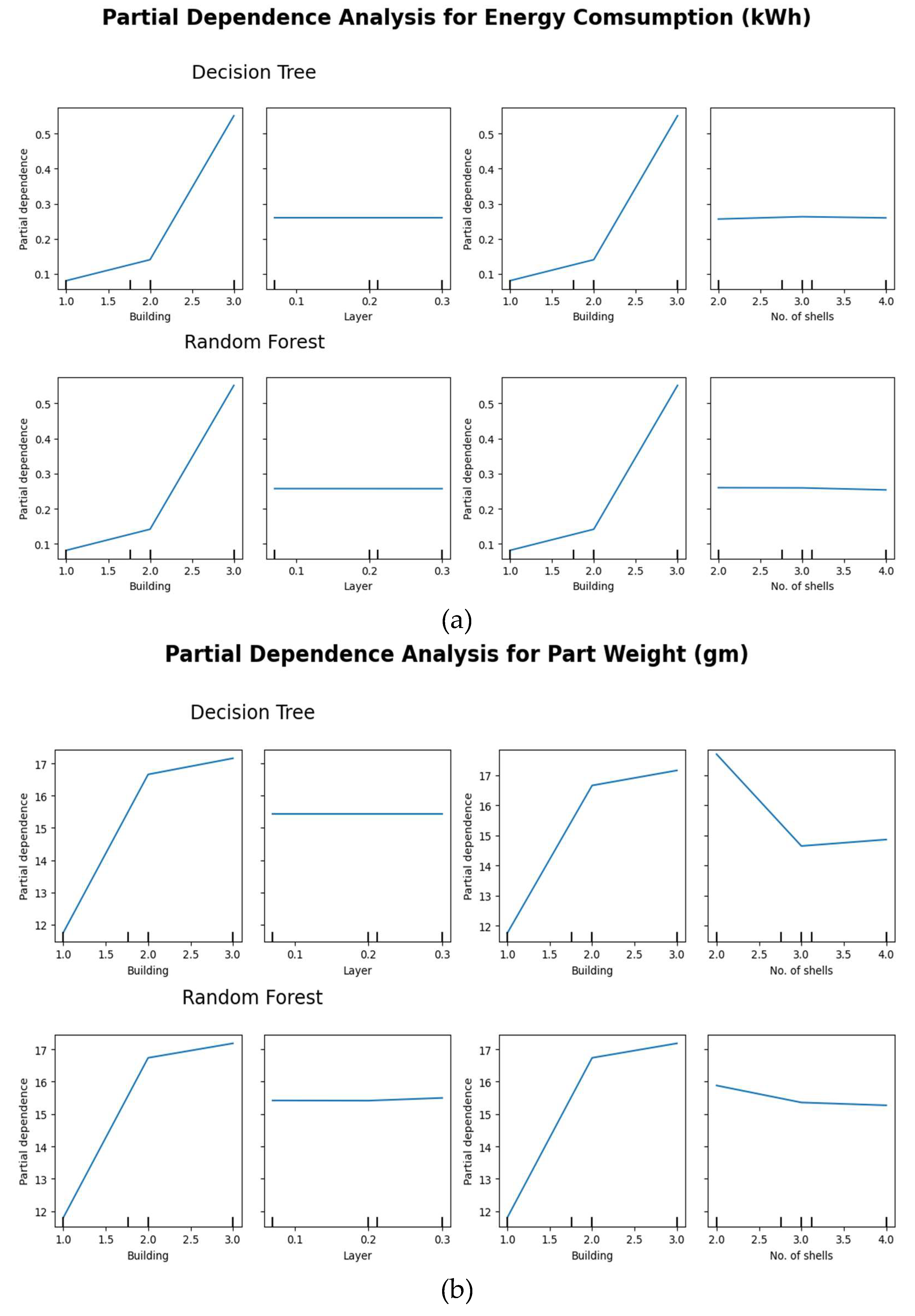
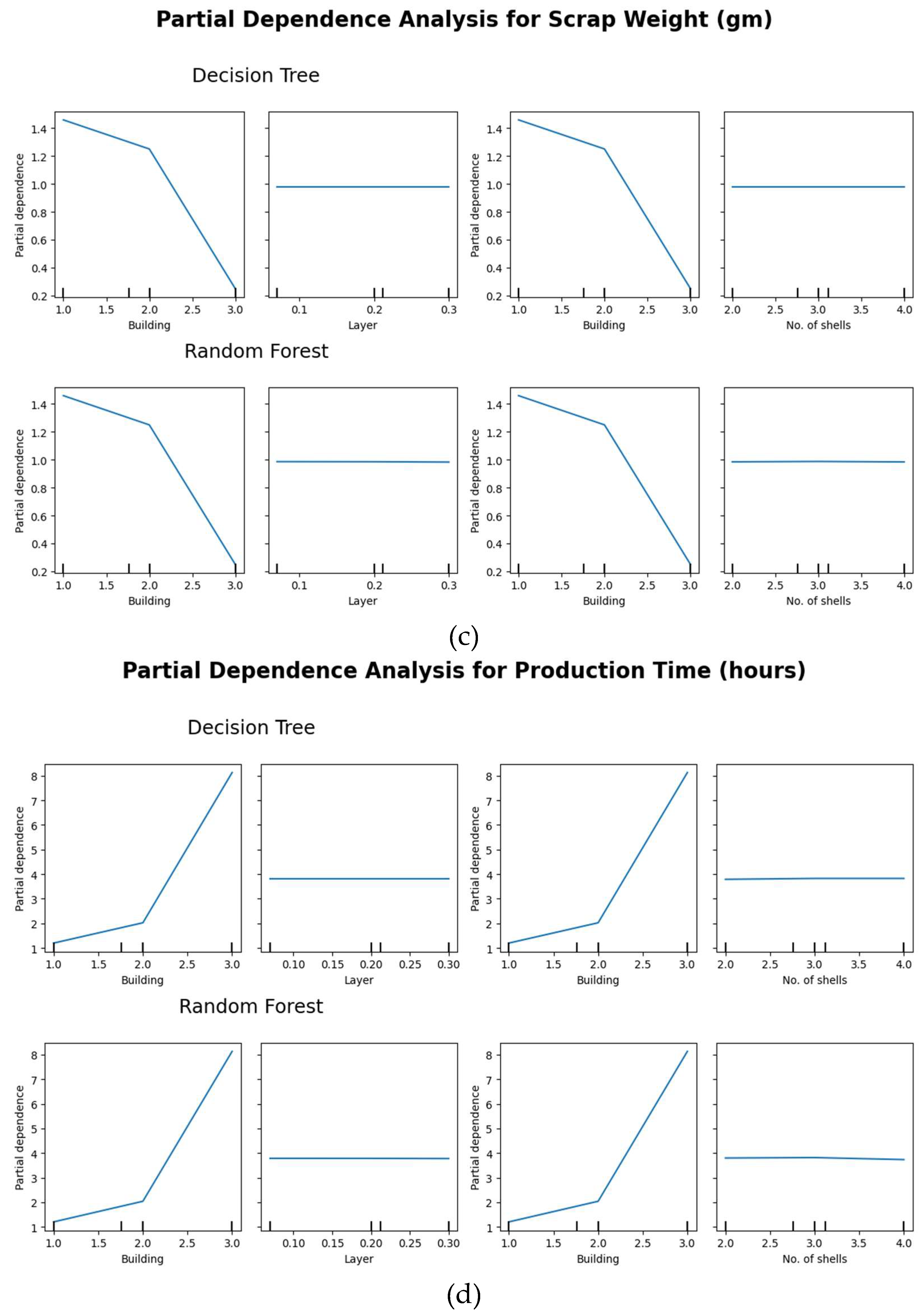
This paper evaluates ML models to identify the most suitable approach for accurately predicting sustainability outcomes of AM processes. By introducing the L-BFGS-B optimization method alongside DT and RF models, this research explores an innovative approach to hyperparameter tuning, enabling more precise and efficient predictions. The models effectively capture relationships between key AM parameters, such as the layer thickness, number of shells, build orientation, infill type, and infill percentage, and sustainability metrics, including the energy consumption, part weight, scrap material, and printing time. The proposed method allows users to optimize AM parameters, reduces the resource consumption, energy usage, and emissions. These advancements contribute significantly to both environmental and economic sustainability in AM. The novel application of L-BFGS-B highlights its potential to enhance the predictive accuracy and process optimization for a scalable framework of sustainable and efficient AM practices.

The research is limited by its focus on the specific material, parameters, and AM technique, which may not fully capture the broader range of possibilities in AM. Expanding the scope to include more materials and methods would provide a more comprehensive understanding of the AM sustainability.

Authors’ Contributions The authors contributed equally to the study.

Funding This work is supported by the Discovery Grants from the Natural Sciences and Engineering Research Council (NSERC) of Canada and Mitacs Lab2Market program.

Data Availability The experimental data are provided in Figure 4.

Code Availability The ML codes will be provided upon request.