Submitted:
21 December 2024
Posted:
23 December 2024
You are already at the latest version
Abstract
This research aims to study by numerical simulation the influence of various parameters on the efficiency of a flash distillation. The main characteristic of this system is that it feed a binary or a multi-components distillation column, such as a debutaniser column, by providing this last one by both a liquid and a gas stream. The study of the flash distillation is carried out in order to emphasis the influence of operating parameters on the gas vaporized fraction (δ). The studied parameters are: temperature and pressure inside the flash tank, feed flow rate, and the feed composition. The obtained results showed that for an ideal mixture, the vaporized fraction is sensitive to the pressure, temperature and feed composition and is non- sensitive to the feed flowrate.
Keywords:
1. Introduction
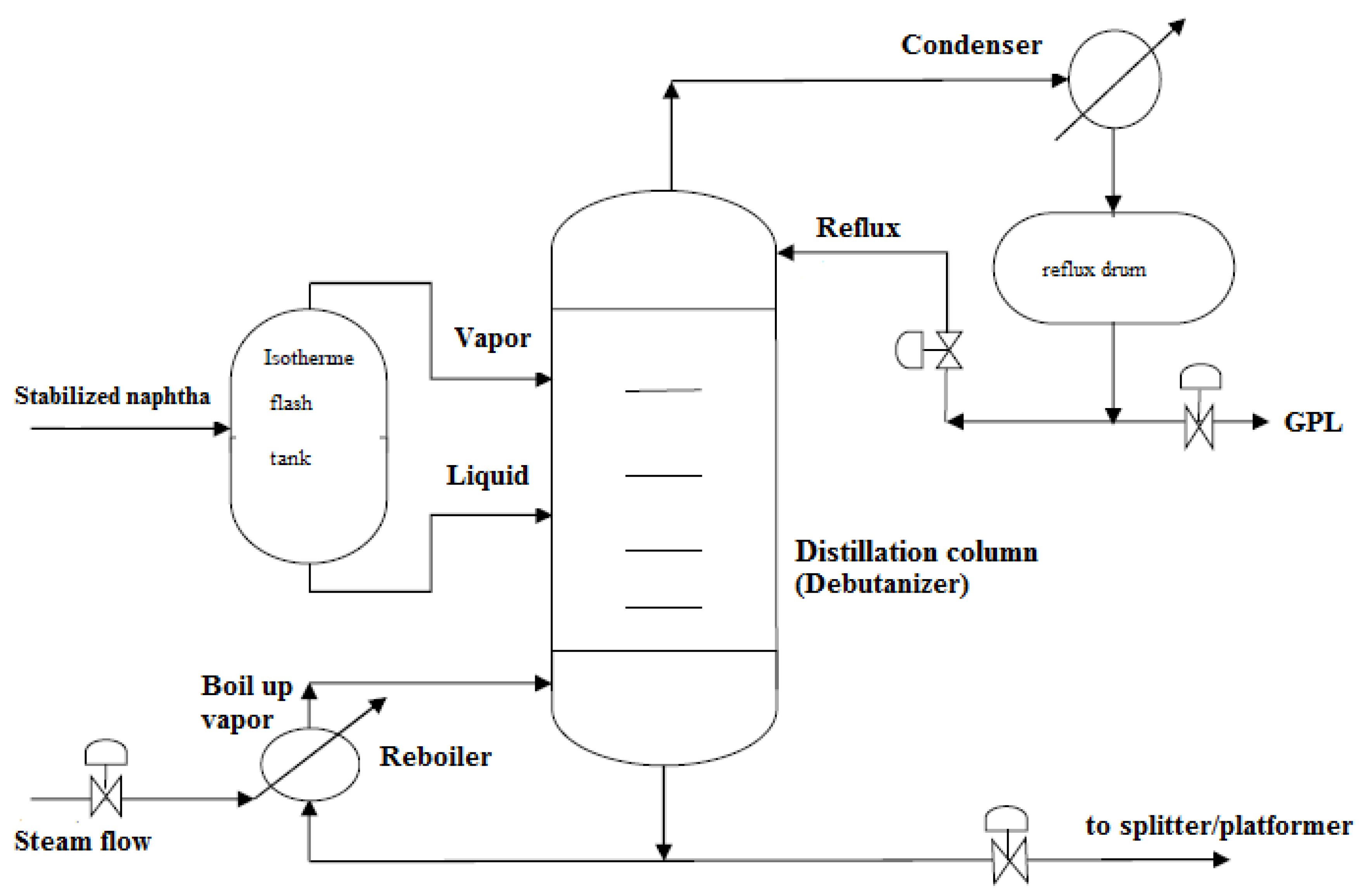
2. The Flash Distillation Unit
3. Model Assumptions
- -
- isothermal operation (isothermal flash);
- -
- steady state mathematical model;
- -
- ideal behavior of the mixture.
4. Mathematical Model and Method of Resolution
- 1.
- Compute the saturated pressure PiS for each component i (i=1,.. Nc), by using Lee-Kesler equation :
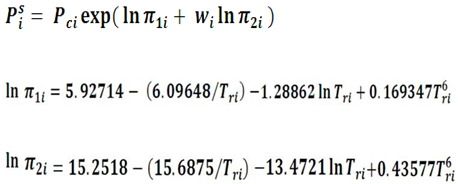
- 2.
- Compute the liquid-vapor equilibrium coefficient kFi = PiS/P ( i=1,.. Nc)
- 3.
- Assume a starting value for δ (δ = 0.1 for example)
- 4.
- Compute VF according to the following equation VF = δ.F
- 5.
- Compute LF according to the following equation LF = F - VF
- 6.
- Compute molar fractions in liquid phase xFi = zFi/(1- δ.(1-kFi)) (i=1,.. Nc)
- 7.
- Compute molar fractions in vapor phase yFci =-kFi. xFi (i=1,.. Nc)
- 8.
-
If | (Σ yFci) -1 | ≤ tolerance then yFi = yFci and stop the computing.Otherwise compute normalized molar fractions in vapor phaseyFi = yFci/ΣyFci (i=1,.. Nc) and go to the next step
- 9.
-
Compute kFi = yFi/xFi for all components (in our case, i=1,..8) according toxFi = zFi/(1- δ.(1-kFi)) (i=1,..Nc) (from step 6)yFi = yFci/ΣyFci (i=1,..Nc) (from step 8)Update δ by using the Newton-Raphson convergence technique:δnew = δold ̶ F(δ)/F’(δ)F(δ) = Σ zFi/(1- δ.(1-kFi)) (i=1,..Nc)F’(δ) = Σ zFi (1-kFi)/(1- δ.(1-kFi))2 (i=1,..Nc)Go to step 4
5. Results and Discussion
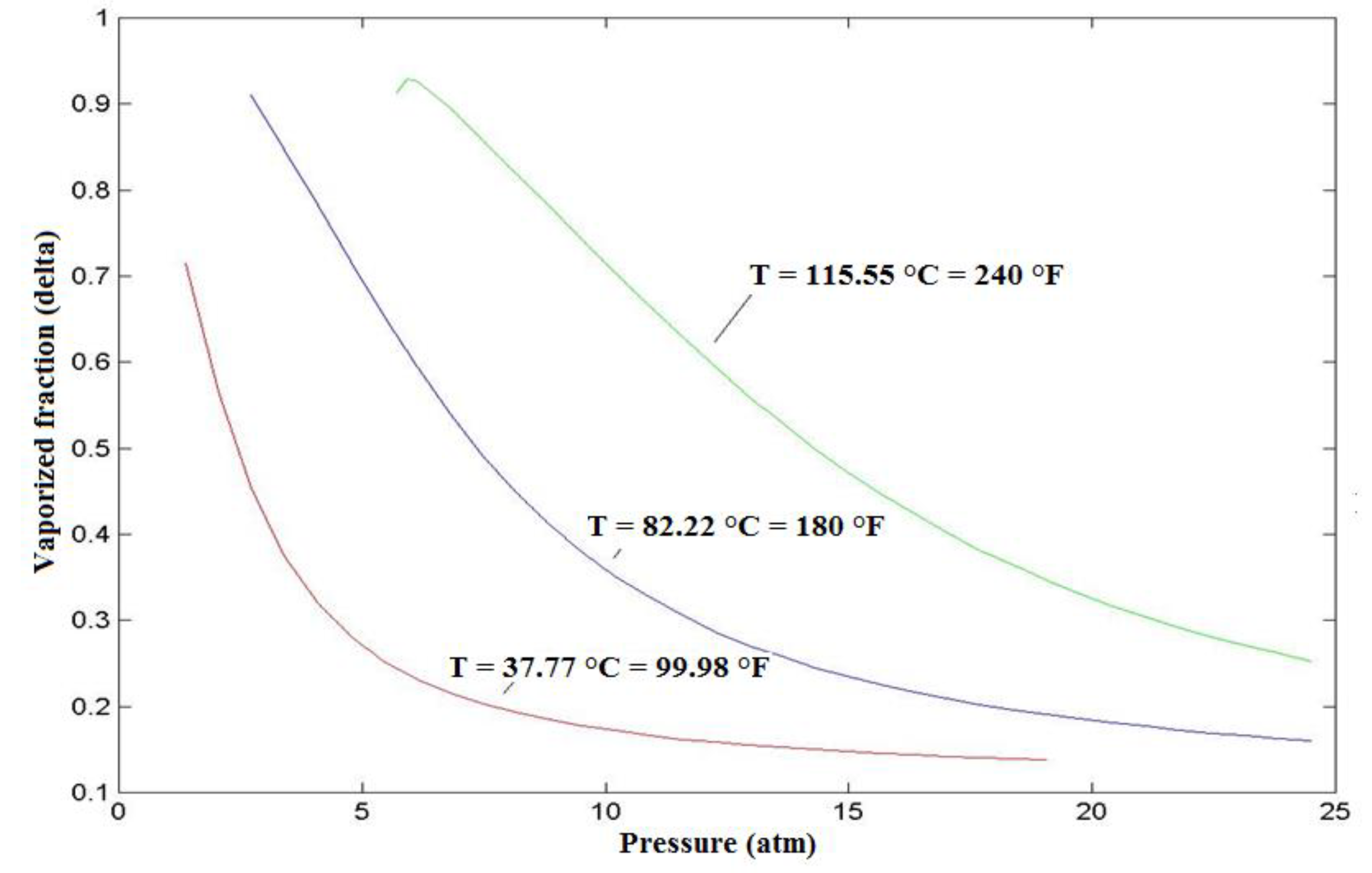
5.1. Influence of Temperature on the Vaporized Fraction
5.2. Influence of Feed Composition on the Vaporized Fraction
| x(1) | 0.001 | 0.101 | 0.301 | 0.101 | 0.501 | 0.001 |
| x(2) | 0.006 | 0.101 | 0.006 | 0.006 | 0.306 | 0.006 |
| x(3) | 0.240 | 0.040 | 0.140 | 0.140 | 0.040 | 0.040 |
| x(4) | 0.315 | 0.015 | 0.215 | 0.015 | 0.015 | 0.015 |
| x(5) | 0.121 | 0.221 | 0.021 | 0.221 | 0.021 | 0.021 |
| x(6) | 0.102 | 0.201 | 0.002 | 0.202 | 0.002 | 0.002 |
| x(7) | 0.131 | 0.231 | 0.031 | 0.231 | 0.031 | 0.431 |
| x(8) | 0.080 | 0.080 | 0.280 | 0.080 | 0.080 | 0.480 |
| δ | 0.491 | 0.428 | 0.611 | 0.396 | 0.911 | 0.188 |
5.3. Influence of Feed Flowrate on the Vaporized Fraction
6. Conclusions
References
- Osman A. Hamed et al. (2000), Thermal performance of multi-stage flash distillation plants in Saudi Arabia, Desalination, 128(3),281-292. [CrossRef]
- David Cargua-Sagbay et al. (2020) Flash Distillation Control Using a Feasible Operating Region: A Sliding Mode Control Approach, Ind Eng Chem Res, 59(5),2013-2024. [CrossRef]
- Bendjaouahdou C, Bendjaouahdou M H (2013) Control of the hot spot temperature in an industrial SO2 converter, Energy Procedia, 36, 428-443. [CrossRef]
- Bendjaouahdou C (2024) Parametric study of a ternary batch distillation column, Research Square (https://doi.org/10.21203/rs.3.rs-5427642/v1) 1 (1), 14. [CrossRef]
- Bendjaouahdou C (2024) Optimization of the Distribution of the Staged Feed in a Plug Flow Tubular Reactor, Preprints.org (10.20944/preprints202412.0703.v1) 1 (1),1-7. [CrossRef]
- A K Jana (2008) chemical process modelling and computer simulation, PHI learning private Limited ISBN-978-81-203-3196-9.
| Parameter | Signification | Value |
|---|---|---|
| Tf | temperature feed | 180 °F |
| P | flash pressure | 110 Psi |
| F | feed flowrate | 880.56 lbmol/h |
| Nc | number of components in the mixture at the inlet of flash tank | 8 |
| Tcf (1) | critical temperature of ethane (i =1) | 90.32 °F |
| Tcf(2) | critical temperature of propane (i =2) | 206.24 °F |
| tcf(3) | critical temperature of iso-butane (i =3) | 274.9 °F |
| tcf(4) | critical temperature of n-butane (i =4) | 305.6 °F |
| tcf(5) | critical temperature of iso-pentane (i =5) | 369.32 °F |
| tcf(6) | critical temperature of n-pentane (i =6) | 385.88 °F |
| tcf(7) | critical temperature of n-hexane (i =7) | 453.92 °F |
| tcf(8) | critical temperature of n-octane (i =8) | 564.44 °F |
| zF(1) | molar fraction of ethane in the flash distillation tank feed | 0.00120174 |
| zF(2) | molar fraction of propane in the flash distillation tank feed | 0.00675980 |
| zF(3) | molar fraction of iso-butane in the flash distillation tank feed | 0.24079915 |
| zF(4) | molar fraction of n-butane in the flash distillation tank feed | 0.31515700 |
| zF(5) | molar fraction of iso-pentane in the flash distillation tank feed | 0.12167645 |
| zF (6) | molar fraction of n-pentane in the flash distillation tank feed | 0.10244855 |
| zF (7) | molar fraction of n-hexane in the flash distillation tank feed | 0.13159080 |
| zF(8) | molar fraction of n-octane in the flash distillation tank feed | 0.08036650 |
| tolerance | value used in the iterative procedure to solve the model | 0.00000001 |
| P = 180 pis | δ | 0.292 | 0.292 | 0.292 | 0.292 |
| F (Ibmol/h) | 580.56 | 680.56 | 880.56 | 1880.56 | |
| P = 110 pis | δ | 0.371 | 0.371 | 0.371 | 0.371 |
| F (Ibmol/h | 580.56 | 680.56 | 880.56 | 1880.56 | |
| P = 80 pis | δ | 0.434 | 0.434 | 0.434 | 0.434 |
| F (Ibmol/h | 580.56 | 680.56 | 880.56 | 1880.56 |
| T=180 °F | δ | 0.371 | 0.371 | 0.371 | 0.371 |
| F (Ibmol/h) | 580.56 | 680.56 | 880.56 | 1880.56 | |
| T = 240 °F | δ | 0.527 | 0.527 | 0.527 | 0.527 |
| F (Ibmol/h | 580.56 | 680.56 | 880.56 | 1880.56 | |
| T = 80 °F | δ | 0.230 | 0.230 | 0.230 | 0.230 |
| F (Ibmol/h | 580.56 | 680.56 | 880.56 | 1880.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





