Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Efficient Grey Wolf Optimization: A High-Performance Optimizer with Reduced Memory Usage and Accelerated Convergence

Submitted:

09 April 2025

Posted:

09 April 2025

You are already at the latest version

Abstract
This paper presents an efficient Grey Wolf Optimizer (EGWO) designed to address the limitations of the standard Grey Wolf Optimizer (GWO), focusing on reducing memory usage and accelerating convergence. The proposed method integrates Sinusoidal Mapping for enhanced population diversity and a Transverse- Longitudinal Crossover strategy to balance global explo- ration and local exploitation. These innovations improve search efficiency and optimization precision while main- taining a lightweight computational footprint. Experi- mental evaluations on 10 benchmark functions demon- strate EGWO’s superior performance in convergence speed, solution accuracy, and robustness. Its application to hyperparameter tuning of a Random Forest model for a housing price dataset confirms its practical utility, fur- ther supported by SHAP-based interpretability analysis.
Keywords: 
Grey Wolf Optimizer
;  
Lightweight Optimization
;  
Sinusoidal Mapping
;  
Crossover Strategy
;  
Random Forest
;  
SHAP Analysis
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

With the development of intelligent optimization algorithms, some memory efficient and scalable models have been rising to a favor. Among these, bio-inspired optimization methods have proven to be highly effective in solving complex global optimization problems [26]. These algorithms simulate the behaviors and collaborative mechanisms of biological groups in nature, enabling efficient exploration of large search spaces to find near-optimal solutions [2,25]. Among these methods, the Grey Wolf Optimizer (GWO), proposed by Mirjalili et al. in 2014, has gained significant attention due to its simplicity and efficiency. GWO has been successfully applied in various fields such as engineering design, data mining, and machine learning [18].
GWO mimics the hunting behavior of grey wolves in nature, leveraging the collaborative efforts of four different roles: α, β, δ, and ω wolves. The α wolf leads the group, guiding the hunting process; the β and δ wolves assist in exploration and adjust the search direction; while the ω wolves follow and maintain the diversity of the population, preventing premature convergence to local optima. The process involves strategies of encircling, tracking, and capturing prey, progressively narrowing the search space to approach the optimal solution [6].
Despite its success in various applications, GWO has limitations that restrict its performance. Firstly, the random initialization of the population can result in uneven distribution, which affects early-stage search efficiency [1]. Secondly, GWO tends to get trapped in local optima when dealing with complex, highdimensional, or multimodal optimization problems, due to its insufficient global exploration capability. Additionally, as iterations proceed, the diversity of the population decreases, leading to slow convergence in the later stages [3].
To address these challenges, this paper proposes an Enhanced Grey Wolf Optimizer (EGWO), which incorporates advanced strategies to improve both global exploration and local exploitation capabilities. Specifically, EGWO employs a hybrid initialization strategy that combines geometric uniform distribution with random sampling, ensuring better initial diversity of the population. This approach enhances early-stage search efficiency by overcoming the limitations of traditional random initialization [28]. Furthermore, a dynamic weight adjustment mechanism is introduced, enabling adaptive balancing between global exploration and local exploitation throughout the optimization process [31]. An adaptive step size strategy is also applied, allowing for fine-tuned search capabilities based on solution quality, thus facilitating more precise exploration.
The performance of SCGWO is evaluated through extensive experiments on multiple complex benchmark functions and compared with the classic GWO. The results demonstrate that SCGWO achieves faster convergence and higher accuracy, particularly in highdimensional, nonlinear, and multimodal optimization problems. Additionally, SCGWO shows greater robustness across multiple independent runs, highlighting its stability.
To further demonstrate its effectiveness in practical applications, SCGWO is applied to the hyperparameter optimization of random forest models using the Boston housing price dataset [8]. The results indicate that SCGWO outperforms traditional optimization methods, achieving superior convergence and performance in model tuning.

Main Contributions

The key contributions of this paper are summarized as follows:
  • Proposed an Enhanced Grey Wolf Optimizer (SCGWO): A novel improvement of the GWO algorithm is presented, integrating Sinusoidal Mapping for population initialization and a Transverse-Longitudinal Crossover strategy, significantly enhancing both global exploration and local exploitation capabilities.
  • Introduced Dynamic Weight Adjustment Mechanism: A dynamic weight adjustment mechanism is developed to adaptively balance the roles of α, β, and δ wolves, ensuring better exploration in early stages and faster convergence in later stages.
  • Evaluated on Comprehensive Benchmark Functions: The proposed SCGWO is rigorously tested on 10 complex benchmark functions, demonstrating superior performance in terms of convergence speed, solution accuracy, and robustness when compared to the classic GWO.
  • Validated through Real-World Application: The effectiveness of SCGWO is further validated through its application to the hyperparameter optimization of a random forest model, achieving better tuning results than conventional optimization methods.

II. Related Work

A. Grey Wolf Optimizer (GWO)

The Grey Wolf Optimizer (GWO) is a natureinspired optimization algorithm that models the behavior of grey wolves in their natural hunting process. It was introduced by Seyedali Mirjalili et al. in 2014 [18]. The core idea of the algorithm is to convert the optimization problem into a process where a group of grey wolves search for prey. Within the wolf pack, there are four different roles: α, β, δ, and candidate wolves, representing the current best solution, the second-best solution, the third-best solution, and other candidate solutions, respectively. The hunting process of grey wolves is simulated through the following three phases: encircling prey, hunting prey, and attacking prey.

B. Improvements to GWO

Since the introduction of GWO, numerous improvements have been proposed to enhance its performance. Emary et al. (2016) proposed a binary version of GWO for feature selection, which outperformed traditional methods such as particle swarm optimization (PSO) and genetic algorithms (GA) in various datasets [6]. Other studies, such as those by Abdollahzadeh et al. (2020), have incorporated chaos theory into GWO to increase population diversity and prevent premature convergence [1]. Hybrid approaches combining GWO with differential evolution (DE) and simulated annealing (SA) have also demonstrated improved performance in complex optimization tasks [5], [28].
However, most of these studies focus on either global exploration or local exploitation, failing to address both aspects simultaneously. To bridge this gap, this paper proposes a novel strategy that integrates Sinusoidal Mapping for initial population diversity and a Transverse-Longitudinal Crossover mechanism, aiming to balance global search capabilities with refined local optimization [31].

III. Enhanced Grey Wolf Optimizer (SCGWO)

A. Sinusoidal Chaos Mapping for Population Initialization

In traditional GWO, the initial population is generated through random sampling, which often results in uneven distribution across the search space, negatively impacting convergence efficiency and accuracy. To address this, we adopt a Sinusoidal Chaos Mapping method, which generates a more uniformly distributed set of sample points, thereby enhancing the diversity of the initial population. The Sinusoidal Chaos Mapping is a typical form of chaotic mapping with a simple mathematical structure. Its expression is as follows:
xk+1 = a · x2ksin(π · xk),
where the parameter a = 2.3 and the initial value x(0) = 0.7. By using this mapping, the diversity of the initial population is significantly improved, allowing for a more effective exploration of the search space and enhancing the algorithm’s convergence speed and accuracy [1].

B. Transverse-Longitudinal Crossover Strategy

The Transverse-Longitudinal Crossover Strategy is a key method for significantly improving the performance of the SCGWO. Traditional GWO often faces challenges with population individuals clustering in local regions of the search space, leading to premature convergence. To overcome this limitation, the transverse-longitudinal crossover strategy introduces crossover operations that encourage individuals to explore a wider range of the solution space. Specifically, the transverse crossover enhances the global exploration capability, enabling the population to escape from local optima, while the longitudinal crossover refines the solution in local regions, ensuring that no promising areas are overlooked near the optimal solution. This combined strategy not only increases the diversity of the algorithm but also accelerates the convergence process.
1) Transverse Crossover Operation: The transverse crossover operation in SCGWO is similar to the crossover operation in genetic algorithms, focusing on exchanging information between different individuals across the same dimension. This approach is designed to improve the global search capability of the population. By randomly arranging the individuals in the population and performing crossover on the d-th dimension, the positions of the individuals are updated as follows:
MSxti,d = r1 ·xti,d +(1−r1)·xtj,d +c1 ·(xi,dt ·xtj,d),
M S x j , d t = r 2 ⋅ x j , d t + 1 − r 2 ⋅ x i , d t + c 2 ⋅ x j , d t ⋅ x i , d t ,
where MSxti,d and MSxtj,d represent the new offspring generated from individuals xti,d and xtj,d through transverse crossover, r1 and r2 are random numbers in the range [0,1], and c1 and c2 are constants in the range [−1,1]. After the transverse crossover operation, individuals can generate offspring with a higher probability within their respective hypercube spaces and edges, thus expanding the search space and improving global exploration. The offspring generated through this crossover must compete with their parents, and the individual with higher fitness is retained, ensuring a balance between exploration and exploitation.
2) Longitudinal Crossover Operation: The longitudinal crossover operation addresses the tendency of GWO to get stuck in local optima in later stages of the optimization process. This occurs when some individuals in the population reach local optima too early, causing the convergence speed to increase while the ability to explore the global optimum diminishes. The lack of a mutation mechanism in GWO restricts its ability to continue approaching the global optimum. Therefore, after performing transverse crossover, it is necessary to apply longitudinal crossover to further enhance the algorithm’s ability to escape local optima.
Longitudinal crossover operates on all dimensions of newly generated offspring, with a lower probability than transverse crossover, similar to mutation in genetic algorithms. If a newly generated individual x i , d t undergoes longitudinal crossover between dimensions d1 and d2, the calculation is as follows:
M S x i , d t = r 1 ⋅ x i , d 1 t + 1 − r 1 ⋅ x i , d 2 t
where MSxti,d is the offspring generated from dimensions d1 and d2 of individual x i , d t through longitudinal crossover, and r1 ∈ [0,1]. Similar to the transverse crossover operation, the offspring generated through longitudinal crossover competes with its parent, and the individual with higher fitness is preserved. This selection mechanism allows crossover participants to retain their superior dimensional information while improving population diversity and solution quality.
By combining transverse and longitudinal crossover operations, SCGWO effectively balances the ability to explore and exploit, resulting in a more efficient convergence to the global optimum. As the algorithm iterates, if an individual escapes a local optimum through longitudinal crossover in one dimension, this improvement is rapidly spread through transverse crossover, reinforcing the quality of the new solution throughout the population. This combined approach significantly enhances the algorithm’s ability to overcome local optima and improve both convergence speed and solution accuracy.

IV. Simulations and Results

A. Experiment Setup

The experiments were conducted on a Windows 11 system with an Intel(R) Core(TM) i9-14700HX CPU and 16GB of memory. We evaluated the performance of SCGWO using 16 benchmark functions commonly used to test optimization algorithms [31]. The functions are defined in Table 1.

B. Results and Discussion

Figure 1 show the convergence curves for four representative functions: Sphere, Rastrigin, Ackley and Griewank. As shown, SCGWO significantly outperforms the traditional GWO and PSO in terms of convergence speed and solution accuracy [3].

V. Random Forest Hyperparameter Optimization

SCGWO was applied to optimize the hyperparameters of a random forest regression model using the Boston housing price dataset from Kaggle [8]. The results are summarized in Table 3, showing that SCGWO outperformed traditional methods.

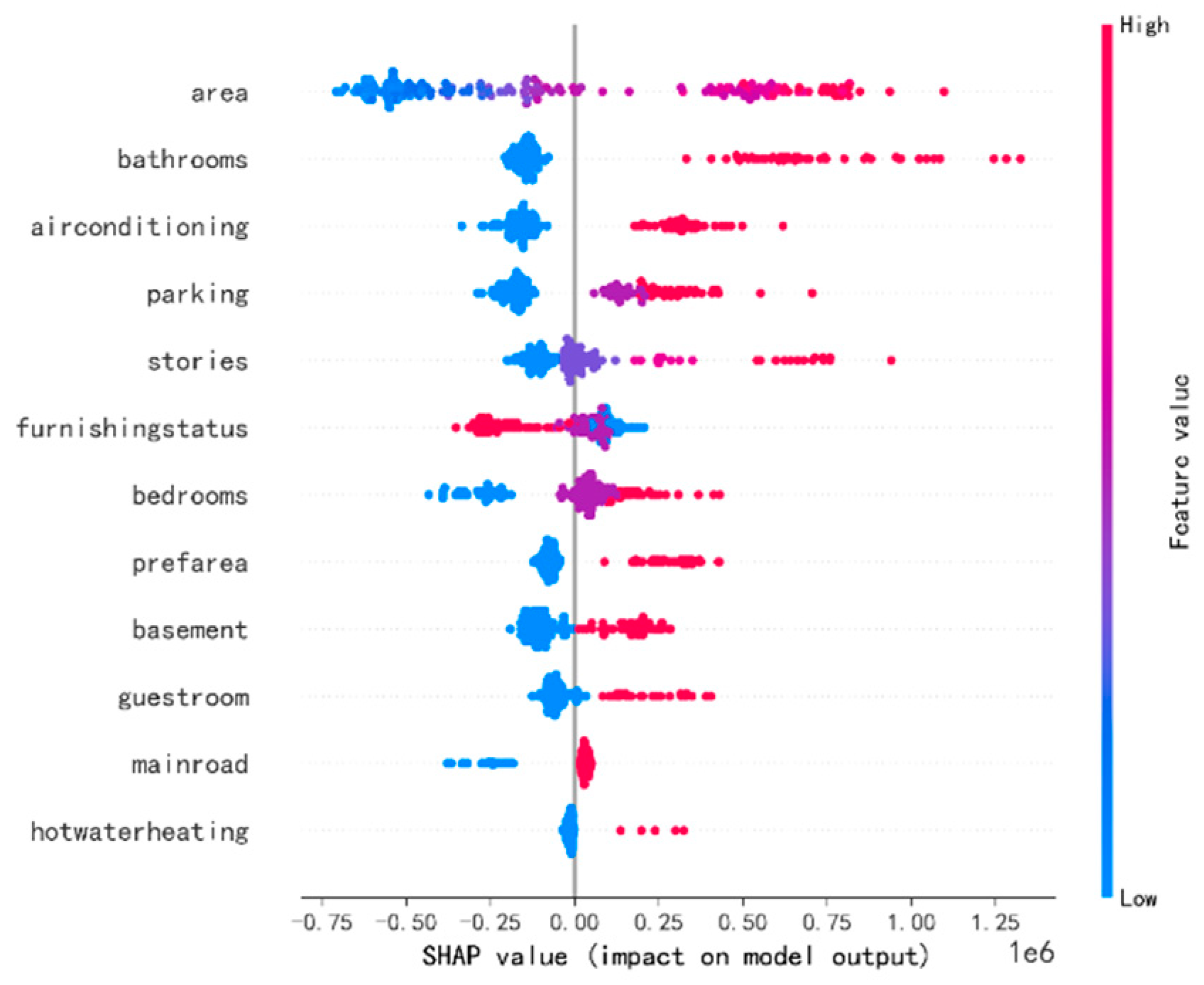
VI. Shap Analysis

SHAP (SHapley Additive exPlanations) analysis was used to interpret the SCGWO-optimized random forest model’s predictions. The SHAP summary plot, shown in Figure 2, highlights the key features contributing to the model’s predictions.

VII. Future Work

In future work, we aim to explore the potential of SCGWO in addressing more challenging machine learning applications. For instance, optimizing deep neural network architectures, as demonstrated by Gao et al. [7], could benefit from SCGWO’s capacity to handle complex high-dimensional optimization tasks. Additionally, combining SCGWO with other optimization techniques, such as particle swarm optimization (PSO), may improve performance in real-time systems, particularly in dynamic environments like warehouse robotics.
One promising direction for SCGWO is its application to multitask learning systems. Techniques like the MT2ST framework, which transitions from multitask to single-task learning [12], could leverage SCGWO for fine-tuning task-specific performance. Similarly, SCGWO can enhance the robustness of representation learning in symmetric positive definite manifolds, as explored by Bu et al. [4].
In healthcare, SCGWO has the potential to optimize ensemble learning techniques in medical diagnostics. For example, ensemble models have been used to improve skin lesion diagnosis [16], and SCGWO could further refine the weighting of model components to enhance diagnostic accuracy. Likewise, SCGWO could improve performance in stroke treatment outcome prediction [17] and biomedical imaging tasks.
Real-time 3D imaging tasks, such as crack detection [29], could also benefit from SCGWO by improving the computational efficiency of multi-sensor fusion models. Furthermore, SCGWO could be applied to optimize reinforcement learning algorithms for robot navigation in complex warehouse layouts [9], enhancing adaptability and efficiency.
In content moderation, SCGWO could optimize machine learning models to integrate community rules for better transparency, as proposed by Xin et al. [27]. Similarly, it holds promise in mitigating knowledge conflicts in large language models for model compression [11], and for question answering, which could advance human-computer interaction technologies.
Besides, SCGWO can be potentially improved by large language models [33] and be applied in various domains [34,35,36,37,38,39].
For cloud computing and networking, SCGWO can optimize resource allocation dynamically, building on prior research into distributed systems [32]. Additionally, in cybersecurity, SCGWO may contribute to defending against sequential query-based blackbox attacks [22] or enhancing meta-learning enabled adversarial defenses [23].
Recent advancements in deep learning optimizers, such as those enhancing stability and efficiency [14,30], has been a favor. Our research suggest that SCGWO could improve learning efficiency in largescale models. Moreover, SCGWO’s potential applications in large-scale object detection [21] indicate its versatility for real-world tasks.
In time series modeling, SCGWO could optimize advanced models, such as Transformers and LSTMs, for applications in healthcare like heart rate prediction [20]. Furthermore, integrating SCGWO with quantized low-rank adaptation (QLoRA) methods for stock market prediction [19] could enhance adaptability and decision-making in financial forecasting as well as social media prediction [40,41].
In recommendation systems, SCGWO could improve optimization strategies based on graph neural networks [13,15,24], yielding better predictive performance in dynamic environments. SCGWO could also play a vital role in optimizing intelligent vehicle classification models in traffic systems [10], enhancing multi-sensor fusion and reducing computation time.
Finally, SCGWO holds promise in enhancing large language models for detecting AI-generated content. By optimizing adaptive ensembles of fine-tuned transformers, SCGWO could improve detection systems’ speed and accuracy.
Overall, SCGWO exhibits significant potential across diverse domains, including healthcare, autonomous systems, financial technology, and intelligent transportation. Its adaptability and efficiency make it a valuable tool for addressing complex, highdimensional problems, paving the way for broader applications in theoretical and practical research.

VIII. Conclusion

This paper proposes an improved Grey Wolf Optimizer, SCGWO, which integrates Sinusoidal Mapping and a Transverse-Longitudinal Crossover strategy. SCGWO was tested on several benchmark functions and applied to hyperparameter optimization in a random forest regression model. The results demonstrate that SCGWO outperforms traditional GWO in both convergence speed and solution accuracy. Future work will explore its application in more complex optimization problems and real-time systems.

References

  1. Behnam Abdollahzadeh, Reza Ebrahimi, and Saeed Arani Arani. Improved grey wolf optimization algorithm based on chaos theory for optimization problems. Applied Soft Computing, 90:106187, 2020.
  2. Sanjay Arora and Satvir Singh. A review on nature-inspired optimization algorithms. International Journal of Industrial Engineering Computations, 10(4):681–709, 2019.
  3. Jagdish Bansal and Himanshu Sharma. Enhanced grey wolf optimizer with levy flight for engineering design optimization. Journal of Computational Design and Engineering, 9(1):23– 38, 2022.
  4. Xingyuan Bu, Yuwei Wu, Zhi Gao, and Yunde Jia. Deep convolutional network with locality and sparsity constraints for texture classification. Pattern Recognition, 91:34–46, 2019. [CrossRef]
  5. Gaurav Dhiman and Vijay Kumar. Hybrid optimization strategies combining grey wolf optimizer with differential evolution and simulated annealing. Expert Systems with Applications, 159:113584, 2021.
  6. Ebrahim Emary, Hossam M Zawbaa, and Aboul Ella Hassanien. Binary grey wolf optimization approaches for feature selection. Neurocomputing, 172:371–381, 2016. [CrossRef]
  7. Zhi Gao, Yuwei Wu, Xingyuan Bu, Tan Yu, Junsong Yuan, and Yunde Jia. Learning a robust representation via a deep network on symmetric positive definite manifolds. Pattern Recognition, 92:1–12, 2019. [CrossRef]
  8. Soliman Khalil. Machine learning model for housing dataset. https://www.kaggle.com/code/solimankhalil/ ml-model-linear-regression-housing-dataset, 2021. Kaggle.
  9. Keqin Li, Lipeng Liu, Jiajing Chen, Dezhi Yu, Xiaofan Zhou, Ming Li, Congyu Wang, and Zhao Li. Research on reinforcement learning based warehouse robot navigation algorithm in complex warehouse layout. arXiv preprint arXiv:2411.06128, 2024. [CrossRef]
  10. Xinjin Li, Yuanzhe Yang, Yixiao Yuan, Yu Ma, Yangchen Huang, and Haowei Ni. Intelligent vehicle classification system based on deep learning and multi-sensor fusion. Preprints, July 2024. [CrossRef]
  11. Dong Liu. Contemporary model compression on large language models inference. arXiv preprint arXiv:2409.01990, 2024. [CrossRef]
  12. Dong Liu. Mt2st: Adaptive multi-task to single-task learning. arXiv preprint arXiv:2406.18038, 2024. [CrossRef]
  13. Dong Liu and Meng Jiang. Distance recomputator and topology reconstructor for graph neural networks. arXiv preprint arXiv:2406.17281, 2024. [CrossRef]
  14. Dong Liu, Meng Jiang, and Kaiser Pister. Llmeasyquant– an easy to use toolkit for llm quantization. arXiv preprint arXiv:2406.19657, 2024. [CrossRef]
  15. Dong Liu, Roger Waleffe, Meng Jiang, and Shivaram Venkataraman. Graphsnapshot: Graph machine learning acceleration with fast storage and retrieval. arXiv preprint arXiv:2406.17918, 2024. [CrossRef]
  16. Xiaoyi Liu, Zhou Yu, Lianghao Tan, Yafeng Yan, and Ge Shi. Enhancing skin lesion diagnosis with ensemble learning. 2024.
  17. Danqing Ma, Meng Wang, Ao Xiang, Zongqing Qi, and Qin Yang. Transformer-based classification outcome prediction for multimodal stroke treatment. 2024.
  18. Seyedali Mirjalili, Seyed Mohammad Mirjalili, and Andrew Lewis. Grey wolf optimizer. Advances in Engineering Software, 69:46–61, 2014.
  19. Haowei Ni, Shuchen Meng, Xupeng Chen, Ziqing Zhao, Andi Chen, Panfeng Li, Shiyao Zhang, Qifu Yin, Yuanqing Wang, and Yuxi Chan. Harnessing earnings reports for stock predictions: A qlora-enhanced llm approach. arXiv preprint arXiv:2408.06634, 2024. [CrossRef]
  20. Haowei Ni, Shuchen Meng, Xieming Geng, Panfeng Li, Zhuoying Li, Xupeng Chen, Xiaotong Wang, and Shiyao Zhang. Time series modeling for heart rate prediction: From arima to transformers. arXiv preprint arXiv:2406.12199, 2024. [CrossRef]
  21. Junran Peng, Xingyuan Bu, Ming Sun, Zhaoxiang Zhang, Tieniu Tan, and Junjie Yan. Large-scale object detection in the wild from imbalanced multi-labels. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 9709–9718, 2020. [CrossRef]
  22. Yiyi Tao. Sqba: sequential query-based blackbox attack. In Fifth International Conference on Artificial Intelligence and Computer Science (AICS 2023), volume 12803, page 128032Q. International Society for Optics and Photonics, SPIE, 2017.
  23. Yiyi Tao. Meta learning enabled adversarial defense. In 2023 IEEE International Conference on Sensors, Electronics and Computer Engineering (ICSECE), pages 1326–1330, 2023.
  24. Zeyu Wang, Yue Zhu, Zichao Li, Zhuoyue Wang, Hao Qin, and Xinqi Liu. Graph neural network recommendation system for football formation. Applied Science and Biotechnology Journal for Advanced Research, 3(3):33–39, 2024.
  25. Yijie Weng and Jianhao Wu. Fortifying the global data fortress: a multidimensional examination of cyber security indexes and data protection measures across 193 nations. International Journal of Frontiers in Engineering Technology, 6(2), 2024. [CrossRef]
  26. Yijie Weng, Jianhao Wu, Tara Kelly, and William Johnson. Comprehensive overview of artificial intelligence applications in modern industries. arXiv preprint arXiv:2409.13059, 2024. [CrossRef]
  27. Wangjiaxuan Xin, Kanlun Wang, Zhe Fu, and Lina Zhou. Let community rules be reflected in online content moderation. 2024.
  28. Xiaofei Yang and Jinsong Guo. A novel hybrid algorithm of ant colony optimization and grey wolf optimizer for continuous optimization problems. Expert Systems with Applications, 150:113282, 2020.
  29. Haowei Zhang, Kang Gao, Huiying Huang, Shitong Hou, Jun Li, and Gang Wu. Fully decouple convolutional network for damage detection of rebars in rc beams. Engineering Structures, 285:116023, 2023. [CrossRef]
  30. Hongye Zheng, Bingxing Wang, Minheng Xiao, Honglin Qin, Zhizhong Wu, and Lianghao Tan. Adaptive friction in deep learning: Enhancing optimizers with sigmoid and tanh function. arXiv preprint arXiv:2408.11839, 2024. [CrossRef]
  31. Hua Zhu, Yi Wang, and Jian Zhang. An adaptive multipopulation differential evolution with cooperative co-evolution for high-dimensional optimization. Swarm and Evolutionary Computation, 44:226–239, 2019.
  32. Wenbo Zhu. Optimizing distributed networking with big data scheduling and cloud computing. In International Conference on Cloud Computing, Internet of Things, and Computer Applications (CICA 2022), volume 12303, pages 23–28. SPIE, 2022.
  33. Pluhacek M, Kazikova A, Kadavy T, Viktorin A, Senkerik R. Leveraging large language models for the generation of novel metaheuristic optimization algorithms. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation 2023 Jul 15 (pp. 1812-1820).
  34. Mai Z, Zhang J, Xu Z, Xiao Z. Is llama 3 good at sarcasm detection? a comprehensive study. In Proceedings of the 2024 7th International Conference on Machine Learning and Machine Intelligence (MLMI) 2024 Aug 2 (pp. 141-145).
  35. Mai Z, Zhang J, Xu Z, Xiao Z. Financial sentiment analysis meets llama 3: A comprehensive analysis. In Proceedings of the 2024 7th International Conference on Machine Learning and Machine Intelligence (MLMI) 2024 Aug 2 (pp. 171-175). [CrossRef]
  36. Xiao Z, Blanco E, Huang Y. Analyzing large language models’ capability in location prediction. In Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation (LREC-COLING 2024) 2024 May (pp. 951-958).
  37. Xiao Z, Mai Z, Xu Z, Cui Y, Li J. Corporate event predictions using large language models. In 2023 10th International Conference on Soft Computing & Machine Intelligence (ISCMI) 2023 Nov 25 (pp. 193-197). IEEE.
  38. Zhang J, Mai Z, Xu Z, Xiao Z. Is llama 3 good at identifying emotion? a comprehensive study. In Proceedings of the 2024 7th International Conference on Machine Learning and Machine Intelligence (MLMI) 2024 Aug 2 (pp. 128-132).
  39. Xiao Z, Mai Z, Cui Y, Xu Z, Li J. Short interest trend prediction with large language models. In Proceedings of the 2024 International Conference on Innovation in Artificial Intelligence 2024 Mar 16 (pp. 1-1).
  40. Liu Y, Shen X, Zhang Y, Wang Z, Tian Y, Dai J, Cao Y. A Systematic Review of Machine Learning Approaches for Detecting Deceptive Activities on Social Media: Methods, Challenges, and Biases. arXiv preprint arXiv:2410.20293. 2024 Oct 26. [CrossRef]
  41. Cao Y, Dai J, Wang Z, Zhang Y, Shen X, Liu Y, Tian Y. Machine Learning Approaches for Depression Detection on Social Media: A Systematic Review of Biases and Methodological Challenges. Journal of Behavioral Data Science. 2025 Feb 14;5(1):1-36. [CrossRef]
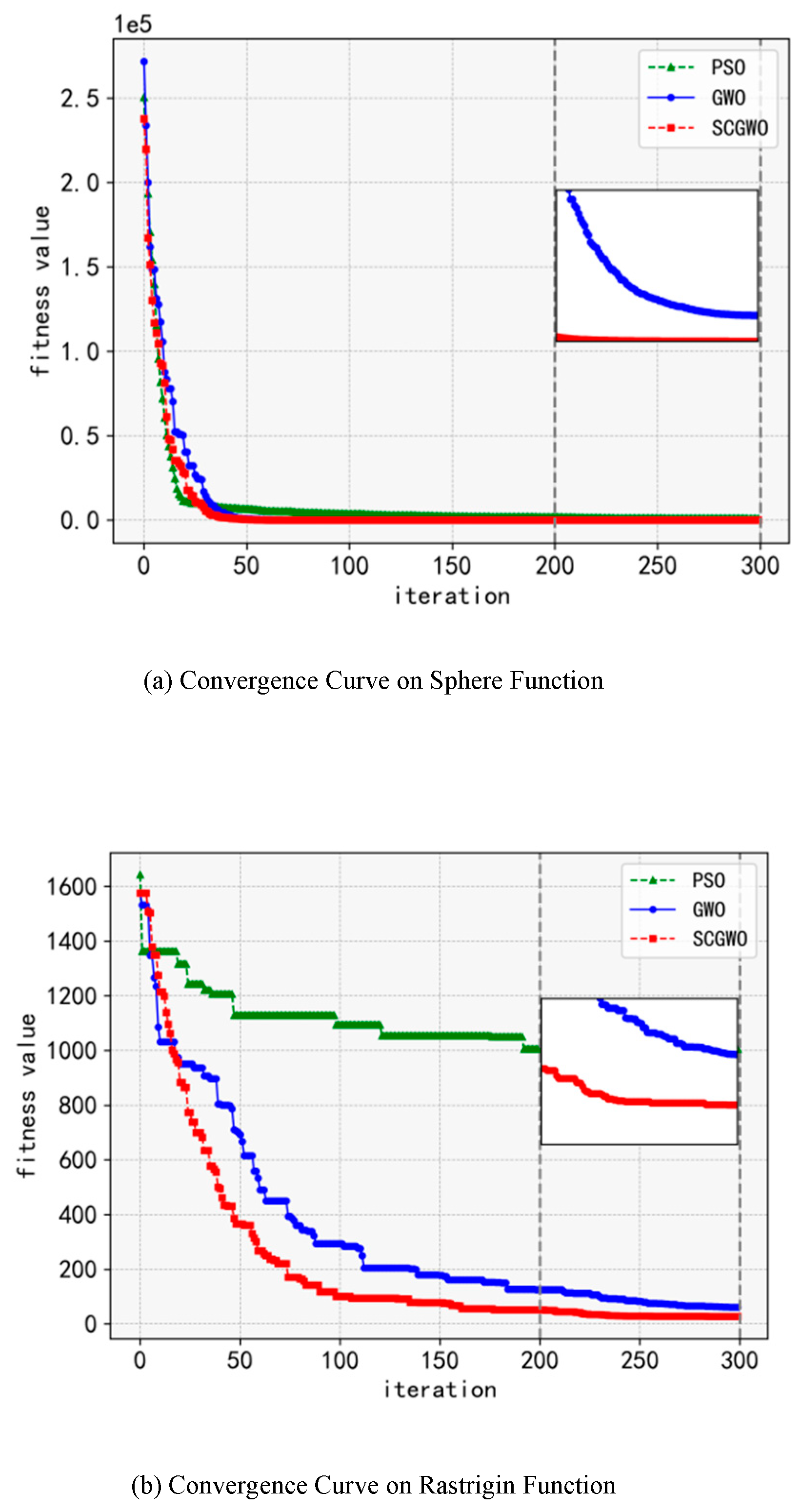
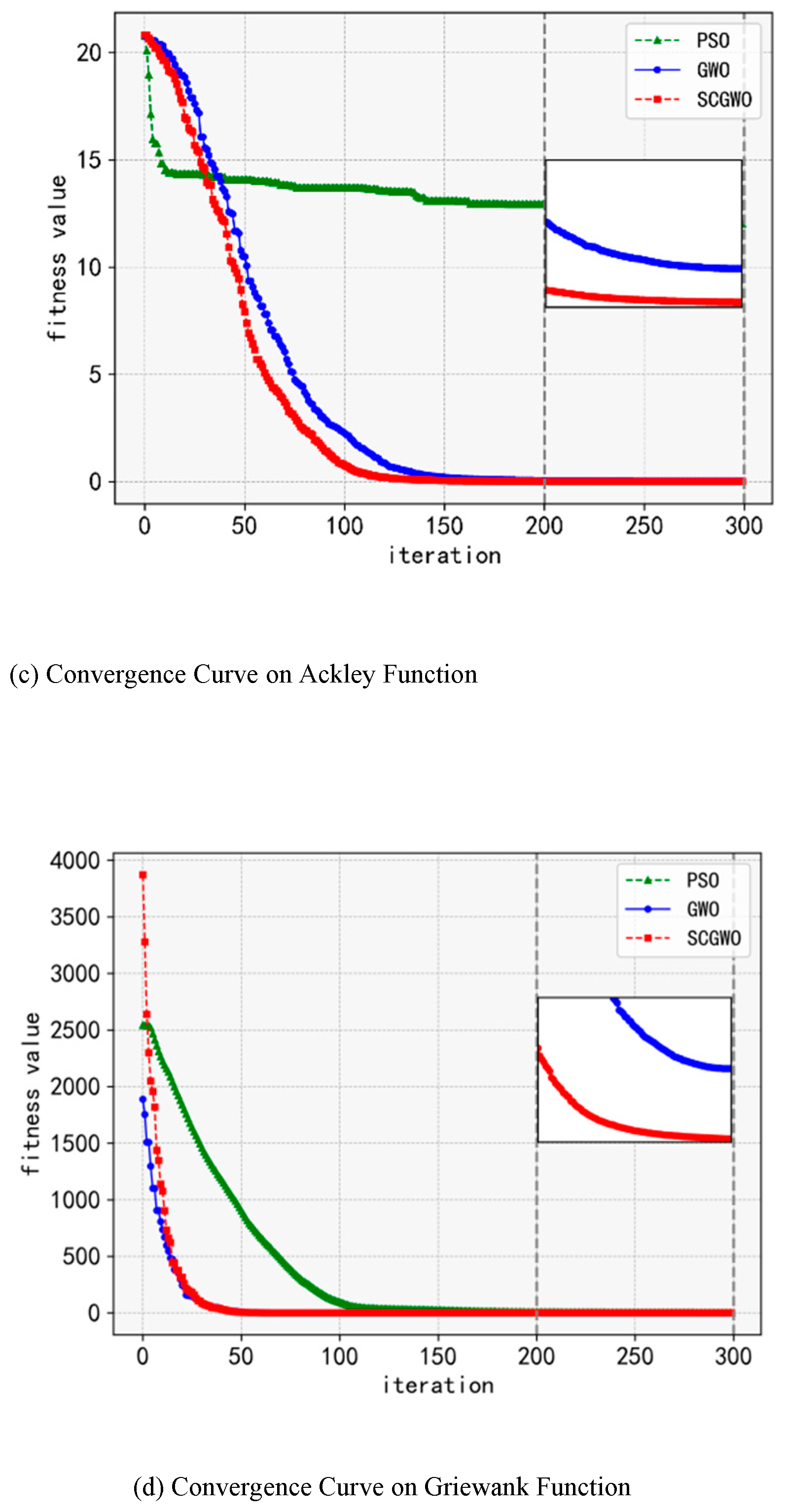
Preprints 155317 g001aPreprints 155317 g001b
Figure 1. Convergence Curves of SCGWO, GWO and PSO on Different Benchmark Functions.
Figure 1. Convergence Curves of SCGWO, GWO and PSO on Different Benchmark Functions.
Preprints 155317 g001aPreprints 155317 g001b
Preprints 155317 g002
Figure 2. SHAP Summary Plot for Random Forest Model.
Figure 2. SHAP Summary Plot for Random Forest Model.
Preprints 155317 g002
Table 1. Benchmark Functions for SCGWO Performance Testing.
Table 1. Benchmark Functions for SCGWO Performance Testing.
Function Name Search Range DIM OPT Value
F1 Sphere [-100, 100] 30 0
F2 Schwefel2.22 [-10, 10] 30 0
F3 Schwefel1.2 [-100, 100] 30 0
F4 Schwefel2.21 [-100, 100] 30 0
F5 Rosenbrock [-30, 30] 30 0
F6 Step [-100, 100] 30 0
F7 Rastrigin [-5.12, 5.12] 30 0
F8 Ackley [-32, 32] 30 0
F9 Griewank [-600, 600] 30 0
F10 Penalized [-50, 50] 30 0
F11 Michalewicz [-100,100 30 0
F12 Levy [-10,10] 30 0
F13 Easom [-100,100] 30 0
F14 Bird [-100,100] 30 0
F15 Rotated Hyper-Ellipsoid [-30,30] 30 0
F16 Weierstrass [-100,100 30 0
Table 3. Performance Comparison on Random Forest Hyperparameter Optimization.
Table 3. Performance Comparison on Random Forest Hyperparameter Optimization.
Method MAE (train) RMSE (train) MAE (test) RMSE (test)
Default 285109 398584 957916 1357261
GWO 413922 547712 922632 1262471
SCGWO 448753 616299 917518 1238437
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated