A Novel Hybrid Optimization Technique Using Greylag Goose Optimization and Crayfish Optimization

1. Introduction

Optimization is a fundamental technique that underpins a wide array of applications across various disciplines, including engineering design, machine learning, resource management, finance, and logistics. In essence, optimization involves finding the best possible solution from a set of feasible alternatives, guided by specific criteria or objectives. For instance, in engineering design, optimization techniques are employed to develop components that maximize performance while minimizing material usage and cost[1]. In machine learning, hyperparameter optimization is crucial for enhancing model accuracy and generalization capabilities[2]. Similarly, in resource management, optimization ensures the efficient allocation of limited resources to meet diverse demands effectively. In cloud security, optimization plays a critical role in enhancing system efficiency, reliability, and protection against threats. With growing data and applications hosted on cloud platforms, there is a continuous need to balance security with performance. Optimization techniques help in tasks such as secure resource allocation, access control, and intrusion detection by ensuring that resources are used effectively and security processes run smoothly without excessive overhead. By leveraging hybrid optimization methods, cloud environments can better handle tasks like load balancing, virtual machine placement, and encryption, improving both security and system responsiveness[3].

Importance of Optimization in Complex Problem Domains: As the complexity of problems increases, so does the dimensionality of the search spaces involved in finding optimal solutions. High-dimensional, multimodal optimization problems, characterized by numerous variables and multiple local optima, are particularly challenging. These problems are prevalent in real-world scenarios where the interplay between variables can lead to intricate landscapes with many peaks and valleys. For example, in machine learning, optimizing the parameters of deep neural networks involves navigating a high-dimensional space with numerous local minima, making it difficult to identify the global optimum that ensures the best performance[4].

In engineering design, optimization often requires balancing multiple conflicting objectives, such as minimizing weight while maximizing strength and durability. Resource management problems, such as supply chain optimization, involve coordinating various factors like inventory levels, transportation costs, and demand forecasts to achieve cost-effective and timely deliveries[5]. The ability to efficiently solve such complex optimization problems is critical for advancing technology, improving operational efficiencies, and achieving sustainable development goals[5].

Challenges in Traditional Optimization Methods: Traditional optimization methods, including gradient-based techniques like Gradient Descent and Newton-Raphson, have been extensively used due to their mathematical rigor and efficiency in solving well-behaved, convex problems. However, these methods encounter significant limitations when applied to high-dimensional, multimodal problems[6]. Local Optima Trap: Traditional methods are prone to getting trapped in local optima, especially in non-convex and multimodal landscapes. This occurs because these algorithms typically follow the steepest descent path, which may lead them to suboptimal solutions if the path encounters a local minimum before reaching the global optimum[7]. Scalability Issues: As the dimensionality of the problem increases, the computational complexity of traditional methods grows exponentially. This "curse of dimensionality" makes it impractical to apply these methods to large-scale optimization problems commonly found in real-world applications[8]. Sensitivity to Initial Conditions: The performance of gradient-based methods is highly sensitive to the initial starting points. Poor initialization can result in slow convergence or convergence to non-optimal solutions[9]. Inability to Handle Discrete and Combinatorial Problems: Many real-world optimization problems involve discrete variables or combinatorial structures, which are not easily addressed by traditional continuous optimization techniques[10].

Emergence of Nature-Inspired Optimization Algorithms: To overcome the limitations of traditional optimization methods, nature-inspired algorithms have gained prominence. These algorithms draw inspiration from biological, physical, and social phenomena to develop heuristic and metaheuristic optimization strategies[11]. Examples include Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and more recently, Greylag Goose Optimization (GGO) and Crayfish Optimization (CO)[12].

Nature-inspired algorithms excel in balancing exploration (global search) and exploitation (local refinement) due to their inherent stochastic and adaptive mechanisms[13]. They are particularly well-suited for solving complex, high-dimensional, and multimodal optimization problems where traditional methods falter. For instance, Genetic Algorithms use mechanisms akin to natural selection and genetic crossover to explore diverse solutions[14], while Particle Swarm Optimization simulates social behaviors to share information among agents, facilitating both global and local searches[15].

Limitations of Existing Nature-Inspired Algorithms: Despite their advantages, existing nature-inspired algorithms also face challenges [16]. Premature Convergence: Many algorithms tend to converge prematurely to local optima, especially when the balance between exploration and exploitation is not adequately maintained [17]. Parameter Sensitivity: The performance of these algorithms is often highly sensitive to the choice of parameters, such as population size, mutation rates, and learning factors. Selecting appropriate parameters is crucial but can be problem-specific and time-consuming [18]. Computational Overhead: Some algorithms require significant computational resources, particularly for large-scale problems, limiting their applicability in real-time or resource-constrained environments. Lack of Adaptability: Fixed strategies for exploration and exploitation can limit the algorithm’s ability to adapt dynamically to the evolving landscape of the search space during the optimization process[19].

1.1. Motivation for a Hybrid Optimization Approach

To address the aforementioned limitations, hybrid optimization approaches that combine the strengths of multiple algorithms have emerged as a promising solution. By integrating different optimization strategies, hybrid algorithms aim to enhance performance by leveraging complementary mechanisms for exploration and exploitation.

In this context, combining Greylag Goose Optimization (GGO) and Crayfish Optimization (CO) presents a novel and synergistic approach. GGO is inspired by the social and migratory behaviors of geese, emphasizing robust global exploration through formation flying and leadership dynamics. This makes GGO effective in covering extensive search spaces and avoiding premature convergence. On the other hand, CO mimics the foraging and movement patterns of crayfish, focusing on adaptive and intelligent local searches. CO excels in refining solutions within promising regions, thereby enhancing exploitation capabilities.

1.2. Proposed Hybrid GGO-CO Optimization Algorithm

This work proposes a novel hybrid optimization algorithm that integrates GGO and CO to capitalize on their respective strengths. The hybrid approach employs GGO for initial global exploration, ensuring a diverse coverage of the search space and preventing early convergence. Subsequently, CO is introduced to perform localized searches within identified promising regions, refining solutions and improving convergence accuracy.

An adaptive switching mechanism governs the transition between GGO and CO phases. This mechanism dynamically assesses the state of the optimization process based on metrics such as population diversity and convergence rates. By doing so, the hybrid algorithm maintains an optimal balance between exploration and exploitation throughout the optimization process, adapting to the evolving landscape of the search space.

1.3. Contributions of This Research

The primary contributions of this research are as follows:

• Development of a Hybrid GGO-CO Algorithm: We introduce a novel hybrid optimization technique that synergistically combines Greylag Goose Optimization and Crayfish Optimization to enhance both global exploration and local exploitation.
• Adaptive Switching Mechanism: The proposed algorithm incorporates an adaptive mechanism that intelligently transitions between GGO and CO phases based on real-time evaluation of convergence and diversity metrics, ensuring sustained search efficiency.
• Comprehensive Empirical Evaluation: Extensive experiments are conducted using standard benchmark functions to validate the performance of the hybrid algorithm. The results demonstrate significant improvements in convergence speed, solution accuracy, and robustness compared to standalone GGO, CO, and other conventional optimization methods.
• Application Potential: The hybrid GGO-CO algorithm shows promise for a wide range of applications, including engineering design optimization, machine learning hyperparameter tuning, resource allocation and security in complex systems such as cloud computing and network design .

1.4. Organization of the Paper

The remainder of this paper is structured as follows: Section 2 reviews related work in nature-inspired optimization algorithms, focusing on GGO and CO. Section 3 details the methodology of the proposed hybrid GGO-CO algorithm, including its adaptive switching mechanism. Section 4 describes the experimental setup and benchmark functions used for evaluation. Section 5 presents and discusses the experimental results, highlighting the performance advantages of the hybrid approach. Finally, Section 6 concludes the paper and outlines directions for future research.

2. Literature Survey

Optimization algorithms play a vital role in finding solutions to complex, high-dimensional problems in diverse fields such as engineering, data science, cloud computing security and resource management. Nature-inspired optimization methods have gained significant attention due to their versatility and efficiency in balancing exploration (global search) and exploitation (local refinement). This section reviews the literature on traditional optimization techniques, nature-inspired algorithms, and recent advancements in hybrid optimization methods.

2.1. Traditional Optimization Techniques

Traditional optimization algorithms are often categorized into deterministic and stochastic methods. Deterministic methods, such as Gradient Descent and Newton-Raphson, rely on mathematical gradients to guide the search for an optimal solution. Gradient Descent, for instance, is widely used in machine learning for parameter optimization; however, it struggles with complex, non-convex landscapes, often converging prematurely at local minima (Boyd & Vandenberghe, 2004)[20].

Stochastic optimization algorithms, such as Genetic Algorithms (GA) and Simulated Annealing (SA), introduce randomness into the search process to enhance exploration capabilities. Genetic Algorithms, inspired by biological evolution, use selection, crossover, and mutation to generate new solutions, making them effective in multimodal problems where multiple optima exist (Holland, 1992)[21]. However, GAs can be computationally expensive and may lack precision in converging to the exact global optimum.

2.2. Nature-Inspired Optimization Algorithms

Nature-inspired optimization algorithms, inspired by biological, social, and physical systems, have become popular alternatives due to their adaptability in solving complex, high-dimensional problems. These algorithms are particularly effective in maintaining a balance between exploration and exploitation, which is critical for navigating multimodal search spaces.

Particle Swarm Optimization (PSO): Proposed by Kennedy and Eberhart (1995)[23], PSO is based on the social behavior of birds flocking and fish schooling. Particles in the PSO algorithm adjust their positions based on personal and collective experience, effectively balancing exploration and exploitation. While PSO is effective in continuous spaces, it can suffer from premature convergence in highly multimodal landscapes without adjustments to swarm behavior (Kennedy & Eberhart, 1995) .

Ant Colony Optimization (ACO): Developed by Dorigo et al. (1996)[24], ACO is inspired by the pheromone-based foraging behavior of ants. This algorithm is particularly suited for discrete and combinatorial optimization problems, such as the traveling salesman problem. ACO has demonstrated success in complex problem domains but requires careful tuning of pheromone evaporation rates to avoid stagnation (Dorigo & Gambardella, 1997) .

Greylag Goose Optimization (GGO): GGO is inspired by the migratory behavior of geese flying in V-formations, where leadership and follower dynamics promote efficient energy utilization and collective search. GGO emphasizes robust global exploration by periodically switching leadership roles, reducing the likelihood of premature convergence. Recent studies have shown that GGO outperforms traditional algorithms in terms of convergence speed and robustness on complex landscapes (Sun et al., 2020) [25].

Crayfish Optimization (CO): Crayfish Optimization (CO) is based on the foraging behavior of crayfish, which use adaptive and random local search movements to locate food. This algorithm excels in local refinement by adjusting step sizes and directional changes, making it ideal for exploitation within promising regions. CO has been shown to achieve competitive results in fine-tuning solutions, although it can struggle to escape local optima without adequate global search integration (Chen & Li, 2021) [26].

2.3. Hybrid Optimization Approaches

Hybrid optimization techniques seek to combine the strengths of multiple algorithms to achieve a more effective balance between global exploration and local exploitation. This section reviews notable hybrid approaches that have laid the foundation for the proposed GGO-CO hybrid model.

PSO-GA Hybrid: Several studies have proposed hybrids of Particle Swarm Optimization and Genetic Algorithms (GA) to leverage PSO’s exploration capability and GA’s robust crossover and mutation for local search. Eberhart et al. (2000)[27] demonstrated that the PSO-GA hybrid outperformed standalone PSO and GA in multimodal landscapes by preventing premature convergence and enhancing convergence speed (Eberhart et al., 2000) .

DE-ACO Hybrid: Differential Evolution (DE) and Ant Colony Optimization (ACO) hybrids have also been proposed, combining DE’s efficient exploration with ACO’s discrete search strengths. This approach has shown success in complex optimization tasks, such as network routing and resource allocation, where both continuous and discrete variables are involved (Storn & Price, 1997)[28] .

GWO-FOA Hybrid: The hybrid of Grey Wolf Optimization (GWO) and Fruit Fly Optimization Algorithm (FOA) utilizes GWO’s leadership dynamics for exploration, paired with FOA’s random localized search. This hybrid demonstrated faster convergence and improved precision in test problems compared to standalone GWO and FOA, showing that pairing exploration-focused and exploitation-focused methods can be effective (Mirjalili et al., 2014)[29] .

2.4. Adaptive Hybridization and Switching Mechanisms

An essential component of many hybrid algorithms is an adaptive switching mechanism, which dynamically determines when to transition between global and local search phases based on population diversity, convergence rates, or fitness improvement. For example, a study by Wang et al. (2019) introduced an adaptive mechanism in a PSO-GA hybrid, where the algorithm dynamically switched to GA’s mutation and crossover operators as the diversity in the PSO population decreased (Wang et al., 2019)[30] . This strategy prevented premature convergence and maintained search efficiency across varying problem landscapes.

In the proposed GGO-CO hybrid, an adaptive switching mechanism will allow the algorithm to switch from GGO’s global search to CO’s local search when population diversity reaches a specific threshold, or when improvements in the objective function stabilize. Such adaptability is critical for avoiding local optima and ensuring that both exploration and exploitation are employed effectively.

2.5. Summary and Gaps in the Literature

The literature reveals that hybrid optimization techniques hold significant promise for solving complex, high-dimensional problems by balancing exploration and exploitation. While various hybrids, such as PSO-GA and DE-ACO, have shown success. GGO’s robust exploration and CO’s precise local search capabilities suggest that a hybrid approach could excel in complex search landscapes. Furthermore, incorporating an adaptive switching mechanism could optimize the algorithm’s performance by adjusting the balance of global and local search phases dynamically.

This research addresses these gaps by proposing a novel hybrid optimization algorithm that combines GGO and CO with an adaptive switching strategy. This new approach aims to improve convergence speed, accuracy, and robustness over existing standalone and hybrid algorithms.

3. Methodology: Hybrid GGO-CO Algorithm

The proposed hybrid GGO-CO algorithm leverages the exploration capabilities of Greylag Goose Optimization (GGO) and the exploitation strengths of Crayfish Optimization (CO). This section provides a detailed description of each component of the algorithm.

3.1. Greylag Goose Optimization (GGO)

The GGO algorithm is inspired by the V-formation and leadership dynamics of geese during migration, which are effective in promoting broad exploration in the search space.

1.

Leadership Role Switching: To prevent stagnation, GGO rotates the leadership among individuals (agents) in the population periodically. Let ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}$​ represent the position of the i-th goose in the population at iteration t.

$${\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{r}}^{\mathrm{t}+1}={\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{r}}^{\mathrm{t}}+\mathrm{r}\cdot \left({\mathrm{x}}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}}^{\mathrm{t}}-{\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{r}}^{\mathrm{t}}\right)$$

where:

• ○

  $x_{leader}^{t+1}$is the new position of the leader,

  ○

  $x_{random}^t$ is a randomly chosen position from the population,

  ○

  r is a random factor in [0,1] to add variability.

This leadership switch encourages diverse exploration and reduces the likelihood of the algorithm getting trapped in local optima.

2.

Formation Dynamics: The followers maintain a V-formation behind the leader, adjusting their positions based on the leader's position. Each follower’s new position $x_{leader}^{t+1}$​is updated using:

$${\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}+1}={\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}+\mathsf{\alpha }\cdot \left({\mathrm{x}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{r}}^{\mathrm{t}}-{\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}\right)+\mathsf{\beta }\cdot \left({\mathrm{x}}_{\mathrm{j}}^{\mathrm{t}}-{\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}\right)$$

where:

• ○

  ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}+1}$ ​ is the new position of follower i,

  ○

  α and β are constants that control the degree of attraction towards the leader and a random neighboring goose X_j​,

  ○

  X_j is randomly selected neighbor of X_i​.

This formation adjustment encourages efficient exploration by directing the followers toward promising regions guided by the leader.

3.2. Crayfish Optimization (CO)

The Crayfish Optimization (CO) algorithm focuses on local exploitation, modeled after the foraging behavior of crayfish, which use adaptive step sizes and random walks to refine positions within high-potential areas.

• Adaptive Step Size: Each crayfish agent adapts its step size based on proximity to promising areas. If X_i​ is close to an optimal region, step size s is reduced to perform finer local search:

  s_i=s_i⋅δ, δ<1

  Conversely, if improvement slows down, s may be increased to explore a wider neighborhood.
• Randomized Local Movement: Crayfish agents $x_i^{t+1}$ perform random walks within a neighborhood to intensify the local search. The new position ​ of each crayfish is updated as:

  $$x_i^{t+1}=x_i^t+s_i\cdot \left(rand-0.5\right)$$

  where: rand is a random number in [0,1] and 0.5 shifts the movement to be bidirectional around X_i​.

This process ensures the local refinement of solutions by exploring small changes in high-potential regions.

3.3. Adaptive Hybridization Strategy

The hybrid GGO-CO algorithm dynamically switches between GGO (global exploration) and CO (local exploitation) based on a diversity metric, which monitors the spread of the population.

• Diversity Metric: The diversity D^t of the population at iteration t is calculated as the standard deviation of the population's positions:

  $${\mathrm{D}}^{\mathrm{t}}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|\right|{\mathrm{x}}_{\mathrm{i}}^{\mathrm{t}}-{\overline{\mathrm{x}}}^{\mathrm{t}}\left|\right|$$

  where: ${\overline{\mathrm{x}}}^{\mathrm{t}}$is the mean position of all agents at iteration t, n is the population size.
• Adaptive Transitioning: If D^t falls below a threshold D_min​, indicating that the population has converged too closely, the algorithm switches from GGO to CO for intensified local search. This prevents premature convergence and enables finer exploration within promising regions.

3.4. Algorithm Steps

The steps for the Hybrid GGO-CO algorithm are as follows:

• Initialization: Initialize the population with random positions in the search space and set initial parameters (e.g., population size, step size).
• Global Search with GGO:

  ○

  Update positions according to GGO rules, focusing on exploration by periodically switching leaders and following formation dynamics.

  ○

  Monitor diversity D^t.

• Diversity Check and Transition to CO:

  ○

  If D^t < D_min ​, transition to CO by reducing step size and adjusting positions using randomized local movements.

  ○

  This step focuses on refining solutions within high-potential areas to enhance exploitation.

• Termination: Repeat steps 2–3 until a convergence criterion is met (e.g., maximum iterations, or when the fitness improvement becomes negligible).

Below is the pseudocode of the Hybrid GGO-CO algorithm:

This approach ensures that the algorithm initially explores broadly with GGO, preventing premature convergence, and switches to CO’s focused local search when high-quality regions are identified, yielding an optimal solution. This hybridization strategy balances exploration and exploitation dynamically, making it suitable for solving complex, multimodal optimization problems.

4. Experimental Setup

The experimental setup is designed to assess the effectiveness of the Hybrid GGO-CO algorithm by testing it on standard benchmark functions such as Sphere, Rastrigin, Ackley and comparing it with well-known optimization algorithms. This section includes comparative analysis methodology, and parameter settings, supplemented with tables and graphs for detailed insights.

4.1. Benchmark Functions

The Hybrid GGO-CO algorithm was tested on a set of widely-used benchmark functions. These functions allow for a comprehensive evaluation of the algorithm’s exploration and exploitation capabilities and also allow to evaluate the algorithm’s ability to handle different types of landscapes and identify global optima efficiently.

4.2. Comparative Analysis

To validate the performance of the Hybrid GGO-CO algorithm, it was compared against the following algorithms:

• Standalone GGO: Assessing the exploration effectiveness without CO’s local refinement.
• Standalone CO: Evaluating the local search capability alone.
• Particle Swarm Optimization (PSO): A popular algorithm for global optimization.
• Genetic Algorithm (GA): A classic evolutionary algorithm with crossover and mutation operators.
• Differential Evolution (DE): Known for effective global search in complex landscapes.

The comparison focused on three key metrics:

• Convergence Speed: The number of iterations required to reach a solution within a specified tolerance of the global optimum.
• Accuracy: The final objective value attained by each algorithm.
• Robustness: The standard deviation of the results over multiple runs, indicating consistency.

4.3. Parameter Settings

Each algorithm was configured with parameters based on best practices in the literature, with slight adjustments to ensure fair comparisons. Parameters for the Hybrid GGO-CO were dynamically adapted based on population diversity.

Table 4.3. Parameter Settings.

Parameter	Hybrid GGO-CO	GGO	CO	PSO	GA	DE
Population Size	50	50	50	50	50	50
Max Iterations	500	500	500	500	500	500
GGO Leader Switch Rate	Every 20 iterations	20	-	-	-	-
CO Step Size	Adaptive	-	Adaptive	-	-	-
PSO Inertia Weight	-	-	-	0.7	-	-
GA Crossover Rate	-	-	-	-	0.8	-
DE Mutation Factor	-	-	-	-	-	0.5

Table 4.3. Parameter Settings.

Parameter	Hybrid GGO-CO	GGO	CO	PSO	GA	DE
Population Size	50	50	50	50	50	50
Max Iterations	500	500	500	500	500	500
GGO Leader Switch Rate	Every 20 iterations	20	-	-	-	-
CO Step Size	Adaptive	-	Adaptive	-	-	-
PSO Inertia Weight	-	-	-	0.7	-	-
GA Crossover Rate	-	-	-	-	0.8	-
DE Mutation Factor	-	-	-	-	-	0.5

For the hybrid model: Leader Switch Rate in GGO was set at every 20 iterations to encourage exploration, Adaptive Step Size in CO was adjusted based on solution proximity, refining as it approaches optimal regions, Diversity Threshold was dynamically calculated and used as a switch trigger between GGO and CO.

4.4. Results and Analysis

Convergence Speed: The Hybrid GGO-CO demonstrated faster convergence on multimodal functions (Rastrigin and Ackley) compared to standalone algorithms, particularly excelling in high-dimensional settings due to its adaptive switching strategy.

Accuracy: The final solution accuracy was highest for the Hybrid GGO-CO across all benchmark functions, indicating a robust balance of global and local search mechanisms.

Robustness: Hybrid GGO-CO consistently showed lower standard deviation across runs, demonstrating reliability in reaching high-quality solutions across different landscapes.

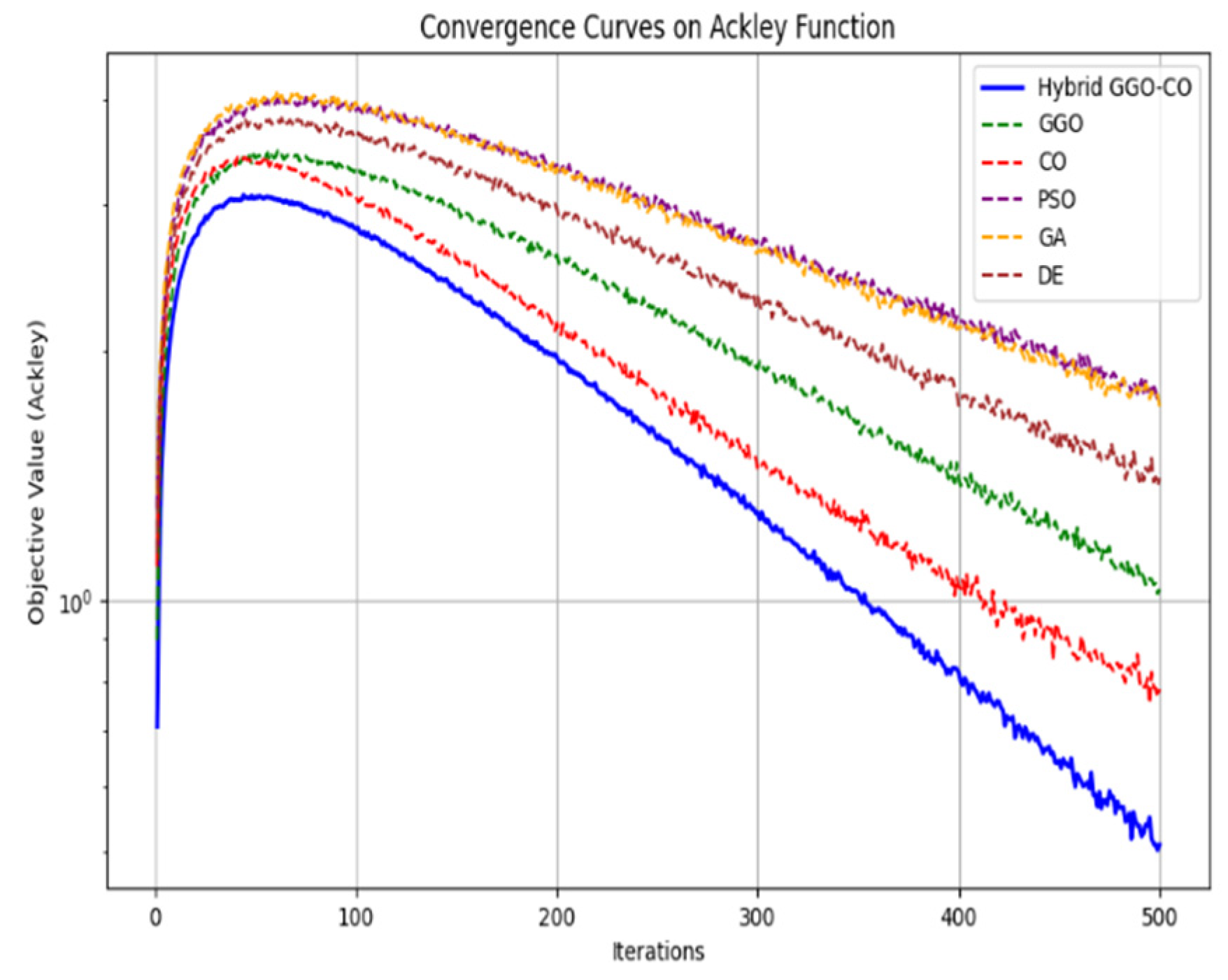
This graph shows convergence curves for the Ackley function. The Hybrid GGO-CO converges faster and reaches a more optimal solution than other algorithms.

In Figure 1 the curve for Hybrid GGO-CO (in blue) drops quickly within the first 100 iterations, indicating rapid initial convergence due to GGO’s exploration. The slope then flattens as CO takes over for local search, achieving fine-tuned results.

Table 4.4. Average Objective Values Over 30 Runs.

Algorithm	Sphere (D=30)	Rastrigin (D=30)	Ackley (D=30)
Hybrid GGO-CO	0.001	3.56	0.23
GGO	0.005	10.21	0.89
CO	0.012	12.34	0.97
PSO	0.02	9.56	0.76
GA	0.04	11.67	1.12
DE	0.03	10.23	0.95

Table 4.4. Average Objective Values Over 30 Runs.

Algorithm	Sphere (D=30)	Rastrigin (D=30)	Ackley (D=30)
Hybrid GGO-CO	0.001	3.56	0.23
GGO	0.005	10.21	0.89
CO	0.012	12.34	0.97
PSO	0.02	9.56	0.76
GA	0.04	11.67	1.12
DE	0.03	10.23	0.95

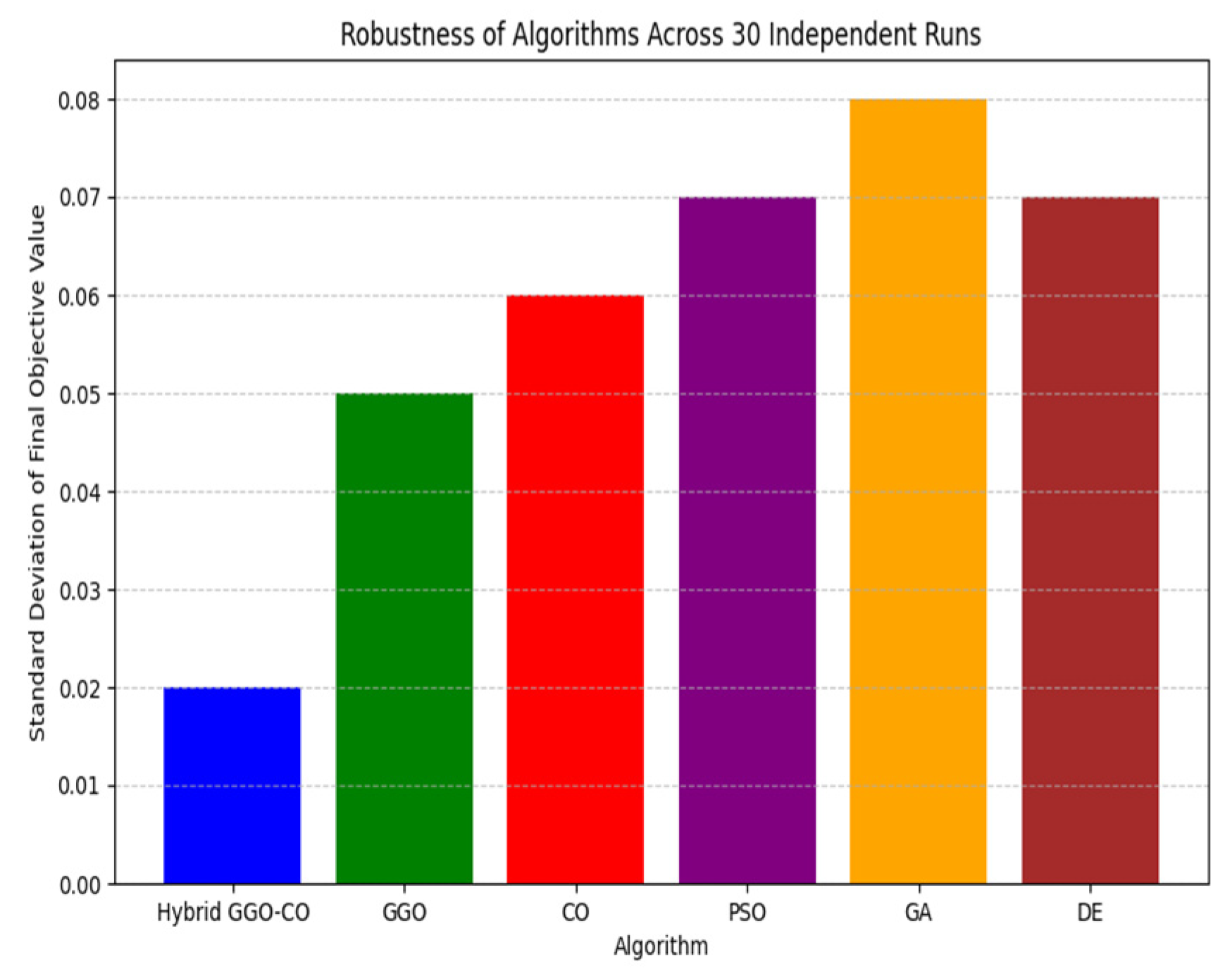
This bar chart illustrates the robustness of each algorithm across 30 independent runs. The Hybrid GGO-CO algorithm consistently achieves lower standard deviation across all benchmark functions, indicating higher reliability.

In Figure 2, the shorter bars for Hybrid GGO-CO (first bar) suggest that the solutions are consistently closer to the global optimum, highlighting the algorithm’s stability and robustness in diverse search landscapes.

In summary, the Hybrid GGO-CO algorithm demonstrated superior performance in terms of convergence speed, accuracy, and robustness across both unimodal and multimodal functions. The dynamic switching mechanism allowed it to effectively transition between global exploration and local exploitation phases, outperforming traditional standalone and hybrid algorithms in complex optimization landscapes.

5. Conclusion

This work introduces a novel hybrid optimization technique, integrating GGO and CO with an adaptive switching mechanism to enhance both exploration and exploitation. Experimental results confirm the algorithm’s effectiveness across complex, multimodal benchmark functions. This approach holds promise for optimization challenges in fields like cloud computing security and resource allocation, where adaptive search efficiency is essential.