Submitted:
19 December 2024
Posted:
20 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background
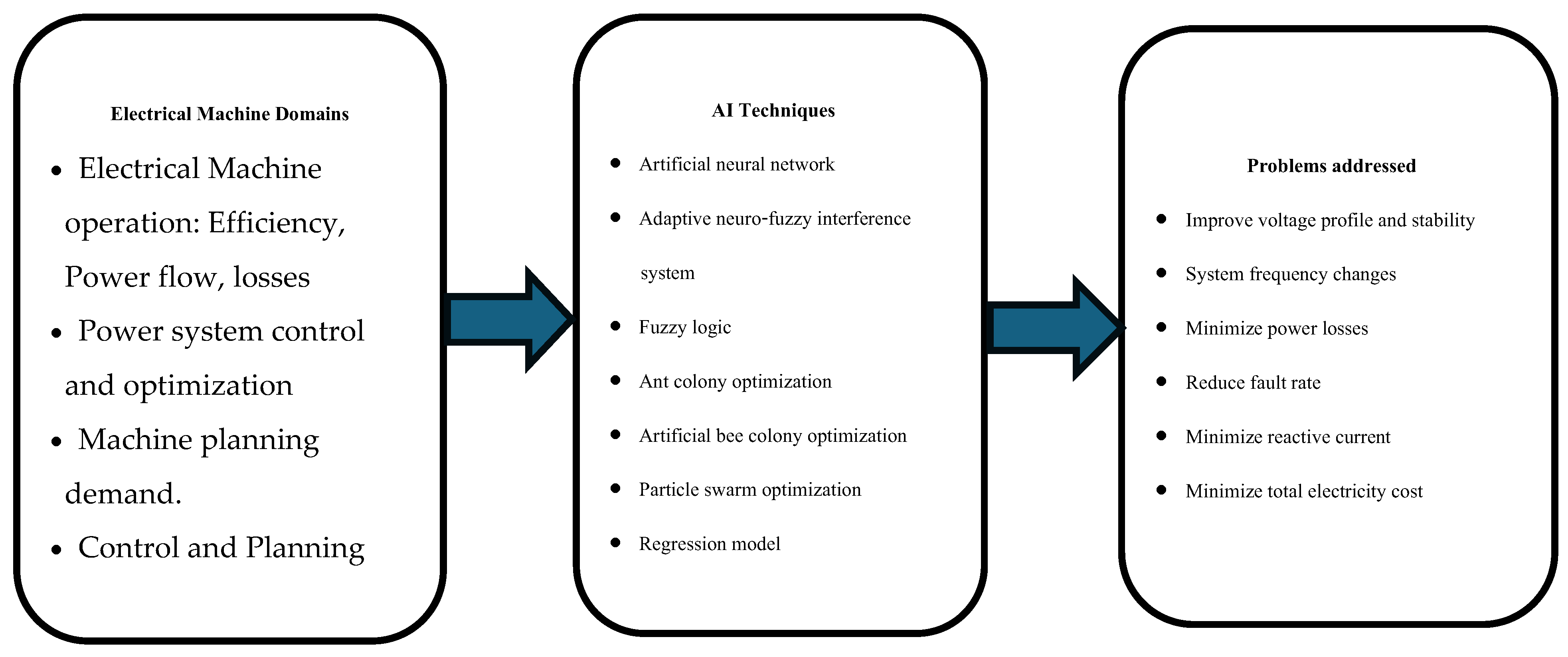
3. AI Technologies Used in the Electric Machine Control
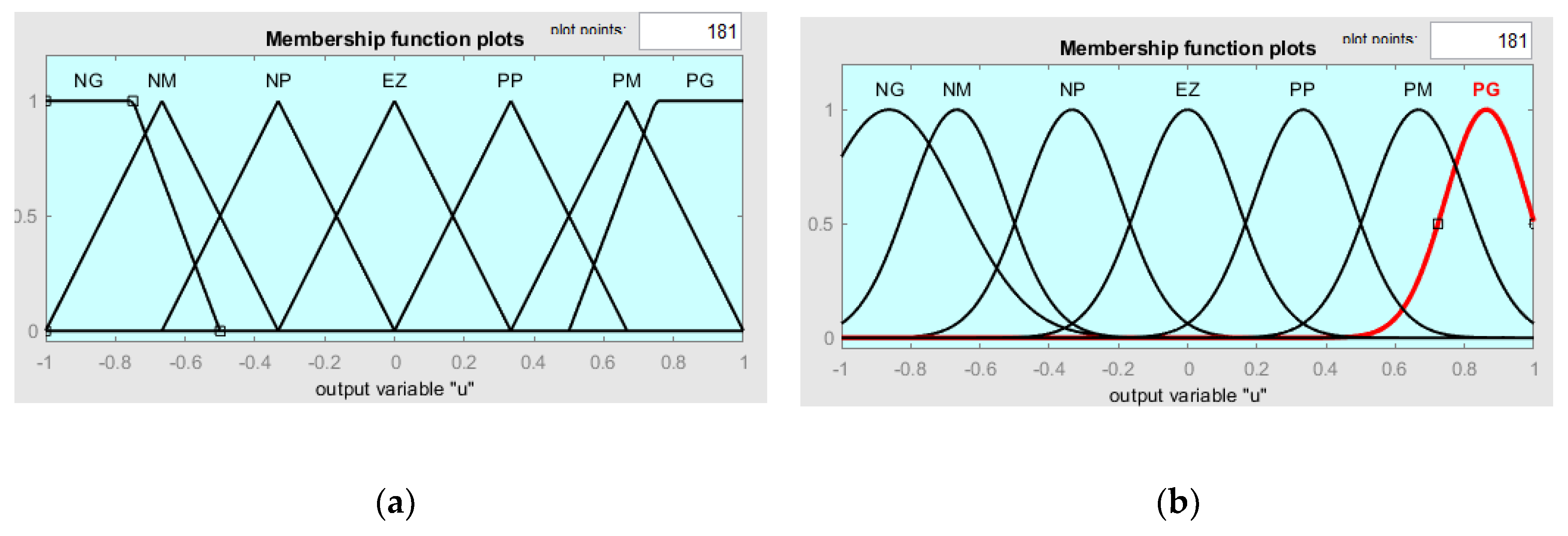
4. Comparison Between Fuzzy Logic and ANFIS
5. Types of Faults in Synchronous Electric Drives
6. Fault Diagnostics Techniques
- Model-Based Approaches:
- i. State Estimation Techniques: Observers and Kalman filters to monitor system states and detect abnormalities.
- ii. Analytical Redundancy: Comparing measurements with expected values from system models.
- Data-Driven Techniques:
- i. Machine Learning: Using supervised learning models (e.g., SVM, neural networks) trained on historical fault data to predict failures.
- ii. Deep Learning: Advanced models (like CNNs and RNNs) for feature extraction from complex datasets such as vibration or current signals.
- iii. Signal Processing: Techniques like FFT (Fast Fourier Transform), wavelet analysis, and time-domain analysis for detecting irregularities in motor currents, vibrations, or acoustic signals.
7. Fault Tolerance in Synchronous Electric Drives
- (i)
- Redundancy: Designing systems with redundant components, such as dual inverters and backup power supplies, that can take over when the primary component fails.
- (ii)
- Reconfigurable Control: Adjusting control algorithms in real-time to compensate for faulty components, such as de-rating motor power or shifting operation modes.
- (iii)
- Fault-Tolerant Control Algorithms: Adjusting the control strategy to handle faults by switching control to a different phase in case of a phase fault and
- (iv)
8. Advanced AI Techniques for Fault Diagnostics and Tolerance
- AI for Predictive Maintenance: AI models can analyze sensor data (temperature, vibration, etc.) to predict potential failures. (i) Real-Time Monitoring: Implementing AI for continuous monitoring of drive systems, enabling rapid detection of abnormalities. (ii) Fuzzy Logic and ANFIS-Based Controllers: Adaptive systems that adjust drive control in real-time to handle faults seamlessly.
- b. Internet of Things (IoT) and Edge Computing: (i) IoT Integration: Sensors across the drive system can communicate data in real-time for centralized analysis. (ii) Edge Computing: Performing diagnostic processing locally on devices for faster and more efficient fault detection [22].
9. Challenges and Future Directions
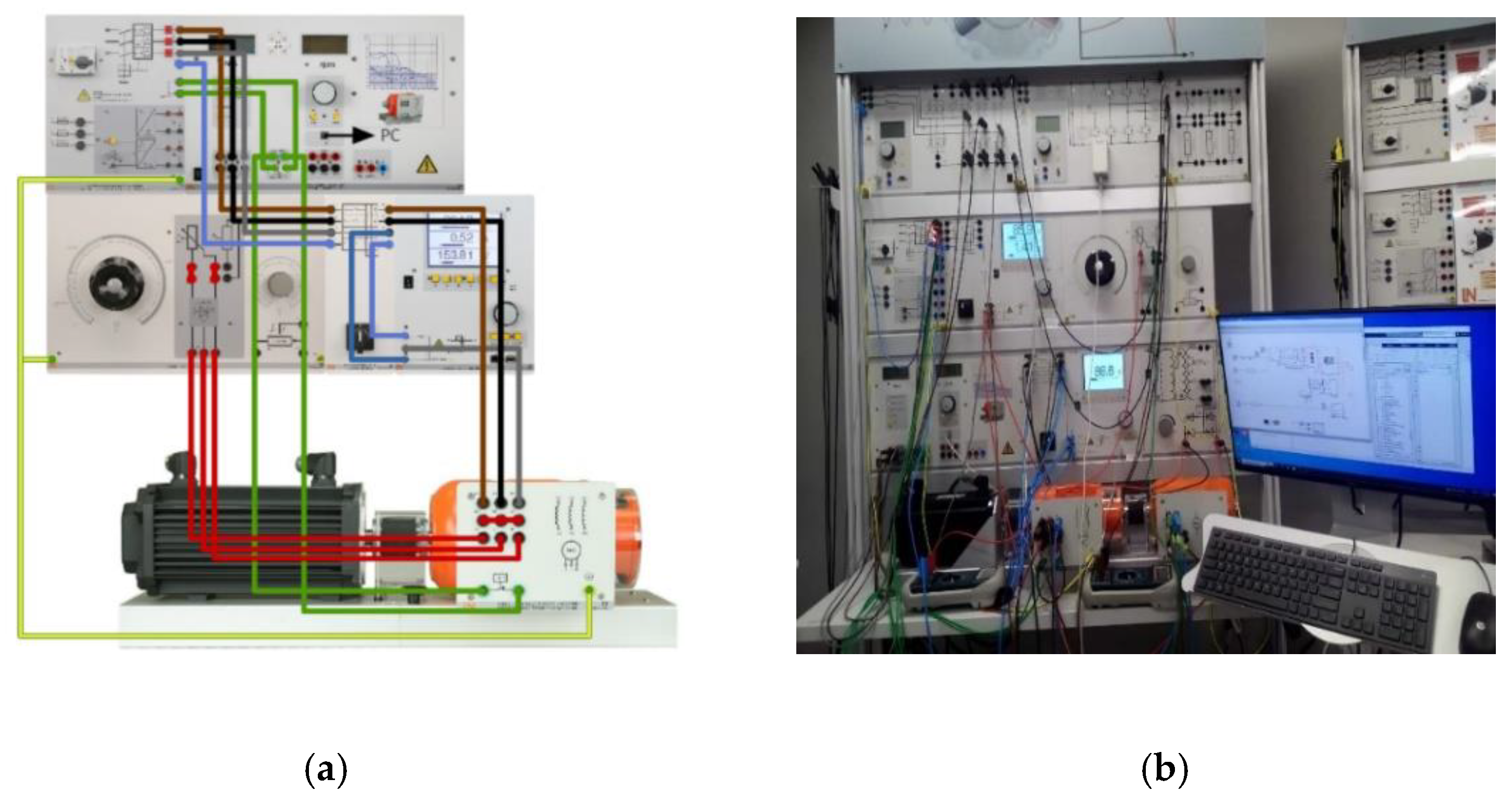
10. Materials and Specifications
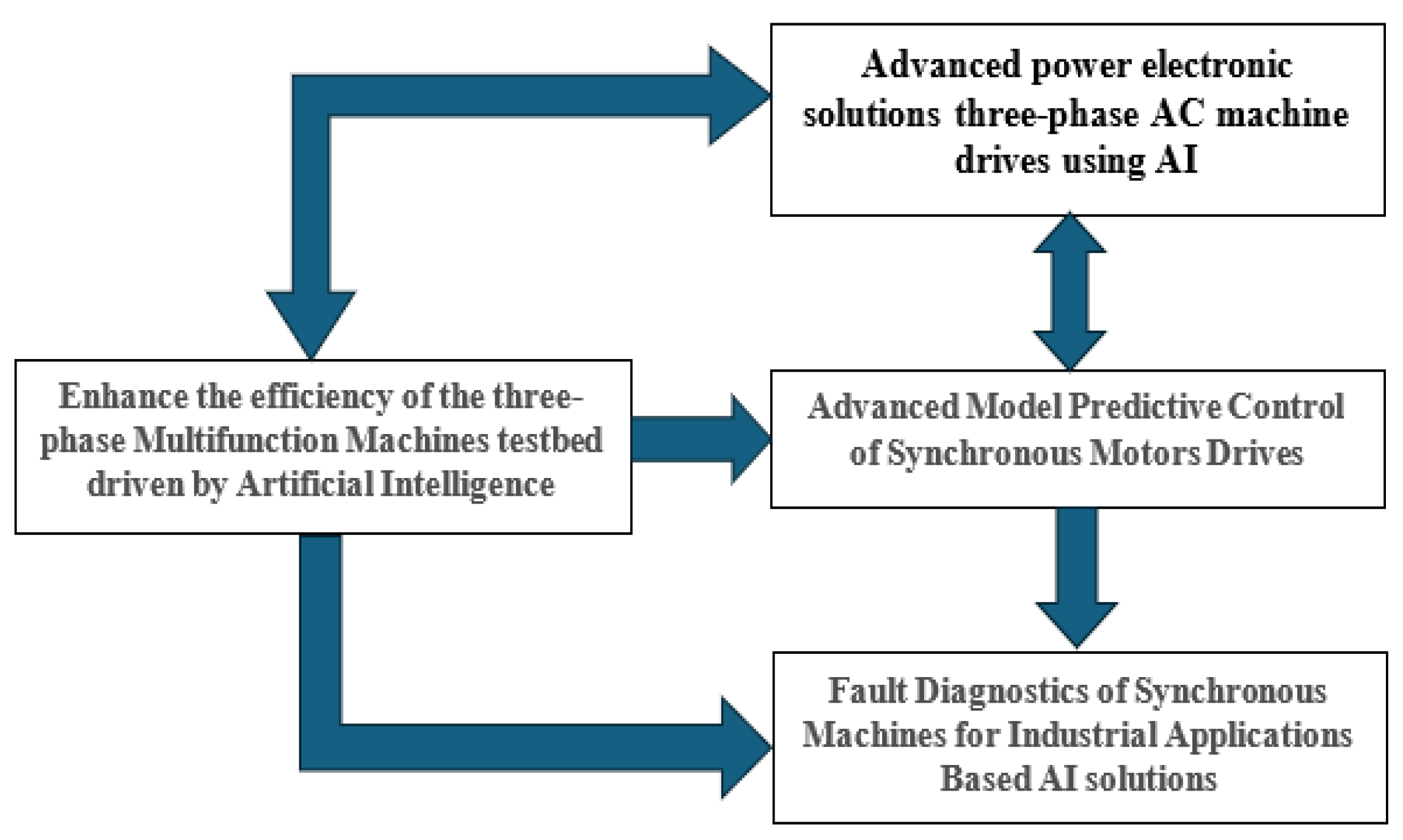
11. Enhance Efficiency with Artificial Intelligence.
11. Modeling the Machine Dynamics
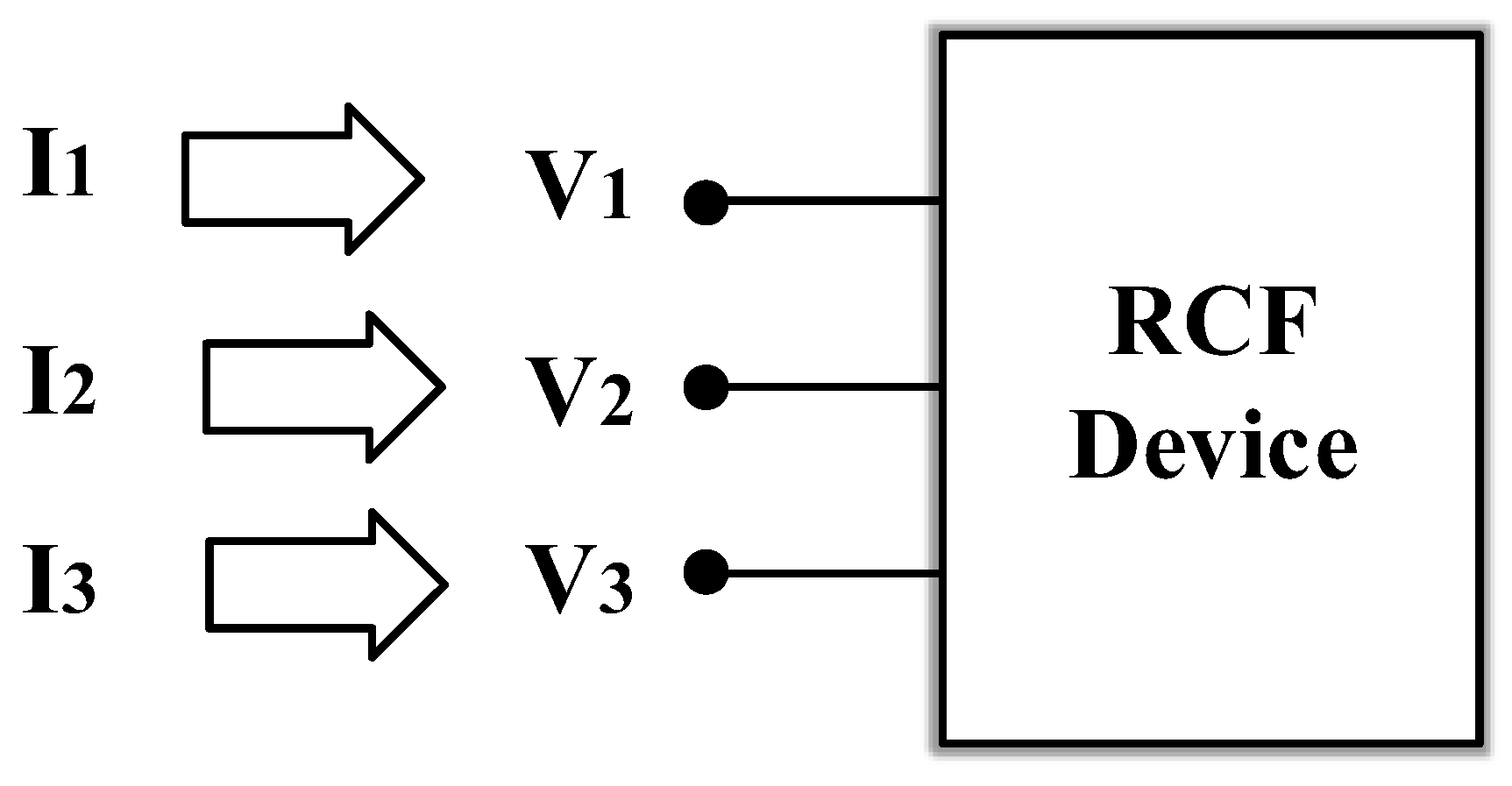
11.1. Resistive Companion Form Modeling Technique
11.2. The d-q Model of a Three-Phase Synchronous Machine
11.3. Park's Transformation
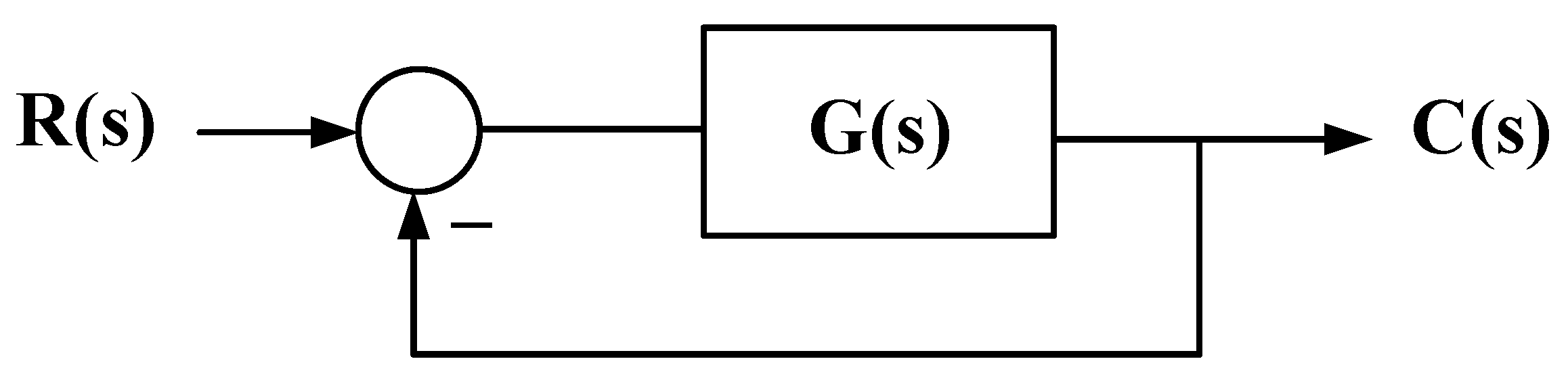
12. Control Strategy with AI
12.1. Optimization with Neural Networks or Fuzzy Logic
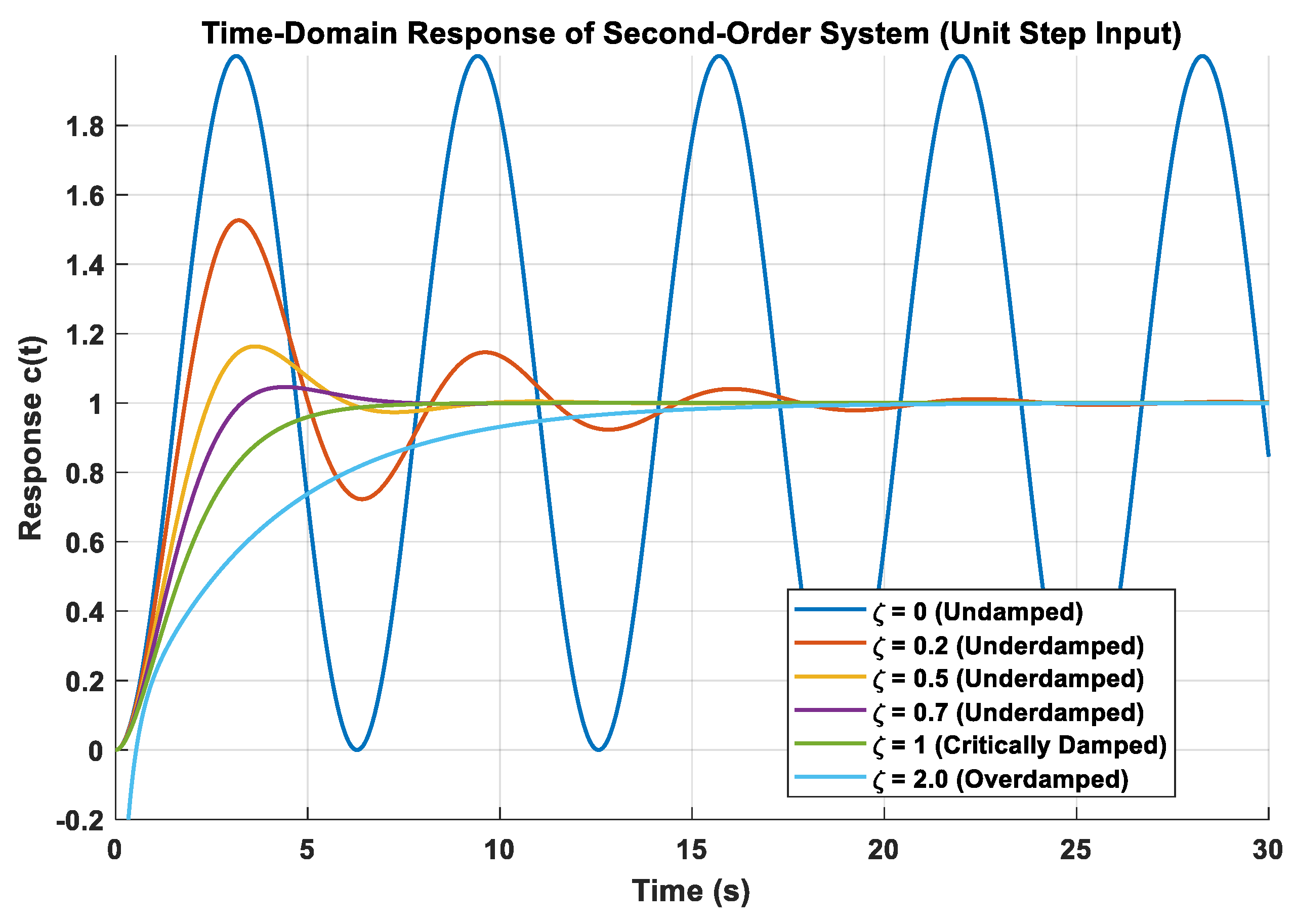
12.2. Time Response of a Second-Order System
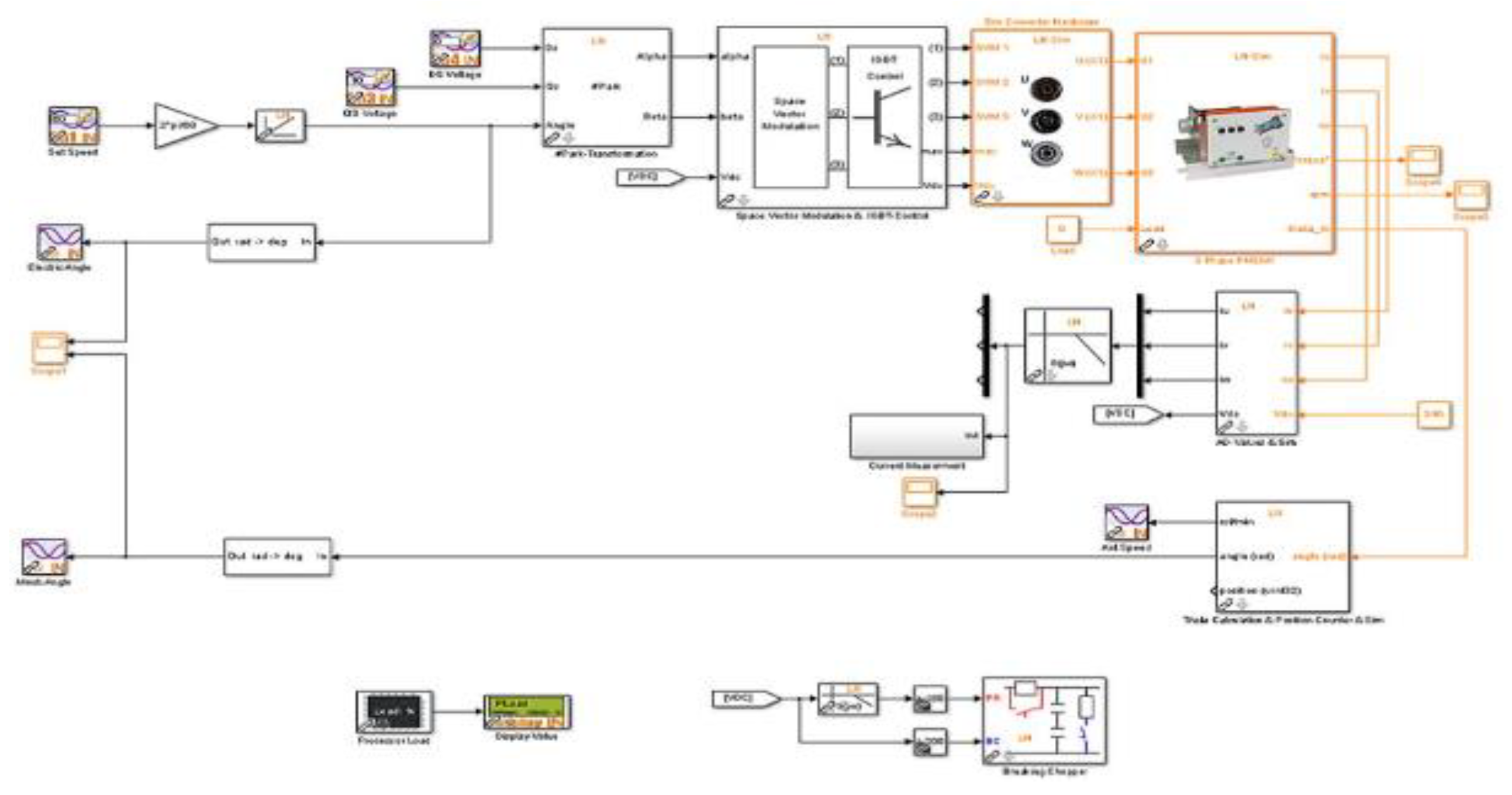
13. Simulation Model
14. Fault Diagnostics
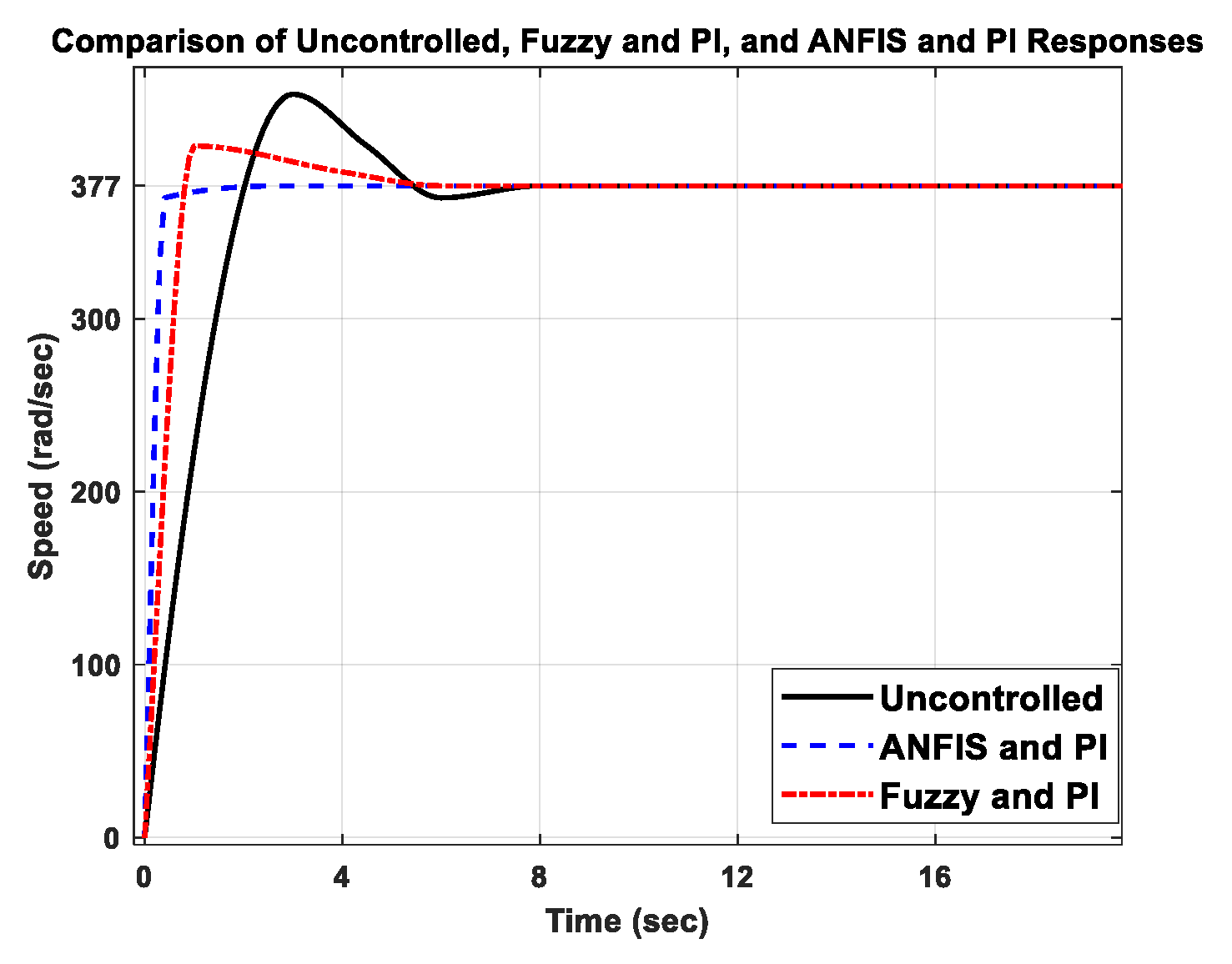
15. Results and Discussion
16. Conclusions
References
- Vargas, M. , Teixeira, D., Jiménez, G., Ladines, M., Machacuay, J., & Ipanaqué, W. Model-Free ANN-based control for Three-Phase Synchronous Motor Speed Control. In 2023 IEEE International Conference on Electronics, Electrical Engineering and Computing (INTERCON), IEEE, 23, pp. 1-8. 20 November.
- Patel, R. A. , & Bhalja, B. R. Condition monitoring and fault diagnosis of the synchronous motor using support vector machine. Electric Power Components and Systems, 2016, 44(6), pp. 683-692.
- Ali, M.; Khalid, M. Multiphase Matrix Converter Modulation for Wind Energy Systems using Genetic Algorithm. 2022 Saudi Arabia Smart Grid (SASGIEEE, 22; pp. 1–5. 20 December.
- Zhou, Y. , Shang, Q., & Guan, C. Three-phase synchronous motor fault diagnosis using attention mechanism and hybrid CNN-MLP by multi-sensor information. IEEE Access, 2023.
- Sunori, S. K. , Mittal, A., Bisht, V. S., Joshi, N., Garia, P., Juneja, P., & Kaliraj, S. Title of the article. Simulation, 122, 23. 3rd International Conference on Electronics and Sustainable Communication Systems (ICESC 2022), -19, 2022. 17 August.
- Preethi, I. , Suryaprakash, S., & Mathankumar, M. A state-of-the-art approach to fault detection in a three-phase synchronous motor using AI techniques. In 2021 5th International Conference on Computing Methodologies and Communication (ICCMC), IEEE, 21, pp. 567-573. 20 April.
- de Araújo, V.G.; Teixeira, R.d.A.; Nascimento, T.F.D.; Salazar, A.O.; Fonseca, D.A.d.M. Application of Artificial Intelligence Techniques for Monitoring and Fault Diagnosis in Three-Phase Induction Motors. 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP). LOCATION OF CONFERENCE, BrazilDATE OF CONFERENCE; pp. 1–8.
- Akin, M.; Canbay, Y.; Ocak, C. Deep Learning Based Phase Current Prediction Model in Three-Phase IGBT Two-Level Inverter for Electrical Drives. 2024 IEEE 18th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG). LOCATION OF CONFERENCE, PolandDATE OF CONFERENCE; pp. 1–6.
- Yaghobi, H. , Ansari, K., & Mashhadi, H. R. Stator Turn-to-Turn Fault Detection of Synchronous Motor Using THD Analysis. Iranian Journal of Science and Technology, 2013, 37(2), pp. 161-182.
- Redondo, M.; Platero, C.A.; Gyftakis, K.N. Turn-to-turn fault protection technique for synchronous machines without additional voltage transformers. 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED). LOCATION OF CONFERENCE, GreeceDATE OF CONFERENCE; pp. 117–121.
- Hoffe, S. J. , Meyer, A. S., & Cronje, W. A. Determination of Shaft Position from Shaft Voltage on a Synchronous Motor. IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), IEEE, 2005.
- Varzaneh, M.G.; Iranshahi, M.; Mansour, I.; Kamali-Omidi, N.; Panah, A.S. Implementing V/F Control of Three-Phase Induction Motors without the Use of Digital Processors for Electric Propulsion Applications. 2023 2nd International Engineering Conference on Electrical, Energy, and Artificial Intelligence (EICEEAI). LOCATION OF CONFERENCE, JordanDATE OF CONFERENCE; pp. 1–4.
- E Okpo, E.; Le Roux, P.F.; Nnachi, A.F. Induction Motor Fault Identification using Support Vector Machine. 2023 6th International Conference on Renewable Energy and Power Engineering (REPE). LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE; pp. 168–174.
- Casadei, D. , Filippetti, F., Rossi, C., Stefani, A., Capolino, G. A., & Yazidi, A. A General Diagnostic Method for Doubly Fed Synchronous Machine Drives Based on Field Oriented Control. IEEE Transactions on Industry Applications, 2005, 50(2), pp. 1206-1213.
- Freire, N. M. A. , Estima, J. O., & Cardoso, A. J. M. A New Approach for Current Sensor Fault Diagnosis in PMSG Drives for Wind Energy Conversion Systems. IEEE Transactions on Industry Applications, 2013, 50(2), pp. 1207-1214.
- Sabir, R. , Rosato, D., Hartmann, S., & Gühmann, C. Detection and Localization of Electrical Faults in a Three Phase Synchronous Motor with Rectifier. In 2019 International Conference on Electrical Drives & Power Electronics (EDPE), IEEE, -26, 2019. 24 September.
- Kiani, M. , Lee, W.-J., Kenarangui, R., & Fahimi, B. Detection of Rotor Faults in Synchronous Motors. IEEE Transactions on Industry Applications, 2008, 50(2), pp. 1206-1213.
- Mahmoud, H. , Abdallah, A., El-Hakim, S., & Shaltout, A. An Inverse Approach for Interturn Fault Detection in Synchronous Machines. IEEE Transactions on Industry Applications, 2016, 52(1), pp. 226-233.
- Awadallah, M. , Morcos, M., Gopalakrishnan, S., & Nehl, T. A Neuro-Fuzzy Approach to Automatic Diagnosis of Stator Inter-Turn Faults. IEEE Transactions on Energy Conversion, 2005, 20(2), pp. 253-259.
- Antonino-Daviu, J. A. , & Penman, J. Fault Detection of Synchronous Machines Using Discrete Wavelet Transform. IEEE Transactions on Industry Applications, 2005, 41(2), pp. 257-265.
- Bouzid, M. , Champenois, G., Bellaaj, N., Signac, L., & Jelassi, K. An Effective Neural Approach for Automatic Location of Stator Interturn Faults in Synchronous Motors. IEEE Transactions on Industrial Electronics, 2008, 55(12), pp. 4277-4289.
- Shah, D. , Nandi, S., & Neti, P. Stator-Interturn-Fault Detection of Doubly Fed Synchronous Motors Using Rotor-Current Signature Analysis. IEEE Transactions on Industry Applications, 2009, 45(5), pp. 1831-1842.
- Soualhi, A. , Clerc, G., & Razik, H. Faults Classification of Synchronous Machine Using Improved Ant Clustering Technique. IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives.
- Kim, C. E. , & Sykulski, J. K. Harmonic Analysis of Output Voltage in Synchronous Motor Using Finite Element Method. IEEE Transactions on Magnetics, 2002, 38(2), pp. 1249-1252.
- Neti, P.; Nandi, S. Stator Inter-turn Fault Detection of Synchronous Machines Using Field Current Signature Analysis. Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
- Antonino-Daviu, J. A. , Penman, J., & Negrea, M. D. On-Line Detection of Faults in Electrical Machines by Wavelet Analysis of Current Signals. IEEE Transactions on Power Electronics, 2018, 23(1), pp. 50-59.
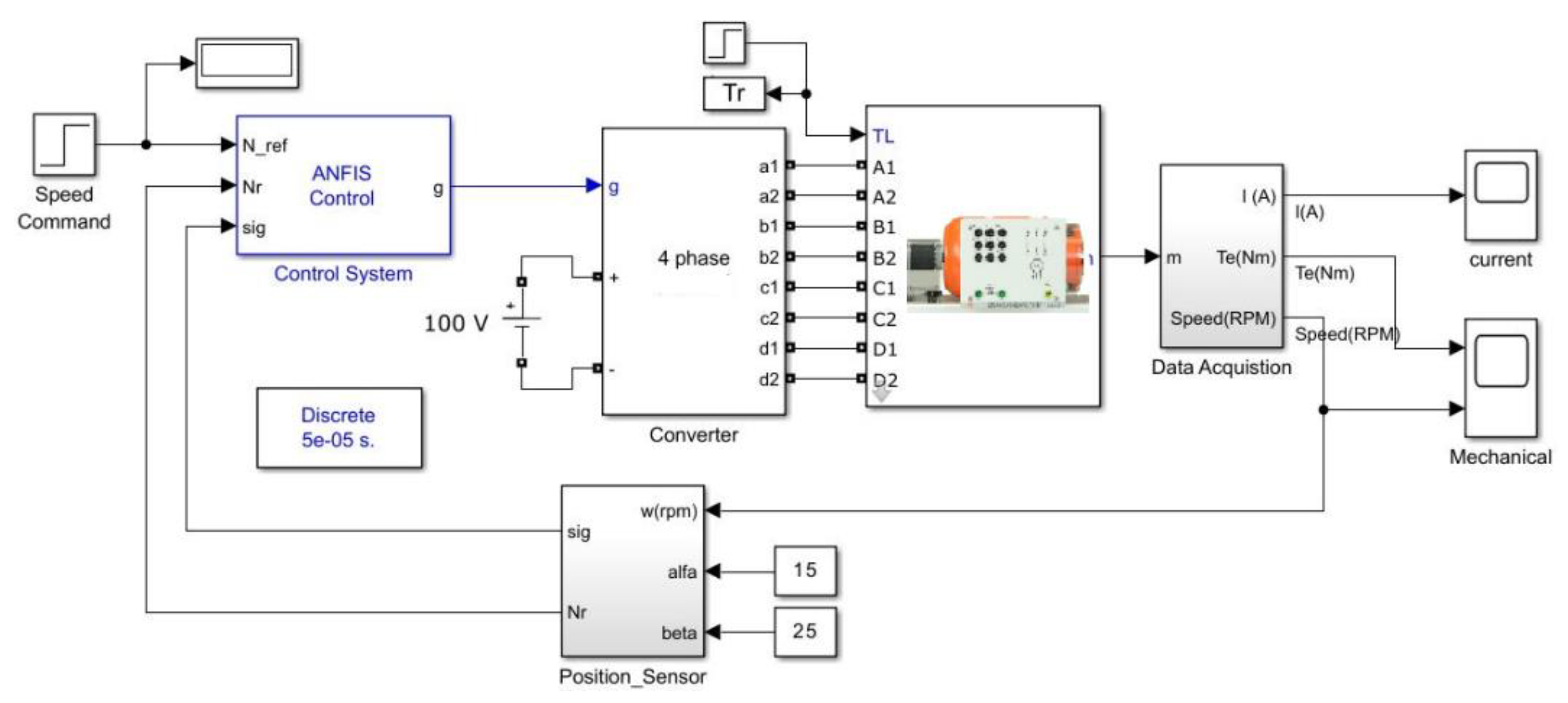

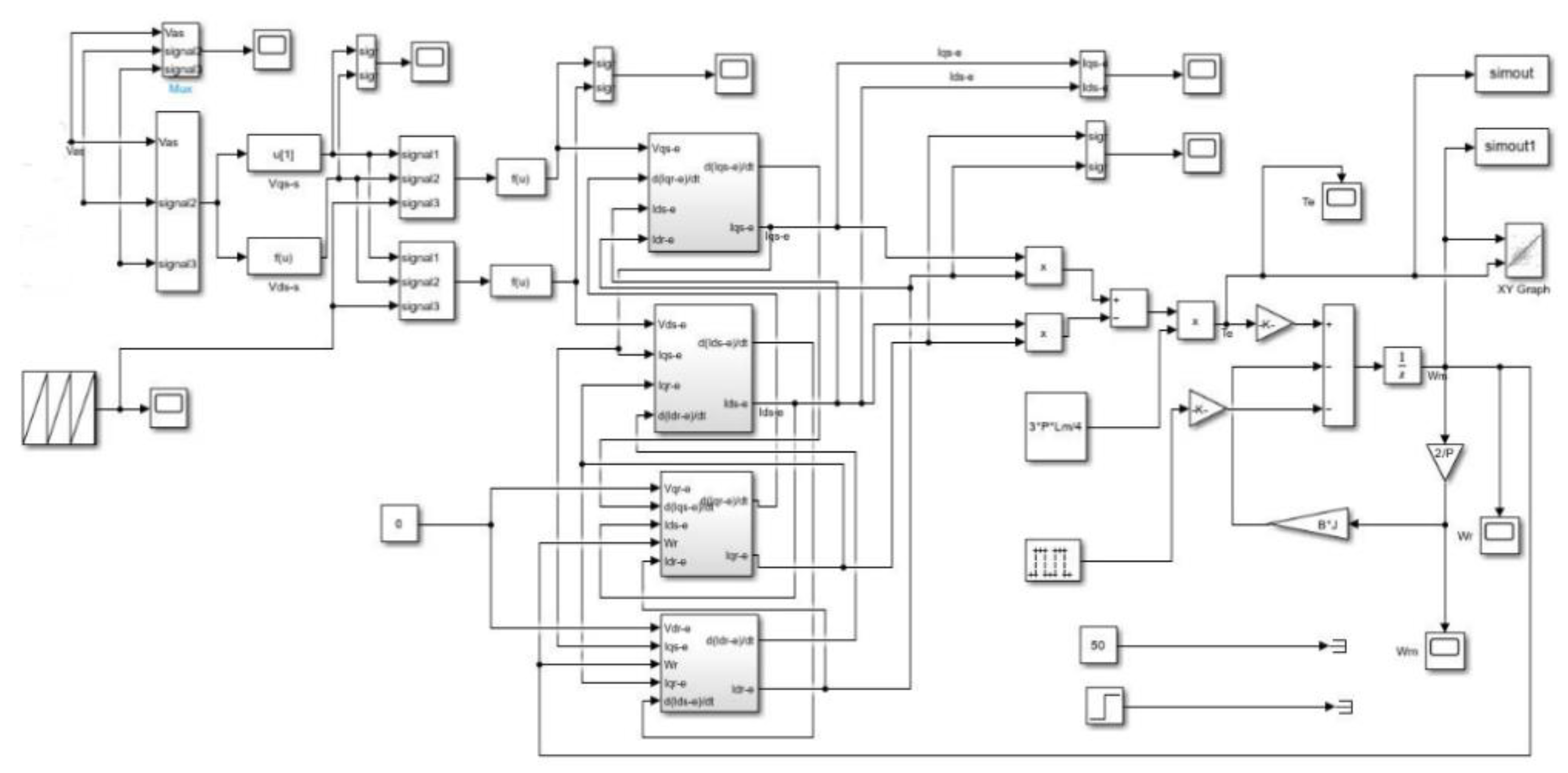
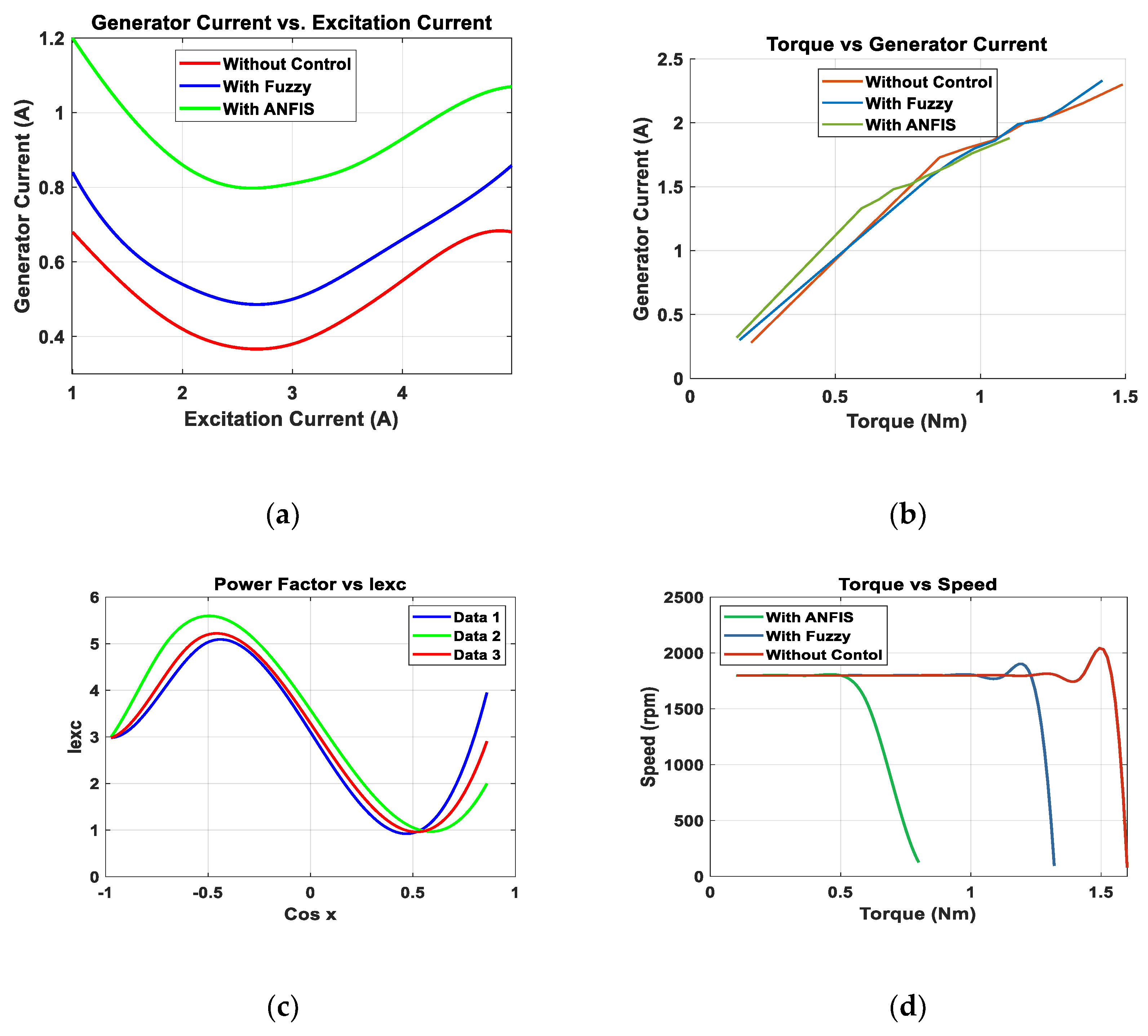
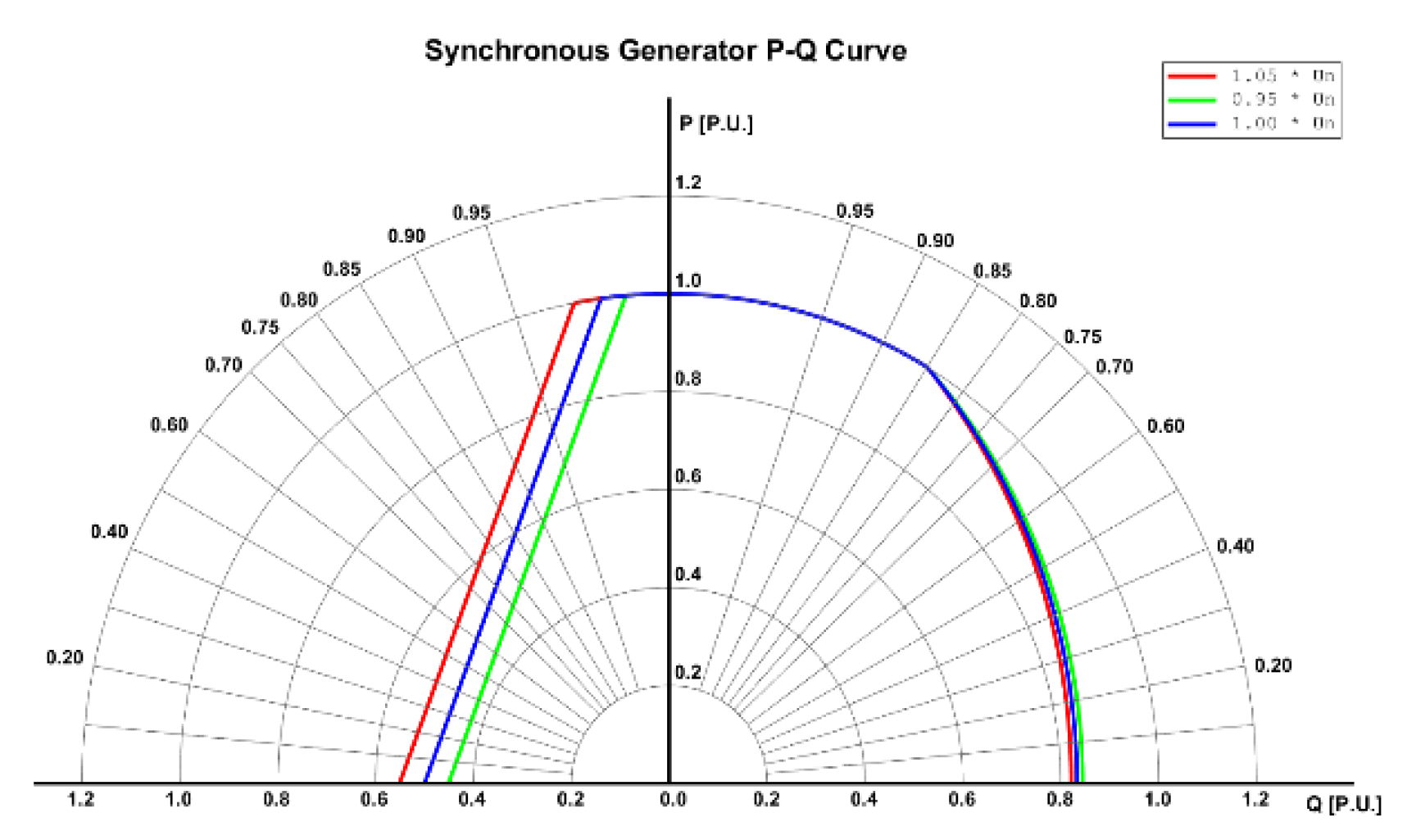
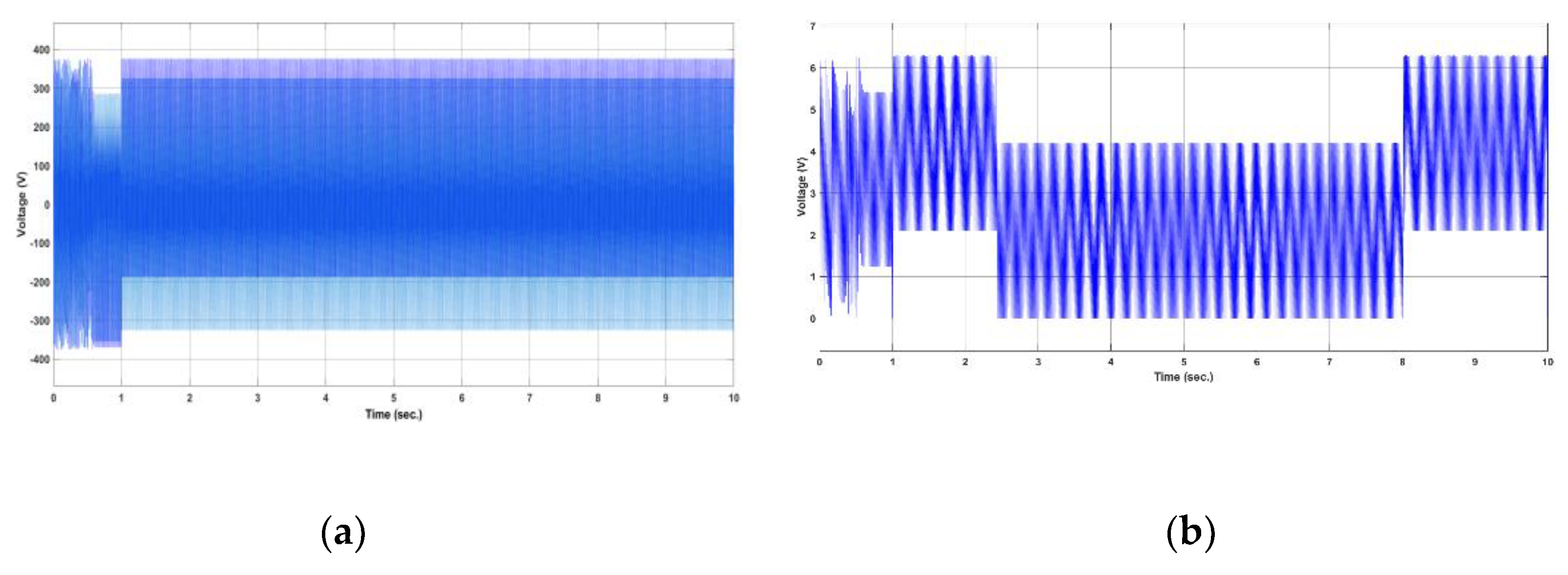
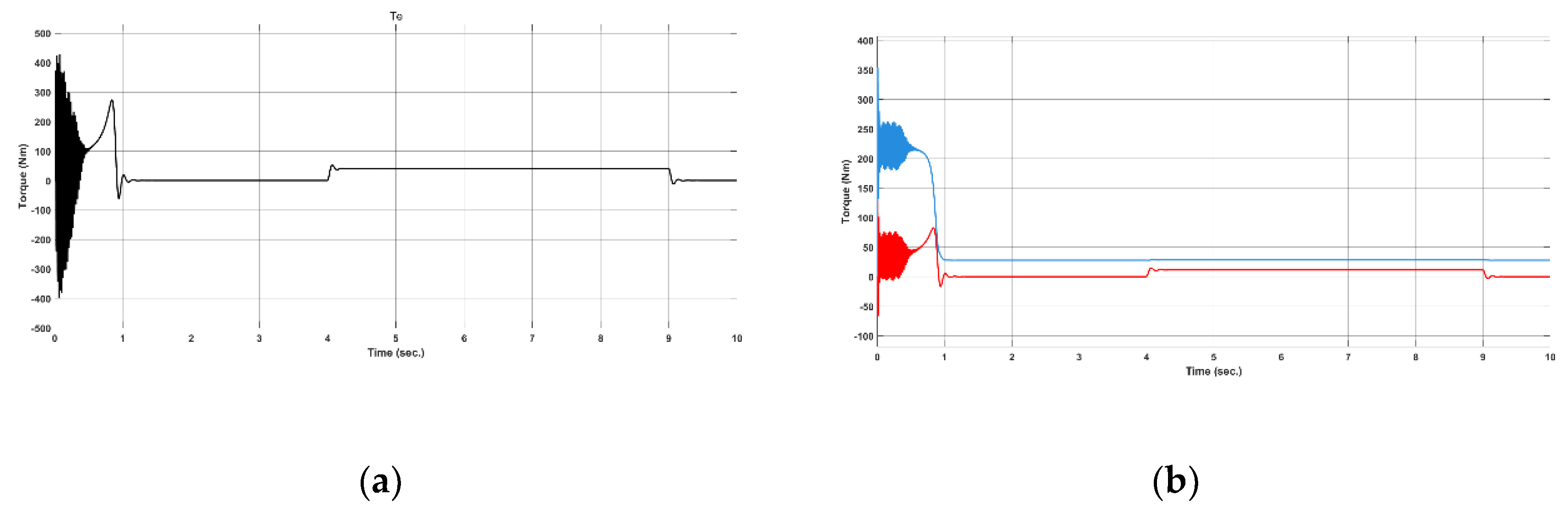
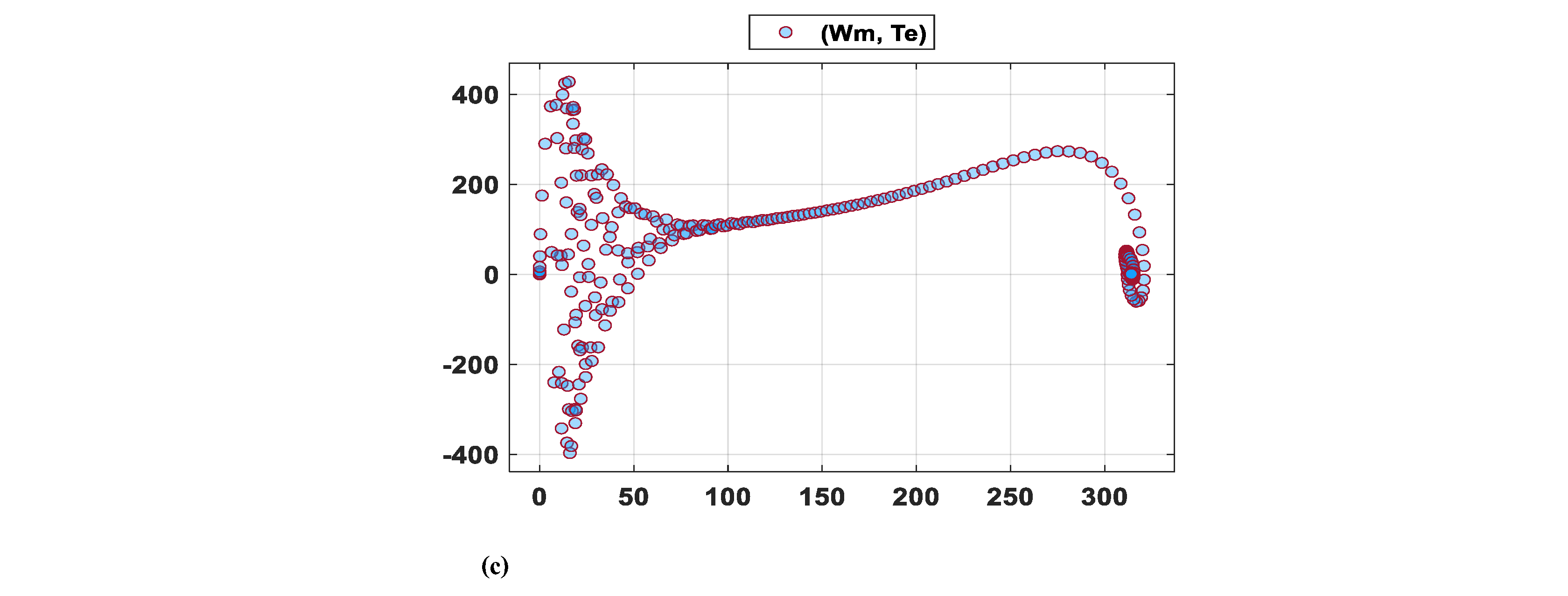
| Researchers | Year | Technology Used | Type of Fault or Control | Results |
|---|---|---|---|---|
| Gonzaga de Araujo et al. | 2023 | Self-forming neural network | fault classification (bearing faults and shaft imbalance) | High efficiency in fault classification |
| Okpo and Lo Ro | 2023 | Support Vector Machines (SVM) | Diagnosis of Unbalanced Voltage and Mechanical Overload Faults | High Accuracy in Fault Diagnosis |
| Vargas et al. | 2023 | Artificial neural network with modified Adam algorithm for | speed control of synchronous motors with better | performance than conventional controllers |
| Akin and Kanbi | 2023 | BiLSTM Network for Phase Current Prediction | Inverter Management High Prediction | Accuracy Compared to Conventional Models |
| Zhou et al. | 2023 | Hybrid model (CNN and MLP) with attention mechanism | Fault diagnosis using vibration signals and electrical signals | High accuracy and stability compared with traditional methods |
| Rich et al. | 2023 | Processor-free V/F control system | Improves safety and reliability in sensitive applications (e.g., marine propulsion) | System effectiveness verified by simulation |
| Ali and Khaled | 2022 | Multiphase Strategy Using Genetic Algorithms | Improving Torque Density and Fault Tolerance in Six-phase Synchronous Motors | Success of the Strategy Supported by Simulation in MATLAB |
| Kumar et al. | 2021 | Machine Learning Algorithms (KNN and SVM) Fault | Diagnosis by Analyzing Vibration Signals and Operational Parameters | Facilitating Fault Diagnosis and Failure Avoidance |
| Preethi and Surya Praka | 2021 | Logit Boosting Algorithm and Sample Optimization Techniques | Fault Classification | High-Performance Fault Detection |
| Hossein Ehya, Arne Nysveen | 2021 | Pattern Recognition Algorithm | Static, Dynamic, and Mixed Eccentricity Faults | Non-invasive, verified on large setups |
| B. Tabbache, M. Benbouzid | 2013 | Virtual-Sensor-Based Approach | Electric Vehicle Powertrain Faults | Enhanced fault tolerance |
| S. Karimi, A. Gaillard | 2009 | Fault-Tolerant Control for WECS | Current Sensor Fault Control for DFIG | Improved stability and fault tolerance |
| Specification | Typical Value |
|---|---|
| Motor Type | Three-phase Synchronous, 300 W |
| Nominal Voltage | 230/400 V |
| Frequency/Pole | 60 Hz, 4-pole |
| Nominal Current | 1.4 A / 2.4 A |
| Nominal Speed | 1800 rpm |
| Nominal Power | 0.3 kW |
| Power Factor | 0.9 (lagging) |
| Dimensions | 340 × 210 × 210 mm |
| Weight | 10 kg |
| Cooling Method | Air-cooled |
| Type | Max. Overshoot (rad/sec) | Rise Time (sec) |
Settling Time (sec) |
Time at Max. Overshoot (sec) |
|---|---|---|---|---|
| Uncontrolled | 53.16 | 2.90 | 8 | 3.10 |
| Fuzzy and PI | 16.79 | 1.10 | 6 | 1.40 |
| ANFIS and PI | - | 0.80 | 4 | 0.9 |
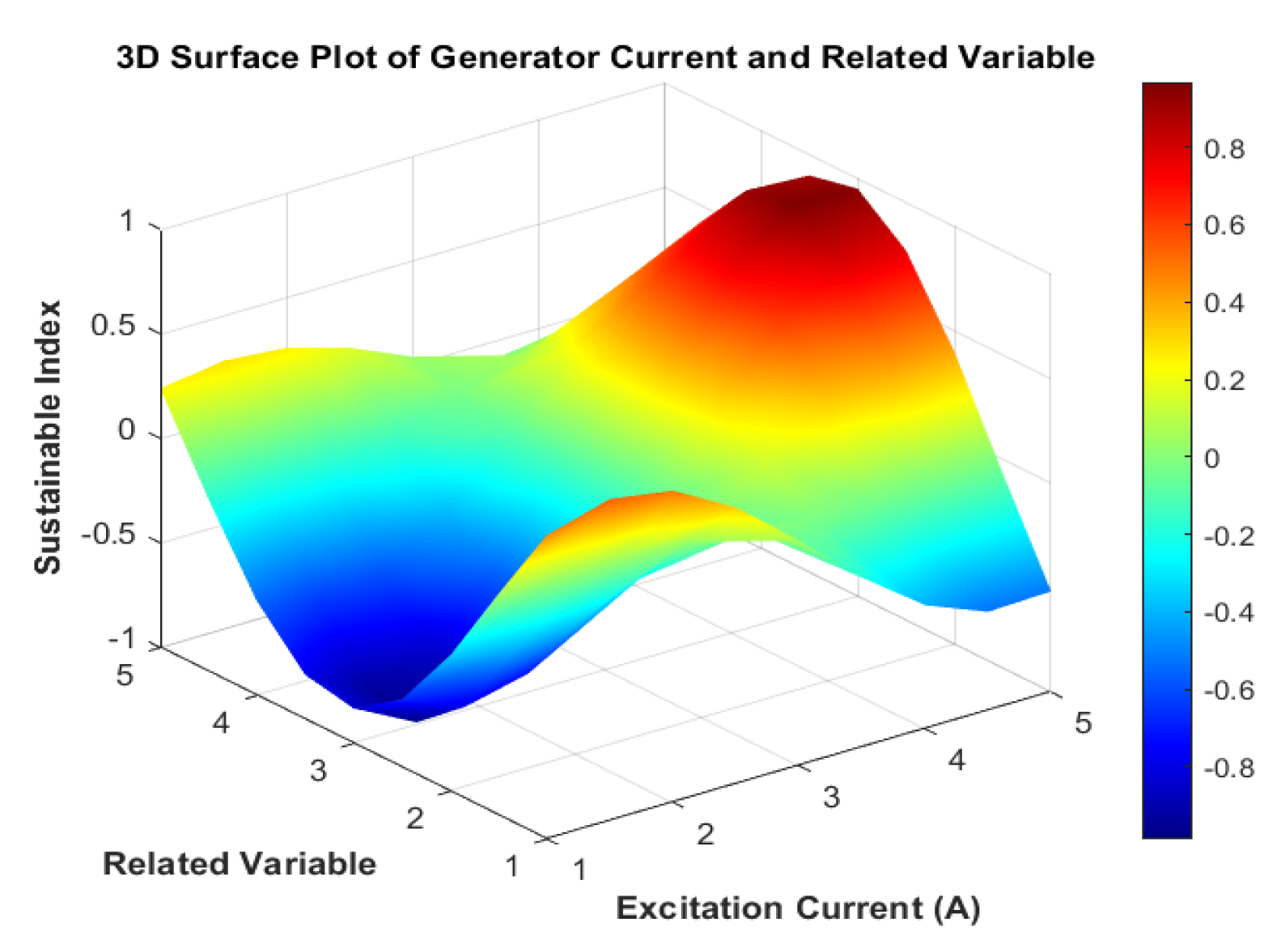
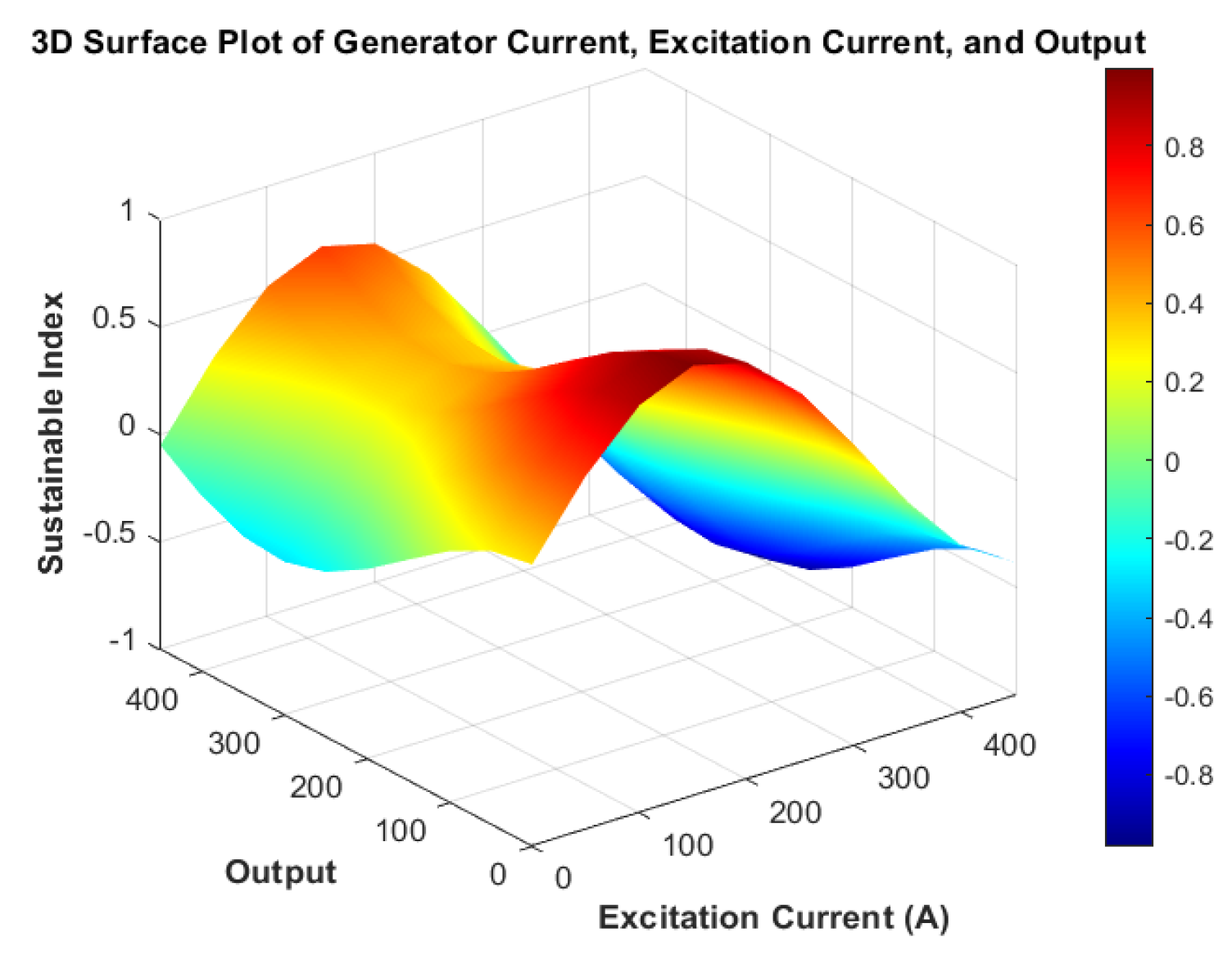
| Variable | Sustainable Index (FSBI) |
|---|---|
| Excitation Current | 0.5–0.9 |
| Motor Current 1 | 0.4–0.8 |
| Motor Current 2 | 0.3–0.7 |
| Motor Current 3 | 0.2–0.6 |
| Output | 0.6–1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




