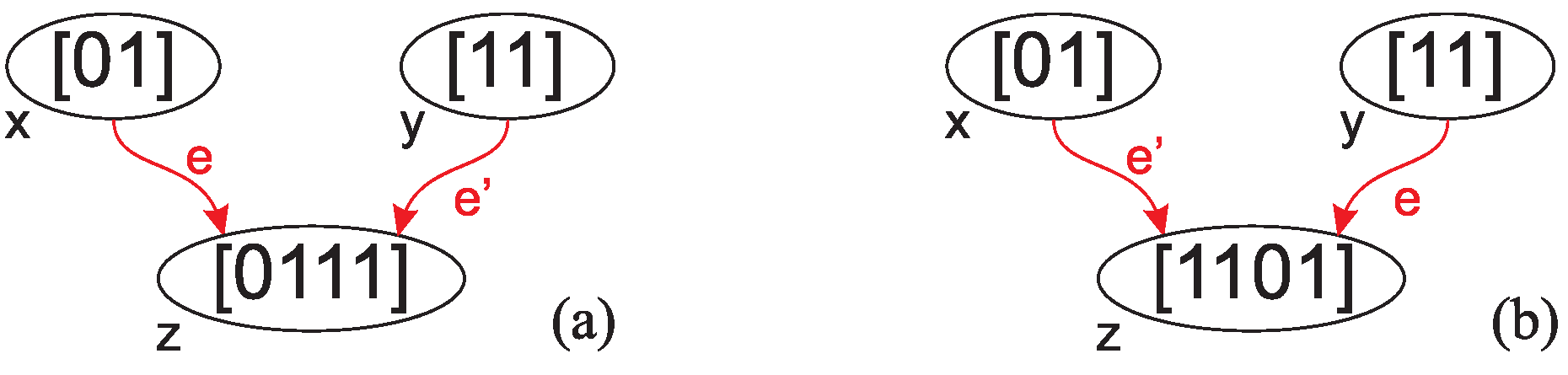On the "Assembly Theory and its Relationship with Computational Complexity"

1. Introduction

A recent study [1] shows that assembly theory offers a distinct approach and answers different questions than computational complexity theory with its focus on minimum descriptions via compressibility and discusses fundamental differences in the ontological basis of assembly theory and the assembly index as a physical observable, which distinguish it from theoretical approaches to formalizing life that are unmoored from measurement. Furthermore, the study [1] claims to contain the proof of the conjecture posed in [2] that the Assembly Index Problem is NP-Complete. In general, it argues to show that any instance of Vertex Cover Problem, which is known to be NP-Hard, can be reformulated as an instance of the Assembly Index Problem. Finally, it leaves open the question of whether the non-commutative concatenation version of string assembly is NP-Complete; its authors see no alternative to reconcile the commutativity of the assembly step with the non-commutativity of the string concatenation (cf. [1], Supplementary Material, footnote 101.).

Here, we show that such a reconciliation is, in fact, possible by providing an alternative definition of the assembly space. We also show that it is the Assembly Steps Problem, not the Assembly Index Problem, which has been shown in [1] to be NP-complete. Hence, finding if a string can be assembled along a given path in a given number of steps is NP-complete. But we do not know if finding the minimal difference between the cardinalities of the final and initial assembly pools that lead to this string, that is, the assembly index of this string [3], is NP-complete.

2. An Alternative Definition of an Assembly Space

An assembly space $\mathsf{\Omega }=(\mathsf{\Gamma },\varphi )$ is defined in [1] (cf. Definition 8) as an acyclic directed graph $\mathsf{\Gamma }=(V,E)$, where $V\left(\mathsf{\Omega }\right)$ is the set of vertices and $E\left(\mathsf{\Omega }\right)$ is the set of edges together with an edge labeling map $\varphi \left(e\right):e\in E\left(\mathsf{\Omega }\right)\to v\in V\left(\mathsf{\Omega }\right)$. $\mathsf{\Gamma }$ contains a finite and non-empty set of vertices $\mathrm{Src}\left(\mathsf{\Gamma }\right)=B_{\mathsf{\Omega }}$ that form the basis of $\mathsf{\Omega }$, each reachable only from itself. All remaining vertices of $\mathsf{\Gamma }$ are reachable from a vertex in $B_{\mathsf{\Omega }}$. The edge labeling map $\varphi$ cleverly defines the assembly step. Namely

$$e=(x,z)\in E\left(\mathsf{\Omega }\right)\wedge \varphi \left(e\right)=y\in V\left(\mathsf{\Omega }\right)\iff \exists e^{\prime }=(y,z)\in E\left(\mathsf{\Omega }\right):\varphi \left(e^{\prime }\right)=x,$$

(1)

allowing to write $e=(x_y,z)$, $e^{\prime }=(y_x,z)$, and

$$e=(x_y,z)\in E\left(\mathsf{\Omega }\right)\iff e^{\prime }=(y_x,z)\in E\left(\mathsf{\Omega }\right).$$

(2)

However, the commutativity of the relation (2) cannot imply the commutativity of the string concatenation. If all assembly objects in $V\left(\mathsf{\Omega }\right)$ are strings $(x_y,xy)\in E\left(\mathsf{\Omega }\right)$ does not imply $(y_x,yx)\in E\left(\mathsf{\Omega }\right)$, as might be expected for string concatenation, but it actually implies also $(y_x,xy)\in E\left(\mathsf{\Omega }\right)$. Therefore, a string assembly space is endowed in [1] with the additional property (cf. [1], Definition 18 and Eq. (10))

$$(x_y,z)\in E\left(\mathsf{\Omega }\right)\Rightarrow z=\left[xy\right]\vee z=\left[yx\right],$$

(3)

and likewise for the edge $(y_x,z)\in E\left(\mathsf{\Omega }\right)$.

However, this conclusion and, thus, the inevitability of the property (3) it entails makes the string associated with the terminating vertex z unresolvable if $x\ne y$. Here, we provide an alternative definition of the assembly space, noting that vertices x, y, or z of the assembly space are not the same as strings $C_x$, $C_y$, or $C_z$ they are associated with.

Definition 1 

(Assembly Space). An assembly space $\mathsf{\Omega }=(\mathsf{\Gamma },\varphi )$ is an acyclic, 2-in-regular digraph $\mathsf{\Gamma }=(V,E)$, where V is a set of vertices $v_k$ associated with strings $C_k$ with b inaccessible vertices associated with $b\in \mathbb{N}$ different basic symbols c of unit length, and the edge labeling map defined as:

$$\forall e=(x,z)\in E\left(\mathsf{\Gamma }\right)\wedge \varphi \left(e\right)=\left\{\begin{array}{cc}y\hfill & \iff \exists !e^{\prime }=(y,z)\in E\left(\mathsf{\Gamma }\right):\varphi \left(e^{\prime }\right)=-x\wedge C_z=C_x\circ C_y=\mathrm{strcat}(C_x,C_y)\hfill \\ -y\hfill & \iff \exists !e^{\prime }=(y,z)\in E\left(\mathsf{\Gamma }\right):\varphi \left(e^{\prime }\right)=x\wedge C_z=C_y\circ C_x=\mathrm{strcat}(C_y,C_x)\hfill \end{array}\right.,$$

(4)

that defines the concatenation order of the strings $C_x$, $C_y$ associated respectively with vertices x, y in the string $C_z$ associated with the vertex z being the endpoint of both edges e and $e^{\prime }$.

The set of b inaccessible vertices forms the initial assembly pool $P_0^{\left(b\right)}\{0,1,\cdots ,b-1\}$[3] and is equivalent to the basis $B_{\mathsf{\Omega }}$ (cf. [1], Eq. (7)). We note that the definition of edge labeling map (4) is possible if only $b>1$, i.e., the initial assembly pool contains more than one distinct basic symbol, as in that case we can say that a given symbol is the 1^st one in the initial assembly pool, another is the 2^nd one, and so on; we can sort them. Otherwise, the notion of a concatenation direction is pointless for one symbol only. The relation (4) preserves the commutativity of the assembly step in terms of the vertices labels, that is $(x_y,z)\in E\left(\mathsf{\Omega }\right)\iff (y_x,z)\in E\left(\mathsf{\Omega }\right)$, but defines the order of concatenation of the strings associated with those labels, as for different strings $C_x\ne C_y\iff C_x\circ C_y\ne C_y\circ C_x$. This is shown in Figure 1.

In an acyclic, 2-in-regular digraph, each accessible vertex has exactly two incoming edges corresponding to the assembly step. This definition extends the previous definition of the assembly space as a quiver [4]; the notion of self-reachability of vertices of an assembly space is misleading as it suggests some self-assembly. Hence, basis objects are inaccessible, not self-reachable (cf. [1], Definition 7).

3. The Assembly Steps Problem is NP-Complete

In order to show that any instance of Vertex Cover Problem $(G,k)$, where $G=(V,E)$ is a graph, $V\left(G\right)$ is the set of vertices and $E\left(G\right)$ is the set of edges and k is the cardinality of a set of vertices that includes at least one vertex of every edge of G, which is known to be NP-Hard, can be reformulated in polynomial time as an instance of the Assembly Index Problem, the following procedure is offered (cf. [1], Section 4.2). For a given instance of the Vertex Cover Problem $(G,k)$, where $\tau \le k\le V\left|G\right|$, and $\tau$ is the vertex cover number (the size of a minimum vertex cover), an instance of the Assembly Index Problem $(\mathsf{\Omega },C_x,a^{(N,b)}\left(C_x\right))$ is constructed, where $\mathsf{\Omega }=(\mathsf{\Gamma },\varphi )$ is a constructed assembly space, and $C_x$ is the target string for which the assembly index $a^{(N,b)}\left(C_x\right)$ is to be determined. It is then claimed that a certificate for the Vertex Cover Problem

$$C=\{v_l\in V\left(G\right)|C_l=\left[0v_{l}0\right]\in V\left({\mathsf{\Omega }}^{\prime }\right)\}$$

(5)

containing a subset $\left\{v_l\right\}$ of vertices of G that includes at least one vertex of every edge of G can be used to produce a certificate $({\mathsf{\Omega }}^{\prime },C_x,a^{(N,b)}\left(C_x\right))$ for the Assembly Index Problem and vice versa, where ${\mathsf{\Omega }}^{\prime }\subset \mathsf{\Omega }$ is a rooted subspace (cf. [1] Definition 15) of the assembly space $\mathsf{\Omega }$ containing only a proper subset $\{C_l=\left[0v_{l}0\right]\}$ of the strings of the form $C_k=\left[0v_{k}0\right],\forall v_k\in V\left(G\right)$. Hence, such an instance of the Assembly Index Problem would be logically equivalent to an instance of the Vertex Cover Problem from which it was constructed.

The construction of $C_x$ (cf. [1], Section 4.2) begins with forming the basis of the assembly space $\mathsf{\Omega }$ (cf. Eqs. (17), (50))

$$B_{\mathsf{\Omega }}=\{0,1,2,\cdots ,|V\left(G\right)\left|\right\},$$

(6)

containing $\left|V\right(G\left)\right|$ symbols of vertices $V\left(G\right)$, and a special symbol that here we call 0 (it is defined as # in [1]). Hence, $b=|B_{\mathsf{\Omega }}|=|V\left(G\right)|+1$. Then, a set of $3\left|V\right(G\left)\right|$ strings

$$C_{k1}=\left[0v_k\right],C_{k2}=\left[v_{k}0\right],C_{k3}=\left[0v_{k}0\right],\forall v_k\in V\left(G\right)$$

(7)

is assembled (Eq. (18)) Subsequently, a set of $\left|E\right(G\left)\right|$ strings

$$C_j=\left[0v_{s_j}0v_{t_j}0\right],\forall e_j=(v_{s_j},v_{t_j})\in E\left(G\right)$$

(8)

is assembled (Eq. (19)). The last step of the construction of $C_x$ is a sequence of $2\left|V\right(G\left)\right|$ strings

$$\begin{array}{cc}\hfill S_0& 0,\hfill \\ \hfill S_k& S_k\circ \left[0v_k\right],\forall v_k\in V\left(G\right),\hfill \\ \hfill S_{\left|V\right(G\left)\right|+1}& S_{\left|V\right(G\left)\right|}\circ \left[v_{1}0\right],\hfill \\ \hfill S_{\left|V\right(G\left)\right|+k}& S_{\left|V\right(G\left)\right|+k-1}\circ \left[v_{k}0\right],\forall v_k\in V\left(G\right),\hfill \end{array}$$

(9a)

and $\left|E\right(G\left)\right|$ strings

$$\begin{array}{cc}\hfill S_{2\left|V\right(G\left)\right|+1}& S_{2\left|V\right(G\left)\right|}\circ \left[0v_{s_1}0v_{t_1}0\right],\hfill \\ \hfill S_{2\left|V\right(G\left)\right|+j}& S_{2\left|V\right(G\left)\right|+j-1}\circ \left[0v_{s_j}0v_{t_j}0\right],\forall e_j=(v_{s_j},v_{t_j})\in E\left(G\right),\hfill \end{array}$$

(9b)

defined in [1] by Eqs. (20)-(25), where the target string $C_x{S}_{2\left|V\right(G\left)\right|+\left|E\right(G\left)\right|}$ is defined as the last string of this sequence and

$$\left|V\right(\mathsf{\Omega }\left)\right|=\left|V\right(G\left)\right|+1+3\left|V\right(G\left)\right|+\left|E\right(G\left)\right|+2\left|V\right(G\left)\right|+\left|E\right(G\left)\right|=6\left|V\right(G\left)\right|+2\left|E\right(G\left)\right|+1.$$

(10)

Finally ([1], Section 4.2.3) it is claimed that given $({\mathsf{\Omega }}^{\prime },C_x,n_{\mathrm{vcp}}\left(C_x\right))$ is a certificate for the Assembly Index Problem if the set (5) is a vertex cover of G with size k, i.e. a certificate for the Vertex Cover Problem is given, wherein $n_{\mathrm{vcp}}\left(C_x\right)$ is the assembly index of string $C_x$ and

$$n_{\mathrm{vcp}}\left(C_x\right)=4|V\left(G\right)|+2|E\left(G\right)|+k\iff |V\left({\mathsf{\Omega }}^{\prime }\right)|=n_{\mathrm{vcp}}\left(C_x\right)+|B_{{\mathsf{\Omega }}^{\prime }}|=5|V\left(G\right)|+2|E\left(G\right)|+k+1,$$

(11)

which depends on k and is minimal if $k=\tau$.

By construction, the basic symbols (6), the edge strings (8), and the sequence strings (9a) and (9b) contained in $\mathsf{\Omega }$ must also be contained in ${\mathsf{\Omega }}^{\prime }$ (certificate). However, the vertex strings (7) of the form $\left[0v_{k}0\right]$ are the exception, as each of the edge strings (8) can be assembled from strings (7) in one of the two mutually exclusive steps (cf. [1] Eqs. (53), (54))

$$\left[0v_{s_j}\right]\circ \left[0v_{t_j}0\right]=\left[0v_{s_j}0v_{t_j}0\right]\mathrm{or}\left[0v_{s_j}0\right]\circ \left[v_{t_j}0\right]=\left[0v_{s_j}0v_{t_j}0\right],$$

(12)

leaving some of the strings $\left[0v_{s_j}0\right]$ or $\left[0v_{t_j}0\right]$ redundant. It can be seen by comparing the cardinalities of the spaces $\mathsf{\Omega }$ (10) and ${\mathsf{\Omega }}^{\prime }$ (11), which - as expected - leads to $k<\left|V\right(G\left)\right|$.

By construction (9a), (9b), the target string has the form

$$C_x=C_{\mathrm{vs}}\circ C_{\mathrm{es}}=[001020\cdots (\left|V\left(G\right)\right|-1\left)0\right|V\left(G\right)|1020\cdots (\left|V\left(G\right)\right|-1\left)0\right|V\left(G\right)\left|0\right]\circ C_{\mathrm{es}},$$

(13)

where the $C_{\mathrm{vs}}$ is a vertex-specific part of $C_x$ depending solely on $\left|V\right(G\left)\right|$ and its explicit form is given by the formula (9a), and the $C_{\mathrm{es}}$ is an edge-specific part of $C_x$, generated by the formula (9b), and depending both on $\left|E\right(G\left)\right|$, edge vertex assignments and the order of labeling of the edges of graph G. However, $|C_{\mathrm{es}}|=5|E\left(G\right)|$, as the length of each edge string (8) is five and there are $\left|E\right(G\left)\right|$ such strings in $C_x$ and ${\mathsf{\Omega }}^{\prime }$. Therefore, the length of the target string is

$$N_x=|C_{\mathrm{vs}}|+|C_{\mathrm{es}}|=(4\left|V\left(G\right)\right|+1)+5|E\left(G\right)|.$$

(14)

Furthermore, by construction $C_{\mathrm{vs}}$ contains two copies of the string $C_{\mathrm{lng}}[1020\cdots (\left|V\left(G\right)\right|-1\left)0\right|V\left(G\right)\left|\right]$ of length $N_{\mathrm{lng}}=2\left|V\left(G\right)\right|-1$ having the assembly index equal to $a_{\mathrm{lng}}=2\left|V\left(G\right)\right|-2$ as it does not contain any repetitions of substrings. We can take advantage of the fact that each m copies of an n-plet $C_n$ contained in a string decrease the assembly index of this string at least by $m(n-1)-a\left(C_n\right)$[3], where $a\left(C_n\right)$ is the assembly index of this n-plet, to estimate the upper bound for the assembly index of $C_x$ reduced by the presence of these two copies of $C_{\mathrm{lng}}$. Furthermore, excluding the degenerate cases of empty and disjoint graphs G, we can further infer some information about $C_x$. That is, since any vertex $v_k\in V\left(G\right)$ is a part of some edge $e_j\in E\left(G\right)$, $C_x$ contains at least two repetitions of doublets $\left[c_{l}0\right]$ (or $\left[0c_l\right]$), with $l=1,2,\cdots ,\left|V\right(G\left)\right|-1$ as the string $C_{\mathrm{lng}}$ also contains $\left|V\right(G\left)\right|-1$ such doublets, and each repetition decreases the assembly index by one. Hence, the upper bound must be further decreased by $\left|V\right(G\left)\right|-1$. Finally, each string $C_x$ contains $\left|E\right(G\left)\right|+1$ repetitions of a doublet $\left[00\right]$ and, hence, the upper bound must be further decreased by $\left|E\right(G\left)\right|$. Therefore, the initial upper bound on the assembly index that amounts to $N_x-1$[5] if $N_x\le b^2+b+1$ [3] decreases to

$$n_{\mathrm{dec}}\left(C_x\right)\le (N_x-1)-\left[2\left(2\right|V\left(G\right)|-2)-\left(2\right|V\left(G\right)|-2)\right]-\left(\right|V\left(G\right)|-1)-|E\left(G\right)|=|V\left(G\right)|+4|E\left(G\right)|+3,$$

(15)

which, in contrast to $n_{\mathrm{vcp}}\left(C_x\right)$ (11), is independent of k.

We have examined a few simple graphs, shown in Figure 2, obtaining the results listed in Table 1.

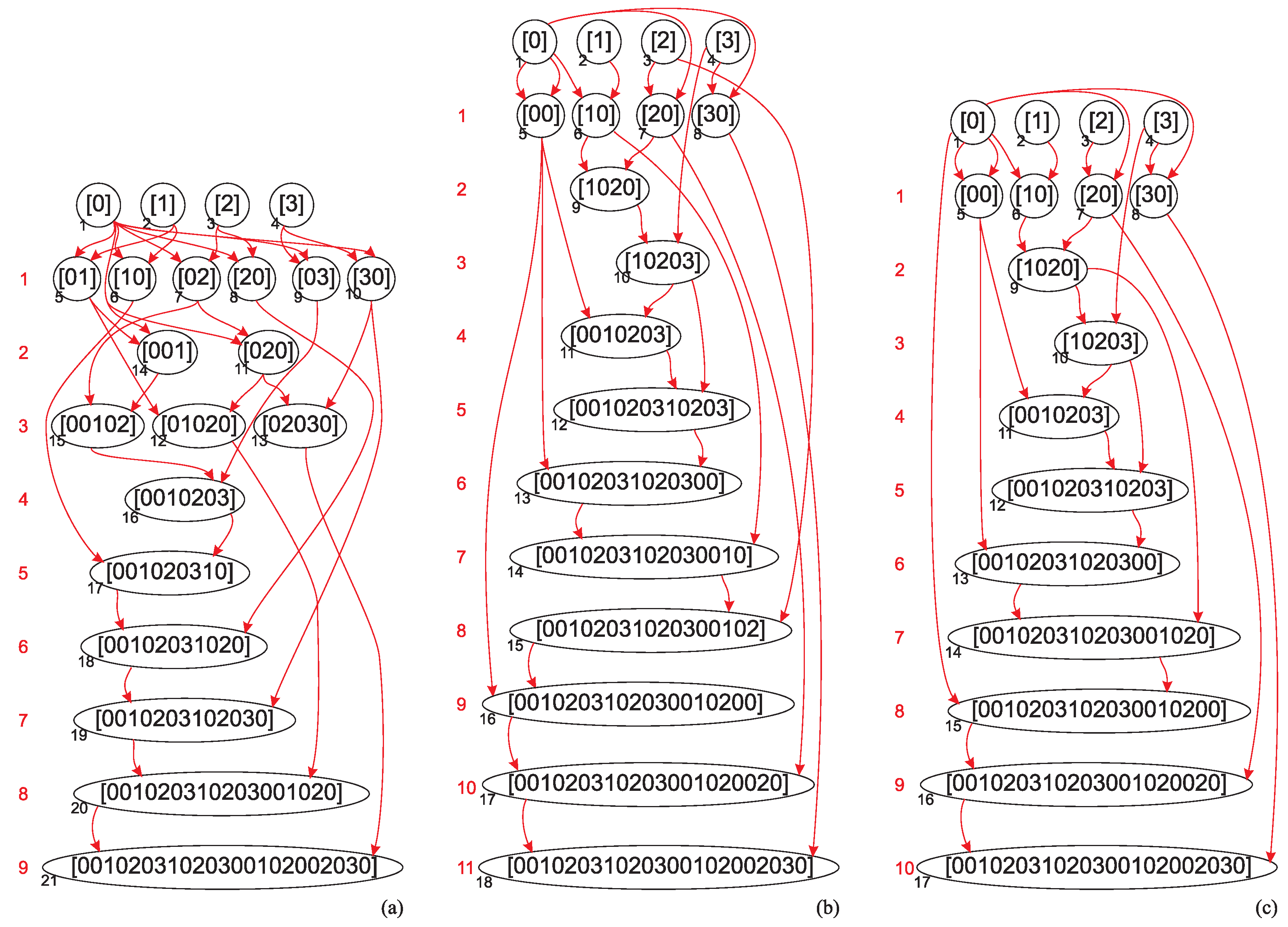
As an example, consider the trivial graph $G=(V,E)$, shown in Figure 2(b) having two edges connected at one vertex. Hence, its vertex cover number is $\tau =1$. In this case, $\left|V\right(\mathsf{\Omega }\left)\right|=23$ and the target string generated by sequences (9a) and (9b) has the form

$$C_x=\left[00102031020300102002030\right].$$

(16)

As the vertex cover of the graph G is the vertex 2, the subspace ${\mathsf{\Omega }}^{\prime }$ (the certificate) is devoid of triplets $\left[010\right]$ and $\left[030\right]$, since the edges $(1,2)$ and $(2,3)$ share the vertex 2, and the edge strings (8) could be assembled as $\left[01\right|020]$ and $\left[020\right|30]$. Therefore, the number of steps on the assembly pathway of $C_x$ defined by ${\mathsf{\Omega }}^{\prime }$, given by the relation (11), amounts to $n_{\mathrm{vcp}}\left(C_x\right)=\left|\mathsf{\Omega }\right|-|B_{\mathsf{\Omega }}|-2=17$, as shown in Figure 3(a) also illustrating the assembly depth [6] ($d\left(C_x\right)=9$) of this string: 7 steps (5-11) for vertex strings (7), 2 steps (12,13) for edge strings (8), 6 steps (14-19) for sequence strings (9a), and 2 steps (20,21) for sequence strings (9b)) which corresponds to the vertex cover number $\tau =1$, if only the string (16) is assembled using the set of allowed assembly operations defined by the equations Eqs. (38)-(45) of [1].

However, imposing such a set of allowed assembly steps deviates from the principles of assembly theory that assume the possibility of assembling any object from any two objects in the assembly pool. Even if we assume that only some steps are allowed and some are not due to peculiarities of the assembled data structures, this is certainly not the case for strings, considered in [1] in the proof of Lemma 3. All strings are possible and mathematically well defined [7]. The evolution of information became possible as soon as a first bit, not a first particle or object, became accessible [2,3,8,9].

Therefore, the assembly index of the string (16) is $a\left(C_x\right)=13$. One of the shortest pathways of the string (16) is shown in Figure 3(c) with $d\left(C_x\right)=10$. A quadruplet $\left[1020\right]$ present in two independent copies is assembled in step 5, 5-plet $C_{\mathrm{lng}}=\left[10203\right]$ present in two copies is assembled in step 6. Furthermore, $C_x$ contains two independent copies of $\left[00\right]$, $\left[10\right]$, and $\left[20\right]$. A slightly longer pathway leading to the string of length (15) is shown in Figure 3(b).

4. Conclusions

The study [1] shows that the Assembly Steps Problem, that is, a problem of determining if a given string can be assembled in a given number of steps according to principles of assembly theory, can be reformulated as the NP-hard Vertex Cover Problem, that is a problem of determining if a given set of vertices of a graph contains at least one vertex of each edge of this graph, and hence the former problem is also NP-hard. Furthermore, the study [1] shows that, since a proposed solution (certificate) to the Assembly Steps Problem can be checked for correctness in polynomial time, the Assembly Steps Problem becomes NP-complete.

However, here, based on a few simple graphs, we have shown that the proposed construction of an assembly space from a graph (a certificate) to map correspondence between the Minimum Vertex Cover Problem and the Assembly Steps Problem does not reflect a shortest pathway leading to this string and hence does not correspond to the Assembly Index Problem.

In this study, we have also answered in the affirmative the question posed in [1]: using the alternative definition of the assembly space 1 and the procedure of constructing the Assembly Steps Problem to correspond to the Vertex Cover Problem [1] shows that the non-commutative concatenation version of the Assembly Steps Problem is also NP-Complete.

Unfortunately, we still do not know if the Assembly Index Problem is NP-Complete.