Submitted:
24 October 2023
Posted:
25 October 2023
You are already at the latest version
Abstract
Keywords:
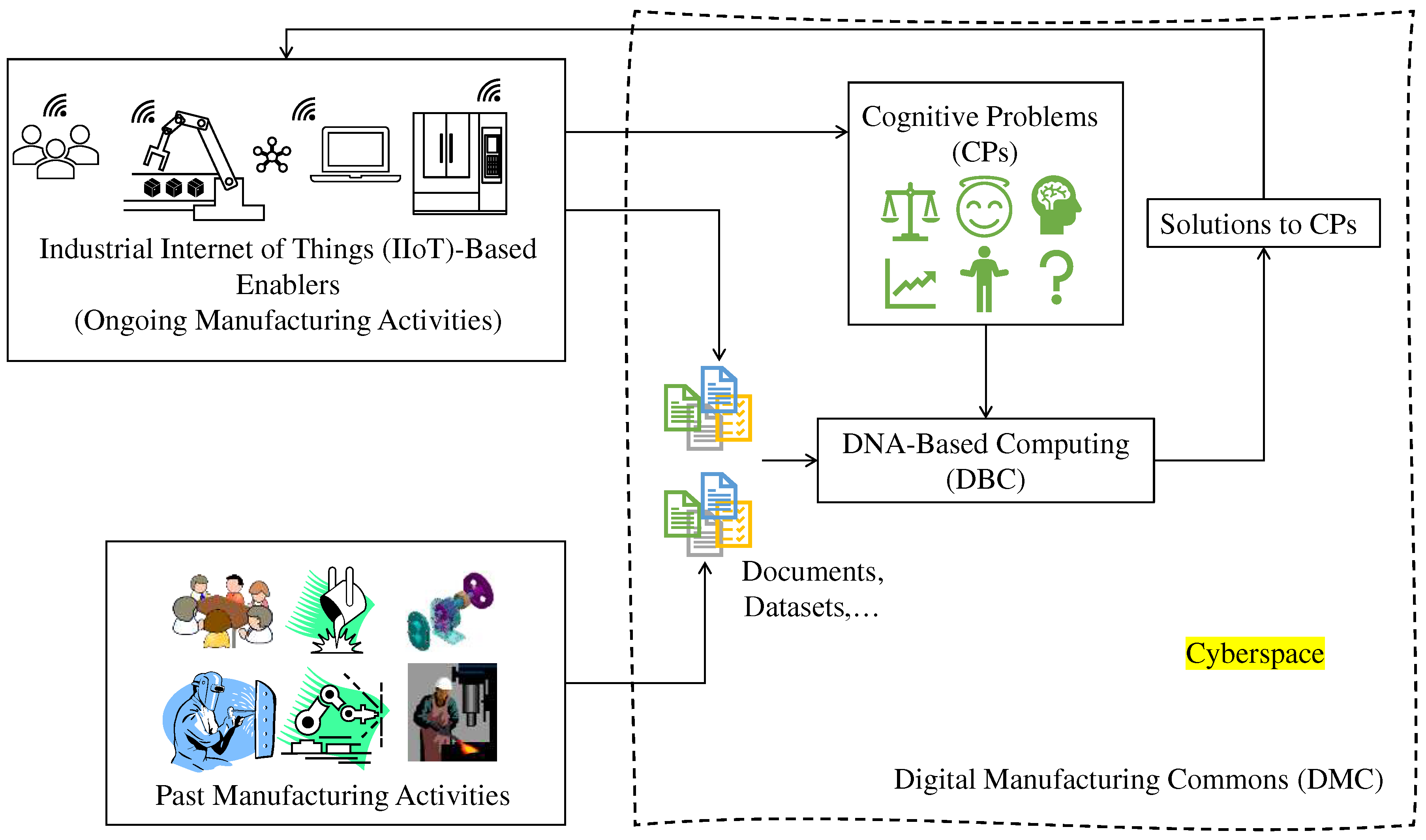
1. Introduction
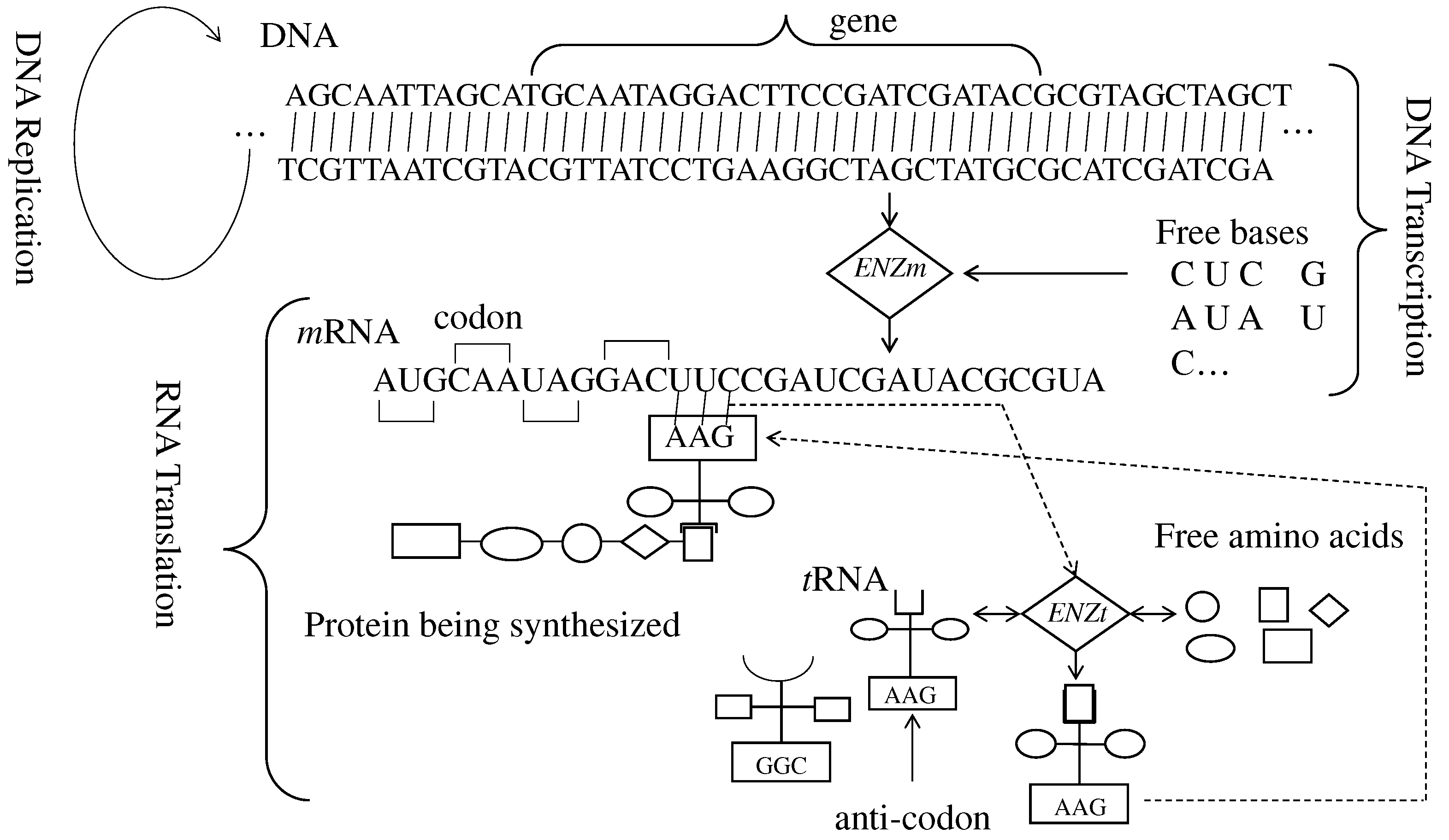
2. Central Dogma of Molecular Biology
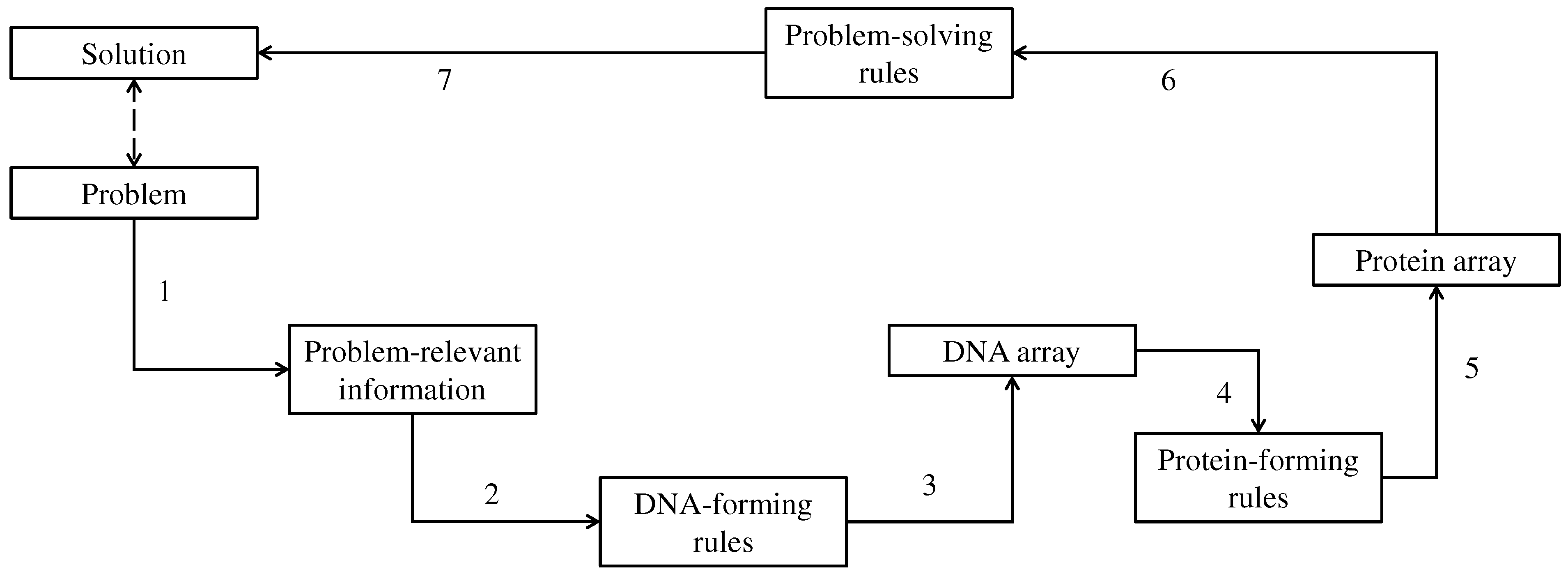
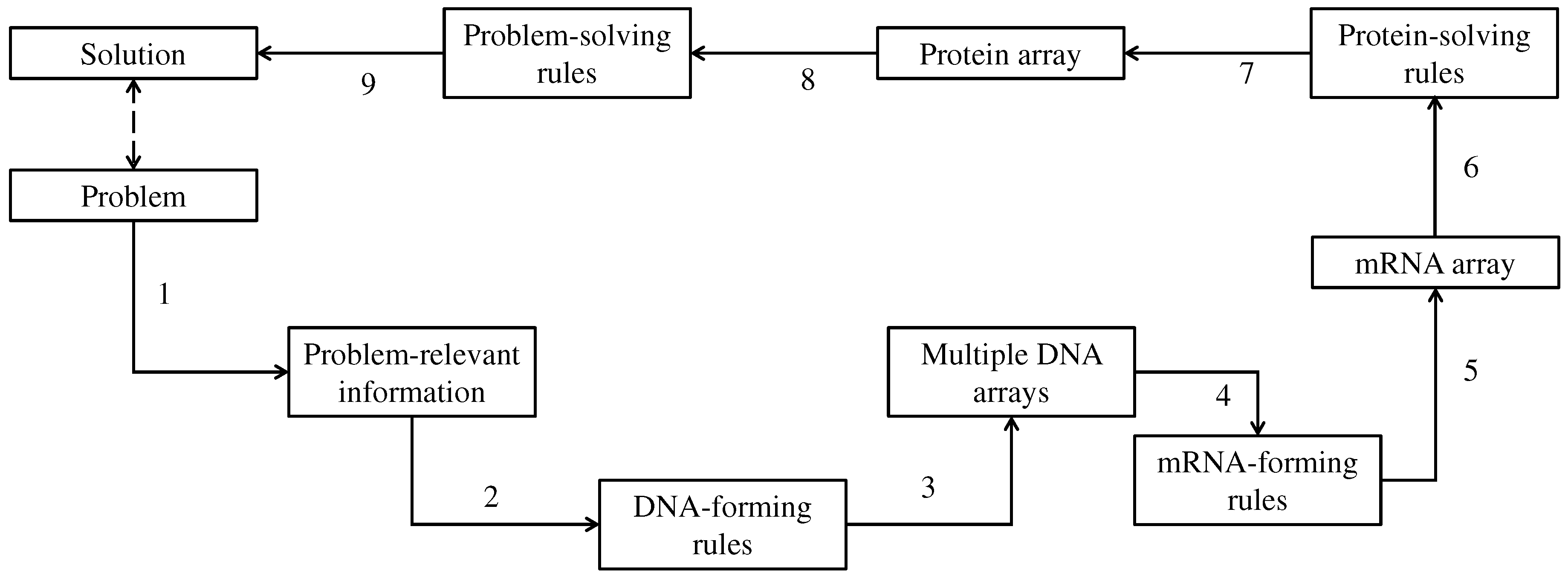
3. DNA-Based Computing (DBC)
- IF codon(i) ∈ {ATT, ATC, ATA} THEN protein(i) = I
- IF codon(i) ∈ {CTT, CTC, CTA, CTG, TTA, TTG} THEN protein(i) = L
- IF codon(i) ∈ {GTT, GTC, GTA, GTG} THEN protein(i) = V
- IF codon(i) ∈ {TTT, TTC} THEN protein(i) = F
- IF codon(i) ∈ {ATG} THEN protein(i) = M
- IF codon(i) ∈ {TGT, TGC} THEN protein(i) = C
- IF codon(i) ∈ {GCT, GCC, GCA, GCG} THEN protein(i) = A
- IF codon(i) ∈ {GGT, GGC, GGA, GGG} THEN protein(i) = G
- IF codon(i) ∈ {CCT, CCC, CCA, CCG} THEN protein(i) = P
- IF codon(i) ∈ {ACT, ACC, ACA, ACG} THEN protein(i) = T
- IF codon(i) ∈ {TCT, TCC, TCA, TCG, AGT, AGC} THEN protein(i) = S
- IF codon(i) ∈ {TAT, TAC} THEN protein(i) = Y
- IF codon(i) ∈ {TGG} THEN protein(i) = W
- IF codon(i) ∈ {CAA, CAG} THEN protein(i) = Q
- IF codon(i) ∈ {AAT, AAC} THEN protein(i) = N
- IF codon(i) ∈ {CAT, CAC} THEN protein(i) = H
- IF codon(i) ∈ {GAA, GAG} THEN protein(i) = E
- IF codon(i) ∈ {GAT, GAC} THEN protein(i) = D
- IF codon(i) ∈ {AAA, AAG} THEN protein(i) = K
- IF codon(i) ∈ {CGT, CGC, CGA, CGG, AGA, AGG} THEN protein(i) = R
- IF codon(i) ∈ {TAA, TAG, TGA} THEN protein(i) = X
4. Results
4.1. Similarity Indexing
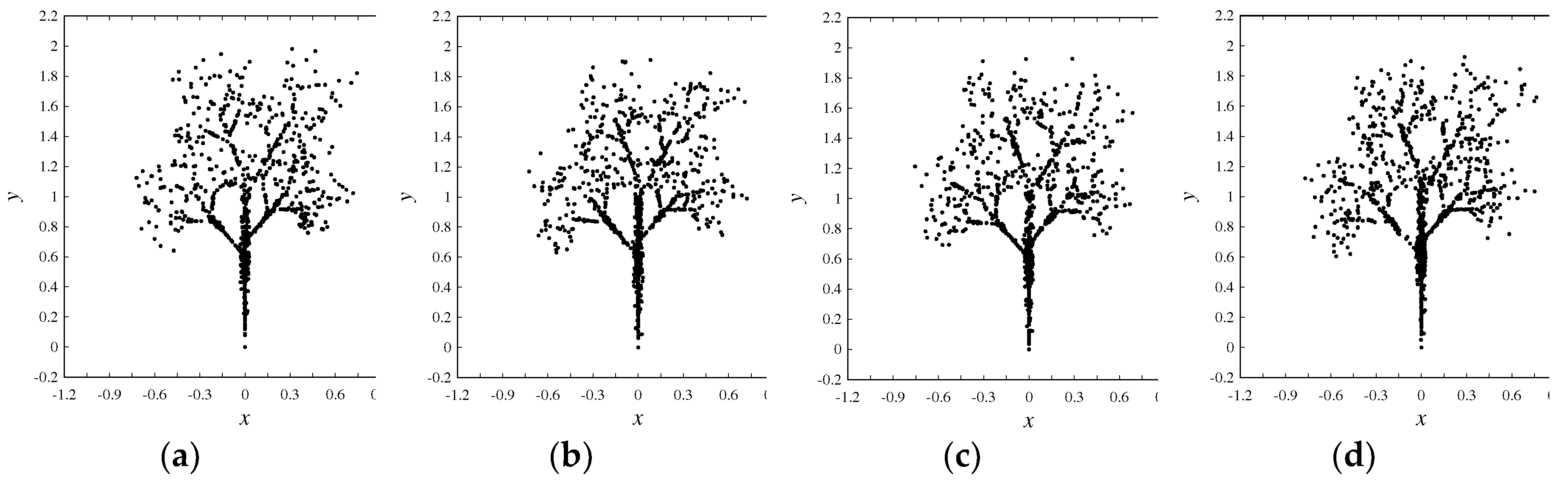
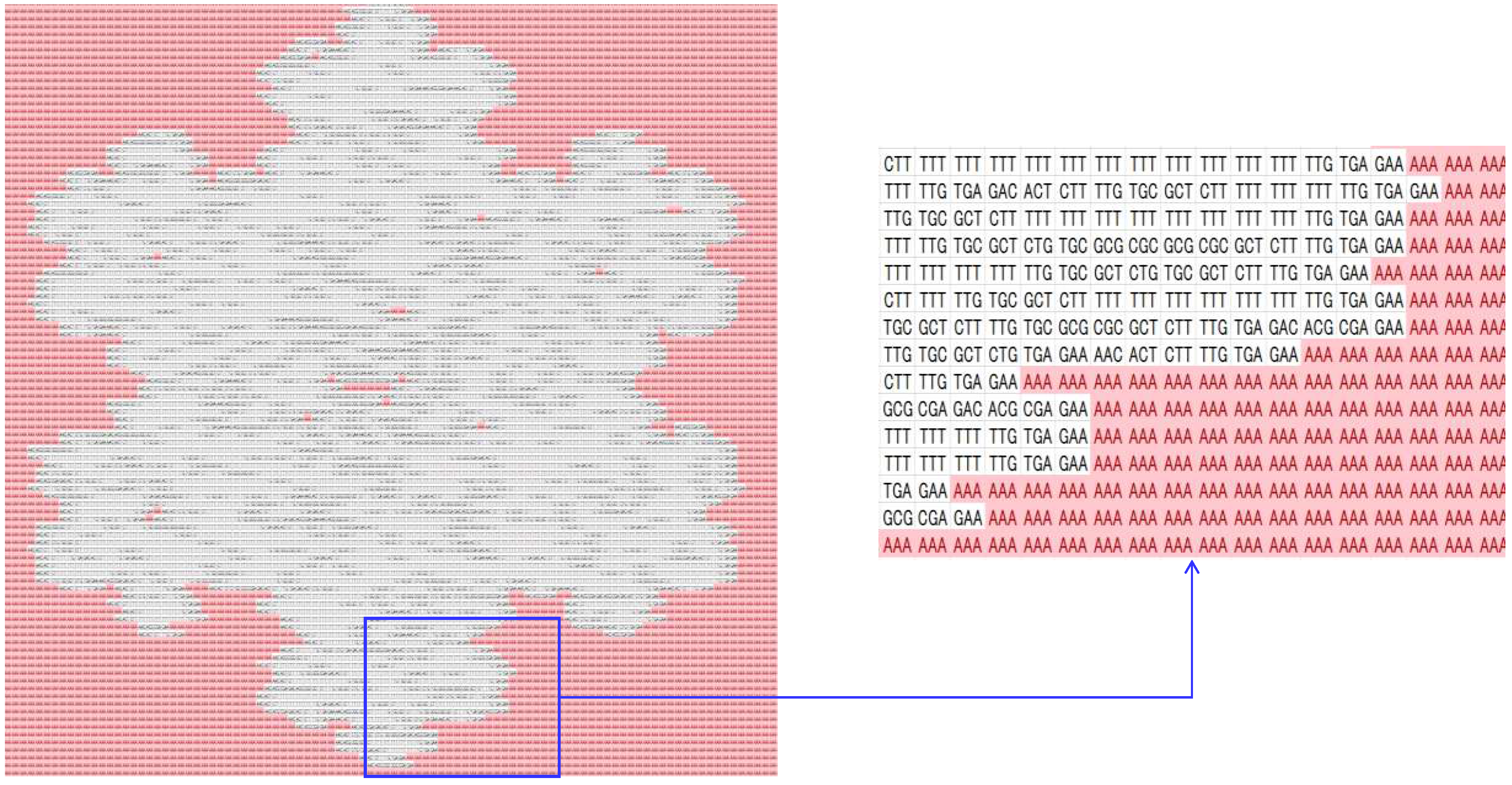
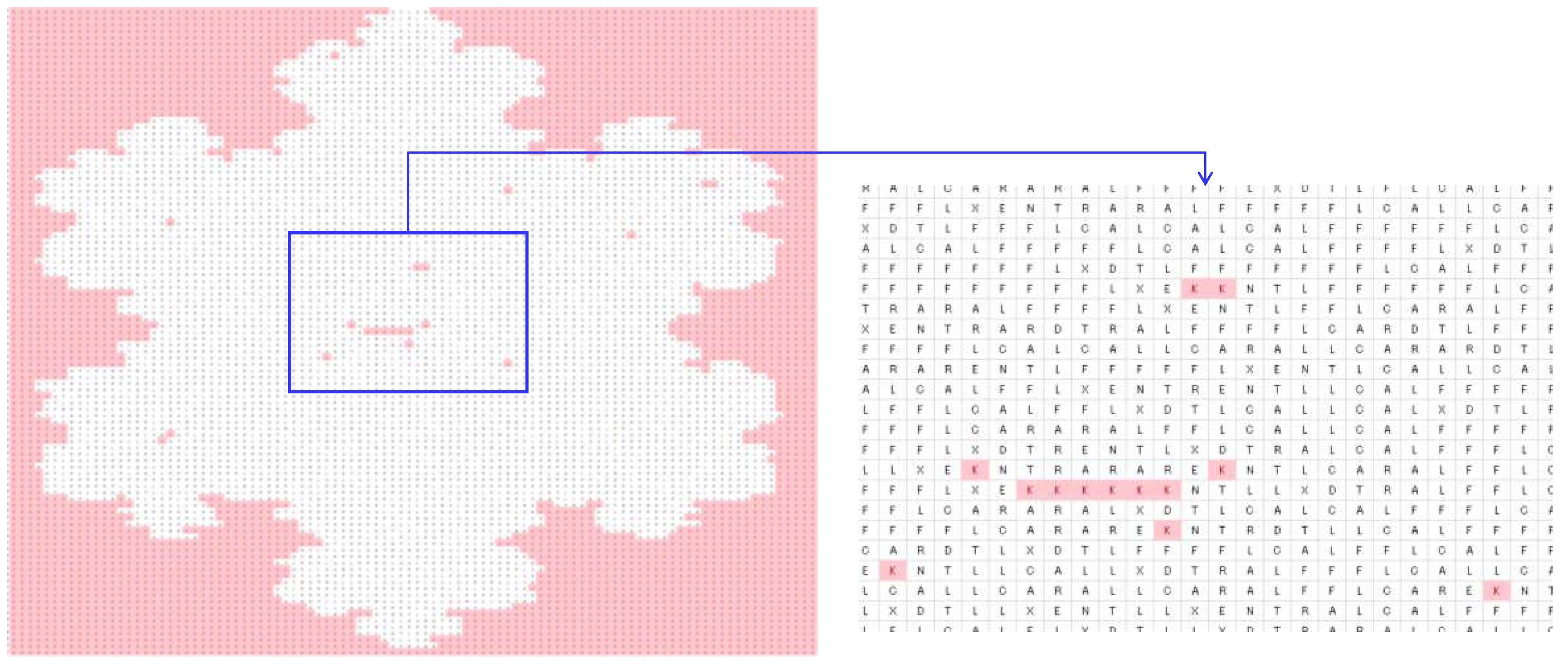
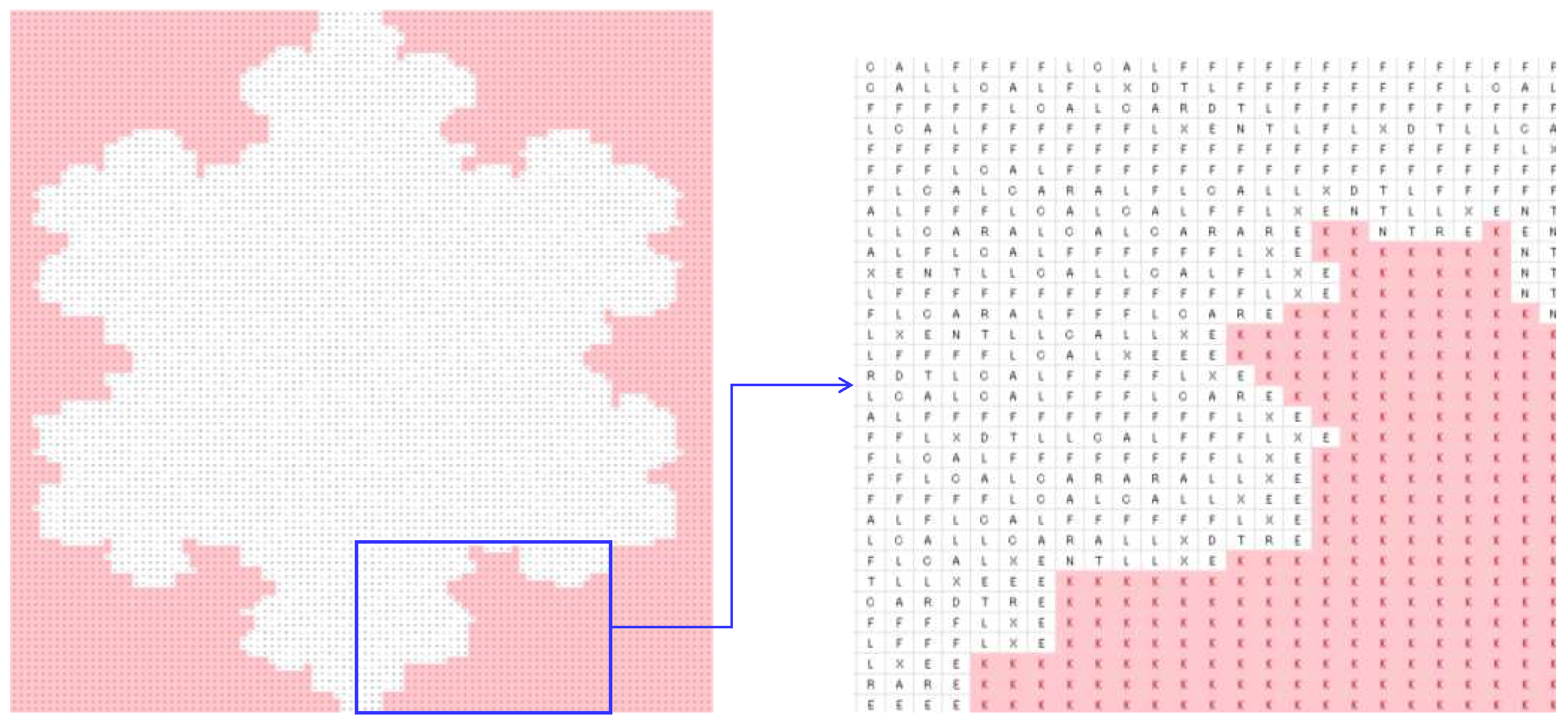
4.2. Image Processing
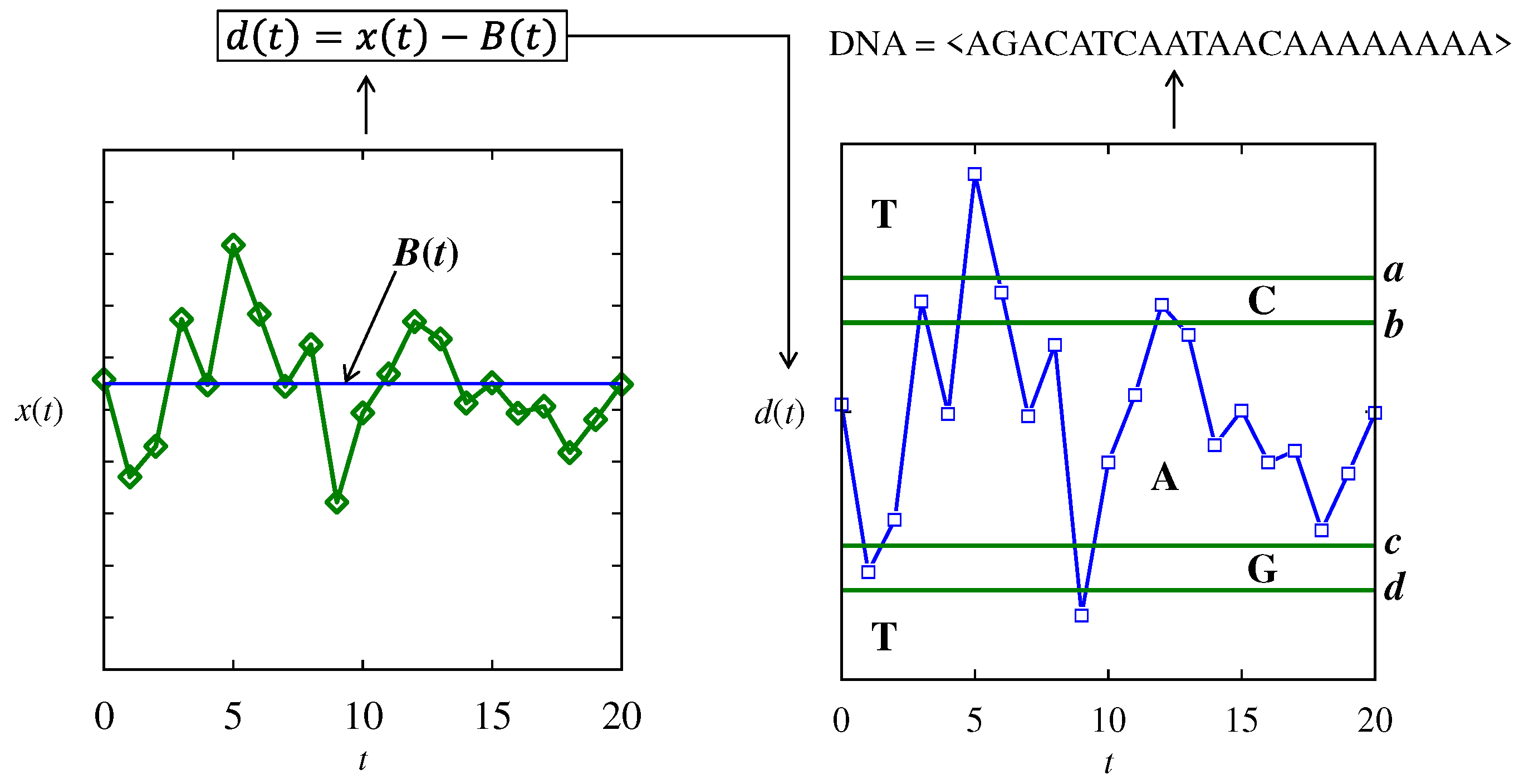
4.3. Pattern Recognition in Time Series Datasets
5. Conclusions
Authors Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kusiak, A. Smart manufacturing, International Journal of Production Research, 2018, 56 (1-2), 508-517. [CrossRef]
- Beckmann, B.; Giani, A.; Carbone, J.; Koudal, P.; Salvo, J.; Barkley, J. Developing the Digital Manufacturing Commons: A National Initiative for US Manufacturing Innovation. Procedia Manufacturing 2016, 5, 182–194. [Google Scholar] [CrossRef]
- Dumitrescu, R.; Riemensperger, F.; Schuh, G. (Eds.). acatech Maturity Index Smart Services: Shaping the Transformation of Businesses to Smart Service Providers (acatech STUDY), Munich 2023. Available Online: https://en.acatech.de/publication/acatech-maturity-index-smart-services/. [CrossRef]
- Sharif Ullah, A. M. M. Modeling and simulation of complex manufacturing phenomena using sensor signals from the perspective of Industry 4.0. Advanced Engineering Informatics 2019, 39, 1–13. [Google Scholar] [CrossRef]
- Ghosh, A. K.; Ullah, A. M. M. S.; Teti, R.; Kubo, A. Developing sensor signal-based digital twins for intelligent machine tools. Journal of Industrial Information Integration 2021, 24, 100242. [Google Scholar] [CrossRef]
- Byrne, G.; Dimitrov, D.; Monostori, L.; Teti, R.; van Houten, F.; Wertheim, R. Biologicalisation: Biological transformation in manufacturing. CIRP Journal of Manufacturing Science and Technology 2018, 21, 1–32. [Google Scholar] [CrossRef]
- Wegener, K.; Damm, O.; Harst, S.; Ihlenfeldt, S.; Monostori, L.; Teti, R.; Wertheim, R.; Byrne, G. Biologicalisation in manufacturing – Current state and future trends. CIRP Annals 2023, 72(2), 781–807. [Google Scholar] [CrossRef]
- Ullah, A.S. What is knowledge in Industry 4.0?. Engineering Reports. 2020; 2, e12217. [CrossRef]
- Ueda, K.; Vaario, J.; Ohkura, K. Modelling of Biological Manufacturing Systems for Dynamic Reconfiguration. CIRP Annals 1997, 46(1), 343–346. [Google Scholar] [CrossRef]
- Ueda, K. A concept for bionic manufacturing systems based on DNA-type information. In Human Aspects in Computer Integrated Manufacturing, Olling, G. J., Kimura, F. Eds.; Elsevier, 1992; pp 853-863. [CrossRef]
- Ueda, K. Intelligent Manufacturing Systems: From Knowledge-base to Emergence-type. Journal of the Japan Society for Precision Engineering 1993, 59(11), 1755–1760, [In Japanese]. [Google Scholar] [CrossRef]
- Denkena, B.; Morke, T. Cyber-Physical and Gentelligent Systems in Manufacturing and Life Cycle: Genetics and Intelligence–Keys to Industry 4.0; Academic Press, 2017.
- Denkena, B.; Dittrich, M.-A.; Stamm, S.; Wichmann, M.; Wilmsmeier, S. Gentelligent processes in biologically inspired manufacturing. CIRP Journal of Manufacturing Science and Technology 2021, 32, 1–15. [Google Scholar] [CrossRef]
- Ullah, A. M. M. S.; Yano, A. Higuchi, M. Protein Synthesis Algorithm and a New Metaphor for Selecting Optimum Tools. JSME International Journal Series C 1997, 40 (3), 540-546. [CrossRef]
- Shuta, Y.; Ullah, A.M.M.S.; Yano, A.; Higuchi, M.; Yamaguchi, T. Grinding Wheel Design Based on the Model of Protein Synthesis. Journal of the Japan Society of Grinding Engineers, 1998, 42 (10) 418-423. [In Japanese].
- Ullah, A. M. M. S. A DNA-based computing method for solving control chart pattern recognition problems. CIRP Journal of Manufacturing Science and Technology 2010, 3(4), 293–303. [Google Scholar] [CrossRef]
- Ullah, A. M. M. S.; D’Addona, D.; Arai, N. DNA based computing for understanding complex shapes. Biosystems 2014, 117, 40–53. [Google Scholar] [CrossRef] [PubMed]
- D’Addona, D. M.; Ullah, A. M. M. S.; Matarazzo, D. Tool-wear prediction and pattern-recognition using artificial neural network and DNA-based computing. Journal of Intelligent Manufacturing 2017, 28(6), 1285–1301. [Google Scholar] [CrossRef]
- Iwadate, K.; Ullah, S. Determining Outer Boundary of a Complex Point-Cloud using DNA Based Computing. Transaction of the Japanese Society for Evolutionary Computation 2020, 11(1), 1–8, [In Japanese]. [Google Scholar] [CrossRef]
- Ghosh, A. K.; Ullah, A. S.; Kubo, A.; Akamatsu, T.; D’Addona, D. M. Machining Phenomenon Twin Construction for Industry 4.0: A Case of Surface Roughness. Journal of Manufacturing and Materials Processing 2020, 4 (1), 11. [CrossRef]
- Kubo, A.; Teti, R.; Ullah, A.S.; Iwadate, K.; Segreto, T. Determining Surface Topography of a Dressed Grinding Wheel Using Bio-Inspired DNA-Based Computing. Materials 2021, 14, 1899. [Google Scholar] [CrossRef] [PubMed]
- Crick F. Central dogma of molecular biology. Nature. 1970 Aug 8;227(5258):561-3. [CrossRef]
- Cobb, M. 60 years ago, Francis Crick changed the logic of biology. PLoS Biol. 2017 Sep 18;15(9):e2003243. [CrossRef]
- Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., Walter, P., 2002, Molecular Biology of the Cell, Fourth Edition. Garland Science, New York.
- Shannon, C. E. A mathematical theory of communication. The Bell System Technical Journal 1948, 27(3), 379–423. [Google Scholar] [CrossRef]
- Barnsley, M. F.; Demko, S. Iterated Function Systems and the Global Construction of Fractals. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 1985, 399(1817), 243–275. [Google Scholar] [CrossRef]
- Sharif Ullah, A. M. M.; Sato, Y.; Kubo, A.; Tamaki, J. Design for Manufacturing of IFS Fractals from the Perspective of Barnsley’s Fern-leaf. Computer-Aided Design and Applications 2015, 12(3), 241–255. [Google Scholar] [CrossRef]

| DNA | mRNA (codon) | tRNA (anti-codon) |
| A | U | A |
| C | G | C |
| G | C | G |
| T | A | U |
| Nucleic acid symbols | ||
| No | Three-letter DNA bases (codons$) | Amino acids (single-letter symbols) |
| 1 | ATT, ATC, ATA | Isoleucine (I) |
| 2 | CTT, CTC, CTA, CTG, TTA, TTG | Leucine (L) |
| 3 | GTT, GTC, GTA, GTG | Valine (V) |
| 4 | TTT, TTC | Phenylalanine (F) |
| 5 | ATG | Methionine (M) |
| 6 | TGT, TGC | Cysteine (C) |
| 7 | GCT, GCC, GCA, GCG | Alanine (A) |
| 8 | GGT, GGC, GGA, GGG | Glycine (G) |
| 9 | CCT, CCC, CCA, CCG | Proline (P) |
| 10 | ACT, ACC, ACA, ACG | Threonine (T) |
| 11 | TCT, TCC, TCA, TCG, AGT, AGC | Serine (S) |
| 12 | TAT, TAC | Tyrosine (Y) |
| 13 | TGG | Tryptophan (W) |
| 14 | CAA, CAG | Glutamine (Q) |
| 15 | AAT, AAC | Asparagine (N) |
| 16 | CAT, CAC | Histidine (H) |
| 17 | GAA, GAG | Glutamic acid (E) |
| 18 | GAT, GAC | Aspartic acid (D) |
| 19 | AAA, AAG | Lysine (K) |
| 20 | CGT, CGC, CGA, CGG, AGA, AGG | Arginine (R) |
| 21 | TAA, TAG, TGA | None (X%) |
| Items | Settings |
| Problem relevant information | A (100 × 100) binary array of the tree |
| DNA-forming rules | 00 = A, 01 = C, 10 = G, 11 = T, continuous reading frame, truncation/addition: truncation |
| Protein-forming rules | As described in Section 3 |
| Rules | |
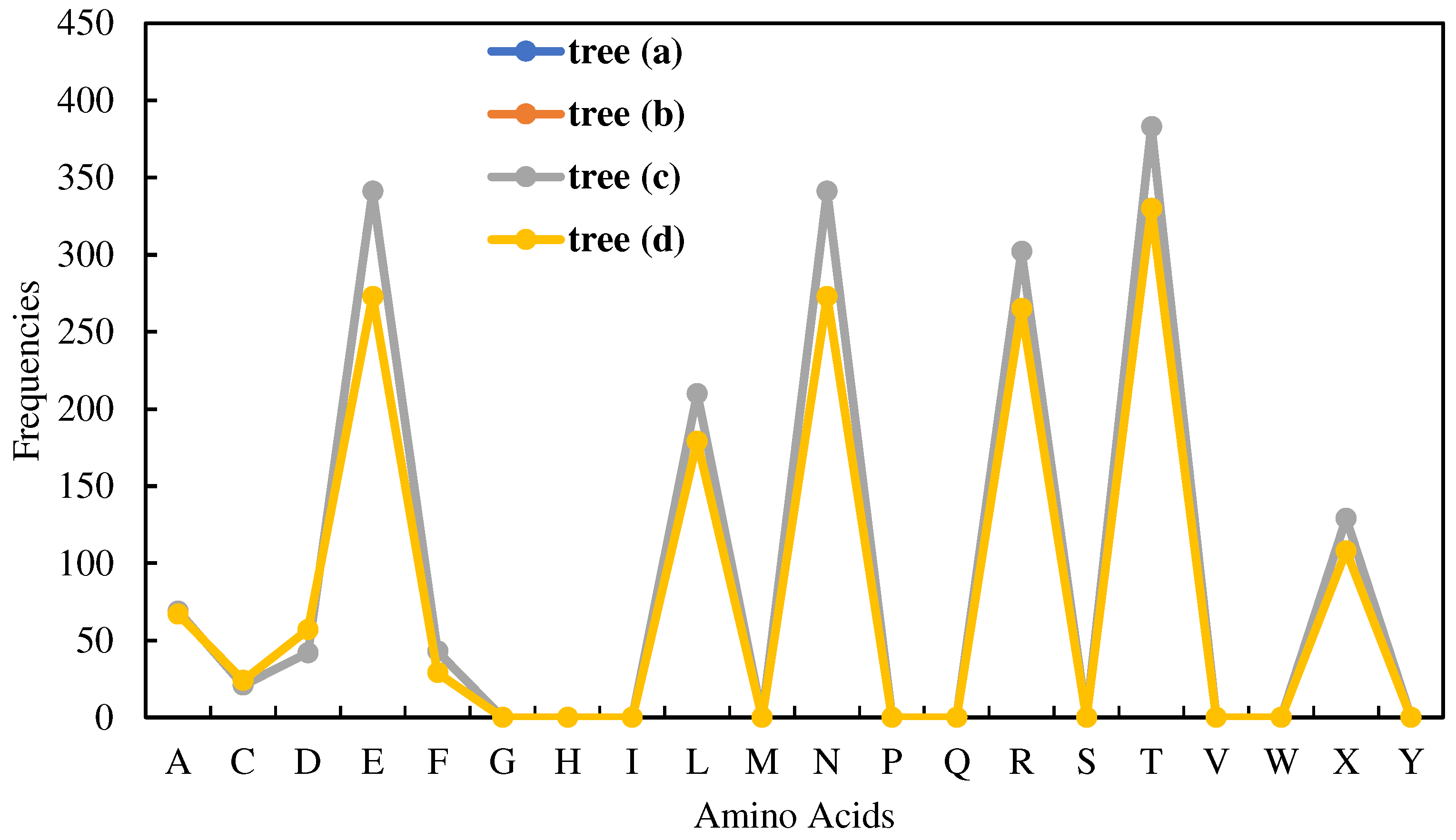
| Zero-frequency amino acids | G, H, I, M, P, Q, S, V, W, and Y |
| Equal-frequency amino acids | E and N (341 for trees Figure 4(a)-(c) and 273 for Figure (d)) |
| Special frequencies | Summation of frequencies of D and N is equal to the frequency of T, i.e., (fr(D) + fr(N) = fr(T) = 383 for trees Figures 4(a)-(c) and 330 for the tree in Figure 4(d)). |
| The least frequent amino acid other than the zero-frequency ones | C |
| List of amino acids in the ascending order of frequencies | fr(A) < fr(X) < fr(L) < fr(R) < fr(E) < fr(N) < fr(T) |
| Items | Settings |
| Baseline and thresholds | B(t) = 100, a = 10, b = 5, c = -5, and d = 10 for all three DNA arrays |
| mRNA-forming rules | Cascading rule among three DNA, DNA1,…,DNA3 mRNA = <…codon = DNA1(i)DNA2(i)DNA3(i)…> |
| Protein-forming rules | As described in Section 3 |
| No | Protein arrays (normal) | Proteins arrays (not normal) | Entropy (normal) [dna] | Entropy (not normal) [dna] | Problem-solving rule holds |
| 1 | KKKPFKKKKKPKKGKKPKFKK | KFKGPFKFKKGFKKGPFGFKK | 0.640 | 0.910 | yes |
| 2 | KGKKKKKKKKKKKKKPKKKGP | FKKGFPGGGKKPKFKFPKGKK | 0.446 | 0.937 | yes |
| 3 | PKGKKGKPPPPGKFKKKKKKK | PGKKKFPFFFFFKFKFFFFFP | 0.782 | 0.782 | yes |
| 4 | PKKPGKPKFFFKKKKPPKKKP | FFGKFKGKKKGFKFGPFKGPK | 0.808 | 0.931 | yes |
| 5 | KGKPKPKPKKKKKGKPKKKGK | KPFGKPKFFPFFKGFGGPPKF | 0.623 | 0.985 | yes |
| 6 | PKGGKFGKKKKKKKKGKKKKK | PPFKKGKGFFFKFFFGGGKKF | 0.610 | 0.931 | yes |
| 7 | KKKGKKKKKKKPKGKKKKKKP | FKKGKFKKPFKGFKFKGFKFF | 0.446 | 0.832 | yes |
| 8 | KKKKPKFPKFKKKKKKKKKKK | GPKFFKKFFPKGPFGKFGPKP | 0.446 | 0.991 | yes |
| 9 | GKKKKFPPKKKPFKPKGPPPK | FPKGKKFFFKKFPGGKGPGKF | 0.842 | 0.969 | yes |
| 10 | PFKKGKKPKKKFKKPKKKKKK | GKFGFKKFKFPFFPFGGFKKK | 0.640 | 0.919 | yes |
| 11 | KKFKKKKPKKKKKPKKGKKKK | FPFFKGFGKFGGFFGKGKPGK | 0.494 | 0.936 | yes |
| 12 | KKKFKKPKKKFFKPKKKKKKK | KFGKFGPKFFGKKPGFKGGGK | 0.512 | 0.936 | yes |
| 13 | KGKKKKKPKKKKKKKKKKKKK | FFKPGFGPGKGKGPKFPPFFF | 0.274 | 0.985 | yes |
| 14 | KKKKKPPKKKKKKGGKGGKPP | GGKFKPFKKFGKKKFKFFFKK | 0.670 | 0.824 | yes |
| 15 | KKKKKPGKKKKKKKKKPKKPK | FKKFGFFKFFFGGGGFGGGPF | 0.428 | 0.832 | yes |
| 16 | PGPKPKKPPKPKKKKKKKKKK | PKGGPPPFFFKFFPFFGPKPK | 0.558 | 0.957 | yes |
| 17 | KGKGKPGKKFKKKKPKKKKKP | FFFFKKPKGKKFKKKPPFFKK | 0.701 | 0.824 | yes |
| 18 | KGKGKKGKKKKFGKPKPKGKK | PKPPFKKKPKFKKFKKFFFPF | 0.727 | 0.773 | yes |
| 19 | GKPKKKKKPFKPPKPKKKKKG | FGPFFKFGFFKKKGKGKGFGP | 0.727 | 0.942 | yes |
| 20 | KPKGKGKKKGKKGKGKPKKGK | GPFGKGKGGFFFFGPGPPGKP | 0.634 | 0.959 | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).