Research on the Sub-synchronous Oscillation Optimization Control Technology of Doubly-Fed Wind Turbine Based on Genetic Algorithm

1. Introduction

By the end of 2022, the cumulative installed photovoltaic capacity and wind power capacity in the world are approximately 1.2TW, and the cumulative installed capacity of wind power is approximately 906GW. According to the Global Wind Energy Report 2024, the total installed capacity of new wind power worldwide will be 117GW by 2023, a year-on-year increase of 50% by 2022. China added 106GW of new wind power capacity in 2022, accounting for 44% of the world’s new capacity, ranking first in the world for 14 consecutive years, from 2009 to 2022[1].

In its latest annual market report on Renewable Energy 2023, the International Energy Agency predicted that the global renewable energy capacity will grow significantly over the next six years, eventually reaching an ambitious target of 7,300 GW. This growing trend reflects not only the growing global focus on clean energy but also the enormous potential for technological advancements and cost reductions. By early 2025, renewables are expected to overtake coal power as the world’s leading source of electricity[2]. This transformation will have a profound impact on the global energy structure, marking an important step in the path of human society to combat climate change and promoting green development.

Sub-synchronous Oscillation (SSO) accidents caused by large-scale doubly fed wind farms after they are integrated into the grid system through series compensation have become a major influencing factors that threaten the safe and stable operation of wind turbines and power grids. In the early 1970s, the first sub-synchronous oscillation accident occurred at the Mohave power plant in the United States, which caused a serious accident in which the shafting of the generator set was broken [3]. In October 2009, owing to a change in the system structure of a doubly fed wind farm in southern Texas, USA, the series compensation degree increased sharply from 50% to 75% during normal operation, triggering an SSO phenomenon of approximately 20 Hz. The voltage and current waveform distortion was severe, resulting in damage to the crowbar circuit and a large number of wind turbines going off the grid [4]. From the end of 2012 to the end of 2013, 58 oscillation events occurred on wind farms in Guyuan, Hebei Province, China. In December 2012, a doubly fed wind farm in Guyuan County, Zhangjiakou City, Hebei Province, China, was connected to a power system with a fixed series compensation, causing a major SSO accident. At the beginning of the accident, the output current of the affected wind turbines quickly became unstable; its maximum amplitude increased abnormally to more than 30%, and the oscillation frequency of the current was stable at approximately 7.9 Hz. Because of this anomaly, the protection mechanism of the wind turbine is triggered, resulting in many wind turbines tripping and leaving the grid, which in turn causes the current in the grid to exhibit an attenuation trend. After taking emergency measures, such as shutting down some wind turbines, the entire system gradually returned to a stable state[5]. In 2016, Tongyu County, Baicheng City, Jilin Province, repeatedly encountered SSO phenomena with frequencies of approximately 5 Hz, but these phenomena disappeared when the related series compensation system was turned off [6].

After much research, scholars have divided SSO into the following three types according to its causes: sub-synchronous resonance (SSR), device-induced sub-synchronous oscillation (SSTI), and sub-synchronous control interaction (SSCI). Ref. [7] proposed that the danger zone of the DFIG induction generator effect is near the right region of the rotation speed, corresponding to the natural resonant frequency of the system. With an increase in the series compensation, the minimum value of the equivalent resistance further decreases, the natural resonant frequency of the system increases, and the danger area of the DFIG induction generator effect moves to the high-wind-speed region and becomes more intense. Ref. [8] illustrates the effect of an induction generator: an increase in the degree of series compensation, decrease in wind speed, and decrease in transmission line resistance can increase the electrical negative damping of the system. When the equivalent electrical negative damping of the system is greater than the sum of the equivalent positive damping of the stator and transmission systems, the output power diverges and oscillates. Ref. [9] pointed out that the sub-synchronous oscillation caused by the device is mainly studied in the field of thermal power units, and there are few studies on wind power because this problem has not been encountered in actual engineering. Ref. [10] summarizes the mechanism of SSCI and the influence of the controller and system parameters on SSCI, and summarizes the research methods and main inhibitory measures of SSCI. Ref. [11] revealed that the interaction between wind turbines and the series compensation system is the key factor that triggers SSO, and further studies have found that the negative damping characteristics of DFIG at sub-synchronous frequencies are the main reason for SSCI. The analysis results show that the oscillation frequency of the wind turbines changes continuously with time, the grid operation mode, and the number of generators. Ref.[12] proposes a control method for attaching a virtual impedance to the rotor-side converter of a doubly fed wind turbine, where the real part of the virtual impedance improves the damping characteristics of the system and thus suppresses the SSO. Ref. [13] proposed a sub-synchronous virtual resistance strategy, which plays the role of increasing the sub-synchronous oscillation damping and suppressing the oscillations by introducing a virtual resistance in the sub-synchronous frequency band in the control of the wind turbine motor side, which can be physically interpreted as a series of virtual resistors in the rotor circuit of the motor. Ref. [14]designs an additional power-controlled sub-synchronous damping controller and provided a strategy for tuning the parameters of this controller to optimize its performance. Ref. [15]proposed a damping controller design method that is more adaptive than the traditional damping controller, which is mainly based on a self-immobilizing controller that can effectively inhibit the SSO phenomenon in a doubly fed wind power system under different operating conditions and improve the stability of the system. Ref.[16] proposed an SSCI damping control strategy based on the multiple-input multiple-output state-space approach and pointed out that the configuration of the SSDC in the rotor-side converter has a better damping performance with a more significant effect than the inclusion of the grid-side converter.

At present, research on the mechanism of SSO has been relatively sufficient, but there is no effective, efficient, and convenient method for the optimization and transformation of doubly fed wind turbines and the inhibition and solution of SSO problems. Based on the research of scholars, this study analyzes the influencing factors of SSO through frequency domain impedance modeling and time domain simulation analysis, proposes an optimal suppression strategy based on the Supplementary Damping Controller (SDC), and optimizes the parameters through a large number of experiments to achieve the best suppression effect to improve the stability and reliability of the overall operation of the system.

The main contributions of this study can be summarized as follow:

• For the first time, the cooperative damping method for the grid-side and rotor-side control systems of the DFIG is proposed to solve the SSO problem of doubly fed wind power via a series-capacitor grid-connected system.
• The parameters, including the gain and phase-shift of the proposed SSO damping method, are optimized using the genetic algorithm to achieve the best performance for all variable operation conditions.
• The proposed optimized SSO damping method is verified with the established model under the RTLAB platform.

The structure of the paper is as follow: The part two establishes the mathematical model and frequency domain impedance model of the doubly fed wind turbine grid-connected system via series complementarity, and deduces the impedance function of the system, to reasonably speculate the influence of the parameters on the SSO; the third part designs the SDC, which is added into the control system of the doubly fed wind turbine, and the fourth part of the article utilizes the genetic algorithm to obtain the optimal parameter settings; the fifth part builds a time-domain simulation model in the RTLAB platform and verifies the suppression effect of SDC, and obtains the control table of parameter settings and SSO amplitude suppression rate through experiments to realize the optimal suppression effect; and finally summary and outlook are obtained.

2. Modeling of the Grid-Connected Systems of Doubly-Fed Wind Turbines Through Series Supplementation

2.1. Mathematical Model of Doubly-Fed Asynchronous Wind Turbines

Doubly fed induction generators (DFIG) are not only the core components of variable-speed constant-frequency wind turbines, but are also a key component in the process of promoting the localization of wind turbines. The design and application of DFIG are of great significance for improving the efficiency and reliability of wind power systems [17].

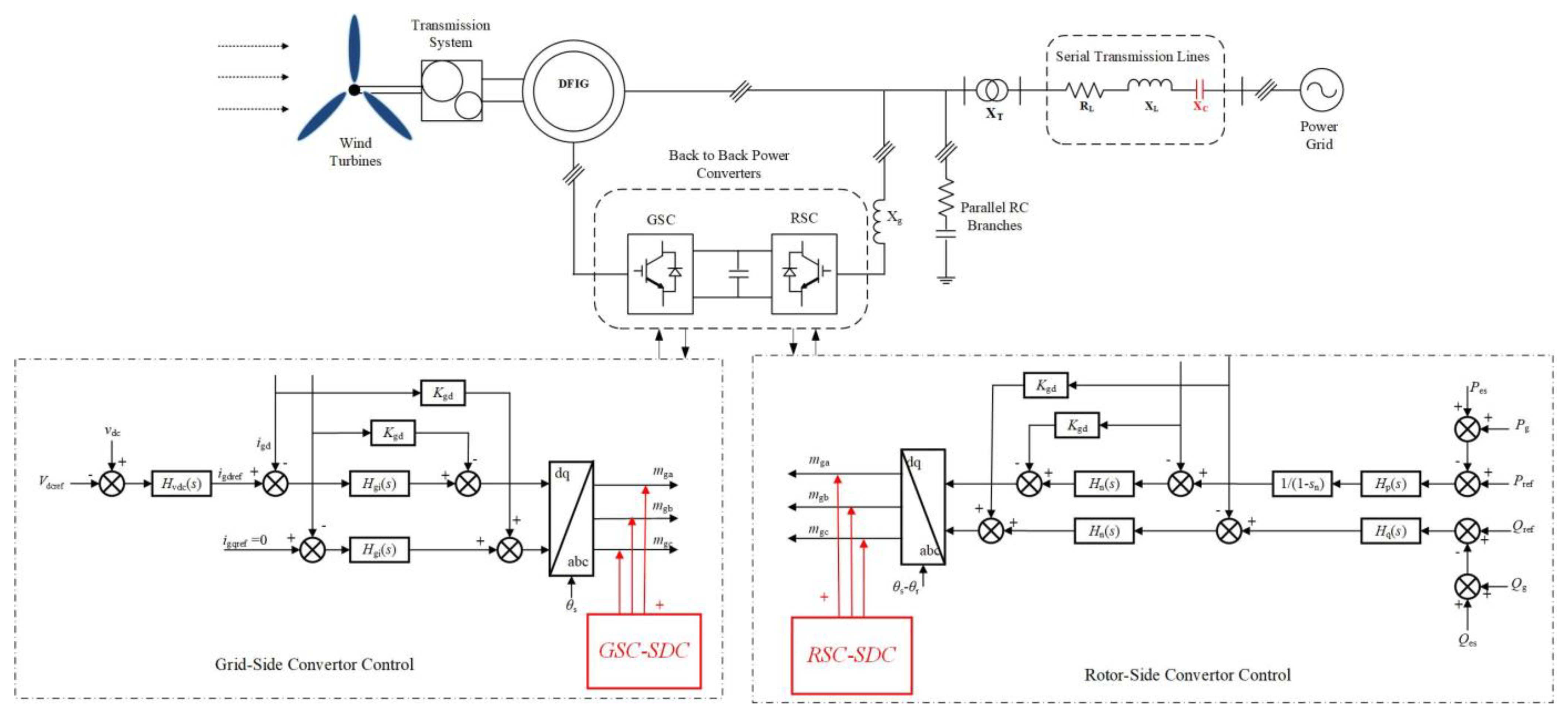
The „doubly-fed” in DFIG’s name comes from its unique structure: the stator is directly connected to the grid, the rotor is connected to the grid through a set of back-to-back converters, and both the stator and rotor are involved in feeding power to the grid. The doubly-fed wind turbine mainly includes a wind turbine, transmission system, doubly fed induction motor, back-to-back power converter, and control system, and its complete topology is shown in Figure 1. These components work together to ensure that the wind turbines can efficiently and consistently convert wind energy into electricity. The back-to-back power converters of the DFIG are composed of rotor-side converters (RSC) and grid-side converters (GSC) to achieve stable energy flow. X_T is the reactance of the step-up transformer, and R_L and X_L are the equivalent resistance and reactance of the transmission line, respectively. where X_C is the reactance of the series compensation capacitor of the transmission line.

This paper proposes an optimized additional damping method for both the rotor and grid-side controllers, which can achieve efficient suppression of sub-synchronous oscillations.

2.2. Grid-Side Converter Control Model

The typical control structure of the GSC is shown in the “Grid-Side Converter Control” part in Figure 1, which consists of two control parts: the outer loop of the DC voltage and the inner loop of the AC current. The balance of the instantaneous active power between the RSC and GSC determines the DC voltage, which is achieved by controlling the active component of the GSC AC current, that is, the d-axis component. Power factor control can be achieved by adjusting the reactive component of the GSC AC current, that is, the q-axis component[18].

The voltage difference between the three modulation voltages of the GSC and that of three-phase AC port acts on the filter inductor to generate a three-phase AC current. The GSC AC loop time-domain model can be expressed as

$$\begin{array}{c}{v}_{gi}=K_m{v}_{dc}{m}_{gl}=v_l+{sL}_f{i}_{gi}\end{array}$$

(1)

Table 1 lists the meaning of each physical quantity.

2.3. Rotor Side Converter Control Model

The typical control structure of the RSC is shown in the “Rotor-Side Converter Control” part of Figure 1. Links related to the slip rate are added to the rotor current control. The total output power of the DFIG unit is controlled by the active and reactive powers of the outer ring. In the inner ring of the alternating current, the d-axis component of the alternating current of the rotor winding can be adjusted to control the active power, and the reactive power can be controlled by adjusting the q-axis component of the alternating current of the rotor winding[19].

The RSC AC port is connected to the rotor winding, and its modulation voltage acts directly on the rotor winding, and the time domain model of the RSC AC loop is

$$\begin{array}{c}{v}_{rl}=K_e{K_{m}v}_{dc}{m}_{rl}\end{array}$$

(2)

Table 1 lists the meaning of each physical quantity.

2.4. Frequency Domain Impedance Model

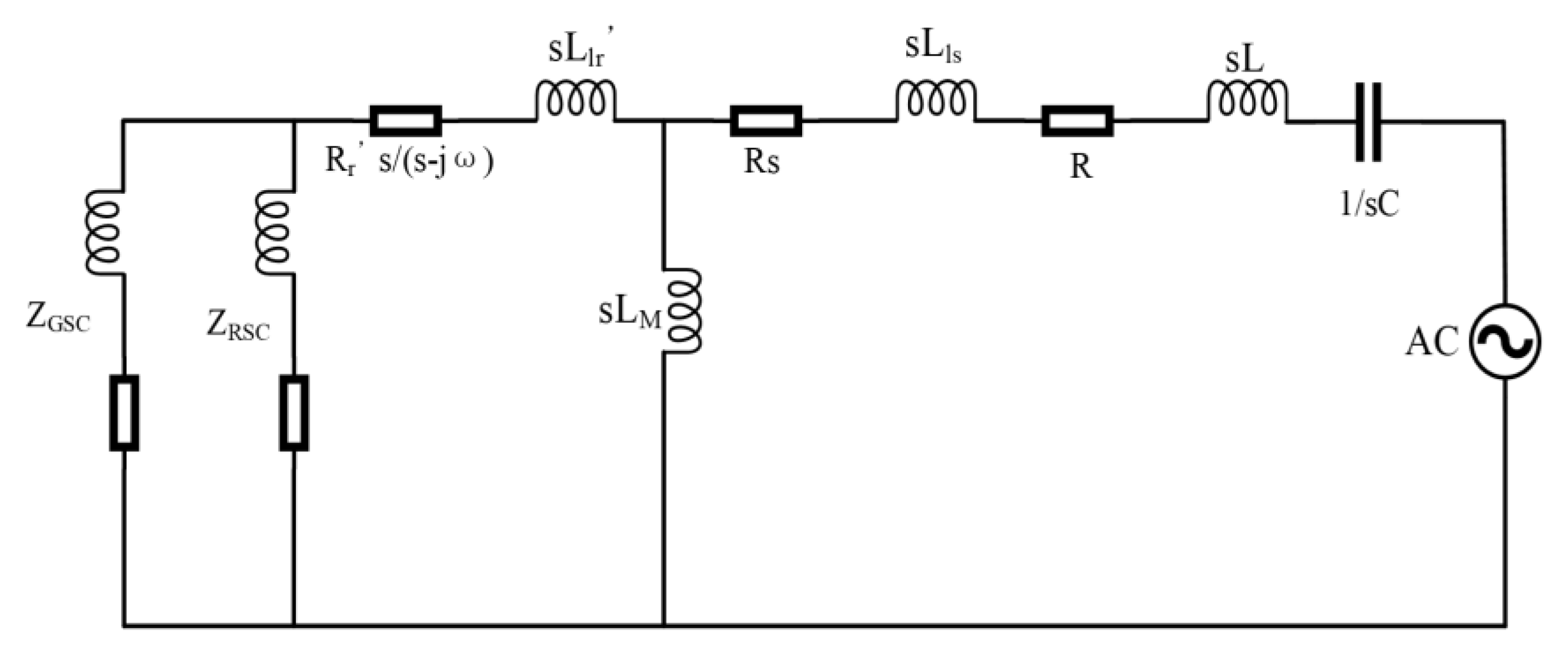
According to Figure 2, the impedance function of the system is constructed as follows:

$$Z={\displaystyle \frac{Z_{GSC}\ast Z_{RSC}}{Z_{GSC}+Z_{RSC}}}+Z_l+Z_s+Z_r$$

(3)

Where Z is the total impedance of the system, Z_l is the line impedance, Z_s is the grid side impedance, Z_r is the rotor side impedance, and Z_GSC and Z_RSC are the impedances of GSC and RSC in the control system, respectively. Each component is given by Equation(4):

$$\begin{array}{c}\left\{\begin{array}{c}{Z}_l=R+sL-{\displaystyle \frac{1}{sC}}\\ Z_s=R_s+s{L}_{ls}\\ Z_r=R_r{\displaystyle \frac{s}{s-j{\omega }_m}}+s{L}_{lr}\\ Z_{GSC}={\displaystyle \frac{s}{s-j{\omega }_m}}\left(K_{pg}+{\displaystyle \frac{K_{ig}}{s-j\omega }}\right)\\ Z_{RSC}={\displaystyle \frac{s}{s-j{\omega }_m}}\left(K_{pr}+{\displaystyle \frac{K_{ir}}{s-j\omega }}\right)\end{array}\right.\end{array}$$

(4)

where R, R_s, and R_l are the line, stator side, and rotor side resistances, respectively. L, L_ls, L_lr and L_M are the line inductance, grid-side inductance, rotor-side inductance, and grid and rotor mutual inductance, respectively; K_pg and K_ig are the proportional and integral coefficients, respectively, in the GSC. K_pr and Kir are the proportional and integral coefficients of RSC, respectively. ω is the nominal angular velocity, take 377 rad/s; ω_m is the angular velocity of the rotor, C is the series compensation capacitance, j is the imaginary number unit, and the resonant frequency can be obtained from s=jω₀. The electrical power from the rotor side is converted to the grid side.

From Equation 3 and Equation 4, it can be seen that the changes in the proportional coefficients of series capacitors C, GSC, and RSC, K_pg and K_pr directly affect the size of the system impedance, while the number of fans affects the system torque, and the wind speed affects the rotor speed, and indirectly changes the size of the system impedance. When the real part of the impedance is negative, the system presents a negative damping state, and there is a risk of SSO.

3. Additional Damping Controller Design

A traditional sub-synchronous damping controller (SDC) is generally a single-input, single-output system that includes gain, phase shifting, and clipping. The controller often uses speed deviation signal Δω, active output P_meas of the fan, and voltage as feedback signals [20].

In this study, an additional damping controller installed in the DFIG control system GSC and RSC is used, and the electrical characteristics of the access point can be equivalent to a controllable impedance. The bus voltage u_abc of the doubly fed wind turbine is selected as the SDC feedback signal, which not only circumvents the problem of communication delays, but also behaves as an open circuit in the industrial frequency range and does not contain components complementary to the sub-synchronous mode in frequency.

3.1. Mechanism of Influence of Cross-Complement Degree on SSO and Simulation Verification

The filter is used to extract the sub-synchronous signal based on the oscillating component of the feedback signal. As the core element in this process, it allows specific sub-synchronous frequency components of the signal to pass through while greatly attenuating other non-essential frequency components [21]. Through this process, the filtering link can ensure that the control system accurately identifies and processes the sub-synchronous oscillation, provides accurate and reliable signal input for the subsequent gain and phase compensation links, optimizes the interaction between the DFIG and the power grid, and improves the stability and performance of the system. In this study, the filtering link in SDC includes two parts: a bandstop filter and a bandpass filter. Its combined transfer function H_F(s) is

$$\begin{array}{l}{H}_F(s)=H_P(s)\cdot H_S(s)\text{}\\ H_P(s)={\displaystyle \frac{\frac{s}{{\omega }_p}}{1+\frac{2\zeta pS}{{\omega }_p}+{\left(\frac{s}{{\omega }_p}\right)}^2}}\text{}\\ H_S(s)={\displaystyle \frac{1+{\left(\frac{s}{{\omega }_S}\right)}^2}{1+\frac{2\zeta sS}{{\omega }_S}+{\left(\frac{s}{{\omega }_S}\right)}^2}}\end{array}$$

(5)

where H_S(s) is the transfer function of the bandstop filter and H_P(s) is the transfer function of the bandpass filter.

3.2. Gain

The effectiveness of additional damping control on the SSO does not depend solely on the choice of the feedback signal of the access point and the design of the filter, but also on the design of a well-designed gain link [18]. By setting the gain coefficient reasonably, it can ensure that the control system can quickly and accurately output the corresponding voltage signal when detecting the sub-synchronous oscillation, so as to effectively suppress the further development of the oscillation and improve the stability and reliability of the entire power system. Within a certain range, the larger the gain K, the better the effect of suppressing the SSO; however, the limiting link needs to be considered, so it should not be set too large.

3.3. Phase Shifting

The PID phase compensation controller has the advantages of a simple structure, easy implementation of the algorithm, and strong robustness. In this study, a simple leading-lag control structure is used to generate a reference signal for the voltage loop, which makes it easy to adjust the gain and phase compensation parameters. The phase compensation formula is as follows:

$${\displaystyle \frac{1-Ts}{1+Ts}}$$

(6)

Where T is the time constant of the phase compensation link.

3.4. Add the Impedance Transfer Function of SDC

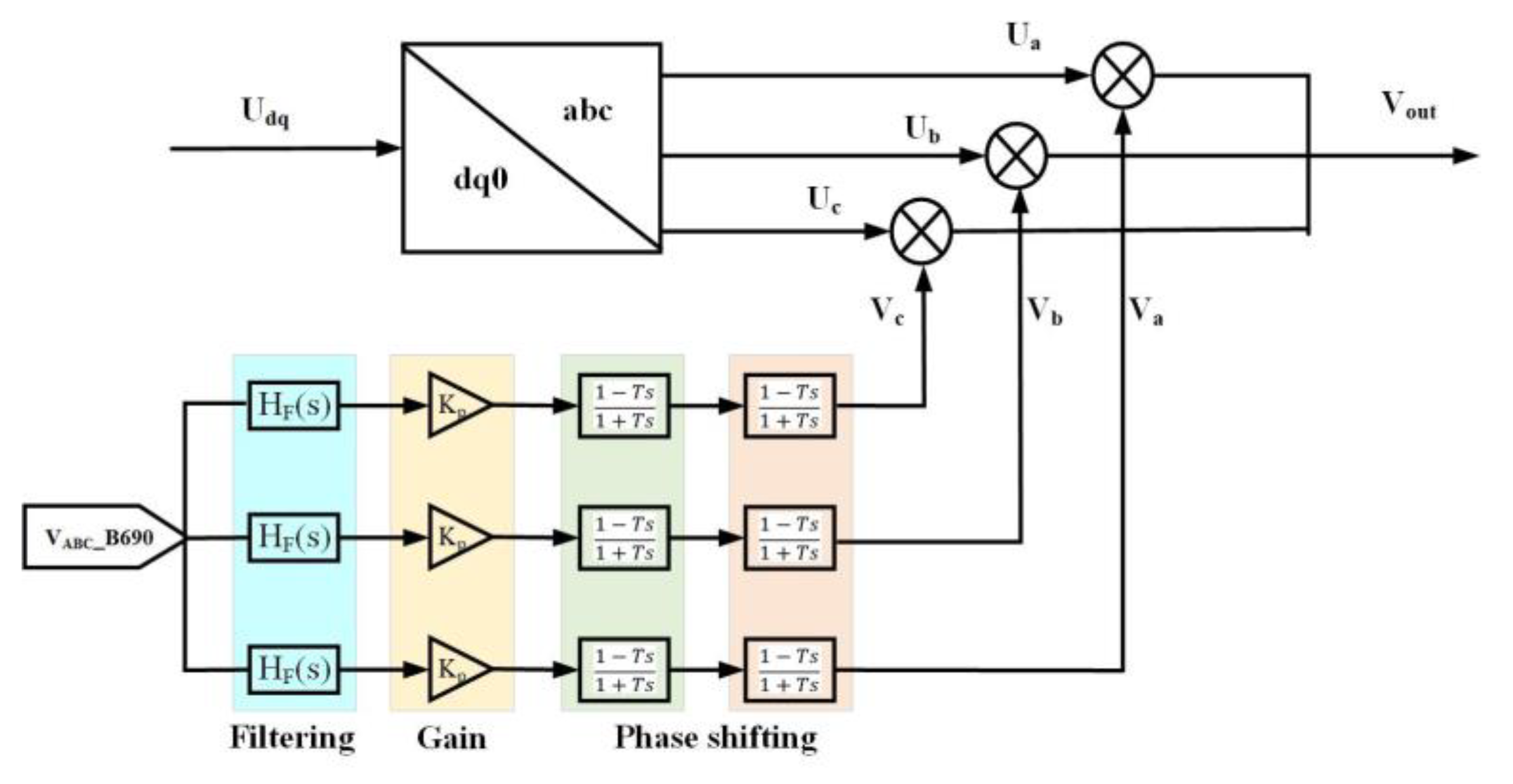
SDC is added to the rotor-side and grid-side control systems, as shown in Figure 3.

Let the impedance transfer function after adding SDC be G(s), then:

$$G(s)={\displaystyle \frac{V_{out}}{U_{abc}}}$$

(7)

Taking phase A as an example, then:

$$\begin{array}{l}{G}_a(s)={\displaystyle \frac{V_{aout}}{U_a}}={\displaystyle \frac{U_a+V_a}{U_a}}=1+{\displaystyle \frac{V_a}{U_a}}\text{}\\ =1+{\displaystyle \frac{V_{a-B690}}{U_a}}[H_F(s)+K_P+{({\displaystyle \frac{1-Ts}{1+Ts}})}^2]\end{array}$$

(8)

where V_out is the output voltage after adding the SDC, and U_abc is the output voltage of the control system without the SDC. V_aout is the output voltage of phase A after adding SDC, U_a is the phase A voltage at the output terminal of the control system without SDC, V_a is the equivalent injection voltage of SDC, V_(a-B690) is the voltage of phase A of the generator, the transfer function of the filter link H_F (s) is given by Equation(5), K_P is the gain.

4. Parameter Optimization

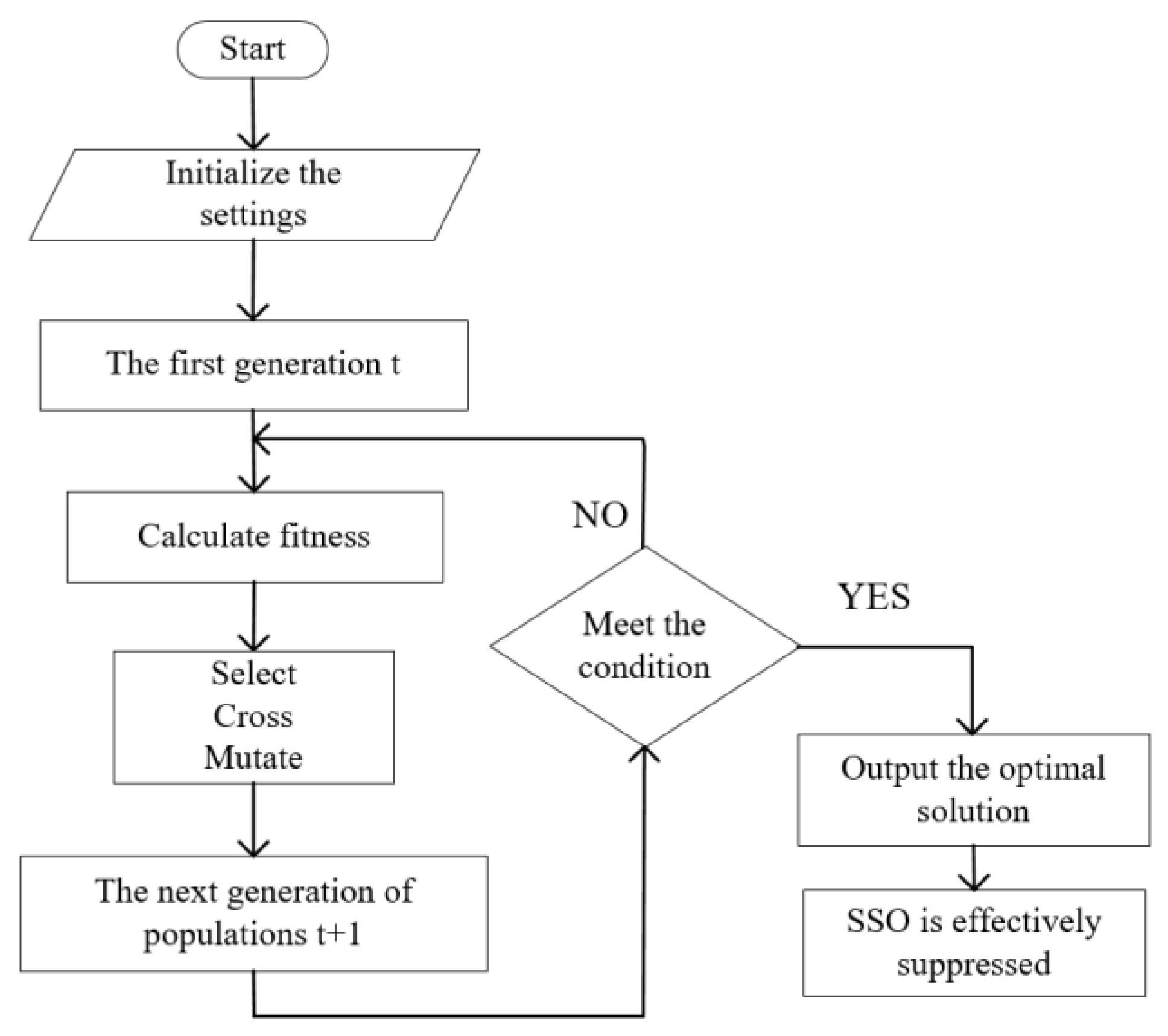
The genetic algorithm(GA) is a method of searching for the optimal solution in a probabilistic manner by simulating the natural evolutionary process[22]. Through mathematical methods and computer simulation operations, the problem-solving process is transformed into a process similar to the selection, crossing, and mutation of chromosome genes in biological evolution, and the optimal solution to the problem is obtained after several iterations and updates.

The parameter optimization method based on genetic algorithm takes the fitness function as the evaluation criterion, uses MATLAB programming to realize the iterative calculation of the parameters of the additional damping controller, and efficiently and quickly calculates the optimal parameters that should be set under different operation conditions to obtain the optimal suppression effect of the sub-synchronous oscillation.

The algorithm implementation steps are as follows:

• Initialize the population: select the dataset within the controllable range of the target parameters, and select the phase shift angle, gain, and serial complement degree as the „genes” that can be operated. The initial parameters are set as follows: the crossing probability P_c is 0.5, the mutation probability P_m is 0.001, and the maximum number of iterations T is five.
• Calculate the fitness values for different parameter combinations.
• The cross-matching order is randomly generated, the cross-matching sequence is determined according to the crossover probability P_c, and the cross-operation is carried out one by one to generate a new group.
• Individuals were randomly selected to determine whether the gene fragment was mutated according to the mutation probability, P_m, and the mutation operation of the single gene fragment was performed to generate a new population.
• Determine whether the suppression requirements are met; otherwise, proceed to Step 2 until the maximum number of iterations is reached, and the optimal solution is retained.

Figure 4. Algorithm implementation step diagram.

Figure 4. Algorithm implementation step diagram.

The optimization objective of this study is to calculate the optimal setting values of the gain K and phase-shift time constant T in the SDC for any operating condition using the GA algorithm, to maximize the SSO amplitude rejection rate.

The index of the amplitude suppression rate is defined to describe the suppression effect of the SSO phenomenon under different SDC parameters. The relevant amplitude suppression rate is expressed as follows:

$$\beta ={\displaystyle \frac{H_a-H_b}{H_b}}$$

(9)

where H_a and H_b represent the amplitude of the oscillation of the output waveform of the a-phase current I_aa before and after the addition of the SDC, respectively.

A mathematical model for parameter optimization is developed as shown in Equation(10):

$$\left\{\begin{array}{l}maxC(\beta ,K,T)\text{}\\ 0\le \beta \le 1\text{}\\ -10\le K_g\le -64\text{}\\ -30\le K_r\le -120\text{}\\ 0.2\le T_g\le 0.99\text{}\\ 0.2\le T_r\le 0.99\end{array}\right.$$

(10)

5. Simulation and Verification of SDC Inhibition Effect

5.1. Simulation and Verification of the Suppression Effect of SDC Add into the Control System

The SDC are installed in the abc axis control structure at the output of the GSC and RSC, and are enabled simultaneously.

In order to verify that the proposed optimization method can effectively suppress SSO under all working conditions, the time domain simulation was carried out with parameters such as gain and phase-shift time constant in SDC as variables. Table 2 lists the parameters of DFIG. The rated power and voltage of the stator were selected as the reference values. I_aa is the phase A current of the bus on the grid side The following working conditions are taken as an example for simulation experiments. The wind speed was set to 6 m/s, the capacity of each DFIG was 1.5 MW, and the number of wind turbines was 100, which were connected to the infinite power grid through the series compensation capacitor of 445F. As shown in Figure 5, the proposed method is tested with RTLAB platform.

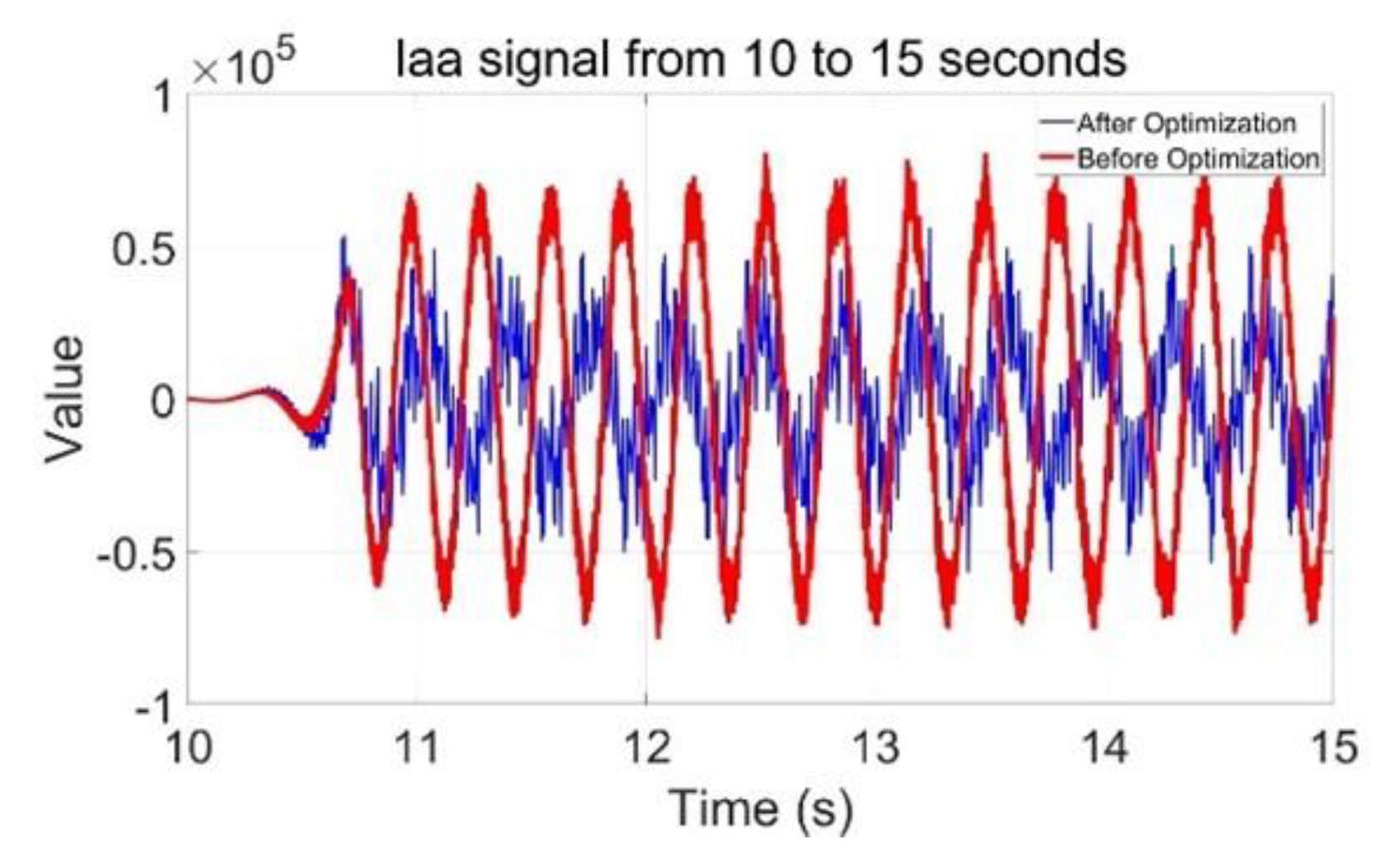
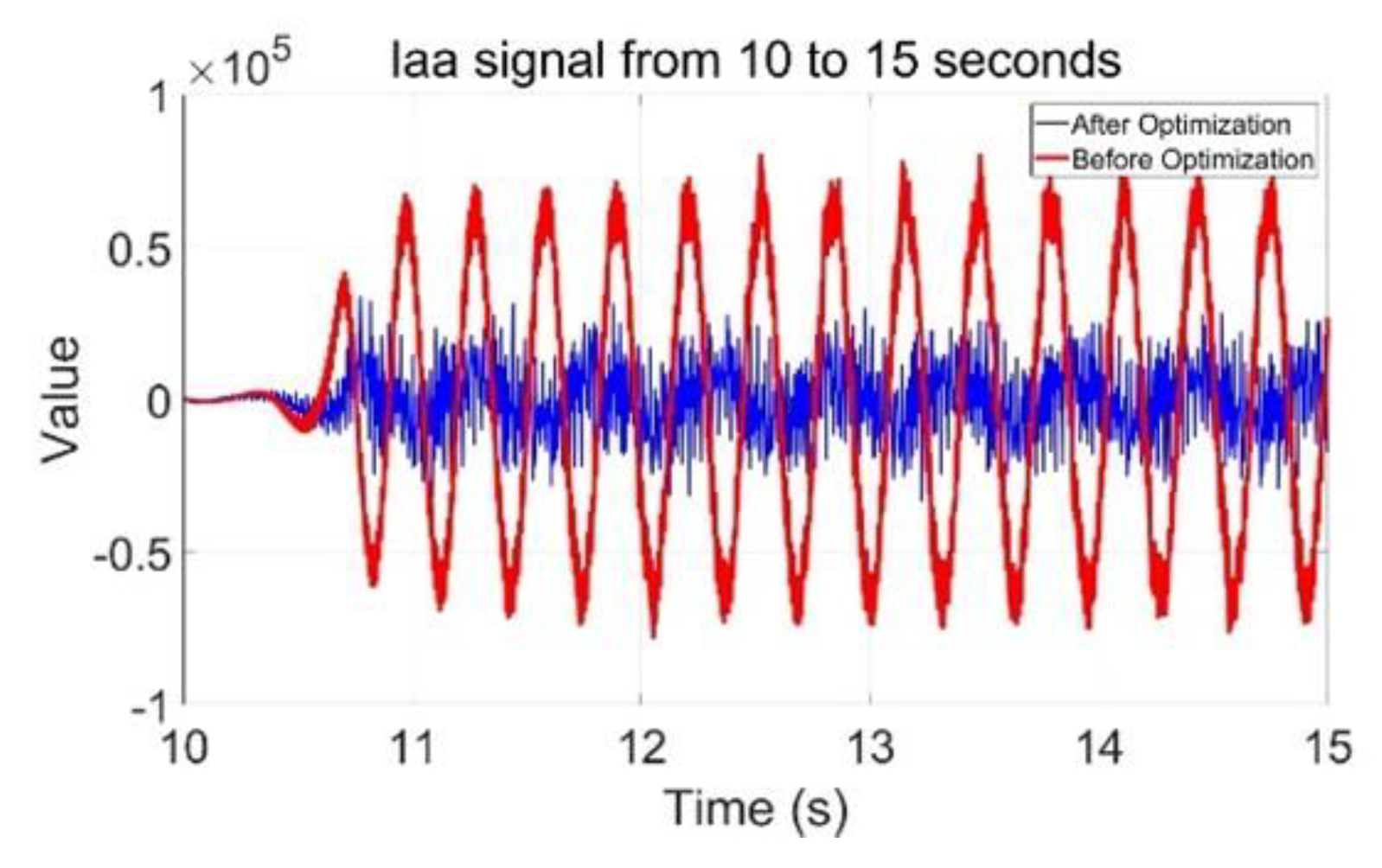
The SDC gains K_g and K_r installed in both GSC and RSC, as well as the phase shift time constants T_g and T_r, are calculated from the GA. The current waveform without SDC under the same operating conditions was compared, and the amplitude suppression rate β was calculated according to Equation(9), which is shown in Table 6. Figure 6 and Figure 7 show the comparison of the current I_aa output waveform of phase A before and after adding SDC; the red line in the figure is the I_aa output waveform before adding the SDC, and the blue line is the I_aa output waveform after SDC is added.

Table 3. GSC+RSC-SDC Parameters And Results.

Number	Kg	Tg	Kr	Tr	β
1	-64	0.99	-110	0.99	84.70%
2	-68	0.99	-120	0.99	85.15%
3	-10	0.2	-30	0.2	37.14%
4	-25	0.5	-60	0.5	65.58%
5	-50	0.8	-70	0.8	78.22%
6	-64	0.95	-100	0.95	85.99%

Table 3. GSC+RSC-SDC Parameters And Results.

Number	Kg	Tg	Kr	Tr	β
1	-64	0.99	-110	0.99	84.70%
2	-68	0.99	-120	0.99	85.15%
3	-10	0.2	-30	0.2	37.14%
4	-25	0.5	-60	0.5	65.58%
5	-50	0.8	-70	0.8	78.22%
6	-64	0.95	-100	0.95	85.99%

After many experiments and analyses of the experimental results, the following conclusions were obtained:

• Comparing Figure 6 and Figure 7, the optimization effect of adding SDC on both the grid side and rotor side is obviously better than adding SDC only to the single-side controller.
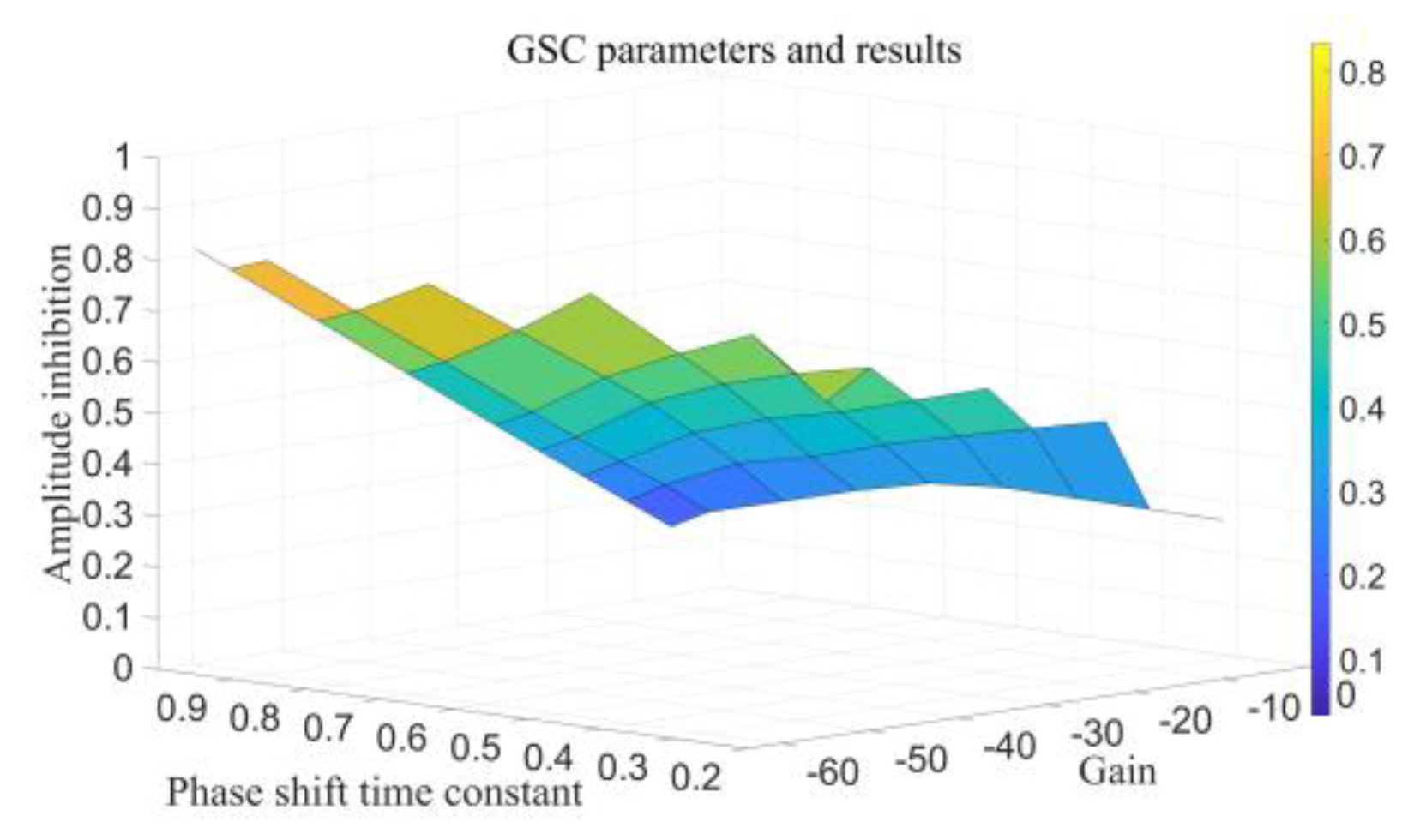
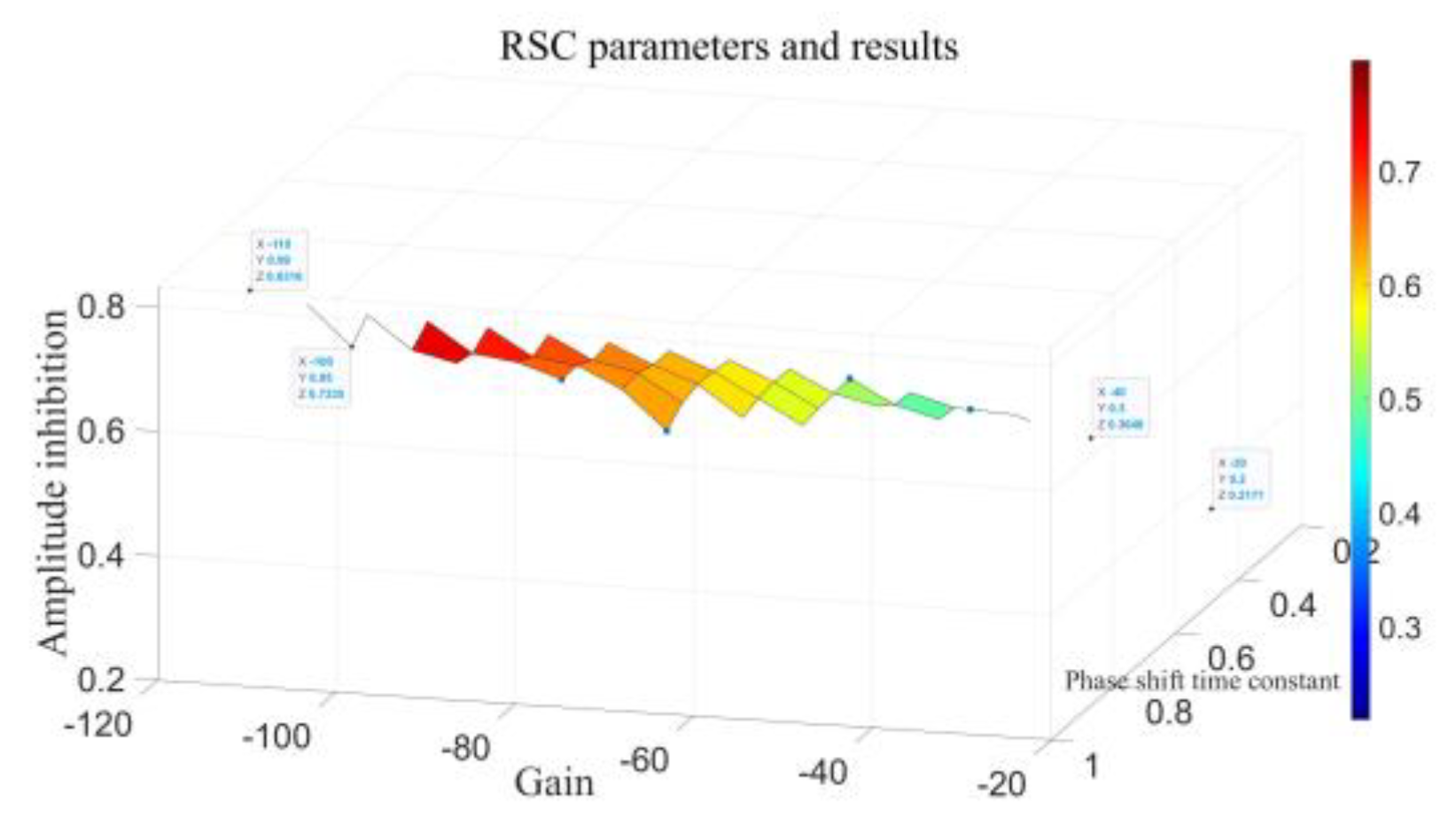
• To achieve optimization, under this working condition, the value range of the SDC gain K_g in the GSC is [-10, -64], the value range of the SDC gain K_r in the RSC is [-30, -120], and the value range of the phase-shift time constant T in the two control systems is [0.2, 0.99].
• The gain K is related to the phase-shift time constant T, and the parameters should be synchronously increased or decreased. When the absolute value of K is extremely large and that of T is extremely small, the system becomes unstable. When the absolute value of K is too small and that of T is too large, the inhibition effect is extremely insignificant, as shown in Figure 8.
• When the absolute values of K and T were increased, the inhibition effect was better. The combined inhibition effect was the best at 85.99% when K_g= -50,T_g= 0.8,K_r= -70 340 and T_r= 0.8, as shown in Figure 7.

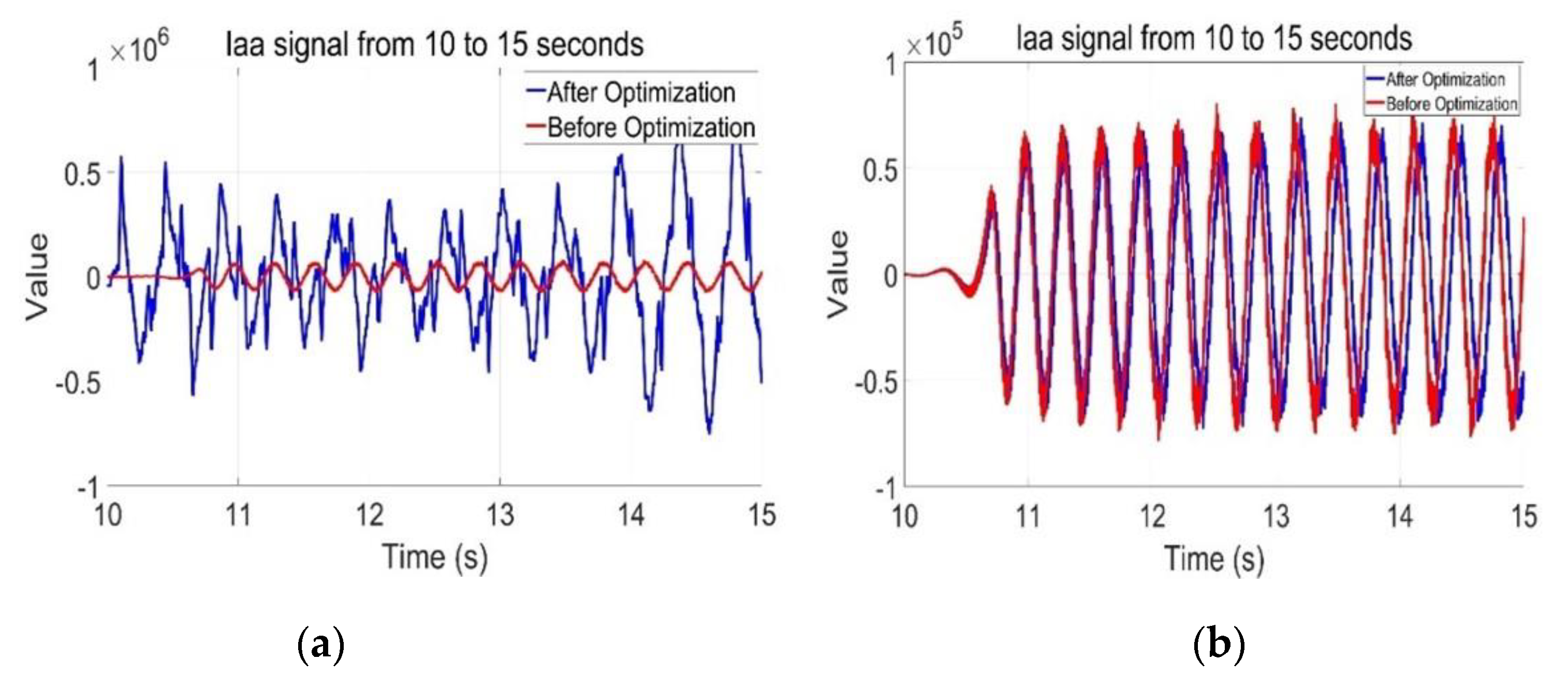
5.2. Simulation and Verification of the Suppression Effect of SDC Injected into the Control System Alone

In this study, SDC is injected into the GSC and RSC control systems, the suppression effect is explored through simulation experiments, and a comparison table between the parameters and the SSO amplitude suppression rate is obtained. The three-dimensional diagram is drawn with code in MATLAB, as shown in Figure 9 and Figure 10 so that the relationship between the parameter setting and the suppression effect can be intuitively seen.

Comparing the inhibition effect with that of the combined injection of SDC, as shown in Table 4, it can be concluded that the joint inhibition effect when SDC is added to both the GSC and RSC systems is better than that of SDC alone in the control system under the same conditions.

6. Conclusions

To solve the SSO problem, this paper proposes an optimized additional damping method for the rotor and grid side control system of the DFIG, which can suppress the SSO successfully under variable operating conditions. First, the impedance model of the DFIG is established. Subsequently, a joint optimization strategy with SDC on both the grid and the rotor sides is proposed. Finally, the model is verified. The verification results show the following:：

• An innovative optimization method based on coordinated control of the rotor and grid sides was proposed. Compared with the method of adding an additional damping controller on only one side of the rotor or grid control system, the combined optimization effect is better, with an amplitude suppression rate reaching 85.99%, which can more effectively solve the SSO problem existing in the doubly-fed wind power grid-connected system via series compensation.
• The genetic algorithm was used to optimize the design of the parameters of the additional damping controller. Through the optimization algorithm, optimized suppression under all working conditions can be achieved with different series compensation degrees, wind speeds, and the number of wind turbines.
• The experimental module was established on the RTLAB platform to simulate the experimental effects under different working conditions and conduct the simulation research. The experimental results are consistent with theoretical derivations, and the experimental conclusions provide a reference value for the setting of various parameter thresholds in engineering practice.

In summary, the SSO suppression method for doubly-fed wind turbines based on the GA proposed in this paper has a certain practical application value in addressing the challenges of power system stability and security, and also features both economy and convenience. It provides a guarantee for the safe and stable operation and efficient power transmission of wind farms and offers new ideas for the integration of artificial intelligence into new power systems.