Advanced Neural Network Strategies for Optimal Power Flow in Contemporary Power Systems: A Comprehensive Review

1. Introduction

The optimal operation of power systems is crucial for ensuring the stability, efficiency, and sustainability of electricity distribution networks. One of the foundational tasks in power system operation is Optimal Power Flow (OPF) calculation. OPF is a mathematical optimization problem that seeks to determine the optimal generation and transmission configuration in a power system, with the aim of minimizing generation costs or losses, while satisfying operational constraints such as voltage limits, generation capacities, and power balance at each node in the system [6]. The accuracy and reliability of OPF calculations directly impact the operation of modern electrical grids, influencing everything from energy prices to grid stability.

The advent of smart grids, the growing integration of renewable energy sources, and the widespread use of power electronics have significantly increased the complexity of these systems. Traditional OPF models primarily addressed deterministic, steady-state conditions under which power generation and load profiles were relatively predictable. However, the increasing penetration of renewable energy sources, such as wind and solar power, has introduced a significant amount of variability and uncertainty into the power grid. The intermittent nature of these resources necessitates more adaptive and dynamic methods of power flow analysis that can respond to the stochastic behavior of generation and demand in real time [7].

Moreover, the rise of new technologies, such as electric vehicles (EVs) and High Voltage Direct Current (HVDC) transmission systems, have introduced additional complexity to OPF problems. EVs, for example, represent a large and highly dynamic load on the system, as their charging patterns are difficult to predict and can vary significantly based on factors such as time of day, weather, and driver behavior [8]. Similarly, HVDC systems, while offering greater efficiency for long-distance power transmission, require new methods of integration and optimization, particularly when coupled with alternating current (AC) grids. The interplay between these various technological elements in modern power systems presents a challenge for traditional methods.

In general, OPF solution methods can be classified into the following types: linear programming, nonlinear programming, Newton’s method, gradient methods, and AI-based methods, as illustrated in Figure 1. In this context, traditional optimization approaches, such as linear programming (LP) and nonlinear programming (NLP), are becoming less effective at capturing the full complexity of modern power systems. These methods often struggle with the high dimensionality and nonlinearity introduced by the complex interactions between traditional AC networks, DC components, and the integration of new technologies. As a result, there is a growing interest in using artificial intelligence (AI), particularly neural networks (NNs), to solve OPF problems more efficiently and effectively [9].

Neural networks have demonstrated significant potential in tackling complex optimization problems across various fields, such as intelligent sensing [10], industrial process optimization [11], and power system operation [12]. Unlike traditional methods, which rely heavily on explicit mathematical formulations of the system’s constraints, neural networks learn directly from historical data, identifying patterns and relationships that may not be immediately apparent through conventional modeling. The ability of neural networks to process large amounts of data and adapt to changing system conditions makes them particularly well-suited for the dynamic nature of modern power grids.

The key advantage of neural networks in OPF calculations lies in their ability to model the nonlinear relationships between system variables, such as the interaction between generation levels, load distribution, and voltage stability. For example, a neural network can learn from data how different operating conditions influence power flow and use this knowledge to predict and optimize future operational states. This capability is especially valuable in dealing with the unpredictability of renewable energy generation and the variability in load demand, allowing for more robust and adaptive optimization strategies.

In addition to their ability to model complex relationships, neural networks also excel in real-time decision-making. Traditional OPF algorithms often require significant computational resources and time to process large datasets, particularly in large-scale systems. In contrast, once trained, neural networks can make predictions and optimizations in real-time, offering a significant improvement in computational efficiency. This makes them particularly suitable for applications in smart grids, where rapid responses are crucial for maintaining grid stability and reliability under fluctuating conditions [11].

However, despite the promise of neural networks in OPF, there are several challenges that must be addressed before they can be widely adopted in operational settings. One of the primary challenges is the quality of data required to train the neural networks. In power systems, data can often be noisy, incomplete, or inconsistent, which can affect the accuracy and reliability of the predictions made by the neural network. Additionally, the complexity of modern power systems means that the training process can be computationally intensive and time-consuming, requiring high-quality datasets that cover a wide range of operating conditions [12].

Another challenge is the interpretability of neural network models. While neural networks are capable of making accurate predictions, the underlying decision-making process is often opaque, making it difficult for operators to understand how the model arrived at a particular solution. This lack of transparency can be problematic in safety-critical applications, where operators need to trust the system's recommendations and be able to verify the validity of its decisions. Efforts are underway to develop techniques for improving the interpretability of neural networks, such as explainable AI (XAI) methods, which aim to make the inner workings of machine learning models more transparent and understandable [13].

Moreover, the increasing reliance on data-driven optimization techniques introduces new challenges in terms of cybersecurity. The integration of AI and neural networks into power system operations makes the grid more vulnerable to information attacks, such as false data injection attacks (FDIAs), which can manipulate the input data used by neural networks and lead to incorrect optimization results. Ensuring the security of neural network-based OPF solutions is therefore an area of active research, with efforts focused on developing robust methods for detecting and mitigating cyber threats in real-time [14].

Despite these challenges, the potential of neural networks to enhance the accuracy, efficiency, and adaptability of OPF calculations in modern power systems is undeniable. This paper provides a comprehensive review of the current state of research on neural network applications in OPF, including the methodologies, case studies, and future development trends. We will discuss how neural networks are being used to address the challenges of renewable energy integration, EV charging optimization, and HVDC system operation, as well as the strategies being developed to overcome the issues of data quality, interpretability, and cybersecurity. Through this review, we aim to provide a roadmap for future research in this exciting and rapidly evolving area.

2. Principles of Application of Neural Networks in Power Systems

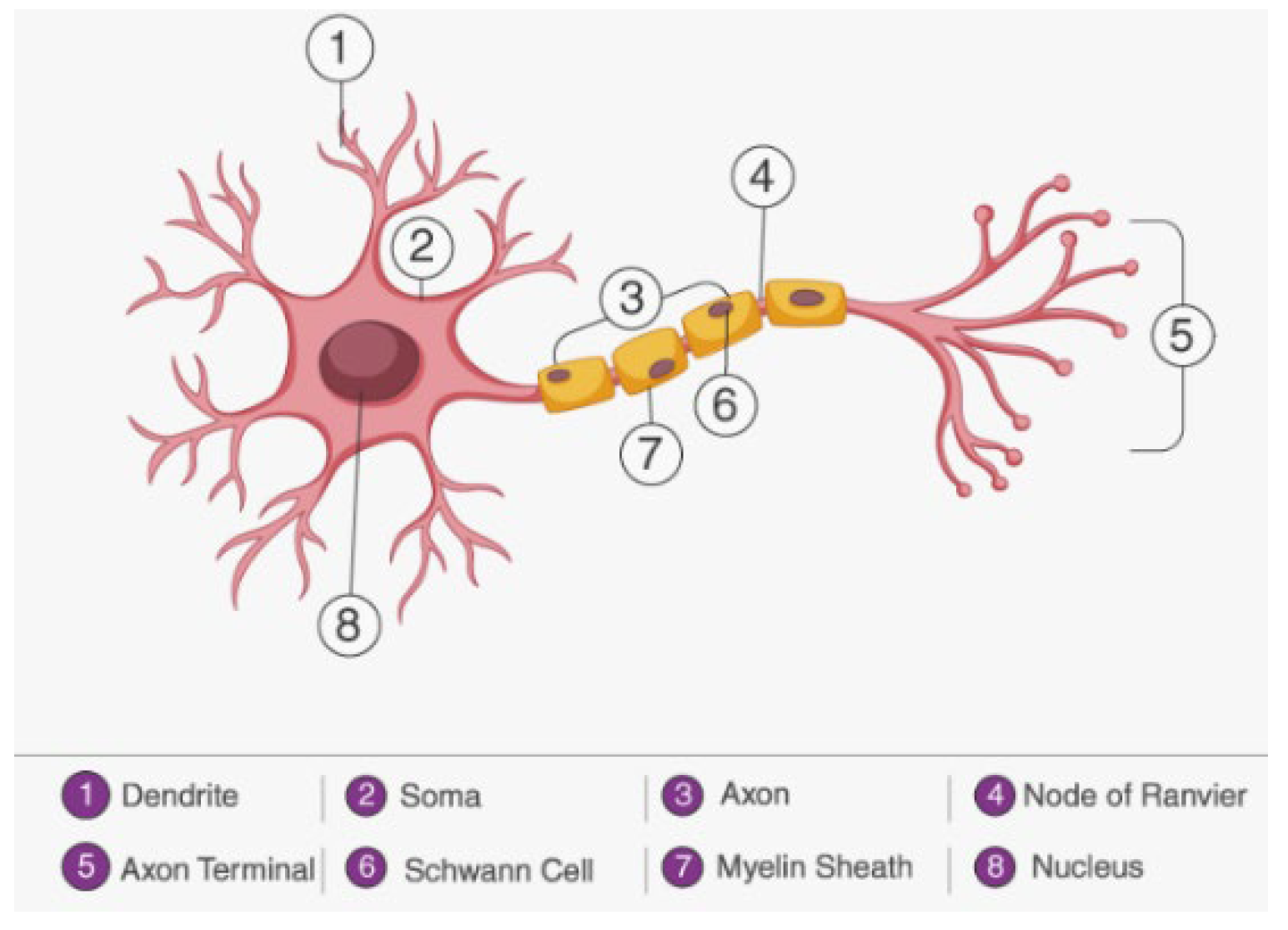
2.1. Fundamentals of Neural Networks

Neural networks are a class of computational models inspired by the structure and function of biological neural systems, as illustrated in Figure 2. A neural network consists of layers of interconnected units, known as neurons, which perform computations on input data. Each neuron receives input signals from either the external environment or from other neurons in the previous layer. These inputs are then processed using weighted sums, followed by an activation function that determines the neuron’s output. This output is passed on to subsequent layers or serves as the network’s final output [15].

The structure of a neural network is typically organized into three main layers: the input layer, where data enters the system; the hidden layers, where the data is processed and transformed through multiple levels of abstraction; and the output layer, which generates the final results of the computation. The learning process of a neural network involves adjusting the weights of the connections between neurons to minimize the difference between the network’s predictions and the actual target values. This adjustment is typically carried out using an optimization algorithm such as backpropagation, which iteratively refines the weights based on the error of the output [15].

Neural networks are particularly powerful in capturing nonlinear relationships between input and output variables, which is one of the reasons they have gained prominence in solving complex problems like those encountered in power systems. Through training, neural networks can learn patterns, making them highly adaptable to dynamic and unpredictable environments such as those in modern electrical grids.

Artificial neural networks consist of an input layer, hidden layers, and an output layer [16]. The input layer receives external data and sends it to the hidden layers for processing. The hidden layers perform feature extraction and high-level abstraction, while the output layer carries out the final classification or prediction. The goal of training neural networks is to minimize the error between the network's output values and the actual label values by adjusting weights and biases, thereby achieving optimal performance for different tasks. There are many methods to train neural networks, with the most common being the backpropagation algorithm [17], as shown in equation (1), where$\partial {\omega }_{\mathrm{ij}}$represents the change in weight from neuron i to neuron j, $\eta$is the learning rate,$\partial \mathrm{L}/\partial {\omega }_{ij}$ denotes the partial derivative of the error function with respect to the weight. In practical applications, by continually adjusting the network structure and parameters, the performance of neural networks can be progressively optimized. Equation (2) represents the perceptron model formula, where$\mathrm{y}$ is the output value,$\omega$is the weight, $x$is the input value,$b$is the bias, and $\sigma$is the active function.

$$\mathsf{\Delta }c{q}_{\mathrm{j}}=-\eta {\displaystyle \frac{\partial \mathrm{L}}{\partial {\omega }_{\mathrm{ij}}}}$$

(1)

$$\mathrm{y}=\sigma (\omega \mathrm{x}+b)$$

(2)

In artificial neural networks, neurons receive input signals from the input layer or the previous layer, compute the weighted sum based on these inputs and weights, and pass this sum through an activation function. The activation function transforms the weighted sum into the output of the neuron, which is then passed on to the next layer or directly output as the final result of the network. The adjustment of neuron weights is aimed at minimizing the error between the network output and the target output. Thus, the role of neurons is to transform input signals into output signals and to facilitate learning and model optimization by adjusting the neuron's weights. Neural networks, through their hierarchical structure and weight adjustments, can learn complex nonlinear relationships and patterns from large amounts of data, enabling efficient processing and predictive capabilities of input data [18].

2.2. Application of Neural Networks in Power Systems

The OPF problem is one of the core issues in the optimization of power system operations, aimed at minimizing the total system loss or cost by adjusting the output of generators and controlling equipment parameters, while meeting various constraints of the power system. The optimal power flow problem can be formalized as the following optimization problem：

$${\min }_{P_G,Q_G,V}\sum _{i=1}^N{C}_i(P_{G,i})$$

(3)

Here,$P_G$,$Q_G$,$V$ are the vectors of active power output and reactive power output from the generators, and the vector of node voltages. he goal of optimal power flow is to minimize the total cost or total loss, which is described by the cost functions of the generators. These cost functions are usually related to the fuel costs and operational costs of the generators.

When solving the objective function, the following constraints must also be satisfied:

$$\left\{\begin{array}{l}{P}_i-P_{G,i}+P_{L,i}=0,\hspace{1em}\forall i\\ Q_i-Q_{G,i}+Q_{L,i}=0,\hspace{1em}\forall i\\ V_{\min }\le V_i\le V_{\max },\hspace{1em}\forall i\end{array}\right.$$

(4)

where $P_i$,$Q_i$ are the total active and reactive power demands at node i, $P_{L,i}$ and$Q_{L,i}$ are the active and reactive power loads at the node。This constraint ensures that the total active and reactive power at each node in the system is balanced, meaning the generator's output power equals the load demand. $V_i$ is the voltage at node i,$V_{\min }$ and $V_{\max }$ are the minimum and maximum voltage limits at the node . This constraint ensures that the voltage at each node in the system operates within a safe range, avoiding the risk of voltage instability or equipment damage.

Considering the constraints above, the resolution of the optimal power flow problem aims to find appropriate outputs for generators, and node voltages, such that the total system loss or cost is minimized while meeting the constraints of power balance and voltage limits. By optimizing the operational strategies of generators, the efficiency and economy of power system operations can be effectively enhanced, reducing energy consumption and environmental impact [19].

The application of neural networks in optimal power flow problems primarily focuses on the following aspects:

1) Flow Calculation Substitution: Traditional optimal power flow calculation methods are usually based on mathematical programming techniques and struggle with handling the complex nonlinearities and large-scale data of power systems [20]. Neural networks, through learning from extensive historical data and pattern recognition, can directly predict node voltage and power distribution, thus substituting traditional mathematical models.

2) Optimization of Scheduling Decisions: In the management of power system operations, neural networks can monitor and predict the state of the grid in real-time, optimizing generator output scheduling and equipment parameter control [21], to maximize the efficiency and economy of the grid. With their strong adaptive learning capability, neural networks can respond quickly and make decisions in dynamically changing grid environments.

3) Flexibility and Real-Time Capability: Compared to traditional mathematical optimization methods, neural networks are better at handling complex nonlinear relationships and interactions between multiple variables in power systems, offering higher flexibility and adaptability [22]. Neural network models can adaptively adjust based on real-time data, providing accurate and real-time power flow calculations that support the needs for real-time operation and intelligent decision-making in power systems [23].

The application of neural networks in optimal power flow problems not only enhances computational efficiency and accuracy but also provides new technical methods and ideas for the management of power system operations [24]. Future research directions include how to further optimize the performance and generalization capabilities of neural network models, and how to combine new technologies such as deep reinforcement learning [24,25], to promote the development of intelligent management and optimization scheduling in power systems.

This section has detailed the basic principles of neural networks, as well as their specific applications and advantages in optimal power flow calculations for power systems. Next, we will further explore specific cases and effects analysis of neural networks in actual grid operations, along with the challenges faced and the prospects for future development.

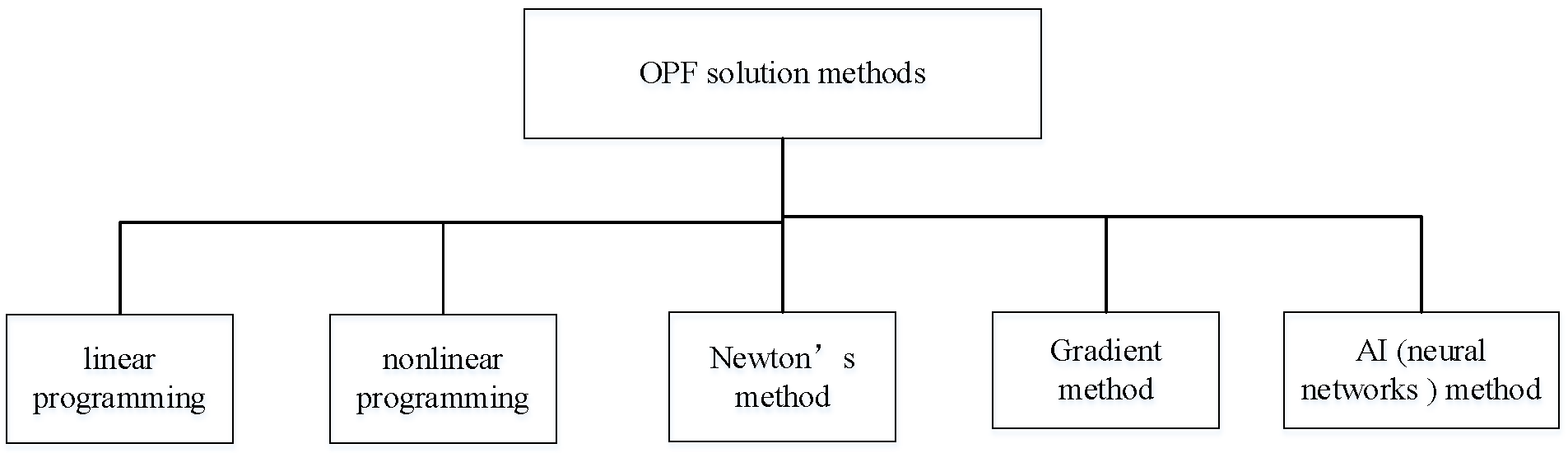
3. Current Status of Neural Network Applications in OPF Calculations

Neural networks, as powerful pattern recognition tools, have broad potential applications in OPF calculations within power systems. The current status of neural network applications in OPF includes choices of network architectures, application of training techniques, and their practical effects in optimizing power systems.

3.1. Role of Neural Networks in OPF Calculations

OPF calculations are critical for the efficient operation of modern power systems. The primary objective of OPF is to determine the optimal power generation and distribution across a grid that minimizes the total cost, such as fuel costs, while adhering to constraints like voltage limits, transmission line capacities, and system stability requirements. The calculation involves adjusting various system parameters, such as generator outputs, load power, and the flow of power across transmission lines and system nodes [26].

Given the complexity of modern power systems, especially with the integration of renewable energy sources, electric vehicles, and flexible demand-side resources, traditional OPF techniques, which rely heavily on mathematical programming, often struggle to handle large-scale, dynamic, and nonlinear systems. Neural networks, however, provide a powerful alternative by learning from historical data and using it to optimize power flow calculations, even in highly complex and dynamic environments.

As a data-driven approach, neural networks can capture the nonlinear dynamics of power systems that are difficult to model with conventional techniques. By processing vast amounts of historical and real-time data, neural networks can uncover hidden patterns and relationships within the system that are critical for efficient power flow management. The input to a neural network model can include real-time measurements from the power system, such as load curves, generator statuses, voltage readings, and line flows [27,28,29]. The model then uses this input to produce an optimized power distribution plan that minimizes operational costs while meeting all system constraints.

3.1.1. Deep Learning-Based OPF Models

One of the key advantages of neural networks in OPF calculations is their ability to leverage deep learning techniques, such as Convolutional Neural Networks (CNNs), Long Short-Term Memory (LSTM) networks, and Transformers, which have proven to be effective in extracting complex patterns and temporal dependencies from data.

• CNNs have been applied in OPF calculations to capture spatial relationships in grid topology and to analyze power flow patterns across different areas of the system. By learning hierarchical representations of system behavior, CNNs can provide more accurate predictions of how changes in one part of the grid affect the rest of the system [30].
• LSTMs are particularly suited for OPF because of their ability to model temporal dependencies and handle sequential data. In power systems, load demands and generation levels vary over time, and LSTMs excel at predicting future power flow conditions based on past data. This ability is critical for real-time scheduling and forecasting in power grids with high penetrations of intermittent renewable energy sources [31].
• Transformers, originally designed for natural language processing, have recently gained attention in power systems for their ability to capture long-range dependencies in data, making them useful for optimizing power flow in large, highly interconnected grids. Transformers can process multiple data streams simultaneously, enhancing the efficiency and robustness of the optimization process [32].

These deep learning models, by learning the intricate relationships within the system’s data, can integrate the system constraints (e.g., voltage limits, generator capacity, transmission line capacity) and optimization objectives (e.g., minimizing generation cost, minimizing losses) into a unified framework. This allows for the generation of optimized power distribution plans that are not only feasible but also highly efficient.

3.1.2. Data-Driven Optimization Methods

Neural networks excel at processing large volumes of historical data, which is critical in capturing the inherent variability and nonlinearity of power systems. Traditional OPF approaches typically rely on predefined models and rules, which can be rigid and fail to adapt quickly to changing grid conditions or unexpected events. In contrast, neural networks use data-driven optimization, which allows them to learn and adapt based on observed system behavior over time.

For example, by analyzing historical data, neural networks can identify recurring patterns in load variations, generation fluctuations, and system faults. They can then use this knowledge to predict future system states and optimize operational decisions accordingly. This adaptive learning allows neural networks to quickly adjust to new conditions without requiring extensive reprogramming or manual tuning, as is often necessary with traditional optimization methods. Moreover, neural networks can effectively handle the uncertainties and dynamic nature of modern power systems, such as the intermittent availability of renewable generation and the fluctuating demand from electric vehicles and other flexible loads [33].

In comparison to traditional optimization techniques, which often rely on deterministic models, data-driven optimization methods are more flexible and scalable, offering better computational efficiency and accuracy, especially in large-scale systems with complex interdependencies.

3.1.3. Real-Time Scheduling and Response Capabilities

One of the most promising applications of neural networks in OPF is their ability to provide real-time scheduling and response capabilities. Power systems today face frequent and sudden changes in demand, supply, and network conditions. For instance, sudden faults, load spikes, or the unexpected variability of renewable energy sources require rapid adjustments to generator outputs and load distribution. Traditional OPF methods often struggle to deliver results in a timely manner, especially when the system is subject to real-time fluctuations.

Neural networks, however, can process real-time data streams from the grid and quickly adjust their predictions and optimization plans. This real-time capability enables neural network-based OPF models to dynamically adjust generator outputs, power flow, and load distribution to respond to changes in demand and supply, thereby enhancing the grid’s stability, reliability, and robustness. By continuously learning from new data, neural networks can anticipate future grid conditions, make real-time adjustments, and even predict potential disruptions before they occur [34]. This capability is especially critical in grids with high penetration of renewable energy, where fluctuations in power generation can cause significant operational challenges.

Moreover, the integration of reinforcement learning techniques with neural networks holds the potential to further improve the real-time optimization of power systems. Reinforcement learning algorithms allow neural networks to learn optimal actions through trial and error, receiving feedback from the environment. This makes them particularly useful for dynamic decision-making in power systems, where system states are constantly changing and the optimization goals may shift based on new constraints or requirements.

3.2. Suitable Network Structures for OPF

Choosing the appropriate neural network architecture is fundamental to achieving effective results in OPF calculations, especially considering the complexity of modern power systems. Different network structures are designed to process specific types of data and achieve particular optimization goals. The selection of the right architecture is crucial, as it directly influences the model's ability to learn from data, make accurate predictions, and adapt to the system's dynamic behavior. The following outlines some of the most widely used neural network architectures in OPF calculations:

3.2.1. Feedforward Neural Networks (FNNs)

FNNs are one of the simplest and most commonly used types of neural networks for various tasks, including OPF calculations. They consist of an input layer, one or more hidden layers, and an output layer. The input layer receives data, which is then passed through the hidden layers where the network processes the data before it reaches the output layer, which generates the prediction or result. FNNs are particularly suitable for processing static data, such as node power and voltage information, that does not involve temporal dependencies or sequential patterns.

In OPF calculations, FNNs can be trained to predict the voltage and power distribution across system nodes based on historical data. By learning from historical operating conditions, such as past load variations and system states, FNNs can estimate how various factors, such as generator output and load allocation, influence the overall system efficiency. Their simplicity and ability to model relationships between inputs and outputs make FNNs an effective tool for OPF when the system is relatively stable and does not experience drastic temporal changes [35].

3.2.2. Recurrent Neural Networks (RNNs)

RNNs are designed specifically to process time-series data, making them highly suitable for applications where temporal dependencies exist. Unlike FNNs, RNNs have a feedback loop, allowing them to retain information about previous time steps, making them capable of handling sequential data. This makes them ideal for modeling systems like power grids, where the system’s state evolves over time, and previous states affect future ones.

In the context of OPF calculations, RNNs can capture the temporal dependencies between nodes in a power system. For instance, they can be used to predict future node voltage changes and load demand fluctuations based on historical data, which is crucial for real-time scheduling decisions. Since power systems are dynamic and subject to continuous changes, RNNs can anticipate the effects of changing loads, generation, and system conditions over time. This ability to model time-dependent relationships allows RNNs to optimize power flow not just at a single point in time but throughout a period of interest, which is especially valuable for long-term optimization in power systems [36].

RNNs, however, can struggle with long-term dependencies due to issues like vanishing gradients, which can limit their ability to capture the full range of temporal effects in complex systems. To address this, Long Short-Term Memory (LSTM) networks, a special type of RNN, have been developed to better retain long-term dependencies in the data and mitigate the vanishing gradient problem, making them even more effective in power system applications [31].

3.2.3. Convolutional Neural Networks

CNNs are primarily known for their use in image processing, where they are used to identify spatial features in images. However, their ability to detect spatial correlations makes them highly suitable for analyzing power system topologies, where the relationship between different components of the system (such as transformers, generators, and loads) can be represented as spatial data.

In OPF calculations, CNNs are applied to spatially structured data, such as the topological relationships between nodes in a power grid. Power systems are essentially networks of interconnected components, and CNNs can help identify patterns in how power is distributed across the grid and how changes in one part of the grid may affect other areas. For example, CNNs can be used to optimize power flow across large grids, where changes at specific nodes influence power flow and voltage stability across multiple regions of the system. By learning hierarchical spatial features from the grid’s topology, CNNs can contribute to more accurate predictions and efficient optimization of power flow calculations. Their ability to recognize local patterns and adjust power flow accordingly enhances both the accuracy and efficiency of OPF solutions [30].

CNNs are particularly effective in handling large-scale and high-dimensional data, where traditional methods may struggle. They can process vast amounts of data in parallel, making them highly efficient for optimizing power systems with many interconnected components. This ability to detect spatial dependencies in power flow makes CNNs especially useful for power systems that span large geographical areas or have complex network structures.

3.2.4. Integrating Multiple Neural Network Architectures

While each of the aforementioned neural network architectures has its strengths, combining them can result in a more powerful and versatile optimization tool. For example, hybrid models that integrate CNNs with RNNs or LSTMs can take advantage of both spatial and temporal features of power systems. This approach could allow for the modeling of both the spatial relationships in the grid and the time-dependent dynamics of power flow, providing a more comprehensive and accurate OPF solution. Transformers, which are capable of capturing long-range dependencies and processing multiple data streams, can further improve these hybrid models by enhancing their efficiency and robustness, especially in large and interconnected power systems [32].

In summary, the choice of neural network architecture is crucial in achieving successful OPF calculations. Feedforward Neural Networks (FNNs) are suitable for static, linear relationships in relatively stable systems. Recurrent Neural Networks (RNNs) excel in time-dependent scenarios, especially when historical data and predictions about future states are required. Convolutional Neural Networks (CNNs), with their ability to model spatial relationships, are beneficial for analyzing grid topology and improving power flow predictions across large-scale grids. Finally, combining different neural network models—such as CNNs, RNNs, and LSTMs—can lead to more sophisticated, data-driven optimization solutions that are highly effective in addressing the complex, nonlinear dynamics of modern power systems.

As neural network technology continues to advance, further optimization of these architectures and the integration of new approaches like deep reinforcement learning will likely improve the adaptability, accuracy, and real-time capabilities of OPF models. The future of OPF will likely see a more seamless integration of multiple neural network techniques, with further development focused on enhancing computational efficiency, improving model interpretability, and addressing challenges related to data quality and system uncertainty [36,37].

4. Challenges and Future Development Trends

While neural networks are widely applied in optimal power flow calculations within power systems, they face multiple challenges such as model structure optimization, security assurance, and stability in complex environments [38]. These challenges demand further strengthening of technical research and application, as well as interdisciplinary integration and innovative thinking, to continuously innovate and develop neural networks in power system optimization. Below, we will explore the specific challenges faced by neural networks in optimal power flow applications and their future development directions.

4.1. Current Challenges

With the increasing complexity of the power market and the growing proportion of renewable energy sources, traditional power system optimization methods have been unable to meet the challenges of modern power demands. Optimal power flow calculation, as a key technology, aims to reduce system operational costs and enhance energy efficiency by optimizing generator output, load distribution, and power transmission efficiency. However, facing challenges such as nonlinearity, dynamic changes, and real-time response in power systems, more flexible and intelligent optimization strategies, such as data-driven models based on neural networks, are required [39]. Therefore, exploring the future development trends of optimal power flow calculations in power systems is crucial for driving the systems towards higher efficiency, reliability, and sustainability.

4.1.1. Data Quality and Availability

In optimal power flow calculations for power systems, data quality and timeliness are key challenges. The power system involves extensive real-time data collection and processing, and the quality and availability of this data directly affect the training and predictive accuracy of neural network models [40].

Difficulty in obtaining and processing real-time data: Operational data of power systems, including generator output, load demands, and line status, require real-time, high-frequency collection and processing [41]. However, many issues such as non-uniform data sources and non-standard data formats make the data acquisition and integration process complex and time-consuming.

Impact of data uncertainty and noise: There are significant amounts of data uncertainty and noise in power systems, such as sudden load changes and data anomalies caused by equipment failures, which can increase the instability and prediction errors of neural network models [42]. Effectively handling and filtering this data noise to improve data quality is crucial for the training and application of neural network models.

4.1.2. Complexity and Computational Efficiency

The complexity of power systems is another significant challenge, especially when dealing with large-scale networks and complex system interactions. Modern power systems typically consist of thousands of nodes and devices, covering extensive geographic areas and complex topological structures. Neural networks need to effectively handle this complexity, understanding the nonlinear relationships and spatiotemporal interactions between nodes to provide accurate power flow calculations and optimization decisions [43]. Although neural networks excel in handling complex issues, their computational complexity and resource demands are high, particularly for real-time applications where there is a need to balance accuracy with computational efficiency. How to achieve rapid power flow calculations and decision optimization in large-scale networks is one of the current important research directions [44].

4.1.3. Impact of Renewable Energy Integration

The integration of renewable energy sources (RES) like wind and solar introduces significant uncertainty in power systems, mainly due to their variable nature [45]. This variability challenges traditional OPF methods, which are designed for more stable and predictable generation sources [46,47]. The increasing penetration of renewable energy requires the development of more adaptable OPF models that can effectively handle such fluctuations without compromising grid stability and efficiency [48,49,50].

Stochastic models have emerged as a solution to address these uncertainties, incorporating the randomness of renewable generation into OPF. For example, reference [51] developed a stochastic OPF model that accounts for intermittent wind generation using HVDC connections. Such models are essential for ensuring grid stability, as they optimize power flow despite the uncertainty inherent in renewable energy sources.

Neural networks, which excel at identifying patterns in large datasets, are particularly suited for predicting and managing fluctuations in renewable generation and load. By learning from historical data, these models can predict future power generation and demand, allowing OPF solutions to be adjusted dynamically. Studies like References [52,53,54] have shown that machine learning algorithms, such as deep reinforcement learning, can be integrated with OPF to enhance real-time decision-making, thus improving the efficiency and reliability of power systems with high renewable energy penetration.

Energy storage systems and demand response play critical roles in mitigating the variability of RES [55]. By storing excess energy during periods of high renewable output and releasing it when demand increases or generation decreases, these technologies help balance the grid [56]. As highlighted by reference [57], flexible load control and storage systems improve the operational efficiency of renewable-powered grids.

Moreover, multi-period forecasting and reinforcement learning have proven effective in managing the volatility of renewable energy generation. These approaches allow for better anticipation of renewable generation patterns, helping grid operators optimize scheduling and power flow.

In summary, integrating renewable energy into OPF calculations presents challenges related to uncertainty and variability, but advances in stochastic optimization, neural networks, and forecasting offer promising solutions. Future research should focus on further developing adaptive models that can dynamically respond to changing renewable generation and improve grid stability.

4.1.4. Challenges of Cyber Attacks

As power systems become increasingly digitized, they face greater vulnerability to cybersecurity threats, such as false data injection attacks (FDIAs) and denial-of-service attacks (DoS), which can manipulate critical data used in OPF calculations [58,59,60]. These cyber threats can lead to incorrect OPF results, causing inefficiencies, system instability, or even catastrophic failures in the grid. Traditional OPF models, which rely on trusted data, are particularly susceptible to such attacks [61,62,63].

To address these challenges, neural networks can be utilized to detect anomalous data patterns that indicate potential cyber intrusions [64,65,66]. By learning the normal behavior of power system parameters (e.g., voltage, power flow), these models can identify discrepancies in real-time data, helping to prevent erroneous OPF calculations.

As renewable energy sources and smart grid technologies become more integrated, the complexity and attack surfaces of power systems increase [67,68,69]. Previous studies pointed out that OPF methods need to account for both the variability of renewables and cybersecurity risks, which requires the development of more robust algorithms. One promising approach is to embed security measures within neural network training and inference processes. Reinforcement learning can help optimize OPF while also safeguarding against attacks by incorporating security constraints during the learning process.

Additionally, robust optimization techniques can be integrated to handle uncertainties introduced by cyber threats [70,71,72]. These methods optimize OPF while considering worst-case scenarios where data integrity may be compromised. Multi-agent systems and distributed learning approaches also offer a way to decentralize data processing, making it harder for cyber attackers to compromise the entire system.

4.1.5. Challenges Posed by Electric Vehicle Integration

The increasing integration of electric vehicles presents unique challenges and opportunities for power system management [73,74]. EVs not only add significant and variable loads to the power grid but also serve as distributed energy resources that can potentially support grid stability through vehicle-to-grid (V2G) technologies. This dual role complicates OPF calculations, requiring the power systems to dynamically adjust to the charging demands of EVs while potentially leveraging their battery storage capabilities to balance supply and demand [75,76,77].

Neural networks can play a vital role in addressing these challenges by predicting EV charging patterns and optimizing charging schedules to minimize impact on the grid. However, this requires robust models that can handle the high variability and potentially large scale of EV integration [78]. The models need to accurately forecast the timing and magnitude of EV charging demand and optimize the grid operations not only to avoid overloading the grid but also to ensure that the energy demands of the EV users are met efficiently [79,80].

Additionally, the integration of EVs increases the grid's exposure to potential cybersecurity risks, as each EV and charging station could potentially be a vector for cyber-attacks [81]. Ensuring the cybersecurity of widely distributed and varied EV charging infrastructure becomes an essential aspect of maintaining overall grid security [82,83].

4.1.6. Challenges Posed by Power Electronics and HVDC Integration

The increasing deployment of power electronics and High Voltage Direct Current (HVDC) transmission systems presents new challenges for power system optimization [84,85]. Power electronics, essential for controlling and converting electrical power in systems that include renewable energy sources and HVDC links, introduce nonlinear dynamics and rapid response capabilities that can complicate OPF calculations [86]. HVDC systems, in particular, alter the traditional power flow dynamics due to their ability to control power flows more flexibly and independently of the alternating current (AC) network configurations [87].

These technologies demand advanced OPF models that can handle the unique characteristics of power electronics, such as rapid switching times and the management of power flow in multi-terminal HVDC systems. The integration of these systems necessitates OPF solutions that can dynamically adjust to the non-conventional power flow patterns and ensure stability and efficiency across interconnected AC and DC networks [88,89].

Additionally, the integration of these advanced technologies increases the need for enhanced operational strategies to manage the increased complexity and ensure reliability. This includes developing models that can predict the interactions between various components and optimize the overall system performance while considering the fast dynamics introduced by power electronics [90].

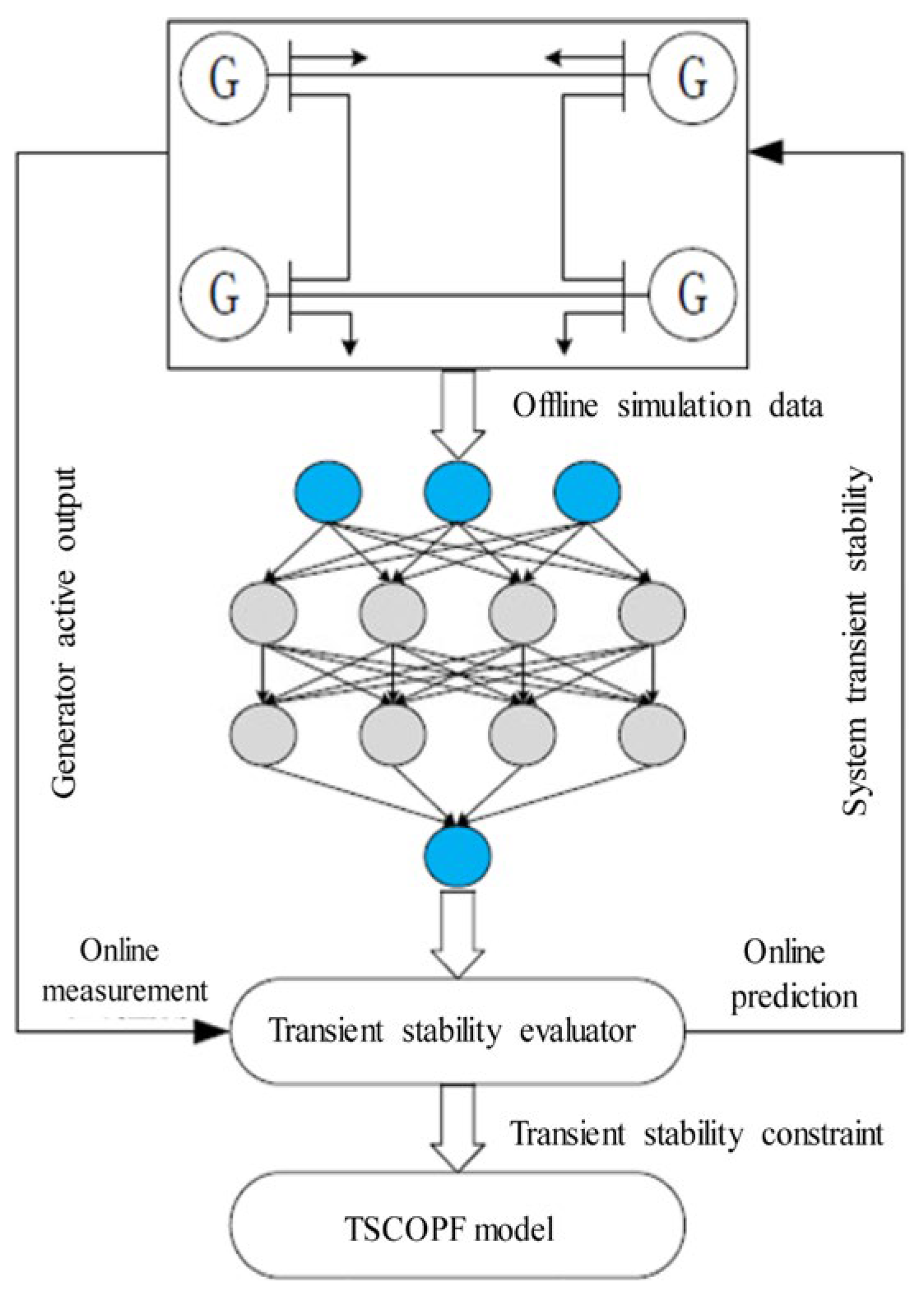
4.1.7. Challenges of Stability-Constrained OPF

Incorporating stability constraints into the OPF problem is essential for maintaining the safe and reliable operation of power systems [91,92,93]. Stability, encompassing aspects like voltage stability [94], frequency stability [95], and transient stability [96], is critical in ensuring that the system remains resilient under normal and fault conditions. However, adding stability constraints complicates the OPF problem due to their nonlinear nature and the need for real-time adjustment. The flowchart of NNs-based transient stability constrained-OPF (TSC-OPF) is shown in Figure 3 [97]. These constraints often require more detailed models and higher computational complexity, as they must consider the dynamic behavior of the system during disturbances or operational changes [97,98].

The first challenge lies in voltage stability, which is affected by the interaction between reactive power and voltage levels. In modern grids, particularly those with high renewable energy penetration, voltage instability can arise from rapid fluctuations in reactive power due to variations in renewable generation, such as wind and solar [99]. Traditional OPF methods are often not well-equipped to handle such nonlinear interactions, and stability constraints must be carefully formulated to prevent voltage instability. Similarly, frequency stability is heavily influenced by the balance between generation and demand. Small disturbances can lead to frequency deviations, requiring fast corrective measures. The transient stability of the system, which involves the grid’s ability to recover from large disturbances, is another significant factor that complicates the inclusion of stability constraints into OPF [100].

Furthermore, the complexity of stability-constrained OPF increases with the size and interconnection of modern power systems [101]. Large-scale grids with numerous interconnected generators, loads, and transmission lines present significant challenges when trying to ensure stability while minimizing operational costs. The nonlinearity of power system equations further exacerbates these challenges, requiring more sophisticated optimization techniques that can handle these complexities without excessive computational delays.

4.2. Future Development Directions

The application prospects of neural networks in power systems are very broad, and future development trends are mainly reflected in the following aspects:

4.2.1. Technological Enhancements for Resilience

Advancements in technology will need to focus on enhancing the resilience of neural networks to both unpredictable nature disasters [102,103,104] and malicious threats posed by cyber-attacks [105]. Developing hybrid models that combine the predictive power of neural networks with the stability and robustness of traditional power flow methods could provide a balanced approach to managing these challenges. Furthermore, incorporating techniques from the fields of cybersecurity and system reliability into the training of neural networks will be pivotal in ensuring that these systems can withstand and adapt to both natural fluctuations and targeted disruptions.

With technological advancements, the advantages of neural networks in data processing are becoming increasingly apparent, especially in handling complex problems in large-scale power systems [103]. Therefore, it is expected that neural networks will play an increasingly important role in power system optimization, providing strong support for the daily operation, maintenance, and long-term planning of power systems.

Combining hybrid neural networks with traditional optimization methods, such as integrating deep learning with mathematical planning methods, can overcome the limitations of each approach, enhancing the predictive capability and robustness of models [104]. Additionally, cross-disciplinary collaboration with fields such as the Internet of Things and big data analysis will also promote innovative applications of neural networks in power systems.

4.2.2. Leveraging Advanced Learning Algorithms

Future research should also explore the use of more sophisticated machine learning algorithms, such as deep reinforcement learning [106,107,108] and federated learning [109,110], which can operate effectively under the dual pressures of renewable integration and cybersecurity threats. These algorithms offer the potential for neural networks to learn optimal strategies in an online manner, continually adapting to new data and conditions while maintaining system security and reliability.

Moreover, future innovation directions for neural networks in optimal power flow calculations in power systems are as follows:

Reinforcement learning [111] and deep reinforcement learning have great potential in optimal power flow calculations. Reinforcement learning, through interaction with the environment, can achieve system optimization based on reward signals, suitable for dynamic and complex decision scenarios in power systems [112]. Combining deep neural networks with reinforcement learning algorithms is expected to play a significant role in real-time optimization and decision-making in power systems.

Developing new power system network architectures [113] and neural network optimization algorithms for specific problems in power systems, such as high-dimensional data processing and dynamic system modeling, is an important research direction for the future. For example, neural networks based on attention mechanisms [114] and adaptive learning rate optimization algorithms can enhance the learning capability and generalization ability of models [115].

Neural networks have achieved certain successes in optimal power flow calculations in power systems [116], but still face many challenges and areas for improvement. By overcoming challenges related to data quality, complexity, and computational efficiency, and combining future technological development trends and innovative directions, neural networks are expected to become a key technology driving the intelligent and efficient development of power systems [117]. As technology progresses and application experience accumulates, the application prospects of neural networks in power system optimization will become even broader and deeper.

4.2.3. Adaptive and Predictive Modeling for EV Integration

Future development trends should focus on creating adaptive and predictive neural network models that can efficiently incorporate EV charging and discharging patterns into OPF calculations [71]. These models could use real-time data from connected vehicles and charging stations to update their predictions and optimizations dynamically. Research into combining deep learning with spatial-temporal modeling could yield neural network architectures particularly suited to managing the complexities introduced by widespread EV adoption [118].

Implementing these advancements will allow for more resilient, efficient, and secure power systems that can fully leverage the benefits of EV integration while mitigating potential risks. This approach ensures that neural networks not only optimize power flow but also adaptively manage the increasingly complex interactions between traditional power systems and new transportation electrification trends.

4.2.4. Advanced Control Strategies for Power Electronics and HVDC Systems

Future development trends in neural network applications for OPF should focus on incorporating models that can specifically address the challenges posed by power electronics and HVDC systems [119]. This includes the development of control strategies that leverage advanced machine learning techniques such as reinforcement learning to optimize power flows in real-time. These strategies must account for the rapid response capabilities and the potential impact of these technologies on system stability [120,121].

Moreover, research should explore the integration of system-wide data analytics to better predict and manage the interactions between HVDC systems and the traditional AC grid [122,123,124]. Neural networks can be instrumental in developing predictive models that help system operators anticipate and mitigate potential issues arising from the complex dynamics of integrated AC-DC systems [125].

By addressing these challenges, neural networks can help harness the full potential of power electronics and HVDC technology, enhancing the operational flexibility and efficiency of modern power systems. This approach ensures that power systems are not only optimized for current technologies but are also prepared to integrate and leverage emerging innovations effectively [126].

4.2.5. Strategies for Improving Stability-Constrained OPF

To address challenges posed by stability constraints, future research should focus on advanced optimization approaches that effectively integrate these constraints. This includes stochastic optimization, which accounts for uncertainties in renewable energy generation and system behavior. Machine learning techniques, especially neural networks, can predict complex, nonlinear system behaviors, including stability-related variables, and optimize power flow to maintain stability under uncertain conditions [127,128].

The integration of real-time data monitoring systems, such as Phasor Measurement Units (PMUs) and Wide Area Measurement Systems (WAMS), can provide continuous feedback on system stability [129,130,131]. This allows neural networks to adjust OPF solutions dynamically, improving the system’s response to disturbances.

Additionally, reinforcement learning techniques can enhance real-time optimization for stability-constrained OPF by enabling systems to learn optimal control actions through trial and error, adjusting power generation, load distribution, and other parameters in response to system changes, such as faults or fluctuations in renewable energy [132]. Furthermore, robust optimization methods should be explored to address contingency scenarios, ensuring OPF solutions are effective and feasible under various potential future conditions, thereby maintaining stability and minimizing costs even in the face of unexpected events or system failures [133,134,135].

5. Conclusions

This article explores the role of neural networks in optimal power flow (OPF) calculations for power systems, highlighting their potential to handle complex optimization problems efficiently. Neural networks excel at capturing the nonlinear characteristics and dynamic changes of power systems, improving computational efficiency and accuracy over traditional methods. Their performance in real-time data processing and predictive analysis further enhances system stability and robustness.

Despite these advantages, challenges remain, including the optimization of neural network models, ensuring their stability in the face of anomalies, and addressing industry standards and policy support. Future research should focus on expanding neural network applications, optimizing models, and integrating new methods like reinforcement learning to promote intelligent and adaptive optimization. Additionally, cross-disciplinary integration with traditional power system modeling and emerging energy management technologies will be crucial for achieving comprehensive system optimization and intelligent management.

Overall, neural networks offer a powerful method for OPF calculations, contributing significantly to improved system efficiency, energy utilization, and the achievement of sustainable development goals. As technology advances, neural networks will play an increasingly integral role in power system optimization.