The Total Entropic Quantity Framework: A Conceptual Foundation for Entropy, Time, and Cosmic Evolution

1. Introduction

The evolution of the universe presents a fundamental tension between the unitary nature of quantum mechanics and the observed growth of entropy on cosmological scales. In a unitary quantum system, the global quantum state evolves without loss of information, preserving quantum purity [1,2]. However, local observations reveal increasing thermodynamic disorder, classical structures, and a distinct arrow of time. Resolving this paradox requires a framework that unifies the global quantum description of the universe with its local thermodynamic behavior. The Total Entropic Quantity (TEQ) framework addresses this challenge by decomposing the total normalized entropy into three components:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right),$$

(1)

where:

• ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ represents observable thermodynamic disorder,
• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ encodes hidden correlations due to quantum entanglement, and
• ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$ quantifies classical correlations in decohered subsystems.

At $t=0$, the universe is posited to exist in a maximally entangled state, characterized by global quantum symmetry, coherence, and purity. In this state, all entropy is latent, with no apparent thermodynamic disorder or classical structures. However, quantum fluctuations, arising inherently from the uncertainty principle, introduce deviations that break the universe’s initial symmetry [3,4]. Gravitational instabilities amplify these fluctuations, leading to the emergence of density contrasts and the formation of localized subsystems. Subsequent interactions within these subsystems drive decoherence [1,5], transforming globally accessible entanglement into locally inaccessible correlations. This process manifests as an increase in apparent entropy and the onset of classical behavior, observed as stable structures such as galaxies and stars.

The TEQ framework offers a natural interpretation of the thermodynamic arrow of time as a consequence of entropy redistribution. While the unitary evolution of the global quantum state preserves total entropy, the growth of apparent entropy reflects the limited access of local observers to the full wavefunction. The emergence of Universal Entropic Time (UET) is rooted in the monotonic increase of ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$, synchronized across cosmic scales through decoherence processes:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(2)

where $\alpha$ is the decoherence-driven growth rate, and $f(\Lambda )$ encodes the influence of the cosmological constant $\Lambda$.

On cosmological scales, the TEQ framework adheres to the cosmological principle, ensuring large-scale homogeneity and isotropy [6]. By integrating entropy dynamics with the Friedmann equations of General Relativity, TEQ connects entropy redistribution to the universe’s geometric evolution:

$$H^2\left(t\right)={\displaystyle \frac{\dot{a}{\left(t\right)}^2}{a{\left(t\right)}^2}}={\displaystyle \frac{8\pi G}{3}}{\rho }_{\mathrm{total}}\left(t\right)-{\displaystyle \frac{k}{a{\left(t\right)}^2}}+{\displaystyle \frac{\Lambda }{3}},$$

(3)

where $H\left(t\right)$ is the Hubble parameter, $a\left(t\right)$ is the scale factor, k is the spatial curvature, and ${\rho }_{\mathrm{total}}\left(t\right)$ is the total energy density.

The TEQ hypothesis unifies the global unitary evolution of the universe with its observed thermodynamic irreversibility, offering a comprehensive framework to understand the emergence of time, causality, and structure. Beyond describing entropy redistribution, TEQ posits a deeper hypothesis: quantum entanglement serves as the foundation for time and space, with decoherence driving the transition from pre-geometric quantum states to classical spacetime.

Furthermore, the TEQ framework aligns with first principles of physics, including unitarity, entropy as coarse-graining, and the role of entanglement in structure formation (Appendix A). While remaining phenomenological in its current form, TEQ establishes a pathway for deriving microscopic descriptions of entropy dynamics, including decoherence rates and entanglement redistribution mechanisms.

This manuscript is organized as follows: Section 2 introduces the TEQ framework, including the entropy decomposition and governing equations. Section 3 explores the implications for the thermodynamic arrow of time, causality, and the observational emergence of apparent entropy. Section 5 summarizes the key findings and outlines directions for future work. Detailed derivations of the entropy equations and their relationship with the Friedmann equations are provided in Appendice A and Appendice B.

2. Theoretical Framework and Entropy Redistribution

The Total Entropic Quantity (TEQ) framework provides a unified theoretical model for entropy redistribution in the universe, capturing the interplay between apparent entropy, quantum coherence, and latent classical disorder. This section formalizes the decomposition of total entropy, outlines the governing equations, and introduces the hierarchical flow of entropy across its components, all while ensuring consistency with the unitary evolution of the universe.

2.1. Decomposition of Total Entropy

The total normalized entropy, ${\tilde{S}}_{\mathrm{total}}\left(t\right)$, is conserved under unitary evolution and decomposes into three components:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right).$$

(4)

Here:

• ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ represents observable thermodynamic disorder, arising from decoherence and local observations [1,5].
• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ encodes entangled latent entropy, reflecting unrealized correlations in the global quantum state [2].
• ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$ quantifies latent classical entropy, corresponding to stable yet unobservable classical correlations in decohered systems.

The TEQ framework ensures that while ${\tilde{S}}_{\mathrm{total}}\left(t\right)$ remains constant, entropy is dynamically redistributed across its components through decoherence, feedback, and realization processes. The detailed derivation of these entropy components, along with their governing equations, can be found in Appendix A.

2.2. Apparent Entropy Dynamics

The growth of apparent entropy, ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$, arises from the conversion of entangled latent entropy into observable thermodynamic disorder. This process is driven by decoherence due to interactions with the environment, which locally transform pure quantum states into mixed states [1]. The evolution of ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ is governed by:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(5)

where $\alpha$ is the growth rate constant determined by decoherence processes, and $f(\Lambda )$ incorporates the cosmological constant $\Lambda$ [7]. Integrating Equation (5) with the initial condition ${\tilde{S}}_{\mathrm{apparent}}\left(0\right)=0$, the solution is:

$${\tilde{S}}_{\mathrm{apparent}}\left(t\right)=1-e^{-\alpha f(\Lambda )t}.$$

(6)

This result reflects the monotonic growth of apparent entropy, consistent with the emergence of the thermodynamic arrow of time observed in decohering subsystems [1,8].

2.3. Entangled Latent Entropy Dynamics

The dynamics of entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, are driven by decoherence processes that transfer correlations into apparent entropy and latent classical entropy. The evolution is expressed as:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{apparent}}\left(t\right),$$

(7)

where $\gamma$ is the decoherence rate, and $\delta$ describes the coupling between entangled latent entropy and apparent entropy. The initial condition at $t=0$ is:

$${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(0\right)=1.$$

(8)

This equation models the loss of accessible global quantum coherence as entanglement becomes locally inaccessible, driving the redistribution of entropy.

2.4. Latent Classical Entropy Dynamics

The latent classical entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$, accounts for classical correlations emerging from decohered subsystems. Its evolution follows from the conservation of total entropy:

$${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)-{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right).$$

(9)

This equation ensures that any reduction in entangled latent entropy or growth in apparent entropy is balanced by changes in the latent classical component.

2.5. Hierarchy of Entropy Redistribution

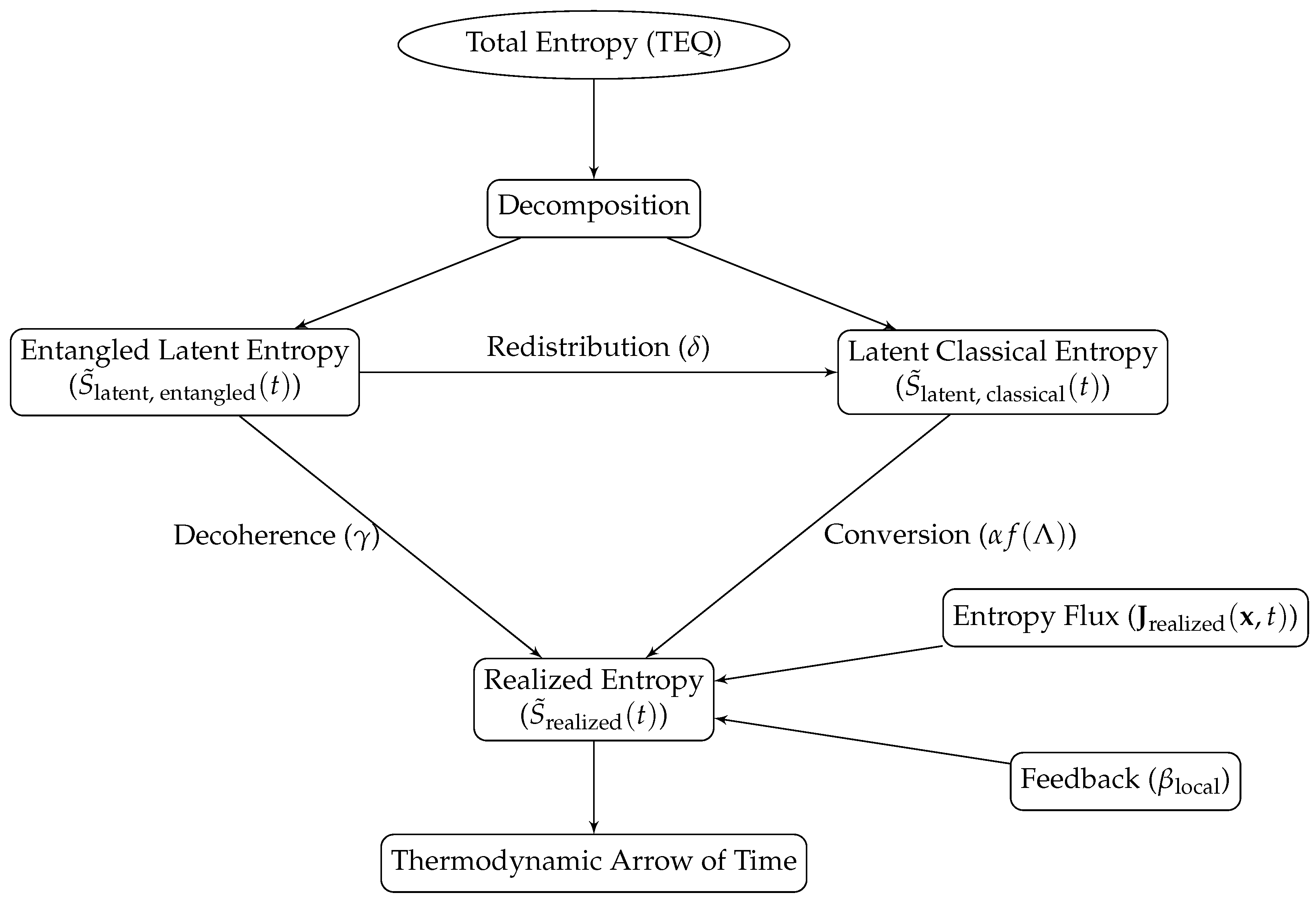
The TEQ framework models a hierarchical flow of entropy, where decoherence and entropy redistribution drive the transition from global entanglement to local observations of thermodynamic disorder:

• Decoherence ($\gamma$) converts entangled latent entropy into apparent and latent classical components.
• Redistribution ($\delta$) facilitates coupling between apparent and entangled latent entropies.
• Realization ($\alpha f(\Lambda )$) drives the monotonic growth of apparent entropy, establishing the thermodynamic arrow of time.

This hierarchical process respects the universe’s unitary evolution, conserving total entropy while decoherence drives the emergence of apparent entropy. As illustrated in Figure 1, entropy redistribution converts latent entanglement into apparent entropy, providing a consistent description across quantum and classical regimes and aligning with the universe’s thermodynamic evolution and large-scale structure.

3. Theoretical Implications of the TEQ Framework

The Total Entropic Quantity (TEQ) framework provides a unified perspective on the emergence of the thermodynamic arrow of time, the synchronization of time, and the origin of causality within a unitary quantum universe. This section explores these implications by reconciling the universe’s global unitary evolution with the local observational growth of entropy.

3.1. The Thermodynamic Arrow of Time

The monotonic growth of apparent entropy, ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$, underpins the thermodynamic arrow of time [8]. While the global quantum state evolves unitarily, preserving purity, local observers perceive an irreversible increase in entropy due to the loss of access to entangled latent correlations. This process arises from decoherence, which converts entangled latent entropy into apparent entropy [1,2,5].

The growth of apparent entropy is governed by:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(10)

where $\alpha$ is a decoherence-driven growth rate constant, and $f(\Lambda )$ is a modulation factor tied to the cosmological constant $\Lambda$ [7]. Integrating Equation (10) yields:

$${\tilde{S}}_{\mathrm{apparent}}\left(t\right)=1-e^{-\alpha f(\Lambda )t},$$

(11)

demonstrating that apparent entropy increases monotonically, consistent with the observed thermodynamic irreversibility of macroscopic processes. This growth is emergent from decoherence and entropy redistribution, aligning quantum unitarity with classical thermodynamics.

Unitary Evolution and Observational Perspective. 

The irreversibility observed in thermodynamic processes does not violate the universe’s unitary evolution. Instead, it arises from the coarse-graining of inaccessible global correlations into local observations. This reconciles the preservation of global quantum purity with the apparent entropy growth observed by subsystems [1,2].

3.2. Synchronization of Time Across the Universe

A key prediction of the TEQ framework is the emergence of a Universal Entropic Time (UET), defined by the monotonic growth of apparent entropy. UET provides a natural and synchronized temporal framework that ties entropy dynamics to cosmic evolution.

Mechanisms of Synchronization. 

The synchronization of time across the universe arises from:

• Global Entropy Growth: The universal increase of ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ provides a global “clock,” monotonically progressing due to decoherence processes [8].
• Cosmic Expansion: The Friedmann equations describe the expansion of the universe, linking the apparent entropy dynamics to the Hubble parameter $H\left(t\right)$:

  $$H^2\left(t\right)={\displaystyle \frac{8\pi G}{3}}{\rho }_{\mathrm{total}}\left(t\right)-{\displaystyle \frac{k}{a{\left(t\right)}^2}}+{\displaystyle \frac{\Lambda }{3}},$$

  (12)

  where ${\rho }_{\mathrm{total}}\left(t\right)$ includes contributions from realized and latent entropy components.
• Entropy Gradients: Local variations in apparent entropy, expressed as $\nabla {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)$, introduce regional deviations in time progression without disrupting the global synchronization of UET [7].

Thus, UET aligns the thermodynamic arrow of time with cosmic expansion, providing a globally consistent temporal framework rooted in entropy dynamics.

3.3. Causality as an Entropic Phenomenon

The TEQ framework naturally embeds causality within the redistribution of entropy. The monotonic flow of entropy from entangled latent to apparent and classical components establishes a universal causal direction consistent with thermodynamic irreversibility [2,8].

Global Causal Order. 

The irreversible growth of apparent entropy defines a causal sequence of events, driven by the governing equation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}>0\forall t\ge 0.$$

(13)

This irreversibility provides a natural origin for the global causal order observed in macroscopic processes.

Local Variations in Causality. 

Spatial variations in entropy, such as $\nabla {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)$, allow for regional deviations in causal flow. The local entropy production rate satisfies:

$$\nabla ·{\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)+{\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)\right),$$

(14)

where ${\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)$ is the entropy flux, and ${\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)$ represents local entropy production.

3.4. Quantum Interpretations and Entropic Dynamics

The Total Entropic Quantity (TEQ) framework provides a thermodynamic foundation for understanding quantum-to-classical transitions by linking entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, to realized entropy, ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$. This transition is governed by decoherence ($\gamma$) and entropy redistribution ($\delta$), processes that underpin both the emergence of classical behavior and the thermodynamic arrow of time.

Quantum Interpretations and Entropy Redistribution

While the TEQ framework describes entropy redistribution through decoherence and latent-to-realized transitions, its behavior under different quantum interpretations provides unique insights into the quantum-to-classical emergence:

• Copenhagen Interpretation: Decoherence ($\gamma$) effectively simulates wavefunction collapse, irreversibly converting latent entropic contributions from quantum coherence into realized entropy ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$. This process aligns with the observed emergence of classical behavior, as quantum correlations are lost and entropy redistributes deterministically [1,2,5].
• Many-Worlds Interpretation (MWI): In MWI, decoherence creates independent branches of the global wavefunction, each representing a classical outcome. While realized entropy ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$ grows within each branch, the total normalized entropy remains globally conserved. Latent entanglement redistributes across an exponentially increasing number of branches, preserving quantum consistency while locally yielding classical probabilities [1,9,10].

Comparison of Predictions. 

The primary difference lies in the interpretation of realized entropy growth:

• In the Copenhagen framework, entropy redistribution corresponds to irreversible quantum-to-classical transitions.
• In MWI, entropic contributions remain distributed across branching wavefunctions, maintaining global unitarity while producing classical behavior within each branch.

Despite their philosophical differences, the Copenhagen Interpretation and MWI provide operationally consistent descriptions of realized entropy growth. In Copenhagen, entropy redistribution corresponds to irreversible quantum-to-classical transitions, while in MWI, it reflects the branching of the wavefunction into classical outcomes. Importantly, both interpretations rely on decoherence ($\gamma$) and entropy redistribution ($\delta$) to explain the observable emergence of classical behavior. The TEQ framework unifies these processes into a single measurable model, remaining agnostic to interpretation while connecting entropy dynamics to the quantum-to-classical transition.

Implications for Quantum-to-Classical Emergence

The evolution of ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ and its transition into ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$ provides a thermodynamic perspective on quantum interpretations. Specifically:

• Decoherence Mechanisms: Modeled by the rate $\gamma$, decoherence describes the loss of quantum coherence, aligning with the observed emergence of classical states [1,2].
• Entropy Redistribution: Governed by $\delta$, the redistribution of entropy between entangled latent and realized components underpins macroscopic irreversibility and the thermodynamic arrow of time [7,8].

By unifying entropy dynamics with quantum decoherence, the TEQ framework bridges the gap between microscopic quantum mechanics and macroscopic thermodynamics. This connection offers a testable model for entropy growth across cosmological scales and provides a foundation for exploring measurable signatures of decoherence and entropy redistribution in observational data.

3.5. The Fate of the Universe: Heat Death

As ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)\to 1$, the universe approaches a state of thermodynamic equilibrium, often referred to as heat death [7,8]. In this asymptotic state, entropy gradients vanish, and no further macroscopic processes occur. The modulation factor $f(\Lambda )$ in Equation (10) suggests that dark energy may influence or delay this progression, linking entropy dynamics to cosmic acceleration and expansion.

The TEQ framework thus provides a self-consistent description of the thermodynamic arrow of time, the emergence of causality, and the synchronization of entropy-driven time, all within the constraints of a globally unitary universe.

4. Speculative Extensions of the TEQ Framework

This section explores speculative extensions of the Total Entropic Quantity (TEQ) framework, hypothesizing its role in the emergence of time, space, and causality. These extensions are motivated by the interplay between apparent entropy, quantum entanglement, and the global unitary evolution of the universe.

4.1. Entanglement as the Source of Time and Space

A key speculative hypothesis within the TEQ framework is that quantum entanglement underlies the emergence of classical notions of time and space. In this view, entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, represents a pre-geometric quantum state where spatial and temporal structures are undefined [11,12].

Pre-Geometric Nature of Entanglement. 

At the level of entangled latent entropy, correlations exist globally without reference to classical space or time:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right).$$

(15)

These correlations are:

• Spaceless: Entanglement exists independently of spatial separation.
• Timeless: The global quantum state evolves unitarily, preserving coherence without a preferred temporal direction [1,2].

Emergence of Time. 

Time emerges through the monotonic growth of apparent entropy as latent entanglement decoheres:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(16)

where the irreversible increase in ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ defines the thermodynamic arrow of time, aligning local observations with entropy redistribution [1,8].

Emergence of Space. 

Building on the ER=EPR conjecture [11] and ideas in holography [12], we speculate that spatial structure arises from the strength of entanglement. Effective spatial distances between regions can be related to entanglement correlations as:

$$d_{\mathrm{effective}}\propto {\displaystyle \frac{1}{\mathrm{Entanglement}\mathrm{Correlation}\mathrm{Strength}}}.$$

(17)

This relationship suggests that as entangled latent entropy decoheres, classical geometry dynamically emerges, linking entropy growth to the formation of space.

4.2. Spacetime Emergence Through Entropy Redistribution

The hierarchical redistribution of entropy, as described in Section 2, provides a mechanism for the emergence of spacetime. The evolution of entangled latent entropy,

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{apparent}}\left(t\right),$$

(18)

captures the transition from pre-geometric quantum states to classical spacetime. Here:

• $\gamma$: Decoherence rate, driving the loss of global quantum coherence.
• $\delta$: Redistribution rate, linking entropic growth to the emergence of classical structure.

Initially, the universe exists as a pure quantum state dominated by ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$. As decoherence progresses, latent entanglement is converted into apparent entropy, giving rise to classical spacetime geometry [1,2]. This process bridges the transition from a pre-geometric quantum regime to the classical description of time and space.

4.3. Residual Coherence and Quantum Branching

Residual quantum coherence, represented by ${\tilde{S}}_{\mathrm{coherence}}\left(t\right)$, captures the incomplete decoherence of entangled states. This residual coherence influences quantum-to-classical transitions and entropy redistribution. The total entangled latent entropy can be expressed as:

$${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)=1-\left({\tilde{S}}_{\mathrm{vN}}\left(t\right)+{\tilde{S}}_{\mathrm{coherence}}\left(t\right)+{\tilde{S}}_{\mathrm{relational}}\left(t\right)\right),$$

(19)

where:

• ${\tilde{S}}_{\mathrm{vN}}\left(t\right)$: Von Neumann entropy, measuring quantum mixedness [13].
• ${\tilde{S}}_{\mathrm{coherence}}\left(t\right)$: Remaining coherence in the system [2].
• ${\tilde{S}}_{\mathrm{relational}}\left(t\right)$: Long-range correlations persisting across the universe [12].

The persistence of residual coherence suggests that the classical-quantum transition may not be strictly irreversible. This mechanism aligns with MWI’s global coherence while challenging Copenhagen’s notion of complete wavefunction collapse, blurring the operational differences between these interpretations.

Blurring the Distinction Between Interpretations. 

The persistence of residual coherence introduces an intriguing possibility: the apparent distinction between the Copenhagen Interpretation and the Many-Worlds Interpretation (MWI) may not be as stark as traditionally assumed. While Copenhagen emphasizes irreversible wavefunction collapse, the presence of residual coherence suggests that this collapse is merely an effective, observer-dependent approximation. From the MWI perspective, residual coherence aligns naturally with the global unitarity of the wavefunction, where branching preserves quantum correlations. This shared reliance on decoherence ($\gamma$) and entropy redistribution ($\delta$) highlights a deeper operational unity between these interpretations. By providing a measurable framework for residual coherence, the TEQ framework raises the possibility that both interpretations represent complementary approximations of the same underlying process, governed by entropy dynamics.

4.4. Observational Consequences

The speculative extensions of the TEQ framework suggest testable predictions across multiple observational domains:

• Cosmic Microwave Background (CMB): Residual coherence may imprint subtle deviations in polarization patterns, particularly in the B-mode spectrum [14].
• Gravitational Waves: Entropic transitions during early universe decoherence could produce detectable signatures in the primordial gravitational wave background [7].
• Large-Scale Structure (LSS): The entropic origin of spacetime may influence entropy gradients, affecting structure formation at cosmological scales [15].

These predictions can be explored using data from current and upcoming experiments, such as CMB-S4 [16], LISA [17], and DESI [15].

4.5. Summary of Speculative Extensions

The TEQ framework suggests that entanglement may underlie the emergence of time and space, with entropy redistribution driving the transition from pre-geometric quantum states to classical spacetime. These ideas align with concepts in quantum gravity, holography, and decoherence, providing a pathway to testable predictions that connect quantum processes to cosmological observations.

5. Conclusions and Future Work

The Total Entropic Quantity (TEQ) framework provides a comprehensive theoretical model for understanding entropy redistribution, the emergence of time, and the thermodynamic evolution of the universe. By bridging microscopic quantum processes with macroscopic thermodynamic trends, the TEQ framework reconciles the global unitary evolution of the universe with the observable growth of apparent entropy. This section summarizes the framework’s key findings, outlines potential observational pathways, and proposes directions for future work.

Interpretational Implications. 

An intriguing result of the TEQ framework is the potential reconciliation between seemingly divergent quantum interpretations. The introduction of residual coherence (${\tilde{S}}_{\mathrm{coherence}}\left(t\right)$) suggests that the Copenhagen Interpretation and Many-Worlds Interpretation may be operationally more aligned than previously thought. The classical-quantum transition, often viewed as an irreversible collapse (Copenhagen) or branching (MWI), can instead be seen as an effective approximation of underlying entropic processes. This perspective highlights the TEQ framework as a unifying model, offering a deeper understanding of how entropy dynamics underlie quantum decoherence, the persistence of global unitarity, and the emergence of classical behavior.

5.1. Conclusions

The key insights of the TEQ framework are as follows:

• Decomposition of Total Entropy: Total normalized entropy is decomposed into three components:

  $${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right),$$

  (20)

  where apparent entropy (${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$) quantifies observable disorder, latent entangled entropy (${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$) stores unrealized quantum correlations, and latent classical entropy (${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$) captures classical disorder in decohered systems [1,2].
• Emergence of the Thermodynamic Arrow of Time: The monotonic growth of apparent entropy, governed by:

  $${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

  (21)

  establishes the thermodynamic arrow of time, providing a temporal direction consistent with decoherence and entropy redistribution processes [7].
• Universal Entropic Time (UET): The growth of apparent entropy defines a global temporal framework–Universal Entropic Time (UET)–which synchronizes entropy dynamics with cosmic expansion, while allowing for local deviations driven by entropy gradients.
• Causality as an Entropic Phenomenon: The directional flow of entropy from latent to apparent components underpins the emergence of causality. The irreversible increase of apparent entropy aligns the thermodynamic arrow of time with the progression of causal events.
• Speculative Extensions: TEQ provides a foundation to explore the emergence of time and space from entanglement. The conversion of latent entangled entropy into apparent entropy through decoherence suggests that quantum correlations form the pre-geometric basis of classical spacetime [11,12].
• Observational Predictions: TEQ predicts measurable signatures in the Cosmic Microwave Background (CMB), primordial gravitational wave spectra, and large-scale cosmic structure, offering testable pathways for validation [14,15].

5.2. Assessment of TEQ from First Principles

The Total Entropic Quantity (TEQ) framework provides a novel perspective on the interplay between entropy, time, and the thermodynamic evolution of the universe. In this section, we evaluate the framework’s validity against fundamental principles of physics to assess its conceptual foundation and highlight pathways for further development.

5.2.1. Consistency with Unitary Evolution

Global unitarity, a cornerstone of quantum mechanics, ensures that the total quantum state evolves without loss of information. Mathematically, the von Neumann entropy $S_{\mathrm{vN}}\left(t\right)=-\mathrm{Tr}(\rho ln\rho )$ remains constant for a closed quantum system, where $\rho \left(t\right)$ is the density matrix of the system.

The TEQ framework respects this principle by decomposing the total normalized entropy into conserved components:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right),$$

(22)

where the individual components ${\tilde{S}}_{\mathrm{apparent}}$, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}$, and ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}$ are functions of t, and where the total entropy ${\tilde{S}}_{\mathrm{total}}$ is conserved. This conservation aligns perfectly with the principle of global unitarity, even as entropy redistributes between subsystems due to decoherence (Appendix A).

5.2.2. Entropy as Coarse-Graining and Knowledge Limits

Entropy as a measure of missing information is foundational to both thermodynamics and information theory. Boltzmann’s entropy, $S=k_{B}lnW$, reflects the number of microstates W consistent with a macroscopic state. In quantum mechanics, this idea generalizes to the von Neumann entropy, capturing the uncertainty in a system’s state.

The TEQ framework extends this principle by interpreting latent entropy components as hidden information about inaccessible microstates:

• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$: Quantum correlations inaccessible due to decoherence.
• ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$: Hidden classical correlations in decohered systems.

The growth of apparent entropy, ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$, arises naturally from the coarse-graining of latent entangled information (Appendix B):

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(23)

where $\alpha$ is the decoherence rate and $f(\Lambda )$ accounts for the modulation by the cosmological constant $\Lambda$.

Thus, TEQ aligns with the principle that entropy growth reflects the observer’s loss of access to microstate information due to decoherence.

5.2.3. Entanglement as the Foundation of Structure

Quantum entanglement is a fundamental feature of quantum mechanics, encoding non-local correlations in the wavefunction. The TEQ framework posits that latent entangled entropy plays a foundational role in:

• Driving entropy redistribution:
  Decoherence converts entanglement into observable thermodynamic disorder.
• Emerging classical behavior:
  The loss of accessible entanglement leads to the growth of ${\tilde{S}}_{\mathrm{apparent}}$, reflecting classical thermodynamic structures.

This view aligns with modern results from open quantum systems (Appendix A) and decoherence theory, where entanglement loss explains the quantum-to-classical transition.

5.2.4. The Arrow of Time and Irreversibility

While the fundamental laws of physics are time-reversible, the emergence of the thermodynamic arrow of time arises from the monotonic growth of entropy. In the TEQ framework, this irreversibility is formalized by the growth of apparent entropy due to decoherence:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}>0,\forall t\ge 0.$$

(24)

This result naturally explains the observed irreversibility in macroscopic systems and aligns with the second law of thermodynamics.

5.2.5. TEQ as a Starting Point

While the TEQ framework aligns with the principles of global unitarity, coarse-graining, and entanglement dynamics, its current form remains phenomenological. The parameters governing entropy dynamics, such as the decoherence rate $\gamma$ and redistribution rate $\delta$, await microscopic derivation from first principles, including:

• Open quantum systems and the Lindblad master equation.
• Quantum field theory in expanding spacetimes.
• Holographic entropy dynamics (e.g., AdS/CFT correspondence).

Future work will focus on deriving these parameters to ensure a fully rigorous foundation for the TEQ framework.

5.2.6. Concluding Remarks

The TEQ framework, as presented, represents a conceptually consistent starting point for unifying entropy, time, and causality. By aligning with established first principles while highlighting areas for further development, TEQ offers a pathway for understanding the deep connections between quantum mechanics, thermodynamics, and cosmology.

5.3. Observational Pathways and Validation

The TEQ framework’s predictions can be tested through several observational avenues:

• Cosmic Microwave Background (CMB): Decoherence effects ($\gamma$) and entropy redistribution processes ($\delta$) may leave imprints on CMB polarization patterns, particularly in the B-mode spectra [14,16].
• Gravitational Waves: Entropy redistribution during inflation and cosmic phase transitions could produce unique signatures in the primordial gravitational wave background, detectable by instruments such as LISA and Cosmic Explorer [17].
• Large-Scale Structure (LSS): Entropy gradients influence the distribution of galaxies and cosmic voids, providing a testable link between latent entropy and cosmic structure formation via surveys like DESI and Euclid [15].
• Black Hole Environments: Regions near black holes offer natural laboratories for entropic processes, where the redistribution of latent entropy can be tested using observations from the Event Horizon Telescope and gravitational wave signals [18].

These pathways provide opportunities to constrain key TEQ parameters ($\alpha$, $\gamma$, $\delta$, $f(\Lambda )$) and validate the framework’s predictions at both cosmological and astrophysical scales. Further details on parameter estimation and observational constraints are provided in Appendix C.

5.4. Future Work

Future research directions to refine and extend the TEQ framework include:

• Microscopic Derivations:
  A critical next step is deriving the governing parameters for entropy dynamics, specifically the decoherence rate $\gamma$ and the redistribution rate $\delta$, from first principles. These derivations must incorporate:
  • Open quantum systems using the Lindblad master equation for decoherence processes.
  • Quantum field theory in expanding spacetimes to formalize entropy redistribution across cosmological scales.
  • Statistical mechanics to validate coarse-graining approximations consistent with entropy growth (Appendix A).
  The explicit dependence of entropy dynamics on t, $\Lambda$, and spatial coordinates $\mathbf{x}$ will be central to ensuring a rigorous foundation for TEQ.
• Theoretical Justification and Quantum Gravity:
  Formalize TEQ’s connection to quantum gravity, holographic entropy dynamics, and emergent spacetime models. Specifically:
  • Investigate how entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, relates to holographic descriptions such as the AdS/CFT correspondence [11,12].
  • Explore the role of entanglement entropy in emergent spacetime geometry, particularly through the ER=EPR conjecture and decoherence-driven classicalization [2,11].
  • Incorporate quantum gravity corrections into the entropy growth equations to address behavior near singularities and Planck-scale phenomena.
• Integration with Cosmic Dynamics:
  Investigate the coupling between entropy redistribution and the evolution of the Hubble parameter $H\left(t\right)$, with particular focus on the role of dark energy $\Lambda$ in entropy growth, cosmic acceleration, and the modulation term $f(\Lambda )$ (Eq. 2).
• Spatial and Nonlinear Dynamics:
  Extend the entropy dynamics to include spatial variations $\nabla ·{\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)$ and nonlinear effects, particularly in dense and structured regions such as galaxy clusters, black holes, and cosmic voids (Appendix B). The resulting equations will incorporate:

  $${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)}{\partial t}}=D_{\mathrm{eff}}{\nabla }^2{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)+\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)\right)+{\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t),$$

  (25)

  where $D_{\mathrm{eff}}$ represents the effective diffusion coefficient.
• Numerical Simulations:
  Develop numerical models to analyze entropy dynamics in inhomogeneous and nonlinear cosmological environments, complementing analytical results. Simulations will focus on:
  • Large-scale entropy redistribution and spatial gradients across cosmic structures.
  • Entropy dynamics in black hole environments, where extreme curvature influences ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}$ and its transition into apparent entropy.
• Empirical Tests and Collaboration:
  Collaborate with observational missions such as CMB-S4, LISA, and DESI to test TEQ predictions and refine its theoretical parameters. Potential signatures include:
  • Imprints of entropy redistribution on CMB polarization spectra [14].
  • Gravitational wave signatures from entropic transitions during inflation and cosmic phase changes [17].
  • Large-scale structure entropy gradients observable in galaxy distributions and voids [15].
• Quantum Interpretations and Residual Coherence:
  The persistence of residual coherence in entangled systems raises questions about the operational distinctions between the Copenhagen Interpretation and the Many-Worlds Interpretation (MWI). Specifically, while the Copenhagen Interpretation posits irreversible wavefunction collapse, the MWI maintains global unitarity through wavefunction branching. Future work will:
  • Quantify the role of residual coherence ${\tilde{S}}_{\mathrm{coherence}}\left(t\right)$ in entropy redistribution, including how it interacts with decoherence ($\gamma$) and redistribution processes ($\delta$) (Appendix A).
  • Investigate whether residual coherence influences quantum-to-classical transitions and identify measurable consequences that could distinguish between wavefunction collapse and branching interpretations.

5.5. Final Remarks

The Total Entropic Quantity (TEQ) framework provides a novel, unified perspective on entropy dynamics, the emergence of time, and the origin of causality within a unitary quantum universe. By decomposing the total normalized entropy into three components–apparent entropy, latent entangled entropy, and latent classical entropy–TEQ bridges the global preservation of quantum coherence with the local growth of observable entropy. This reconciliation offers a consistent description of thermodynamic evolution across microscopic, macroscopic, and cosmological scales.

While the current framework is phenomenological, it aligns with foundational principles of quantum mechanics, thermodynamics, and statistical physics. TEQ serves as a conceptual starting point for addressing open questions about the interplay between quantum entanglement, thermodynamic irreversibility, and the emergence of classical behavior.

Key challenges remain, including the derivation of decoherence rates ($\gamma$) and entropy redistribution rates ($\delta$) from first principles, as well as formalizing the role of entanglement in emergent spacetime geometry. The integration of TEQ with quantum field theory, holographic entropy models, and quantum gravity represents a natural pathway for future development.

Empirical tests, including observations of the Cosmic Microwave Background, gravitational waves, and large-scale structure, will play a central role in validating the framework’s predictions and constraining its parameters. As such, TEQ provides a foundation for further theoretical refinement and observational exploration, with the potential to advance our understanding of the universe’s fundamental structure, from its quantum origins to its macroscopic evolution.

In summary, the TEQ framework represents a promising step toward unifying the thermodynamic arrow of time, causality, and cosmic evolution. While still in its early stages, it offers both a conceptual foundation and a roadmap for future progress, reinforcing the notion that understanding entropy lies at the heart of unraveling the universe’s deepest mysteries.

Appendix A.1. Growth of Apparent Entropy

The growth of apparent entropy, ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$, describes the irreversible conversion of latent entropy into observable thermodynamic disorder due to decoherence processes. Its governing equation is:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right),$$

(A1)

where:

• $\alpha$ is the decoherence-driven growth rate constant.
• $f(\Lambda )$ incorporates the influence of the cosmological constant $\Lambda$ on the phase space of available states [7].

Assumptions. 

• Proportionality to Remaining Latent Entropy: The rate of realized entropy growth is proportional to the remaining latent entropy, analogous to thermodynamic systems with exponential relaxation [8,19]:

  $${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}\propto \left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right).$$
• Cosmic Expansion Influence: The cosmological constant modulates entropy growth, scaling the phase space of decohering states.
• Initial Condition: At $t=0$, the apparent entropy is zero:

  $${\tilde{S}}_{\mathrm{apparent}}\left(0\right)=0.$$

Derivation. 

Starting from the proportionality assumption:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right).$$

Separating variables:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{apparent}}}{1-{\tilde{S}}_{\mathrm{apparent}}}}=\alpha f(\Lambda )dt.$$

Integrating both sides:

$$-ln\left(1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)\right)=\alpha f(\Lambda )t+C,$$

where C is the integration constant. Using the initial condition ${\tilde{S}}_{\mathrm{apparent}}\left(0\right)=0$, we find $C=0$. Exponentiating:

$$1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)=e^{-\alpha f(\Lambda )t}.$$

Rearranging yields:

$${\tilde{S}}_{\mathrm{apparent}}\left(t\right)=1-e^{-\alpha f(\Lambda )t}.$$

(A2)

This solution demonstrates the monotonic increase of apparent entropy, consistent with the thermodynamic arrow of time.

Appendix A.2. Dynamics of Entangled Latent Entropy

The evolution of entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, reflects its gradual conversion into apparent entropy and redistribution within the TEQ framework. Its governing equation is:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{apparent}}\left(t\right),$$

(A3)

where:

• $\gamma$ is the decoherence rate, quantifying the decay of global quantum coherence [1].
• $\delta$ is the redistribution rate, describing coupling to apparent entropy growth.

Assumptions. 

• Decoherence-Driven Decay: The decay of ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ follows exponential behaviour decay typical of decoherence processes [1,5]. Entangled latent entropy decays exponentially with rate $\gamma$.
• Feedback Contribution: A fraction of apparent entropy growth feeds back into the entangled latent component.
• Initial Condition: At $t=0$, entangled latent entropy is maximal:

  $${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(0\right)=1.$$

Derivation. 

Starting with the governing equation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{apparent}}\left(t\right).$$

Substitute ${\tilde{S}}_{\mathrm{apparent}}\left(t\right)$ from Eq. (A2):

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta \left(1-e^{-\alpha f(\Lambda )t}\right).$$

This linear differential equation describes the time evolution of entangled latent entropy.

Appendix A.3. Conservation of Total Entropy

The conservation of total normalized entropy ensures:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{apparent}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1.$$

(A4)

Rearranging for the latent classical entropy gives:

$${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1-{\tilde{S}}_{\mathrm{apparent}}\left(t\right)-{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right).$$

(A5)

This equation guarantees that total entropy is conserved, consistent with the unitary evolution of the universe [1,2].

Appendix B.1. Generalized Apparent Entropy Dynamics

In the presence of spatial inhomogeneities, the evolution of apparent entropy is governed by a continuity equation:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)}{\partial t}}+\nabla ·{\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)\right)+{\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t),$$

(A6)

where:

• ${\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)$: Local apparent entropy field.
• ${\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)$: Entropy flux vector describing the spatial transport of apparent entropy.
• ${\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)$: Local entropy production or depletion term.
• $\alpha f(\Lambda )$: Global growth rate, modulated by the cosmological constant $\Lambda$ [7].

Derivation. 

Entropy conservation in the presence of spatial fluxes and sources is expressed as:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)}{\partial t}}+\nabla ·{\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)={\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t).$$

(A7)

Adding the global growth term $\alpha f(\Lambda )(1-{\tilde{S}}_{\mathrm{apparent}})$, we obtain Eq. (A6).

Appendix B.2. Entropy Flux and Diffusion

The entropy flux ${\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)$ is modeled using Fick’s law for diffusive processes:

$${\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)=-D_{\mathrm{eff}}\nabla {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t),$$

(A8)

where:

• $D_{\mathrm{eff}}$: Effective diffusion coefficient for apparent entropy, which may depend on local conditions, such as curvature or energy density.
• $\nabla {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)$: Gradient of the apparent entropy field.

Substitution. 

Substituting Eq. (A8) into Eq. (A6) yields the diffusion equation for apparent entropy:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)}{\partial t}}=D_{\mathrm{eff}}{\nabla }^2{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)+\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)\right)+{\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t).$$

(A9)

This equation describes the diffusion of apparent entropy under local gradients, combined with global entropy growth and local production.

Appendix B.3. Dynamics of Entangled Latent Entropy

The evolution of entangled latent entropy incorporates spatial transport, decoherence, and feedback processes. Generalizing Eq. (A3) to include spatial variations:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)}{\partial t}}+\nabla ·{\mathbf{J}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)+\delta {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t),$$

(A10)

where:

• ${\mathbf{J}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)=-D_{\mathrm{ent}}\nabla {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)$: Entangled entropy flux.
• $D_{\mathrm{ent}}$: Effective diffusion coefficient for entangled latent entropy.
• $\gamma$: Decoherence rate.
• $\delta$: Redistribution rate between entangled and apparent entropy.

Substitution. 

Substituting the flux term into Eq. (A10) yields:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)}{\partial t}}=D_{\mathrm{ent}}{\nabla }^2{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)+\delta {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t).$$

(A11)

This equation captures the diffusion of entangled latent entropy and its coupling to apparent entropy.

Appendix B.4. Conservation of Total Entropy

The conservation of total normalized entropy in the presence of spatial fluxes is expressed as:

$${\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{total}}(\mathbf{x},t)}{\partial t}}+\nabla ·{\mathbf{J}}_{\mathrm{total}}(\mathbf{x},t)=0,$$

(A12)

where:

$${\mathbf{J}}_{\mathrm{total}}(\mathbf{x},t)={\mathbf{J}}_{\mathrm{apparent}}(\mathbf{x},t)+{\mathbf{J}}_{\mathrm{latent},\mathrm{entangled}}(\mathbf{x},t)+{\mathbf{J}}_{\mathrm{latent},\mathrm{classical}}(\mathbf{x},t).$$

This equation ensures that total entropy remains conserved, with spatial fluxes balancing local changes across all entropy components.

Appendix C.1. Key Governing Parameters

The evolution of entropy components in the TEQ framework depends on the following parameters:

• $\alpha$: Growth rate constant for apparent entropy, describing the conversion of latent entropy into thermodynamic disorder.
• $f(\Lambda )$: Modulation factor related to the cosmological constant $\Lambda$, defined as:

  $$f(\Lambda )={\displaystyle \frac{\Lambda }{{\Lambda }_0}},$$

  (A13)

  where ${\Lambda }_0$ is a reference value.
• $\gamma$: Decoherence rate, governing the loss of quantum coherence in entangled latent entropy.
• $\delta$: Redistribution rate, quantifying entropy exchange between entangled latent entropy and apparent entropy.

These parameters dictate the behavior of the governing equations derived in Appendice A and Appendice B.

Appendix C.2. Constraints from Cosmic Microwave Background (CMB)

The CMB provides direct observational evidence for entropy dynamics in the early universe. Key signatures include:

• Polarization Patterns: Decoherence ($\gamma$) produces corrections to E-mode and B-mode polarization spectra through entropy redistribution [14].
• Temperature Anisotropies: Redistribution processes ($\delta$) influence small-scale anisotropies in the temperature power spectrum.

Parameter Constraints. 

Using observational data from Planck [14] and future CMB experiments such as CMB-S4 and the Simons Observatory, constraints on $\gamma$ and $\delta$ can be derived. The entropy feedback modifies the primordial power spectrum as:

$$\Delta P\left(k\right)\propto \delta {\tilde{S}}_{\mathrm{apparent}}\left(t_{\mathrm{dec}}\right)e^{-\gamma t_{\mathrm{dec}}},$$

(A14)

where $t_{\mathrm{dec}}$ is the photon decoupling time.

Appendix C.3. Constraints from Large-Scale Structure (LSS)

Entropy gradients and diffusion processes leave measurable imprints on the spatial distribution of galaxies and cosmic voids. Relevant observables include:

• Galaxy Entropy Profiles: Apparent entropy gradients, $\nabla {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)$, influence the thermodynamic state of galaxy clusters.
• Void Baselines: Cosmic voids provide a low-entropy baseline, constraining the evolution of latent classical entropy.

Parameter Constraints. 

Galaxy surveys such as DESI [20] and Euclid can be used to fit observed entropy profiles to TEQ predictions. Entropy diffusion is described by:

$${\nabla }^2{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)=-{\displaystyle \frac{1}{D_{\mathrm{eff}}}}\left[{\displaystyle \frac{\partial {\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)}{\partial t}}-\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{apparent}}(\mathbf{x},t)\right)\right],$$

(A15)

where $D_{\mathrm{eff}}$ is the effective diffusion coefficient.

Appendix C.4. Gravitational Wave Signatures

Primordial gravitational waves provide a unique probe of early-universe decoherence and entropy redistribution. Observational pathways include:

• Spectral Imprints: Decoherence-driven entropy transitions modify the stochastic gravitational wave background.
• Phase Transitions: Entropy redistribution during inflationary transitions produces detectable gravitational wave signals [7].

Parameter Constraints. 

The gravitational wave energy density spectrum, ${\Omega }_{\mathrm{GW}}\left(f\right)$, is sensitive to $\gamma$ and $\alpha$:

$${\Omega }_{\mathrm{GW}}\left(f\right)\propto \gamma \left(1-e^{-\alpha f(\Lambda )t}\right),$$

(A16)

where f is the gravitational wave frequency. Experiments such as LISA and Cosmic Explorer can place constraints on $\gamma$ and $\alpha$.

Appendix C.5. Black Hole Environments

Black hole systems offer extreme conditions for testing entropy redistribution and decoherence. Observational tests include:

• Event Horizons: Entropy gradients near black hole horizons can be probed through imaging (e.g., Event Horizon Telescope) [18].
• Black Hole Mergers: Gravitational wave signals from merging black holes carry signatures of entropy fluxes and redistribution.

Parameter Constraints. 

Entropy redistribution modifies black hole entropy, introducing corrections to the Bekenstein-Hawking formula:

$$S_{\mathrm{BH}}\left(t\right)={\displaystyle \frac{k_{B}A}{4l_p^2}}+\delta {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right),$$

(A17)

where A is the black hole horizon area and $l_p$ is the Planck length. Such corrections can be tested through gravitational wave signals and horizon-scale imaging.

Appendix C.6. Summary of Parameter Constraints

The observational pathways discussed above provide constraints for the key parameters in the TEQ framework:

• $\alpha$: Constrained through CMB temperature spectra and gravitational wave backgrounds.
• $\gamma$: Derived from decoherence imprints in the CMB and primordial gravitational wave signals.
• $\delta$: Constrained via large-scale entropy gradients and black hole entropy corrections.
• $f(\Lambda )$: Estimated from the modulation of entropy growth and its connection to cosmic expansion.