Dissonance, Sound Spectrum and Musical Scale for Ancient Idiophones and Aerophones

1. Introduction

Idiophones for rhythm and aerophones for melody are probably what our ancestors played over 50000 years ago [1]. The evolution of ancient musicality is unknown, but we can try to deduce how early musical instruments sounded by analyzing their acoustic properties and combining this with the importance of their tuning and temperament [2].

Archaeological sites have revealed many musical instruments made of stone, bone, wood or metal. All civilizations have developed such instruments simultaneously and although Western and Eastern music partly developed independently, we can find common ground in both musical areas by comparing ancient instruments developed in both geographical ends.

Documented styles and scales of early idiophones such as the Javanese gambang or the Thai renat [3] in the East and the Gambian bala or the Basque txalaparta in the West [4], [5] seem to be absolutely different. Although their respective cultures have evolved separately we may find similar instruments whose acoustic principles we can analyze.

Thai culture has been in contact with other civilizations for centuries, and Thai music and musical instruments have been influenced by China, Indonesia and India, among others. Some of the musical instruments used in Thai classical music are a type of xylophone (the renat ek and its low-pitched version, the renat thum), and melodic aerophones such as the pi and other melodic instruments such as the jakeh (a type of zither).

The txalaparta is an ancient idiophone, originally from the Basque Country (european region in the Western Pyrenees) whose peculiarities as a percussion instrument and its mysterious history have aroused great interest among musicologists and historians. The first historical reference to the txalaparta appears in 1882 in a book on cider production in the Basque Country ([6], p. 129), although there are earlier mentions of toberas (a metal variant of the txalaparta). The first of these is in a legal document from 1688 ([7], pp. 52-53). Melodic instruments such as the alboka (an ancient type of clarinet) were mentioned in 1443 in the Basque Country [8]. Very little is known about the practice of the txalaparta and alboka before the 20th century, but anthropologists, historians, musicians and other scholars have placed the instrument on a new path of growth, use and cultural renewal of great international interest.

Our approach here is based on the basic acoustic properties of some ancient musical instruments, which can give us some insight into how they might have been played. The study is structured as follows: Section 2 introduces a brief review of the classical identification of dissonance applied to musical sounds. Then, Section 3 presents a basic method for calculating dissonance in sounds of any spectrum and we propose a simple computational technique for easy calculation of dissonance curves. In Section 4 the method is applied both to harmonic and non-harmonic instruments. In particular it is shown how the corresponding twelve-semitone scale, approximately equal tempered, is directly obtained. Also, by application of dissonance curves to modern xylophones, valuable interpretation of their musical characteristics is deduced. In Section 5 the proposed technique is applied to the non-harmonic renat and txalaparta and their related Thai and Basque traditional instruments, respectively. Interesting properties of these ancient instruments as well as appropriate scales for their use are found and discussed.

2. Dissonance in Musical Sound

One of the best known studies of the perception of consonance and dissonance in music was by H. Helmholtz [9], who proposed a model of dissonance based on the phenomenon of beats. When two pure tones of close frequencies sound simultaneously, the interference of the two tones produces beats. The beats become slower as the frequencies of the tones become more similar, and disappear when the frequencies coincide. Slow beats are typically perceived as smooth waves, but fast beats tend to be rough and unpleasant, with maximum roughness observed when the beats occur around 32 times per second. Considering that every sound can be broken down into sinusoidal partials, Helmholtz concluded that the dissonance perceived when listening to two tones simultaneously is caused by the rapid beating of the partials. Thus, according to Helmholtz, consonance is the absence of such dissonant beats.

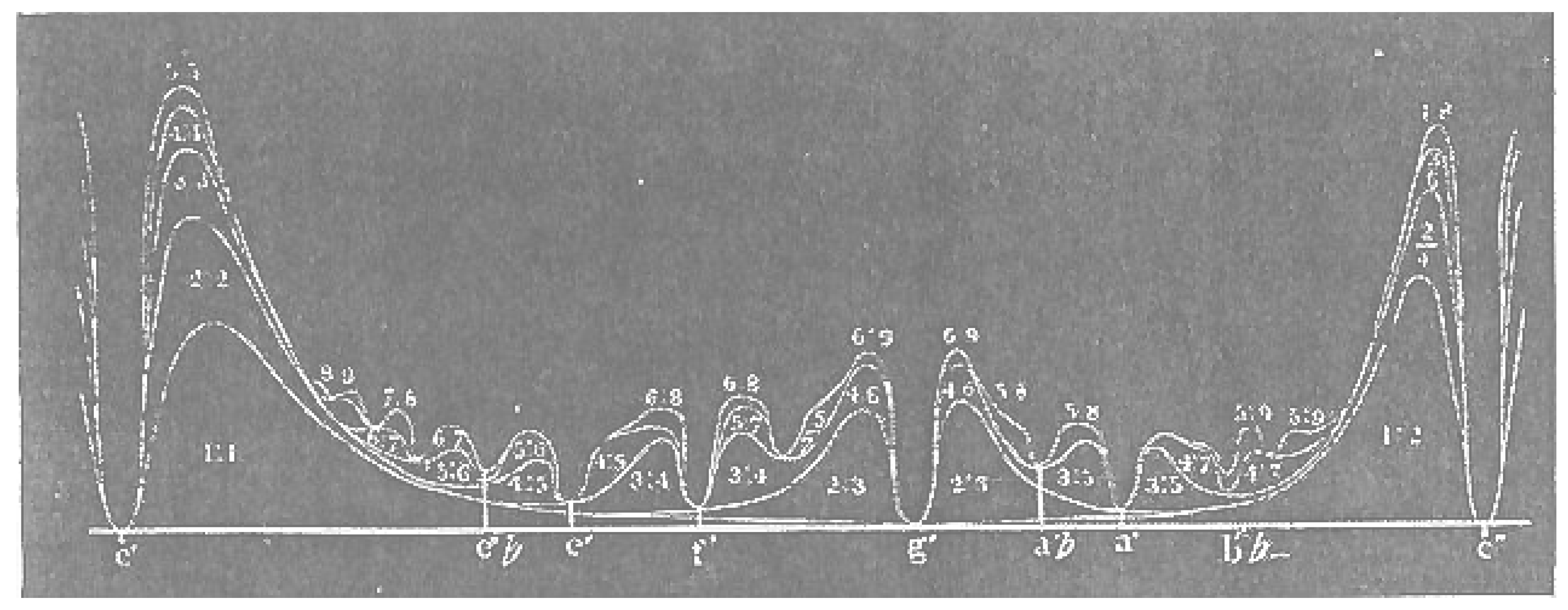
Assuming that the roughness of all interacting partials of two tones add up, the dissonance of any interval can be calculated simply by considering all possible combinations of pairs of partials and summing their contributions. Helmholtz performed this type of calculation for harmonic sounds such as those produced by violins [10], and presented the results graphically in diagrams such as the one shown in Figure 1, taken directly from [9]. The horizontal axis represents the interval between the two tones. One remains at a constant frequency (labelled $c^{\prime }$), and the other moves from $c^{\prime }$ to the upper octave (labelled $c^{\prime \prime }$). The height of the curves (vertical axis) is proportional to the roughness produced by the partials whose frequency ratios are labelled on the plot, using the maximum roughness criterion for 32 Hz beats. The result is a plot that has minima (intervals where minimum roughness occurs) near many of the intervals of the major scale, suggesting a relationship between the phenomenon of beats and the musical notions of consonance and dissonance.

Helmholtz’s work was of enormous importance and opened up many avenues in psychoacoustic research, many of which are still being developed. One of the most famous refinements of Helmholtz’s work on consonance and dissonance is due to R. Plomp and W.J.M. Levelt [11], who carried out a series of experiments on the perception of consonance and dissonance sensations on volunteers with no musical knowledge, using two pure tones whose relative dissonance was judged by the listeners. These experiments with pure tones made it possible to refine Helmholtz’s 32 Hz criterion and to use more closely the concept of critical bandwidth, which is not independent of frequency. Based on their results, Plomp and Levelt were able to calculate dissonance curves for non-pure harmonic tones.

According to the theoretical procedure described in [12], which in turn builds on the work of Plomp and Levelt [11], we present a computational method for calculating general dissonance curves. The method allows the calculation of dissonance curves for both harmonic and non-harmonic sounds. This makes it possible to relate a sound spectrum (of an instrument) to a musical scale (defined by intervals that have dissonance minima).

3. Calculation of dissonance curves

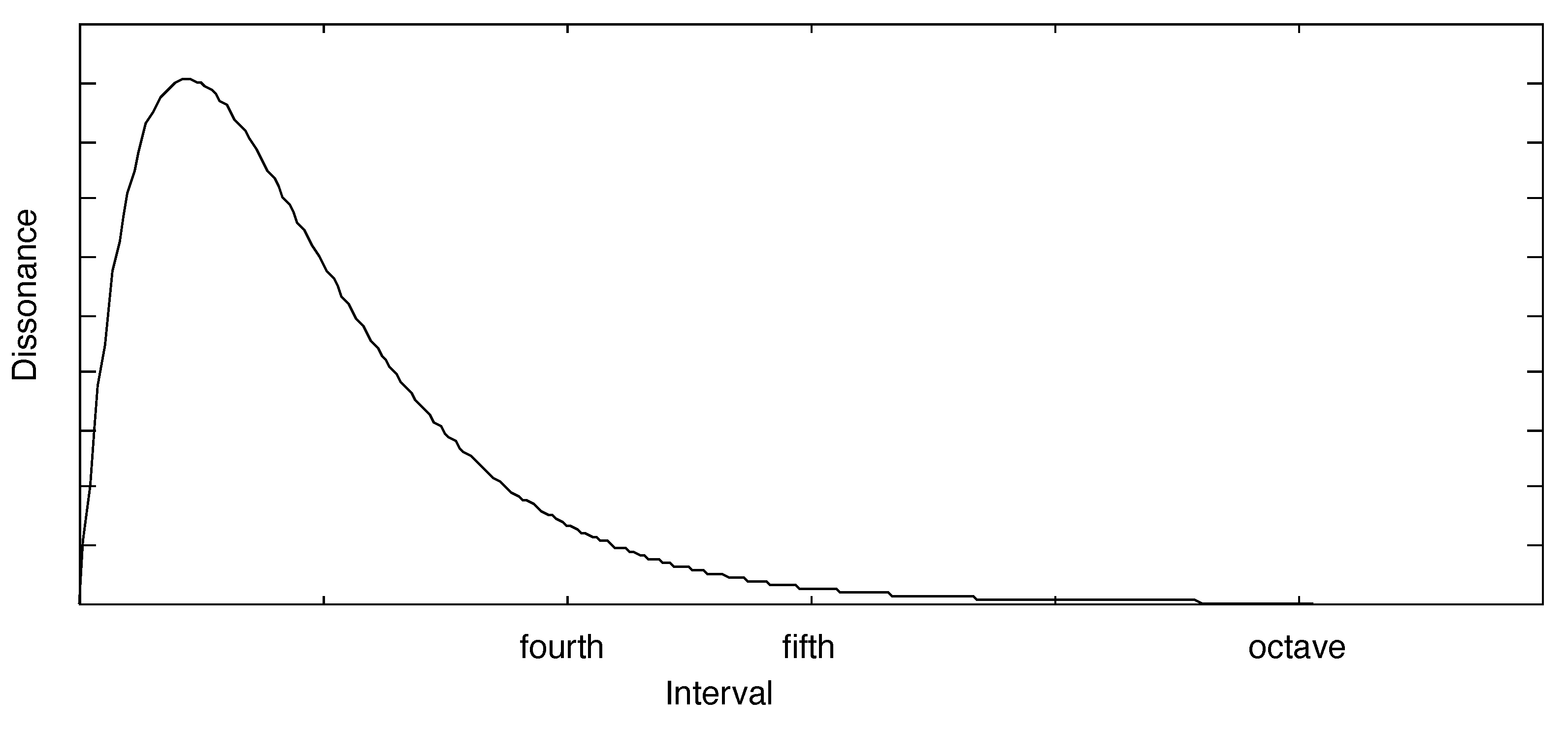
Next, we present a computational method for calculating dissonance curves. The first step in obtaining a closed form for calculating dissonance as a function of interval is to encapsulate Plomp and Levelt’s pure tone curve in a mathematical formula. The dissonance curve for two simultaneous pure tones obtained experimentally by Plomp and Levelt (Figure 2) can be conveniently parameterized by a model of the form:

$$d\left(x\right)=e^{-b_{1}x}-e^{-b_{2}x}$$

(1)

where x represents the frequency difference between the two sinusoids, and $b_1$ and $b_2$ determine how quickly the curves rise and fall. Using a least squares fit, the respective values for $b_1=3.5$ and $b_2=5.75$ are obtained.

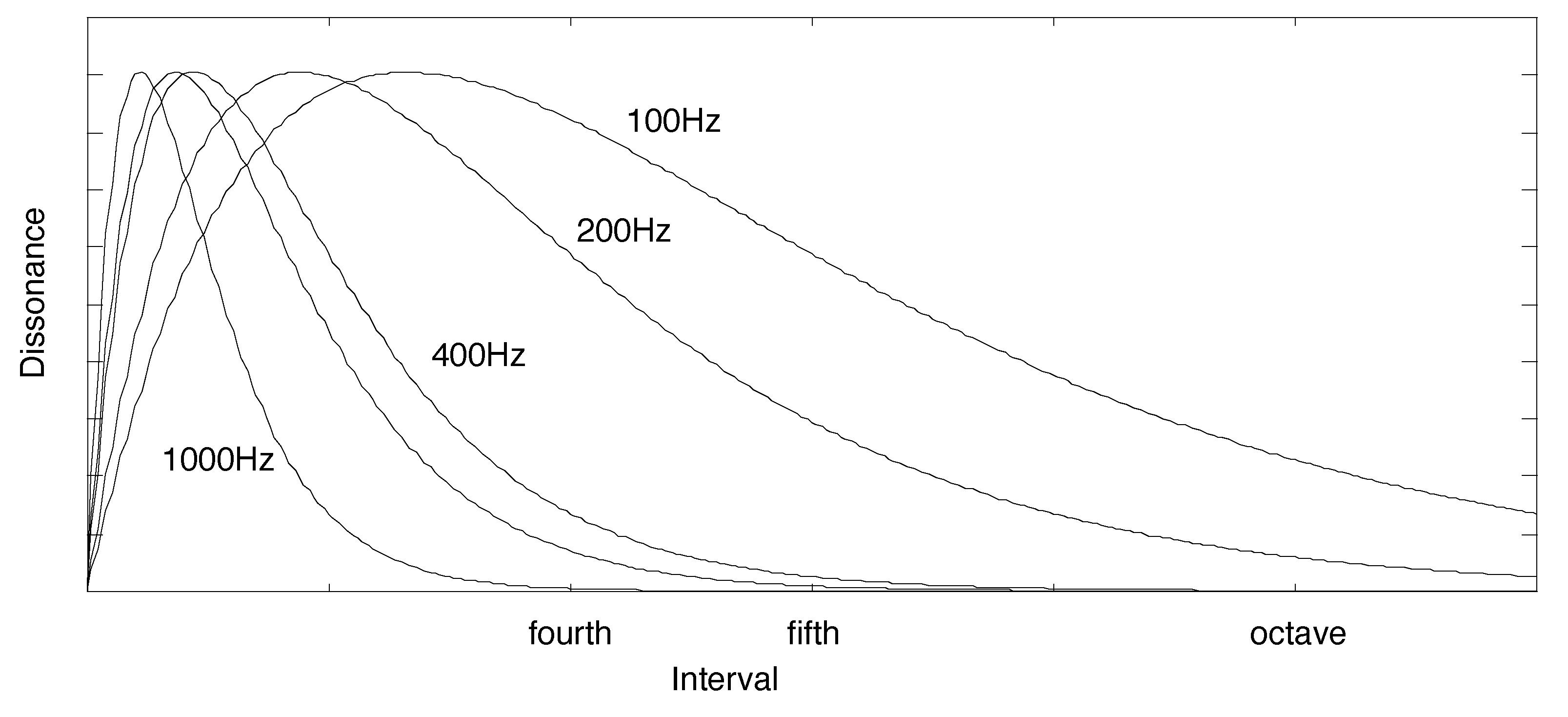
On the other hand, the Plomp-Levelt curves depend on the absolute frequency (and not only on the difference between the frequencies of the two tones), as shown in Figure 3. This family of curves can be expressed in a single functional as described in [12]:

$$d(f_1,f_2,a_1,a_2)=a_1{a}_2\left[e^{-b_{1}s(f_2-f_1)}-e^{-b_{2}s(f_2-f_1)}\right]$$

(2)

where $f_1$ y $f_2$ are the frequencies ($f_1\le f_2$) of the sinusoidal tones and $a_1$ and $a_2$ are the respective amplitudes. The parameter s has the form:

$$s={\displaystyle \frac{x^{*}}{s_1{f}_1+s_2}}$$

(3)

where $x^{*}$ is the maximum of (1). For the above values for $b_1$ and $b_2$ this results that $x^{*}=0.24$. The parameters s in (3) allow the functional to interpolate between the different curves in Figure 3, by moving the dissonance curve along the frequency axis so that it starts at $f_1$ and that the maximum dissonance occurs at the corresponding frequency. Using the Plomp-Levelt curves, the parameters can be adjusted to the values of $s_1=0.0207$ and $s_2=18.96$.

In general, a sound F of fundamental frequency $f_1$ is a collection of n sine waves of frecuencies $f_1<f_2<\dots <f_n$ and amplitudes $a_j$, so that the intrinsic dissonance of F can be calculated as the sum of the dissonances of all the pairs of partials:

$$D_F=\sum _{i=1}^n\sum _{j=1}^{n}d(f_i,f_j,a_i,a_j)$$

(4)

Finally, if two tones of F sound simultaneously in an interval of ratio $\alpha$ (i.e. F and $\alpha F$ sound, where $\alpha F$ contains the frequencies $\alpha f_1,\alpha f_2,\dots ,\alpha f_n$, with amplitudes $a_j$), then the dissonance of F in the interval $\alpha$ will be the sum of the two intrinsic dissonances of the two tones, plus the sum of the dissonances of the pairs of partials taken one at each tone:

$$D_F\left(\alpha \right)=D_F+D_{\alpha F}+\sum _{i=1}^n\sum _{j=1}^{n}d(f_i,\alpha f_i,a_i,a_j)$$

(5)

Thus, the dissonance curve generated by F is defined as the function $D_F\left(\alpha \right)$ in all intervals of interest $\alpha$.

In the following we list the Python programs that have been developed and that will be used to generate the dissonance curves in the rest of the work. First, there is a function called medidadisonancia, which takes as arguments a vector of frequencies and amplitudes and calculates the dissonance according to the method described above:

import numpy as np

def medidadisonancia(f, amp):

   # given a set of partials in f, with amplitudes given in amp,

   # this function computes the dissonance

   # constants for initialization

   Xestr = 0.24

   S1 = 0.0207

   S2 = 18.96

   C1 = 5

   C2 = -5

   A1 = -3.51

   A2 = -5.75

   N = len(f)

   D = 0

   f, ind = zip(*sorted(zip(f, range(N))))

   ams = [amp[i] for i in ind]

   for i in range(1, N):

       Fmin = f[:N-i+1]

       S = Xestr / (S1 * np.array(Fmin) + S2)

       Fdif = np.array(f[i:N]) - np.array(f[:N-i+1])

       a = np.array(ams[i:N]) * np.array(ams[:N-i+1])

       Dnueva = a * (C1 * np.exp(A1 * S * Fdif) + C2 * np.exp(A2 * S * Fdif))

       D += np.sum(Dnueva)

   d = D

   return d

The above function is called repeatedly from a main program in which the sound spectrum is defined. For example, the following program draws the dissonance curve for a harmonic sound with a fundamental frequency of 500 Hz and six harmonics, all of equal amplitude:

import numpy as np

import matplotlib.pyplot as plt

freq = 500 * np.array([1, 2, 3, 4, 5, 6, 7])

amp = np.ones(freq.shape)

rango = 2.3

inc = 0.01

diso = [0]

# call to function medidadisonancia for each interval

for alfa in np.arange(1 + inc, rango, inc):

   f = np.concatenate((freq, alfa * freq))

   a = np.concatenate((amp, amp))

   d = medidadisonancia(f, a)

   diso.append(d)

plt.plot(np.arange(1, rango, inc), diso)

plt.show()

These simple programs allow very fast and efficient calculation of dissonance curves for arbitrary sounds, and will be used in the following sections to construct the examples presented.

4. Dissonance Curves for Harmonic and Non-Harmonic Sounds

The dissonance curves can be calculated to predict the characteristics of general kind of musical instruments taking into account their corresponding spectra.

4.1. Curves for Harmonic Sounds

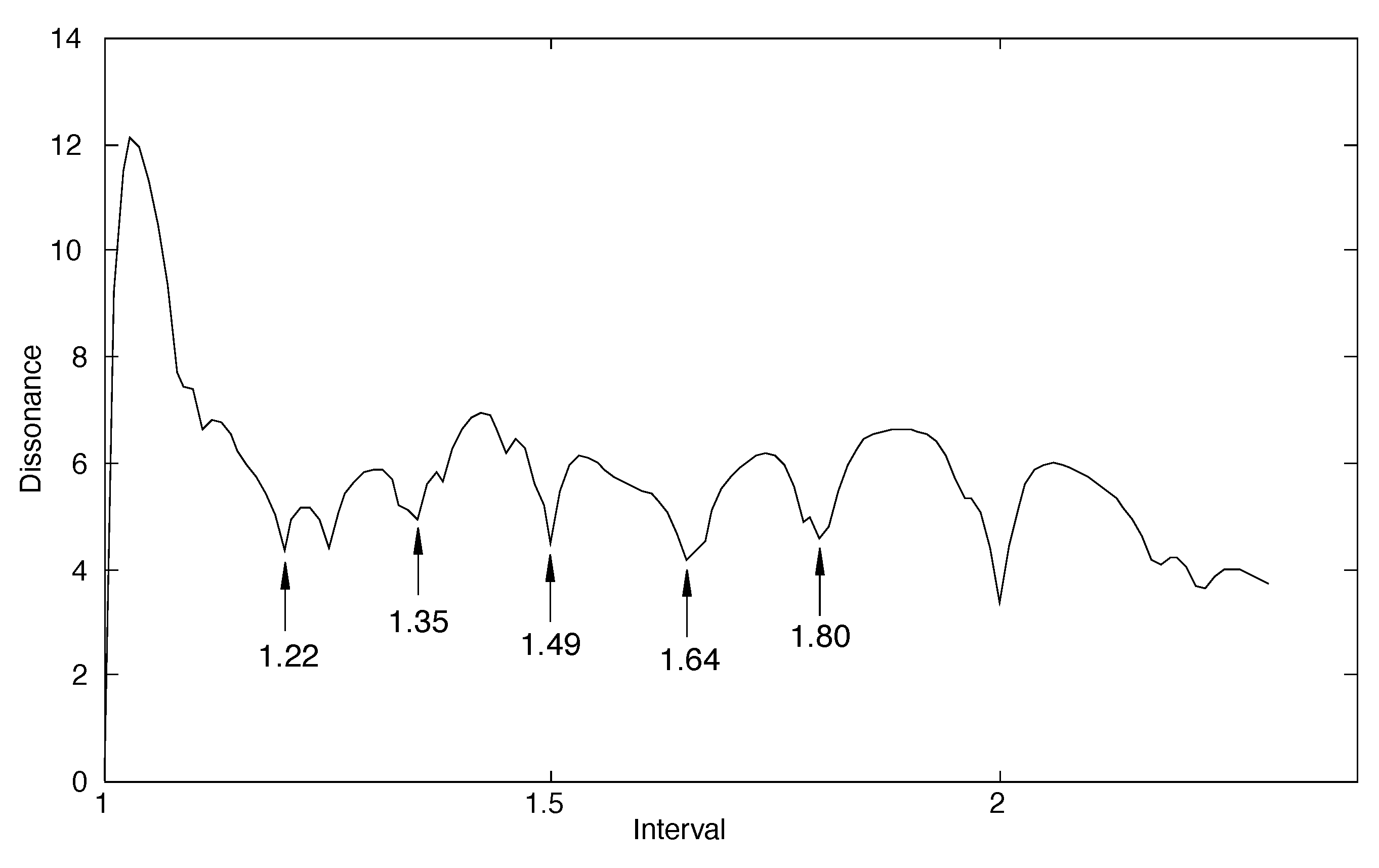
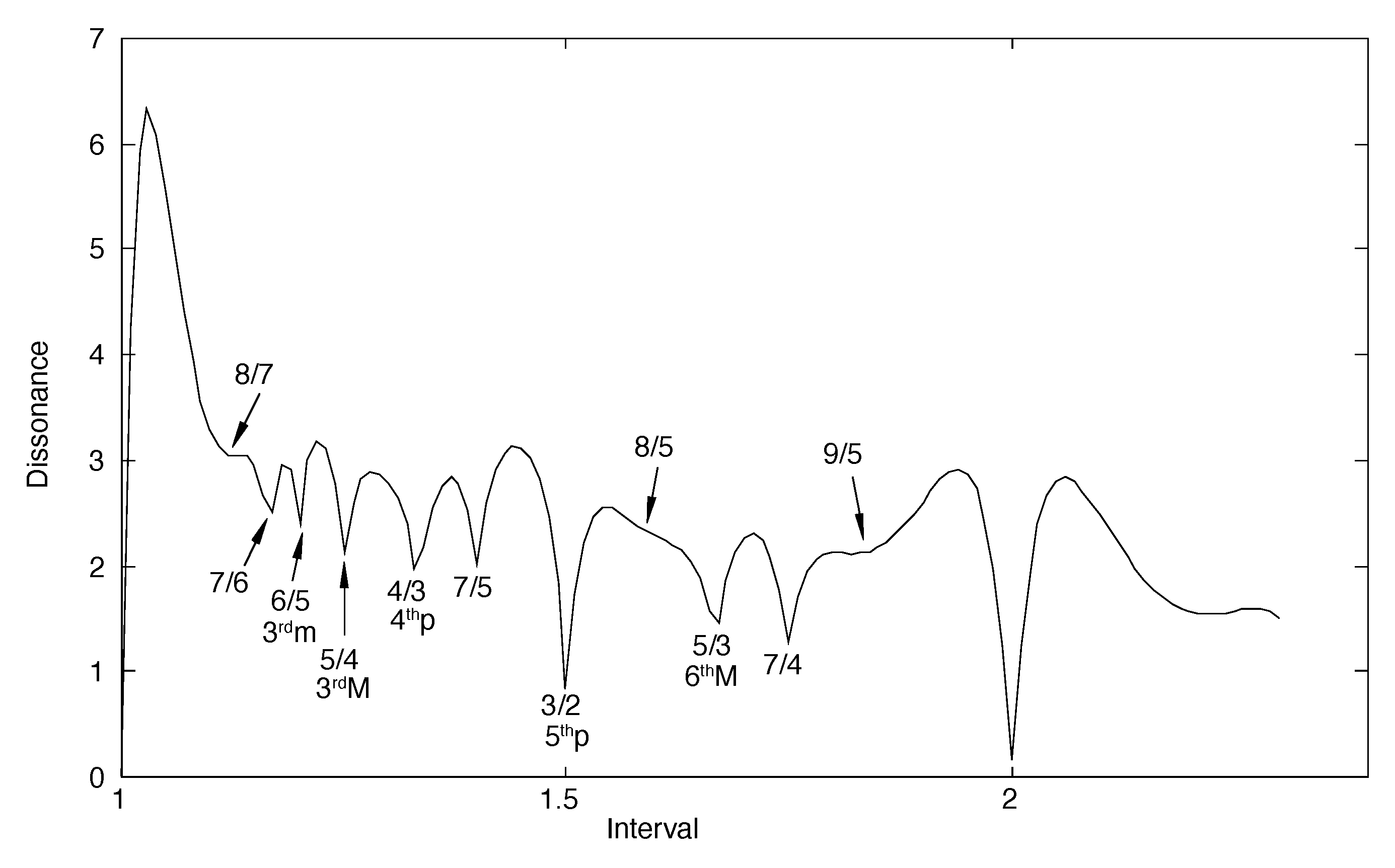
Using the programs listed in the previous section, Figure 4 is generated, which is the dissonance curve corresponding to a harmonic sound with a fundamental frequency of 500 Hz and six additional harmonics. The result is very illustrative. As it can be seen, the curve has minima where the frequencies are related by simple numbers. In addition, the consonant intervals of the octave ($2/1$), the perfect fifth ($3/2$), the major sixth ($5/3$), the perfect fourth ($4/3$), and the major and minor thirds ($5/4$ and $6/5$, respectively) stand out. Other intervals that can be approximately identified are the augmented sixth (about $7/4$), the augmented fourth (about $7/5$) and the major second (about $7/6$). Finally, the dissonant intervals of the minor second (approximately $8/7$), minor sixth ($8/5$) and seventh (approximately $9/5$) are also identified.

Overall, the dissonance curve for harmonic sounds allows the definition of the 12 semitone scale in common use, simply by identifying the intervals of the scale of minimum dissonance. In this sense, it can be said that the harmonic spectrum and the 12 semitone scale (typical of most modern Western musical instruments) are closely related.

4.2. Dissonance Curve for Xylophone Bars

Having applied the method of dissonance curves to harmonic sounds, we can now ask what consonances and dissonances are to be expected when non-harmonic spectrum instruments are used. In this sense, it is quite possible that intervals that are commonly considered to be consonant or dissonant will change their characteristics when played on non-harmonic instruments. It is also possible that, given the dissonance curve of a non-harmonic instrument being studied, a more appropriate associated scale can be defined, better than the usual one of twelve approximately equal tempered tones.

The following applicatoin example is based on the experimental response spectrum of xylophone bars presented in [13]. According to these experimental data, the response of a ’Royal Percussion’ Studio-49 (Germany) xylophone bar tuned to an A4 is not harmonic and has a spectrum:

$$F=[f,4.0f,9.1f,14.8f,19.9f,25.5f];f=437.1Hz$$

(6)

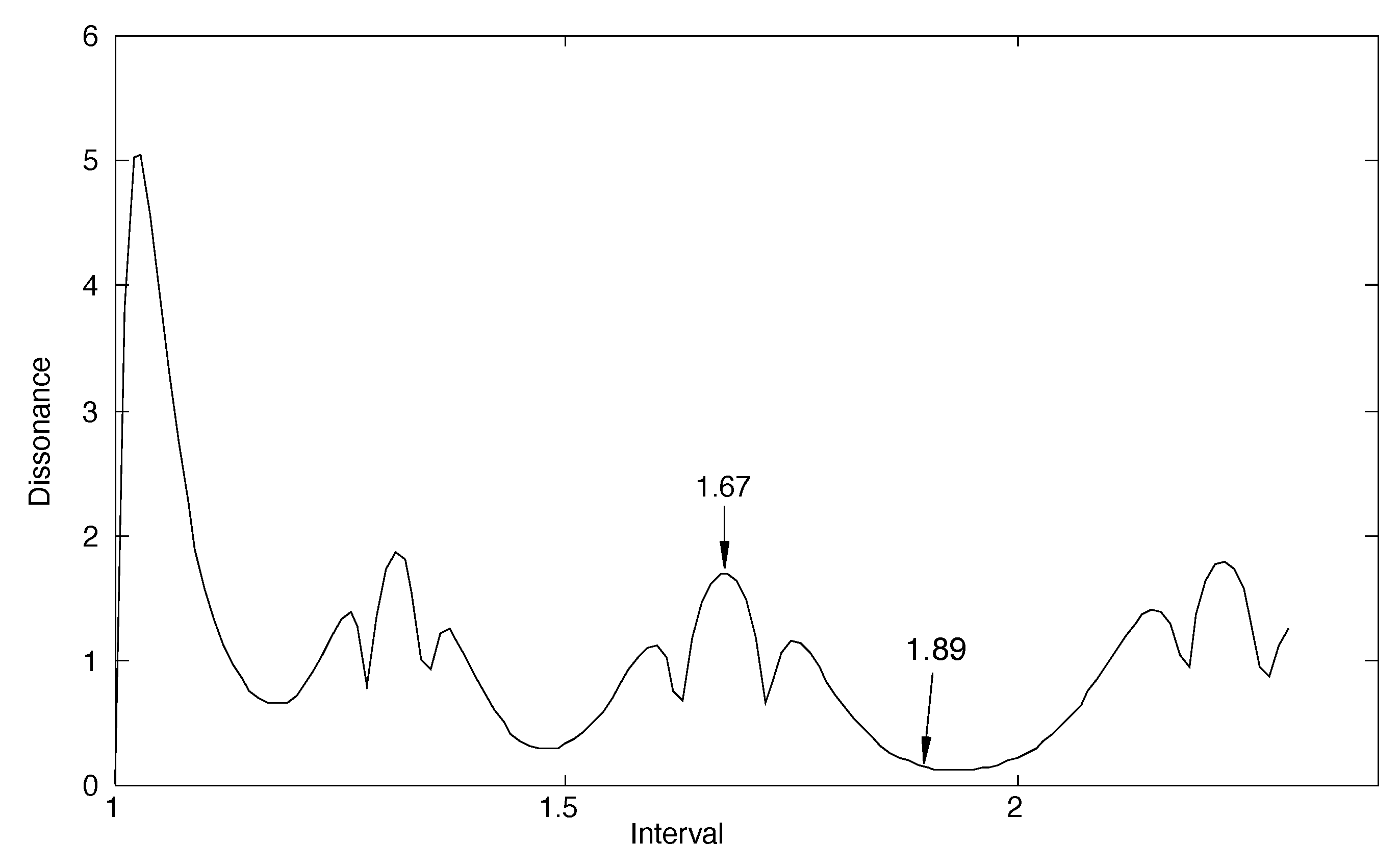
Using these data, and assuming that all partials have the same amplitude (which is not the case in the experiments, of course), the dissonance curve shown in Figure 5 is constructed. The dissonance predicted by the curve is generally lower than that of the harmonic tones (compare Figure 4 and Figure 5). Perhaps the most notable differences between the two curves are the relative dissonance expected for the major sixth interval (interval 1.67) and the predicted consonance for the seventh interval (interval 1.89) in the xylophone bars, both of which are the opposite for the harmonic sounds.

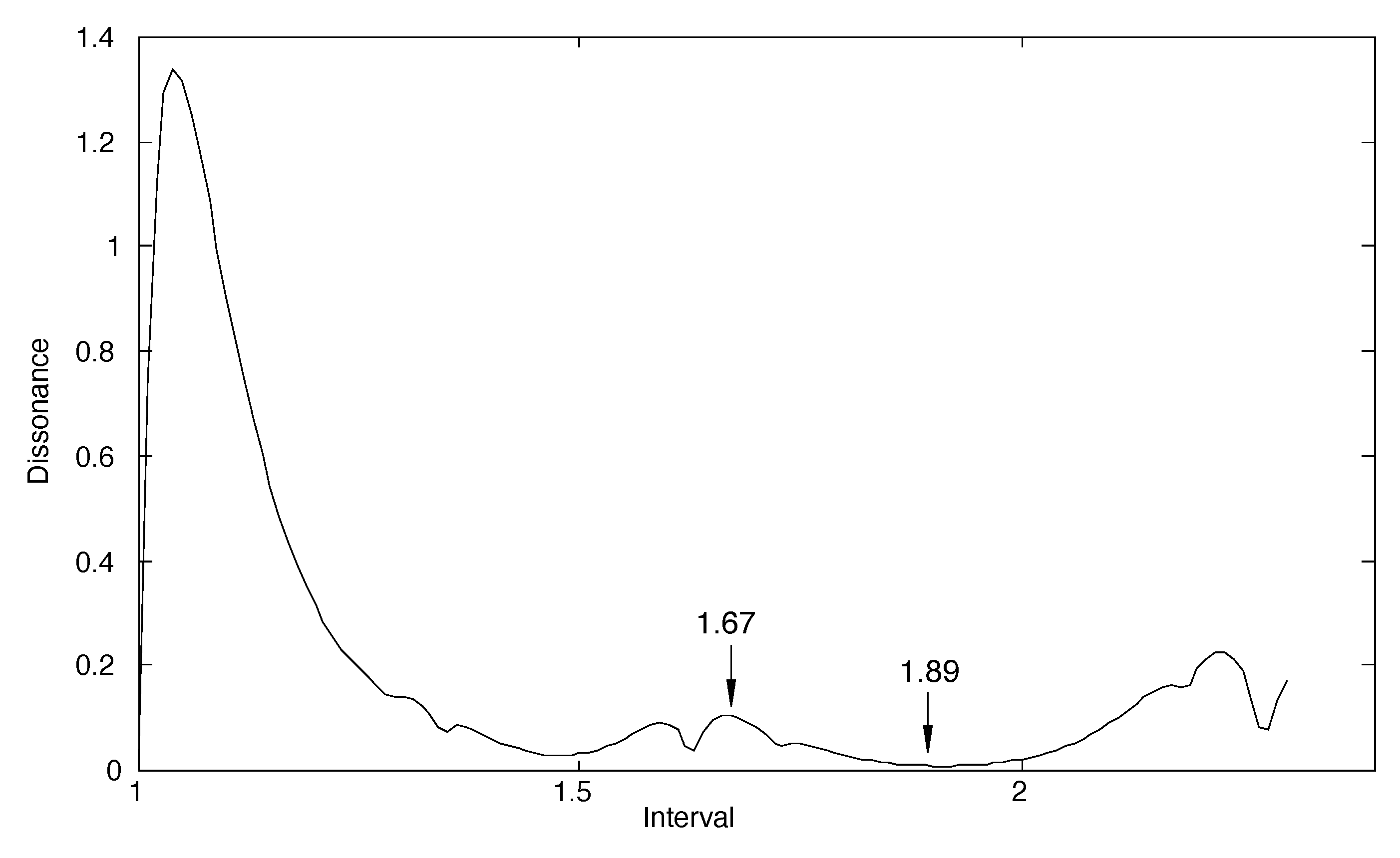
Using the data from [13] again to weight the relative contribution of the partials, their relative amplitudes in the spectrum of the measured bar are approximately as follows:

$$A=[1,0.631,0.3162,0.2818,0.1585,0.1]$$

(7)

Taking (6) and (7) a new dissonance curve can be constructed, as shown in Figure 6. As can be seen, the dissonances predicted by this last curve are much lower than those given in Figure 5, which is not surprising since the high frequency partials are now much less frictional..

5. Application to East and West Traditional Instruments

The ordinary Basque txalaparta consists of wooden planks laid horizontally on two supports and struck with wooden sticks by four hands. Due to the rural origins of the instrument, it is very common to use planks from local trees such as oak, chestnut or alder, and ash sticks, similar to the short handles of rural tools. The metal bar used in the old smithies of the Basque Country was a bronze tube weighing several kilos, with a slightly flattened conical shape, and as such it had all the prerequisites for good sonority for the toberas. According to all the evidence, this must have been the instrument that was originally played at weddings. This percussion instrument has been used together with aerophones such as the alboka capable of providing penta or heptatonic melodies.

A surprising aspect of traditional Thai music is that it is played in a scale that is very close to an equal tempered heptatonic scale, which means that its intervals never coincide (except in the octave) with those of the twelve semitone equal tempered scale. The renat, for example, is a xylophone tuned approximately to a single equal tempered heptatonic scale. The modes of vibration of the renat bars and the txalaparta planks are similar to those of an ideal bar, whose spectrum contains the following first four partials [14]:

$$F_{txalaparta,renat}=[f,2.76f,5.4f,8.9f]$$

(8)

Combining this with a harmonic sound such as the pi, the jakeh or the alboka and taking six partials, gives the mixed dissonance curve that would be produced by playing melodic and percussion instruments together (Figure 7). As can be seen, the curve has dissonance minima in the intervals:

$$D_{min}=[1,1.22,1.35,1.49,1.64,1.80,2]$$

(9)

which largely coincides with the division of the octave into seven equal tempered intervals:

$$7_{eqtemp}=[1,1.10,1.22,1.35,1.49,1.64,1.81,2]$$

(10)

Although it is not the intention here to make categorical statements on the basis of the graphs obtained, since the analysis carried out does nor claim to be complete, it can be said that the heptatonic scale and the spectrum of traditional Thai and Basque instruments are associated in the sense used in this study, which provides arguments to try to explain the use of this scale in the aforementioned traditional music.

By studying the dissonance curves of modern xylophones (Figure 6), we can see that they have evolved into symphonic idiophones, which can be used in conjunction with all kinds of instruments and scales, either with the modern twelve semitone equal tempered scale of Western music, or with the introduction of Eastern microtones. However, the ancient rhythmic idiophones, both Western and Eastern, by their very acoustic nature, allow us to explain how the ’strange’ equal tempered heptatonic scale arises, which fits perfectly with their contemporary melodic aerophones, such as the Thai pi or the Basque alboka, respectively.

6. Conclusions

This study has introduced the idea of the dissonance curve of a given spectrum sound and has presented a computationally efficient method for calculating such curves. It has been shown how the twelve-tone (approximately equal tempered) musical scale is related to the (harmonic) spectrum of most musical instruments in the sense that its dissonance curve has minima in the intervals of the scale.

In addition, the method of dissonance curves has been used in several examples of instruments involving both harmonic and non-harmonic spectra. It has been shown how modern xylophones have evolved to reach true symphonic characteristics, that can coexist with any oriental or western musical instruments.

Finally, an application of the dissonance curve method to traditional Thai and Basque instruments has provided a simple explanation for the initially surprising fact that the equal heptatonic scale is widely used in Thai music, and that a traditional aerophone such as the alboka, capable of producing just simple pentatonic or heptatonic melodies, fits perfectly well with ancient percussion Basque idiophones such as the txalaparta.