Submitted:
11 December 2024
Posted:
12 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
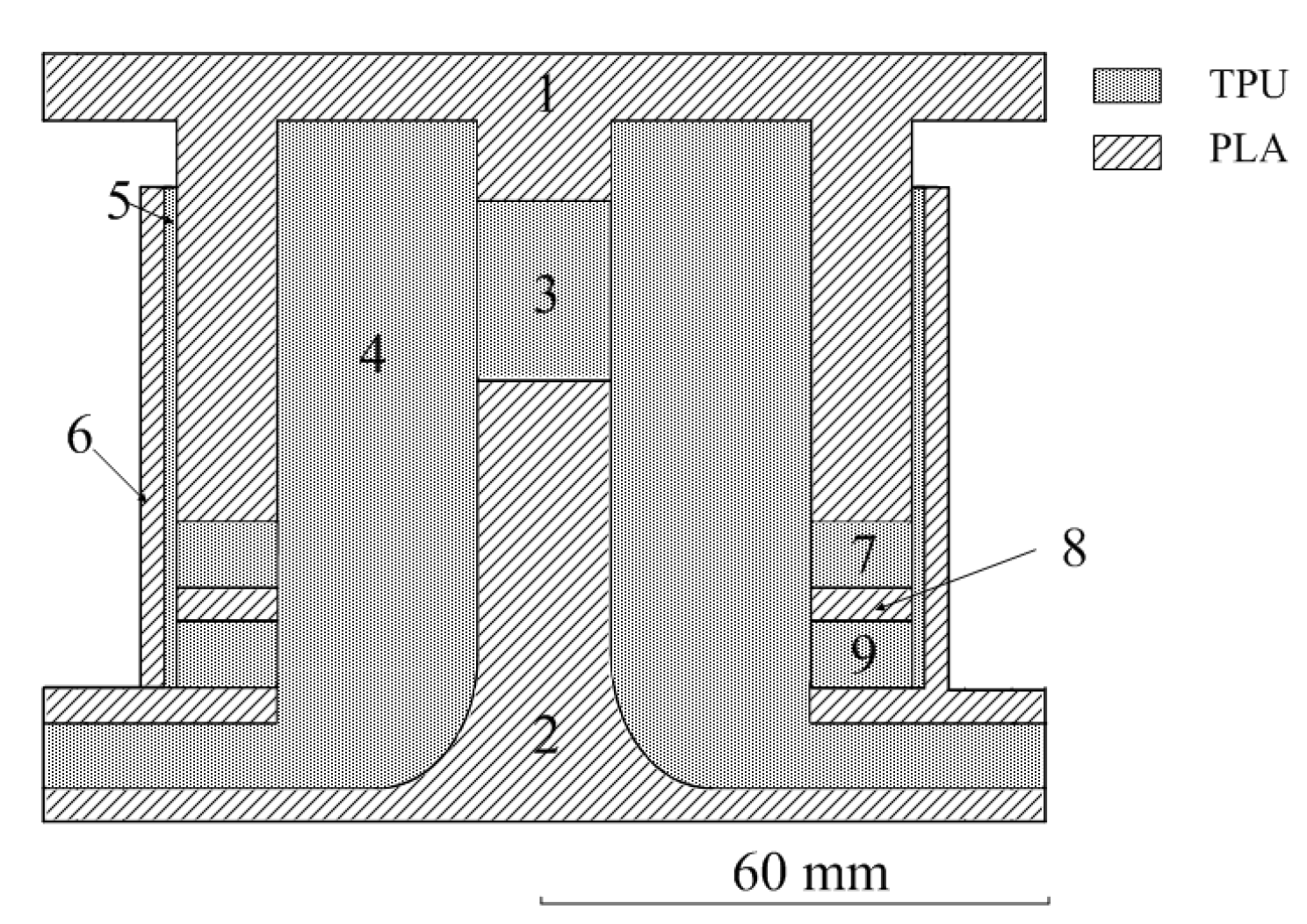
2. Construction of ST Isolator
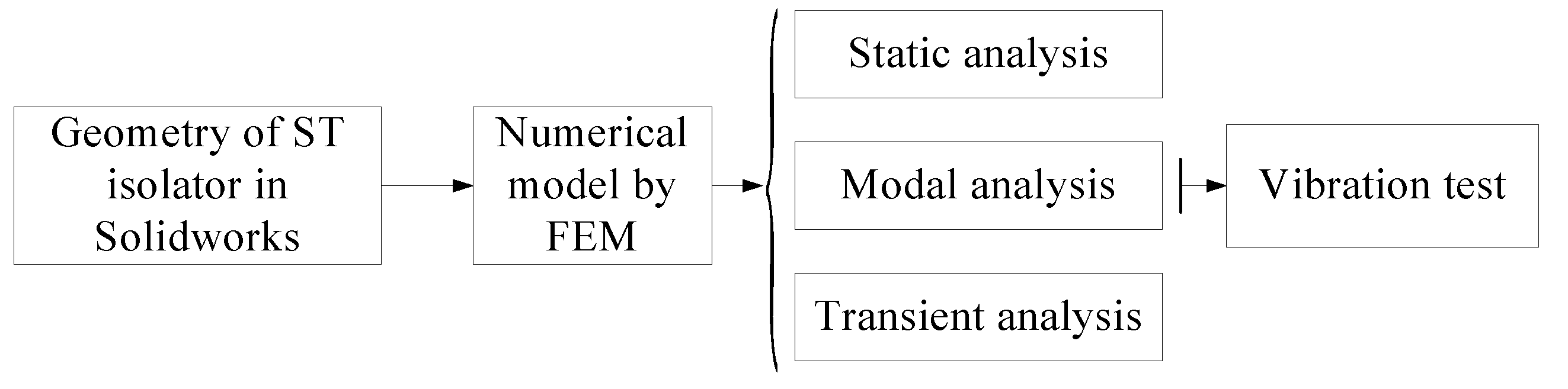
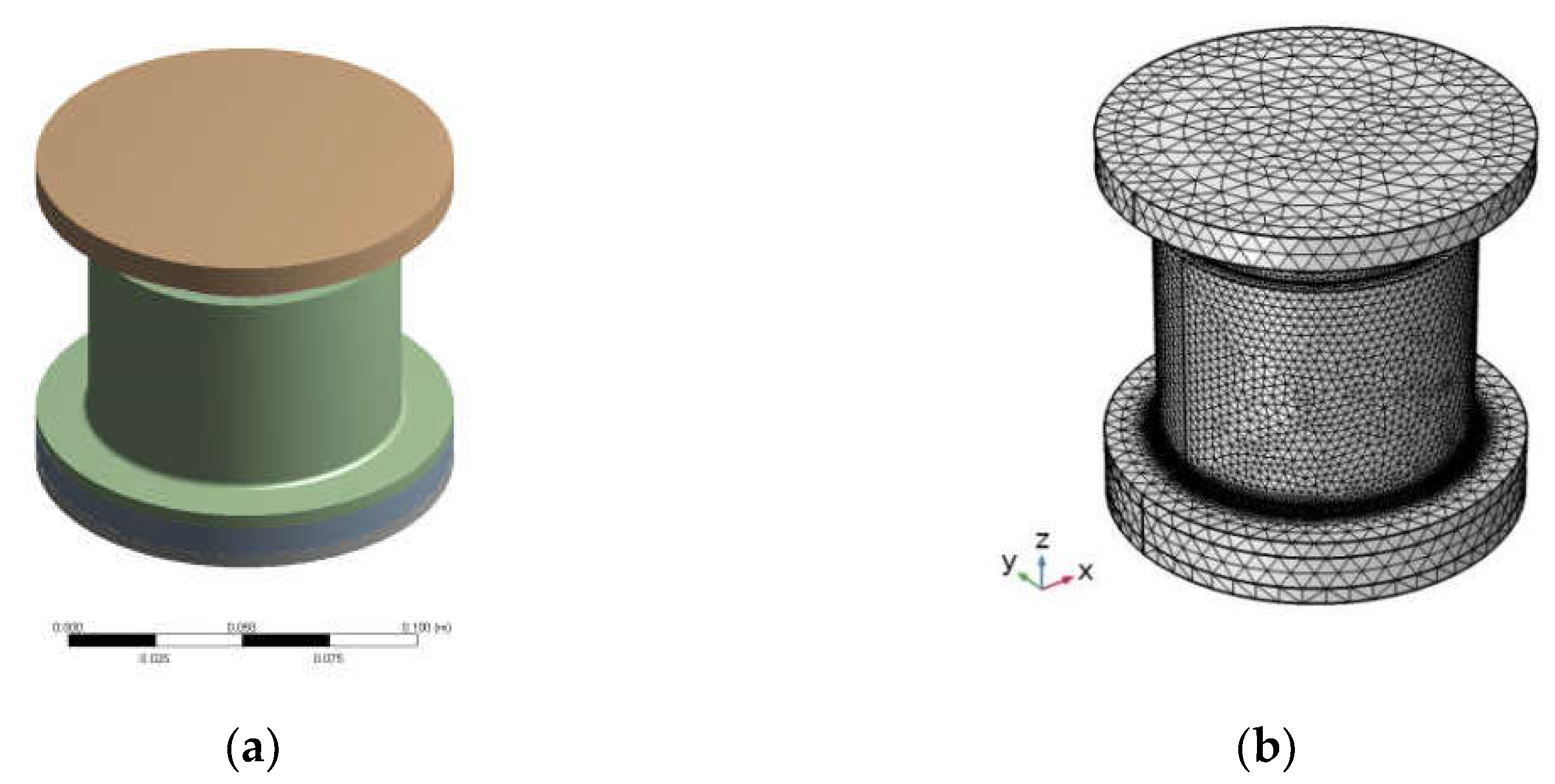
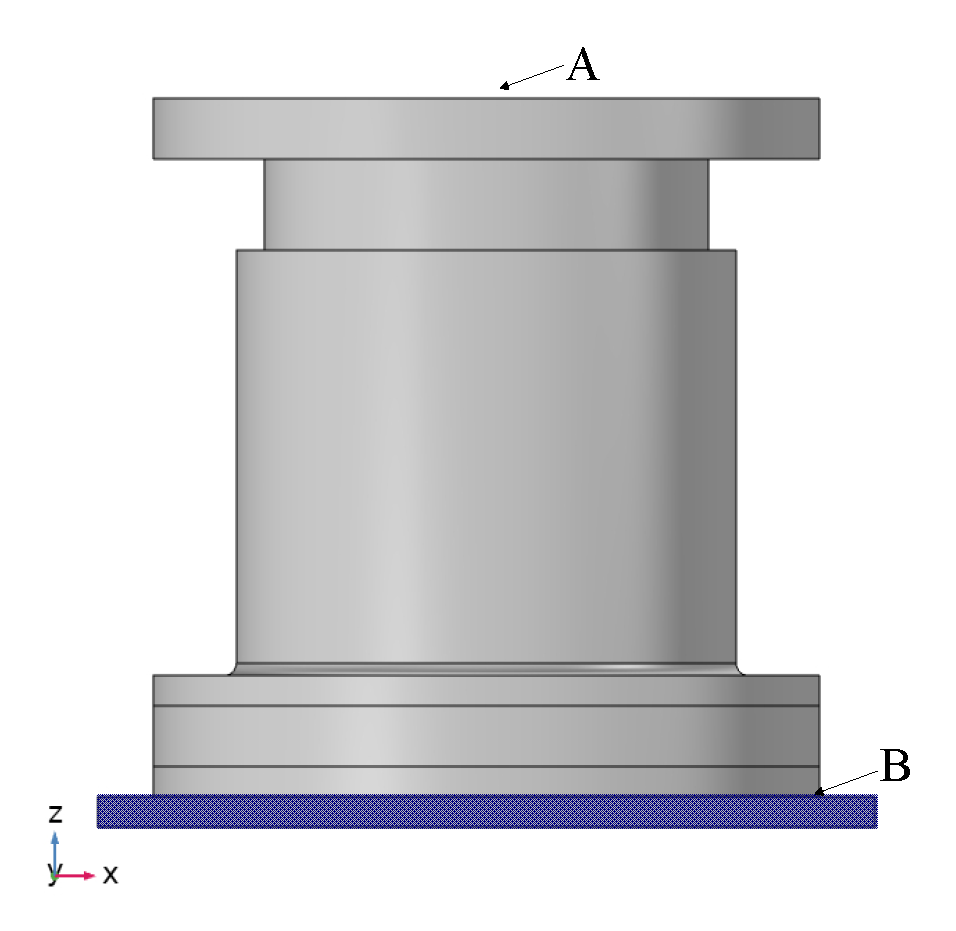
3. Modeling of ST Isolator
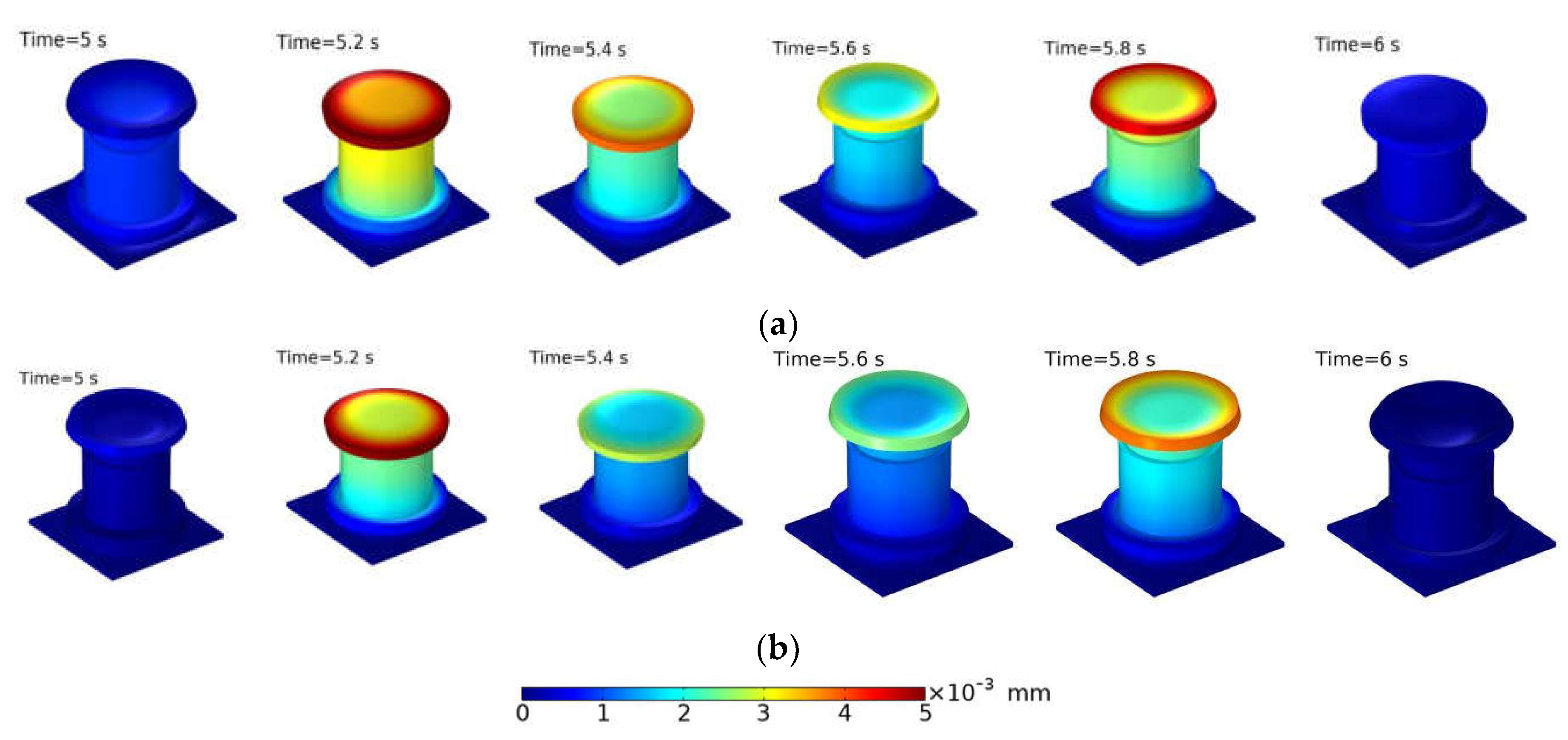
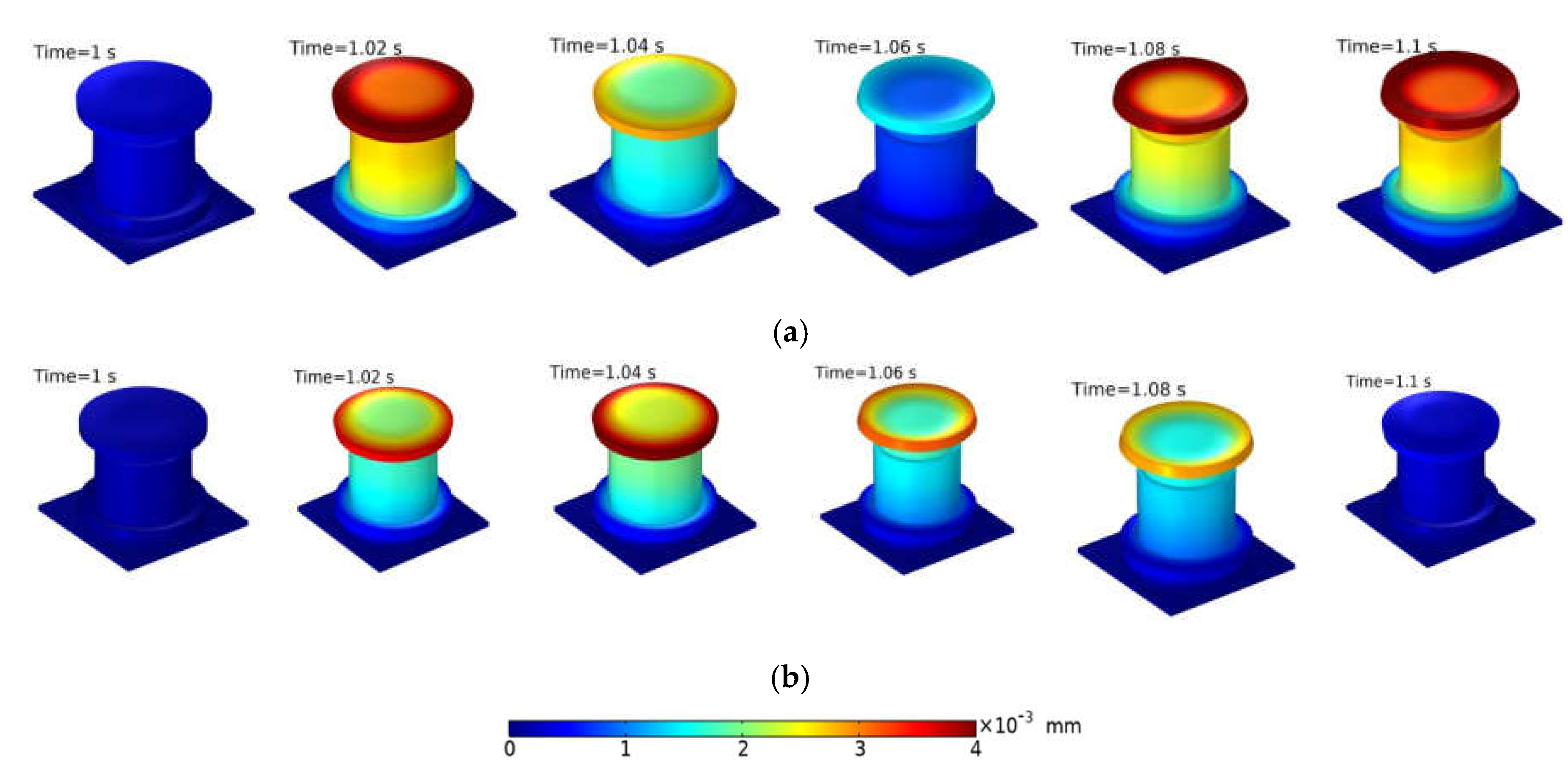
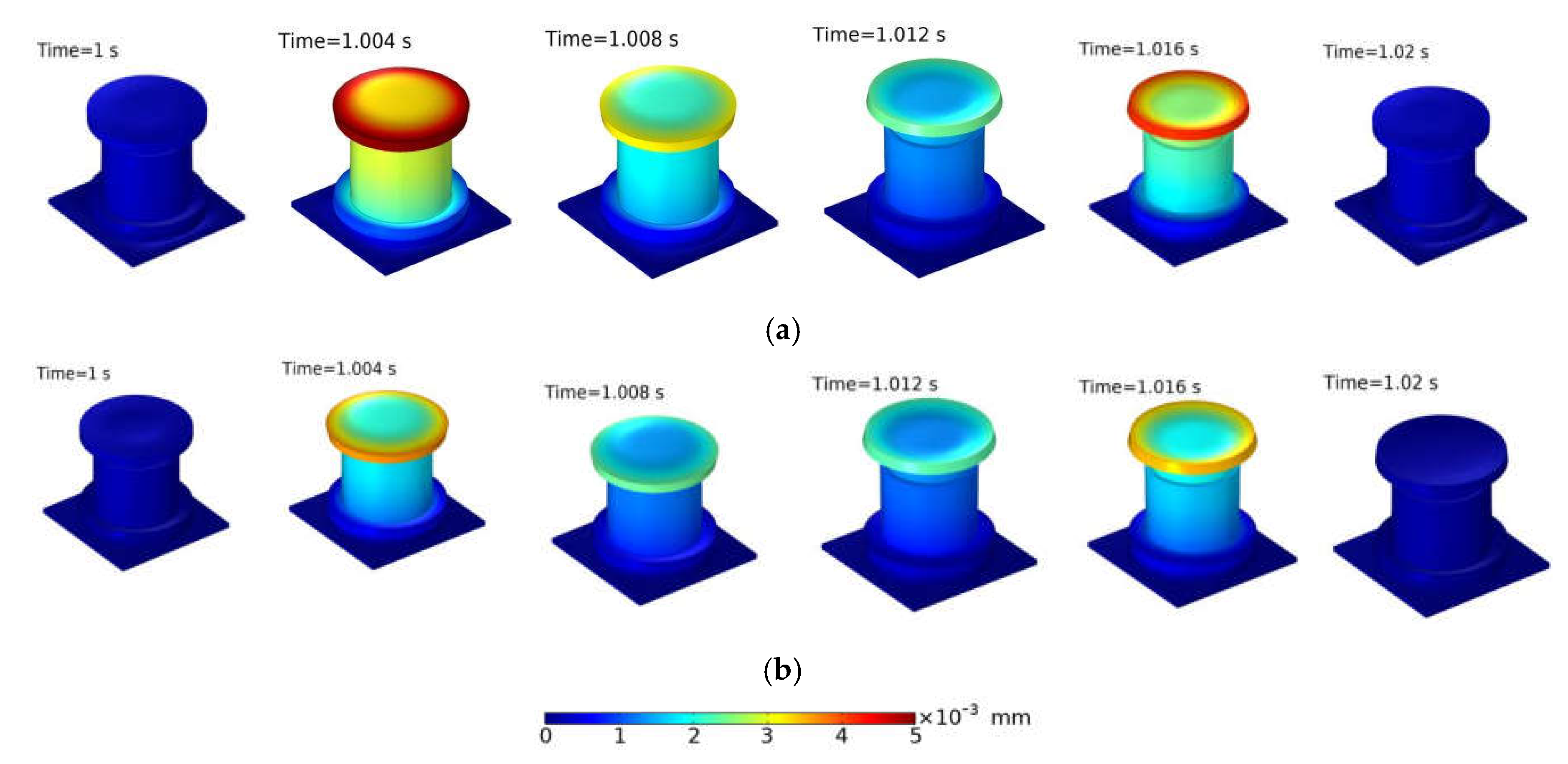
4. Mechanics Analysis and Discussion of ST Isolator
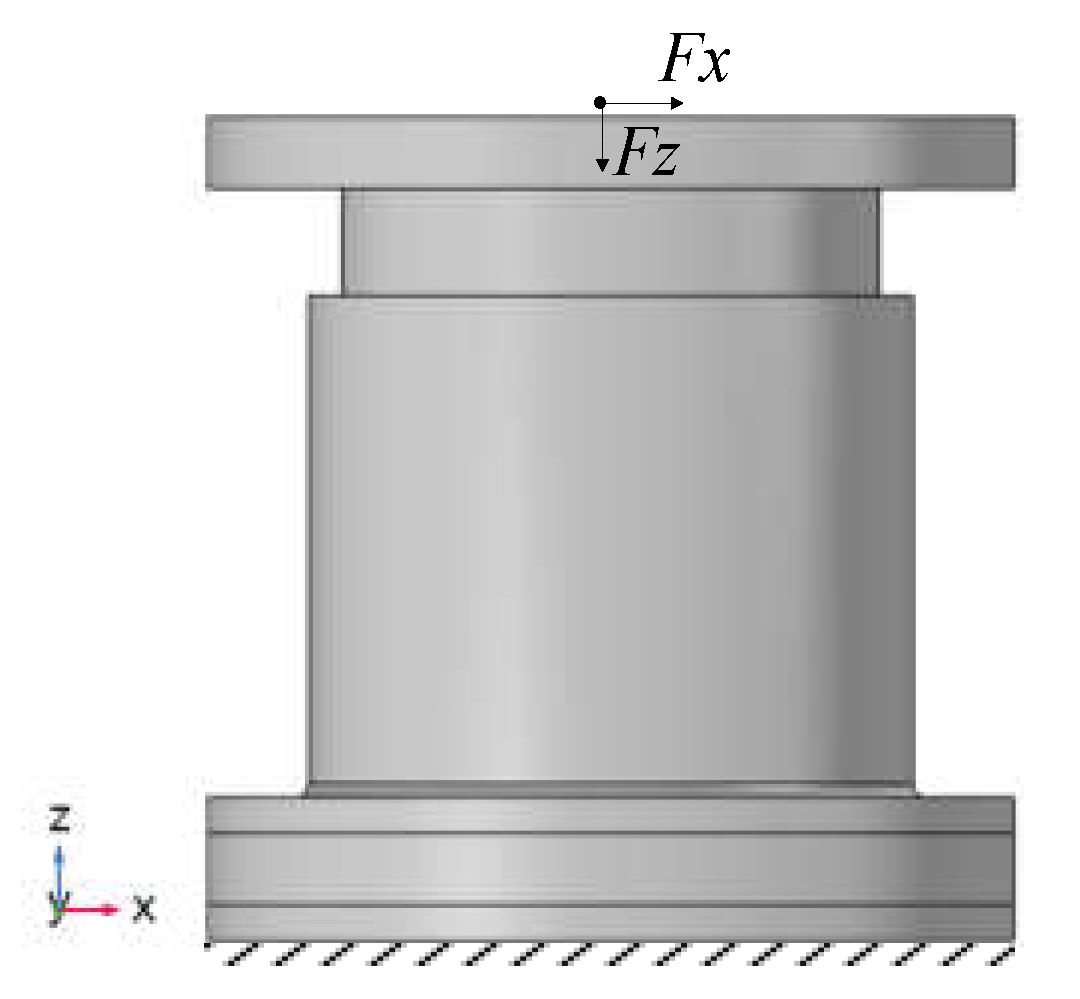
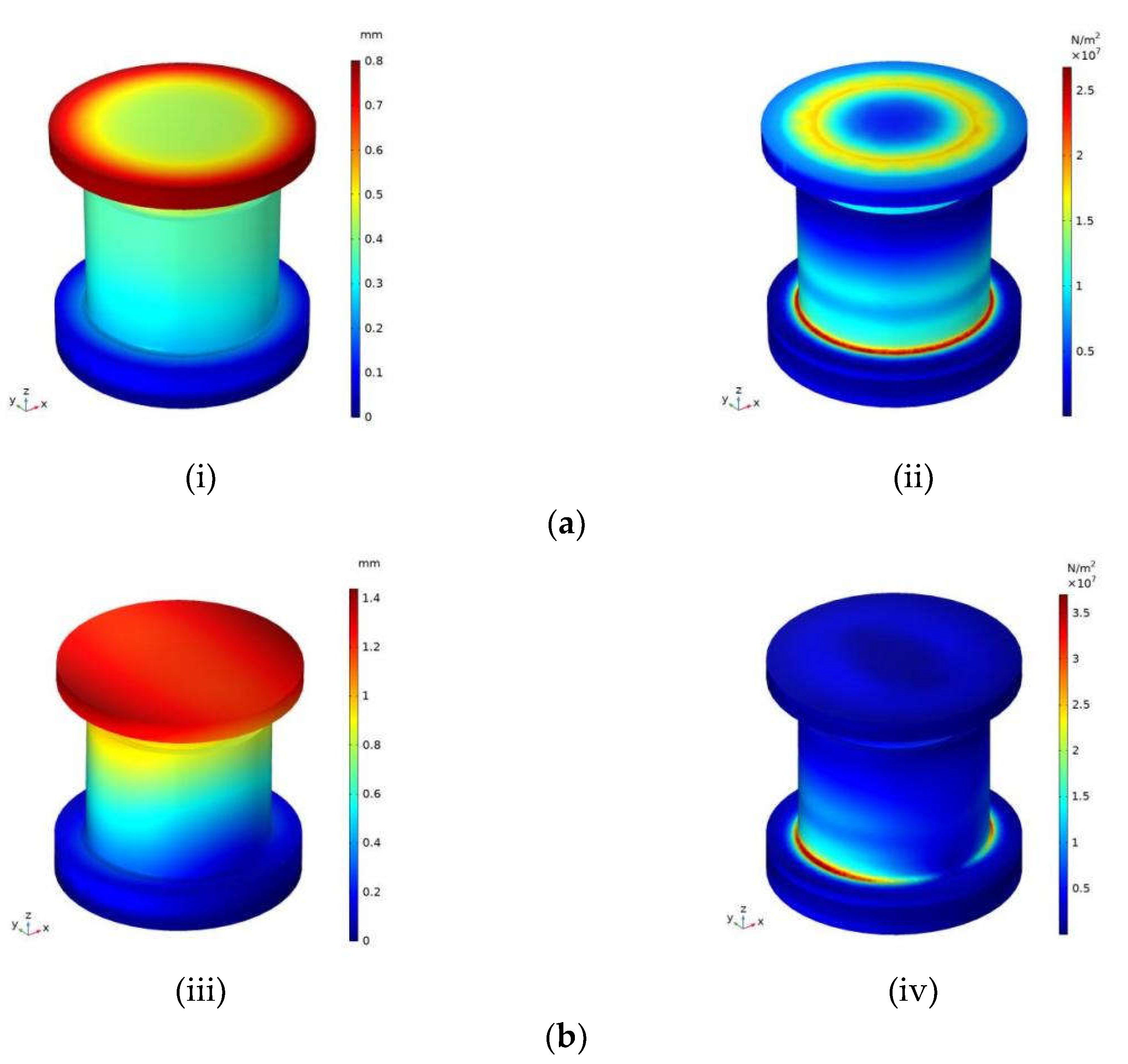
4.1. Static Load Analysis and Discussion
4.2. Modal Analysis and Discussion
4.3. Transient Analysis and Discussion
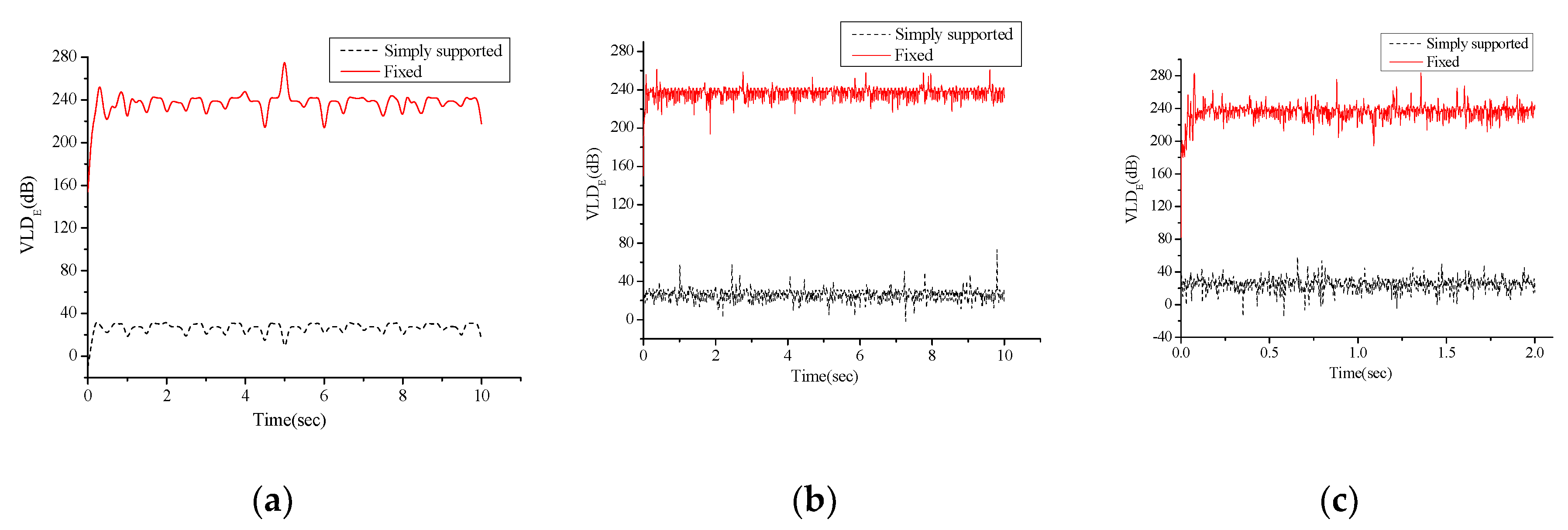
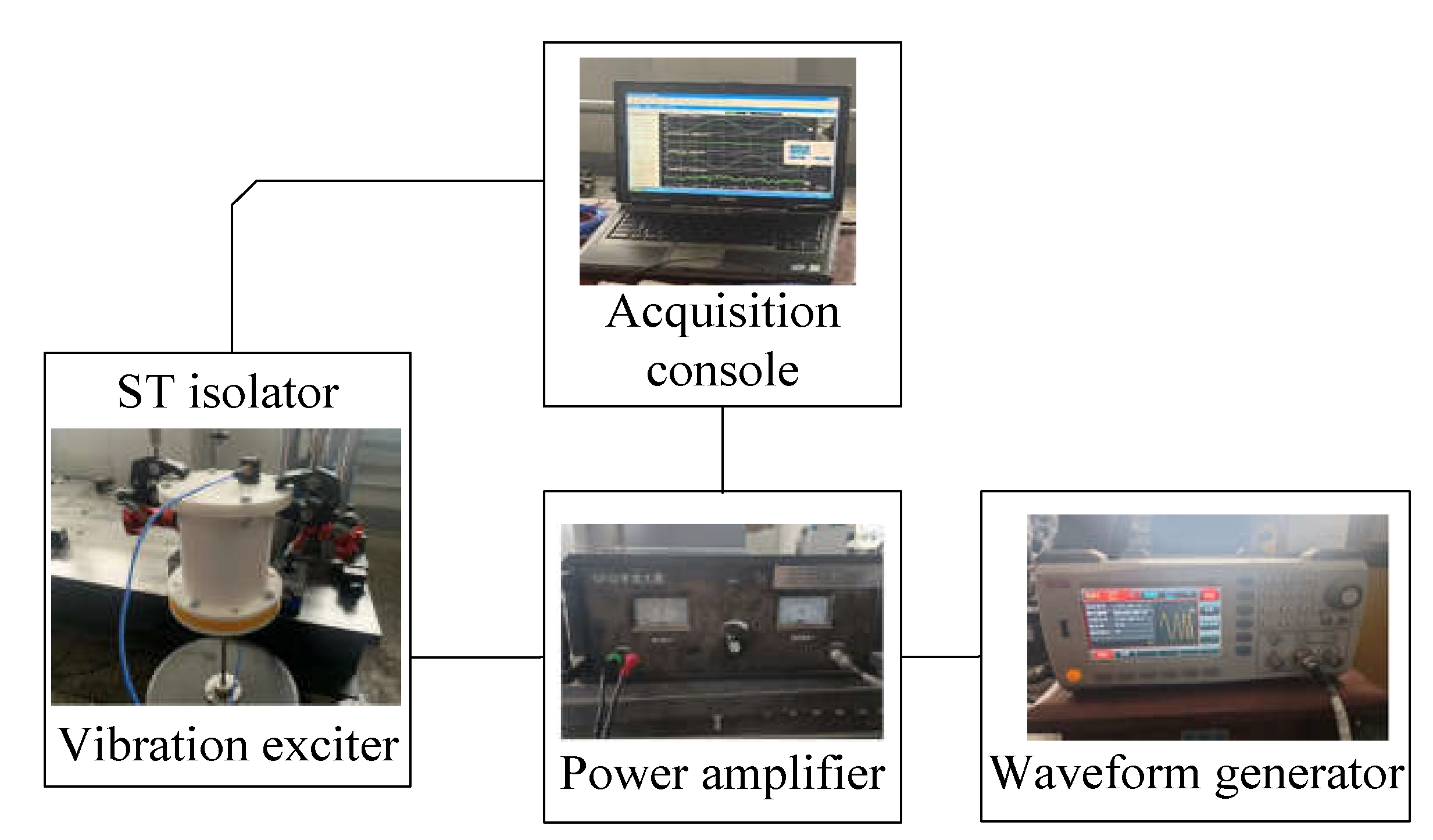
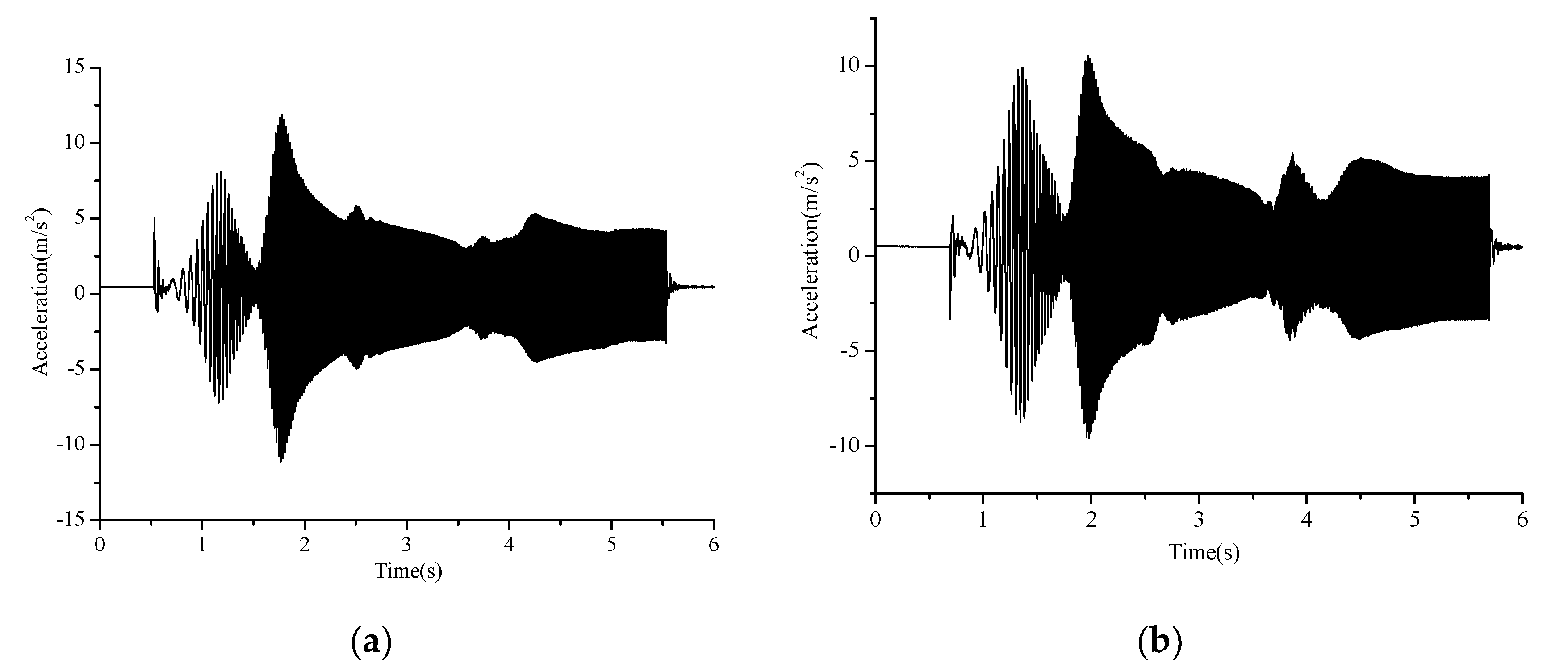
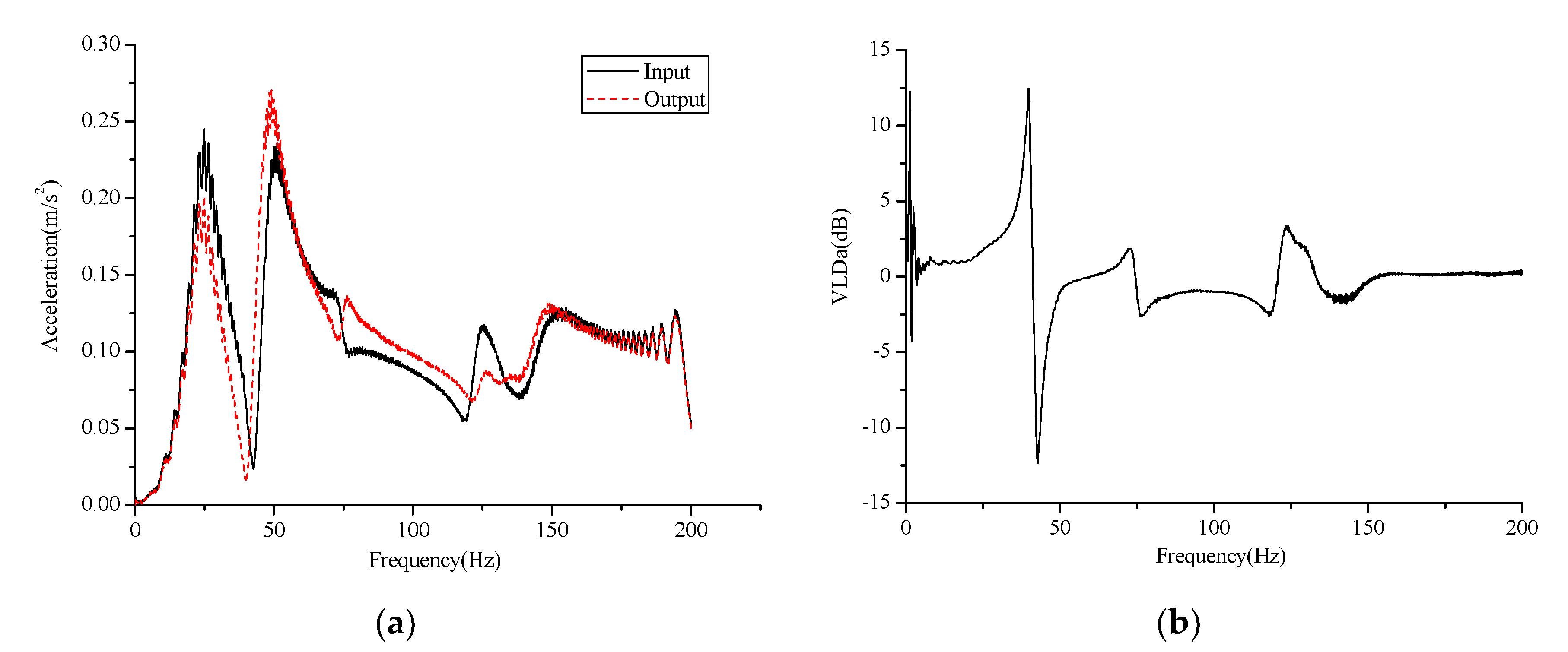
4.4. Vibration Test and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- M. K. Ren, X. L. Xie, Z. W. Huang, and Z. Y. Zhang. Novel rubber-electromagnetic composite active/passive vibration isolator. J Vib Shock (In Chinese) 2021, 40(23), pp. 32-37.
- P. Gao, H. Liu, C. L. Xiang, and P. F. Yan. Study on torsional isolator and absorber comprehensive vibration reduction technology for vehicle powertrain. J Mech Eng(In Chinese) 2021, 57(14), pp. 244-252.
- W. Zhang, W. B. Wang, and S. B. Li. Dynamics and isolation performance of a nonlinear vibration isolator with a bistable cosine-shaped beam. J Vib Shock(In Chinese) 2022, 41(02), pp. 113-122.
- Kan Y, J.C. J, and Terry B. A novel integrated quasi-zero stiffness vibration isolator for coupled translational and rotational vibrations. Mech Syst Signal Pr 2021, 149, p. 107340.
- Y. C. Wang, S. Ma, Y. Li, and W. Xu. Application of active control technology on ship vibration and noise. J Naval Univ Eng(In Chinese) 2021, 33(04), pp. 56-64.
- Z. Q. Lu, D.H. Gu, D. Hu, L.Walter, and L.Q. Chen. A ring vibration isolator enhanced by shape memory pseudoelasticity. Appl Math Model 2021, 100, pp. 1-15. [CrossRef]
- K. Viswanath Allamraju, and K. Sharath Kumar. Finite element analysis of a spring isolator. Mater Today: Proc 2022, 60(p.2), pp. 949-952. [CrossRef]
- Q.L. Zhang, S.Y. Xia, D.L. Xu, and Z.K. Peng. A torsion-translational vibration isolator with quasi-zero stiffness. Nonlinear Dynam 2020, 99, pp. 1467-1488. [CrossRef]
- F. Zhao, J.C. Ji, K. Ye, and Q.T. Luo. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int J Mech Sci 2021, 192, p. 106093. [CrossRef]
- V. Tiwari, S.C. Sharma, and S. P. Harsha. A comparative study on the behavior of ride quality due to deflated state of air spring using different properties of hyperelastic material. Int J Struct Stab Dy 2022, 22(10), p. 2241001. [CrossRef]
- X. Y. Zheng ,Z.Y. Ren, L.L. Shen ,B. Zhang, and H.B. Bai. Dynamic Performance of Laminated High-Damping and High-Stiffness Composite Structure Composed of Metal Rubber and Silicone Rubber. Materials 2021, 14(1), pp.187-187. [CrossRef]
- X.B. Cao, C. Wei, J.Q. Liang, and L.X. Wang. Design and dynamic analysis of metal rubber isolators between satellite and carrier rocket system. Mech Sci 2019, 10(1), pp.71-78. [CrossRef]
- H.W. Wang, S.P. Cao, X.H. Luo, Z.T. Zhang, and Q.J. Wu. Experimental study on the effect of rubber isolator on the vibration of piston pump. Proceedings of the 6th International Conference on Control, Mechatronics and Automation, Tokyo, 12-14 October 2018.
- Z. Jin, Y.L. Zhao, and X.Yang. Study on hyperelastic constitutive model of marine isolation rubber. J Ship Mech(In Chinese) 2023, 27(1), pp.144-152.
- S.J. Lee, G. T. Truong, J.E. Lee, S.H. Park, and K.K. Choi. Dynamic characteristics of combined isolation systems using rubber and wire isolators. Nucl Eng Technol 2022, 54, pp.1071-1084. [CrossRef]
- R. Rahnavard, and R. J. Thomas. Numerical evaluation of steel-rubber isolator with single and multiple rubber cores. Eng Struct 2019, 198, p. 109532. [CrossRef]
- Z.Q. Lu, and L.Q. Chen. Some recent progresses in nonlinear passive isolations of vibrations. Chin J Theor Appl Mech 2017, 49(03), pp. 550-564.
- X.T. Sun, J.W. Qian, Z.F. Qi, and J. Xu. Review on research progress of nonlinear vibration isolation and time-delayed suppression method. Adv Mech(In Chinese) 2023, 53(02), pp.308-356.
- Ali Z, Mahdi B, H. Ramin, P. Liam, M. Fard, and B.F. Rolfe. 3D-printed programmable mechanical metamaterials for vibration isolation and buckling control. Sustainability 2022, 14(11), p.6831, 2022.
- S. Herkal, M.M. Rahman, N. Satish, H V V Jayanthi, and A. Pulickel. 3D printed metamaterials for damping enhancement and vibration isolation: Schwarzites. Mech Syst Signal Process 2023, 185, p. 109819.
- Choi YT, Yoo B, Park J, Pines DJ, and Wereley NM. Design and performance of a 3D-Printed magnetorheological fluid-based adaptive vibration isolator. Front Mater 2023, 10, p.1142590. [CrossRef]
- A. Winner, N. Hieu, and B. Hamzeh. Layered metamaterial beam structures with local resonators for vibration attenuation: model and experiment. Front Mech Eng 2021, 7, p.768508.
- R. Davood, S. Kianoosh, P. Mostafa, A. Mohammad, S. Elyas, G. Ismaeil, B. Majid,A. Karen,B. Mahdi,and B. Mostafa. Shape memory performance assessment of FDM 3D printed PLA-TPU composites by Box-Behnken response surface methodology. Int J Adv Manuf Technol 2023, 127(1-2), pp. 935-950.
- F. Vahid, K. H. Ali, G. Vahabodin, D. Goldis, and O. Maryam. Hydroxyapatite/TPU/PLA nanocomposites: morphological, dynamic-mechanical, and thermal study. Green Process Synth 2022, 11(1), pp. 996-1012.
- Sangharatna M. Ramteke, H. Chelladurai, M. Amarnath. Diagnosis of liner scuffing fault of a diesel engine via vibration and acoustic emission analysis. J Vib Eng Technol 2019,10, pp: 1-19. [CrossRef]
- Seokhwon Lee, Jongdae Kang, Sungwook Park. Measurement and Modeling of crank train friction in light-duty diesel engines. J Mech Sci Technol 2020, 34(2), pp:889-903. [CrossRef]
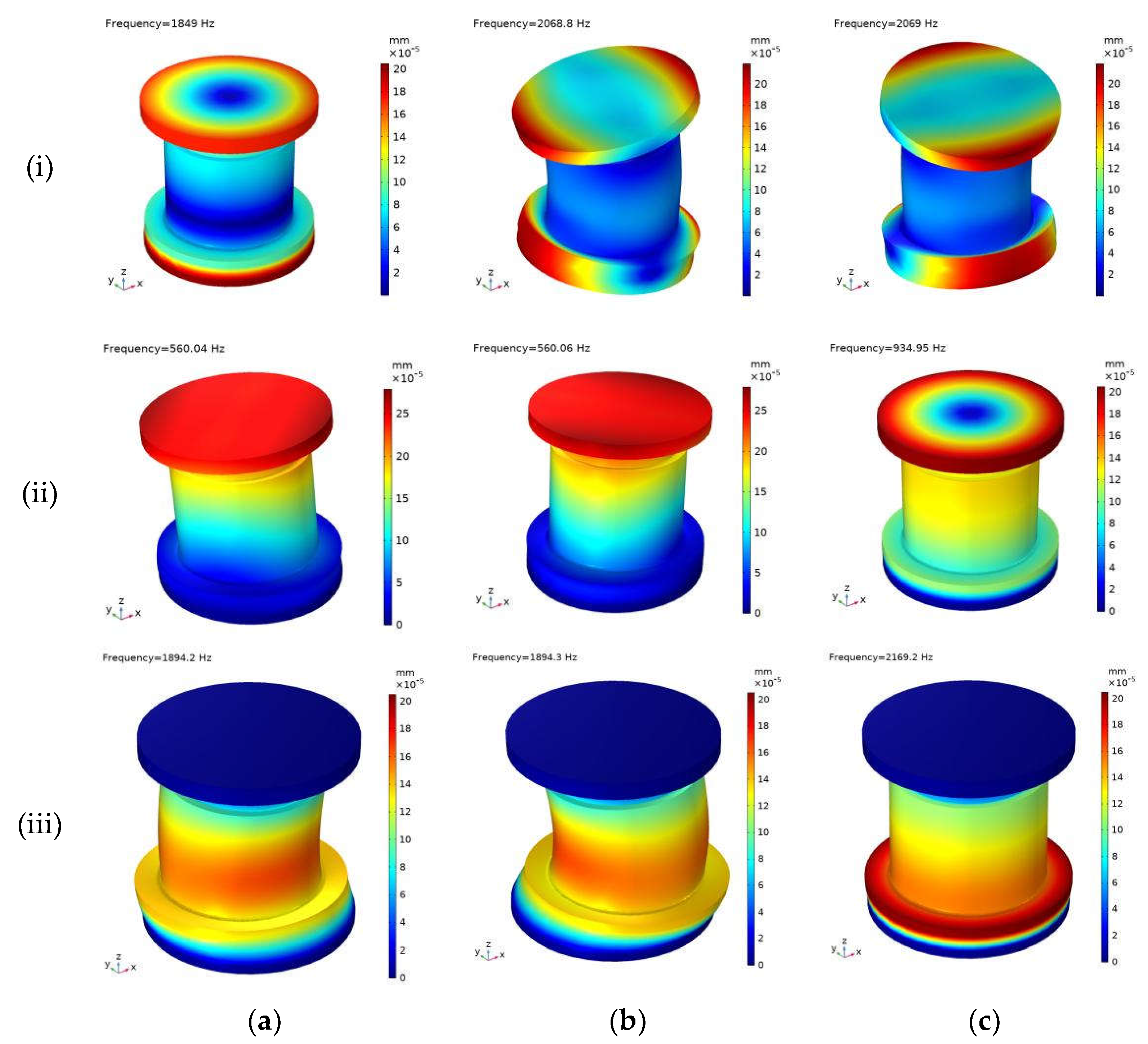
| Order number | Natural | Bottom fixed | Bottom and top fixed |
|---|---|---|---|
| 1 | 1849 | 560.04 | 1894.2 |
| 2 | 2068.8 | 560.06 | 1894.3 |
| 3 | 2069 | 934.95 | 2169.2 |
| 4 | 2361.7 | 1441.4 | 2823.9 |
| 5 | 2362 | 1634.6 | 2824 |
| Frequency(Hz) | Input(m/s2) | Output(m/s2) | VLDa(dB) |
|---|---|---|---|
| 10 | 0.074 | 0.060 | 1.82 |
| 20 | 0.486 | 0.379 | 2.16 |
| 30 | 0.382 | 0.273 | 2.92 |
| 40 | 0.299 | 0.120 | 7.93 |
| 50 | 0.316 | 0.234 | 2.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





