Quantum Relativity (Explanation of the Curvature of Space-Time)

1. Introduction

This research was created for the purpose of answering questions about physics phenomena that have not been answered. Such as explaining the phenomenon of the quantum jump of the electron and the phenomenon of cumulative entanglement. What happens in the phenomenon of the quantum jump of the electron is that when we give the electron energy, this energy causes the electron to move from the energy level that it occupies to the higher energy level without crossing the distance between the two orbits,

which leads to the occurrence of the phenomenon of the quantum jump of the electron.[1] (Svidzinsky et al., 2014)

The role of this scientific paper is to provide a scientific explanation of how the quantum leap occurs without crossing the distance between the orbits. The theory of quantum entanglement is a connection between two quantum entangled particles. If one particle is observed, the other particle is affected by it at the same moment. This is what Einstein objected to; because when the electron traveled this distance in the same period of time, this would lead to the existence of a speed faster than the speed of light. Einstein proved it in special relativity. The maximum speed in the universe is the speed of light. Therefore, the phenomenon of quantum entanglement does not agree with Einstein’s laws. After the validity of quantum laws was proven. There has become a conflict between the laws of relativity that apply to the universe and the quantum laws that apply to atoms. This scientific paper aims to resolve this conflict between the laws of relativity and quantum laws. By establishing a law derived from the laws of relativity to apply to quantum laws. (Equation number 1)

This law in equation 1 is known as quantum relativity because it links the laws of relativity and quantum theory. This law is derived from general relativity. The law works to explain the phenomenon of the quantum leap and the phenomenon of quantum entanglement, as it explains that when energy is given to the atom, the atom does not gain energy, but rather space-time gains that energy. We will discuss the interpretation of this theory in detail later.

• The goal of this scientific research is to answer the explanation of the phenomenon of quantum leap and quantum entanglement and to add some modifications in the Bohr model.

2. Equations

These laws want to explain the results of the final derivation process of this research and what this research wants to prove.

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(n\right)}^4\times {\left({\epsilon }_0\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(h_p\times C\right)}^4}}{T}_{\mu \nu }$$

(1)

where G_µν represents the Einstein tensor, e is the electron charge, G is the universal gravitational constant, T_µν is the energy-momentum tensor, me is the electron mass, h_p is the Planck constant, ε₀ is the vacuum permittivity, r_n is the Bohr radius, Z is the atomic number, n is the energy level, C is the speed of light. This is a law that links the four constants (gravity, electron charge, Planck constant, and speed ) into one law.

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(n\times \lambda \right)}^4\times {\left({\epsilon }_0\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

(2)

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times \left(n\times \mathrm{\hslash }\right)}^4}{{\left(r_n\right)}^2\times {\left(\lambda \right)}^2}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

where E_n represents the photon energy, $\lambda$ is the wavelength. This law explains the final result of the derivation. This law proves the creation of a relationship that links the photon energy and curvature of space-time.

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(\lambda \right)}^4\times {\left({\epsilon }_0\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(E_t\right)}^4}}{T}_{\mu \nu }$$

(3)

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times {\left(n\right)}^8\times \left(\mathrm{\hslash }\right)}^4}{{\left(r_n\right)}^2\times {\left(\lambda \right)}^2}}{\displaystyle \frac{G}{{\left(E_t\right)}^4}}{T}_{\mu \nu }$$

where E_t represents the energy of the total photon.

$$E_{\left(p\right)}^2={\displaystyle \frac{{\left(2\pi \times n\right)}^4\times {\left(2\times {\epsilon }_0\right)}^2}{{\left(r_n\right)}^2\times {\left(m_e\times Z\right)}^2}}{\displaystyle \frac{{\left(\mathrm{\hslash }\times C\right)}^5}{{\left(e\right)}^4\times G}}$$

(4)

where E_p represents the Planck energy. This law links Planck energy with other cosmological constants.

$$\mathit{E}={\displaystyle \frac{{\mathit{n}}^{\mathbf{2}}\times {\mathit{h}}_{\left(\mathit{a}\right)}^{\mathbf{2}}\times \mathbf{2}\mathit{K}\mathit{E}}{{\left(\mathit{Z}\right)}^{\mathbf{2}}}}+\mathit{n}\times \mathit{P}\times {\displaystyle \frac{\mathit{\omega }}{\mathit{k}\times \mathit{\alpha }\times \mathit{Z}}}$$

(5)

$$\mathit{E}=\mathit{m}\times {\mathit{C}}^{\mathbf{2}}+\mathit{P}\times \mathit{C}$$

where E represents the energy, h_{( a)} is the atomic constant, KE is the kinetic energy, P is the momentum, $\omega$ is the angular velocity, k is the wave vector, and$\alpha$ is the fine-structure constant. This law explains the final result of the derivation. This law proves the creation of a relationship that links energy and kinetic energy. That the lost kinetic energy comes out in the form of radiant energy.

$$E=\hslash \times C\times n\times k$$

(6)

$$E=n\times h_{\left(p\right)}\times \nu$$

where $\mathrm{\hslash }$ represents the reduced Planck constant, $\nu$ is the frequency. This law explains the final result of the derivation. This law proves the creation of a relationship that links the energy of the total photon and wave vector.

$$H={\displaystyle \frac{e^4\times {\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2\times G}{{\left(\hslash \times C\right)}^3}}$$

(7)

$${\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2={\left(m_e\right)}^2\times {k_e}^2={\displaystyle \frac{{\left(m_e\right)}^2}{{\left(4\pi \times {\epsilon }_0\right)}^2}}$$

where H represents the Cosmic Constant (David cosmological constant), ${\left(k_e\right)}_{{\left(m\right)}_1 }$is the Agglomerated mass permittivity constant, $k_e$ is the Coulomb constant. This law works to link the four constants ( gravity, electron charge, Planck constant, and speed ) into one law.

$$X={\displaystyle \frac{e^2\times {\left(k_e\right)}_m\times G}{{\left(\hslash \times C\right)}^2}}$$

(8)

$${\left(k_e\right)}_m ={\left(m_e\right)}^2\times k_e={\displaystyle \frac{{\left(m_e\right)}^2}{\left(4\pi \times {\epsilon }_0\right)}}$$

$$X=\alpha \times R={\displaystyle \frac{\alpha \times {\left(m_e\right)}^2}{{\left(m_p\right)}^2}}={\displaystyle \frac{\alpha \times {\left(m_e\right)}^2\times G}{\mathrm{\hslash }\times C}}={\displaystyle \frac{e^2\times {\left(m_e\right)}^2\times G}{\left(4\pi \times {\epsilon }_0\right)\times {\left(\mathrm{\hslash }\times C\right)}^2}}={\displaystyle \frac{e^2\times {\left(k_e\right)}_m\times G}{{\left(\mathrm{\hslash }\times C\right)}^2}}$$

where X represents the unknown force X (David constant), ${\left(k_e\right)}_m$ is the mass permittivity constant. This is a law that links the four constants ( gravity, electron charge, Planck constant, and speed ) into one law.

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{8\pi \times \overline{\mathrm{\hslash }}\times e^2\times {\left(Z\right)}^2}{n^2\times E^2}}{T}_{\mu \nu }$$

(9)

$$\overline{\mathrm{\hslash }}=k_e\times X={\displaystyle \frac{e^2\times {\left(m_e\right)}^2}{{\left(4\pi \times {\epsilon }_0\right)}^2\times \mathrm{\hslash }\times C\times {\left(m_p\right)}^2}}={\displaystyle \frac{H\times \mathrm{\hslash }\times C}{e^2}}={\displaystyle \frac{H\times k_e}{\alpha }}$$

$$\overline{\hslash }={\displaystyle \frac{e^2\times {\left( {\left(k_e\right)}_{{\left(m\right)}_1 }\right)}^2\times G}{{\left(\hslash \times C\right)}^2}}$$

where $\overline{\hslash }$ represents the multiverse constant. This law wants to prove is the creation of a relationship that links the curvature of space-time and the energy of the total photon.

$$n^2\times {\hslash }^2={\left(k_e\right)}_{{\left(m\right)}_1}\times r\times e^2$$

(10)

$${\left(k_e\right)}_{{\left(m\right)}_1 }=\left(m_e\right)\times k_e={\displaystyle \frac{\left(m_e\right)}{\left(4\pi \times {\epsilon }_0\right)}}$$

This law affects the Planck constant and the charge of the electron.

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

(11)

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4\times {\left({\mu }_0\times {\epsilon }_0\right)}^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

where ${\mu }_{ 0}$ Vacuum permeability.

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}\times {\left({\mathsf{\epsilon }}_0\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

(12)

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 1.1797075656\times {\mathbf{10}}^{-\mathbf{74}}\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{\mathrm{ }1}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$${\mathit{E}}_{\mathit{n}}={\mathit{h}}_{\left(\mathit{p}\right)}\times \mathit{\nu }$$

where $h_{\left(p\right)}$ represents the Planck constant, $\nu$ is the frequency.

$$a={\displaystyle \frac{G\times m\times \alpha \times {\left(Z\right)}^2}{R\times {\left(r_n\right)}^2}}$$

(13)

$$E_n={\displaystyle \frac{n\times G\times {\left(m_p\right)}^2\times Z}{r_n}}$$

where $a$ represents the acceleration.

3. These laws have been modified from the mix Planck laws

$${\mathit{t}}_{\left(\mathit{p}\right)}={\displaystyle \frac{{\mathit{l}}_{\mathit{p}}^3}{{\mathit{l}}_{\mathit{p}}^2\times \mathit{C}}}$$

(14)

Definition of time: Create a movement on a spatially fixed three-dimensional body that exists on the surface area of space-time at the body's fixed motion speed

$$t_{\left(p\right)}={\displaystyle \frac{n}{2\times \nu \times sin\left(\mathsf{\Theta }\right)}}\mathrm{ }$$

(15)

Definition of time: Create a movement on a spatially fixed three-dimensional body that exists on the surface area of space-time at the angle at which a stationary body moves

• How quantum entanglement occurs?
  What happens is that the electron connects to the other electron through space-time, as space-time acts like a quantum tunnel that connects the two electrons. In this way, the electron does not penetrate the speed of light, But in relation to large objects, you see that it has crossed the speed of light.
• This hypothesis was based on scientific foundations, the most important of which is:

  1) 

  the connection between relativity and quantum mechanics occurs via quantum entanglement and loop gravitational entanglement.

  2) 

  quantum entanglement occurs by the contraction of space-time.

  3) 

  space-time contraction occurs by space-time absorbing energy.

  4) 

  the quantum jump of the electron occurs as a result of the contraction of space-time.

4. Derivation of Equations

Completing the derivation of the laws resulting from quantum relativity (quantum world)

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$$n\times \lambda =2\pi \times r_n$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\times {\left(\mathit{n}\times \mathit{\lambda }\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

This is derivation number 1

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$${\mu }_0\times {\epsilon }_0=\left({\displaystyle \frac{1}{{\left(C\right)}^2}}\right)$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(C\right)}^4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E=m\times C^2$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(E\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E_t=E\times \alpha \mathrm{ }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(E_t\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$E_t=\mathrm{ }{E}_n\times n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

This is derivation number 2

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$n\times \lambda =2\pi \times r_n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \times {\left(n\times \lambda \right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4\times {\left({\mu }_0\times {\epsilon }_0\right)}^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$${\mu }_0\times {\epsilon }_0=\left({\displaystyle \frac{1}{{\left(C\right)}^2}}\right)$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(C\right)}^4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E=m\times C^2$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(E\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E_t=E\times \alpha \mathrm{ }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(E_t\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E_t=\mathrm{ }{E}_n\times n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

This is derivation number 3

$$a={\displaystyle \frac{G\times m\times \alpha \times {\left(Z\right)}^2}{R\times {\left(r_n\right)}^2}}$$

$$a={\displaystyle \frac{v^2}{r}}$$

$${\displaystyle \frac{v^2}{r}}={\displaystyle \frac{G\times m\times \alpha \times {\left(Z\right)}^2}{R\times {\left(r_n\right)}^2}}$$

$$v^2={\displaystyle \frac{G\times m\times \alpha \times {\left(Z\right)}^2}{R\times r_n}}\mathrm{ }\mathrm{ }{\displaystyle \frac{{\left(n\right)}^2\times \alpha }{{\left(n\right)}^2\times \alpha }}$$

$${\left(\mathit{C}\right)}^2={\displaystyle \frac{{\left(n\right)}^2\times v^2}{{\left(\alpha \right)}^2}}$$

$${\left(\mathit{C}\right)}^2={\displaystyle \frac{{\left(n\right)}^2\times G\times m\times {\left(Z\right)}^2}{R\times r_n\times \alpha }}\mathrm{ }\mathrm{ }{\displaystyle \frac{m}{m}}$$

$${\left(\mathit{C}\right)}^2={\displaystyle \frac{{\left(n\right)}^2\times G\times m\times {\left(Z\right)}^2}{R\times r_n\times \alpha }}\mathrm{ }\mathrm{ }{\displaystyle \frac{m}{m}}$$

$$\mathit{E}=\mathit{m}\times {\mathit{C}}^{\mathbf{2}}$$

$$E={\displaystyle \frac{{\left(n\right)}^2\times G\times {\left(m_e\right)}^2\times {\left(Z\right)}^2}{R\times r_n\times \alpha }}$$

$${\mathit{E}}_{\mathit{t}}=\mathit{E}\times \mathit{\alpha }\mathrm{ }$$

$$E_t={\displaystyle \frac{{\left(n\right)}^2\times G\times {\left(m_e\right)}^2\times Z}{R\times r_n}}$$

$$E_t=\mathrm{ }{E}_n\times n$$

$$E_n={\displaystyle \frac{n\times G\times {\left(m_e\right)}^2\times Z}{R\times r_n}}$$

$$R={\displaystyle \frac{{\left(m_e\right)}^2}{{\left(m_p\right)}^2}}$$

where $m_p$ represents the Planck mass.

$$E_n={\displaystyle \frac{n\times G\times {\left(m_p\right)}^2\times Z}{r_n}}$$

This is derivation number 4

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(n\right)}^4\times {\left({\epsilon }_0\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(h_p\times C\right)}^4}}{T}_{\mu \nu }$$

$$\mathrm{\hslash }={\displaystyle \frac{h_p}{2\pi }}$$

$$n\times \mathrm{\hslash }=m_e\times v\times r_n$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left(2\pi \times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(n\right)}^4\times {\left(\mathrm{\hslash }\times {\epsilon }_0\right)}^2\times {\left(h_p\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(C\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times {\left(Z\right)}^2}{{\left(n\right)}^2\times {\left({\epsilon }_0\right)}^2\times {\left(\mathrm{v}\right)}^2\times {\left(h_p\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(C\right)}^4}}{T}_{\mu \nu }$$

$$v={\displaystyle \frac{\left(2\pi \times r_n\right)}{T}}={\displaystyle \frac{2\pi \times r_n\times \nu \times \alpha \times Z}{{\left(n\right)}^2}}$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(n\right)}^2\times \left(2\pi \right)}{{\left({\epsilon }_0\right)}^2\times {\left(2\pi \times r_n\times \nu \times \alpha \right)}^2\times {\left(h_p\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(C\right)}^4}}{T}_{\mu \nu }$$

$$E_n=h_{\left(p\right)}\times \nu$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(n\right)}^2\times \left(2\pi \right)}{{\left({\epsilon }_0\right)}^2\times {\left(\left(2\pi \right)\times r_n\times \alpha \right)}^2\times {\left(E_n\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(C\right)}^4}}{T}_{\mu \nu } {\displaystyle \frac{{\left(4\pi \right)}^2\times {\left(\hslash \right)}^2}{{\left(4\pi \right)}^2\times {\left(\hslash \right)}^2}}$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{{\left(4\pi \right)}^2\times {\left(n\right)}^4\times \left(\hslash \right)}^2\times \left(2\pi \right)}{{\left(\left(2\pi \right)\times r_n\times \alpha \right)}^2\times {\left(E_n\right)}^2}}{\displaystyle \frac{{\left(\alpha \right)}^4\times G}{{\left(C\right)}^2}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{{\left(4\pi \right)}^2\times {\left(n\right)}^4\times \left(\hslash \right)}^2\times \left(2\pi \right)}{{\left(\left(2\pi \right)\times r_n\times \alpha \right)}^2\times {\left(E_n\right)}^2}}{\displaystyle \frac{{\left(\alpha \right)}^2\times G}{{\left(\mathsf{\lambda }\times \nu \right)}^2}}{T}_{\mu \nu } {\displaystyle \frac{{\left(h_p\right)}^2}{{\left(h_p\right)}^2}}$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^2\times {\left(\mathsf{\lambda }\right)}^2}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^2\times {\left(\mathsf{\lambda }\right)}^2}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu } {\displaystyle \frac{{\left(2\pi \right)}^2}{{\left(2\pi \right)}^2}}$$

$$n\times \lambda =2\pi \times r_n$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^5\times {4\times \left(\hslash \right)}^4}{{\left(\mathsf{\lambda }\right)}^4}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^2\times {\left(\mathsf{\lambda }\right)}^2}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu } {\displaystyle \frac{{\left(n\right)}^2}{{\left(n\right)}^2}}$$

$$n\times \lambda =2\pi \times r_n$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{2\pi \times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^4}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

This is derivation number 5

5. Method

My name is Ahmed. I have made a theoretical derivation of the equation of general relativity as explained in this research for the purpose of obtaining an equation that can be applied within the quantum world so that it describes the movement of the electron during the quantum jump in the Bohr model. After that, the researcher Samira reviewed the research and verified it, and then she worked on applying this theory to the movement of the electron during the occurrence of the quantum leap, using previous research and matching it with the results of this equation to determine its validity.

• This part of the research will explain the spectrum of the hydrogen atom in a new way, as the results presented in these tables from previous research match the results extracted from the equation, and this is consistent with the validity of this equation. Because the new equation is consistent with the photon energy equation. We will discuss that part of the research in the results and discussion.
• Table 5 shows the measurement results tested.[3] (Nanni, 2015)
  
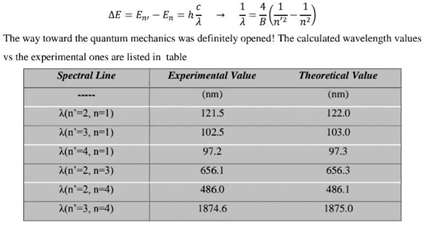
• Table 5 it represents the theoretical and experimental value of the hydrogen atom. Using the photon energy law mentioned above, this table.

Figure 1. Bohr hydrogen atomic model incorporating de Broglie’s .[4] (Jordan, 2024).

Figure 1. Bohr hydrogen atomic model incorporating de Broglie’s .[4] (Jordan, 2024).

This drawing, taken from previous research, shows how the quantum leap occurs through interference, as my equation showed. When interference occurs between the orbit occupied by the electron and the energy level higher than the electron’s orbit, it occurs in the form of wave interference of this type as a result of a contraction in the fabric of space-time. The black circle represents the orbit occupied by the electron, while the red color represents how interference occurs from the orbit higher to the orbit occupied by the electron in the form of wave interference. In other words, the upper level works to contract, forming a wave equal to the same wave as the level occupied by the electron through the de Broglie equation. n × λ = 2π × r

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times {\left(m_e\times Z\right)}^2}{{\left(n\times \lambda \right)}^4\times {\left({\epsilon }_0\right)}^2}}{\displaystyle \frac{{\left(e\right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

Because the equation connects more than one equation into a single equation. As

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{8\pi \times G}{C^4}}{T}_{\mu \nu }$$

$$\Delta E_n={\displaystyle \frac{h_p\times C}{\lambda }}$$

$$n\times \lambda =2\pi \times r_n$$

Figure 2. The observed emission line spectrum of atomic hydrogen in chapter 2 atoms.[5] (Manini, 2020).

Figure 2. The observed emission line spectrum of atomic hydrogen in chapter 2 atoms.[5] (Manini, 2020).

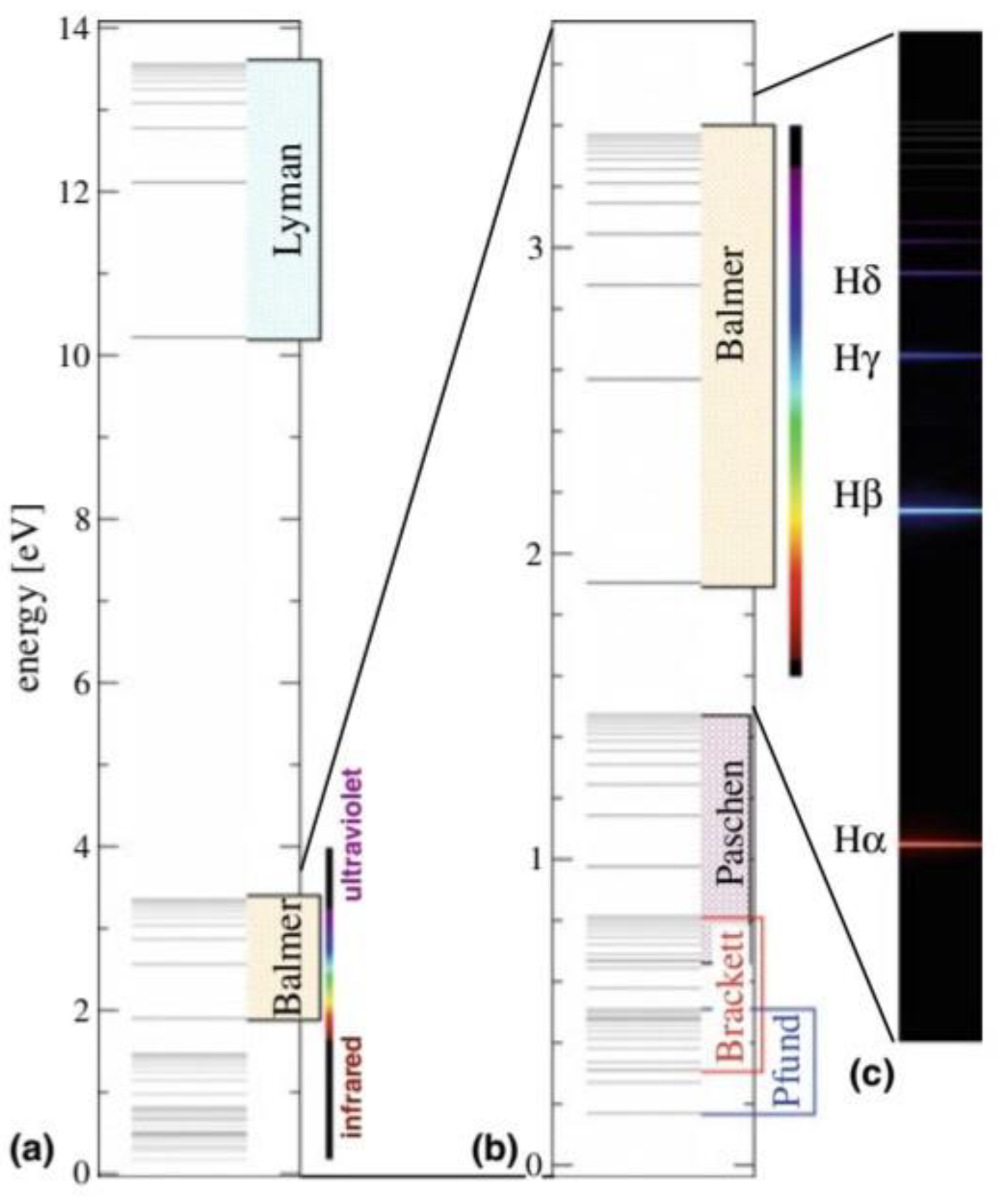
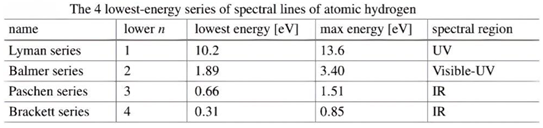
• Table 6 shows the measurement results of one of the previous researches related to the spectrum of the hydrogen atom in chapter 2 atoms.[5] (Manini, 2020)
• This shape is a result of the fact that the electron, after a quantum leap occurred as a result of an interference between the orbital that it occupies and the energy level above it, was in an unstable state. Therefore, when the highest level of energy returns to its position, it releases energy in the form of spectral lines. These lines are determined according to the amount of energy, as shown in the picture.

6. Results Obtained

This scientific research aims to prove a theory by comparing the practical results of this theory with the original results and making the comparison in a table. We will discuss that here.

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{h}}_{\mathit{p}}\times \mathit{C}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\displaystyle \frac{{\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}}{{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}}}={\displaystyle \frac{\mathbf{8}\mathsf{\pi }\times \mathit{G}}{{\mathit{C}}^{\mathbf{4}}}}=\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}$$

(16)

$${\mathit{r}}_{\mathit{n}}^{\mathbf{2}}={\displaystyle \frac{{\left(\mathit{n}\right)}^{\mathbf{4}}\times {\left(\mathbf{8.854187813}\times {\mathbf{10}}^{-\mathbf{12}}\right)}^{\mathbf{2}}\times \mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\right)\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\times \mathit{Z}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{6.62607004}\times {\mathbf{10}}^{-\mathbf{34}}\times \mathbf{299792458}\right)}^{\mathbf{4}}}{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{4}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}}$$

$${\mathit{r}}_{\mathit{n}}^{\mathbf{2}}={\displaystyle \frac{\mathbf{2.800285118}\times {\mathbf{10}}^{-\mathbf{21}}\times {\left(\mathit{n}\right)}^{\mathbf{4}}}{{\left(\mathit{Z}\right)}^{\mathbf{2}}}}$$

After substituting the constants into equation number 1. This derivation proves that the equation can be applied to the Bohr radius.

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\displaystyle \frac{{\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}}{{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}}}={\displaystyle \frac{\mathbf{8}\mathsf{\pi }\times \mathit{G}}{{\mathit{C}}^{\mathbf{4}}}}=\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$$n\times \lambda =2\pi \times r_n$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\times {\left(\mathit{n}\times \mathit{\lambda }\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\right)\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}\times {\left(\mathbf{8.854187813}\times {\mathbf{10}}^{-\mathbf{12}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{4}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\mathbf{2.9248775108}\times {\mathbf{10}}^{-\mathbf{123}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}}}{\displaystyle \frac{\mathbf{1}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}={\displaystyle \frac{\mathbf{2.9248775108}\times {\mathbf{10}}^{-\mathbf{123}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{2}}}}{\displaystyle \frac{\mathbf{1}}{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}$$

$${\mathit{E}}_{\mathit{n}}=\mathbf{1.089397123}\times {\mathbf{10}}^{-\mathbf{20}}\mathit{J}\times {\displaystyle \frac{{\left(\mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}}$$

$${\mathit{E}}_{\mathit{n}}={\mathit{h}}_{\left(\mathit{p}\right)}\times \mathit{\nu }$$

where $h_{\left(p\right)}$ represents the Planck constant, $\nu$ is the frequency.

$${\mathit{G}}_{\mathsf{\mu }\mathsf{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathsf{\mu }\mathsf{\nu }}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left({\mathit{m}}_{\mathit{e}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left({\mathsf{\epsilon }}_{\mathbf{0}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathit{e}\right)}^{\mathbf{4}}\times \mathit{G}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathsf{\mu }\mathsf{\nu }}$$

$${\displaystyle \frac{{\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathit{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}}{{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}}}={\displaystyle \frac{\mathbf{8}\mathit{\pi }\times \mathit{G}}{{\mathit{C}}^{\mathbf{4}}}}=\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}$$

$${\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}}^{\mathbf{4}}={\displaystyle \frac{\left({\left(\mathbf{2}\mathsf{\pi }\right)}^{\mathbf{3}}\times {\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\right)\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}\times {\left(\mathbf{8.854187813}\times {\mathbf{10}}^{-\mathbf{12}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{4}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}$$

$${\Delta E_n}^4=5.5603822503\times {10}^{-79}J\times {\displaystyle \frac{{\left(r_n\times Z\right)}^2}{{\left(n\times \lambda \right)}^4}}$$

$${\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}}^{\mathbf{4}}={\displaystyle \frac{\mathbf{5.5603822503}\times {\mathbf{10}}^{-\mathbf{79}}\mathit{J}}{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{4}}}}\times {\displaystyle \frac{{\left({\mathit{r}}_{\mathit{n}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}}}=\mathbf{8.4384579108}\times {\mathbf{10}}^{-\mathbf{4}}\mathit{e}\mathit{V}\times {\displaystyle \frac{{\left({\mathit{r}}_{\mathit{n}}\times \mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\times \mathsf{\lambda }\right)}^{\mathbf{4}}}}\mathrm{ }\mathrm{ }$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774208} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left({\mathit{r}}_{\mathit{n}}\times \mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}\times \mathsf{\lambda }}}$$

(17)

After, that, we linked the equation number ( 2, 15 ). The unit of measurement for photon energy is electron volt (eV), the wavelength is (nm), and Bohr radius is a (nm).

$${\mathit{E}}_{\mathit{n}}={\mathit{E}}_{\mathbf{2}}-{\mathit{E}}_{\mathbf{1}}$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\displaystyle \frac{-\mathbf{13.605693099} \mathit{e}\mathit{V}}{\mathbf{1}}}\times \left({\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{2}}\right)}^{\mathbf{2}}}}-{\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{1}}\right)}^{\mathbf{2}}}}\right)$$

$$\Delta E_n=0.17043774208 eV\times {\displaystyle \frac{{\left(r_n\times Z\right)}^{\frac{2}{4}}}{n\times \lambda }}$$

$$\lambda =0.17043774208 eV\times {\displaystyle \frac{{\left(r_n\times Z\right)}^{\frac{2}{4}}}{n\times \Delta E_n}}$$

$$\lambda =0.17043774208 eV\times {\displaystyle \frac{{\left(\left(0.052917720266 nm\times {\left(n\right)}^2\right)\times Z\right)}^{\frac{2}{4}}}{n\times \frac{-13.605693099 eV}{1}\times \left(\frac{{\left(Z\right)}^2}{{\left(n_2\right)}^2}-\frac{{\left(Z\right)}^2}{{\left(n_1\right)}^2}\right)}}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$$

• Example of a hydrogen atom in the Balmer series.

We remove the energy level $\left(n\right) form the equation while obtaining the wavelength.$

$$\lambda =0.17043774208 eV\times {\displaystyle \frac{{\left(\left(0.052917720266 nm\right)\times 1\right)}^{\frac{2}{4}}}{\frac{-13.605693099 eV}{1}\times \left(\frac{{\left(1\right)}^2}{{\left(3\right)}^2}-\frac{{\left(1\right)}^2}{{\left(2\right)}^2}\right)}}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$$

$$\lambda =656.11226671 nm$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\displaystyle \frac{{\mathit{h}}_{\mathit{p}}\times \mathit{C}}{\mathsf{\lambda }}}={\displaystyle \frac{\mathbf{1239.8419637} \mathit{e}\mathit{V} \mathit{n}\mathit{m}}{\mathsf{\lambda }}}$$

(18)

Photon energy equation.

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774208} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left({\mathit{r}}_{\mathit{n}}\times \mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}\times \mathsf{\lambda }}}$$

Example of a hydrogen atom.

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774208} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left(\mathbf{0.052917720266} \mathbf{n}\mathbf{m}\times {\left(\mathit{n}\right)}^{\mathbf{2}}\times \mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}\times \mathsf{\lambda }}}$$

• Example of a hydrogen atom in the Balmer series.

We remove the energy level $\left(n\right)$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774208} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left(\mathbf{0.052917720266} \mathbf{n}\mathbf{m}\times \mathbf{1}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathbf{656.11227245} \mathbf{n}\mathbf{m}}}=1.8896795971 \mathrm{eV}$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$${\mu }_0\times {\epsilon }_0=\left({\displaystyle \frac{1}{{\left(C\right)}^2}}\right)$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(C\right)}^4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$E=m\times C^2$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(E\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$E_t=E\times \alpha \mathrm{ }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(E_t\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^6\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }\mathrm{ }$$

$$E_t=\mathrm{ }{E}_n\times n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$${\displaystyle \frac{G_{\mu \nu }+\Lambda g_{\mu \nu }}{T_{\mu \nu }}}={\displaystyle \frac{8\pi \times G}{C^4}}=2.0766474428\times {10}^{-43}$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

Compensation is made in law.

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(9.1093837015\times {10}^{-31}\right)}^2\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }{\left(7.297352563\times {10}^{-3}\right)}^2\times 6.67430\times {10}^{-11}}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }1}{{\left(\Delta E_n\right)}^2}}{T}_{\mu \nu }$$

$$n\times \lambda =2\pi \times r_n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \times {\left(n\times \lambda \right)}^2\right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }1}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{\mathrm{ }1}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$${\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{2}}={\displaystyle \frac{\left(\mathbf{2}\mathit{\pi }\right)\times \mathbf{1.1797075656}\times {\mathbf{10}}^{-\mathbf{74}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}}}{\displaystyle \frac{\mathbf{1}}{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}$$

$${\mathit{E}}_{\mathit{n}}=\mathbf{2.3834486327}\times {\mathbf{10}}^{-\mathbf{16}}\mathit{J}\times {\displaystyle \frac{\sqrt{\left(\mathbf{2}\mathit{\pi }\right)}\times \mathit{Z}}{\mathit{n}}}$$

$${\mathit{E}}_{\mathit{n}}={\mathit{h}}_{\left(\mathit{p}\right)}\times \mathit{\nu }$$

where $h_{\left(p\right)}$ represents the Planck constant, $\nu$ is the frequency.

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^4\times {\lambda }^2}}{\displaystyle \frac{\mathrm{ }1}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$$\Delta E_n={\displaystyle \frac{h_p\times C}{\lambda }}$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{\mathrm{ }1}{{\left(h_p\times C\right)}^2}}{T}_{\mu \nu }$$

$$\Delta E_n={\displaystyle \frac{h_p\times C}{\lambda }}$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 1.1797075656\times {10}^{-74}\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{\mathrm{ }1}{{\left(\Delta E_n\times \lambda \right)}^2}}{T}_{\mu \nu }$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\displaystyle \frac{\left((\mathbf{2}\mathsf{\pi }\times \mathbf{2.5066282746})\times {\mathit{r}}_{\mathit{n}}\right)\times \sqrt{\mathbf{1.1797075656}\times {\mathbf{10}}^{-\mathbf{74}}}\times \mathit{Z}}{{\left(\mathit{n}\right)}^{\mathbf{2}}\times \mathsf{\lambda }}}{\displaystyle \frac{\mathbf{1}}{\sqrt{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}}$$

$$\Delta E_n=5.9744197324\times {10}^{-16}J\times {\displaystyle \frac{2\pi \times r_n\times Z}{{\left(n\right)}^2\times \lambda }}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$$

$$\Delta E_n={\displaystyle \frac{5.9744197324\times {10}^{-16}}{1.60217662\times {10}^{-19}}}=3728.9395301 eV$$

$$\Delta E_n=3728.9395301 eV\times {\displaystyle \frac{2\pi \times r_n\times Z}{{\left(n\right)}^2\times \lambda }}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }$$

The unit of measurement for photon energy is electron volt (eV), the wavelength is (nm), and Bohr radius is a (nm).

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\mathit{E}}_{\mathbf{2}}-{\mathit{E}}_{\mathbf{1}}$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\displaystyle \frac{-\mathbf{13.605693099} \mathit{e}\mathit{V}}{\mathbf{1}}}\times \left({\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{2}}\right)}^{\mathbf{2}}}}-{\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{1}}\right)}^{\mathbf{2}}}}\right)$$

$$\Delta E_n=3728.9395301 eV\times {\displaystyle \frac{ 2\pi \times r_n\times Z}{{\left(n\right)}^{2 }\times \lambda }}$$

$$\lambda =3728.9395301 eV\times {\displaystyle \frac{ 2\pi \times r_n\times Z}{{\left(n\right)}^{2 }\times \Delta E_n}}$$

$$\lambda =3728.9395301 eV\times {\displaystyle \frac{ 2\pi \times \left(0.052917720266 nm\times {\left(n\right)}^2\right)\times Z}{{\left(n\right)}^{2 }\times \frac{-13.605693099 eV}{1}\times \left(\frac{{\left(Z\right)}^2}{{\left(n_2\right)}^2}-\frac{{\left(Z\right)}^2}{{\left(n_1\right)}^2}\right)}}$$

• Example of a hydrogen atom in the Balmer series.

We remove the energy level $\left(n\right)form the equation while obtaining the wavelength.$

$$\lambda =3728.9395301 eV\times {\displaystyle \frac{ 2\pi \times \left(0.052917720266 nm \right)\times Z}{\frac{-13.605693099 eV}{1}\times \left(\frac{{\left(Z\right)}^2}{{\left(3\right)}^2}-\frac{{\left(Z\right)}^2}{{\left(2\right)}^2}\right)}}$$

$$\lambda =656.11227252 nm$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left({\left(2\pi \right)}^3\times {\left(r_n\right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$n\times \lambda =2\pi \times r_n$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \times {\left(n\times \lambda \right)}^2\right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^6\times {\left({\mu }_0\times {\epsilon }_0\right)}^2\times {\lambda }^2}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4\times {\left({\mu }_0\times {\epsilon }_0\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$${\mu }_0\times {\epsilon }_0=\left({\displaystyle \frac{1}{{\left(C\right)}^2}}\right)$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(C\right)}^4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$E=m\times C^2$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(E\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$E_t=E\times \alpha$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(E_t\right)}^2\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^4}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$${ E}_t= E_n\times n$$

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4\times {\left({\mu }_0\times {\epsilon }_0\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$${\displaystyle \frac{G_{\mu \nu }+\Lambda g_{\mu \nu }}{T_{\mu \nu }}}={\displaystyle \frac{8\pi \times G}{C^4}}=2.0766474428\times {10}^{-43}$$

$${ G}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^4\times Z^2}{{\left(n\right)}^4\times {\left({\mu }_0\times {\epsilon }_0\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^4\times G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

Compensation is made in law.

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\left(\left(\mathbf{2}\mathsf{\pi }\right)\right)\times \mathbf{4}\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\right)}^{\mathbf{4}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{4}}\times {\left(\mathbf{4}\mathit{\pi }\times {\mathbf{10}}^{-\mathbf{7}}\times \mathbf{8.854187813}\times {\mathbf{10}}^{-\mathbf{12}}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{7.297352563}\times {\mathbf{10}}^{-\mathbf{3}}\right)}^{\mathbf{4}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}\mathit{ }$$

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\mathbf{2.6457310534}\times {\mathbf{10}}^{-\mathbf{104}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{4}}}}{\displaystyle \frac{\mathbf{1}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}\mathit{ }$$

$${\displaystyle \frac{{\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathit{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}}{{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}}}={\displaystyle \frac{\mathbf{8}\mathit{\pi }\times \mathit{G}}{{\mathit{C}}^{\mathbf{4}}}}=\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}$$

$${\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{4}}={\displaystyle \frac{\mathbf{2.6457310534}\times {\mathbf{10}}^{-\mathbf{104}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{4}}}}{\displaystyle \frac{\mathbf{1}}{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}\mathit{ }$$

$${\mathit{E}}_{\mathit{n}}={\displaystyle \frac{\mathbf{5.9744197312}\times {\mathbf{10}}^{-\mathbf{16}}\times {\left(\mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}}}\mathit{ }$$

$${\mathit{E}}_{\mathit{n}}={\mathit{h}}_{\left(\mathit{p}\right)}\times \mathit{\nu }$$

where $h_{\left(p\right)}$ represents the Planck constant, $\nu$ is the frequency.

$$G_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\displaystyle \frac{\left(2\pi \right)\times 4\times {\left(m_e\right)}^2\times Z^2}{{\left(n\right)}^2}}{\displaystyle \frac{ {\left(\alpha \right)}^2\times G}{{\left(E_n\right)}^2}}{T}_{\mu \nu }$$

Compensation is made in law.

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\left(\left(\mathbf{2}\mathsf{\pi }\right)\right)\times \mathbf{4}\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\right)}^{\mathbf{2}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{7.297352563}\times {\mathbf{10}}^{-\mathbf{3}}\right)}^{\mathbf{2}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{2}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}\mathit{ }$$

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\mathbf{7.4123212429}\times {\mathbf{10}}^{-\mathbf{74}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}}}{\displaystyle \frac{\mathbf{1}}{{\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{2}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}$$

$${\displaystyle \frac{G_{\mu \nu }+\Lambda g_{\mu \nu }}{T_{\mu \nu }}}={\displaystyle \frac{8\pi \times G}{C^4}}=2.0766474428\times {10}^{-43}$$

$${\left({\mathit{E}}_{\mathit{n}}\right)}^{\mathbf{2}}={\displaystyle \frac{\mathbf{7.4123212429}\times {\mathbf{10}}^{-\mathbf{74}}\times {\mathit{z}}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}}}{\displaystyle \frac{\mathbf{1}}{\mathbf{2.0766474428}\times {\mathbf{10}}^{-\mathbf{43}}}}\mathit{ }$$

$${\mathit{E}}_{\mathit{n}}={\displaystyle \frac{\mathbf{5.9744197312}\times {\mathbf{10}}^{-\mathbf{16}}\times \mathit{z}}{\mathit{n}}}\mathit{ }$$

$${\mathit{E}}_{\mathit{n}}={\mathit{h}}_{\left(\mathit{p}\right)}\times \mathit{\nu }$$

where $h_{\left(p\right)}$ represents the Planck constant, $\nu$ is the frequency.

$$H={\displaystyle \frac{e^4\times {\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2\times G}{{\left(\hslash \times C\right)}^3}}$$

$${\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2={\left(m_e\right)}^2\times {k_e}^2={\displaystyle \frac{{\left(m_e\right)}^2}{{\left(4\pi \times {\epsilon }_0\right)}^2}}$$

$$H={\displaystyle \frac{{\left(1.60217662\times {10}^{-19}\right)}^4\times {\left(8.1871057811\times {10}^{-21}\right)}^2\times 6.67430\times {10}^{-11}}{{\left(1.0545718\times {10}^{-34}\times 299792458\right)}^3}}$$

$${\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2={\left(9.1093837015\times {10}^{-31}\right)}^2\times {\left(8987551792.05816\right)}^2$$

$${\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)}^2={\displaystyle \frac{{\left(9.1093837015\times {10}^{-31}\right)}^2}{{\left(4\pi \times 8.854187813\times {10}^{-12}\right)}^2}}$$

$$\left({\left(k_e\right)}_{{\left(m\right)}_1}\right)=8.1871057811\times {10}^{-21}$$

$$H=9.3286224511\times {10}^{-50}$$

$$E_{\left(p\right)}^2={\displaystyle \frac{{\left(2\pi \times n\right)}^4\times {\left(2\times {\epsilon }_0\right)}^2}{{\left(r_n\right)}^2\times {\left(m_e\times Z\right)}^2}}{\displaystyle \frac{{\left(\hslash \times C\right)}^5}{{\left(e\right)}^4\times G}}$$

$${\mathit{E}}_{\left(\mathit{p}\right)}^{\mathbf{2}}={\displaystyle \frac{{\left(\mathbf{2}\mathit{\pi }\times \mathit{n}\right)}^{\mathbf{4}}\times {\left(\mathbf{2}\times \mathbf{8.854187813}\times {\mathbf{10}}^{-\mathbf{12}}\right)}^{\mathbf{2}}}{{\left({\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\times {\left(\mathbf{9.1093837015}\times {\mathbf{10}}^{-\mathbf{31}}\times \mathit{Z}\right)}^{\mathbf{2}}}}{\displaystyle \frac{{\left(\mathbf{1.0545718}\times {\mathbf{10}}^{-\mathbf{34}}\times \mathbf{299792458}\right)}^{\mathbf{5}}}{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{4}}\times \mathbf{6.67430}\times {\mathbf{10}}^{-\mathbf{11}}}}$$

$${\mathit{E}}_{\left(\mathit{p}\right)}^{\mathbf{2}}=\mathbf{0.42299568152}\times {\displaystyle \frac{{\left(\mathit{n}\right)}^{\mathbf{4}}}{{\left(\mathbf{2}\mathit{\pi }\times {\mathit{r}}_{\mathit{n}}\right)}^{\mathbf{2}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}}$$

$${\mathit{E}}_{\left(\mathit{p}\right)}=\mathbf{0.65038118171}\mathit{ }\times {\displaystyle \frac{{\left(\mathit{n}\right)}^{\mathbf{2}}}{\mathbf{2}\mathit{\pi }\times {\mathit{r}}_{\mathit{n}}\times \mathit{Z}}}$$

$${\mathit{E}}_{\left(\mathit{p}\right)}={\mathit{m}}_{\mathit{p}}\times {\left(\mathit{C}\right)}^{\mathbf{2}}$$

where E_p represents the Planck energy.

$$X={\displaystyle \frac{e^2\times {\left(k_e\right)}_m\times G}{{\left(\hslash \times C\right)}^2}}$$

$${\left(k_e\right)}_m ={\left(m_e\right)}^2\times k_e={\displaystyle \frac{{\left(m_e\right)}^2}{\left(4\pi \times {\epsilon }_0\right)}}$$

$$X={\displaystyle \frac{{\left(1.60217662\times {10}^{-19}\right)}^2\times 7.4579487965\times {10}^{-51}\times 6.67430\times {10}^{-11}}{{\left(1.0545718\times {10}^{-34}\times 299792458\right)}^2}}$$

$${\left(k_e\right)}_m ={\left(9.1093837015\times {10}^{-31}\right)}^2\times k_e={\displaystyle \frac{{\left(9.1093837015\times {10}^{-31}\right)}^2}{\left(4\pi \times 8.854187813\times {10}^{-12}\right)}}$$

$${\left({\mathit{k}}_{\mathit{e}}\right)}_{\mathit{m}}\mathit{ }=\mathbf{7.4579487965}\times {\mathbf{10}}^{-\mathbf{51}}$$

$$\mathit{X}=\mathbf{1.2783570986}\times {\mathbf{10}}^{-\mathbf{47}}$$

$${\mathit{h}}_{\left(\mathit{a}\right)}={\displaystyle \frac{\mathbf{1}}{\mathit{\alpha }}}$$

$${\mathit{h}}_{\left(\mathit{a}\right)}={\displaystyle \frac{\mathbf{1}}{\mathbf{7.297352563}\times \mathbf{1}{\mathbf{0}}^{-\mathbf{3}}}}$$

$$\overline{\hslash }={\displaystyle \frac{H\times \hslash \times C}{e^2}}$$

$$\overline{\mathit{\hslash }}={\displaystyle \frac{\mathbf{9.3286224511}\times {\mathbf{10}}^{-\mathbf{50}}\times \mathbf{1.0545718}\times {\mathbf{10}}^{-\mathbf{34}}\times \mathbf{299792458}}{{\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{2}}}}$$

$$\overline{\mathit{\hslash }}=\mathbf{1.1489300633}\times {\mathbf{10}}^{-\mathbf{37}}$$

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathit{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\mathbf{8}\mathit{\pi }\times \overline{\mathit{\hslash }}\times {\mathit{e}}^{\mathbf{2}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\mathit{n}}^{\mathbf{2}}\times {\mathit{E}}^{\mathbf{2}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}$$

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathit{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\mathbf{8}\mathit{\pi }\times \mathbf{1.1489300633}\times {\mathbf{10}}^{-\mathbf{37}}\times {\left(\mathbf{1.60217662}\times {\mathbf{10}}^{-\mathbf{19}}\right)}^{\mathbf{2}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}\times {\mathit{E}}^{\mathbf{2}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}$$

$${\mathit{G}}_{\mathit{\mu }\mathit{\nu }}+\mathit{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\displaystyle \frac{\mathbf{7.412321244}\times {\mathbf{10}}^{-\mathbf{74}}\times {\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left(\mathit{n}\right)}^{\mathbf{2}}\times {\mathit{E}}^{\mathbf{2}}}}{\mathit{T}}_{\mathit{\mu }\mathit{\nu }}$$

$$E_n={\displaystyle \frac{n\times G\times {\left(m_p\right)}^{\mathbf{2}}\times Z}{r_n}}$$

$$E_n={\displaystyle \frac{n\times 3.161526722\times {10}^{-26}\times Z}{r_n}}$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^3\times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^2\times {\left(\mathsf{\lambda }\right)}^2}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{{\left(2\pi \right)}^5\times {4\times \left(\hslash \right)}^4}{{\left(\mathsf{\lambda }\right)}^4}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

$$G_{\mu \nu }+\Lambda g_{\mu \nu }={\displaystyle \frac{2\pi \times {4\times \left(n\times \hslash \right)}^4}{{\left(r_n\right)}^4}}{\displaystyle \frac{G}{{\left(E_n\right)}^4}}{T}_{\mu \nu }$$

Space-time represents in the equation the force of attraction of the nucleus for the electron. Where we take the hydrogen atom compared to the sodium atom. We find after comparison that the undulations that occur in the sodium atom are higher than those that occur in the hydrogen atom. That is, during the occurrence of the quantum jump of the electron, the higher energy level than the level occupied by the electron undulates. So the number of ripples (ripple amplitude) is higher than that of the hydrogen atom during the occurrence of the quantum jump, and this is consistent with the de Broglie equation. n × λ is represented by a ratio to space-time. It is the number of ripples that occur in the energy level higher than the level occupied by the electron until interference occurs between the two levels, the higher energy level and the level occupied by the electron. In other words, as the number of orbitals occupied by the electron increases, the number of ripples that occur at the higher energy levels increases, causing the curvature (contraction) of the fabric of space-time. The interference between the two levels occurs in a wave form so that the quantum jump of the electron occurs. The photon's energy is represented by a ratio to the fabric of space-time, the force that causes the fabric of space-time to bend (contract). The more energy increases, the more space-time contracts through the occurrence of quantum disturbances at the highest energy level, which makes the highest energy level generate waves similar to the orbital number occupied by the electron. Because of these disturbances that occur at the highest energy level, the two levels interfere with each other, the highest energy level, and the level occupied by the electron. A quantum leap occurs, and this is consistent with the quantum Zeno effect, where the electron will remain fixed in its position. This is what my equation indicates, as I explain that these quantum fluctuations occur through a contraction in the fabric of space-time. This contraction occurs as a result of this tissue absorbing energy. Because of this, contraction affects the energy levels in the atom. This contraction works to contract the energy level higher than the level occupied by the electron. Wave interference occurs between the highest energy level and the level occupied by the electron, and a quantum jump occurs from the observer’s perspective. But from the electron's perspective, it remains fixed in its position.

The Casimir effect is according to a law that states that after all the objects acting on the plates disappear until imaginary particles are detected. My equation proves that there is one thing that was not included in the calculations, which is the effect of space-time. Since the plates have a static mass that works to curve space-time, and the presence of imaginary particles works when they collide with each other, they disappear. But according to the law of conservation of energy, the energy will not disappear and will affect the fabric of space-time, making it turbulent like a water wave, and these disturbances that occur on it form waves. This wave works to impact the panels from moving in and out, and because the external disturbances are higher than the internal ones, they cause the panels to move towards each other.

This relationship shows that although we cannot measure what happens when an electronic quantum jump occurs. This law also shows that there is a relationship between the energy of the photon and the fabric of space-time, even if it is not measured by measuring devices. Because measuring devices are considered primitive devices when making the process of measuring the quantitative world. What is being measured are the spectra of the elements being measured, not what happens to the electron when the quantum jump of the electron to the higher level. Second, Maxwell told Rutherford that the electron changes direction as it orbits the nucleus, so it must lose energy to cause a collision with the nucleus, which it does not. My equation tells me the electron moves in a large circle around the nucleus. A body moving in a large circle whose direction of motion is in a straight line. Thus, the electron moves in a straight line. Newton's law states that an object at rest remains at rest unless acted upon by an external or internal force. Likewise, an object in motion stays in motion unless an external or internal force affects its movement, the electron does not lose energy.

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774208} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left({\mathit{r}}_{\mathit{n}}\times \mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}\times \mathsf{\lambda }}}$$

(17)

After, that, we linked the equation number ( 2, 16 ). The unit of measurement for photon energy is electron volt (eV), the wavelength is (nm), and Bohr radius is a (nm).

Table 7. Comparing my theoretical results through my equation with previous results.

Theoretical value (My work)					Experimental value
Spectral Line	Energy		λ		λ
λ(n’=2, n=1)	10.204269824	eV	121.50227268	nm	121.5 nm
λ(n’=3, n=1)	12.093949421	eV	102.51754257	nm	102.5 nm
λ(n’=4, n=1)	12.75533728	eV	97.20181814	nm	97.20 nm
λ(n’=3, n=2)	1.8896795971	eV	656.11227245	nm	656.1 nm
λ(n’=4, n=2)	2.5510674561	eV	486.0090907	nm	486.0 nm
λ(n’=4, n=3)	0.66138785898 eV		1874.6064927	nm	1874.6 nm

Table 7. Comparing my theoretical results through my equation with previous results.

Theoretical value (My work)					Experimental value
Spectral Line	Energy		λ		λ
λ(n’=2, n=1)	10.204269824	eV	121.50227268	nm	121.5 nm
λ(n’=3, n=1)	12.093949421	eV	102.51754257	nm	102.5 nm
λ(n’=4, n=1)	12.75533728	eV	97.20181814	nm	97.20 nm
λ(n’=3, n=2)	1.8896795971	eV	656.11227245	nm	656.1 nm
λ(n’=4, n=2)	2.5510674561	eV	486.0090907	nm	486.0 nm
λ(n’=4, n=3)	0.66138785898 eV		1874.6064927	nm	1874.6 nm

The results of the experimental value were obtained by using the results of previous research on the hydrogen atom. I prove in Table 7 that the results of the equations are identical to their original results in Table 5, which indicates the validity of this law

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\mathit{E}}_{\mathbf{2}}-{\mathit{E}}_{\mathbf{1}}$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}={\displaystyle \frac{-\mathbf{13.605693099} \mathit{e}\mathit{V}}{\mathbf{1}}}\times \left({\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{2}}\right)}^{\mathbf{2}}}}-{\displaystyle \frac{{\left(\mathit{Z}\right)}^{\mathbf{2}}}{{\left({\mathit{n}}_{\mathbf{1}}\right)}^{\mathbf{2}}}}\right)$$

$$\mathsf{\Delta }{\mathit{E}}_{\mathit{n}}=\mathbf{0.17043774059} \mathit{e}\mathit{V}\times {\displaystyle \frac{{\left(\left(\mathbf{0.052917720265} \mathit{n}\mathit{m}\times {\left(\mathit{n}\right)}^{\mathbf{2}}\right)\times \mathit{Z}\right)}^{\frac{\mathbf{2}}{\mathbf{4}}}}{\mathit{n}\times \mathsf{\lambda }}}$$

• These are the results of a relationship between energy and wavelength. The observed results show that whenever the energy increases, the wavelength decreases, as shown by this equation in the hydrogen atom.

7. Conclusions

After the idea of research has been clarified using theoretical and practical scientific evidence to explain the phenomenon of the quantum leap and quantum entanglement from a new perspective, these equations would be used in the following:

1) serving humanity in the advancement of scientific research.

2) using these equations to explore space and quantum world.

3) using these equations in developing communications machines