Theoretical Variants of Bct-Si Allotropes, Composed of Rings and Cubes, Fused

1. Structures

To define the possible bct - C₄ variants, we have based ourselves on the results of some works ^{[ 3, 4}, which predict graphene allotropes, of sp² hybridization, based on the Demsity Function Theory (DFT). Specifically, the structures C4 -10 -I, C4 - 8 - R and C4 - 12- These results have been translated into a three-dimensional sp³ hybridization, corresponding to a bct-type structure, composed of flat square rings, C₄ or Si₄.

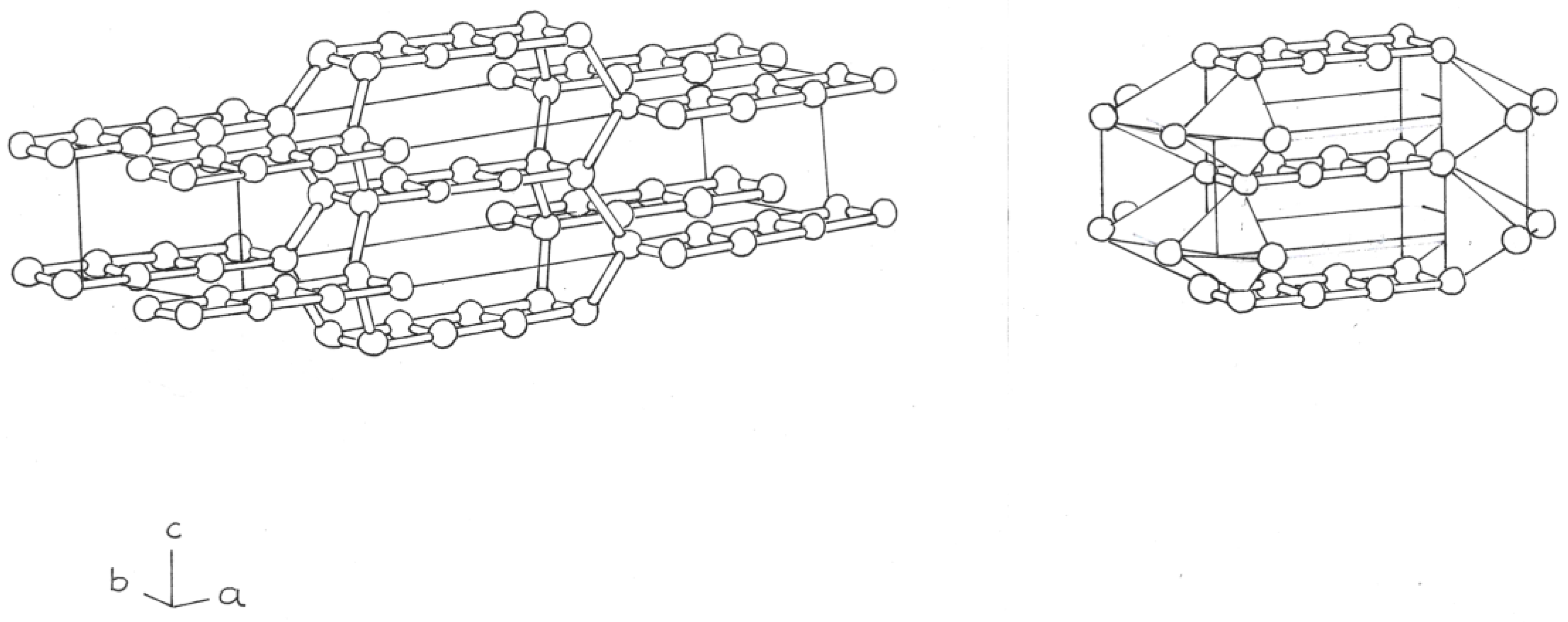
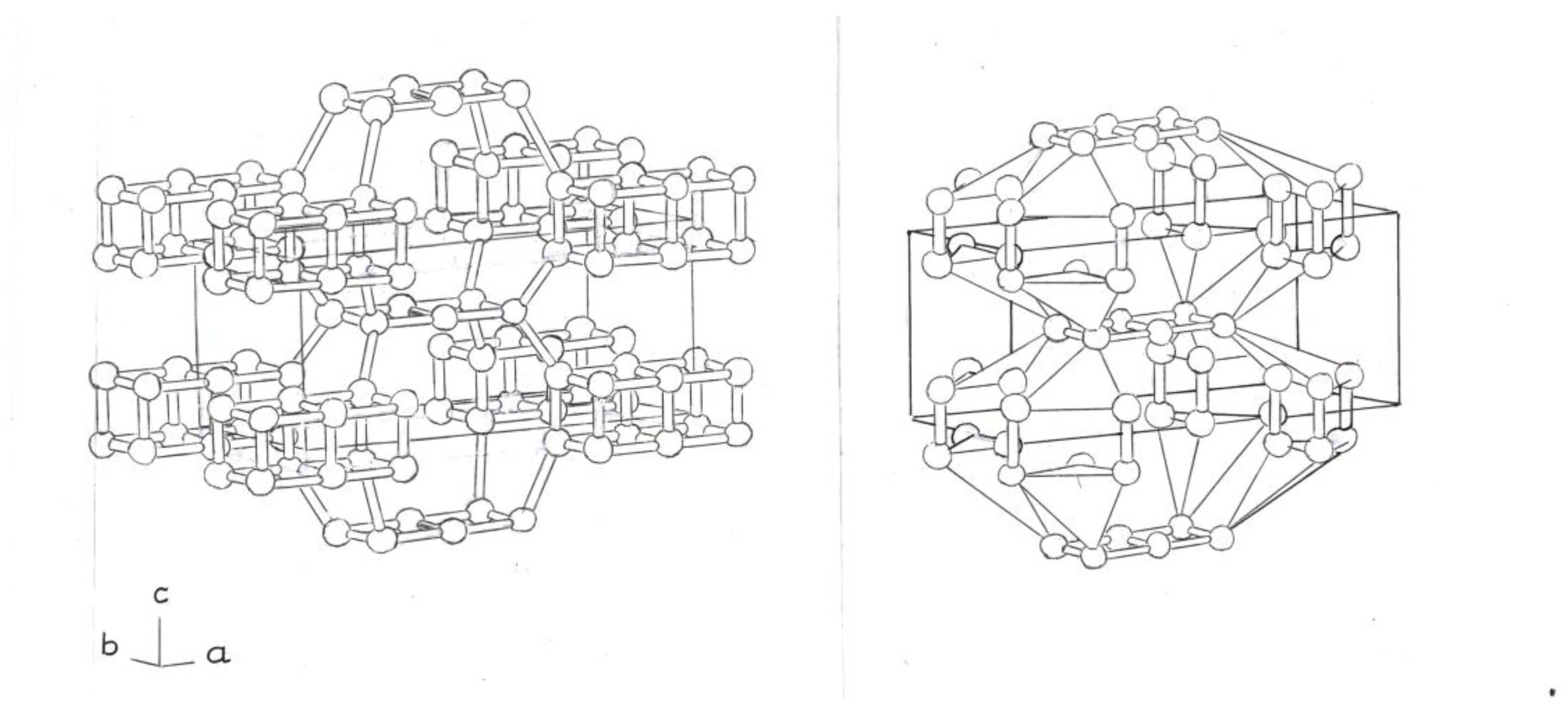
The first of these new structures, derived from the simpler bct - Si₄ phase, is formed by two fused Si₄ rings, with single and double bonds; in the two atoms of the two rings, (Figure 1)

Another variant phase would be composed of three flat square rings, Si₄. The ends of the central ring would be formed by two simple links, at the top and bottom of it; and two double bonds, on the sides of the central ring. (Figure 2)

Both phases form 8 tetrahedra, 5 silicon atoms, adjacent, at the ends (Figure 1 and Figure 2, right).

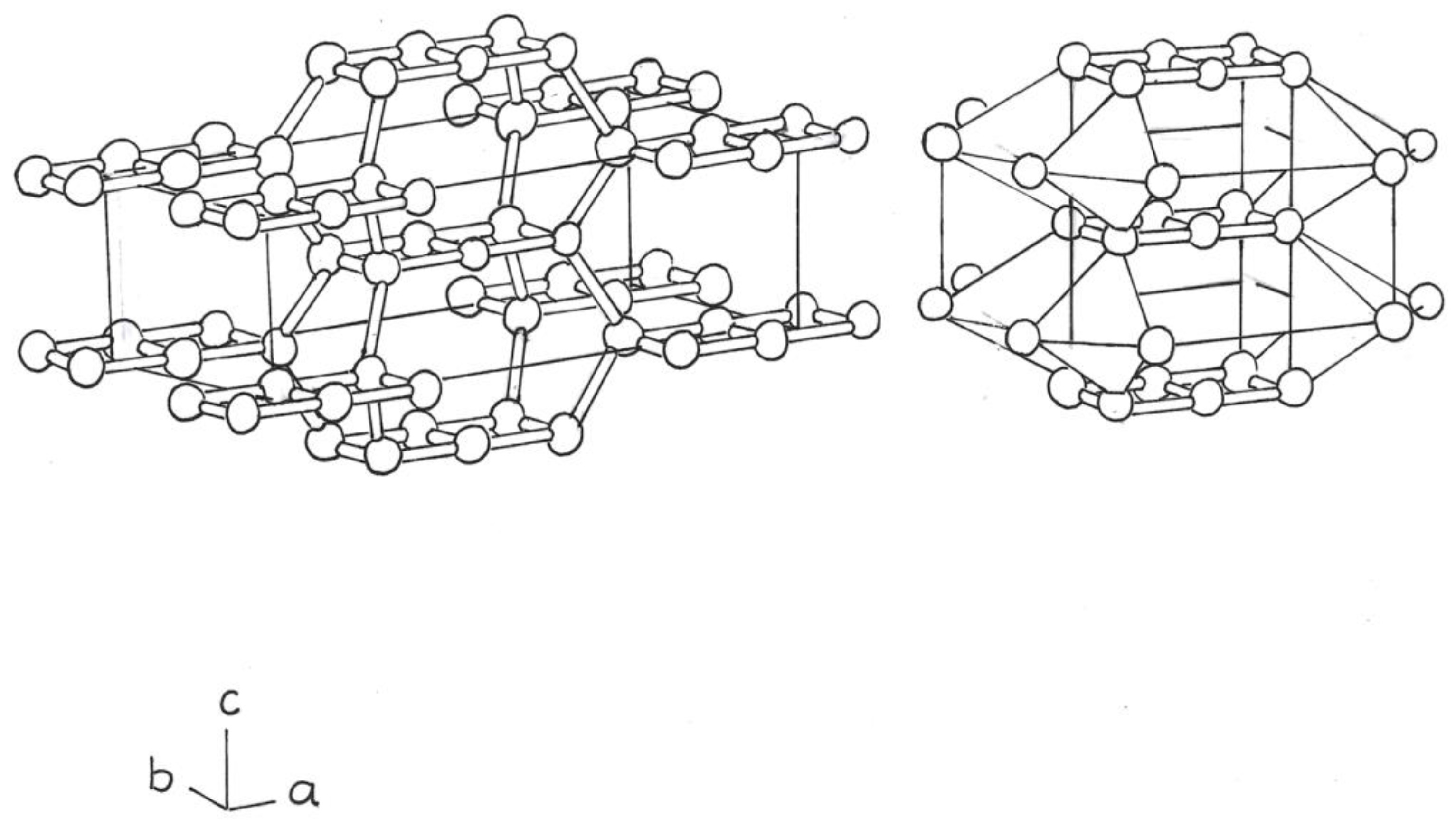
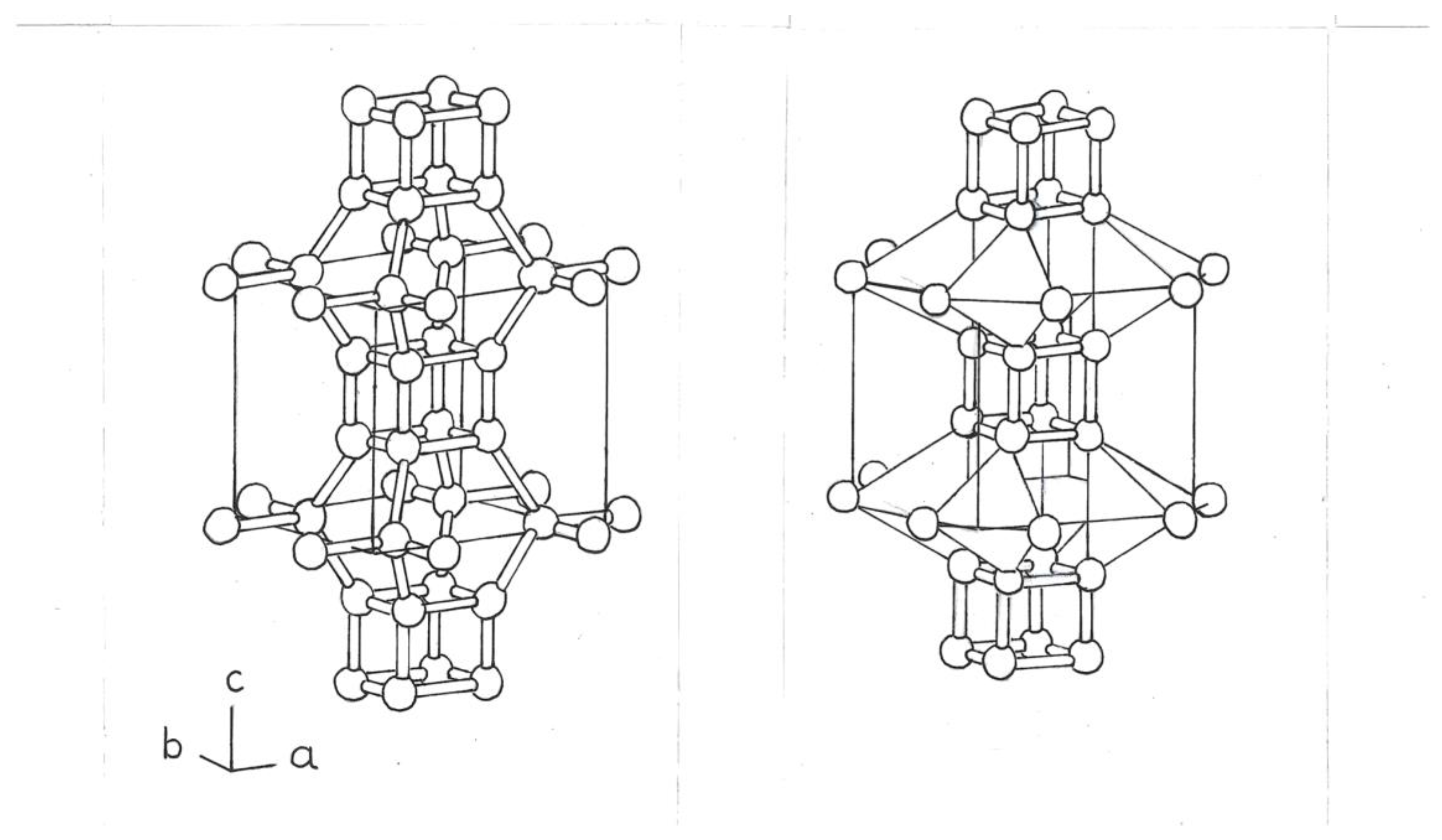
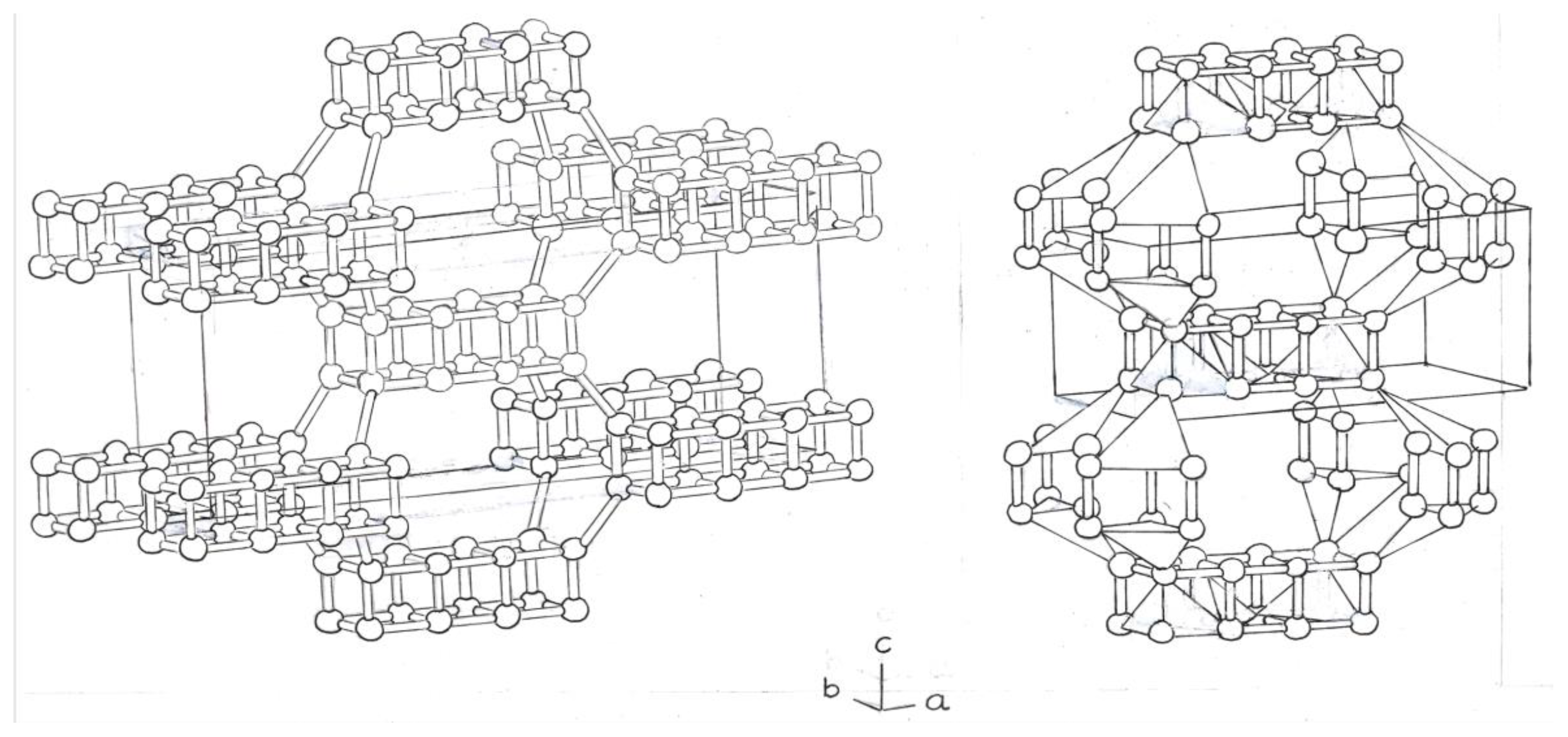
The next phase would be composed of a Si₈ cube, centered, and eight Si₄ rings on the edges of a tetrahedron (Figure 3).

The tetrahedra, at the top, are separated from those at the bottom, by dense bonds of the Si atoms, of the central cbo, Si₈ (Figure 3b).

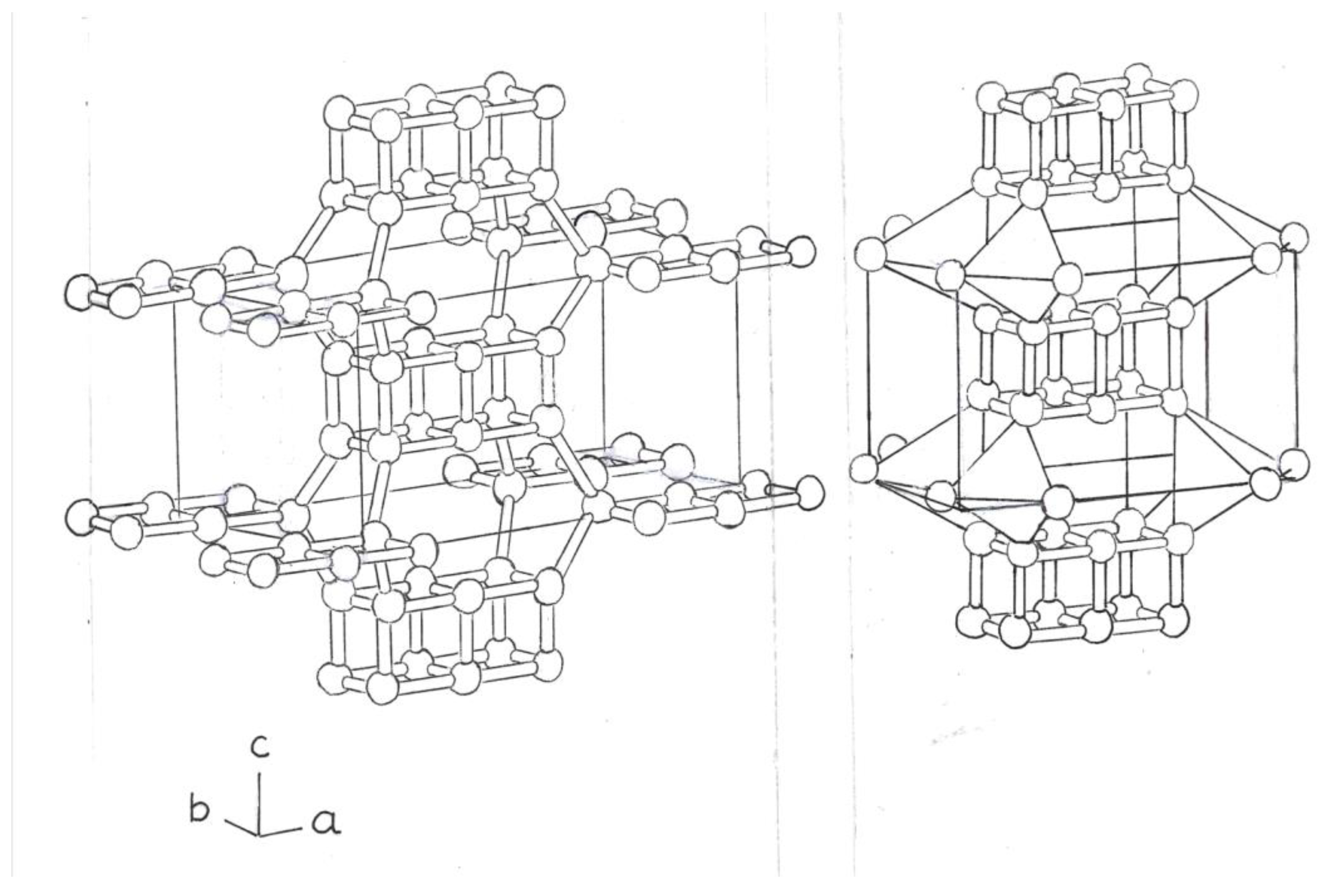
The following variants would be formed by two cubes of Si₈, and two rings, Si₄, fused together. The 2 central atoms, Si, form double and single bonds. (Figure 4)

Another variant, of the previous one, would be formed by three flat rings, Si₄, fused; and three cubes, also composed of silicon atoms, Si₈, fused, in this case, in the form of a double prism. (Figure 5).

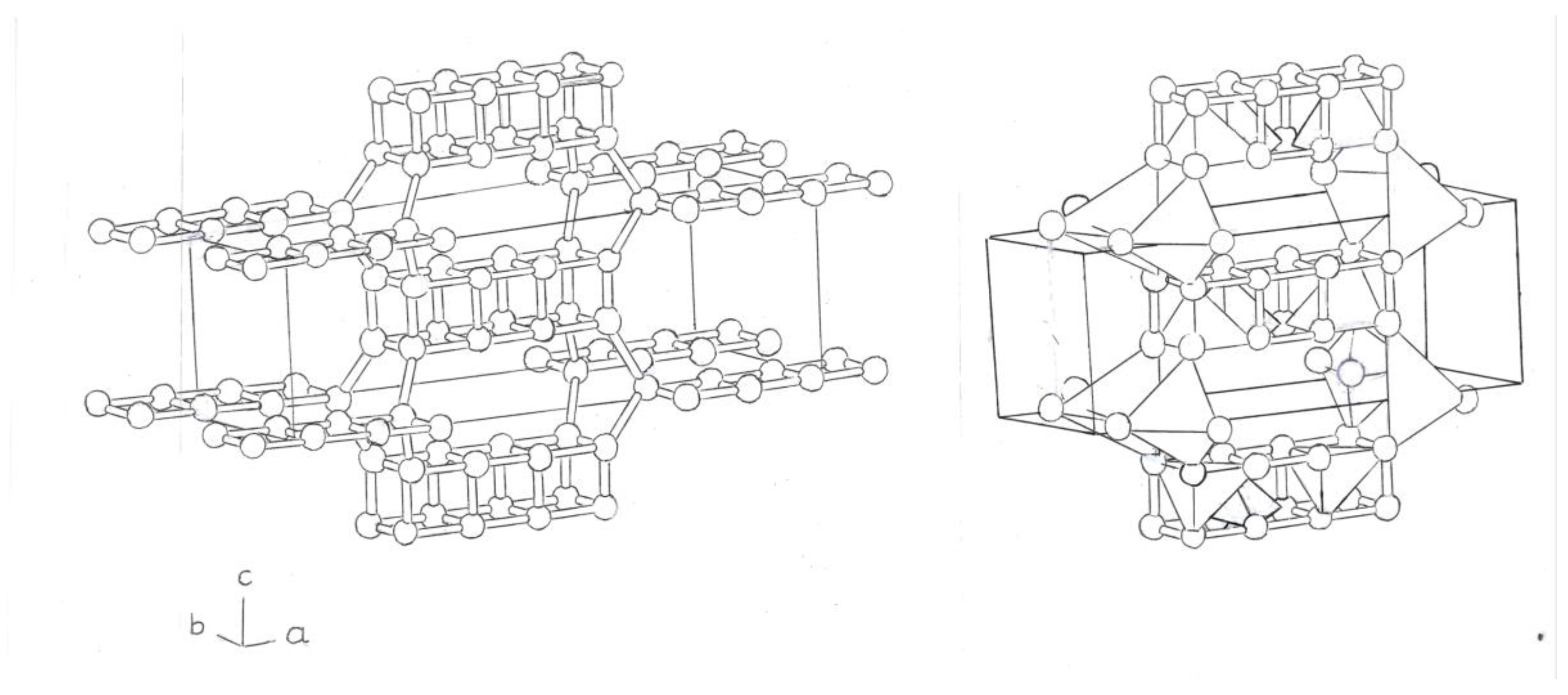
It is also possible to form a Bct phase, composed of two fused Si₈ cubes, at the edges of a tetrahedron; and two flat rings, centered on the body (Figure 6). The central atoms, of the double rings, fused, form single and double bonds.

The tetrahedrons that form between the planes and cubes of Si₄ and Si₈, fused, will be separated by single bonds, which form the silicon cubes, Si₈.

A new Bct phase, a variant of the previous one, would be composed of fused prisms, with three cubes, Si₈; located at the edges and in the center of the tetrahedron ( Figure 7 ) . All the atoms of Si, , form simple bonds in it.

All these new Bct phases form 8 octahedrons, with other Si atoms adjacent; located on the edges of the tetrahedron. The difference between them would lie in the direct contact between them, in the case of being composed of fused flat rings (Figure 1 and Figure 2). Or because they are separated by a simple link, as in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7.

2. Calculation Model

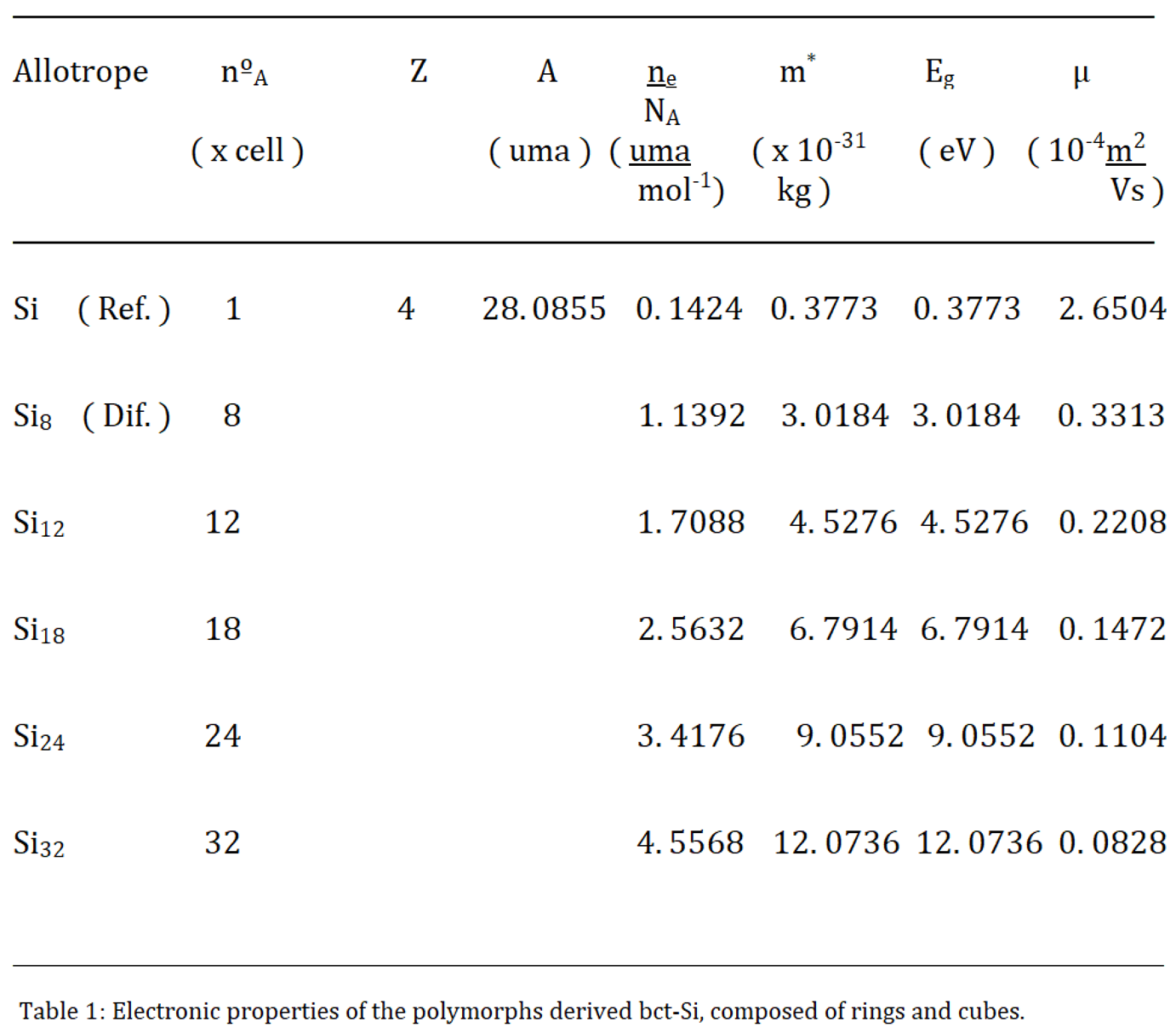
2.1. Electronic Properties

The electrons that move freely through the solid, from the electrons of density, were established by the free electron gas model of Drude and Sommerfeld [4,5].

N_A, is Avogadro's number or constant, Z indicates the electronic valence number, A is the atomic mass of the chemical element (in g/mol), ρm, is the mass density (mass, divided by volume) and ne, They are the conduction electrons, or number of free electrons. This is the basic equation to calculate its concentration.

For a unit cell, we can simplify the equation to the form:

In this equation, we replace the mass density, ρm, with nºA, which is the number of atoms that make up the unit cell [6].

The effective or dynamic mass of the electron is defined by the formula:

where, m*, is the effective mass of the electrons, σ, is the electronic conductivity, e, is the charge of an electron, and τ, is the Relaxation Time; which is the average time between consecutive collisions of an electron. It is an average value, since not all collisions occur at regular intervals.

There is a relationship between this effective or dynamic mass of free electrons in motion, and the forbidden energy gap or band gap [7].

And between these and electronic mobility [7], which measures the efficiency of semiconductors.

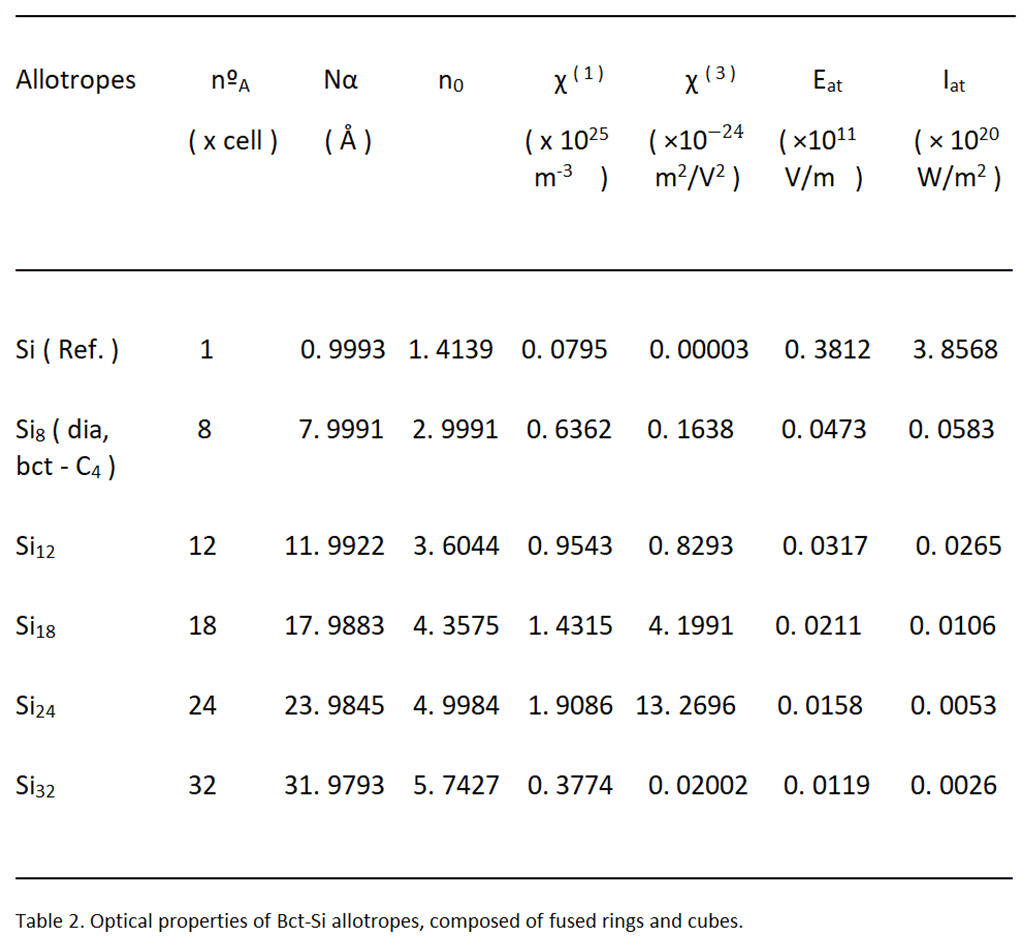
2.2. Optical Properties

To begin to study the optical properties of these allotropes, variants of the bct - Si₄, we must begin to calculate the atomic or electron polarity [10]. of the silicon atoms, which compose them.

where, a_R, the Bohr radius of the components [11] and 4πε₀, the inverse of Coulomb's constant, 1/k.

From this, we can define the linear refractive index, n₀ [12], as:

In this equation, N is the number of atoms per unit volume in the material or unit cell.

Under these circumstances, we can already calculate the linear, or first-order, susceptibility χ⁽¹⁾ of the solid medium [13].

And, from this, we can derive third-order susceptibility [13].

The strength of the electric field, atomic (E_at), is determined by the charge of the electron [14], and the Bohr radius of silicon [11], in the form:

The charge of the electron (e = 1.602 × 10⁻¹⁹ C), comes in coulombs.

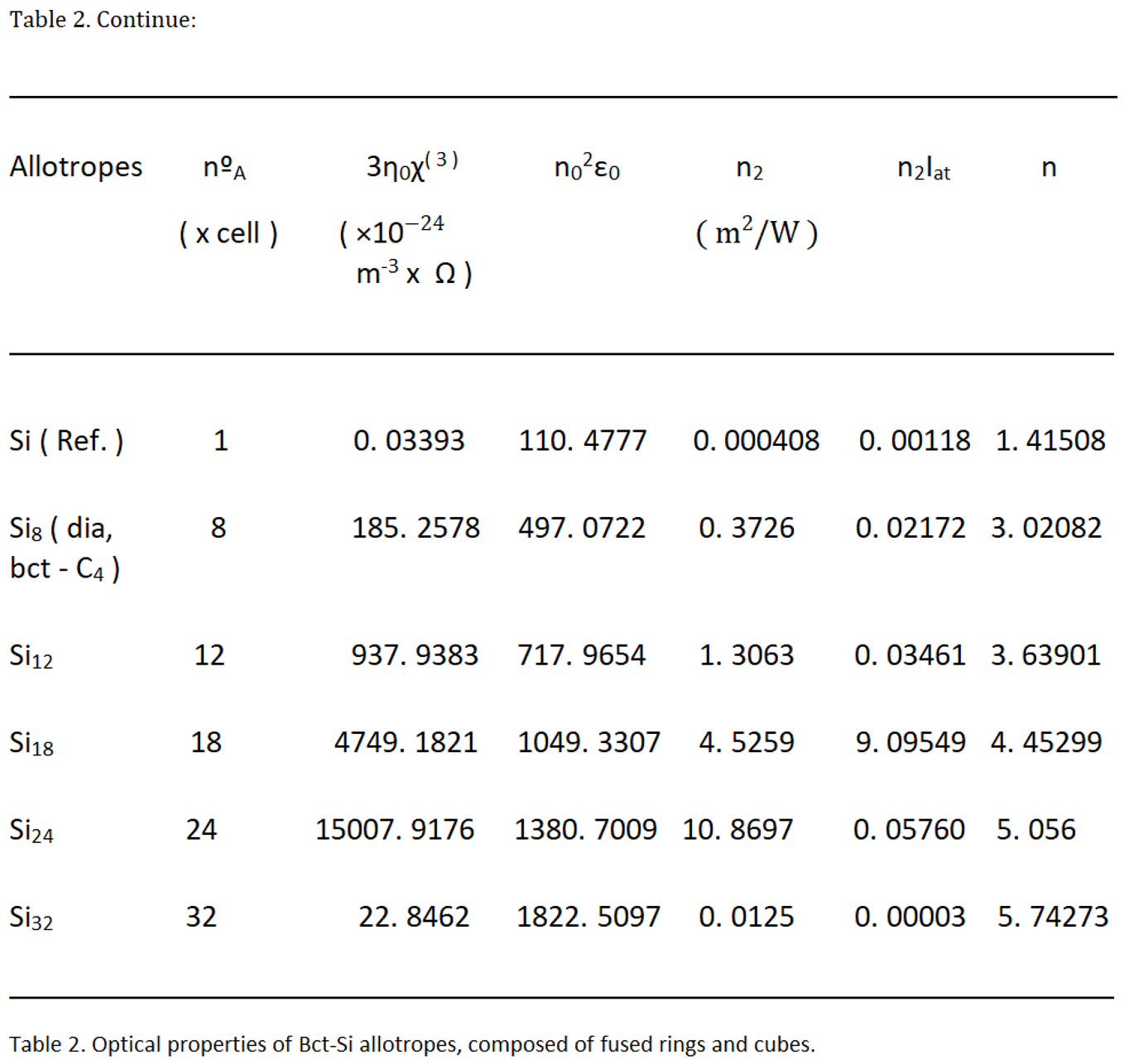
The impedance, the vacuum, has a value of η₀ = 377 ohms (Ω ). That will allow us to calculate the refractive index, of second order, n₂. This nonlinear refractive index, n₂, relates the vacuum impedance, η₀ , with the third-order susceptibility χ⁽³⁾, with a directly proportional relationship, between them; and with the linear refractive index, n₀, in this case inversely proportional, with respect to the first two.

Light intensity, at the atomic level, is related to the amplitude of the electric field, atomic; with equation [15].

Also called Kerr's optical coefficient. Finally, we can calculate the optical Kerr effect, using the equation [16]: