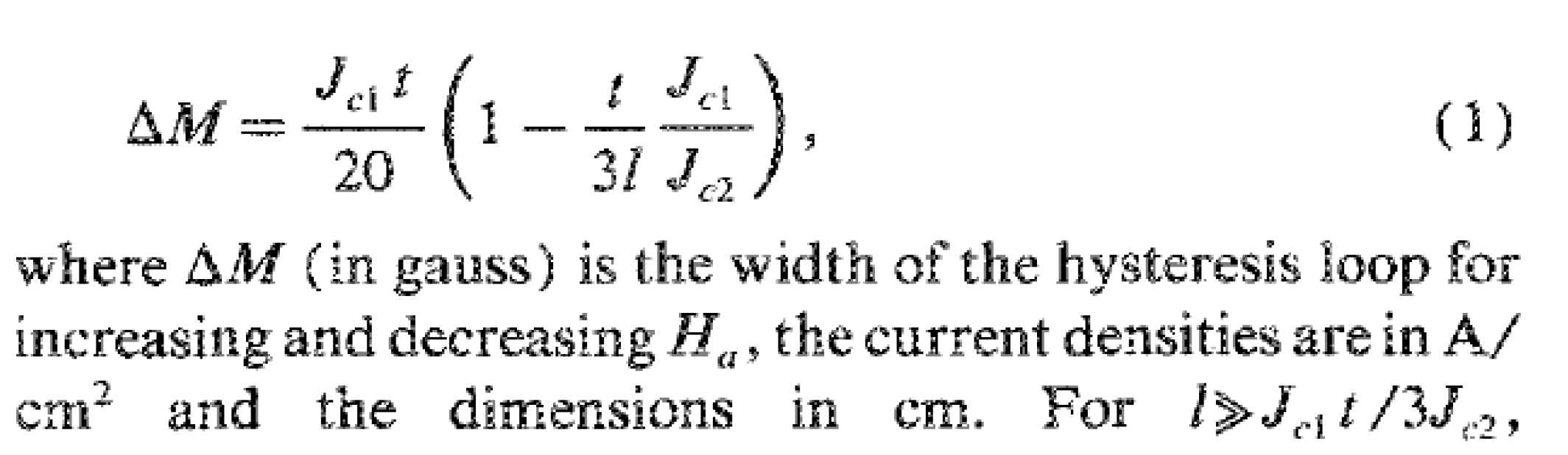Prerpints.org logo
Preprint
Communication

This version is not peer-reviewed.

Equation for Calculation of Critical Current Density Using the Bean's Model with Self-Consistent Magnetic Units to Prevent Unit Conversion Errors

A peer-reviewed article of this preprint also exists.

Submitted:

04 December 2024

Posted:

05 December 2024

You are already at the latest version

Abstract
This study analyzes the calculation of the critical current density Jc,mag by means of the Bean's critical state model, using the equation formulated by Gyorgy et al. and other similar equations derived from Gyorgy et al. reported in literature. While estimations of Jc,mag using the Bean's model are widely done, improper use of different equations with different magnetic units and pre-factors, leads to confusion and to significant errors in the reported values of Jc,mag. We propose a SINGLE general equation for calculation of Jc,mag for a rectangular parallelepiped sample in perpendicular field using the Bean's critical state model, underlying how the simple conversion of magnetic units can lead to a Jc,mag in the desired units, without the need to introduce any other correction or use other specific equations depending on the units of Jc,mag. This resolves all ambiguities and aligns with the correct dimensional analysis, eliminates discrepancies in the calculated Jc,mag and will avoid further propagation of errors in the literature. In this equation, the numerical pre-factor is dimensionless, independent of the unit system used.
Keywords: 
Critical current density
;  
magnetic properties
;  
Bean's critical state model
;  
magnetic units system
;  
unit conversions
Subject: 
Physical Sciences  -   Condensed Matter Physics
This study analyzes the calculation of the critical current density Jc,mag by means of the Bean's critical state model, using the equation formulated by Gyorgy et al. and other similar equations derived from Gyorgy et al. reported in literature. While estimations of Jc,mag using the Bean's model are widely done, improper use of different equations with different magnetic units and pre-factors, leads to confusion and to significant errors in the reported values of Jc,mag. We propose a SINGLE general equation for calculation of Jc,mag for a rectangular parallelepiped sample in perpendicular field using the Bean's critical state model, underlying how the simple conversion of magnetic units can lead to a Jc,mag in the desired units, without the need to introduce any other correction or use other specific equations depending on the units of Jc,mag. This resolves all ambiguities and aligns with the correct dimensional analysis, eliminates discrepancies in the calculated Jc,mag and will avoid further propagation of errors in the literature. In this equation, the numerical pre-factor is dimensionless, independent of the unit system used. There is tremendous excitement for many large-scale applications of superconductors as reported in Goyal et al. [1]. In particular, energy generation via commercial nuclear fusion is presently of great interest [1]. There is significant research ongoing world-wide to improve the performance of superconducting wires based on various coated conductor technologies to improve the performance and lower the cost of these wires and these have been previously reported. In such studies, characterization of the critical current densities by transport and magnetization is of paramount interest. However, calculation of critical current densities, Jc,mag, based on magnetization of a coated conductor represented as a rectangular parallelepiped sample in perpendicular magnetic field poses a challenge in terms of expressions used and self-consistency of magnetic units used in past studies and reported in the literature. A commonly used expression to calculate the critical current density in a majority of these publications is the Bean's Model [2,3]. However, since Bean did not report a specific expression to calculate Jc,mag in the considered geometry, the actual formula used in most prior publications is the equation shown below (at a given field and temperature), reported by Gyorgy et al. [4] and derived on the basis of the Bean's model. This formula has been used extensively in numerous publications in the literature, only a few of which are cited here [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]:
J c , m a g B , T = 20 × Δ M w × 1 − w 3 l
where the current density, Jc,mag, is typically desired in [A/cm2], and the unit-volume full-width of the hysteresis loop for decreasing and increasing applied magnetic field ΔM= μ(B−,T)− μ(B+,T)/(w×l×t) is typically measured in [emu/cm3] (i.e. in gaussian units). The dimensions for the width w, the length l, and the thickness t are typically measured in [cm]. The calculation of critical current density based on magnetization poses a challenge in terms of self-consistency of magnetic units used in past studies and reported in the literature.
In their equation for the calculation of Jc,mag in the general case of anisotropic critical currents, Gyorgy et al. [4] explicitly state that Δ M is in gauss, and when the field is applied perpendicular to one surface of dimensions l by t of a rectangular parallelepiped sample, it is expressed by:
Preprints 141914 g001
Figure 1. Expression for the calculation of Jc,mag as reported in Gyorgy et al. (expression 1, page 283), in the general case for anisotropic critical current densities Jc1≠Jc2.
Figure 1. Expression for the calculation of Jc,mag as reported in Gyorgy et al. (expression 1, page 283), in the general case for anisotropic critical current densities Jc1≠Jc2.
Preprints 141914 g001
Assuming that Jc1=Jc2=Jc the expression (1) becomes:
Δ M = J c t 20 1 − t 3 l
From Gyorgy et al., it is clear that if ΔM is expressed in gauss, and the dimensions in cm, the resulting current density is in A/cm2, without any other conversion of units. This can be checked also by considering the data and specific examples reported in Gyorgy et al.
In practice, magnetometers such the SQUID Magnetometer and the PPMS (VSM and ACMS options) give magnetic moment in emu, and sample dimensions are in cm. The interest is in the estimation of current density, Jc,mag, in A/cm2. The moment is converted to volume magnetization, M, by dividing with the sample volume, giving units of M to be emu/cm3.
In order to use Gyorgy et al. with the correct magnetic units, ΔM in emu/cm3 has to be converted to gauss. A standard table of magnetic unit conversions is shown in databases of IEEE and NIST [34,35], where (Volume) Magnetization M can be in emu/cm3, and when M is multiplied by 4π, the (Volume) Magnetization is in gauss (G). Then the calculation using Gyorgy et al. gives Jc,mag, in A/cm2.
Following the equation for Jc,mag reported in many works in literature, where the magnetization is expressed in emu/cm3 [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] the second route to obtaining the magnetic critical current density in A/cm2, is by converting ΔM in emu/cm3 to SI units of A/m with the expression 1 emu/cm3 = 103 A/m or 1 emu/cm3 = 10 A/cm [34,35]. With this conversion of ΔM to A/cm, using expression (1), yields Jc,mag, in A/cm2.
The third route is to use the expression (1) of Gyorgy et al., have ΔM in emu/cm3, and assume that the number 20 in expression (1) has the units of A⸱cm2/emu. Although not reported in regularly published works, this procedure can be found on some papers deposited on freely accessible online repositories of electronic preprint manuscripts [36,37].
There is also a fourth route, using the expression (1) with ΔM in emu/mm3, the sample’s dimensions in mm, some unclearness between the use of the magnetic moment or the magnetization, and the obtained Jc,mag in A/mm2 [38,39]
In the first and second cases above, whether ΔM is expressed in gauss or converted (as it should be done) from emu/cm3 to A/cm, an error is obtained when using Gyorgy et al.'s expression (1), which is the commonly cited formula in the literature to calculate Jc,mag using the Bean's model. In fact, in the first case when ΔM is converted to gauss, a factor 12.56 higher Jc,mag is obtained, whereas in the second case Jc,mag results 10 times higher. Although the third route provides the correct numerical value, it is conceptually wrong because it artificially introduces a non-dimensionless pre-factor 20 [A⸱cm2/emu], not predicted by the theory, just to force the dimensional balance of an equation with non-coherent units (as it will be shown in the following). In addition, if different magnetic and/or dimensional units are used, the pre-factor of 20 needs to have different "assumed" units, as it should be for the equation used in the fourth route above, as example.
The scenarios cited above lead to confusion and errors in the calculated Jc,mag using the Bean's model. It is difficult to ascertain how Gyorgy et al. has been applied in numerous and extensive previous publications, since in most cases, the measured moment and/or volume magnetization and sample dimensions are typically not reported. However, it is likely that such errors have been made in previous studies, because it is unusual to expect the pre-factor, an integer number, to have complicated and non-intuitive units of A⸱cm2/emu (or A⸱mm2/emu, or A⸱cm2/Gauss or whatever, depending on the authors), specially, given that these units for 20 are not clearly specified in literature.
The correct formula [40]for calculation of Jc,mag starting from the Magnetization M, within the Bean’s critical state model, for a rectangular parallelepiped sample with isotropic critical current densities and with volume w x b x d, when the magnetic field is applied perpendicular to the largest face with dimension w by b (with w ≤ b), and with self-consistent magnetic units that should be used is:
J c = 2 × Δ μ V × w × 1 − w 3 b
If Δ μ (where μ is the magnetic moment) is expressed in [A m2], the volume V = ( w   b   d ) is in [m3], and the sample side lengths w and b are in [m], the Δ M results in A m and the Jc is expressed in SI units as A m 2 m 3 × m = A m 2   . Here, the number 2 is dimensionless. So:
2 × Δ M A / m w m × 1 − w m 3 b m = J c , m a g A / m 2
As indicated in ref. [34,35], it is possible to convert the magnetic moment from [A m2] to emu, and the lengths from m to cm, by means of:
Δ μ e m u = 10 3 e m u / A m 2 Δ μ A m 2
V c m 3 = 10 6 c m 3 / m 3 V m 3
and w c m = 10 2 c m / m w m
Using these conversions, the Jc in the equation [1] can be expressed as e m u c m 3   × 1 c m = e m u c m 4   with a conversion factor of
10 3 10 6 × 1 10 2 = 10 − 5
with respect to the equation (2) in SI units.
But e m u c m 3 = 10 3 A m and, the simple final conversion from A m to A c m can be considered, and so we can write e m u c m 3 = 10 1 A c m .
In this way we obtain the units conversion from cgs emu system to some kind of “hybrid” cgs/SI system (or “practical CGS system”). With this conversion, the Jc in the equation (2) expressed as e m u c m 3   × 1 c m   with a conversion factor of 10-5, can be expressed in A c m   × 1 c m = A c m 2   with a conversion factor of 10 − 5 × 10 1 = 10 − 4 with respect to the equation in SI units, which is exactly what is expected if the conversion A m 2   = 10 − 4 A c m 2   is applied to the final result obtained in SI units from the equation (2). So, the conversion from the results of equation (2) expressed in different unit system is simply done by correctly applying the unit conversions [34,35], as for any formula in science, without the need to create different equations for different unit systems and add dimensional pre-factors to the existing equation.
So, if the magnetic moment is in emu and the sample’s dimensions in cm, the described approach leads to write the equation (2) by making the used units explicit:
J c , m a g = 2 × Δ M e m u / c m 3 w c m × 1 − w c m 3 b c m
where it is evident that an expression having the dimensions of e m u / c m 3 / c m gives as result a quantity having the dimensions of e m u / c m 4 , definitely not practical for a current density. For this reason, this form of the equation 4 can be re-written in more practical units, by the previously indicated conversion e m u c m 3   = 10 1 A c m   which makes the dimensionless number 2 in the equation 4 to become the dimensionless number 20 in the 2nd form of the equation 4 and, therefore, the current density to be expressed in the more practical dimensions of A / c m 2 :
20 × Δ M A / c m w c m × 1 − w c m 3 b c m = J c , m a g A / c m 2
The above discussion clearly shows that equation (2) is the correct one for the sample geometry described in the text, and it can be used independently of the fact that one has the magnetic moment in [A m2] (and dimensions in meters) or in [emu] (and dimensions in centimetres), by using the conversion of units, without adding any non-dimensionless pre-factor:
when the magnetic moment is in [A m2] and the dimensions in meters, their use in equation (2) leads to the equation (3) where the current density is directly in A / m 2
when the magnetic moment is in [emu] and the dimensions in centimetres, their use in equation (2) leads to the equation (4) where the current density is in the unpractical e m u / c m 4 . In order to have the current density expressed in more practical units, the conversion e m u c m 3   = 10 1 A c m   can be used, which introduces a multiplicative dimensionless term 10 that transforms the number 2 into 20, and leads to a current density expressed in A / c m 2 (equation (5)). On the contrary, the expression J c = 20 × Δ M   w × 1 − w 3 l where ΔM is stated to be in emu/cm3 and Jc is resulting in A/cm2 is misleading, because the dimensions on the right and left-hand side of the equation are not coherent and erroneously suggest the need for a further unit conversion.
This approach is also consistent with Poole et al. [40], where the equation to obtain the critical current density using the Bean’s model are reported for several geometries. These equations are obtained by starting from the general equation (13.24) for the magnetic moment of an arbitrary shaped sample, and Poole et al. say that: “Equation (13.24) is an SI formula in which current density j is in amperes per square meter, magnetic field B is in tesla, and lengths are in meters. When practical units are used whereby j is measured in A/cm2, magnetic field in Gauss, and length in centimetres, the factor 1 2 in Eq. (13.24) is replaced by 1/20. To convert the formulae below for the magnetic moment to practical units simply divide by 10.”
In fact, let’s start from the definition of magnetic moment μ, as reported in ref. [40] -page 396, equation 13.24:
μ = 1 2 ∫ V r × j r d 3 r
and for simplicity in the notation let’s denote the integrated quantity as X, so: X = ∫ V r × j r d 3 r .
The equation (6) is an SI equation, the pre-factor 1 2 is dimensionless, and if the current density j is expressed in A/m2, and the lengths in meters (m), the value of X results to be expressed in:
(m) x (A/m2) x (m3) = (A m4/m2) = A m2, coherently with the dimension of the magnetic moment μ in SI [34,35].
Following what reported in ref. [40], when practical units are used, the current density j is expressed in A/cm2, and the lengths in centimetres (cm) the value of X results to be expressed in: (cm) x (A/cm2) x (cm3) = (A cm4/cm2) = A cm2. In this way, the equation (6) in practical units appears as:
μ e m u = 1 2 X A c m 2
But: emu = 10-3 (A m2) = 10 (A cm2) [34,35] and so equation (7) is:
10 μ A c m 2 = 1 2 X A c m 2
or
μ A c m 2 = 1 20 X A c m 2
and for the magnetization M = μ/V:
M = μ [ A c m 2 ] V c m 3 = 1 20 ∫ V r × j r d 3 r V A c m
where the current density j is expressed in A/cm2, and the lengths in centimetres (cm), and the pre-factor 1/20 is still dimensionless, coherently with the equation (5). Following this approach, as also reported by Poole et al. [40] to obtain in particular the equation 13.30 at page 396, the expressions (2-5) can be calculated with the proper units and numerical pre-factors.
Since we have analysed how to perform the calculation of Jc both in SI and in the ‘hybrid’ cgs-emu/SI system, it is worth to consider also what happens in the emu system, where electric current is not an independent physical quantity and can be expressed in abampere (abA), also called biot (Bi). More precisely [41]:
a b A = B i = c m 1 / 2 g 1 / 2 s − 1
The conversion to SI electric current unit is [41]:   1 B i = 10   A .
Remembering that the term “emu” used as unit for the magnetic moment μ is not an unit but just indicates electromagnetic units, it is important to specify that in emu system, the unit for the magnetic moment μ = π I a 2 of a circular loop of radius a carrying a current I is e r g / G a u s s , that, of course, as indicated in the Goldfarb’s paper [42] can be expressed in terms of Bi as:
e r g / G a u s s = B i ∙ c m 2
Therefore, the equation (2) above can be used in emu system by indicating Δ μ in B i ∙ c m 2 , the volume V in c m 3 and the length in w in c m , so leading to a current density expressed in B i ∙ c m 2 c m 3   × 1 c m = B i c m 2   , i.e.:
J c , m a g = 2 × Δ M B i / c m w c m × 1 − w c m 3 b c m = J c , m a g B i c m 2
that is definitely not practical. Since 1 B i = 10   A , the expression above can be written also as:
J c , m a g = 2 × 10 × Δ M A / c m w c m × 1 − w c m 3 b c m = 20 × Δ M A / c m w c m × 1 − w c m 3 b c m = J c , m a g A / c m 2
namely again the expression for J c , m a g in practical units, were the pre-factor 20 is still dimensionless.
After proving the non-dimensionality of the pre-factor 20, it is probably easier to interpret the equations (2-5):
Starting from the equation (2) above in this paper, with the use of the SI units system where the magnetic moment μ is expressed in A m 2 and the dimensions are in meters m the calculation is direct and the critical current density J c , m a g is direcly obtained in A / m 2 . Since many magnetometers present their output in emu (although in several models it is possible to choose the units for the output), the same equation (2) can be used by inserting the magnetic moment μ in emu and the dimensions in centimetres c m , leading for J c , m a g a certain value (for practical reasons, let’s call “Z” this value, simply resulting from the numbers given to the quantities in equation (2)) in e m u / c m 4   . If the value “Z” in e m u / c m 4   is multiplied by 10, because of the conversion
e m u c m 3 = 10 A c m
the J c , m a g results in A / c m 2 .
This makes the equation (4) to be converted into the equation (5), without adding any non-dimensionless pre-factors. This is also what Poole et al. [40] mean when at page 396 they write “To convert the formulae below for the magnetic moment to practical units simply divide by 10”.
To conclude, no matter if one has the physical quantities expressed in SI, in practical units or in emu, the equation to be used (for the geometrical conditions already stated above) is equation (2), and depending on the final units that are needed for the current density, one has just to use the standard conversion units [34,35,41,42], avoiding to make the error of mixing non-coherent units, and to compensate that error by artificially introducing dimensional pre-factors to force the dimensional balance of the equation. We hope that this will clarify any doubt about the application of the correct equations and units for the calculation of the critical current density from magnetic measurements, in particular, for a rectangular parallelepiped sample in perpendicular field, although the same approach can be extended also to analogous equations for different geometries [40].
In order to check the validity of the discussed approach, the consistency of the measurement units and the absence of any non-dimensionless pre-factor in the expression for the calculation of the critical current density by the equation (2) above in any unit system, it can be helpful to make an example of the typical calculation of J c , m a g , if one has on hand the magnetic moment and the dimensions of the sample.
Let’s consider a hypothetical sample with these characteristics:
QUANTITY VALUE IN EMU-CGS VALUE IN SI SYSTEM
Thickness d = 200 nm 2 ∙ 10 − 5   c m 2 ∙ 10 − 7   m
Width w = 4 mm 4 ∙ 10 − 1   c m 4 ∙ 10 − 3   m
Length b = 4 mm 4 ∙ 10 − 1   c m 4 ∙ 10 − 3   m
Volume (wbd) 32 ∙ 10 − 7   c m 3 32 ∙ 10 − 13   m 3
Δ(Magnetic moment) = Δ μ 3   e m u 3 ∙ 10 − 3   A ∙ m 2
Within the Bean’s critical state model, for a rectangular parallelepiped sample with isotropic critical current densities and with volume w x b x d, when the magnetic field is applied perpendicular to the largest face with dimension w by b (with w ≤ b) the equation to be used for J c , m a g is the equation (2) above in this paper (or equivalently the equation (13.30) in ref. [40]).
So, by considering μ in emu and the dimensions in c m , the following calculations apply:
J c = 2 × Δ μ V × w × 1 − w 3 b = 2 × 3 e m u 32 ∙ 10 − 7 c m 3 × 4 ∙ 10 − 1 c m × 2 3
= 6 e m u 128 ∙ 10 − 7 c m 3 × 10 − 1 c m × 3 2 = 0.0703 ∙ 10 8 e m u c m 4
Using the conversion e m u c m 3 = 10 A c m , this can be written as:
J c = 0.0703 ∙ 10 8 e m u c m 3 1 c m = 0.0703 ∙ 10 8 ∙ 10 1 A c m 1 c m = 0.0703 ∙ 10 9 A c m 2 = 7.03 ∙ 10 7 A c m 2
and, since 1 A c m 2 = 10 4 A m 2
J c = 7.03 ∙ 10 7 A c m 2 = 7.03 ∙ 10 7 ∙ 10 4 A m 2 = 7.03 ∙ 10 11 A m 2
On the other hand, by considering μ in A ∙ m 2 and the dimensions in m , the following calculations apply:
J c = 2 × Δ μ V × w × 1 − w 3 b = 2 × 3 ∙ 10 − 3 A ∙ m 2 32 ∙ 10 − 13 m 3 × 4 ∙ 10 − 3 m × 2 3
= 6 ∙ 10 − 3 A ∙ m 2 128 ∙ 10 − 13 m 3 × 10 − 3 m × 3 2 = 0.0703 ∙ 10 13 A m 2 = 7.03 ∙ 10 11 A m 2
as obtained above, and since 1 A m 2 = 10 − 4 A c m 2
J c = 7.03 ∙ 10 11 A m 2 = 7.03 ∙ 10 11 ∙ 10 − 4 A c m 2 = 7.03 ∙ 10 7 A c m 2
as obtained above, with self-consistency and no ambiguity with respect to the magnetic units on the left and right side of the equation (2), without modifying the equation depending on the used unit system, and without artificially introducing any dimensional pre-factors to force the dimensional balance of the equation.
In summary, the formula for calculation of Jc,mag starting from the Magnetization M, within the Bean’s critical state model, for a rectangular parallelepiped sample with isotropic critical current densities and with volume w x b x d, when the magnetic field is applied perpendicular to the largest face with dimension w by b (with w ≤ b), and with self-consistent magnetic units that should be used is:
2 × Δ M w × 1 − w 3 b = J c , m a g
where, ΔM is the width of the volume magnetization loop. In this equation, the pre-factor, number 2, is dimensionless similar to numbers in any scientific formula or expression. The units of M can be modified using appropriate magnetic unit conventions and so can the units of sample dimensions w, b and d to arrive at Jc,mag in the desired units, thereby, removing any ambiguities related to units of the pre-factor. Use of this expression will resolve continued propagation of errors in the literature, is consistent with correct dimensional analysis, and eliminates discrepancies in the calculated Jc,mag.

References

  1. Goyal, A., Kumar, R., Yuan, H. et al. Significantly enhanced critical current density and pinning force in nanostructured, (RE)BCO-based, coated conductor. Nat Commun 2024, 15, 6523. [Google Scholar] [CrossRef] [PubMed]
  2. C.P. Bean. P. Bean. Phys. Rev. Len. 1962, 8, 250.
  3. C.P. Bean. P. Bean. Rev. Mod. Phys. 1964, 36, 31.
  4. E. M. Gyorgy; R. B. van Dover; K. A. Jackson; L. F. Schneemeyer; J. V. Waszczak. Anisotropic critical currents in Ba2YCu3O7 analyzed using an extended Bean model, Appl. Phys. Lett. 1989, 55, 283–285. [Google Scholar] [CrossRef]
  5. Li M., Chen L., You W-L., Ge J., Zhang J. Giant increase of critical current density and vortex pinning in Mn doped KxFe2−ySe2 single crystals. Appl. Phys. Lett. 2014, 105, 192602. [Google Scholar] [CrossRef]
  6. Haberkorn N., Xu M., Schmidt J., Suárez S., Bud’ko S.L., Canfield P.C. Understanding vortex dynamics in CaK(Fe,Ni)4As4 and Ba(Fe,Co)2As2 single crystals under the influence of random point disorder. Supercond. Sci. Technol. 2024, 37, 115003. [Google Scholar] [CrossRef]
  7. Liu Y., Wang T., Xu Z., Hong W., Peng W., Lin Z-R.,Luo H. and Mu G. Influences of quenching treatment and cobalt-doping on the thermally activated flux-flow behavior in KCa2(Fe1−xCox)4As4F2. Supercond. Sci. Technol. 2023, 36, 095008. [Google Scholar] [CrossRef]
  8. Wang A.,1 Wu L., Ivanovski V. N., Warren J. B., Tian J., Zhu Y.and Petrovic C. Critical current density and vortex pinning in tetragonal FeS1−xSex (x = 0,0.06). Phys. Rev. B 2016, 94, 094506. [Google Scholar] [CrossRef]
  9. Wang Y., Li M., Pei C.,Gao L., Bu K., Wang D.,Liu X., Yan L., Qu J., Li N., Wang B., Fang Y., Qi Y. and Yang W. Critical current density and vortex phase diagram in the superconductor Sn0.55In0.45Te. Phys. Rev. B 2022, 106, 054506. [Google Scholar] [CrossRef]
  10. S. Eley, K. Khilstrom, R. Fotovat, Z. L. Xiao, A. Chen, D. Chen, M. Leroux, U. Welp, W. K. Kwok; L. Civale. Glassy Dynamics in a heavy ion irradiated NbSe2 crystal. Sci. Rep. 2018, 8, 13162. [Google Scholar] [CrossRef]
  11. V. A. Vlasenko, A. V. Sadakov, T. A. Romanova, S. Yu Gavrilkin, A. V. Dik, O. A. Sobolevskiy, B. I. Massalimov, D. A. Chareev, A. N. Vasiliev, E. I. Maltsev and T. E. Kuzmicheva. Evolution of vortex matter, phase diagram, and upper critical field in the FeSe1−xSx system. Supercond. Sci. Technol. 2021, 34, 035019. [Google Scholar] [CrossRef]
  12. E. Galstyan, R. Pratap, G. Majkic, M. Kochat, D. Abraimov, J. Jaroszynski and V. Selvamanickam. In field critical current and pinning mechanisms at 4.2 K of Zr added REBCO coated conductors. Supercond. Sci. Technol. 2020, 33, 074007. [Google Scholar] [CrossRef]
  13. Taen, T.; Ohtake, F.; Pyon, S.; Tamegai, T.; Kitamura, H. Critical current density and vortex dynamics in pristine and proton-irradiated Ba 0.6 K 0.4 Fe 2 As 2. Superconductor Science and Technology 2015, 28, 085003. [Google Scholar] [CrossRef]
  14. J Narayan, A Bhaumik, R Sachan, High temperature superconductivity in distinct phases of amorphous B-doped Q-carbon, J. Appl. Phys. 2018, 123, 135304. [CrossRef]
  15. Sun, Y.; Pyon, S.; Tamegai, T.; Kobayashi, R.; Watashige, T.; Kasahara, S.; Matsuda, Y.; Shibauchi, T. Critical current density, vortex dynamics, and phase diagram of single-crystal FeSe. Physical Review B 2015, 92, 144509. [Google Scholar] [CrossRef]
  16. Nakajima, Y.; Tsuchiya, Y.; Taen, T.; Tamegai, T.; Okayasu, S.; Sasase, M. Enhancement of critical current density in Co-doped BaFe2As2 with columnar defects introduced by heavy-ion irradiation. Physical Review B - Condensed Matter and Materials Physics 2009, 80, 012510. [Google Scholar] [CrossRef]
  17. Haberkorn, N.; Maiorov, B.; Usov, I.O.; Weigand, M.; Hirata, W.; Miyasaka, S.; Tajima, S.; Chikumoto, N.; Tanabe, K.; Civale, L. Influence of random point defects introduced by proton irradiation on critical current density and vortex dynamics of Ba(Fe0.925Co0.075)2As2 single crystals. Physical Review B - Condensed Matter and Materials Physics 2012, 85, 014522. [Google Scholar] [CrossRef]
  18. Lei, H.; Hu, R.; Petrovic, C. Critical fields, thermally activated transport, and critical current density of β-FeSe single crystals. Physical Review B - Condensed Matter and Materials Physics 2011, 84, 1–5. [Google Scholar] [CrossRef]
  19. Plain, J.; Puig, T.; Sandiumenge, F.; Obradors, X.; Rabier, J. Microstructural influence on critical currents and irreversibility line in melt-textured YBa2Cu3O7-x reannealed at high oxygen pressure. Physical Review B 2002, 65, 104526. [Google Scholar] [CrossRef]
  20. S. Pyon, S. Taya, Y. Kobayashi, A. Takahashi, W. Li, T. Taen, T. Wang, G. Mu, H. Kitamura, A. Ichinose and T. Tamegai. Critical Current Density and Vortex Dynamics in Pristine and Irradiated KCa2Fe4As4F2. Materials 2021, 14, 5283. [Google Scholar] [CrossRef]
  21. Taen, T.; Tsuchiya, Y.; Nakajima, Y.; Tamegai, T. Critical current densities and vortex dynamics in FeTexSe1-x single crystals. Physica C 2010, 470, 1106–1108. [Google Scholar] [CrossRef]
  22. Tao, J.; Deng, Q.; Yang, H.; Wang, Z.; Zhu, X.; Wen, H.H. Magnetization relaxation, critical current density, and vortex dynamics in a Ba0.66K0.32BiO3+δ single crystal. Physical Review B - Condensed Matter and Materials Physics 2015, 91, 214516. [Google Scholar] [CrossRef]
  23. Yi, X.; Xing, X.; Meng, Y.; Zhou, N.; Wang, C.; Sun, Y.; Shi, Z. Anomalous Second Magnetization Peak in 12442-Type RbCa2Fe4As4F2 Superconductors. Chinese Physics Letters 2023, 40, 027401. [Google Scholar] [CrossRef]
  24. Shahbazi, M.; Wang, X.L.; Choi, K.Y.; Dou, S.X. Flux pinning mechanism in BaFe1.9Ni0.1As2 single crystals: Evidence for fluctuation in mean free path induced pinning. Applied Physics Letters 2013, 103, 032605. [Google Scholar] [CrossRef]
  25. Sun, Y.; Taen, T.; Tsuchiya, Y.; Pyon, S.; Shi, Z.; Tamegai, T. Magnetic relaxation and collective vortex creep in FeTe0.6Se0.4 single crystal. EPL 2013, 103, 57013. [Google Scholar] [CrossRef]
  26. Cheng, W.; Lin, H.; Shen, B.; Wen, H.H. Comparative study of vortex dynamics in CaKFe4As4 and Ba0.6K0.4Fe2As2 single crystals. Science Bulletin 2019, 64, 81–90. [Google Scholar] [CrossRef]
  27. Ishida, S.; Iyo, A.; Ogino, H.; Eisaki, H.; Takeshita, N.; Kawashima, K.; Yanagisawa, K.; Kobayashi, Y.; Kimoto, K.; Abe, H.; et al. Unique defect structure and advantageous vortex pinning properties in superconducting CaKFe4As4. NPJ Quantum Materials 2019, 4, 1–7. [Google Scholar] [CrossRef]
  28. Hossaini, S.J.; Ghorbani, S.R.; Arabi, H.; Wang, X.L.; Lin, C.T. Temperature and field dependence of the flux pinning mechanisms in Fe1.06Te0.6Se0.4O single crystal. Solid State Communications 2016, 246, 29–32. [Google Scholar] [CrossRef]
  29. Eley, S.; Leroux, M.; Rupich, M.W.; Miller, D.J.; Sheng, H.; Niraula, P.M.; Kayani, A.; Welp, U.; Kwok, W.K.; Civale, L. Decoupling and tuning competing effects of different types of defects on flux creep in irradiated YBa2Cu3O7-δ coated conductors. Superconductor Science and Technology 2017, 30, 1–22. [Google Scholar] [CrossRef]
  30. A O Ijaduola, S H Wee, A Goyal, P M Martin, J Li, J R Thompson, and D K Christen, Critical currents, magnetic relaxation and pinning in NdBa2Cu3O7 films with BaZrO3-generated columnar defects. Supercond. Sci. Technol. 2012, 25, 045013. [CrossRef]
  31. J. R. Thompsom, JWSinclair, D K Christen, Yifei Zhang, Y L Zuev, C Cantoni, Yimin Chen and V Selvamanickam. Field, temperature, and angle dependent critical current density Jc(H, T, θ) in coated conductors obtained via contact-free methods. Supercond. Sci. Technol. 2010, 23, 014002. [Google Scholar] [CrossRef]
  32. J. R. Thompsom, Y R Sun, H. R. Kerchner, D. K. Christen, B. C. Sales, and B. C. Chakoumakos, A. D. Mat-wick and L. Civale and J. 0. Thomson Enhanced current density J, and extended irreversibility in single-crystal Bi2Sr2Ca1Cu208 via linear defects from heavy ion irradiation. Appl. Phys. Lett. 60 (18), 4 May 1992.
  33. Yadav, C.S.; Paulose, P.L. Upper critical field, lower critical field and critical current density of Fe1.06Te0.6Se0.4O single crystals. New Journal of Physics 2009, 11, 103046. [Google Scholar] [CrossRef]
  34. https://www.nist.gov/system/files/documents/pml/electromagnetics/magnetics/magnetic_units.pdf.
  35. https://ieeemagnetics.org/files/ieeemagnetics/2022-04/magnetic_units.pdf.
  36. E. F. Talantsev and J. L. Tallon, Fundamental nature of the self-field critical current in superconductors, https://arxiv.org/abs/2409.16758 and https://www.researchgate.net/publication/384365582_Fundamental_nature_of_the_self-field_critical_current_in_superconductors.
  37. C. Tarantini, D. C. C. Tarantini, D. C. Larbalestier, Procedures for proper validation of record critical current density claims, https://arxiv.org/abs/2410.22195.
  38. Zerong Zhang, Zhan Gao, Yanan Wang, Jianli Meng, Junsheng Cheng, Qiuliang Wang, The role of copper in the formation of the Nb3Sn superconducting phase, Intermetallics, 2023, 155, 107848.
  39. Bo Zheng, Wei Xie, Yuhao Liu, Xiyu Zhu, Xue Ming, Yuhang Zhang, and Hai-Hu Wen, Optimization of Magnetic Stability in Nb3Sn Materials Near Stoichiometric Composition, IEEE Trans. On Appl. Supercond. 2024, 34, 8200910.
  40. Superconductivity – 2nd Edition, C.P. Poole, H.A. Farach, R.J. Creswick, R. Prozorov, ISBN 978-0-12-088761-3, Academic Press, Elsevier, 2007.
  41. H.E. Knoepfel, “MAGNETIC FIELDS: A Comprehensive Theoretical Treatise for Practical Use”, Wiley-Interscience Publication, John Wiley and sons inc., (2000) - ISBN-10: 0471322059; ISBN-13: 978-0471322054 – page 543.
  42. R. B. Goldfarb, “Electromagnetic Units, the Giorgi System, and the Revised International System of Units,” IEEE Magnetics Letters, vol. 9, pp. 1–5, 2018. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated