Mott Law exp(T₀/T)^1/4 and Scaling Properties of Oxygen Defect Tenorite CuO_0.75

1. Introduction

On the eve of localization theories in disordered systems Landauer [1] put forward the systematic calculation of the electric conductivity of metals containing point defects and derived an equation σ = e²/h·[ΣT_i]; summation is extended over scattering obstacles. Equation is widely used in semiconducting nanostructures, and pre-factor is named Landauer quantum conductance entering in various localization theories, quantum Hall effect, and symbolizes a way toward more universality in the solid state research.

The groundbreaking progress on localization in disordered systems, followed by Anderson [2] and Mott [3], triggered a further tremendous search for universality of magnetic and electric properties in solid state physics, optics, etc. The quantum mechanical functions in localized systems are confined in a finite region and they decay exponentially at higher distances. The localization phenomena cover various materials [4,5] and optics [6-8]. Experimental data, however, derived from the real objects are scarce and dominantly restricted to the resistive measurements [9,10], while accompanied magnetic effects, superposed to resistivity data are rare to trace in the scientific literature.

This paper aims to describe the preparation of the novel copper oxide CuO_0.75, indicated by disordered oxygen vacancies, while the X-ray diffraction data stress out maintaining the original structure of the tenorite CuO. In addition to the resistivity, CuO_0.75 displays an interesting set of magnetic effects, which start by cooling from T~122 K and are followed by antiferromagnetic transition at T~51 K. In the next step, the experimental data will be discussed in terms of Mott and Anderson theories, as well as, modern scaling models. However, difficulties arise from the fact that theories and models dominantly deal with metals, while CuO_0.75 is non-metal indicated by a huge dielectric permittivity ε ~ 1.3·10³, evaluated independently in these experiments.

2. Experimental

Oxygen defect form CuO_0.75 was produced from the powdered cuprous oxide Cu₂O of the particle size 0.5 microns and heated at 388 K in 4 bars oxygen atmosphere. Prior to reaction the powder was heated in vacuum at 423 K in order to remove the traces of gases: like moisture, CO₂ and SO₂. The slow reaction was monitored during 10 – 12 days by use of the pressure gauge and terminated when oxygen pressure was reduced to the value indicating the necessary stoichiometry CuO_0.75. The final product was raw and very hard cluster. Oxygen content was additionally verified by decomposition in 2 bar H₂ atmosphere at 673 K.

The powder obtained by subsequent reground of the raw cluster (R-sample) was pressed into pellets of 8 mm in diameter and d=0.9 mm thickness. In order to measure the four probes electric resistance, the 100 microns gold wires were pressed together with powder. Raw CuO_0.75 is an insulator, but it was observed that conductance may be induced by applied DC current starting with 1 µA and gradually increasing up to 1.5 mA during repeated annealing-cooling cycles (DC-samples) in argon atmosphere. Annealing temperature was 908 K, while the final conductivity of DC samples at room temperature (RT) saturated at 0.08–1.25·10^–2 Ω^–1m^–1. It may be a tedious work to explain this interesting phenomenon in terms conventional chemical and metallurgical methodology. More recent findings [11,12] may provide some introductory ideas and hints on possible stimulation of disorder and corresponding increase of the conductivity by use of the conducting currents.

3. Results

Copper oxide CuO is narrow band p-type semiconductor and crystallographic unit cell belongs to the monoclinic group C2/c with cell dimensions a = 0.4683 nm, b = 0.3421 nm, c = 0.5129 nm; α = 90^°, β = 90^°, γ = 99.784 ^°. Unit cell contains 4 units formulas, and density is ρ= 5.94 g·cm^–3, while the oxygen defect form CuO_0.75 exhibits ρ=5.64 g·cm^–3. Due to one oxygen vacancy per unit cell, CuO_0.75 is expected to be a mixed valence oxide with equal number of Cu²⁺ and Cu⁺ cations. In this respect, CuO_0.75 resembles the copper oxide Cu₄O₃, known as paramelaconite, with the structure indicating CuO₂ chains along c-axis [13]. 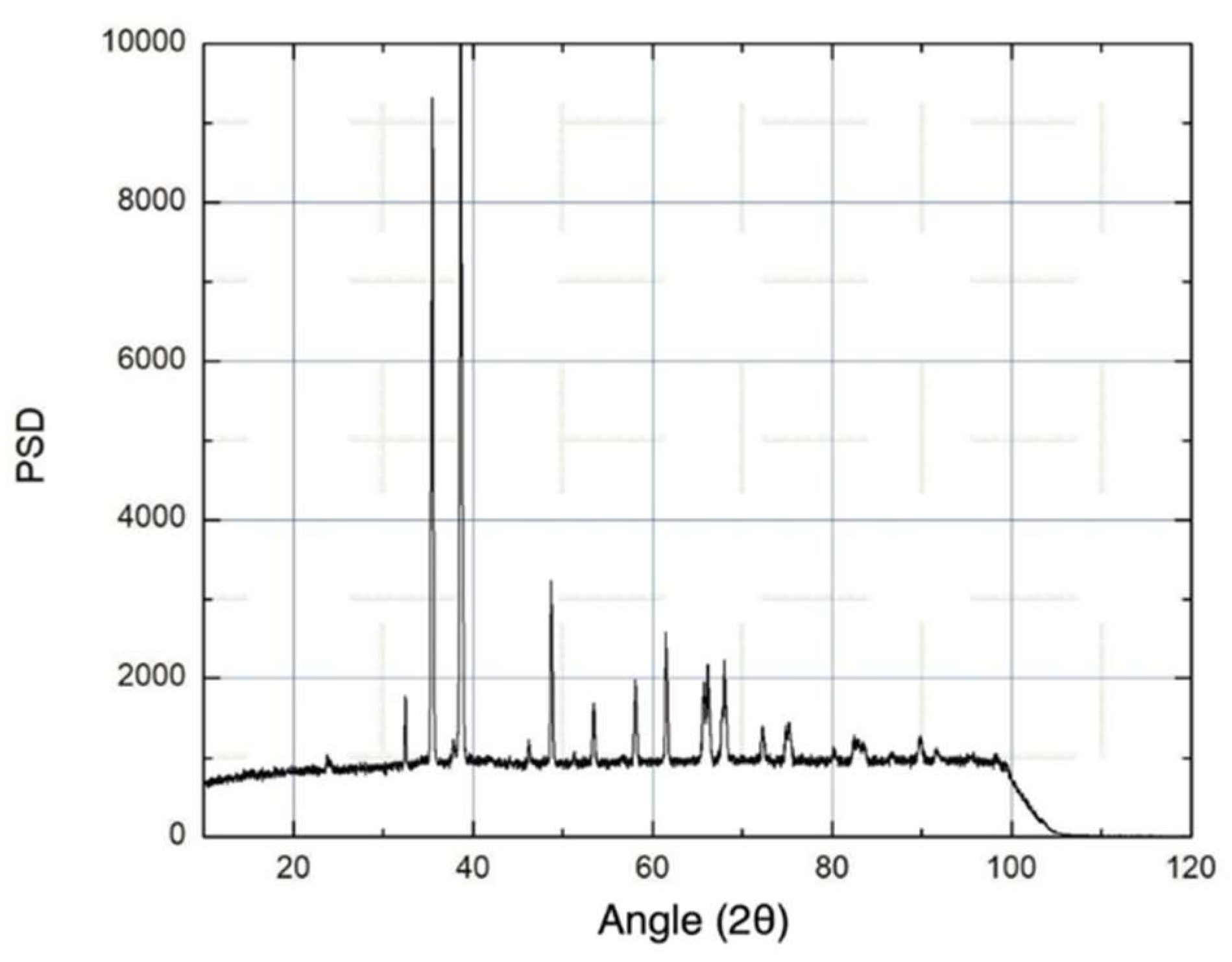Pinsard-Gaudart and co-workers reported [14] the antiferromagnetic transition in Cu₄O₃ at 42 K.XRD data of CuO_0.75 are shown in Figure 1.

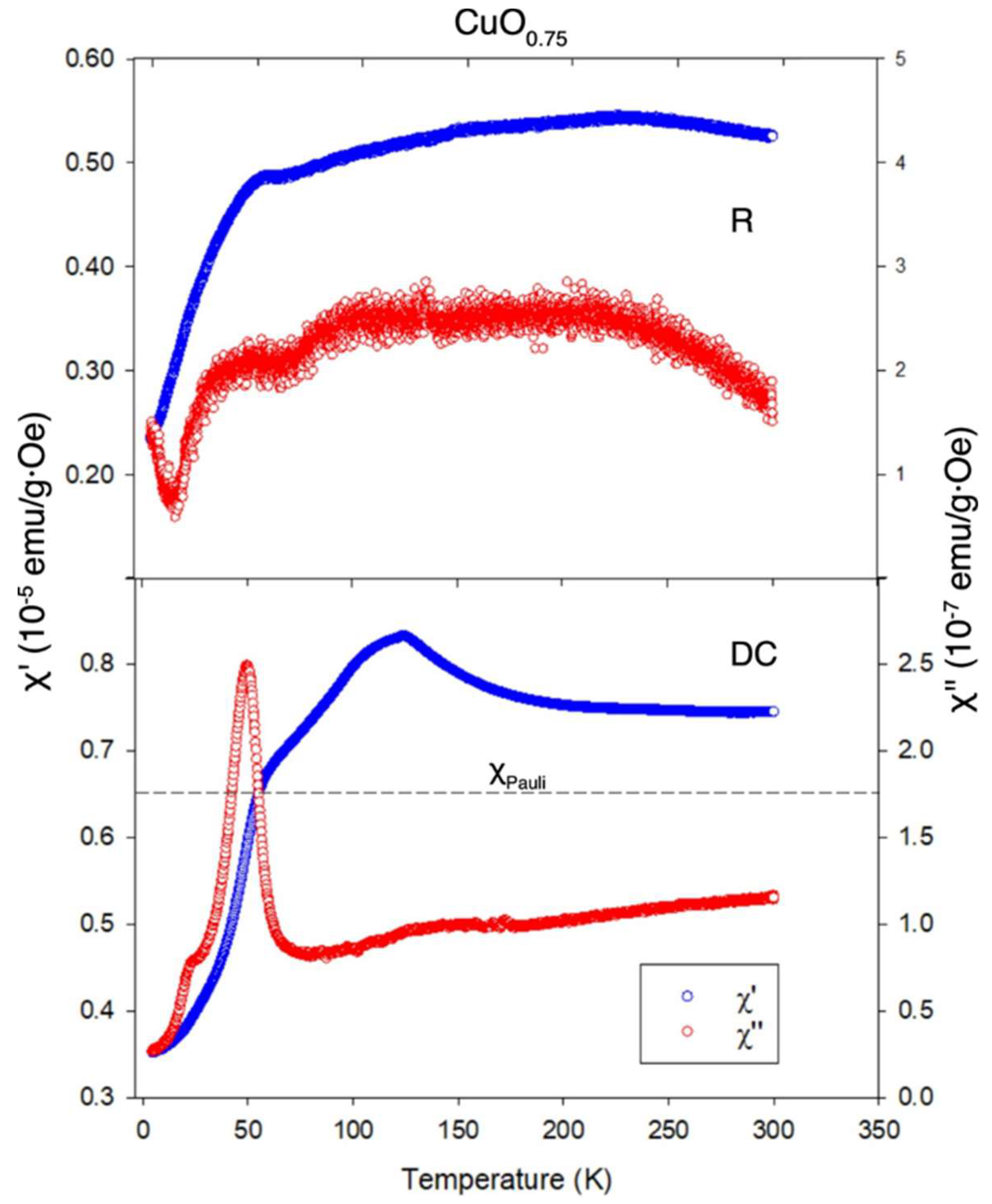
High resolution measurements of AC susceptibility were performed on R- and DC-samples by use of Cryobind susceptometer, and real and imaginary parts are shown in Figure 2. Samples exhibit a surprising temperature dependence of the susceptibility, and several effects are included. By heating to RT, the magnetic susceptibility reveals three features. At T = 51 K, both DC- and R-samples, undergo an antiferromagnetic transition. The next feature appears in DC sample at T = 101 K, while at T_C = 122 K, DC-sample resembles the paramagnetic transition. Both cited transitions are absent in the raw R-sample. At T > 122 K DC sample obeys the Stoner expression χ= χ_p / [1 – U·N(E_F)], while the quantities χ_p, U and N(E_F) are in the respective order; Pauli susceptibility, Coulomb repulsion energy U(Joule·m³) and density of states (DOS) on the Fermi surface. The Pauli susceptibility χ_P and DOS were evaluated from the inverse susceptibility 1/χ plotted versus 1/T. Horizontal dashed line reflects a contribution of the Pauli susceptibility and foreign ingredients; the latter must be subtracted, after an independent measurement on non-reacted Cu₂O. Dimensionless Pauli susceptibility is χ_p=2.9·10^–6, while DOS was calculated [15] from χ_p = μ₀·μ_B²·N(E_F), giving N(E_F) = 2.8·10⁴⁶ Joule^–1·m^–3. The Fermi energy E_F was separately derived from number of states n = 1/V₀ = 2.4·10²⁸ m^–3, and V₀ means the volume of the crystallographic unit cell. Fermi wave number is given as k_F = (3π²·n)^1/3, and E_F = 3.3 eV.

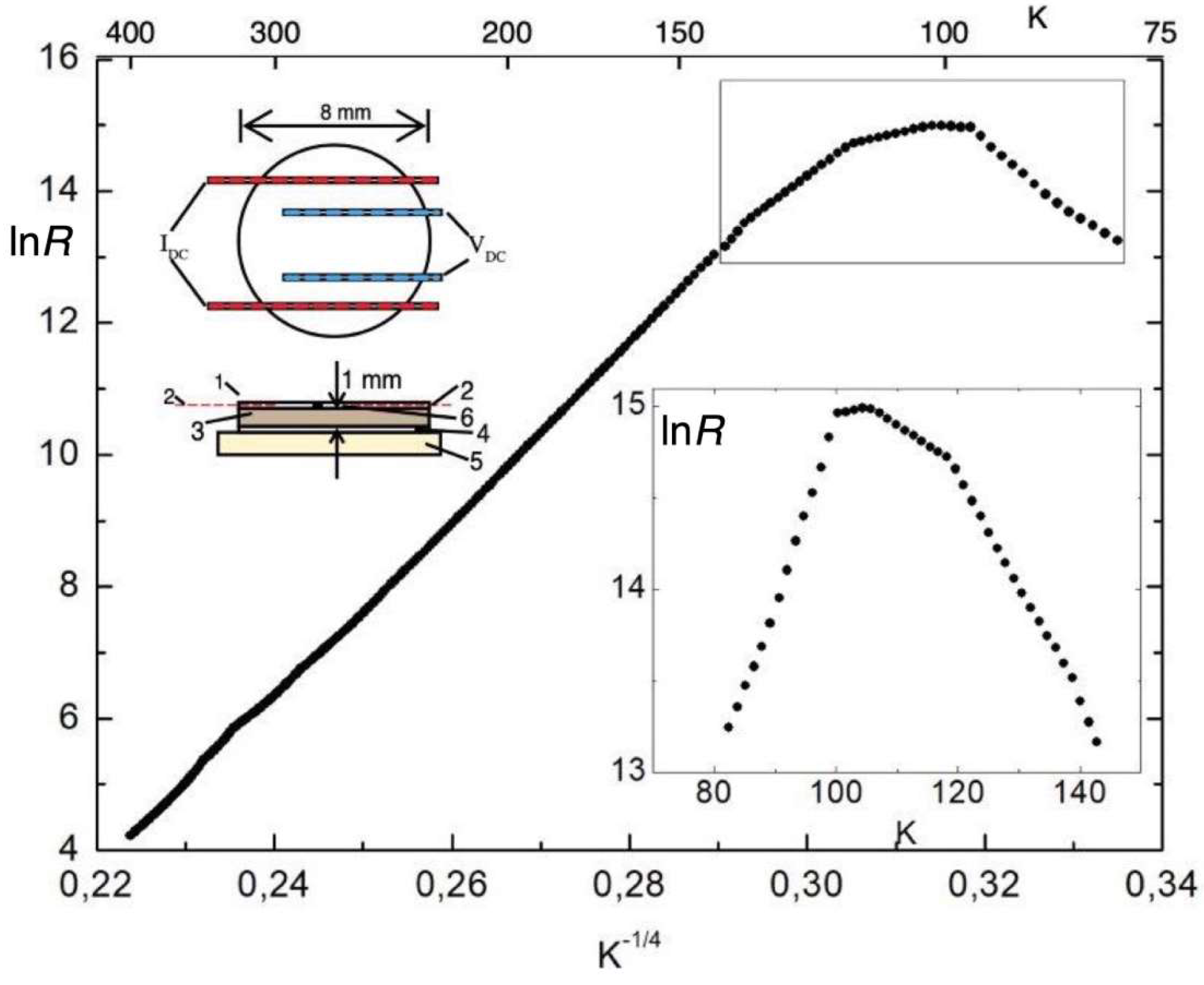
Figure 3 presents the resistance of DC-sample measured by cooling and heating in the range 415 – 80 K. It is evident the linear dependence of lnR on T ^{– 1/4} down to T_C = 122 K, when strong linear increase converts in stagnation, which is followed by the sharp downturn at T =101 K. Linear dependence of lnR on T^–1/4 is the characteristic behavior of the disordered 3 dimensional (3D) system indicated by localization of the electronic states. Anderson put forward that, in disordered systems, diffusion theories of the conductivity must be replaced by models based upon quantum jumps between the localized states. Continuing upon such a course, Mott developed theory¹⁷ of the variable range hopping, and logarithm of the resistivity was derived as

lnρ=2αR+ 1/(4απ/3)k_BTR³N(E_F) R = [αk_BTN(E_F)]^–1/4

(1)

where 1/α and R are localization length and hopping range respectively. This expression was fitted to the measured dependence lnR on T^–1/4 in the temperature interval 122 – 415 K when metallic state sets up by further heating. An evaluation of the localization length gives α^–1= 2.1·10^–9 m, while the variable range length at T =122 K is R = 2.3·10^–9 m. R decreases slowly by heating, and Mott expression of the level spacing between two states reads Δ=α³/N (E_F)~18.8meV.

Measured electric conductance of CuO_0.75 at T= 415 K was G₀= 1.5·10^–2Ω^–1, and evaluated conductivity is σ₀ = 0.17 Ω^–1·cm^–1.When this value should be compared to Mott minimum metallic conductivity σ_min= π²·e²/8·z·h·c [ref.16, p.31], it must be encountered the dielectric permittivity of CuO_0.75, ε = 1.3·10³ in the temperature interval 100 – 415 K. The renormalized value reads σ = ε·σ₀ ~ 221 Ω^–1cm^–1, and it is comparable to the Mott value σ_min= 300 Ω^–1·cm^–1. In further calculations we replace lattice parameter c by α^-1 distant localized scatters.

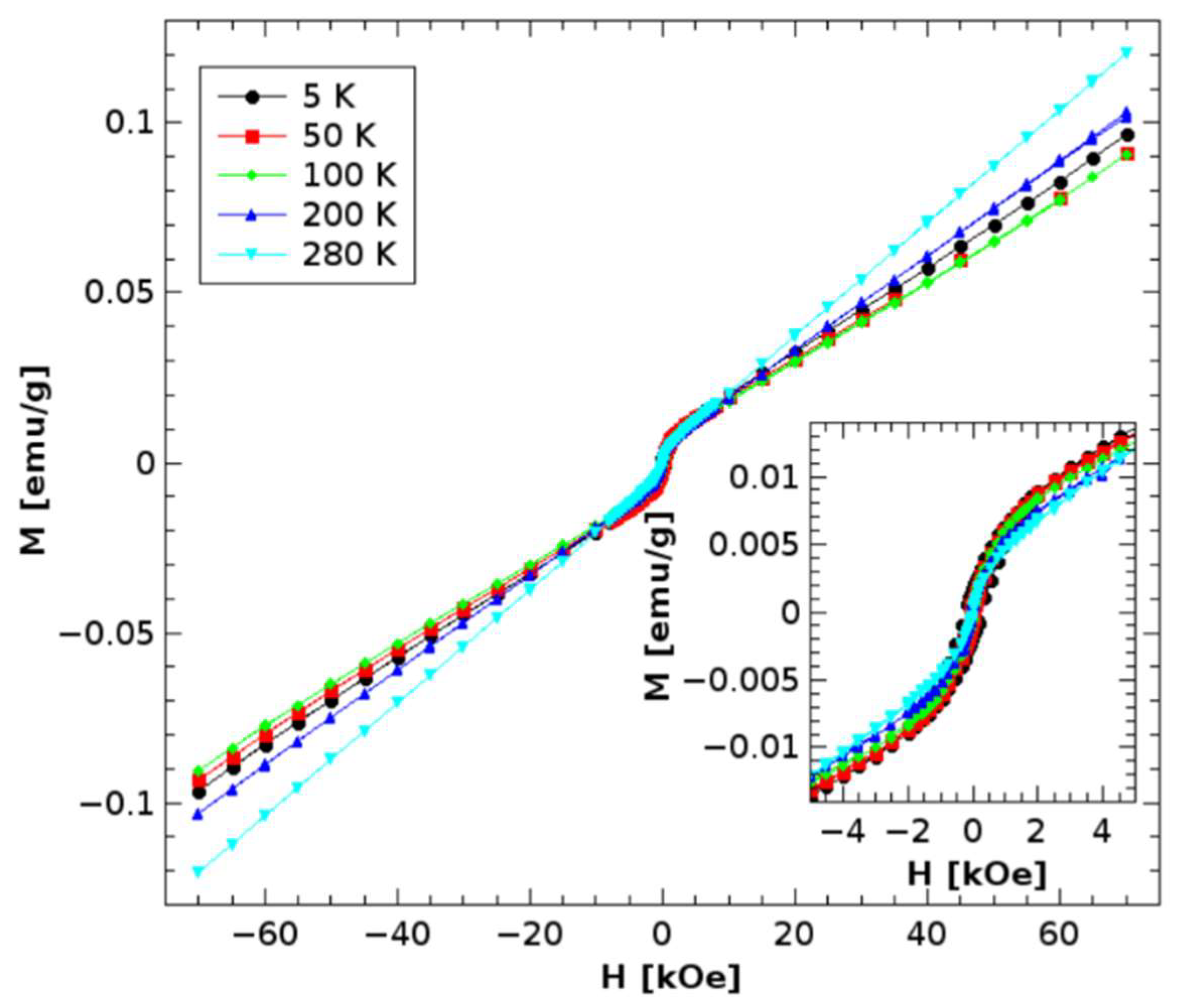
The measurements of hysteresis performed by use of SQUID, are presented in Figure 4. Measurements of magnetization, dependent on magnetic field at various stable temperatures, sound for antiferromagnetic state below 50 K. Bending of hysteresis around small fields could originate from superparamagnetism of nano-clusters, which may reflect the localized states bound to distinct regions.

4. Discussion

Pinsard-Gaudart and co-workers calculated in paramelaconite Cu₄O₃ the magnetic double-exchange interaction E = 48,3 K between nearest neighbor Cu²⁺ cations Cu²⁺–O–Cu²⁺ (NN). Such a mechanism may also be certain in CuO_0.75, with oxygen vacancies involved in double-exchange Cu²⁺–Vo–Cu²⁺ or Cu²⁺–Vo–Cu⁺. In support, Gao and co-workers [17] reported a weak ferromagnetism mediated by oxygen vacancies in CuO nanoparticles.

Downturn of the resistance in CuO_0.75 below 122 K may be explained by Zener model of the magnetic double exchange conductivity. Model was originally applied to the resistance [18] properties of strontium doped manganite (La_1-xSr_x)MnO₃. An exchange is favored by the polarization of the hopping electrons between aligned cation spins Mn⁴⁺–O–Mn³⁺, which, in turn, enhances the electric conductance and the magnetization due to the itinerant electron contribution. Zener evaluated the electric conductance G_Z =x·e²E/h·k_BT. E and x are exchange energy and fraction of ions involved in the exchange respectively. G_Z may compete the resistance divergence T^–1/4 in CuO_0.75 at T < 122 K giving rise to a possible two fluid conductance. Calculated Zener conductivity reads σ_Z ~ 380 Ω^-1·cm^-1, while relative dielectric permittivity is absent in the evaluation.

Thouless [19] introduced dimensionless conductance g=G·h/e². However, the ratio of the measured and Landauer conductance is impractical for testing the scaling theories by experiment, since measured conductance G is dependent on the sample thickness d, as being no uniquely defined parameter. We introduce dimensionless conductivity g = ε·α⁻¹·G·h/d·e², and g gives Thouless energy E_T =g·Δ. Δ = 18.8 meV is the, above evaluated, level spacing, and from the resistance at T =415 K, Thouless energy reads E_T = 9.8 meV giving T_C=132 K, which should be compared to transition temperature T = 122 K. Thouless energy and corresponding temperature mark the melting of the localized to extended states, while, upon heating, the T^–1/4 regime starts at temperature T= 122 K, and extends up to 415 K.

In the next step, an attempt is presented to compare the resistance data to scaling model put forward by Abrahams and co-workers (AALR) [20]. The problem arises to define the universal scaling length L based on given experimental data. The choice proposed by AALR is the mean free path l, although l is doubtful because of strong dependence on temperature. Following a search for common points of AALR model, Mott theory and our experimental data, we introduce localization decay L=α^–1 as a scaling length, since it is independent of temperature. AALR theory introduces parameter β=d(lng)/d(lnL) indicating β = 0 at the metal-insulator transition. The comparatively easy calculation, for the case CuO_0.75, starts with an elimination of the temperature in Equation (1), which gives the dimensionless conductivity g =(ε·α^-1·h·σ₀/e²)·exp–αR[2 + ¾π]. This expression matches the AALR result for 3D system, and little more algebra results in β = lng, giving β= 0 for g = 1, means that metal-insulator transition may be expected when the renormalized conductivity ε·α_o approaches the Landauer quantum conductivity e²·α/h proceeded between two localized points distant α^-1. In the case CuO_0.75 this happens at T~ 415 K, when exp(T₀ /T)^1/4 regime starts by cooling.

5. Conclusions

In conclusion, a novel copper oxide CuO_0.75 was prepared. It is indicated by one oxygen vacancy per unit cell and exhibits the crystallographic structure of a tenorite CuO. In the interval 122 – 415 K, electric resistance is temperature dependent according to the Mott law exp[(T₀/T)^1/4]. Anderson theory of localization and Mott theory of variable hopping were successfully applied, and characteristic length of exponential decay of the localized state was evaluated α^–1= 2.1 nm, while variable hopping range is R=2.3·10^–9 m at T =122 K. It has been shown that Mott’s concept of minimum conductivity in metals σ_min may be extended to nonmetal CuO_0.75, giving rise to a possible universal physical constant. In addition, σ_min has been evaluated by taking in account a calculated [21] ratio of critical localization potential and band width V_crit/B = 2, confirming this result as to be correct. Dimensionless Thouless conductivity g was calculated and corresponding Thouless energy E_T, converted to temperature, gives T~142 K. In order to apply scaling theory of Abrahams and co-workers (AALR), L =α^–1 is chosen as a scaling length, while β function reads β= lng. At T = 122 K magnetic measurements reveal the transition to a double exchange interaction indicated by Zener conductivity, which is comparable to the Mott conductivity σ_min. CuO_0.75 undergoes an antiferromagnetic transition at 51 K.