Submitted:
04 December 2024
Posted:
05 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
2.1. System Dynamics Modeling and Its Applications in Manufacturing and Supply Chain Management
2.2. System Dynamics Modeling for Sustainable Supply Chain Management
2.3. Hemp-Reinforced Polymer Composite Manufacturing for Sustainability
2.5. Identified Research Gap and the Study’s Proposed Contribution
3. Hypothesis and Research Questions (RQ)
4. Materials and Methods
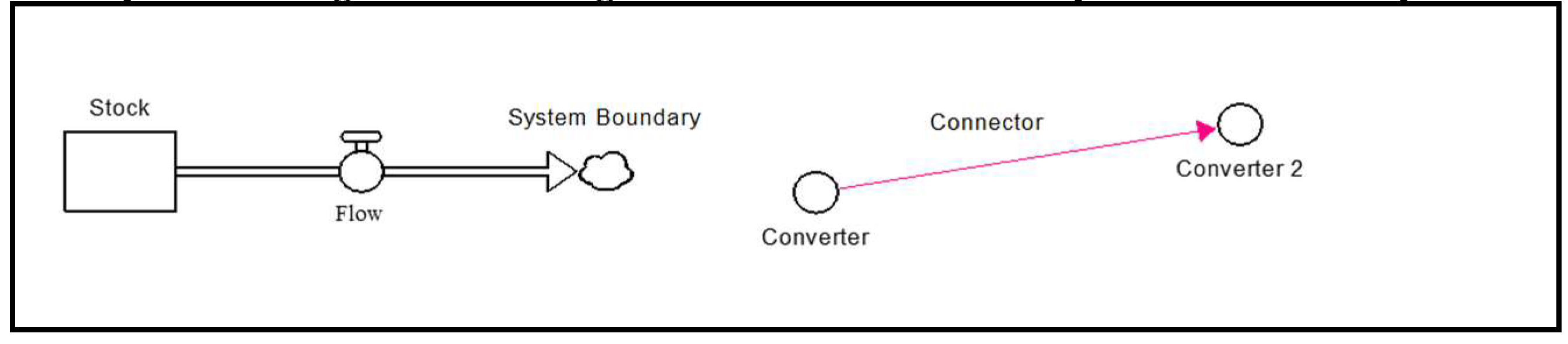
4.1. SDM Software
- Define the objective of the supply chain.
- Set the project scope by identifying its boundaries, inputs, and outputs.
- Specify the functional unit, such as the number of goods produced per day.
- Build the STELLA® model using the four building blocks: stocks, flows, converters, and connectors.
- Add equations with conditional statements, like "if_then_else," to the flows.
- Set initial conditions for each stock and converter.
- Run the model and observe the behavior of stocks and flows for a given scenario.
- Adjust inputs and rerun the model for different scenarios, aiming to minimize material flows and waste.
4.2. Elements of SDM
- Specifying appropriate units of measurement for each model variable to avoid formulation errors.
- Ensuring model equations are unit-consistent, meaning the left and right sides of each equation must simplify to the same units.
- Maintaining consistent units of measurement across all stocks within a flow chain.
- Assigning an initial value to all stocks at time equals zero.
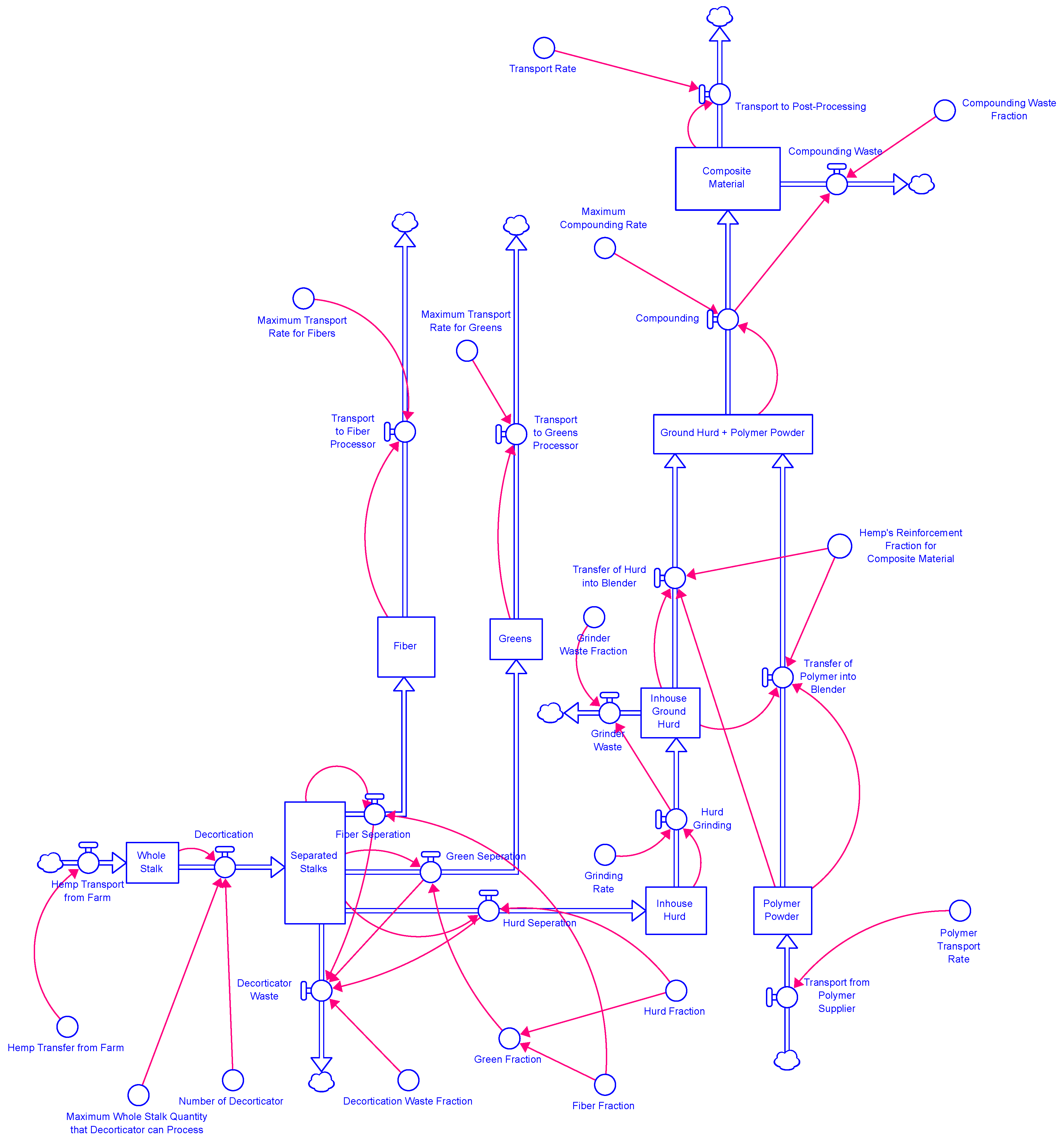
4.3. Supply Chain Model of Hemp-Reinforced Polymer Composite Manufacturing.
- Harvested and retted hemp stalks are delivered to the manufacturing facility to begin the production process. It is assumed that farms can consistently supply the facility with sufficient material. Any processes prior to delivering harvested and retted hemp stalks are outside the scope of this model.
- Hemp stalks are processed through decortication, separating them into three components: bast fiber, hurd, and greens.
- "Greens" refer to any residues and leaves separated during decortication that are neither bast fiber nor hurd.
- Bast fiber and greens are transported to their respective manufacturing facilities.
- Each step of the process generates a nominal amount of waste.
- Thermoplastic polymer powder or pellets are purchased from suppliers and delivered to the manufacturing facility.
- The reinforcement fraction for the composite material is specified by an external customer purchasing the material.
- The composite material is processed into compounded pellets, which are then transported to customers for further processing. The conversion of pellets into final products is beyond the scope of this model.
- The current model does not account for supply chain disruptions such as equipment failures, transportation delays, or labor shortages (though these time-dependent elements could be added in future versions of the model).
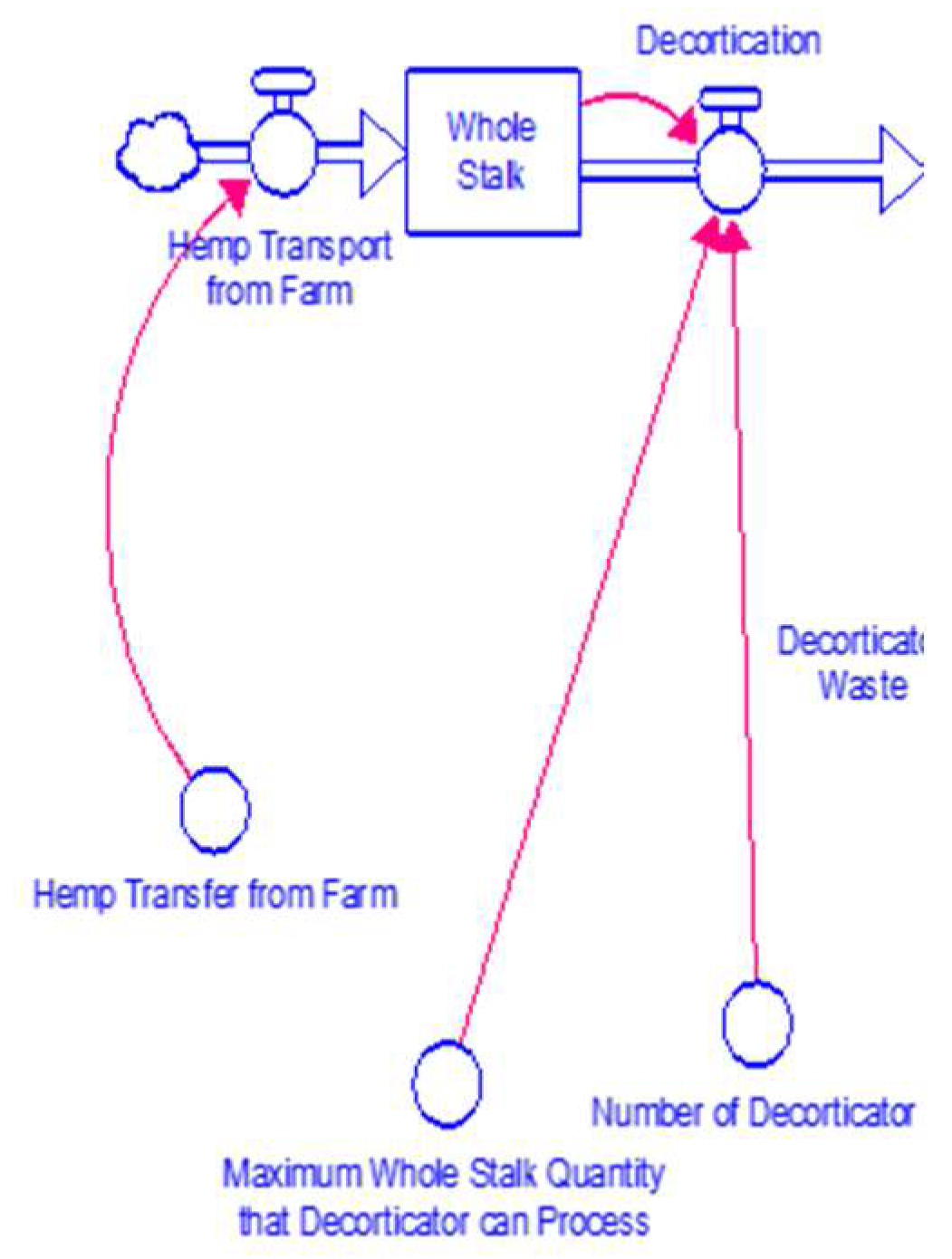
4.4. Development of SDM Converters, Flow Equations, and Stock Equations for This Model
4.4.1. SDM Converters in Figure 3
4.4.2. SDM Flow Equations in Figure 3
4.4.3. SDM Stock Equation in Figure 3
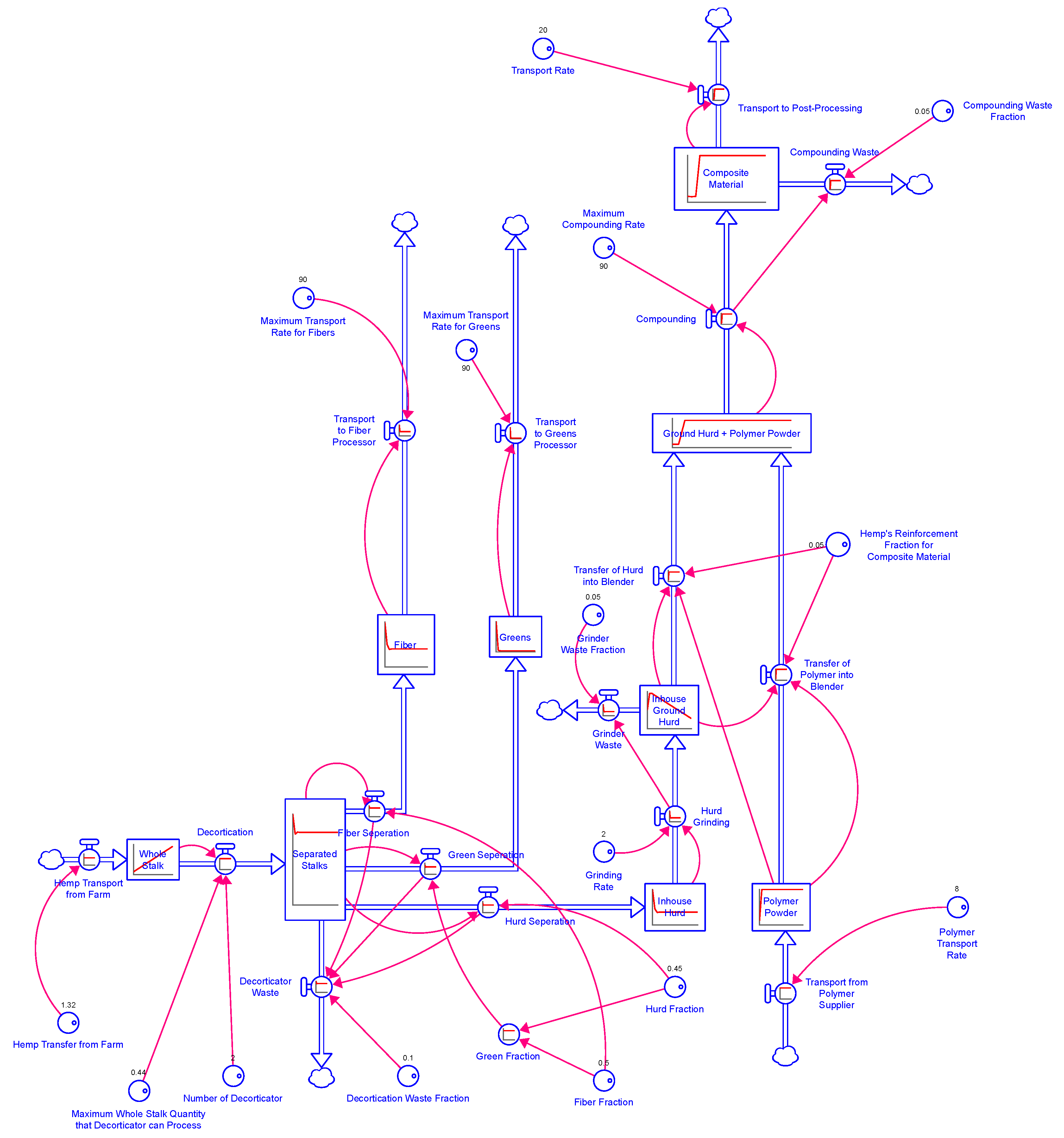
5. Simulation Results
5.1. Initial Simulation
- Inhouse Ground Hurd stock declines, with values dropping from 1.66 tons on day 6 to 1.34 tons on day 10, and further to 0.552 tons on day 20.
- Whole Stalk stock rises, increasing from 3.2 tons on day 6 to 4.96 tons on day 10, and reaching 9.36 tons by day 20.
5.2. Stabilized Supply Chain Simulation
- The stock of Inhouse Ground Hurd stabilizes at 1.69 tons/day after 6 days.
- The stock of Whole Stalk also stabilizes at 1.32 tons/day and no longer increases over time.
- Evaluate the Final Stock:
- If the value does not change with time, move to the next upstream stock in the supply chain.
- If the value does change with time, proceed to step 2.
- 2.
- Adjust Input Flow Converters:
- If the value continues to change, proceed to step 3.
- If the value remains unchanged, go to step 4.
- 3.
- Repeat Adjustments:
- 4.
- Move Upstream:
5.3. Analysis of Stable Supply Chain
- A 22% increase in the availability of polymer (material).
- A 12% reduction in the grinding rate (process).
- An increase of 1 decorticator (equipment).
6. Conclusions, Limitations, and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
|
Serial Nos. |
Name of the Flow | Equations | Unit |
| 1 | Compounding | IF ("Ground_Hurd_+_Polymer_Powder"/DT) < Maximum_Compounding_Rate THEN "Ground_Hurd_+_Polymer_Powder"/DT ELSE Maximum_Compounding_Rate | Tons/day |
| 2 | Compounding Waste | Compounding * Compounding_Waste_Fraction | Tons/day |
| 3 | Decortication | IF((Whole_Stalk/DT)<Maximum_whole_stalk_quantity_that_decorticator_can_process *Number_of_Decorticator) THEN (Whole_Stalk/DT) ELSE (Maximum_whole_stalk_quantity_that_decorticator_can_process * Number_of_Decorticator) | Tons/day |
| 4 | Decorticator Waste | (Fiber_Seperation+Green_Seperation+Hurd_Seperation)*Decortication_Waste_Fraction | Tons/day |
| 5 | Fiber Separation | Separated_Stalks/DT * Fiber_Fraction | Tons/day |
| 6 | Green Separation | Separated_Stalks/DT * Green_Fraction | Tons/day |
| 7 | Grinder Waste | Hurd_Grinding * Grinder_Waste_Fraction | Tons/day |
| 8 | Hemp Transport from Farm | Hemp_Transfer_from_Farm | Tons/day |
| 9 | Hurd Grinding | IF (Inhouse_Hurd/DT<Grinding_Rate) THEN Inhouse_Hurd/DT ELSE Grinding_Rate | Tons/day |
| 10 | Hurd Separation | Hurd_Fraction * Separated_Stalks/DT | Tons/day |
| 11 | Transfer of Hurd into Blender | IF ((Inhouse_Ground_Hurd/(Inhouse_Ground_Hurd+Polymer_Powder)>Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product) THEN (Polymer_Powder/DT)*Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product/(1-Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product) ELSE Inhouse_Ground_Hurd/DT | Tons/day |
| 12 | Transfer of Polymer into Blender | IF ((Inhouse_Ground_Hurd/(Inhouse_Ground_Hurd+Polymer_Powder)>Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product) THEN Polymer_Powder/DT ELSE ((Inhouse_Ground_Hurd/DT)*(1-Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product)/Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product) | Tons/day |
| 13 | Transport from Polymer Supplier | Polymer_Transport_Rate | Tons/day |
| 14 | Transport to Fiber Processor | IF ((Fiber/DT) < Maximum_Transport_Rate_for_Fibers) THEN Fiber/DT ELSE Maximum_Transport_Rate_for_Fibers | Tons/day |
| 15 | Transport to Greens Processor | IF ((Greens/DT) < Maximum_Transport_Rate_for_Greens) THEN Greens/DT ELSE Maximum_Transport_Rate_for_Greens | Tons/day |
| 16 | Transport to post-processing | IF Composite_material/DT < Transport_Rate THEN Composite_material/DT ELSE Transport_Rate | Tons/day |
|
Serial Nos. |
Stocks (all numbers are per day) |
Stock’s Variable Name |
Equation of Stock | Unit |
| 1 | Composite Material | Composite_Material | Composite Material (t-dt) + Compounding (t) - Compounding Waste (t) - Transport Rate (t) | Tons |
| 2 | Fiber | Fiber | Fiber (t-dt) + Fiber Separation (t) - Transport to Fiber Processor (t) | Tons |
| 3 | Greens | Greens | Greens (t-dt) + Green Separation (t) - Transport to Greens Processor (t) | Tons |
| 4 | Ground Hurd + Polymer Powder | Ground_Hurd_+_ Polymer_Powder |
Ground Hurd + Polymer Powder (t-dt) + Transfer of Hurd into Blender (t) + Transfer of Polymer into Blender (t) - Compounding (t) | Tons |
| 5 | Inhouse Ground Hurd | Inhouse_Ground_Hurd | Inhouse Ground Hurd (t-dt) + Hurd Grinding (t) - Grinding Waste (t) - Transfer of Hurd into Blender (t) | Tons |
| 6 | Inhouse Hurd | Inhouse_Hurd | Inhouse Hurd (t-dt) + Hurd Separation (t) - Hurd Grinding (t) | Tons |
| 7 | Polymer Powder | Polymer_Powder | Polymer Powder (t-dt) + Transport from Polymer Supplier (t) - Transfer of Polymer into Blender (t) | Tons |
| 8 | Separated Stalks | Separated_Stalks | Separated Stalks (t-dt) + Decortication (t) - Fiber Separation (t) - Green Separation (t) - Hurd Separation (t) | Tons |
| 9 | Whole Stalk | Whole_Stalk | Whole Stalk (t-dt) + Hemp Transport from Farm (t) – Decortication (t) | Tons |
|
Serial Nos. |
Converters | Converter’s Variable Name | Unit |
| 1 | Compounding Waste Fraction | Compounding_Waste_Fraction | Unitless |
| 2 | Decortication Waste Fraction | Decortication_Waste_Fraction | Unitless |
| 3 | Fiber Fraction | Fiber_Fraction | Unitless |
| 4 | Green Fraction | Green_Fraction | Unitless |
| 5 | Grinder Waste Fraction | Grinder_Waste_Fraction | Unitless |
| 6 | Grinding Rate | Grinding_Rate | Tons/day |
| 7 | Hemp Transfer from Farm | Hemp_Transfer_from_Farm | Tons/day |
| 8 | Hemp's Reinforcement Fraction for 3D Printed Final Product |
Hemp's_Reinforcement_Fraction_for_3D_Printed_Final_Product | Unitless |
| 9 | Hurd Fraction | Hurd_Fraction | Unitless |
| 10 | Maximum Compounding Rate | Maximum_Compounding_Rate | Tons/day |
| 11 | Maximum Transport Rate for Fibers | Maximum_Transport_Rate_for_Fibers | Tons/day |
| 12 | Maximum Transport Rate for Greens | Maximum_Transport_Rate_for_Greens | Tons/day |
| 13 | Maximum Whole Stalk Quantity that Decorticator can Process |
Maximum_Whole_Stalk_Quantity_that_Decorticator_can_Process | Tons/day |
| 14 | Number of Decorticators | Number_of_Decorticators | Unitless |
| 15 | Polymer Transport Rate | Polymer_Transport_Rate | Tons/day |
| 16 | Transport Rate | Transport_Rate | Tons/day |
Appendix B
| Serial Nos. | Compounding | Compounding Waste | Decortication | Decorticator Waste | Fiber Separation | Green Separation | Grinder Waste | Hemp Transport from Farm |
| 1 | 1 | 0.05 | 0.88 | 0.1 | 0.5 | 0.05 | 0.05 | 1.32 |
| 2 | 1.05 | 0.0526 | 0.88 | 0.078 | 0.39 | 0.039 | 0.0225 | 1.32 |
| 3 | 8.42 | 0.421 | 0.88 | 0.0802 | 0.401 | 0.0401 | 0.0176 | 1.32 |
| 4 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 5 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 6 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 7 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 8 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 9 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 10 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 11 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 12 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 13 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 14 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 15 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 16 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 17 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 18 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 19 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
| 20 | 8.42 | 0.421 | 0.88 | 0.08 | 0.4 | 0.4 | 0.018 | 1.32 |
|
Serial Nos. |
Hurd Grinding | Hurd Separation | Transfer of Hurd into Blender | Transfer of Polymer into Blender | Transport from Polymer Supplier | Transport to Fiber Processor | Transport to Greens Processor | Transport to post-processing |
| 1 | 1 | 0.45 | 0.0526 | 1 | 8 | 1 | 1 | 1 |
| 2 | 0.45 | 0.351 | 0.421 | 8 | 8 | 0.5 | 0.05 | 0.95 |
| 3 | 0.351 | 0.361 | 0.421 | 8 | 8 | 0.39 | 0.039 | 1 |
| 4 | 0.361 | 0.36 | 0.421 | 8 | 8 | 0.401 | 0.0401 | 8 |
| 5 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 6 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 7 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 8 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 9 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 10 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 11 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 12 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 13 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 14 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 15 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 16 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 17 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 18 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 19 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
| 20 | 0.36 | 0.36 | 0.421 | 8 | 8 | 0.4 | 0.04 | 8 |
|
Serial Nos. |
Composite material | Fiber | Greens | Ground Hurd + Polymer Powder | Inhouse Ground Hurd | Inhouse Hurd | Polymer Powder | Separated Stalks | Whole Stalk |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0.95 | 0.5 | 0.05 | 1.05 | 1.9 | 0.45 | 8 | 0.78 | 1.44 |
| 3 | 1 | 0.39 | 0.039 | 8.42 | 1.9 | 0.351 | 8 | 0.802 | 1.88 |
| 4 | 8 | 0.401 | 0.0401 | 8.42 | 1.82 | 0.361 | 8 | 0.8 | 2.32 |
| 5 | 8 | 0.4 | 0.4 | 8.42 | 1.74 | 0.36 | 8 | 0.8 | 2.76 |
| 6 | 8 | 0.4 | 0.4 | 8.42 | 1.66 | 0.36 | 8 | 0.8 | 3.2 |
| 7 | 8 | 0.4 | 0.4 | 8.42 | 1.58 | 0.36 | 8 | 0.8 | 3.64 |
| 8 | 8 | 0.4 | 0.4 | 8.42 | 1.5 | 0.36 | 8 | 0.8 | 4.08 |
| 9 | 8 | 0.4 | 0.4 | 8.42 | 1.42 | 0.36 | 8 | 0.8 | 4.52 |
| 10 | 8 | 0.4 | 0.4 | 8.42 | 1.34 | 0.36 | 8 | 0.8 | 4.96 |
| 11 | 8 | 0.4 | 0.4 | 8.42 | 1.26 | 0.36 | 8 | 0.8 | 5.4 |
| 12 | 8 | 0.4 | 0.4 | 8.42 | 1.18 | 0.36 | 8 | 0.8 | 5.84 |
| 13 | 8 | 0.4 | 0.4 | 8.42 | 1.11 | 0.36 | 8 | 0.8 | 6.28 |
| 14 | 8 | 0.4 | 0.04 | 8.42 | 1.03 | 0.36 | 8 | 0.8 | 6.72 |
| 15 | 8 | 0.4 | 0.04 | 8.42 | 0.947 | 0.36 | 8 | 0.8 | 7.16 |
| 16 | 8 | 0.4 | 0.04 | 8.42 | 0.868 | 0.36 | 8 | 0.8 | 7.6 |
| 17 | 8 | 0.4 | 0.04 | 8.42 | 0.789 | 0.36 | 8 | 0.8 | 8.04 |
| 18 | 8 | 0.4 | 0.04 | 8.42 | 0.71 | 0.36 | 8 | 0.8 | 8.48 |
| 19 | 8 | 0.4 | 0.04 | 8.42 | 0.631 | 0.36 | 8 | 0.8 | 8.92 |
| 20 | 8 | 0.4 | 0.04 | 8.42 | 0.552 | 0.36 | 8 | 0.8 | 9.36 |
Appendix C
|
Serial Nos. |
Compounding | Compounding Waste | Decortication | Decorticator Waste | Fiber Separation | Green Separation | Grinder Waste | Hemp Transport from Farm |
| 1 | 1 | 0.05 | 1 | 0.1 | 0.5 | 0.05 | 0.05 | 1.32 |
| 2 | 1.05 | 0.0526 | 1.32 | 0.09 | 0.45 | 0.045 | 0.0225 | 1.32 |
| 3 | 10.3 | 0.513 | 1.32 | 0.123 | 0.615 | 0.0615 | 0.0203 | 1.32 |
| 4 | 10.3 | 0.513 | 1.32 | 0.12 | 0.599 | 0.0599 | 0.0277 | 1.32 |
| 5 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 1.32 |
| 6 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 7 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 8 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 9 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 10 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 11 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 12 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 13 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 14 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 15 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 16 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 17 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 18 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 19 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
| 20 | 10.3 | 0.513 | 1.32 | 0.12 | 0.6 | 0.06 | 0.027 | 0.32 |
|
Serial Nos. |
Hurd Grinding | Hurd Separation | Transfer of Hurd into Blender | Transfer of Polymer into Blender | Transport from Polymer Supplier | Transport to Fiber Processor | Transport to Greens Processor | Transport to post-processing |
| 1 | 1 | 0.45 | 0.0526 | 1 | 9.75 | 1 | 1 | 1 |
| 2 | 0.45 | 0.405 | 0.513 | 9.75 | 9.75 | 0.5 | 0.05 | 0.95 |
| 3 | 0.405 | 0.554 | 0.513 | 9.75 | 9.75 | 0.45 | 0.045 | 1 |
| 4 | 0.554 | 0.539 | 0.513 | 9.75 | 9.75 | 0.615 | 0.0615 | 9.75 |
| 5 | 0.539 | 0.54 | 0.513 | 9.75 | 9.75 | 0.599 | 0.0599 | 9.75 |
| 6 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 7 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 8 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 9 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 10 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 11 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 12 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 13 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 14 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 15 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 16 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 17 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 18 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 19 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
| 20 | 0.54 | 0.54 | 0.513 | 9.75 | 9.75 | 0.6 | 0.06 | 9.75 |
|
Serial Nos. |
Composite material | Fiber | Greens | Ground Hurd + Polymer Powder | Inhouse Ground Hurd | Inhouse Hurd | Polymer Powder | Separated Stalks | Whole Stalk |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0.95 | 0.5 | 0.05 | 1.05 | 1.9 | 0.45 | 9.75 | 0.9 | 1.32 |
| 3 | 1 | 0.45 | 0.045 | 10.3 | 1.81 | 0.405 | 9.75 | 1.23 | 1.32 |
| 4 | 9.75 | 0.615 | 0.0615 | 10.3 | 1.68 | 0.554 | 9.75 | 1.2 | 1.32 |
| 5 | 9.75 | 0.599 | 0.0599 | 10.3 | 1.7 | 0.539 | 9.75 | 1.2 | 1.32 |
| 6 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 7 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 8 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 9 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 10 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 11 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 12 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 13 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 14 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 15 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 16 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 17 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 18 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 19 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
| 20 | 9.75 | 0.6 | 0.06 | 10.3 | 1.69 | 0.54 | 9.75 | 1.2 | 1.32 |
References
- Radzicki, M.J.; Taylor, R.A. Introduction to system dynamics. US Department of Energy http://www. systemdynamics. org/DL-IntroSysDyn/inside. htm. 1997. [Google Scholar]
- Angerhofer, B.J.; Angelides, M.C. System dynamics modelling in supply chain management: research review. In 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165), 2000; IEEE: Vol. 1, pp 342-351.
- Pérez-Pérez, J.F.; Parra, J.F.; Serrano-Garcia, J. A system dynamics model: Transition to sustainable processes. Technology in Society 2021, 65, 101579. [Google Scholar] [CrossRef]
- Radzicki, M.J.; Taylor, R.A. Origin of system dynamics: Jay W. Forrester and the history of system dynamics. US Department of Energy’s introduction to system dynamics, 2008. [Google Scholar]
- Richardson, G.P. Core of System Dynamics. System Dynamics: Theory and Applications, 2020; 11–20. [Google Scholar]
- Forrester, J.W. (1961). Industrial Dynamics. Waltham MA, Pegasus Communications, 1961. [Google Scholar]
- Sterman, J.D. Business Dynamics: Systems thinking and modeling for a complex world. MacGraw-Hill Company, 2000. [Google Scholar]
- Winkler, H.; Franke, S.; Franke, F.; Jabs, I.; Fischer, D.; Thürer, M. Systems Thinking Approach for Production Process Optimization Based on KPI Interdependencies. In IFIP International Conference on Advances in Production Management Systems, 2023; Springer: pp 662-675.
- Gejo-García, J.; Reschke, J.; Gallego-García, S.; García-García, M. Development of a system dynamics simulation for assessing manufacturing systems based on the digital twin concept. Applied Sciences 2022, 12, 2095. [Google Scholar] [CrossRef]
- Ajayeoba, A.O.; Adebiyi, K.A.; Raheem, W.A.; Fajobi, M.O.; Musa, A.I. System Dynamic: An Intelligent Decision-Support System for Manufacturing Safety Intervention Program Management. In Automation and Innovation with Computational Techniques for Futuristic Smart, Safe and Sustainable Manufacturing Processes, Springer, 2023; pp 315-337.
- Litwin, P.; Szymusik, A. System Dynamics in Manufacturing Processes Modelling and Analysis. In International Conference Innovation in Engineering, 2024; Springer: pp 14-26.
- Saarinen, L.; Oddsdottir, H.; Rehman, O. Resilience through appropriate response: a simulation study of disruptions and response strategies–case COVID-19 and the grocery supply chain. Operations Management Research 2024, 1–22. [Google Scholar] [CrossRef]
- John, T.; DeWitt, W.; Keebler, J.S.; Min, S.; Nix, N.; Smith, C.; Zacharia, Z. Defining Supply Chain Management. Journal of Business Logistics. 2001. [Google Scholar]
- Harland, C. Supply Chain Management: Concepts, Challenges and Future Research Directions; Springer Nature, 2024.
- Mentzer, J.T.; DeWitt, W.; Keebler, J.S.; Min, S.; Nix, N.W.; Smith, C.D.; Zacharia, Z.G. Defining supply chain management. Journal of Business logistics 2001, 22, 1–25. [Google Scholar] [CrossRef]
- Seuring, S.; Müller, M. From a literature review to a conceptual framework for sustainable supply chain management. Journal of cleaner production 2008, 16, 1699–1710. [Google Scholar] [CrossRef]
- Pullman, M.; Wu, Z. Food supply chain management: building a sustainable future; Routledge, 2021.
- Kaur, G.; Kander, R. The sustainability of industrial hemp: a literature review of its economic, environmental, and social sustainability. Sustainability 2023, 15, 6457. [Google Scholar] [CrossRef]
- Shahzad, A. Hemp fiber and its composites–a review. Journal of composite materials 2012, 46, 973–986. [Google Scholar] [CrossRef]
- Deshmukh, G.S. Advancement in hemp fibre polymer composites: a comprehensive review. Journal of Polymer Engineering 2022, 42, 575–598. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. Journal of theoretical biology 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Schunk, D.; Plott, B. Using simulation to analyze supply chains. In 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165); IEEE, 2000; Vol. 2, pp. 1095–1100. [Google Scholar]
- Rebs, T.; Brandenburg, M.; Seuring, S. System dynamics modeling for sustainable supply chain management: A literature review and systems thinking approach. Journal of cleaner production 2019, 208, 1265–1280. [Google Scholar] [CrossRef]
- Kaur, G.; Kander, R. Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability. Sustainability 2023, 15, 15353. [Google Scholar] [CrossRef]
- Bianchi, C.; Cosenz, F.; Marinković, M. Designing dynamic performance management systems to foster SME competitiveness according to a sustainable development perspective: empirical evidences from a case-study. International Journal of Business Performance Management 31 2015, 16, 84–108. [Google Scholar] [CrossRef]
- Kibira, D.; Jain, S.; McLean, C. A system dynamics modeling framework for sustainable manufacturing. In Proceedings of the 27th annual system dynamics society conference; 2009; Vol. 301, pp. 1–22. [Google Scholar]
- Elmasry, S.; Shalaby, M.; Saleh, M. A System dynamics simulation model for scalable-capacity manufacturing systems. International Conference of the System Dynamics Society, 2012. [Google Scholar]
- Georgiadis, P.; Vlachos, D. The effect of environmental parameters on product recovery. European Journal of Operational Research 2004, 157, 449–464. [Google Scholar] [CrossRef]
- Torres de Miranda Pinto, J. Integrating life cycle analysis into system dynamics: the case of steel in Europe. 2019.
- Rebs, T.; Thiel, D.; Brandenburg, M.; Seuring, S. Impacts of stakeholder influences and dynamic capabilities on the sustainability performance of supply chains: A system dynamics model. Journal of Business Economics 2019, 89, 893–926. [Google Scholar] [CrossRef]
- Khorram Niaki, M.; Nonino, F. Additive manufacturing management: a review and future research agenda. International Journal of Production Research 2017, 55, 1419–1439. [Google Scholar] [CrossRef]
- Luna, L.F.; Andersen, D.L. Using Qualitative Methods in the Conceptualization and Assessment of System Dynamics Models. In Proceedings of the 20th International System Dynamics Conference, System Dynamics Society, Palermo, Italy; Citeseer, 2002; Vol. 28. [Google Scholar]
- Guest, J.; Skerlos, S.; Daigger, G.; Corbett, J.; Love, N. The use of qualitative system dynamics to identify sustainability characteristics of decentralized wastewater management alternatives. Water science and technology 2010, 61, 1637–1644. [Google Scholar] [CrossRef]
- Brundtland, G.H. Our common future world commission on environment and developement. 1987.
- Boroujeni, F.M.; Fioravanti, G.; Kander, R. Synthesis and characterization of cellulose microfibril-reinforced polyvinyl alcohol biodegradable composites. Materials 2024, 17, 526. [Google Scholar] [CrossRef]
- Joshi, S.V.; Drzal, L.; Mohanty, A.; Arora, S. Are natural fiber composites environmentally superior to glass fiber reinforced composites? Composites Part A: Applied science and manufacturing 2004, 35, 371–376. [Google Scholar] [CrossRef]
- Van der Werf, H.M.; Turunen, L. The environmental impacts of the production of hemp and flax textile yarn. industrial crops and products 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Dittenber, D.B.; GangaRao, H.V. Critical review of recent publications on use of natural composites in infrastructure. Composites Part A: applied science and manufacturing 2012, 43, 1419–1429. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Composites Part A: Applied Science and Manufacturing 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Flax fibre and its composites–A review. Composites Part B: Engineering 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Ichim, M.; Filip, I.; Stelea, L.; Lisa, G.; Muresan, E.I. Recycling of Nonwoven Waste Resulting from the Manufacturing Process of Hemp Fiber-Reinforced Recycled Polypropylene Composites for Upholstered Furniture Products. Sustainability 2023, 15, 3635. [Google Scholar] [CrossRef]
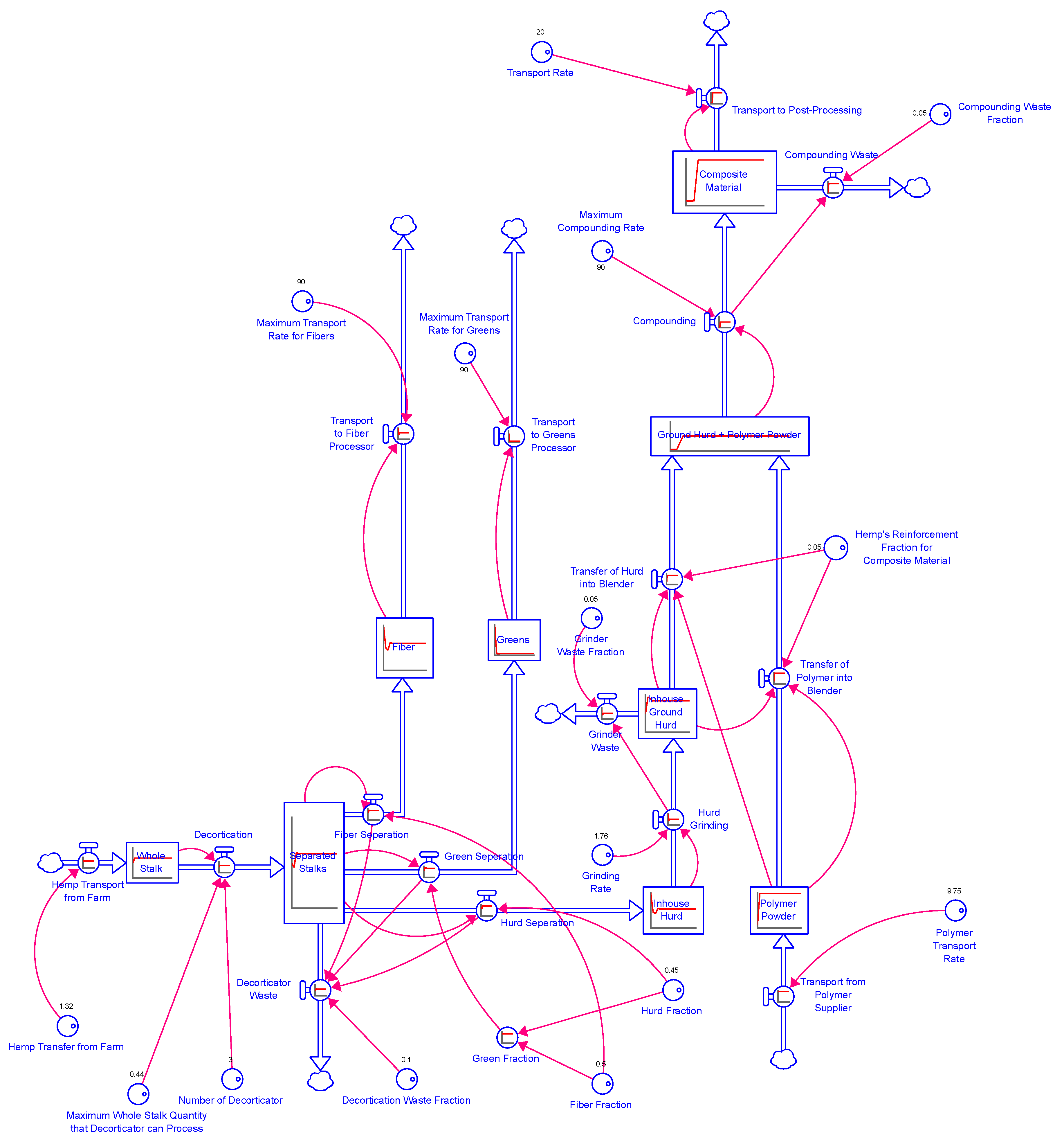
|
Serial Nos. |
Stocks |
Description |
| 1 | Composite Material | Quantity of hemp-reinforced polymer composite material produced |
| 2 | Fiber | Separated quantity of fiber after the decortication of the whole stalk |
| 3 | Greens | Separated quantity of greens after the decortication of whole stalk |
| 4 | Ground Hurd + Polymer Powder | Mix quantity of ground hurd and polymer powder to produce composite material |
| 5 | Inhouse Ground Hurd | Quantity of inhouse ground hurd after grinding inhouse hurd |
| 6 | Inhouse Hurd | Quantity of in-house hurd after separating greens and fiber from the whole stalk through decortication. |
| 7 | Polymer Powder | Quantity of polymer powder bought from polymer supplier to produce composite material. |
| 8 | Separated Stalks | Quantity of separated stalk after the decortication of whole stalk. |
| 9 | Whole Stalk | Quantity of the whole stalk bought into the unit from hemp farm for producing composite material. |
|
Serial Nos. |
Converters | Description | |
| 1 | Compounding Waste Fraction | The fraction of compounding material waste generated from the compounding process | |
| 2 | Decortication Waste Fraction | The fraction of decorticating waste generated from the decortication of whole stalks. | |
| 3 | Fiber Fraction | The fraction of fiber separated from whole stalks after decortication. | |
| 4 | Green Fraction | The fraction of green separated from whole stalks after decortication. | |
| 5 | Grinder Waste Fraction | The fraction of grinder waste generated from hurd grinding. | |
| 6 | Grinding Rate | Rate at which inhouse hurd is grinded. | |
| 7 | Hemp Transfer from Farm | The quantity of hemp transferred from the farm into the factory. | |
| 8 | Hemp's Reinforcement Fraction for Composite Material | The reinforcement fraction of hemp to produce composite material. | |
| 9 | Hurd Fraction | The fraction of hurd separated from whole stalks after decortication. | |
| 10 | Maximum Compounding Rate | Maximum rate at which inhouse ground hurd and polymer powder are compounded. | |
| 11 | Maximum Transport Rate for Fibers | Maximum rate at which fibers are transported to post-processor. | |
| 12 | Maximum Transport Rate for Greens | Maximum rate at which greens are transported to post-processor. | |
| 13 | Maximum Whole Stalk Quantity that Decorticator can Process |
The maximum quantity that the decorticator can process. | |
| 14 | Number of Decorticators | The number of decorticators required. | |
| 15 | Polymer Transport Rate | The quantity of polymer transported into the factory. | |
| 16 | Transport Rate | The quantity of composite material transported to post-processor. | |
|
Serial Nos. |
Flows | Description |
| 1 | Compounding | Rate at which mixture of ground hurd and polymer powder is compounded. |
| 2 | Compounding Waste | Rate of waste generation by compounding. |
| 3 | Decortication | Rate at which the whole stalk is decorticated. |
| 4 | Decorticator Waste | Rate of waste generation from decortication process. |
| 5 | Fiber Separation | Rate at which fiber is separated from the whole stalk. |
| 6 | Green Separation | Rate at which green is separated from the whole stalk. |
| 7 | Grinder Waste | Rate of waste generation from grinding inhouse hurd. |
| 8 | Hemp Transport from Farm | Quantity of hemp transported into the factory from the hemp farm. |
| 9 | Hurd Grinding | Rate at which inhouse hurd is grinded. |
| 10 | Hurd Separation | Rate at which hurd is separated from the whole stalk. |
| 11 | Transfer of Hurd into Blender | Rate at which inhouse ground hurd is transferred into blender. |
| 12 | Transfer of Polymer into Blender | Rate at which polymer is transferred into blender. |
| 13 | Transport from Polymer Supplier | Quantity of polymer transported into the factory from polymer supplier. |
| 14 | Transport to Fiber Processor | Quantity of fiber transported to fiber processor. |
| 15 | Transport to Greens Processor | Quantity of greens transported to greens processor. |
| 16 | Transport to post-processing | Quantity of composite material transported to post-processing unit. |
|
Serial Nos. |
Converters | Converter’s Variable Name | Unit |
| 1 | Hemp Transfer from Farm | Hemp_Transfer_from_Farm | Tons/day |
| 2 | Maximum Whole Stalk Quantity that Decorticators can Process |
Maximum_Whole_Stalk_Quantity_that_Decorticators_can_Process | Tons/day |
| 3 | Number of Decorticators | Number_of_Decorticators | Unitless |
|
Serial Nos. |
Name of the Flow | Equations | Unit |
| 1 | Hemp Transport from Farm | Hemp_Transfer_from_Farm | Tons/day |
| 2 | Decortication | IF((Whole_Stalk/DT)<Maximum_whole_stalk_quantity_that_decorticators_can_process * Number_of_Decorticators) THEN (Whole_Stalk/DT) ELSE (Maximum_whole_stalk_quantity_that_decorticator_can_process * Number_of_Decorticators) | Tons/day |
|
Serial Nos. |
Name of the Stock | Equation of Stock | Unit |
| 1 | Whole Stalk | Whole Stalk (t-dt) + Hemp Transport from Farm (t) – Decortication (t) | Tons |
|
Serial Nos. |
Converters | Initial Simulation’s Converter/ Input Values | Unit |
| 1 | Compounding Waste Fraction | 0.05 | Unitless |
| 2 | Decortication Waste Fraction | 0.1 | Unitless |
| 3 | Fiber Fraction | 0.5 | Unitless |
| 4 | Green Fraction | 0.05 | Unitless |
| 5 | Grinder Waste Fraction | 0.05 | Unitless |
| 6 | Grinding Rate | 2 | Tons/day |
| 7 | Hemp Transfer from Farm | 1.32 | Tons/day |
| 8 | Hemp's Reinforcement Fraction for 3D Printed Final Product |
0.05 | Unitless |
| 9 | Hurd Fraction | 0.45 | Unitless |
| 10 | Maximum Compounding Rate | 90 | Tons/day |
| 11 | Maximum Transport Rate for Fibers | 90 | Tons/day |
| 12 | Maximum Transport Rate for Greens | 90 | Tons/day |
| 13 | Maximum Whole Stalk Quantity that Decorticator can Process | 0.3 | Tons/day |
| 14 | Number of Decorticators | 2 | Unitless |
| 15 | Polymer Transport Rate | 8 | Tons/day |
| 16 | Transport Rate | 20 | Tons/day |
| Converters | Stable Simulation Converter/Input Values | Unit | |
| 1 | Compounding Waste Fraction | 0.05 | Unitless |
| 2 | Decortication Waste Fraction | 0.1 | Unitless |
| 3 | Fiber Fraction | 0.5 | Unitless |
| 4 | Green Fraction | 0.05 | Unitless |
| 5 | Grinder Waste Fraction | 0.05 | Unitless |
| 6 | Grinding Rate | 1.76 | Tons/day |
| 7 | Hemp Transfer from Farm | 1.32 | Tons/day |
| 8 | Hemp's Reinforcement Fraction for 3D Printed Final Product |
0.05 | Unitless |
| 9 | Hurd Fraction | 0.45 | Unitless |
| 10 | Maximum Compounding Rate | 90 | Tons/day |
| 11 | Maximum Transport Rate for Fibers | 90 | Tons/day |
| 12 | Maximum Transport Rate for Greens | 90 | Tons/day |
| 13 | Maximum Whole Stalk Quantity that Decorticator can Process |
0.44 | Tons/day |
| 14 | Number of Decorticators | 3 | Unitless |
| 15 | Polymer Transport Rate | 9.75 | Tons/day |
| 16 | Transport Rate | 20 | Tons/day |
| Serial Nos. (from their respective tables) | Converters | Initial Simulation Converter/Input Values | Stable Simulation Converter/Input Values |
| 6 | Grinding Rate | 2 | 1.76 |
| 13 | Nos of Decorticators | 2 | 3 |
| 15 | Polymer Transport Rate | 8 | 9.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





