Strained Graphene as Pristine Graphene with Deformed Momentum Operator

1. Introduction

Two decades have elapsed since the successful isolation of graphene membranes [1,2], which are known for their exceptional properties, such as high thermal and electronic conductivity, transparency in the visible spectrum, and remarkable stiffness and flexibility [3]. Despite the extensive research into its potential technological applications, graphene continues to offer exciting opportunities to explore fundamental physics. The charge carriers in graphene, which behave as massless Dirac fermions in two dimensions, exhibit a (pseudo)-ultrarelativistic character, creating a natural link between condensed matter physics and high-energy physics. This behavior is no longer exclusive to graphene but is also found in a wide variety of two-dimensional materials [4,5,6,7] with pseudo-relativistic effective degrees of freedom, further strengthening the connection between these fields and offering numerous avenues for exploration.

One example is the emerging field of straintronics [8], also known as origami electronics [9]. Straintronics involves altering the electronic properties of graphene through mechanical deformations. Both theoretical [10,11,12,13,14,15,16,17,18,19,20] and experimental [21] studies have yielded intriguing results. In some materials, these deformations arise naturally due to intrinsic anisotropy [22,23,24,25,26]. In comparison to pristine graphene, the presence of anisotropy shifts the Dirac points and distorts the Dirac cones, tilting them and changing their circular cross-section thus inducing anisotropy in the Fermi velocity [10,11]. While strain effects can be incorporated by modifying hopping parameters to account for atomic displacement in the crystal lattice [10,11,12], at low energies, these phenomena are elegantly described by the dynamics of Dirac fermions in curved space-time, a subject rich in its own right [27].

In this paper, we establish the existence of a duality between the equations of motion for charge carriers in strained graphene or any other anisotropic material described by a 2D-Dirac equation and those arising from a deformation of the momentum operator of the flat theory which can be explicitly related to a function of the coordinates of the membrane that describe the strain anisotropy. We exemplify such a duality considering uniaxial and shear strained materials subjected to an external uniform magnetic field [13,14,15,16]. A connection is established between the deformation and the anisotropic (uniform and non-uniform) character of the Fermi velocity [17]. We have organized the remaining of this paper as follows: The next section is devoted to establish the duality of the equations of motion. Section 3 is left to discuss in detail the effects of the deformation on the energy spectrum and states of the resulting Dirac operator. Final remarks are presented at the ending Section.

2. Equivalence Between Strain and Momentum Operator Deformations

Dirac materials, particularly graphene, are described effectively by a 2D-Dirac Hamiltonian in the form

$$H_D=v_F\sigma ·{\mathbf{p}}^0,$$

(1)

which for pristine graphene consist in taking the Fermi velocity $v_F\simeq c/300$, where c the speed of light in vacuum (see, for instance, Ref. [28]). From elasticity theory, we can relate the component of the inhomogeneous Fermi velocity to the strain tensor, which in turn is written in terms of the displacement and vertical deformations, and vice versa. In this way, one can track back the effect of the mechanical deformation or curvature to the electronic properties of graphene through the modification of the Fermi velocity. Thus, we can write:

$$H_D={\mathbf{v}}_F·\sigma ·{\mathbf{p}}^0,$$

(2)

where the Fermi velocity tensor ${\mathbf{v}}_F$ is represented by the matrix

$${\mathbf{v}}_F=v_F\left(\mathbf{I}+{\mathbf{F}}^{\top }\right),$$

(3)

with $v_F$ denoting the ordinary Fermi velocity, $\mathbf{I}$ the $n\times n$ identity matrix, ⊤ denotes the matrix transpose and the matrix F given by

$$\mathbf{F}\left(\mathbf{x}\right)=\left(\begin{array}{ccc}{f}_{11}\left(\mathbf{x}\right)& \cdots & f_{1n}\left(\mathbf{x}\right)\\ ⋮& \ddots & ⋮\\ f_{n1}\left(\mathbf{x}\right)& \cdots & f_{nn}\left(\mathbf{x}\right)\end{array}\right),$$

(4)

being $f_k^i\left(\mathbf{x}\right):{\mathbb{R}}^n\to \mathbb{R}$ an well-behaved function of the n-dimensional position vector $\mathbf{x}$. We know that the components of the Fermi velocity tensor can be written as [11,17]

$${\left({\mathbf{v}}_F\right)}_{ij}=v_F\left({\delta }_{ij}+(1-\beta ){\mathbf{u}}_{ij}-{\displaystyle \frac{1}{2}}{\partial }_{i}h{\partial }_{j}h\right),$$

(5)

where $\beta$ is the Grüneisen parameter ($\beta \simeq 2-3$ in graphene) and $\mathbf{u}$ is the strain tensor, which is commonly written in terms of the displacement vector $u\left(\mathbf{x}\right)$ and the vertical displacement of the graphene membrane $h\left(\mathbf{x}\right)$ due to deformations as

$${\mathbf{u}}_{ij}={\displaystyle \frac{1}{2}}\left({\partial }_i{u}_j+{\partial }_j{u}_i+{\partial }_{j}h{\partial }_{i}h\right).$$

(6)

However, in this work, we analyze the case where the matrix factor $\left(\mathbf{I}+{\mathbf{F}}^{\top }\right)$ of the Fermi velocity ${\mathbf{v}}_F$, can be associated to the momentum. Thus, defining a deformed momentum operator as follows:

$$\mathbf{p}=(\mathbf{I}+{\mathbf{F}}^{\top }){\mathbf{p}}^0,$$

(7)

where the components of ${\mathbf{p}}^0$ satisfy the canonical Heisenberg uncertainty relations

$$[x^i,p_j^0]=i\hslash {\delta }_j^i,$$

(8)

among the coordinate and momentum operators of a quantum mechanical system with n degrees of freedom. Then, modifying these relations according to

$$[x^i,p_j]=i\hslash ({\delta }_j^i+f_k^i\left(\mathbf{x}\right){\delta }_j^k),$$

(9)

we notice that the previous relation is expressed as a function of the coordinates. It is straightforward to check that the generalized momentum operators

$$p_i\equiv \left({\delta }_i^k+f_i^k\left(\mathbf{x}\right)\right)p_k^0,$$

(10)

fulfill the deformed uncertainty relations (9). We must mention the strain could be treated as a curvature. Indeed, by considering $p_k^0\to S_k^i{p}_i^0$, with the canonical commutation rules, we have

$$[x^i,S_j^k{p}_k^0]=S_j^k[x^i,p_k^0]=i\hslash S_j^i,$$

(11)

as in (9). However, this is a point of discussion that we postpone for a future occasion, since various authors suggest the strain can be treated as pseudo-magnetic potential [10]. Here, we focus on the algebraic and physical aspects of the deformed momentum operator (10).

An interesting way to observe the impact of the deformed momentum operator is by means of the algebras formed through quadratures. In other words, we take the operators $a_j$ and $a_j^{†}$ defined as

$$a_j\equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(x^j+i{p}_j\right),a_j^{†}\equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(x^j-i{p}_j\right).$$

(12)

By constructing the commutators $[a_j,a_k^{†}]$ and $[a_j,a_k]$, we arrive at

$$\begin{array}{cc}\hfill & [a_j,a_k^{†}]=\hslash {\delta }_k^j+{\displaystyle \frac{\hslash }{2}}\left(f_k^j+f_j^k+i\left(\nabla \times F+\left(F·\nabla \right)\times F\right){\mathbf{p}}^0\right),\hfill \\ \hfill & [a_j,a_k]={\displaystyle \frac{\hslash }{2}}\left(i\left(\nabla \times F+\left(F·\nabla \right)\times F\right){\mathbf{p}}^0-\left(f_k^j-f_j^k\right)\right),\hfill \end{array}$$

(13)

where $(\nabla \times F){\mathbf{p}}^0=\left({\partial }_k{f}_j^l-{\partial }_j{f}_k^l\right)p_k^0$ and $\left(\left(F·\nabla \right)\times F\right){\mathbf{p}}^0=\left(f_k^l{\partial }_l{f}_j^q-f_j^l{\partial }_l{f}_k^q\right)p_q^0$. When we compare with the canonical Heisenberg uncertainty relation (8), the canonical quadrature algebra is $[a_j,a_k^{†}]=\hslash {\delta }_k^j$ and $[a_j,a_k]=0$. Thus, the deformation generated by the deformed momentum operator as in (9) can be seen, in general, as a linear polynomial deformation (on the momentum) of the quadrature algebra. Nevertheless, there exists cases where the factor accompanying the momentum could vanish, for example in the case of a (anti)diagonal Fermi velocity. In this instance, the deformation of the quadrature algebra only depends on the strain applied to graphene, which help us to understand some physical consequences of the strain as we will shortly see.

On the other hand, from Equation (3), it is easy to identify the components of the strain tensor (6) simply as

$${\mathbf{u}}_{ij}={\displaystyle \frac{{\mathbf{F}}_{ji}-\frac{1}{2}{\partial }_{i}h{\partial }_{j}h}{1+\beta }},$$

(14)

which allow to identify the components of the displacement vector in terms of the deformed momentum operator, namely, of the components of the matrix $\mathbf{F}$ as

$${\partial }_i{u}_j+{\partial }_j{u}_i={\displaystyle \frac{2}{1+\beta }}{\mathbf{F}}_{ji}-{\displaystyle \frac{\beta }{1+\beta }}{\partial }_{i}h{\partial }_{j}h.$$

(15)

Here, because $\beta$ is fixed as constant in our discussion, we can consider two possible cases, $h=0$ and $u^i=0$. Let us see the implications in each case. Note Equation (15) implies that $\mathbf{F}$ is symmetric.

• For in-plane deformations, $h=0$ and thus, from Equation (15) we have the following relations

  $$\begin{array}{ccc}\hfill {\partial }_x{u}_1& =& {\displaystyle \frac{1}{1+\beta }}{F}_{11}\left(\mathbf{x}\right),\hfill \end{array}$$

  (16)

  $$\begin{array}{ccc}\hfill {\partial }_1{u}_2+{\partial }_2{u}_1& =& {\displaystyle \frac{2}{1+\beta }}{F}_{12}\left(\mathbf{x}\right),\hfill \end{array}$$

  (17)

  $$\begin{array}{ccc}\hfill {\partial }_y{u}_2& =& {\displaystyle \frac{1}{1+\beta }}{F}_{22}\left(\mathbf{x}\right).\hfill \end{array}$$

  (18)

  Now, integrating over a square area with diagonal between the points (0,0) and $(x,y)$, we find $u_1\left(\mathbf{x}\right)$ and $u_2\left(\mathbf{x}\right)$ from eqs. (16) and (18) to be explicitly given as

  $$\begin{array}{ccc}\hfill u_1\left(\mathbf{x}\right)-u_1\left(\mathbf{0}\right)& =& {\displaystyle \frac{1}{1+\beta }}{\int }_0^x{F}_{11}(s,y)ds,\hfill \end{array}$$

  (19)

  $$\begin{array}{ccc}\hfill u_2\left(\mathbf{x}\right)-u_2\left(\mathbf{0}\right)& =& {\displaystyle \frac{1}{1+\beta }}{\int }_0^y{F}_{22}(x,s)ds.\hfill \end{array}$$

  (20)

  Furthermore, because of eq. (17), we can write

  $${\int }_0^y{\displaystyle \frac{\partial }{\partial x}}{F}_{22}\left(x,s\right)ds+{\int }_0^x{\displaystyle \frac{\partial }{\partial y}}{F}_{11}\left(s,y\right)ds=2F_{12}\left(\mathbf{x}\right),$$

  (21)

  and hence the full set of in-plane deformations can be expressed in terms of $F_{11}\left(\mathbf{x}\right)$ and $F_{22}\left(\mathbf{x}\right)$. In summary, for the displacement vector $\mathbf{u}\left(\mathbf{x}\right)$ we have

  $$\mathbf{u}\left(\mathbf{x}\right)=\left(\begin{array}{c}{\displaystyle \frac{1}{1+\beta }{\int }_0^x{F}_{11}(s,y)ds}\\ {\displaystyle \frac{1}{1+\beta }{\int }_0^y{F}_{22}(x,s)ds}\end{array}\right)+{\mathbf{u}}_0,$$

  (22)

  where

  $${\mathbf{u}}_0\equiv \left(\begin{array}{c}{u}_1\left(\mathbf{0}\right)\\ u_2\left(\mathbf{0}\right)\end{array}\right).$$

  (23)
• For out of plane deformations, $u^i=0\Rightarrow {\partial }_{i}h{\partial }_{j}h={\displaystyle \frac{2}{\beta }}{F}_{ij}\left(\mathbf{x}\right)$, which leads to the following system of equations

  $$\begin{array}{ccc}\hfill {\left({\partial }_{x}h\right)}^2& =& {\displaystyle \frac{2}{\beta }}{F}_{11}\left(\mathbf{x}\right),\hfill \end{array}$$

  (24)

  $$\begin{array}{ccc}\hfill {\partial }_{x}h{\partial }_{y}h& =& {\displaystyle \frac{2}{b}}{F}_{12}\left(\mathbf{x}\right),\hfill \end{array}$$

  (25)

  $$\begin{array}{ccc}\hfill {\left({\partial }_{y}h\right)}^2& =& {\displaystyle \frac{2}{\beta }}{F}_{22}\left(\mathbf{x}\right).\hfill \end{array}$$

  (26)
  From Equation (24) we obtain $h\left(\mathbf{x}\right)$,

  $${\displaystyle h\left(\mathbf{x}\right)=\sqrt{\frac{2}{\beta }}{\int }_0^x{F}_{11}(s,y)ds+h\left(\mathbf{0}\right).}$$

  (27)

  Now, replacing Eqs. (24) and (26) in Equation (25) we obtain $F_{12}\left(\mathbf{x}\right)$ in terms of the diagonal elements of a $\mathbf{F}$ as

  $$\sqrt{F_{11}\left(\mathbf{x}\right)F_{22}\left(\mathbf{x}\right)}=F_{12}\left(\mathbf{x}\right).$$

  (28)
  Moreover, from Equation (26), we have that the diagonal elements are related through

  $${\int }_0^x\sqrt{F_{11}\left(s,y\right)}ds={\int }_0^y\sqrt{F_{22}\left(x,s\right)}ds.$$

  (29)

Hence, we have obtain all possible in-plane and out-of-plane deformations of the graphene membrane in terms of a deformed momentum operator. Let us explore the implications next.

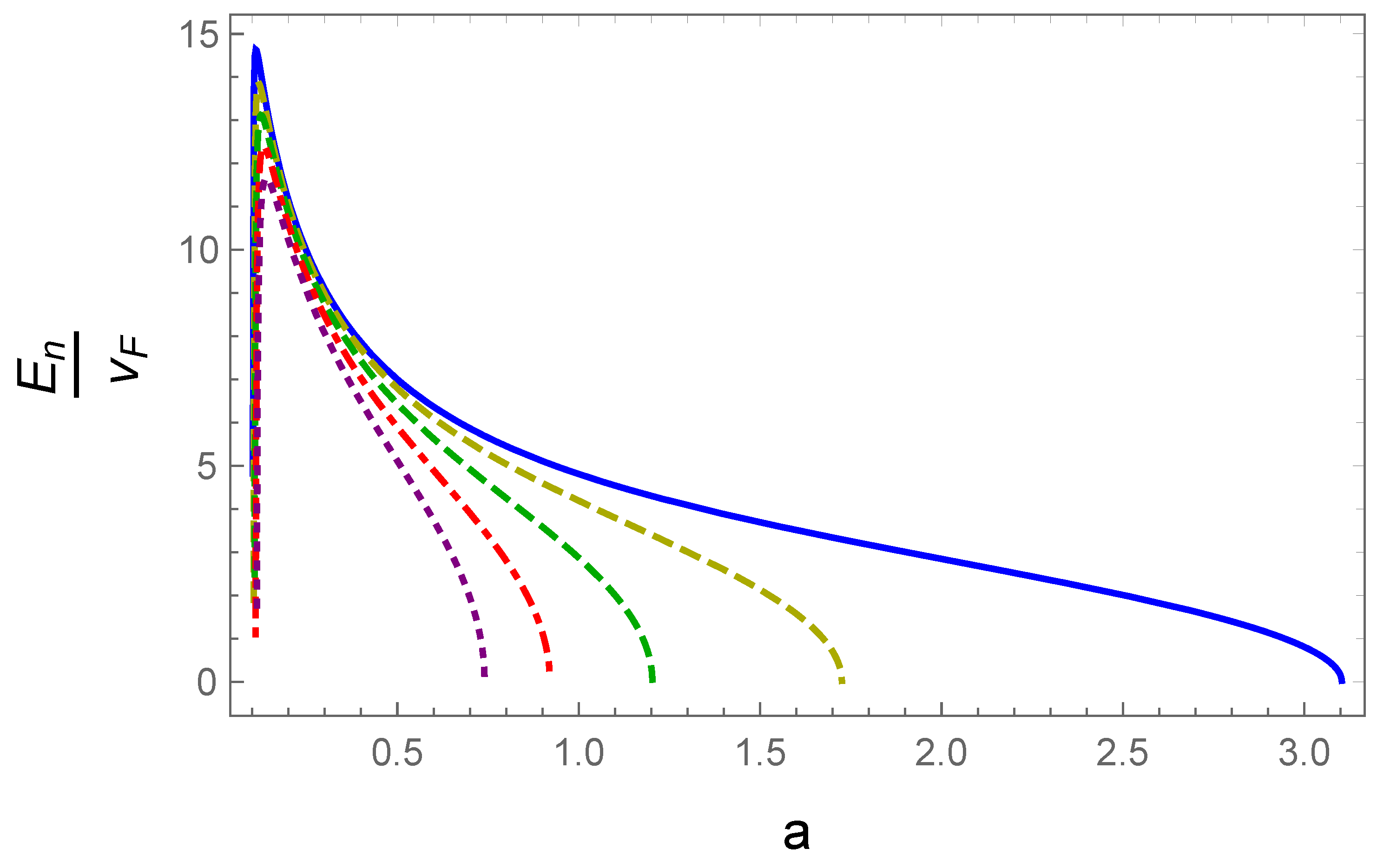
3. Bound States for Inhomogeneous Fermi Velocities

We consider the anisotropic Dirac equation in the presence of a magnetic field, assuming irrelevant for the time being any possible scalar potential that might emerge. Thus, denoting as ${\mathbf{v}}_F$ the tensor Fermi velocity, our starting point is

$${\mathbf{v}}_F·\sigma ·\left({\mathbf{p}}^0+e\mathbf{A}\right){\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right).$$

(30)

In search for the eigenstates and eigenenergies of the general system expressed in Equation (30), we shall consider some specific forms of the Fermi velocity commonly discussed in literature.

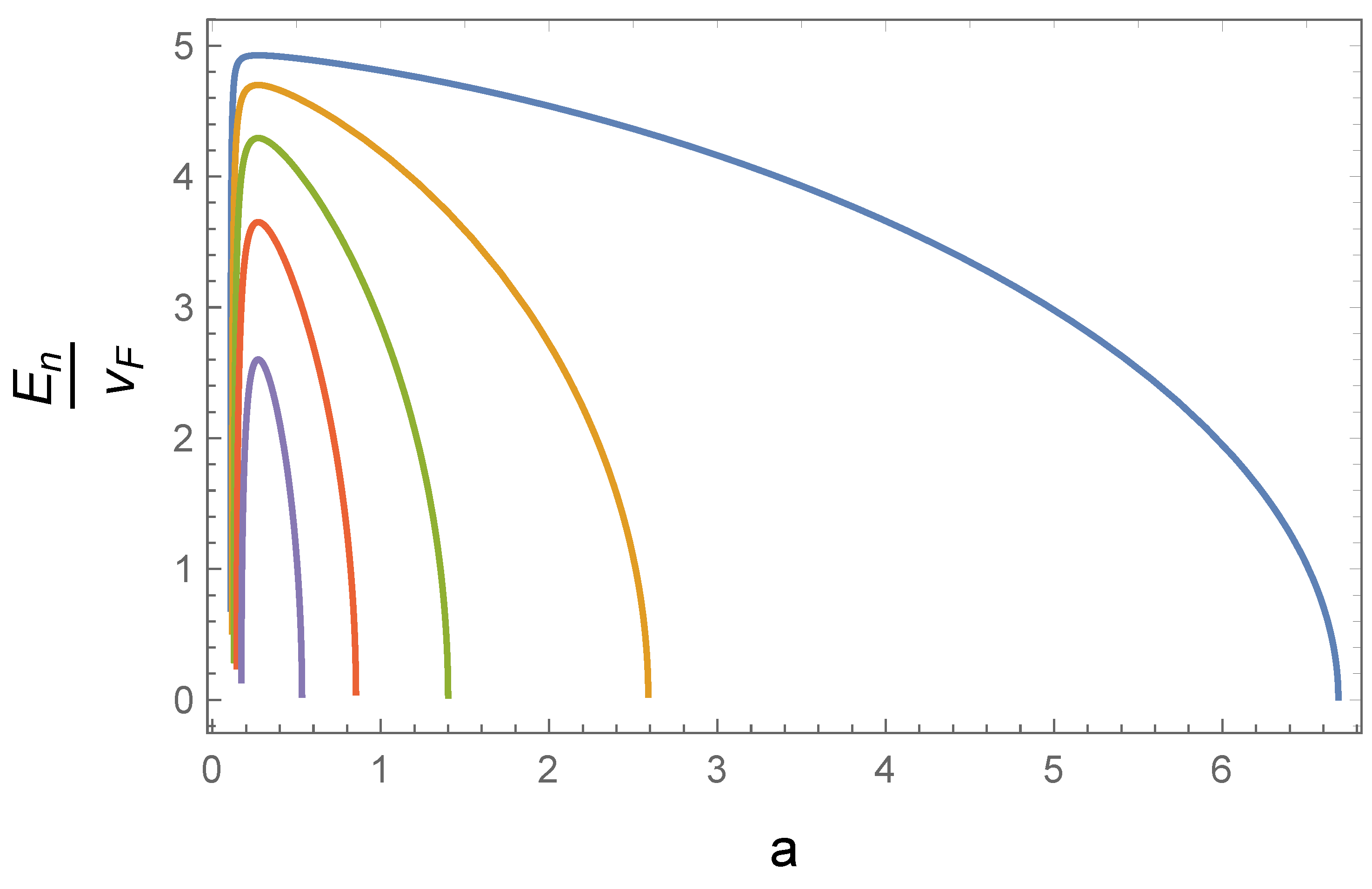
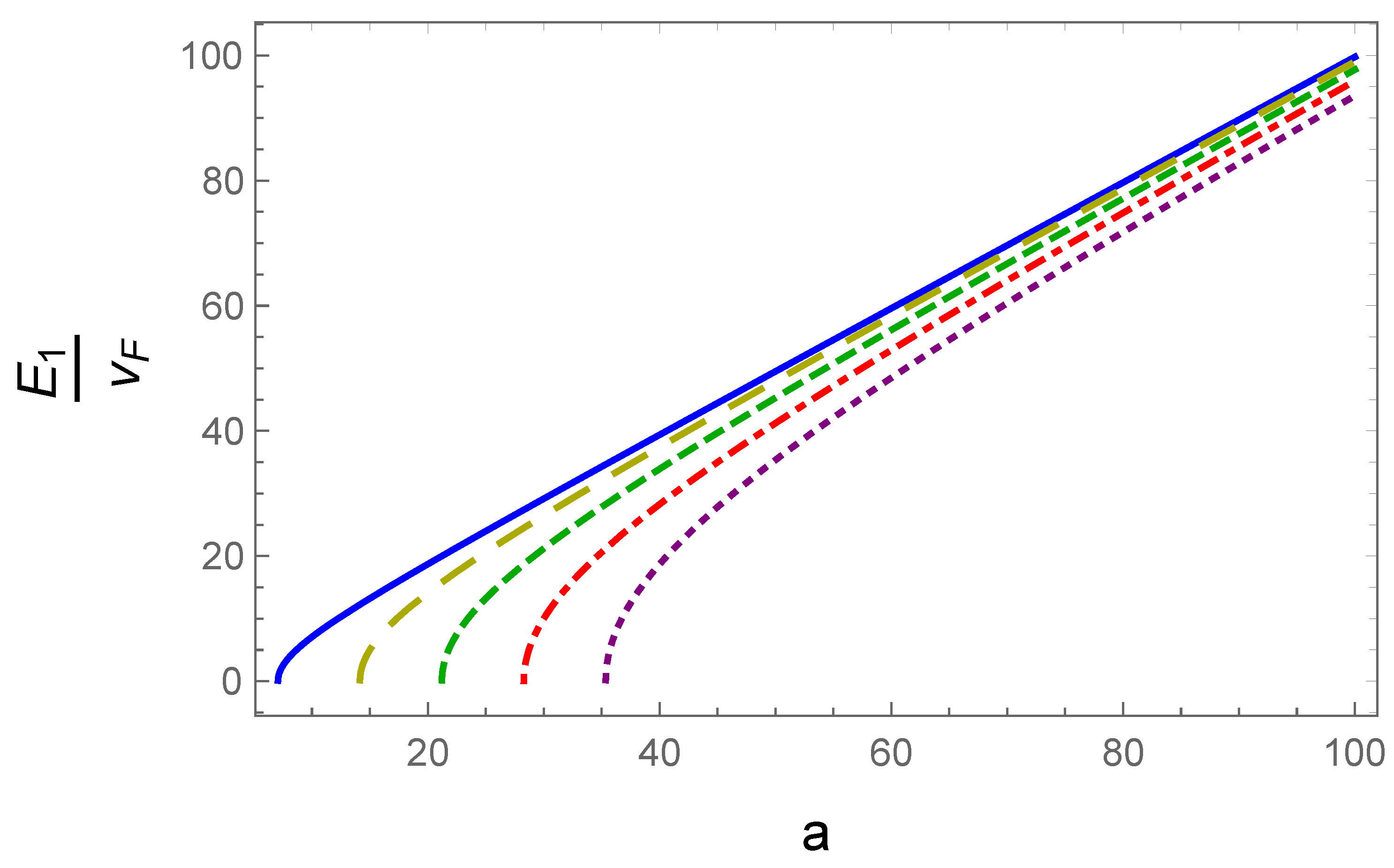
3.1. Uniform Unidirectional Deformation

Let us consider the case of graphene under uniaxial, homogeneous strain vastly discussed in literature [11,12,13,14,15,16,17]. Such strain deforms the Dirac cones to develop an elliptic cross-section. Nevertheless, it is well known that a mechanical deformation of this type does not generate any pseudomagnetic field whatsoever [10]. In order to address the impact of strain and thus of the deformed momentum operator on bound states, we additionally consider a uniform magnetic field pointing perpendicularly to the graphene membrane. Thus, the scenario we consider is described by the tensor Fermi velocity

$${\mathbf{v}}_F=v_F\left(\begin{array}{cc}a& 0\\ 0& b\end{array}\right),$$

(31)

where a and b are dimensionless constants (the case $a=b$ corresponds to the pristine case). As for the magnetic field, we consider the Landau gauge vector potential $\mathbf{A}={(0,B_{0}x,0)}^{\top }$ such that $\mathbf{B}$ is of uniform strength $B_0$ along the perpendicular direction to the graphene sample. Thus, the anisotropic Dirac equation is cast in the form 1

$$v_F\left(a{\sigma }_x{p}_x^0+b{\sigma }_y\left(p_y^0+e{B}_{0}x\right)\right){\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right),$$

(32)

By noticing that $p_y^0$ is conserved, we take the spinor of the form

$${\mathsf{\Psi }}_n\left(\mathbf{x}\right)=e^{i{p}_{y}y}\left(\begin{array}{c}f\left(x\right)\\ ig\left(x\right)\end{array}\right)\equiv e^{i{p}_{y}y}{\psi }_n\left(x\right),$$

(33)

where $p_y$ denotes the eigenvalue of $p_y^0$. Then, by considering the magnetic length ${\ell }_{B_0}^2\equiv 1/\left(e{B}_0\right)$ and the scale ${\ell }_{E_n}\equiv v_F/E_n$, we introduce the dimensionless variables

$$u=\sqrt{r}{\displaystyle \frac{x}{{\ell }_{B_0}}},c_{B_0}\equiv \sqrt{r}{p}_y{\ell }_{B_0},{\lambda }_n\equiv {\displaystyle \frac{1}{\sqrt{ab}}}{\displaystyle \frac{{\ell }_{B_0}}{{\ell }_{E_n}}},r={\displaystyle \frac{b}{a}},$$

(34)

such that the Dirac equation is cast in the form

$$\left(\begin{array}{c}{\displaystyle \left(\frac{d}{du}+\left(c_{B_0}+u\right)\right)g\left(u\right)}\\ {\displaystyle \left(\frac{d}{du}-\left(c_{B_0}+u\right)\right)f\left(u\right)}\end{array}\right)={\lambda }_n\left(\begin{array}{c}f\left(u\right)\\ -g\left(u\right)\end{array}\right).$$

(35)

The resulting coupled system of equations can be decoupled by taking f or g from one of the equations and inserting it in the other. In doing so, we are lead with the following system of equations

$$\begin{array}{ccc}\hfill \left[-{\displaystyle \frac{d^2}{d{u}^2}}+V_{+}\left(u,c_{B_0}\right)\right]f\left(u\right)& =& {\lambda }_n^{2}f\left(u\right),\hfill \\ \hfill \left[-{\displaystyle \frac{d^2}{d{u}^2}}+V_{-}\left(u,c_{B_0}\right)\right]g\left(u\right)& =& {\lambda }_n^{2}g\left(u\right),\hfill \end{array}$$

(36)

with

$$V_{\pm }\left(u,c_{B_0}\right)\equiv {\left(c_{B_0}+u\right)}^2\pm {\displaystyle \frac{d}{du}}\left(c_{B_0}+u\right)={\left(c_{B_0}+u\right)}^2\pm 1.$$

(37)

The system (36) possesses the structure of a supersymmetric quantum mechanical pair of Hamiltonians related through the superpotential

$$W\left(u,c_{B_0}\right)\equiv u+c_{B_0}.$$

(38)

Furthermore, the potentials $V_{\pm }$ are shape invariant, since we can write

$$V_{+}\left(u,c_{B_0}\right)-V_{-}\left(u,c_{B_0}\right)={\left(c_{B_0}+u\right)}^2+1-\left({\left(c_{B_0}+u\right)}^2-1\right)=2,$$

(39)

namely,

$$V_{+}\left(u,c_{B_0}\right)=V_{-}\left(u,c_{B_0}\right)+2.$$

(40)

In this form, by taking $a_1=c_{B_0}$, $a_2=f\left(a_1\right)=c_{B_0}$, upon iterating we have that the k-th term of this sequence is $a_k=f^k\left(a_1\right)=c_{B_0}$ and hence $R\left(a_k\right)=2$. This means that the eigenvalue

$${\lambda }_n^{2\left(-\right)}=\underset{k=1}{\sum ^n}R\left(a_k\right)=2n.$$

(41)

Supersymmetric Quantum Mechanics (SUSY-QM) is an abundant framework [31,32,33,34] in quantum mechanics, which have proven useful for solving Dirac equation, particularly in materials as graphene [35,36,37]. By inserting the above result (41) in the fist of the equations in (36), we are lead to

$$\left[{\displaystyle \frac{d^2}{d{u}^2}}-{\left(c_{B_0}+u\right)}^2-1\right]f\left(u\right)=-2nf\left(u\right).$$

(42)

Let $t=c_{B_0}+u$ and let us search for a solution of the form $f\left(t\right)=e^{-{\displaystyle \frac{t^2}{2}}}H\left(t\right)$. It is straightforward to verify that $H\left(t\right)$ verifies

$$\left[{\displaystyle \frac{d^2}{d{t}^2}}-2t{\displaystyle \frac{d}{dt}}+2\left(n-{\displaystyle \frac{1}{2}}\right)\right]H\left(t\right)=0,$$

(43)

From where we can identify $H\left(t\right)=H_{n-{\displaystyle \frac{1}{2}}}\left(t\right)$, where $H_n\left(t\right)$ are Hermite polynomials [38]. Therefore, $f\left(t\right)$ corresponds to a Whittaker function. Additionally, we have that

$$\left({\displaystyle \frac{d}{dt}}-t\right)e^{-{\displaystyle \frac{t^2}{2}}}{H}_{n-{\displaystyle \frac{1}{2}}}\left(t\right)=-\sqrt{2n}g\left(t\right),$$

(44)

from where we can write the spinor, in its original variables, as

$${\psi }_n\left(u\right)=e^{-{\displaystyle \frac{{\left(c_{B_0}+u\right)}^2}{2}}}\left(\begin{array}{c}{H}_{n-{\displaystyle \frac{1}{2}}}\left(c_{B_0}+u\right)\\ {\displaystyle \frac{i}{\sqrt{2n}}}{H}_{n+{\displaystyle \frac{1}{2}}}\left(c_{B_0}+u\right)\end{array}\right),$$

(45)

whereas the energy eigenvalue becomes

$$E_n=\sqrt{ab}{v}_F\sqrt{2ne{B}_0}.$$

(46)

The effect of the deformation in this case is to bring closer or apart the Landau levels, depending on the value of $\xi =\sqrt{ab}$, as has been extensively discussed in literature (see, for instance, [12,13]). The complete change in the cross section of Dirac cones can me taken into account by redefining the Fermi velocity $v_F\to \xi v_F$. The effect of strain on the Landau levels is sketched in Figure 1.

The explicit calculation of the quadrature commutators gives the following results:

$$[a_x,a_x^{†}]=\hslash a,[a_y,a_y^{†}]=\hslash b,[a_x,a_y^{†}]=0,[a_x,a_y]=0.$$

(47)

We can observe that the non-vanishing quadrature commutators are directly proportional to the diagonal elements of the strain tensor, which are related to the geometrical parameters of the elliptic cross-section of the Dirac cones [12].

3.2. Shear Strain

Let us now consider a Fermi velocity arising from shear strain deformation,

$${\mathbf{v}}_F=v_F\left(\begin{array}{cc}0& a\\ a& 0\end{array}\right)=a{v}_F{\sigma }_x.$$

(48)

Such a deformation does not generate pseudomagnetic fields [11]. Thus, for bound states, we consider the influence of an external uniform magnetic field perpendicular to the sample. Working in the Landau gauge $\mathbf{A}={(-B_{0}y,0,0)}^{\top },$ our starting point is

$$\sigma ·a{v}_F{\sigma }_x·\left(\mathbf{p}+e\mathbf{A}\right){\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right).$$

(49)

Because $p_x^0$ is conserved, we take

$${\mathsf{\Psi }}_n\left(\mathbf{x}\right)=e^{i{p}_{x}x}\left(\begin{array}{c}f\left(y\right)\\ ig\left(y\right)\end{array}\right)\equiv e^{i{p}_{x}x}{\psi }_n\left(y\right).$$

(50)

Next, we define ${\ell }_{B_0}^2\equiv 1/\left(e{B}_0\right)$ and ${\ell }_{E_n}\equiv \left(v_F\right)/E_n$, the spinor $\psi \left(y\right)$ verifies

$$-i\left({\ell }_{B_0}{\displaystyle \frac{d}{dy}}+{\sigma }_z\left(k_x{\ell }_{B_0}-{\displaystyle \frac{y}{{\ell }_{B_0}}}\right)\right){\sigma }_x{\psi }_n\left(y\right)={\displaystyle \frac{1}{a}}{\displaystyle \frac{{\ell }_{B_0}}{{\ell }_{E_n}}}{\psi }_n\left(y\right).$$

(51)

In terms of the dimensionless variables

$$u\equiv {\displaystyle \frac{y}{{\ell }_{B_0}}},c_{B_0}\equiv k_x{\ell }_{B_0},{\lambda }_n\equiv {\displaystyle \frac{1}{a}}{\displaystyle \frac{{\ell }_{B_0}}{{\ell }_{E_n}}},$$

(52)

the Dirac equation is cast in the form

$$-i\left({\displaystyle \frac{d}{du}}+{\sigma }_z\left(c_{B_0}-u\right)\right){\sigma }_x{\psi }_n\left(u\right)={\lambda }_n{\psi }_n\left(u\right).$$

(53)

Notice that replacing $u\to -u$ amounts to write the above equation as

$$-i\left(-{\displaystyle \frac{d}{du}}+{\sigma }_z\left(c_{B_0}+u\right)\right){\sigma }_x{\psi }_n\left(-u\right)={\lambda }_n{\psi }_n\left(-u\right),$$

(54)

which is equivalent to the coupled system of equations

$$\begin{array}{ccc}\hfill \left({\displaystyle \frac{d}{du}}-\left(c_{B_0}+u\right)\right)g\left(-u\right)& =& -{\lambda }_{n}f\left(-u\right),\hfill \\ \hfill \left({\displaystyle \frac{d}{du}}+\left(c_{B_0}+u\right)\right)f\left(-u\right)& =& {\lambda }_{n}g\left(-u\right),\hfill \end{array}$$

(55)

namely, it is the same as in (35). Thus, we readily find

$${\psi }_n\left(u\right)=e^{-{\displaystyle \frac{{\left(c_{B_0}-u\right)}^2}{2}}}\left(\begin{array}{c}{\displaystyle \frac{1}{\sqrt{2n}}}{H}_{n+{\displaystyle \frac{1}{2}}}\left(c_{B_0}-u\right)\\ i{H}_{n-{\displaystyle \frac{1}{2}}}\left(c_{B_0}-u\right)\end{array}\right),$$

(56)

where ${\lambda }_n=\sqrt{2n}$ and thus

$$E_n=a{v}_F\sqrt{2ne{B}_0},$$

(57)

as before, we notice that the effect of shear strain is precisely the same as the parameter $\xi$ in the uniform uniaxial case. In this case, the effect of deformation is seen through the redefinition $v_F\to a{v}_F$. The effect of shear strain on the lowest Landau level is shown in Figure 2.

In this case, the quadrature commutators turn out to be

$$[a_x,a_y^{†}]=\hslash a,[a_y,a_x^{†}]=\hslash a,[a_x,a_x^{†}]=[a_y,a_y^{†}]=0,[a_x,a_y]=0.$$

(58)

Since the shear strain also cancels the momentum term in the commutators in Equation (13), the effect of this strain is similar to the uniform uniaxial case. Again, we can see that quadrature commutators yield the Fermi velocity matrix elements. Thus, they are directly related to the geometrical parameters of the deformed Dirac cones.

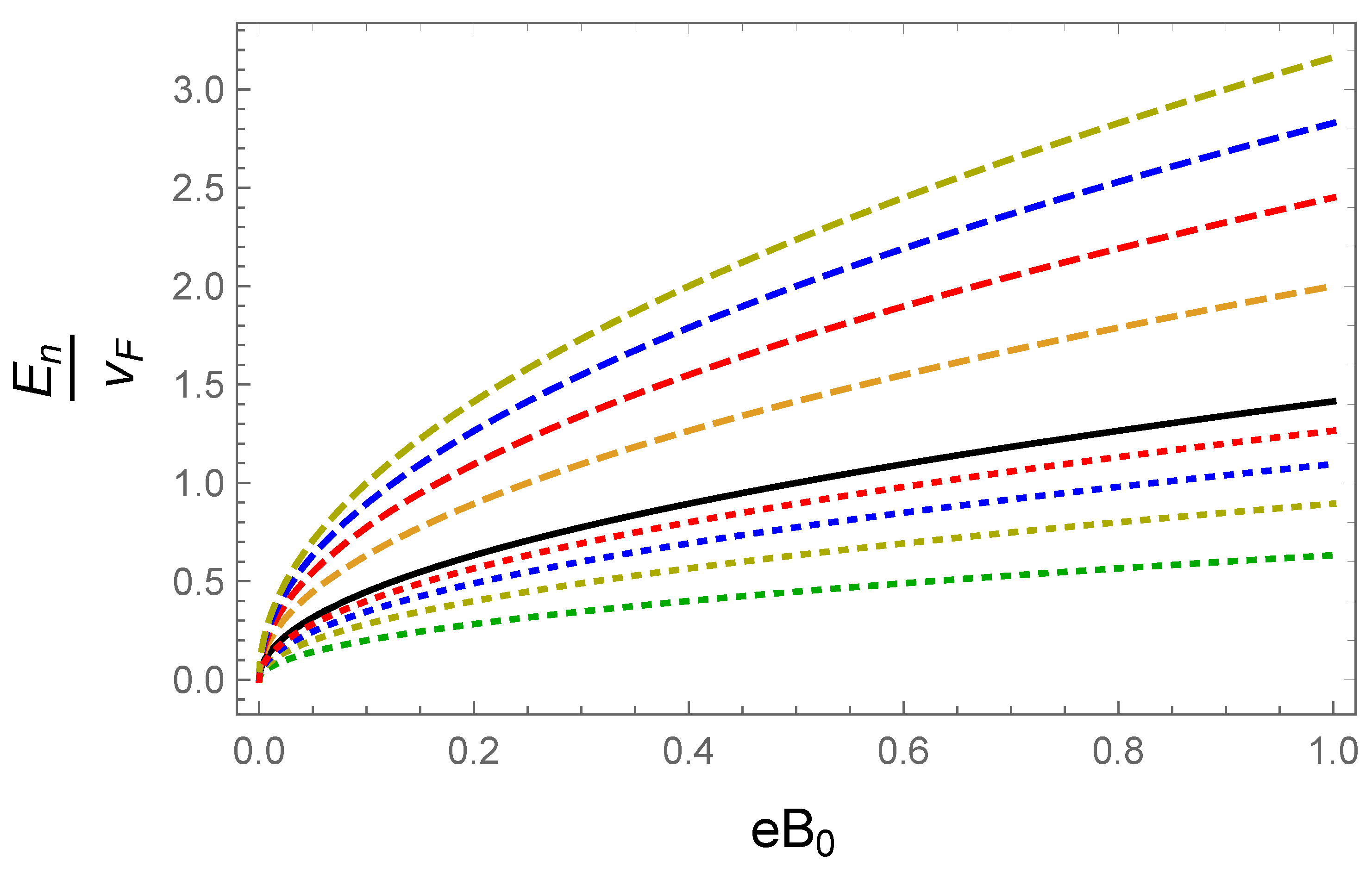
3.3. Diagonal Inhomogeneous Fermi Velocity

Let us now consider the case

$${\mathbf{v}}_F=v_F\left(\begin{array}{cc}ax& 0\\ 0& b\end{array}\right),$$

(59)

with b is dimensionless, but a has dimensions of inverse length. The strain tensor that generates this profile of the Fermi velocity generates a pseudomagnetic field defined through the vector potential with components

$$A_x=-{\displaystyle \frac{B_0}{x}},A_y=0,$$

(60)

that generate a singular pseudomagnetic field of strength $B_0/x^2$ oriented perpendicularly to the graphene membrane. The Dirac equation for this singular pseudomagnetic field has been discussed in [13]. In this article we are interested in the sole effect of the inhomogeneous Fermi velocity, for which the Dirac equation reads

$$\sigma ·v_F\left(\begin{array}{cc}ax& 0\\ 0& b\end{array}\right)\mathbf{p}{\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right).$$

(61)

Again, from the fact that $p_y^0$ is conserved, we take

$${\mathsf{\Psi }}_n\left(\mathbf{x}\right)=e^{i{p}_{y}y}\left(\begin{array}{c}f\left(x\right)\\ ig\left(x\right)\end{array}\right)\equiv e^{i{p}_{y}y}{\psi }_n\left(x\right).$$

(62)

Thus, the Dirac equation becomes

$$-i{v}_F\left(ax{\displaystyle \frac{d}{dx}}+b{\sigma }_z{k}_y\right){\sigma }_x{\psi }_n\left(x\right)=E_n{\psi }_n\left(x\right).$$

(63)

Let $u=ln\left(ax\right)$. Thus,

$$-i\left({\displaystyle \frac{d}{du}}+c_k{\sigma }_z\right){\sigma }_x{\psi }_n\left(u\right)={\lambda }_n{\psi }_n\left(u\right),$$

(64)

with ${\lambda }_n=1/\left(a{\ell }_{E_n}\right)$ and $c_k=b{p}_y/a$. This equation is equivalent to the coupled system of equations

$$\begin{array}{ccc}\hfill \left({\displaystyle \frac{d}{du}}+c_k\right)g\left(u\right)& =& {\lambda }_{n}f\left(u\right),\hfill \\ \hfill \left({\displaystyle \frac{d}{du}}-c_k\right)f\left(u\right)& =& -{\lambda }_{n}g\left(u\right).\hfill \end{array}$$

(65)

The system can be decoupled in the standard procedure, leading to

$$\begin{array}{ccc}\hfill \left({\displaystyle \frac{d^2}{d{u}^2}}-\left(c_k^2-{\lambda }_n^2\right)\right)f\left(u\right)& =& 0,\hfill \\ \hfill \left({\displaystyle \frac{d^2}{d{u}^2}}-\left(c_k^2-{\lambda }_n^2\right)\right)g\left(u\right)& =& 0.\hfill \end{array}$$

(66)

The former equation has as solution

$$f\left(x\right)=Asin\left(\sqrt{c_k^2-{\lambda }_n^2}ln\left(ax\right)+{\theta }_1\right),$$

(67)

while the latter can be expressed as

$$g\left(u\right)=A\left[{\displaystyle \frac{c_k}{{\lambda }_n}}sin\left(\sqrt{c_k^2-{\lambda }_n^2}u+{\theta }_1\right)-{\displaystyle \frac{\sqrt{c_k^2-{\lambda }_n^2}}{{\lambda }_n}}cos\left(\sqrt{c_k^2-{\lambda }_n^2}u+{\theta }_1\right)\right],$$

(68)

but considering that

$${\left({\displaystyle \frac{c_k}{{\lambda }_n}}\right)}^2+{\displaystyle \frac{c_k^2-{\lambda }_n^2}{{\lambda }_n^2}}=2{\left({\displaystyle \frac{c_k}{{\lambda }_n}}\right)}^2-1,$$

(69)

we write

$$g\left(u\right)=A\sqrt{2{\left({\displaystyle \frac{c_k}{{\lambda }_n}}\right)}^2-1}sin\left(\sqrt{c_k^2-{\lambda }_n^2}u-\varphi +{\theta }_1\right),$$

(70)

with

$$cos\left(\varphi \right)\equiv {\displaystyle \frac{\frac{c_k}{{\lambda }_n}}{\sqrt{2{\left(\frac{c_k}{{\lambda }_n}\right)}^2-1}}}.$$

(71)

Then, we can write

$${\psi }_n\left(x\right)=A\left(\begin{array}{c}sin\left(\sqrt{c_k^2-{\lambda }_n^2}ln\left(ax\right)+{\theta }_1\right)\\ isin\left(\sqrt{c_k^2-{\lambda }_n^2}ln\left(ax\right)+{\theta }_1-\varphi \right)\end{array}\right).$$

(72)

We assume that, along the x-direction the layer extends between $ax=1$ and $ax=aL$. Thus ${\psi }_n\left({\displaystyle \frac{1}{a}}\right)={\psi }_n\left(L\right)=0$. The first condition implies ${\theta }_1=0$, while the sencond, $\sqrt{c_k^2-{\lambda }_n^2}ln\left(aL\right)=n\pi$ with n an integer. Thus

$${\psi }_n\left(x\right)=A\left(\begin{array}{c}sin\left(n\pi {\displaystyle \frac{ln\left(ax\right)}{ln\left(aL\right)}}\right)\\ isin\left(n\pi {\displaystyle \frac{ln\left(ax\right)}{ln\left(aL\right)}}-\varphi \right)\end{array}\right)=A\left(\begin{array}{c}sin\left(n\pi {log}_{aL}\left(ax\right)\right)\\ isin\left(n\pi {log}_{aL}\left(ax\right)-\varphi \right)\end{array}\right),$$

(73)

whereas for the energy eigenvalue we have ${\lambda }_n=\sqrt{c_k^2-{\left(n{\displaystyle \frac{\pi }{ln\left(aL\right)}}\right)}^2}$, and thus

$$E_n=v_{F}a\sqrt{c_k^2-{\left(n{\displaystyle \frac{\pi }{ln\left(aL\right)}}\right)}^2}.$$

(74)

We observe that in this case, the effect of the parameters a and b is more intricate than in previous cases, because its effect does not correspond to a simple redefinition of the Fermi velocity, but it also enters in the parameter $c_k$. These energy levels are depicted in Figure 3. Observe the collapse of these levels with the size of the sample at fixed strain and vice versa.

On the other hand, using Equations in (13), we have that

$$[a_x,a_x^{†}]=\hslash ax,[a_y,a_y^{†}]=\hslash b,[a_x,a_y^{†}]=0,[a_x,a_y]=0.$$

(75)

The deformation in the quadrature algebra is in terms of the elements of the Fermi velocity in (59). As we have seen, a strain described by a diagonal Fermi velocity leads us to quadrature commutators related to deformation in the Dirac cones. In this case, such deformation varies linearly in the coordinate x but it is constant in y-direction.

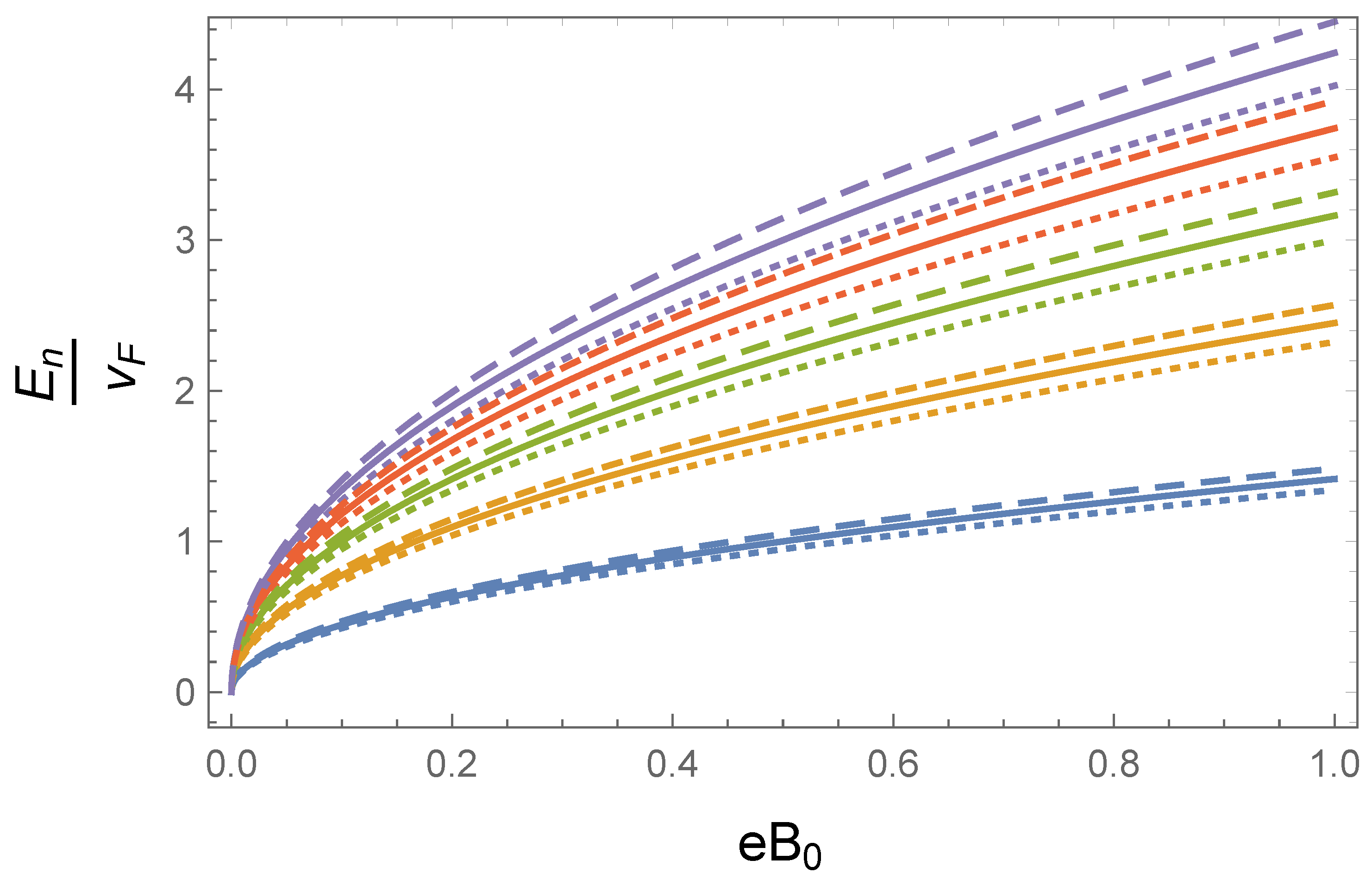
Adding an External Magnetic Field

We consider again the inhomogeneous Fermi velocity (59) and add the influence of a uniform magnetic field perpendicular to the graphene sample, $\mathbf{B}=B_0\widehat{k}$. In Landau gauge, $\mathbf{A}={\left(0B_{0}x0\right)}^T$, Dirac equation becomes

$$\sigma ·v_F\left(\begin{array}{cc}ax& 0\\ 0& b\end{array}\right)\left(\mathbf{p}+e\mathbf{A}\right){\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right).$$

(76)

Writing the spinor as

$${\mathsf{\Psi }}_n\left(\mathbf{x}\right)=e^{i{p}_{y}y}\left(\begin{array}{c}f\left(x\right)\\ ig\left(x\right)\end{array}\right)\equiv e^{i{p}_{y}y}{\psi }_n\left(x\right),$$

(77)

we notice that $\psi \left(x\right)$ verifies

$$-i\left(x{\displaystyle \frac{d}{dx}}+{\sigma }_z\left(b{\displaystyle \frac{p_y}{a}}+b{\displaystyle \frac{x}{a{\ell }_{B_0}^2}}\right)\right){\sigma }_x{\psi }_n\left(x\right)={\displaystyle \frac{1}{a{\ell }_{E_n}}}{\psi }_n\left(x\right).$$

(78)

In terms of the dimensionless variables

$$q=b{\displaystyle \frac{x}{a{\ell }_{B_0}^2}},c_k\equiv b{\displaystyle \frac{p_y}{a}},{\lambda }_n\equiv {\displaystyle \frac{1}{a{\ell }_{E_n}}},$$

(79)

the spinor $\psi$ verifies

$$-i\left(q{\displaystyle \frac{d}{dq}}+\left(c_k+q\right){\sigma }_z\right){\sigma }_x{\psi }_n\left(q\right)={\lambda }_n{\psi }_n\left(q\right),$$

(80)

which is equivalent to the coupled system of equations

$$\begin{array}{ccc}\hfill \left(q{\displaystyle \frac{d}{dq}}+\left(c_k+q\right)\right)g\left(q\right)& =& {\lambda }_{n}f\left(q\right)\hfill \\ \hfill \left(q{\displaystyle \frac{d}{dq}}-\left(c_k+q\right)\right)f\left(q\right)& =& -{\lambda }_{n}g\left(q\right).\hfill \end{array}$$

(81)

By decoupling the system in the standard procedure, we are lead to

$$\begin{array}{ccc}\hfill \left[q{\displaystyle \frac{d}{dq}}q{\displaystyle \frac{d}{dq}}-{\left(c_k+q\right)}^2-q\right]f\left(q\right)& =& -{\lambda }_n^{2}f\left(q\right)\hfill \\ \hfill \left[q{\displaystyle \frac{d}{dq}}q{\displaystyle \frac{d}{dq}}-{\left(c_k+q\right)}^2+q\right]g\left(q\right)& =& -{\lambda }_n^{2}g\left(q\right).\hfill \end{array}$$

(82)

To cast the system of equations (82) in a tractable form, let $u=ln\left(q\right)$. Then, we find straigtforwardly that

$$\begin{array}{ccc}\hfill \left[-{\displaystyle \frac{d^2}{d{u}^2}}+V_{+}\left(u,c_k\right)\right]f\left(u\right)& =& {\lambda }_n^{2}f\left(u\right)\hfill \\ \hfill \left[-{\displaystyle \frac{d^2}{d{u}^2}}+V_{-}\left(u,c_k\right)\right]g\left(u\right)& =& {\lambda }_n^{2}g\left(u\right),\hfill \end{array}$$

(83)

with

$$V_{\pm }\left(u,c_k\right)={\left(c_k+e^u\right)}^2\pm {\displaystyle \frac{d}{du}}\left(c_k+e^u\right)={\left(c_k+e^u\right)}^2\pm e^u,$$

(84)

Namely, the system (83) has a supersymmetric structure with the superpotential

$$W\left(u,c_{B_0}\right)\equiv c_k+e^u.$$

(85)

Furthermore, noticing that

$$V_{+}\left(u,c_k\right)-V_{-}\left(u,c_k^{\prime }\right)={\left(c_k\right)}^2-{\left(c_k^{\prime }\right)}^2+2\left(c_k-c_k^{\prime }\right)e^u+2e^u,$$

(86)

which after the shift $c_k\to c_k-1$ , $c_k^{\prime }=c_k$ lead to

$$V_{+}\left(u,c_k-1\right)-V_{-}\left(u,c_k\right)={\left(c_k-1\right)}^2-{\left(c_k\right)}^2,$$

(87)

namely, the system is also shape invariant, $V_{+}\left(u,a_1\right)=V_{-}\left(u,a_2\right)+R\left(a_1\right)$. By taking

$$a_1=c_k-1,a_2=f\left(a_1\right)=c_k=\left(c_k-1\right)+1,R\left(a_1\right)={\left(a_1\right)}^2-{\left(a_2\right)}^2,$$

(88)

we have that

$${\lambda }_n^{2\left(-\right)}=\underset{k=1}{\sum ^n}R\left(a_k\right)=n\left(2-\left(2c_k+n\right)\right),$$

(89)

and thus the energy eigenvalue is

$$E_n=a{v}_F\sqrt{n\left(2\left(1-c_k\right)-n\right)}.$$

(90)

Interestingly, these energy eigenvalues are independent of the external magnetic field. Furthermore, besides the zero mode, only one additional bound state corresponding to $n=1$ is formed. The corresponding eigenvalue as a function of a for different values of b and fixed $k_y$ is shown in Figure 4.

As for the states themselves, from the first eq. in (82), we can write

$$\left[{\displaystyle \frac{d^2}{d{q}^2}}+{\displaystyle \frac{1}{q}}{\displaystyle \frac{d}{dq}}-{\displaystyle \frac{2\left(c_k+\frac{1}{2}\right)}{q}}-1+{\displaystyle \frac{{\lambda }_n^2-c_k^2}{q^2}}\right]f\left(q\right)=0.$$

(91)

Notice that ${\lambda }_n^2-c_k^2=2n-{\left(c_k+n\right)}^2\equiv {\mathsf{\Theta }}_{nk}$. Thus, by letting $f\left(q\right)=e^{q}h\left(q\right)$, we are lead to

$$\left[{\displaystyle \frac{d^2}{d{q}^2}}+{\displaystyle \frac{1}{q}}\left(1+2q\right){\displaystyle \frac{d}{dq}}-{\displaystyle \frac{2c_k}{q}}+{\displaystyle \frac{{\mathsf{\Theta }}_{nk}}{q^2}}\right]h\left(q\right)=0.$$

(92)

We search for $h\left(q\right)$ of the form $h\left(q\right)=q^{s}w\left(q\right)$ for s to be determined by demanding normalizability of the solution. It is stragthforward to see that the function $w\left(q\right)$ verifies

$$\left[{\displaystyle \frac{d^2}{d{q}^2}}+{\displaystyle \frac{1}{q}}\left(1+2s+2q\right){\displaystyle \frac{d}{dq}}-{\displaystyle \frac{2c_k}{q}}+{\displaystyle \frac{s\left(s-1\right)+{\mathsf{\Theta }}_{nk}}{q^2}}\right]w\left(q\right)=0.$$

(93)

For the solution to be normalizable, we demand $s\left(s-1\right)+{\mathsf{\Theta }}_{nk}=0\Rightarrow {\left(s-{\displaystyle \frac{1}{2}}\right)}^2={\displaystyle \frac{1}{4}}-{\mathsf{\Theta }}_{nk}$, namely

$$s_{\pm }={\displaystyle \frac{1}{2}}\pm \sqrt{{\displaystyle \frac{1}{4}}-{\mathsf{\Theta }}_{nk}}.$$

(94)

Thus, with the additional change of variable $t=-2q$, we can write

$$\left[t{\displaystyle \frac{d^2}{d{t}^2}}+\left(1+2s_{+}-t\right){\displaystyle \frac{d}{dt}}-\left(-c_k\right)\right]w\left(t\right)=0,$$

(95)

which corresponds to a confluent hypergeometric equation with solutions

$$w\left(q\right)=C_{1}M\left(-c_k,1+2s_{+},-2q\right)+C_{2}U\left(-c_k,1+2s_{+},-2q\right),$$

(96)

and correspondingly

$$f\left(q\right)=C_1{e}^q{q}^{s_{+}}M\left(-c_k,1+2s_{+},-2q\right)+C_2{e}^q{q}^{s_{+}}U\left(-c_k,1+2s_{+},-2q\right).$$

(97)

From the second equation in (81), we can write

$$\begin{array}{ccc}\hfill g\left(q\right)& =& -{\displaystyle \frac{1}{{\lambda }_n}}{e}^q{q}^{s_{+}}\left\{C_1{s}_{+}\left(M\left(-c_k,2s_{+}+1,-2q\right)-c_{k}M\left(1-c_k,2s_{+}+1,-2q\right)\right)\right.\hfill \\ & & \left.-C_2\left[\left(c_k+2s_{+}+2\right)U\left(-c_k,s_{+},-2q\right)+s_{+}U\left(-c_k,2s_{+}+1,-2q\right)\right]\right\}.\hfill \end{array}$$

(98)

This completes the final form of the spinors under this deformation.

3.4. Inhomogeneous Strain in Two Variables

Let us now consider a separable linear dependence of the inhomegeneous Fermi velocity as

$${\mathbf{v}}_F=v_F\left(\begin{array}{cc}ax& 0\\ 0& by\end{array}\right)$$

(99)

where a and b are constants with dimensions of inverse length. The corresponding Dirac equation acquires the form

$$\sigma ·v_F\left(\begin{array}{cc}ax& 0\\ 0& by\end{array}\right)\mathbf{p}{\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right)$$

(100)

can be cast in the convenient form

$$-i{v}_F\left(ax{\displaystyle \frac{d}{dx}}-i{\sigma }_{z}by{\displaystyle \frac{d}{dy}}\right){\sigma }_x{\mathsf{\Psi }}_n\left(\mathbf{x}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{x}\right).$$

(101)

Let

$$u=ln\left(ax\right),v=ln\left(by\right),r\equiv {\displaystyle \frac{b}{a}}.$$

(102)

Then, the Dirac equation acquires the form

$$-i{v}_{F}a\left({\displaystyle \frac{d}{du}}-ir{\sigma }_z{\displaystyle \frac{d}{dv}}\right){\sigma }_x{\mathsf{\Psi }}_n\left(\mathbf{u}\right)=E_n{\mathsf{\Psi }}_n\left(\mathbf{u}\right),$$

(103)

where $\mathbf{u}=(u,v)$. By taking

$${\mathsf{\Psi }}_n\left(\mathbf{u}\right)=e^{i{k}_{v}v}\left(\begin{array}{c}f\left(u\right)\\ ig\left(u\right)\end{array}\right)\equiv e^{i{k}_{v}v}{\psi }_n\left(u\right),$$

(104)

the spinor $\psi \left(u\right)$ verifies

$$-i{v}_F\sqrt{ab}\left({\displaystyle \frac{1}{\sqrt{r}}}{\displaystyle \frac{d}{du}}+\sqrt{r}{k}_v{\sigma }_z\right){\sigma }_x{\psi }_n\left(u\right)=E_n{\psi }_n\left(u\right).$$

(105)

Now, defining

$$t\equiv \sqrt{r}u,c_k\equiv \sqrt{r}{k}_v.$$

(106)

Then, we have that

$$-i\left({\displaystyle \frac{d}{dt}}+c_k{\sigma }_z\right){\sigma }_x{\psi }_n\left(t\right)={\lambda }_n{\psi }_n\left(t\right),$$

(107)

with ${\lambda }_n\equiv 1/\sqrt{ab}{\ell }_{E_n}$. This differential equation is the same as in eq. (64). Therefore, assuming again that the graphene sample extends between $ax=1$ and $ax=aL$, we have that

$${\psi }_n\left(x\right)=A\left(\begin{array}{c}sin\left(n\pi {\displaystyle \frac{ln\left(ax\right)}{ln\left(aL\right)}}\right)\\ isin\left(n\pi {\displaystyle \frac{ln\left(ax\right)}{ln\left(aL\right)}}-\varphi \right)\end{array}\right)=A\left(\begin{array}{c}sin\left(n\pi {log}_{aL}\left(ax\right)\right)\\ isin\left(n\pi {log}_{aL}\left(ax\right)-\varphi \right)\end{array}\right).$$

(108)

Finally, by letting $\sqrt{c_k^2-{\lambda }_n^2}\sqrt{r}ln\left(aL\right)=n\pi$, we have that

$${\lambda }_n=\sqrt{c_k^2-{\left({\displaystyle \frac{n}{\sqrt{r}}}{\displaystyle \frac{\pi }{ln\left(aL\right)}}\right)}^2},$$

(109)

and thus the energy eigenvalues becomes

$$E_n=v_F\sqrt{ab}\sqrt{c_k^2-{\displaystyle \frac{1}{r}}{\left(n{\displaystyle \frac{\pi }{ln\left(aL\right)}}\right)}^2}.$$

(110)

These energy eigenvalues are depicted in Figure 5.

Finally, computing the quadrature algebra, we arrive at:

$$[a_x,a_x^{†}]=\hslash ax,[a_y,a_y^{†}]=\hslash by,[a_x,a_y^{†}]=0,[a_x,a_y]=0.$$

(111)

Once again, the deformation for the quadrature algebra is in terms of the elements of the Fermi velocity. Moreover, the deformation of the Dirac cones varies linearly in both directions.

4. Final Remarks

In this article we have identified and exploited the duality between the equations of motion of a Dirac theory with deformed momentum operator in flat graphene and a those arising from mechanical deformation or natural corrugation of the membrane which can be parametrized by the inhomogeneous shape of the Fermi velocity. In this regard, a strained membrane can be described as a pristine sample with a deformed momentum operator. The impact of the deformation of the uncertainty relations has been explored in bound states by considering strained membranes of graphene in the presence of a background uniform magnetic field. For the examples under consideration in this work, we have obtained the energy spectrum and the corresponding eigenstates. The impact of deformations is explored in detail for the energy eigenvalues, which deviate from the corresponding pristine spectra in parametric form in terms of the deformation parameters. Furthermore, the deformation of the momentum operator is analyzed by means of a quadrature algebra allowing to identify the physical consequences of a strain applied to graphene, as the deformation of the Dirac cones for an inhomogeneous strain described by a diagonal Fermi velocity. Also, we can determine strain deformations with the same effect, as the uniaxial strain and the share strain, since both cancel the term directly proportional to the momentum in the quadrature commutators.

For the future, we are planning to study the consequences of a strain deformation that remains the linear term on the momentum in the quadrature algebra, as well as, to extend this framework addressing the curvature formalism by considering non-commutative geometry, in which new dualities would be better identified.