Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Cross Section Calculations for Electron-Impact Ionization of Pyrimidine Molecule and its Halogenated Derivatives: 2-Chloropyrimidine, 5-Chloropyrimidine, 2-Bromopyrimidine and 5-Bromopyrimidine

A peer-reviewed article of this preprint also exists.

Submitted:

30 November 2024

Posted:

03 December 2024

You are already at the latest version

Abstract
Total cross section for single electron-impact ionization of pyrimidine (C4H4N2), 2–chloropyrimidine (2-C4H3ClN2), 5–chloropyrimidine (5-C4H3ClN2), 2–bromopyrimidine (2-C4H3BrN2) and 5–bromopyrimidine (5-C4H3BrN2) molecules has been calculated with the binary-encounter-Bethe model from the ionization threshold up to 5 keV. The input data for the BEB calculations concerning electronic structure of the studied targets have been obtained with quantum chemical methods including the Hartree-Fock (H-F) and the outer valence Green function (OVGF) methods. The calculated cross section for ionization of pyrimidine molecule due to electron impact is compared with available experimental and theoretical data. The question of the magnitude the pyrimidine ionization cross section is also discussed. Efficiency of the ionization process of studied halogenated derivatives of pyrimidine is also discussed.
Keywords: 
electron-impact ionization
;  
binary-encounter-Bethe model
;  
pyrimidine
;  
2-chloropyrimidine
;  
5-chloropyrimidine
;  
2-bromopyrimidine
;  
5-bromopyrimidine
;  
electron scattering
Subject: 
Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

Detailed and deep understanding of electron scattering from atom and molecules is crucial for interpretation the relevant phenomena occurring in many different environments including natural and technological ones [1,2]. Among all possible processes accompanying the interaction of electrons with molecules, electron-impact ionization and dissociative electron attachment (DEA), leading to the formation of positive and negative ions, respectively, seem to be very important due to the role these products play in chemical reactions. Also in the context of the interaction of primary ionizing radiation ( α , β ± , γ and etc.) with biomatter, secondary products such as low energy electrons, ions and radicals play an important role in the final effect of irradiation. The discovery of the fact that low-energy (0 eV – 20 eV) secondary electrons can induce DNA damage, including single- and double strand breaks by dissociative electron attachment (DEA) process indicated the need to take their contribution into account in radiotherapy [3,4,5,6]. Such secondary low-energy (0 eV – 100 eV) electrons are created in large quantities by ionizing radiation ( ∼ 4 × 10 4 per 1 MeV of primary ionizing radiation) [7]. In the next stages of radiolysis, they may lead to further ionization of the medium or be captured in the electron attachment process. The effect of the interaction of primary ionizing radiation and secondary products with living cells and the DNA they contain can be modeled in Monte-Carlo simulations. For example the Geant4-DNA package [8,9] allows to include into simulations many of electron interaction processes with biological environment, like elastic electron scatterring (7.4 eV – 1 MeV), electron–impact electronic excitation (9 eV – 1MeV), electron–impact vibrational excitation (2 eV – 100 eV), electron–impact ionization (11 eV – 1 MeV) and electron attachment by studied target (4 eV – 13 eV). This Monte-Carlo toolkit enables thorough investigations covering the physical, pre-chemical and chemical phases of early DNA damage induced by primary ionizing radiation, including indirect DNA damage induced by secondary ionizing particles, including low-energy electrons [10]. For such simulations, a complete set of high-quality data on the efficiency of the interaction, most often described by the cross-section for a given reaction, of primary ionizing radiation and secondary products is necessary. Since it is not possible to determine such data for all relevant chemical compounds and all possible interaction energies and all scattering channels in a reasonable time by means of measurements or advanced quantum-mechanical numerical calculations, reliable simple models are necessary. In order to develop such models, it is necessary to conduct thorough experimental and theoretical studies concerning, among others, the interactions of electrons with biomatter and simple molecular analogues of its components (see e.g., Ref. [11,12] and references therein).
Pyrimidine (1,3-diazine) is a six-membered, aromatic, heterocyclic organic compound in which two CH groups of the benzene molecule are replaced by nitrogen atoms at positions (1) and (3) of the ring (Figure 1). In studies on the damage to biological tissues by ionizing radiation in cancer radiotherapy, pyrimidine has been widely recognized as a precursor and/or analog of the nucleobases – cytosine, thymine and uracil, which are the structural units of DNA and RNA. Moreover, derivatives of halogenated pyrimidines can incorporate into DNA and act as radiosensitizers making it more sensitive to radiation damage. Therefore, intensive research is being carried out on new compounds based on pyrimidine and its derivatives, which can act as radiosensitizers, potential antioxidants and selective anticancer agents [13,14,15]. Taking all the above facts into account, it is not surprising that relatively many studies have been carried out on electron scattering on pyrimidine molecules, including electron-impact ionization studies.
The theoretical and experimental work to date on collisional interactions of electrons with pyrimidine molecules can be briefly summarized as follows. Total electron-scattering cross section of pyrimidine was measured using the linear transmission spectrometer for energies from 20 eV to 5 keV [16] and for electron energies ranging from 8 eV to 500 eV using a magnetically confined experimental setup [17]. The same work reported integral elastic and inelastic electron-scattering cross sections calculated with the spherical complex optical potential model [16]. The stopping power for electron in pyrimidine was calculated based on measured the mean energy loss and theoretical total and elastic cross sections obtained with the screening-corrected additivity rule method [23]. Relatively many works concern measurements of the differential cross-section for elastic electron scattering from pyrimidine [18,19,20,21,22]. Differential cross sections for elastic electron scattering on pyrimidine for selected electron energies ranging from 1 eV to 20 eV and at scattering angles up to 180° have also been measured using an electron-impact spectrometer with hemispherical analyzer and a magnetic angle changer [24]. Experimental integral elastic cross section as a function of electron energy in the range 0.1–14 eV, as well as calculated ones with the-fixed-nuclei Schwinger variational and R-matrix methods have been also reported [24]. Experimental, as well as theoretical works also concerned electronic and vibrational excitation of pyrimidine by electron impact [24,25,26] Total and elastic cross sections for electron scattering from pyrimidine molecule were also calculated with a spherical complex optical potential formalism for an extensive energy range of 10 eV to 5 keV [28]. Resonances occurring due to low energy electron interaction with pyrimidine in the elastic channel were studied with R-matrix method [29]. Cross sections data set, including among others total, differential and total elastic cross sections, for an impact of electron in the energy range between 10 eV and 1 keV on pyrimidine molecules has been reported [30]. Very recently, a comprehensive set of calculated scattering cross section data of pyrimidine, including elastic one computed with the single-centre-expansion formalism, for impinging electron energies ranging from 1 eV to 5 keV has been also reported [31].
Of course, a relatively large number of works concern the ionization of the pyrimidine molecule induced by collisions with electrons. The experimental total and partial cross sections for electron-impact ionization of pyrimidine molecule were obtained employing the total ion collection technique and the quadrupole mass spectrometer from the ionization threshold up to 150 eV [32]. Total ionization cross section of pyrimidine was also determined form measured doubly differential electron-impact ionization cross section of pyrimidine [33]. Absolute total and partial dissociative ionization cross sections were also measured for electron impact energies ranging from 70 to 400 eV through time of flight mass spectrometry and calculated using semi-empirical approach [34]. Total ionization cross section obtained by integrating the measured double-differential ionization cross sections was also reported [30]. Theoretical studies on the calculations of electron-impact ionization cross section of pyrimidine molecules include computations using the spherical complex optical potential formalism with complex scattering potential ionization contribution method [35] and quantum-mechanical study based on the first Born approximation [36]. Total and/or partial ionization cross sections due to electron impact calculated with the binary-encounter-Bethe method have been also reported in several works [30,31]. Please note that preliminary version of our calculations of electron-impact ionization cross section of pyrimidine molecules has been also presented previously [37].
Much less work has been done on the interaction of electrons with halogenated pyrimidines. Here we note studies on the formation of temporary anion states due to low energy impact on haloprymidines [38] and the theoretical study of shape resonance states occurring during the interaction of low-energy electrons with halopyrimidines [39].
The objective of the present work is to provide carefully and precisely calculated electron-impact ionization cross sections for pyrimidine and its simple halogenated derivatives i.e., 2-chloropyrimidine, 5-chloropyrimidine, 2-bromopyrimidine and 5-bromopyrimidine.

2. Computational Methods

Essentially, theoretical method and numerical procedures employed in the present work are almost the same as in our previous studies, in which we have calculated electron-impact ionization cross sections for building blocks of DNA and RNA [40,41], and some simple biologically relevant molecules [42,43,44]. For this reason we provide below a rather concise and short description of the method and calculations used in this work.
Electron-impact ionization cross section (ICS) has been calculated with the binary-encounter-Bethe (BEB) method [45,46]. The BEB model is the simplified version of the binary-encounter-dipole (BED) method [45] that combines the binary-encounter theory [47] suitable for low electron impact energies with the Bethe theory valid for high electron impact energies [48]. While this method is still a model and semi-empirical approach to the ionization phenomenon, it does not contain any arbitrary parameters. Thus, the advantage of the BEB model is that all quantities necessary to calculate ICS have a well-defined physical meaning and can be calculated or evaluated quite accurately using standard quantum chemical methods. Of course, the accuracy of such quantum chemical calculations, and therefore the quality of the obtained ICS, depends to a large extent on the level of the theory applied and the basis sets used.
Within BEB formalism the electron-impact ionization cross section for a given molecular orbital can be calculated from the following formula
σ B E B = S t + u + 1 ln t 2 1 − 1 t 2 + 1 − 1 t − ln t t + 1 ,
where u = U / B , t = T / B , S = 4 π a 0 2 N R 2 / B 2 , a 0 = 0 . 5292 Å, R = 13 . 61 eV, U is the kinetic orbital energy, T is the energy of impinging electrons and N is the orbital occupation number. Finally, the total cross section for electron-impact ionization, σ i o n , can be calculated as the sum of σ B E B for all molecular orbitals (MO):
σ ion = ∑ i = 1 n M O σ n M O B E B
To obtain the electron binding energies B, kinetic energy of all molecular orbitals, U, and orbital occupation numbers, N, quantum chemical computations have been performed using Gaussian code [49]. At first, we have performed geometry optimization of the studied molecules in the ground state within C 2 ν symmetry with the Hartree-Fock (HF) method with 6-311++G(2d,2p) Gaussian basis sets. In the next step, using the obtained geometries of the studied molecules, single point energy calculations were performed. The HF method with the same 6-311++G(2d,2p) Gaussian basis sets was also used in these calculations.
Since the energies of the highest occupied molecular orbitals (HOMO) obtained in this way usually are higher from those measured experimentally (even by about 1-3 eV), we performed also outer valence Green function calculations of correlated electron affinities and ionization potentials [50,51,52,53] using the GAUSSIAN code [49]. The resulting value of the ionization threshold for pyrimidine molecule is 9 . 804 eV which is rather in good agreement with measured data: 9 . 9 eV [54], 9 . 71 eV [55], 9 . 35 eV [56], 9 . 73 eV [57] and 9 . 21 eV [58]. Please note that data from Refs. [56,58] are photoelectron spectral values of the adiabatic ionization energy while the higher values are the vertical ionization energies [57]. For the remaining studied compounds calculated the first ionization energies are: 9 . 865 eV, 9 . 911 eV, 10 . 04 eV and 10 . 12 eV for 5-bromopyrimidine, 2-bromopyrimidine, 5-chloropyrimidine and 2-chloropyrimidine, respectively. The results of reported HF calculations for binding energies and orbital kinetic energies are presented in the Appendix A in the Table A1, Table A2 and Table A3. The values of the HOMOs energies calculated using the OVGF method are also listed there in the Table A4.
The BEB results obtained in the manner described are counting ionization cross sections that include a contribution from a single ionization. Therefore, they should be considered as a lower limits to experimental results in which the contribution from multiple ionization can also be included [46]. It is worth to note here that, despite the previous remark, the BEB model is well–known theoretical method that allows obtaining reliable ionization cross sections for molecules. ICSs obtained with the BEB method usually are in good agreement (within ± 15 %) with experimental data [59,60,61].

3. Results and Discussion

The numerical values of the calculated cross sections for electron–impact ionization of studied targets, for energies ranging from the ionization threshold to 5 keV are summarized in the Table 1. Computed in this work ionization cross section for pyrimidine molecules is shown in Figure 2. It is compared with the available experimental results [30,32,33,34]. The results of the present calculations are in very good agreement with the experimental results obtained by integrating the measured double-differential ionization cross sections[30]. Fairly good agreement is also seen between the present results and the recently evaluated total ionization cross section, also obtained from double-differential electron impact ionization cross sections [33]. The latter are slightly higher, but taking into account the declared measurement uncertainty of 30%, these differences can be considered as approximately insignificant. However, present data are higher by about 20% than the results measured through time of flight mass spectrometry [34]. This does not apply only for the energies from the ionization threshold up to 70 eV, at which the results of both the mentioned experiments [30,34] and our calculations are in almost perfect agreement. This may indicate that in the experiment with the time of flight mass spectrometer [34] at higher impact-electron-energies not all formed ions were recorded and that the contribution from the inner–shell ionization was also slightly underestimated. The results obtained with the use of the total ion collection technique [32], except the low energy range from the ionization threshold up to 30 eV are much smaller than the predictions of the present calculations and other experimental data [30,33,34]. This difference is even up to 50%.
In the same figure (Figure 2), for comparison, the total cross sections for the ionization of pyrimidine determined in all previous theoretical calculations [30,31,34,35,36] are shown. All calculated pyrimidine ionization cross sections have very similar shapes. However, there are visible differences in the maximum positions and predicted cross section values. In particular, the results of semiempirical calculations [34] and those based on the first Born approximation [36] indicate a maximum position at about 60 eV, while the others predict maxima at about 80 eV. The present results are in good agreement with previously calculated BEB ionization cross section [30]. The minor discrepancies are due to small differences in the calculations of the electronic structure of pyrimidine in both studies. However, the results of the latest calculations [31], also using the BEB method, are systematically lower than our data and the earlier results of BEB method calculations [30]. The maximum differences are up to 10%. It is worth adding that these results [31] were obtained using binding energies calculated at the HF level with cc-pVTZ basis set [31] without taking into account any correlation energy which usually leads to an underestimation of the cross-section value in the BEB method. The results of semi-empirical calculations [34] and those obtained using the first Born approximation [36] are in satisfactory agreement with the results of the remaining calculations only for the energies in the range from the ionization threshold to about 30 eV. They predict, as we mentioned above, the location of the ionization maximum at an energy of about 60 eV. Moreover, the semi-empirical calculations [34] gave the maximum higher than the present ones by about 10%, while the results obtained in the first Born approximation [36] for energies greater than 80 eV are systematically lower than the present ones by about 10%. The results obtained with the spherical complex optical potential formalism and complex scattering potential ionization contribution method [35] are the least consistent with the other calculations. However, they are in good agreement with the ionization cross section measured with the use of the total ion collection technique [32].
Since, as can be seen in Figure 2, there are quite significant discrepancies between the predictions of theoretical calculations and the results of various experiments, an important question is which of these results is the most realistic. To provide a preliminary answer to this question the experimentally determined ionization cross sections of benzene molecules [62,63] are depicted in Fig Figure 2. Benzene is isoelectronic with pyrimidine and therefore such a comparison may be useful in this analysis to some extent. Of course, the same number of electrons in a molecule does not mean the same total cross-section for ionization. The most important here are molecular electronic structure and, consequently, the binding energies of the individual electrons. Taking into account the differences in the structure of benzene and pyrimidine, it can be expected that the ionization cross section of benzene will be higher than that of pyrimidine. Despite this, it can be expected that the ionization results of benzene and pyrimidine should not differ drastically. Hence, analyzing the data presented in Figure 2, it seems that experimental results measured with the total ion collection technique [32] which differ from those for benzene by almost twice can be at least slightly underestimated.
In Figure 3 present computed ICS for pyrimidine molecules are compared with previously reported theoretical BEB data for pyridazine [43]. Since both compounds are isomeric, it is not surprising that the ionization cross sections calculated for them are very similar. The cross section for pyridazine has slightly higher values in the whole range of compared energies. Additionally in Figure 3 experimental ICS for pyridazine measured with quadrupole mass spectrometer are shown [43]. It is important to stress here that this data are normalized. Specifically, the total measured cation efficiency was normalized to the calculated cross section, assuming that the measured cross section should be equal at its maximum to the calculated maximum. For comparison, the experimental ionization cross section for pyrimidine [63] normalized to the present computed ICS are also depicted in Figure 3. Normalization was performed assuming that the maximum in the measured cross section occurring at 85 eV should be equal to the maximum calculated value, i.e., 12 . 10 × 10 − 20 m2. As can be seen in Figure 3, the resulting normalized experimental cross section is in quite good agreement with our calculation results for all other common energies.
To determine whether the ionization cross section of pyrimidine should have values similar to those of pyridazine and not differ too much from the cross sections of benzene in Figure 4, we compared the absolute total cross sections for electron scattering from pyrimidine [16,17] and benzene molecules [64,65,66]. Total cross section (TCS) is a quantity giving valuable information on the overall scattering phenomena. Moreover, TCS can be usually measured in absolute scale over wide energy range without any normalization procedure and can thus serve as quantitative tests of the reliability of theoretical models.
Of course, the TCS includes the contribution from all scattering channels opened at a given collision energy. However, in our analysis it is important to note that at higher collision energies (above ∼ 100 eV) the dominant contribution to the scattering process comes from elastic collisions and overall ionization processes. As can be seen from Figure 4, the experimental TCS data for benzene are in reasonable agreement. The differences between these results do not exceed 20%. TCSs for pyrimidine were measured with two different electron-transmission experiments in which results were obtained using the electrostatic apparatus with highly reduced magnetic field [16], and with a system using magnetically confined electron beam [17]. Above 60 eV, both TCS data sets [16,17] are very similar, and importantly, they do not differ significantly from the results for benzene, especially from older experimental data [64,65]. In the latter case, the differences between these results are generally within the total declared measurement uncertainties. It is worth to note that experimental electron-impact differential scattering cross sections for elastic scattering from benzene and pyrimidine are quite similar [67]. This is of course not a direct proof, but taking into account the previously described comparative analysis of the results for pyrimidine ionization, it can be expected that the presented ICS results calculated for pyrimidine molecules are very likely to have reliable values. However, further studies of the efficiency of the ionization processes in electron collisions with pyrimidine, primarily experimental, are necessary to finally resolve this problem.
In Figure 5, calculated in this work, within BEB approximation, total cross sections for electron–impact ionization of pyrimidine, 2-chloropyrimidine, 5-chloropyrimidine, 2-bromopyrimidine and 5-bromopyrimidine are presented and compared. For all studied compounds maximum of the ICS is located at around 80 eV. For the halogenated derivatives of pyrimidine, the cross–section values are very similar in the entire energy range studied. However, the highest cross-section is for 2-bromopyrimidine, reaching a maximum of 14 . 17 × 10 − 20 m2. For 5-bromopyrimidine, the maximum ICS value is 13 . 99 × 10 − 20 m2. For 2-chloropyrimidine and 5-chloropyrimidine, the maximum ICS value is similar and amounts to 13 . 84 × 10 − 20 m2 and 13 . 73 × 10 − 20 m2, respectively. This tendency in the dependencies between the cross-section values for these compounds is visible from almost the ionization threshold up to 500 eV. In the case of 2-chloropyrimidine and 5-chloropyrimidine respective ionization cross sections almost coincide at incident electron energies above 500 eV. Obviously, a similar dependence can be observed for 2-bromopyrimidine and 5-bromopyrimidine. This reflects the fact that at higher energies the small differences in the electronic structure of these isomeric pairs do not play a significant role. However, they do affect the ionization efficiency at lower energies. The electron-impact ionization cross-section of pyrimidine is significantly lower than the ICSs for its halogenated derivatives and reaches a maximum of 12 . 10 × 10 − 20 m2. This indicates a potentially high efficiency of the response of halogenated pyrimidines and radiosensitizers based on them to ionizing radiation in comparison with pyrimidine.

4. Conclusions

The BEB method was used to calculate the ionization cross sections for ionization induced by collisions with electrons of pyrimidine and its halogenated derivatives. All parameters necessary for the BEB method were carefully determined using quantum chemical methods. The cross sections for ionization of pyrimidine are generally consistent with the results of experiments based on doubly differential electron-impact ionization cross sections measurements. The results obtained for pyrimidine are comparable with the results for its isomeric compound - pyridazine. The process of ionization of halogenated derivatives of pyrimidine is much more efficient than the process of pyrimidine ionization . This indicates a possible potential use of these compounds as a base for new radiosensitizers. The need for further experimental and theoretical work on the ionization of pyrimidine and its derivatives by electron interaction was also pointed out.

Author Contributions

Conceptualization, P.M. and B.Ż.; methodology, P.M.; software, B.Ż.; validation, P.M. and B.Ż.; formal analysis, P.M. and B.Ż.; investigation, P.M. and B.Ż.; data curation, P.M. and B.Ż.; writing—original draft preparation, P.M.; writing—review and editing, P.M. and B.Ż.; All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Acknowledgments

This work has been supported in part by the Polish Ministry of Science and Higher Education (MNiSzW Project 2024). Numerical computations have been performed at the Academic Computer Center (TASK) in Gdańsk.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BEB Binary–encounter–Bethe
BED Binary–encounter-dipole
HF Hartree–Fock
ICS Ionization cross section
OVGF Outer valence Green function
TCS Total cross section

Appendix A. Binding Energies, B, Kinetic Orbital Energies U and HOMOs Energies of the Studied Targets

This appendix summarizes the calculated in this work data on the binding energies, B, and kinetic orbital energies, U, of the compounds studied, calculated in this work. All results are given in electronvolt. In Appendix A.1 the results obtained with Hartree-Fock method with 6-311++G(2d,2p) Gaussian basis sets are tabulated in Table A1, Table A2 and Table A3. The ionization energies of the selected highest occupied molecular orbitals computed with outer valence Green function method are tabulated in Table A4 of Appendix A.2. All calculations were performed with Gaussian code [49].

Appendix A.1. Calculated with the HF Method Binding Energies B, Kinetic Orbital Energies U of the Studied Targets

Table A1. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for pyrimidine molecule.
Table A1. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for pyrimidine molecule.
Orbital No. B (eV) U (eV)
1 423.70 602.02
2 423.70 602.02
3 307.75 436.01
4 307.37 435.98
5 307.37 435.98
6 306.0 435.86
7 36.188 49.142
8 32.871 56.227
9 29.490 45.438
10 24.570 45.287
11 24.509 45.486
12 20.373 28.960
13 19.422 45.659
14 17.855 35.506
15 16.362 37.558
16 16.136 40.181
17 15.964 29.630
18 12.927 50.071
19 11.650 36.887
20 11.329 50.811
21 10.372 30.498
Table A2. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for 2-chloropyrimidine (column 2 and 3) and 5-chloropyrimidine molecules (column 4 and 5).
Table A2. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for 2-chloropyrimidine (column 2 and 3) and 5-chloropyrimidine molecules (column 4 and 5).
Orbital No. B (eV) U (eV) B (eV) U (eV)
1 2852.9 3731.1 2853.4 3731.1
2 424.16 602.00 424.13 602.02
3 424.16 602.01 424.13 602.02
4 309.71 436.13 308.08 436.01
5 307.84 435.99 307.95 435.87
6 307.84 435.99 307.82 435.97
7 306.44 435.85 307.81 436.08
8 287.58 593.54 288.09 593.55
9 218.69 560.89 219.20 560.91
10 218.61 561.98 219.12 562.03
11 218.60 562.07 219.12 562.05
12 37.053 49.944 36.686 49.013
13 33.520 56.392 33.318 56.271
14 31.419 61.358 32.204 62.570
15 29.034 58.689 28.678 60.286
16 25.241 45.425 25.224 45.271
17 24.247 51.509 24.414 51.024
18 20.215 34.408 20.679 30.373
19 20.116 45.191 20.211 45.843
20 17.870 41.651 17.228 54.826
21 16.944 31.629 16.981 37.236
22 16.822 37.613 16.661 30.324
23 16.212 50.782 16.589 41.560
24 13.492 54.721 14.032 51.316
25 13.221 50.513 13.350 53.848
26 12.666 60.695 13.279 61.505
27 12.154 37.355 12.082 36.944
28 11.733 54.286 11.625 52.252
29 10.351 39.768 10.204 41.309
Table A3. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for 2-bromopyrimidine (column 2 and 3) and 5-bromopyrimidine molecules (column 4 and 5).
Table A3. Binding energies B (eV) and kinetic orbital energies U (eV) calculated at the HF level for 2-bromopyrimidine (column 2 and 3) and 5-bromopyrimidine molecules (column 4 and 5).
Orbital No. B (eV) U (eV) B (eV) U (eV)
1 13334 16195 13335 16195
2 1772.9 3195.1 1773.5 3195.1
3 1592.2 3166.6 1592.8 3166.6
4 1592.2 3166.9 1592.7 3166.9
5 1592.2 3166.9 1592.7 3166.9
6 424.20 602.00 424.13 602.02
7 424.20 602.01 424.13 602.02
8 309.57 436.14 308.11 436.01
9 307.85 435.98 307.86 435.76
10 307.85 435.99 307.85 435.97
11 306.39 435.85 307.79 436.20
12 267.70 766.10 268.24 766.10
13 202.77 709.25 203.31 709.26
14 202.55 710.98 203.09 711.05
15 202.53 711.12 203.08 711.07
16 86.836 586.40 87.380 586.39
17 86.732 587.14 87.268 587.00
18 86.709 587.01 87.266 587.21
19 86.450 587.89 86.996 587.86
20 86.450 587.85 86.996 587.90
21 36.971 49.811 36.677 49.056
22 33.520 56.435 33.324 56.278
23 30.376 51.103 30.881 56.097
24 27.840 77.019 27.691 75.621
25 25.227 45.492 25.192 45.371
26 24.106 55.105 24.292 54.455
27 20.118 34.612 20.677 30.583
28 20.082 45.384 20.141 45.914
29 17.737 41.273 16.966 37.295
30 16.817 37.635 16.706 40.492
31 16.812 30.927 16.568 29.828
32 15.685 52.194 16.185 59.049
33 13.052 59.804 13.126 55.832
34 12.248 49.590 13.012 52.312
35 12.158 37.334 12.235 62.538
36 12.018 52.657 12.087 36.963
37 11.181 68.587 11.498 57.508
38 10.165 47.962 10.039 47.489

Appendix A.2. Calculated with the OVGF Method HOMOs Energies of the Studied Targets

Table A4. Ionization energies (eV) of the HOMOs calculated with the OVGF method.
Table A4. Ionization energies (eV) of the HOMOs calculated with the OVGF method.
C4H4N2 2-C4H3ClN2 5-C4H3ClN2 2-C4H3BrN2 5-C4H3BrN2
18.144 18.561 18.023 18.529
17.851 17.923 17.768 17.808
18.302 16.220 15.839 16.047 15.062
17.293 15.278 15.129 15.107 15.080
16.204 15.027 15.045 14.982 15.006
14.693 14.678 14.890 14.100 14.767
14.630 11.845 13.108 11.655 12.290
14.565 12.382 12.297 11.603 11.591
11.331 11.675 11.690 11.599 11.583
11.327 11.640 11.632 10.497 11.204
10.461 10.178 10.075 10.301 10.184
9.804 10.120 10.040 9.911 9.865

References

  1. Joshipura, K. N.; Mason, N. Atomic-Molecular Ionization by Electron Scattering, 1st ed.; Cambridge Univ. Press: Cambridge, United Kingdom, 2019; pp. 177–217.
  2. Szmytkowski, Cz.; Możejko, P. Recent total cross section measurements in electron scattering from molecules. Eur. Phys. J. D 2020, 74, 90. [CrossRef]
  3. Boudaiffa, B.; Cloutier, P.; Hunting, D.; Huels, M. A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 2000, 287, 1658–1600. [CrossRef]
  4. Sanche, L. Beyond radical thinking. Nature 2009, 461, 358–359. [CrossRef]
  5. McKee, A. D.; Schaible, M. J.; Rosenberg, R. A.; Kundu, S.; Orlando, T. M. Low energy secondary electron induced damage of condensed nucleotides. J. Chem. Phys. 2019, 150, 204709. [CrossRef]
  6. Gao, Y.; Zheng, Li.; Sanche, L. Low–energy electron damage to condensed–phase DNA and its constituents. Int. J. Mol. Sci. 2021, 22, 7879. [CrossRef]
  7. Cobut, V.; Fongillo, Y.; Patau, J. P.; Goulet, T.; Fraser, M. J.; Jay-Gerin, J. P. Monte-Carlo simulation of fast electron and proton tracks in liquid water.I. Physical and physico-chemical aspects. Radiat. Phys. Chem., 1998, 51, 229–243.
  8. Villagrasa, C.; Francis, Z.; Incerti, S. Physical models implemented in the Geant4-DNA extension of the Geant-4 toolkit for calculating initial radiation damage at the molecular level. Radiat. Prot. Dosim. 2011, ı143, 214–218.
  9. Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; Beck, B. R.; Bogdanov, A. G.; Brandt, D.; Brown, J. M. C.; Burkhardt, H.; Canal, Ph.; Cano-Ott, D.; Chauvie, S.; Cho, K.; Cirrone, G. A. P.; Cooperman, G.; Cortés-Giraldo, M. A.; Cosmo, G.; Cuttone, G.; Depaola, G.; Desorgher, L.; Dong, X.; Dotti, A.; Elvira, V. D.; Folger, G.; Francis, Z.; Galoyan, A.; Garnier, L.; Gayer, M.; Genser, K. L.; Grichine, V. M.; Guatelli, S.; Gueye, P.; Gumplinger, P.; Howard, A.S.; Hřivnáčová, I.; Hwang, S.; Incerti, S.; Ivanchenko, A.; Ivanchenko, V. N.; Jones, F. W.; Jun, S. Y.; Kaitaniemi, P.; Karakatsanis, N.; Karamitros, M.; Kelsey, M.; Kimura, A.; Koi, T.; Kurashige, H.; Lechner, A.; Lee, S. B.; Longo, F.; Maire, M.; Mancusi, D.; Mantero, A.; Mendoza, E.; Morgan, B.; Murakami, K.; Nikitina, T.; Pandola, L.; Paprocki, P.; Perl, J.; Petrović, I.; Pia, M. G.; W. Pokorski, W.; Quesada, J. M.; Raine, M.; Reis, M. A.; Ribon, A.; Ristić Fira, A.; F. Romano, F.; Russo, G.; Santin, G.; Sasaki, T.; Sawkey, D.; Shin, J. I.; Strakovsky, I. I.; Taborda, A.; Tanaka, S.; Tomé, B.; Toshito, T.; Tran, H. N.; Truscott, P. R.; Urban, L.; Uzhinsky, V.; Verbeke, J. M.; Verderi, M.; Wendt, B. L.; Wenzel, H.; Wright, D. H.; Wright, D. M.; Yamashita, T.; Yarba, J.; Yoshida, H. Recent developments in Geant4 Nucl. Instr. Meth. Phys. Res. A 2016, ı835, 186–225.
  10. Rosales, L. F.; Incerti, S.; Francis, Z.; Bernal, M. A. Accounting for radiation–induced indirect damage on DNA with the Geant 4–DNA code. Phys. Med. 2018, 51, 108–116. [CrossRef]
  11. Costa, F.; Traoré-Dubuis, A.; Álvarez, L.; Lozano, A. I.; Ren, X.; Dorn, A.; Limão-Vieira, P.; Blanco, F.; Oller, J. C.; Muñoz, A.; Garcáa-Abenza, A.; Gorfinkiel, J. D.; Barbosa, A. S.; Bettega, M. H. F.; Stokes, P.; White, R. D.; Jones, D. B.; Brunger M. J.; García, G. A Complete cross section set for electron scattering by pyridine: Modelling electron transport in the energy range 0–100 eV. Int. J. Mol. Sci. 2020, 21, 6947. [CrossRef]
  12. Lozano, A. I.; Álvarez, L.; García-Abenza, A.; Guerra C.; Kossoki, F.; Rosado, J.; Blanco, F.; Oller, J. C.; Hasan, M.; Centurion, M.; Weber, T.; Slaughter, D. S.; Mootheril, D. M.; Dorn, A.; Kumar, S.; Limão-Vieira, P.; Colmenares, R.; García, G. Electron scattering from 1-methyl-5-nitroimidazole: Cross–sections for modeling electron transport through potential radiosensitizers. Int. J. Mol. Sci. 2023, 24, 12182. [CrossRef]
  13. Tylińska, B.; Wiatrak, B.; Czyżnikowska, Ż.; Cieśla-Niechwiadowicz, A.; Gębarowska, E.; Janicka-Kłos, A. Novel pyrimidine derivatives as potential anticancer agents: Synthesis, biological evaluation and molecular doking study. Int. J. Mol. Sci. 2023, 22, 3825. [CrossRef]
  14. Al-Tuwaijri, H. M.; Al-Abdullah, E. S.; El-Rashedy, A. A.; Anasari, S. A.; Almomen, A.; Alshibl, H. M.; Haiba, M. E.; Alkahtani, H. M. New indazol–pyrimidine–based derivatives as selective anticancer agents: Design, synthesis, and in silico studies. Molecules 2023, 28, 3664. [CrossRef]
  15. Myriagkou, M.; Papakonstantinou, E.; Deligiannidou, G.-E.; Patsilinakos, A.; Kontogiorgis, Ch.; Pontiki, E. Novel pyrimidine derivatives as antioxidant and anticancer agents: Design, synthesis and molecular modeling studies. Molecules 2023, 28, 3913. [CrossRef]
  16. Baek, W. Y.; Arndt, A.; Bug, M. U.; Rabus, H.; Wang, M. Total electron–scattering cross sections of pyrimidine. Phys. Rev. A 2013, 88, 032702. [CrossRef]
  17. Fuss, M. C.; Sanz, A. G.; Blanco, F.; Oller, J. C.; Limão-Vieira, P.; Brunger, M. J.; García, G. Total electron scattering cross sections for pyrimidine and pyrazine as measured using a magnetically confined experimental system. J. Phys. Conf. Ser. 2014, 488, 012048. [CrossRef]
  18. Maljković, J. B.; Milosavljević, A. R.; Blanco, F.; and Šević, D.; Garcıa, G.; Marinković, B. P. Absolute differential cross sections for elastic scattering of electrons from pyrimidine Phys. Rev. A 2009, 79, 052706. [CrossRef]
  19. Palihawadana, P.; Sullivan, J.; Brunger, M. J.; Winstead, C.; McKoy, V.; Garcıa, G.; Blanco, F.; Buckman, S. Low–energy elastic electron interactions with pyrimidine. Phys. Rev. A 2011, 84, 062702. [CrossRef]
  20. Palihawadana, P.; Machacek, J. R.; Makochekanwa, C.; Sullivan, J. P.; Brunger, M. J.; Winstead, C.; McKoy, V.; Garcıa, G.; Blanco, F.; Buckman, S. J. Electron and positron scattering from pyrimidine. J. Phys. Conf. Ser. 2012, 388, 052079. [CrossRef]
  21. Maljković, J. B. Absolute differential cross sections for elastic electron scattering from small biomolecules. J. Phys. Conf. Ser. 2014, 565, 012005. [CrossRef]
  22. W. Y. Baek, W. Y.; Bug, M. U.; Rabus, H. Differential elastic electron–scattering cross sections of pyrimidine in the energy range between 20 eV and 1 keV. Phys. Rev A 2014, 89, 062716. [CrossRef]
  23. Colmenares, R.; Sanz, A. G.; Fuss, M. C.; Blanco, F.; García, G. Stopping power for electrons in pyrimidine in the energy range 20–3000eV. Appl. Radiat. Isotopes 2014, 83 Part B, 91-94. [CrossRef]
  24. Regeta, K.; Allan, M.; Winstead, C.; McKoy, V.; Mašın, Z.; Gorfinkiel, J. D. Resonance effects in elastic cross sections for electron scattering on pyrimidine: Experiment and theory. J. Chem. Phys. 2016, 144, 024301. [CrossRef]
  25. Jones, D. B.; Bellm, S. M.; Blanco, F.; García G.; Limão-Vieira, P. Brunger, M. J. Differential cross sections for electron impact excitation of pyrimidine. J. Chem. Phys. 2012, 137, 074304. [CrossRef]
  26. Jones, D. B.; Ellis-Gibbings, L.; García, G.; Nixon, K. L.; Lopes, M. C. A., Brunger, M. J. Intermediate energy cross sections for electron–impact vibrational–excitation of pyrimidine. J. Chem. Phys. 2015, 143, 094304. [CrossRef]
  27. Regeta K.; Allan, M.; Mašín, Z.; Grofinkiel, J. D. Absolute cross sections for electronic excitation of pyrimidine by electron impact. J. Chem. Phys., 2016, 144, 024302. [CrossRef]
  28. Sinha, N.; Antony, B. Electron and positron interaction with pyrimidine: A theoretical investigation. J. Appl. Phys. 2018, 123, 124906. [CrossRef]
  29. Mašín, Z.; Gornfinkiel, J. D. Effect of the Third π★ Resonance on the angular distributions for electron–pyrimidine scattering. Eur. Phys. J. D 2016, 70, 150. [CrossRef]
  30. Bug, M. U.; Baek W. Y.; Rabus, H.; Villagrasa, C.; Meylan, S.; Rosenfeld, A. B. An electron–impact cross section data set (10 eV–1 keV) of DNA constituents based on consistent experimental data: A requisite for Monte Carlo simulations. Radiat. Phys. Chem. 2017, 130, 459–479. [CrossRef]
  31. Luthra, M.; Bharadvaja, A.; Prashant, A.; Baluja, K. L. Electron scattering from pyrimidine up to 5 keV. Braz. J. Phys. 2024, 54, 116. [CrossRef]
  32. Linert, I.; Dampc, M.; Mielewska, B.; Zubek, M. Cross sections for ionization and ionic fragmentation of pyrimidine molecules by electron collisions. Eur. Phys. J. D 2012, 66, 20. [CrossRef]
  33. Dinger, M.; Baek, W. Y.; Rabus, H. Comparative experimental and theoretical study on doubly differential electron–impact ionization cross sections of pyrimidine. Phys. Rev. A 2024, 109, 062813. [CrossRef]
  34. Wolff, W.; Luna, H.; Sigaud, L.; Tavares, A. C.; Montenegro, E. C. Absolute total and partial dissociative cross sections of pyrimidine at electron and proton intermediate impact velocities. J. Chem. Phys. 2014, 140, 064309. [CrossRef]
  35. Gupta, D.; Naghma, R.; Antony, B. Electron Impact total ionisation cross section for simple bio–molecules: A theoretical approach. Mol. Phys. 2014, 112, 1201–1209. [CrossRef]
  36. Champion, Ch.; Quinto, M. A.; Weck, Ph. F. Electron– and proton–induced ionization of pyrimidine. Eur. Phys. J. D 2015, 69, 127. [CrossRef]
  37. Żywicka, B.; Możejko P. Electron–impact ionization cross sections calculations for purine and pyrimidine molecules. In Proceedings of the 6th Conference on Elementary Processes in Atomic Systems, Bratislava, Slovakia, 9–12 July 2014; 236–239.
  38. Modelli, A.; Bolognesi, P.; Avaldi, L. Temporary anion states of pyrimidine and halopyrimidines. J. Phys. Chem. A 2011, 115, 10775–10782. [CrossRef]
  39. Barbosa, A. S.; Bettega, M. H. F. Shape resonances in low–energy–electron collisions with halopyrimidines. J. Chem. Phys. 2013, 139, 214301. [CrossRef]
  40. Możejko, P.; Sanche, L. Cross section calculations for electron scattering from DNA and RNA bases. Radiat. Environ. Biophys. 2003, 42, 201–211. [CrossRef]
  41. Możejko, P.; Sanche, L. Cross sections for electron scattering from selected components of DNA and RNA. Radiat. Phys. Chem. 2005, 73, 77–84. [CrossRef]
  42. Możejko, P. Calculations of electron impact ionization cross section for simple biomolecules: Formic and acetic acids. Eur. Phys. J. Special Topics 2007, 144, 233–237. [CrossRef]
  43. Dampc, M.; Możejko, P.; Zubek, M. Electron impact ionization and cationic fragmentation of the pyridazine molecules. Eur. Phys. J. D 2018, 72, 216. [CrossRef]
  44. Szmytkowski, Cz.; Stefanowska, S.; Tańska, N.; Żywicka, B.; Ptasińska-Denga, E.; Możejko, P. Cross sections for electron collision with pyridine [C5H5N] molecule. Mol. Phys. 2018, 117, 395–403. [CrossRef]
  45. Kim, Y. K.; Rudd, M. E. Binary–encounter–dipole model for electron–impact ionization. Phys. Rev. A 1994, 50, 3954–3967. [CrossRef]
  46. Hwang, W.; Kim, Y. K.; Rudd, M. E. New model for electron--impact ionization cross sections of molecules. J. Chem. Phys. 1996, 104, 2956-2966. [CrossRef]
  47. Vriens, L. Binary–encounter and classical collision theories. In Case Studies in Atomic Physics 1; McDaniel, E. W., McDowell, M. R. C., Eds.; North-Holland Publishing Company, Amsterdam, Netherlands, 1969; pp. 335–398.
  48. Bethe, H. Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie. Ann. Phys. 1930, 397, 325–400. [CrossRef]
  49. Frisch, M. J.; et al, GAUSSIAN 03, Revision B.05, Gaussian: Pittsburgh, USA, 2003.
  50. Cederbaum, L. S. One–body Green’s function for atoms and molecules: Theory and application. J. Phys. B 1975, 8, 290–303. [CrossRef]
  51. von Niessen, W.; Schirmer, J.; Cederbaum, L. S. Computational methods for the one–particle Green’s function. Comp. Phys. Rep. 1984, 1, 57–125. [CrossRef]
  52. Ortiz, J. V. Electron binding energies of anionic alkali metal atoms from partial fourth order electron propagator theory calculations. J. Chem. Phys. 1988, 89, 6348–6352. [CrossRef]
  53. Zakrzewski, V. G.; von Niessen, W. Vectorizable algorithm for Green function and many--body perturbation methods. J. Comp. Chem. 1994, 14, 13–18. [CrossRef]
  54. Berthod, H.; Giessner-Prettre, C.; Pullman, A. Theoretical study of the electronic properties of the purine and pyrimidine components of the nucleic acids. Theoret. Chim. Acta 1966, 5, 53-–68. [CrossRef]
  55. Kunii, T.L.; Kuroda, H. Ionization potentials and electron affinities of carbo- and heterocyclic π–conjugated molecules. Theoret. Chim. Acta 1968, 11, 97–106. [CrossRef]
  56. Yencha, A.J.; El-Sayed, M.A. Lowest ionization potentials of some nitrogen heterocyclics. J. Chem. Phys. 1968, 48, 3469–3475. [CrossRef]
  57. Hush, N.S.; Cheung, A.S., Ionization potentials and donor properties of nucleic acid bases and related compounds. Chem. Phys. Lett. 1975, 34, 11–13. [CrossRef]
  58. Schwell, M.; Jochims, H.-W.; Baumgartel, H.; Leach, S. VUV Photophysics and dissociative photoionization of pyrimidine, purine, imidazole and benzimidazole in the 7–18 eV photon energy range. Chem. Phys. 2008, 353 145–162. [CrossRef]
  59. Y.-K. Kim, W. Hwang, N.M. Weinberger, M.A. Ali, M.E. Rudd, M. E. Electron-impact ionization cross sections of atmospheric molecules. J. Chem. Phys. 1997, 106 1026–1033. [CrossRef]
  60. Karwasz, G. P.; Możejko, P.; Song, M.–Y. Electron–impact ionization of fluoromethanes–Review of experiments and binary–encounter models. Int. J. Mass. Spectrom. 2014, 365-366 232–237. [CrossRef]
  61. Tanaka, H.; Brunger, M. J.; Campbell, L.; Kato, H.; Hoshino, M.; Rau, A. R. P. Scaled plane–wave Born cross sections for atoms and molecules. Rev.Mod. Phys. 2016, 88, 025004. [CrossRef]
  62. Lampe, F. W., Franklin, J. L.; Field, F. H. Cross sections for ionization by electrons. J. Am. Chem. Soc. 1957, 79, 6129–6132. [CrossRef]
  63. Schram, B. L.; Van der Wiel, M. J.; de Heer, F. J.; Moustafa, H. R. Absolute gross ionization cross sections for electrons (0.6–12 keV) in hydrocarbons. J. Chem. Phys. 1966, 44, 49–54. [CrossRef]
  64. Możejko, P.; Kasperski, G.; Szmytkowski, Cz.; Karwasz, G. P.; Brusa, R. S.; Zecca, A. Absolute total cross section measurements for electron scattering on benzene molecules. Chem. Phys. Lett. 1996, 257, 309–313. [CrossRef]
  65. Makochekanwa, C.; Sueoka, O.; M. Kimura, M. Comparative study of electron and positron scattering from benzene (C6H6) and hexafluorobenzene (C6F6) molecules. Phys. Rev. A 2003, 68, 032707. [CrossRef]
  66. Costa; F.; Alvarez; L.; Lozano; A. I.; Blanco, F.; Oller, J. C.; Muñoz, A.; Souza Barbosa, A.; Bettega, M. H. F.; Ferreira da Silva, F.; Limão-Vieira, P.; White; R. D.; Brunger, M. J.; García, G. Experimental and theoretical analysis for total electron scattering cross sections of benzene. J. Chem. Phys. 2019, 151, 084310.
  67. Jones, D. B.; Bellm, S. M.; Limão-Vieira, P.; Brunger, M. J. Low–energy electron scattering from pyrimidine: Similarities and differences with benzene. Chem. Phys. Lett. 2012, 535, 30–34. [CrossRef]
Preprints 141426 g001
Figure 1. Schematic drawing of pyrimidine molecules and its halogenated derivatives.
Figure 1. Schematic drawing of pyrimidine molecules and its halogenated derivatives.
Preprints 141426 g001
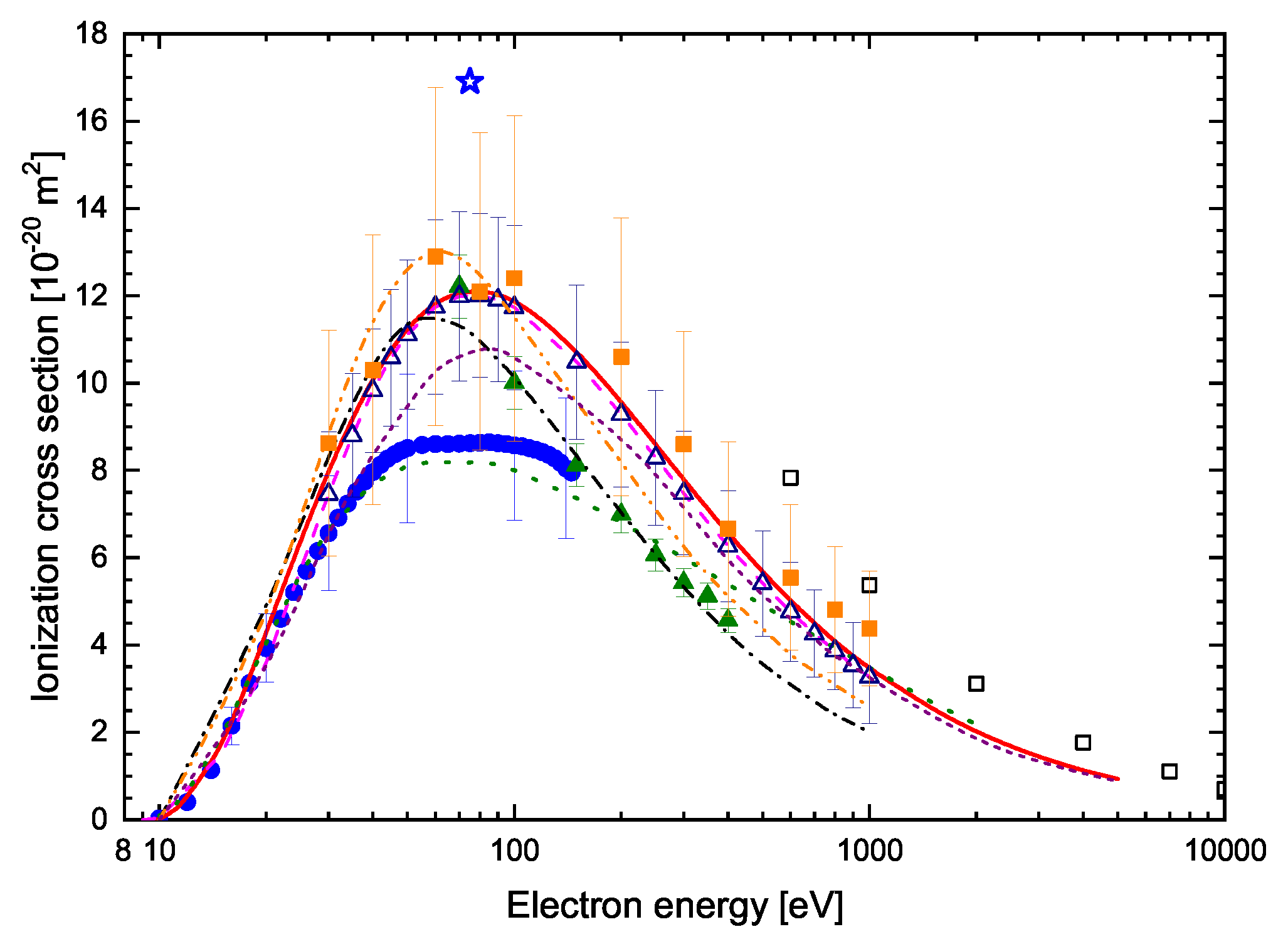
Preprints 141426 g002
Figure 2. Comparison of the ionization cross sections due to electron impact on pyrimidine molecule. Experimental ICS: full circles, [32]; full triangles, [34]; open triangles, [30], full squares, [33]. Theoretical: solid line, present BEB results; dash line, [30]; dot line, [35]; dash dot line, [36]; dash dot dot line, [34]; short dash line, [31]. For comparison experimental cross sections for electron-impact ionization of benzene molecule are also shown: open star, [62]; open squares, [63].
Figure 2. Comparison of the ionization cross sections due to electron impact on pyrimidine molecule. Experimental ICS: full circles, [32]; full triangles, [34]; open triangles, [30], full squares, [33]. Theoretical: solid line, present BEB results; dash line, [30]; dot line, [35]; dash dot line, [36]; dash dot dot line, [34]; short dash line, [31]. For comparison experimental cross sections for electron-impact ionization of benzene molecule are also shown: open star, [62]; open squares, [63].
Preprints 141426 g002
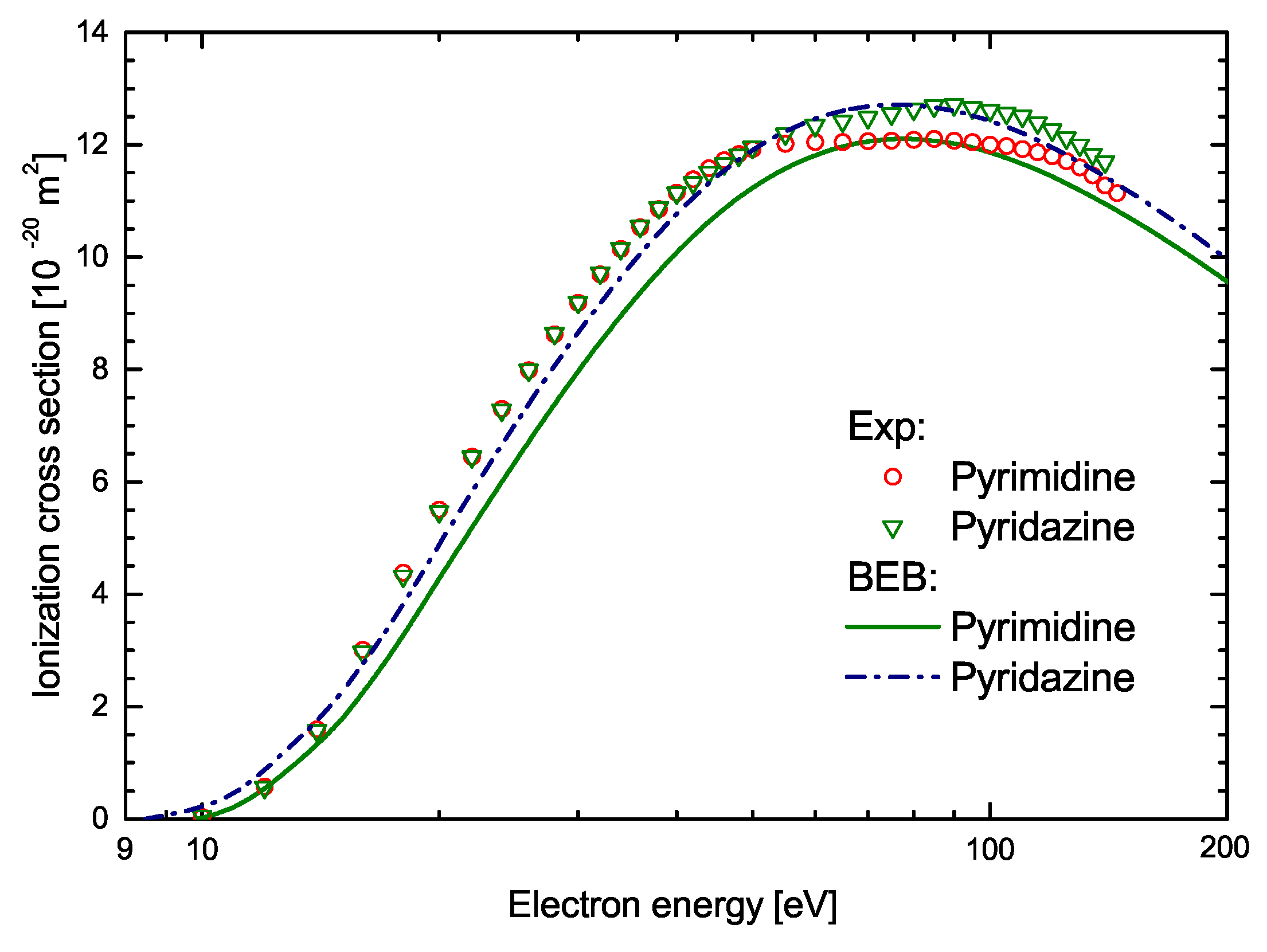
Preprints 141426 g003
Figure 3. Comparison of the electron-impact ionization cross sections for pyridazine and pyrimidine molecules. Experimental and theoretical data for pyridazine are from Ref. [43]. The solid line represents present theoretical data for pyrimidine and the open circles are experimental data [32] for this compound normalized using the calculated results.
Figure 3. Comparison of the electron-impact ionization cross sections for pyridazine and pyrimidine molecules. Experimental and theoretical data for pyridazine are from Ref. [43]. The solid line represents present theoretical data for pyrimidine and the open circles are experimental data [32] for this compound normalized using the calculated results.
Preprints 141426 g003
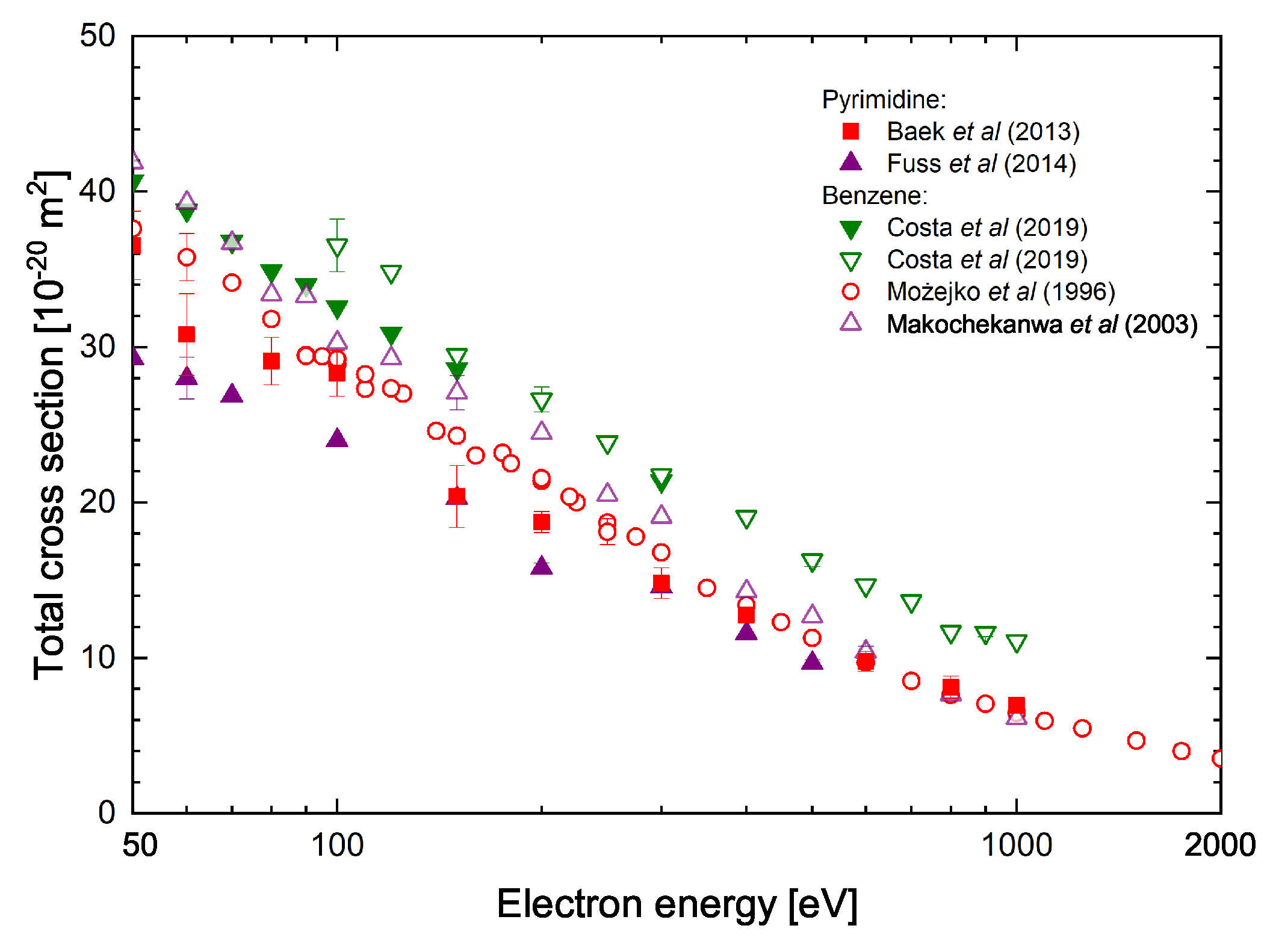
Preprints 141426 g004
Figure 4. Comparison of the total scattering cross sections (TCS) for electron scattering from benzene (C6H6) and pyrimidine (C4H4N2) molecules measured for intermediate energy range. TCS for pyrimidine molecules: full squares, [16]; full triangles, [17]. TCS for benzene molecules: open circles, [64]; open triangles, [65]; open and full down triangles [66].
Figure 4. Comparison of the total scattering cross sections (TCS) for electron scattering from benzene (C6H6) and pyrimidine (C4H4N2) molecules measured for intermediate energy range. TCS for pyrimidine molecules: full squares, [16]; full triangles, [17]. TCS for benzene molecules: open circles, [64]; open triangles, [65]; open and full down triangles [66].
Preprints 141426 g004
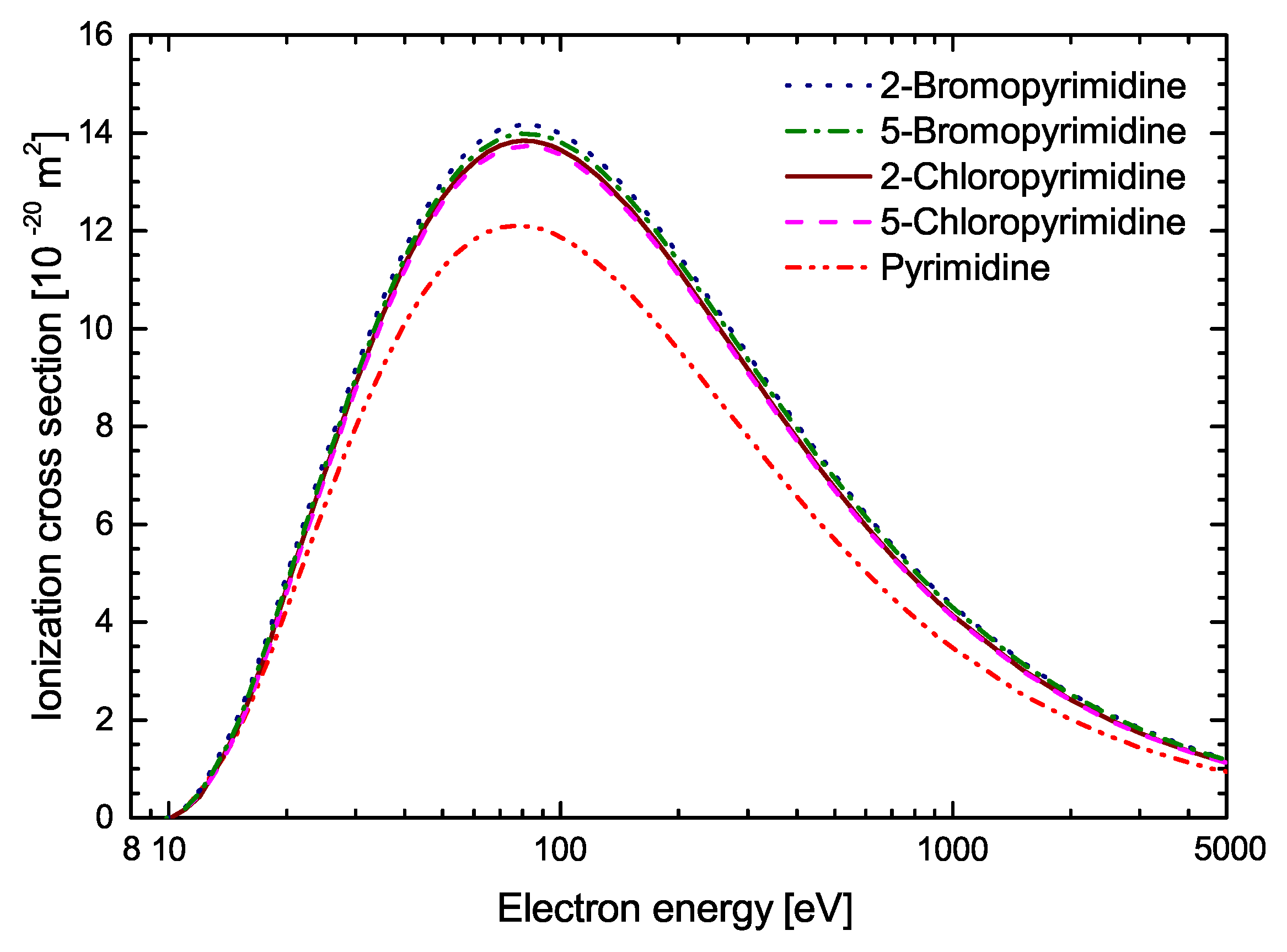
Preprints 141426 g005
Figure 5. Comparison of the calculated with BEB method ionization cross sections induced by electron collisions with pyrimidine (dash dot dot line), 2-chloropyrimidine (solid line), 5-chloropyrimidine (dash line), 2-bromopyrimidine (dot line) and 5-bromopyrimidine (dash dot dot line) molecules.
Figure 5. Comparison of the calculated with BEB method ionization cross sections induced by electron collisions with pyrimidine (dash dot dot line), 2-chloropyrimidine (solid line), 5-chloropyrimidine (dash line), 2-bromopyrimidine (dot line) and 5-bromopyrimidine (dash dot dot line) molecules.
Preprints 141426 g005
Table 1. Ionization cross section for electron-impact ionization of pyrimidine and its halogenated derivatives in units of 10 − 20 m2.
Table 1. Ionization cross section for electron-impact ionization of pyrimidine and its halogenated derivatives in units of 10 − 20 m2.
Energy [eV] C4H4N2 2-C4H3ClN2 5-C4H3ClN2 2-C4H3ClN2 5-C4H3ClN2
9.804 0.00000
9.865 0.00000
9.900 0.00934 0.00355
9.911 0.00000
10.00 0.01920 0.00883 0.01366
10.04 0.00000
10.12 0.00000
11 0.1877 0.1697 0.1930 0.2058 0.1899
12 0.5286 0.4370 0.4573 0.5588 0.5013
13 0.9283 0.8912 0.8583 1.052 0.9616
14 1.319 1.368 1.318 1.540 1.437
15 1.744 1.844 1.775 2.050 1.904
16 2.244 2.402 2.342 2.628 2.508
17 2.753 2.981 2.924 3.223 3.099
18 3.267 3.547 3.485 3.798 3.668
19 3.785 4.131 4.053 4.393 4.244
20 4.283 4.692 4.610 4.959 4.805
25 6.380 7.055 6.960 7.341 7.168
30 7.992 8.874 8.775 9.175 8.995
35 9.199 10.26 10.15 10.57 10.39
40 10.11 11.31 11.21 11.63 11.45
45 10.77 12.10 11.99 12.43 12.24
50 11.25 12.68 12.57 13.01 12.82
55 11.59 13.11 12.99 13.43 13.24
60 11.82 13.40 13.29 13.73 13.55
65 11.97 13.61 13.50 13.94 13.75
70 12.06 13.74 13.63 14.07 13.88
75 12.10 13.81 13.70 14.14 13.96
80 12.10 13.84 13.73 14.17 13.99
85 12.08 13.83 13.72 14.16 13.98
90 12.02 13.79 13.69 14.12 13.94
95 11.95 13.73 13.63 14.06 13.89
100 11.87 13.65 13.55 13.98 13.81
110 11.67 13.46 13.36 13.79 13.63
125 11.33 13.11 13.01 13.44 13.28
150 10.72 12.46 12.37 12.79 12.64
175 10.13 11.80 11.72 12.13 12.00
200 9.568 11.18 11.10 11.51 11.38
250 8.594 10.09 10.01 10.40 10.29
300 7.789 9.171 9.105 9.477 9.374
350 7.122 8.407 8.347 8.701 8.608
400 6.564 7.763 7.708 8.046 7.960
450 6.090 7.214 7.163 7.487 7.407
500 5.683 6.741 6.694 7.004 6.930
600 5.020 5.968 5.926 6.213 6.148
700 4.503 5.362 5.325 5.592 5.534
800 4.089 4.874 4.841 5.091 5.039
900 3.748 4.473 4.443 4.678 4.630
1000 3.463 4.137 4.109 4.331 4.287
1500 2.530 3.031 3.011 3.186 3.155
2000 2.009 2.411 2.395 2.542 2.516
2500 1.674 2.011 1.998 2.124 2.104
3000 1.440 1.731 1.720 1.831 1.813
3500 1.266 1.523 1.513 1.612 1.597
4000 1.131 1.361 1.353 1.443 1.429
4500 1.024 1.233 1.225 1.307 1.295
5000 0.9359 1.127 1.120 1.196 1.185
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated